Abstract
Influence of rotation, relaxation times, magnetic field, initial stress and gravity field on attenuation coefficient (Imaginary part of frequency equation root) and Rayleigh waves velocity (the real part of frequency equation root) in an elastic half-space of granular medium is studied. The analytical solution is obtained by using Lame’s potential techniques. The numerical calculations are carried out for the frequency equation of Rayleigh waves velocity. The results are displayed graphically. Some results of previous investigations are deduced as special cases from this study.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The study of granular medium in recent times has been necessiated by its possible applications in soil mechanics, geophysical prospecting, mining engineering, earthquake science, etc. The dynamical problem of magneto-thermoelasticity has received much attention in the literature during the past decade. In recent years the theory of magneto-thermoelasticity which deals with the interactions among strain, temperature and electromagnetic fields has drawn the attention of many researchers because of its extensive uses in divers field, such as geophysics for understanding the effect of Earth’s magnetic field on seismic waves, damping of acoustic waves in magnetic field, emissions of electromagnetic radiations from nuclear devices, development of highly sensitive superconduction magnetometer, electrical power engineering, optics etc. The dynamical problem in granular medium of generalized magneto-thermoelastic waves has been studied in recent times, necessitated by its possible applications in Soil mechanics, earthquakes Science, Geophysics, mining Engineering and Plasma physics, etc. In the motion of a deformable body, quantities at each point of it can’t be recognized with out some uncertainty, and must be regarded as average values over a small region about the point. Abd-Alla and Mahmoud discussed magneto-thermoelastic problem in rotating non-homogeneous orthotropic hollow cylindrical under the hyperbolic heat conduction model [1]. Generalized magneto-thermoelastic Rayleigh waves in a granular medium under influence of gravity field and initial stress, also effect of the rotation on the radial vibrations in a non-homogeneous orthotropic hollow cylinder is discussed by Abd-Alla et al. [2, 4]. Mahmoud et al. [3, 5] discussed effect of the rotation on plane vibrations in a transversely isotropic infinite hollow cylinder, they solved effect of the rotation on wave motion through cylindrical bore in a micropolar porous cubic crystal.
The dynamical problem of a generalized thermoelastic granular infinite cylinder under initial stress has been illustrated by El-Naggar [6]. Abd-Alla et al. [7–12] studied wave propagation modeling in cylindrical human long wet bones with cavity, propagation of S-wave in a non-homogeneous anisotropic incompressible and initially stressed medium under influence of gravity field, effect of the rotation on a non-homogeneous infinite cylinder of orthotropic material, effect of magnetic field and non-homogeneity on the radial vibrations in hollow elastic cylinder, on Problem of Transient Coupled Thermoelasticity of an Annular Fin, effect of the rotation, and they studied magnetic field and initial stress on peristaltic motion of micropolar fluid, influences of rotation, magnetic field, initial stress and gravity on Rayleigh waves in a homogeneous orthotropic elastic half-space. Abd-Alla and Mahmoud [13–15] solved effect of the rotation on propagation of thermoelastic waves in a non-homogeneous infinite cylinder of isotropic material, analytical solution of wave propagation in non-homogeneous orthotropic rotating elastic media, magneto-thermo-viscoelastic interactions in an unbounded non-homogeneous body with a spherical gravity subjected to a periodic loading. Effect of the non-homogeneity on wave propagation on orthotropic elastic media, effect of rotation and magnetic field through porous medium on Peristaltic transport of a Jeffrey fluid in tube are investigated by Mahmoud [16, 17]. Rayleigh waves in a thermoelastic granular medium under initial stress has been explained by Ahmed [18]. Recently, Ahmed [19] discussed the influence of gravity on the propagation of waves in granular medium. Problem of Rayleigh waves propagation in an orthotropic thermoelastic medium under gravity and initial stress is discussed by Abd-Alla and Ahmed [20]. Abouelregal [21] presented Rayleigh waves in a thermoelastic solid half space using dual-phase-lag model. The medium under consideration is granular half-space overlying by a different granular layer and initial stress present in this medium have considerable effect in the propagation of Rayleigh waves, Ahmed [18].
This study focuses on the study of Rayleigh waves with models fitting with the earth. The granular medium under consideration is a discontinuous one and is composed of large or small grains. The effects of rotation, magnetic and gravity fields and initial stress on the propagation of Rayleigh waves in a granular media under incremental thermal stresses are investigated. The roots of this equation are in general complex, the real part measures the Rayleigh wave velocity and the imaginary part of an appropriate root measures the attenuation of the waves. When there is no coupling between the temperature and the strain field in the absence of the initial stress, the derived frequency equation reduces to an equation in the form of ninth-order determinant.
2 Formulation of the problem
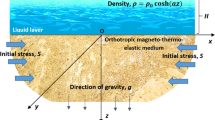
Let us consider a system of orthogonal Cartesian axes oxyz, the interface and the free surface of the granular layer resting on the granular half-space of different material being the planes z=K, and z=0, respectively. The origin o is any point on the free surface, z-axis is positive along the direction towards the exterior of the half-space, and the x-axis is positive along the direction of Rayleigh waves propagation. The both media are under initial compression stress P along x-direction and primary magnetic field  parallel to y-axis, as well as gravity field and incremental thermal stresses as shown in Fig. 1.
parallel to y-axis, as well as gravity field and incremental thermal stresses as shown in Fig. 1.
The state of deformation in the granular medium is described by the displacement vector \(\vec{u}(u,0,w) \) and \(\vec{\xi}(\xi,\eta,\zeta) \) are components of rotation vector of the grain about its center of gravity. The electromagnetic field is governed by Maxwell equations, under the consideration that the medium is a perfect electric conductor taking into account the absence of the displacement current.
The heat conduction equation in Lord and Shulman theory is given by

The vector equation of motion is

where  is the centripetal acceleration due to the time varying motion only and
is the centripetal acceleration due to the time varying motion only and  is the Coriolis acceleration. Here
is the Coriolis acceleration. Here  is the dynamic displacement vector measured from steady state deformed position and supposed to be small, F
j
are the components of Lorentz’s body forces vector.
is the dynamic displacement vector measured from steady state deformed position and supposed to be small, F
j
are the components of Lorentz’s body forces vector.
Equation (2) has three Cartesian components:
where  and
and
The stress-strain-temperature relations have the forms
where η, ζ and ξ are the components of rotation vector of the grain about its center of gravity.
Noted that, the fundamental equations of the Lord and Shulman’s theory can be obtained when δ=1 and τ 1=0. Green and Lindsay model (G-L) can be also obtained as a special case when δ=0. In the absence of the relaxation times τ 1 and τ 2, (1) reduces to the classical theory of thermoelasticity, where
From (5) and (6), (3) and (4) tend to
3 Solution of the problem
We assume that the displacements \(\vec{u}\) are derivable from the displacement potentials Φ and Ψ by the relation

which reduces to
Substituting from (14) into (7), (9) and (11), the wave equations tend to


where
Using (14), the heat conduction equation (1) becomes:


Where the coupling coefficient ε appears in temperature equation only
From (16) and (17), by eliminated η, we get

For a plane harmonic wave propagation in the x-direction, we assume
Substituting from (25) into (8), (10) and (12), one may obtain:
where q 2=ikcs 2−k 2, \(D=\frac{d}{dz}\).
Solutions of (26b) and (26c) are:
where, A 1, A 2, B 1 and B 2 are arbitrary constants, from (26a) and (27) we obtain
then
Substituting from (23) and (24) into (20) and (22), we obtain:


where
The solutions of (30) and (31) take the form:


Where the constants E j and F j are related with the constants C j and D j as the form
where N 1, N 2, N 3 and N 4 are taken to be the complex roots of equation




From (16), (24), (25), (32a) and (32b), we obtain:
Using (32a) and (32b), we obtain

With the lower medium, we use the symbols with dashes, for ξ 1, ζ1, η 1, T, Φ1, Ψ1 and q, for z>K,




4 Boundary conditions and frequency equation
In this section, we obtain the frequency equation for the boundary conditions which specify on the interface z=K, i.e.,



The boundary condition on the free surface z=0 are


from the conditions (iii), (v), (vi), (vii), we get




hence
The other significant boundary conditions are responsible for the following relations

By eliminating C j , D j and \(D^{\prime}_{j}\) from the relevant results, we will get a determinant of a twelfth-order form which determines the wave velocity and attenuation coefficient.
5 Special cases and discussion
5.1 In presence of rotation and absence of the gravity field
In this case, we put the gravity field g=0, and the rotation Ω≠0, (30) and (31) take the form:


which take the solutions
where
where






Also,


With the lower medium, we use the symbols with dashes, for ξ 1, ζ1, η 1, T, Φ1, Ψ1 and q, for z>K,



Using the boundary conditions, we get:

Equation (54) has complex roots, the real part gives Rayleigh wave velocity and the imaginary part gives the attenuation coefficient due to the friction of the granular nature of the medium. Analytically, one may observed that the Rayleigh wave velocity and attenuation coefficient depend on the rotation, magnetic field, initial stress, gravity field, granular rotation and thermal relaxation times. It’s shown from (34) that due to effect of the thermal field and gravity field change from fourth-order to eight-order which involves four positive roots. The transcendental equation (54) in the determinant form, represents the required wave velocity equation of wave propagated in generalized magneto-thermoelastic granular body under the influence of rotation, gravity field and initial stress.
5.2 In presence of rotation, relaxation times, granularity and there is no coupling (ε=0) between the temperature and strain field
In this case, presence of rotation (Ω≠0), no gravity field (g=0), no initial stress (P=0), no magnetic field (H o =0), coupled parameter (ε=0) and the ratio of the coefficients of heat transfer (θ=0), we obtain:




After tanking γ→0, boundary conditions become:

Equation (59) has complex roots, the real part gives Rayleigh wave velocity and the imaginary part gives the attenuation coefficient. The frequency equation (54) which determines the wave velocity equation for the Rayleigh waves in a granular medium, when the rotation and initial stress are absent, we have
Finally, if there is (i) no rotation, magnetic field, thermal relaxation times, gravity field, and granular rotation is vanishes and (ii) absence of the magnetic field, thermal relaxation times, gravity field, there is uncoupling between temperature and strain field, and the granular rotation is vanishes, the results obtained by Ahmed [18, 19] are deduced as special case from this study with slight changes in symbols with additional to the graphs that not included in the last work.
For a computation work by half-interval method program, we use Sand Stone as a granular medium and Nephiline as a granular layer taking into consideration that the friction coefficient F=0.5 and third elastic constants M 1=0.4, M 2=0.6.
5.3 In presence of rotation, there are no coupling (ε=0) between the temperature and strain field, there are no relaxation times and granularity
In this case presence of rotation (Ω≠0), no relaxation times (τ 1=τ 2=0) no gravity field (g=0), no initial stress (P=0), no magnetic field (H o =0), coupled parameter (ε=0) and the ratio of the coefficients of heat transfer (θ=0), and the friction coefficient F=0, we obtain:


So, (59) tends to
Equation (61) has complex roots, the real part gives Rayleigh wave velocity and the imaginary part gives the attenuation coefficient, where

6 Numerical results and discussion
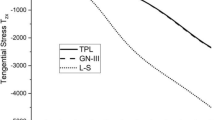
In order to show theoretical results and present some numerical results obtained. We investigate the variation of attenuation coefficient (imaginary part of frequency equation root) and Rayleigh wave velocity in a perfectly conducting granular medium under effect of rotation Ω, magnetic field, initial stress P and gravity field g, for computational work. From Fig. 3a shows the effects of rotation Ω on variation of attenuation coefficient with respect to initial stress with the various values of rotation Ω, k=10−5, τ 1=10−2, K=10−3, H o =4×103 which it decreases with increasing of initial stress and it increases with increasing of rotation Ω.
Figure 2(a,b) shows variation of the attenuation coefficient (imaginary part of frequency equation root) and velocity of Rayleigh waves (real part of frequency equation root), with respect to initial stress, for the various values of gravity field; we found that the attenuation coefficient and velocity of Rayleigh waves decreased with increasing values of initial stress P and gravity field g. From Fig. 3b, it’s noticed that the various values of Rayleigh wave velocity are fixed for the small values of initial stress P, jump to its maximum value that help an engineers in their applications, and run to its fixed value.
Figure 4(a,b) shows the effects of rotation Ω and magnetic field H o on variation of attenuation coefficient and Rayleigh wave velocity with respect to initial stress with the various values of magnetic field H o , k=10−5, τ 1=10−2, K=10−3, which it decreases with increasing of initial stress and it decreases with increasing of magnetic field H o . Figure 5(a,b) shows the effects of rotation Ω and wave number k on variation of attenuation coefficient and Rayleigh wave velocity with respect to initial stress with the various values of wave number k, τ 1=10−2, K=10−3, H o =4×103, which it decreases with increasing of initial stress and it decreases with increasing of wave number k. Figure 6(a,b) shows the effects of rotation Ω and relaxation time τ 1 on variation of attenuation coefficient and Rayleigh wave velocity with respect to initial stress with the various values of relaxation time, k=10−5, K=10−3, H o =4×103, which it decreases with increasing of initial stress and it increases with increasing of relaxation time τ 1.
Figure 7(a,b) shows the effects of rotation Ω on attenuation coefficient and Rayleigh wave velocity c with respect to thickness K with the various values of rotation, k=10−5, τ 1=10−2, K=10−3, H o =4×103, which it increases with increasing of thickness K and it increases with decreasing of rotation Ω. Figure 8 shows the effects of rotation Ω on non-dimensional frequency, which it increases with increasing of thickness K and it decreases with increasing the rotation. Figure 9 shows the effects of magnetic field H o on non-dimensional frequency, which it increases with increasing of thickness K and it increases with increasing the magnetic field. Figure 10 shows the effects of relaxation time on non-dimensional frequency, which it increases with increasing of thickness K and it increases with increasing the relaxation time. Figure 11 shows the effects of wave number on non-dimensional frequency, which it increases with increasing of thickness K and it increases with increasing the wave number. Figure 12 shows the effects of gravity field on non-dimensional frequency, which it has no effect for small values of thickness K and it has Trivial effect for higher values, non-dimensional frequency increases with increasing of thickness K and it increases with increasing the gravity field.
Finally, from the previous results obtained in general case and special cases, it is shown that the rotation, magnetic field, initial stress, gravity field, thermal relaxation times, and granular rotations have utilitarian aspects on Rayleigh wave velocity and attenuation coefficient.
7 Conclusion
The effects of rotation, relaxation times, magnetic field, gravity field, initial stress and wave number are very pronounced on attenuation coefficient, Rayleigh wave velocity and non-dimensional frequency. When the medium is an orthotropic and the effect of rotation is neglected, the frequency equation reduces to previous work. Special cases are investigated. The results indicate that the effect of rotation is very sensitive.
Abbreviations
- T :
-
is temperature difference (θ−T 0)
- θ :
-
is the ratio of the coefficients of heat transfer
- t :
-
is the time
-
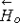 :
: -
is the constant primary magnetic field vector
-
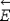 :
: -
is the electric intensity
- s :
-
is the specific heat per unit mass
- ρ :
-
is the density of the material
- P :
-
is the initial stress
- F :
-
is the coefficient of friction
- F j :
-
are the components of Lorentz’s body forces vector
- τ 1,τ 2 :
-
are the mechanical relaxation times
- g :
-
is the earth gravity
- \(\vec{u}\) :
-
is the component of displacement vector
- T o :
-
is reference temperature solid
-
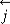 :
: -
is the electric current density
- ω ij :
-
is the rotation vector
- μ e :
-
is the magnetic permeability
- k :
-
is the wave number
- c :
-
is speed of Rayleigh waves
- λ,μ :
-
are the Lame’ constants
- M :
-
is the third elastic constant
- κ :
-
is thermal conductivity
- K :
-
is the thickness
-
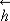 :
: -
is the perturbed magnetic field over the constant primary magnetic field
- σ ij :
-
is the stress tensor
- ε :
-
is coupling coefficient
- (ξ,η,ζ):
-
are components of rotation vector of the grain about its center of gravity
References
Abd-Alla AM, Mahmoud SR (2010) Magneto-thermo-elastic problem in rotating non-homogeneous orthotropic hollow cylindrical under the hyperbolic heat conduction model. Meccanica 45(4):451–462
Abd-Alla AM, Abo-Dahab SM, Hammad HA, Mahmoud SR (2011) On generalized magneto-thermoelastic Rayleigh waves in a granular medium under influence of gravity field and initial stress. J Vib Control 17(1):115–128
Mahmoud SR, Abd-Alla AM, AL-Shehri NA (2011) Effect of the rotation on plane vibrations in a transversely isotropic infinite hollow cylinder. Int J Mod Phys B 25, 26:3513–3528
Abd-Alla AM, Mahmoud SR, AL-Shehri NA (2010) Effect of the rotation on the radial vibrations in a non-homogeneous orthotropic hollow cylinder. Open Mech J 4:58–64
Mahmoud SR, Abd-Alla AM, Matooka BR (2011) Effect of the rotation on wave motion through cylindrical bore in a micropolar porous cubic crystal. Int J Mod Phys B 25(20):2713–2728
El-Naggar AM (1992) On the dynamical problem of a generalized thermoelastic granular infinite cylinder under initial stress. Astrophys Space Sci 190:177–190
Abd-Alla AM, Mahmoud SR, Abo-Dahab SM (2011) Wave propagation modeling in cylindrical human long wet bones with cavity. Meccanica 46(6):1413–1428
Abd-Alla AM, Mahmoud SR, Abo-Dahab SM, Helmi MIR (2011) Propagation of S-wave in a non-homogeneous anisotropic incompressible and initially stressed medium under influence of gravity field. Appl Math Comput 217(9):4321–4332
Abd-Alla AM, Mahmoud SR, AL-Shehri NA (2011) Effect of the rotation on a non-homogeneous infinite cylinder of orthotropic material. Appl Math Comput 217(22):8914–8922
Abd-Alla AM, Mahmoud SR, Abo-Dahab SM (2011) On problem of transient coupled thermoelasticity of an annular fin. Meccanica. doi:10.1007/s11012-011-9513-2. Published online: 7 December 2011
Abd-Allaa AM, Yahya GA, Mahmoud SR, Alosaimi HS (2011) Effect of the rotation, magnetic field and initial stress on peristaltic motion of micropolar fluid. Meccanica. doi:10.1007/s11012-011-9528-8. Published online: 14 December 2011
Abd-Alla AM, Mahmoud SR, Abo-Dahab SM, Helmi MIR (2010) Influences of rotation, magnetic field, initial stress and gravity on Rayleigh waves in a homogeneous orthotropic elastic half-space. Appl Math Sci 4(2):91–108
Abd-Alla AM, Mahmoud SR (2010) Effect of the rotation on propagation of thermoelastic waves in a non-homogeneous infinite cylinder of isotropic material. Int J Math Anal 4(42):2051–2064
Mahmoud SR, Abd-Alla AM (2012, in press) Analytical solution of wave propagation in non-homogeneous orthotropic rotating elastic media. J Mech Sci Technol
Abd-Alla AM, Mahmoud SR (2011) Magneto-thermo-viscoelastic interactions in an unbounded non-homogeneous body with a spherical homogeneity cavity subjected to a periodic loading. Appl Math Sci 5(29):1431–1447
Mahmoud SR (2010) Effect of the non- on wave propagation on orthotropic elastic media. Int J Contemp Math Sci 5(45):2211–2224
Mahmoud SR (2011) Effect of rotation and magnetic field through porous medium on peristaltic transport of a Jeffrey fluid in tube. Math Probl Eng 2011:971456. doi:10.1155/2011/971456
Ahmed SM (1999) Rayleigh waves in a thermoelastic granular medium under initial stress. Appl Math Comput 101:269–280
Ahmed SM (2000) Influence of gravity field on the propagation of waves in granular medium. Int J Math Math Sci 23(9):627–637
Abd-Alla AM, Ahmed SM (1998) Rayleigh waves in an orthotropic thermoelastic medium under gravity and initial stress. Earth Moon Planets 75:185–197
Abouelregal AE (2011) Rayleigh waves in a thermoelastic solid half space using dual-phase-lag model. Int J Eng Sci 49:781–791
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Mahmoud, S.R. Influence of rotation and generalized magneto-thermoelastic on Rayleigh waves in a granular medium under effect of initial stress and gravity field. Meccanica 47, 1561–1579 (2012). https://doi.org/10.1007/s11012-011-9535-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-011-9535-9





















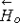 :
: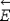 :
: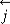 :
: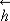 :
: