Abstract
We propose a novel quantum integrable model for every non-simply laced simple Lie algebra \({{\mathfrak {g}}}\), which we call the folded integrable model. Its spectra correspond to solutions of the Bethe Ansatz equations obtained by folding the Bethe Ansatz equations of the standard integrable model associated with the quantum affine algebra \(U_q(\widehat{{{\mathfrak {g}}}'})\) of the simply laced Lie algebra \({{\mathfrak {g}}}'\) corresponding to \({{\mathfrak {g}}}\). Our construction is motivated by the analysis of the second classical limit of the deformed W-algebra of \({{\mathfrak {g}}}\), which we interpret as a “folding” of the Grothendieck ring of finite-dimensional representations of \(U_q(\widehat{{{\mathfrak {g}}}'})\). We conjecture, and verify in a number of cases, that the spaces of states of the folded integrable model can be identified with finite-dimensional representations of \(U_q({}^L{\widehat{{{\mathfrak {g}}}}})\), where \(^L{\widehat{{{\mathfrak {g}}}}}\) is the (twisted) affine Kac–Moody algebra Langlands dual to \({\widehat{{{\mathfrak {g}}}}}\). We discuss the analogous structures in the Gaudin model which appears in the limit \(q \rightarrow 1\). Finally, we describe a conjectural construction of the simple \({{\mathfrak {g}}}\)-crystals in terms of the folded q-characters.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Integrable models
Exactly solvable quantum integrable models have played a prominent role in mathematical physics ever since the groundbreaking work of Hans Bethe [3] in which he described the spectrum of the Hamiltonian of the XXX spin chain in terms of the solutions of what we call today the Bethe Ansatz equations. The XXX spin chain naturally corresponds to the Yangian of \({{\mathfrak {s}}}{{\mathfrak {l}}}_2\), and it can be generalized to quantum spin chain models corresponding to the Yangian of an arbitrary simple Lie algebra \({{\mathfrak {g}}}\) or the corresponding quantum affine algebra \(U_q({\widehat{{{\mathfrak {g}}}}})\). In this paper, we focus on the latter model, which we call XXZ-type model associated with \(U_q({\widehat{{{\mathfrak {g}}}}})\).
Using the universal R-matrix of \(U_q({\widehat{{{\mathfrak {g}}}}})\), one assigns a commuting family of Hamiltonians \(t_V(z), z \in {{\mathbb {C}}}\), of this model, to every finite-dimensional representation V of \(U_q({\widehat{{{\mathfrak {g}}}}})\), which is called an auxiliary space. These Hamiltonians, which are called the transfer-matrices, act on any finite-dimensional representation W of \(U_q({\widehat{{{\mathfrak {g}}}}})\), which is called a space of states (or physical space) of the model. Moreover, the transfer-matrix construction extends to a compatible family of ring homomorphisms
sending the class of V in the Grothendieck ring \({\text {Rep}} U_q({\widehat{{{\mathfrak {g}}}}})\) of \(U_q({\widehat{{{\mathfrak {g}}}}})\) to the corresponding transfer-matrix \(t_V(z)\) acting on W (viewed as a formal power series in z with coefficients in \({\text {End}}(W)\)). We will assume throughout that \(q\in {\mathbb {C}}^\times \) is not a root of unity.
In a generic situation, the spectra of these quantum Hamiltonians are expected to be in one-to-one correspondence with the solutions of the generalized Bethe Ansatz equations. For the XXZ-type model associated with \(U_q({\widehat{{{\mathfrak {g}}}}})\), where \({\widehat{{{\mathfrak {g}}}}}\) is an arbitrary affine Kac–Moody algebra (twisted or untwisted) they were proposed in [54, 55, 57]. A pair of authors of the present paper subsequently conjectured in [25] an explicit formula for the eigenvalues of the transfer-matrices \(t_V(z)\) corresponding to a given solution of these generalized Bethe Ansatz equations. This formula is written in terms of the q-character of V.
Another pair of authors of the present paper then extended the above construction to a larger algebra of quantum Hamiltonians [19]. Namely, the homomorphism \(h_W\) extends to a homomorphism
where \({\text {Rep}}'\) stands for the Grothendieck ring of the category  introduced in [33] or its dual category
introduced in [33] or its dual category  . The corresponding transfer-matrices \(t_V(z,u)\) are formal power series in z with coefficients depending on an element u of the Cartan subgroup H of the simply-connected Lie group G associated with \({{\mathfrak {g}}}\). The category
. The corresponding transfer-matrices \(t_V(z,u)\) are formal power series in z with coefficients depending on an element u of the Cartan subgroup H of the simply-connected Lie group G associated with \({{\mathfrak {g}}}\). The category  is topologically generated by the prefundamental representations \(R_j^\pm (z), j \in I\), where I is the set of vertices of the Dynkin diagram of \({{\mathfrak {g}}}\). Hence, the eigenvalues of the quantum Hamiltonians are determined by the eigenvalues of the Q-operators \(Q_j^\pm (z,u) = t_{R_j^\pm }(z,u)\), the transfer-matrices associated in [19] with the prefundamental representations \(R_j^\pm (z)\).
is topologically generated by the prefundamental representations \(R_j^\pm (z), j \in I\), where I is the set of vertices of the Dynkin diagram of \({{\mathfrak {g}}}\). Hence, the eigenvalues of the quantum Hamiltonians are determined by the eigenvalues of the Q-operators \(Q_j^\pm (z,u) = t_{R_j^\pm }(z,u)\), the transfer-matrices associated in [19] with the prefundamental representations \(R_j^\pm (z)\).
It was proved in [19] that up to a universal factor depending on the representation W, all eigenvalues of \(Q_j^+(z,u)\) on W (which are a priori formal power series in z) are in fact polynomials in z. Moreover, it follows from [19, 20] that the roots of these polynomials are solutions of the Bethe Ansatz equations (more precisely, the u-dependent version of the Bethe Ansatz equations) under a certain non-degeneracy condition. (This condition was subsequently dropped in [15].) Finally, it was shown in [19] that the eigenvalues of the transfer-matrix \(t_V(z,u)\) corresponding to a finite-dimensional representation V can be expressed in terms of the eigenvalues of the \(Q_j^+(z,u)\) and the q-character of V, proving the conjecture of [25]. These results provide a link between the spectra of the XXZ-type model associated with \(U_q({\widehat{{{\mathfrak {g}}}}})\) and the solutions of the corresponding Bethe Ansatz equations (BAE).
Explicitly, if the space of states W is the tensor product of irreducible finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\) with the Drinfeld polynomials \(P_{i,k}, i \in I, k=1,\ldots ,N\), then the BAE have the form:
with one equation for each root \(w^{(i)}_r, r = 1,\ldots ,m_i\), of the ith Baxter polynomial \(Q^+_i(z)\), with i ranging over the set I. Here \((B_{ij})\) is the symmetrized Cartan matrix of \({{\mathfrak {g}}}\): \(B_{ij} = d_i C_{ij}\), where \((C_{ij})\) is the Cartan matrix and the \(d_i\) are relatively prime integers, and we set \(q_i = q^{d_i}\).
Note that a typical factor on the right-hand side of (1.3) looks like this:
1.2 Miura q-opers and folded Bethe Ansatz equations
In a recent paper [21], certain geometric objects on \({{\mathbb {C}}}{{\mathbb {P}}}^1\) called Miura (G, q)-opers were introduced. It was shown in [21] (see also the earlier work [42] in the case \(G=SL_n\)) that there is a one-to-one correspondence between the set of Miura (G, q)-oper satisfying a non-degeneracy condition and the set of solutions of a system of equations which look very similar to the BAE associated with \(U_q({\widehat{{{\mathfrak {g}}}}})\).Footnote 1
In these equations, a typical factor with \(i \ne j\) reads
where \((C_{ij})\) is the Cartan matrix of \({{\mathfrak {g}}}\). If \({{\mathfrak {g}}}\) is simply laced, formulas (1.4) and (1.5) coincide and so the equations are just the standard BAE associated with \(U_q({\widehat{{{\mathfrak {g}}}}})\). Therefore, in this case one obtains a “dual” description of the spectrum in terms of Miura (G, q)-opers, giving rise to what in [21] was called the qDE/IM correspondence.
However, if \({{\mathfrak {g}}}\) is not simply laced, we obtain this way a different system of equations. A Yangian version of these equations first appeared in the work of Mukhin and Varchenko [47, 48]. We note that for \({{\mathfrak {g}}}=B_\ell \) similar equations were also obtained in [8] in the context of 3d quiver gauge theories.
In this paper, we will call these equations the folded Bethe Ansatz equations because they can be obtained by “folding” the BAE for the simply laced simple Lie algebra \({{\mathfrak {g}}}'\) that gives rise to \({{\mathfrak {g}}}\) (i.e. \({{\mathfrak {g}}}'\) is equipped with an automorphism of order 2 or 3 whose invariant Lie subalgebra is \({{\mathfrak {g}}}\)).
To explain this folding procedure and to illustrate the difference between the two types of BAE, consider the case of \({{\mathfrak {g}}}=C_\ell \). Then, \({{\mathfrak {g}}}' = A_{2\ell -1}\). In this case, \(d_i=1\) for \(i=1,\ldots ,\ell -1\) and \(d_\ell = 2\). Therefore, only factors (1.4) for \(C_\ell \) with \(i \ne j\) and the powers of q different from \(\pm 1\) (which are the only powers of q appearing in the factors with \(i \ne j\) in the simply laced cases) occur for \(i=\ell , j=\ell -1\) or the other way around. The first of them is
On the other hand, since the entry \(C_{\ell -1,\ell }\) of the Cartan matrix of \({{\mathfrak {g}}}=C_\ell \) is equal to \(-2\), the corresponding factor (1.5) reads
It can be obtained by folding the expression of the form:
appearing in the BAE of the simply laced Lie algebra \({{\mathfrak {g}}}'=A_{2\ell -1}\). Indeed, the automorphism of the Dynkin diagram of \(A_{2\ell -1}\) preserves the \(\ell \)th vertex and exchanges the \((\ell -1)\)st and the \((\ell +1)\)st vertices. If we accordingly identify the variables \(w^{(\ell -1)}_s\) and \(w^{(\ell +1)}_s\) in the expression (1.8), we obtain the factor (1.7). This is what we mean by folding the BAE of a simply laced Lie algebra \({{\mathfrak {g}}}'\).
Note that the difference between (1.7) and (1.6) (as its RHS shows) is the difference between \(f(w)^2\) and \(f(wq)f(wq^{-1})\).
Remark 1.1
After the first version of this paper was posted on arXiv, Heng-Yu Chen and Taro Kimura informed us about their paper [7], in which they considered two classical limits of the deformed W-algebra  in the context of the corresponding 5D fractional quiver gauge theory introduced in [41] (where these classical limits are interpreted as the two Nekrasov–Shatashvili limits). They obtained a version of the folded Bethe Ansatz equations of the present paper from the analysis of the partition function of this theory in one of these limits. They did not consider the folded integrable model, which is the main focus of the present paper, where these equations naturally appear from certain subspaces of finite-dimensional representations of quantum affine algebras (see Sect. 5). \(\square \)
in the context of the corresponding 5D fractional quiver gauge theory introduced in [41] (where these classical limits are interpreted as the two Nekrasov–Shatashvili limits). They obtained a version of the folded Bethe Ansatz equations of the present paper from the analysis of the partition function of this theory in one of these limits. They did not consider the folded integrable model, which is the main focus of the present paper, where these equations naturally appear from certain subspaces of finite-dimensional representations of quantum affine algebras (see Sect. 5). \(\square \)
1.3 Folded integrable model
According to [21], non-degenerate Miura (G, q)-opers encode solutions of the folded BAE. But which integrable model do these equations correspond to?
In this paper (Sect. 5), we propose a conjectural answer to this question. Namely, we conjecture the existence of what we will call the folded integrable model for every non-simply laced simple Lie algebra \({{\mathfrak {g}}}\), whose spectra give rise to solutions of the folded BAE (under a genericity condition). This folded integrable model combines in a non-trivial way representations of the quantum affine algebra \(U_q(\widehat{{{\mathfrak {g}}}'})\), where \({{\mathfrak {g}}}'\) is the corresponding simply-laced Lie algebra (these appear as the auxiliary spaces of the folded model) and representations of the quantum affine algebra \(U_q({}^L{\widehat{{{\mathfrak {g}}}}})\), where \(^L{\widehat{{{\mathfrak {g}}}}}\) is the twisted affine Kac–Moody algebra which is Langlands dual to \({\widehat{{{\mathfrak {g}}}}}\) (these appear as the spaces of states of the folded model).
Remark 1.2
Note that to the twisted quantum affine algebra \(U_q({}^L{\widehat{{{\mathfrak {g}}}}})\) one can also associate an XXZ-type quantum integrable model. It is constructed in the same way as for the untwisted quantum affine algebras, and its spectra correspond to the solutions of the BAE that were proposed in [55, 57]. But this model is different from the folded model. Namely, the typical factors of the BAE of this model read
so they differ from the factors (1.5).
For example, in the case of \({{\mathfrak {g}}}=C_\ell \), instead of the factor (1.7), we have
Thus, it can be obtained by folding the expression (1.8) if we also multiply the spectral parameter by \(-1\), i.e. identify \(w^{(\ell -1)}_s\) and \(-w^{(\ell +1)}_s\) in (1.8) (rather than \(w^{(\ell -1)}_s\) and \(w^{(\ell +1)}_s\)). In other words, the difference between (1.7) and (1.10) is the difference between \(f(w)^2\) and \(f(w) f(-w)\). And similarly for other Lie algebras corresponding to an automorphism of order 2. In the case of \({{\mathfrak {g}}}=G_2\), when the automorphism has order 3, it is the difference between \(f(w)^3\) and \(f(w)f(w\epsilon )f(w\epsilon ^{-1})\), where \(\epsilon = e^{2\pi i/3}\). \(\square \)
1.4 QQ-system
There is an important intermediate object between the spectra of the XXZ-type model associated with \(U_q({\widehat{{{\mathfrak {g}}}}})\) and the corresponding BAE called the QQ-system. It was introduced in [45, 46] in the context of affine opers. In [20], it was shown that this QQ-system naturally arises in the context of the homomorphisms \(h'_W\) (see the above formula (1.2)). Namely, in addition to the set of prefundamental representations \(R^+_j(z), j \in I\), discussed above there is another set of representations, denoted by \(X_j(z), j \in I\), in the category  , such that properly rescaled classes of these two sets satisfy the QQ-system. In other words, if we assign to \(R^+_j(z), j \in I\), the above Q-operators \(Q_j(z,u)\) and to \(X_j(z), j \in I\), the transfer-matrix \(\widetilde{Q}_j(z,u)\) (the image of \(X_j(z)\) under the homomorphism \(h'_W\), where W is a finite-dimensional representation of \(U_q({\widehat{{{\mathfrak {g}}}}})\)), then these operators, properly rescaled, will satisfy the QQ-system.Footnote 2 Note that for \({{\mathfrak {g}}}={{\mathfrak {s}}}{{\mathfrak {l}}}_2\), this is the quantum Wronskian relation introduced in [4], which provided the initial motivation for this line of research.
, such that properly rescaled classes of these two sets satisfy the QQ-system. In other words, if we assign to \(R^+_j(z), j \in I\), the above Q-operators \(Q_j(z,u)\) and to \(X_j(z), j \in I\), the transfer-matrix \(\widetilde{Q}_j(z,u)\) (the image of \(X_j(z)\) under the homomorphism \(h'_W\), where W is a finite-dimensional representation of \(U_q({\widehat{{{\mathfrak {g}}}}})\)), then these operators, properly rescaled, will satisfy the QQ-system.Footnote 2 Note that for \({{\mathfrak {g}}}={{\mathfrak {s}}}{{\mathfrak {l}}}_2\), this is the quantum Wronskian relation introduced in [4], which provided the initial motivation for this line of research.
Thus, the QQ-system encodes universal relations between the classes of the representations \(R^+_j(z)\) and \(X_j(z), j \in I\) in \({\text {Rep}}'\) which translate under the homomorphism (1.2) into relations between the corresponding transfer-matrices, and hence their eigenvalues, on any representation W.Footnote 3
As explained in [20, 45, 46], the Bethe Ansatz equations (1.3) follow directly from the QQ-system under a certain non-degeneracy condition. In fact, from the point of view of the preceding paragraph, the QQ-system is more fundamental to the question of describing the spectra of the XXZ-type models than the Bethe Ansatz equations.
Likewise, for the folded BAE, as shown in [21], these equations are equivalent to the QQ-system proposed in [21] (under a non-degeneracy condition). We will call the latter system the folded QQ-system because it can be obtained by folding the QQ-system associated with the simply laced Lie algebra \({{\mathfrak {g}}}'\). Thus, this system appears as an intermediate object between Miura (G, q)-opers and the folded BAE.
In this paper, we show that this folded QQ-system also appears naturally as a relation satisfied by the transfer-matrices of our (conjectural) folded integrable model associated with a non-simply laced Lie algebra \({{\mathfrak {g}}}\). The folded BAE equations follow from the folded QQ-system under a non-degeneracy condition.
1.5 Deformed W-algebras
Valuable insights about the folded quantum integrable model can be learned from the deformed W-algebras introduced by two of the authors of the present paper in [24]. Recall that this is a two-parameter algebra  associated with a simple Lie algebra \({{\mathfrak {g}}}\). Recently, the algebra
associated with a simple Lie algebra \({{\mathfrak {g}}}\). Recently, the algebra  found interesting applications in the study of four-dimensional supersymmetric gauge theories, see [1, 10, 40, 41, 53].
found interesting applications in the study of four-dimensional supersymmetric gauge theories, see [1, 10, 40, 41, 53].
The deformed W-algebra has two classical limits, in which the algebra becomes commutative, and equipped with a Poisson structure: the first occurs when \(t \rightarrow 1\) and the second when \(q \rightarrow 1\).
The first limit,  , is relatively well understood. It is isomorphic to the center \(Z_q({\widehat{{{\mathfrak {g}}}}})\) of \(U_q({\widehat{{{\mathfrak {g}}}}})\) at the critical level. The corresponding commutative algebra of generating fields can be identified, via a version of the transfer-matrix construction (see [23, 56]), with the representation ring \({\text {Rep}} U_q({\widehat{{{\mathfrak {g}}}}})\).Footnote 4 Moreover, under this identification the free field realization of
, is relatively well understood. It is isomorphic to the center \(Z_q({\widehat{{{\mathfrak {g}}}}})\) of \(U_q({\widehat{{{\mathfrak {g}}}}})\) at the critical level. The corresponding commutative algebra of generating fields can be identified, via a version of the transfer-matrix construction (see [23, 56]), with the representation ring \({\text {Rep}} U_q({\widehat{{{\mathfrak {g}}}}})\).Footnote 4 Moreover, under this identification the free field realization of  becomes the q-character homomorphism (this was the motivation behind the definition of the q-characters in [25]).
becomes the q-character homomorphism (this was the motivation behind the definition of the q-characters in [25]).
If \({{\mathfrak {g}}}\) is simply laced, then the second classical limit,  , coincides with the first one upon replacing t with q. But if \({{\mathfrak {g}}}\) is not simply laced, the second limit is substantially different from the first one. In [24],
, coincides with the first one upon replacing t with q. But if \({{\mathfrak {g}}}\) is not simply laced, the second limit is substantially different from the first one. In [24],  was linked to the t-deformed Drinfeld–Sokolov reduction of the loop group associated with G introduced in [26, 59] and some observations were made connecting elements of
was linked to the t-deformed Drinfeld–Sokolov reduction of the loop group associated with G introduced in [26, 59] and some observations were made connecting elements of  to the q-characters of \(U_q({\widehat{{{\mathfrak {g}}}}}^\vee )\), where \({\widehat{{{\mathfrak {g}}}}}^\vee \) is the twisted affine algebra associated with \({{\mathfrak {g}}}'\) and \(\sigma \). But that’s pretty much all that has been known about the limit \(q \rightarrow 1\) until now.
to the q-characters of \(U_q({\widehat{{{\mathfrak {g}}}}}^\vee )\), where \({\widehat{{{\mathfrak {g}}}}}^\vee \) is the twisted affine algebra associated with \({{\mathfrak {g}}}'\) and \(\sigma \). But that’s pretty much all that has been known about the limit \(q \rightarrow 1\) until now.
In the present paper, we argue that it is this limit that is relevant to the “folded structures” that we discuss here, including the folded Bethe Ansatz equations and the folded integrable models. Thus, we can learn a lot about these models by studying this limit. Its hybrid nature, i.e. the fact that it mixes in a non-trivial way quantum affine algebras \(\widehat{{{\mathfrak {g}}}'}\) and \(^L{\widehat{{{\mathfrak {g}}}}}\), shows that  is a fascinating Poisson algebra that deserves further investigation.
is a fascinating Poisson algebra that deserves further investigation.
The deformed W-algebra  creates a bridge between the two classical limits, and hence between the XXZ-type quantum integrable model associated with \(U_q({\widehat{{{\mathfrak {g}}}}})\) and the corresponding folded quantum integrable model. However, the non-commutative nature of
creates a bridge between the two classical limits, and hence between the XXZ-type quantum integrable model associated with \(U_q({\widehat{{{\mathfrak {g}}}}})\) and the corresponding folded quantum integrable model. However, the non-commutative nature of  makes deriving practical consequences of this bridge a daunting task. For this reason, in this paper we replace
makes deriving practical consequences of this bridge a daunting task. For this reason, in this paper we replace  with its simplified commutative version introduced by two of the authors in [18] under the name interpolating (q, t)-characters. Using a slight refinement of these objects, we make our conjectures concerning the folded quantum integrable models more precise. This also enables us to explicitly verify our conjectures in a number of non-trivial cases (see Sect. 7).
with its simplified commutative version introduced by two of the authors in [18] under the name interpolating (q, t)-characters. Using a slight refinement of these objects, we make our conjectures concerning the folded quantum integrable models more precise. This also enables us to explicitly verify our conjectures in a number of non-trivial cases (see Sect. 7).
1.6 Connection to qKZ equations and quantum q-Langlands correspondence
It is known that the critical level limit of the solutions of the qKZ equations corresponding to \(U_q({\widehat{{{\mathfrak {g}}}}})\) gives rise to eigenvectors of the XXZ-type model associated with \(U_q({\widehat{{{\mathfrak {g}}}}})\). Thus, the qKZ system provides a deformation of the latter model.Footnote 5 This can also be seen from the fact that for a large class of representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\), the difference operators of the qKZ system become in the critical level limit the transfer-matrices of the XXZ-type model (see Proposition 10.1).
In [1], a quantum q-Langlands correspondence was proposed. For a simply laced simple Lie algebra \({{\mathfrak {g}}}\), it sets up a correspondence between solutions of the qKZ system associated with \(U_t({\widehat{{{\mathfrak {g}}}}})\) and the deformed conformal blocks associated with  . Here q depends on the level of \(U_t({\widehat{{{\mathfrak {g}}}}})\) in such a way that the limit \(q \rightarrow 1\) corresponds to the critical level limit. In this limit, the quantum q-Langlands correspondence essentially becomes the statement that the Hamiltonians of the XXZ-type model associated with \(U_t({\widehat{{{\mathfrak {g}}}}})\) correspond to elements of
. Here q depends on the level of \(U_t({\widehat{{{\mathfrak {g}}}}})\) in such a way that the limit \(q \rightarrow 1\) corresponds to the critical level limit. In this limit, the quantum q-Langlands correspondence essentially becomes the statement that the Hamiltonians of the XXZ-type model associated with \(U_t({\widehat{{{\mathfrak {g}}}}})\) correspond to elements of  . If \({{\mathfrak {g}}}\) is simply laced, then
. If \({{\mathfrak {g}}}\) is simply laced, then  indeed coincides with \({\text {Rep}} U_t({\widehat{{{\mathfrak {g}}}}})\), so this statement comes down to the existence of the homomorphisms \(h_W\) given by formula (1.1).
indeed coincides with \({\text {Rep}} U_t({\widehat{{{\mathfrak {g}}}}})\), so this statement comes down to the existence of the homomorphisms \(h_W\) given by formula (1.1).
However, if \({{\mathfrak {g}}}\) is not simply laced, the algebra  is no longer isomorphic to \({\text {Rep}} U_t({\widehat{{{\mathfrak {g}}}}})\) and hence does not give rise to the Hamiltonians of the standard XXZ-type model associated with \(U_t({\widehat{{{\mathfrak {g}}}}})\), which are the transfer-matrices associated with finite-dimensional representations of \(U_t({\widehat{{{\mathfrak {g}}}}})\). Rather, as we argue in this paper, it gives rise to the Hamiltonians of the folded quantum integrable model associated with \({{\mathfrak {g}}}\). These Hamiltonians correspond to the transfer-matrices associated with finite-dimensional representations of \(U_t(\widehat{{{\mathfrak {g}}}'})\) rather than \(U_t({\widehat{{{\mathfrak {g}}}}})\).
is no longer isomorphic to \({\text {Rep}} U_t({\widehat{{{\mathfrak {g}}}}})\) and hence does not give rise to the Hamiltonians of the standard XXZ-type model associated with \(U_t({\widehat{{{\mathfrak {g}}}}})\), which are the transfer-matrices associated with finite-dimensional representations of \(U_t({\widehat{{{\mathfrak {g}}}}})\). Rather, as we argue in this paper, it gives rise to the Hamiltonians of the folded quantum integrable model associated with \({{\mathfrak {g}}}\). These Hamiltonians correspond to the transfer-matrices associated with finite-dimensional representations of \(U_t(\widehat{{{\mathfrak {g}}}'})\) rather than \(U_t({\widehat{{{\mathfrak {g}}}}})\).
This suggests that for non-simply laced \({{\mathfrak {g}}}\) the quantum q-Langlands correspondence might be more subtle. Namely, it follows from the preceding paragraph that the system of q-difference equations appearing on one side of this correspondence is not the usual qKZ system associated with \(U_t({\widehat{{{\mathfrak {g}}}}})\). If this were the usual qKZ system associated with \(U_t({\widehat{{{\mathfrak {g}}}}})\), then in the critical limit we would recover the eigenvectors of the XXZ-type model associated with \(U_t({\widehat{{{\mathfrak {g}}}}})\), but this would be inconsistent with the limit on the other side of the correspondence which yields  . As we discussed above, the latter is not the algebra of Hamiltonians of the XXZ-type model associated with \(U_t({\widehat{{{\mathfrak {g}}}}})\), but rather the algebra of Hamiltonians of the folded quantum integrable model introduced in the present paper.
. As we discussed above, the latter is not the algebra of Hamiltonians of the XXZ-type model associated with \(U_t({\widehat{{{\mathfrak {g}}}}})\), but rather the algebra of Hamiltonians of the folded quantum integrable model introduced in the present paper.
What should replace the qKZ system associated with \(U_t({\widehat{{{\mathfrak {g}}}}})\) in the quantum q-Langlands correspondence for non-simply laced \({{\mathfrak {g}}}\)? The above discussion shows that this modified qKZ system should have the property that the leading terms of its solutions in the critical level limit are eigenvectors of the folded integrable system associated with \({{\mathfrak {g}}}\). As far as we know, the existence of such modified qKZ system is an open question at the moment (naive ways to “fold” the qKZ system associated with \({{\mathfrak {g}}}'\) don’t seem to work, see “Appendix” of this paper). But we expect that this question can be answered using the geometric and K-theoretic methods of [1]. Perhaps, these equations can also be constructed purely algebraically. We hope to return to this question elsewhere.
1.7 The Gaudin limit
To gain further insights, it is instructive to consider the limit in which the second parameter, denoted by t in the previous subsection, also goes to 1. In this limit, the XXZ-type model associated with \(U_t({\widehat{{{\mathfrak {g}}}}})\) becomes the Gaudin model associated with \({{\mathfrak {g}}}\) [12, 16]; more precisely, its modification with a twist parameter \(\chi \), an element of the Cartan subalgebra of \({{\mathfrak {g}}}\) [13, 14, 58]. It turns out that in the limit \(t \rightarrow 1\) the folded integrable model associated with \({{\mathfrak {g}}}\) that we discuss in this paper becomes the Gaudin model associated with \(^L{{\mathfrak {g}}}\). Thus, in the Gaudin limit we do not find any new quantum integrable models. In part, this is because in this limit the irreducible finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\) decompose into a direct sum of irreducible representations of the finite-dimensional Lie algebra \({{\mathfrak {g}}}\), so the affine Langlands duality \({\widehat{{{\mathfrak {g}}}}}\rightarrow {}^L{\widehat{{{\mathfrak {g}}}}}\) reduces to the finite-dimensional Langlands duality \({{\mathfrak {g}}}\rightarrow {}^L{{\mathfrak {g}}}\), which was discovered in [12].
However, even in this limit, as we will show in Sect. 9, one can observe some intriguing effects related to folding. In particular, using the results of [13], we will construct embeddings of tensor products of irreducible representations of \(^L{{\mathfrak {g}}}\) into tensor products of the corresponding irreducible representations of \({{\mathfrak {g}}}'\) (see Theorem 9.5). In fact, it’s a family of embeddings depending on \(\chi \) (which is assumed to be regular and generic). It maps eigenvectors of the \(^L{{\mathfrak {g}}}\)-Gaudin model with the twist \(\chi \) to eigenvectors of the corresponding \({{\mathfrak {g}}}'\)-Gaudin model. Under a certain assumption (see Conjecture 9.10 in the case of a single irreducible representation) this embedding can be constructed explicitly.
1.8 Plan of the paper
In Sect. 2, we fix our notation for the Lie algebras and two-parameter Cartan matrices. In Sect. 3, we recall the definition of the deformed W-algebra  from [24]. We then consider its two classical limits. The first limit, \(t \rightarrow 1\), is relatively well understood; it can be identified with the Grothendieck ring of finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\) as we recall in Sect. 3.3. In Sect. 3.4 we obtain a description of the second limit, \(q \rightarrow 1\) (which was much less understood), analogous to the description of the \(t \rightarrow 1\) limit (see Propositions 3.2 and 3.3). In Sect. 4, we recall the relation between the \(t \rightarrow 1\) limit of the deformed W-algebra and the ring of q-characters of finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\). We then relate the \(q \rightarrow 1\) limit to what we call the ring of folded t-characters of finite-dimensional representations of \(U_t(\widehat{{\mathfrak {g}}'})\), where \({{\mathfrak {g}}}'\) is the simply laced Lie algebra from which \({{\mathfrak {g}}}\) is obtained as the Lie subalgebra fixed by an automorphism (see Theorem 4.3). We also discuss the link between this limit and the difference Drinfeld–Sokolov reduction. Finally, in Sect. 4.6 we introduce the folded Bethe Ansatz equations.
from [24]. We then consider its two classical limits. The first limit, \(t \rightarrow 1\), is relatively well understood; it can be identified with the Grothendieck ring of finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\) as we recall in Sect. 3.3. In Sect. 3.4 we obtain a description of the second limit, \(q \rightarrow 1\) (which was much less understood), analogous to the description of the \(t \rightarrow 1\) limit (see Propositions 3.2 and 3.3). In Sect. 4, we recall the relation between the \(t \rightarrow 1\) limit of the deformed W-algebra and the ring of q-characters of finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\). We then relate the \(q \rightarrow 1\) limit to what we call the ring of folded t-characters of finite-dimensional representations of \(U_t(\widehat{{\mathfrak {g}}'})\), where \({{\mathfrak {g}}}'\) is the simply laced Lie algebra from which \({{\mathfrak {g}}}\) is obtained as the Lie subalgebra fixed by an automorphism (see Theorem 4.3). We also discuss the link between this limit and the difference Drinfeld–Sokolov reduction. Finally, in Sect. 4.6 we introduce the folded Bethe Ansatz equations.
In Sect. 5, we describe the folded quantum integrable model in which the spectra of the Hamiltonians conjecturally correspond to solutions of the folded Bethe Ansatz equations (see Conjectures 5.15 and 5.16). In Sect. 6, we recall the interpolating (q, t)-characters from [18], which may be viewed as commutative algebra analogues of elements of the non-commutative W-algebra  . We then construct a refined version of the interpolating (q, t)-characters. They are elements of a ring depending on the parameters q and t, which is equipped with 5 interesting specialization homomorphisms to the rings of q- and t-characters of various affine Kac–Moody algebras related to \({{\mathfrak {g}}}\) (see Theorem 6.6). In Sect. 6.5, we partially prove our conjectures in the important case of \(\sigma \)-fundamental representations (these are the irreducible finite-dimensional representations of \(U_q(\widehat{{{\mathfrak {g}}}'})\) with the \(\sigma \)-invariant highest monomials of smallest possible degrees). In Sect. 7, we present a number of explicit examples confirming our Conjectures 5.15 and 5.16. In Sect. 8, we formulate a conjecture linking the folded t-characters to Kashiwara’s extension of Nakajima’s monomial model of crystals to non-simply laced Lie algebras. In Sect. 9, we consider the Gaudin limit of the folded quantum integrable models. In the “Appendix” we discuss a possible construction of a folded version of the qKZ equations for non-simply laced Lie algebras.
. We then construct a refined version of the interpolating (q, t)-characters. They are elements of a ring depending on the parameters q and t, which is equipped with 5 interesting specialization homomorphisms to the rings of q- and t-characters of various affine Kac–Moody algebras related to \({{\mathfrak {g}}}\) (see Theorem 6.6). In Sect. 6.5, we partially prove our conjectures in the important case of \(\sigma \)-fundamental representations (these are the irreducible finite-dimensional representations of \(U_q(\widehat{{{\mathfrak {g}}}'})\) with the \(\sigma \)-invariant highest monomials of smallest possible degrees). In Sect. 7, we present a number of explicit examples confirming our Conjectures 5.15 and 5.16. In Sect. 8, we formulate a conjecture linking the folded t-characters to Kashiwara’s extension of Nakajima’s monomial model of crystals to non-simply laced Lie algebras. In Sect. 9, we consider the Gaudin limit of the folded quantum integrable models. In the “Appendix” we discuss a possible construction of a folded version of the qKZ equations for non-simply laced Lie algebras.
2 Notation and setup
2.1 Lie algebra
Let \({{\mathfrak {g}}}\) be a simple Lie algebra of rank \(\ell \) and \(I = \{ 1,\ldots ,\ell \}\) the set of vertices of the Dynkin diagram of \({{\mathfrak {g}}}\). Let \((\cdot ,\cdot )\) be the invariant inner product on \({{\mathfrak {g}}}\), normalized so that the square of the maximal root equals 2. Let \(\{ \alpha _1,\ldots ,\alpha _\ell \}\) and \(\{ \omega _1,\ldots ,\omega _\ell \}\) be the sets of simple roots and of fundamental weights of \({{\mathfrak {g}}}\), respectively. We have:
Let d be the maximal number of edges connecting two vertices of the Dynkin diagram of \({{\mathfrak {g}}}\). Thus, \(d=1\) for simply laced \({{\mathfrak {g}}}\), \(d=2\) for \(B_\ell , C_\ell , F_4\), and \(d=3\) for \(G_2\). We set \(\epsilon = e^{i\pi /d}\).
Set
where
All \(d_i\)’s are integers, which are relatively prime with each other. For simply laced \({{\mathfrak {g}}}\), D is the identity matrix.
Now let \(C = (C_{ij})_{1\le i,j\le \ell }\) be the Cartan matrix of \({{\mathfrak {g}}}\). We have:
Denote by \((I_{ij})_{1\le i,j\le \ell }\) the incidence matrix,
Let \(B= (B_{ij})_{1\le i,j\le \ell }\) be the following matrix:
i.e.,
The weights \(\rho \) and \(\rho ^\vee \) are defined by \((\rho ^\vee ,\alpha _i) = 1\), \(d(\rho ,\alpha _i) = d_i\) for any \(1\le i\le \ell \).
2.2 Lie algebras involved
We list here all Lie algebras involved in our study:
-
\({{\mathfrak {g}}}\) is a simple finite-dimensional Lie algebra.
-
\(^L{{\mathfrak {g}}}\) is its Langlands dual Lie algebra. For example, if \({{\mathfrak {g}}}=B_\ell \), then \(^L{{\mathfrak {g}}}=C_\ell \).
-
\({\widehat{{{\mathfrak {g}}}}}\) is the untwisted affine Kac–Moody algebra, which is the central extension of \({{\mathfrak {g}}}[t,t^{-1}]\). For example, if \({{\mathfrak {g}}}=B_\ell \), then \({\widehat{{{\mathfrak {g}}}}}= B_\ell ^{(1)}\).
-
\(\widehat{^L{{\mathfrak {g}}}}\) is the untwisted affine Kac–Moody algebra, which is the central extension of \(^L{{\mathfrak {g}}}[t,t^{-1}]\). For example, if \({{\mathfrak {g}}}=B_\ell \), then \(\widehat{^L{{\mathfrak {g}}}} = C_\ell ^{(1)}\).
-
\(^L{\widehat{{{\mathfrak {g}}}}}\) is the affine Kac–Moody algebra that is affine Langlands dual to \({\widehat{{{\mathfrak {g}}}}}\). If \({{\mathfrak {g}}}\) is simply laced, then \(^L{\widehat{{{\mathfrak {g}}}}}= {\widehat{{{\mathfrak {g}}}}}\). But if \({{\mathfrak {g}}}\) is non-simply laced, then \(^L{\widehat{{{\mathfrak {g}}}}}\) is a twisted affine Kac–Moody algebra. Note that \(^L{\widehat{{{\mathfrak {g}}}}}\) contains \(^L{{\mathfrak {g}}}\) as the constant Lie subalgebra. For example, if \({{\mathfrak {g}}}=B_\ell \), then \(^L{\widehat{{{\mathfrak {g}}}}}= A_{2\ell -1}^{(2)}\) (whose constant subalgebra is \(^L{{\mathfrak {g}}}= C_\ell \)); and if \({{\mathfrak {g}}}=C_\ell \), then \(^L{\widehat{{{\mathfrak {g}}}}}= D_{\ell +1}^{(2)}\) (whose constant subalgebra is \(^L{{\mathfrak {g}}}= B_\ell \)).
-
\({{\mathfrak {g}}}'\) is the unique simply laced Lie algebra equipped with an automorphism \(\sigma \) of order d such that the Lie subalgebra of \(\sigma \)-invariants in \({{\mathfrak {g}}}'\) is \({{\mathfrak {g}}}\) (i.e. \({{\mathfrak {g}}}=({{\mathfrak {g}}}')^\sigma \)). For example, if \({{\mathfrak {g}}}=B_\ell \), then \({{\mathfrak {g}}}'=D_{\ell +1}\); and if \({{\mathfrak {g}}}=C_\ell \), then \({{\mathfrak {g}}}'=A_{2\ell -1}\).
-
\({\widehat{{{\mathfrak {g}}}}}^\vee \) is \({\widehat{{{\mathfrak {g}}}}}\), if \({{\mathfrak {g}}}\) is simply laced. If \({{\mathfrak {g}}}\) is non-simply laced, then \({\widehat{{{\mathfrak {g}}}}}^\vee \) is the twisted affine Kac–Moody algebra corresponding to \({{\mathfrak {g}}}'\) and \(\sigma \). Note that its constant Lie subalgebra is \({{\mathfrak {g}}}\) itself. For example, \((B_\ell ^{(1)})^\vee = D_{\ell +1}^{(2)}\) (its constant subalgebra is \(B_\ell \)), and \((C_\ell ^{(1)})^\vee = A_{2\ell -1}^{(2)}\) (its constant subalgebra is \(C_\ell \)). Note also that we have \({\widehat{{{\mathfrak {g}}}}}^\vee = {}^L(\widehat{^L{{\mathfrak {g}}}})\).
It might be better to denote \({\widehat{{{\mathfrak {g}}}}}^\vee \) by \({{\mathfrak {g}}}'{}^{(d)}\), but we will use below the notation \({\widehat{{{\mathfrak {g}}}}}^\vee \) because it was used in [24].
Let us denote by \(I'\) the set of vertices of the Dynkin diagram of \({{\mathfrak {g}}}'\). Then, \(\sigma \) acts on \(I'\) and the quotient is in bijection with the set I of vertices of the Dynkin diagram of I. Note that the automorphism \(\sigma \) of the Dynkin diagram of \({{\mathfrak {g}}}'\) acts on the objects labeled by the nodes of this diagram (such as simple roots, fundamental weights, etc.).
2.3 Two-parameter Cartan matrices
We follow the notation of [24], Sect. 2, except that we replace q by \(q^{-1}\) (however, for \(t=1\) this notation is consistent with the notation of [25]).
Now let q, t be nonzero complex numbers which are not roots of unity. We will use the standard notation for \(n\in {\mathbb {Z}}\)
Let
We define \(\ell \times \ell \) matrices C(q, t), D(q, t), and \(B(q,t)\) by the formulas
Thus,
It is easy to see that the matrix \(B(q,t)\) is symmetric. For simply laced \({{\mathfrak {g}}}\),
We note that the determinants of these matrices are nonzero polynomials in q and t. Hence, they are invertible over the field of rational functions in q and t.
Clearly, the limits of C(q, t), D(q, t), and \(B(q,t)\) as both \(q \rightarrow 1\) and \(t \rightarrow 1\) coincide with C, D, and \(B\), respectively. We also have
and
Let \(C(q) = C(q,1)\). It is invertible over the field of rational functions in q. We denote its inverse by \(\widetilde{C}(q)\).
3 Deformed W-algebras and screening operators
In this section, we recall the definition of the deformed W-algebra  and related objects from [24]. We will then look at the two classical limits \(t \rightarrow 1\) and \(q \rightarrow 1\), which are defined as the intersections of the kernels of two sets of classical screening operators. The \(t \rightarrow 1\) limit was described in [22, 24, 25] and is closely related to the Grothendieck ring \({\text {Rep}} U_q({\widehat{{{\mathfrak {g}}}}})\) and the corresponding q-characters (as we recall in the next section). A new result of this section is the analogous description of the \(q \rightarrow 1\) limit (see Propositions 3.2 and 3.3).
and related objects from [24]. We will then look at the two classical limits \(t \rightarrow 1\) and \(q \rightarrow 1\), which are defined as the intersections of the kernels of two sets of classical screening operators. The \(t \rightarrow 1\) limit was described in [22, 24, 25] and is closely related to the Grothendieck ring \({\text {Rep}} U_q({\widehat{{{\mathfrak {g}}}}})\) and the corresponding q-characters (as we recall in the next section). A new result of this section is the analogous description of the \(q \rightarrow 1\) limit (see Propositions 3.2 and 3.3).
3.1 Heisenberg algebra 
Let  be the Heisenberg algebra with generators \(a_i[n], i=1,\ldots ,\ell ; n \in {{\mathbb {Z}}}\), and relations
be the Heisenberg algebra with generators \(a_i[n], i=1,\ldots ,\ell ; n \in {{\mathbb {Z}}}\), and relations
where \(1\le i,j\le \ell ;n,m\in {{\mathbb {Z}}}{\setminus }\{0\}\).
Here and in what follows, it is understood that the 0th generator commutes with all other generators: \([a_i[0],a_j[m]] = 0\), for all \(m \in {{\mathbb {Z}}}\).
The algebra  becomes commutative in the limit \(q \rightarrow 1\) and in the limit \(t\rightarrow 1\).
becomes commutative in the limit \(q \rightarrow 1\) and in the limit \(t\rightarrow 1\).
The generators \(a_i[n]\) are “root” type generators of  . There is a unique set of “fundamental weight” type generators, \(y_i[n], i=1,\ldots ,\ell ; n \in {{\mathbb {Z}}}\), that satisfy:
. There is a unique set of “fundamental weight” type generators, \(y_i[n], i=1,\ldots ,\ell ; n \in {{\mathbb {Z}}}\), that satisfy:
They have the following commutation relations:
where \((M_{ij}(q,t))_{1\le i,j\le \ell }\) is the following matrix
We have
We will use the colon notation for the standard normally ordered product of elements of this algebra. Introduce the generating series
Recall that \((\rho ^\vee ,\alpha _i) = 1, d(\rho ,\alpha _i) = d_i\).
Formula (3.5) implies that
Thus, for \({\mathfrak {g}}\) of non-simply laced type, the two classical limits of \(A_i(z)\) are quite different: When \(t \rightarrow 1\), we have
but when \(q \rightarrow 1\), we have a much simpler expression
Remark 3.1
(1) The first limit (3.9) coincides with the monomial \(A_{i,z}\) which appears in the theory of q-characters of finite-dimensional representations of quantum affine algebras introduced in [25]. This is not surprising because, as explained in [25] and in Sect. 4.1, the q-characters may be viewed as limits of the fields from \({\mathbf{W}}_{q,t}\) as \(t \rightarrow 1\).
(2) There is a surprising connection between the second limit (3.10) and Kashiwara’s extension to non-simply laced \({{\mathfrak {g}}}\) [38] of Nakajima’s monomial model for crystals of \(U_t({{\mathfrak {g}}})\) [51]. Let us recall that Nakajima’s monomial realization was originally motivated by its relation with the q-characters in the symmetric cases. It turned out that this crystal realization was a consequence of the embedding theorem [36], which makes sense in the symmetrizable case [38]. But the relation between the monomial model and the q-characters was lost for non-simply laced types. Here we suggest an analogous relation, in which the role of the \(t \rightarrow 1\) classical limit of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) (whose free field realization is essentially the same as the q-character homomorphism, see Remark 4.1) is played by the \(q \rightarrow 1\) classical limit.
Recall that in the monomial model the vertices of the crystal are represented by certain monomials in the variables \(Y_i(t^k)^{\pm 1}\), and the crystal operators are obtained by multiplying them with some special monomials corresponding to the simple roots. In the simply laced case, these are the monomials \(A_{i,a}^{\pm 1}\) occurring in the q-character theory (as in formula (3.9)). But in the non-simply laced case the monomials \(A_{i,a}^{\pm 1}\) in formula (3.9) do not work. Instead, as explained in [38], we have to replace these monomials \(A_{i,a}^{\pm 1}\) with other monomials. A direct comparison shows that Kashiwara’s monomials coincide with the monomials in the above formula (3.10). We formulate a precise conjecture about this in Sect. 8 below. \(\square \)
3.2 Screening operators and definition of 
Recall that we have two sets of screening operators introduced in [24]: \(S^+_i(z)\) and \(S^-_i(z)\), \(i=1,\ldots ,\ell \). They satisfy the difference equations:
and
The deformed W-algebra  was defined in [24] as the intersection of kernels of the residues \(S^+_i\) of \(S^+_i(z), i \in I\), or of the residues \(S^-_i\) of \(S^-_i(z), i \in I\).
was defined in [24] as the intersection of kernels of the residues \(S^+_i\) of \(S^+_i(z), i \in I\), or of the residues \(S^-_i\) of \(S^-_i(z), i \in I\).
More precisely,  was defined in [24] as the associative topological algebra depending on two parameters q and t, which is topologically generated by the Fourier coefficients of certain fields from a deformed chiral algebra \({{\mathbf {W}}}_{q,t}({\mathfrak {g}})\). The latter was defined in [24] as the maximal subalgebra commuting with the screening operators \(S_i^\pm , i \in I\), in a deformed chiral algebra \({\mathbf{H}}_{q,t}({\mathfrak {g}})\) constructed from the Heisenberg algebra
was defined in [24] as the associative topological algebra depending on two parameters q and t, which is topologically generated by the Fourier coefficients of certain fields from a deformed chiral algebra \({{\mathbf {W}}}_{q,t}({\mathfrak {g}})\). The latter was defined in [24] as the maximal subalgebra commuting with the screening operators \(S_i^\pm , i \in I\), in a deformed chiral algebra \({\mathbf{H}}_{q,t}({\mathfrak {g}})\) constructed from the Heisenberg algebra  .
.
In the classical limits \(t \rightarrow 1\) (resp. \(q \rightarrow 1\)), \({\mathbf{H}}_{q,t}({\mathfrak {g}})\) becomes commutative:
The corresponding classical limit of \({\mathbf{W}}_{q,t}({\mathfrak {g}})\) is a commutative subalgebra of this polynomial algebra, which is equal to the intersection of the kernels of the classical screening operators \(S^+_i\) (resp. \(S^-_i\)), \(i \in I\).
We will call these limits as the classical W-algebras and denote them by  and
and  , respectively. Below we describe both of these algebras. We will see that they are quite different if \({{\mathfrak {g}}}\) is non-simply laced.
, respectively. Below we describe both of these algebras. We will see that they are quite different if \({{\mathfrak {g}}}\) is non-simply laced.
3.3 The \(t \rightarrow 1\) limit
In the limit \(t \rightarrow 1\), the family \(S^+_i, i \in I\), survives and gives rise to the following derivations:
acting by the formula
The following isomorphism was proved in [25, Proposition 6] and [22, Proposition 5.2]:
where \(A_i(z)\) is given by formula (3.9).
Now set

Thus,  is the \(t \rightarrow 1\) limit of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\). The following theorem was proved in [22, Theorem 5.1].
is the \(t \rightarrow 1\) limit of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\). The following theorem was proved in [22, Theorem 5.1].
Theorem 3.1
-
(1)
The commutative algebra
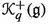 is isomorphic to \({\text {Rep}}_z U_q({\widehat{{{\mathfrak {g}}}}})\), the Grothendieck ring of the tensor subcategory
is isomorphic to \({\text {Rep}}_z U_q({\widehat{{{\mathfrak {g}}}}})\), the Grothendieck ring of the tensor subcategory  of the category of finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\) whose objects are representations with the Jordan–Hölder constituents having Drinfeld polynomials with roots in \(q^{{\mathbb {Z}}}\).
of the category of finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\) whose objects are representations with the Jordan–Hölder constituents having Drinfeld polynomials with roots in \(q^{{\mathbb {Z}}}\). -
(2)
Under this isomorphism, the embedding
 becomes the q-character homomorphism.
becomes the q-character homomorphism.
From Theorem 3.1, we obtain a natural basis of  consisting of the q-characters of simple modules from
consisting of the q-characters of simple modules from  . It is known that these are parametrized by dominant monomials, i.e. monomials in the variables \(Y_j(zq^{n_j})\), \(j \in I\), \(n_j\in {\mathbb {Z}}\), with only non-negative powers. In particular, the elements of this basis corresponding to the degree one dominant monomials \(Y_j(zn^j)\) coincide with the q-characters of the corresponding fundamental representations (those are known to contain a unique dominant monomial, see [25, Corollary 4,(1)]).
. It is known that these are parametrized by dominant monomials, i.e. monomials in the variables \(Y_j(zq^{n_j})\), \(j \in I\), \(n_j\in {\mathbb {Z}}\), with only non-negative powers. In particular, the elements of this basis corresponding to the degree one dominant monomials \(Y_j(zn^j)\) coincide with the q-characters of the corresponding fundamental representations (those are known to contain a unique dominant monomial, see [25, Corollary 4,(1)]).
3.4 The \(q \rightarrow 1\) limit
Now consider the limit \(q \rightarrow 1\). Then, it is the family \(S^-_i, i \in I\), that survives and gives rise to the derivations
acting by the formula
where \(A_i(z) = Y_i(zt) Y_i(zt^{-1}) Y_j(z)^{-I_{ji}}\) (formula (3.10)).
We have the following analogue of the isomorphism (3.15) (it is equivalent to (3.15) if \({{\mathfrak {g}}}\) is simply laced, but for a non-simply laced Lie algebra \({{\mathfrak {g}}}\) this statement is new, as far as we know).
Proposition 3.2
We have
where \(A_i(z) = Y_i(zt) Y_i(zt^{-1}) \prod _{j \ne i} Y_j(z)^{-I_{ji}}\,(\)formula (3.10)).
The proof is obtained by applying the argument used in the proof of (3.15) in [22, Proposition 5.2].
Now set

Thus,  is the \(q \rightarrow 1\) limit of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\).
is the \(q \rightarrow 1\) limit of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\).
Unlike the limit \(t \rightarrow 1\) (see Theorem 3.1), for non-simply laced \({{\mathfrak {g}}}\) we do not have an identification of  with the Grothendieck ring of a category of representation. Nonetheless, we do have a basis in
with the Grothendieck ring of a category of representation. Nonetheless, we do have a basis in  analogous to the basis of the q-characters of simple modules in
analogous to the basis of the q-characters of simple modules in  .
.
Proposition 3.3
-
(1)
Every element of
 is characterized by the multiplicities of the dominant monomials contained in it (i.e. monomials in the \(Y_{j,t^{n_j}}\), \(j \in I\), \(n_j\in {\mathbb {Z}}\), with only non-negative powers).
is characterized by the multiplicities of the dominant monomials contained in it (i.e. monomials in the \(Y_{j,t^{n_j}}\), \(j \in I\), \(n_j\in {\mathbb {Z}}\), with only non-negative powers). -
(2)
For every dominant monomial m, there is a unique element F(m) of
 such that m is the unique dominant monomial of F(m). Therefore, we obtain a basis \(\{ F(m) \}\) of
such that m is the unique dominant monomial of F(m). Therefore, we obtain a basis \(\{ F(m) \}\) of  parametrized by dominant monomials m.
parametrized by dominant monomials m.
Proof
The proof is the same as the proof in [28, Theorem 5.13]. All that remains is to check the existence of the \(F(Y_i(zq^n))\) for rank 2 Lie algebras. For simply laced types, this is true because we can use the ordinary q-characters of the fundamental representations. For type \(B_2\), we find the following elements:
and for type \(G_2\) we find
This completes the proof, up to the fact that the algorithm may produce elements \(F(Y_i(zq^n))\) with an infinite number of terms. But it follows from Theorem 4.3 that the elements \(F(Y_i(zq^n))\) can also be obtained as folded q-characters of fundamental representations of \(U_q(\widehat{{\mathfrak {g}}'})\), which do have finite numbers of terms. \(\square \)
It follows from Proposition 3.3 that we have natural analogues \(F(Y_i(zt^n))\) of the q-characters of the fundamental representations. We also have natural analogues of q-characters of the Kirillov–Reshetikhin modules (see Sect. 4.1).
Remark 3.2
This discussion motivates the following natural question: Is there a Hopf algebra  (an analogue of \(U_t({\widehat{{{\mathfrak {g}}}}})\)) together with an injective (t-character) homomorphism
(an analogue of \(U_t({\widehat{{{\mathfrak {g}}}}})\)) together with an injective (t-character) homomorphism

where  is a subring of the Grothendieck ring of the category of finite-dimensional representations of
is a subring of the Grothendieck ring of the category of finite-dimensional representations of  , whose image is
, whose image is  ?
?
It is tempting to try to answer this question using an automorphism \(\sigma \) of the quantum affine algebra \(U_t(\widehat{{{\mathfrak {g}}}'})\) defined by formula (5.2) below. The subalgebra \((U_t(\widehat{{{\mathfrak {g}}}'}))^\sigma \) of \(\sigma \)-invariants acts on every finite-dimensional representation V of \(U_t(\widehat{{{\mathfrak {g}}}'})\). However, it is not clear how to define a comultiplication on the algebra \((U_t(\widehat{{{\mathfrak {g}}}'}))^\sigma \). Hence, it is not clear how one could define a quantum integrable model this way. \(\square \)
3.5 The deformed W-algebra for general q and t
The structure of the deformed chiral algebra \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) for general values of q and t is much more complicated than that of its classical limits discussed above. Conjecture 1 of [24] implies that every basis element of  given by the q-character of a simple module over \(U_q({\widehat{{{\mathfrak {g}}}}})\) can be deformed to a basis element of \({\mathbf{W}}_{q,t}({{\mathfrak {g}}})\) (i.e. an element of \({{\mathbf {H}}}_{q,t}({{\mathfrak {g}}})\) which lies in the kernel of the screening operators).
given by the q-character of a simple module over \(U_q({\widehat{{{\mathfrak {g}}}}})\) can be deformed to a basis element of \({\mathbf{W}}_{q,t}({{\mathfrak {g}}})\) (i.e. an element of \({{\mathbf {H}}}_{q,t}({{\mathfrak {g}}})\) which lies in the kernel of the screening operators).
However, apart from a few explicit examples presented in [24], there is no proof of existence of these elements in general. On the other hand, in [18] a simplified, commutative version of  was introduced, called the space of interpolating (q, t)-characters. These are defined from certain subrings which are modeled on what we expect the kernels of the screening operators to be (based on the description of the kernels of screening operators associated with the ordinary q-characters). We will recall this construction, and add further details to it, in Sect. 6.
was introduced, called the space of interpolating (q, t)-characters. These are defined from certain subrings which are modeled on what we expect the kernels of the screening operators to be (based on the description of the kernels of screening operators associated with the ordinary q-characters). We will recall this construction, and add further details to it, in Sect. 6.
At the moment, the relation between the interpolating (q, t)-characters and the deformed W-algebra \({\mathbf{W}}_{q,t}({{\mathfrak {g}}})\) is conjectural. However, as we will see below, for our purposes the (q, t)-characters provide a good substitute for elements of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\).
4 Classical limits of the deformed W-algebra and q-characters
In this section, we first recall some details on the relation between the \(t \rightarrow 1\) limit of the deformed W-algebra and the q-characters of finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\). We then relate the \(q \rightarrow 1\) limit to what we call folded t-characters of finite-dimensional representations of \(U_t(\widehat{{\mathfrak {g}}'})\) (see Theorem 4.3).
4.1 Reminder on the q-characters of representations of quantum affine algebras
First, consider the untwisted quantum affine algebra \(U_q(\widehat{{\mathfrak {g}}})\). Let \({\text {Rep}} U_q(\widehat{\mathfrak {g}})\) be the Grothendieck ring of finite-dimensional representations of \(U_q(\widehat{\mathfrak {g}})\). The q-character homomorphism [25] is an injective ring homomorphism

If we replace each \(Y_{i,a}\) by \(y_i\), we recover the usual character homomorphism for the \(U_q(\mathfrak {g})\)-module obtained by restriction of \(U_q(\widehat{\mathfrak {g}})\)-module, which encodes its grading by the lattice of integral weights of a Cartan subalgebra of the Lie algebra \(\mathfrak {g}\). In what follows, we will refer to these integral weights as \(\mathfrak {g}\)-weights. In particular, each monomial in  has a \(\mathfrak {g}\)-weight.
has a \(\mathfrak {g}\)-weight.
It is proved in [22, 25] (see also Theorem 3.1 above) that
where
and \(A_{i,a}\) is defined by formula (3.9), where we replace \(Y_j(za)\) with \(Y_{j,a}\).
Remark 4.1
Note that in the context of deformed W-algebras, it is convenient to restrict ourselves to the variables \(Y_j(zq^{n_j}), n_j \in {{\mathbb {Z}}}\) (i.e. restrict ourselves to the multiplicative lattice of spectral parameters \(a = zq^n, n \in {{\mathbb {Z}}}\)). But in the context of q-characters, we usually consider all spectral parameters \(a \in {{\mathbb {C}}}^\times \) and denote the corresponding variables by \(Y_{j,a}\) (see [25, Sect. 7] for more detail).
In particular, comparing formulas (3.16) and (3.15) with formulas (4.1) and (4.2), respectively, we find that if we replace the variables \(Y_j(zq^{n_j}), n_j \in {{\mathbb {Z}}}\), by the variables \(Y_{j,a}, a \in {{\mathbb {C}}}^\times \), then  becomes \({\text {Im}}(\chi _q)\). That’s what we mean by the statement that the \(t \rightarrow 1\) limit of the free field realization of \({\mathbf{W}}_{q,t}({{\mathfrak {g}}})\) corresponds to the q-character homomorphism of \(U_q({\widehat{{{\mathfrak {g}}}}})\). \(\square \)
becomes \({\text {Im}}(\chi _q)\). That’s what we mean by the statement that the \(t \rightarrow 1\) limit of the free field realization of \({\mathbf{W}}_{q,t}({{\mathfrak {g}}})\) corresponds to the q-character homomorphism of \(U_q({\widehat{{{\mathfrak {g}}}}})\). \(\square \)
A monomial in  is called dominant if it is a product of positive powers of the \(Y_{i,a}, i\in I, a\in {\mathbb {C}}^\times \). A simple \(U_q(\widehat{\mathfrak {g}})\)-module is uniquely characterized by the highest monomial (in the sense of its \(\mathfrak {g}\)-weight) in its q-character (this monomial encodes the data of the Drinfeld polynomials; for the definition of the latter, see Theorem 12.2.6 of [6]). This monomial is dominant. An element of \(\text {Im}(\chi _q)\) is characterized by the multiplicities of its dominant monomials. A \(U_q(\widehat{\mathfrak {g}})\)-module is said to be affine-minuscule if its q-character has a unique dominant monomial.
is called dominant if it is a product of positive powers of the \(Y_{i,a}, i\in I, a\in {\mathbb {C}}^\times \). A simple \(U_q(\widehat{\mathfrak {g}})\)-module is uniquely characterized by the highest monomial (in the sense of its \(\mathfrak {g}\)-weight) in its q-character (this monomial encodes the data of the Drinfeld polynomials; for the definition of the latter, see Theorem 12.2.6 of [6]). This monomial is dominant. An element of \(\text {Im}(\chi _q)\) is characterized by the multiplicities of its dominant monomials. A \(U_q(\widehat{\mathfrak {g}})\)-module is said to be affine-minuscule if its q-character has a unique dominant monomial.
If a dominant monomial is in \(\mathbb {Z}[Y_{i,a}^{\pm 1}]_{i\in I, a\in q^{{\mathbb {Z}}}}\), then the q-character of the corresponding simple module also belongs to this subring.
A Kirillov–Reshetikhin (KR) module of \(U_q(\widehat{\mathfrak {g}})\) is a simple module with the highest monomial of the form \(Y_{i,a}Y_{i,aq_i^2}\cdots Y_{i,aq_i^{2(k-1)}}\) with \(a\in {\mathbb {C}}^\times \), \(i\in I\) and \(k\ge 0\).
It was proved in [29, 52] that the KR modules of \(U_q(\widehat{\mathfrak {g}})\) are affine-minuscule. For \(k=1\), that is for fundamental representations, this was proved in [22].
4.2 Twisted affine algebras
Next, consider the twisted quantum affine algebra \(U_t({}^L\widehat{\mathfrak {g}})\), and let \({\text {Rep}} U_t({}^L\widehat{\mathfrak {g}})\) be the Grothendieck ring of the category of its finite-dimensional representations.
The twisted t-character homomorphism [30] is an injective ring homomorphism
where we have set
These are the analogues of the \(d_i\) for the Langlands dual Lie algebra \({}^L\mathfrak {g}\).
As in the untwisted case, we have the notions of dominant monomials, affine-minuscule modules and KR modules. An element of \(\text {Im}(\chi _t)\) is again characterized by its dominant monomial and the KR modules of \(U_t({}^L\widehat{\mathfrak {g}})\) are affine-minuscule, as proved in [30].
If a dominant monomial is in \(\mathbb {Z}[Z_{i,a^{d_i^\vee }}^{\pm 1}]_{a\in \epsilon ^\mathbb {Z}t^\mathbb {Z}, i\in I}\), then the twisted t-character of the corresponding simple module also belongs to this subring.
The image of \(\chi _t\) is equal to
where
where we write \(i \sim j\) if \(I_{ij} \ne 0\) (recall that \((I_{ij})\) denotes the incidence matrix).
Note that a special definition should be used for the monomials \(B_{i,a}\) in the case of type \(A_{2n}^{(2)}\), but we are not considering this case here because this affine Kac–Moody algebra is not dual to an untwisted affine algebra (note that \(A_{2n}^{(2)}\) does not appear in Sect. 2.2).
According to Theorem 3.1, the \(t \rightarrow 1\) limit  of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) is isomorphic to \({\text {Rep}} U_q({\widehat{{{\mathfrak {g}}}}})\) so that the embedding of \({{\mathbf {W}}}_{q,1}({{\mathfrak {g}}})\) into \({{\mathbf {H}}}_{q,1}({{\mathfrak {g}}})\) becomes the q-character homomorphism.
of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) is isomorphic to \({\text {Rep}} U_q({\widehat{{{\mathfrak {g}}}}})\) so that the embedding of \({{\mathbf {W}}}_{q,1}({{\mathfrak {g}}})\) into \({{\mathbf {H}}}_{q,1}({{\mathfrak {g}}})\) becomes the q-character homomorphism.
Our task is to relate the \(q \rightarrow 1\) limit  of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) to t-characters of representations of quantum affine algebras. We start with two examples and then derive a general result. The upshot is that
of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) to t-characters of representations of quantum affine algebras. We start with two examples and then derive a general result. The upshot is that  is spanned by what we will call folded t-characters of \(U_t(\widehat{{{\mathfrak {g}}}'})\), where \({{\mathfrak {g}}}'\) is the simply laced Lie algebra equipped with an automorphism whose invariant Lie subalgebra is \({{\mathfrak {g}}}\) (the Dynkin diagram of \({{\mathfrak {g}}}\) can be obtained by folding the Dynkin diagram of \({{\mathfrak {g}}}'\)). These are the t-characters of the finite-representations of \(U_t(\widehat{{{\mathfrak {g}}}'})\) in which we identify the variables \(Y_i(z)\) and \(Y_{\sigma (i)}(z)\) for all \(i \in I'\).
is spanned by what we will call folded t-characters of \(U_t(\widehat{{{\mathfrak {g}}}'})\), where \({{\mathfrak {g}}}'\) is the simply laced Lie algebra equipped with an automorphism whose invariant Lie subalgebra is \({{\mathfrak {g}}}\) (the Dynkin diagram of \({{\mathfrak {g}}}\) can be obtained by folding the Dynkin diagram of \({{\mathfrak {g}}}'\)). These are the t-characters of the finite-representations of \(U_t(\widehat{{{\mathfrak {g}}}'})\) in which we identify the variables \(Y_i(z)\) and \(Y_{\sigma (i)}(z)\) for all \(i \in I'\).
4.3 Examples
Consider the case \({{\mathfrak {g}}}=B_\ell \). Then, we have the following formula for the element \(T_1(z)\) of \({{\mathbf {W}}}_{q,t}(B_\ell )\) corresponding to the first fundamental representation of \(U_q(B^{(1)}_\ell )\) (see [24], Sect. 5.1.2). Set
Here and below we set \(Y_0(z)=1\). According to [24],
commutes with the screening operators \(S^\pm _i, i=1,\ldots ,\ell \) and hence belongs to \({{\mathbf {W}}}_{q,t}(B_\ell )\).
The \(t \rightarrow 1\) limit of the rational function
is equal to 1. Hence, the limit of the above formula for \(T_1(z)\) as \(t \rightarrow 1\) has \(2\ell +1\) terms, and one can check that it coincides with the q-character of the first fundamental representation of \(U_q(B_\ell ^{(1)})\).
Now consider the \(q \rightarrow 1\) limit of (4.4). Note that \(f_\ell (1,t) = 2\), so in this limit the term \(\Lambda _0(z)\) appears with coefficient 2. As observed in [24, Sect. 6.3], the \(q \rightarrow 1\) limit of \(T_1(z)\) looks like the t-character of \(U_t(D_{\ell +1}^{(2)})\) in which we remove all \(\epsilon \) factors. For this reason, it was conjectured in [24, Sect. 6.3] that the \(q \rightarrow 1\) limit of the elements of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) in general (which are, by definition, elements of  ) should be given by the t-characters of finite-dimensional representations of \(U_t({\widehat{{{\mathfrak {g}}}}}^\vee )\) in which we remove the \(\epsilon \) factors (note that \(D_{\ell +1}^{(2)} = (B_\ell ^{(1)})^\vee \)).
) should be given by the t-characters of finite-dimensional representations of \(U_t({\widehat{{{\mathfrak {g}}}}}^\vee )\) in which we remove the \(\epsilon \) factors (note that \(D_{\ell +1}^{(2)} = (B_\ell ^{(1)})^\vee \)).
This conjecture is likely to be true, but the problem is that we don’t know how to interpret this removal of \(\epsilon \) factors in terms of representation theory, and therefore, this does not help us with constructing the corresponding integrable models. Hence, in this paper we give a different interpretation of this limit.
To explain it, let’s look more closely at the \(q \rightarrow 1\) limit of the formula (4.4) for \(T_1(z)\). This is an element of  given by the same formula (4.4), where now
given by the same formula (4.4), where now
Let’s compare this formula with the \(q \rightarrow 1\) limit of the formula for \(T_1(z)\) from \({{\mathbf {W}}}_{q,t}(D_{\ell +1})\) (see [24], Sect. 5.1.4). It is an element  given by formula (4.4) but now with
given by formula (4.4) but now with
By inspecting these formulas, we obtain the following result (recall that  is defined in formula (3.19)).
is defined in formula (3.19)).
Lemma 4.1
If we identify the generators \(Y_{\ell +1}(z)\) with \(Y_\ell (z)\) for \(D_{\ell +1}\), then the formula for \(T_1(z)\) in  becomes the formula for \(T_1(z)\) in
becomes the formula for \(T_1(z)\) in  .
.
Now observe that in this case \({{\mathfrak {g}}}=B_\ell \) and \({{\mathfrak {g}}}'=D_{\ell +1}\), with the corresponding automorphism \(\sigma \) exchanging the \(\ell \)th and the \((\ell +1)\)st nodes of the Dynkin diagram. Hence, the identification of Lemma 4.1 corresponds precisely to the folding of the Dynkin diagram of \(D_\ell \), which gives the Dynkin diagram of \(B_\ell \).
Let us apply the same procedure in the case \({{\mathfrak {g}}}=C_\ell \). Then, \({{\mathfrak {g}}}'=A_{2\ell -1}\) and \(\sigma \) exchanges the ith and the \(2\ell -i\)th nodes of the Dynkin diagram. Comparing formulas in Sects. 5.1.1 and 5.1.3 of [24], we obtain
Lemma 4.2
Let us identify the generators \(Y_{2\ell -i}(z), i=1,\ldots ,\ell -1\), with \(Y_i(z)\) for \(A_{2\ell -1}\). Then, the formula for \(T_1(z)\) in  becomes the formula for \(T_1(z)\) in
becomes the formula for \(T_1(z)\) in  .
.
4.4 General case
Formula (3.10) shows that if we impose the relations \(Y_i(z) = Y_{\sigma (i)}(z)\) for all \(i \in I'\), then the generators \(A_i(z), i \in I'\) of  go to the corresponding generators \(A_i(z), i \in I\), of
go to the corresponding generators \(A_i(z), i \in I\), of  . Here and below, abusing notation, we identify \(i \in I'\) with its image in \(I = I'/\langle \sigma \rangle \).
. Here and below, abusing notation, we identify \(i \in I'\) with its image in \(I = I'/\langle \sigma \rangle \).
Thus, we have natural commutative diagram

with the vertical maps being surjective and the horizontal maps being injective. This proves the following theorem stating that  is spanned by the t-characters of \(U_t(\widehat{{{\mathfrak {g}}}'})\) in which we identify \(Y_i(z)\) with \(Y_{\sigma (i)}(z)\).
is spanned by the t-characters of \(U_t(\widehat{{{\mathfrak {g}}}'})\) in which we identify \(Y_i(z)\) with \(Y_{\sigma (i)}(z)\).
Theorem 4.3
There is a surjective homomorphism  that fits in the commutative diagram
that fits in the commutative diagram

We will call the composition of the left vertical and the lower horizontal maps the folded t-character homomorphism and denote it by \(^{{\text {f}}}\chi _t\):
It extends naturally to the entire \({\text {Rep}} U_t(\widehat{{{\mathfrak {g}}}'})\). We will also call  the folded t-character ring.
the folded t-character ring.
Thus, we obtain an interpretation of the \(q \rightarrow 1\) limit  of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) as a “folding” of the Grothendieck ring of finite-dimensional representations of \(U_t(\widehat{{{\mathfrak {g}}}'})\).
of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) as a “folding” of the Grothendieck ring of finite-dimensional representations of \(U_t(\widehat{{{\mathfrak {g}}}'})\).
4.5 Connection to the Drinfeld–Sokolov reduction and the center of quantum affine algebra
In this subsection, we briefly discuss links between the classical limits of  and other (Poisson) algebras.
and other (Poisson) algebras.
First, Conjecture 3 of [24] states that the limit \(q \rightarrow 1\) of  is isomorphic, as a Poisson algebra, to the Poisson algebra obtained by the deformed Drinfeld–Sokolov reduction of G((z)) with parameter \(p=t^d\). This was confirmed by an explicit computations in the case of \({{\mathfrak {g}}}=C_2\) presented in “Appendix” B of [24].
is isomorphic, as a Poisson algebra, to the Poisson algebra obtained by the deformed Drinfeld–Sokolov reduction of G((z)) with parameter \(p=t^d\). This was confirmed by an explicit computations in the case of \({{\mathfrak {g}}}=C_2\) presented in “Appendix” B of [24].
Second, recall that the \(t \rightarrow 1\) limit of  is isomorphic, as a commutative algebra, to the center \(Z_q({\widehat{{{\mathfrak {g}}}}})\) of \(U_q({\widehat{{{\mathfrak {g}}}}})\) at the critical level. Indeed, we can associate elements of \(Z_q({\widehat{{{\mathfrak {g}}}}})\) with finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\) using a “double” of the transfer-matrix construction [23, 56], and hence connect \(Z_q({\widehat{{{\mathfrak {g}}}}})\) to \({\text {Rep}} U_q({\widehat{{{\mathfrak {g}}}}})\), which is
is isomorphic, as a commutative algebra, to the center \(Z_q({\widehat{{{\mathfrak {g}}}}})\) of \(U_q({\widehat{{{\mathfrak {g}}}}})\) at the critical level. Indeed, we can associate elements of \(Z_q({\widehat{{{\mathfrak {g}}}}})\) with finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\) using a “double” of the transfer-matrix construction [23, 56], and hence connect \(Z_q({\widehat{{{\mathfrak {g}}}}})\) to \({\text {Rep}} U_q({\widehat{{{\mathfrak {g}}}}})\), which is  . In [23], it was shown that in the case of \({{\mathfrak {g}}}=A_\ell \) this is in fact an isomorphism of Poisson algebra. We expect this to be true for a general \({{\mathfrak {g}}}\) as well.
. In [23], it was shown that in the case of \({{\mathfrak {g}}}=A_\ell \) this is in fact an isomorphism of Poisson algebra. We expect this to be true for a general \({{\mathfrak {g}}}\) as well.
If there exists an algebra  satisfying the properties of Remark 3.2, then it is reasonable to expect that the center of
satisfying the properties of Remark 3.2, then it is reasonable to expect that the center of  at its “critical level” is isomorphic to the \(q \rightarrow 1\) limit of
at its “critical level” is isomorphic to the \(q \rightarrow 1\) limit of  .
.
Remark 4.2
Note that the limit of \(Z_q({\widehat{{{\mathfrak {g}}}}})\) as \(q \rightarrow 1\) is the center of \(U({\widehat{{{\mathfrak {g}}}}})\) at the critical level. According to the Feigin–Frenkel isomorphism, the latter is isomorphic to the classical W-algebra of the Langlands dual Lie algebra \(^L{{\mathfrak {g}}}\) (and not of \({{\mathfrak {g}}}\)). This is consistent with the fact that in the \(q \rightarrow 1\) limit the screening operators \(S^+_i\), whose joint kernel is the Poisson algebra  , become the screening operators of the classical W-algebra of \(^L{{\mathfrak {g}}}\). \(\square \)
, become the screening operators of the classical W-algebra of \(^L{{\mathfrak {g}}}\). \(\square \)
4.6 Bethe Ansatz equations from deformed W-algebras
First, consider the limit \(t \rightarrow 1\), in which we obtain the algebra of q-characters of finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\). In [25, Sect. 6.3], it was shown how to derive the corresponding Bethe Ansatz equation (BAE) from these q-characters. Namely, according to the conjecture in [25, Sect. 6.1], which was proved in [19], the eigenvalues of the transfer-matrices on the representation \(W = \bigotimes _{j=1}^N V({{\mathbf {P}}}_j)\) can be expressed (up to an overall factor) as the q-characters in which we replace the variables \(Y_{i,a}\) by the ratios \(Q_i(aq_i^{-1})/Q_i(aq_i)\) of the corresponding Baxter polynomials. Then, the seeming poles corresponding to the monomials of the form M and \(M A_{i,aq_i}^{-1}\) in the q-characters should cancel each other. Using formula (3.9), we obtain the following BAE:
where \(\{ w^{(i)}_k \}\) is the set of roots of the ith Baxter polynomial \(Q_i(z)\), and \(P_{j,i}(z), j=1,\ldots ,N; i=1,\ldots ,\ell \), are the Drinfeld polynomials of W.
Remark 4.3
This formula corrects a typo in formula (6.6) of [25]; namely, the entries \(C_{li}\) of the Cartan matrix there should be replaced by the entries \(B_{li}\) of the symmetrized Cartan matrix. \(\square \)
Thus, the key point in deriving these BAE is formula (3.9) expressing variables \(A_i(z)\) in terms of \(Y_j(z)\).
Now consider the limit \(q \rightarrow 1\) and apply the argument of [25, Sect. 6.3] to formula (3.10) instead of (3.9). In the same way as in [25], we then obtain the following equations:
This system is equivalent to the system of Bethe Ansatz equations obtained in [21] (formula (6.16)). It can also be obtained by folding the BAE corresponding to \({{\mathfrak {g}}}'\). See Sect. 1.2 for the explanation of the procedure of folding. We summarize this in the following statement.
Proposition 4.4
The system (4.8) corresponding to the Lie algebra \({{\mathfrak {g}}}\) is equivalent to the system obtained by folding the BAE (4.7) corresponding to the Lie algebra \({{\mathfrak {g}}}'\), i.e. assuming that \(m_i=m_{\sigma (i)}\) for all \(i \in I'\), identifying \(w^{(i)}_r \equiv w^{\sigma (i)}_r\), and writing the equations in terms of the variables \(w^{(i)}_r, i \in I\).
5 Folded integrable models
In this section, we describe a novel quantum integrable model in which the spectra of the Hamiltonians correspond (conjecturally) to solutions of the Bethe Ansatz equations (4.8).
5.1 Action of an automorphism \(\sigma \)
Let W be a simple finite-dimensional representation of \(U_q(\widehat{{{\mathfrak {g}}}'})\) whose highest monomial is \(\sigma \)-invariant, i.e. it is a monomial in the elements \(\widetilde{Y}_{i,a}\) defined in Sect. 6.1.Footnote 6 Denote the corresponding highest \({{\mathfrak {g}}}'\)-weight by \(\Lambda (W)\). Clearly, \(\sigma (\Lambda (W)) = \Lambda (W)\).
Denote by P the set of all \({{\mathfrak {g}}}'\)-weights and by \(P^\sigma \) its subset of \(\sigma \)-invariant \({{\mathfrak {g}}}'\)-weights. For \(\gamma \in P\), denote by \(W_\gamma \subset W\) the weight \(\gamma \) subspace of W. Let \(\widehat{W}\) be the direct sum of the subspaces of W corresponding to \(\sigma \)-invariant \({{\mathfrak {g}}}'\)-weights \(\gamma \):
In particular, \(\widehat{W}\) contains the one-dimensional highest weight subspace \(W_{\Lambda (W)}\) of W.
Next, let \(\widetilde{W}\subset W\) be the direct sum of \(\ell \)-weight subspaces of W corresponding to the \(\sigma \)-invariant \(\ell \)-weights (equivalently, \(\sigma \)-invariant monomials in \(\chi _q(W)\)). Associating with each \(\ell \)-weight the corresponding \({{\mathfrak {g}}}'\)-weight, we obtain a grading on \(\widetilde{W}\) by \(\sigma \)-invariant \({{\mathfrak {g}}}'\)-weights:
We have an inclusion \(\widetilde{W} \subset \widehat{W}\) respecting the grading by (\(\sigma \)-invariant) \({{\mathfrak {g}}}'\)-weights:
The restriction of this inclusion to \(\widetilde{W}_{\Lambda (W)}\) is an isomorphism. Next, we define an automorphism of \(U_q(\widehat{{{\mathfrak {g}}}'})\) corresponding to \(\sigma \) (abusing notation, we denote it in the same way).
Lemma 5.1
There is a unique algebra automorphism \(\sigma \) of \(U_q(\widehat{{{\mathfrak {g}}}'})\) defined on the Drinfeld generators by the formulas
Proof
One checks directly that the map \(\sigma \) preserves the relations between the Drinfeld generators. \(\square \)
We associate with W its twist by the automorphism \(\sigma \). Namely, if \(\rho : U_q(\widehat{{{\mathfrak {g}}}'}) \rightarrow {\text {End}}(W)\) is the action of \(U_q(\widehat{{{\mathfrak {g}}}'})\) on W, we define the \(\sigma \)-twisted action of \(U_q(\widehat{{{\mathfrak {g}}}'})\) on the same vector space by the formula
Lemma 5.2
-
(1)
The representations \((W,\rho )\) and \((W,\rho _\sigma )\) are isomorphic, and there is a unique linear automorphism \(\widehat{\sigma }: W\rightarrow W\), such that
$$\begin{aligned} \rho (\sigma (g)) = \widehat{\sigma }\rho (g) \widehat{\sigma }^{-1}, \qquad \forall g\in U_q(\widehat{{{\mathfrak {g}}}'}) \end{aligned}$$(5.3)and the restriction of \(\widehat{\sigma }\) to \(W_{\Lambda (W)}\) is the identity.
-
(2)
The operator \(\widehat{\sigma }\) maps every \({{\mathfrak {g}}}'\)-weight (resp. \(\ell \)-weight) subspace of W corresponding to the \({{\mathfrak {g}}}'\)-weight \(\gamma \) (resp. monomial M in \(Y_{i,a}\)) to a \({{\mathfrak {g}}}'\)-weight (resp. \(\ell \)-weight) subspace corresponding to \(\sigma (\gamma )\) (resp. \(\sigma (M)\)). In particular, it preserves the subspaces \(\widehat{W}\) and \(\widetilde{W}\) and their graded components corresponding to \(\sigma \)-invariant \({{\mathfrak {g}}}'\)-weights and \(\ell \)-weights, respectively.
Proof
-
(1)
Drinfeld’s classification of irreducible finite-dimensional representations of \(U_q(\widehat{{{\mathfrak {g}}}'})\) (see [6]) shows that such a representation W is generated by its one-dimensional highest weight subspace \(W_\Lambda \) and is determined by the eigenvalues of the Cartan–Drinfeld generators \(h_{i,r}\) on it, which are recorded by the highest monomial of its q-character (see Sect. 4.1). Formulas (5.2) imply that \(W_\Lambda \) is still the highest weight subspace of W under the twisted representation \(\rho _\sigma \). The \(\sigma \)-invariance of the highest monomial of the representation \((W,\rho )\) implies that the highest monomial of \((W,\rho _\sigma )\) is the same. Therefore, there is an isomorphism \(\widehat{\sigma }: W \rightarrow W\) intertwining the representations \((W,\rho )\) and \((W,\rho _\sigma )\) of \(U_q(\widehat{{{\mathfrak {g}}}'})\) and preserving the one-dimensional subspace \(W_\Lambda \). It follows that \(\widehat{\sigma }\) satisfies formula (5.3). By Schur’s lemma, there is a unique such \(\widehat{\sigma }\) that is equal to the identity on \(W_\Lambda \).
-
(2)
Let \(\{ X_i, i \in I' \}\) be either \(\{ k_i, i \in I' \}\) or \(\{ h^{{\text {ss}}}_{i,r}, i \in I' \}\) with a fixed \(r \ne 0\), where \(h^{{\text {ss}}}_{i,r}\) is the semi-simplification of the action of \(h_{i,r}\) on W. Suppose that v is a joint eigenvector of \(\{ X_i, i \in I' \}\), in W with the eigenvalues \(\lambda _i, i \in I'\). Then
$$\begin{aligned} X_i \cdot \widehat{\sigma }(v) = \widehat{\sigma }(\widehat{\sigma }^{-1} X_i \widehat{\sigma })\cdot v = \widehat{\sigma }X_{\sigma ^{-1}(i)} \cdot v = \lambda _{\sigma ^{-1}(i)} \widehat{\sigma }(v). \end{aligned}$$(5.4)This completes the proof.
\(\square \)
Remark 5.1
Let \(W^{\widehat{\sigma }}\subset W\) be the subspace of vectors fixed by \(\widehat{\sigma }\). It contains \(W_{\Lambda (W)}\) and is stable under the action of the subalgebra \(U_q(\widehat{{{\mathfrak {g}}}'})^\sigma \) of \(\sigma \)-invariant elements of \(U_q(\widehat{{{\mathfrak {g}}}'})\). However, in general \(W^{\widehat{\sigma }}\) is not stable under the action of the Cartan generators \(k_i^{\pm 1}, i \in I'\) or the Cartan–Drinfeld generators, and hence does not have a well-defined character or q-character. Besides, the invariant subalgebra \(U_q(\widehat{{{\mathfrak {g}}}'})^\sigma \) does not have a natural structure of Hopf algebra and has other deficiencies, as can be shown by an argument similar to that of [30, Section 2.7].
This is why we consider instead the subspaces \(\widehat{W}\) and \(\widetilde{W}\). Their graded subspaces are preserved by \(\widehat{\sigma }\), and hence \(\widehat{W}\) and \(\widetilde{W}\) have well-defined character and q-character, respectively. \(\square \)
5.2 XXZ-type model associated with \(U_q(\widehat{{\mathfrak {g}}}')\)
Consider the Borel subalgebra \(U_q(\widehat{{{{\mathfrak {b}}}}}')\) of \(U_q(\widehat{{{\mathfrak {g}}}'})\) and its category  which contains the prefundamental representations \(R_j^+(a)\), \(R_j^-(a)\) (\(j\in I'\), \(a\in {\mathbb {C}}^\times \)) constructed in [33].
which contains the prefundamental representations \(R_j^+(a)\), \(R_j^-(a)\) (\(j\in I'\), \(a\in {\mathbb {C}}^\times \)) constructed in [33].
For every \(j \in I'\), we have the Q-operator \(Q_j^\pm (z,u) = t_{R_j^\pm }(z,u)\) associated in [19] with the prefundamental representation \(R_j^\pm (z)\). This operator is a formal power series in z, and it also depends on an element u of the Cartan subgroup \(H'\) of the simply connected Lie group \(G'\) associated with \({{\mathfrak {g}}}'\).
More generally, for any V in the Grothendieck ring  , we have the corresponding transfer-matrix \(t_V(z,u)\).
, we have the corresponding transfer-matrix \(t_V(z,u)\).
The transfer-matrices  (in particular, operators \(Q_j^\pm (z,u), j \in I'\)) commute with each other. These are the Hamiltonians of the XXZ-type model associated to \(U_q(\widehat{{\mathfrak {g}}}')\). Every finite-dimensional representation W of \(U_q(\widehat{{{\mathfrak {g}}}'})\) decomposes into a direct sum of the generalized eigenspaces of these Hamiltonians. In this paper, we will focus on the eigenvalues of these Hamiltonians and ignore the structure of the corresponding Jordan blocks. Hence, we introduce the semi-simplification \(Q^{\pm , {\text {ss}}}_i(z,u)\) of \(Q_i^\pm (z,u)\), i.e., the unique diagonalizable operator on W whose eigenspaces and eigenvalues are the generalized eigenspaces and eigenvalues of \(Q_i^\pm (z,u)\). It follows that each \(Q^{{\text {ss}},\pm }_i(z,u)\) can be expressed as a polynomial in the original operator \(Q_i^\pm (z,u)\), and therefore, \(Q^{\pm , {\text {ss}}}_i(z,u)\) commutes with all \(Q_j^\pm (z,u)\) and with all \(Q^{\pm , {\text {ss}}}_j(z,u), j \in I'\).
(in particular, operators \(Q_j^\pm (z,u), j \in I'\)) commute with each other. These are the Hamiltonians of the XXZ-type model associated to \(U_q(\widehat{{\mathfrak {g}}}')\). Every finite-dimensional representation W of \(U_q(\widehat{{{\mathfrak {g}}}'})\) decomposes into a direct sum of the generalized eigenspaces of these Hamiltonians. In this paper, we will focus on the eigenvalues of these Hamiltonians and ignore the structure of the corresponding Jordan blocks. Hence, we introduce the semi-simplification \(Q^{\pm , {\text {ss}}}_i(z,u)\) of \(Q_i^\pm (z,u)\), i.e., the unique diagonalizable operator on W whose eigenspaces and eigenvalues are the generalized eigenspaces and eigenvalues of \(Q_i^\pm (z,u)\). It follows that each \(Q^{{\text {ss}},\pm }_i(z,u)\) can be expressed as a polynomial in the original operator \(Q_i^\pm (z,u)\), and therefore, \(Q^{\pm , {\text {ss}}}_i(z,u)\) commutes with all \(Q_j^\pm (z,u)\) and with all \(Q^{\pm , {\text {ss}}}_j(z,u), j \in I'\).
Thus, for every \(u \in H'\), we have a direct sum decomposition of W into joint eigenspaces of the operators \(Q^{\pm ,{\text {ss}}}_j(z,u), j \in I'\). The following is proved in [19, Theorem 5.9] and [20].
Theorem 5.3
Let W be a simple module over \(U_q(\widehat{{{\mathfrak {g}}}'})\). Then,
-
(1)
The eigenvalues of \(Q^{+,{\text {ss}}}_j(z,u)\) on W are polynomials in z, up to an overall function in z depending only on W. Generically, the roots of these polynomials yield a solution of the BAE (4.7) corresponding to \({{\mathfrak {g}}}'\).
-
(2)
Every joint eigenspace of \(Q^{\pm , {\text {ss}}}_j(z,u), j \in I'\), on W is a subspace of a \({{\mathfrak {g}}}'\)-weight subspace of W corresponding to the \({{\mathfrak {g}}}'\)-weight \(\Lambda (W) - \sum _{j \in I'} n_j \alpha _j\), where \(n_j\) is the degree of the Baxter polynomial encoding the eigenvalue of \(Q^{+,{\text {ss}}}_j(z,u)\).
We call the polynomials in part (1) of this theorem the Baxter polynomials.
Part (1) of the theorem implies that the decomposition of W into a direct sum of joint eigenspaces of \(Q^{\pm , {\text {ss}}}_j(z,u), j \in I'\), is a refinement of the decomposition of W into a direct sum of its \({{\mathfrak {g}}}'\)-weight subspaces. In other words, for every \(u \in H'\) and \(\gamma \in P\) (the set of \({{\mathfrak {g}}}'\)-weights), the corresponding component \(W_\gamma \) of W is a direct sum

where  is the set of distinct joint eigenvalues of \(Q^{\pm , {\text {ss}}}_j(z,u), j \in I'\), on \(W_\gamma \), and \(W_{\gamma ,\lambda }(u)\) is the eigenspace corresponding to
is the set of distinct joint eigenvalues of \(Q^{\pm , {\text {ss}}}_j(z,u), j \in I'\), on \(W_\gamma \), and \(W_{\gamma ,\lambda }(u)\) is the eigenspace corresponding to  . Here, \(\lambda \) denotes a collection \(\{ \lambda _j^{\pm }(z,u), j \in I' \}\) of joint eigenvalues of \(Q^{\pm , {\text {ss}}}_j(z,u), j \in I'\)
. Here, \(\lambda \) denotes a collection \(\{ \lambda _j^{\pm }(z,u), j \in I' \}\) of joint eigenvalues of \(Q^{\pm , {\text {ss}}}_j(z,u), j \in I'\)
As shown in [19, Proposition 5.5], \(Q_j^+(z,u)\) has a well-defined \(u \rightarrow 0\) limit, which is equal to
This is a generating series of the Cartan–Drinfeld generators
According to this formula, we can recover all Cartan–Drinfeld generators \(h_{k,-m}, k\in I', m > 0\) from the \(T_j(z), j \in I'\).
It follows that the set  has a well-defined \(u \rightarrow 0\) limit, which we denote by
has a well-defined \(u \rightarrow 0\) limit, which we denote by  . Moreover,
. Moreover,  can be identified with the set of \(\ell \)-weights with the underlying \({{\mathfrak {g}}}'\)-weight \(\gamma \). For each \(\ell \)-weight
can be identified with the set of \(\ell \)-weights with the underlying \({{\mathfrak {g}}}'\)-weight \(\gamma \). For each \(\ell \)-weight  , the eigenspace \(W_{\gamma ,\lambda }(0)\) is the corresponding \(\ell \)-weight subspace of \(W_\gamma \).
, the eigenspace \(W_{\gamma ,\lambda }(0)\) is the corresponding \(\ell \)-weight subspace of \(W_\gamma \).
Remark 5.2
The \(u \rightarrow 0\) limit of the Q-operator \(Q_j^-(z,u)\) is equal to \((T_j(z))^{-1}\). This follows from a direct computation or from the decomposition of \(R_{i,a}^+\otimes R_{i,a}^-\) in  . Indeed, it is equal to the class [1] of the trivial one-dimensional representation plus the classes of simple representations whose highest weights are equal to positive linear combinations of the simple roots, which implies that they do not contribute to the \(u\rightarrow 0\) limit. \(\square \)
. Indeed, it is equal to the class [1] of the trivial one-dimensional representation plus the classes of simple representations whose highest weights are equal to positive linear combinations of the simple roots, which implies that they do not contribute to the \(u\rightarrow 0\) limit. \(\square \)
5.3 The invariant subspace
Let us apply the automorphism \(\sigma \) of the algebra \(U_q(\widehat{{{\mathfrak {g}}}'})\) given by formula (5.2) to the transfer-matrices \(t_V(z,u)\). Recall that they are constructed by taking the trace of u times the universal R-matrix  of \(U_q(\widehat{{{\mathfrak {g}}}'})\) over V (see, e.g. [19]).
of \(U_q(\widehat{{{\mathfrak {g}}}'})\) over V (see, e.g. [19]).
Lemma 5.4
The automorphism \(\sigma \) is an automorphism of the Hopf algebra structure on \(U_q(\widehat{{{\mathfrak {g}}}'})\). Moreover, it preserves the universal R-matrix  of \(U_q(\widehat{{{\mathfrak {g}}}'})\):
of \(U_q(\widehat{{{\mathfrak {g}}}'})\):  .
.
Proof
One checks directly that the comultiplication defined on the Drinfeld–Jimbo generators is invariant under \(\sigma \). For the ith Drinfeld–Jimbo generators, where \(i \in I'\), this is obvious. For the 0th Drinfeld–Jimbo generators, we use a formula expressing them in terms of the Drinfeld generators from [6, p. 393].
The universal R-matrix of \(U_q(\widehat{{{\mathfrak {g}}}'})\) corresponds to the canonical element in the double of \(U_q({{{\mathfrak {b}}}}_+)\) under the identification of this double (modulo the Cartan subalgebra with \(U_q(\widehat{{{\mathfrak {g}}}'})\)), see [9]. It follows from its definition that the automorphism \(\sigma \) is compatible with the double structure and therefore it sends the canonical element to itself. Hence, it preserves the universal R-matrix of \(U_q(\widehat{{{\mathfrak {g}}}'})\). \(\square \)
For any representation V in the category  , denote by \(\sigma ^*(V)\) the twist of V by the automorphism \(\sigma \) defined as in Sect. 5.1. It is clear that \(\sigma ^*\) induces an automorphism of the Grothendieck ring
, denote by \(\sigma ^*(V)\) the twist of V by the automorphism \(\sigma \) defined as in Sect. 5.1. It is clear that \(\sigma ^*\) induces an automorphism of the Grothendieck ring  . By construction, \(\sigma ^*(R^\pm _{j,a}) \simeq R^\pm _{\sigma (j),a}\). Note also that \(\sigma \) defines an automorphism of the Cartan subgroup \(H'\) of \(G'\).
. By construction, \(\sigma ^*(R^\pm _{j,a}) \simeq R^\pm _{\sigma (j),a}\). Note also that \(\sigma \) defines an automorphism of the Cartan subgroup \(H'\) of \(G'\).
Lemma 5.5
We have
From now on, we will assume that u is \(\sigma \)-invariant, and hence defines an element of \(H = (H')^\sigma \), which is a Cartan subgroup of the group \(G = (G')^\sigma \). With this assumption, formulas (5.7) become
Now we come to a key definition.
Definition 5.6
We define the invariant subspace of W as
where \(P^\sigma \) is the set of \(\sigma \)-invariant \({{\mathfrak {g}}}'\)-weights and
Since the prefundamental representations (topologically) generate the entire Grothendieck ring  , we have
, we have

Using formula (5.8) in the same way as in the proof of Lemma 5.2, we obtain the following result.
Lemma 5.7
\(W_\gamma (u)\) is preserved by \(\widehat{\sigma }\).
We can also describe \(W_\gamma (u)\) as a span of joint eigenvectors of \(Q_j^{\pm ,{\text {ss}}}(z,u), j \in I'\).
Lemma 5.8
\(W_\gamma (u)\) is equal to the span of the joint eigenvectors of \(Q_j^{\pm ,{\text {ss}}}(z,u), j \in I'\), in \(W_\gamma \) with eigenvalues \(\lambda _j^{\pm }(z,u), j \in I'\), such that \(\lambda _j^{\pm }(z,u) = \lambda _{\sigma (j)}^{\pm }(z,u)\) for all \(j \in I'\). In other words, in the notation of Sect. 5.2,
Proof
Every vector \(v \in W_\gamma \) can be written as a linear combination of joint eigenvectors of \(Q_j^{\pm ,{\text {ss}}}(z,u), j \in I'\):
where \(v_\lambda \) denotes an eigenvector with the collection of joint eigenvalues \(\lambda = \{ \lambda _j^{\pm }(z,u), j \in I' \}\). Now, if \(v \in W_\gamma (u)\), then
which implies that every collection \(\lambda = \{ \lambda _j^{\pm }(z,u), j \in I' \}\) appearing in the decomposition (5.11) with a nonzero coefficient \(a_\lambda \) must be \(\sigma \)-invariant, i.e. \(\lambda _j^{\pm }(z,u) = \lambda _{\sigma (j)}^{\pm }(z,u)\) for all \(j \in I'\). \(\square \)
Now, the discussion after Theorem 5.3 implies
Lemma 5.9
We have \(W_\gamma (0) = \widetilde{W}_\gamma \), i.e. \(W_\gamma (0)\) is spanned by the \(\ell \)-weight vectors corresponding to the \(\sigma \)-invariant \(\ell \)-weights whose underlying \({{\mathfrak {g}}}'\)-weight is \(\gamma \in P^\sigma \).
Remark 5.3 shows, however, that we do not expect the statement analogous to Lemma 5.9 to hold for \(W_\gamma (u)\) with \(u \ne 0\).
Lemma 5.7 implies that W(u) is preserved by \(\widehat{\sigma }\). Lemma 5.9 implies that \(W(0) = \widetilde{W}\). We also record the following useful result.
Lemma 5.10
Suppose that \(v \in W\) is an eigenvector of \(Q_j^{\pm ,{\text {ss}}}(z,u), j \in I'\) (resp. an \(\ell \)-weight vector) such that \(\widehat{\sigma }(v) = \mu v\), where \(\mu \) is a scalar (thus, \(\mu \) is a d-th root of unity). Then, the set of eigenvalues of \(Q_j^{\pm ,{\text {ss}}}(z,u), j \in I'\) on v (resp. the \(\ell \)-weight of v) is \(\sigma \)-invariant.
Proof
Let \(\lambda ^\pm _j(z,u), j \in I'\), be the eigenvalues of \(Q_j^{\pm ,{\text {ss}}}(z,u), j \in I'\) on v. Using formulas (5.8) and (5.3), we obtain that
for all \(j \in I'\). The proof for \(\ell \)-weight vectors is similar. \(\square \)
Remark 5.3
In general, joint eigenspaces of the operators \(Q^{\pm , {\text {ss}}}_j(z,u), j \in I'\), in \(W_\gamma \) are not spanned by \(\ell \)-weight vectors. In other words, these eigenspaces differ from their limits as \(u \rightarrow 0\). For example, let us take as W the tensor product \(V_1\otimes V_a\) of two fundamental representations of \(U_q(\widehat{sl}_2)\) with the highest weight monomial \(Y_1 Y_a\). The \(\ell \)-weight vectors in it are computed for example in [31, Example 3.3]. Let \(\{ w_+,w_- \}\) and \(\{ v_+,v_- \}\) be bases of weight vectors in \(V_1\) and \(V_a\), respectively, with \(w_+\) and \(v_+\) being the highest weight vectors. Then, \(w_-\otimes v_+\) is an \(\ell \)-weight vector whose \(\ell \)-weight is \(Y_{q^2}^{-1}Y_{a}\).
On the other hand, the action of \(Q^+(z,u)\) on the 0-weight subspace of \(V_1\otimes V_a\), which is spanned by \(w_- \otimes v_+\) and \(w_+ \otimes v_-\), can be computed following [19, Example 7.8]. The result is
where T(z) is the \(u \rightarrow 0\) limit of \(Q^+(z,u)\), which can be expressed (see formula (5.6) above) as a generating function of the Cartan–Drinfeld elements, and \(f_1\), \(f_0\) are the Drinfeld–Jimbo generators.
In particular, if we denote by g(z) the eigenvalue of T(z) on \(w_+\otimes v_+\), then we obtain
Hence, \(w_-\otimes v_+\) is not an eigenvector of \(Q^+(z,u)\) if \(u\ne 0\). \(\square \)
5.4 Eigenvalues of transfer-matrices on the invariant subspace
Since the operators \(Q^{\pm , {\text {ss}}}_j(z,u), j \in I'\), commute with each other, they have a well-defined joint spectrum on the invariant subspace W(u). Using Proposition 4.4 (the fact that the system of folded BAE (4.8) for \({{\mathfrak {g}}}\) is obtained by folding of the system of BAE (4.7) for \({{\mathfrak {g}}}'\)) and Theorem 5.3, we can now link the eigenvalues of \(Q^{\pm , {\text {ss}}}_j(z,u), j \in I'\), on W(u) and solutions of the folded BAE (4.8) for \({{\mathfrak {g}}}\).
Theorem 5.11
Suppose that the Baxter polynomials encoding the joint eigenvalues of \(Q^{+, {\text {ss}}}_j(z,u)\), \(j \in I'\), on a vector in W(u) are generic, so that their roots satisfy the BAE (4.7) for \({{\mathfrak {g}}}'\). Then, after the identification of the roots of these polynomials corresponding to \(Q^{+, {\text {ss}}}_j(z,u)\) and \(Q^{+, {\text {ss}}}_{\sigma (j)}(z,u)\), we obtain a solution of the folded BAE (4.8).
Next, the following result is proved in [19, Theorem 5.11]:
Theorem 5.12
The eigenvalues of the transfer-matrix \(t_V(z,u)\), where V is in \({\text {Rep}} U_q(\widehat{{{\mathfrak {g}}}'})\), on a simple module W can be expressed (up to an overall factor) as the q-character of V, in which we replace each \(Y_{i,a}, i \in I\), by a ratio of the corresponding Baxter polynomials.
We now use this result to describe the eigenvalues of \(t_V(z,u)\) on \(W(u) \subset W\).
Theorem 5.13
Let V be a finite-dimensional representation of \(U_q(\widehat{{{\mathfrak {g}}}'})\). Then, the transfer-matrix \(t_V(z,u)\) preserves the subspace W(u) and its generalized eigenvalues are given (up to an overall factor) by the folded t-character \(^{{\text {f}}}\chi _t(V)\) (obtained by identifying \(Y_{i,a}\) with \(Y_{\sigma (i),a}\) in \(\chi _t(V)\)) in which we further replace each \(Y_{i,a}\) by a ratio of the corresponding Baxter polynomials.
This theorem gives us the sought-after link between the spectra of commuting quantum Hamiltonians and solutions of the folded Bethe Ansatz equations. Namely, the quantum Hamiltonians are the transfer-matrices \(t_V(z,u)\) of the XXZ-type model associated with \(U_q(\widehat{{{\mathfrak {g}}}'})\) (so the auxiliary spaces are representations of \(U_q(\widehat{{{\mathfrak {g}}}'})\), or more general objects of the corresponding category  ), but we restrict them to the invariant subspaces W(u) of the irreducible finite-dimensional representations W of \(U_q(\widehat{{{\mathfrak {g}}}'})\) and consider the corresponding spectra (so the spaces of states are the subspaces \(W(u) \subset W\)).
), but we restrict them to the invariant subspaces W(u) of the irreducible finite-dimensional representations W of \(U_q(\widehat{{{\mathfrak {g}}}'})\) and consider the corresponding spectra (so the spaces of states are the subspaces \(W(u) \subset W\)).
However, for non-simply laced \({{\mathfrak {g}}}\) this answer does not quite define a quantum integrable model since we have not yet described the invariant subspaces W(u) as representations of a Hopf algebra. In the next subsection, we conjecture such a description. More precisely, we conjecture that there is a certain distinguished subspace \(\overline{W}(u) \subset W(u)\) which is isomorphic to a representation of the twisted quantum affine algebra \(U_q({}^L{\widehat{{{\mathfrak {g}}}}})\). If this is true, then we can indeed describe the spaces of states as representations of a Hopf algebra, and then we indeed obtain a quantum integrable model.
5.5 Defining the folded integrable model
As before, let W be a simple representation of \(U_q(\widehat{{{\mathfrak {g}}}'})\) whose highest monomial is \(\sigma \)-invariant, i.e. it is a monomial in the elements \(\widetilde{Y}_{i,a}\) defined in Sect. 6.1.
Recall that for a Lie algebra \({{\mathfrak {g}}}\), we refer to the integral weights of the Cartan subalgebra of \({{\mathfrak {g}}}\) as \({{\mathfrak {g}}}\)-weights. We will use the following simple fact demonstrated below in Sect. 9.1:
Lemma 5.14
There is a natural isomorphism between the lattice \(P^\sigma \) of \(\sigma \)-invariant \({{\mathfrak {g}}}'\)-weights and the lattice \(^LP\) of \(^L{{\mathfrak {g}}}\)-weights.
In particular, since W(u) and \(\widetilde{W} = W(0)\) are, by definition, vector spaces graded by \(P^\sigma \), we can view them as vector spaces graded by the lattice \(^LP\) of \(^L{{\mathfrak {g}}}\)-weights.
Conjecture 5.15
-
(i)
For generic u, there is an isomorphism \(W(u) \simeq \widetilde{W}\) of vector spaces graded by \(^L{{\mathfrak {g}}}\)-weights.
-
(ii)
For generic u, there is a subspace \({\overline{W}}(u)\) of W(u) which is stable under the operators \(Q^{\pm ,{\text {ss}}}_j(z,u)\) and isomorphic, as a vector space graded by \({}^L{{\mathfrak {g}}}\)-weights, to the vector space underlying a \(U_q({}^L{\widehat{{{\mathfrak {g}}}}})\)-module M(W) (which does not depend on u).
In Sect. 7, we explicitly verify this conjecture, as well as Conjecture 5.16, in a number of examples. In Sect. 6.5, we identify the representation M(W), in terms of the closely related Conjecture 5.16, for the simplest \(U_q(\widehat{{{\mathfrak {g}}}'})\)-modules with \(\sigma \)-invariant highest monomials (modulo Conjecture 6.11).
Remark 5.4
A possible candidate for \(\overline{W}(u)\) is the subspace \({\mathbf{W}}(u) := \bigoplus _{\gamma \in P^\sigma } {\mathbf{W}}_\gamma (u)\), where
The difference with formula (5.9) is that we now consider the operators \(Q_j^\pm (z,u)\), rather than their semi-simplifications. We expect that for generic u, \({\mathbf{W}}(u)\) is isomorphic to \({\mathbf{W}}(0) \subset W(0) = \widetilde{W}\), which is defined similarly in terms of \(T_j(z)\) (not their semi-simplifications).
Another candidate for \(\overline{W}(u)\) is the subspace \({\mathbf{W}}^\sigma (u) \subset {\mathbf{W}}(u)\) spanned by the \(\sigma \)-invariant generalized eigenvectors. \(\square \)
Conjecture 5.15 means that for any non-simply laced simple Lie algebra \({\mathfrak {g}}\), there exists a folded quantum integrable system with the quantum Hamiltonians being the transfer-matrices \(t_V(z,u)\), corresponding to finite-dimensional representations V of \({\text {Rep}} U_t(\widehat{{{\mathfrak {g}}}'})\), or more general objects of the corresponding category  (these are the auxiliary spaces of this integrable model). These Hamiltonians act on vector spaces that underlie finite-dimensional representations of \(U_t({}^L{\widehat{{{\mathfrak {g}}}}})\) (these are the spaces of states of this integrable model) and, according to Theorem 5.13, the spectra of \(t_V(z,u)\) can be expressed in terms of the folded t-character of V and the corresponding Baxter polynomials. Moreover, by Theorem 5.11, the roots of these Baxter polynomials correspond to solutions of the folded BAE (4.8) associated with \({{\mathfrak {g}}}\).
(these are the auxiliary spaces of this integrable model). These Hamiltonians act on vector spaces that underlie finite-dimensional representations of \(U_t({}^L{\widehat{{{\mathfrak {g}}}}})\) (these are the spaces of states of this integrable model) and, according to Theorem 5.13, the spectra of \(t_V(z,u)\) can be expressed in terms of the folded t-character of V and the corresponding Baxter polynomials. Moreover, by Theorem 5.11, the roots of these Baxter polynomials correspond to solutions of the folded BAE (4.8) associated with \({{\mathfrak {g}}}\).
Remark 5.5
-
(1)
In all examples we have studied so far, with W a simple module, we found a simple \(U_q({}^L{\widehat{{{\mathfrak {g}}}}})\)-module M(W) that satisfies the statements of this conjecture.
-
(2)
Suppose that a weight subspace \(\widehat{W}_\gamma , \gamma \in P^\sigma \), of \(\widehat{W}\) is one-dimensional. Then, the automorphism \(\widehat{\sigma }\) from Lemma 5.2 must act on \(\widehat{W}_\gamma \) as a nonzero scalar. By Lemma 5.10, this implies that \(\widehat{W}_\gamma = \widetilde{W}_\gamma \) and \(\widehat{W}_\gamma = W_\gamma (u)\) for all u. Hence the statement of part (i) of the conjecture is clear for such weight subspaces.
-
(3)
In the statement of part (ii) of the conjecture, one might be tempted to replace \(U_t({}^L{\widehat{{{\mathfrak {g}}}}})\) with \(U_t(\widehat{^L{{\mathfrak {g}}}})\). Indeed, the statement involves a vector space \(\overline{W}(u)\) graded by \(^L{{\mathfrak {g}}}\)-weights, and therefore it could come from a representation of \(U_t({}^L{{\mathfrak {g}}})\) (the quantum group of the simple finite-dimensional Lie algebra \(^L{{\mathfrak {g}}}\)), which is a subalgebra of both \(U_t({}^L{\widehat{{{\mathfrak {g}}}}})\) and \(U_t(\widehat{^L{{\mathfrak {g}}}})\). In fact, in the examples we have considered so far (see Sect. 7), the character of \(\overline{W}(u)\) is not only the character of a representation of \(U_t({}^L{\widehat{{{\mathfrak {g}}}}})\) but also the character of a representation of \(U_t(\widehat{^L{{\mathfrak {g}}}}\)). But the representations of \(U_t(\widehat{^L{{\mathfrak {g}}}})\) that appear here are significantly less natural than the representations of \(U_t({}^L{\widehat{{{\mathfrak {g}}}}})\). For instance, as we illustrate below (see Sects. 7.2, 7.3, 7.4, 7.5), in most cases they are not simple, and often contain direct sums of copies of the trivial representation as direct summands (even for representations of small dimension). Even more importantly, if we consider representations of \(U_t(\widehat{^L{{\mathfrak {g}}}})\), we can only reproduce the ordinary character of its restriction to \(U_t({}^L{{\mathfrak {g}}})\), and not its t-character. On the other hand, in all examples we consider below, we can reproduce the t-character of a \(U_t({}^L{\widehat{{{\mathfrak {g}}}}})\)-module M(W) using interpolating (q, t)-characters, see Conjecture 5.16 below.
-
(4)
It would be interesting to write explicit formulas for the action of \(U_t({}^L{\widehat{{{\mathfrak {g}}}}})\) on M(W), at least in the cases when \(M(W) \simeq \widetilde{W}\).
\(\square \)
We will give a more detailed description of the module M(W), and hence a more precise formulation of Conjecture 5.15, using the theory of interpolating (q, t)-characters which we will recall (and refine) in Sect. 6. Namely, we have the following conjecture.
Conjecture 5.16
The t-character \(\chi _t(M(W))\) of the \(U_t\left( {}^L{\widehat{{{\mathfrak {g}}}}}\right) \)-module M(W) can be obtained via the specialization map \(\Pi _t\) from an element  . In fact, \(X_{q,t}\) has the following three specializations:
. In fact, \(X_{q,t}\) has the following three specializations:

where
-
 is the folded t-character of the \(U_t\left( \widehat{{\mathfrak {g}}'}\right) \)-module W,
is the folded t-character of the \(U_t\left( \widehat{{\mathfrak {g}}'}\right) \)-module W, -
 is the folded t-character of a \(U_t\left( \widehat{\left( {}^L{\mathfrak {g}}\right) '}\right) \)-module \(W'\).
is the folded t-character of a \(U_t\left( \widehat{\left( {}^L{\mathfrak {g}}\right) '}\right) \)-module \(W'\).
5.6 The subspace \(\overline{W}(u)\)
Here, we discuss the question of how to describe the subspace \({\overline{W}}(u)\subset W(u)\) in general.
Note that the fixed subspace \(W^{\widehat{\sigma }}\subset W\) is not necessarily stable under the action of the operators \(Q_j^{\pm ,{\text {ss}}}(z,u)\) in general. But let us introduce the subspace \(W^\sigma (u) \subset W^{\widehat{\sigma }}\) spanned by all joint eigenvectors of \(Q_j^{\pm ,{\text {ss}}}(z,u)\), \(j\in I'\), which belong to \(W^{\widehat{\sigma }}\).
Recall the decomposition (5.10) of \(W_\gamma (u)\):
Lemma 5.17
We have
where \(W^\sigma _{\gamma ,\lambda }(u)\) is the \(\widehat{\sigma }\)-invariant subspace of \(W_{\gamma ,\lambda }(u)\).
Proof
According to Theorem 5.3,(1), every joint eigenvector v of \(Q_j^{\pm ,{\text {ss}}}(z,u)\), \(j\in I'\), belongs to a weight subspace \(W_\gamma \subset W, \gamma \in P\). By Lemma 5.2,(2) \(\widehat{\sigma }\) maps \(W_\gamma , \gamma \in P\), to \(W_{\sigma (\gamma )}\). Therefore, if \(\widehat{\sigma }(v) = v\), then \(v \in W_\gamma , \gamma \in P^\sigma \). Next, we have the decomposition (5.5) of \(W_\gamma , \gamma \in P^\sigma \), into eigenspaces of \(Q_j^{\pm ,{\text {ss}}}(z,u)\). Applying formula (5.4) with \(X_i = Q_i^{\pm ,{\text {ss}}}(z,u)\), \(j\in I'\), we obtain that if \(v \in W_{\gamma ,\lambda }\), then \(\widehat{\sigma }(v) \in W_{\gamma ,\sigma (\lambda )}\). Hence, if \(\widehat{\sigma }(v) = v\), then \(\sigma (\lambda )=\lambda \). It follows that the subspace \(W_{\gamma ,\lambda }\) with \(\gamma \in P^\sigma \) and \(\sigma (\lambda )=\lambda \) is preserved by \(\widehat{\sigma }\). Thus, \(W_{\gamma ,\lambda }\) decomposes into a direct sum of eigenspaces of \(\widehat{\sigma }\), which are labeled by the d-th roots of unity. Denoting the invariant part (on which \(\widehat{\sigma }\) acts the identity) by \(W^\sigma _{\gamma ,\lambda }(u)\), we obtain the decomposition (5.14). \(\square \)
There is an analogue of the subspace \(W^\sigma (u) \subset W(u)\) for \(u=0\); namely, the subspace \(\widetilde{W}^\sigma \) spanned by all \(\widehat{\sigma }\)-invariant \(\ell \)-weight vectors in W. In the same way as in the proof of Lemma 5.17, one shows that
where \(\widetilde{W}^\sigma _{\gamma ,M}\) is \(\widehat{\sigma }\)-invariant part of the \(\ell \)-weight subspace of \(\widetilde{W}_\gamma , \gamma \in P^\sigma ,\) whose \(\ell \)-weight corresponds to a monomial M (note that \(\widetilde{W}^\sigma _{\gamma ,M}\) is preserved by \(\widehat{\sigma }\) if and only if M is a \(\sigma \)-invariant monomial, see Lemma 5.2,(2)). Thus, \(\widetilde{W}^\sigma \) is a subspace of \(\widetilde{W} = W(0)\).
We expect that \({\overline{W}}(u)\) is a subspace of \(\widetilde{W}^\sigma \) (although they are not equal in general, as we can see from the example in Sect. 7.5). In addition to the examples that will be presented in Sect. 7, some supporting evidence comes from the following result in the finite-type case.
Let W be a simple finite-dimensional representation of \(U_q({\mathfrak {g}}')\) with a \(\sigma \)-invariant highest weight. Then, as in the affine case, \(\sigma \) gives rise to an automorphism \(\widehat{\sigma }\) of W. Let \(W^\sigma \) be the span of all weight vectors in W which belong to \(W^{\widehat{\sigma }}\). In the same way, as in the proof of Lemma 5.17, one shows that
where \(W^\sigma _\gamma \) is the subspace of \(\widehat{\sigma }\)-invariant vectors in \(W_\gamma , \gamma \in P^\sigma \). Recall from Lemma 5.14 that we can view elements of the set \(P^\sigma \) of \(\sigma \)-invariant \({{\mathfrak {g}}}'\)-weight spaces as \(^{L}{\mathfrak {g}}\)-weights. Thus, the character \(\chi (W^\sigma )\) is a linear combination of \(^{L}{\mathfrak {g}}\)-weights.
Proposition 5.18
\(\chi (W^\sigma )\) is invariant under the action of the Weyl group of \(^L{{\mathfrak {g}}}\), and hence it is the character of a virtual representation of \(U_q({}^{L}{\mathfrak {g}})\).
Proof
For \(i \in I'\), denote by \(U_i\) the \(U_q({{\mathfrak {s}}}{{\mathfrak {l}}}_2)\) subalgebra of \(U_q({{\mathfrak {g}}}')\) generated by \(e_i\), \(f_i\), \(k_i^{\pm 1}\).
Let us show that \(\chi (W^\sigma )\) is invariant under the simple reflections of \(^{L}{\mathfrak {g}}\) associated with the \(\sigma \)-orbits of \(i\in I'\). This is clear if \(\sigma (i) = i\) as \(W^\sigma \) is stable under the action of \(U_i\) and hence its character is invariant under the ith reflection of \(^{L}{\mathfrak {g}}\).
Suppose \(\sigma (i)\ne i\). Since \({{\mathfrak {g}}}'\) is not of type \(A_{2n}\), the subalgebra \(U_i^\sigma \) of \(U_q({\mathfrak {g}}')\) generated by the \(U_q({{\mathfrak {s}}}{{\mathfrak {l}}}_2)\) subalgebras \(U_{\sigma ^k(i)}\), \(1\le k\le d\), is isomorphic to \(U_q({{\mathfrak {s}}}{{\mathfrak {l}}}_2)^{\otimes d}\). To simplify notation, let us assume that \(d = 2\) (the proof for \(d = 3\) is quite similar).
Viewed as a representation of \(U_i^\sigma \), W is semi-simple:
where \(L_j^{(1)}\) and \(L_j^{(2)}\) are simple representations of the subalgebras \(U_i\) and \(U_{\sigma (i)}\), respectively.
If x is a weight vector which belongs to \(W^\sigma \) (i.e. the weight of x is \(\sigma \)-invariant), then so are the vectors \({\overline{e}}.x\) and \({\overline{f}}.x\), where
Hence, \(W^\sigma \) is stable under \({\overline{e}}\) and \({\overline{f}}\).
Let \(\omega \) be a weight such that that the weight subspace \((W^\sigma )_\omega \) is nonzero. Then, \(\omega (\alpha _i^\vee ) = \omega (\alpha _{\sigma (i)}^\vee ) = m\in {\mathbb {Z}}\). Suppose that \(m\ge 0\). Using the decomposition (5.16), we can write any weight vector v in \((W^\sigma )_\omega \) as \(v = \sum _j v_j\), where
\((L^{(1)}_j)_m\) and \((L^{(2)}_j)_m\) being the weight subspaces corresponding to weight m in \(L^{(1)}_j\) and \(L^{(2)}_j\), respectively. From representation theory of \(U_q({{\mathfrak {s}}}{{\mathfrak {l}}}_2)\) we know that these weight subspaces are one-dimensional, so \(v_j = v_j^{(1)} \otimes v_j^{(2)}\) is a pure tensor. Moreover, we have
Hence, we obtain an injective linear map :
and so
if \(m\ge 0\).
The opposite inequality is obtained by considering the action of \(\overline{e}^m\) on \((W^\sigma )_{\omega - m(\alpha _i + \alpha _{\sigma (i)})}\). This completes the proof. \(\square \)
We expect that this virtual representation is an actual representation of \(U_q({}^{L}{\mathfrak {g}})\) (although it is not clear to us how to construct the corresponding action of \(U_q({}^{L}{\mathfrak {g}})\)). In Sect. 9.7, we will show (assuming Conjecture 9.10) that in the limit \(q \rightarrow 1\) it is possible to construct an explicit embedding of the irreducible representation of \(^L{{\mathfrak {g}}}\) with the highest weight corresponding to that of W (which is \(\sigma \)-invariant by our assumption) into \(W^\sigma \).
In the rest of this section, we discuss the corresponding QQ-system.
5.7 The QQ-system
The QQ-system (or \(Q\widetilde{Q}\)-system in the terminology of [20]) of type \(\widehat{{\mathfrak {g}}'}\) reads
where \(C'\) (resp. \(\alpha _i'\)) is the Cartan matrix (resp. a simple root) of \({\mathfrak {g}}'\). It was written in [45] in the context of affine opers, and established [20] as a system of relations in  , with the \(Q_{i,a}\) and \(\widetilde{Q}_{i,a}\) being the properly normalized classes of certain simple modules; namely, the module \(R_{i,a}^+\) for \(Q_{i,a}\) and another module, which we denote by \(X_{i,aq_i^{-2}}'\), divided by an invertible element which does not depend on a (recall that here we consider the category
, with the \(Q_{i,a}\) and \(\widetilde{Q}_{i,a}\) being the properly normalized classes of certain simple modules; namely, the module \(R_{i,a}^+\) for \(Q_{i,a}\) and another module, which we denote by \(X_{i,aq_i^{-2}}'\), divided by an invertible element which does not depend on a (recall that here we consider the category  , see [20, Remark 3.2 (iii)]). The \(\left[ -\frac{\alpha _i'}{2}\right] \) are classes of certain one-dimensional representations in
, see [20, Remark 3.2 (iii)]). The \(\left[ -\frac{\alpha _i'}{2}\right] \) are classes of certain one-dimensional representations in  . Then, on W(u), the eigenvalues of \(Q_{j,a}\) are identified with those of \(Q_{\sigma (j),a}\) and the eigenvalues of \(\widetilde{Q}_{i,a}\) are identified with the eigenvalues of \(\widetilde{Q}_{\sigma (j),a}\). Hence, we obtain the following result.
. Then, on W(u), the eigenvalues of \(Q_{j,a}\) are identified with those of \(Q_{\sigma (j),a}\) and the eigenvalues of \(\widetilde{Q}_{i,a}\) are identified with the eigenvalues of \(\widetilde{Q}_{\sigma (j),a}\). Hence, we obtain the following result.
Theorem 5.19
The following QQ-system holds on the invariant subspace W(u):
where C is the Cartan matrix of \({\mathfrak {g}}\), \(Q_{i,a}\) (resp. \(\widetilde{Q}_{i,a}\)) is, up to an invertible constant, the Q-operator \(Q_{i,a}^+\) (resp. the transfer-matrix associated with \(X_{i,aq_i^{-2}}\)).
Note that for a non-simply laced \({{\mathfrak {g}}}\), this is neither the QQ-system of type \(\widehat{{\mathfrak {g}}}\) (as defined in [20, 46]) nor the QQ-system of the twisted type \(\widehat{{\mathfrak {g}}}^\vee \) conjectured in [20, Section 3.3]. But this system is equivalent to the QQ-system obtained in [21] in the context of Miura (G, q)-opers (we note that a Yangian version of this system first appeared in the work of Mukhin and Varchenko [47, 48]). We will call it the folded QQ-system associated with \({{\mathfrak {g}}}\).
According to Theorem 5.19, the spectra of the Hamiltonians of the folded integrable model introduced in this section give rise to solutions of the folded QQ-system. This is in agreement with Theorem 5.11 because, as shown in [21], under a genericity condition there is a bijection between solutions of the folded QQ-system and solutions of the folded BAE (4.8).
Remark 5.6
-
(1)
Recall that each character \(\omega \in H^*\) of the commutative group H gives a one-dimensional representation \(U_q(\widehat{{\mathfrak {b}}})\)-module \([\omega ]\) which is in
 and in
and in  . We obtain a subring
. We obtain a subring  of representations whose simple constituents are of this form. These are called constant elements as the associated transfer-matrices are constant (independent of the spectral parameter). The ordinary character of a representation in
of representations whose simple constituents are of this form. These are called constant elements as the associated transfer-matrices are constant (independent of the spectral parameter). The ordinary character of a representation in  can be viewed as an element of \(K_0(H)\).
can be viewed as an element of \(K_0(H)\). -
(2)
According to [20], the precise relation between the solutions of \(Q\widetilde{Q}\)-system (5.17) and elements of
 is as follows. The variables \(Q_{i,z}\) and \(\widetilde{Q}_{i,z}\) correspond to the classes \([L_{i,z}^+]\) and \([X_{i,zq_i^{-2}}]\), respectively, renormalized by constant invertible elements of
is as follows. The variables \(Q_{i,z}\) and \(\widetilde{Q}_{i,z}\) correspond to the classes \([L_{i,z}^+]\) and \([X_{i,zq_i^{-2}}]\), respectively, renormalized by constant invertible elements of  . However, Keyu Wang has pointed out that the proof of [20, Lemma 4.11] is incomplete. In that lemma a formula \(\chi (X_{i,a}) = (1 - [-\alpha _i])^{-1}\prod _{j\ne i}\chi _j^{-C_{j,i}}\) for the character of \(X_{i,a}\) was given in terms of the characters \(\chi _i = \chi (L_{i,a}^+)\) of the prefundamental representations, and the normalization used in [20] (see the preceding paragraph) was based on this formula. Although we believe that this character formula is correct (and so the normalization used in [20] is correct), at the moment we do not have a proof of this character formula. Hence, we propose to slightly modify formulas (3.1) and (3.2) in [20] for the normalizing factors, so we can avoid relying on this character formula. We explain this normalization in the next subsection.
. However, Keyu Wang has pointed out that the proof of [20, Lemma 4.11] is incomplete. In that lemma a formula \(\chi (X_{i,a}) = (1 - [-\alpha _i])^{-1}\prod _{j\ne i}\chi _j^{-C_{j,i}}\) for the character of \(X_{i,a}\) was given in terms of the characters \(\chi _i = \chi (L_{i,a}^+)\) of the prefundamental representations, and the normalization used in [20] (see the preceding paragraph) was based on this formula. Although we believe that this character formula is correct (and so the normalization used in [20] is correct), at the moment we do not have a proof of this character formula. Hence, we propose to slightly modify formulas (3.1) and (3.2) in [20] for the normalizing factors, so we can avoid relying on this character formula. We explain this normalization in the next subsection. -
(3)
According to Theorem 5.19 and to Sect. 5.4, eigenvectors in the subspace W(u) give solutions of the folded QQ-system (or, under some genericity condition, of the folded BAE (4.8)). However, we then restrict to a smaller subspace \({\overline{W}}(u)\) of W(u), which means that we only take a subset of these solutions (we will see in the example in Sect. 7.5 that \({\overline{W}}(u)\) can in fact be strictly smaller than W(u)). This is likely related to the fact that taking various limits of elements of the deformed W-algebras, or various specializations of the corresponding interpolating (q, t)-characters (as discussed in Sect. 6), may very well have different numbers of monomials. Hence, it is natural to expect that there is a characterization of the solutions corresponding to the eigenvectors that belong to the subspace \({\overline{W}}(u)\) through a similar kind of interpolation, which would enable us to tell which solutions of the folded QQ-system (and the folded BAE) correspond to the representation M(W) for the Langlands dual quantum affine and which do not. At the moment, this remains as an open question.
\(\square \)
5.8 Normalization of \(Q_{i,z}\) and \(\widetilde{Q}_{i,z}\)
Proposition 5.20
The functions
where
solve the \(Q\widetilde{Q}\)-system (in the notation of [20]).
Remark 5.7
Here, in contrast to [20], we do not specify a precise relation between the \(\widetilde{\chi }_i\) and the \(\chi _i\). In addition, for symmetry, we have chosen to renormalize \([L_{i,z}^+]\) by dividing by \(\chi _i\), although in [20] \(Q_{i,z}\) is \([L_{i,z}^+]\) without renormalization. Both normalizations are compatible, as the \(Q\widetilde{Q}\)-system written with the normalization in [20] implies that the variables in the Proposition above satisfy also the \(Q\widetilde{Q}\)-system. \(\square \)
Proof
We give the proof of the proposition for the category  . The analogous result in
. The analogous result in  is obtained in the same way.
is obtained in the same way.
We establish the following q-character formula
where \(\widetilde{\varvec{\Psi }}_{i,1}\) is the highest \(\ell \)-weight of \(X_{i,1}\) and \(\chi _{i,1} = \sum _{m\ge 0}(A_{i,1}A_{i,q_i^{-2}}\cdots A_{i,q_i^{-2m}})^{-1}\). This formula implies the \(Q\widetilde{Q}\)-system in  by the arguments given in [20].
by the arguments given in [20].
The proof of (5.18) is based on the results in [20], except that we do not use the complete proof of [20, Lemma 4.11], but only [20, Lemma 4.10]. Indeed, it implies only
where for \(m\ge 0\), \(\chi (m)\in K_0(H)\) is a constant element. It suffices to prove that \(\chi (m)\) do not depend on m.
To do this, consider for \(r\ge 0\) the representation \(X_{i,1}^{(r)} = L(\widetilde{\varvec{\Psi }}_{i,1} \varvec{\Psi }_{i,q_i^{-2r}})\). Then, we obtain from [32, Theorem 8.1] that
Hence, the class of \(X_{i,1}\otimes L_{i,q_i^{-2r}}^+\) can be decomposed as a sum
where \(\chi _r'\in K_0(H)\) is an invertible constant, the \(n_{\varvec{\Psi }'}\) are positive integers and the \(\ell \)-weight \(\varvec{\Psi }'\) which occur in the sum are, up to a constant, of the form
for some \(m \ge 0\). We claim that only \(\ell \)-weights \(\varvec{\Psi }'\) with \(m\ge r\) can occur, that is the class of \(L(\widetilde{\varvec{\Psi }}_{i,1} \varvec{\Psi }_{i,q_i^{-2r}}A_{i,1}^{-1}\cdots A_{i,q_i^{-2m}}^{-1})\) cannot occur in the decomposition for \(m < r\).
Indeed, for \(m < r\), \(A_{i,q_i^{-2m}}^{-1}\) is a factor of one of the \(\ell \)-weight of the simple module \(L(\widetilde{\varvec{\Psi }}_{i,1} \varvec{\Psi }_{i,q_i^{-2r}}A_{i,1}^{-1}\cdots A_{i,q_i^{-2m}}^{-1})\). This follows from an \({{\mathfrak {s}}}{{\mathfrak {l}}}_2\)-reduction, as an elementary analysis shows that \(A_{q^{-2m}}^{-1}\) occurs in an \(\ell \)-weight of the representation in the \({{\mathfrak {s}}}{{\mathfrak {l}}}_2\)-case
which is the tensor product of \(L(\varvec{\Psi }_{q^2}\varvec{\Psi }_{q^{-2m}}^{-1})\) evaluation representation of a Verma module and \(L(\varvec{\Psi }_{q^{-2m-2}}^{-1}\varvec{\Psi }_{q^{-2r}})\) finite-dimensional representation. So, if this representation appeared in the decomposition, then all its \(\ell \)-weights would be occur in the q-character of \(X_{i,1}\otimes L_{i,q_i^{-2r}}^+\). In particular, \(A_{i,q_i^{-2m}}^{-2}\) would be the factor of one of the \(\ell \)-weights of \(X_{i,1}\otimes L_{i,q_i^{-2r}}^+\), which is a contradiction.
Now, as \(\chi _q(X_{i,1}\otimes L_{i,q_i^{-2r}}^+) = \chi _q(X_{i,1})[\varvec{\Psi }_{i,q_i^{-2r}}^+]\chi _i\), by identifying for \(m\le r\) the coefficients of \((A_{i,1}A_{i,q_i^{-2}}\cdots A_{i,q_i^{-2m}})^{-1}\), we obtain:
This implies that all the \(\chi (m)\) are equal and we obtain the q-character formula (5.18). \(\square \)
6 Interpolating (q, t)-characters
Our approach to the folded quantum integrable systems associated with quantum affine algebras, as formulated in Conjectures 5.15 and 5.16, involves the interpolating (q, t)-characters introduced in [18] as a tool for the study of a certain Langlands duality between finite-dimensional representations of quantum affine algebras. In this section, we extend and refine the definition of the interpolating (q, t)-characters from [18]. They are defined as elements of the refined Grothendieck ring  , which is defined in this section (Theorem 6.6). It turns out that they have 5 interesting specializations corresponding to various q- and t-characters. Moreover, the interpolating (q, t)-characters may be viewed as commutative analogues of elements of the deformed W-algebra \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\).
, which is defined in this section (Theorem 6.6). It turns out that they have 5 interesting specializations corresponding to various q- and t-characters. Moreover, the interpolating (q, t)-characters may be viewed as commutative analogues of elements of the deformed W-algebra \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\).
6.1 Notation for monomials
For \(j \in I'\), a node of the Dynkin diagram of \({{\mathfrak {g}}}'\), let us set
For \(i\in I\), a node of the Dynkin diagram of \({{\mathfrak {g}}}\), let us set
Note that \(d_i\) can equal \(d-1\) (resp. \(d-2\)) only if \(d=2\) (resp. \(d=3\)), and recall that \(\epsilon = e^{i\pi /d}\).
Note that \(L(W_{i,a})\) is a KR module over \(U_q(\widehat{{\mathfrak {g}}})\). It is a fundamental representation if \(d_i = d\) (in particular, for simply laced types, these representations are always fundamental).
6.2 Polynomial rings and specialization homomorphisms
Now we recall the definition of the ring of interpolating (q, t)-characters from [18] and then define a refined version of this ring. We start with some preliminary definitions.
Consider the ring

where \(\alpha \) is an indeterminate.
Remark 6.1
For simply laced types,  is just \({\mathbb {Z}}[Y_{i,a}^{\pm 1}, \alpha ]_{i\in I, a\in q^{{\mathbb {Z}}}t^{{\mathbb {Z}}}}\). \(\square \)
is just \({\mathbb {Z}}[Y_{i,a}^{\pm 1}, \alpha ]_{i\in I, a\in q^{{\mathbb {Z}}}t^{{\mathbb {Z}}}}\). \(\square \)
The ring of interpolating (q, t)-characters  was defined in [18] as a subring of a quotient
was defined in [18] as a subring of a quotient  of
of  . This quotient is defined from the specialization maps
. This quotient is defined from the specialization maps

by the formula

For our purposes, we also want to use the additional specialization homomorphisms

These specialization homomorphisms are well defined on  , but \({\overline{\Pi }}_t\) does not descend to
, but \({\overline{\Pi }}_t\) does not descend to  if \(d>1\) (indeed, \(\alpha ^2 - \alpha \) projects onto 0 in
if \(d>1\) (indeed, \(\alpha ^2 - \alpha \) projects onto 0 in  , but \({\overline{\Pi }}_t(\alpha ^2 - \alpha ) = d^2 - d\)). For this reason, we will work with an intermediate quotient
, but \({\overline{\Pi }}_t(\alpha ^2 - \alpha ) = d^2 - d\)). For this reason, we will work with an intermediate quotient

for which we have surjective ring homomorphisms

Remark 6.2
-
(1)
The interpolating (q, t)-characters are defined below as elements of a subalgebra of the commutative algebra
 . Their purpose is to imitate the properties of elements of the non-commutative deformed W-algebra \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\). In particular, the variable \(\alpha \) is introduced in order to imitate the behavior of the rational functions like (4.5) arising in the formulas for elements of the deformed W-algebra \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) such as (4.4). This is why in the above specializations we set \(\alpha \) equal to 1, 0, or d depending on the situation.
. Their purpose is to imitate the properties of elements of the non-commutative deformed W-algebra \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\). In particular, the variable \(\alpha \) is introduced in order to imitate the behavior of the rational functions like (4.5) arising in the formulas for elements of the deformed W-algebra \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) such as (4.4). This is why in the above specializations we set \(\alpha \) equal to 1, 0, or d depending on the situation. -
(2)
There is a polynomial \(P(\alpha )\) in \(\alpha \) so that \(\alpha ^d P(\alpha )\) is equal to \(\alpha \) in the quotient
 (for example, using a Lagrange interpolating polynomial). Hence, for an arbitrary monomial m in the variables \(Y_{i,a}^{\pm 1}\), as \(\alpha ^N m\) is in
(for example, using a Lagrange interpolating polynomial). Hence, for an arbitrary monomial m in the variables \(Y_{i,a}^{\pm 1}\), as \(\alpha ^N m\) is in  for N large enough, \(\alpha m\) makes sense in
for N large enough, \(\alpha m\) makes sense in  . \(\square \)
. \(\square \)
Let us recall some terminology from [18]. By a monomial in  we will understand an element m of the form \(P(\alpha )M\), where \(P(\alpha )\) is a polynomial in \(\alpha \) and M is a monomial in the \(Y_{j,a}^{\pm 1}\). Note that a monomial in
we will understand an element m of the form \(P(\alpha )M\), where \(P(\alpha )\) is a polynomial in \(\alpha \) and M is a monomial in the \(Y_{j,a}^{\pm 1}\). Note that a monomial in  may be written in various ways as for example \(\alpha Y_{i,a} = \alpha Y_{i,at}\) and \((1 - \alpha )Y_{i,aq^{2d}} = (1 - \alpha )Y_{i,a}\). A monomial is said to be i-dominant if it can be written by using only the variables \(\alpha \), \(Y_{i,a}\) and \(Y_{j,a}^{\pm 1}\), where \(j\ne i\). Let \(B_i\) be the set of i-dominant monomials and for \(J\subset I\), let \(B_J = \cap _{j\in J} B_j\). Finally, let \(B = B_I\) be the set of dominant monomials.
may be written in various ways as for example \(\alpha Y_{i,a} = \alpha Y_{i,at}\) and \((1 - \alpha )Y_{i,aq^{2d}} = (1 - \alpha )Y_{i,a}\). A monomial is said to be i-dominant if it can be written by using only the variables \(\alpha \), \(Y_{i,a}\) and \(Y_{j,a}^{\pm 1}\), where \(j\ne i\). Let \(B_i\) be the set of i-dominant monomials and for \(J\subset I\), let \(B_J = \cap _{j\in J} B_j\). Finally, let \(B = B_I\) be the set of dominant monomials.
We will use the analogous definition of i-dominant (resp. dominant) monomials in  .
.
Lemma 6.1
A monomial in  is i-dominant if and only if its specializations under \(\Pi _q\), \({\overline{\Pi }}_t\) and \(\Pi _t\) are all i-dominant.
is i-dominant if and only if its specializations under \(\Pi _q\), \({\overline{\Pi }}_t\) and \(\Pi _t\) are all i-dominant.
Proof
The direct implication is clear. For the converse, let us first consider a monomial m in  which is a product of various \(Y_{i,a}^{\pm 1}\), \(a\in q^{{\mathbb {Z}}}t^{{\mathbb {Z}}}\) (for this question, we may discard the other variables \(Y_{j,a}^{\pm 1}\) with \(j\ne i\)). Suppose m specializes to i-dominant monomials
which is a product of various \(Y_{i,a}^{\pm 1}\), \(a\in q^{{\mathbb {Z}}}t^{{\mathbb {Z}}}\) (for this question, we may discard the other variables \(Y_{j,a}^{\pm 1}\) with \(j\ne i\)). Suppose m specializes to i-dominant monomials
for the respective specializations \(t = 1\), \(q = \epsilon \), \(q=1\). Then, the sum
of the various powers of the various variables is the same for \(m_1\), \(m_2\) and \(m_3\). We also have for any \(\epsilon ' = \epsilon ^R\), \(R\in {\mathbb {Z}}\), the relation
Hence we can construct an i-dominant monomial M in  so that its specializations at \(t = 1\) and \(q = \epsilon \) are \(m_1\) and \(m_2\), respectively. Such a monomial is not unique, but, for example, the powers in the variables in M can be defined inductively by a standard combinatorial algorithm, starting from the \(r_0\), \(s_0\) where \(r_0\) (resp. \(s_0\)) is minimal so that \(u_{i,r_0}(m_1)\ne 0\) (resp. \(u_{i,s_0}(m_3)\ne 0\)). Then, M specializes necessarily to \(m_3\) at \(q = 1\) as for any \(s\in {\mathbb {Z}}\)
so that its specializations at \(t = 1\) and \(q = \epsilon \) are \(m_1\) and \(m_2\), respectively. Such a monomial is not unique, but, for example, the powers in the variables in M can be defined inductively by a standard combinatorial algorithm, starting from the \(r_0\), \(s_0\) where \(r_0\) (resp. \(s_0\)) is minimal so that \(u_{i,r_0}(m_1)\ne 0\) (resp. \(u_{i,s_0}(m_3)\ne 0\)). Then, M specializes necessarily to \(m_3\) at \(q = 1\) as for any \(s\in {\mathbb {Z}}\)
In particular, m gets identified with M in  and so m is i-dominant. The case when the monomial has a factor depending of \(\alpha \) is treated in a similar way. \(\square \)
and so m is i-dominant. The case when the monomial has a factor depending of \(\alpha \) is treated in a similar way. \(\square \)
Remark 6.3
The analogous statement is not true in  for non-simply laced types (with \(r > 1\)). For example, \(Y_{i,1}Y_{i,t}^{-1}Y_{i,tq^d}\) is not i-dominant, but specializes at \(t = 1\), \(q = \epsilon \), \(q = 1\), respectively, to \(Y_{i,q^d}\), \(Y_{i,1}\), \(Y_{i,1}\) which are all i-dominant. But in
for non-simply laced types (with \(r > 1\)). For example, \(Y_{i,1}Y_{i,t}^{-1}Y_{i,tq^d}\) is not i-dominant, but specializes at \(t = 1\), \(q = \epsilon \), \(q = 1\), respectively, to \(Y_{i,q^d}\), \(Y_{i,1}\), \(Y_{i,1}\) which are all i-dominant. But in  this monomial gets identified with \(Y_{i,q^d}\), and so it is i-dominant, in accordance with Lemma 6.1. \(\square \)
this monomial gets identified with \(Y_{i,q^d}\), and so it is i-dominant, in accordance with Lemma 6.1. \(\square \)
6.3 Definition of interpolating (q, t)-characters
Recall the definition of the ring  of interpolating (q, t)-characters from [18]. It is defined as the intersection of subrings
of interpolating (q, t)-characters from [18]. It is defined as the intersection of subrings  , \(i\in I\), by analogy with the characterization of \({\text {Im}} \chi _q\) as the intersection of the subrings \({\mathfrak {K}}_{i,q}\) (see formulas (4.1) and (4.2)) as well as the definition of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) as the intersection of the kernels of the screening operators in [24] and Sect. 3.2.
, \(i\in I\), by analogy with the characterization of \({\text {Im}} \chi _q\) as the intersection of the subrings \({\mathfrak {K}}_{i,q}\) (see formulas (4.1) and (4.2)) as well as the definition of \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) as the intersection of the kernels of the screening operators in [24] and Sect. 3.2.
We will need the following analogues of the generating series \(A_i(z)\) in the deformed W-algebra \({{\mathbf {W}}}_{q,t}({{\mathfrak {g}}})\) given by formula (3.6):
Definition 6.2
Let  be the subring of
be the subring of  generated by the variables \(\alpha \), \(W_{j,a}^{\pm 1}\), \(\alpha Y_{j,a}^{\pm 1}\) (\(j\ne i\), \(a\in q^{{\mathbb {Z}}}t^{{\mathbb {Z}}}\)), the \(\alpha Y_{i,a}(1 + \widetilde{A}_{i,aq_it}^{-1})\) (\(a\in q^{{\mathbb {Z}}}t^{{\mathbb {Z}}}\)) and
generated by the variables \(\alpha \), \(W_{j,a}^{\pm 1}\), \(\alpha Y_{j,a}^{\pm 1}\) (\(j\ne i\), \(a\in q^{{\mathbb {Z}}}t^{{\mathbb {Z}}}\)), the \(\alpha Y_{i,a}(1 + \widetilde{A}_{i,aq_it}^{-1})\) (\(a\in q^{{\mathbb {Z}}}t^{{\mathbb {Z}}}\)) and
where \(a\in q^{{\mathbb {Z}}}t^{{\mathbb {Z}}}\).
Following [18], we define the ring  of interpolating (q, t)-characters associated with \({{\mathfrak {g}}}\) as the following ring intersection:
of interpolating (q, t)-characters associated with \({{\mathfrak {g}}}\) as the following ring intersection:

Remark 6.4
If \({{\mathfrak {g}}}\) is simply laced,
coincides with \(A_{i,qt}\). Hence,  is the image in
is the image in  of:
of:

\(\square \)
The following result was proved in [18].
Theorem 6.3
-
(i)
 is nonzero.
is nonzero. -
(ii)
Every element
 (resp.
(resp.  , \(i\in I\)) is uniquely determined by the multiplicities of the dominant monomials (resp. i-dominant monomials) occurring in F.
, \(i\in I\)) is uniquely determined by the multiplicities of the dominant monomials (resp. i-dominant monomials) occurring in F. -
(iii)
For each dominant monomial m, there is a unique
 such that m is the unique dominant monomial occurring in \(F_{q,t}(m)\) (moreover, there is an algorithm to construct \(F_{q,t}(m)\) explicitly).
such that m is the unique dominant monomial occurring in \(F_{q,t}(m)\) (moreover, there is an algorithm to construct \(F_{q,t}(m)\) explicitly).
In particular, the interpolating (q, t)-character \(F_{q,t}(Y_{i,a})\) corresponding to the ith fundamental representation is well defined, as are the interpolating (q, t)-characters
corresponding to the KR modules.
Remark 6.5
(1) In general, the ring  cannot be lifted to a subring of
cannot be lifted to a subring of  satisfying the properties listed in Theorem 6.3. For example, suppose that \(d_i = d - 1\) and consider the following element:
satisfying the properties listed in Theorem 6.3. For example, suppose that \(d_i = d - 1\) and consider the following element:
Viewed as an element of  , it can be identified with \(\alpha W_{i,1} \widetilde{A}_{i,1}^{-1}\) which belongs to
, it can be identified with \(\alpha W_{i,1} \widetilde{A}_{i,1}^{-1}\) which belongs to  and is an i-dominant monomial.
and is an i-dominant monomial.
However, viewed as an element of  , it does not contain any i-dominant monomials. This contradicts property (ii) of Theorem 6.3.
, it does not contain any i-dominant monomials. This contradicts property (ii) of Theorem 6.3.
(2) If \({{\mathfrak {g}}}\) is simply laced, there is no such obstruction and we can consider interpolating (q, t)-characters as elements of  . These are just the ordinary q-characters, but with the quantum parameter qt instead of q. More precisely, for \(r\in {\mathbb {Z}}\), let
. These are just the ordinary q-characters, but with the quantum parameter qt instead of q. More precisely, for \(r\in {\mathbb {Z}}\), let  be the subring of elements of
be the subring of elements of  involving only variables \(Y_{i,q^d (tq)^s}^{\pm 1}\), \(i\in I\), \(s\in {\mathbb {Z}}\). Then,
involving only variables \(Y_{i,q^d (tq)^s}^{\pm 1}\), \(i\in I\), \(s\in {\mathbb {Z}}\). Then,  is isomorphic to
is isomorphic to  as it is obtained from
as it is obtained from  by the automorphism shifting spectral parameters by \(q^d\). Moreover,
by the automorphism shifting spectral parameters by \(q^d\). Moreover,

By Remark 6.4,  is the image in
is the image in  of
of

where

is the ordinary q-character homomorphism, but with quantum parameter q replaced by qt and  is the subcategory of finite-dimensional representations of \(U_{qt}(\widehat{{{\mathfrak {g}}}})\) whose simple constituents have Drinfeld polynomials have roots that are powers of qt. \(\square \)
is the subcategory of finite-dimensional representations of \(U_{qt}(\widehat{{{\mathfrak {g}}}})\) whose simple constituents have Drinfeld polynomials have roots that are powers of qt. \(\square \)
Theorem 6.4
 can be lifted to a subring
can be lifted to a subring  so that we have a commutative diagram:
so that we have a commutative diagram:

This theorem follows from Theorem 6.6.
6.4 The refined ring of interpolating (q, t)-characters
Let us consider the completion  of the ring
of the ring  which includes infinite linear combinations of monomials whose \({{\mathfrak {g}}}\)-weights belong to a finite union of cones \(\{\mu \preceq \omega \}\), with \(\preceq \) being the standard ordering (as for the q-characters in the category
which includes infinite linear combinations of monomials whose \({{\mathfrak {g}}}\)-weights belong to a finite union of cones \(\{\mu \preceq \omega \}\), with \(\preceq \) being the standard ordering (as for the q-characters in the category  ). Next, we define the subrings
). Next, we define the subrings  in the same way as the subrings
in the same way as the subrings  of
of  , except that we include infinite which make sense in
, except that we include infinite which make sense in  . Note that the elements generating
. Note that the elements generating  are well defined in
are well defined in  and in
and in  by (2) in Remark 6.2.
by (2) in Remark 6.2.
Definition 6.5
We define the refined ring of interpolating (q, t)-characters  as the intersection
as the intersection

Theorem 6.6
The refined ring of interpolating (q, t)-characters  satisfies the same properties as the properties of
satisfies the same properties as the properties of  listed in Theorem 6.3. In particular, it contains a unique element
listed in Theorem 6.3. In particular, it contains a unique element

for each dominant monomial m.
Proof
All proofs in [18] remain valid if we replace  by
by  . More precisely,
. More precisely,
(i) follows from (iii).
(ii) The property for the i-dominant monomials is proved as for [18, Lemma 4.1]. In the simply laced cases (\(d = 1\)), the proof is the same as for ordinary q-character as discussed above (see Remark 6.5). If \(d = 2\), the crucial point is indeed that the formula (6.6) has an i-dominant monomial: its respective specializations under \({\overline{\Pi }}_t\), \(\Pi _q\), \(\Pi _t\) are 0, \(Y_{i,q^{-1}}Y_{i,q}A_{i,1}^{-1}\), 0, which are i-dominant. Hence, expression (6.6) identifies with \(\alpha (2 - \alpha ) Y_{i,q^{-1}}Y_{i,q}A_{i,1}^{-1}\) in  which is i-dominant. An analogous reasoning gives the result for \(d = 3\).
which is i-dominant. An analogous reasoning gives the result for \(d = 3\).
The property for dominant monomials is proved exactly as in [18, Lemma 4.2] from the property we just obtained for the i-dominant monomials.
(iii) This is proved as in [18, Section 4.2]: an algorithm is proposed which produces the \(F(W_{i,a})\) for any i, a, and from which the F(m) are obtained as algebraic combinations of these \(F(W_{i,a})\). For the \(F(W_{i,a})\), the algorithm and the proof that it does not fail are the same. This proof is obtained by induction on the rank of the Lie algebra. That is why we have to check for \(n = 1\) (type \(A_1\)) and \(n = 2\) (types \(A_1\times A_1\), \(A_2\), \(C_2\), \(G_2\)). The simply laced cases are clear by Remark 6.4. For type \(C_2\), the formulas obtained in [18] for  work as well for
work as well for  :
:
For the type \(G_2\), the formulas obtained in [18, Section 5.2] work as well. \(\square \)
Now let us consider the various specializations of  . We have first the three specializations corresponding to the respective specializations of the deformed
. We have first the three specializations corresponding to the respective specializations of the deformed  -algebras at \(t = 1\), \(q = \epsilon \) and \(q = 1\).
-algebras at \(t = 1\), \(q = \epsilon \) and \(q = 1\).
-
The specialization \(\Pi _q = \Pi _{t = 1, \alpha = 1}\): we get the q-character of a \(U_q(\widehat{{\mathfrak {g}}})\)-module, that is an element of
 (this is proved in [18]).
(this is proved in [18]). -
The specialization \(\Pi _t = \Pi _{q = \epsilon , \alpha = 0}\): we get the t-character of a \(U_t({}^L\widehat{{\mathfrak {g}}})\)-module (this is proved in [18]).
-
The specialization \({\overline{\Pi }}_t = \Pi _{q = 1, \alpha = d}\): we get the t-character of an element of
 (in light of Proposition 3.2, the proof is parallel to the proof for the other specializations since
(in light of Proposition 3.2, the proof is parallel to the proof for the other specializations since  ). Hence, it can also be viewed as the folded t-character of a \(U_t(\widehat{{\mathfrak {g}}'})\)-module (see Sect. 4.3).
). Hence, it can also be viewed as the folded t-character of a \(U_t(\widehat{{\mathfrak {g}}'})\)-module (see Sect. 4.3).
There are also two additional interesting specializations:
-
The specialization \(\Pi _t' = \Pi _{q = 1, \alpha = 0}\): it is well defined as the composition of \(\Pi _t\) and the homomorphism
$$\begin{aligned} {\mathbb {Z}}[W_{i,a}^{\pm 1}]_{i\in I, a\in t^{{\mathbb {Z}}}\epsilon ^{{\mathbb {Z}}}}\rightarrow {\mathbb {Z}}[{\overline{Y}}_{i,a}^{\pm 1}]_{i\in I, a\in t^{{\mathbb {Z}}}} \end{aligned}$$(see formula (6.1) for the definition of \({\overline{Y}}_{i,a}\)) identifying \(\epsilon \) with 1. We get the t-character of an element of
 which is defined in terms of the variables \({\overline{Y}}_{i,a}\) instead of \(Y_{i,a}\) (this is parallel to the proof for the other specializations as
which is defined in terms of the variables \({\overline{Y}}_{i,a}\) instead of \(Y_{i,a}\) (this is parallel to the proof for the other specializations as  ). Hence, it can also be viewed as the folded t-character of a \(U_t\left( \widehat{\left( {}^L{\mathfrak {g}}\right) '}\right) \)-module (see Sect. 4.3).
). Hence, it can also be viewed as the folded t-character of a \(U_t\left( \widehat{\left( {}^L{\mathfrak {g}}\right) '}\right) \)-module (see Sect. 4.3). -
The specialization \({\overline{\Pi }}_q = \Pi _{t = 1, \alpha = 0}\): we obtain elements of \(\text {Im}(\chi _q^L)\), i.e. q-characters of modules over the Langlands dual quantum affine algebra \(U_q({}^L\widehat{{\mathfrak {g}}})\), as defined in [32, Section 12] (in the context of the parametrization of simple representations of shifted quantum affine algebras).
5 interesting specializations of the refined ring of interpolating (q, t)-characters:

Remark 6.6
To get the t-characters of \(U_t({}^L\widehat{{\mathfrak {g}}})\)-modules in the sense of [30] (as recalled above), one has to change the sign in the definition of the variables \(Z_{i,a}\), as described in [18] (formula (2) for \(r = 2\) and Section 3.2 for \(r = 3\)). In this paper, to simplify our notation, we do not make this sign change. \(\square \)
Remark 6.7
In [18, Lemma 4.16], we proved that the generators of  , i.e. the fundamental elements \(F_{q,t}(W_{i,a})\), are finite linear combinations of monomials. In the case of the refined ring
, i.e. the fundamental elements \(F_{q,t}(W_{i,a})\), are finite linear combinations of monomials. In the case of the refined ring  the algorithm in the proof of Theorem 6.6 produces the fundamental elements \({\overline{F}}_{q,t}(W_{i,a})\) but so far we have only been able to prove that they are (possibly infinite) linear combinations of monomials with weights in the union of finitely many cones. That’s why we have allowed such linear combinations in the definition of the
the algorithm in the proof of Theorem 6.6 produces the fundamental elements \({\overline{F}}_{q,t}(W_{i,a})\) but so far we have only been able to prove that they are (possibly infinite) linear combinations of monomials with weights in the union of finitely many cones. That’s why we have allowed such linear combinations in the definition of the  above. However, we also know that the specializations under \(\Pi _q\), \(\Pi _t\), \({\overline{\Pi }}_t\) and \(\Pi _t'\) of an interpolating (q, t)-character with a finite number of dominant monomials are finite linear combinations. This follows from Proposition 6.10. Therefore, finiteness of elements of
above. However, we also know that the specializations under \(\Pi _q\), \(\Pi _t\), \({\overline{\Pi }}_t\) and \(\Pi _t'\) of an interpolating (q, t)-character with a finite number of dominant monomials are finite linear combinations. This follows from Proposition 6.10. Therefore, finiteness of elements of  follows from Conjecture 6.11 saying that the coefficients of all monomials in \({\overline{F}}_{q,t}(W_{i,a})\) are positive (see Corollary 6.12). \(\square \)
follows from Conjecture 6.11 saying that the coefficients of all monomials in \({\overline{F}}_{q,t}(W_{i,a})\) are positive (see Corollary 6.12). \(\square \)
Example 6.7
Let us consider the interpolating (q, t)-character (6.7) corresponding to the second fundamental representation of \(U_q(C_2^{(1)})\). In this case, we have \(^L{\widehat{{{\mathfrak {g}}}}}= D_3^{(2)}, \widehat{{{\mathfrak {g}}}'} = A_3^{(1)}, \widehat{({}^L{{\mathfrak {g}}})'} = D_3^{(1)} \simeq A_3^{(1)}\) (the last isomorphism involves switching the indices \(1 \leftrightarrow 2 \in \{1,2,3\} = I'\)).
The above 5 specializations (listed in the same clockwise order) are, respectively,
-
the q-character of the fundamental representation \(L(Y_{2,1})\) of \(U_q(C_2^{(1)})\):
$$\begin{aligned} Y_{2,1} + Y_{2,q^4}^{-1} Y_{1,q}Y_{1,q^3} \!+\! Y_{1,q}Y_{1,q^5}^{-1} \!+\! Y_{1,q^3}^{-1}Y_{1,q^5}^{-1}Y_{2,q^2} \!+\! Y_{2,q^6}^{-1}, \end{aligned}$$ -
the twisted t-character of the fundamental representation \(L(Z_{2,1})\) of \(U_t(D_3^{(2)})\):
$$\begin{aligned} Z_{2,1} + Z_{2,t^2}^{-1} Z_{1,-t^2} + Z_{1,-t^6}^{-1}Z_{2,-t^2} + Z_{2,-t^4}^{-1}, \end{aligned}$$ -
the t-character in
 of highest monomial \(Y_{2,1}\): $$\begin{aligned} Y_{2,1} + Y_{2,t^2}^{-1} Y_{1,t}^2 + 2 Y_{1,t}Y_{1,t^3}^{-1} + Y_{1,t^3}^{-2}Y_{2,t^2} + Y_{2,t^4}^{-1}, \end{aligned}$$
of highest monomial \(Y_{2,1}\): $$\begin{aligned} Y_{2,1} + Y_{2,t^2}^{-1} Y_{1,t}^2 + 2 Y_{1,t}Y_{1,t^3}^{-1} + Y_{1,t^3}^{-2}Y_{2,t^2} + Y_{2,t^4}^{-1}, \end{aligned}$$also equal to the folded t-character of the fundamental representation \(L(Y_{2,1})\) of \(U_t(A_3^{(1)})\),
-
the t-character in
 of highest monomial \({\overline{Y}}_{2,1}\): $$\begin{aligned} {\overline{Y}}_{2,1} + {\overline{Y}}_{2,t^2}^{-1} {\overline{Y}}_{1,t} + {\overline{Y}}_{1,t^3}^{-1} {\overline{Y}}_{2,t^2} + {\overline{Y}}_{2,t^4}^{-1}, \end{aligned}$$
of highest monomial \({\overline{Y}}_{2,1}\): $$\begin{aligned} {\overline{Y}}_{2,1} + {\overline{Y}}_{2,t^2}^{-1} {\overline{Y}}_{1,t} + {\overline{Y}}_{1,t^3}^{-1} {\overline{Y}}_{2,t^2} + {\overline{Y}}_{2,t^4}^{-1}, \end{aligned}$$which after switching the indices 1 and 2 is equal to the folded t-character of the fundamental representation \(L(Y_{1,1})\) of \(U_t(A_3^{(1)})\), defined in terms of the variables \({\overline{Y}}_{i,a}\) instead of \(Y_{i,a}\).
-
the Langlands dual q-characters of the fundamental representation \(L(Z_{2,1})\) of \(U_q(D_3^{(2)})\)
$$\begin{aligned} W_{2,1} + W_{2,q^4}^{-1} W_{1,q^2} + W_{1,q^4}^{-1}W_{2,q^2} + W_{2,q^6}^{-1}. \end{aligned}$$
Example 6.8
Let us consider the interpolating (q, t)-character (6.8) corresponding to the representation \(L(W_{1,1})\) of \(U_q(C_2^{(1)})\). The 5 specializations are, respectively,
-
the q-character of the 11-dimensional representation \(L(Y_{1,q^{-1}}Y_{1,q})\) of \(U_q(C_2^{(1)})\).
-
the twisted t-character of the fundamental representation \(L(Z_{1,-1})\) of \(U_t({}^L\widehat{{\mathfrak {g}}}) = U_t(D_3^{(2)})\).
$$\begin{aligned} Z_{1,-1} + Z_{1,-t^4}^{-1}Z_{2,t}Z_{2,-t} + Z_{2,-t}Z_{2,t^3}^{-1} + Z_{2,-t^3}^{-1}Z_{2,t} + Z_{2,t^3}^{-1}Z_{2-t^3}^{-1} Z_{1,-t^4} + Z_{1,-t^8}^{-1}. \end{aligned}$$ -
the t-character in
 of highest monomial \(Y_{1,1}^2\): $$\begin{aligned} \Big (Y_{1,1} + Y_{1,t^2}^{-1}Y_{2,t} + Y_{2,t^3}^{-1}Y_{1,t^2} + Y_{1,t^4}^{-1}\Big )^2, \end{aligned}$$
of highest monomial \(Y_{1,1}^2\): $$\begin{aligned} \Big (Y_{1,1} + Y_{1,t^2}^{-1}Y_{2,t} + Y_{2,t^3}^{-1}Y_{1,t^2} + Y_{1,t^4}^{-1}\Big )^2, \end{aligned}$$also equal to the folded t-character of the representation \(L(Y_{1,1}Y_{3,1})\) of \(U_t(A_3^{(1)})\)
-
the t-character in
 of highest monomial \({\overline{Y}}_{1,1}\): $$\begin{aligned} {\overline{Y}}_{1,1} + {\overline{Y}}_{1,t^2}^{-1}{\overline{Y}}_{2,t}^2 +2{\overline{Y}}_{2,t}{\overline{Y}}_{2,t^3}^{-1} +{\overline{Y}}_{2,t^3}^{-2}{\overline{Y}}_{1,t^2} +{\overline{Y}}_{1,t^4}^{-1} \end{aligned}$$
of highest monomial \({\overline{Y}}_{1,1}\): $$\begin{aligned} {\overline{Y}}_{1,1} + {\overline{Y}}_{1,t^2}^{-1}{\overline{Y}}_{2,t}^2 +2{\overline{Y}}_{2,t}{\overline{Y}}_{2,t^3}^{-1} +{\overline{Y}}_{2,t^3}^{-2}{\overline{Y}}_{1,t^2} +{\overline{Y}}_{1,t^4}^{-1} \end{aligned}$$which after switching the indices 1 and 2 is equal to the folded t-character of the fundamental representation \(L(Y_{2,1})\) of \(U_t(A_3^{(1)})\), defined in terms of the variables \({\overline{Y}}_{i,a}\) instead of \(Y_{i,a}\).
-
the Langlands dual q-characters of the fundamental representation \(L(Z_{2,1})\) of \(U_q(D_3^{(2)})\)
$$\begin{aligned}&W_{1,1} + W_{1,q^2}^{-1}W_{2,1}W_{2,q^2} +W_{2,q^2}W_{2,q^4}^{-1} +W_{1,q^2}^{-1}W_{1,q^4}W_{2,q^6}^{-1}Y_{2,t}\\&\quad +W_{2,q^4}^{-1}W_{2,q^6}^{-1}W_{1,q^4} +W_{1,q^6}^{-1}. \end{aligned}$$
Example 6.9
Let us consider the interpolating (q, t)-character (6.9) corresponding to the first fundamental representation of \(U_q(C_2^{(1)})\). The specializations under \(\Pi _t\), \(\Pi _t'\), \({\overline{\Pi }}_q\) are zero because of the \(\alpha \) factor. The specializations under \(\Pi _q\) and \({\overline{\Pi }}_t\) are, respectively:
-
the q-character of the fundamental representation \(L(Y_{1,1})\) of \(U_q(C_2^{(1)})\):
$$\begin{aligned} Y_{1,1} + Y_{1,q^2}^{-1}Y_{2,q} + Y_{2,q^5}^{-1} Y_{1,q^4} + Y_{1,q^6}^{-1}, \end{aligned}$$ -
the t-character in
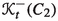 of highest monomial \(2Y_{1,1}\): $$\begin{aligned} 2( Y_{1,1} + Y_{1,t^2}^{-1}Y_{2,t} + Y_{2,t^3}^{-1} Y_{1,t^2} + Y_{1,t^4}^{-1}) \end{aligned}$$
of highest monomial \(2Y_{1,1}\): $$\begin{aligned} 2( Y_{1,1} + Y_{1,t^2}^{-1}Y_{2,t} + Y_{2,t^3}^{-1} Y_{1,t^2} + Y_{1,t^4}^{-1}) \end{aligned}$$also equal to (the double of) the folded t-character of the representation \(L(Y_{1,1})\) of \(U_t(A_3^{(1)})\).
6.5 \(\sigma \)-fundamental interpolating (q, t)-characters
In this subsection, we identify the representation M(W) of \(U_q({}^L{\widehat{{{\mathfrak {g}}}}})\) in terms of Conjecture 5.16 for the simplest \(U_q(\widehat{{{\mathfrak {g}}}'})\)-modules with \(\sigma \)-invariant highest monomials. These monomials have the form \(Y_{i,a}\) if \(\sigma (i)=i\) and \(\prod _{1\le k \le d} Y_{\sigma ^k(i),a}\) if \(\sigma (i)\ne i\). For this reason, we call these \(U_q(\widehat{{{\mathfrak {g}}}'})\)-modules \(\sigma \)-fundamental. Note, however, that the corresponding \(U_t({}^L\widehat{{\mathfrak {g}}})\)-modules (see the second part of Proposition 6.10) are in fact fundamental.
Consider a \(U_q(\widehat{{{\mathfrak {g}}}'})\)-module of the form \(L(\widetilde{Y}_{i,a}), i \in I\) (the set of vertices of the Dynkin diagram of \({{\mathfrak {g}}}= ({{\mathfrak {g}}}')^\sigma \)) and with \(a\in q^{{\mathbb {Z}}}\).
Let

We call it the ith \(\sigma \)-fundamental interpolating (q, t)-character. The following proposition shows that \(X^{(i)}_{q,t}\) satisfies the properties of the element \(X_{q,t}\) whose existence is stated in Conjecture 5.16 in the case when \(W = L(\widetilde{Y}_{i,a})\).
Proposition 6.10
The specializations of \(X^{(i)}_{q,t}\) under \(\Pi _q\), \(\Pi _t\), \({\overline{\Pi }}_t\), \(\Pi _t'\), \({\overline{\Pi }}_q\) are respectively
-
the q-character of the simple \(U_q(\widehat{{\mathfrak {g}}})\)-module of highest monomial \(W_{i,a}\). It is a KR module (a fundamental representation if \(d_i = d\)).
-
the t-character of the fundamental \(U_t({}^L\widehat{{\mathfrak {g}}})\)-module of highest monomial \(Z_{i,(a_{q = \epsilon })^{d_i^\vee }}\) (see (4.3) for the definition of \(d_i^\vee \)), with \(a_{q = \epsilon }\) the specialization of a at \(q = \epsilon \).
-
the t-character of the element \(F({\overline{Y}}_{i,a}) = F(Y_{i,a})^{d_i^\vee }\) in
 (defined in terms of the variables \(Y_{j,b}\)) of highest monomial \({\overline{Y}}_{i,a}\). It is also the folded t-character of the simple \(U_t(\widehat{{\mathfrak {g}}'})\)-module of highest monomial \(\widetilde{Y}_{i,a}\) (this is a tensor product of the fundamental representations).
(defined in terms of the variables \(Y_{j,b}\)) of highest monomial \({\overline{Y}}_{i,a}\). It is also the folded t-character of the simple \(U_t(\widehat{{\mathfrak {g}}'})\)-module of highest monomial \(\widetilde{Y}_{i,a}\) (this is a tensor product of the fundamental representations). -
the t-character of the element \(F({\overline{Y}}_{i,a})\) in
 (which is defined in terms of the variables \({\overline{Y}}_{j,b}\) instead of \(Y_{j,b}\)) of highest monomial \({\overline{Y}}_{i,a}\). It is also, after the appropriate permutation of indices, equal to the folded t-character of the fundamental \(U_t\left( \widehat{\left( {}^L{\mathfrak {g}}\right) '}\right) \)-module of highest monomial \(Y_{i,a}\).
(which is defined in terms of the variables \({\overline{Y}}_{j,b}\) instead of \(Y_{j,b}\)) of highest monomial \({\overline{Y}}_{i,a}\). It is also, after the appropriate permutation of indices, equal to the folded t-character of the fundamental \(U_t\left( \widehat{\left( {}^L{\mathfrak {g}}\right) '}\right) \)-module of highest monomial \(Y_{i,a}\). -
the Langlands dual q-character of the fundamental \(U_q({}^L\widehat{{\mathfrak {g}}})\)-module of highest monomial \(Z_{i,a^{d_i^\vee }}\).
Proof
By construction, following the algorithm in [18, Section 4.2.4], the interpolating (q, t)-character \(F_{q,t}(W_{i,a})\) is the sum of \(W_{i,a}\) plus other monomials of the form:
where \(j_k\in I\), \(b_j\in aq^{{\mathbb {Z}}}t^{{\mathbb {Z}}}\) and the \(\widetilde{A}_{j,b}\) are given by formula (6.4). Though the argument in [18] concerns \(F_{q,t}(W_{i,a})\), the algorithm constructing \(X_{q,t}^{(i)} = \overline{F}_{q,t}(W_{i,a})\) in  is the same, hence we obtain that \(X_{q,t}^{(i)}\) satisfies the same property. This implies that each of the 5 specializations considered in the statement of the proposition has a unique dominant monomial; namely, the corresponding specialization of the highest monomial \(W_{i,a}\). Then, as explained in [18], the first two specializations are, respectively, the q-character of a KR module of \(U_q(\widehat{{\mathfrak {g}}})\) and the t-character of a fundamental module of \(U_t({}^L\widehat{{\mathfrak {g}}})\), which are known to have a unique dominant monomial by [29, 30]. The third specialization is an element of
is the same, hence we obtain that \(X_{q,t}^{(i)}\) satisfies the same property. This implies that each of the 5 specializations considered in the statement of the proposition has a unique dominant monomial; namely, the corresponding specialization of the highest monomial \(W_{i,a}\). Then, as explained in [18], the first two specializations are, respectively, the q-character of a KR module of \(U_q(\widehat{{\mathfrak {g}}})\) and the t-character of a fundamental module of \(U_t({}^L\widehat{{\mathfrak {g}}})\), which are known to have a unique dominant monomial by [29, 30]. The third specialization is an element of  with a unique dominant monomial \({\overline{Y}}_{i,a}\); hence, it is equal to \(F({\overline{Y}}_{i,a})\). Moreover, the simple \(U_t(\widehat{{\mathfrak {g}}'})\)-module of highest monomial \(\widetilde{Y}_{i,a}\) is a simple tensor product of fundamental representations, and, as a consequence of [22], its (folded) t-character belongs to \({\overline{Y}}_{i,a} + {\overline{Y}}_{i,a}A_{i,at}^{-1}{\mathbb {Z}}[A_{j,b}^{-1}]_{j\in I, b\in at^{{\mathbb {Z}}}}\), with the \(A_{j,b}\) as in formula (3.10). Hence, it has a unique dominant monomials and is equal to \(F({\overline{Y}}_{i,a})\). We use an analogous argument for the fourth specialization. For the last specialization, this is the Langlands dual q-character which is precisely defined as the specialization of the interpolating (q, t)-character \(F_{q,t}(W_{i,a})\). \(\square \)
with a unique dominant monomial \({\overline{Y}}_{i,a}\); hence, it is equal to \(F({\overline{Y}}_{i,a})\). Moreover, the simple \(U_t(\widehat{{\mathfrak {g}}'})\)-module of highest monomial \(\widetilde{Y}_{i,a}\) is a simple tensor product of fundamental representations, and, as a consequence of [22], its (folded) t-character belongs to \({\overline{Y}}_{i,a} + {\overline{Y}}_{i,a}A_{i,at}^{-1}{\mathbb {Z}}[A_{j,b}^{-1}]_{j\in I, b\in at^{{\mathbb {Z}}}}\), with the \(A_{j,b}\) as in formula (3.10). Hence, it has a unique dominant monomials and is equal to \(F({\overline{Y}}_{i,a})\). We use an analogous argument for the fourth specialization. For the last specialization, this is the Langlands dual q-character which is precisely defined as the specialization of the interpolating (q, t)-character \(F_{q,t}(W_{i,a})\). \(\square \)
The following conjecture is true in all examples known to us.
Conjecture 6.11
\(X^{(i)}_{q,t}\) can be written in such a way that all coefficients of its monomials are positive.
Corollary 6.12
If Conjecture 6.11 holds, then \(X^{(i)}_{q,t}\) is a polynomial and therefore every element of  is a polynomial (a finite linear combination of monomials).
is a polynomial (a finite linear combination of monomials).
Proof
Positivity of coefficients of \(X^{(i)}_{q,t}\) implies that if \(X^{(i)}_{q,t}\) were an infinite combination of monomials, then so would be \({\overline{\Pi }}_t(X^{(i)}_{q,t})\), which is not the case. Since the elements \(X^{(i)}_{q,t}\) generate  , it follows that every element of
, it follows that every element of  is finite as well. \(\square \)
is finite as well. \(\square \)
Remark 6.8
The statement analogous to Conjecture 6.11 for the elements \(F_{q,t}(W_{i,a})\) of the original ring  is also a conjecture. At present, we are not aware of a uniform proof of this statement or of Conjecture 6.11. We expect, however, that it is possible to write an explicit positive and finite expression for these elements for Lie algebras \({{\mathfrak {g}}}\) of classical types, and to check the statement with the help of a computer for \({{\mathfrak {g}}}\) of exceptional types. There is a similar question for the corresponding elements of the deformed W-algebra. We hope to discuss this in another paper.
is also a conjecture. At present, we are not aware of a uniform proof of this statement or of Conjecture 6.11. We expect, however, that it is possible to write an explicit positive and finite expression for these elements for Lie algebras \({{\mathfrak {g}}}\) of classical types, and to check the statement with the help of a computer for \({{\mathfrak {g}}}\) of exceptional types. There is a similar question for the corresponding elements of the deformed W-algebra. We hope to discuss this in another paper.
Assuming Conjecture 6.11, we obtain a proof of the second part of Conjecture 5.15,(ii) (modulo Conjecture 5.15,(i)) and Conjecture 5.16 for \(W=L(\widetilde{Y}_{i,a})\).
Theorem 6.13
Let \(W = L(\widetilde{Y}_{i,a})\), \(i\in I\), \(a\in {\mathbb {C}}^\times \). Suppose that Conjecture 6.11 holds. Then, there exists a subspace \({\overline{W}}\subset \widetilde{W}\) isomorphic, as a vector space graded by \({}^L{{\mathfrak {g}}}\)-weights, to a \(U_q({}^L{\widehat{{{\mathfrak {g}}}}})\)-module M(W), which is the simple \(U_t({}^L\widehat{{\mathfrak {g}}})\)-module of highest monomial \(Z_{i,(a_{q = \epsilon })^{d_i^\vee }}\). Moreover, it satisfies Conjecture 5.16 for the interpolating (q, t)-character \(X^{(i)}_{q,t}\).
Proof
We have seen in Proposition 6.10 that \({\overline{\Pi }}_t(X^{(i)}_{q,t})\) is the folded t-character of W and that \(\Pi _t(X^{(i)}_{q,t}) = \chi _t(M(W))\) where M(W) is the fundamental \(U_t({}^L\widehat{{\mathfrak {g}}})\)-module of highest monomial \(Z_{i,(a_{q = \epsilon })^{d_i^\vee }}\). The positivity of \(X^{(i)}_{q,t}\) implies that the multiplicities of weights in \(\Pi _t(X^{(i)}_{q,t})\) (for which \(\alpha = 0\)) are lower than in \({\overline{\Pi }}_t(X^{(i)}_{q,t})\) (for which \(\alpha = d\)). Hence, the result. \(\square \)
7 Examples
In this section, we present five explicit examples confirming Conjectures 5.15 and 5.16.
7.1 First example: the fundamental representation \(L(Y_{2,1})\) of \(U_q(A_3^{(1)})\)
Consider the Lie algebra \({{\mathfrak {g}}}'\) of type \(A_3\) with the automorphism \(\sigma \) exchanging the nodes 1 and 3 of its Dynkin diagram. We have the Lie algebra \({{\mathfrak {g}}}= C_2\) with \(d_1 = 1\), \(d_2 = 2\) and its Langlands dual is \({}^L{{\mathfrak {g}}}= B_2\). We also have \(\left( {}^L{\mathfrak {g}}\right) ' = A_3\), but with the nodes 1 and 3 exchanged in comparison with the original \({{\mathfrak {g}}}'\), and \(^L{\widehat{{{\mathfrak {g}}}}} = D_3^{(2)}\).
Then, the algebra \(U_q(\widehat{{{\mathfrak {g}}}'}) = U_q(A_3^{(1)})\) acts on its 6-dimensional fundamental representation \(W = L(Y_{2,1})\) whose q-character is
We have the Q-operators \(Q_i^\pm (z,u) = t_{R_i^\pm }(z,u)\) associated with the prefundamental representations \(R_i^+(z), i=1,2,3\), of \(U_q(\widehat{{{\mathfrak {g}}}'})\). The roots of the corresponding Baxter polynomials satisfy the BAE (4.7) of type \(A_3^{(1)}\). Now we consider the subspace W(u) of W where the actions of \(Q_1^{\pm ,\text {ss}}(z,u)\) and \(Q_3^{\pm ,\text {ss}}(z,u)\) coincide. We also have the 4-dimensional subspace \(\widehat{W}\subset W\) which is the direct sum of the \(\sigma \)-invariant weight subspaces W and the subspace \(\widetilde{W}\) which is the direct sum of the \(\ell \)-weight subspaces corresponding to the \(\sigma \)-invariant \(\ell \)-weights (or monomials in the q-character).
In the present case, all \(\sigma \)-invariant weights have multiplicity 1. Therefore, by Remark 5.5,(2), for all values of u we have
Thus, part (i) of Conjecture 5.15 is verified in this case.
This implies that only \(\sigma \)-invariant solutions of the BAE (4.7) appear in this case. Identifying the eigenvalues of the operators \(Q_1^{\pm ,\text {ss}}(z) = Q_3^{\pm ,\text {ss}}(z)\), we obtain the folded BAE (4.8) corresponding to the Lie algebra \({{\mathfrak {g}}}= C_2\).
The q-character of the subspace \(\widetilde{W}\) is given by the formula
Setting \(\widetilde{Y}_{1,q} = Y_{1,q}Y_{3,q}\), one gets
The corresponding character
is equal to the character of a fundamental representation of \(U_t({}^L\widehat{{\mathfrak {g}}}) = U_t(D_3^{(2)})\). Thus, part (ii) of Conjecture 5.15 is verified.
Finally, we discuss Conjecture 5.16 in the present case. We have the interpolating (q, t)-character (6.7) of the second fundamental representation of \(U_q(C_2^{(1)})\) studied in Example 6.7. We verify Conjecture 5.16:
The specialization of the interpolating (q, t)-character (6.7) under \(\Pi _t\) is equal to the t-character of the fundamental representation M(W) of \(U_t({}^L{\widehat{{{\mathfrak {g}}}}}) = U_t(D_3^{(2)})\).
Its specialization under \({\overline{\Pi }}_t\) is the folded t-character of the \(U_t(\widehat{{{\mathfrak {g}}}'}) = U_t(A_3^{(1)})\)-module W.
Its specialization under \(\Pi _t'\) is (after switching the indices 1 and 2) the folded t-character of \(W'\), the fundamental representation \(L(Y_{1,1})\) of \(U_t(A_3^{(1)})\), defined in terms of the variables \({\overline{Y}}_{i,a}\) instead of \(Y_{i,a}\).
Thus, we find that both Conjectures 5.15 and 5.16 hold in this case. In other words, we obtain an example of the folded quantum integrable system associated with \({{\mathfrak {g}}}=C_2\) whose spectra correspond to the solutions of the folded BAE equation (4.8) associated with \({{\mathfrak {g}}}=C_2\), with the space of states being isomorphic to a representation of \(U_q({}^L{\widehat{{{\mathfrak {g}}}}} = D_3^{(2)})\).
7.2 Second example: representation \(L(Y_{1,1}Y_{2n-1,1})\) of \(U_q(A_{2n-1}^{(1)})\)
We work with the Lie algebras \({{\mathfrak {g}}}' = A_{2n-1}\), \({{\mathfrak {g}}}= C_n\), \({}^L{{\mathfrak {g}}}= B_n\), \(\left( {}^L{\mathfrak {g}}\right) ' = D_{n+1}\) and \(^L{\widehat{{{\mathfrak {g}}}}} = D_{n+1}^{(2)}\) (we assume that \(n\ge 2\)).
Consider the representation \(W=L(Y_{1,1}Y_{2n-1,1})\) of \(U_q(A_{2n-1}^{(1)})\). It is \(4n^2\)-dimensional and is isomorphic to the tensor product of the fundamental representations \(L(Y_{1,1})\otimes L(Y_{2n-1,1})\). Its q-character has 2n \(\sigma \)-invariant monomials, including one with multiplicity 2:
All weight subspaces of W are one-dimensional, except for the 0-weight subspace \(W_0\) of W which is 2n-dimensional, containing as a proper subspace its intersection with \(\widetilde{W}\), which is the 2-dimensional \(\ell \)-weight space associated with the \(\sigma \)-invariant monomial \(Y_{n,q^{n-1}}Y_{n,q^{n+1}}^{-1}\) (the other \(n-1\) monomials of weight 0 are not \(\sigma \)-invariant). This \(\ell \)-subspace is therefore precisely the intersection \(\widetilde{W} \cap W_0\), and Lemma 5.2,(2) implies that \(\widehat{\sigma }\) preserves this \(\ell \)-weight subspace. We are going to show that \(\widehat{\sigma }\) acts on it as the identity.
Let v be a generating vector of the weight subspace \(W_{\alpha _n}\), which is one-dimensional, and hence is an \(\ell \)-weight subspace. The corresponding monomial is \(Y_{n,q^{n-1}}^2Y_{n-1,q^n}^{-1}Y_{n-1,q^n}^{-1}\). Under the action of the \(U_q(\widehat{{{\mathfrak {s}}}{{\mathfrak {l}}}}_2)\) subalgebra corresponding to the node n, the vector v generates a representation of dimension 4 with a 2-dimensional 0-weight space, which is spanned by the \(x_{n,m}^-.v\), \(m\in {\mathbb {Z}}\). Since \(W_{\alpha _n}\) is preserved by \(\widehat{\sigma }\), it follows that \(\widehat{\sigma }(v) = \pm v\). In fact, it is easy to see that \(\widehat{\sigma }(v) = v\) by restricting W to \(U_q({{\mathfrak {g}}})\) and taking the limit \(q \rightarrow 1\). Then, W decomposes into the direct sum of the adjoint representation of \(A_{2n-1}\) and the trivial one-dimensional representation, and the weight subspace \(W_{\alpha _n}\) appears in the former. It is easy to see that the operator \(\widehat{\sigma }\) acts on the adjoint representation as the automorphism induced by the automorphism \(\sigma \) of the Dynkin diagram of \(A_{2n-1}\) (whose invariant Lie subalgebra is \(C_n\)). From this we readily obtain that \(\widehat{\sigma }\) acts as the identity on \(W_{\alpha _n}\).
Next, we have \(\sigma (x_{n,m}^-) = x_{n,m}^-\) for any \(m\in {\mathbb {Z}}\), so we obtain that \(\widehat{\sigma }(x_{n,m}^-.v) = x_{n,m}^-.v\). This implies that the vectors in \(\widetilde{W}\cap W_0\) are indeed \(\widehat{\sigma }\)-invariant. This implies that \(\widetilde{W}^\sigma = \widetilde{W}\).
Now we derive from this that for generic u the intersection \(W(u) \cap W_0\) is two-dimensional.
We have the 2n-dimensional weight subspace \(W_0\) of W. By analyzing the q-character of W, we have found that it decomposes into a direct sum of \(n-1\) two-dimensional subspaces, each containing two \(\ell \)-weight subspaces corresponding to a pair of monomials \(M_1 \ne M_2\) such that \(\sigma (M_1)=M_2\) (and therefore \(\widehat{\sigma }\) interchanges them, according to Lemma 5.2,(2)), and the two-dimensional \(\ell \)-weight subspace corresponding to the \(\sigma \)-invariant monomial \(Y_{n,q^{n-1}}Y_{n,q^{n+1}}^{-1}\) on which \(\widehat{\sigma }\) acts as the identity, as we have shown above. This implies that the trace of \(\widehat{\sigma }\) on \(W_0\) is equal to 2.
On the other hand, \(W_0\) also has a basis of joint eigenvectors of \(Q_i^{\pm ,{\text {ss}}}(u), i \in I'\), with eigenvalues \(\lambda (u) = (\lambda ^\pm _i(u))\). By applying the argument of Lemma 5.2,(2), we find that \(\widehat{\sigma }\) maps such an eigenvector to another one with eigenvalues \(\sigma (\lambda (u))\). In the limit \(u \rightarrow 0\) the eigenspaces of \(Q_i^{\pm ,{\text {ss}}}(u), i \in I'\) become \(\ell \)-weight spaces. Hence, we find from the preceding paragraph that for generic u we have at least \(2(n-1)\) eigenvalues \(\lambda (u)\) which are not \(\sigma \)-invariant, and the set of these eigenvalues breaks into \(n-1\) pairs, with the eigenvalues in each pair (and the corresponding one-dimensional eigenspaces) exchanged by \(\sigma \). If the remaining 2 eigenvalues were not \(\sigma \)-invariant, then the corresponding 2 one-dimensional eigenspaces would have to be exchanged by \(\sigma \). But then the trace of \(\widehat{\sigma }\) on \(W_0\) would be equal to 0, which is a contradiction. Therefore, for generic u there must be one \(\sigma \)-invariant eigenvalue \(\lambda (u)\) with multiplicity 2, such that the corresponding two-dimensional eigenspace is \(\widehat{\sigma }\)-invariant (this is the necessary condition for the trace of \(\widehat{\sigma }\) on this subspace, and hence on \(W_0\), to be equal to 2). But then this two-dimensional subspace is contained in W(u), and moreover in \(W^\sigma (u)\). This implies that \(W(u) \cap W_0 = W^\sigma (u) \cap W_0\) is two-dimensional.
Since the other weight spaces are 1-dimensional, it follows from Remark 5.5,(2) that for generic u we have
as vector spaces graded by \(^L{{\mathfrak {g}}}\)-weights, in agreement with Conjecture 5.15,(1). Moreover, we obtain that \(W(u) = W^\sigma (u)\).
Now, setting \(\widetilde{Y}_{i,a} = Y_{i,a}Y_{2n-i,a}\) for \(1\le i\le n-1\), we obtain that
The corresponding character is
which coincides with the character of the \((2n+2)\)-dimensional fundamental representation M(W) of \(U_t({}^L\widehat{{\mathfrak {g}}}) = U_t(D_{n+1}^{(2)})\). Moreover, as we will see below, the specialization \(\Pi _t\) of corresponding interpolating (q, t)-character gives rise to the t-character of this representation of \(U_t(D_{n+1}^{(2)})\).
The above character can also be interpreted as the character of the direct sum of the \((2n+1)\)-dimensional fundamental representation and the trivial representation of \(U_t(\widehat{{}^L{\mathfrak {g}}}) = U_t(B_{n}^{(1)})\). But we cannot obtain its t-character from the interpolating (q, t)-character below because this t-character contains the monomial 1 (compare with the discussion in Remark 5.5,(3)).
The interpolating (q, t)-character of the simple representation \(L(Y_{1,q^{-1}}Y_{1,q})\) of \(U_q(C_n^{(1)})\) is given by formula (6.8) in Example 6.8 for \(n = 2\). For general n, the statements about its specializations follow from Proposition 6.10:
Its specialization under \({\overline{\Pi }}_t\) it is equal to \(^{{\text {f}}}\chi _t(W)\).
Its specialization under \(\Pi _t\) is the t-character of the fundamental representation M(W) of \(U_t({}^L\widehat{{\mathfrak {g}}}) = U_t(D_{n+1}^{(2)})\).
Its specialization under \(\Pi _t'\) is (after switching the indices i and \(n + 1 -i\)) is the folded t-character of \(W'\), the fundamental representation \(L(Y_{n,1})\) of \(U_t(A_{2n - 1}^{(1)})\), defined in terms of the variables \({\overline{Y}}_{i,a}\) instead of \(Y_{i,a}\).
All of this is in agreement with Conjectures 5.15 and 5.16.
7.3 Third example: the fundamental representation \(L(Y_{3,1})\) of \(U_q(A_5^{(1)})\)
Consider the Lie algebra \({{\mathfrak {g}}}'\) of type \(A_5\) with \(\sigma \) being the unique automorphism of the Dynkin diagram of order 2. Then, \({{\mathfrak {g}}}= C_3\) with \(d_1 = d_2 = 1\), \(d_3 = 2\) and its Langlands dual Lie algebra is \({}^L{{\mathfrak {g}}}= B_3\). We also have \(\left( {}^L{\mathfrak {g}}\right) ' = D_4\) and \(^L{\widehat{{{\mathfrak {g}}}}} = D_5^{(2)}\).
The fundamental representation \(L(Y_{3,1})\) of \(U_q(\widehat{{{\mathfrak {g}}}'}) = U_q(A_5^{(1)})\) is 20-dimensional. It has 8 invariant monomials:
In this case, all ordinary weights have multiplicity 1. Therefore, Remark 5.5,(2) implies that for any u we have
Setting \(\widetilde{Y}_{1,a} = Y_{1,a}Y_{5,a}\) and \(\widetilde{Y}_{2,a} = Y_{2,a}Y_{4,a}\), we obtain that \(\chi _q(\widetilde{W})\) equals
The corresponding character is
which is the character of the third fundamental representation M(W) of \(U_t({}^L\widehat{{\mathfrak {g}}}) = U_t(D_5^{(2)})\).
Actually, it is also the character of the fundamental representation \(L(Y_{3,1})\) of \(U_t(\widehat{{}^L{{\mathfrak {g}}}}) = U_t(B_3^{(1)})\). But we cannot obtain the t-character of this representation from the interpolating (q, t)-character, whereas we can do it for the third fundamental representation of \(U_t(D_5^{(2)})\) (see the discussion in Remark 5.5,(3)).
In fact, the interpolating (q, t)-character of the simple representation \(L(Y_{3,1})\) of \(U_q(\widehat{{{\mathfrak {g}}}}) = U_q(C_3^{(1)})\) was computed in [18, Section 4.5] (note however that there was a typo there for the monomials \(Y_{2,q^5t^3}\) and \(Y_{2,q^7t^5}\), which we correct here):
There are 14-monomials, 8 with multiplicity 1 and 6 with multiplicity \(\alpha \).
Its specialization under \({\overline{\Pi }}_t\), has 20 terms, and it is equal to \(\chi _t(W)\) after identification of the variables \(Y_{1,a} \sim Y_{5,a}\), \(Y_{2,a} \sim Y_{4,a}\).
Its specialization under \(\Pi _t\) has 8 terms:
and is the t-character of the fundamental representation M(W) of \(U_t({}^L\widehat{{\mathfrak {g}}}) = U_t(D_5^{(2)})\).
Its specialization under \(\Pi _t'\) is the folded t-character
of the fundamental representation \(L(Y_{3,1})\) of \(U_t\left( \widehat{\left( {}^L{\mathfrak {g}}\right) '}\right) = U_t(D_4^{(1)})\), defined in terms of the variables \({\overline{Y}}_{i,a}\) instead of \(Y_{i,a}\).
All of this is in agreement with Conjectures 5.15 and 5.16.
7.4 Fourth example: the trivalent fundamental representation \(L(Y_{1,1})\) of \(U_q(D_4^{(1)})\)
Now we consider the Lie algebra \({{\mathfrak {g}}}'\) of type \(D_4\) with an automorphism \(\sigma \) of order 3 and denote by \(i = 1\) the trivalent node. Then, \({{\mathfrak {g}}}= G_2\) with \(d_1 = 3\), \(d_2 = 1\) and its Langlands dual Lie algebra is \({}^L{{\mathfrak {g}}}= G_2\) with \(d_1^\vee = 1\) and \(d_2^\vee = 3\). We also have \(\left( {}^L{\mathfrak {g}}\right) ' = D_4\) (but with the trivalent node now being \(i = 2\)) and \(^L{\widehat{{{\mathfrak {g}}}}} = D_4^{(3)}\).
Let us consider the example of the fundamental representation \(W = L(Y_{1,1})\) of \(U_q(\widehat{{{\mathfrak {g}}}'}) = U_q(D_4^{(1)})\). Its q-character is computed in [50, Example 5.3.2]. It has 27 monomials, all of multiplicity 1 except one (\(Y_{1,q^2}Y_{1,q^4}^{-1}\)) of multiplicity 2. It has 8 invariant monomials for an automorphism \(\sigma \) of order 3, including one of multiplicity 2:
All weight spaces of W are one-dimensional, except for the 0-weight space \(W_0\) of W which is 5-dimensional, containing as a proper subspace its intersection with \(\widetilde{W}\), which is the 2-dimensional \(\ell \)-weight space associated with \(Y_{1,q^2}Y_{1,q^4}^{-1}\) (the other 3 monomials of weight 0 are \(Y_{2,q}Y_{2,q^5}^{-1}\), \(Y_{3,q}Y_{3,q^5}^{-1}\), \(Y_{4,q}Y_{4,q^5}^{-1}\), which are not \(\sigma \)-invariant).
Let v be a generating vector of the weight space \(W_{\alpha _1}\), which is one-dimensional and whose corresponding monomial is \(Y_{1,q^2}^2Y_{2,q}^{-1}Y_{3,q}^{-1}Y_{4,q}^{-1}\). Under the action of the \(U_q(\widehat{{{\mathfrak {s}}}{{\mathfrak {l}}}}_2)\)-subalgebra corresponding to the node 1, the vector v generates a representation of dimension 4 with a 2-dimensional 0-weight space. We obtain as in Sect. 7.2 above that for generic u we have \({\text {dim}} W(u)\cap W_0 = {\text {dim}} \widetilde{W}\cap W_0 = 2\).
Since the other weight spaces are 1-dimensional, it follows from Remark 5.5,(2) that for generic u we have
as vector spaces graded by \(^L{{\mathfrak {g}}}\)-weights. Moreover, it follows that \(W^\sigma (u) = W(u)\) and \(\widetilde{W}^\sigma = \widetilde{W}\).
Setting \(\widetilde{Y}_{2,a} = Y_{2,a}Y_{3,a}Y_{4,a}\), we obtain that
The corresponding character
is the character of the first fundamental representation M(W) of \(U_t({}^L\widehat{{\mathfrak {g}}}) = U_t(D_4^{(3)})\).
Note that it is also the character of the direct sum of the first fundamental representation and the trivial one-dimensional representation of \(U_t(\widehat{{}^L{{\mathfrak {g}}}}) = U_t(G_2^{(1)})\). Therefore, we cannot obtain the t-character of this representation of \(U_t(G_2^{(1)})\) from the corresponding interpolating (q, t)-character, whereas we can do it for the first fundamental representation of \(U_t(D_4^{(3)})\) (compare with the discussion in Remark 5.5,(3)).
In fact, the interpolating (q, t)-character of the simple representation \(L(Y_{1,1})\) of \(U_q(G_2^{(1)})\) was computed in [18, Section 5.2]. It has 15 monomials, 8 with multiplicity 1 and 7 with multiplicity \(\alpha \).
Its specialization under \({\overline{\Pi }}_t\) has 29 terms and is equal to \(^{{\text {f}}}\chi _t(W)\).
Its specialization under \(\Pi _t\), has 8 terms:
and is the t-character of the fundamental representation M(W) of \(U_t({}^L\widehat{{\mathfrak {g}}}) = U_t(D_4^{(3)})\).
Its specialization under \(\Pi _t'\) is the folded t-character
of the fundamental representation \(L(Y_{1,1})\) of \(U_t\left( \widehat{\left( {}^L{\mathfrak {g}}\right) }'\right) = U_t(D_4^{(1)})\), defined in terms of the variables \({\overline{Y}}_{i,a}\) instead of \(Y_{i,a}\).
All of this is in agreement with Conjectures 5.15 and 5.16.
7.5 Fifth example: a simple tensor product of 4 fundamental representations of \(U_q(A_3^{(1)})\)
Here we study an example in which \({\overline{W}}(u)\) is not equal to the whole space W(u).
We work with the same Lie algebras \({{\mathfrak {g}}}' = A_3\), \({{\mathfrak {g}}}= C_2\), \({}^L{{\mathfrak {g}}}= B_2\), \(\left( {}^L{\mathfrak {g}}\right) ' = A_3\) and \(^L{\widehat{{{\mathfrak {g}}}}} = D_3^{(2)}\) as in the first example.
Consider the following simple tensor product of 4 fundamental representations of \(U_q (\widehat{{{\mathfrak {g}}}'}) = U_q(A_3^{(1)})\),
Its highest monomial \(Y_{1,1}^2Y_{3,1}^2\) is \(\sigma \)-invariant.
It is the tensor square of the 16-dimensional representation \(W_1 = L(Y_{1,1}Y_{3,1})\) studied in Sect. 7.2 (with \(n = 2\)), whose invariant subspace \(\widetilde{W}_1 = W_1(0)\) has dimension 6. Its dimension is 256, and its subspace \(\widetilde{W} = W(0)\) contains a subspace of dimension \(6^2 = 36\) corresponding to the square of the q-character of the invariant subspace \(\widetilde{W}_1\) of \(L(Y_{1,1}Y_{3,1})\):
However, the analysis of the q-character
shows that \(\widetilde{W}\) is larger: it has dimension 54 and \(\chi _q(\widetilde{W})\) equals
But the corresponding character is not equal to the character of a representation of the twisted quantum affine algebra \(U_q(D_3^{(2)})\). Indeed, the dimensions of the simple \(U_q(D_3^{(2)})\)-modules whose highest \(^L{{\mathfrak {g}}}\)-weight is \(y_1^2\) are 36 (simple tensor square of the first fundamental representation), 35 (\(L(Z_{1,t}Z_{1,t^4})\)) or 32 (KR modules). The dimension of the remaining space and the multiplicity of the highest weight \(y_2^2\) within it are, respectively, 18 and \(2y_2^2\), 19 and \(2y_2^2\), 22 and \(3y_2^2\). But the dimension of the simple modules of highest weight \(y_2^2\) are 16 (simple tensor product of fundamental representation), 15 (\(L(Z_{2,t}Z_{2,t^4})\)) or 10 (KR modules). This means that this is not the character of a representation of \(U_q(D_3^{(2)})\).
Hence, in this case \({\overline{W}}(u)\) cannot be equal to the whole W(u). Rather, it should be a subspace of the space isomorphic to the one whose q-character is (7.2). We expect that M(W) is a simple tensor square of the first fundamental representation of \(U_q(D_3^{(2)})\). The computation of the specialization \(\Pi _t\) of the corresponding interpolating (q, t)-interpolating character confirms it.
We also note that M(W) is smaller than \(\widetilde{W}^\sigma \) in this case. Indeed, the weight spaces associated with the \(^L{{\mathfrak {g}}}\)-weights \(2\omega _1^\vee \), \(2\omega _2^\vee \) and \(\omega _1^\vee \) have respective dimensions 1, 4 and 8 in \(\widetilde{W}\) of dimension 54. The dimensions of the corresponding weight spaces in \(\widetilde{W}^\sigma \) are 1, 3 and 6 (indeed, denoting by v a highest weight vector of W, the generators for \(2\omega _2^\vee \) are \(x_{1,0}^-x_{3,0}^-.v\), \(x_{1,1}^-.x_{3,1}^-.v\), \((x_{1,0}^-x_{3,1}^-+x_{1,1}^-x_{3,0}^-).v\), and for \(\omega _1^\vee \) their images under the action of \(x_{2,0}^-\) and \(x_{2,1}^-\)). So the dimension of \(\widetilde{W}^\sigma \) is smaller than 51, and then by a symmetry argument (by considering the opposite weights), it is smaller than 48. We have seen that the dimensions of the simple modules over \(U_q(D_3^{(2)})\) of highest weight \(\omega _1^\vee \) are 36, 35 or 32. The dimension of the remaining space in \(\widetilde{W}^\sigma \) is smaller than 12, 13 and 20, respectively, and the multiplicity of the weights \(2\omega _2^\vee \), \(\omega _1^\vee \) within are, respectively, \(y_2^2 + 2y_1\), \(y_2^2 + 2y_1\) and \(2y_2^2 + 3y_1\). But the dimensions of the simple modules of highest weight \(2\omega _2^\vee \) are 16, 15 or 10. Only the last case is possible, and it corresponds to a KR-module which contributes to \(\omega _1^\vee \) with multiplicity 1. In all cases, the remaining space has dimension smaller than 3 with a space associated with \(\omega _1^\vee \) of dimension 1. This means that this is not the character of a representation of \(U_q(D_3^{(2)})\).
Now let us interpret this in terms of the interpolating (q, t)-character of the simple representation \(L(Y_{1,q^{-1}}Y_{1,q})^{\otimes 2}\) of \(U_q(C_2^{(1)})\), that is the square of the formula (6.8) studied in Example 6.8.
Its specialization under \({\overline{\Pi }}_t\) is equal to \(^{{\text {f}}}\chi _t(W)\).
Its specialization under \(\Pi _t\) is the t-character of the 36-dimensional simple representation \(M(W) = L(Z_{1,-1})^{\otimes 2}\) of \(U_t({}^L\widehat{{\mathfrak {g}}}) = U_t(D_3^{(2)})\).
Its specialization under \(\Pi _t'\) is (after switching the indices 1 and 2) the folded t-character of \(W'\), the 36-dimensional simple representation \(L(Y_{2,1})^{\otimes 2}\) of \(U_t(A_3^{(1)})\), defined in terms of the variables \({\overline{Y}}_{i,a}\) instead of \(Y_{i,a}\).
8 Connection to monomial crystals
In this section, we formulate a conjecture linking folded t-characters to Kashiwara’s extension of Nakajima’s monomial model of crystals to non-simple laced Lie algebras. We have previously mentioned it in Remark 3.1,(2).
Recall that a \({\mathfrak {g}}\)-crystal is a set C together with an assignment to each element \(c\in C\) a \({\mathfrak {g}}\)-weight \(\text {wt}(c)\); the crystal operators \(\widetilde{e}_i,\widetilde{f}_i : C\rightarrow C\sqcup \{0\}, i \in I\) (crystallized versions of Chevalley operators of \(U_q({\mathfrak {g}})\)); and maps \(\epsilon _i,\phi _i : C\rightarrow {\mathbb {Z}}\) satisfying the axioms of the crystal theory (in general, \(\epsilon _i,\phi _i\) could have infinite values, but we do not consider this possibility here). There is a corresponding notion of morphisms and isomorphisms of \({\mathfrak {g}}\)-crystals as well as that of \({\mathfrak {g}}\)-subcrystals. For example, each simple finite-dimensional representation \(V(\lambda )\) of \(U_q({\mathfrak {g}})\) of highest weight \(\lambda \) is known to have a crystal basis. The set of its elements has the structure of a \({\mathfrak {g}}\)-crystal, which is denoted by  . This \({\mathfrak {g}}\)-crystal is called a simple crystal and it has various realizations. One of them is the monomial crystal which was introduced by Nakajima [51] and further studied by Kashiwara [38]. We now recall the definition.
. This \({\mathfrak {g}}\)-crystal is called a simple crystal and it has various realizations. One of them is the monomial crystal which was introduced by Nakajima [51] and further studied by Kashiwara [38]. We now recall the definition.
Let \(s:I\rightarrow \{0,1\}\) (\(i\mapsto s_i\)) be a map such that \(C_{i,j}\le -1\) implies \(s_i+s_j=1\). Consider the set of monomials  generated by the \(Y_{i,q^{r}}^{\pm 1}\) such that \(r \equiv s_i \text { mod } [2]\).
generated by the \(Y_{i,q^{r}}^{\pm 1}\) such that \(r \equiv s_i \text { mod } [2]\).
For  , define its \({\mathfrak {g}}\)-weight by the formula
, define its \({\mathfrak {g}}\)-weight by the formula
Next, set for \(i\in I\),
Finally, define  for \(i\in I\) by the formulas
for \(i\in I\) by the formulas
where the \(A_{j,q^d}\) are given by formula (3.10) and
Theorem 8.1
-
(1)
The collection
 is a \({\mathfrak {g}}\)-crystal. It is called the monomial crystal.
is a \({\mathfrak {g}}\)-crystal. It is called the monomial crystal. -
(2)
For a dominant
 , let
, let  be the \({\mathfrak {g}}\)-subcrystal generated by m. Then,
be the \({\mathfrak {g}}\)-subcrystal generated by m. Then,  is isomorphic, as a \({\mathfrak {g}}\)-crystal, to
is isomorphic, as a \({\mathfrak {g}}\)-crystal, to  .
.
For example, for \({\mathfrak {g}} = A_2\) we have

and for \({\mathfrak {g}} = C_2\) we have

Observe that the first set (8.1) is the set of monomials of the q-character of a fundamental representation of \(U_q(A_2^{(1)})\), but the second set (8.2) in not the set of monomials of the q-character of a representation of \(U_q(C_2^{(1)})\).
In fact, if \({{\mathfrak {g}}}\) is a simply laced Lie algebra, there is a precise relation between the monomial crystals and the q-characters of modules over \(U_q({\widehat{{{\mathfrak {g}}}}})\) discovered by Nakajima [51]. Namely, it is proved in [51, Theorem 3.3] that for a dominant monomial m in  , the set
, the set  of monomials (without multiplicities) of the q-character of the standard module V(m) associated with m (i.e. V(m) is the corresponding tensor product of the fundamental representations) is a \({\mathfrak {g}}\)-subcrystal of the monomial crystal
of monomials (without multiplicities) of the q-character of the standard module V(m) associated with m (i.e. V(m) is the corresponding tensor product of the fundamental representations) is a \({\mathfrak {g}}\)-subcrystal of the monomial crystal  (in particular, its union with \(\{0\}\) is stable by the crystal operators). Moreover, for each dominant \({{\mathfrak {g}}}\)-weight \(\lambda \), there is a choice of a dominant monomial
(in particular, its union with \(\{0\}\) is stable by the crystal operators). Moreover, for each dominant \({{\mathfrak {g}}}\)-weight \(\lambda \), there is a choice of a dominant monomial  of weight \(\text {wt}(m) = \lambda \) so that the \({{\mathfrak {g}}}\)-crystal
of weight \(\text {wt}(m) = \lambda \) so that the \({{\mathfrak {g}}}\)-crystal  is equal to
is equal to  . By Theorem 8.1,(2),
. By Theorem 8.1,(2),  is isomorphic, as a \({\mathfrak {g}}\)-crystal, to the corresponding simple crystal
is isomorphic, as a \({\mathfrak {g}}\)-crystal, to the corresponding simple crystal  [51, Proposition 3.4] (for a fundamental weight \(\lambda = \omega _i\) we can choose \(m = Y_{i,a}\)).
[51, Proposition 3.4] (for a fundamental weight \(\lambda = \omega _i\) we can choose \(m = Y_{i,a}\)).
We will now conjecture an analogous result for non-simply laced \({{\mathfrak {g}}}\), with the q-characters of representations of quantum affine algebras in  replaced by the t-characters in the folded t-character ring
replaced by the t-characters in the folded t-character ring  introduced in Sect. 4.4. Note that we now denote the quantum parameter in
introduced in Sect. 4.4. Note that we now denote the quantum parameter in  by t instead of q to fit the notation of the previous sections.
by t instead of q to fit the notation of the previous sections.
Conjecture 8.2
-
(1)
The set of monomials (without multiplicities) of a product of the fundamental elements
 , with
, with  , is a \({\mathfrak {g}}\)-subcrystal of the monomial crystal
, is a \({\mathfrak {g}}\)-subcrystal of the monomial crystal  .
. -
(2)
For each dominant weight \(\lambda \), there is a product of the fundamental elements \(F(Y_{i,a})\) with highest monomial
 of weight \(\lambda \) whose set of monomials is equal to
of weight \(\lambda \) whose set of monomials is equal to  and hence is a \({\mathfrak {g}}\)-crystal isomorphic to
and hence is a \({\mathfrak {g}}\)-crystal isomorphic to  . \(\square \)
. \(\square \)
In particular, for \(i\in I\), we expect that the set of monomials (without multiplicities) occurring in  is equal to
is equal to  and so is isomorphic, as a \({\mathfrak {g}}\)-crystal, to
and so is isomorphic, as a \({\mathfrak {g}}\)-crystal, to  . We also expect that \(\widetilde{W} = W'\) in this case (see Conjecture 5.16).
. We also expect that \(\widetilde{W} = W'\) in this case (see Conjecture 5.16).
For example, we have the following element in  :
:
The set of its monomials is the set (8.2), which is equal to  , and so it is isomorphic, as a \({\mathfrak {g}}=C_2\)-crystal, to
, and so it is isomorphic, as a \({\mathfrak {g}}=C_2\)-crystal, to  .
.
One of our motivations for this conjecture in the following. Consider the representation \(L(\widetilde{Y}_{i,1})\) of \(U_q(\widehat{\left( {}^L{\mathfrak {g}}\right) '})\). It is a simple tensor product of fundamental representations. By Theorem 8.1, the set of monomials of its q-character,  , has the structure of a simple \(\left( {}^L{\mathfrak {g}}\right) '\)-crystal.
, has the structure of a simple \(\left( {}^L{\mathfrak {g}}\right) '\)-crystal.
Now, the action of \(\sigma \) on  is an automorphism of \(\left( {}^L{\mathfrak {g}}\right) '\)-crystal. It then follows from the general results on crystals in [37] that the subset of monomials
is an automorphism of \(\left( {}^L{\mathfrak {g}}\right) '\)-crystal. It then follows from the general results on crystals in [37] that the subset of monomials  fixed by \(\sigma \) has the structure of a simple \({}^L({}^L{{\mathfrak {g}}}) = {{\mathfrak {g}}}\)-crystal isomorphic to
fixed by \(\sigma \) has the structure of a simple \({}^L({}^L{{\mathfrak {g}}}) = {{\mathfrak {g}}}\)-crystal isomorphic to  .
.
On the other hand, the identification of variables \(Y_{j,b}\equiv Y_{j,\sigma (b)}\) is injective on  . Hence, the set
. Hence, the set  can be identified with a subset
can be identified with a subset  of the set of monomials of the folded t-character
of the set of monomials of the folded t-character

Hence, this subset  inherits the structure of a simple \({{\mathfrak {g}}}\)-crystal.
inherits the structure of a simple \({{\mathfrak {g}}}\)-crystal.
In Proposition 6.10, we have established that \(\chi _t^L(L(\widetilde{Y}_{i,a}))\) is the specialization of the interpolating (q, t)-character  under \({\overline{\Pi }}_t\). But the specialization under \(\Pi _t'\) of the same interpolating (q, t)-character \(F_{q,t}(W_{i,1})\) is
under \({\overline{\Pi }}_t\). But the specialization under \(\Pi _t'\) of the same interpolating (q, t)-character \(F_{q,t}(W_{i,1})\) is  (defined in terms of the variables \({\overline{Y}}_{j,b}\) instead of \(Y_{j,b}\)).
(defined in terms of the variables \({\overline{Y}}_{j,b}\) instead of \(Y_{j,b}\)).
We expect that the monomials of \(F({\overline{Y}}_{i,1})\) correspond through this interpolation to the monomials in the subset  , and so the set of these monomials should inherit the structure of a \({{\mathfrak {g}}}\)-crystal. This leads us to the statement of Conjecture 8.2. Proving this identification requires a finer analysis. We plan to come back to this question in another paper.
, and so the set of these monomials should inherit the structure of a \({{\mathfrak {g}}}\)-crystal. This leads us to the statement of Conjecture 8.2. Proving this identification requires a finer analysis. We plan to come back to this question in another paper.
For example, consider \({\mathfrak {g}} = C_2\) as above. Then, \(\left( {}^L{\mathfrak {g}}\right) ' = A_3\) and the set of monomials of \(L(\widetilde{Y}_{1,1}) \simeq L(Y_{1,0})\otimes L(Y_{3,1})\) has 15 elements

(\(Y_{2,1}Y_{2,3}^{-1}\) occurs with multiplicity 2 in the q-character). The set of fixed monomials is

It has the structure of a \(C_2\)-crystal isomorphic to  by the general results mentioned above. In this explicit example, we can check directly that the above identification gives the \(C_2\)-crystal (8.2). Indeed, by folding, this set is identified with
by the general results mentioned above. In this explicit example, we can check directly that the above identification gives the \(C_2\)-crystal (8.2). Indeed, by folding, this set is identified with

which is a subset of the set of monomials of \(\chi _t^f(L(\widetilde{Y}_{1,1}))\). The corresponding interpolating (q, t)-character \({\overline{F}}_{q,t}(W_{1,1})\) is given by Formula (6.8) in type \(B_2\) (with 1 and 2 exchanged), see Example 6.8. Its specialization under \({\overline{\Pi }}_t\) is the folded t-character of the representation \(L(\widetilde{Y}_{1,1})\) above. Its specialization under \(\Pi _t'\) is the t-character of an element in  , whose set of monomials is the set
, whose set of monomials is the set  and is equal to
and is equal to
Exchanging the indices 1 and 2, we recover the set (8.2) (with the variables \({\overline{Y}}_{i,a}\) instead of the \(Y_{i,a}\)) as expected.
9 The Gaudin model
In this section, we consider the Gaudin limit of the folded integrable model discussed above. In this case, Bethe Ansatz equations simplify and we can study more directly the links between the objects associated with the Lie algebras \({{\mathfrak {g}}}, {}^L{{\mathfrak {g}}}\), and \({{\mathfrak {g}}}'\).
9.1 The appearance of \(^L{{\mathfrak {g}}}\)
First, some general observations about finite-dimensional representations of these three Lie algebras. Recall that \({{\mathfrak {g}}}'\) is a simply laced Lie algebra with an automorphism \(\sigma \) of order 2 or 3, and \({{\mathfrak {g}}}\) is its Lie subalgebra of \(\sigma \)-invariant elements. Let \({{\mathfrak {h}}}'\) be a Cartan subalgebra of \({{\mathfrak {g}}}'\). Then, its subspace \( {{\mathfrak {h}}}\) of \(\sigma \)-invariant elements is a Cartan subalgebra of \({{\mathfrak {g}}}\).
Consider for simplicity the case when \(\sigma \) has order 2. The case of order 3 can be analyzed in a similar way.
The Cartan subalgebra \({{\mathfrak {h}}}'\) is generated by the coroots \(\check{\alpha }'_i, i \in I'\). Here \(I'\) is the set of vertices of the Dynkin diagram of \({{\mathfrak {g}}}'\). Recall that \(\sigma \) acts on \(I'\), and the set I of vertices of the Dynkin diagram of \({{\mathfrak {g}}}\) is the quotient of \(I'\) by this action. For each \(i \in I\), let \(J_i\) be the preimage of i in \(I'\). It either consists of one element stable by \(\sigma \), or two elements exchanged by \( \sigma \). The coroot generators \(\check{\alpha }_i, i \in I\), of \({{\mathfrak {h}}}\) are
In other words, they have the form
Consider now the dual spaces \(({{\mathfrak {h}}}')^*\) and \({{\mathfrak {h}}}^*\). We have a surjective map \( ({{\mathfrak {h}}}')^* \twoheadrightarrow {{\mathfrak {h}}}^*\) dual to the inclusion \({{\mathfrak {h}}}\hookrightarrow {{\mathfrak {h}}}'\). We can try to embed \({{\mathfrak {h}}}^*\) into \( ({{\mathfrak {h}}}')^*\) so that the pairing between the image of this embedding of \({{\mathfrak {h}}}^*\) and \({{\mathfrak {h}}}\subset {{\mathfrak {h}}}'\) is the pairing we have on \({{\mathfrak {h}}}\), but then an interesting thing happens: if \(\sigma (i)=i\), then we can take as the image of the corresponding fundamental weight \(\omega _i\) of \({{\mathfrak {g}}}\) in \(({{\mathfrak {h}}}')^*\) to be equal to \(\omega '_i\), the ith fundamental weight of \({{\mathfrak {g}}}'\). But if \(\sigma (i) \ne i\), then we have to take half the sum of the fundamental weights:
Indeed, we need to have \(\langle \omega _i,\check{\alpha }_j \rangle = \delta _{ij}\), and then formula (9.2) shows that we must insert the factor \(\frac{1}{2}\). The same factor appears in the expressions for the simple roots of \({{\mathfrak {g}}}\).
This has an important consequence: the integral weight lattice associated with \({{\mathfrak {g}}}\) does not embed into the integral weight lattice of \({{\mathfrak {g}}}'\). Instead, we have an embedding of the integral weight lattice associated not with \({{\mathfrak {g}}}\) but with \(^L{{\mathfrak {g}}}\)—the Langlands dual Lie algebra!—into the integral weight lattice of \({{\mathfrak {g}}}'\).
Actually, this is clear from the fact that \(^L{{\mathfrak {h}}}= {{\mathfrak {h}}}^*\), and so \(({}^L{{\mathfrak {h}}})^* = {{\mathfrak {h}}}\), which, as we have seen above, naturally embeds into \({{\mathfrak {h}}}'\). We then identify the latter with \( ({{\mathfrak {h}}}')^*\) using the unique W-invariant bilinear form normalized so that the square length of each root of \({{\mathfrak {g}}}'\) is equal to 2. Thus, we obtain an embedding \(({}^L{{\mathfrak {h}}})^* \hookrightarrow ({{\mathfrak {h}}}')^*\). Under this embedding, a fundamental weight of \(^L{{\mathfrak {g}}}\) is mapped to
Unlike formula (9.3), there is no factor \(\frac{1}{2}\) now. The same holds for the simple roots of \(^L{{\mathfrak {g}}}\). Thus, we have proved the statement of Lemma 5.14 that there is a natural isomorphism between the lattice of integral \(^L{{\mathfrak {g}}}\)-weights and the lattice of \(\sigma \)-invariant \({{\mathfrak {g}}}'\)-weights.
Now suppose that we have a finite-dimensional irreducible representation W of \({{\mathfrak {g}}}'\) whose highest weight \(\lambda \) is \(\sigma \)-invariant. By analogy with Lemma 5.2, we then prove that there is a unique automorphism \(\widehat{\sigma }\) of W which intertwines the representation of \({{\mathfrak {g}}}'\) on W with its \(\sigma \)-twist and acts as identity on the highest weight subspace. As in Sect. 5.6, define the subspace \(W^\sigma \subset W\) as the direct sum of the \(\widehat{\sigma }\)-invariant parts of the weight subspaces of W corresponding to \(\sigma \)-invariant weights. According to Proposition 5.18, its character is the character of a virtual representation of \(^L{{\mathfrak {g}}}\). In Sect. 9.7, we will show that in fact it is possible (modulo Conjecture 9.10) to explicitly embed the irreducible representation of \(^L{{\mathfrak {g}}}\) with the highest weight corresponding to \(\lambda \) into \(W^\sigma \).
So, an interesting switch happens: we start with a simply laced Lie algebra \({{\mathfrak {g}}}'\) with an automorphism \(\sigma \) whose fixed-point Lie subalgebra is \({{\mathfrak {g}}}\). Of course, every irreducible representation W of \({{\mathfrak {g}}}'\) restricts to a representation of \({{\mathfrak {g}}}\). However, because the integral weight lattice of \({{\mathfrak {g}}}\) does not embed into the integral weight lattice of \({{\mathfrak {g}}}'\), it’s not natural to describe it in terms of weight spaces corresponding to the \(\sigma \)-invariant weights of \({{\mathfrak {g}}}'\). Instead, it turns out that we can construct inside the direct sum of \(\sigma \)-invariant weight subspaces of W (actually, inside its subspace \(W^\sigma \)) an irreducible representation of the Langlands dual Lie algebra \(^L{{\mathfrak {g}}}\), which at first glance has nothing to do with \({{\mathfrak {g}}}'\). This can be done using the results of [13] on the spectra of the Hamiltonians of the Gaudin model.
Remark 9.1
In [17] and references therein, it was shown that representations of \(^L{{\mathfrak {g}}}\) can be extracted from irreducible finite-dimensional representations of \({{\mathfrak {g}}}\). In contrast, here we aim to extract representations of \(^L{{\mathfrak {g}}}\) from irreducible representations of \({{\mathfrak {g}}}'\). It would be interesting to see whether there is a connection between the two approaches. \(\square \)
9.2 Gaudin model for \({{\mathfrak {g}}}'\)
Here we discuss the Gaudin model associated with \({{\mathfrak {g}}}'\), more precisely, its modification with the twist parameter \(\chi ' \in {{\mathfrak {h}}}'\). It appears as the \(q \rightarrow 1\) limit of the XXZ-type quantum integrable model associated with \(U_q(\widehat{{{\mathfrak {g}}}'})\) (\(\chi '\) is the analogue of the parameter \(u \in H'\) of the XXZ-type model).
We will use the results of [12,13,14, 16, 58]. Let \(\lambda _k, k=1,\ldots ,N\), be a collection of dominant integral weights of \({{\mathfrak {g}}}'\). Denote by \(V'_{\lambda _k}\) the corresponding irreducible finite-dimensional representations of \({{\mathfrak {g}}}'\). For a collection \(z_k, k=1,\ldots ,N\), of distinct complex numbers, let \(V'_{\lambda _k}(z_k), k=1,\ldots ,N\), be the corresponding evaluation representations of the current algebra \({{\mathfrak {g}}}'[z]\). Consider their tensor product
and its subspace of weight
These are the spaces of states of the Gaudin model associated with \({{\mathfrak {g}}}'\).
Next we discuss the Bethe Ansatz equations. Their solutions are in one-to-one correspondence with the Miura \({{\mathfrak {g}}}'\)-opers on \({{\mathbb {C}}}{{\mathbb {P}}}^1\) with trivial monodromy representation. They can be represented by \({{\mathfrak {g}}}'\)-valued connections on \({{\mathbb {C}}}{{\mathbb {P}}}^1\) of the form
Here the \(f'_i, i \in I'\), are generators of the lower nilpotent subalgebra of \({{\mathfrak {g}}}'\), and we are using the above identification between \({{\mathfrak {h}}}'\) and \(({{\mathfrak {h}}}')^*\) by means of the normalized bilinear form; namely, \(\{ \check{\lambda }_k \}\) denote the elements of \({{\mathfrak {h}}}' \subset {{\mathfrak {g}}}'\) corresponding to \(\{ \lambda _k \in ({{\mathfrak {h}}}')^* \}\), and \(\{ \check{\alpha }'_i, i \in I' \}\) is the set of simple coroots of \({{\mathfrak {g}}}'\), which correspond to the simple roots \(\{ \alpha '_i, i \in I'\}\) under the identification \(({{\mathfrak {h}}}')^* \simeq {{\mathfrak {h}}}\).
We will assume that \(w_j\)’s are distinct complex numbers such that \(w_j \ne z_k\) for all j and k.
Proposition 9.1
[12, 14, 16] The condition that connection (9.7) has trivial monodromy is equivalent to the following system of Bethe Ansatz equations:
These equations can be obtained by taking the limit \(q \rightarrow 1\) of the Bethe Ansatz equations (4.7) of the XXZ-type model associated with \(U_q(\widehat{{{\mathfrak {g}}}'})\). The monic polynomial with the roots \(w_j\) where \(i_j=i\) (i.e. those points on \({{\mathbb {C}}}{{\mathbb {P}}}^1\backslash \infty \) at which the connection (9.7) has residue \(\check{\alpha }'_i\)),
is the analogue of the Baxter polynomial \(Q_i(z), i \in I'\) (see Theorem 5.3) in the Gaudin model.
Note that if we apply a permutation to the set of roots of each polynomial \(Q_i(z)\) (which we recall are assumed to be distinct) we also obtain a solution of the system (9.8). In what follows, by a solution of Bethe Ansatz equations we will understand an equivalence class of solutions under these permutations.
In [12, 14, 16] a joint eigenvector of the Gaudin Hamiltonians (Bethe vector) is constructed for each solution of the BAE (9.8). It is known, however, that for general \(\lambda _k\)’s and \(\gamma \) these Bethe vectors do not yield a basis of the weight subspace of (9.5) of weight \(\gamma \) given by formula (9.6). In fact, explicit examples have been constructed in [49] showing that for \(\chi = 0\) this is so even for generic \(z_k\)’s (and fixed \(\lambda _k\)’s and \(\gamma \)). We are not aware of such counterexamples for generic \(\chi '\), so it is possible that in this case Bethe vectors do yield a basis for generic \(z_k\)’s. For \(N=1\), this is the statement of Conjecture 9.10 below.
As explained in [16, Sect. 5.5] (in the case \(\chi '=0\), but the picture is similar for all \(\chi '\)) that the true parameters of the spectra of the quantum Gaudin Hamiltonians are not the Miura \({{\mathfrak {g}}}'\)-opers of the form (9.7) but rather \({{\mathfrak {g}}}'\)-opers on \({{\mathbb {C}}}{{\mathbb {P}}}^1\) with trivial monodromy, regular singularities at \(z_1,\ldots ,z_N\) with respective residues \(\check{\lambda }_1,\ldots ,\check{\lambda }_N\) (coweights of \({{\mathfrak {g}}}'\) corresponding to the weight \(\lambda _1,\ldots ,\lambda _N\)), and irregular singularity at \(\infty \) of order 2 with 2-residue corresponding to \(\chi '\) (see [13, 14] for more details). Denote the set of these \({{\mathfrak {g}}}'\)-opers by \({\text {Op}}^\chi _{(\check{\lambda }_i),(z_i)}({{\mathfrak {g}}}')\).
Theorem 9.2
[13] For any regular \(\chi ' \in {{\mathfrak {h}}}'\) and any collection \(z_1\ldots ,z_N\) there is a bijection between \({\text {Op}}^\chi _{(\check{\lambda }_i),(z_i)}({{\mathfrak {g}}}')\) and the spectrum of the Gaudin Hamiltonians on the space (9.5). Moreover, the eigenspace corresponding to every \({{\mathfrak {g}}}'\)-oper in \({\text {Op}}^\chi _{(\check{\lambda }_i),(z_i)}({{\mathfrak {g}}}')\) is always one-dimensional. In addition, for generic \(z_1\ldots ,z_N\) and \(\chi '\) the Gaudin Hamiltonians are diagonalizable.
In other words, for any regular \(\chi \) and general \(z_1\ldots ,z_N\) there is at most one Jordan block for each joint eigenvalue of the Gaudin Hamiltonians (this is expressed in [13, Corollary 5] as the statement that the commutative algebra of Gaudin Hamiltonians has a cyclic vector in (9.5)). Moreover, for generic \(\chi \) and \(z_1\ldots ,z_N\) all Jordan blocks have size 1 (see [13, Corollary 6]).
Following the argument in [16, Sect. 5.5] in the case \(\chi '=0\), one can show that every \({{\mathfrak {g}}}'\)-oper in \({\text {Op}}^\chi _{(\check{\lambda }_i),(z_i)}({{\mathfrak {g}}}')\) corresponds to a unique Miura \({{\mathfrak {g}}}'\)-oper of the form
where the \(w_j, j=1,\ldots ,m\), are distinct complex numbers such that \(w_j \ne z_k\) for all j and k; \(g_k, k=1,\ldots ,N\), and \(\widetilde{g}_j, i=1,\ldots ,m\), are elements of the Weyl group of \({{\mathfrak {g}}}'\); and \(\check{\rho }'\) is the sum of the dominant coweights of \({{\mathfrak {g}}}'\).
A Miura \({{\mathfrak {g}}}'\)-oper of the form (9.10), and the corresponding \({{\mathfrak {g}}}'\)-oper, are called non-degenerate (see [16, Sect. 5.2]) if \(g_k=1\) for all \(k=1,\ldots ,N\), and each \(\widetilde{g}_j\) is a simple reflection \(s_{i_j}\) from the Weyl group of \({{\mathfrak {g}}}'\). Since \(\check{\rho }' - s_{i_j}(\check{\rho }') = \check{\alpha }_{i_j}'\), a Miura \({{\mathfrak {g}}}'\)-oper of the form (9.10) is non-degenerate \({{\mathfrak {g}}}'\)-oper if and only if it has the form (9.7). Further, according to Proposition 9.1, the no-monodromy condition is then equivalent to BAE (9.8).
Theorem 9.2 implies that non-degenerate Miura \({{\mathfrak {g}}}'\)-opers of the form (9.7) satisfying (9.8) correspond to a subset in the spectrum of the Gaudin Hamiltonians on the weight subspace of (9.5) of weight \(\gamma \). But in general, this is not the entire spectrum; there may be other joint eigenvalues of the Gaudin Hamiltonians on this weight subspace which correspond to degenerate Miura \({{\mathfrak {g}}}'\)-opers of the form (9.10) with at least one \(g_k\) not equal to the identity or at least one of the \(\widetilde{g}_j\) not equal to a simple reflection, or both. For such Miura \({{\mathfrak {g}}}'\)-opers, the equations expressing the no-monodromy condition are more complicated, as are the corresponding eigenvectors (though they can be constructed in principle by a certain algorithm). See [16, Sect. 5.5] for more details.
9.3 Gaudin model for \(^L{{\mathfrak {g}}}\)
Next, consider the Gaudin model for the Lie algebra \(^L{{\mathfrak {g}}}\) with a twist by \(\chi \in ({}^L{{\mathfrak {h}}})^* = {{\mathfrak {h}}}\). The space of states of the model is then a tensor product of evaluation representations of the current algebra \(^L{{\mathfrak {g}}}[z]\) corresponding to irreducible finite-dimensional representations of \(^L{{\mathfrak {g}}}\):
where \(\mu _1,\ldots ,\mu _N\) are dominant integral weights of \(^L{{\mathfrak {g}}}\) and \(z_1,\ldots ,z_N\) are distinct complex numbers. According to the results of [12,13,14, 16], the spectrum of the Gaudin Hamiltonians exhibits Langlands duality; namely, the joint eigenvalues of the \(^L{{\mathfrak {g}}}\)-Gaudin Hamiltonians are described in terms of \({{\mathfrak {g}}}\)-opers rather than \(^L{{\mathfrak {g}}}\)-opers.
More precisely, let \(\check{\mu }_k \in {{\mathfrak {h}}}= ({}^L{{\mathfrak {h}}})^*\) be the integral coweight of \({{\mathfrak {g}}}\) corresponding to \(\mu _k\). Let \({\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) be the set of \({{\mathfrak {g}}}\)-opers on \({{\mathbb {C}}}{{\mathbb {P}}}^1\) with trivial monodromy, regular singularities at \(z_1,\ldots ,z_N\) with respective residues \(\check{\mu }_1,\ldots ,\check{\mu }_N\), and irregular singularity at \(\infty \) of order 2 with 2-residue corresponding to \(\chi \) (see [13, 14] for details). Then, we have the following analogue of Theorem 9.2.
Theorem 9.3
[13] For any regular \(\chi \in {{\mathfrak {h}}}\) and any collection \(z_1\ldots ,z_N\) there is a bijection between \({\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) and the spectrum of the \(^L{{\mathfrak {g}}}\)-Gaudin Hamiltonians on the space of (9.11). Moreover, the eigenspace corresponding to every \({{\mathfrak {g}}}\)-oper in \({\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) is always one-dimensional. In addition, for generic \(z_1\ldots ,z_N\) and \(\chi \) the Gaudin Hamiltonians are diagonalizable.
9.4 Embedding of the space of states
This theorem has an intriguing consequence. Note that each coweight \(\check{\mu }_k\) of \({{\mathfrak {g}}}\) defines a coweight \(\check{\mu }'_k\) of \({{\mathfrak {g}}}'\) while the corresponding weight \(\mu _k\) of \(^L{{\mathfrak {g}}}\) defines a weight of \({{\mathfrak {g}}}'\), and the element \(\chi \in {{\mathfrak {h}}}\) defines an element \(\chi ' \in {{\mathfrak {h}}}'\).
Next, define the nilpotent generators \(f_i, i \in I\), of \({{\mathfrak {g}}}\) by the formulas
Then, we obtain that the embedding \({{\mathfrak {g}}}\hookrightarrow {{\mathfrak {g}}}'\) maps the principal nilpotent element of \({{\mathfrak {g}}}\) to that of \({{\mathfrak {g}}}'\):
In the same way, we obtain that the element \(\check{\rho }\) of \({{\mathfrak {g}}}\) (the sum of its dominant coweights) maps to the corresponding element \(\check{\rho }'\) of \({{\mathfrak {g}}}'\). Recall that there is a unique nilpotent element \(p_+ \in {{\mathfrak {g}}}\) which is a linear combination of the generators \(e_i, i \in I\), such that \(\{ p_-,2\check{\rho },p_+ \}\) is an \({{\mathfrak {s}}}{{\mathfrak {l}}}_2\) triple in \({{\mathfrak {g}}}\). Likewise, we have an \({{\mathfrak {s}}}{{\mathfrak {l}}}_2\) triple \(\{ p'_-,2\check{\rho }',p'_+ \}\) in \({{\mathfrak {g}}}'\). Uniqueness implies that \(p'_+\) is the image of \(p_+\) in \({{\mathfrak {g}}}'\).
Using these \({{\mathfrak {s}}}{{\mathfrak {l}}}_2\) triples, we construct the Kostant slices \(K({{\mathfrak {g}}})\) and \(K({{\mathfrak {g}}}')\) of regular conjugacy classes in \({{\mathfrak {g}}}\) and \({{\mathfrak {g}}}'\), respectively. Namely,
where \(\{ p_j \}_{j=1,\ldots ,\ell }\) is a basis of the subspace of \({\text {ad}} p_+\)-invariants in the upper nilpotent subalgebra \({{\mathfrak {n}}}_+\) of \({{\mathfrak {g}}}\), such that \([\check{\rho },p_j] = d_j p_j\), with \(\{ d_1,\ldots ,d_\ell \}\) being the set of exponents of \({{\mathfrak {g}}}\). The Kostant slice \(K({{\mathfrak {g}}}')\) in \({{\mathfrak {g}}}'\) is defined similarly. The fact that the embedding \({{\mathfrak {g}}}\hookrightarrow {{\mathfrak {g}}}'\) maps the above \({{\mathfrak {s}}}{{\mathfrak {l}}}_2\) triples to each other then implies that we have a natural embedding
Beilinson and Drinfeld have constructed [2] canonical representatives of \({{\mathfrak {g}}}\)-opers in terms of \(K({{\mathfrak {g}}})\) (see [14, Sect. 4.2]). Using the embedding (9.13), we obtain the following.
Lemma 9.4
There is a natural embedding
Now we derive from Theorem 9.3 and Lemma 9.4 the following surprising result.
Theorem 9.5
For generic regular \(\chi \in {{\mathfrak {h}}}\), such that \(\chi ' \in {{\mathfrak {h}}}'\) is regular, and generic \(z_1,\ldots ,z_N\) there exists an embedding of the tensor product (9.11) of simple \(^L{{\mathfrak {g}}}\)-modules with highest weights \(\mu _k\) into the tensor product of the simple \({{\mathfrak {g}}}'\)-modules with the corresponding highest weights \(\mu '_k\):
Proof
By Theorem 9.3, for generic \(\chi \) and \(z_1,\ldots ,z_N\) there exists an eigenbasis \(\{ e_m \}\) of the Gaudin Hamiltonians in (9.11) labeled by \({{\mathfrak {g}}}\)-opers \(m \in {\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) with each \({{\mathfrak {g}}}\)-oper corresponding to exactly one basis vector. Under the embedding (9.14), each of these \({{\mathfrak {g}}}\)-opers gives a \({{\mathfrak {g}}}'\)-oper \(m' \in {\text {Op}}^{\chi '}_{(\check{\mu }'_i),(z_i)}({{\mathfrak {g}}}')\). Applying Theorem 9.3 in the case of the Lie algebra \({{\mathfrak {g}}}'\) and the tensor product of simple \({{\mathfrak {g}}}\)-modules with the corresponding highest weights \(\mu '_k, k=1,\ldots ,N\), we find that each \(m'\) obtained this way corresponds to the one-dimensional eigenspace \(E_{m'}\) of the Hamiltonians of the \({{\mathfrak {g}}}'\)-Gaudin model. Mapping each basis vector \(e_m\) in (9.11) to a nonzero vector in \(E_{m'}\), we obtain the desired embedding. \(\square \)
The embedding (9.15) is not unique since we can rescale the images of the basis elements \(e_m\) by arbitrary nonzero numbers. Another issue is that the embedding (9.14) is defined in a rather abstract way (using Kostant slices). It turns out that we can obtain a more concrete realization of (9.14) if all \({{\mathfrak {g}}}\)-opers in \({\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) are non-degenerate, and hence correspond to solutions of the Bethe Ansatz equations. In this case we can also construct the corresponding eigenvectors (Bethe vectors) explicitly, so we obtain a more concrete realization of the embedding (9.15) as well. This may be viewed as an analogue of the statement of our main Conjecture 5.15 in the case of simple Lie algebras. We explain it in the next subsection.
Remark 9.2
Alternatively, under the conditions of Theorem 9.5 we can construct a surjective map
instead of an embedding (9.15). Indeed, the inclusion (9.14) gives rise to a surjective homomorphism of the corresponding algebras of functions
The corresponding algebras of \({{\mathfrak {g}}}\)- and \({{\mathfrak {g}}}'\)-Gaudin Hamiltonians were denoted in [13] by  and
and  . According to Theorem 9.3, for generic regular \(\chi \in {{\mathfrak {h}}}\) and generic \(z_1,\ldots ,z_N\), the algebra \({\text {Fun}} {\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) is equal to the image of
. According to Theorem 9.3, for generic regular \(\chi \in {{\mathfrak {h}}}\) and generic \(z_1,\ldots ,z_N\), the algebra \({\text {Fun}} {\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) is equal to the image of  in the algebra of endomorphisms of \(\bigotimes _{k=1}^N V_{\mu _k}(z_k)\). Moreover, \({\text {Fun}} {\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) then has a cyclic vector in \(\bigotimes _{k=1}^N V_{\mu _k}(z_k)\). If we choose such a cyclic vector, we obtain an isomorphism of vector spaces
in the algebra of endomorphisms of \(\bigotimes _{k=1}^N V_{\mu _k}(z_k)\). Moreover, \({\text {Fun}} {\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) then has a cyclic vector in \(\bigotimes _{k=1}^N V_{\mu _k}(z_k)\). If we choose such a cyclic vector, we obtain an isomorphism of vector spaces
On the other hand, according to Theorem 9.2, \({\text {Fun}} {\text {Op}}^{\chi '}_{(\check{\mu }'_i),(z_i)}({{\mathfrak {g}}}')\) is the quotient of the image of  in the algebra of endomorphisms of \(\bigotimes _{k=1}^N V_{\mu _k}(z_k)\) by its radical. Choosing a cyclic vector of
in the algebra of endomorphisms of \(\bigotimes _{k=1}^N V_{\mu _k}(z_k)\) by its radical. Choosing a cyclic vector of  in \(\bigotimes _{k=1}^N V'_{\mu '_k}(z_k)\) and using the homomorphism (9.17), we obtain a surjective map (9.16).
in \(\bigotimes _{k=1}^N V'_{\mu '_k}(z_k)\) and using the homomorphism (9.17), we obtain a surjective map (9.16).
This construction can be generalized to the case when \(\chi \) is a regular nilpotent element of \({{\mathfrak {g}}}\) and \(\chi \) is the corresponding element of \({{\mathfrak {g}}}'\). Then, we can choose as the cyclic vectors the highest weight vectors in the tensor products (9.16), so that the resulting map becomes canonical up to a scalar.
Constructing surjective maps (9.16) may seem more appealing than constructing the embeddings (9.15). However, in the case when all \({{\mathfrak {g}}}\)-opers in \({\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) are non-degenerate, the embedding (9.15) can be linked to the inclusion of the sets of solutions of the corresponding Bethe Ansatz equations, as we explain in the next subsection. Therefore, we can make contact to the folded integrable models. (Moreover, the embedding (9.15) can then be constructed rather explicitly using Bethe vectors, see Sect. 9.7.) It is for this reason that we focus on the embeddings (9.15) rather than the surjections (9.16), even though the latter also deserve to be studied. \(\square \)
9.5 Embedding in the case of non-degenerate \({{\mathfrak {g}}}\)-opers
As in the case of \({{\mathfrak {g}}}'\)-opers discussed in Sect. 9.2, each \({{\mathfrak {g}}}\)-oper in \({\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) can be represented in a unique way by a Miura \({{\mathfrak {g}}}\)-oper given by a formula similar to (9.10). Among them are the non-degenerate Miura \({{\mathfrak {g}}}\)-opers of the form
where \(\check{\alpha }_i, i \in I\), are the simple coroots of \({{\mathfrak {g}}}\). The no-monodromy condition on (9.19) is equivalent to the Bethe Ansatz equations similar to (9.8) (see equation (6.11) in [14]):
The image of a non-degenerate Miura \({{\mathfrak {g}}}\)-oper (9.19) under the embedding (9.14) is particularly easy to describe. Namely, we interpret formula (9.19) as a Miura \({{\mathfrak {g}}}'\)-oper of the form (9.7) as follows: According to formula (9.12), the first summation in (9.19) is equal to the first summation in (9.7). Next, the second summation in (9.19) is equal to the second summation in (9.7) with \(\check{\lambda }_k=\check{\mu }'_k\).
Finally, every term in the third summation in (9.19) can be written as the sum of terms appearing in the third summation of (9.7). Namely, for \(i \in I'\) such that \(\sigma (i) = i\), we map
and for \(i \in I\) such that if \(\sigma (i) \ne i\), we map
In other words, each term corresponding to \(i \in I\) such that \(\sigma (i) = i\) in (9.19) gives us the corresponding term in (9.7), whereas in the case \(\sigma (i) \ne i\) it gives us the sum of two terms in (9.7).
Observe that if the terms (9.22) are present in (9.19), then the corresponding \({{\mathfrak {g}}}'\)-Miura oper (9.7) is degenerate because its residue at the corresponding point \(w_j\) is equal to
(the simple reflections \(s_i\) and \(s_{\sigma (i)}\) commute with each other, so it doesn’t matter in which order we take their product).
Thus, the Miura \({{\mathfrak {g}}}'\)-opers we obtain this way have the form (9.10), with \(g_k=1\) for all \(k=1,\ldots ,N\), and \(\widetilde{g}_j\) being equal to the simple reflection \(s_i\) of the Weyl group of \({{\mathfrak {g}}}'\) if the residue of this Miura \({{\mathfrak {g}}}'\)-oper at \(w_j\) is equal to a \(\sigma \)-invariant simple coroot \(\check{\alpha }'_{i}\) of \({{\mathfrak {g}}}'\), but \(\widetilde{g}_j\) is equal to the product of two simple reflections, \(s_i s_{\sigma (i)}\), if residue at \(w_j\) is equal to (9.23). We have obtained the following result.
Proposition 9.6
Under the embedding (9.14), every non-degenerate \({{\mathfrak {g}}}\)-oper in \({\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) which is represented by a Miura \({{\mathfrak {g}}}\)-oper of the form (9.19) maps to the \({{\mathfrak {g}}}'\)-oper in \({\text {Op}}^{\chi '}_{(\check{\mu }'_i),(z_i)}({{\mathfrak {g}}}')\) represented by the Miura \({{\mathfrak {g}}}'\)-oper
According to Theorem 9.2, the Miura \({{\mathfrak {g}}}'\)-oper (9.24) defines a point in the spectrum of the \({{\mathfrak {g}}}'\)-Gaudin model.
9.6 Folded Bethe Ansatz equations
From the point of view of the Bethe Ansatz equations, we interpret this as follows. In the system of BAE (9.8), it makes sense to impose the condition
for all \(i \in I'\). That’s because for \(i \ne \sigma (i)\) we have \(\langle \check{\alpha }'_i,\check{\alpha }'_{\sigma (i)} \rangle = 0\), so no singularities occur in equations (9.8). Equivalently, this condition may be expressed as \(Q_i(z) = Q_{\sigma (i)}(z)\) for all \(i \in I\), so this is the Gaudin model analogue of the condition we used to define the folding of the Bethe Ansatz equations in the XXZ-type model associated with \(U_q(\widehat{{{\mathfrak {g}}}'})\) (see Proposition 4.4).
Lemma 9.7
The system (9.8) of Bethe Ansatz equations of the \({{\mathfrak {g}}}'\)-Gaudin model together with the condition \(Q_i(z) = Q_{\sigma (i)}(z)\) for all \(i \in I'\) is equivalent to the system (9.20) of Bethe Ansatz equations of the \(^L{{\mathfrak {g}}}\)-Gaudin model.
Thus, the folding of the BAE of the \({{\mathfrak {g}}}'\)-Gaudin model gives the BAE of the \(^L{{\mathfrak {g}}}\)-Gaudin model. In particular, we obtain that the \(q \rightarrow 1\) limit of the system (4.8) of folded Bethe Ansatz equations for \(U_q(\widehat{{{\mathfrak {g}}}'})\) coincides with the Bethe Ansatz equations of the \(^L{{\mathfrak {g}}}\)-Gaudin model.
Now we define an analogue of the space W(u) from Sect. 5.3, with the role of the twist parameter u played by \(\chi \) (more precisely, this is an analogue of the subspace \({\mathbf{W}}(u) \subset W(u)\) introduced in Remark 5.4). Recall that we have identified the lattice of integral \(^L{{\mathfrak {g}}}\)-weights (equivalently, integral \({{\mathfrak {g}}}\)-coweights) with the lattice of \(\sigma \)-invariant integral \({{\mathfrak {g}}}'\)-weights (equivalently, integral \({{\mathfrak {g}}}'\)-coweights). We have a collection \(\check{\mu }_k, k=1,\ldots ,N\), of \({{\mathfrak {g}}}\)-coweights. Let \(\mu _k, k=1,\ldots ,N\), be the corresponding \(^L{{\mathfrak {g}}}\)-weights and \(\mu '_k, k=1,\ldots ,N\), the corresponding \({{\mathfrak {g}}}'\)-weights. Consider the following representation of \({{\mathfrak {g}}}'\):
Definition 9.8
The subspace \(W(\chi )\) of W is the span of eigenvectors of the \({{\mathfrak {g}}}'\)-Gaudin Hamiltonians with the twist parameter \(\chi \) whose eigenvalues correspond to solutions of the BAE (9.8) satisfying the condition \(Q_i(z) = Q_{\sigma (i)}(z), i \in I'\).
Theorems 9.2 and 9.3 and Lemma 9.7 imply the following.
Theorem 9.9
Suppose that the \(^L{{\mathfrak {g}}}\)-Gaudin Hamiltonians are diagonalizable on the tensor product (9.11) and all \({{\mathfrak {g}}}\)-opers in \({\text {Op}}^\chi _{(\check{\mu }_i),(z_i)}({{\mathfrak {g}}})\) are non-degenerate, so they correspond to non-degenerate Miura \({{\mathfrak {g}}}\)-opers of the form (9.19) or equivalently, solutions of the corresponding Bethe Ansatz equations. Then, there is a natural embedding of the corresponding set of solutions of the BAE of this \(^L{{\mathfrak {g}}}\)-Gaudin model into the spectrum of the \({{\mathfrak {g}}}'\)-Gaudin model with the spaces of states (9.26). Moreover, we obtain an embedding
where W is the tensor product (9.26) of representations of \({{\mathfrak {g}}}'\) and \(W(\chi )\) is given in Definition 9.8.
We can construct the embedding (9.27) explicitly using the formulas given in [14] for the eigenvectors (Bethe vectors) of the \(^L{{\mathfrak {g}}}\)-Gaudin model associated with solutions of the corresponding BAE. In the next subsection, we will explain this in the case \(N=1\).
9.7 The case \(N=1\)
If \(N=1\), the space (9.11) is an irreducible representation \(V_\mu \) of \(^L{{\mathfrak {g}}}\) with highest weight \(\mu \in ({}^L{{\mathfrak {h}}})^*\) and (9.26) is the irreducible representation \(V'_{\mu '}\) of \({{\mathfrak {g}}}'\) with the \(\sigma \)-invariant \({{\mathfrak {g}}}'\)-highest weight \(\mu '\) corresponding to \(\mu \). As before, we denote by \(\check{\mu }\) and \(\check{\mu }'\) the corresponding coweights of \({{\mathfrak {g}}}\) and \({{\mathfrak {g}}}'\). Let \(\chi \) be a regular element of the Cartan subalgebra of \({{\mathfrak {g}}}\). As before, we will denote by \(\chi '\) its image in \({{\mathfrak {h}}}'\), and we will assume that it is a regular element of \({{\mathfrak {h}}}'\) as well.
The Gaudin model for general N is invariant under simultaneous shifts of the spectral parameters \(z_i\). Using this symmetry, we will set the only parameter \(z_1\) in the case \(N=1\) equal to 0. The algebra of Gaudin Hamiltonians in this case is known as the shift of argument subalgebra  of the universal enveloping algebra \(U({{\mathfrak {g}}})\) (see [13, 14, 58]).
of the universal enveloping algebra \(U({{\mathfrak {g}}})\) (see [13, 14, 58]).
The corresponding non-degenerate Miura \({{\mathfrak {g}}}\)-opers (9.19) have the form
This Miura \({{\mathfrak {g}}}\)-oper has trivial monodromy if and only if the following BAE are satisfied (see formula (6.16) of [14]):
Suppose that these equations are satisfied. Then, as shown in [14], the following Bethe vector is an eigenvector of the Gaudin Hamiltonians (provided that it is nonzero) of weight \(\gamma = \mu - \sum _{j=1}^m \alpha _{i_j}\):
where the sum is over all permutations \(\tau \) on m letters (see formula (6.15) of [14]).
According to Theorem 9.3, for generic \(\chi \) the spectrum of the algebra  of Gaudin Hamiltonians on \(V_\mu \) is simple and in bijection with the set \({\text {Op}}^\chi _{\check{\mu },0}({{\mathfrak {g}}})\) of \({{\mathfrak {g}}}\)-opers on \({{\mathbb {C}}}{{\mathbb {P}}}^1\) with trivial monodromy, regular singularity at 0 with the residue \(\check{\mu }\), and irregular singularity of order 2 at \(\infty \) with the 2-residue \(\chi \).
of Gaudin Hamiltonians on \(V_\mu \) is simple and in bijection with the set \({\text {Op}}^\chi _{\check{\mu },0}({{\mathfrak {g}}})\) of \({{\mathfrak {g}}}\)-opers on \({{\mathbb {C}}}{{\mathbb {P}}}^1\) with trivial monodromy, regular singularity at 0 with the residue \(\check{\mu }\), and irregular singularity of order 2 at \(\infty \) with the 2-residue \(\chi \).
Conjecture 9.10
For generic regular \(\chi \in {{\mathfrak {h}}}\), all \({{\mathfrak {g}}}\)-opers appearing in the spectrum of this Gaudin model are non-degenerate, and so the spectrum is parametrized by Miura \({{\mathfrak {g}}}\)-opers (9.28) with trivial monodromy, or equivalently, by collections \(\{ w_1,\ldots ,w_m \}\) and \(\{ \check{\alpha }_{i_1},\ldots ,\check{\alpha }_{i_m} \}\) solving the system of BAE (9.29). Moreover, the corresponding Bethe vectors (9.30) form an eigenbasis of  in the irreducible representation \(V_\mu \) of \({{\mathfrak {g}}}\).
in the irreducible representation \(V_\mu \) of \({{\mathfrak {g}}}\).
Assuming this conjecture, we can construct explicitly an embedding of \(V_\mu \) into the irreducible representation \(V'_{\mu '}\) of \({{\mathfrak {g}}}'\). Namely, suppose that we have collections \(\{ w_1,\ldots ,w_m \}\) and \(\{ \check{\alpha }_{i_1},\ldots ,\check{\alpha }_{i_m} \}\) satisfying the BAE (9.29) of the \(^L{{\mathfrak {g}}}\)-Gaudin model. Then, we have the corresponding non-degenerate Miura \({{\mathfrak {g}}}\)-oper (9.28) with trivial monodromy, to which we associate a Miura \({{\mathfrak {g}}}'\)-oper with trivial monodromy via Proposition 9.6. It has the form (9.24):
We wish to associate with this Miura \({{\mathfrak {g}}}'\)-oper an eigenvector of the \({{\mathfrak {g}}}'\)-Gaudin Hamiltonians in \(V'_{\mu '}\). There are two ways to do it, which give the same result. The first is to apply the construction of [14, Sect. 6.3] but insert at every point \(w_j\) such that \(\sigma (i_j) \ne i_j\) the vector \(e_{i_j,-1}^R e_{\sigma (i_j),-1}^R|0\rangle \) in the corresponding Wakimoto module, rather than \(e_{i_j,-1}^R|0\rangle \) (see formula (6.4) in [14]). The second way (which is more direct) is to apply formula (9.30) directly to the \({{\mathfrak {g}}}'\)-oper (9.31). The problem is that if \(i_j\) is such that \(\sigma (i_j) \ne i_j\), then the corresponding \(w_j\) appears twice giving rise to seeming singularities in (9.30). However, since for \(\sigma (i) \ne i\) we always have \([f_i,f_{\sigma (i)}] = 0\), it is easy to see that these singularities cancel out, so we do obtain a well-defined vector \(\phi '(w_1^{i_1},\ldots ,w_m^{i_m})\) in \(V'_{\mu '}\). It then follows that it is an eigenvector of the \({{\mathfrak {g}}}'\)-Gaudin Hamiltonians with the eigenvalue corresponding to the \({{\mathfrak {g}}}'\)-oper in \({\text {Op}}^{\chi '}_{\check{\mu }',0}({{\mathfrak {g}}}')\) represented by (9.31). Moreover, it is a weight vector of the same weight as \(\phi (w_1^{i_1},\ldots ,w_m^{i_m})\); namely, \(\gamma = \mu - \sum _{j=1}^m \alpha _{i_j}\) (here we identify \(^L{{\mathfrak {g}}}\)-weights with \(\sigma \)-invariant \({{\mathfrak {g}}}'\)-weights).
Now recall that in Sect. 5.6 we defined the invariant subspace \((V'_{\mu '})^\sigma \) of \(V'_{\mu '}\) as the direct sum of the subspaces of \(\widehat{\sigma }\)-invariant vectors in all weights subspaces of \(V'_{\mu '}\) corresponding to \(\sigma \)-invariant weights. Using the explicit formula for \(\phi '(w_1^{i_1},\ldots ,w_m^{i_m})\), we obtain that it belongs to \((V'_{\mu '})^\sigma \). We summarize this as follows.
Lemma 9.11
The vector \(\phi '(w_1^{i_1},\ldots ,w_m^{i_m}) \in V'_{\mu '}\) is a well-defined eigenvector of the \({{\mathfrak {g}}}'\)-Gaudin Hamiltonians corresponding to the \({{\mathfrak {g}}}'\)-oper in \({\text {Op}}^{\chi '}_{\check{\mu }',0}({{\mathfrak {g}}}')\) which is the image of the \({{\mathfrak {g}}}\)-oper in \({\text {Op}}^\chi _{\check{\mu },0}({{\mathfrak {g}}})\) represented by (9.28) under the embedding (9.14). Moreover, it is \(\sigma \)-invariant, so it belongs to \((V'_{\mu '})^\sigma \).
This implies the following statement.
Theorem 9.12
Suppose that \(\chi \) is generic, so that Conjecture 9.10 holds. Assume also that the vectors \(\phi '(w_1^{i_1},\ldots ,w_m^{i_m})\) are nonzero in \(V'_{\mu '}\). Then the map \(V_\mu \rightarrow V'_{\mu '}\) sending \(\phi (w_1^{i_1},\ldots ,w_m^{i_m}) \in V_\mu \) to \(\phi '(w_1^{i_1},\ldots ,w_m^{i_m}) \in V'_{\mu '}\) defines an embedding of \(V_\mu \) into \(V'_{\mu '}\) whose image is the subspace \(V'_{\mu '}(\chi )\) (see Definition 9.8). Moreover, \(V'_{\mu '}(\chi )\) is contained in \((V'_{\mu '})^\sigma \).
We view this result as an analogue of our main Conjecture 5.15.
9.8 Example
Let \(V'_{\alpha '_{{\text {max}}}}\) be the adjoint representation of \({{\mathfrak {g}}}'\). Its highest weight is the maximal root \(\alpha '_{{\text {max}}}\) of \({{\mathfrak {g}}}'\), which is \(\sigma \)-invariant. It is easy to describe the automorphism \(\widehat{\sigma }: {{\mathfrak {g}}}' \rightarrow {{\mathfrak {g}}}'\) from Lemma 5.2 (adapted to simple Lie algebras) in this case.
Lemma 9.13
The automorphism \(\widehat{\sigma }: V'_{\alpha '_{{\text {max}}}} \rightarrow V'_{\alpha '_{{\text {max}}}}\) is equal to \(\sigma ^{-1}\).
Proof
For \(g \in {{\mathfrak {g}}}'\), we have \(\rho (g) \cdot x = [g,x], \forall x \in W={{\mathfrak {g}}}'\). Hence, \(\rho _\sigma (g) \cdot x = [\sigma (g),x]\). The operator \(\widehat{\sigma }\) is uniquely defined by the equation
and the condition that the restriction of \(\widehat{\sigma }\) to the highest weight subspace of W is the identity. We claim that \(\widehat{\sigma }= \sigma ^{-1}\) satisfies these conditions. Indeed, it acts as the identity on the highest weight subspace of \(W={{\mathfrak {g}}}'\), and the equation (9.32) is equivalent to
Setting \(\widehat{\sigma }= \sigma ^{-1}\), we obtain
which follows from the fact that \(\sigma \) is an automorphism of \({{\mathfrak {g}}}'\). \(\square \)
Now let \({{\mathfrak {g}}}' = A_{2n-1} = {{\mathfrak {s}}}{{\mathfrak {l}}}_{2n}\) with its order two automorphism \(\sigma \). Then, \({{\mathfrak {g}}}= C_n = sp_{2n}\) and \(^L{{\mathfrak {g}}}= B_n = so_{2n+1}\). The highest weight \(\alpha '_{{\text {max}}}\) of the adjoint representation of \({{\mathfrak {g}}}'\) is equal to \(\omega '_1+\omega '_{2n-1}\) in this case. By the above lemma, \(\widehat{\sigma }= \sigma ^{-1} = \sigma \). Therefore, we have following description of the invariant subspace \((V'_{\omega '_1+\omega '_{2n-1}})^\sigma \) (the direct sum of the subspaces of \(\widehat{\sigma }\)-invariant vectors in all weights subspaces of \(V'_{\omega '_1+\omega '_{2n-1}}\) corresponding to \(\sigma \)-invariant weights).
Lemma 9.14
\((V'_{\omega '_1+\omega '_{2n-1}})^\sigma \) is the direct sum of the root subspaces of \(V'_{\omega '_1+\omega '_{2n-1}}\) corresponding to the roots
as well as the n-dimensional invariant subspace of the zero weight subspace of W, which is the Cartan subalgebra of \({{\mathfrak {g}}}=C_n\) inside the Cartan subalgebra of \({{\mathfrak {g}}}'\).
Expressing \(\sigma \)-invariant \({{\mathfrak {g}}}'\)-weights as \(^L{{\mathfrak {g}}}\)-weights, we obtain:
Lemma 9.15
\((V'_{\omega '_1+\omega '_{2n-1}})^\sigma \) is isomorphic, as a vector space graded by \(^L{{\mathfrak {g}}}\)-weights, to the direct sum of the first fundamental representation \(V_{\omega _1} = {{\mathbb {C}}}^{2n+1}\) of \(^L{{\mathfrak {g}}}=so_{2n+1}\) and \((n-1)\) copies of the trivial representation of \(^L{{\mathfrak {g}}}\).
Assuming Conjecture 9.10, we obtain that we can embed \(V_{\omega _1}\) into \(V'_{\omega '_1+\omega '_{2n-1}}\) in such a way that the image is the subspace \(V'_{\omega '_1+\omega '_{2n-1}}(\chi )\) (the span of eigenvectors of the \({{\mathfrak {g}}}'\)-Gaudin Hamiltonians for which \(Q_i(z) = Q_{\sigma (i)}(z), i \in I'\)). The latter is the analogue of the subspace W(u) from Sect. 5.3 which we used to define the folded integrable model. Moreover, using Proposition 9.12 we can construct this embedding explicitly, using the Bethe vectors (9.30), and this shows that \(V'_{\omega '_1+\omega '_{2n-1}}(\chi )\) is contained in \((V'_{\omega '_1+\omega '_{2n-1}})^\sigma \). The weight subspaces of these two vector spaces coincide for all nonzero weights, but their weight 0 subspaces are different: the former is 1-dimensional and the latter is n-dimensional.
Remark 9.3
At first glance, it may appear that this result is in contradiction with the results of Sect. 7.2, where we considered a similar example in the case of the quantum affine algebras associated with \({{\mathfrak {g}}}'=A_{2n-1}\) and \({{\mathfrak {g}}}=C_n\). Namely, we showed that if we take as W the irreducible representation \(L(Y_{1,1}Y_{2n-1,1})\) of \(U_q(A_{2n-1}^{(1)})\), then its subspace W(u) defined in Sect. 5.6 is \((2n+2)\)-dimensional for generic u. This means that the corresponding subspace in the limit \(q \rightarrow 1\) should have dimension at least \(2n+2\). And yet, we have found that in the case of the adjoint representation of \(A_{2n-1}\) the analogous subspace \(V'_{\omega '_1+\omega '_{2n-1}}(\chi )\) (which is the image of \(V_{\omega _1}\) in \(V'_{\omega '_1+\omega '_{2n-1}}\)) has dimension \(2n+1\) for generic \(\chi \).
The explanation is that the evaluation representation of \(U_q(A_{2n-1}^{(1)})\) corresponding to the adjoint representation of \(A_{n-1}\) (of dimension \(4n^2-1\)) is not \(L(Y_{1,1}Y_{2n-1,1})\) but \(L(Y_{1,1}Y_{2n-1,q^{2n}})\). The highest monomial of \(L(Y_{1,1}Y_{2n-1,q^{2n}})\) is not \(\sigma \)-invariant and therefore we cannot define the operator \(\widehat{\sigma }\) and related structures on \(L(Y_{1,1}Y_{2n-1,q^{2n}})\). On the other hand, the highest monomial of \(L(Y_{1,1}Y_{2n-1,1})\) is \(\sigma \)-invariant, but the dimension of this representation is \(4n^2\), i.e. it is greater than the dimension of the adjoint representation \(V'_{\omega '_1+\omega '_{2n-1}}\) of \(A_{n-1}\) by 1. Hence, it is not surprising that the subspace W(u) of \(W=L(Y_{1,1}Y_{2n-1,1})\) has dimension greater by 1 than the dimension of \(V'_{\omega '_1+\omega '_{2n-1}}(\chi )\). In fact, as shown in Sect. 7.2, the weight 0 subspace of W(u) is two-dimensional and can be identified with the weight 0 subspace of a 4-dimensional irreducible representation of the \(U_q(\widehat{{{\mathfrak {s}}}{{\mathfrak {l}}}}_2)\) subalgebra of \(U_q(A_{2n-1}^{(1)})\) corresponding to node n of the Dynkin diagram of \(A_{2n-1}\). But the corresponding irreducible representation of the \({{\mathfrak {s}}}{{\mathfrak {l}}}_2\) Lie subalgebra corresponding to node n is 3-dimensional and so its weight 0 subspace is 1-dimensional. This is the weight 0 subspace of \(V'_{\omega '_1+\omega '_{2n-1}}(\chi )\).
As the result, W(u) is actually isomorphic, as a vector space graded by weights of \(^L{{\mathfrak {g}}}= B_n\), to an irreducible representation of \(U_q({}^L{\widehat{{{\mathfrak {g}}}}})\), where \(^L{\widehat{{{\mathfrak {g}}}}}= D^{(2)}_{n+1}\), whereas \(V'_{\omega '_1+\omega '_{2n-1}}(\chi )\) is isomorphic to an irreducible representation of \(^L{{\mathfrak {g}}}= B_n\). \(\square \)
Remark 9.4
The above example gives us a nice illustration of how the affine Langlands duality of the folded integrable model becomes in the limit \(q \rightarrow 1\) the finite-dimensional Langlands duality of the Gaudin model. The point is that when we take the \(q \rightarrow 1\) limit, we restrict finite-dimensional representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\) to \(U_q({{\mathfrak {g}}})\) and then take the limit \(q \rightarrow 1\) (the latter is an equivalence of categories if q is generic). The smallest finite-dimensional representation W of \(U_q({\widehat{{{\mathfrak {g}}}}})\) with \(\sigma \)-invariant highest monomial that has \(\mu \) as the highest \(^L{{\mathfrak {g}}}\)-weight is usually isomorphic, as a \(U_q({{\mathfrak {g}}})\)-module, to the direct sum of \(V_\mu \) and many other irreducible representations.Footnote 7 So it is not surprising that the intersection of an irreducible representation M(W) of \(U_q({}^L{\widehat{{{\mathfrak {g}}}}})\), which is embedded into W according to Conjecture 5.15,(2), with \(V_\mu \) would be an irreducible representation of \(U_q({}^L{{\mathfrak {g}}})\).
This is closely related to another seeming paradox. According to a result of [13] that we used in this section, every eigenspace in the space of states of the Gaudin model is one-dimensional (if the Gaudin Hamiltonians are not diagonalizable, this means that there can be at most one Jordan block for every joint eigenvalue). In particular, for every irreducible representation \(V_\mu \) of \(^L{{\mathfrak {g}}}\), the joint eigenspace of the algebra  is one-dimensional for all joint eigenvalues. On the other hand, we expect that the analogous spaces in the folded integrable model for generic q can have dimensions greater than one. The explanation is that components other than \(V_\mu \) in the decomposition of W as a representation of \(U_q({{\mathfrak {g}}})\) may well contain (in the limit \(q \rightarrow 1\)) additional eigenvectors of
is one-dimensional for all joint eigenvalues. On the other hand, we expect that the analogous spaces in the folded integrable model for generic q can have dimensions greater than one. The explanation is that components other than \(V_\mu \) in the decomposition of W as a representation of \(U_q({{\mathfrak {g}}})\) may well contain (in the limit \(q \rightarrow 1\)) additional eigenvectors of  . \(\square \)
. \(\square \)
9.9 Conclusion
It follows that, somewhat surprisingly, we can realize the \(^L{{\mathfrak {g}}}\)-Gaudin model inside the \({{\mathfrak {g}}}'\)-Gaudin model by embedding the space of states (9.11) of the former into the space of states (9.26) of the latter in such a way that on the dual side this corresponds to the embedding of the Miura \({{\mathfrak {g}}}\)-opers (9.19) into the Miura \({{\mathfrak {g}}}'\)-opers (9.7). This is an intriguing consequence of the Langlands duality in the Gaudin models discovered in [12] and the results of [13], which deserves further study.
The embedding of the Miura \({{\mathfrak {g}}}\)-opers (9.19) into the Miura \({{\mathfrak {g}}}'\)-opers (9.7) means that the Baxter polynomials \(Q_i(z)\) and \(Q_{\sigma (i)}(z)\) (see formula (9.9)) associated with a \({{\mathfrak {g}}}'\)-oper obtained this way will be equal. Thus, the folding of the \({{\mathfrak {g}}}'\)-Gaudin model is equivalent to the \(^L{{\mathfrak {g}}}\)-Gaudin model. This statement may be viewed as a \(q \rightarrow 1\) limit of Conjecture 5.15, so it provides support for this conjecture.
Availability of data
Data sharing is not applicable to this article as no datasets were generated or analyzed during the study.
Notes
More precisely, there is a homomorphism \({\text {Rep}} U_q({\widehat{{{\mathfrak {g}}}}}) \rightarrow Z_q({\widehat{{{\mathfrak {g}}}}})[[z^{\pm 1}]]\), so that every \(V \in {\text {Rep}} U_q({\widehat{{{\mathfrak {g}}}}})\) gives rise to a formal power series \(T_V(z)\), and the Fourier coefficients of these series topologically generate \(Z_q({\widehat{{{\mathfrak {g}}}}})\), see [25, Section 8.1].
The XXZ-type model is already quantum, but here by a deformation we mean a non-commutative deformation of the commutative algebra of quantum Hamiltonians of the XXZ-type model. Therefore, it is a kind of “second quantization.”
More generally, we could consider the case when W is a tensor product of simple representations, with the same invariance property for its highest monomial (but not necessarily for each simple factor). However, we will not do so in this paper.
In the case of \({{\mathfrak {g}}}={{\mathfrak {s}}}{{\mathfrak {l}}}_n\), every finite-dimensional irreducible representation of \(U_q({{\mathfrak {s}}}{{\mathfrak {l}}}_n)\) can be lifted to \(U_q(\widehat{{\mathfrak {s}}}{{\mathfrak {l}}}_n)\), but the highest monomial of the resulting representation of \(U_q(\widehat{{\mathfrak {s}}}{{\mathfrak {l}}}_n)\) is not \(\sigma \)-invariant, see the above example. The representations with \(\sigma \)-invariant monomials are generally much larger.
References
Aganagic, M., Frenkel, E., Okounkov, A.: Quantum q-Langlands correspondence. Trans. Moscow Math. Soc. 79, 1–83 (2018)
Beilinson, A., Drinfeld, V.: Opers. arXiv:math/0501398
Bethe, H.: Zur Theorie der Metalle I. Eigenwerte und Eigenfunktionen der linearen Atomkette. Z. Phys. 71, 205–226 (1931)
Bazhanov, V.V., Lukyanov, S.L., Zamolodchikov, A.B.: Integrable structure of conformal field theory. III. The Yang-Baxter Relation. Commun. Math. Phys. 200, 297–324 (1999)
Chari, V.: Braid group actions and tensor products, IMRN, pp. 357–382 (2002)
Chari, V., Pressley, A.: A Guide to Quantum Groups. Cambridge University Press, Cambridge (1994)
Chen, H.-Y., Kimura, T.: Quantum integrability from non-simply laced quiver gauge theory. JHEP 2018, 165 (2018)
Dey, A., Hanany, A., Koroteev, P., Mekareeya, N.: On three-dimensional quiver gauge theories of type B. JHEP 09, 067 (2017)
Drinfeld, V.G.: Quantum groups. In: Proceedings of the International Congress of Mathematicians, pp. 798–820. AMS (1987)
Elliott, C., Pestun, V.: Multiplicative Hitchin systems and supersymmetric gauge theory. Selecta Math. 25, 64 (2018)
Feigin, B., Frenkel, E.: Quantization of soliton systems and Langlands duality. In: Exploration of New Structures and Natural Constructions in Mathematical Physics. Advanced Studies in Pure Mathematics, volume61, Mathematical Society of Japan, Tokyo, pp. 185–274 (2011). arXiv:0705.2486
Feigin, B., Frenkel, E., Reshetikhin, N.: Gaudin model, Bethe Ansatz and critical level. Commun. Math. Phys. 166, 27–62 (1994)
Feigin, B., Frenkel, E., Rybnikov, L.: Opers with irregular singularity and spectra of the shift of argument subalgebra. Duke Math. J. 155, 337–363 (2010)
Feigin, B., Frenkel, E., Laredo, V.T.: Gaudin models with irregular singularities. Adv. Math. 223, 873–948 (2010)
Feigin, B., Jimbo, M., Miwa, T., Mukhin, E.: Finite type modules and Bethe Ansatz equations. Ann. Henri Poincaré 18, 2543–2579 (2017)
Frenkel, E.: Gaudin model and opers. In: Kulish, P. (ed.) Infinite Dimensional Algebras and Quantum Integrable Systems. Progress in Mathematics, vol. 237, pp. 1–60. Birkhäuser, Basel (2005)
Frenkel, E., Hernandez, D.: Langlands duality for representations of quantum groups. Math. Ann. 349(3), 705–746 (2011)
Frenkel, E., Hernandez, D.: Langlands duality for finite-dimensional representations of quantum affine algebras. Lett. Math. Phys. 96(1–3), 217–261 (2011). arXiv:0902.0447
Frenkel, E., Hernandez, D.: Baxter’s relations and spectra of quantum integrable models. Duke Math. J. 164, 2407–2460 (2015). arXiv:1308.3444
Frenkel, E., Hernandez, D.: Spectra of quantum KdV Hamiltonians, Langlands duality, and affine opers. Commun. Math. Phys. 362(2), 361–414 (2018)
Frenkel, E., Koroteev, P., Sage, D.S., Zeitlin, A.M.: \(q\)-Opers, \(QQ\)-systems, and Bethe Ansatz. J. Eur. Math. Soc. (to appear) arXiv:2002.07344
Frenkel, E., Mukhin, E.: Combinatorics of \(q\)-characters of finite-dimensional representations of quantum affine algebras. Commun. Math. Phys. 216(1), 23–57 (2001)
Frenkel, E., Reshetikhin, N.: Quantum affine algebras and deformations of the Virasoro and \({\cal{W} }\)-algebras. Commun. Math. Phys. 178, 237–264 (1996)
Frenkel, E., Reshetikhin, N.: Deformations of \({\cal{W}}\)-algebras associated to simple Lie algebras. Commun. Math. Phys. 197, 1–32 (1998). arXiv:q-alg/9708006
Frenkel, E., Reshetikhin, N.: The \(q\)-characters of representations of quantum affine algebras and deformations of \({\cal{W}}\)-algebras. In: Jing, N., Misra, K. (eds.) Recent Developments in Quantum Affine Algebras and Related Topics, Contemporary Mathematics, vol. 248, pp. 163–205. AMS (1999)
Frenkel, E., Reshetikhin, N., Semenov-Tian-Shansky, M.: Drinfeld-Sokolov reduction for difference operators and deformations of \({\cal{W} }\)-algebras I. Commun. Math. Phys. 192, 605–629 (1998)
Frenkel, I., Reshetikhin, N.: Quantum affine algebras and holonomic difference equations. Commun. Math. Phys. 146, 1–60 (1992)
Hernandez, D.: Algebraic approach to q, t-characters. Adv. Math. 187(1), 1–52 (2004)
Hernandez, D.: The Kirillov–Reshetikhin conjecture and solutions of \(T\)-systems. J. Reine Angew. Math. 596, 63–87 (2006)
Hernandez, D.: Kirillov–Reshetikhin conjecture: the general case, IMRN, pp. 149–193 (2010). arXiv:0704.2838
Hernandez, D.: Simple tensor products. Invent. Math. 181, 649–675 (2010)
Hernandez, D.: Representations of shifted quantum affine algebras. To appear in IMRN. arXiv:2010.06996
Hernandez, D., Jimbo, M.: Asymptotic representations and Drinfeld rational fractions. Compos. Math. 148, 1593–1623 (2012)
Hernandez, D., Leclerc, B.: Cluster algebras and quantum affine algebras. Duke Math. J. 154, 265–341 (2010)
Hernandez, D., Leclerc, B.: A cluster algebra approach to \(q\)-characters of Kirillov–Reshetikhin modules. J. Eur. Math. Soc. 18, 1113–1159 (2016)
Kashiwara, M.: The crystal base and Littelmann’s refined Demazure character formula. Duke Math. J. 71, 839–858 (1993)
Kashiwara, M.: Similarity of crystal bases. Contemp. Math. 194, 177–186 (1996)
Kashiwara, M.: Realizations of crystals. In: Combinatorial and Geometric Representation Theory (Seoul, 2001), Contemporary Mathematics, vol. 325, pp. 133–139 (2003)
Kashiwara, M., Kim, M., Oh, S., Park, E.: Monoidal categorification and quantum affine algebras. Compos. Math. 156, 1039–1077 (2020)
Kimura, T., Pestun, V.: Quiver W-algebras. Lett. Math. Phys. 108, 1351–1381 (2018)
Kimura, T., Pestun, V.: Fractional quiver W-algebras. Lett. Math. Phys. 108, 2425–2451 (2018)
Koroteev, P., Sage, D., Zeitlin, A.: \((SL(N), q)\)-opers, the \(q\)-Langlands correspondence, and quantum/classical duality. Commun. Math. Phys. 381(2), 641–672 (2021)
Koroteev, P., Zeitlin, A.: \(q\)-Opers, \(QQ\)-systems, and Bethe Ansatz II: generalized minors. arXiv:2108.04184
Leclerc, B.: Imaginary vectors in the dual canonical basis of \(U_q(n)\). Transform. Groups 8, 95–104 (2003)
Masoero, D., Raimondo, A., Valeri, D.: Bethe Ansatz and the spectral theory of affine Lie algebra-valued connections. The simply-laced case. Commun. Math. Phys. 344, 719–750 (2016)
Masoero, D., Raimondo, A., Valeri, D.: Bethe Ansatz and the spectral theory of affine Lie algebra-valued connections. The non simply-laced case. Commun. Math. Phys. 349, 1063–1105 (2017)
Mukhin, E., Varchenko, A.: Populations of solutions of the XXX Bethe equations associated to Kac–Moody algebras. In: Infinite-Dimensional Aspects of Representation Theory and Applications, Contemporary Mathematics, vol. 392, pp. 95–102. AMS (2005)
Mukhin, E., Varchenko, A.: Discrete Miura opers and solutions of the Bethe ansatz equations. Commun. Math. Phys. 256, 565–588 (2005)
Mukhin, E., Varchenko, A.: Multiple orthogonal polynomials and a counterexample to the Gaudin Bethe Ansatz Conjecture. Trans. Am. Math. Soc. 359, 5383–5418 (2007)
Nakajima, H.: \(t\)-analogue of the \(q\)-characters of finite dimensional representations of quantum affine algebras. In: Physics and Combinatorics, pp. 196–219 (2000)
Nakajima, H.: \(t\)-analogs of \(q\)-characters of quantum affine algebras of type \(A_n\), \(D_n\). In: Combinatorial and Geometric Representation Theory (Seoul, 2001), Contemporary Mathematics, vol. 325, pp. 141–160. AMS (2003)
Nakajima, H.: \(t\)-analogs of \(q\)-characters of Kirillov–Reshetikhin modules of quantum affine algebras. Represent. Theory 7, 259–274 (2003)
Nekrasov, N.: BPS/CFT correspondence: non-perturbative Dyson–Schwinger equations and qq-characters. JHEP 1603, 181 (2016)
Ogievetsky, E., Wiegmann, P.: Factorized S-matrix and the Bethe ansatz for simple Lie groups. Phys. Lett. B 168, 360–366 (1986)
Reshetikhin, N.: The spectrum of the transfer matrices connected with Kac–Moody algebras. Lett. Math. Phys. 14, 235–246 (1987)
Reshetikhin, Yu.N., Semenov-Tian-Shansky, M.A.: Central extensions of quantum current groups. Lett. Math. Phys. 19, 133–142 (1990)
Reshetikhin, N., Weigmann, P.: Towards the classification of completely integrable quantum field theories (the Bethe-Ansatz associated with Dynkin diagrams and their automorphisms). Phys. Lett. B 189, 125–131 (1987)
Rybnikov, L.: Argument shift method and Gaudin model. Funct. Anal. Appl. 40, 188–199 (2006)
Semenov-Tian-Shansky, M.A., Sevostyanov, V.: Drinfeld–Sokolov reduction for difference operators and deformations of W-algebras II. General semisimple case. Commun. Math. Phys. 192, 631–647 (1998)
Acknowledgements
We thank M. Aganagic, P. Koroteev, A. Okounkov, and A. Zeitlin for useful discussions. E.F. and D.H. were partially supported by a grant from the France-Berkeley Fund of UC Berkeley. N.R. was partially supported by the NSF grant DMS-1902226.
Author information
Authors and Affiliations
Corresponding author
Additional information
In memory of Hugues Charnallet.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Toward constructing a folded version of the qKZ equations for non-simply laced Lie algebras
Appendix: Toward constructing a folded version of the qKZ equations for non-simply laced Lie algebras
The qKZ equations [27] for \(U_q({\widehat{{{\mathfrak {g}}}}})\) (with the twist parameter u, which is an element of the Cartan subgroup H as above), can be written in the form
Here, each \(V_i\) denotes an irreducible finite-dimensional representation of \(U_q({\widehat{{{\mathfrak {g}}}}})\), \(V_i(z_i)\) is its shift by the spectral parameter \(z_i\), and \(R^{V_jV_i}_{j,i}(z_j/z_i)\) is the R-matrix acting on \(V_j(z_j) \otimes V_i(z_i)\) normalized so that it acts as the identity on \(v_j \otimes v_i\), where \(v_j\) and \(v_i\) are highest weight vectors in \(V_j(z_j)\) and \(V_i(z_i)\), respectively. Also, \(u_j\) denotes \(u|_{V_j}\).
Let us denote the operator on the right-hand side of the jth equation by \(K_j(p)\).
The critical level limit corresponds to \(p \rightarrow 1\). In this limit, we have
Recall that for an auxiliary representation V of \(U_q({\widehat{{{\mathfrak {g}}}}})\) we have the transfer matrix \(t_V(z,u)\). These transfer-matrices commute with each other for a fixed u and different V and z. In what follows, we will use the same notation \(t_V(z,u)\) for the action of the transfer-matrix \(t_V(z,u)\) on the tensor product \(V_N(z_N) \otimes \ldots \otimes V_1(z_1)\). Thus,
where the subscript a indicates the auxiliary representation V(z).
Proposition 10.1
Suppose that \(V_j\) is such that up to a scalar, \(R^{V_jV_j}(1) = P\), the permutation operator on \(V_j(z) \otimes V_j(z)\) sending \(x \otimes y\) to \(y \otimes x\). Then, \(K_j(1) = t_{V_j}(z_j,u)\).
Proof
If \(R^{V_jV_j}(1) = P\), then formula (10.3) with \(V(z) = V_j(z_j)\) becomes
Using the identify \(A_a P_{aj} = P_{aj} A_j\), we rewrite the RHS of (10.4) as
Next, using the cyclic property of the trace, we rewrite (10.5) as:
Using formula \(A_a P_{aj} = P_{aj} A_j\) again, we rewrite (10.6) as:
In the last formula, the only operator depending on the auxiliary space is \(P_{aj}\) and its trace over the auxiliary space is the identity operator on \(V_j(z_j)\). Hence, (10.7) is equal to \(K_j(1)\). \(\square \)
Next, we discuss under what conditions \(R^{VV}(1) = P\).
Lemma 10.2
Let V be an irreducible representation of \(U_q({\widehat{{{\mathfrak {g}}}}})\) such that \(V \otimes V\) is also irreducible. Then, \(R^{VV}(1) = P\).
Proof
It follows from the definition that \(P \circ R^{VV}(1)\) is an intertwining operator \(V \otimes V \rightarrow V \otimes V\). If \(V \otimes V\) is irreducible, then by Schur’s lemma it is a scalar operator. Under our normalization, it then has to be the identity operator, and hence \(R^{VV}(1) = P\). \(\square \)
Note that a representation V satisfying the condition of Lemma 10.2 is called real in [34]. Not all irreducible representations of \(U_q({\widehat{{{\mathfrak {g}}}}})\) are real, as shown in [44], see [34, Sect. 13.6]. However, there is a large class of real representations: Kirillov–Reshetikhin modules.
Proposition 10.3
Let V be any Kirillov–Reshetikhin module over \(U_q({\widehat{{{\mathfrak {g}}}}})\). Then, \(V \otimes V\) is irreducible.
Proof
There are several possible arguments. It follows from [5] that \(V\otimes V\) is cyclic and cocyclic, and hence is irreducible. The statement also follows from the fact that the square of the q-character of a Kirillov–Reshetikhin module has a unique dominant monomial; namely, its highest monomial. The latter follows from the results of [35, Sect. 3.2.2]. In addition, the statement has been established by a different method in [39]. \(\square \)
Note however that even if \(V \otimes V\) is reducible, we may still have \(R^{VV}(1) = P\). It would be interesting to describe all irreducible representations V of \(U_q({\widehat{{{\mathfrak {g}}}}})\) satisfying the condition \(R^{VV}(1) = P\).
In any case, the above results readily imply that in the case when all \(V_j\)’s are Kirillov–Reshetikhin modules, the operators \(K_j(1), j=1,\ldots ,N\), are commuting Hamiltonians of the XXZ-type integrable model associated with \(U_q({\widehat{{{\mathfrak {g}}}}})\). It is in this sense that we say that one recovers this integrable model in the critical level limit of the qKZ equations.
Similarly, under the above condition on \(V_j\), the operator \(K_j(p)\) is the transfer-matrix \(t_{V_j}(z_j,u)\) acting on
However, because of the shifts by \(p^{-1}\) these operators do not commute with each other if \(p \ne 1\).
Now suppose that \({{\mathfrak {g}}}\) is a non-simply laced simple Lie algebra. We would like to construct a “folded qKZ system” such that in the critical level limit the operators on the right hand side become the Hamiltonians of the folded quantum integrable model described in this paper. This means, in particular, that they should correspond to transfer-matrices of \(U_q(\widehat{{{\mathfrak {g}}}'})\) rather than \(U_q({\widehat{{{\mathfrak {g}}}}})\). Thus, each \(V_i(z_i)\) should be a representation of \(U_q(\widehat{{{\mathfrak {g}}}'})\).
Unfortunately, naive attempts to construct this folded qKZ system appear to fail:
-
(1)
For each \(V_i(z_i)\), we have its subspace \((V_i(z_i))(u)\) defined as above and we can take the tensor product of these subspaces, \(\otimes _{i=1}^N (V_i(z_i))(u)\). However, it is not clear why this subspace would be preserved by the operators \(K_j\) or their p-deformed versions \(K_j(p)\) appearing on the RHS of (10.1).
-
(2)
We take the subspace V(u) of the entire tensor product \(V=\otimes _{i=1}^N V_i(z_i)\). According to Conjecture 5.15,(ii), it contains a subspace isomorphic to a representation M(V) of \(U_q(^L\widehat{{{\mathfrak {g}}}})\). Moreover, since the algebra of transfer-matrices of \(U_q(\widehat{{{\mathfrak {g}}}'})\) commutes with the Baxter operators \(Q_j(z), j \in I'\), it follows that all transfer-matrices of \(U_q(\widehat{{{\mathfrak {g}}}'})\) preserve this subspace V(u). In particular, the operators \(K_j\) given by formula (10.2), being the transfer-matrices of \(U_q(\widehat{{{\mathfrak {g}}}'})\), preserve V(u). But the problem is that on the right-hand side of these qKZ equations we have the operators \(K_j(p)\) with \(p\ne 1\), which are the transfer matrices acting on the tensor product of representations in some of which (namely, the ones with \(i=1,\ldots ,j-1\)) there is a multiplicative shift in the spectral parameter by \(p^{-1}\). It is not clear why these operators should preserve V(u) (where V is the tensor product of the representations \(V_i(z_i)\) without any shift by \(p^{-1}\)).
Hence, at the moment it is unclear to us how to fold the qKZ equations for \(U_q(\widehat{{{\mathfrak {g}}}'})\) in such a way that in the critical level limit we recover the commuting Hamiltonians of the folded quantum integrable model associated with \(U_q({\widehat{{{\mathfrak {g}}}}})\).
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Frenkel, E., Hernandez, D. & Reshetikhin, N. Folded quantum integrable models and deformed W-algebras. Lett Math Phys 112, 80 (2022). https://doi.org/10.1007/s11005-022-01565-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11005-022-01565-8





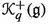 is isomorphic to
is isomorphic to  of the category of finite-dimensional representations of
of the category of finite-dimensional representations of  becomes the q-character homomorphism.
becomes the q-character homomorphism. is characterized by the multiplicities of the dominant monomials contained in it (i.e. monomials in the
is characterized by the multiplicities of the dominant monomials contained in it (i.e. monomials in the  such that m is the unique dominant monomial of F(m). Therefore, we obtain a basis
such that m is the unique dominant monomial of F(m). Therefore, we obtain a basis  parametrized by dominant monomials m.
parametrized by dominant monomials m. is the folded t-character of the
is the folded t-character of the  is the folded t-character of a
is the folded t-character of a  and in
and in  . We obtain a subring
. We obtain a subring  of representations whose simple constituents are of this form. These are called constant elements as the associated transfer-matrices are constant (independent of the spectral parameter). The ordinary character of a representation in
of representations whose simple constituents are of this form. These are called constant elements as the associated transfer-matrices are constant (independent of the spectral parameter). The ordinary character of a representation in  can be viewed as an element of
can be viewed as an element of  is as follows. The variables
is as follows. The variables  . However, Keyu Wang has pointed out that the proof of [
. However, Keyu Wang has pointed out that the proof of [ . Their purpose is to imitate the properties of elements of the non-commutative deformed W-algebra
. Their purpose is to imitate the properties of elements of the non-commutative deformed W-algebra  (for example, using a Lagrange interpolating polynomial). Hence, for an arbitrary monomial m in the variables
(for example, using a Lagrange interpolating polynomial). Hence, for an arbitrary monomial m in the variables  for N large enough,
for N large enough,  .
.  is nonzero.
is nonzero. (resp.
(resp.  ,
,  such that m is the unique dominant monomial occurring in
such that m is the unique dominant monomial occurring in  (this is proved in [
(this is proved in [ (in light of Proposition
(in light of Proposition  ). Hence, it can also be viewed as the folded t-character of a
). Hence, it can also be viewed as the folded t-character of a  which is defined in terms of the variables
which is defined in terms of the variables  ). Hence, it can also be viewed as the folded t-character of a
). Hence, it can also be viewed as the folded t-character of a  of highest monomial
of highest monomial  of highest monomial
of highest monomial  of highest monomial
of highest monomial  of highest monomial
of highest monomial 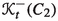 of highest monomial
of highest monomial  (defined in terms of the variables
(defined in terms of the variables  (which is defined in terms of the variables
(which is defined in terms of the variables  is a
is a  , let
, let  be the
be the  is isomorphic, as a
is isomorphic, as a  .
. , with
, with  , is a
, is a  .
. of weight
of weight  and hence is a
and hence is a  .
.