1 Introduction

The use of gravity data remains important in a wide array of subsurface modeling applications including in the exploration for geothermal energy and mineral resources. There are a couple reasons for this. First, regional gravity data are widely available, and therefore useful in the early stages of subsurface exploration by providing basic constraints on the shape and depth of sedimentary basins (Thakur et al. 2012; Nishijima and Naritomi 2017). This step is often the starting point for building geologic models that form the basis of a subsurface study. The second reason gravity data are important is that it is relatively inexpensive to acquire new data, either by surface-based or airborne surveys (Wooldridge 2010; Martelet et al. 2013). Because regional data is often available in an area of interest, new data can be acquired to target previously identified gravity anomalies at a higher resolution (denser survey spacing). Depending on the underlying geology, high-resolution gravity data may be used to infer and constrain the location of faults, either on its own or in conjunction with other geophysical data (Athens et al. 2016; Maithya et al. 2020).

However, one of the common problems of interpreting gravity anomalies is non-uniqueness, meaning that for any given gravity field there are multiple mathematical solutions to the inverse problem (Sleep and Fujita 1997). Of course, not all mathematical solutions are valid geologic solutions. By using prior geologic knowledge, the set of possible solutions can be greatly reduced allowing for insightful interpretation of the subsurface (Saltus and Blakely 2011; Crombez et al. 2020). Nevertheless, the problem of addressing non-uniqueness, coupled with typically large uncertainties on rock density values, remains challenging in both the forward modeling and inverse modeling paradigms (Nabighian et al. 2005), albeit for different reasons. Whereas in the forward modeling paradigm, it is relatively straightforward to directly incorporate geologic knowledge in the process of building a model, but it is difficult to then assess model uncertainty due to often-used manual process of model building (Phelps 2016). In contrast, there is the opposite problem in the inverse modeling paradigm. Inverse modeling can be easily extended to Bayesian frameworks to quantify model uncertainty, but it is often challenging to incorporate geologic knowledge into the regularization process (Giraud et al. 2019). Despite recent progress, inverse solutions still commonly suffer from a lack of geologic realism due to smoothing of sharp boundaries (Fullagar and Pears 2007).

Assessing model uncertainty without reducing geologic realism is particularly important in resource exploration in faulted terranes (Manzocchi et al. 2008). However, quantifying structural uncertainty is generally not straightforward; there is often a balance between ensuring that generated models are geologically valid and fully assessing model uncertainty (Caumon et al. 2007). While aspects of what is considered geologically valid is open to debate, the concept of structural restoration is widely used as a starting point for evaluating structural interpretations. If a model cannot be restored to its initial undeformed state, then it is an unacceptable structural interpretation (Woodward et al. 1989). This constraint, however, poses a practical challenge for generating alternative geologic models because grid cells (or finite elements) must be updated each time a fault is added or removed to maintain consistent bedding across faults.

The purpose of this study is to create a framework for gravity inversion that directly accounts for structural uncertainty. The first intended contribution is to show how to parameterize structural models for uncertainty quantification using a kinematic modeling approach that guarantees models are structurally restorable. This approach will then be applied in the main contribution of inverting gravity data for model uncertainty. To invert gravity data, Monte Carlo simulation is used to generate an initial set of prior model realizations that span the solution space. Following Monte Carlo, model realizations that are close to the solution space are refined using the gradual deformation method (GDM) (Hu et al. 2001), which perturbs models while preserving spatial structures specified in the prior model. It will also be shown that the initial set of prior model realizations can be used to train a surrogate model to greatly decrease computation time in high dimension models. To organize the paper, related methods for representing structural uncertainty are reviewed before proceeding with new contributions using a synthetically generated reference model of faulted stratigraphy. Finally, inversion results are shown using field-observed data from Dixie Valley, Nevada.

2 Related Work on Representing Structural Uncertainty

In recent years, there is broad recognition that solving inverse problems for a single model is insufficient for quantitative analysis and decision making in subsurface applications (Scheidt et al. 2018). Rather, what is desired is a suite of models that can be used to quantify the probability of model parameters representing physical properties in the earth. Stochastic inverse modeling approaches address this need by reframing the inverse problem using Bayes’ rule (Mosegaard and Tarantola 1995). In a Bayesian framework, solutions to the inverse problem are presented as a conditional probability distribution of a model given observed data. Because the relationship between model parameters and data is non-linear, it is common to use Monte Carlo-based methods to determine the posterior distribution by sampling from a prior model of uncertainty specifying parameter distributions.

As described by Suzuki and Caers (2008), one of the main challenges in Bayesian inverse problems in the earth sciences is specifying a prior model for spatial parameters that ensures model realizations are geologically realistic. This issue of representing spatial variability has led to the development of a wide array of geostatistical simulation techniques. These include variogram-based methods that are routinely used to simulate spatial fields such as permeability and porosity (Goovaerts 1997), and multipoint geostatistical methods that utilize a training image to capture more complex spatial patterns such as meandering sand channels (Strebelle 2002). Despite many advances in the field of geostatistics to represent spatial variability, structural features with variable topological relationships remain particularly difficult to simulate because of the need to represent both faults and corresponding displacements of geologic horizons.

One approach to represent structural uncertainty is to perturb a reference model (Caumon et al. 2007). However, in data sparse problems in which topological relationships are uncertain or a reference model is not available, a method that can simulate geologic models with geologically consistent structural features may be advantageous for full uncertainty quantification of structural features. One way to approach this problem is through physics-based modeling of time-varying deformation (simulating from an undeformed state to a deformed state), either using a continuum constitutive approach (Exadaktylos et al. 2003; Crook et al. 2006; Nollet et al. 2012) or the discrete element method (Abe et al. 2011; Finch and Gawthorpe 2017; Hardy 2019). In either approach, alternative geologic models can be generated from these deterministic physical models by varying the boundary conditions and mechanical properties of geologic horizons in the model. The advantage of a physics-based simulation approach is that it directly incorporates the physical equations that govern the structural features being modeled. However, there are major computational limitations inherent to both of these methods that reduce their applicability to uncertainty quantification problems that require numerous simulations to be run.

Kinematic modeling is an alternative to physics-based modeling to simulate fault displacements (Wellmann et al. 2016; Godefroy et al. 2018). In contrast to physics-based modeling, kinematic modeling is purely geometrical and does not simulate stress transfer. For this reason, kinematic modeling is significantly more computationally efficient and comparatively flexible. To utilize kinematic modeling in a stochastic process, deformation can be thought of as a sequence of random fault operations that displace geologic horizons. Furthermore, by changing the order of fault operations, the topology of a model is also changed (Cherpeau et al. 2010). In order to ensure geologic realism, stochastic simulation of faults is often implemented to follow a set of geologic rules based on prior geologic knowledge about the distribution of faults in a study area (Cherpeau et al. 2010; Aydin and Caers 2017; Godefroy et al. 2019).

3 Stochastic Generation of Geologic Models with Kinematic Restorability

In this section, a method is described to stochastically simulate geologic models that guarantees kinematic restorability. The approach is particularly apt for simulating faulted stratigraphy in extensional terranes where deformation can be represented by rigid-body displacements. By using rigid-body displacements, this method enforces that geologic horizons on either side of a fault will have the same thickness at the fault surface. The decision to employ rigid-body displacements, a simplification of typical fault displacement models (Barnett et al. 1987; Gibson et al. 1989), is discussed in Sect. 7.

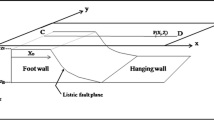
Generation of geologic models and kinematic operations are performed using a custom Python code using standard scientific libraries (e.g. numpy, pandas). The first step of the simulation is to initialize a set of regularly spaced points in a domain that is sufficiently large to account for subsequent displacements (Fig. 1a). Following initialization, normal faulting is simulated by applying a sequence of rigid-body displacement operations to the set of points. Each fault in the sequence is defined by a location, dip, slip, and orientation. Displacements are applied with relative motion, meaning that the hanging wall moves downward while the footwall moves upwards. The result of this process is a mapping of each point’s location pre- and post-faulting that can be used to generate realizations of geologic models with continuous rock properties that are offset by faults (Fig. 1b).

Rock properties are generated using geostatistical simulation (Goovaerts 1997), and then assigned to points in the pre-faulting state and mapped to point locations in the post-faulting state. One advantage of generating properties in the pre-faulted space is that it enables properties to be simulated as a function of their stratigraphic position rather than their post-faulted location (Souche et al. 2014). The specific parameterization of the geostatistical simulation will depend on the problem of interest and the data available. Although not the focus in this study, there are many examples in the literature of using Gaussian simulations to create highly realistic earth models (Beucher and Renard 2016). For this study, Sequential Gaussian Simulation is performed using the Stanford Geostatistical Modeling Software (SGeMS) (Remy et al. 2009). The specific geostatistical model parameterization used in this study will be discussed in Sect. 5. One final step after generating the post-faulting point set is to interpolate points that are within the final domain boundary onto a regular two-dimensional grid for geophysical forward modeling. In addition to interpolating rock properties, fault locations (Fig. 1c) are also interpolated to create binary fault map images.

Fig. 1
figure 1

Generating a geologic model. a Points in the pre-faulting state. Color represents density values. Black box denotes the location of the final domain extent. b Points in the post-faulting state. c Fault locations. Color represents fault ID

Full size image

4 Gravity Inversion Approach for Quantifying Structural Uncertainty

In this section, a high-level overview is provided of the techniques used in the gravity inversion approach. The goal of the approach is to invert gravity data for a suite of models in order to quantify the probability of model properties of interest. The first step is to use Monte Carlo simulation to sample models from a prior distribution. Second, prior model realizations that are close to the solution space are refined using the gradual deformation method (GDM) to improve models fits while preserving desired geologic properties such as kinematically restorable cross-sections. Optionally, a surrogate machine learning model can be used to reduce the number of geophysical forward calculations thereby reducing computation time. Following the overview provided in this section, these ideas are implemented in two example inversion problems in Sects. 5 and 6.

4.1 Sampling from a Prior Model Using Monte Carlo Simulation

The first technique is to use Monte Carlo simulation to sample models that span the solution space. Because this study is concerned with understanding structural uncertainty, the model \({\varvec{m}}\) is defined as a structural-density model consisting of two components

$$\begin{aligned} {\varvec{m}}=\{{\varvec{\chi }}, {\varvec{\zeta }}\}, \end{aligned}$$
(1)

where \({\varvec{\chi }}\) are variables describing the structural model (e.g. the location, dip, and slip of faults), and \({\varvec{\zeta }}\) describes the density model (e.g. the spatial distribution of rock density within the domain).

Next, model uncertainty is represented as a probability distribution \(f({\varvec{m}})\) referred to as the prior model of uncertainty. The parameterization and parameter distributions specified in the prior model depend on prior geologic knowledge about the geologic setting. This is typically one of the more challenging aspects of any Bayesian uncertainty quantification method because it requires that prior understanding is explicitly stated. For now, it is assumed that the prior model has been specified; later a specific example of how to parameterize a two-dimensional model for an asymmetric basin typical of the Basin and Range geologic province.

Having specified the prior model, Monte Carlo is used to sample from \(f({\varvec{m}})\) to generate a set of L model realizations \(\{{\varvec{m}}^{(1)}, {\varvec{m}}^{(2)},\dots , {\varvec{m}}^{(L)}\}\). Finally, these realizations are used to compute a set of L gravity realizations \({\varvec{d}}\) using the following forward function

$$\begin{aligned} {\varvec{d}}=g({\varvec{m}}), \end{aligned}$$
(2)

where g is a deterministic function that computes the gravity forward calculation of each model, transforming realizations of \({\varvec{m}}\) into realizations of \({\varvec{d}}\). The forward calculation is performed using SimPEG, an open source python package for geophysical applications (Cockett et al. 2015). The actual field-observed gravity data is denoted as \({\varvec{d_{obs}}}\).

4.2 Applying GDM to Optimize Fitting of Gravity Data

In this step, prior model realizations that are close to the solution space are refined to match observed gravity data. To select models that are close to the solution space, a distance metric is needed. For gravity inverse modeling, there is a large body of research emphasizing the importance of gravity gradient analysis for constraining depth, size, and geometry of density source bodies (Butler 1995; Blakely 1996). Therefore the distance metric is defined as the mean squared error of the gravity gradient

$$\begin{aligned} J=\frac{1}{n}\Vert {\varvec{d_{obs}}}' - {\varvec{d}}' \Vert ^{2}_{2}, \end{aligned}$$
(3)

where \({\varvec{d}}'\) is the gradient of gravity data realizations \({\varvec{d}}\).

After selecting prior models that minimize the distance metric, small adjustments are likely still needed to improve the fit of data; this means adjusting the location, dip, and slip of faults, as well as density model variables. At the same time, it is essential that refinement of model realizations is performed in such a way that it preserves properties specified in the prior model, such as that model realizations are structurally restorable. One way to accomplish this is by applying GDM, which was developed to perturb models defined by Gaussian random functions while preserving spatial variability (Hu et al. 2001). The key idea of GDM is the recognition that each stochastic model realization is defined by a random vector drawn from a specified distribution; by perturbing the random vector, the corresponding model realization is also perturbed. In GDM, perturbations of random Gaussian vectors are generated using

$$\begin{aligned} {\varvec{v_{\theta }}}={\varvec{v_1}}\cos (\theta )+{\varvec{v_2}}\sin (\theta ), \end{aligned}$$
(4)

where \({\varvec{v_1}}\) and \({\varvec{v_2}}\) are independent standard Gaussian random vectors, and \(\theta \) is a scalar value. Typically, \(\theta \in (0,\frac{\pi }{2})\) such that \({\varvec{v_1}}\) and \({\varvec{v_2}}\) are returned at the limits of the bounds. Because \({\varvec{v_1}}\) and \({\varvec{v_2}}\) are independent standard Gaussian random vectors, \({\varvec{v_{\theta }}}\) will also be standard Gaussian. For models defined by random samples from non-Gaussian distributions, such as a uniform distribution, a normal-score transformation can be applied prior to applying Eq. 4.

Since its development, GDM and related perturbation-based algorithms have been applied to many case studies, mostly commonly for history matching well data (Hoffman and Caers 2005; Le Ravalec and Mouche 2012). In a typical implementation, the GDM equation is used to minimize an objective function as part of an iterative optimization algorithm (Algorithm 1). The optimization algorithm is initiated by sampling a proposed model realization (i.e. a Gaussian vector) followed by a loop that iteratively updates the proposed model. For each iteration, a second Gaussian vector (representing an independent stochastic model realization) is drawn from the prior model, and the GDM equation is applied to generate a set of perturbed model realizations. For each perturbed realization, the data forward function (Eq. 2) is applied and the objective function (Eq. 3) is calculated. The proposed model realization is then updated to be the perturbed realization that minimizes the objective function for that iteration step. Minimization can be performed using any standard univariate optimization technique such as Brent’s Method. In some iterations, the minimum will be found where \(\theta =0\) (the proposed model realization for that step), in which case there is no decrease in the objective function for that step.

figure a

4.3 Surrogate Machine Learning Model

To reduce the number of forward model calculations required by the GDM optimization algorithm (Algorithm 1), an optional step is to train a surrogate machine learning model to predict whether a sampled model realization is close to the solution space. By only running the geophysical forward calculation on prior models predicted to be close to the solution space, computation time can be significantly improved in the optimization algorithm. The surrogate model can also be used to efficiently generate additional prior model realizations that are close to the solution space via importance sampling, although this is not employed in this study.

The surrogate model can be trained on prior model realizations previously generated by Monte Carlo simulation. To achieve this, it is proposed to first reduce the dimension of model realizations using a dimension reduction technique such as Principal Component Analysis (PCA). This step transforms two-dimensional model grids \({\varvec{m}}\) to vectors \({\varvec{m}}^*\) that can be used as the input to a machine learning model. Thus, the surrogate model h aims to estimate the mismatch J (Eq. 3), given a model in reduced dimension space

$$\begin{aligned} {\hat{J}}=h({\varvec{m}}^*). \end{aligned}$$
(5)

By setting up the model to predict the mismatch J (a scalar value) rather than predicting \({\varvec{d}}\) (a vector), the prediction problem is relatively simple. Once the model is trained, it can be applied to accept/reject samples based on a chosen threshold value (e.g. the 10% quantile of J). If the sample is predicted to be close to \({\varvec{d_{obs}}}\) (less than the threshold value), then the forward function (Eq. 2) is applied. Else, the geophysical forward model is not run. Using this approach, the forward model is only run on samples likely to be relevant, saving significant computation time depending on the accuracy of the surrogate model and the computational cost of the forward function. There are any number of machine learning models h that can be used as the surrogate model. In this study, a Random Forest model is employed, which is a widely used ensemble tree-based method (Breiman 1999).

4.4 A Combined Approach

Whereas Monte Carlo is efficient at exploring the full model space \(f({\varvec{m}})\), a necessary feature for full uncertainty quantification, it is highly inefficient at sampling accurately from the posterior distribution \(f({\varvec{m}}\mid {\varvec{d_{obs}}})\). In contrast, GDM is the opposite. It is efficient at matching data, but because it relies on a simple low-dimensional parameterization, it is challenging to sample from high-dimensional posterior distributions, and may have a tendency to be trapped in local minima (solutions that do not match data). Therefore, one way to improve the efficiency of GDM is to use the best models from Monte Carlo simulation as the starting point for GDM. In effect, Monte Carlo has already explored \(f({\varvec{m}})\) and GDM needs only to refine models that are close to \({\varvec{d_{obs}}}\) to learn the posterior distribution \(f({\varvec{m}}\mid {\varvec{d_{obs}}})\). This will be shown in detail in the next section.

5 Synthetic Modeling Example

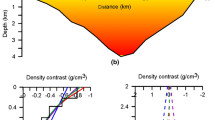
To illustrate the gravity inversion approach, a reference density model is used to represent the true earth model (Fig. 2). The synthetically created reference model is intended to represent an idealized normal fault system with three faults of varying dips and slips that offset layered stratigraphy. By using a reference model with known properties, the inversion results can be compared to the truth.

Fig. 2
figure 2

Reference model for synthetic case study problem. a Gravity field (red) and gradient of the gravity field (black). b Density model in units of kg /m\(^{3}\). From left to right, the three faults in the model have dips of 55\(\circ \), 60\(\circ \), and 65\(\circ \), and slips of 0.3, 0.5, and 0.4  km

Full size image

5.1 Parameterization of Geologic Models

The structural model and density model are controlled by two sets of parameters (Eq. 1). With regards to the structural model, the number of faults, location, dip, and slip are considered to be uncertain, and therefore probability distributions for each of these parameters are specified in the prior model of uncertainty (Table 1). The specific distributions are chosen to be large, reflecting the fact that very little prior knowledge of the study area is assumed (i.e. a narrowly defined base case model does not need to be proposed). However, in a real study, these distributions could be constrained given prior knowledge from other data sources; the parameterization and probability distributions are problem specific.

To sample from the prior model, each fault is sampled independently and the orientation (i.e. which side of the domain is the hanging wall vs footwall) is sampled with equal probability. This means that if the number of faults drawn from the prior distribution is 3, then there will be 3 sets of parameters specifying the location, dip, and slip of 3 independent rigid-body displacement operations. As a consequence, the dimension of the parameterization depends on the number of faults

$$\begin{aligned} {\varvec{\chi }}=\{{\varvec{rb_1}},{\varvec{rb_2}},\dots ,{\varvec{rb_n}}\}, \end{aligned}$$
(6)

where \({\varvec{rb}}\) defines a rigid-body displacement parameterized by a location, dip, slip, and orientation. Rigid-body displacement operations are applied sequentially when generating model realizations (Fig. 1), and thus the age relationship between faults is controlled by the sequence order (Cherpeau et al. 2010).

The second set of prior parameters controls the density model. Following a similar approach to Phelps (2016), density is modeled using a geostatistical approach. To capture the observation that borehole density is spatially correlated and generally increasing with depth, the density field is decomposed into a trend and residual. The trend is defined by a gradient of density with depth. The residual is defined by a parameter specifying the correlation length of a Gaussian random field (Goovaerts 1997). For this study, only vertical changes in density are considered, meaning that density is simulated in one-dimension and then extended to a two-dimensional grid resulting in the appearance of layered stratigraphy. However, this approach is easily extended to modeling spatial correlation in two-dimensional and three-dimensional domains provided there is sufficient data to define the horizontal correlation lengths.

Table 1 Prior model of uncertainty for synthetic modeling example
Full size table

5.2 Monte Carlo Simulation

Following the steps of the gravity inversion approach, 80,000 prior model realizations were generated by Monte Carlo simulation. Figure 3 shows a random subset of the prior model realizations. For each realization, a geologic model was generated and the data forward function (Eq. 2) was applied to simulate the gravity field. This number of prior models took approximately 15 min to simulate at a model resolution of \(100 \times 50\) grid cells utilizing 4 compute nodes and multi-processing on a computer cluster.

The number of prior models required is largely dependent on the complexity of the data and the specification of the prior model. If the observed gravity field \({\varvec{d_{obs}}}\) falls well outside of the prior distribution, then either more samples need to be generated or the specification of the prior model needs to be revised. In this example, 80,000 prior model realizations were determined to be sufficient to select model realizations that are close to the solution space for detailed refinement using GDM. Figure 4 shows 100 prior model realizations that were selected for refinement. While these prior model realizations exhibit varying number of faults in different age sequences (Fig. 4b), they are all close to matching the gradient of the observed gravity data.

Fig. 3
figure 3

Monte Carlo results. a 200 of 80,000 forward gravity calculations drawn from the prior model. b Mean density of prior model realizations. c Example prior model realization [same color scale and axes as (b)]

Full size image
Fig. 4
figure 4

Prior model realizations selected to be refined by GDM. a Gravity gradient data realizations showing 100 model and data realizations selected using the objective function (Eq. 3). b Fault maps corresponding to 5 selected starting models. Colors show the order of faulting

Full size image

5.3 Training Surrogate Model

Using 3000 of the 80,000 prior model realizations, a Random Forest regression model, implemented in the Scikit-learn library in Python (Pedregosa et al. 2011), was trained to predict the distance J in Eq. 3 (the objective function in Algorithm 1). Before training the Random Forest model, the dimension of model realizations (\(50 \times 100\) grid cells) was reduced using PCA (Fig. 5). The input variables for the Random Forest model are the first 60 PC components, which were found to explain 90% of the variance of the prior models. The training set of 3000 models was then split into a training and test set using a 70/30 split, and the Random Forest model was trained using standard hyperparameters. Prediction performance on the test set shows a correlation coefficient of 0.91 comparing the model predicted values to the true values, suggesting relatively high prediction accuracy (Fig. 6).

Fig. 5
figure 5

Dimension reduction using principal component analysis (PCA). a Scatterplot of first two principal component (PC) scores. b Scree plot showing cumulative explained variance for first 200 PCs. c Eigenfaces of first 8 PCs

Full size image
Fig. 6
figure 6

Test set performance of surrogate model to predict the objective function (Eq. 3) in Algorithm 1

Full size image

5.4 Refining Data Fit Using GDM

Having selected 100 prior model realizations that are close to the solution space, the final step is to apply the GDM optimization algorithm (Algorithm 1) to refine the selected models. However, because GDM perturbs standard Gaussian random vectors of equivalent dimension (Eq. 4), there are two issues with the parameterization of the prior model. The first issue is that model parameters are sampled from uniform distributions (Table 1). To transform uniform samples to standard Gaussian samples, a normal-score transformation is applied. The second issue is that the dimension of the samples drawn from the prior model is variable depending on the number of faults in the structural model for that sample (Eq. 6). To ensure that there is a constant sample dimension during GDM optimization, the number and orientation of faults in the structural model are fixed to that of the selected starting model. While the number and orientation of faults are fixed for each run of the optimization algorithm, the process is repeated many times using different starting models from the 100 selected prior models, thus generating posterior models with varying fault models.

Note that this problem of solving an inverse problem with a variable number of parameters to optimize is generally referred to as the trans-dimensional inverse problem (Sambridge et al. 2006). The solution proposed in this study is to sample from the trans-dimensional space using Monte Carlo simulation and then refine a selected subset of models using GDM, a constant-dimension optimization approach. Whether this approach generalizes to other trans-dimensional inverse problems requires further investigation.

Figure 7 shows an example iteration step of GDM optimization where a model realization, denoted as \({\varvec{m}}^{(1)}\), is gradually deformed to another model realization, denoted as \({\varvec{m}}^{(2)}\), using the GDM equation (Eq. 3). In this example, the number and orientation of faults in the structural model is fixed to 3 faults (2 down-to-the-right and 1 down-to-the-left) based on the selected starting model. Although the number and orientation of faults are the same in both model realizations, \({\varvec{m}}^{(1)}\) and \({\varvec{m}}^{(2)}\), the location, dip, slip of each fault, as well as the density model, are perturbed as the value of theta ranges from 0 to \(\pi /2\). Corresponding to the set of perturbed model realizations, the gradient of the gravity field is also perturbed, and the objective function is minimized where \(\theta =0.35\).

Fig. 7
figure 7

Minimization of objective function for a single iteration. a Gradient of the gravity field. b Objective function. c Geologic model

Full size image

Figure 8 shows an example of GDM optimization over 500 iterations, using a different starting model with 4 faults. This example shows typical behavior in which the objective function decreases quickly through the first  100 iterations before the rate of decrease plateaus.

Fig. 8
figure 8

Example realization of GDM optimization algorithm. a Objective function by iteration. b Gradient of the gravity field for selected iterations. c Geologic models for iterations corresponding to large decreases in the objective function

Full size image

5.5 Inversion Results

The GDM optimization algorithm (Algorithm 1) was run multiple times for each of the 100 starting models selected from prior model realizations. In total, 2000 models were run of which 100 were determined to have converged to match the gradient of the gravity data (Fig. 9a). To match the gravity data (in addition to matching the gradient), a simple post-processing step is needed to shift each model’s density values by a scalar constant; in this example the datum shift was generally in the range of ±100 kg /m\(^{3}\). Together, these 100 models form a suite of posterior model realizations of \(f({\varvec{m}}\mid {\varvec{d_{obs}}})\) (Fig. 9b).

Fig. 9
figure 9

Gravity field fits for 100 posterior models. a Gradient of the gravity field. b Gravity field

Full size image

Aggregating the posterior density models and calculating the mean value by grid cell produces a mean density model (Fig. 10a) that closely resembles the true density model (Fig. 2b). Although stratigraphic layers have been smoothed by the aggregation, the mean of the posterior models clearly shows three zones of deformation corresponding to the three faults in the true model (Fig. 3b). In addition to aggregating the density values by grid cell, faults can be similarly aggregated by transforming fault locations into a binary image (0 for no fault present, 1 for fault). The mean of the posterior binary fault models is the probability of a fault by grid cell (Fig. 10b). As expected, fault locations are most tightly constrained near the surface of the domain where the gravity field is most sensitive to source bodies. Below 0.5  km depth, fault probabilities become more diffuse due to the range of fault dips in the suite of posterior models.

Visualizing individual posterior models highlights the full range of uncertainty in both density and structure represented in these models (Fig. 10c). For example, these models show different number of faults, age relationships, and stratigraphic thicknesses. Nevertheless, the gravity field associated with each of these models matches the observed gravity field.

Fig. 10
figure 10

Posterior models. a Mean density by grid cell. b Mean binary fault map. c Example posterior models

Full size image

To investigate how prior uncertainty was reduced, posterior density models were compared to the prior density models. Figure 11a shows the ratio of the prior model variance to the posterior model variance, illustrating that the majority of uncertainty reduction occurred in the top 250 m depth. Figure 11b shows density with depth at a single location in the center of the domain. Whereas the mean of the prior density profiles is linear, the mean of the posterior density profiles follows the long wavelength trend of the true model’s density profile. However, the posterior density models do not appear to resolve short wavelength features of the true model. This suggests that the gravity field is not sensitive to high resolution changes in density.

Fig. 11
figure 11

Density uncertainty reduction. a The ratio of prior density variance to posterior density variance plotted by grid cell. b Density profiles extracted at \(x = 2\)  km. Solid lines show the mean of the prior and posterior distributions, dashed lines show the 5th and 95th percentile range. The red line is the density-depth profile from the true model

Full size image

In addition to a reduction of uncertainty in the density model, there is also a reduction of uncertainty in the structural model. Figure 12 shows the distribution of dips and slips corresponding to the locations of the three prominent zones of deformation in the posterior fault probability map (Fig. 10b). Recall that the prior specifies a uniform distribution for dip and slip. For each histogram plot, the true value (from the true model) lies within the posterior distribution.

Fig. 12
figure 12

Reduction of uncertainty of fault displacements for each of the three prominent zones of deformation in the posterior probability map. a Distribution of dip values. Red line indicates the true dip value from the reference model. b Distribution of slip values for the same faults

Full size image

6 Dixie Valley Case Study

To compare the proposed gravity inversion approach to a conventional forward modeling approach, a gravity profile from Dixie Valley, Nevada, previously modeled in Okaya and Thompson (1985), was inverted. The gravity model developed by Okaya and Thompson (reproduced in Fig. 13) shows an asymmetric basin formed by stair-stepped normal faults. As described in the original study, gravity observations were acquired along a transect across Dixie Valley and modeled using polygonal shapes to represent different facies units. In addition to gravity observations, Okaya and Thompson also collected rock samples to compute average density values, and a seismic reflection survey that was used to constrain a portion of the gravity forward model.

Using the gravity observations from Dixie Valley, the general inversion procedure follows the previously detailed synthetic modeling example except the prior parameterization was changed in two ways (Table 2). First, rather than modeling density using a one-dimensional Gaussian field (i.e. layered stratigraphy), density was modeled as a linear trend where density increases linearly with depth. This is parameterized in the prior model by two parameters controlling the gradient and intercept of the linear relationship. The second change to the prior model was to create a domain representing crystalline basement rock that is fixed to 2, 800 kg m\(^{3}\) (the value used in the Okaya and Thompson model). The primary purpose of these two changes is to create models that will allow us to compare inversion results with the Okaya and Thompson model, and not to reinterpret the geology of Dixie Valley, Nevada. A secondary purpose is to show that the inversion approach can accommodate different prior model parameterizations beyond what was shown in the synthetic modeling example.

Fig. 13
figure 13

Gravity forward model reproduced from Okaya and Thompson (1985)

Full size image
Table 2 Prior model of uncertainty for Dixie Valley case study
Full size table

In total, 25 posterior models were generated (Fig. 14) that fit the Dixie Valley gravity data (Fig. 15a). As shown in the synthetic modeling example, the inversion results can be summarized by visualizing the mean of the posterior models by grid cell (Fig. 15b) and the mean of the fault locations (Fig. 15c). In general, these two summary maps show broad agreement with the original Okaya and Thompson model, depicting an asymmetric basin defined by a stair-step basement topography. In terms of structural uncertainty, Fig. 15c shows four prominent zones of deformation (labeled a-d) as well as a fifth zone of deformation that is more diffuse (labeled e). These zones of deformation closely align with interpreted fault and facies changes in the Okaya and Thompson model. Figure 16 shows the distribution of dip and slip for the first zone of deformation (label a). Supporting the interpretation of Okaya and Thompson, the distribution of dips tends towards lower dips (50–60\(\circ \)), although higher dips are also possible. One noteworthy difference in interpretation is the absence of a shallow dipping layer towards the third zone of deformation (label c) that is part of the Okaya and Thompson model. In fact, evidence for the dipping layer primarily comes from the seismic reflection profile utilized in the Okaya and Thompson model, which was not used to inform the gravity inversion in the present study. Thus, this difference in interpretation primarily stems from what prior knowledge was incorporated in the respective studies.

Fig. 14
figure 14

Subset of Posterior models

Full size image
Fig. 15
figure 15

Inversion results. a Posterior model fits. b Posterior mean density by grid cell. c Posterior binary mean fault probability map

Full size image
Fig. 16
figure 16

Distribution of fault parameters for deformation zone a in Fig. 15c

Full size image

7 Discussion

The gravity inversion approach proposed in this study demonstrates a methodology to sample the posterior distribution of geologic models that match observed gravity data. Rather than manually tuning or calibrating models, as commonly done in conventional forward modeling approaches, this approach only requires an appropriately defined prior model of uncertainty. The advantage is that once the prior model is specified, a full suite of models can be generated, enabling quantification of structural and density uncertainty.

The approach can also be extended to utilize more sophisticated approaches to generating structural models. In the example problems presented in this study, rigid-body displacements were used to model offsets along normal faults, which results in a uniform displacement of geologic horizons along the fault surface and assumes there is infinite fault extension along planar faults. Thus, this model does not account for the fact that displacement on fault surfaces is well established to taper towards the edges of faults (Barnett et al. 1987; Gibson et al. 1989). Nevertheless, because the gravity fit is mostly sensitive to the top 250 m of the model (Fig. 11), the use of rigid-body displacements appears justified; the gravity fit would not be sensitive to a tapered fault displacement. For modeling problems that require more geologic realism, methods that model true fault displacement distributions (Hollund et al. 2002; Godefroy et al. 2018) could potentially be employed in place of the method used in this study. The only requirement is that structural models can be represented by Gaussian vectors, which allows models to be perturbed by drawing independent samples.

Another way the inversion approach can be extended is to incorporate hard data such as density well logs. In this case, the generation of geologic models (Fig. 1) would need to be modified to use a conditional simulation. Similar to the previously described approach, the first step is to simulate the pre- and post-faulting point locations. Once the post-faulting point locations are known, the location of hard data in the post-faulting state can be transformed to their pre-faulting location and then used to generate a conditional geostatistical density realization. The rest of the inversion approach would proceed as previously described.

In terms of computation time, the approach requires upwards of hundreds of thousands of forward geophysical calculations depending on the complexity of the problem and the number of posterior models generated. In the synthetic model example, around 10,000,000 forward calculations were required to refine 2000 models using GDM, of which 100 were accepted as posterior models. However, employing a surrogate model to filter non-relevant models reduced the number of forward calculations to around 1,000,000. At a grid resolution of 5000 grid cells, a single gravity forward calculation takes approximately 0.13 s; with parallel processing across 4 compute nodes on a computer cluster, the total computation time was about 12 h.

Figure 17 shows a time comparison of the surrogate prediction model to the geophysical forward calculation at different model grid resolutions. Recall that in the surrogate modeling approach, a model realization is transformed by PCA, and then the objective function is predicted by the surrogate model using the PC components as the input vector. In contrast, in the geophysical forward calculation, the model realization is directly simulated by the geophysical forward calculation (Eq. 2) and then the objective function is calculated (Eq. 3). For both methods, the time comparison is the computation time to transform 100 model realizations to distances defined by the objective function, and assumes the surrogate model was already trained and the PCA matrix already computed. Based on this comparison, the surrogate model is far more computationally efficient. Furthermore, the need for the surrogate model becomes particularly apparent at higher grid dimensions, such as for high-resolution two-dimensional models or extending the inversion framework to three-dimensional models.

In addition to incorporating a surrogate model to the inversion framework, there are a variety of other ways computation time can be further reduced. Most of the GDM optimization results show that the objective function stops decreasing after 100 to 200 iterations (Fig. 8a). This suggests that the number of GDM iterations could be reduced by as much as 50% by implementing a smarter stopping criterion. Instead of completing all 500 iterations, the algorithm could be halted if, for example, the previous 50 iterations resulted in no decrease in the objective function. Another way to improve the efficiency of the optimization algorithm is to incorporate more prior geologic knowledge into the prior model. For instance, the approximate location of faults may be known a priori by geologic or geophysical methods such as well data, topographic features (Haugerud et al. 2003; Arrowsmith and Zielke 2009), and gradient analysis of potential-field data (Phillips et al. 2007). This knowledge can be added to the prior model of uncertainty to create a more narrowly defined prior model.

Fig. 17
figure 17

Forward model and surrogate model computation time comparison per 100 realizations corresponding to density grids with dimension \(50 \times 25, 100 \times 50, 150 \times 75\), and \(200 \times 100\)

Full size image

8 Conclusions

The main contribution of this paper is an extensible gravity inversion approach that directly incorporates structural uncertainty into the inversion framework. The approach begins by defining a prior model of uncertainty for a geologic model composed of a structural model and a density model. The decomposition of the prior model creates flexibility to use different methods for the stochastic generation of faults and density. In this paper, fault displacements are generated using rigid-body displacements, while density realizations are created using unconditional Gaussian simulation. Depending on the specific problem, other stochastic methods may be more suitable. Following specification of the prior, the posterior distribution is learned by a combined approach of Monte Carlo simulation and application of GDM to refine the best fitting models.

In order to test the performance of the inversion approach, a reference model was synthetically created to represent an idealized normal fault-controlled basin. The reference model consisted of three normal faults with varying dip, slip, and orientation. After specifying a prior model with large uncertainties for structure and density, 100 posterior models were generated that match the observed gravity data from the reference model. Each posterior model is guaranteed to be structurally restorable and is an independent realization drawn from the prior, providing a far greater quantification of uncertainty than conventional gravity inversion approaches. Following the example using a synthetic model, the inversion approach was further validated by comparing inversion results to a previously published gravity forward model of Dixie Valley, Nevada.

By generating a suite of posterior models rather than a single forward model, a host of new analysis techniques is possible to help guide exploration and understanding of the subsurface. For example, structure characterization can be assessed probabilistically, which could be used to optimize well placement in geothermal exploration and development. This analysis can also be extended to value of information problems in which one quantifies the reduction of uncertainty given acquisition of additional data.