1 Introduction

One major sources of uncertainty that affects mine planning and production scheduling optimization is the geological characteristics of the mineral deposit, which comprises grades, metals, material types, and other rock properties of interest. Typically, these attributes are interpolated from a relatively limited number of data (Dimitrakopoulos 2011). To describe orebodies, spatially correlated random fields are commonly used and the geological uncertainty is quantified and assessed via a set of simulations. Over the past two decades, new spatial stochastic simulation techniques have been developed for simulating univariate random fields. However, for deposits with multiple elements, existing methods for joint modeling of non-Gaussian spatially correlated multivariate random fields are limited. To address spatial complexity, including the non-linearity of geological features and connectivity of extreme values, there is a need to consider new, efficient high-order joint simulation methods, similar to existing methods employed to simulate univariate spatial attributes.

There are many existing methods used for the joint simulation of multiple spatially correlated attributes including second-order Gaussian simulations based on sequential co-simulation (Boogaart et al. 2014; Mueller et al. 2014; Soares 2001; Verly 1993), and decorrelation approaches, such as principal component analysis (David 1988; Wackernagel 1998), the multivariate normal score transform (Bandarian et al. 2010; Boogaart et al. 2016; Leuangthong and Deutsch 2003), projection pursuit multivariate transform (Barnett et al. 2014), U-WEDGE transformation (Mueller and Ferreira 2012) and minimum–maximum autocorrelation factors (Boucher and Dimitrakopoulos 2008, 2012; Dimitrakopoulos and Fonseca 2003; Mueller et al. 2014; Rondon 2012; Switzer and Green 1984), among others (Chilès and Delfiner 2012; Journel and Huijbregts 1978; Maleki and Emery 2015). Most of the co-simulation techniques that are not based on decorrelation are both cumbersome to implement and inefficient for deposits with more than two attributes of interest, thus providing a reason to search for simplified models of co-regionalization (Almeida and Journel 1994). In the decorrelation framework, variables are transformed into uncorrelated (orthogonal) factors such that each factor can be independently simulated and then back-transformed into the simulated original variables.

Principal component analysis (PCA) and the multivariate normal score transform mentioned above decorrelate variables only at lag-zero; whereas minimum–maximum autocorrelation factors (MAF) and the U-WEDGE transformation provide uncorrelated factors at all lags. The decorrelation techniques above assume Gaussianity and/or take into account only second-order spatial statistics, thus carry the same limitations as all second-order joint simulation methods. The benefit of using complex high-order or multiple-point univariate simulation methods for the independent factors would be lost in the back-transformation step. This paper therefore aims to address these related limitations by developing a high-order joint simulation framework, built upon past developments in high-order simulation methods (Dimitrakopoulos et al. 2010; Mustapha and Dimitrakopoulos 2010).

Approaches for the decorrelation of non-Gaussian variables may be based on principal component cumulant analysis (Morton 2010; Morton and Lim 2010; Savas and Lim 2009) and independent component analysis or ICA (Comon 1994). The first method relies on finding principal cumulant components that account for most of the variation in all high-order cumulants, just as PCA obtains maximum variance components. In ICA approaches, transformation into independent factors is performed by maximization of different independence measures (Hyvärinen 1999), such as likelihood and network entropy, mutual information and Kullback–Leibler divergence, non-linear cross-correlations, non-linear PCA criteria, high-order cumulant tensors, weighted covariance matrices, negative entropy, and general contrast functions.

In this paper, a new measure of independence for ICA is first proposed. The measure is based on the diagonal domination condition of high-order cumulants of factors: the absolute values of diagonal elements that are substantially greater than non-diagonal ones. This is similar to minimum–maximum autocorrelation framework (Desbarats and Dimitrakopoulos 2000; Switzer and Green 1984), where non-diagonal terms of covariance-variance matrix are minimized and diagonal terms are maximized. It is not hard to see that the diagonal domination condition will maximize independence between factors because, for independent variables, the high-order cumulants are diagonal. However, unlike Gaussian variables, there can be no transformation into completely independent factors (Morton and Lim 2010). From this perspective, using the diagonal domination condition seems natural, because, in contrast to any strong diagonalization condition, it is possible to obtain maximally diagonal cumulants for all orders simultaneously. The advantage of the proposed technique is that it uses the high-order statistics of a multivariate dataset directly.

After performing a high-order orthogonalization, the resultant decorrelated factors can be simulated using any method which takes into account high-order spatial relations. Specifically, multiple-point simulation (MPS) algorithms (Journel 2005, 2007; Strebelle and Cavelius 2013; Zhang 2015), filtersim (Zhang et al. 2006), and simpat (Arpat and Caers 2007), cdfsim (Mustapha et al. 2013), ccsim (Tahmasebi et al. 2012), direct sampling (Mariethoz et al. 2010; Mariethoz and Renard 2010; Rezaee et al. 2013), and others (Chugunova and Hu 2008; De Vries et al. 2008; Honarkhah 2011; Li et al. 2013; Lochbühler et al. 2013; Straubhaar et al. 2011); multi-point approaches based on Markov random fields (Toftaker and Tjelmeland 2013); and finally, multi-scale MPS simulations based on discrete wavelet decomposition (Chatterjee et al. 2012). MPS techniques use pattern-based algorithms and depend on a so-termed training image (TI) and its spatial statistics rather than hard data. As a result, simulated realizations may not reproduce the spatial statistics of the data, and thus are called TI-driven methods. These issues become apparent in mining applications where there is a reasonable amount of data, unlike other major applications of the aforementioned methods used in the characterization of petroleum reservoirs (Goodfellow et al. 2012; Osterholt and Dimitrakopoulos 2007).

To address this issue, the high-order geostatistical simulation framework based on high-order spatial statistics is used (Dimitrakopoulos et al. 2010; Mustapha and Dimitrakopoulos 2010; Mustapha et al. 2011). The high-order simulation framework provides an alternative data-driven algorithm, which infers high-order spatial relationships from data rather while a TI complements the simulation process and does not require any distribution-related assumptions. The algorithm estimates local conditional density functions based on a non-parametric Legendre polynomial series approximation (Lebedev 1965) and the high-order spatial statistics of available data, which may be complemented by relations derived from a training image.

In the following sections, first the basic definitions for high-order spatial statistics are briefly reviewed and are followed by the proposed joint high-order simulation approach using simultaneous decorrelation of high-order cumulants. Subsequently, a multi-element dataset from an iron ore deposit is used to test and assess the proposed joint high-order simulation approach. Conclusions follow.

2 The Proposed Method

2.1 High-Order Spatial Statistics: A Recall

Let \((\Omega ,\mathfrak {I},P)\) be a probability space and Z(x) be a real stationary and ergodic random field in \({\mathbb {R}}^n\) defined at \(x_{i} \in D\subseteq {\mathbb {R}}^n(n=1,2,3)\) for \(i=1\ldots N\), where N is the number of points in a discrete grid \(D\subseteq {\mathbb {R}}^n\). Assuming Z(x) is a “zero-mean” \(E[Z(x)]\equiv 0\) random variable, then the cumulants of Z(x) are defined by the MacLaurin expansion of the cumulant generating function (Rosenblatt 1985)

$$\begin{aligned}&K(\omega )=\ln \left( {E\left[ {e}^{\omega Z}\right] } \right) =\sum \limits _{r=1}^\infty {\mathrm{Cum}[\underbrace{Z(x),Z(x),\ldots ,Z(x)}_r]} \frac{{\omega }^{r}}{r!} \nonumber \\&\mathrm{Cum}[\underbrace{Z(x),Z(x), ,Z(x)}_r]=\frac{\mathrm{d}^{r}}{\mathrm{d}\omega ^{r} }\left[ {\ln \left( {E\left[ {e}^{\omega Z}\right] } \right) } \right] , \end{aligned}$$
(1)

where \(\mathrm{Cum}[\underbrace{Z(x),Z(x),\ldots ,Z(x)}_r]\) is the rth-order cumulant of the random variable Z(x). Similarly, the spatial cumulant of the random field Z(x) of order r is

$$\begin{aligned} c_{r}^{z} (h_{1} ,\ldots ,h_{r-1} )=\mathrm{Cum}\left[ {Z(x_{0} ),Z(x_{1} ),\ldots ,Z(x_{r-1} )} \right] . \end{aligned}$$
(2)

According to Eq. (1), the high-order spatial cumulants are expressed as functions of moments. For example, the cumulant of order one is a mean of random field Z(x)

$$\begin{aligned} c_{1}^{z} =E\left[ {Z(x)} \right] =0. \end{aligned}$$
(3)

The second-order cumulant of the random field Z(x) is the covariance

$$\begin{aligned} c_{2}^{z} (h)=E\left[ {Z(x_{0} )Z(x_{1} )} \right] -E\left[ {Z(x_{0} )} \right] E\left[ {Z(x_{1} )} \right] =E\left[ {Z(x_{0} )Z(x_{1} )} \right] . \end{aligned}$$
(4)

Its third-order cumulant is

$$\begin{aligned} c_{3}^{z} (h_{1} ,h_{2} )&=E\left[ {Z(x_{0} )Z(x_{1} )Z(x_{2} )} \right] -E\left[ {Z(x_{0} )} \right] E\left[ {Z(x_{1} )Z(x_{2} )} \right] \nonumber \\&\quad -E\left[ {Z(x_{1} )} \right] E\left[ {Z(x_{0} )Z(x_{2} )} \right] -E\left[ {Z(x_{2} )} \right] E\left[ {Z(x_{0} )Z(x_{1} )} \right] \nonumber \\&\quad -E\left[ {Z(x_{0} )} \right] E\left[ {Z(x_{1} )} \right] E\left[ {Z(x_{2} )} \right] =E\left[ {Z(x_{0} )Z(x_{1} )Z(x_{2} )} \right] , \end{aligned}$$
(5)

and so on. The spatial cumulants are experimentally obtained by scanning the available data with a given template \(T_{r}^{e_{1} ,e_{2} ,\ldots e_{r-1} } (h_1,h_2,\ldots h_{r-1} )\), which represents a particular geometry of points in space

$$\begin{aligned}&T_{r}^{e_{1} ,e_{2} ,\ldots e_{r-1} } (h_{1} ,h_{2} ,\ldots h_{r-1})\nonumber \\&\quad =\{(x,x+h_{i} e_{i} ,i=1\ldots r-1)|\{x,x+h_{i} e_{i} ,i=1\ldots r-1\}\subset \hbox {available data},\nonumber \\ \end{aligned}$$
(6)

where \(e_{i} \) and \(h_{i} \) are unit directional vectors and distances from \(x_{0} \) to \(x_{i} \), respectively. For example, in Eq. (5), the third-order cumulant with a given template \(T_{2}^{e_{1} ,e_{2} } (h_1,h_2)\) is calculated as

$$\begin{aligned} c_{3}^{z} (h_1,h_2)=\frac{1}{N_{h_1,h_2} }\sum \limits _{k=1}^{N_{h_1,h_2} } {Z(x_{k} )Z(x_{k} +h_{1} e_{1} )Z(x_{k} +h_{2} e_{2} )}, \nonumber \\ \quad \{x_{k} ,x_{k} +h_{i} e_{i} ,i=1\ldots r-1\}\subset T_{2}^{e_{1} ,e_{2} } (h_1,h_2)\}, \end{aligned}$$
(7)

where \(N_{h_{1} ,h_{2} } \) is the number of elements of \(T_{2}^{e_{1} ,e_{2} } (h_1,h_2)\).

For further definitions and details pertaining to the calculation of high-order cumulants, the reader is referred to Dimitrakopoulos et al. (2010).

Let us summarize pertinent properties of cumulants:

  1. 1.

    Cumulants are multi-linear

    $$\begin{aligned} \mathrm{Cum}(A_{\alpha i} Z(x_{i} ),A_{\beta j} Z(x_{j} ),A_{\gamma k} Z(x_{k} ))=A_{\alpha i} A_{\beta j} A_{\gamma k} \mathrm{Cum}(Z(x_{i} ),Z(x_{j} ),Z(x_{k} )), \end{aligned}$$
    (8)

    where A is an arbitrary matrix.

  2. 2.

    Cumulants of independent variables are diagonal.

  3. 3.

    Cumulants of Gaussian variables with an order greater than two are equal to zero.

2.2 Joint High-Order Simulation

2.2.1 Algorithm Overview

The joint simulation algorithm is based on transformation of correlated variables into a factor space, where factors are simulated independently using high-order simulation (Mustapha and Dimitrakopoulos 2010) and are subsequently back-transformed into the original data space. The joint simulation algorithm is as follows.

Algorithm A.1

  1. 1.

    Find the transformation matrix A of initial correlated data \(\mathbf{Z}(x)=\{Z_{1} {(x),Z_{2}(x)},\) \({\ldots ,Z}_{k} (x)\}\) into orthogonal factors \(\mathbf{Y}(x)=\{Y_{1}(x),Y_{2}(x),\ldots ,Y_{k}(x)\}\) using the herein proposed decorrelation technique.

  2. 2.

    Simulate each of the factors independently using the high-order univariate simulation algorithm.

  3. 3.

    Back-transform simulated factors \(\mathbf{Y}(x)\) into data space using the matrix \(\mathbf{A}^{-1}\).

The decorrelation technique and high-order univariate simulation are explained next.

2.2.2 Decorrelation with Diagonal Dominant Cumulants

Let \(\mathbf{Z }(x)=\{Z_{1} (x),Z_{2} (x),\ldots ,Z_{K} (x)\}\) be a stationary and ergodic non-Gaussian vector random function (RF) in \({\mathbb {R}}^{n}\), which represents K attributes of a natural phenomenon. Without loss of generality, \(\mathbf{Z}(x)\) is zero-mean and high-order cumulants \(\mathrm{Cum}(Z_{1} (x),Z_{2} (x),\ldots ,Z_{r} (x))\) of order r. Furthermore, all K RFs are measured at each sample location. Consider the linear pointwise transformation of \(\mathbf{Z}(x)\) into factors \(\mathbf{Y }(x)=\{Y_{1} (x),Y_{2} (x),\ldots ,Y_{K}(x)\}\)

$$\begin{aligned} \mathbf{Y}(x)=\mathbf{AZ}(x). \end{aligned}$$
(9)

All factors are assumed to be independent. Using the cumulant properties described above, only diagonal elements of high-order joint-cumulants are not equal to zero

$$\begin{aligned} \mathrm{Cum}(Y_{k_{1} } (x),Y_{k_{2} } (x),\ Y_{k_{r} } (x))\ne 0, \mathrm{if \,only}\, k_{1} =k_{2} = \cdots = k_{r} . \end{aligned}$$
(10)

In general, the joint-cumulants of different orders cannot be diagonalized simultaneously. Therefore, in this work, it is not assumed that joint-cumulants of factors \(\mathbf{Y}(x)\) are diagonal; however, they have a strong diagonal domination. For a second-order tensor (i.e., a matrix), a diagonal domination condition is

$$\begin{aligned} |\mathrm{Cum}(Y_{i} (x),Y_{i} (x))|\ge \sum _{j\ne i} {|\mathrm{Cum}(Y_{i} (x),Y_{j} (x))|} \forall i. \end{aligned}$$
(11)

For high-order tensors, the diagonal domination condition is the domination of the diagonal elements over the sum of non-diagonals

$$\begin{aligned}&|\mathrm{Cum}(Y_{k} (x),Y_{k} (x),\ldots Y_{k} (x))|\nonumber \\&\quad \ge \sum _{k_{1} } {\sum _{k_{2} } \cdots } \sum _{k_{r} } {|\mathrm{Cum}(Y_{k_{1} } (x),Y_{k_{2} } (x),\ldots Y_{k_{r} } (x))| } \forall k, \end{aligned}$$
(12)

where the sums are taken for all indices \(k_{1} ,k_{2} ,\ldots ,k_{r} \) except for the case where all indexes are equal to k.

Although factors \(\mathbf{Y}(x)\) with diagonal dominant cumulants are not totally independent, they are likely to have low level of dependence to facilitate their application as it is shown in a subsequent section. As a result, the factors \(\mathbf{Y}(x)\) can be simulated independently and the back-transformed variables \(\mathbf{Z}(x)\) are expected to have the same high-order spatial statistics as the drill-hole data.

2.2.3 Objective Function

To obtain the transformation matrix \(\mathbf{A}\) using the diagonal dominant condition (12), the following objective function is minimized

$$\begin{aligned} F(\mathbf{A})=\sum _d {\alpha _{d} F_{d} (\mathbf{A})} , \end{aligned}$$
(13)

where d is the order of the cumulant, \(\alpha _{d} \) are constants, and \(F_{d} (\mathbf{A})\) are defined by

$$\begin{aligned} F_{d} (\mathbf{A})&=\sum \limits _{k_{0} } {\frac{\sum \limits _{k_{1} } {\sum \limits _{k_{2} } {\cdots \sum \limits _{k_{d-1} } {\left\| {\mathrm{Cum}(Y_{k_{0} } (x),Y_{k_{1} } (x),\ldots ,Y_{k_{d-1} } (x))} \right\| _{2} } } } }{\left\| {\mathrm{Cum}(Y_{k_{0} } (x),Y_{k_{0} } (x),\ldots ,Y_{k_{0} } (x))} \right\| _{2} }} \nonumber \\&=\sum \limits _{k_{0} } {1+\frac{\sum \limits _\mathrm{non-diagonal} {\left\| {\mathrm{Cum}(Y_{k_{0} } (x),Y_{k_{1} } (x),\ldots ,Y_{k_{d-1} } (x))} \right\| _{2} } }{\left\| {\mathrm{Cum}(Y_{k_{0} } (x),Y_{k_{0} } (x),\ldots ,Y_{k_{0} } (x))} \right\| _{2} }}, \end{aligned}$$
(14)

where factors \(Y_{k_{0} } \) are functions of the matrix \(\mathbf{A}\), because \(\mathbf{Y}(x)=\mathbf{AZ}(x)\). Coefficients \(\alpha _{d} \) are decreasing for high-order cumulants to prioritize the decorrelation for low-order statistics. In this work, the same weights \(\alpha _{d} =O\left( {\frac{1}{d!}} \right) \) are used, as suggested by Morton and Lim (2010) for the principal cumulant component analysis technique. It is not hard to see that the second term in Eq. (13) is the inverse diagonal domination condition (11), and minimizing the objective function (14) will result in maximizing the diagonal domination of the joint cumulant. To minimize the objective function (13), the limited-memory Broyden–Fletcher–Goldfarb–Shanno optimization algorithm is used (Perry 1977). The gradients for objective function are calculated analytically from Eq. (14).

2.2.4 Univariate High-Order Simulation

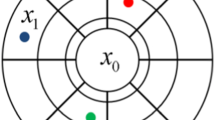
After transforming the initial correlated data, \(\mathbf{Z }(x)=\{Z_{1} (x),Z_{2} (x),\ldots ,Z_{p} (x)\}\), into orthogonal factors, \(\mathbf{Y }(x)=\{Y_{1} (x),Y_{2} (x),\ldots ,Y_{p} (x)\}\), each factor \(Y_{p} (x)\) is simulated independently. Let \(Y(x_{i} )\) or \(Y_{i} \) be a random field indexed in \({\mathbb {R}}^{n}\), \(x_{i} \in \Omega \subseteq {\mathbb {R}}^{n}(n=1,2,3)\), where N is the number of points in a discrete grid \(\Omega \subseteq {\mathbb {R}}^{n}\). The focus of high-order simulation techniques is to simulate the realization of random field \(Y(x_{i} )\) for all nodes of a discrete grid \(\Omega \) with given set of conditioning data \(d_{M} =\{Y(x_{\alpha } ),\alpha =1\ldots M\}\). The high-order simulation method proposed by Mustapha and Dimitrakopoulos (2010) uses Legendre polynomials and coefficients in terms of cumulants to approximate the conditional probability density function for each node on the simulation grid. The algorithm runs sequentially for every node. The simulation algorithm is outlined as follows.

Algorithm A.2

  1. 1.

    Define random path for visiting all unsampled nodes on the simulation grid.

  2. 2.

    For each node \(x_{0} \) in the path:

    1. (a)

      Find the closest sampled grid nodes \(x_{1} ,x_{2} ,\ldots x_{n} \) .

    2. (b)

      Define the template shape \(T_{n+1}^{e_{1} ,e_{2} ,\ldots e_{n} } (h_{1} ,h_{2} ,\ldots ,h_{n} )\), according to Eq. (6), for unsampled location \(x_{0} \) using its neighbors.

    3. (c)

      Search for all replicates of the template by scanning the initial data with the template \(T_{n+1}^{e_{1} ,e_{2} ,\ldots e_{n} } (h_{1} ,h_{2} ,\ldots ,h_{n} )\). Considering a spatial location \(x_{m} \) as a reference, the set of replicates obtained is defined as

      $$\begin{aligned} \begin{array}{l} \{Y(x_{m} ),Y(x_{m} + h_{1} ),\ldots Y(x_{m} +h_{n} ),m=1 \ldots M\}, \\ \{x_{m} ,x_{m} +h_{1} ,x_{m} +h_{n} \}\in T_{n+1}^{e_{1} ,e_{2} ,\ldots e_{n} } (h_{1} ,h_{2} ,\ldots ,h_{n} ), \\ \end{array} \end{aligned}$$
      (15)

      where M is the number of replicates and \(x_{m} \) is the central node of the replicate.

    4. (d)

      Calculate the coefficients of the Legendre polynomial approximation

      $$\begin{aligned} L_{i_{0} ,i_{1} ,\ldots i_{n} } =\frac{1}{M}\sum _{m=0}^M {P_{i_{0} } (Y(x_{m} )),P_{i_{1} } (Y(x_{m} +h_{1} ))} \ldots P_{i_{n} } (Y(x_{m} +h_{n} )), \end{aligned}$$
      (16)
      $$\begin{aligned} P_{i_{n} } (y)=\frac{1}{2^{{i}_{n}}!}\sqrt{\frac{2}{2{{i}_{n}}+1}}\left( {\frac{d^{n}}{dy^{n}}} \right) [(y-1)^{i_n}], \end{aligned}$$
      (17)

      where \(P_{i_{n} } \) is normalized Legendre polynomial of order \(i_{n} \)

    5. (e)

      Build the conditional probability density function \(f_{Y_{0}}(y_{0} |y_{1} ,y_{2} ,\ldots ,y_{n} )\) for the random variable \(Y_{0} \) at the unsampled location \(x_{0} \) given the conditioning data \(y_{1} ,\ldots y_{n} \) at the corresponding neighbors \(x_{1} ,x_{2} ,... x_{n} \)

      $$\begin{aligned} f_{Y_{0} } (y_{0} |y_{1} ,y_{2} ,\ldots ,y_{n} )=C\sum _{i_{0} =0}^r {\sum _{i_{1} =0}^r {\ldots \sum _{i_{M} =0}^r {L_{i_{0} ,i_{1} ,\ldots i_{M} } P_{i_{0} } (y_{0} )} } } P_{i_{1} } (y_{1} )\ldots P_{i_{n} } (y_{n} ),\nonumber \\ \end{aligned}$$
      (18)

      where C is normalization coefficient defined as \(C=1/\int _ {f_{Y_{0}}}(y_{0} |y_{1} ,y_{2} ,\ldots ,y_{n})dy_{0}\), and is the maximum order of approximation.

    6. (f)

      Draw a uniform random value in \(\left[ 0,1\right] \) to generate a simulated value from the conditional distribution \(f_{Y_{0} } (y_{0} |y_{1} ,y_{2} ,\ldots ,y_{n} )\) a simulated value \(Y_{0} \).

    7. (g)

      Add to the set of sample hard data and the previously simulated values.

  3. 3.

    Repeat Steps 3a–g for the next points in the random path defined in Step 2.

Finally, factors are back-transformed into data space using (9).

3 Application at an Iron Ore Dataset

3.1 Study Area and Data

This section explores the application of the proposed diagonal domination technique for the joint simulation on the iron ore dataset. The domain considered in this study represents a portion of the deposit, and is 2-km long by 1.6-km wide. A horizontal section with both exploration drill-hole and blast-hole data serves as the dataset (Fig. 1a, c) and TI (Fig. 1b, d) for the case study, respectively. The study area includes 293 drill-holes on a near-regular 50-m grid. Each composite (sample) contains five ore-quality attributes: iron (Fe), silica (SiO\(_{\mathrm {2}})\), alumina (Al\(_{\mathrm {2}}\)O\(_{\mathrm {3}})\), phosphorus (P) and loss of ignition (LOI). The deposit in the area of study is discretized into 93 \(\times \) 145 grid, each grid block is 10 by 10 m long.

Fig. 1
figure 1

Iron ore dataset: a drill-hole data of iron content; b training image of iron content; c drill-hole data of silica content, d training image of silica content. Colors are shown in log-scale

Full size image
Fig. 2
figure 2

Histograms of a iron content in drill-hole data; b iron content in training image; c silica content in drill-hole data; d silica content in training image

Full size image
Fig. 3
figure 3

Scatter plots of iron and alumina content: a drill-hole data; b training image or blast-holes; c drill-hole data in log-scale; d training image or blast-holes in log-scale

Full size image

Figure 2 shows the distributions for the iron and silica content, respectively. The cross-plot of iron and alumina content for the drill-hole data and TI are shown in Fig. 3a, b. It is apparent that the distributions strongly deviate from the Gaussian distribution, given that they are skewed with long tails. Moreover, the elements are highly correlated; this correlation is traced not only in second-order statistics, but also in high-order statistics. Evidently, standard Gaussian techniques and decorrelation approaches that use second-order statistics, such as PCA or MAF, fail to transform non-Gaussian correlated variables into independent factors due to the presence of high-order correlations.

Due to the power law distributions of the grades, the log-scale cross-plots better visualize important features of distributions (Fig. 3c, d), and therefore all subsequent results are presented in log-scale. The distributions and cross-plots for the rest of the elements are presented in the Appendix.

3.1.1 High-Order Cumulant Visualization

To visualize the high-order cumulants, an unfolding technique is used (Kiers 2000), whereby high-order cumulants are unfolded into the matrixes, which tend to have minimum difference between the number of columns and rows such that

$$\begin{aligned} n_\mathrm{row}&=M^{\left\lfloor {r/2} \right\rfloor } \nonumber \\ n_\mathrm{column}&=m^{r}/n_\mathrm{row}, \end{aligned}$$
(19)

where \(n_\mathrm{row} \) and \(n_\mathrm{column} \) are the number of rows and columns of the resulting matrix, respectively, r is the order of cumulant, M is the number of variables, and \(\left\lfloor {r/2} \right\rfloor \) is the largest previous integer of r / 2. For example, the third-order cumulant with dimensions \(3\times 3\times 3\) and the fourth-order cumulant with dimensions \(3\times 3\times 3\times 3\) are unfolded into matrices of sizes \(3\times 9\) and \(9\times 9\), respectively.

Fig. 4
figure 4

Unfolded \(3\times 3\times 3\times 3\) cumulant. Each cell is an element of the cumulant and solid, dashed, and dot-dashed squares are slices. Grey cells are diagonal elements of the cumulant tensor

Full size image

An unfolded fourth-order cumulant, \(C_{i,j,k,l} \), with dimensions \(3\times 3\times 3\times 3\) is shown in Fig. 4. Its matrix representation consists of \(9\times 9\) elements, depicted by cells. Gray cells represent diagonal elements: \(C_{1,1,1,1} \), \(C_{2,2,2,2} \), and \(C_{3333} \) of the fourth-order cumulant \(C_{i,j,k,l} \). Each slice of cumulant \(C_{i,j,k,l} \) with fixed indexes i and k is the matrix \(3\times 3\) and these slices compose the resulting \(9\times 9\) matrix. For example, the slice \(i=1\) and \(k=1\) is shown by solid square in Fig. 4 and the slice with \(i=3\) and \(k=1\) is shown by dot-dashed square. The correspondence between the indexes of a tensor i, j, k, l and its matrix representation indexes ij, kl is given by

$$\begin{aligned} ij&=3i+j \nonumber \\ kl&=3k+l. \end{aligned}$$
(20)

3.2 Decorrelation Results

For the purpose of present study, only the high-order cumulants up to order five are calculated, as this seems sufficient. To better understand the correlation between variables, each cumulant is shown in absolute values and is scaled so that the diagonal elements are equal to one. In the other words, values close to zero represent low correlation and values close to one represent a strong correlation. Initial variables are ordered in the following way: \(Z_{1} \) is the iron content (Fe), \(Z_{2} \) is the silica content (SiO\(_{\mathrm {2}})\), \(Z_{3} \) is the alumina content \((\hbox {A}1_{2} \hbox {O}_{3} )\), \(Z_{4} \) is the phosphorus content (P), and \(Z_{5} \) is the loss on ignition (LOI). All cumulants are represented in matrix form using the unfolding technique described in a previous section. Thus, the first element of each matrix is located in upper-left corner. Colors represent the levels of correlation: red represents a strong correlation, whereas blue represents a low correlation.

Fig. 5
figure 5

Covariance matrix of the original variables (a) and the decorrelation factors (b). Each cell is an element of the matrix. Colors are the levels of correlation: red represents a strong correlation, whereas blue represents a small correlation

Full size image

The second-order cumulants shown in Fig. 5a are the covariance matrix of initial variables. Each number on the axes represents an element: iron (1), silica (2), alumina (3), phosphorus (4), and LOI (5). The second-order cumulants are shown in Fig. 5b, which is the covariance matrix of the factors. Each number on the axes corresponds to a particular factor. As can be seen in Fig. 5a, the iron content (\(Z_{1} )\), is highly correlated with the content of silica (\(Z_{2} )\) and alumina content (\(Z_{3} )\), respectively. The phosphorus (\(Z_{4} )\) and LOI (\(Z_{5} )\) have low correlations with the other attributes. In the factor space (Fig. 5b), all non-diagonal elements have values less than 0.01, which means there is almost no correlation between factors.

Fig. 6
figure 6

Third-order cumulant of the original variables (a) and the decorrelation factors (b). Cells are elements of the cumulant. Each slice of the cumulant is separated by black vertical line shows three-variate correlations of the element from the labels on the top axis with other two variables

Full size image

The second-order cumulants reflect the correlation between two variables, whereas the third-order cumulants in Fig. 6a, b represents the dependence between the values of three variables. As previously mentioned in Sect. 3.2, the third-order tensor \(5\times 5\times 5\) can be unfolded to \(5\times 25\) matrix. Each slice of the cumulants separated by a black vertical line shows the three-variate correlations of the variable from the labels on the top axis with other two variables. For example, the correlation between iron content, the first variable \(Z_{1} \), and two other variables \(Z_{j} ,Z_{k} ,j,k=1\ldots 5\) is represented by the left part of the image, columns 1–5. Similar to the second-order cumulant (Fig. 5), the iron content shows a high level of correlation with silica and alumina.

The third-order correlation of LOI content, the fifth variable \(Z_{5} \), and two other variables \(Z_{j} ,Z_{k} ,j,k=1\ldots 5\) is represented by the right part of the image with columns from 20 to 25. It is not hard to see that, as in case with the second-order cumulant, LOI has a low correlation with the other variables. However, there are green values in the last column of the Fig. 6a, which show low correlation between LOI, iron and silica contents. Thus, using the third-order cumulant map, it is possible to detect complex dependencies among the variables that cannot be identified using second-order statistics. In the factor space (Fig. 6b), there are high values only for diagonal elements of the third-order cumulant; therefore, the factors are also decorrelated for order three.

Fig. 7
figure 7

Fourth-order cumulant of initial variables. Cells are elements of the cumulant. Each slice of the cumulant separated by black lines shows four-variate correlations of the element from the labels on the top axis, the element from the labels on the right axis and other two variables

Full size image
Fig. 8
figure 8

Fourth-order cumulant of decorrelation factors. Cells are elements of the cumulant. Each slice of the cumulant separated by black lines shows four-variate correlations of the factor from the labels on the top axis, the factor from the labels on the right axis and other two factors. Red cells correspond to diagonal terms \(C_{1,1,1,1} ,C_{2,2,2,2} ,\ldots C_{5,5,5,5} \)

Full size image

The fourth-order cumulants are shown in Figs. 7 and 8. The fourth-order tensor \(5\times 5\times 5\times 5\) can be unfolded to \(25\times 25\) matrix. Each slice of the cumulants separated by black lines shows four-variate correlations of the variable from the labels on the top axis, the element from the labels on the right axis and other two variables. For example, the correlations between phosphorus, silica and the contents of the other two elements are represented by the slice with the indexes four and two on the top and right axes, or cells with column indexes 16–20 and row indexes 6–10.

According to Fig. 7, there is a high dependence between iron, silica, and alumina contents, represented by orange and red colors in the upper-left part of the graph. In the factor space (Fig. 8), high values are only present for the diagonal elements of the forth-order cumulant; therefore, the factors are also decorrelated for the fourth-order. A similar tendency can be seen for the fifth-order cumulants (Figs. 9, 10).

Fig. 9
figure 9

Fifth-order cumulant of initial variables. Each cell is element of the cumulant

Full size image
Fig. 10
figure 10

Fifth-order cumulant of factors. Each cell is element of the cumulant. Colors show the levels of correlation: red color is maximum correlation, blue color is no correlation. Red cells correspond to diagonal terms \(C_{11111} ,C_{22222} ,\ldots C_{55555}\)

Full size image

3.3 Simulation Results

After decorrelation, drill-hole data and TI are transformed into factor space using Eq. (9). Thus, the contents for the five elements (Fe, SiO\(_{\mathrm {2}}\), Al\(_{\mathrm {2}}\)O\(_{\mathrm {3}}\), P, and LOI) are transformed into five factors which have a low level of correlation. Each of the factors is then simulated separately using the Algorithm A.2 and back-transformed into contents of elements. The final 20 realizations contain 93\(\times \)145 points at a 10 m by 10 m grid, with simulated Fe, SiO\(_{\mathrm {2}}\), Al\(_{\mathrm {2}}\)O\(_{\mathrm {3}}\), P, and LOI content. Examples are shown in Fig. 11, and a realization for all elements is presented in the Appendix.

Fig. 11
figure 11

Two simulations of iron content (a, b) and silica content (c, d). Colors are shown in log-scale

Full size image

By visual inspection, the simulations in Fig. 11 reproduce the spatial distribution of ore content and preserve connected structures of high values. Besides that, the areas with low-values of iron content on the north-east and south-west parts of image (blue areas in Fig. 11a, b) coincide with high values of silica content (red areas in Fig. 11c, d). These observations are confirmed by quantitative analysis in subsequent validation by: (1) quantile–quantile plots (QQ-plots) between drill-hole data and simulated values; (2) cross-plot comparison of drill-hole data and simulation values; (3) zero-lag cumulant validation; (4) variogram and cross-variogram validation; (5) high-order spatial cumulant and spatial cross-cumulant validation (De Laco and Maggio 2011).

Fig. 12
figure 12

QQ-plots of a iron, b phosphorus, c alumina, d silica, and e LOI contents. Grey lines are simulated realizations with drill-hole data, blue line is the TI with drill-hole data, and red line is drill-hole with drill-hole data

Full size image

In Fig. 12, QQ-plots of the simulated realization and the drill-hole data are indicated by grey lines. In addition, QQ-plots of the training image and the drill-hole data are depicted by blue and red lines, respectively. Despite the decorrelation and related data transformations, the simulations do reproduce the distributions of the drill-hole data reasonably well. The scatter plots between iron, silica and alumina contents are shown in Figs. 13, 14 and 15. Graphs on the left represent scatter plots of drill-hole data, whereas graphs on the right scatter plots of one of the simulated realizations. The general shape of the clouds of points remains preserved. Next, the reproduction of the cumulants at lag-zero is investigated to demonstrate the performance of the proposed decorrelation technique. As in Sect. 2.2.3, all cumulants are shown in absolute values and scaled to better depict the correlations: the values close to zero represent low correlations, whereas values that are close to one represent high correlations. The second-order cumulant (i.e., the covariance matrix) of a simulation is shown in Fig. 16. It is noted that the simulations reproduce the covariance of drill-hole data (Fig. 5a).

Fig. 13
figure 13

Scatter plot between Fe and SiO\(_{\mathrm {2}}\), for the data (a) and simulation #1 (b). Contents are shown in log-scale

Full size image
Fig. 14
figure 14

Scatter plot between Fe and Al\(_{\mathrm {2}}\)O\(_{\mathrm {3}}\), for the data (a) and simulation #1 (b). Contents are shown in log-scale

Full size image
Fig. 15
figure 15

Scatter plot between SiO\(_{\mathrm {2}}\) and Al\(_{\mathrm {2}}\)O\(_{\mathrm {3}}\), for the data (a) and simulation #1 (b). Contents are shown log-scale

Full size image
Fig. 16
figure 16

Covariance matrix and third-order cumulant of simulation #1. Each cell is element of the matrix

Full size image

The third-order cumulant is generally also reproduced; however, some of the correlations are underestimated in the third-order cumulant of simulated realizations; for example, elements with indices (2,20), (2,23), and (2,24) have values of approximately 0.5 for the drill-hole data (Fig. 6a) and approximately 0.1 for simulations (Fig. 16b).

Fig. 17
figure 17

Fourth-order cumulant of simulation #1. Cells are elements of the cumulant. Each slice of the cumulant separated by black lines shows four-variate correlations of the element from the labels on the top axis, the element from the labels on the right axis and other two variables. Colors show the levels of correlation: red color is maximum correlation, blue color is no correlation

Full size image
Fig. 18
figure 18

Fifth-order cumulant of simulation #1. Each cell is element of the cumulant. Colors show the levels of correlation: red color is maximum correlation, blue color is no correlation

Full size image

The fourth-order cumulant of the simulation (Fig. 17) depicts more discrepancies from the drill-hole data (Fig. 7); however, the overall structure is preserved. Finally, the fifth-order cumulant (Fig. 18) of the simulation is underestimated when compared to the cumulants of the drill-hole data (Fig. 9). There are several reasons of these deviations in high-order cumulants. First of all, the condition (13) favors decomposition of lower order, because they have greater impact on joint distribution of multiple correlated variables. Secondly, the high-order cumulants that are obtained from the drill-hole data are sampling statistics and, therefore, the estimation error is inevitably introduced to results. Finally, similar to variogram analysis, the fluctuations are consequence of ergodicity and the estimations of high-order statistics differ among simulations.

Figure 19 shows a variogram (left) of the iron content, and a cross-variogram (right) between iron and alumina. The variogram of univariate spatial distribution for iron is well-reproduced. The cross-variogram shows some slightly lower values than the data, which is a result of the fact that the decorrelation technique does not take into account high-order cross-cumulants at non-zero lags.

Fig. 19
figure 19

Variogram of iron content (a), and cross-variogram of iron and alumina contents (b) for 20 simulations (grey lines) and drill-hole data (black points). Contents are taken in log-values

Full size image
Fig. 20
figure 20

The third-order spatial cumulant maps for iron content of a initial data and b simulation #1. Colors are the levels of correlation: red color is maximum correlation and blue color is no correlation.

Full size image
Fig. 21
figure 21

The third-order cross-spatial cumulant maps for a iron and alumina contents of initial data and b simulation #1. Colors are the levels of correlation: red color is maximum correlation and blue color is no correlation

Full size image
Fig. 22
figure 22

The fourth-order spatial cumulant maps for iron contents of initial data (upper) and simulation #1 (lower). Colors are the levels of correlation: red color is maximum correlation and blue color is no correlation

Full size image

A similar analysis is performed for the third-order spatial cumulant and the third-order spatial cross-cumulant. For the calculation of the third-order spatial cumulant map of iron content (Fig. 20), an L-shape template and Eq. (6) are used. The L-shape template lag’s directions are (1, 0) and (0, 1), so for each cell the triplets \(Z_{1} (x,y)\), \(Z_{1} (x+i\mathrm{d}x,y)\), \(Z_{1} (x,y+j\mathrm{d}y)\) are used. Here \((x,y)\in \Omega \), \(i=1\ldots 30\), \(j=1\ldots 30\), and \(\mathrm{d}x, \mathrm{d}y\), are grid block sizes, that is 10 m \(\times \) 10 m. For the cross-cumulant map of iron and alumina the same template is used, but points are taken from different variables \(Z_{1} (x,y)\), \(Z_{3} (x+i\mathrm{d}x,y)\), \(Z_{3} (x,y+j\mathrm{d}y)\). As can be seen in Fig. 20, there is a good reproduction of the spatial features, and the area of high- and low-values of the data’s spatial cumulant (Fig. 20a) corresponds to the areas on the cumulant map of the simulated realization (Fig. 20b). The third-order spatial cross-cumulant map of a simulated realization (Fig. 21b) has also structures similar to drill-hole data (Fig. 21a).

The fourth-order spatial cumulants of the iron content are shown in Fig. 22, and are calculated using a template with directions (1, 0), (0, 1), and (1, 1): for each cell, the four-point relationship \(Z_{1} (x,y)\), \(Z_{1} (x+i\mathrm{d}x,y)\), \(Z_{1} (x,y+j\mathrm{d}y)\), and \(Z_{1} (x+k\mathrm{d}x,y+k\mathrm{d}y)\) is used. Here the \((x,y)\in \Omega \), lags are indexed by \(i=1\ldots 30\), \(j=1\ldots 30\), and \(k=1\ldots 30\); dx, dy are grid block sizes, that is 10 m \(\times \) 10 m. According to Fig. 22, the fourth-order cumulant is reproduced quite well, thus four-point relationships available in data are preserved in the simulations.

4 Conclusions

This paper proposes a new method for the joint high-order simulation of non-Gaussian spatially correlated variables. Typically, mineral deposits are modelled using a finite number of samples, and are multi-element thus require joint simulations of the pertinent attributes of interest. These variables are often non-Gaussian, with complex spatial connectivity and joint connectivity of extreme values that are critical to the uses of simulated models, such mine panning optimization and reservoir multi-face flow simulation.

The proposed technique extends the univariate high-order simulation framework to address multiple correlated variables based on a new decorrelation approach that generates uncorrelated factors using the so-termed diagonal domination condition for high-order cumulants. Specifically, the joint high-order simulation method presented decorrelates variables to independent factors, simulates these factors independently, then, factors are then back-transformed to correlated high-order realizations of the pertinent attributes of interest in a way that high-order spatial relations and cross-relations are reproduced.

The algorithm presented herein is tested using iron ore deposit data. The results show that the newly proposed method transforms initial variables into factors with a low level of dependence. Using high-order statistics both at the decorrelation step and the simulation step permits the ability to generate jointly simulated grades with the same complex spatial statistics as the initial data. It is noted that the spatial high-order cross-statistics may be underestimated, thus the need to validate results given that high-order statistics at lag-zero are considered. In general, the application shows the feasibility and excellent performance of the proposed method.

One related issue to be discussed is the availability of suitable training images, which, given the interest in high-order relations, is not trivial. In the case of mineral deposits, the two known options are to (1) in an operating mine use as a dense dataset for a TI, such as the blast-hole data used herein. In the absence of the first option; (2) one may consider dense information that may be available from a similar orebody. In other cases, different opportunities may exist.

Fig. 23
figure 23

Histograms of alumina content: a drill-hole data; b training image

Full size image

Further research will address the improvement of the decorrelation condition, namely cross-cumulants at various lags will be added to objective function (13). In addition, the non-linear transformation model will be applied to initial variables instead of linear model (8).