1 Introduction

Geological structures in mineral and petroleum exploration can be approximated by simple geological structures such as a fault, a sphere, a cylinder, or a dike. According to this approximation, many methods have been introduced for interpreting magnetic field anomalies due to simple geometric models in an attempt to best-estimate the magnetic parameters values, for example, the depth to the buried body, the amplitude coefficient, and the effective magnetization angle. The interpretation methods include matching standardized curves (Gay 1963, 1965; McGrath and Hood 1970), characteristic points and distance approaches (Grant and West 1965; Abdelrahman 1994), monograms (Prakasa Rao et al. 1986), Hilbert transforms (Mohan et al. 1982), Fourier transform techniques (Bhattacharyya 1965), correlation factors between successive least-squares residual anomalies (Abdelrahman and Sharafeldin 1996), least-squares minimization methods (Silva 1989; McGrath and Hood 1973), linearized least-squares method (Salem et al. 2004), normalized local wave number method (Salem and Smith 2005), analytic signal derivatives (Salem 2005), and Euler deconvolution method (Salem and Ravat 2003).

Werner deconvolution method (1953) is designed to analyze magnetic fields of dipping magnetized dikes by separating the anomaly due to a particular dike from the interference of neighboring dikes. The application of the Werner deconvolution method has been thoroughly discussed by Hartiman et al. (1971), Jain (1976), and Ku and Sharp (1983). Ku and Sharp (1983) further refined the Werner deconvolution method using iteration for reducing and eliminating the interference field and then applied Marquardt’s nonlinear least-squares method to further refine automatically the first approximation provided by deconvolution. Nabighian and Hansen (2001) showed the extension of Euler deconvolution algorithm in order to be a generalization and unification of two-dimensional Euler deconvolution and Werner deconvolution. They showed that the three-dimensional extension can be realized using generalized Hilbert transforms. The resulting algorithm is both a generalization of extended Euler deconvolution to three dimensions and a three-dimensional extension of Werner deconvolution.

Recently simulated annealing methods (Gokturkler and Balkaya 2012) and deterministic approaches (Mehanee 2014a, b) have been successfully used to solve similar nonlinear inversion problems of geometrically simple idealized bodies. Alternatively, in this paper, a practical interpretation method is introduced for interpreting magnetic field anomalies and best-estimate of model parameters values, for example the depth to the top or to the center of the body, the effective magnetization inclination, and the amplitude coefficient related to a buried thin dike or a horizontal cylinder-like structure. The method is based on the use of the deconvolution technique to avoid the local minima where, we transformed the nonlinear programming problem, which describes the suitable simple geometric-shaped model of structure into a linear programming one. This linear programming problem is thereafter solved by the very well-known algorithm in linear programming called the simplex algorithm of Dantzig (Phillips et al. 1976). However, the use of deconvolution technique, in this paper, allows transforming the non-convex and nonlinear mathematical program into linear one and this linear program has been thereafter solved by the simplex method for definitely reaching the global minima.

The reliability and validity of the proposed interpretation method is demonstrated first through using synthetic data sets corrupted by different white Gaussian random noise levels and second through reinterpreting real field magnetic anomalies taken from the United States and Brazil. A comparable and acceptable agreement is shown between the results derived by this method and those obtained by other interpretation methods.

Moreover, the depth obtained by such a method is found to be in high accordance with that obtained from the real field data information.

2 Method

2.1 Interpretation of Magnetic Anomaly due to a Thin Dike Model

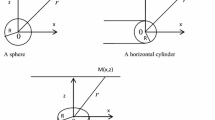
The general expression for the magnetic anomaly \((V)\) at any point \(P(x)\) along the \(x-\)axis of an arbitrary magnetized thin dike-like structure in a Cartesian coordinate system (Fig. 1) can be given according to Atchuta Rao et al. (1980), Abdelrahman and Sharafeldin (1996), and Gay (1963) as

$$\begin{aligned} V(x_i )=k\frac{x_i \sin \theta +z\cos \theta }{x_i^2 +z^2}\quad (i=1,\ldots ,N), \end{aligned}$$
(1)
Fig. 1
figure 1

Cross-sectional view of a two-dimensional thin dike model

Full size image

where \(z\) is the depth to the top of the buried thin dike body, \(\theta \) is the effective magnetization angle or the index parameter, \(k\) is the amplitude coefficient, and \(x_i (i=1,\ldots .,N)\) is the horizontal position coordinate. The values of \(k\) and \(\theta \)for the vertical, horizontal and total field anomalies for the case of thin dikes are given in Table 1. In this table, \(\xi \) is the magnetic susceptibility contrast, \(I_0 \) is the true inclination of the geometric field, \(T_0^{'} \) and \(I_0^{'} \) are, respectively, the effective intensity and effective inclination of the geometric field in the vertical plane normal to the strike of the body, \(t\)and \(d\) are, respectively, the thickness and the dip of the dike, and \(\alpha \) is the strike of the body measured in the clockwise direction from magnetic north. The set of Eq. 1 consists of \(N\) nonlinear equations in function of the parameters \(k\), \(\theta \) and \(z\). To avoid this nonlinearity, the following proposed deconvolution technique will be used. First and for simplification, \(V_i \) is used instead of \(V(x_i )\quad (i=1,\ldots ,N)\) in the rest of this paper. Multiplying the two sides of Eq. 1 by the term \(( {x_i^2 +z^2})\) and arranging them, it can be found

$$\begin{aligned} V_i x_i^2 +V_i q_1 -x_i q_2 -q_3 =0\quad (i=1,\ldots ,N), \end{aligned}$$
(2)

where, in Eq. 2.

$$\begin{aligned}&q_1 =z^2,\end{aligned}$$
(3)
$$\begin{aligned}&q_2 =k\sin \theta ,\end{aligned}$$
(4)
$$\begin{aligned}&q_3 =kz\cos \theta . \end{aligned}$$
(5)
Table 1 Characteristic amplitude coefficient \(k\) and index parameter \(\theta \)for vertical, horizontal and total magnetic anomalies resulting from thin dikes and horizontal cylinders
Full size table

The set of Eq. 2 consists of \(N\) linear equations in function of the new parameters \(q_1 \),\(q_2 \), and \(q_3 \), where \(q_1 \) is restricted to be nonnegative variable, \(q_2 \) and \(q_3 \) are free variables. To find the optimal solution \((q_1 ,q_2 ,q_3 )\) of the set of linear Eq. 2, with respect to the non-negativity of \(q_1 \), it can be found by solving the following nonlinear program onto the real space \(R^3\)

$$\begin{aligned} \min _{q\in R^3} \quad f(q)=\sum \limits _{i=1}^N {( {V_i x_i^2 +V_i q_1 -x_i q_2 -q_3 })} ^2, \end{aligned}$$
(6)

subject to \(q_1 \ge 0\) and \(q_2, q_3 \) being free. The quadratic objective function \(f(q)\)of (6) is being defined as a sum of squared linear functions in function of \(q\), then it is convex onto the real space\(R^3\). Furthermore \(q_2 \)and \(q_3 \) are free variables, where no restrictions exist, and then \(q_1 ,q_2 ,q_3 \) will be changed to become as follows

$$\begin{aligned} \left. \begin{array}{l} q_1 =p_1 \\ q_2 =p_2 -p_4 \\ q_3 =p_3 -p_4 \\ \end{array} \right\} , \end{aligned}$$
(7)

where \(p_1 ,p_2 ,p_3 ,p_4 \ge 0\).

Introducing these new variables into (6), the following nonlinear program can be obtained, which is subjected to non-negativity constraints on variables \(p_1 ,p_2 ,p_3 \) and \(p_4 \)

$$\begin{aligned} \min _{p\in R^4} \,\,\,\varphi (p)=\sum \limits _{i=1}^N {( {V_i x_i^2 +V_i p_1 -x_i p_2 +x_i p_4 -p_3 +p_4 })} ^2, \end{aligned}$$
(8)

subject to \(p_1 ,p_2 ,p_3 ,p_4 \ge 0\).

The new quadratic objective function \(\varphi (p)\)of (8) is being also defined as the sum of squared linear functions of \(p\), then it is convex onto the nonnegative orthant of the real space \(R^4\). In order to find the optimal solution\(( {p_1 ,p_2 ,p_3 ,p_4 })\in R^4\) of (8), it is necessary and sufficient to find the optimal solution to the following set of nonlinear equations

$$\begin{aligned} \left. \begin{array}{l} p_i \ge 0\quad \forall i=1,\ldots ,4 \\ p_i \frac{\partial \varphi (p)}{\partial p_i }=0\quad \forall i=1,\ldots ,4 \\ \frac{\partial \varphi (p)}{\partial p_i }\ge 0\quad \forall i=1,\ldots ,4\\ \end{array} \right\} . \end{aligned}$$
(9)

Equations 9 are called the optimality conditions of Karush–Kuhn–Tuker (KKT) according to Phillips et al. (1976). Since Eq. 9 are nonlinear, they can be easily transformed into a linear optimization program by adding non-negative artificial variables \(u\in R^4\) as follows

$$\begin{aligned} \left. \begin{array}{l} \min \;\sum \nolimits _{i=1}^4 {u_i } \\ \mathrm{subject\,to}\,\,\frac{\partial \varphi (p)}{\partial p_i }-u_i =0\quad \forall i=1,\ldots ,4 \\ \quad p_i ,u_i \ge 0\quad \forall i=1,\ldots ,4 \\ \end{array} \right\} . \end{aligned}$$
(10)

The objective function \(\sum \nolimits _{i=1}^4 {u_i } \) of (10) is linear and consequently convex. The following feasible set

$$\begin{aligned}&X=\left\{ p,u\in R^4:\frac{\partial \varphi (p)}{\partial p_i }-u_i =0\quad (i=1,\ldots ,4), \right. \\&\quad \left. \,\mathrm{and}\quad p_i ,u_i \ge 0\quad (i=1,\ldots ,4) \right\} , \end{aligned}$$

is defined by linear equations and it is consequently convex on the nonnegative orthant of \(R^8\). After executing the above-mentioned mathematical steps, all the conditions needed and necessarily for the simplex algorithm are now satisfied.

Differentiating \(\varphi (p)\)as a function of \(p\), the linear program (10) can be rewritten as follows

$$\begin{aligned} \left. \begin{array}{l} \min \quad u_1 +u_2 +u_3 +u_4 \quad \mathrm{subject\;to} \\ \left( {\sum \limits _{i=1}^N {V_i^2 }}\right) p_1 -\left( {\sum \limits _{i=1}^N {V_i x_i }}\right) p_2 -\left( {\sum \limits _{i=1}^N {V_i } }\right) p_3 +\left( {\sum \limits _{i=1}^N {V_i(1+x_i )} }\right) p_4 -u_1 =-\left( {\sum \limits _{i=1}^N {V_i^2 x_i^2 } }\right) \\ -\left( {\sum \limits _{i=1}^N {V_i x_i } }\right) p_1 +\left( {\sum \limits _{i=1}^N {x_i^2 } }\right) p_2 +\left( {\sum \limits _{i=1}^N {x_i } }\right) p_3 -\left( {\sum \limits _{i=1}^N {x_i (1+x_i )} }\right) p_4 -u_2 =-\left( {\sum \limits _{i=1}^N {V_i x_i^3 } }\right) \\ -\left( {\sum \limits _{i=1}^N {V_i } }\right) p_1 +\left( {\sum \limits _{i=1}^N {x_i } }\right) p_2 +Np_3 -\left( {\sum \limits _{i=1}^N {(1+x_i )}}\right) p_4 -u_3 =-\left( {\sum \limits _{i=1}^N {V_i x_i^2 } }\right) \\ \left( {\sum \limits _{i=1}^N {V_i (1+x_i )} }\right) p_1 -\left( {\sum \limits _{i=1}^N {x_i (1+x_i )} }\right) p_2 -\left( {\sum \limits _{i=1}^N {(1+x_i )} }\right) p_3 \quad +\left( {\sum \limits _{i=1}^N {(1+x_i )^2} }\right) p_4 -u_4 =\\ -\left( {\sum \limits _{i=1}^N {V_i x_i^2 (1+x_i )} }\right) \\ \quad p_1 ,p_2 ,p_3 ,p_4 ,u_1 ,u_2 ,u_3 ,u_4 \ge 0 \\ \end{array} \right\} .\nonumber \\ \end{aligned}$$
(11)

The linear program (11) is then solved by the Simplex algorithm in order to find the optimal values of \(( {p_1 ,p_2 , p_3, p_4 ,u_1 ,u_2 ,u_3 ,u_4 })\in R^{8}\), which are satisfying the KKT optimality conditions (9) for the nonlinear program (8). This solution is surely a global minima, and consequently the optimal valuesof \(( {q_1 ,q_2 ,q_3 })\in R^3\) can be obtained by using Eq. 7. For more details about the simplex algorithm of Dantzig for linear programming optimization, readers are referred to Phillips et al. (1976), Hillier and Lieberman (1986) and Bradley et al. (1977). It is useful to mention here that the linear program (11) cannot be solved by one of the unconstrained mathematical optimization algorithms as the steepest descent algorithm, conjugate gradients algorithms, Hooke and Jeeves’s algorithm, and the simulated annealing algorithms, but it should be solved using one of the constrained mathematical optimization algorithms as the simplex algorithm and the interior point algorithms.

After obtaining the optimal values of \(q_1 \), \(q_2 \) and \(q_3 \), the best-estimate of the depth to the top of the buried thin dike body (\(z)\) can be easily found using Eq. 3 as

$$\begin{aligned} z=\sqrt{q_1 } . \end{aligned}$$
(12)

The best-estimate of the effective magnetization angle (\(\theta )\) and the amplitude coefficient (\(k)\) can be obtained using simultaneously Eqs. 4 and 5 as

$$\begin{aligned} \theta =\arctan \left( {z\frac{q_2 }{q_3 }}\right) ,\end{aligned}$$
(13)
$$\begin{aligned} k=\mp \sqrt{q_2^2 +\frac{q_3^2 }{z^2}}. \end{aligned}$$
(14)

The sign of \(k\)can be assigned depending on the statistical criterion of preference called the root mean square error (RMSE) (Collins 2003). The RMSE is based on the minimal value between the field data anomaly and the computed one and also by using the estimated values of \(z\),\(\theta \) and \(k\)calculated before. The mathematical formula of this criterion is given as

$$\begin{aligned} \mathrm{RMSE}=\sqrt{\frac{\sum \nolimits _{i=1}^N {( {V_i ( \mathrm{Observed})-V_i ( \mathrm{Computed})})^2} }{N}}, \end{aligned}$$

where \(V_i ( \mathrm{Observed})\) and \(V_i ( \mathrm{Computed}) \quad (i=1,\ldots ,N)\) are the observed and the computed values at the point \(x_i \;(i=1,\ldots ,N)\), respectively.

2.2 Interpretation of a Synthetic Magnetic Anomaly due to a Thin Dike Model with different Levels of Gaussian Random Noise

A synthetic magnetic anomaly \(V(x_i )\;(i=1,\ldots ,N)\) due to a thin dike-like structure is generated from Eq. 1 using the following values of model parameters: depth to the top of the structure \(z=15\) unit length, effective magnetization angle \(\theta =60^{\circ }\), and amplitude coefficient \(k=1{,}500~\)nT.m. Based on this generated synthetic anomaly, two additional magnetic anomalies are regenerated, by perturbing them with different Gaussian random noise maximum levels of 7 and 10 %, respectively. Both regenerated magnetic anomalies are consequently interpreted by the new proposed method, where the estimated model parameters values are shown in Table 2 and Fig. 2.

Fig. 2
figure 2

Diagram for the computed anomaly and synthetic data set with adding a maximum of 10 % random noise

Full size image
Table 2 Interpretation of a synthetic magnetic anomaly due to a thin dike model with different maximum levels of Gaussian random noise
Full size table

The results presented in Table 2 show that the estimated parameter values, derived by this interpretation method, are very close to the true values of parameters, which clearly indicate the efficiency and the capability of the proposed interpretation method. Moreover, it is noticed from Table 2 that the parameter \(k\) (the amplitude coefficient) are more influenced and exhibits more sensibility to the random noise. Being \(k\)a multiplier factor, that explains such a sensibility. To minimize the big deviation between the estimated and the true values of the multiplier parameter\(k\), when the field data is more contaminated by gross random noise, it is therefore advisable to estimate \(k\)by the following equation instead of Eq. 14

$$\begin{aligned} k=\frac{\sum \nolimits _{i=1}^N {V_i \alpha _i } }{\sum \nolimits _{i=1}^N {\alpha _i^2 } }, \end{aligned}$$
(15)

where \(\alpha _i =\frac{x_i \sin \theta +z\cos \theta }{x_i^2 +z^2}\quad \quad ( {i=1,2,\ldots ,N}).\)

Equation 15 is easily derived from the minimization of the \(L_2 \) Euclidean distance, between the field data anomaly and the computed one, taking into consideration the computed values of the depth to the top of the body (\(z)\) and the effective magnetization angle (\(\theta )\) by Eqs. 12 and 13.

2.3 Interpretation of Magnetic Anomaly due to a Horizontal Vylinder Model

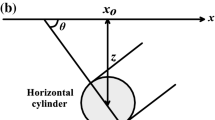
The general expression for the magnetic anomaly \((V)\) observed at a point \(P(x)\) along the \(x\)-axis due to an infinitely extended horizontal cylinder in a Cartesian coordinate system (Fig. 3), is given by Prakasa Rao et al. (1986) as

$$\begin{aligned} V(x_i )=k\frac{( {z^2-x_i^2 })\cos \theta +2x_i z\sin \theta }{( {x_i^2 +z^2})^2}\quad (i=1,\ldots ,N). \end{aligned}$$
(16)
Fig. 3
figure 3

Geometry of the horizontal cylinder magnetized by induction in the Earth’s field

Full size image

The notations in this expression have the same meaning as those presented in Eq. 1 except \(z\) is the depth to the center of the buried structure. The values of \(k\) and \(\theta \)for the vertical, horizontal and total field anomalies for the case of horizontal cylinders are also given in Table 1. In this table, \(s\)is the cross-sectional area of the horizontal cylinder. Multiplying the two sides of Eq. 16 by the term \(( {x_i^2 +z^2})^2\) and arranging them, it can be found

$$\begin{aligned} V_i x_i^4 +2V_i x_i^2 q_1 +V_i q_2 +x_i^2 q_3 -2x_i q_4 -q_5 =0\quad (i=1,\ldots ,N), \end{aligned}$$
(17)

where, in Eq. 17

$$\begin{aligned}&q_1 =z^2,\end{aligned}$$
(18)
$$\begin{aligned}&q_2 =z^4,\end{aligned}$$
(19)
$$\begin{aligned}&q_3 =k\cos \theta ,\end{aligned}$$
(20)
$$\begin{aligned}&q_4 =kz\sin \theta ,\end{aligned}$$
(21)
$$\begin{aligned}&q_5 =kz^2\cos \theta , \end{aligned}$$
(22)

The optimal solution \((q_1 ,q_2 ,q_3 ,q_4 ,q_5 )\)of the set of linear equations (17), with respect to the non-negativity of \(q_1 \)and \(q_2 \), it can be found by solving the following nonlinear program onto the real space\(R^5\)

$$\begin{aligned} \min _{q\in R^5} \;\,f(q)=\sum \limits _{i=1}^N {( {V_i x_i^4 +2V_i x_i^2 q_1 +V_i q_2 +x_i^2 q_3 -2x_i q_4 -q_5 })} ^2. \end{aligned}$$
(23)

Subject to \(q_1 \ge 0,q_2 \ge 0\) and \(q_3 ,q_4 ,q_5 \) being free.

Furthermore \(q_3 ,q_4 ,q_5 \) are free variables, no restrictions exist, and then \(q_1 ,q_2 ,q_3 ,q_4 ,q_5 \) will be changed as follows

$$\begin{aligned} \left. \begin{array}{l} q_1 =p_1 \\ q_2 =p_2 \\ q_3 =p_3 -p_6 \\ q_4 =p_4 -p_6 \\ q_5 =p_5 -p_6 \\ \end{array} \right\} , \end{aligned}$$
(24)

where \(p_1 ,p_2 ,p_3 ,p_4 ,p_5 ,p_6 \ge 0.\)

Introducing those new variables into (23), it can be obtained the following nonlinear program which is subjected to non-negativity constraints on variables \(p_1 ,p_2 ,p_3 ,p_4 ,p_5 \) and \(p_6 \)

$$\begin{aligned}&\min _{p\in R^6} \;\,\varphi (p)\nonumber \\&=\sum \limits _{i=1}^N {( {V_i x_i^4+2V_i x_i^2 p_1 +V_i p_2 +x_i^2 p_3-2x_i p_4 -p_5 +( {-x_i^2 +2x_i +1})p_6 })}^2, \nonumber \\&{\hbox {Subject to}}\quad p_1 ,p_2 ,p_3 ,p_4 ,p_5 ,p_6 \ge 0. \end{aligned}$$
(25)

The KKT optimality conditions (9) for the nonlinear program (25) are satisfied through solving the following linear program

$$\begin{aligned} \left. \begin{array}{l} \min \quad u_1 +u_2 +u_3 +u_4 +u_5 +u_6 \quad subject\;to \\ 4\left( {\sum \nolimits _{i=1}^N {V_i^2 } x_i^4 }\right) p_1 +2\left( {\sum \nolimits _{i=1}^N {V_i^2 x_i^2 } }\right) p_2 +2\left( {\sum \nolimits _{i=1}^N {V_i x_i^4 } }\right) p_3 -4\left( {\sum \nolimits _{i=1}^N {V_i x_i^3 } }\right) p_4 -2\left( {\sum \nolimits _{i=1}^N {V_i x_i^2} }\right) \\ p_5 +2\left( {\sum \nolimits _{i=1}^N {V_i x_i^2 (-x_i^2 +2x_i +1)} }\right) p_6 -u_1 =-2\left( {\sum \nolimits _{i=1}^N {V_i^2 x_i^6 } }\right) \\ 2\left( {\sum \nolimits _{i=1}^N {V_i^2 } x_i^2 }\right) p_1 +\left( {\sum \nolimits _{i=1}^N {V_i^2 } }\right) p_2 +\left( {\sum \nolimits _{i=1}^N {V_i x_i^2 } }\right) p_3 -2\left( {\sum \nolimits _{i=1}^N {V_i x_i} }\right) p_4 -\left( {\sum \nolimits _{i=1}^N {V_i } }\right) \\ p_5 + \left( {\sum \nolimits _{i=1}^N {V_i (-x_i^2 +2x_i +1)} }\right) p_6 -u_2 =-\left( {\sum \nolimits _{i=1}^N {V_i^2 x_i^4 } }\right) \\ 2\left( {\sum \nolimits _{i=1}^N {V_i} x_i^4 }\right) p_1 +\left( {\sum \nolimits _{i=1}^N {V_i x_i^2 } }\right) p_2 +\left( {\sum \nolimits _{i=1}^N {x_i^4 } }\right) p_3 -2\left( {\sum \nolimits _{i=1}^N {x_i^3 } }\right) p_4 -\left( {\sum \nolimits _{i=1}^N {x_i^2 } }\right) \\ p_5 +\left( {\sum \nolimits _{i=1}^N {x_i^2 (-x_i^2 +2x_i +1)} }\right) p_6 -u_3 =-\left( {\sum \nolimits _{i=1}^N {V_i x_i^6 } }\right) \\ \quad -4\left( {\sum \nolimits _{i=1}^N {V_i} x_i^3 }\right) p_1 -2\left( {\sum \nolimits _{i=1}^N {V_i x_i} }\right) p_2 -2\left( {\sum \nolimits _{i=1}^N {x_i^3 } }\right) p_3 +4\left( {\sum \nolimits _{i=1}^N {x_i^2 } }\right) p_4 +2\left( {\sum \nolimits _{i=1}^N {x_i } }\right) \\ p_5-2\left( {\sum \nolimits _{i=1}^N {x_i (-x_i^2 +2x_i +1)} }\right) p_6 -u_4 =2\left( {\sum \nolimits _{i=1}^N {V_i x_i^5 } }\right) \\ \quad -2\left( {\sum \nolimits _{i=1}^N {V_i } x_i^2 }\right) p_1 -\left( {\sum \nolimits _{i=1}^N {V_i} }\right) p_2 -\left( {\sum \nolimits _{i=1}^N {x_i^2 } }\right) p_3 +2\left( {\sum \nolimits _{i=1}^N{x_i } }\right) \\ p_4 +Np_5 -\left( {\sum \nolimits _{i=1}^N {(-x_i^2 +2x_i +1)} }\right) p_6 -u_5 =\left( {\sum \nolimits _{i=1}^N {V_i x_i^4 } }\right) \\ 2\left( {\sum \nolimits _{i=1}^N {V_i} x_i^2 (-x_i^2 +2x_i +1)}\right) p_1 +\left( {\sum \nolimits _{i=1}^N {V_i (-x_i^2 +2x_i +1)} }\right) p_2 +\left( {\sum \nolimits _{i=1}^N{x_i^2 (-x_i^2 +2x_i +1)} }\right) \\ p_3 -2\left( {\sum \nolimits _{i=1}^N {x_i (-x_i^2 +2x_i +1)} }\right) p_4 -\left( {\sum \nolimits _{i=1}^N {(-x_i^2 +2x_i +1)} }\right) p_5 +\left( {\sum \nolimits _{i=1}^N{(-x_i^2 +2x_i +1)^2} }\right) \\ p_6 -u_6 = -\left( {\sum \nolimits _{i=1}^N {V_i x_i^4 (-x_i^2 +2x_i +1)} }\right) \\ \quad p_1 ,p_2 ,p_3 ,p_4 ,p_5 ,p_6 ,u_1 ,u_2 ,u_3 ,u_4 ,u_5 ,u_6 \ge 0 \\ \end{array} \right\} .\nonumber \\ \end{aligned}$$
(26)

The linear program (26) is then solved by the Simplex algorithm to find the optimal values of \(( {p_1 ,p_2 ,p_3 ,p_4 ,p_5 ,p_6 ,u_1 ,u_2 ,u_3 ,u_4 ,u_5 ,u_6 })\in R^{12}\) which are satisfying the KKT optimality conditions (9) for the nonlinear program (25). This solution is surely a global minima, and consequently, the optimal values of \(( {q_1 ,q_2 ,q_3 ,q_4 ,q_5 })\in R^5\) can be obtained by using Eq. 24. After obtaining the optimal values of \(q_1 \), \(q_2 \),\(q_3 \),\(q_4 \)and \(q_5 \), the best- estimate of the depth to the center of the buried horizontal cylinder body (\(z)\) can be easily found using simultaneously Eqs. 18 and 19 as

$$\begin{aligned} z=\frac{1}{2}\left( {q_1^{\frac{1}{2}} +q_2^{\frac{1}{4}} }\right) . \end{aligned}$$
(27)

The best-estimate of the effective magnetization angle (\(\theta )\) and the amplitude coefficient (\(k)\) can easily be obtained using simultaneously Eqs. 20, 21 and 22 as

$$\begin{aligned}&\theta =\arctan \frac{1}{2}\left( {\frac{1}{z}\frac{q_4 }{q_3 }+z\frac{q_4 }{q_5 }}\right) ,\end{aligned}$$
(28)
$$\begin{aligned}&k=\mp \sqrt{\frac{1}{2}\left( {q_3^2 +2\frac{q_4^2 }{z^2}+\frac{q_5^2 }{z^4}}\right) } . \end{aligned}$$
(29)

It is worth noting that, the sign of \(k\) can be also assigned depending on the statistical criterion of preference (RMSE). The RMSE is based on both the minimal value between the field data anomaly and the computed one and also on the use of the estimated values of \(z\),\(\theta \) and \(k\) calculated before.

Moreover, when the field data are more contaminated by gross random noise, it is therefore advisable to estimate the multiplier parameter \(k\)by the following equation instead of Eq. 29

$$\begin{aligned} k=\frac{\sum \nolimits _{i=1}^N {V_i \beta _i } }{\sum \nolimits _{i=1}^N {\beta _i^2 } }, \end{aligned}$$
(30)

where \(\beta _i =\frac{( {z^2-x_i^2 })\cos \theta +2\,x_i \,z\sin \theta }{( {x_i^2 +z^2})^2}\quad ( {i=1,2,\ldots ,N}).\)

Equation 30 is also derived from the minimization of the\(L_2 \)-Euclidean distance, between the field data anomaly and the computed one, taking into consideration the computed values of the depth to the center of the body (\(z)\) and the effective magnetization angle (\(\theta )\) by Eqs. 27 and 28.

3 Applications

Two field magnetic anomalies over various geological structures are interpreted by the proposed method and discussed below.

3.1 Interpretation of a Field Magnetic Anomaly due to a Thin Dike Model

Figure 4 shows a magnetic field anomaly resulted from a profile of 750 \(m\)-long over the Pima Copper mine, Arizona; United States (Abdelrahman and Sharafeldin 1996; Gay 1963). This magnetic anomaly has been reinterpreted by the proposed method with considering a priori that the source which causes this anomaly is due to a thin dike model. Using Eqs. 12, 13 and 14 the estimated values of the model parameters are obtained as

$$\begin{aligned} z=64.1\,\mathrm{m},\quad \theta =-44.7^{\circ },\quad k=42{,}700\;\mathrm{nT.m},\quad \mathrm{RMSE}_1 =32\,\mathrm{nT}. \end{aligned}$$
Fig. 4
figure 4

Magnetic field anomaly over the Pima copper deposit in Arizona, United States. The computed anomaly by the proposed interpretation method is also shown

Full size image

The depth to the top of the thin dike (\(z=64.1\;\mathrm{m})\) is found to be in very good agreement with that obtained from drilling (\(z=64\;\mathrm{m})\). The computed magnetic anomaly has been drawn according to these estimated values of model parameters as shown in Fig. 4. The comparison between field and computed anomalies clearly indicates the close agreement between them, which attests the capability and the validity of the method. The results acquired by the presented method are shown in Table 3 and Fig. 4, which include also the results derived using the standardized curves method previously reported by Gay (1963), the results obtained using the least-squares minimization (Abdelrahman and Sharafeldin 1996), and the results obtained using the Fair function minimization (Tlas and Asfahani 2011a). The magnetic anomaly has also been reinterpreted by the proposed method with considering a priori that the source which causes this anomaly is due to a horizontal cylinder model. Using Eqs. 27, 28 and 29 the estimated values of the model parameters are obtained as

$$\begin{aligned} z=496.9\,\mathrm{m},\quad \theta =-88.9^{\circ },\quad k=3.9\times 10^7\;\mathrm{nT.m}^2,\quad \mathrm{RMSE}_2 =213.7\,\mathrm{nT}. \end{aligned}$$
Table 3 Interpretation of the Pima copper mine anomaly, Arizona, United States
Full size table

From the calculation of \(\mathrm{RMSE}_1 \) and \(\mathrm{RMSE}_2 \), it is clear that, the value of \(\mathrm{RMSE}_2 \) is greater than the value of \(\mathrm{RMSE}_1 \). Hence, it is not absolutely preferable to model the source which causes this anomaly as a horizontal cylinder but it is better to be modeled as a dike.

3.2 Interpretation of a Field Magnetic Anomaly due to a Horizontal Cylinder Model

Figure 5 shows a magnetic field anomaly measured over a profile of 24.64 m-long above a Mesozoic diabase intruded into Paleozoic sediment from the Parnaiba basin, Brazil (Abdelrahman and Sharafeldin 1996; Silva 1989). This magnetic anomaly has been reinterpreted by the proposed method with considering a priori that the source which causes this anomaly is due to a horizontal cylinder model. The specificity of this field anomaly is that the upper part of the body was weathered and the magnetite presence was oxidized, where most of its magnetic property have been lost, according to Silva (1989). This geological situation indicates that the magnetic anomaly is largely affected by gross random noise levels. The model parameter values could therefore be estimated using Eqs. 27, 28 and 30, where the estimated values are

$$\begin{aligned} z=3.4\,\mathrm{m},\quad \theta =41.3^{\circ },\quad k=-645.6\;\mathrm{nT.m}^2,\quad \mathrm{RMSE}_1 =38\;\mathrm{nT}. \end{aligned}$$
Fig. 5
figure 5

Magnetic field anomaly over an outcropping horizontal cylinder in the Parnaiba basin, Brazil. The computed anomaly by the proposed interpretation method is also shown

Full size image

The depth to the center of the horizontal cylinder (\(z=3.4\;m)\) is found to be in very good agreement with that reported by both Silva (1989), using the \(M\)-fitting technique and Abdelrahman and Sharafeldin (1996), using the least-squares minimization technique (\(z=3.5\;\mathrm{m})\). The computed magnetic anomaly has been drawn according to the estimated values of model parameters as shown in Fig. 5. The results acquired by the presented method are shown in Table 4 and Fig. 5, which include also the results derived using the \(M\)-fitting technique previously reported by Silva (1989), the results obtained using the least-squares minimization (Abdelrahman and Sharafeldin 1996), and the results derived using the deconvolution technique (Tlas and Asfahani 2011).

Table 4 Interpretation of the Parnaiba anomaly, Brazil
Full size table

The magnetic anomaly has been also reinterpreted by the proposed method with considering a priori that the source which causes this anomaly is due to a thin dike model.

The simplex algorithm indicates that the linear program (11) is unbounded and the calculated value of RMSE\(_2\) was very high. Hence, it is not absolutely recommended to model the source which causes this anomaly as a thin dike but it is better to be modeled as a horizontal cylinder. Finally, it is useful to mention here that there is no loss of generality in assuming the source geometry is known a priori, in addition, it does not impose any restrictions on the generality of the proposed interpretation method. However, in the case of any magnetic field anomaly, where its source geometry is unknown, the next two steps are to be followed.

First, the magnetic field anomaly is interpreted with considering the source geometry as a thin dike, where the root mean square error \(\mathrm{RMSE}_1 \) is computed between the observed field anomaly and the computed one. Second, the magnetic field anomaly is re-interpreted with considering the source geometry as a horizontal cylinder, where the root mean square error \(\mathrm{RMSE}_2 \) is computed between the observed field anomaly and the computed one. The comparison between the two values \(\mathrm{RMSE}_1 \) and \(\mathrm{RMSE}_2 \) allows selecting minimal value of RMSE, which exactly determines the suitable source geometry related to the treated field anomaly.

4 Conclusions

Herewith a new approach is proposed in this paper for the interpretation of magnetic anomalies due to simple geometric-shaped models such as thin dike, and horizontal cylinder. The proposed method is based on both the deconvolution technique to avoid the local minima and on the simplex algorithm for linear programming to best-estimate the model parameters values, for example the depth to the top or to the center of the buried structure, the effective magnetization angle and the amplitude coefficient from magnetic anomaly profile. The reliability and capability of this interpretation method have been first demonstrated through testing and corrupting the synthetic data sets by different white Gaussian random noise levels of 7 and 10 %. The synthetic modeling results acquired show that the estimated parameter values derived by this new method are very close to the assumed true values of parameters. The validity of this method is also demonstrated through reinterpreting real field magnetic anomalies taken from the United States and Brazil. A comparable and acceptable agreement is shown between the results derived by the proposed method and those obtained by other interpretation methods. Moreover, the depth obtained by such a method is found to be in high accordance with that obtained from the real field data information.

This interpretation method can be easily put in a MATLAB code. Furthermore, the method is being based on the familiar algorithm in linear programming, called the simplex algorithm of Dantzig, the convergence towards the best estimation of parameters values is assured and rapidly reached. This new methodology is therefore recommended for routine analysis of magnetic anomalies in an attempt to determine the best-estimate values of parameters related to thin dikes and horizontal cylinder-like structures.