The strength of solids depends on the specific features of material structure and the presence of defects in it. Foreign inclusions and cavities induce stress concentration in materials. In the present work, based on the strain criterion of strength, we study the features of deformation and fracture of elastoplastic bodies in the neighborhood of elastic spheroidal inclusions.

Formulation of the Problem

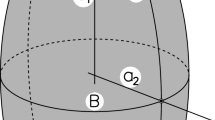
Consider uniaxial tension of an infinite elastoplastic body, containing a thin elastic inclusion in the plane normal to the load axis. We assume that the inclusion surface is a surface of revolution symmetric with respect to the plane z = 0 (Fig. 1).

Fig. 1
figure 1

Schematic illustration of the section of a body with a spheroidal inclusion and prefracture zones by the planes φ = 0 (a) and z = 0 (b).

Full size image

With increase in the load, a zone is formed near the inclusion where the material is deformed beyond the limits of elasticity. We mentally cut out the inclusion and prefracture zone, adjoining it, from the body. Their action on the base material is replaced, in view of the small thickness of the inclusion and prefracture zone and the smoothness of their surfaces, by certain stresses on the cavity surface. In the region of contact of the materials of the inclusion and matrix, we represent the stresses according to the model of a compliant inclusion [1]

$$ {{{\upsigma }}_z}(r) = \frac{{\left[ {u_z^*} \right]}}{{2h(r)}}{E_1},\quad {{{\upsigma }}_{rz}} = 0 $$
(1)

and, at the boundary between inelastically and elastically deformed materials, take them constant and equal to σ T :

$$ {{{\upsigma }}_z} = {{{\upsigma }}_T},\quad {{{\upsigma }}_{rz}} = 0. $$
(2)

Here, 2 h(r) is the inclusion thickness, [u z *(r)] is the displacement jump of points of the inclusion surface, and E 1 is the Young’s modulus of the material.

Since the thickness of the formed cavity is small, we may carry boundary conditions from the surface to median plane (z = 0) . As a result, we reduce the axially symmetric problem of tension of an infinite body with a thin inclusion to the solution of the following boundary-value problem for a circular cut of diameter 2(a + R):

$$ \begin{array}{*{20}{c}} {{{{\upsigma }}_{zz}} = \left\{ {\begin{array}{*{20}{c}} { - p + \frac{{\left[ {u_z^*} \right]}}{{2h(r)}}{E_1},} \hfill & {0 \leq r \leq a,} \hfill \\ { - p + {{{\upsigma }}_T},} \hfill & {a \leq r \leq a + R,} \hfill \\ \end{array} } \right.} \hfill \\ {{u_z} = 0,\quad a + R < r < \infty, } \hfill \\ {{{{\upsigma }}_{rz}} = 0,\quad 0 \leq r < \infty .} \hfill \\ \end{array} $$
(3)

In axially symmetric problems, the displacements and stresses are usually expressed via two harmonic functions ϕ and ψ:

$$ 2{{\upmu }}{u_r} = - \frac{{\partial \phi }}{{\partial r}} - z\frac{{\partial {{\uppsi }}}}{{\partial r}},\quad 2{{\upmu }}{u_z} = {{\upkappa \psi }} - \frac{{\partial \phi }}{{\partial z}} - z\frac{{\partial {{\uppsi }}}}{{\partial z}}, $$
(4)
$$ \begin{array}{*{20}{c}} {{{{\upsigma }}_z} = 2\left( {1 - {{\upnu }}} \right)\frac{{\partial {{\uppsi }}}}{{\partial z}} - \frac{{{\partial^2}\phi }}{{\partial {z^2}}} - z\frac{{{\partial^2}{{\uppsi }}}}{{\partial {z^2}}},} \hfill \\ {{{{\upsigma }}_{rz}} = \frac{\partial }{{\partial r}}\left[ {\left( {1 - {{\upnu }}} \right){{\uppsi }} - \frac{{\partial \phi }}{{\partial z}} - z\frac{{\partial {{\uppsi }}}}{{\partial z}}} \right],} \hfill \\ {{{\upkappa }} = 3 - 4{{\upnu }},\quad {{\upmu }} = \frac{{2\left( {1 + {{\upnu }}} \right)}}{E},} \hfill \\ \end{array} $$
(5)

where υ and E are the Poisson’s ratio and Young’s modulus of the base material.

The functions ϕ and ψ can be represented by the Hankel integral expansions:

$$ \phi = \int\limits_0^\infty {{A_1}\left( {{\upxi }} \right){e^{{{\upxi }}z}}{J_0}\left( {{{\upxi }}r} \right)\frac{{d{{\upxi }}}}{{{\upxi }}}}, \quad {{\uppsi }} = \int\limits_0^\infty {{A_2}\left( {{\upxi }} \right){e^{ - {{\upxi }}z}}{J_0}\left( {{{\upxi }}r} \right)d{{\upxi }}}, $$
(6)

where A 1(ξ) and A 2(ξ) are unknown functions. Using the condition of absence of tangential stresses in the plane z = 0 , we can establish the relation between the functions A 1(ξ) and A 2(ξ):

$$ {A_2}\left( {{\upxi }} \right) = - \frac{{{A_1}\left( {{\upxi }} \right)}}{{1 - {{\upnu }}}}. $$

Then, in view of expressions (5) and (6), we obtain from two first conditions (3) a system of paired integral equations

$$ \begin{array}{*{20}{c}} { - \int\limits_0^\infty {{{\upxi }}{A_1}\left( {{\upxi }} \right){J_0}\left( {{{\upxi }}r} \right)d{{\upxi }} = \left\{ {\begin{array}{*{20}{c}} { - p + \frac{{\left[ {u_z^*} \right]}}{{2h(r)}}{E_1},} \hfill & {0 \leq r \leq a,} \hfill \\ { - p + {{{\upsigma }}_T}} \hfill & {a \leq r \leq a + R,} \hfill \\ \end{array} } \right.} } \hfill \\ {\quad \quad \frac{{1 - {{\upnu }}}}{{{\upmu }}}\int\limits_0^\infty {{A_1}\left( {{\upxi }} \right){J_0}\left( {{{\upxi }}r} \right)d{{\upxi }} = 0}, \quad a + R \leq r \leq \infty .} \hfill \\ \end{array} $$
(7)

Further, we differentiate the second of Eqs. (7) with respect to r and introduce the following notation of unknown displacements u z (r) of the cut surface on the segment 0 < r < a + R :

$$ \begin{array}{*{20}{c}} {\frac{{1 - {{\upnu }}}}{{{\upmu }}}\int\limits_0^\infty {{{\left. {{A_1}\left( {{\upxi }} \right){J_1}\left( {{{\upxi }}r} \right){{\upxi }}d{{\upxi }} = \frac{{\partial {u_z}(r)}}{{\partial z}}} \right|}_{z = 0}} = u_z^{\prime}(r)}, \quad 0 < r < a + R,} \hfill \\ {\quad \quad \quad \frac{{1 - {{\upnu }}}}{{{\upmu }}}\int\limits_0^\infty {{A_1}\left( {{\upxi }} \right){J_1}\left( {{{\upxi }}r} \right){{\upxi }}d{{\upxi }} = 0}, \quad a + R < r < \infty .} \hfill \\ \end{array} $$
(8)

Applying the inverse Hankel transformation to relations (8), we obtain from the first equation (7) after certain calculations an integro-differential equation in unknown displacements of the cut surface (z = 0, 0 < r < a + R):

$$ \frac{2}{{{\uppi }}}\int\limits_0^{a + R} {K\left( {r,t} \right)u_z^{\prime}(t)dt} = \frac{{1 - {{\upnu }}}}{{{\upmu }}}\left\{ {\begin{array}{*{20}{c}} { - p + \frac{{\left[ {u_z^*(r)} \right]}}{{2h(r)}}{E_1},} \hfill & {0 \leq r \leq a,} \hfill \\ { - p + {{{\upsigma }}_T}} \hfill & {a \leq r \leq a + R,} \hfill \\ \end{array} } \right. $$
(9)

where

$$ K\left( {r,t} \right) = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{r}K\left( {\frac{t}{r}} \right) + \frac{{{r^2}}}{{{t^2} - {r^2}}}E\left( {\frac{t}{r}} \right),} \hfill & {t < r,} \hfill \\ {\frac{t}{{{t^2} - {r^2}}}E\left( {\frac{r}{t}} \right),} \hfill & {t > r.} \hfill \\ \end{array} } \right. $$
(10)

Here, K(t/r) and E(t/r) are the first- and second-kind complete elliptic integrals. We assume that u z *(r) ≈ u z (r) + u z 0(r), u z 0(r) = ph(r)/E is the displacement of points of the inclusion surface in a homogeneous (without inclusions) body under the action of external forces p.

Redefining the function u z ′ on the segment − a − R < r < 0 and introducing dimensionless variables

$$ {{\uptau }} = \frac{t}{{a + R}},\quad {{\uprho }} = \frac{r}{{a + R}}, $$

we may write Eq. (9) in the form

$$ \begin{array}{*{20}{c}} {\frac{1}{{{\uppi }}}\int\limits_{ - 1}^1 {{K_1}\left( {{{\uprho }},{{\uptau }}} \right)\frac{{u_z^{\prime}\left( {\left( {a + R} \right){{\uptau }}} \right)d{{\uptau }}}}{{{{\uptau }} - {{\uprho }}}}} = \frac{{1 - {{\upnu }}}}{{{\upmu }}}\left[ { - p + \left( {p{{\uplambda }} + {{\upbeta }}\frac{{{u_z}\left( {\left( {a + R} \right){{\uprho }}} \right)}}{{h\left( {\left( {a + R} \right){{\uprho }}} \right)}}{E_1}} \right)H\left( {\frac{a}{{a + R}} - \left| {{\uprho }} \right|} \right)} \right.} \hfill \\ {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left. { + {{{\upsigma }}_T}H\left( {\left| {{\uprho }} \right| - \frac{a}{{a + R}}} \right)} \right],\quad \left| {{\uprho }} \right| \leq 1,} \hfill \\ \end{array} $$
(11)
$$ {K_1}\left( {{{\uprho }},{{\uptau }}} \right) = \left\{ {\begin{array}{*{20}{c}} {\frac{{{{{\uptau }}^2} - {{{\uprho }}^2}}}{{\left| {{{\uptau \rho }}} \right|}}K\left( {\frac{{{\uptau }}}{{{\uprho }}}} \right) + \frac{{\left| {{\uprho }} \right|}}{{\left| {{\uptau }} \right|}}E\left( {\frac{{{\uptau }}}{{{\uprho }}}} \right),} \hfill & {\left| {{\uprho }} \right| < \left| {{\uptau }} \right|,} \hfill \\ {E\left( {\frac{{{\uprho }}}{{{\uptau }}}} \right),} \hfill & {\left| {{\uptau }} \right| < \left| {{\uprho }} \right|,} \hfill \\ \end{array} } \right. $$
(12)

where H(ρ) is the Heaviside function, and λ = E 1/E.

We establish the size of prefracture zones R near the inclusion, as in the δ c -model [2], from the condition of boundedness of the stresses at the cut edges. The singular integro-differential equation is solved by the method of Gauss–Chebyshev quadrature formulas (see, e.g., [3]). According to relation (1), we determine the strain in the inclusion as

$$ {{\upvarepsilon }}_z^* = \frac{{\left[ {u_z^*(r)} \right]}}{{2h(r)}}. $$
(13)

In particular, at points close to the inclusion tip (r → a) , this relation can be written in the form

$$ {{\upvarepsilon }}_z^* \approx \frac{{\left[ {u_z^*(a)} \right]}}{{2{{\uprho }}}}, $$
(14)

where ρ is the curvature radius of the inclusion tip.

Using the condition of compatibility of strains of the inclusion and matrix at the point we establish the maximal strain near the inclusion:

$$ {{\upvarepsilon }}_z^{\max } = \frac{{\left[ {u_z^*(a)} \right]}}{{2{{\uprho }}}}. $$
(15)

The solution of Eq. (11) enables us to determine the sizes of prefracture zones (R/a) near a spheroidal inclusion with semiaxes a and b (a > b) (Fig. 2). We have established (Fig. 2a) that smaller prefracture zones are formed in the neighborhood of a spheroidal inclusion than near a cylindrical elliptic one (plane problem), the load intensities and curvature radii of inclusions being equal.

Fig. 2
figure 2

Dependence of the size of prefracture zone near an inclusion on the load intensity (a) and inclusion rigidity (b) (dashed lines show the results of solution of the plane problem of tension of a body with an elliptic inclusion [4], and solid lines correspond to the solution of three-dimensional problem).

Full size image

The influence of rigidity of the inclusion material on the size of prefracture zones in its neighborhood for fixed external load is illustrated in Fig. 2b. We see that, with increase in Young’s modulus of the inclusion material, the sizes of prefracture zones in its neighborhood decrease.

To establish the critical load p c , when a crack is initiated in the neighborhood of a spheroidal inclusion, we use the strain criterion of strength, according to which local fracture takes place when the maximal tensile strain reaches its ultimate level ε c :

$$ {{{\upvarepsilon }}_{\max }} = \frac{{\left[ {u_z^*(a)} \right]}}{{2{{\uprho }}}} = {{{\upvarepsilon }}_c}. $$
(16)

We assume that the deformability and strength of the inclusion and its adhesion with the base material are sufficient for initial fracture to occur in the matrix near the inclusion. In Figs. 3 and 4, we show the influence of geometrical and elastic parameters of the inclusion on the critical load.

Fig. 3
figure 3

The critical load of a body with an inclusion vs. the inclusion rigidity (a) and thickness (b) (Eε c /σ0 = 10) (for explanation, see Fig. 2)

Full size image
Fig. 4
figure 4

Influence of the ultimate strain of materials on the critical load of a body with an inclusion (for explanation, see Fig. 2).

Full size image

Conclusions

The strain in the neighborhood of a spheroidal inclusion in an elastic isotropic body under uniaxial tension depends on the intensity of applied loads (p), the characteristic size of the inclusion (a) , its thickness [h(r)], and the mechanical properties of materials (E, E i , and σ T ). As to fracture, through plate-like inclusions are more dangerous as compared with internal spheroidal. The difference between the solutions of plane and three-dimensional problems of this type can reach 30%.