1 Background

With the swift technological progress in micro and nanofabrication, practical applications of micro and nanostructures in recently developed engineering instruments such as micro and nanoelectromechanical systems (MEMS and NEMS) have extensively increased owing to their little dimensions, high sensitivity and rapid response. Consequently, researchers’ attention has been devoted to analysis of behavior of miniaturized mechanical elements like micro and nanoplates. Given the findings of several experimental tests (Ma and Clarke 1995; Stölken and Evans 1998; Chong and Lam 1999), the mechanical behavior of micro and nanostructures is sorely dependent on their size, known as the small-scale effect. For the reason that the relations of classical theory (CT) of elasticity don’t have any material length scale parameters, it is impotent to elaborate size-dependent responses of small-scaled structures. Accordingly, several higher-order continuum theories have been instituted for making the estimations of CT more precise at micro and nano dimensions. As the most well-known of these theories, one can enumerate the couple stress theory (CST) (Toupin 1964), modified couple stress theory (MCST) (Yang et al. 2002), strain gradient theory (SGT) (Lam et al. 2003), nonlocal theory (NT) (Eringen 1972) and nonlocal strain gradient theory (NSGT) (Lim et al. 2015). In MCST, employing a length scale parameter, apart from the classical stress tensor, a symmetric higher-order stress tensor is also introduced. In the last decade, applying the nonclassical elasticity theories, many researchers have surveyed the role of size-dependency in the responses of miniaturized structural elements like beams (Esen et al. 2021; Lu et al. 2022; Liu et al. 2020, 2021; Sarparast et al. 2022; Yu et al. 2022; Zhang et al. 2022; Allahkarami et al. 2018; Hosseini and Arvin 2021; Ebrahimi-Mamaghani et al. 2020; Weng et al. 2021; Xie et al. 2022; Esfahani et al. 2019; Huang et al. 2022; Borjalilou et al. 2019; Farokhi and Ghayesh 2016), plates (Razavilar et al. 2016; Xiao et al. 2021; Akgöz and Civalek 2015; Yin et al. 2022; Golmakani et al. 2021; Gürses et al. 2012; Chang et al. 2022; Tong et al. 2021) and shells (Liu et al. 2022; Farokhi and Ghayesh 2018; Melaibari et al. 2022; Li et al. 2022a) in different situations.

On the evidence of several empirical investigations, heat transfer in a small-scaled structure is extremely dependent on its size. Since the classical heat conduction model, known as the Fourier law, lacks any scale parameters to account for the size effect, various nonclassical models have been put forward to address the shortcomings of the classical model. As the most prominent of these models, one can name models Lord-Shulman (LS model) (Lord and Shulman 1967), Moore-Gibson-Thompson (MGT model) (Quintanilla 2019), Guyer-Krumhansl (GK model) (Guyer and Krumhansl 1966), Green-Naghdi (GN model) (Green and Naghdi 1993), dual-phase-lag (DPL model) (Tzou 2014) and three-phase-lag (TPL model) (Choudhuri 2007). In the GK model, a phase lag parameter is used to account for the size effect on the time domain and a nonlocal parameter is exploited to incorporate the size effect into the space domain.

Thermoelastic damping (TED) has been recognized as a substantial dissipation mechanism for energy loss in a wide range of miniaturized structural elements. As a result of the stress field induced by flexural oscillations, a portion of the structure under tension enlarges, whereas another portion under compression shrinks. Given the coupling between the strain field and temperature, the structure attempts to reestablish thermal equilibrium by heat transfer in the direction of its thickness. This is an irreversible thermal process that results in entropy generation and energy dissipation in the form of thermoelastic damping. To estimate the amount of TED in structures analytically, mainly two approaches of energy dissipation (ED) and complex frequency (CF) are utilized. In the following, the most significant analytical works in the field of TED in small-scaled structures are introduced. The first analytical studies on TED have been carried out by Zener (Zener 1937). In the framework of ED approach, he extracted an explicit solution for evaluating TED in small-sized Euler–Bernoulli beams. With the help of the definition of TED on the basis of CF approach, Lifshitz and Roukes (Lifshitz and Roukes 2000) employed Fourier law of heat conduction to arrive at a single term and exact relation for predicting TED value in thin beams. By means of ED approach, Fang et al. (Fang et al. 2013) developed a mathematical model for expressing TED value in circular plates in the context of CT and Fourier law. In a similar research, Li et al. (Li et al. 2012) provided a comprehensive model to compute TED value in rectangular and circular microplates. Ge and Sarkar (Ge and Sarkar 2022) applied MCST alongside the nonlocal dual-phase-lag (NDPL) model to appraise small-scale effect on TED value in rectangular cross-sectional miniaturized rings. In another study, according to MCST and TPL model, Kumar and Mukhopadhyay (Kumar and Mukhopadhyay 2020) derived a closed-form solution for TED in rectangular plates. In an article by Borjalilou et al. (Borjalilou et al. 2020), NT together with DPL model have been utilized to arrive at an analytical formula for TED in Euler–Bernoulli nanobeams. Based on the NSGT and GK model, Ge et al. (Ge et al. 2021) provided a mathematical model for TED in miniaturized rectangular plates. In a paper by Shi et al. (Shi et al. 2021), TED in nanobeams has been examined by inclusion of dual-phase-lagging and surface effects in governing equations. By using NT, MCST, and MGT model simultaneously, Kumar and Mukhopadhyay (Kumar and Mukhopadhyay 2022) proposed a size-dependent model for TED in nanobeam resonators. Borjalilou and Asghari (Borjalilou and Asghari 2020) exploited SGT and DPL model for computing TED value in rectangular microplates with different boundary conditions. In a work done by Zhou and Li (Zhou and Li 2021), TED in rectangular cross sectional micro and nanorings has been examined on the basis of CT and DPL model. By making use of NT and GK model, Li et al. (Li et al. 2022b) attained an analytical solution to determine size-dependent TED value in circular cylindrical nanoshells.

Given the issues raised above, thermoelastic damping (TED) is one of the undeniable sources of energy loss in microstructures. On the other hand, it was found that structural and heat transfer areas in mechanical elements with small dimensions are sorely sensitive to their size. Ergo the application of size-dependent theories of elasticity and models of heat conduction for credible interpretation of TED phenomenon in small-scaled structures is inescapable. The current article is devoted to thermoelastic damping modeling in circular microplates based upon the modified couple stress theory (MCST) and Guyer-Krumhansl (GK) heat conduction model within the complex frequency (CF) approach for the first time. After deriving the coupled size-dependent equations of motion and heat conduction, the solution of heat conduction equation is extracted to arrive at the temperature distribution in circular microplate. Substitution of the temperature profile in the motion equation results in the frequency equation affected by small-scale and thermoelastic coupling effects. With the aid of this equation, the real and imaginary parts of frequency can be separated. In the last place, by means of the definition of TED in the framework of the CF approach, a closed-form single-term solution containing nonclassical structural and thermal parameters is achieved to predict size-dependent TED value in circular microplates. By accomplishing a comparative study, the credibility of the developed formulation is appraised. Via several numerical examples, an all-out study is also carried out to enlighten the impact of various factors like length scale parameter of MCST and thermal nonlocal parameter of GK model, boundary conditions, geometrical parameters, material type and environmental temperature on TED value.

2 Guyer-Krumhansl model of heat conduction

For an isotropic material, the constitutive relation of heat conduction in the framework of Guyer-Krumhansl (GK) model is described via the relation above (Guyer and Krumhansl 1966):

$${\varvec{q}} + \tau \frac{{\partial {\varvec{q}}}}{{\partial t}} = - k {\varvec{\nabla}} \theta + l_{Q}^{2} \left[ {{{\nabla}} ^{2} \textbf{q} + 2{\varvec{\nabla}} \left( {{\varvec{\nabla}} \, \cdot \,\textbf{q}} \right)} \right]$$
(1)

in which \({\varvec{q}}\) and \(\theta\) refer to heat flux vector and temperature increment, respectively. Parameter \(\theta\) is calculated from relation \(T-{T}_{0}\), where \(T\) and \({T}_{0}\) represent instantaneous and reference temperatures, respectively. Parameter \(k\) stands for the thermal conductivity of material. Material constant \(\tau\) is also relaxation time or phase lag parameter. Moreover, parameter \({l}_{Q}\) denotes thermal nonlocal parameter that allows the model to incorporate nonlocal effect within heat conduction equation. When \({l}_{Q}\) is set to zero, Eq. (1) reduces to the constitutive relation of LS model. In addition, by ignoring terms including parameters \(\tau\) and \({l}_{Q}\), constitutive relation of GK model is replaced with that of Fourier law. The equation of conservation of energy for an isotropic material is expressed by:

$$-{\varvec{\nabla}}\,\, \cdot\,\,{\varvec{q}}+Q=\rho {c}_{v}\frac{\partial \theta }{\partial t}+{T}_{0}\beta \frac{\partial e}{\partial t}$$
(2)

In the relation above, parameters \(Q\), \(\rho\) and \({c}_{v}\) denote volumetric heat source, mass density and specific heat per unit mass, respectively. Furthermore, parameter \(\beta =E\alpha /(1-2\nu )\) is called thermal modulus in which material constants \(E\), \(\alpha\) and \(\nu\) represent the modulus of elasticity, thermal expansion coefficient and the Poisson ratio, respectively. Additionally, variable \(e\) refers to the volumetric strain, which is equal to the trace of strain tensor. In the absence of heat source \(Q\), combination of Eqs. (1) and (2), and elimination of heat flux vector \({\varvec{q}}\) gives the following heat conduction equation:

$$\left(1+\tau \frac{\partial }{\partial t}\right)\left(\rho {c}_{v}\frac{\partial \theta }{\partial t}+{T}_{0}\beta \frac{\partial e}{\partial t}\right)=\left(k+3{l}_{Q}^{2}\rho {c}_{v}\frac{\partial }{\partial t}\right){\nabla }^{2}\theta$$
(3)

3 Modified couple stress theory

According to the modified couple stress theory (MCST), the first variation of strain energy \(U\) of a structure occupying the volume \(V\) is calculated by Yang et al. (2002):

$$\delta U={\iiint }_{V}\left({\sigma }_{ij}\delta {\varepsilon }_{ij}+{m}_{ij}\delta {\chi }_{ij}^{s}\right)dV$$
(4)

in which \({\sigma }_{ij}\) and \({m}_{ij}\) represent the components of the Cauchy stress tensor \({\varvec{\sigma}}\) and deviatoric part of the couple stress tensor \({\varvec{m}}\), respectively. Additionally, variables \({\varepsilon }_{ij}\) and \({\chi }_{ij}^{s}\) stand for the components of the strain tensor \({\varvec{\varepsilon}}\) and the symmetric part of rotation gradient tensor \({{\varvec{\chi}}}^{s}\), respectively. These two tensors can be obtained via the following relations:

$${\varvec{\varepsilon}}=\frac{1}{2}\left[{\varvec{\nabla}} {\varvec{u}}+{\left({\varvec{\nabla}} {\varvec{u}}\right)}^{T}\right]$$
(5a)
$${{\varvec{\chi}}}^{s}=\frac{1}{2}\left[{\varvec{\nabla}} \boldsymbol{\varphi }+{\left({\varvec{\nabla}} \boldsymbol{\varphi }\right)}^{T}\right]$$
(5b)

in which \({\varvec{u}}\) is the displacement vector. Moreover, \(\boldsymbol{\varphi }\) denotes the infinitesimal rotation vector, which can be determined by relation below:

$$\boldsymbol{\varphi }=\frac{1}{2}\mathrm{curl}\left({\varvec{u}}\right)=\frac{1}{2}{\varvec{\nabla}} \times {\varvec{u}}$$
(6)

For an isotropic material, thermoelastic constitutive relations between the stresses and the kinematic parameters are given by:

$${\varvec{\sigma}}=\lambda e{\varvec{I}}+2\mu{\varvec{\varepsilon}}-(3\lambda +2\mu )\alpha \theta {\varvec{I}}$$
(7a)
$${\varvec{m}}=2\mu {l}_{M}^{2}{{\varvec{\chi}}}^{s}$$
(7b)

in which parameters \(\lambda\) and \(\mu\) are known as Lame constants, which can be expressed in terms of elasticity modulus \(E\) and the Poisson ratio \(\nu\) as \(\lambda =E\nu /\left(1+\nu \right)\left(1-2\nu \right)\) and \(\mu =E/2\left(1+\nu \right)\). Parameter \({l}_{M}\) is also the material length scale parameter.

4 Coupled thermoelastic equations of circular microplates in the framework of MCST and GK model

4.1 Motion equation

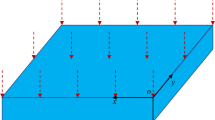
Configuration and coordinate system of a circular plate with radius \(a\) and thickness \(h\) are depicted in Fig. 1. The components of displacement field of the Kirchhoff axisymmetric thin plates can be written by:

$${u}_{r}=-z\frac{\partial w\left(r,t\right)}{\partial r} , {u}_{\phi }=0 , {u}_{z}=w(r,t)$$
(8)

where \({u}_{r}\), \({u}_{\phi }\) and \({u}_{z}\) denote displacements in the radial, circumferential and transverse directions, respectively. With the aid of Eqs. (5a) and (8), the strains are obtained as follows:

Fig. 1
figure 1

Schematic view of a circular plate

Full size image
$${\varepsilon }_{rr}=-z\frac{{\partial }^{2}w}{\partial {r}^{2}} , {\varepsilon }_{\phi \phi }=-\frac{z}{r}\frac{\partial w}{\partial r}$$
(9)

Moreover, the nonzero components of tensor \({{\varvec{\chi}}}^{s}\) can be derived as below:

$${\chi }_{r\phi }^{s}={\chi }_{\phi r}^{s}=\frac{1}{2}\left(-\frac{{\partial }^{2}w}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial w}{\partial r}\right)$$
(10)

By inserting the last two relations into Eq. (4) and performing some calculations, the first variation of strain energy takes the following form:

$$\begin{aligned} \delta U & = 2\pi \int _{0}^{a} \left[ { - M_{{rr}} \delta \left( {\frac{{\partial ^{2} w}}{{\partial r^{2} }}} \right) - \frac{1}{r}M_{{\phi \phi }} \delta \left( {\frac{{\partial w}}{{\partial r}}} \right)} \right. \\ & \left. { - Y_{{r\phi }} \delta \left( {\frac{{\partial ^{2} w}}{{\partial r^{2} }}} \right) + \frac{1}{r}Y_{{r\phi }} \delta \left( {\frac{{\partial w}}{{\partial r}}} \right)} \right]rdr \\ \end{aligned}$$
(11)

where the stress resultants \({M}_{rr}\) and \({M}_{\phi \phi }\), and the couple stress resultant \({Y}_{r\phi }\) are defined via the following relations:

$${M}_{rr}={\int }_{-h/2}^{+h/2}{\sigma }_{rr}zdz\,\, and\,\, {M}_{\phi \phi }={\int }_{-h/2}^{+h/2}{\sigma }_{\phi \phi }zdz$$
(12a)
$${Y}_{r\phi }={\int }_{-h/2}^{+h/2}{m}_{r\phi }dz$$
(12b)

The first variation of kinetic energy \(K\) of an isotropic circular plate is given by:

$$\delta K=\rho \underset{V}{\overset{}{\iiint }}\left[\left(\frac{\partial {u}_{r}}{\partial t}\right)\delta \left(\frac{\partial {u}_{r}}{\partial t}\right)+\left(\frac{\partial {u}_{\phi }}{\partial t}\right)\delta \left(\frac{\partial {u}_{\phi }}{\partial t}\right)+\left(\frac{\partial {u}_{z}}{\partial t}\right)\delta \left(\frac{\partial {u}_{z}}{\partial t}\right)\right]dV$$
(13)

By substituting Eq. (8) into Eq. (13) and overlooking the rotary inertia effect, the relation above becomes:

$$\delta K=2\pi \rho h{\int }_{0}^{a}\left(\frac{\partial w}{\partial t}\right)\delta \left(\frac{\partial w}{\partial t}\right)rdr$$
(14)

Based on the Hamilton principle, one can write:

$${\int }_{{t}_{1}}^{{t}_{2}}\left(\delta U-\delta K\right)dt=0$$
(15)

By inserting Eqs. (11) and (13) into Eq. (14) and integrating by parts by means of Green’s theorem, the motion equation is derived as follows:

$$\frac{{\partial }^{2}{M}_{rr}}{\partial {r}^{2}}+\frac{2}{r}\frac{\partial {M}_{rr}}{\partial r}-\frac{1}{r}\frac{\partial {M}_{\phi \phi }}{\partial r}+\frac{{\partial }^{2}{\begin{array}{c}Y\\ \end{array}}_{r\phi }}{\partial {r}^{2}}++\frac{3}{r}\frac{\partial {Y}_{r\phi }}{\partial r}=\rho h\frac{{\partial }^{2}w}{\partial {t}^{2}}$$
(16)

In addition, the boundary conditions are obtained as:

$$\delta w = 0\,\,OR\,\,\frac{\partial }{{\partial r}}\left( {rM_{{rr}} } \right) - M_{{\phi \phi }} + Y_{{r\phi }} + \frac{\partial }{{\partial r}}\left( {rY_{{r\phi }} } \right) = 0$$
(17a)
$$\delta \left(\frac{\partial w}{\partial r}\right)=0\,\,OR\,\, r{M}_{rr}+r{Y}_{r\phi }=0$$
(17b)

Given the plane stress condition due to the thinness of plate, one can consider \({\sigma }_{zz}=0\). By applying this condition to Eq. (7a), one can get:

$${\varepsilon }_{zz}=-\frac{\nu }{1-\nu }\left({\varepsilon }_{rr}+{\varepsilon }_{\phi \phi }\right)+\frac{1+\nu }{1-\nu }\alpha \theta$$
(18)

Substitution of Eq. (9) into relation above yields:

$${\varepsilon }_{zz}=\frac{\nu z}{1-\nu }\left(\frac{{\partial }^{2}w}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial w}{\partial r}\right)+\frac{1+\nu }{1-\nu }\alpha \theta$$
(19)

By inserting Eqs. (9) and (19) into Eq. (7a), one can obtain:

$${\sigma }_{rr}=-\frac{Ez}{1-{\nu }^{2}}\left(\frac{{\partial }^{2}w}{\partial {r}^{2}}+\frac{\nu }{r}\frac{\partial w}{\partial r}\right)-\frac{E\alpha }{1-\nu }\theta$$
(20a)
$${\sigma }_{\phi \phi }=-\frac{Ez}{1-{\nu }^{2}}\left(\nu \frac{{\partial }^{2}w}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial w}{\partial r}\right)-\frac{E\alpha }{1-\nu }\theta$$
(20b)

By substituting relations above into Eq. (12a), the stress resultants \({M}_{rr}\) and \({M}_{\phi \phi }\) take the following forms:

$${M}_{rr}=-D\left(\frac{{\partial }^{2}w}{\partial {r}^{2}}+\frac{\nu }{r}\frac{\partial w}{\partial r}\right)-\frac{{M}_{T}}{1-\nu } \,\,{and}\,\, {M}_{\phi \phi }=-D\left(\nu \frac{{\partial }^{2}w}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial w}{\partial r}\right)-\frac{{M}_{T}}{1-\nu }$$
(21)

in which \(D\) is the bending rigidity of plate given by:

$$D=\frac{E{h}^{3}}{12(1-{\nu }^{2})}$$
(22)

Besides, \({M}_{T}\) is thermal moment obtained via the relation above:

$${M}_{T}=E\alpha {\int }_{-h/2}^{+h/2}\theta zdz$$
(23)

On the other hand, substitution of Eq. (10) into Eq. (7b) results in the following relation:

$${m}_{r\phi }={m}_{\phi r}=\mu {l}_{M}^{2}\left(-\frac{{\partial }^{2}w}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial w}{\partial r}\right)$$
(24)

By inserting relation above into Eq. (12b), the couple stress resultants are determined as follows:

$${Y}_{r\phi }={Y}_{\phi r}=\mu {l}_{M}^{2}h\left(-\frac{{\partial }^{2}w}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial w}{\partial r}\right)=\kappa D\left(-\frac{{\partial }^{2}w}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial w}{\partial r}\right)$$
(25)

where

$$\kappa =\frac{\mu {l}_{M}^{2}h}{D}=6(1-\nu ){\left(\frac{{l}_{M}}{h}\right)}^{2}$$
(26)

It is evident that by taking no notice of size effect, we have \(\kappa =0\). Now, by substituting Eqs. (21) and (25) into Eq. (16) and sorting terms, one can acquire the coupled thermoelastic equation of motion in terms of transverse displacement \(w\) as follows:

$$D\left(1+\kappa \right){\nabla }^{4}w+\frac{1}{1-\nu }{\nabla }^{2}{M}_{T}+\rho h\frac{{\partial }^{2}w}{\partial {t}^{2}}=0$$
(27)

in which \({\nabla }^{2}=\left({\partial }^{2}/\partial {r}^{2}\right)+\left(1/r\right)\left(\partial /\partial r\right)\) and \({\nabla }^{4}={\nabla }^{2}({\nabla }^{2})\). Furthermore, by inserting Eqs. (21) and (25) into Eqs. (17a) and (17b) and simplifying the results, boundary conditions take the following forms:

$$\delta w = 0\,\,OR\,\,\frac{{\partial ^{3} w}}{{\partial r^{3} }} + \frac{1}{r}\frac{{\partial ^{2} w}}{{\partial r^{2} }} - \frac{1}{{r^{2} }}\frac{{\partial w}}{{\partial r}} = 0$$
(28a)
$$\delta \left(\frac{\partial w}{\partial r}\right)=0\,\,OR\,\, \left(1+\kappa \right)\frac{{\partial }^{2}w}{\partial {r}^{2}}+\left(\nu -\kappa \right)\frac{1}{r}\frac{\partial w}{\partial r}=0$$
(28b)

4.2 Heat conduction equation

Given that in thin structures, the amount of temperature gradient in the direction of thickness is remarkable compared to the other two directions, the heat conduction Eq. (3) can be replaced by the following equation:

$$\left(1+\tau \frac{\partial }{\partial t}\right)\left(\rho {c}_{v}\frac{\partial \theta }{\partial t}+{T}_{0}\beta \frac{\partial e}{\partial t}\right)=\left(k+3{l}_{Q}^{2}\rho {c}_{v}\frac{\partial }{\partial t}\right)\frac{{\partial }^{2}\theta }{\partial {z}^{2}}$$
(29)

By referring to Eqs. (9) and (19), the volumetric strain \(e\) can be obtained as:

$$e=-\frac{1-2\nu }{1-\nu }z{\nabla }^{2}w+\frac{1+\nu }{1-\nu }\alpha \theta$$
(30)

By making use of equation above in Eq. (29) and sorting terms, the heat conduction equation becomes:

$$(\chi +3{l}_{Q}^{2}\frac{\partial }{\partial t})\frac{{\partial }^{2}\theta }{\partial {z}^{2}}+\frac{{\Delta }_{E}z}{\alpha \left(1-\nu \right)}(1+\tau \frac{\partial }{\partial t})\frac{\partial }{\partial t}({\nabla }^{2}w)=\left[1+{\Delta }_{E}\frac{1+\nu }{\left(1-2\nu \right)\left(1-\nu \right)}\right](1+\tau \frac{\partial }{\partial t})\frac{\partial \theta }{\partial t}$$
(31)

with \(\chi =k/\rho {c}_{v}\) and \({\Delta }_{E}=E{\alpha }^{2}{T}_{0}/\rho {c}_{v}\). Given the minute amount of \({\Delta }_{E}\) for most materials (that is \({\Delta }_{E}\ll 1\)), the final and simplified form of the heat conduction equation can be expressed as follows:

$$\chi \left( {1 + \tau _{Q} \frac{\partial }{{\partial t}}} \right)\frac{{\partial ^{2} \theta }}{{\partial z^{2} }} + \frac{{\Delta _{E} z}}{{\alpha \left( {1 - \nu } \right)}}\left( {1 + \tau \frac{\partial }{{\partial t}}} \right)\frac{\partial }{{\partial t}}(\nabla ^{2} w) = \left( {1 + \tau \frac{\partial }{{\partial t}}} \right)\frac{{\partial \theta }}{{\partial t}}$$
(32)

in which

$${\tau }_{Q}=\frac{3{l}_{Q}^{2}}{\chi }.$$
(33)

5 Determination of TED value

In this section, the goal is to provide an analytical relation for calculating TED value. For this purpose, the CF approach is exploited by considering the following forms for deflection and temperature increment:

$$w\left(r,t\right)=W\left(r\right){e}^{i\omega t} \,\,{and}\,\, \theta \left(r,z,t\right)=\Theta (r,z){e}^{i\omega t}$$
(34)

where \(\omega\) represents the complex frequency. By inserting the relations above into Eq. (32) and sorting terms, one can arrive at the following partial differential equation (PDE):

$$\frac{{\partial }^{2}\Theta }{\partial {z}^{2}}+{p}^{2}\Theta ={p}^{2}\frac{{\Delta }_{E}}{\alpha \left(1-\nu \right)}z{\nabla }^{2}W$$
(35)

where \(p\) is a complex parameter with the following definition:

$$p=\sqrt{\frac{\omega }{\chi }}\sqrt{{a}_{1}-i{a}_{2}}=\frac{\xi \eta }{h}-i\frac{\xi {a}_{2}}{h\eta }$$
(36)

in which

$$\xi =h\sqrt{\frac{\omega }{2\chi }} , \eta =\sqrt{{a}_{1}+\sqrt{{a}_{1}^{2}+{a}_{2}^{2}}} , {a}_{1}=\frac{(\tau -{\tau }_{Q})\omega }{1+{\tau }_{Q}^{2}{\omega }^{2}} , {a}_{2}=\frac{1+{\tau }_{Q}\tau {\omega }^{2}}{1+{\tau }_{Q}^{2}{\omega }^{2}}$$
(37)

The solution of Eq. (35) can be written as follows:

$$\Theta \left(r,z\right)={C}_{1}\mathrm{sin}\left(pz\right)+{C}_{2}\mathrm{cos}(pz)+\frac{{\Delta }_{E}}{\alpha \left(1-\nu \right)}z{\nabla }^{2}W$$
(38)

The unknown coefficients \({C}_{1}\) and \({C}_{2}\) to be computed by imposing thermal boundary conditions on the general solution given in relation above. For a thermally insulated plate on its upper and lower surfaces (that is \(\partial \Theta /\partial z=0\) at \(z=\pm h/2\)), the temperature distribution is obtained as follows:

$$\Theta (r,z)=\frac{{\Delta }_{E}}{\alpha \left(1-\nu \right)}{\nabla }^{2}W\left[z-\frac{\mathrm{sin}(pz)}{p\mathrm{cos}(\mathit{ph}/2)}\right]$$
(39)

Substitution of Eqs. (34) and (39) into Eq. (23) gives:

$${M}_{T}=D\left(1-{\nu }^{2}\right){\Delta }_{E}\left[1+f\left(\omega \right)\right]{\nabla }^{2}W{e}^{i\omega t}$$
(40)

where

$$f\left( \omega \right) = \frac{{24}}{{h^{3} p^{3} }}\left[ {\frac{{hp}}{2} - tan\left( {\frac{{hp}}{2}} \right)} \right]$$
(41)

By inserting Eqs. (34) and (40) into motion Eq. (27), the frequency equation is extracted as follows:

$$D\left\{1+\kappa +\frac{1+\nu }{1-\nu }{\Delta }_{E}\left[1+f\left(\omega \right)\right]\right\}{\nabla }^{4}W=\rho h{\omega }^{2}W$$
(42)

By removing the terms containing the thermal coefficients from the equation above, the frequency equation in the isothermal case is derived as follows:

$$D\left(1+\kappa \right){\nabla }^{4}W=\rho h{\omega }_{0}^{2}W$$
(43)

in which \({\omega }_{0}\) stands for the couple stress-based isothermal frequency. The method of calculating \({\omega }_{0}\) is explained in section Appendix. Comparison of the last two relations gives:

$$\omega ={\omega }_{0}\sqrt{\frac{1+\kappa +\frac{1+\nu }{1-\nu }{\Delta }_{E}\left[1+f\left(\omega \right)\right]}{1+\kappa }}={\omega }_{0}\sqrt{1+\frac{1}{1+\kappa }\frac{1+\nu }{1-\nu }{\Delta }_{E}\left[1+f\left(\omega \right)\right]}$$
(44)

As mentioned earlier, \({\Delta }_{E}\) is insignificant for most materials. Therefore, by using the Taylor series up to the first order, the relation above can be approximated as follows:

$$\omega ={\omega }_{0}\left\{1+\frac{{\Delta }_{E}}{2}\frac{1}{1+\kappa }\frac{1+\nu }{1-\nu }\left[1+f\left(\omega \right)\right]\right\}$$
(45)

Owing to the weak impact of thermoelastic coupling, in the relation above, \(f\left(\omega \right)\) can be replaced by \(f({\omega }_{0})\) as below:

$$\omega ={\omega }_{0}\left\{1+\frac{{\Delta }_{E}}{2}\frac{1}{1+\kappa }\frac{1+\nu }{1-\nu }\left[1+f({\omega }_{0})\right]\right\}$$
(46)

Based on the complex frequency approach, the magnitude of TED can be estimated via the following relation (Lifshitz and Roukes 2000):

$$TED=2\left|\frac{Im(\omega )}{Re(\omega )}\right|$$
(47)

in which \(Re(\omega )\) and \(Im(\omega )\) represent the real and imaginary parts of complex frequency \(\omega\), respectively. According to Eq. (45), one can write:

$$Re\left(\omega \right)={\omega }_{0}\left\{1+\frac{{\Delta }_{E}}{2}\frac{1}{1+\kappa }\frac{1+\nu }{1-\nu }\left[1+Re\left(f\left({\omega }_{0}\right)\right)\right]\right\}$$
(48a)
$$Im\left(\omega \right)={\omega }_{0}\frac{{\Delta }_{E}}{2}\frac{1}{1+\kappa }\frac{1+\nu }{1-\nu }Im\left(f\left({\omega }_{0}\right)\right)$$
(48b)

where \(Re\left(f\left({\omega }_{0}\right)\right)\) and \(Im\left(f\left({\omega }_{0}\right)\right)\) stand for the real and imaginary parts of complex function \(f\left({\omega }_{0}\right)\), respectively. By considering Eqs. (36) and (41), and implementing some mathematical manipulations, one can derive \(Re\left(f\left({\omega }_{0}\right)\right)\) and \(Im\left(f\left({\omega }_{0}\right)\right)\) as follows:

$$Re\left(f\left({\omega }_{0}\right)\right)=12\frac{{\eta }^{2}-\frac{{a}_{2}^{2}}{{\eta }^{2}}}{{\xi }^{2}{({\eta }^{2}+\frac{{a}_{2}^{2}}{{\eta }^{2}})}^{2}}-24\frac{({\eta }^{3}-3\frac{{a}_{2}^{2}}{\eta })\mathrm{sin}\left(\xi \eta \right)+(3\eta {a}_{2}-\frac{{a}_{2}^{3}}{{\eta }^{3}})\mathrm{sinh}(\frac{\xi {a}_{2}}{\eta })}{{\xi }^{3}{\left({\eta }^{2}+\frac{{a}_{2}^{2}}{{\eta }^{2}}\right)}^{3}(\mathrm{cos}\left(\xi \eta \right)+\mathrm{cosh}(\frac{\xi {a}_{2}}{\eta }))}$$
(49a)
$$Im\left(f\left({\omega }_{0}\right)\right)=24\frac{{a}_{2}}{{\xi }^{2}{({\eta }^{2}+\frac{{a}_{2}^{2}}{{\eta }^{2}})}^{2}}-24\frac{(3\eta {a}_{2}-\frac{{a}_{2}^{3}}{{\eta }^{3}})\mathrm{sin}\left(\xi \eta \right)-({\eta }^{3}-3\frac{{a}_{2}^{2}}{\eta })\mathrm{sinh}(\frac{\xi {a}_{2}}{\eta })}{{\xi }^{3}{({\eta }^{2}+\frac{{a}_{2}^{2}}{{\eta }^{2}})}^{3}(\mathrm{cos}\left(\xi \eta \right)+\mathrm{cosh}(\frac{\xi {a}_{2}}{\eta }))}$$
(49b)

As stated earlier, the value of \({\Delta }_{E}\) is very small in such a way that \({\Delta }_{E}\ll 1\). By considering this point and placing Eqs. (48a) and (48b) into Eq. (47), one can estimate TED value through the following relation:

$$TED=\frac{{\Delta }_{E}}{1+\kappa }\frac{1+\nu }{1-\nu }Im\left(f\left({\omega }_{0}\right)\right)$$
(50)

In the last place, substitution of Eq. (49b) into relation above yields the following relation for TED in circular microplates according to MCST and GK model:

$$TED = 24\frac{{\Delta _{E} }}{{1 + \kappa }}\frac{{1 + \nu }}{{1 - \nu }}\left[ {\frac{{a_{2} }}{{\xi ^{2} \left( {\eta ^{2} + \frac{{a_{2}^{2} }}{{\eta ^{2} }}} \right)^{2} }} - \frac{{\left( {3\eta a_{2} - \frac{{a_{2}^{3} }}{{\eta ^{3} }}} \right){\text{sin}}\left( {\xi \eta } \right) - \left( {\eta ^{3} - 3\frac{{a_{2}^{2} }}{\eta }} \right){\text{sinh}}\left( {\frac{{\xi a_{2} }}{\eta }} \right)}}{{\xi ^{3} \left( {\eta ^{2} + \frac{{a_{2}^{2} }}{{\eta ^{2} }}} \right)^{3} \left( {{\text{cos}}\left( {\xi \eta } \right) + {\text{cosh}}\left( {\frac{{\xi a_{2} }}{\eta }} \right)} \right)}}} \right]$$
(51)

It is important to emphasize that in the absence of nonclassical material constants \({l}_{M}\), \({l}_{Q}\) and \(\tau\), one can get \(\kappa ={a}_{1}=0\) and \({a}_{2}=\eta =1\). By inserting these values into Eq. (51), it is clear that the relation above is converted to that derived by Li et al. (Li et al. 2012) on the basis of CT and Fourier law of heat conduction.

6 Numerical results and discussion

In this section, several numerical examples are provided to analyze size effect on TED value in circular microplates. First of all, a comparative study is made between the results of this work and those published in an article in the literature. A complete parametric study is also conducted to ascertain the impact of crucial factors such as length scale parameter of MCST and thermal nonlocal parameter of GK model, boundary conditions, geometrical parameters, material type and environmental temperature on TED value.

To assess the validity of presented solution, the findings of this study are compared with those of the research of Li et al. (Li et al. 2018). In their work, TED analysis in functionally graded (FG) circular microplates through CT and Fourier model has been carried out. Accordingly, unconventional mechanical and thermal material parameters, i.e. \({l}_{M}\), \({l}_{Q}\) and \(\tau\) must be set to zero in the presented formula to compare the results of these two researches. Moreover, the material gradient parameter for FG materials defined in Li et al. (2018) must be set to zero. Thus, the case full ceramic (i.e. Si3N4) is selected, whose mechanical and thermal constants at \({T}_{0}=300\,\, \mathrm{K}\) are given in Table 1. The variation of TED estimated in this study and that calculated in Li et al. (2018) are displayed as a function of thickness \(h\) in Fig. 2 for a clamped circular microplate with fixed radius \(a = 200\) μm. It can be observed that the results exhibit a very good accordance with each other.

Table 1 Material constants of Si3N4 at \({T}_{0}=300 K\) (Li et al. 2018)
Full size table
Fig. 2
figure 2

Comparison between TED values obtained in this study and a study in the literature

Full size image

For the section of parametric study, numerical examples are prepared for both clamped (C) and simply-supported (SS) circular microplates made of silicon with fixed geometrical ratio of \(a/h=20\) at reference temperature \({T}_{0}=300\)K, except where other conditions are examined. Mechanical and thermal material constants of silicon together with those of gold and diamond at \({T}_{0}=300\)K are given in Table 2 (Zhou et al. 2019).

Table 2 Mechanical and thermal constants of silicon, gold and diamond at \({T}_{0}=300 K\) (Zhou et al. 2019)
Full size table

The variation of TED value versus the thickness of microplate is illustrated for five values of \({l}_{M}\) (i.e. \(l_{M} = 0,0.5,1,1.5\;and\;2\mu m\)) in Figs. 3a and b for C and SS constraints, respectively. When \(l_{M} = 0\)μm, the results correspond with those of CT. To depict the curves, the thermal nonlocal parameter is supposed to be \({l}_{Q}=100 \,\,{\text{nm}}\). It is observed that for both C and SS boundary conditions, MCST estimates lower amounts of TED in comparison with CT. Moreover, with the increase of the magnitude of \({l}_{M}\), TED value lessens. It is also obvious that as the thickness of microplate gets larger, the small-scale effect weakens in such a way that the discrepancy between the predictions of MCST and CT almost fades. Regarding the boundary conditions, it can be said that for thinner microplates, the amount of TED in clamped microplates is higher, but as the microplate becomes thicker, TED value in simply-supported microplates exceeds its value in clamped microplates. Furthermore, the critical thickness (i.e. the thickness at which the peak value of TED occurs) of clamped microplates is smaller than that of simply-supported microplates.

Fig. 3
figure 3

The effect of \({l}_{M}\) on the variation of TED with respect to thickness of a Clamped b Simply-supported microplates with fixed geometrical ratio of \(a/h=20\)

Full size image

For C and SS boundary conditions, Figs. 4a and 4b indicate TED values computed by GK and CTE models as a function of the thickness of microplate for five different values of thermal nonlocal parameter (i.e. \({l}_{Q}=0, 50, 100, 150 \,\,and\,\, 200\,\, \mathrm{nm}\)). For extracting these diagrams, the length scale parameter is taken as \(l_{M} = 1\)μm. According to these figures, by employing GK model, a lower value is obtained for TED than for Fourier model, although for SS boundary conditions, the impact of GK model on TED is much less than its effect on TED for C boundary conditions. It is also observed that the increase of thermal nonlocal parameter \({l}_{Q}\) shrinks the amount of TED.

Fig. 4
figure 4

The effect of \({l}_{Q}\) on the variation of TED with respect to thickness of a Clamped b Simply-supported microplates with fixed geometrical ratio of \(a/h=20\)

Full size image

For different amounts of \({l}_{M}\), Figs. 5a and b examines the variation of TED value with respect to geometrical ratio \(a/h\) for C and SS boundary conditions, respectively. To draw these curves, \(h = 0.5\)μm and \({l}_{Q}=100 \mathrm{nm}\) are selected. Similar to Figs. 3a and 3b, it can be seen that higher magnitudes of \({l}_{M}\) yield the diminution in TED value. It is also evident that for smaller ratios \(a/h\), the amount of TED for C boundary conditions is higher than SS ones, but with the increase of \(a/h\), TED value of SS boundary conditions becomes greater than its value in clamped microplates.

Fig. 5
figure 5

The impact of \({l}_{M}\) on the variation of TED versus geometrical ratio of \(a/h\) of a Clamped b Simply-supported microplates with fixed thickness of \(h = 0.5\) μm

Full size image

To highlight the influence of thermal nonlocal parameter \({l}_{Q}\) on TED in microplates with variable ratio of \(a/h\), the variation of TED value as a function of ratio \(a/h\) for C and SS boundary conditions is shown in Figs. 6a and 6b, respectively. These curves are plotted by assuming \(h = 0.5\) μm and \({l}_{M}=1\) μm. It is easily perceived that GK model anticipates less values for TED than Fourier model. Moreover, the difference between the results of GK and Fourier models for SS boundary conditions is much less compared to C boundary conditions.

Fig. 6
figure 6

The impact of \({l}_{Q}\) on the variation of TED versus geometrical ratio of \(a/h\) of a Clamped b Simply-supported microplates with fixed thickness of \(h=0.5\) μm

Full size image

For C boundary conditions, the changes of TED with respect to both scale parameters \({l}_{M}\) and \({l}_{Q}\) are demonstrated in Figs. 7, 9 and 11 for plates made of silicon, gold and diamond, respectively. The same results are assessed for SS edge conditions in Figs. 8, 10 and 12 for silicon, gold and diamond plates, respectively. These surfaces are plotted for four different values of thickness of plate (i.e. \(h = 0.25,0.5,0.75\,\,{\mathrm{and}}\,\,{\mathrm{1}}\,\,\,\,\mu{\text{ m}}\)). As it turns out, for all three materials, the amount of TED wanes with both increasing the value of \({l}_{M}\) and increasing the value of \({l}_{Q}\), although the impact of \({l}_{M}\) on this decline is far greater than that of \({l}_{Q}\). According to these plots, it is also ascertained that the highest and lowest values of TED occur in microplates made of gold and diamond. This can be a momentous criterion for designing high quality factor microplate resonators. Moreover, by comparing the results for the specific thicknesses considered in these figures, one can deduce that the energy loss caused by TED in clamped microplates is greater than that in the plates with SS boundary conditions (Figs. 9, 10, 11 and 12).

Fig. 7
figure 7

The variation of TED with respect to both \({l}_{M}\) and \({l}_{Q}\) of clamped silicon microplates with fixed geometrical ratio of \(a/h=20\) a \(h = 0.25\) μm b \(h=0.5\) μm c \(h=0.75\) μm d \(h=1\) μm

Full size image
Fig. 8
figure 8

The variation of TED with respect to both \({l}_{M}\) and \({l}_{Q}\) of simply-supported silicon microplates with fixed geometrical ratio of \(a/h=20\) a \(h=0.25\) μm b \(h=0.5\) μm c \(h=0.75\) μm d \(h=1\) μm

Full size image
Fig. 9
figure 9

The variation of TED with respect to both \({l}_{M}\) and \({l}_{Q}\) of clamped gold microplates with fixed geometrical ratio of \(a/h=20\) a \(h=0.25\) μm b \(h=0.5\) μm c \(h=0.75\) μm d \(h=1\) μm

Full size image
Fig. 10
figure 10

The variation of TED with respect to both \({l}_{M}\) and \({l}_{Q}\) of simply-supported gold microplates with fixed geometrical ratio of \(a/h=20\) a \(h=0.25\) μm b \(h=0.5\) μm c \(h=0.75\) μm d \(h=1\) μm

Full size image
Fig. 11
figure 11

The variation of TED with respect to both \({l}_{M}\) and \({l}_{Q}\) of clamped diamond microplates with fixed geometrical ratio of \(a/h=20\) a \(h=0.25\) μm b \(h=0.5\) μm c \(h=0.75\) μm d \(h=1\) μm

Full size image
Fig. 12
figure 12

The variation of TED with respect to both \({l}_{M}\) and \({l}_{Q}\) of simply-supported diamond microplates with fixed geometrical ratio of \(a/h=20\) a \(h=0.25\) μm b \(h=0.5\) μm c \(h=0.75\) μm d \(h=1\) μm

Full size image

For C and SS edge conditions, Figs. 13 and 14 respectively appraise the influence of reference temperature \({T}_{0}\) on the magnitude of TED in silicon microplates as the function of thickness. Material properties of silicon at five different values of \({T}_{0}\) (i.e. \({T}_{0}=40, 80, 160, 293 \,\,and\,\, 400 K\)) are listed in Table 3 (Zhou et al. 2019). It is obvious that for both classical and nonclassical models, as well as for both boundary conditions studied, TED intensifies with increasing ambient temperature. This is consistent with the hypothesis that TED has a remarkable amount at room temperature and is one of the dominant sources of energy dissipation.

Fig. 13
figure 13

The effect of \({T}_{0}\) on the variation of TED with respect to thickness of clamped microplates with fixed geometrical ratio of \(a/h=20\) a \({l}_{M}=0\) μm and \({l}_{Q}=0 \mathrm{nm}\) b \({l}_{M}=2\) μm and \({l}_{Q}=200 \mathrm{nm}\)

Full size image
Fig. 14
figure 14

The effect of \({T}_{0}\) on the variation of TED with respect to thickness of simply-supported microplates with fixed geometrical ratio of \(a/h=20\) a \({l}_{M}=0\) μm and \({l}_{Q}=0 \mathrm{nm}\) b \({l}_{M}=2\) μm and \({l}_{Q}=200 \mathrm{nm}\)

Full size image
Table 3 Material properties of silicon at different reference temperatures (Zhou et al. 2019)
Full size table

7 Summary and conclusion

In the current study, by accommodating size effect within both constitutive equations of elasticity and heat conduction, a size-dependent model for evaluation of thermoelastic damping (TED) in circular microplates has been provided. With the aim of extracting the nonclassical equations of motion and heat conduction, the modified couple stress theory (MCST) and Guyer-Krumhansl (GK) heat conduction model have been employed. By working out the heat conduction equation, the closed-form of temperature distribution in the circular microplate has been specified. By inserting the obtained solution for temperature in the motion equation, the size-dependent frequency equation has been derived in the presence of thermoelastic coupling effect. By comparing this equation with its isothermal case, the real and imaginary parts of complex frequency have been extracted. Via the description of TED according to the complex frequency (CF) approach, an analytical single-term expression including structural and thermal scale parameters has been established to anticipate the amount of TED in circular microplates. To survey the reliability of the provided model, the findings obtained on the basis of presented relation have been compared with those reported in the literature. By providing a variety of numerical examples, a parametric study has also been performed to elucidate the role of different factors like length scale parameter of MCST and thermal nonlocal parameter of GK model, boundary conditions, geometrical properties, material and reference temperature in the magnitude of TED. According to the results given in the previous section, the momentous findings of this research can be summarized as follows:

  • The couple stress-based model of circular microplates results in a smaller value of TED. Moreover, for greater values of \({l}_{M}\), the amount of this diminution gets larger.

  • Incorporation of thermal nonlocal parameter \({l}_{Q}\) into governing equations lessens the magnitude of TED.

  • As the dimensions of plate get larger, the influence of \({l}_{M}\) and \({l}_{Q}\) gradually disappears and TED value estimated by the presented formulation tends to that obtained by the classical model.

  • The impact of edge conditions on the amount of TED depends on the thickness of the plate, so that at lower thicknesses, TED value is greater for clamped plates, and at higher thicknesses TED value is larger for simply-supported plates.

  • The material of plate plays a vital role in the amount of TED and consequently the optimal design of the plate in the field of energy loss. Among plates made of silicon, gold, and diamond, the highest and lowest amounts of TED take place in gold and diamond plates, respectively.

  • As the reference temperature rises to room temperature, the magnitude of TED heightens pronouncedly, confirming the importance of mechanism of thermoelastic damping as one of the principal factors of energy dissipation at room temperature.