1 Introduction

Functionally graded materials, FGMs are new kind of composites, which possess smooth continuous variation of microstructure and mechanical characteristics without internal boundaries and sharp interfacial stress variations, (Elishakoff et al. 2015; Nie and Zhong 2010). In these materials, the properties are continuously varied in a given direction, (Malekzadeh and Heydarpour 2012). FGMs are commonly made of ceramic and metal mixture. The ceramic materials are characterized by its good thermal resistance as well as anti-oxidant behavior. On the other hand, metallic materials have excellent strength and superior fracture toughness, (Jha et al. 2013). Due to large applicability of the FGMs such as automotive industry, nuclear structures, and aircraft industry, serious attempts were performed by many researchers to study and analyze the mechanical behavior of this modern category of composite materials, (Kieback et al. 2003; Naebe and Shirvanimoghaddam 2016; Sarathchandra et al. 2018). Many attempts had been performed to combine metal-ceramic mixture in FGMS, Japanese researchers succeeded to develop a combination between metal and ceramic with thermal gradation 1000 k through thickness of 10 mm, (Esen et al. 2021). Interests of studying and analyzing the FGMs have several aspects such as distribution of the material properties and deformation theories, (Liew et al. 2015) or their applicability such as beam, plate, and shell structures under thermal, mechanical or thermo-mechanical analysis, (static, buckling, free and forced vibration) (Eltaher et al. 2014; Attia and Abdelrahman 2018).

Regarding the property graduation point of view, the FGMs properties can be varied through one or several spatial directions by controlling the volume fraction of the constituents, (Ghatage et al. 2020). Many mathematical forms are used to express the volume fraction distribution throughout a given direction of FGMs. Both the power law and exponential functions are the most common mathematical models used to express the properties distribution, (Mohammadian 2021). Many efforts have been done to relate the volume fraction at any point to the magnitude of the property such as rule of mixture or Mori–Tanaka Scheme which assuming no interaction between phases or applying Tamura-Tomota-Ozawa (TTO) model given by Tamura that consider for the bonding effect (Jha et al. 2013; Nikbakht et al. 2019. Other researchers give more interest in the response of FGMs so they assumed an arbitrary distribution of properties for studying without regarding to the way they could achieve such gradation, (Sofiyev 2019). Yongdong et al. (2005) investigated stresses in functionally graded beams based on effective principal axes method.

On the other hand, considering the deformation theories point of view, the well-known Euler–Bernoulli beam theory (EBBT) is the oldest and simplest beam theory that described beam deformation, Li and Batra (2013). In thick beams, which possess transverse shear strain EBBT was unable to efficiently describe the mechanical behavior of such types of beams. Shear deformation beam theories are required for effective investigation of the mechanical behavior of thick beams. The first order shear deformation theory, developed by Timoshenko and Ehrenfest and known as Timoshenko beam theory (TBT), is considered as the simplest theory in which the shear deformation effect was incorporated through the analysis of beams, Elishakoff (2020). In this theory, the shear effect is considered by assuming that the edges after deformation is not perpendicular to each other anymore but still straight. To achieve that assumption, the transverse deformation and rotation have to be independent of each other with \({C}^{0}\) continuity, Elishakoff (2019). Applying the TBT to detect the mechanical behavior of slender beams and thin plates using the same interpolation function for the transverse deflection and rotation, shear locking (SL) phenomena is appeared. In such case a nonzero transverse shear strain is detected, (Oñate 2013).

Many techniques have been developed to overcome shear locking (SL) in the analyses of slender beams and thin plates. Some of the most commonly applied techniques are the reduced integration techniques; Lin et al. (2020), the assumed shear strain field technique, The discrete Kirchhoff methodology, and the mixed interpolation of tensorial components (MITC) (Oñate2013; Wang et al. 2014; Lin et al. 2020). Although these techniques are efficient to remove shear locking, the accuracy of the finite elements may be reduced. Seeking for simple and accurate locking free finite element model, formulations based on interpolation functions that embody interdependency between bending and shear deformation have been developed, [Reddy (1997); Mukherjee and Prathap(2001); Edem (2006)]. For efficient investigation of nonlinear behavior of structures and alleviate shear and membrane locking phenomena that commonly occurred in shell structures, finite element based on isogeometric analysis was developed on higher order interpolation function bases (Liu et al. 2020; Liu and Jeffers 2017, 2018).

Anther weakens of TBT is coming out from the straightness of edges assumption that lead to constant transverse shear stress distribution through thickness and to overcome that problem there is a need to apply shear correction factor, (Menaa et al. 2012; Sina et al. 2009; Wei et al. (2012)). To eliminate the weakness encountered in TBT due to straightness assumption, the second order shear deformation beam theory was proposed, (Khoshgoftar 2019). A more precise beam theory is the third order shear theory which allow parabolic shear strain through thickness and verify the zero-shear stress condition at the upper and lower surface of beam, (Reddy 1984; Thai and Vo (2012; Maia et al. 2020; Attia and Mohamed, 2020). More comprehensive shear deformation theories have been discussed in many research articles (Touratier 1991; Soldatos 1992; Karama et al. 2003; Carrera 2003; Abdelrahman and Eltaher 2020; Bouazza and Zenkour 2020; Boussoula et al. 2020; Jiang et al. 2020; Nguyen et al. (2020a, b); Qin et al. 2020; Shafei et al. 2020; Van Do et al. 2020).

Considering the applications point of view, recently, analysis of the static as well as dynamic behavior of functionally graded beams (FGBs) have been studied through many beam’s theories for various type of material gradation function, (Esen 2020a; Le et al. 2020; Xie et al. 2020a). For unidirectional functionally graded materials, (Sankar 2001) investigated the static mechanical behavior of unidirectional functionally graded beam (UFGB) based on EBBT. Applying the EBBT, the free vibration behaviorof axially functionally graded beam (AFGB) with non-uniform cross section was investegated by (Huang and Li 2010) while the free vibration behavior of TBT was analyzed by (Huang et al. 2013).

Considering the variation of the material properties throughout the axial and thickness dirctions, (Alshorbagy et al. 2011) presented the free vibration charactristic for FGBs based on EBBT. (Lee and Lee 2017) developed exact transfer matrix method for analyzing the free vibration response of FGBs. (Şimşek 2010) performed the fundamental frequency analysis of FGB using the first-order and different higher-order shear deformation beam theories. (Jing et al. 2016) combined TBT with finite volume method to analysis the static and free vibration response of FGM. (Nguyen et al. 2013) have developed the first order shear deformation theory to obtain the static and free vibration solution of one dimension FGBs. (Kadoli et al. 2008). Studied the static behavior of metal-ceramic FGBs under ambient temperature using higher order beam theory (RBT). (Pradhan and Chakraverty 2015) Introduced generalized power-law exponent based shear deformation beam theory (PESDBT) to analysis the free vibration response of FGB with power-law material variation through the thickness. Atmane et al. (2017) investigated effect of thickness stretching and porosity on mechanical behavior of functionally graded beams. Within the framework of the improved third-order shear deformable theory, Xie et al. (2020b) investigated the nonlinear vibration and dynamic response.

For more improvement of the functionally graded material characteristics, two directional material graduation become necessary for many applications, (Tlidji et al. 2019). Applying different beam theories, (Karamanlı 2017) has introduced a static bending solution of two directional functionally graded beams with power law variation. (Pydah and Sabale 2017) studied the static behvoiur of curved bi-directional FGB using EBBT. Using both power and exponential laws for FGMs, (Huang and Ouyang 2020) have introduced closed form solution for the static bending of two directional functionally graded Timoshenko beam FGTBs under various boundary and loading conditions. Applying the higher order shear deformation theory, (Huang 2020) analyzed both static and free vibration behaviors of two directional FGB. Based on the exponential graduation law, (Karamanlı 2018) has studied the free vibration behavior of two direction FGBs using Reddy beam theory (RBT). Based on state space approach, (Deng and Cheng 2016) have studied the dynamic behavior of two direction FGBs based on TBT. Based on neural network-differential evolution approach, (Truong et al. 2020) developed an optimization technique for bidirectional functionally graded materials distribution to investigate the free vibration behavior of beams. (Lu and Chen 2020), studied the parametric dynamics of bidirectional functionally graded (BDFG) beams subjected to a time-dependent axial force. Based on finite element analysis. (Viet et al. 2020) Investigated the free vibration characteristics of sectioned unidirectional/bidirectional functionally graded material cantilever (Zhang et al. 2020a, b) proposed multifunctional nonlinear composite structure consisting of functionally graded beams and piezoelectric sheets for energy harvesting systems. Jamshidi et al. (2019) proposed an optimization procedure to achieve optimal post-buckling behavior of 2D functionally graded beams.

Regarding the functionally graded strucures under moving loads, many attempts have been performed to study and analyze functionally graded beams and structural element s under moving loads. (Şimşek et al. 2012) investigated the dynamic behavior of axially functionally graded EBBT subjected to moving load. In the context of finite element formulation, Esen et al. (2018) developed a finite element formulation to analyze the dynamic behavior of functionally graded Timoshenko beams under accelerating moving load. Applying Timoshenko beam hypothesis, (Nguyen et al. 2017) introduced the free vibration analysis of two directional FGB under moving load. Comparison between the dynamic behaviors of two directional functionally graded beams based on EBBT and TBT under moving load was performed by (Şimşek 2015). Wang et al. (2018) investigated vibration behavior of longitudinally moving sigmoid functionally graded material plates with porosities. (Nguyen et al. 2020a), investigated the dynamic behavior of a bidirectional functionally graded sandwich beam under non-uniform motion of a moving load. Based on higher order shear deformation beam theory, Wang et al. (2020) investigated the transient response of a sandwich porous beam uniformly distributed moving mass. Further readings on functionally graded beams under moving loads may be found in (Zhang and Liu, 2020; Esen (2019a, b, 2020a); Akbas et al. (2020), Özarpa and Esen 2020a, b, Ebrahimi et al. 2020).

Among these resources, there was no evidence of developing dynamic finite element model capable of investigating the static as well as the dynamic behavior of symmetrical functionally graded first order shear deformation beams under moving load considering the shear locking conditions. The present study aims to present a dynamic finite element model to study and analyze the mechanical behavior of bidirectional symmetrical functionally graded beams under moving loads. The first order shear deformation theory is adopted to incorporate the transverse shear strain effect. To avoid the shear locking effect, different polynomial interpolation functions technique is adopted based on five nodded isoparametric finite elements. Thus zero shear strain condition for thin beams is satisfied with no need for assuming new strain field or eliminating any of the true kinematic constraints. The proposed numerical procedure is verified and compared. Static, free and forced vibration behaviors are investigated and analyzed. The rest of the manuscript is organized as follows:—The mathematical model is presented in Sect. 2. Section 3 aims to present the finite element formulation and solution procedure. In Sect. 4, the verification of the proposed numerical procedure is presented. The numerical results and discussions are presented in Sect. 5. Finally, the concluding remarks are presented in Sect. 6.

2 Mathematical model

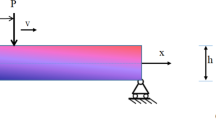
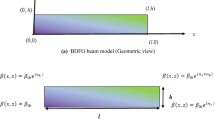
Consider a straight functionally graded beam of length L, uniform thickness h and width b as shown in Fig. 1. The material properties are assumed to be gradually changed in both thickness and length directions. According to the power law function, the symmetrical material distribution through thickness and length can be expressed as, Elishakoff et al. (2015):

$$P\left(x,z\right)=\left({P}_{1}-{P}_{2}\right){\left(\left|\frac{z}{h}\right|+0.5\right)}^{{r}_{z}}{\left(\left|\frac{x}{L}\right|+0.5\right)}^{{r}_{x}}+{P}_{2}$$
(1a)

where \(P\) is the property, \({P}_{\mathrm{1,2}}\) are the reference properties, \({r}_{x}\) and \({r}_{z}\) are the gradation index through the length and thickness respectively.

Fig. 1
figure 1

Geometry of bidirectional functionally graded Beam under moving load

Full size image

Due to the graded properties of the beam material, the neutral axis at which zero normal stress is attained will not be coincided with mid plane axis and will be dislocated by distance d through z direction. Due to the dislocation of neutral axis from the mid-plane axis there will be axial displacement \({u}_{o}\) associated with bending displacement \(\theta ,\) (Oñate 2013). The location of the neutral axis can be given by, (Eltaher et al. 2013)

$$d=\frac{{\int }_{-h/2}^{h/2}zE\left(x,z\right) dz}{{\int }_{-h/2}^{h/2}E\left(x,z\right) dz}$$
(1b)

For material with symmetrical distribution of the material properties along the mid-plane; the neutral axis dislocation is equal zero. Based on first order shear deformation theory, the displacement field can be expressed as, (Elishakoff (2019, 2020); Hu et al. 2020)

$$u\left(x,z,t\right)={u}_{0}\left(x,t\right)- \left(z-d\right)\theta \left(x,t\right), w\left(x,z,t\right)={w}_{0}\left(x,t\right), v\left(x,z,t\right)=0$$
(2)

where \({u}_{0}\) is the axial displacement,\({w}_{0}\) is the transverse displacement and \(\theta\) is the cross-sections rotation. Based on the displacement field given by Eq. (2), the kinematic relations can be written as.

The axial and shear strain in matrix form can be defined by

$$\left\{\begin{array}{c}{\varepsilon }_{x}\\ {\gamma }_{xz}\end{array}\right\}=\left[\begin{array}{ccc}1& -(z-d)& 0\\ 0& 0& 1\end{array}\right]\left\{\begin{array}{c}\frac{\partial {u}_{0}\left(x,t\right)}{\partial x}\\ \frac{\partial \theta \left(x,t\right)}{\partial x}\\ \frac{\partial {w}_{0}\left(x,t\right)}{\partial x}-\theta \left(x,t\right)\end{array}\right\}=S\widehat{\varepsilon }$$
(3)

where \(\frac{\partial {u}_{0}\left(x,t\right)}{\partial x}\) represent the beam elongation, \(\frac{\partial \theta \left(x,t\right)}{\partial x}\) represent beam curvature and \(\frac{\partial {w}_{0}\left(x,t\right)}{\partial x}-\theta \left(x,t\right)\) represent the beam transverse shear and all this component are represent the generalized strain vector \(\widehat{\varepsilon }\). The material constitutive relations for bidirectional functionally graded materials can be expressed as

$$\left\{\begin{array}{c}{\sigma }_{x}\\ {\tau }_{xz}\end{array}\right\}=\left[\begin{array}{ccc}E(x,z)& -(z-d)E(x,z)& 0\\ 0& 0& {k}_{z}G(x,z)\end{array}\right]\widehat{\varepsilon }$$
(4)

where \({\sigma }_{x} \mathrm{and} {\tau }_{xz}\) are the normal and shear components of Cauchy stress tensor; respectively. E(x,z) and G(x,z) are the elasticity and rigidity moduli of the bidirectional functionally graded materials; respectively.\({k}_{z}\) is the shear correction factor. The balance of the internal forces is found by.

$$N = \mathop \int \limits_{A}^{ } \sigma_{x} dA,\;M = - \mathop \int \limits_{A}^{ } \left( {z - d} \right)\sigma_{x} dA,\;Q = \mathop \int \limits_{A}^{ } \tau_{xz} dA$$
(5)

where N, M and Q are respectively the normal, bending and shear forces. By substituting with Eq. (4) into Eq. (5), and rewrite the forces in matrix form as,

$$\widehat{\sigma }=\left\{\begin{array}{c}N\\ M\\ Q\end{array}\right\}=\left[\begin{array}{ccc}{D}_{a}& {D}_{ab}& 0\\ {D}_{ab}& {D}_{b}& 0\\ 0& 0& {D}_{s}\end{array}\right] \widehat{\varepsilon }=\widehat{D} \widehat{\varepsilon }$$
(6)

where \({D}_{a}, {D}_{b}, {D}_{ab}, {D}_{s}\) are respectively the axial stiffness, bending stiffness, coupling axial-bending stiffness, and shear stiffness which can be given by, (Eltaher et al. 2014)

$$\left[{D}_{a} {D}_{ab} {D}_{b}\right]={\int }_{A}\left[1 z {z}^{2} \right]E\left(x,z\right)dA \mathrm{and }{D}_{s}={\int }_{A}{k}_{z}G\left(x,z\right)dA$$
(7)

The strain energy of functionally graded Timoshenko beam given by, (Esen 2020b)

$$U=\frac{1}{2}{\iiint }_{\Omega }\left({\sigma }_{xx}{\varepsilon }_{xx}+{\tau }_{xz}{\gamma }_{xz}\right)d\Omega =\frac{1}{2}{\int }_{0}^{L}\left[{D}_{a}{\left(\frac{\partial {u}_{0}\left(x,t\right)}{\partial x}\right)}^{2}-2{D}_{ab}\left(\frac{\partial {u}_{0}\left(x,t\right)}{\partial x}\right)\left(\frac{\partial \theta \left(x,t\right)}{\partial x}\right)+{D}_{b}{\left(\frac{\partial \theta \left(x,t\right)}{\partial x}\right)}^{2}+{\kappa }_{z}{D}_{s}{\left(\frac{\partial {w}_{0}\left(x,t\right)}{\partial x}-\theta \left(x,t\right)\right)}^{2}\right] dx$$
(8)

The kinetic energy of functionally graded Timoshenko beam can be expressed as, ( Özarpa and Esen 2020a, b)

$$T=\frac{1}{2}{\int }_{0}^{L}\left[{I}_{a}\left\{{\left(\frac{\partial {u}_{0}\left(x,t\right)}{\partial t}\right)}^{2}+{\left(\frac{\partial {w}_{0}\left(x,t\right)}{\partial t}\right)}^{2}\right\}+{I}_{b}{\left(\frac{\partial \theta \left(x,t\right)}{\partial t}\right)}^{2}-2{I}_{ab}\left(\frac{\partial {u}_{0}\left(x,t\right)}{\partial t}\right)\left(\frac{\partial \theta \left(x,t\right)}{\partial t}\right)\right] dx$$
(9)

where \({I}_{a}, {I}_{b}, {I}_{ab}\) are respectively the inertia components of the functionally graded beam which can be expressed as, (Eltaher et al. 2014)

$$\left[{I}_{a} {I}_{ab} {I}_{b}\right]={\int }_{A}\left[1 z {z}^{2} \right]\rho \left(x,z\right)dA$$
(10)

The potential of the moving load (V) is simply given by, (Nguyen et al. 2017)

$$V=-{\int }_{0}^{L}P{w}_{0}\left(x,t\right)\delta \left({x}_{P}-vt\right)dx$$
(11)

where δ(.) is the Dirac delta function, and x is the abscissa, measured from the left end of the beam. Applying the virtual displacement principle as

$${\int }_{0}^{t}\left(\delta T-\delta U-\delta V\right)dt=0$$
(12)

Evaluating the variations and performing the integral leads to the following dynamic equations of motion of functionally graded Timoshenko beam under moving load: -

$${I}_{a}\frac{{\partial }^{2}{u}_{0}\left(x,t\right)}{\partial {t}^{2}}-{I}_{ab}\frac{{\partial }^{2}\theta \left(x,t\right)}{\partial {t}^{2}}={D}_{a}\frac{{\partial }^{2}{u}_{0}\left(x,t\right)}{\partial {x}^{2}}-{D}_{ab}\frac{\partial \theta (x,t)}{\partial x}$$
(13)
$${I}_{a}\frac{{\partial }^{2}{w}_{0}\left(x,t\right)}{\partial {t}^{2}}-P\delta \left({x}_{P}-vt\right)={\kappa }_{z}{D}_{s}\left[\frac{{\partial }^{2}{w}_{0}(x,t)}{\partial {x}^{2}}+\frac{\partial \theta (x,t)}{\partial x}\right]$$
(14)
$${I}_{b}\frac{{\partial }^{2}\theta \left(x,t\right)}{\partial {t}^{2}}-{I}_{ab}\frac{{\partial }^{2}{u}_{0}\left(x,t\right)}{\partial {t}^{2}}={D}_{b}\frac{{\partial }^{2}\theta \left(x,t\right)}{\partial {x}^{2}}-{D}_{ab}\frac{{\partial }^{2}{u}_{0}\left(x,t\right)}{\partial {x}^{2}}+{\kappa }_{z}{D}_{s}\left[\frac{\partial {w}_{0}\left(x,t\right)}{\partial x}-\theta \left(x,t\right)\right]$$
(15)

3 Finite element formulation

3.1 Discretized finite element equation of motion

To seek for an efficient numerical tool to solve the dynamic equations of motion (13–15), the finite element is adopted. To derive the dynamic finite elements equilibrium equations, the virtual displacement principle is applied as, (Abdelrahman and El-Shafei 2020):

$$\delta \left(T+U-V\right)=0$$
(16)

where, T, U, V are respectively the variation, the total kinetic energy, the total strain energy, and the work done by the external forces. Substituting for the kinetic, strain energies and the work done, Eq. (16) can be expressed, (Nguyen et al. 2017):

$$\delta \left(\frac{1}{2}{\int }_{0}^{L}\left[{I}_{a}\left\{{\left(\frac{\partial {u}_{0}\left(x,t\right)}{\partial t}\right)}^{2}+{\left(\frac{\partial {w}_{0}\left(x,t\right)}{\partial t}\right)}^{2}\right\}+{I}_{b}{\left(\frac{\partial \theta \left(x,t\right)}{\partial t}\right)}^{2}-2{I}_{ab}\left(\frac{\partial {u}_{0}\left(x,t\right)}{\partial t}\right)\left(\frac{\partial \theta \left(x,t\right)}{\partial t}\right)\right] dx\right)+\delta \left(\frac{1}{2}{\int }_{0}^{L}\left[{D}_{a}{\left(\frac{\partial {u}_{0}\left(x,t\right)}{\partial x}\right)}^{2}-2{D}_{ab}\left(\frac{\partial {u}_{0}\left(x,t\right)}{\partial x}\right)\left(\frac{\partial \theta \left(x,t\right)}{\partial x}\right)+{D}_{b}{\left(\frac{\partial \theta \left(x,t\right)}{\partial x}\right)}^{2}+{\kappa }_{z}{D}_{s}{\left(\frac{\partial {w}_{0}\left(x,t\right)}{\partial x}-\theta \left(x,t\right)\right)}^{2}\right] dx\right)-\delta \left({\int }_{0}^{L}P{w}_{0}\left(x,t\right)\delta \left({x}_{P}-vt\right)dx\right)=0$$
(17)

To overcome the shear locking problem, five noded isoparametric element with ten degrees of freedom, shown in Fig. 2 and mixed shape function is adopted, (Baier-Saip et al. 2020). The displacement field can be interpolated as:

$$\left\{\begin{array}{c}u\\ w\end{array}\right\}=\left[\begin{array}{ccc}1& -(z-d)& 0\\ 0& 0& 1\end{array}\right] \left[\begin{array}{cccccccccc}{N}_{1}& 0& 0& 0& {N}_{2}& 0& 0& {N}_{3}& 0& 0\\ 0& 0& {N}_{1}& 0& 0& {N}_{2}& 0& 0& 0& {N}_{3}\\ 0& {\overline{N} }_{1}& 0& {\overline{N} }_{2}& 0& 0& {\overline{N} }_{3}& 0& {\overline{N} }_{4}& 0\end{array}\right]\left\{a\right\}$$
(18)

where the quadratic shape functions, used for the axial and rotational degrees of freedom,\({u}_{o}\),\(\theta\) are given by, (Oñate 2013)

Fig. 2
figure 2

five nodes beam element

Full size image
$${N}_{1}\left(\xi \right)=\frac{1}{2}\xi \left(\xi -1\right), {N}_{2}\left(\xi \right)=\left(1-{\xi }^{2}\right), {N}_{3}(\xi )=\frac{1}{2}\xi (\xi +1)$$
(19.a)

While cubic shape functions used for the transverse deflection, w0 and given by

$${\overline{N} }_{1}\left(\xi \right)=\frac{-9}{16}\left(\xi +\frac{1}{3}\right)\left(\xi -\frac{1}{3}\right)\left(\xi -1\right), {\overline{N} }_{2}\left(\xi \right)=\frac{27}{16}\left(\xi +1\right)\left(\xi -\frac{1}{3}\right)\left(\xi -1\right),$$
$${\overline{N} }_{3}\left(\xi \right)=\frac{-27}{16}\left(\xi +1\right)\left(\xi +\frac{1}{3}\right)\left(\xi -1\right), {\overline{N} }_{4}(\xi )=\frac{9}{16}(\xi +\frac{1}{3})(\xi -\frac{1}{3})(\xi +1)$$
(19.b)
$${a}^{T}=\left[\begin{array}{ccc}{u}_{01}& {w}_{01}& {\theta }_{1}\end{array} \begin{array}{ccc}{w}_{02}& {u}_{02}& {\theta }_{2}\end{array} \begin{array}{ccc}{w}_{03}& {u}_{03}& {w}_{04}\end{array} {\theta }_{3}\right]$$
(19.c)

With \(\xi\) is the local coordinate system,\(\xi =\frac{2}{{l}^{e}}\left(x-{x}_{c}\right)\), \({l}^{e}\) is the element length, \({x}_{c}\) is the coordinate of the element center. Based on the assumed displacement interpolation functions, the kinematic relations can be expressed as

$$\left\{\begin{array}{c}{\varepsilon }_{x}\\ {\gamma }_{xz}\end{array}\right\}=\left[\begin{array}{ccc}1& -(z-d)& 0\\ 0& 0& 1\end{array}\right] \left[\begin{array}{cccccccccc}\frac{d\xi }{dx}\frac{d{N}_{1}}{d\xi }& 0& 0& 0& \frac{d\xi }{dx}\frac{d{N}_{2}}{d\xi }& 0& 0& \frac{d\xi }{dx}\frac{d{N}_{3}}{d\xi }& 0& 0\\ 0& 0& \frac{d\xi }{dx}\frac{d{N}_{1}}{d\xi }& 0& 0& \frac{d\xi }{dx}\frac{d{N}_{2}}{d\xi }& 0& 0& 0& \frac{d\xi }{dx}\frac{d{N}_{3}}{d\xi }\\ 0& \frac{d\xi }{dx}\frac{d{\overline{N} }_{1}}{d\xi }& -{N}_{1}& \frac{d\xi }{dx}\frac{d{\overline{N} }_{2}}{d\xi }& 0& -{N}_{2}& \frac{d\xi }{dx}\frac{d{\overline{N} }_{3}}{d\xi }& 0& \frac{d\xi }{dx}\frac{d{\overline{N} }_{4}}{d\xi } & -{N}_{3}\end{array}\right] \left\{a\right\}$$
(20)

With \(\frac{d\xi }{dx}=\frac{2}{{l}^{e}}\) Substituting Eqs. (6), (18), and (20) into Eq. (17), the variational form can be written as

$$\frac{1}{2}{\int }_{0}^{l} \delta {\dot{a}}^{T}{N}^{T}CN\dot{a}dx+\frac{1}{2}{\int }_{0}^{l} \delta {a}^{T}{B}^{T}\widehat{D}Badx-\left[\left(P\times {\left({N}_{w}\right)}_{at x={x}_{P}}\right)\delta a+{\int }_{0}^{l}f{N}_{w}\delta a dx\right]=0$$
(21)

where C is the equivalent inertia components of the functionally graded material, which is given by

$$\left[C\right]={\int }_{A}\rho \left(x,z\right){s}^{T}s dA={\int }_{A}\rho \left(x,z\right)\left[\begin{array}{cc}1& 0\\ -(z-d)& 0\\ 0& 1\end{array}\right]\left[\begin{array}{ccc}1& -(z-d)& 0\\ 0& 0& 1\end{array}\right] dA=\left[\begin{array}{ccc}{I}_{a}& -{I}_{ab}& 0\\ -{I}_{ab}& {I}_{b}& 0\\ 0& 0& {I}_{a}\end{array}\right]$$
(22)

While \({x}_{P}\) presents the position of the moving load, for steady state velocity, \({x}_{P}={v}_{p}\times t,\) \({N}_{w}\) is the shape function vector for the transverse deflection, w, which can be expressed as

$${N}_{w}={\left[\begin{array}{ccc}0& {\overline{N} }_{1}& 0\end{array} \begin{array}{ccc}{\overline{N} }_{2}& 0& 0\end{array} \begin{array}{ccc}{\overline{N} }_{3}& 0& {\overline{N} }_{4} 0\end{array}\right]}^{T}$$
(23)

Evaluating the variations in Eq. (21) and recalling Gauss quadrature to evaluate the integrals, the following discretized form of the dynamic equation of motion is obtained:-

$$\sum_{e=1}^{NE}\left[{M}^{e}\right]\left\{\ddot{a}\right\}+\sum_{e=1}^{NE}\left[{K}^{e}\right]\left\{a\right\}=\left\{Q\right\}$$
(24)

where \(NE\) are the total number of finite elements, and \(\left[{M}^{e}\right], \left[{K}^{e}\right], \mathrm{and} Q\) are respectively the element mass and stiffness matrices and the external force vector, which are obtained as

$$\left[{M}^{e}\right]=\frac{{l}^{e}}{2}{\int }_{-1}^{1}{N}^{T}CN d\xi , \left[{K}^{e}\right]=\frac{{l}^{e}}{2}{\int }_{-1}^{1}{B}^{T}\widehat{D} B d\xi \,and\, Q=P\times {\left({N}_{w}\right)}_{at x={x}_{P}}+\frac{{l}^{e}}{2}{\int }_{-1}^{1}f{N}_{w} d\xi$$
(25)

3.2 Solution methodology

To study and analyze the mechanical behavior of the functionally graded Timoshenko beam, both static and dynamic behavior are investigated. The static behavior is investigated by neglecting the inertia effects and assuming that the load is applied gradually with no shocks. Thus, the governing equilibrium equations is simplified into the following form:

$$\sum_{e=1}^{NE}\left[{K}^{e}\right]\left\{a\right\}=\left\{Q\right\}$$
(26)

On the other hand, the free vibration behavior is investigated by neglecting the effect of the external applied load leading to the following equation of motion:

$$\sum_{e=1}^{NE}\left[{M}^{e}\right]\left\{\ddot{a}\right\}+\sum_{e=1}^{NE}\left[{K}^{e}\right]\left\{a\right\}=0$$
(27)

Assuming harmonic response, then the unknown displacement, velocity, and acceleration can be expressed as

$$a=A{e}^{i{w}_{n}t}, \dot{a}=A{iw}_{n}{e}^{i{w}_{n}t}, \mathrm{and}\, \ddot{a}=-A{w}_{n}^{2}{e}^{i{w}_{n}t}$$
(28)

By substituting in the discretized Eq. (27), the free vibration behavior can be obtained by solving the following eigen value problem: -

$$\left[K-{w}_{n}^{2}M\right]\left\{A\right\}=0$$
(29)

where \({w}_{n}\) represent the natural frequency and \(\left\{A\right\}\) is the vibration mode vector.

Finally, the forced vibration response is investigated by solving the dynamic equation of motion, Eq. (24) using implicit integration techniques. The most common scheme for implicit time integration is the Newmark scheme in which assume linear variation of acceleration through time step as below, (Borst et al. 2012):

$${\dot{a}}^{t+\Delta t}={\dot{a}}^{t}+\Delta t\left(\left(1-\gamma \right){\ddot{a}}^{t}+\gamma {\ddot{a}}^{t+\Delta t}\right)$$
(30)
$${a}^{t+\Delta t}={a}^{t}+\Delta t{\dot{a}}^{t}+\frac{1}{2}{\Delta t}^{2}\left(\left(1-2\beta \right){\ddot{a}}^{t}+2\beta {\ddot{a}}^{t+\Delta t}\right)$$
(31)

where \(\beta\) and \(\gamma\) are parameter determine the stability of the system. For unconditionally stability of linear system

$$2\beta \ge \gamma \ge \frac{1}{2}$$
(32)

The acceleration can be expressed as below by rearranging the previous equation for displacement

$${\ddot{a}}^{t+\Delta t}=\frac{1}{{\beta \Delta t}^{2}}\left({a}^{t+\Delta t}-{a}^{t}-\Delta t{\dot{a}}^{t}-\frac{1}{2}{\Delta t}^{2}{\ddot{a}}^{t}\left(1-2\beta \right)\right)$$
(33)

Recall equation of motion, Eq. (24):

$$M{\ddot{a}}^{t+\Delta t}+K{a}^{t+\Delta t}=Q(t)$$
(34)

By substitute with acceleration and displacement in equation of motion:

$$M\left(\frac{1}{{\beta \Delta t}^{2}}\left({a}^{t+\Delta t}-{a}^{t}-\Delta t{\dot{a}}^{t}-\frac{1}{2}{\Delta t}^{2}{\ddot{a}}^{t}\left(1-2\beta \right)\right)\right)+K{a}^{t+\Delta t}=Q(t)$$
$$\left[K+\frac{1}{{\beta \Delta t}^{2}}M\right]{a}^{t+\Delta t}={Q}^{t+\Delta t}+M\left(\frac{{a}^{t}}{{\beta \Delta t}^{2}}+\frac{{\dot{a}}^{t}}{\beta \Delta t}+{\ddot{a}}^{t}\left(\frac{1}{2\beta }-1\right)\right)$$
$$\left[\widehat{K}\right]\left\{{a}^{t+\Delta t}\right\}=\left\{\widehat{R}\right\}$$
(35)

where

$$\left[\widehat{K}\right]=\left[K+\frac{1}{{\beta \Delta t}^{2}}M\right]$$
(36)
$$\left\{\widehat{R}\right\}={Q}^{t+\Delta t}+M\left(\frac{{a}^{t}}{{\beta \Delta t}^{2}}+\frac{{\dot{a}}^{t}}{\beta \Delta t}+{\ddot{a}}^{t}\left(\frac{1}{2\beta }-1\right)\right)$$
(37)

4 Verification of the developed procedure

Within this section, the developed numerical procedure is verified by comparing the obtained results with the available results in literature. Static as well as dynamic behaviors of bidirectional functionally graded beams are verified and compared. For all verification cases, the material properties distribution of the functionally graded material is graduated through the axial and transverse directions according to the following form:

$$P\left(x,z\right)={P}_{0}{e}^{{r}_{x}\left(\frac{x}{L}+0.5\right)+{r}_{z}\left(\frac{z}{h}+0.5\right)}$$
(38)

where \(P\) is the property, \({P}_{0}\) is the reference property, \({r}_{x}\) and \({r}_{z}\) are the gradation index through the axial and transverse directions, respectively.

4.1 Static behavior

The static analysis is performed on a beam under uniformly distributed load of intensity, \({q}_{0}\) with reference material properties given by \({E}_{0}=70 GPa\), and \(\nu =0.3\) and geometrical properties given by \(l=1.0 m\), \(b=0.1 m\) for two different values beam aspect ratio, \(\frac{L}{h}\) = 5 and 20 for different axial and transvers material graduation index.

Comparison between the obtained results and those obtained by (Huang and Ouyang 2020) for the maximum normalized deflection, \(\overline{W }\left(x\right)=\frac{100 {E}_{0}{h}^{3}b}{{q}_{0}{L}^{4}}w\left(x\right)\) at different values of the axial and transverse material graduation index for L/h = 5 and 20 for simply supported, SS and clamped- simple, CS beams are illustrated in Table 1. It is observed that an excellent agreement is detected with the corresponding results obtained by (Huang and Ouyang 2020).

Table 1 Dimensionless maximum transverse deflections of the SS and CS TDFG beam with the exponential-law gradient at L/h = 5
Full size table

On the other hand, comparison between the obtained results and that obtained by(Huang and Ouyang 2020) for the variation of normalized normal stress, \({\tilde{\sigma }}_{xx}\left(0,z\right)=\frac{b h}{{q}_{0}L}{\sigma }_{xx}\left(0,z\right)\) and the normalized shear stress, \({\overline{\tau }}_{xz}\left(\frac{-L}{2},z\right)=\frac{b h}{{q}_{0}L}{\tau }_{xz}\left(\frac{-L}{2},z\right)\) with the normalized beam thickness for z/h = 5 are shown in Fig. 3. It may be noticed that the obtained results are in excellent agreement with the corresponding analytical results obtained by (Huang and Ouyang 2020).

Fig. 3
figure 3

Dimensionless stress through the thickness for CS TDFG beam

Full size image

4.2 Dynamic behavior

To check the validity of the developed procedure to investigate the vibration behavior of bidirectional functionally graded beams, the dynamic analysis is performed on a beam with reference material properties given by \({E}_{0}=210 GPa\), \({\rho }_{0}=7850 kg/{m}^{3}\) and \(\mu =0.3\) and geometrical properties given by \(h=1 m\), \(b=0.5 m\) and \(\frac{L}{h}\) ratio equal to 5 and 20. The developed numerical procedure is applied to investigate the free as well as the forced vibration behavior under moving load for SS and CS beams. Comparison between the obtained nondimensional frequency parameter,\({\lambda }_{1}=\frac{{\omega }_{1}{L}^{2}}{h}\sqrt{\frac{{\rho }_{0}}{{E}_{0}}}\) and that obtained by (Şimşek 2015) at different material graduation index for L/h = 5 for SS and CS bidirectional Timoshenko functionally graded, BDTFG beams are depicted in Table 2. It may be observed that an excellent agreement between the obtained results and the corresponding results obtained by (Şimşek 2015).

Table 2 Dimensionless first natural frequency of SS and CS bidirectional Timoshenko-Ehrenfest functionally graded, BDTEFG beam at L/h = 5
Full size table

To check the forced vibration response of bidirectional functionally graded Timoshenko beams under the moving load, the developed procedure is applied to detect the forced vibration response under moving load and the obtained results for the maximum non-dimensional deflection, \(w\left(0,t\right)\times \frac{48 {E}_{0}I}{{P}_{0}{L}^{3}}\) will be compared with the corresponding results obtained by (Şimşek 2015). Variations of the maximum non-dimensional deflection, \(\overline{W }\left(0,t\right)=w(0,t)\times \frac{48 {E}_{0}I}{{P}_{0}{L}^{3}}\) with the moving load velocity at different material graduation index for both SS and CS beams for L/h = 15 are shown in Fig. 4. While the dependency of the maximum non-dimensional deflection, \(\overline{W }\left(0,t\right)\) on the normalized time, \(\overline{t }=\frac{t}{{t}_{f}}\) where \({t}_{f}\) is the time required for the moving load \({v}_{p}=20 m/s\) to reach the end of the beam, at L/h = 5 for both SS and CS beams is illustrated in Fig. 5. It is observed that, comparing between the obtained results and those obtained by (Şimşek 2015), there is and excellent agreement is found validating the developed numerical procedure.

Fig. 4
figure 4

Variation of the maximum normalized dynamic deflection with the moving load velocity for \(\frac{L}{h}=15\),\({v}_{p}=20 m/s\)

Full size image
Fig. 5
figure 5

Time history of the normalized dynamic deflection with the dimensionless time for \(\frac{L}{h}=5\) and \({v}_{p}=20 m/s\)

Full size image

5 Numerical results and discussion

In this section, the static and dynamic behaviors of bidirectional functionally graded beam with different boundary conditions will be studied and analyzed. Symmetrical material distribution through thickness and length based on power-law function will be applied throughout calculations as indicated in Eq. (1a). The reference properties are based on ceramics of alumina with Young’s modulus \({E}_{1}=380 GPa\), density \({\rho }_{1}=3960 kg/{m}^{3}\) and Poisson’s ratio \(\mu =0.3\) and aluminum metal with Young’s modulus \({E}_{2}=70 GPa\), density \({\rho }_{2}=2700 kg/{m}^{3}\) and Poisson’s ratio \(\mu =0.3\), Wang and Zu (2018). Figure 6 shows the effect of graduation index in the variation of properties values is illustrated for young modulus. The geometrical properties assumed to be \(h=1 m\), \(b=0.5 m\). To investigate the influence of the boundary conditions on the mechanical behavior of BDTFG beams, four different boundary conditions are considered; Simply supported, SS, Simple-clamped, SC, clamped- clamped CC, and clamped free, CF.

Fig. 6
figure 6

The distributions of modulus of elasticity through length and thickness ((a) \({r}_{x}=0,{r}_{z}=0\); (b) \({r}_{x}=0,{r}_{z}=1\); (c) \({r}_{x}=0,{r}_{z}=5\); (d) \({r}_{x}=0,{r}_{z}=10\); (e) \({r}_{x}=1,{r}_{z}=0\); (f) \({r}_{x}=1,{r}_{z}=1\); (g) \({r}_{x}=1,{r}_{z}=5\); (k) \({r}_{x}=1,{r}_{z}=10\))

Full size image

5.1 Static bending behavior

To investigate the static bending behavior of bidirectional functionally graded Timoshenko beam under uniformly distributed load having an intensity of \({q}_{0}\) for different boundary conditions, consider the beam with the geometrical and material characteristics described in Sect. 5. The normalized normal stress at the midplane, \({\tilde{\sigma }}_{xx}\left(x,\frac{h}{2}\right)=\frac{b h}{{q}_{0}L}{\sigma }_{xx}\left(x,\frac{h}{2}\right)\) profiles throughout the normalized axial coordinate, \(\frac{x}{L}\) at axial gradation index, \({r}_{x}=1\) and beam aspect ratio, \(\frac{L}{h}=5\) for different values of transverse gradation index, \({r}_{z}\) at different boundary conditions are illustrated in Fig. 7. It is noticed that increasing the material transverse gradation index increases the material content of metal which increases the overall material flexibility thus increasing the normalized normal stress for all beam boundary conditions. On the other hand, the normalized normal stress significantly affected by the beam boundary condition,; the CF produces the largest values of the maximum normalized normal stress at the midplane while both SS and CC almost produces the same area under the normalized normal stress profile.

Fig. 7
figure 7

Dimensionless normal stress through the normalized axial coordinate

Full size image

To investigate the effectiveness of the developed procedure to efficiently detect the shear stress profile throughout the beam length, the normalized shear stress,\({\overline{\tau }}_{xz}\left(x,\frac{h}{2}\right)=\frac{2b h}{{q}_{0}L}{\tau }_{xz}\left(x,\frac{h}{2}\right)\) profiles throughout the normalized coordinate,\(\frac{x}{L}\) are investigated using 5 noded Timoshenko beam element with different shape function (DITBT) and 3 noded Timoshenko beam element with equal convention shape function (CTBT) for two different values of beam aspect ratio for SS, CF, CC, and CS boundary conditions, as illustrated in Fig. 8. It is observed that both DITBT and CTBT formulations are capable to predict the exact solution in case of thick beam, \(\frac{L}{h}=5\). On the other hand, for slender beam, \(\frac{L}{h}=20\); CTBT indicate inconsistency in shear stress profile due to the disability of convention CTBT to vanish the shear strain to coincide with the exact solution of EBBT and produces oscillatory normalized shear stress profiles due to shear locking phenomena. By using mixed shape function in which the displacement is interpolated with higher order interpolation function than rotation (DITBT), the vanish condition of shear strain is satisfied. As noticed for the normalized normal stress, also the normalized shear stress profiles increase with increasing the material gradation index due to increasing the material content of metal. Moreover, larger values of the maximum normalized shear stress are detected for CF boundary condition comparing with that obtained in SS, CS and CC boundary conditions.

Fig. 8
figure 8

Dimensionless shear stress through the normalized axial coordinate for different BCs

Full size image

5.2 Free vibration analysis

The developed procedure is applied to solve the eigen value problem to obtain the fundamental frequency of vibrational motion. The influence of the axial and transvers gradation index on the fundamental frequency is detected. Variations of the nondimensional frequency parameter for the first vibration mode, \({\lambda }_{1}=\frac{{\omega }_{1}{L}^{2}}{h}\sqrt{\frac{{\rho }_{1}}{{E}_{1}}}\) with the transverse gradation index, \({r}_{z}\) at different values of the axial gradation index, \({r}_{x}\) for different beam boundary conditions for BDTFG beam with metallic core are depicted in Fig. 9. It is noticed that, keeping one of the material gradation index constant and increasing the other results in decreasing the first nondimensional natural frequency due to the overall decrease in the system stiffness as well as the inertia effect with the increase of gradation indices. As it is known from theory of vibration the natural frequency is directly proportional to the modulus of elasticity and inversely proportional to the mass density that is why for the first moment it could be thought that the modulus elasticity has the dominated effect in natural frequency but this is not clear yet as for the given material ingredients the elasticity can change from minimum value \(70 GPa\) to maximum value \(380 GPa\) with 5.4 times increasing ratio while density can change from minimum value \(2700 Kg/{m}^{3}\) to maximum value of \(3960 Kg/{m}^{3}\) with 1.46 times increasing ratio which to tend to be constant density compared to the change in elasticity and that is mean the effect of density variation is not cleared for the given material ingredients. In these results the change in natural frequency is tend to obey the change in density by decreasing with the increasing of density otherwise increasing with the increasing of elasticity which mean for the same changing ratio for elasticity and density; the density will has the dominated effect in natural frequency.

Fig. 9
figure 9

The non-dimensional first natural frequency versus \({r}_{z}\) for \(\frac{L}{h}=5\), for BDTFG beams with almost metallic core

Full size image

Reversing the material distribution such that beam core is almost ceramic, dependency of the first nondimensional natural frequency on the material gradation indices for different beam boundary conditions for (L/h = 5) beams are illustrated in Table 3. It is observed that, keeping constant value of one of the material gradation index, increasing the material gradation index in either transverse or axial direction increases the material content of ceramic leading to higher values of stiffness and consequently higher values of natural frequencies are observed. Moreover, at higher values of the material graduation index in either axial or transverse direction, (\({r}_{x}\) or \({r}_{z}=10\)) almost constant nondimensional frequency parameter is detected. Comparing between the boundary conditions, CF beams produces the smallest nondimensional natural frequencies while the largest nondimensional natural frequencies are detected for CC beams. Additionally, beam aspect ratio significantly affect the detected natural frequency. Higher values of natural frequency are detected with increasing beam aspect ratio.

Table 3 Dimensionless first natural frequency of bidirectional Timoshenko-Ehrenfest functionally graded BDTEFG beam with ceramic core for SS, CS, CC, and CF boundary conditions at L/h = 5
Full size table

5.3 Forced vibration response under moving load

The forced vibration time response under moving point load of intensity of \({P}_{o}\), is investigated for material gradation indices and different beam boundary conditions. The load velocity is set to be equal \({v}_{p}=20 m/s\) and the aspect ratio, \(L/h\) equal 20. The normalized central deflection, \(\overline{W }\left(0,t\right)=w(0,t)\times \frac{48 {E}_{1}I}{{P}_{0}{L}^{3}}\) profiles for SS, CS and CC and The normalized free end deflection, \(\overline{W }\left(L/2,t\right)=w(L/2,t)\times \frac{48 {E}_{1}I}{{P}_{0}{L}^{3}}\) profiles for CF versus the normalized time, \(\overline{t }=\frac{t {v}_{p}}{L}\) for different values of material gradation index are depicted in Fig. 10. It is observed that the material gradation indices significantly affect the forced vibration response under moving load; increasing the material gradation index in axial and transverse directions increases the transvers deflection for all beam boundary conditions due to decreasing the overall system stiffness which increases the system flexibility.

Fig. 10
figure 10

Time history of the normalized dynamic deflection with the dimensionless time for \(\frac{L}{h}=20\) and \({v}_{p}=20 m/s\) for BDTFG beams with metallic core

Full size image

Additionally, the boundary condition significantly affects both value and smoothness of the nondimensional transverse deflection with time. CC beam behaves quasi-statically under the action moving load, \(\left(0\le \overline{t }\le 1\right)\) and after removing the action of load \(\left(\overline{t }>1\right).\) On the other hand both CS and CF behave quasi-statically throughout the time interval of load application, \(\left(0\le \overline{t }\le 1\right)\) while oscillating waves are associated with the transverse deflection profile after load leaving the beam span, \(\left(\overline{t }>1\right)\). On contrary to the CC, SS beam produces a normalized transverse bending profiles associated with oscillating wave during the intervals of application and removal of load. Moreover, the maximum normalized deflection is detected for CF beam while the smallest value is produced by the CC beam.

On the other hand this trend is reversed if the material properties are distributed such that beam core is fully ceramic. As shown in Fig. 11, the maximum normalized transverse deflection under moving load decreases with increasing the material gradation index.

Fig. 11
figure 11

Time history of the normalized dynamic deflection with the dimensionless time for \(\frac{L}{h}=20\) and \({v}_{\mathrm{p}}=20\mathrm{ m}/\mathrm{s}\) for different BCs. for BDTFG beams with ceramic core

Full size image

It is observed that the effect of increasing the moving load velocity is controlled by the material gradation indices, the beam aspect ratio and the beam boundary conditions. Depending on the beam aspect ratio and the boundary conditions, increasing the moving load velocity below the critical speed produces either constant transverse deflection profile or slow rate increasing one. On the other hand, for thin beams, L/h = 20, as the speed increases over the critical value the transverse deflection increases until reaching maximum value then decreases or proceeds with a constant value depending on the material gradation indices and boundary conditions. Moreover, for CF thick beams, the moving load velocity has insignificant effect on the maximum transverse deflection. Thin beams behave quasi-statically as the moving load speed increases above its critical value while transverse deflection profile associated with oscillating waves is detected for thick beams. The amplitudes of the associated waves depend on the beam boundary conditions; waves with increasing amplitudes are observed for SS, CS, and CC while it is completely disappeared for CF thick beams.

The speed of the applied moving load significantly the maximum transvers deflection. Variations of the normalized maximum transverse deflection, deflection \({\overline{W} }_{max.}\left(x,t\right)=w(x,t)\times \frac{48 {E}_{1}I}{{P}_{0}{L}^{3}}\), evaluated at the mid beam \(\left(x=0\right)\) for SS, CS and CC and at the free end of the beam \(\left(x=\frac{L}{2}\right)\) for CF beam, with the applied moving load speed for different material gradation index in the axial and transverse directions for both thin and thick beams are respectively illustrated in Figs. 12 and 13.

Fig. 12
figure 12

Variation of the maximum normalized dynamic deflection with the load velocity for \(\frac{L}{h}=20\), for different BCs

Full size image
Fig. 13
figure 13

Variation of the maximum normalized dynamic deflection with moving load velocity for \(\frac{L}{h}=5\) for different BCs

Full size image

6 Conclusions

Static and dynamic mechanical behaviors of bidirectional symmetrical functionally graded Timoshenko beams considering the shear locking effect is investigated through finite element procedure. Different polynomial shape functions are used to avoid shear locking phenomena occurs in thin beams. The material properties of the functionally graded materials are assumed to be graduated through both axial and transverse directions according to the power law function. To maintain the outer fibers of the beam against rubbing conditions or strengthen beam core, symmetrical material properties distribution is assumed such that both upper and bottom surface are harder than beam core or core be hardener than top and bottom beam fibers. The differential equations of motion are derived using the virtual displacement principle. To avoid shear locking, the dynamic finite element equations of motion are derived on mixed shape function basis. The incremental solution procedure based on implicit direct integration technique is presented. The developed numerical methodology is verified for static and dynamic analysis and good agreement is observed. Numerical results are obtained and discussed. Based on the considered material and geometrical parameters, the following concluding remarks are revealed:

  • The material gradation index in the axial and transverse direction significantly affect the mechanical behavior of bidirectional symmetrical functionally graded materials; increasing the material gradation index increases the flexibility of beam and consequently larger values of the transverse deflection and the produced stresses are detected while smaller values of the natural frequencies are observed.

  • To seek efficient detection of the mechanical behavior of Timoshenko beams, finite elements based on mixed shape functions could be used to avoid shear locking phenomena occurs in thin beam structures.

  • The mechanical behavior of bidirectional symmetrical functionally graded Timoshenko beam under moving load significantly affected by the beam boundary conditions. For thin beams, L/h = 20, CC beam produces a more stable dynamic behavior under moving load compared with SS, CF, CS beams.

  • The applied moving load speed has a significant effect on the forced vibration response, this effect is controlled with the material gradation index, beam aspect ratio, and the beam boundary conditions.

  • Beam aspect ratio significantly affects the forced time response. This ratio should be carefully chosen to attain stable dynamic performance.

  • Symmetrical material gradation could be used for enhancing the mechanical performance of beam structural components according to the required objective.