Vibration characteristics of moving sigmoid functionally graded plates containing porosities

Abstract

This study investigates vibration characteristics of longitudinally moving sigmoid functionally graded material (S-FGM) plates containing porosities. Two types of porosity distribution, i.e., the even and uneven distributions, are taken into account. In accordance with the sigmoid distribution rule, the material properties of porous S-FGM plates vary smoothly along the plate thickness direction. The nonlinear geometrical relations are adopted by using the von Kármán non-linear plate theory. Based on the d’Alembert’s principle, the nonlinear governing equation of the system is derived. Then, the governing equation is discretized to a set of ordinary differential equations via the Galerkin method. These discretized equations are subsequently solved by using the method of harmonic balance. Analytical solutions are verified with the aid of the adaptive step-size fourth-order Runge–Kutta method. By using the perturbation technique, the stability of the steady-state response is highlighted. Finally, both natural frequencies and nonlinear forced responses of moving porous S-FGM plates are examined. Results demonstrate that the moving porous S-FGM plates exhibit hardening spring characteristics in the nonlinear frequency response. Moreover, it is shown that the type of porosity distribution, moving speed, porosity volume fraction, constituent volume fraction and in-plane pretension all have significant influence on the nonlinear forced responses of moving porous S-FGM plates.

1 Introduction

Functionally gradient materials (FGMs) are a new type of advanced composite materials composed of two or more phases. FGMs are first introduced by a group of Japanese scientists for the purpose of aerospace application. Due to their promising mechanical and material properties such as smooth stress distribution, less stress concentration and high joint strength of different materials, FGMs have received wide applications in modern engineering including rocket nozzles, turbine blades, power machinery and electronics. Some available techniques can be used to synthesize FGMs such as multi-step sequential infiltration technique, non-pressure sintering technique and self-propagating high temperature synthesis technique.

Owing to the existence of technical issues in the process of preparing FGMs, porosities or micro-voids may happen inside the FGMs. For example, Zhu et al. (2001) reported that many porosities can happen inside the materials when preparing FGMs by means of the non-pressure sintering technique; the existence of porosities attenuates dramatically the strength of FGMs. In addition, it was found that (Wattanasakulpong et al. 2012) porosities happen mainly in the middle zone of the FGMs that are prepared via the multi-step sequential infiltration technique. This is because that it is difficult to infiltrate the secondary material into the middle zone ideally, nevertheless infiltrating the material into the top and bottom zones is easier, leading to less porosities in these two zones. In consideration of the existence of pososities inside FGMs, it is essential to take into account porosity effect on dynamic behavior of FGM structures containing porosities.

Because of the wide application of FGM plates in various engineering fields, this type of composite structures has drawn much attention. Most researches of FGM plates are related to stress and buckling studies, by contrast, dynamics analyses of FGM plates are not large (Swaminathan et al. 2015). Some of these disquisitions are briefly mentioned here. Nguyen (2015) calculated natural frequencies of FGM plates by using a higher-order hyperbolic shear deformation theory. Atmane et al. (2010) analyzed free vibration of FGM plates on Winkler-Pasternak elastic foundations. The free vibration problem of variable thickness two-directional circular FGM plates on elastic foundations was carried out by Alipour et al. (2010). Gupta et al. (2016) calculated natural frequencies of a shear deformable FGM plate with various boundary conditions utilizing the finite element method. Based on the three dimensional theory of elasticity, Jin et al. (2015) carried out free vibration analysis of annular sector FGM plates. The free vibration of FGM sandwich plates was analyzed by Alibeigloo and Alizadeh (2015), who considered two types of plate conformation. Using the third-order shear deformation theory, Zhang et al. (2010) studied the chaotic motion of simply-supported thick FGM plates through the method of multiple scales. Based on the von Kármán non-linear plate theory, Allahverdizadeh et al. (2014) analyzed dynamic response of a rectangular FGM plate considering a single-mode approximation. Thai et al. (2014) researched the bending, buckling and free vibration of FGM sandwich plates according to the first-order shear deformation theory. Utilizing the Mindlin plate theory along with modified couple stress theory, Ke et al. (2013) performed the axisymmetric non-linear free vibration analysis of FGM microplates. Alijani et al. (2011) adopted the Lagrange method together with the pseudo-arc-length continuation technique to obtain non-linear dynamic response of FGM plates. Hao et al. (2011, 2014) investigated periodic, quasi periodic and chaotic motions of FGM plates under various boundary constrains. Yang et al. (2010) studied the non-linear frequency characteristics and transient response of cracked FGM plates by using Reddy third-order shear deformation plate theory. Recently, based on the classical plate theory, Wang and Zu (2017c, e) investigated the nonlinear steady-state response of traveling FGM plates with and without fluid effect in the von Kármán-type sense.

The foregoing researches all suppose the constituent material of FGMs is perfect without inclusion or porosities existing inside the materials. A few studies are carried out on free vibrations of FGM structures with porosities. Based on the classical beam theory, Wattanasakulpong and Ungbhakorn (2014) obtained linear and nonlinear frequencies of FGM Euler–Bernoulli beams with porosities. Ebrahimi and Zia (2015) analyzed nonlinear frequency characteristics of FGM Timoshenko beams with porosities using the method of multiple scales. Ait Atmane et al. (2017) calculated the natural frequencies of a porous FGM beam resting on elastic foundations. Considering a porous FGM nanoplate resting on Winkler–Pasternak foundations, porosity effect on the free vibration of the system was shown by Mechab et al. (2016).

Additionally, longitudinally moving structures can be found in many engineering applications such as deployment of appendages in aerospace, robotic manipulators, transmission belts and satellite tethers. Longitudinally moving beams, plates and shells made of metal materials have been studied extensively (Ding and Chen 2010; Ding et al. 2012; Marynowski and Kapitaniak 2014; Wang et al. 2013; Yang et al. 2016a, b; Yang and Zhang 2014; Zhang et al. 2014). Recently, Wang et al. (2015, 2016a, b) and Wang and Zu (2017a, b) considered moving metallic plates in contact with liquid; they reported a series of work on various aspect of the coupled structure including natural frequencies, mode functions, critical speed, stability, internal resonance and parametric resonance.

The concept of the sigmoid functionally graded materials (S-FGMs) is introduced by Chi and Chung (2006a) in 2006. The advantage of S-FGMs is that they can reduce stress concentration more effectively (Chi and Chung 2006a). For instance, it is reported that (Chi and Chung 2002) the usage of S-FGMs can dramatically reduce the stress intensity factors in a cracked structure. Some investigations have been conducted on bending, stress, and free vibration analyses of S-FGM structures. Ben-Oumrane et al. (2009) performed static deformation and stress analyses of S-FGM beams. Bending and stresses of S-FGM plates are studied by several researchers by means of various methods (Chi and Chung 2006b; Fereidoon et al. 2011; Han et al. 2009). Atmane et al. (2011) investigated the free vibration of S-FGM beams with variable cross-section, where three boundary conditions were considered. Due to the complexity of constituent distribution of S-FGMs, there are still no studies on large-deflection vibrations of S-FGM plates.

In this paper, the vibration characteristics are investigated on longitudinal moving S-FGM plates with porosities for the first time. Two types of porosity distribution, i.e., even and uneven distributions, are taken into account. In accordance with the sigmoid distribution rule, the material properties of porous S-FGM plates vary smoothly along the plate thickness direction. The nonlinear geometrical relations are adopted by using the von Kármán non-linear plate theory. Based on the d’Alembert’s principle, the governing equation of moving porous S-FGM plates is derived. Then, the governing equation is discretized to a set of ordinary differential equations via the Galerkin method. These discretized equations are subsequently solved by using the method of harmonic balance. Analytical solutions are verified with the aid of the adaptive step-size fourth-order Runge–Kutta method. By using the perturbation technique, the stability of the steady-state response is highlighted. Finally, the present study examines both natural frequency and nonlinear forced response characteristics for longitudinally moving S-FGM plates with porosities.

2 Problem formulation

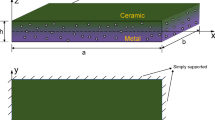
Consider a rectangular porous S-FGM plate with length a, width b, thickness h and Cartesian coordinate system $(O,x,y,z)$ where the origin O is at one of the plate corners as shown in Fig. 1a. The plate moves longitudinally in the x-axis direction at a constant velocity V. The S-FGM is a mixture of metal and ceramic, in which the top surface of the plate is pure metal and the bottom surface is pure ceramic. The S-FGM contains porosities and Fig. 1b shows two types of porosity distribution, i.e., evenly distributed porosity (Porosity-I for short) and unevenly distributed porosity (Porosity-II for short). Displacement components of points in the mid-plane of the plate are denoted by u, v and w in the x, y and z directions from the static equilibrium, respectively. Besides, there is pretention applied on the plate in the x-axis direction, which is denoted by N ₀.

Fig. 1

Schematic of a moving rectangular S-FGM plate with porosities: a Cartesian coordinate system; b plate cross-sections for two types of porosity

Supposing porosities disperse equally among the metal and ceramic phases, the effective material properties of the imperfect FGM plate, with a porosity volume fraction α ($\alpha \ll1$), are given by the modified form:

$$ P\left( z \right) = P_{m} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {V_{m} \left( z \right) - \frac{\alpha }{2}} \right] + P_{c} {\kern 1pt} \left[ {V_{c} \left( z \right) - \frac{\alpha }{2}} \right] $$

(1)

where P _m and P _c are, respectively, the material properties of metal and ceramic; and V _m and V _c are their volume fractions, respectively.

The volume fraction relations of constituents are given by $V_{m} + V_{c} = 1$ (Wattanasakulpong and Chaikittiratana 2015). For the purpose of realizing the smooth distribution of stresses, Chi and Chung (2006a) proposed a sigmoid FGM (S-FGM), which is defined as

$$ \left\{ \begin{aligned} V_{c1} \left( z \right) = 1 - \frac{1}{2}\left( {\frac{h/2 - z}{h/2}} \right)^{N} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le z \le h/2 \hfill \\ V_{c2} \left( z \right) = \frac{1}{2}\left( {\frac{h/2 + z}{h/2}} \right)^{N} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - h/2 \le z \le 0 \hfill \\ \end{aligned} \right. $$

(2)

in which $N$ denotes the power-law index which is nonnegative real number, V _ci (i = 1, 2) the volume fractions of ceramic in different areas.

The general material properties P _i (i = 1, 2), for the S-FGM plate with evenly distributed porosities (Porosity-I), are stated as

$$ \left\{ \begin{aligned} P_{1} \left( z \right) = \left( {P_{c} - P_{m} } \right) \, \left[ {1 - \frac{1}{2}\left( {\frac{h/2 - z}{h/2}} \right)^{N} } \right] + P_{m} - \frac{\alpha }{2}\left( {P_{c} + P_{m} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} (0 \le z \le h/2) \hfill \\ P_{2} \left( z \right) = \left( {P_{c} - P_{m} } \right) \, \frac{1}{2}\left( {\frac{h/2 + z}{h/2}} \right)^{N} + P_{m} - \frac{\alpha }{2}\left( {P_{c} + P_{m} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} ( - h/2 \le z \le 0) \hfill \\ \end{aligned} \right. $$

(3)

Accordingly, the general Young’s modulus E _i , Poisson ratio $\nu_{i}$ and mass density $\rho_{i}$ (i = 1, 2) of the Porosity-I S-FGM plate take the form

$$ \left\{ \begin{aligned} E_{1} \left( z \right) = \left( {E_{c} - E_{m} } \right) \, \left[ {1 - \frac{1}{2}\left( {\frac{h/2 - z}{h/2}} \right)^{N} } \right] + E_{m} - \frac{\alpha }{2}\left( {E_{c} + E_{m} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (0 \le z \le h/2) \hfill \\ E_{2} \left( z \right) = \left( {E_{c} - E_{m} } \right) \, \frac{1}{2}\left( {\frac{h/2 + z}{h/2}} \right)^{N} + E_{m} - \frac{\alpha }{2}\left( {E_{c} + E_{m} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ( - h/2 \le z \le 0) \hfill \\ \end{aligned} \right. $$

(4)

$$ \left\{ \begin{aligned} \nu_{1} \left( z \right) = \left( {\nu_{c} - \nu_{m} } \right) \, \left[ {1 - \frac{1}{2}\left( {\frac{h/2 - z}{h/2}} \right)^{N} } \right] + \nu_{m} - \frac{\alpha }{2}\left( {\nu_{c} + \nu_{m} } \right),{\kern 1pt} \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (0 \le z \le h/2) \hfill \\ \nu_{2} \left( z \right) = \left( {\nu_{c} - \nu_{m} } \right) \, \frac{1}{2}\left( {\frac{h/2 + z}{h/2}} \right)^{N} + \nu_{m} - \frac{\alpha }{2}\left( {\nu_{c} + \nu_{m} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ( - h/2 \le z \le 0) \hfill \\ \end{aligned} \right. $$

(5)

$$ \left\{ \begin{aligned} \rho_{1} \left( z \right) = \left( {\rho_{c} - \rho_{m} } \right) \, \left[ {1 - \frac{1}{2}\left( {\frac{h/2 - z}{h/2}} \right)^{N} } \right] + \rho_{m} - \frac{\alpha }{2}\left( {\rho_{c} + \rho_{m} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (0 \le z \le h/2) \hfill \\ \rho_{2} \left( z \right) = \left( {\rho_{c} - \rho_{m} } \right) \, \frac{1}{2}\left( {\frac{h/2 + z}{h/2}} \right)^{N} + \rho_{m} - \frac{\alpha }{2}\left( {\rho_{c} + \rho_{m} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} ( - h/2 \le z \le 0) \hfill \\ \end{aligned} \right. $$

(6)

For the S-FGM plate with unevenly distributed porosities (Porosity-II), on the other hand, the material properties in Eqs. (4–6) can be replaced by (Wattanasakulpong and Chaikittiratana 2015)

$$ \left\{ \begin{aligned} E_{1} \left( z \right) = \left( {E_{c} - E_{m} } \right) \, \left[ {1 - \frac{1}{2}\left( {\frac{h/2 - z}{h/2}} \right)^{N} } \right] + E_{m} - \frac{\alpha }{2}\left( {E_{c} + E_{m} } \right)\left( {1 - \frac{2\left| z \right|}{h}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \quad {\kern 1pt} (0 \le z \le h/2) \hfill \\ E_{2} \left( z \right) = \left( {E_{c} - E_{m} } \right) \, \frac{1}{2}\left( {\frac{h/2 + z}{h/2}} \right)^{N} + E_{m} - \frac{\alpha }{2}\left( {E_{c} + E_{m} } \right)\left( {1 - \frac{2\left| z \right|}{h}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} ( - h/2 \le z \le 0) \hfill \\ \end{aligned} \right. $$

(7)

$$ \left\{ \begin{aligned} \nu_{1} \left( z \right) = \left( {\nu_{c} - \nu_{m} } \right) \, \left[ {1 - \frac{1}{2}\left( {\frac{h/2 - z}{h/2}} \right)^{N} } \right] + \nu_{m} - \frac{\alpha }{2}\left( {\nu_{c} + \nu_{m} } \right)\left( {1 - \frac{2\left| z \right|}{h}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} \quad {\kern 1pt} (0 \le z \le h/2) \hfill \\ \nu_{2} \left( z \right) = \left( {\nu_{c} - \nu_{m} } \right) \, \frac{1}{2}\left( {\frac{h/2 + z}{h/2}} \right)^{N} + \nu_{m} - \frac{\alpha }{2}\left( {\nu_{c} + \nu_{m} } \right)\left( {1 - \frac{2\left| z \right|}{h}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} \quad ( - h/2 \le z \le 0) \hfill \\ \end{aligned} \right. $$

(8)

$$ \left\{ \begin{aligned} \rho_{1} \left( z \right) = \left( {\rho_{c} - \rho_{m} } \right) \, \left[ {1 - \frac{1}{2}\left( {\frac{h/2 - z}{h/2}} \right)^{N} } \right] + \rho_{m} - \frac{\alpha }{2}\left( {\rho_{c} + \rho_{m} } \right)\left( {1 - \frac{2\left| z \right|}{h}} \right),{\kern 1pt} \quad {\kern 1pt} {\kern 1pt} (0 \le z \le h/2) \hfill \\ \rho_{2} \left( z \right) = \left( {\rho_{c} - \rho_{m} } \right) \, \frac{1}{2}\left( {\frac{h/2 + z}{h/2}} \right)^{N} + \rho_{m} - \frac{\alpha }{2}\left( {\rho_{c} + \rho_{m} } \right)\left( {1 - \frac{2\left| z \right|}{h}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} \quad {\kern 1pt} ( - h/2 \le z \le 0) \hfill \\ \end{aligned} \right. $$

(9)

where the Poisson ratio is additionally treated as variable in comparison with Ref. (Wattanasakulpong and Chaikittiratana 2015).

In this study, the S-FGM is made of Alumina (ceramic) and Nickel (metal) whose material properties at room temperature are obtained as:

$$ {\text{Alumina:}}\;E_{c} = 3.2023 \times 10^{11} {\text{N}}\;{\text{m}}^{ - 2} ,\;\nu_{c} = 0.26\;{\text{and }}\rho_{c} = 3950\;{\text{kg}}\;{\text{m}}^{ - 3} $$

$$ {\text{Nickel: }}E_{m} = 2.05098 \times 10^{11} {\text{N}}\;{\text{m}}^{ - 2} ,\;\nu_{m} = 0.31\;{\text{and}}\;\rho_{m} = 8900\;{\text{kg}}\;{\text{m}}^{ - 3} $$

To demonstrate the mechanics characteristics of the S-FGM plate with porosities, the change rules of Young’s moduli along with the thickness are plotted for perfect and porous S-FGM plates in Fig. 2. The porosity volume fraction is chosen as α = 0.1 and three constituent volume fractions, namely, N = 0.3, 3 and 5, are taken into account. From the figure, one can find the Young’s moduli show sigmoid distributions, thus the FGM is termed as S-FGM.

Fig. 2

Change rule of Young’s moduli of perfect and porous S-FGM plates with different constituent volume fractions: a N = 0.3; b N = 1; c N = 5

Additionally, one can find that the perfect S-FGM has the biggest Young’s modulus while the Porosity-I (even distribution) S-FGM has the smallest one; the Porosity-II (uneven distribution) S-FGM possesses Young’s modulus that is in the middle of the two previously mentioned. Besides, the Young’s modulus of Porosity-II S-FGM is piecewise smooth; it has the same value as that of Porosity-I S-FGM at the middle plane of the plate, and has the same value as that of perfect S-FGM at the top and bottom surface.

Based on the classical thin plate theory, the strain relations of a thin porous S-FGM plate are stated as (Amabili 2008)

$$ \varepsilon_{x} = \varepsilon_{x}^{0} + z\chi_{x} $$

(10)

$$ \varepsilon_{y} = \varepsilon_{y}^{0} + z\chi_{y} $$

(11)

$$ \gamma_{xy} = \gamma_{xy}^{0} + 2z\chi_{xy} $$

(12)

in which $\varepsilon_{x}$, $\varepsilon_{y}$ and $\gamma_{xy}^{{}}$ are strain components at an arbitrary point of the plate, $\chi_{x}$, $\chi_{y}$ and $\chi_{xy}$ the changes in the curvature and torsion of the middle surface, $\varepsilon_{x}^{0}$, $\varepsilon_{y}^{0}$ and $\gamma_{xy}^{0}$ the middle surface strains, z the distance of an arbitrary point to the middle surface of the porous S-FGM plate.

According to the von Kármán non-linear plate theory, the stain-displacement relations are written as (Amabili 2008)

$$ \left\{ {\varepsilon_{x}^{0} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \varepsilon_{y}^{0} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma_{xy}^{0} } \right\} = \left\{ {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\partial v}{\partial y} + \frac{1}{2}\left( {\frac{\partial w}{\partial y}} \right)^{2} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\partial v}{\partial x} + \quad \frac{\partial u}{\partial y} + \frac{\partial w}{\partial x}\frac{\partial w}{\partial y}} \right\} $$

(13)

$$ \left\{ {\chi_{x} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \chi_{y} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \chi_{xy} } \right\} = \left\{ { - \frac{{\partial^{2} w}}{{\partial x^{2} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{{\partial^{2} w}}{{\partial y^{2} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{{\partial^{2} w}}{\partial x\partial y}} \right\} $$

(14)

The stress–strain relations for a porous S-FGM plate, under plane stress condition, are given by

$$ \left\{ \begin{aligned} \sigma_{x} \hfill \\ \sigma_{y} \hfill \\ \tau_{xy} \hfill \\ \end{aligned} \right\}{ = }\left[ {\begin{array}{*{20}c} {Q_{ 1 1}^{(i)} } & {Q_{ 1 2}^{(i)} } & 0\\ {Q_{ 2 1}^{(i)} } & {Q_{ 2 2}^{(i)} } & 0\\ 0& 0& {Q_{ 6 6}^{(i)} } \\ \end{array} } \right]{\kern 1pt} {\kern 1pt} \left\{ \begin{aligned} \varepsilon_{x} \hfill \\ \varepsilon_{y} \hfill \\ \gamma_{xy} \hfill \\ \end{aligned} \right\} $$

(15)

in which $\sigma_{x}$, $\sigma_{y}$ and $\tau_{xy}$ denote the in-plane stress components; $Q_{jk}^{(i)}$ (i = 1, 2; $j,k = 1,2,6$) are the reduced stiffnesses in the following form for an isotropic material (i = 1 for $0 \le z \le h/2$; i = 2 for $- h/2 \le z \le 0$)

$$ Q_{ 1 1}^{(1)} = Q_{ 2 2}^{(1)} = \frac{{E_{1} \left( z \right)}}{{ [ 1- \nu_{1} \left( z \right)_{{}}^{ 2} ]}}{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (0 \le z \le h/2) $$

(16a)

$$ Q_{ 1 1}^{(2)} = Q_{ 2 2}^{(2)} = \frac{{E_{2} \left( z \right)}}{{ [ 1- \nu_{2} \left( z \right)_{{}}^{ 2} ]}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ( - h/2 \le z \le 0) $$

(16b)

$$ Q_{ 1 2}^{(1)} = Q_{ 2 1}^{(1)} = \frac{{E_{1} \left( z \right) \cdot \nu_{1} \left( z \right)}}{{[ 1- \nu_{1} \left( z \right)_{{}}^{ 2} ]}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (0 \le z \le h/2) $$

(17a)

$$ Q_{ 1 2}^{(2)} = Q_{ 2 1}^{(2)} = \frac{{E_{2} \left( z \right) \cdot \nu_{2} \left( z \right)}}{{[ 1- \nu_{2} \left( z \right)_{{}}^{ 2} ]}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ( - h/2 \le z \le 0) $$

(17b)

$$ Q_{ 6 6}^{(1)} = \frac{{E_{1} \left( z \right)}}{{ 2[ 1+ \nu_{1} \left( z \right)]}}, \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (0 \le z \le h/2) $$

(18a)

$$ Q_{ 6 6}^{(2)} = \frac{{E_{2} \left( z \right)}}{{ 2[ 1+ \nu_{2} \left( z \right)]}}, \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ( - h/2 \le z \le 0) $$

(18b)

The stress and moment resultants of a porous S-FGM plate are stated as

$$ \left\{ {N_{x} ,N_{y} ,N_{xy} } \right\} = \int_{ - h/2}^{h/2} {\left\{ {\sigma_{x} ,\sigma_{y} ,\tau_{xy} } \right\}{\kern 1pt} {\kern 1pt} {\kern 1pt} } {\text{d}}z $$

(19)

$$ \left\{ {M_{x} ,M_{y} ,M_{xy} } \right\} = \int_{ - h/2}^{h/2} {\left\{ {\sigma_{x} ,\sigma_{y} ,\tau_{xy} } \right\}{\kern 1pt} {\kern 1pt} {\kern 1pt} z{\kern 1pt} } {\text{d}}z $$

(20)

Applying Eqs. (10) (11) (12) and (15) in Eqs. (19–20) results in the constitutive relation:

$$ {\mathbf{\rm N}} = {\mathbf{S}} \cdot {\varvec{\upvarepsilon}} $$

(21)

where N and ε are defined, respectively, as

$$ {\mathbf{\rm N}}_{{}}^{\text{T}} {\mathbf{ = }}\left[ {\begin{array}{*{20}c} {N_{x} } & {N_{y} } & {N_{xy} } & {M_{x} } & {M_{y} } & {M_{xy} } \\ \end{array} } \right] $$

(22)

$$ {\varvec{\upvarepsilon}}_{{}}^{\text{T}} {\mathbf{ = }}\left[ {\begin{array}{*{20}c} {\varepsilon_{x}^{ 0} } & {\varepsilon_{y}^{ 0} } & {\gamma_{xy}^{0} } & {\chi_{x} } & {\chi_{y} } & {\chi_{xy} } \\ \end{array} } \right] $$

(23)

and S is given by

$$ {\mathbf{S}} = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{1 2} } & 0 & {B_{11} } & {B_{1 2} } & 0 \\ {A_{ 1 2} } & {A_{ 2 2} } & 0 & {B_{ 1 2} } & {B_{ 2 2} } & 0 \\ 0 & 0 & {A_{ 6 6} } & 0 & 0 & {B_{ 6 6} } \\ {B_{11} } & {B_{1 2} } & 0 & {D_{11} } & {D_{1 2} } & 0 \\ {B_{ 1 2} } & {B_{ 2 2} } & 0 & {D_{ 1 2} } & {D_{ 2 2} } & 0 \\ 0 & 0 & {B_{ 6 6} } & 0 & 0 & {D_{ 6 6} } \\ \end{array} } \right] $$

(24)

in which $A_{jk}$, $B_{jk}$ and $D_{jk}$ ($j,k = 1,2,6$) denote, respectively, the extensional, coupling and bending stiffness coefficients, which are calculated by

$$ \left\{ {A_{jk} ,B_{jk} ,D_{jk} } \right\} = \int_{0}^{h/2} {Q_{jk}^{(1)} \left\{ {1,z,z^{2} } \right\}dz + } \int_{ - h/2}^{0} {Q_{jk}^{(2)} \left\{ {1,z,z^{2} } \right\}dz} $$

(25)

Employing the d’Alembert’s principle, the nonlinear equation of motion describing out-of-plane vibration of a longitudinally moving porous S-FGM plate is derived as

$$ \begin{aligned} \int_{0}^{{\frac{h}{2}}} {\rho_{1} \frac{{{\text{d}}^{2} w}}{{{\text{d}}t^{2} }}} {\text{d}}z + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} \frac{{{\text{d}}^{2} w}}{{{\text{d}}t^{2} }}} {\text{d}}z - \frac{{\partial^{2} M_{x} }}{{\partial x^{2} }} - 2\frac{{\partial^{2} M_{xy} }}{\partial x\partial y} - \frac{{\partial^{2} M_{y} }}{{\partial y^{2} }} - \hfill \\ \quad \left( {N_{x} + N_{0} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} - N_{y} \frac{{\partial^{2} w}}{{\partial y^{2} }} - 2N_{xy} \frac{{\partial^{2} w}}{\partial x\partial y} + c\left( {\frac{\partial w}{\partial t} + V\frac{\partial w}{\partial x}} \right) + F(x,y,t) = 0 \hfill \\ \end{aligned} $$

(26)

where c denotes the damping coefficient, and the total derivative in the first two terms takes the form

$$ \frac{{{\text{d}}^{2} w}}{{{\text{d}}t^{2} }} = \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2V\frac{{\partial^{2} w}}{\partial x\partial t} + V^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} $$

(27)

In Eq. (26), F denotes the lateral excitation and is considered as practical point excitation with the form (Wang 2014; Wang et al. 2010; Wang and Zu 2017d)

$$ F(x,y,t) = F_{0} \cos \left( {\omega t} \right)\delta \left( {x - x_{0} } \right)\delta \left( {y - y_{0} } \right) $$

(28)

where $F_{0}$ is the force amplitude, $\delta$ the Dirac delta function, $\omega$ the circular frequency of the force, $x_{0}$ and $y_{0}$ the in-plane coordinates in x- and y- direction, respectively. In this paper, the excitation is applied at the center of the plate, i.e., $x_{0} { = }a/2$ and $y_{0} { = }b/2$.

Inserting Eqs. (10–12), (15), (19–20) (27) and (28) into Eq. (26) gives the partial differential equation in term of transverse displacement:

$$ \begin{aligned} D_{11} \frac{{\partial^{4} w}}{{\partial x^{4} }} + (2D_{12} + 4D_{66} )\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + D_{22} \frac{{\partial^{4} w}}{{\partial y^{4} }} - N_{0} \frac{{\partial^{2} w}}{{\partial x^{2} }} + c\left( {\frac{\partial w}{\partial t} + V\frac{\partial w}{\partial x}} \right) \hfill \\ \quad + \frac{1}{2}\left[ { - A_{22} \frac{{\partial^{2} w}}{{\partial y^{2} }}\left( {\frac{\partial w}{\partial y}} \right)^{2} - A_{12} \frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial y}} \right)^{2} - A_{12} \frac{{\partial^{2} w}}{{\partial y^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right. \hfill \\ \quad - \left. {A_{11} \left( {\frac{\partial w}{\partial x}} \right)^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} - 2B_{22} \frac{{\partial^{3} w}}{{\partial y^{3} }}\frac{\partial w}{\partial y} - 2B_{11} \frac{\partial w}{\partial x}\frac{{\partial^{3} w}}{{\partial x^{3} }}} \right] \hfill \\ \quad + \frac{1}{2}(4B_{12} - 4B_{66} )\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{1}{2}( - 2B_{12} - 4B_{66} )\frac{\partial w}{\partial y}\frac{{\partial^{3} w}}{{\partial x^{2} \partial y}} \hfill \\ \quad + \frac{1}{2}(4B_{66} - 4B_{12} )\left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} + \frac{1}{2}( - 2B_{12} - 4B_{66} )\frac{\partial w}{\partial x}\frac{{\partial^{3} w}}{{\partial x\partial y^{2} }} \hfill \\ \quad +\int_{0}^{{\frac{h}{2}}} {\rho_{1} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2V\frac{{\partial^{2} w}}{\partial x\partial t} + V^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} {\text{d}}z + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2V\frac{{\partial^{2} w}}{\partial x\partial t} + V^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} {\text{d}}z \hfill \\ \quad - 2A_{66} \frac{\partial w}{\partial x}\frac{\partial w}{\partial y}\frac{{\partial^{2} w}}{\partial x\partial y} + F_{0} \cos \left( {\omega t} \right)\delta \left( {x - x_{0} } \right)\delta \left( {y - y_{0} } \right) = 0{\kern 1pt} {\kern 1pt} \hfill \\ \end{aligned} $$

(29)

in which the normal and shear stresses resulting from in-plane deformation are neglected due to the fact that natural frequencies of in-plane oscillation are much higher than those of out-of-plane oscillation, as shown in (Yang et al. 2011).

3 Solution techniques

It is well known that the low order modes are dominant in vibrations of moving plates. The displacement function containing the lowest two modes that satisfies exactly the simply supported boundary condition is given by

$$ w(x,y,t) = A_{{\bar{m},{\kern 1pt} \bar{n}}} (t){\kern 1pt} \sin \left( {\frac{{\bar{m}\pi x}}{a}} \right){\kern 1pt} \sin \left( {\frac{{\bar{n}\pi y}}{b}} \right) + A_{{\bar{j},{\kern 1pt} \bar{k}}} (t){\kern 1pt} \sin \left( {\frac{{\bar{j}\pi x}}{a}} \right){\kern 1pt} \sin \left( {\frac{{\bar{k}\pi y}}{b}} \right) $$

(30)

where $\bar{m}$ and $\bar{j}$ are the half-wave numbers in the length direction and $\bar{n}$ and $\bar{k}$ are half-wave numbers in the width direction of the plate; $A_{{\bar{m},{\kern 1pt} \bar{n}}} (t){\kern 1pt}$ and $A_{{\bar{j},{\kern 1pt} \bar{k}}} (t){\kern 1pt}$ stand for generalized coordinates of the lowest two modes with respect to time t.

By using the Galerkin method, the governing partial differential equation can be discretized to a set of ordinary differential equations (ODEs), which are obtained by the following calculation

$$ \left\{ {\text{ODEs}} \right\} = \int_{0}^{b} {\int_{0}^{a} {Eq.{\kern 1pt} {\kern 1pt} {\kern 1pt} (29)} }_{{}} F_{g} (x,y)_{{}} {\text{d}}x_{{}} {\text{d}}y $$

(31)

where $F_{g}$ (g = 1, 2) are proper weight functions defined as

$$ F_{g} \left( {x,y} \right) = \left\{ \begin{aligned} \hfill \sin (\bar{m}\pi x/a)\sin (\bar{n}\pi y/b)\text{ }g = 1 \\ \hfill \sin (\bar{j}\pi x/a)\sin (\bar{k}\pi y/b)\text{ }g = 2 \\ \end{aligned} \right.\text{ } $$

(32)

The derivation of Eq. (31) is tedious and has been conducted by employing the Mathematica software (Wolfram 1999). Eventually, one can obtain three non-linear second order ordinary differential equations with respect to generalized coordinates:

$$ \left\{ \begin{aligned} \bar{J}_{1} \ddot{A}_{{\bar{m},{\kern 1pt} \bar{n}}} (t) + \bar{J}_{2} \dot{A}_{{\bar{m},{\kern 1pt} \bar{n}}} (t) + \bar{J}_{3} \dot{A}_{{\bar{j},{\kern 1pt} \bar{k}}} (t) + \bar{J}_{4} A_{{\bar{m},{\kern 1pt} \bar{n}}} (t) + \bar{J}_{5} A_{{\bar{j},{\kern 1pt} \bar{k}}} (t) + \hfill \\ \bar{J}_{6} A_{{\bar{m},{\kern 1pt} \bar{n}}}^{3} (t) + \bar{J}_{7} A_{{\bar{m},{\kern 1pt} \bar{n}}} (t)A_{{\bar{j},{\kern 1pt} \bar{k}}}^{2} (t) + \bar{J}_{8} A_{{\bar{m},{\kern 1pt} \bar{n}}}^{2} (t) + \bar{J}_{9} A_{{\bar{j},{\kern 1pt} \bar{k}}}^{2} (t) + \bar{J}_{10} \cos (\omega t) = 0 \hfill \\ \hfill \\ \bar{K}_{1} \ddot{A}_{{\bar{j},{\kern 1pt} \bar{k}}} (t) + \bar{K}_{2} \dot{A}_{{\bar{m},{\kern 1pt} \bar{n}}} (t) + \bar{K}_{3} \dot{A}_{{\bar{j},{\kern 1pt} \bar{k}}} (t) + \bar{K}_{4} A_{{\bar{m},{\kern 1pt} \bar{n}}} (t) + \hfill \\ \bar{K}_{5} A_{{\bar{j},{\kern 1pt} \bar{k}}} (t) + \bar{K}_{6} A_{{\bar{j},{\kern 1pt} \bar{k}}}^{3} (t) + \bar{K}_{7} A_{{\bar{m},{\kern 1pt} \bar{n}}}^{2} (t)A_{{\bar{j},{\kern 1pt} \bar{k}}} (t) + \bar{K}_{8} A_{{\bar{m},{\kern 1pt} \bar{n}}} (t)A_{{\bar{j},{\kern 1pt} \bar{k}}}^{{}} (t) = 0 \hfill \\ \end{aligned} \right. $$

(33)

in which the over-dot denotes derivative with respect to t; $\bar{J}_{i}$ and $\bar{K}_{j}$ ($i = 1,2, \ldots ,10$, $j = 1,2, \ldots ,8$) are the integral coefficients related to the geometrical and material properties of the system. In Appendix, their analytic formulations are presented.

Let us introduce the following non-dimensional variables to simplify the calculation:

$$ \tau { = }\omega_{{\bar{m},{\kern 1pt} \bar{n}}} t,\quad \varOmega { = }\omega /\omega_{{\bar{m},{\kern 1pt} \bar{n}}} ,\quad q_{1} (\tau ){ = }A_{{\bar{m},{\kern 1pt} \bar{n}}} (t)/h,\quad q_{2} (\tau ){ = }A_{{\bar{j},{\kern 1pt} \bar{k}}} (t)/h $$

(34)

in which $\omega_{{\bar{m},{\kern 1pt} \bar{n}}}$ defines the lowest natural frequency of the longitudinally moving porous S-FGM plate.

Applying Eq. (34) in Eq. (33) leads to the following non-dimensional ordinary differential equations

$$ \left\{ {\begin{array}{*{20}l} J_{1} \ddot{q}_{1} (\tau ) + J_{2} \dot{q}_{1} (\tau ) + J_{3} \dot{q}_{2} (\tau ) + J_{4} q_{1} (\tau ) + J_{5} q_{2} (\tau ) + J_{6} q_{1}^{3} (\tau ) + \hfill \\ \quad \quad J_{7} q_{1} (\tau )q_{2}^{2} (\tau ) + J_{8} q_{1}^{2} (\tau ) + J_{9} q_{2}^{2} (\tau ) + J_{10} \cos (\varOmega \tau ) = 0 \hfill \\ \hfill \\ K_{1} \ddot{q}_{2} (\tau ) + K_{2} \dot{q}_{1} (\tau ) + K_{3} \dot{q}_{2} (\tau ) + K_{4} q_{1} (\tau ) + K_{5} q_{2} (\tau ) + \hfill \\ \quad \quad K_{6} q_{2}^{3} (\tau ) + K_{7} q_{1}^{2} (\tau )q_{2} (\tau ) + K_{8} q_{1}^{{}} (\tau )q_{2} (\tau ) = 0 \hfill \\ \hfill \\ \end{array} } \right. $$

(35)

where $J_{i}$ and $K_{j}$ ($i = 1,2, \ldots ,10$, $j = 1,2, \ldots ,8$) are new integral coefficients resulting from the above dimensionless transformation.

By using the method of harmonic balance, we express the solutions of Eq. (35) as the following truncated Fourier series forms

$$ q_{1} (\tau ) = A_{0} + \sum\limits_{n = 1}^{H} {[A_{2n - 1} { \cos }(n\varOmega \tau ) + A_{2n} { \sin }(n\varOmega \tau )]} $$

(36)

$$ q_{2} (\tau ) = B_{0} + \sum\limits_{n = 1}^{H} {[B_{2n - 1} { \cos }(n\varOmega \tau ) + B_{2n} { \sin }(n\varOmega \tau )]} $$

(37)

in which $A_{n}$ and $B_{n}$ ($n = 0,1, \ldots ,H$) define the Fourier coefficients, H the total of harmonics maintained in the truncated Fourier series.

Substituting Eqs. (36–37) into Eq. (35) and then gathering each harmonic components including $\cos \left( {n\varOmega \tau } \right)$ and $\sin \left( {n\varOmega \tau } \right)$ ($n = 0,1, \ldots ,H$) in the resulting equations, one may obtain $4H + 2$ algebraic equations related to Fourier coefficients $A_{n}$ and $B_{n}$ ($n = 0,1, \ldots ,H$). These equations are expressed for H = 1 as

$$ {\text{Fun}}_{k} \left( {A_{i} ,B_{i} ,\varOmega } \right) = 0\quad k = 0,1, \ldots ,6;\quad i = 0,1,2 $$

(38)

where Fun _k stand for algebraic expressions associated to unknowns $A_{i}$, $B_{i}$ ($i = 0,1,2$) and $\varOmega$; these expressions are quite cumbersome and omitted here. From Eq. (39), $A_{i}$ and $B_{i}$ can be calculated for a given $\varOmega$; thus one can obtain solutions of $q_{1}$ and $q_{2}$ with the aid of Eqs. (36–37).

4 Stability of steady state response

For the purpose of distinguishing the stable and unstable vibration responses in the analytical solutions, let us introduce the perturbation terms as follows

$$ \left\{ \begin{array}{l} q_{1} \hfill \\ q_{2} \hfill \\ \end{array} \right\} = \left\{ \begin{array}{l} A_{0} + \Delta A_{0} (\tau ) + [A_{1} + \Delta A_{1} (\tau )]{ \cos }(\varOmega \tau ) + [A_{2} + \Delta A_{2} (\tau )]{ \sin }(\varOmega \tau ) \hfill \\ B_{0} + \Delta B_{0} (\tau ) + [B_{1} + \Delta B_{1} (\tau )]{ \cos }(\varOmega \tau ) + [B_{2} + \Delta B_{2} (\tau )]{ \sin }(\varOmega \tau ) \hfill \\ \end{array} \right\} $$

(39)

where $\Delta A_{i} (\tau )$ and $\Delta B_{i} (\tau )$ $(i = 0,1,2)$ denote the perturbance of steady-state response.

Applying Eq. (39) in (35) and then gathering the harmonic components containing trigonometric functions $\cos (n\varOmega \tau )$ and $\sin (n\varOmega \tau )$ $(n = 0,1)$, one may get a set of perturbation equations with respect to perturbation terms. These equations are stated as:

$$ {\dot{\mathbf{X}}} = {\varvec{\Psi}}({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau ) $$

(40)

where

$$ {\mathbf{X}} = \left[ {\begin{array}{*{20}c} {\Delta A_{0} (\tau )} & {\Delta \dot{A}_{0} (\tau )} & {\Delta B_{0} (\tau )} & {\Delta \dot{B}_{0} (\tau )} & \cdots & {\Delta A_{k} (\tau )} & {\Delta \dot{A}_{k} (\tau )} & {\Delta B_{k} (\tau )} & {\Delta \dot{B}_{k} (\tau )} \\ \end{array} } \right]^{\text{T}} \quad (k = 0,1,2) $$

(41)

$$ {\mathbf{Y}} = \left[ {\begin{array}{*{20}c} {A_{0} } & {B_{0} } & {A_{1} } & {B_{1} } & {A_{2} } & {B_{2} } \\ \end{array} } \right]^{\text{T}} $$

(42)

$$ {\varvec{\Psi}} = \left[ {\begin{array}{*{20}c} {\varPsi_{1} \left( {{\mathbf{X}},{\mathbf{Y}},\tau } \right)} & {\varPsi_{2} \left( {{\mathbf{X}},{\mathbf{Y}},\tau } \right)} & \cdots & {\varPsi_{j} \left( {{\mathbf{X}},{\mathbf{Y}},\tau } \right)} \\ \end{array} } \right]^{T} \quad \left( {J = 1, \ldots ,12} \right) $$

(43)

The performance of the Taylor series expansion for ${\varvec{\Psi}}$ at X = 0 yields

$$ {\dot{\mathbf{X}}} = {\mathbf{PX}} $$

(44)

where P stands for the Jacobian matrix which is given by

$$ {\mathbf{P}} = \left( {\begin{array}{*{20}c} {P_{11} } & {P_{12} } & \ldots & {P_{1J} } \\ {P_{21} } & {P_{22} } & \ldots & {P_{2J} } \\ \vdots & \vdots & \ddots & \vdots \\ {P_{I1} } & {P_{I2} } & \ldots & {P_{IJ} } \\ \end{array} } \right)_{12 \times 12} $$

(45)

where I = J=12, and the inside elements are ($i = 1,2, \ldots ,I$):

$$ \begin{aligned} P_{i1} = \left. {\frac{{\partial \varPsi_{i} ({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau )}}{{\partial \Delta A_{0} (\tau )}}} \right|_{{{\mathbf{X}}{ = }0}} P_{i2} = \left. {\frac{{\partial \varPsi_{i} ({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau )}}{{\partial \Delta \dot{A}_{0} (\tau )}}} \right|_{{{\mathbf{X}}{ = }0}} P_{i3} = \left. {\frac{{\partial \varPsi_{i} ({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau )}}{{\partial \Delta B_{0} (\tau )}}} \right|_{{{\mathbf{X}}{ = }0}} \hfill \\ P_{i4} = \left. {\frac{{\partial \varPsi_{i} ({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau )}}{{\partial \Delta \dot{B}_{0} (\tau )}}} \right|_{{{\mathbf{X}}{ = }0}} P_{i5} = \left. {\frac{{\partial \varPsi_{i} ({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau )}}{{\partial \Delta A_{1} (\tau )}}} \right|_{{{\mathbf{X}}{ = }0}} P_{i6} = \left. {\frac{{\partial \varPsi_{i} ({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau )}}{{\partial \Delta \dot{A}_{1} (\tau )}}} \right|_{{{\mathbf{X}}{ = }0}} \hfill \\ P_{i7} = \left. {\frac{{\partial \varPsi_{i} ({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau )}}{{\partial \Delta B_{1} (\tau )}}} \right|_{{{\mathbf{X}}{ = }0}} P_{i8} = \left. {\frac{{\partial \varPsi_{i} ({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau )}}{{\partial \Delta \dot{B}_{1} (\tau )}}} \right|_{{{\mathbf{X}}{ = }0}} P_{i9} = \left. {\frac{{\partial \varPsi_{i} ({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau )}}{{\partial \Delta A_{2} (\tau )}}} \right|_{{{\mathbf{X}}{ = }0}} \hfill \\ P_{i10} = \left. {\frac{{\partial \varPsi_{i} ({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau )}}{{\partial \Delta \dot{A}_{2} (\tau )}}} \right|_{{{\mathbf{X}}{ = }0}} P_{i11} = \left. {\frac{{\partial \varPsi_{i} ({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau )}}{{\partial \Delta B_{2} (\tau )}}} \right|_{{{\mathbf{X}}{ = }0}} P_{i12} = \left. {\frac{{\partial \varPsi_{i} ({\mathbf{X}}\text{,}{\mathbf{Y}}\text{,}\tau )}}{{\partial \Delta \dot{B}_{2} (\tau )}}} \right|_{{{\mathbf{X}}{ = }0}} \hfill \\ \end{aligned} $$

(46)

Stable responses require that all the eigenvalues of Eq. (45) possess negative real part. By contrast, the existence of one or more positive real part in eigenvalues will correspond to the instable responses.

5 Results and discussion

For the sake of validating the analysis, we first consider a simply-supported rectangular homogeneous plate with a = 0.515 m, b = 0.184 m, h = 0.0003 m, $E = 69 \times 10^{9} \, {\text{Pa}}$, $\rho = 2700\;{\text{kg}}/{\text{m}}^{3}$ and $\nu = 0.33$, which has been studied by Amabili (2004). The natural frequencies of the plate can be obtained by neglecting the nonlinear, damping and external excitation terms in Eq. (33). The natural frequencies obtained by means of the present method are compared with those given in (Amabili 2004), as seen in Table 1, where m and n are the half-wave numbers in the length and width direction. It is clear that good agreement between the present results and those in the literature has been achieved.

Table 1 Comparison of natural frequencies of a simply-supported rectangular homogeneous plate (n = 1) (in Hz)

To further validate the present analysis, a simply-supported FGM rectangular plate composed of SUS304 and Si₃N₄ is considered here, which has been investigated by Alijani et al. (2011). This plate has the following geometry: length a = 0.2 m, width b = 0.2 m and thickness h = 0.025 m. The Poisson ratio is considered as a constant $\mu \;{ = }\;0.28$. The frequency parameter $\omega^* = \omega a^{2} /h\sqrt {\rho_{m} (1 - \mu^{2} )/E_{m} }$ of the FGM plate is obtained and the results are listed together with those calculated by using Kirchhoff plate theory (Alijani et al. 2011), as can be seen in Table 2. Also, very good agreement between the present results and those in the literature is achieved.

Table 2 Comparison of frequency parameter $\omega^{*} = \omega a^{2} /h\sqrt {\rho_{m} (1 - \mu^{2} )/E_{m} }$ for a SUS304/Si₃N₄ FGM plate at room temperature

Next, the study is related to a simply-supported longitudinally moving Nickel/Alumina S-FGM plate with porosities, whose geometrical parameters are: length a = 0.4 m, width b = 0.1 m and thickness h = 0.001 m. It is obvious that this is a thin plate due to the width-to-thickness ratio being b/h = 100.

Table 3 lists the first two natural frequencies of the moving Porosity-I S-FGM plate for various power-low indices and porosity volume fractions, where V = 10 m/s and N ₀ = 1000 N/m. One may find that the natural frequencies decrease as the porosity volume fraction increases for small power-law index. However, this trend is inverted under relatively large power-law index, for example N = 6, as can be seen in the table. Besides, it is noted that at a given porosity volume fraction, the natural frequencies of the system reduce with the increase of the power-law index.

Table 3 Natural frequencies of simply-supported moving Porosity-I S-FGM plate (in rad/s)

Depicted in Fig. 3 is the variation of the first two natural frequencies of the moving Porosity-I S-FGM plate along with speed under different constituent volume fractions, where α = 0.1 and N ₀ = 1000 N/m. Based on this figure, it is found that as the moving speed increases, the natural frequencies of the plate decrease gradually. Moreover, the impact of power-law index gets great on natural frequencies when its value is relatively large. For instance, the natural frequencies change more when N alters from 5 to 6, as compared with N altering from 0.3 to 5.

Fig. 3

Variation of natural frequencies of the moving Porosity-I S-FGM plate under different constituent volume fractions: a the fundamental natural circular frequency; b the second-order natural circular frequency

The frequency-response relationships of the moving Porosity-I S-FGM plate are shown in Fig. 4, where V = 10 m/s, α = 0.1, N ₀ = 1000 N/m, F ₀ = 5 N, $c = 30\;{\text{Ns}}/{\text{m}}^{3}$ and N = 5. The figure gives the maximum amplitudes of each generalized coordinates during the vibration period. The steady-state responses are examined for their stability and the stable and unstable responses are described by solid and dashed lines, respectively. From the figure, it can be found that both the first and second modes are different from zero in the vicinity of the lowest natural frequency. This indicates that the two modes are both excited near the fundamental mode. Additionally, different from the general frequency response, the present frequency-response curves possess two peaks for each generalized coordinate. That is because the additional peak comes from the nonlinear modal interaction between the two modes. On the frequency-response curves of each generalized coordinate, four stable branches are detected by the stability analysis; they are denoted by S1, S2, S3 and S4, as seen in the figure. Furthermore, one may find that the frequency-response relationships exhibit hardening-spring characteristics for the longitudinally moving Porosity-I S-FGM plate.

Fig. 4

Frequency-response curves of the moving Porosity-I S-FGM plate: a maximum of $q_{1} (\tau )$; b maximum of $q_{2} (\tau )$

In order to verify the analytical method developed in the present study, numerical solutions are performed by using the adaptive step-size fourth-order Runge–Kutta method. The numerical solutions are obtained via direct integration of ordinary differential Eqs. (35), where the initial condition is assumed as $q_{1} (0)\;{ = }\;q_{2} (0)\;{ = }\;\dot{q}_{1} (0)\;{ = }\;\dot{q}_{2} (0)\;{ = }\;0$. In Fig. 5, the results from the approximate analytical method and those from the Runge–Kutta method are presented together. It is seen that the agreement between numerical and approximate analytical solutions is quite good, demonstrating the method developed in the present study is valid and accurate.

Fig. 5

Comparison of the harmonic balance method and Runge–Kutta method: a maximum of $q_{1} (\tau )$; b maximum of $q_{2} (\tau )$

Figures 6 and 7 show the frequency-response relationships of the moving Porosity-I S-FGM plate for the speed V = 3 m/s and V = 30 m/s, respectively. The other parameters are kept the same as those in Fig. 4. It should be noted that these curves also contain stable and unstable solutions. However, our concentration here is on the general characteristics thus the stability is not shown for brevity. From Fig. 4 (V = 10 m/s), Figs. 6 and 7, it is found the moving speed affects the response characteristics dramatically. When the speed is slow, as seen in Fig. 6 for V = 3 m/s, the two modes are uncoupled thus there exists only one peak for each mode. With the increase of moving speed, the nonlinear mode interaction phenomenon appears between the two modes and thus another peak emerges for each mode. Moreover, the second peak of each generalized coordinate shrinks when the speed increases from V = 10 m/s (Fig. 4) to 30 m/s (Fig. 7); it is interesting that for the generalized coordinate q ₂, the smaller peak moves from the front to the back of the larger peak, as seen in Figs. 4 and 7.

Fig. 6

Frequency-response curves of the moving Porosity-I S-FGM plate for V = 3 m/s: a maximum of $q_{1} (\tau )$; b maximum of $q_{2} (\tau )$

Fig. 7

Frequency-response curves of the moving Porosity-I S-FGM plate for V = 30 m/s: a maximum of $q_{1} (\tau )$; b maximum of $q_{2} (\tau )$

Increasing the in-plane pretension from N ₀ = 1000 N/m (Fig. 4) to N ₀ = 10,000 N/m and then to N ₀ = 100,000 N/m, Figs. 8 and 9 are generated; the other system parameters are the same as those in Fig. 4. Comparing Figs. 4, 8 and 9 reveals that the nonlinear mode interaction can be uncoupled by increase the in-plane pretension. It is seen the additional peak nearly vanishes when N ₀ = 10,000 N/m and N ₀ = 100,000 N/m in Figs. 8 and 9; only very small peak occurs additionally for the generalized coordinate q ₂, showing the effect of nonlinear mode interaction is insignificant when the in-plane pretension is at a large value.

Fig. 8

Frequency-response curves of the moving Porosity-I S-FGM plate for P = 10000 N/m: a maximum of $q_{1} (\tau )$; b maximum of $q_{2} (\tau )$

Fig. 9

Frequency-response curves of the moving Porosity-I S-FGM plate for P = 100000 N/m: a maximum of $q_{1} (\tau )$; b maximum of $q_{2} (\tau )$

In Fig. 10, the effect of porosity is studied on frequency-response relationships of the moving Porosity-I S-FGM plate; three porosity volume fractions are considered here, i.e., α = 0 (perfect S-FGM), α = 0.1 and α = 0.2. The parameters in the figure are V = 10 m/s, N ₀ = 1000 N/m, F ₀ = 5 N, $c = 30\;{\text{Ns}}/{\text{m}}^{3}$ and N = 5. From the figure, an obvious trend is detected that as the porosity volume fraction increases, the response amplitudes of each generalized coordinate increase too. The perfect S-FGM plate has the lowest response amplitude compared with porous ones. Besides, the frequency-response curves move slightly to the low frequency region with the raise of porosity volume fraction.

Fig. 10

Frequency-response curves of the moving Porosity-I S-FGM plate with different porosity volume fractions: a maximum of $q_{1} (\tau )$; b maximum of $q_{2} (\tau )$

Figure 11 shows the effect of constituent volume fraction on the frequency-response relationships of the moving Porosity-I S-FGM plate. Three power-law indexes are considered here, i.e., N = 0.3, N = 3 and N = 5. The other parameters are set as V = 10 m/s, N ₀ = 1000 N/m, F ₀ = 5 N, $c = 30\;{\text{Ns}}/{\text{m}}^{3}$ and α = 0.1. It is clear that the power-law index affects the dynamic response characteristics of the moving porous S-FGM plate. With the increasing of power-law index, the resonant response amplitudes of each mode first decrease and then increase. Additionally, one can find an obvious phenomenon that the resonance domain of the system moves to the low frequency region when the power-law index increases to N = 5. This is because the larger power-law index leads to the lower natural frequency of the system, as discussed before in Fig. 3.

Fig. 11

Frequency-response curves of the Porosity-I S-FGM plate with different constitute volume fractions: a maximum of $q_{1} (\tau )$; b maximum of $q_{2} (\tau )$

Figure 12 gives the frequency-response relationships of the moving Porosity-II S-FGM plate. Three porosity volume fractions, i.e., α = 0, α = 0.1 and α = 0.2, are compared. The selected parameters are the same as those in Fig. 10 for comparison purpose. For the Porosity-II S-FGM plate, the frequency response relationships also show hardening spring characteristics, and there exists two peaks for each generalized coordinate. These characteristics are the same as those for Porosity-I plate. However, the effect of porosity volume fraction is different on Porosity-I and Porosity-II plate. In the Porosity-II plate, the resonance domain moves to the higher frequency region and the resonant amplitudes decrease when the porosity volume fraction rises, as seen in Fig. 12. This tendency is totally opposite compared with that in Porosity-I plate (Fig. 10), showing the two types of porosity distribution have different influences on the resonance domain and resonant amplitude of the moving S-FGM plate.

Fig. 12

Frequency-response curves of the moving Porosity-II S-FGM plate with different porosity volume fractions: a maximum of $q_{1} (\tau )$; b maximum of $q_{2} (\tau )$

6 Concluding remarks

Vibration characteristics are investigated on longitudinal moving S-FGM plates with porosities. Two types of porosity distribution, i.e., even and uneven distributions, are taken into account. In accordance with the sigmoid distribution rule, the material properties of porous S-FGM plates vary smoothly along the plate thickness direction. Based on the d’Alembert’s principle, the nonlinear governing equation of moving porous S-FGM plates is derived incorporating the von Kármán non-linear geometrical relations. The governing equation is discretized via the Galerkin method and then solved by using the method of harmonic balance. Analytical solutions are verified with the aid of the adaptive step-size fourth-order Runge–Kutta method. Additionally, the stability of the steady-state response is highlighted. For the longitudinally moving porous S-FGM plate, the frequency-response relationships exhibit hardening-spring characteristics. More than one resonance peak can happen for the first two modes due to the nonlinear mode interaction. Additionally, both moving speed and in-plane pretention affect the vibration characteristics and they can change the mode interaction situation of the system. Moreover, the large-deflection forced response of the structure can be influenced by the constituent volume fraction. It is further observed that the Porosity-I and Porosity-II have different effects on the resonance domain and resonant amplitude of the moving S-FGM plate.

Appendix

The coefficient formulations in Eq. (33) are as follows

$$ \begin{aligned} \bar{J}_{1} = 1 \hfill \\ \bar{J}_{2} = \frac{c}{{\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{-\frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} }} \hfill \\ \bar{J}_{3} = - \frac{16V}{3a} \hfill \\ \bar{J}_{4} = \frac{{\pi^{4} D_{11} }}{{a^{4} \left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} + \frac{{2\pi^{4} D_{12} }}{{a^{2} b^{2} \left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{-\frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} + \hfill \\ \quad \quad {\kern 1pt} \frac{{4\pi^{4} D_{66} }}{{a^{2} b^{2} \left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} + \frac{{\pi^{2} N_{0} }}{{a^{2} \left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{-\frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} \hfill \\ {\kern 1pt} \quad \quad - \frac{{\pi^{2} V^{2} }}{{a^{2} }} + \frac{{\pi^{4} D_{22} }}{{b^{4} \left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{-\frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} \hfill \\ \bar{J}_{5} = - \frac{8cV}{{3a\left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{-\frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} \hfill \\ \bar{J}_{6} = {{\left( {\frac{{3\pi^{4} A_{11} }}{{32a^{4} }} + \frac{{3\pi^{4} A_{12} }}{{16a^{2} b^{2} }} - \frac{{\pi^{4} A_{66} }}{{8a^{2} b^{2} }} + \frac{{3\pi^{4} A_{22} }}{{32b^{4} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{3\pi^{4} A_{11} }}{{32a^{4} }} + \frac{{3\pi^{4} A_{12} }}{{16a^{2} b^{2} }} - \frac{{\pi^{4} A_{66} }}{{8a^{2} b^{2} }} + \frac{{3\pi^{4} A_{22} }}{{32b^{4} }}} \right)} {\left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}}} \right. \kern-0pt} {\left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} \hfill \\ \bar{J}_{7} = {{\left( {\frac{{3\pi^{4} A_{11} }}{{4a^{4} }} + \frac{{21\pi^{4} A_{12} }}{{16a^{2} b^{2} }} - \frac{{\pi^{4} A_{66} }}{{a^{2} b^{2} }} + \frac{{3\pi^{4} A_{22} }}{{16b^{4} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{3\pi^{4} A_{11} }}{{4a^{4} }} + \frac{{21\pi^{4} A_{12} }}{{16a^{2} b^{2} }} - \frac{{\pi^{4} A_{66} }}{{a^{2} b^{2} }} + \frac{{3\pi^{4} A_{22} }}{{16b^{4} }}} \right)} {\left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}}} \right. \kern-0pt} {\left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} \hfill \\ \bar{J}_{8} = {{\left( {\frac{{32\pi^{2} B_{11} }}{{9a^{4} }} + \frac{{160\pi^{2} B_{12} }}{{9a^{2} b^{2} }} + \frac{{32\pi^{2} B_{66} }}{{9a^{2} b^{2} }} + \frac{{32\pi^{2} B_{22} }}{{9b^{4} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{32\pi^{2} B_{11} }}{{9a^{4} }} + \frac{{160\pi^{2} B_{12} }}{{9a^{2} b^{2} }} + \frac{{32\pi^{2} B_{66} }}{{9a^{2} b^{2} }} + \frac{{32\pi^{2} B_{22} }}{{9b^{4} }}} \right)} {\left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{-\frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}}} \right. \kern-0pt} {\left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{-\frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} \hfill \\ \bar{J}_{9} = {{\left( {\frac{{3584\pi^{2} B_{11} }}{{45a^{4} }} + \frac{{512\pi^{2} B_{12} }}{{9a^{2} b^{2} }} + \frac{{1664\pi^{2} B_{66} }}{{45a^{2} b^{2} }} + \frac{{128\pi^{2} B_{22} }}{{45b^{4} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{3584\pi^{2} B_{11} }}{{45a^{4} }} + \frac{{512\pi^{2} B_{12} }}{{9a^{2} b^{2} }} + \frac{{1664\pi^{2} B_{66} }}{{45a^{2} b^{2} }} + \frac{{128\pi^{2} B_{22} }}{{45b^{4} }}} \right)} {\left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{-\frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}}} \right. \kern-0pt} {\left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{-\frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} \hfill \\ \bar{J}_{10} = \frac{{4F_{0} }}{{ab\left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{-\frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}}\sin \left( {\frac{{\pi x_{0} }}{a}} \right)\sin \left( {\frac{{\pi y_{0} }}{b}} \right) \hfill \\ \end{aligned} $$

(47)

$$ \begin{aligned} \bar{K}_{1} { = }1 \hfill \\ \bar{K}_{2} { = }\frac{16V}{3a} \hfill \\ \bar{K}_{3} { = }\frac{c}{{\left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} \hfill \\ \bar{K}_{4} { = }\frac{8cV}{{3a\left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} \hfill \\ \bar{K}_{5} { = }\frac{1}{{a^{4} b^{4} \left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}}(\pi^{4} a^{4} D_{22} - 4\pi^{2} a^{2} b^{4} V^{2} \left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right) \hfill \\ {\kern 1pt} \quad \quad + 4\pi^{2} a^{2} b^{4} N_{0}^{{}} + 8\pi^{4} a^{2} b^{2} D_{12} + 16\pi^{4} a^{2} b^{2} D_{66} + 16\pi^{4} b^{4} D_{11} ) \hfill \\ \bar{K}_{6} { = }\frac{{\pi^{4} (3a^{4} A_{22} + 24a^{2} A_{12} b^{2} - 16a^{2} A_{66} b^{2} + 48A_{11} b^{4} )}}{{32a^{4} b^{4} \left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} \hfill \\ \bar{K}_{7} { = }\frac{{\pi^{4} (3a^{4} A_{22} + 9a^{2} A_{12} b^{2} - 4a^{2} A_{66} b^{2} + 12A_{11} b^{4} )}}{{16a^{4} b^{4} \left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} \hfill \\ \bar{K}_{8} { = }\frac{{128\pi^{2} (2a^{4} B_{22} + 25a^{2} b^{2} B_{12} - 4a^{2} b^{2} B_{66} + 5b^{4} B_{11} )}}{{45a^{4} b^{4} \left( {\int_{0}^{{\frac{h}{2}}} {\rho_{1} (z){\text{d}}z} + \int_{{ - \frac{h}{2}}}^{0} {\rho_{2} (z){\text{d}}z} } \right)}} \hfill \\ \end{aligned} $$

(48)