Stress analysis of steel beams strengthened with a bonded hygrothermal aged composite plate

Abstract

In this paper, the problem of interfacial stresses in steel beams strengthened with bonded hygrothermal aged composite laminates is analyzed using linear elastic theory. The analysis is based on the deformation compatibility approach developed by Tounsi (Int. J. Solids Struct. 43:4154–4174, 2006) where both the shear and normal stresses are assumed to be invariant across the adhesive layer thickness. The adopted model takes into account the adherend shear deformations by assuming a linear shear stress through the depth of the steel beam. This solution is intended for application to beams made of all kinds of materials bonded with a thin composite plate. For steel I-beam section, a geometrical coefficient ξ is determined to show the effect of the adherend shear deformations. This research is helpful for the understanding on mechanical behaviour of the interface and design of such structures.

1 Introduction

Advanced composite materials have been used successfully for repairing metallic aircraft structures for a number of years (Baker 1984; Megueni et al. 2003, 2007). In Civil Engineering, composite plates have mainly been used to rehabilitate concrete structure, although the strengthening of metallic structures using FRP is gaining significant interesting in recent years. The main advantages of FRP are their high strength-to-weight ratio and their excellent resistance against corrosion and chemical attacks. An important topic arising in the study of plated steel beams is the evaluation of interactions at steel–FRP interface. These interactions, in fact, permit the transmission of stresses from the core to the plate; if they go over a limit value the premature failure of the strengthened beam can occur.

The determination of interfacial stresses has been researched for the last decade for steel or concrete beams bonded with either steel or advanced composite materials. In particular, several closed-form analytical solutions have been developed (Vilnay 1988; Roberts 1989; Roberts and Haji-Kazemi 1989; Stratford and Cadei 2006; Malek et al. 1998; Smith and Teng 2001; Benyoucef et al. 2006; Tounsi 2006). All these solutions are for linear elastic materials and employ the same key assumption that the adhesive is subject to normal and shear stresses that are constant across the thickness of the adhesive layer. It is this key assumption that enables relatively simple closed-form solutions to be obtained. In the existing solutions, two different approaches have been employed. Roberts (1989) and Roberts and Haji-Kazemi (1989) used a staged analysis approach, while Vilnay (1988), Stratford and Cadei (2006), Malek et al. (1998) and Smith and Teng (2001) considered directly deformation compatibility conditions. Recently, Tounsi and his co-workers (Benyoucef et al. 2006; Tounsi 2006) developed theoretical solutions for interfacial stresses in concrete beams strengthened with FRP plate based also on deformation compatibility conditions. Benyoucef et al. (2006) present an alternative theoretical interfacial stress analysis, where, the FRP plate fibre orientation is considered and the flexural rigidity of the composite plate is estimated using lamination theory. Tounsi (2006) presented a new theoretical solution in which the adherend shear deformations have been included.

In this paper, we present an alternative theoretical interfacial analysis for simply supported steel beams bonded with a thin hygrothermal aged FRP plate. It is well known that during the operational life, the variation of temperature and moisture reduces the elastic moduli and degrades the strength of composite material (Megueni et al. 2003, 2007; Shen and Springer 1981; Adams and Miller 1977; Bowles and Tompkins 1989; Shen 2001; Tounsi and Amara 2005; Amara et al. 2005; Tounsi et al. 2005). The material properties of the bonded composite plate are assumed to be functions of temperature and moisture. This effect is studied here, due to technological considerations. For example, when we use these plates to reinforce beams, they can be already exposed to the environmental conditions. Thus, these plates are aged with time and the mechanical properties will be reduced. In this study, we aim to show if the reduction in stiffness due to hygrothermal ageing has an effect on the interfacial stresses. Both ambient temperature and moisture are assumed to have a uniform distribution. The plate is fully saturated such that the variation of temperature and moisture are independent of time and position. The adopted model describes better the actual response of the FRP-steel hybrid beam and permits the evaluation of the interfacial stresses, the knowledge of which is very important in the design of such structures.

2 The method of solution

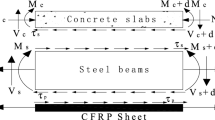
A differential section dx, can be cut out from the FRP strengthened steel beam (Fig. 1), as shown in Fig. 2. The composite beam is made from three materials: steel, adhesive layer and FRP reinforcement. In the present analysis, linear elastic behaviour is regarded to be for all the materials; the adhesive is assumed to only play a role in transferring the stresses from the steel to the FRP reinforcement and the stresses in the adhesive layer do not change through the direction of the thickness.

Fig. 1

Simply supported beam strengthened with bonded composite plate

Fig. 2

Forces in infinitesimal element of a soffit-plated beam

2.1 Basic equation of elasticity

The strain ε ₁(x) in the steel beam near adhesive interface can be expressed as

$$ \varepsilon_{1} \left( x \right) = \frac{{{\text{d}}u_{1} \left( x \right)}}{{{\text{d}}x}} = \varepsilon_{1}^{M} \left( x \right) + \varepsilon_{1}^{N} \left( x \right) $$

(1)

where u ₁ (x) is the longitudinal displacement at the base of steel beam. $\varepsilon_{1}^{M} \left( x \right)$ is the strain induced by the bending moment at the adherend 1 and it is written as follow:

$$ \varepsilon_{1}^{M} \left( x \right) = \frac{{t_{1} }}{{2E_{1} I_{1} }}M_{1} \left( x \right) $$

(2)

where M ₁(x), is the bending moment applied in the steel beam at its mid-height; E ₁ is Young’s moduli of the steel; I ₁ is the second moment area; t ₁ is the depth of steel beam. $\varepsilon_{1}^{N} \left( x \right)$ is the unknown longitudinal strain of the steel beam, at the adhesive interface and it is due to the longitudinal forces. This strain is given as follow:

$$ \varepsilon_{1}^{N} \left( x \right) = \frac{{{\text{d}}u_{1}^{N} (x)}}{{{\text{d}}x}} $$

(3)

where $u_{ 1}^{N}$ represents the longitudinal force-induced adhesive displacement at the interface between the steel beam and the adhesive.

To determine the unknown longitudinal strain $\varepsilon_{1}^{N} \left( x \right)$, shear deformation of the steel beam is incorporated in this analysis. It is reasonable to assume that the shear stresses, which develop in the adhesive, are continuous across the adhesive–adherend interface. In addition, equilibrium requires the shear stress to be zero at the free surface. Using the same methodology developed by Tounsi (2006), this effect is taken into account. The importance of including shear-lag effect of the adherents was also shown by Tsai et al. (1998). In the present analysis, shear deformations of the FRP plate is ignored. However, a linear shear stress through the depth of the steel beam is assumed.

$$ \sigma_{xy\left( 1 \right)} = \frac{\tau \left( x \right)}{{t_{1} }}y $$

(4)

Equation 4 is based on zero shear stresses at the top surface of the upper adherend (i.e. at y = 0) and σ _xy(1) = τ _a at y = t ₁. Then with a linear material constitutive relationship the adherend shear strain γ ₁for the adherend 1 (steel beam) is written as:

$$ \gamma_{xy\left( 1 \right)} = \gamma_{1} = \frac{{\tau_{a} }}{{G_{1} t_{1} }}y $$

(5)

G ₁ is the transverse shear moduli of the adherend 1 (steel beam), and τ _a  = τ(x).

The longitudinal displacement functions $U_{1}^{N}$ for the upper adherend, due to the longitudinal forces, is given by

$$ U_{1}^{N} \left( y \right) = U_{1}^{N} \left( 0 \right) + \int\limits_{0}^{y} {\gamma_{1} \left( y \right){\text{d}}y} = U_{1}^{N} \left( 0 \right) + \frac{{\tau_{a} }}{{2G_{1} t_{1} }}y^{2} $$

(6)

where $U_{1}^{N} \left( 0 \right)$ represents the displacement at the top surface of the upper adherend (due to the longitudinal forces).

Note that due to the perfect bonding of the joints, the displacements are continuous at the interfaces between the adhesive and adherends. As a result, the $u_{1}^{N}$ (the adhesive displacement at the interface between the adhesive and upper adherend) should be the same as the upper adherend displacement at the interface. Based on Eq. 6 the $u_{1}^{N}$ can be expressed as:

$$ u_{1}^{N} = U_{1}^{N} \left( {y = t_{1} } \right) = U_{1}^{N} \left( 0 \right) + \frac{{\tau_{a} t_{1} }}{{2G_{1} }} $$

(7)

Using Eq. 7, Eq. 6 can be rewritten as:

$$ U_{1}^{N} \left( y \right) = u_{1}^{N} + \frac{{\tau_{a} }}{{2G_{1} t_{1} }}y^{2} - \frac{{\tau_{a} t_{1} }}{{2G_{1} }} $$

(8)

The longitudinal resultant force, N ₁ for the upper adherends having I section (Fig. 1), is:

$$ N_{1} = b_{1} \int\limits_{0}^{{t_{0} }} {\sigma_{1}^{N} \left( y \right){\text{d}}y + b_{0} \int\limits_{{t_{0} }}^{{t_{1} - t_{0} }} {\sigma_{1}^{N} \left( y \right){\text{d}}y} } + b_{1} \int\limits_{{t_{1} - t_{0} }}^{{t_{1} }} {\sigma_{1}^{N} \left( y \right){\text{d}}y} $$

(9)

where $\sigma_{1}^{N}$ is longitudinal normal stress for the upper adherend. By changing this stress into function of displacement and substituting Eq. 8 into the displacement, Eq. 9 can be rewritten as:

$$ N_{1} = E_{1} b_{1} \int\limits_{0}^{{t_{0} }} {\frac{{{\text{d}}U_{1}^{N} }}{{{\text{d}}x}}{\text{d}}y + E_{1} b_{0} \int\limits_{{t_{0} }}^{{t_{1} - t_{0} }} {\frac{{{\text{d}}U_{1}^{N} }}{{{\text{d}}x}}{\text{d}}y} } + E_{1} b_{1} \int\limits_{{t_{1} - t_{0} }}^{{t_{1} }} {\frac{{{\text{d}}U_{1}^{N} }}{{{\text{d}}x}}{\text{d}}y} $$

(10)

$$ N_{1} = E_{1} A_{1} \left[ {\frac{{{\text{d}}u_{1}^{N} }}{{{\text{d}}x}} - \frac{1}{{6G_{1} t_{1} A_{1} }}\left( {b_{1} \left( {(t_{1} - t_{0} )^{3} - t_{0}^{3} - t_{1}^{3} + 6t_{1}^{2} t_{0} } \right) + b_{0} \left( {3t_{1}^{2} \left( {t_{1} - 2t_{0} } \right) - \left( {t_{1} - t_{0} } \right)^{3} + t_{0}^{3} } \right)} \right)\frac{{{\text{d}}\tau (x)}}{{{\text{d}}x}}} \right] $$

(11)

Hence, the longitudinal strains induced by the longitudinal forces Eq. 3 can be expressed as

$$ \varepsilon_{1}^{N} (x) = \frac{{{\text{d}}u_{1}^{N} }}{{{\text{d}}x}} = \frac{{N_{1} }}{{E_{1} A_{1} }} + \frac{1}{{6G_{1} t_{1} A_{1} }}\left( {b_{1} \left( {(t_{1} - t_{0} )^{3} - t_{0}^{3} - t_{1}^{3} + 6t_{1}^{2} t_{0} } \right) + b_{0} \left( {3t_{1}^{2} \left( {t_{1} - 2t_{0} } \right) - \left( {t_{1} - t_{0} } \right)^{3} + t_{0}^{3} } \right)} \right)\frac{{{\text{d}}\tau (x)}}{{{\text{d}}x}} $$

(12)

Substituting Eqs. 2 and 12 into Eq. 1, this latter becomes:

$$ \begin{gathered} \varepsilon_{1} \left( x \right) = \frac{{{\text{d}}u_{1} \left( x \right)}}{{{\text{d}}x}} = \frac{{t_{1} }}{{2E_{1} I_{1} }}M_{1} \left( x \right) + \frac{{N_{1} \left( x \right)}}{{E_{1} A_{1} }} + \hfill \\ \frac{{b_{1} \left( {\left( {t_{1} - t_{0} } \right)^{3} - t_{0}^{3} - t_{1}^{3} + 6t_{1}^{2} t_{0} } \right) + b_{0} \left( {3t_{1}^{2} \left( {t_{1} - 2t_{0} } \right) - \left( {t_{1} - t_{0} } \right)^{3} + t_{0}^{3} } \right)}}{{6G_{1} t_{1} A_{1} }}\frac{{{\text{d}}\tau (x)}}{{{\text{d}}x}} \hfill \\ \end{gathered} $$

(13)

A ₁ is the cross-sectional area.

On the other hand, the laminate theory is used to determine the stress and strain of the externally bonded composite plate in order to investigate the whole mechanical performance of the composite-strengthened structure. The effective moduli of the composite laminate are varied by the orientation of the fibre directions and arrangements of the laminate patterns. The classical laminate theory (CLT) is used to estimate the strain of the composite plate (Herakovich 1998), i.e.

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon^{0} } \\ k \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A^{'} } & {B^{'} } \\ {C^{'}} & {D^{'} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} N \\ M \\ \end{array} } \right\} $$

(14)

where $[A^{'} ] = [A]^{ - 1} + [A]^{ - 1} [B][D^{x} ]^{ - 1} [B][A]^{ - 1} , [B^{'} ] = - [A^{ - 1} ][B][D^{x} ]^{ - 1} ,{\text{ [C']}} = - [D^{x} ]^{ - 1} [B][A]^{ - 1} ,[D'] = ([D] - [B][A]^{ - 1} [B])^{ - 1} , [D^{x} ] = [D] - [B][A]^{ - 1} [B]$ and Extensional matrix:

$$ A_{ij} = \sum\limits_{k = 1}^{NN} {\overline{Q}_{ij}^{(k)} } \left( {(y_{2} )_{k} - (y_{2} )_{k - 1} } \right) $$

(15)

Extensional-bending coupled matrix:

$$ B_{ij} = \frac{1}{2}\sum\limits_{k = 1}^{NN} {\overline{Q}_{ij}^{(k)} \left( {(y_{2}^{2} )_{k} - (y_{2}^{2} )_{k - 1} } \right)} $$

(16)

Flexural matrix:

$$ D_{ij} = \frac{1}{3}\sum\limits_{k = 1}^{NN} {\overline{Q}_{ij}^{(k)} \left( {(y_{2}^{3} )_{k} - (y_{2}^{3} )_{k - 1} } \right)} $$

(17)

The subscript NN represents the number of laminate layers of the FRP plate. Parameter $\overline{Q}_{ij}$ can be estimated by using the off-axis orthotropic plate theory (Herakovich 1998). Assume that the ply arrangement of the plate is symmetrical with respect to the mid-plane axis y ₂ = 0. A great simplification in laminate analysis then occurs by assuming that the coupling matrix B is identically zero (Herakovich 1998). Therefore Eqs. 14–17 can be simplified to the following matrix form for a plate with a width of b ₂:

$$ \left\{ {\varepsilon^{0} } \right\} = \left[ {A^{'} } \right] \left\{ N \right\}_{2} \;{\text{and }}\left\{ k \right\} = \left[ {D^{'} } \right] \left\{ M \right\}_{2} $$

(18)

where:

$$ \left\{ {\varepsilon^{0} } \right\}_{2} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\};\left\{ N \right\}_{2} = \left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{y} } \\ {N_{xy} } \\ \end{array} } \right\}_{2} ;\left\{ k \right\} = \left\{ {\begin{array}{*{20}c} {k_{x} } \\ {k_{y} } \\ {k_{xy} } \\ \end{array} } \right\}\;{\text{and}}\;\left\{ M \right\}_{2} = \left\{ {\begin{array}{*{20}c} {M_{x} } \\ {M_{y} } \\ {M_{xy} } \\ \end{array} } \right\}_{2} $$

(19)

In the present study, only an axial load N _x and the bending moment M _x in the beam’s longitudinal axis are considered, i.e. N _y  = N _xy  = 0 and M _y  = M _xy  = 0. Therefore, Eq. 18 can be simplified to:

$$ \varepsilon_{x}^{0} = A_{11}^{'} N_{x} \frac{1}{{b_{2} }}\quad{\text{and}}\quad k_{x} = D_{11}^{'} M_{x} \frac{1}{{b_{2} }} $$

(20)

Using CLT, the strain at the top of the FRP plate 2 is given as:

$$ \varepsilon_{2} \left( x \right) = \varepsilon_{x}^{0} - k_{x} \frac{{t_{2} }}{2} $$

(21)

Substituting Eq. 20 in 21 gives the following equation:

$$ \varepsilon_{2} \left( x \right) = \frac{{{\text{d}}u_{2} \left( x \right)}}{{{\text{d}}x}} = - D_{11}^{'} \frac{{t_{2} }}{{2b_{2} }}M_{2} \left( x \right) + A_{11}^{'} \frac{{N_{2} \left( x \right)}}{{b_{2} }} $$

(22)

where:

$$ N_{2} \left( x \right) = N_{x} \quad{\text{and}}\quad M_{2} \left( x \right) = M_{x} $$

(23)

The subscripts 1 and 2 denote adherends 1 and 2, respectively. M(x), N(x) and V(x) are the bending moment, axial and shear forces in each adherend.

It is well known in many studies (Shen and Springer 1981; Adams and Miller 1977; Bowles and Tompkins 1989; Shen 2001; Tounsi and Amara 2005; Amara et al. 2005; Tounsi and Amara 2005) that the material properties of composite are function of temperature and moisture. In terms of a micro-mechanical model of laminate, the material properties may be written as (Tsai and Hahn 1980)

$$ E_{L} = V_{f} E_{f} + V_{m} E_{m} $$

(24)

$$ \frac{1}{{E_{T} }} = \frac{{V_{f} }}{{E_{f} }} + \frac{{V_{m} }}{{E_{m} }} - V_{f} V_{m} \frac{{\nu_{f}^{2} \left( {\frac{{E_{m} }}{{E_{f} }}} \right) + \nu_{m}^{2} \left( {\frac{{E_{f} }}{{E_{m} }}} \right) - 2\nu_{f} \nu_{m} }}{{V_{f} E_{f} + V_{m} E_{m} }} $$

(25)

$$ \frac{1}{{G_{LT} }} = \frac{{V_{f} }}{{G_{f} }} + \frac{{V_{m} }}{{G_{m} }} $$

(26)

$$ \nu_{LT} = V_{f} \nu_{f} + V_{m} \nu_{m} $$

(27)

In the above equations, V _f and V _m are the fibre and matrix volume fractions and are related by

$$ V_{f} + V_{m} = 1 $$

(28)

E _f , G _f and ν _f are the Young’s modulus, shear modulus and Poisson’s ratio, respectively, of the fibre, and E _m , G _m and ν _m are corresponding properties for the matrix. It is assumed that E _m is a function of temperature and moisture, as is shown in Sect. 3, then E _L , E _T and G _LT are also functions of temperature and moisture. By adopting the equilibrium conditions of the steel beam, we have: Along x-direction:

$$ \frac{{{\text{d}}N_{1} (x)}}{{{\text{d}}x}} = - \tau (x)b_{2} $$

(29)

where τ(x) is shear stress in the adhesive layer. Along y-direction:

$$ \frac{{{\text{d}}V_{1} (x)}}{{{\text{d}}x}} = - \left[ {\sigma_{n} (x)b_{2} + q} \right] $$

(30)

where V ₁(x) is shear force applied in the steel beam; σ _n (x) is normal stress in the adhesive layer; q is the uniformly distributed load and b ₁ is width of steel beam. Moment equilibrium:

$$ \frac{{{\text{d}}M_{1} (x)}}{{{\text{d}}x}} = V_{1} (x) - \tau (x)b_{2} \frac{{t_{1} }}{2} $$

(31)

The equilibrium of the external FRP reinforcement along x-, y-direction and moment equilibrium can be also written as: Along x-direction:

$$ \frac{{{\text{d}}N_{2} (x)}}{{{\text{d}}x}} = \tau (x)b_{2} $$

(32)

Along y-direction:

$$ \frac{{{\text{d}}V_{2} (x)}}{{{\text{d}}x}} = \sigma_{n} (x)b_{2} $$

(33)

Moment equilibrium:

$$ \frac{{{\text{d}}M_{2} (x)}}{{{\text{d}}x}} = V_{2} (x) - \tau (x)b_{2} \frac{{t_{2} }}{2} $$

(34)

where V ₂(x) is shear force applied in the external FRP reinforcement.

2.2 Shear stress distribution along the FRP–steel interface

The shear stress in the adhesive can be expressed as follows:

$$ \tau \left( x \right) = K_{s} \Updelta u(x) = K_{s} \left[ {u_{2} \left( x \right) - u_{1} \left( x \right)} \right] $$

(35)

where K _s is shear stiffness of the adhesive per unit length and can be deduced as:

$$ K_{s} = \frac{\tau (x)}{\Updelta u(x)} = \frac{\tau (x)}{{\Updelta u(x)/t_{a} }}\frac{1}{{t_{a} }} = \frac{{G_{a} }}{{t_{a} }} $$

(36)

Δu(x) is relative horizontal displacement at the adhesive interface; G _a is the shear modulus in the adhesive and t _a is the thickness of the adhesive.Differentiating Eqs. 13, 22 and 35 with respect to x, respectively:

$$ \frac{{{\text{d}}\tau (x)}}{{{\text{d}}x}} = K_{S} \left( {A_{11}^{'} \frac{{N_{2} (x)}}{{b_{2} }} - D_{11}^{'} \frac{{t_{2} }}{{2b_{2} }}M_{2} (x) - \frac{{t_{1} }}{{2E_{1} I_{1} }}M_{1} (x) - \frac{{N_{1} (x)}}{{E_{1} A_{1} }}} \right) - \frac{{K_{S} }}{{6G_{1} t_{1} A_{1} }}\left[ {b_{1} \left( {\left( {t_{1} - t_{0} } \right)^{3} - t_{0}^{3} - t_{1}^{3} + 6t_{1}^{2} t_{0} } \right) + b_{0} \left( {3t_{1}^{2} \left( {t_{1} - 2t_{0} } \right) - \left( {t_{1} - t_{0} } \right)^{3} + t_{0}^{3} } \right)} \right]\frac{{{\text{d}}\tau (x)}}{{{\text{d}}x}} $$

(37)

Assuming equal curvature in the beam and the FRP plate, the relationship between the moments in the two adherends can be expressed as:

$$ M_{1} \left( x \right) = RM_{2} \left( x \right) $$

(38)

with

$$ R = \frac{{E_{1} I_{1} D_{11}^{'} }}{{b_{2} }} $$

(39)

Note that Eq. 38 is an approximation which was also used by previous researchers studying interfacial stresses between a beam and a strengthening plate, and was found to lead to accurate results (Smith and Teng 2001).

Moment equilibrium of the differential segment of the plated beam in Fig. 2 gives:

$$ M_{T} \left( x \right) = M_{1} \left( x \right) + M_{2} \left( x \right) + N\left( x \right)\left[ {\frac{{t_{1} + t_{2} }}{2} + t_{a} } \right] $$

(40)

where, M _T (x) is the total applied moment and from Eqs. 29 and 32, the axial forces are given as:

$$ N_{1} \left( x \right) = - N\left( x \right) = - b_{2} \int\limits_{0}^{x} {\tau \left( x \right)} {\text{ and }}N_{2} (x) = N(x) = b_{2} \int\limits_{0}^{x} {\tau \left( x \right)} $$

(41)

The bending moment in each adherend, expressed as a function of the total applied moment and the interfacial shear stress, is given as

$$ M_{1} \left( x \right) = \frac{R}{R + 1}\left[ {M_{T} \left( x \right) - b_{2} \int\limits_{0}^{x} {\tau \left( x \right)\left( {\frac{{t_{1} + t_{2} }}{2} + t_{a} } \right){\text{d}}x} } \right] $$

(42)

and

$$ M_{2} \left( x \right) = \frac{1}{R + 1}\left[ {M_{T} \left( x \right) - b_{2} \int\limits_{0}^{x} {\tau \left( x \right)\left( {\frac{{t_{1} + t_{2} }}{2} + t_{a} } \right){\text{d}}x} } \right] $$

(43)

The first derivative of the bending moment in each adherend gives:

$$ \frac{{{\text{d}}M_{1} \left( x \right)}}{{{\text{d}}x}} = \frac{R}{R + 1}\left[ {V_{T} \left( x \right) - b_{2} \tau \left( x \right)\left( {\frac{{t_{1} + t_{2} }}{2} + t_{a} } \right)} \right] $$

(44)

and

$$ \frac{{{\text{d}}M_{2} \left( x \right)}}{{{\text{d}}x}} = \frac{1}{R + 1}\left[ {V_{T} \left( x \right) - b_{2} \tau \left( x \right)\left( {\frac{{t_{1} + t_{2} }}{2} + t_{a} } \right)} \right] $$

(45)

Differentiating Eq. 37:

$$ \frac{{{\text{d}}^{2} \tau (x)}}{{{\text{d}}x^{2} }} = K_{S} \left( {\frac{{A_{11}^{'} }}{{b_{2} }}\frac{{{\text{d}}N_{2} (x)}}{{{\text{d}}x}} - D_{11}^{'} \frac{{t_{2} }}{{2b_{2} }}\frac{{{\text{d}}M_{2} (x)}}{{{\text{d}}x}} - \frac{{t_{1} }}{{2E_{1} I_{1} }}\frac{{{\text{d}}M_{1} (x)}}{{{\text{d}}x}} - \frac{1}{{E_{1} A_{1} }}\frac{{{\text{d}}N_{1} (x)}}{{{\text{d}}x}}} \right) - \frac{{K_{S} }}{{6G_{1} t_{1} \left( {2b_{1} t_{0} + b_{0} \left( {t_{1} - 2t_{0} } \right)} \right)}}\left[ {b_{1} \left( {\left( {t_{1} - t_{0} } \right)^{3} - t_{0}^{3} - t_{1}^{3} + 6t_{1}^{2} t_{0} } \right) + b_{0} \left( {3t_{1}^{2} \left( {t_{1} - 2t_{0} } \right) - \left( {t_{1} - t_{0} } \right)^{3} + t_{0}^{3} } \right)} \right]\frac{{{\text{d}}^{2} \tau (x)}}{{{\text{d}}x^{2} }} $$

(46)

Substitution of the shear forces (Eqs. 44 and 45) and axial forces Eq. 41 into Eq. 46 gives the following governing differential equation for the interfacial shear stress.

$$ \frac{{{\text{d}}^{2} \tau \left( x \right)}}{{{\text{d}}x^{2} }} - K_{1} \left( {A_{11}^{'} + \frac{{b_{2} }}{{E_{1} A_{1} }} + \frac{{\left( {\frac{{t_{1} + t_{2} }}{2}} \right)\left( {\frac{{t_{1} + t_{2} }}{2} + t_{a} } \right)}}{{E_{1} I_{1} D_{11}^{'} + b_{2} }}b_{2} D_{11}^{'} } \right)\tau \left( x \right) + \frac{{K_{1} }}{2}\left( {\frac{{t_{1} + t_{2} }}{{E_{1} I_{1} D_{11}^{'} + b_{2} }}D_{11}^{'} } \right)V_{T} \left( x \right) = 0 $$

(47)

where

$$ K_{1} = \frac{1}{{\left( {\frac{{t_{a} }}{{G_{a} }} + \frac{{t_{1} }}{{3G_{1} }}\xi } \right)}} $$

(48)

and ξ is a geometrical coefficient which is given as

$$ \xi = \frac{1}{{2A_{1} t_{1}^{2} }}\left[ {b_{1} \left( { - t_{0}^{3} + 6t_{0} t_{1}^{2} - t_{1}^{3} + \left( {t_{1} - t_{0} } \right)^{3} } \right) + b_{0} \left( {3t_{1}^{2} \left( {t_{1} - 2t_{0} } \right) - \left( {t_{1} - t_{0} } \right)^{3} + t_{0}^{3} } \right)} \right] $$

(49)

For a rectangular section (b ₁  = b ₀ ), ξ = 1 which corresponds to the same expression given by Tounsi (2006) by neglecting shear deformations of the FRP plate. However, for I-beam section (the present case) we have ξ < 1.For simplicity, the general solutions presented below are limited to loading which is either concentrated or uniformly distributed over part or the whole span of the beam, or both. For such loading, d² V _T (x)/dx ² = 0, and the general solution to Eq. 47 is given by:

$$ \tau \left( x \right) = B_{1} \cosh \left( {\lambda x} \right) + B_{2} \sinh \left( {\lambda x} \right) + m_{1} V_{T} \left( x \right) $$

(50)

where

$$ \lambda^{2} = K_{1} \left( {A_{11}^{'} + \frac{{b_{2} }}{{E_{1} A_{1} }} + \frac{{\left( {\frac{{t_{1} + t_{2} }}{2}} \right)\left( {\frac{{t_{1} + t_{2} }}{2} + t_{a} } \right)}}{{E_{1} I_{1} D_{11}^{'} + b_{2} }}b_{2} D_{11}^{'} } \right) $$

(51)

and

$$ m_{1} = \frac{{K_{1} }}{{2\lambda^{2} }}\left( {\frac{{t_{1} + t_{2} }}{{E_{1} I_{1} D_{11}^{'} + b_{2} }}D_{11}^{'} } \right) $$

(52)

B ₁ and B ₂ are constant coefficients determined from the boundary conditions. In the present study, a simply supported beam is investigated which is subjected to a uniformly distributed load as shown in Fig. 1. The interfacial shear stress for this load case at any point is written as:

$$ \tau \left( x \right) = \left[ {\frac{{m_{2} a}}{2}\left( {L - a} \right) - m_{1} } \right]\frac{{qe^{ - \lambda x} }}{\lambda } + m_{1} q\left( {\frac{L}{2} - a - x} \right) \quad 0 \le x \le L_{p} $$

(53)

where q is the uniformly distributed load and x, a, L and L _p are defined in Fig. 1. And m ₂ is given as follow:

$$ m_{2} = \frac{{K_{1} t_{1} }}{{2E_{1} I_{1} }} $$

(54)

In the case where the RC beam is subjected to a two symmetric point loads as shown in Fig. 3, the general solution for the interfacial shear stress is given by the following expressions Tounsi (2006) a < b

$$ \tau (x) = \left\{ {\begin{array}{*{20}c} {\frac{{m_{2} }}{\lambda }Pae^{ - \lambda x} + m_{1} P\cosh (\lambda x)e^{ - k}\quad 0 \le x \le (b - a )} \\ {\frac{{m_{2} }}{\lambda }Pae^{ - \lambda x} + m_{1} P\sinh (k)e^{ - \lambda x}\quad (b - a )\le x \le \frac{{L_{p} }}{2}} \\ \end{array} } \right. $$

(55)

a > b

$$ \tau (x) = \frac{{m_{2} }}{\lambda }Pbe^{ - \lambda x}\quad 0 \le x \le L_{p} $$

(56)

where P is the concentrated load and k = λ(b − a). The expression of m ₁ and m ₂ takes into considerations the shear deformation of adherends.

Fig. 3

Comparison of interfacial shear stress of the steel plated RC beam with the experimental results

2.3 Normal stress distribution along the FRP–steel interface

The normal stress in the adhesive can be expressed as follows:

$$ \sigma_{n} \left( x \right) = K_{n} \Updelta w\left( x \right) = K_{n} \left[ {w_{2} \left( x \right) - w_{1} \left( x \right)} \right] $$

(57)

where K _n is normal stiffness of the adhesive per unit length and can be deduced as:

$$ K_{n} = \frac{{\sigma_{n} \left( x \right)}}{\Updelta w\left( x \right)} = \frac{{\sigma_{n} \left( x \right)}}{{\Updelta w\left( x \right)/t_{a} }}\left( {\frac{1}{{t_{a} }}} \right) = \frac{{E_{a} }}{{t_{a} }} $$

(58)

w ₁(x) and w ₂(x) are the vertical displacements of adherend 1 and 2, respectively.Differentiating Eq. 50 twice results in:

$$ \frac{{{\text{d}}^{2} \sigma_{n} \left( x \right)}}{{{\text{d}}x^{2} }} = K_{n} \left[ {\frac{{{\text{d}}^{2} w_{2} \left( x \right)}}{{{\text{d}}x^{2} }} - \frac{{{\text{d}}^{2} w_{1} \left( x \right)}}{{{\text{d}}x^{2} }}} \right] $$

(59)

Considering the moment–curvature relationships for the beam to be strengthened and the external reinforcement, respectively:

$$ \frac{{{\text{d}}^{2} w_{1} \left( x \right)}}{{{\text{d}}x^{2} }} = - \frac{{M_{1} \left( x \right)}}{{E_{1} I_{1} }}, \quad \frac{{{\text{d}}^{2} w_{2} \left( x \right)}}{{{\text{d}}x^{2} }} = - \frac{{D_{11}^{'} M_{2} \left( x \right)}}{{b_{2} }} $$

(60)

Based on the equilibrium Eqs. 29–34, the governing differential equations for the deflection of adherends 1 and 2, expressed in terms of the interfacial shear and normal stresses, are given as follows:Adherend 1:

$$ \frac{{{\text{d}}^{4} w_{1} \left( x \right)}}{{{\text{d}}x^{4} }} = \frac{1}{{E_{1} I_{1} }}b_{2} \sigma_{n} \left( x \right) + \frac{{t_{1} }}{{2E_{1} I_{1} }}b_{2} \frac{{{\text{d}}\tau \left( x \right)}}{{{\text{d}}x}} + \frac{q}{{E_{1} I_{1} }} $$

(61)

Adherend 2:

$$ \frac{{{\text{d}}^{4} w_{2} \left( x \right)}}{{{\text{d}}x^{4} }} = - D_{11}^{'} \sigma_{n} \left( x \right) + D_{11}^{'} \frac{{t_{2} }}{2}\frac{{{\text{d}}\tau \left( x \right)}}{{{\text{d}}x}} $$

(62)

Substitution of Eqs. 59 and 60 into the fourth derivation of the interfacial normal stress obtainable from Eq. 55 gives the following governing differential equation for the interfacial normal stress:

$$ \frac{{{\text{d}}^{4} \sigma_{n} \left( x \right)}}{{{\text{d}}x^{4} }} + \frac{{E_{a} }}{{t_{a} }}\left( {D_{11}^{'} + \frac{{b_{2} }}{{E_{1} I_{1} }}} \right)\sigma_{n} \left( x \right) - \frac{{E_{a} }}{{t_{a} }}\left( {D_{11}^{'} y_{2} - \frac{{t_{1} b_{2} }}{{2E_{1} I_{1} }}} \right)\frac{{{\text{d}}\tau \left( x \right)}}{{{\text{d}}x}} + \frac{{qE_{a} }}{{t_{a} E_{1} I_{1} }} = 0 $$

(63)

The general solution to this fourth-order differential equation is:

$$ \sigma_{n} \left( x \right) = e^{ - \beta x} \left[ {C_{1} \cos \left( {\beta x} \right) + C_{2} \sin \left( {\beta x} \right)} \right] + e^{\beta x} \left[ {C_{3} \cos \left( {\beta x} \right) + C_{4} \sin \left( {\beta x} \right)} \right] - n_{1} \frac{{{\text{d}}\tau \left( x \right)}}{{{\text{d}}x}} - n_{2} q $$

(64)

For large values of x it is assumed that the normal stress approaches zero, and as a result C ₃ = C ₄ = 0. The general solution therefore becomes:

$$ \sigma_{n} \left( x \right) = e^{ - \beta x} \left[ {C_{1} \cos \left( {\beta x} \right) + C_{2} \sin \left( {\beta x} \right)} \right] - n_{1} \frac{{{\text{d}}\tau \left( x \right)}}{{{\text{d}}x}} - n_{2} q $$

(65)

where

$$ \beta = {\sqrt[4]{{\frac{{E_{a} }}{{4t_{a} }}}\left( {\frac{{b_{2} }}{{E_{1} I_{1} }} + D_{11}^{'} } \right)}} $$

(66)

$$ n_{1} = \left( {\frac{{t_{1} b_{2} - D_{11}^{'} E_{1} I_{1} t_{2} }}{{2\left( {D_{11}^{'} E_{1} I_{1} + b_{2} } \right)}}} \right) $$

(67)

and

$$ n_{2} = \frac{1}{{D_{11}^{'} E_{1} I_{1} + b_{2} }} $$

(68)

The constants C ₁ and C ₂ in Eq. 63 are written as follow:

$$ C_{1} = \frac{{E_{a} }}{{2\beta^{3} t_{a} E_{1} I_{1} }}\left[ {V_{T} \left( 0 \right) + \beta M_{T} \left( 0 \right)} \right] - \frac{{n_{3} }}{{2\beta^{3} }}\tau \left( 0 \right) + \frac{{n_{1} }}{{2\beta^{3} }}\left( {\frac{{{\text{d}}^{4} \tau \left( 0 \right)}}{{{\text{d}}x^{4} }} + \beta \frac{{{\text{d}}^{3} \tau \left( 0 \right)}}{{{\text{d}}x^{3} }}} \right) $$

(69)

$$ C_{2} = - \frac{{E_{a} }}{{2\beta^{2} t_{a} E_{1} I_{1} }}M_{T} \left( 0 \right) - \frac{{n_{1} }}{{2\beta^{2} }}\frac{{{\text{d}}^{3} \tau \left( 0 \right)}}{{{\text{d}}x^{3} }} $$

(70)

where

$$ n_{3} = \frac{{E_{a} b_{2} }}{{t_{a} }}\left( {\frac{{t_{1} }}{{2E_{1} I_{1} }} - \frac{{D_{11}^{'} t_{2} }}{{2b_{2} }}} \right) $$

(71)

The above expressions for the constants C ₁ and C ₂ have been left in terms of the bending moment M _T (0) and shear force V _T (0) at the end of the soffit plate.

3 Results and discussion

A computer code based on the preceding equations was written to compute the interfacial stresses in a steel beam bonded with a hygrothermal aged FRP plate.

Graphite/epoxy composite material was selected in the present examples as a bonded plate. However, the analysis is equally applicable to other types of composite material. For these examples the thickness of each ply is 0.125 mm, the width is b ₂  = 150 mm and the material properties adopted are (Adams and Miller 1977; Bowles and Tompkins 1989; Shen 2001; Tounsi and Amara 2005; Amara et al. 2005; Tounsi and Amara 2005): E_f = 230.0 GPa, G_f = 9.0 GPa, ν_f = 0.203, ν_m = 0.34 and E _m  = (3.51 − 0.003T − 0.142C) GPa, in which T = T ₀  + ΔT and T ₀  = 25°C (room temperature), and C = C ₀  + ΔC and C ₀  = 0 wt% H₂O.

Using the formula of the Young’s modulus E _m and the relations (24)–(28), we calculate E _L , E _T , G _LT and ν_LT.

3.1 Comparison with experimental results

To validate the present method, a rectangular section (ξ = 1) is used here. One of the tested beams bonded with steel plate by Jones et al. (1988), beam F31, is analysed here using the present improved solution. The beam is simply supported and subjected to four-point bending, each at the third point. The geometry and materials properties of the specimen are summarized in Table 1.

Table 1 Dimensions and material properties

The interfacial shear stress distributions in the beam bonded with a soffit steel plate under the applied load 60 kN, i.e. P = 30 kN in Fig. 3, are compared between the experimental results and those obtained by the present method. As it can be seen from Fig. 3, the predicted theoretical results are in reasonable agreement with the experimental results.

3.2 Theoretical parametric study

In this section, numerical results of the present solutions are presented to study the effect of various parameters on the distributions of the interfacial stresses in a steel beam bonded with an FRP plate. These results are intended to demonstrate the main characteristics of interfacial stress distributions in these strengthened beams.

The steel beam is simply supported and subjected to a uniformly distributed load q = 50 kN/m. The Young’s modulus and Poisson’s ratio are respectively: E ₁  = 210 GPa and υ₁  = 0.3. The span of the steel beam is 3,000 mm; the width is b ₁  = 150 mm; the total depth is t ₁  = 300 mm; the depth of the flange is t ₀  = 10.7 mm; the thickness of the web is b ₀  = 7.1 mm; the distance from the support to the end of the plate is 300 mm.

The geometric and material properties of the adhesive layer are: the thickness is t _a  = 4 mm; the Young’s modulus and Poisson’s ratio are respectively, E _a  = 3 GPa and υ _a  = 0.35.

3.2.1 Fiber volume fractions effect

Figure 4 shows, the effect of fiber volume fractions V _f (= 0.5, 0.6 and 0.7) on the variation of shear and normal adhesive stresses. It can be seen that the interfacial shear stresses are reduced with decreases in fiber volume fraction. However, almost no effect is observed on the variation of interfacial normal stresses.

Fig. 4

The effect of fiber volume fraction on the variation of both shear and normal adhesive stresses in steel beam bonded with composite plate [016]_S. ΔT = 0°C, ΔC = 0%

3.2.2 Hygrothermal effect on the adhesive stresses

This effect is studied here, due to technological considerations. For example, when we use these plates to strengthen beams, they can be already exposed to the environmental conditions. Thus, these plates are aged with time and the mechanical properties will be reduced. In this study, we aim to show if the reduction in stiffness of the bonded composite plate due to hygrothermal ageing has an effect on the interfacial stresses.

From results presented in Fig. 5 we can conclude that the hygrothermal ageing of the bonded composite plate has no effect on the variation of adhesive stresses.

Fig. 5

Hygrothermal effect on the variation of both shear and normal adhesive stresses in steel beam bonded with composite plate [016]_S. (Vf = 0.7)

3.2.3 Effect of the adhesive layer thickness

Figure 6 shows the effects of the thickness of the adhesive layer on the interfacial stresses. It is seen that increasing the thickness of the adhesive layer leads to significant reduction in the peak interfacial stresses. Thus using thick adhesive layer, especially in the vicinity of the edge, is recommended.

Fig. 6

Effect of adhesive layer thickness on interfacial stresses in steel beam bonded with composite plate [016]_S. (Vf = 0.7). ΔT = 0°C, ΔC = 0%

3.2.4 Effect of FRP plate thickness

Peak shear and peeling stresses for various thicknesses of the FRP plate within the range of 1–6 mm appear in Fig. 7. The results reveal that thickness of the FRP plates significantly increases the edge peeling and shear stresses. This relation is an outcome of the local bending effects in the FRP plate governed by the flexural rigidity of the plate. Thus any increase in the flexural rigidity leads to an increase in the magnitude of the edge stresses.

Fig. 7

Influence of thickness of frp plate on edge stresses in steel beam bonded with composite plate [016]_S. (Vf = 0.7). ΔT = 0°C, ΔC = 0%

3.2.5 Effect on Plate Length of the strengthened beam region L _p

The influence of length of the strengthened beam region L _p appears in Fig. 8. It is seen that, as the plate terminates further away from the supports, the interfacial stresses increase significantly. This result reveals that in any case of strengthening, including cases where retrofitting is required in a limited zone of maximum bending moments at midspan, it is recommended to extend the strengthening strip as close as possible to the support lines.

Fig. 8

Effect of plate length on edge stresses interfacial stresses in steel beam bonded with composite plate [016]_S. (Vf = 0.7). ΔT = 0°C, ΔC = 0%

4 Conclusion

A systematic rigorous general approach for the analysis of interfacial stresses in steel beams strengthened with externally bonded hygrothermal aged FRP plate has been presented. This approach is based on elastic foundation model in which the adherend shear deformations have been included by assuming a linear shear stress through the depth of the steel beam. By comparing with experimental results, the present closed-solution provides satisfactory predictions to the interfacial shear stress in the plated beams.

The material properties of FRP plate were considered to be dependent on temperature and moisture, which are given explicitly in terms of the fibre and matrix properties and the fibre–volume ratio. The conclusions from this research can be outlined as follows.

• There are stress concentrations at the end of the FRP plate. The normal stress concentration is a tensile stress but quickly towards to zero through a small oscillation. The initial delamination of the FRP plate from steel beam results from joints effects of the shear and normal stress at the end of the FRP plate.

• The interfacial shear stresses are reduced with decreases in fiber volume fraction. However, almost no effect is observed on the variation of interfacial normal stresses.

• No effect on the variation of adhesive stresses is observed when we use hygrothermal aged FRP plate to strengthen the steel beam.

• The interfacial stresses are influenced by the geometry parameters such as thickness of the adhesive layer and FRP plate in range of the different degrees. It is shown that the edge stresses and levels increase obviously with the increase of the thickness of the FRP plate. However, it is seen that increasing the thickness of the adhesive layer leads to significant reduction in the peak interfacial stresses.

• Another outcome based on the parametric study indicates that extending the FRP strip as close as possible to the support reduces the stresses at the edge.