1 Introduction

Various sheet-metal forming processes, e.g., drawing, stamping, and cupping are used extensively to produce products with desired shape and functionality (Kalpakjian 1991). A computer-aided design analysis of these forming processes using a commercial finite element (ABAQUS 2003; ANSYS 2007) generally consists of modeling large plastic deformation of a sheet metal and requires the input of the effective true stress–true strain curve of the material over a wide range of plastic strains. The effective true stress–true strain curve, represented either in a set of discrete data points or in one of commonly used analytical strain-hardening models, is typically obtained from a standard uniaxial tensile test on sheet metals. However, it is well known that after a certain amount of uniform elongation in the tensile test, non-uniform deformation due to diffuse necking occurs at a critical strain (Hill 1952; Hutchinson and Miles 1973; Nichols 1980) and the stress state at the narrowest cross-section within the neck region subsequently becomes increasingly biaxial and tri-axial, which limits the accuracy and reliability of experimentally measured uniaxial stress–strain data beyond the uniform elongation. In addition, the plastic deformation becomes highly heterogeneous and concentrates within the necked region (Tvergaard 1993; Tong and Zhang 2001) and the conventional means of an extensometer is no longer applicable to the axial strain measurement inside the neck. It is thus questionable to simply extrapolate these measured stress–strain data of a sheet metal beyond the uniform elongation when one analyzes the forming failures of the sheet metal occurring at much larger strains.

Bridgman (1952) developed some approximate analytical solutions for obtaining more accurately the effective true stress–true strain curve of metals beyond diffuse necking by using various simplifying assumptions about the neck geometry and stress and strain distribution inside the neck. As discussed in some details by Ling (1996) and Joshi et al. (1992), the use of original analytical results by Bridgman for tensile samples made of either cylindrical rods or flat sheets requires the measurement of (1) the radius of curvature of the neck profile along the axial direction and (2) the radius or width of the smallest cross-section, which are both difficult to obtain with sufficient accuracy. In practice, the average axial true stress and true strain computed from only the measured diameter of the smallest cross-section of a cylindrical rod specimen were often regarded as the effective true stress and true strain without further correction (Segal et al. 2006; Poortmans et al. 2007). The true stress computed with the Bridgman correction factor was found to attain a maximum and then strain softening behavior for an alpha-brass sheet before localized necking (Joshi et al. 1992). Furthermore, the analytical results by Bridgman are not expected to be applicable when localized necking is being developed in a thin sheet sample (Ling 1996).

Following the pioneering work by Bridgman, many research efforts have been carried out in recent years in developing a variety of new techniques and approaches by taking the advantage of the increasing availability of new experimental measurement tools and finite element analysis tools. These new methods differ mainly in their use of the various experimental measurements and whether or not a finite element analysis is required each time. Zhang and Li (1994) developed a customized finite element analysis program to obtain the true stress–true strain curve of a round smooth steel bar up to fracture based on the experimental tensile load-axial displacement curve. Their program adjusts the trace of the effective stress–strain curve step-by-step iteratively to reduce the difference between simulated and experimental load-displacement curves at each displacement increment to a pre-set tolerance level. Joun et al. (2008) implemented in their own finite element analysis code the similar iterative adjustments at some selected increments of elongation in a tension test of a cylindrical rod specimen beyond diffuse necking. The current true stress at the current average axial true strain was corrected by a ratio of the measured axial load over the computed axial load. While such a step-by-step iterative optimization procedure implemented during the finite element analysis was found to be effective, it is difficult to be implemented in a general purpose commercial finite element program. Ling (1996) instead analyzed the uniaxial tension of various copper sheets in the finite element analysis program ABAQUS by using a combined power-law (for small strain) and linear (large strain) strain hardening model with a single adjustable weight parameter. The true stress–true strain curve was obtained by adjusting only the weight parameter via a trial-and-error manner to minimize the difference between simulated and experimental load-displacement curves. As the experimental load-displacement data over the entire gage length are usually less accurate after the onset of diffuse necking (even with the use of an extensometer) and less sensitive to the plastic straining details inside the neck (especially the localized neck), the obtained true stress–true strain curves may be less reliable at very large strains.

Zhang et al. (1999) proposed a method based on the experimental load-thickness curve to determine the true stress–true strain curve of rectangular cross-section tensile coupons with a width-to-thickness aspect ratio from 1 to 8. They presented an empirical cross-section area reduction equation in terms of the current thickness at the minimum section of the test coupon based on extensive 3D finite element analysis results so the average true stress as well as true strain at the minimum section can be computed from the measurement of the current sheet thickness. The so-called Bridgman-Le Roy correction equations were then applied to obtain the effective true stress–true strain of the material. Their method requires the thickness reduction measurement at the prior known minimum section of the test coupon and is valid up to localized necking. This method has been also extended to anisotropic materials (Zhang et al. 2001a, 2001b). Scheider et al. (2004) found that the cross-section area reduction equation proposed by Zhang et al. (1999) is not sufficiently accurate and thickness reduction at the minimum section is difficult to measure. They proposed instead the use of the experimental load-width curve to determine the true stress–true strain curve of rectangular cross-section tensile coupons. By using the digital image correlation technique, the displacement field of the neck region of the tensile coupon was obtained first and then the width at the minimum section was determined by a polynomial fitting of the displacements of edge nodes of the neck. The effective true strain was obtained from the axial and transverse surface strains measured by digital image correlation and the true stress was computed using the measured load, current width at the minimum section (neck), and an empirical correction factor. The correction factor is a nonlinear function of both the effective true strain and the minimum width of the neck. It was also determined empirically from some extensive 3D finite element analysis results. Yang and Tong (2008) defined the effective true strain in the same way but computed the effective true stress directly using the average axial true stress and the average axial and transverse surface strain. They carried out a 3D finite element analysis on two tapered tensile coupon geometries for five different dual-phase steel materials (two base metals, two heat-affected zones, and one weld metal) and found the effective true stress–true strain curves obtained in such a way are reasonably accurate up to a strain level of 1. Dan et al. (2007) used a coarse grid method to obtain the local average axial true strain and then the average axial true stress in low-carbon steel sheet coupons with various gage lengths. Although their true stress–true strain curves were found more or less to be independent of the coupon geometry (gage length) but their data are valid only at moderately large strains just shortly after diffuse necking as no additional correction due to a tri-axial stress state within the neck was introduced at all.

In the present study, we describe an iterative correction procedure using a general purpose commercial 3D finite element analysis (FEA) program to obtain improved effective true stress–true strain curves of aluminum, copper, steel, and titanium sheet metal tension coupons with various gage section geometries up to very large strains just prior to the final tearing failure. Instead of relying on the global load-displacement data, the average axial true stress–true strain curve measured locally at the minimum section of the neck region will be used both as the initial guess of the effective true stress–true strain curve in the finite element analysis and as the target which the FE-computed average axial true stress–true strain curve will be compared with. The correction made to the input true stress–true strain curve is carried out in a post-processing step entirely outside the finite element analysis program. It will be shown that the method proposed here can achieve more accurate and robust results than the simpler correction methods described above but without the complexity and cost of using the entire whole-field displacement data in an inverse model parameter identification analysis (Kajberg and Lindkvist 2004). The iterative correction procedure presented here is based on some early preliminary works carried out in our group (Zhang et al. 2000; Tong and Zhang 2001; Tao 2006) and it has been further expanded and refined in this study.

In the following, the experimental procedure is first described briefly for tensile testing of the selected five materials and their tension coupon geometries. Calculations of the average axial true-stress and true strain curves of these materials are described based on the local strain measurements inside the neck using digital image correlation. The isotropic elastic-plastic finite element analysis (FEA) of the five uniaxial tension tests is then presented. The iterative correction procedure as a post-processing step is described in details to obtain the accurate effective true stress–true strain curves of the materials. The numerical analysis results are presented to show the robustness and effectiveness of the proposed iterative correction procedure as they converge quickly in only two to three finite element analysis sessions per tension coupon to the experimental measurements of all five materials investigated. Some suggestions are offered for possible improvements in both experimental measurements and finite element analyses and conclusions of this study are also given.

2 Materials and experimental procedure

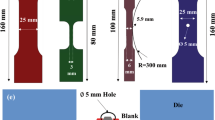
Four thin sheet metals (aluminum, copper, steel and titanium) plus one miniature steel square bar have been chosen for this study. The geometries, finite element mesh details, and material elastic constants are listed in Tables 1 and 2, respectively for each material. The aspect ratio of the minimum section of tension coupons is between 1 and 7.35. The use of some tension coupons with a tapered gage section (Richmond et al. 1983) facilitates a better control of the location of the diffuse and localized necking region. A desktop mini-tensile testing apparatus shown in Fig. 1 was used for stretching both compact and miniature sized tension test coupons in all experiments reported here. During each tensile test, a series of digital images (e.g., see Fig. 2) of the gage section of the test coupon were acquired and these images were then processed by a digital image correlation (DIC) analysis program to generate the local distribution of in-plane biaxial strain components in the gage section. Flat tensile test coupons are in fact better suitable for such a whole-field strain measurement technique than cylindrical coupons. Details of the experimental procedure and image and load data analyses can be found elsewhere (Tong et al. 2005, 2007; Marya et al. 2006; Tong and Zhang 2007).

Table 1 Summary of materials and geometries of five tension coupons
Full size table
Table 2 Summary of finite element models and elastic constants of materials
Full size table
Fig. 1
figure 1

The top view of the mini-tensile testing apparatus with a copper tension coupon mounted

Full size image
Fig. 2
figure 2

Selected digital images of the aluminum tension coupon (a) before the application of axial loading; (b) at the maximum axial load point; (c) during diffuse necking; (d) prior to final fracture

Full size image

Once the surface distribution of the axial true strain ε x (x, y) at the narrowest section of a necked region was measured from the experiment, an average true axial strain \( \bar \varepsilon _{x} \) and an average axial true stress \( \bar \sigma _{x} \) at the cross-section of the tension coupon gage section were computed, respectively from

$$ \bar \varepsilon _{x} = \int\limits_{S} {\varepsilon _{x} (x,y){\text{d}}x{\text{d}}y} , $$
(1)

and

$$ \bar \sigma _{x} = \frac{{F_{x} }}{A} \approx \frac{{F_{x} }}{{A_{0} }}\exp (\bar \varepsilon _{x} ), $$
(2)

where x is the coordinate along the tensile loading direction, y is the coordinate transverse to the tensile loading direction (see Fig. 3), S is the size of the narrowest neck region chosen on the coupon surface, A 0 and A are the initial and current minimum cross-section areas of the neck region, and F x is the measured axial load. The surface area S is defined by the minimum width b of the neck region and a finite dimension in the axial direction Δx, which was the axial dimension of the subset used in computing the surface axial strain from the surface displacement data in the digital image correlation analysis. Computation of the true stress by Eq. 2 uses the approximate value of the current cross-section area A of the tension coupon based on the assumption of volume constancy under plastic straining:

$$ A{\text{d}}L = A_{0} {\text{d}}L_{0} \quad {\text{or}}\quad A = A_{0} \frac{{{\text{d}}L_{0} }}{{{\text{d}}L}} \approx A_{0} {\text{e}}^{{ - \bar \varepsilon _{x} }} . $$
(3)
Fig. 3
figure 3

Finite element meshes with boundary conditions of the four thin sheet metal tension coupons: (a) aluminum; (b) copper; (c) steel; (d) titanium

Full size image

An area integral (over a finite surface area S covering the region with the entire narrowest width of the neck region and a finite length in the x-direction) instead of a line integral is given in Eq. 1 in order to emphasize the fact that the average axial true strain still has a limited spatial resolution (or a finite “gage length”) even though it was obtained locally. As the axial load can be measured fairly accurately using a precision load cell, the reliability of the average axial true stress–true strain curve \( \bar \sigma _{x} (\bar \varepsilon _{x} ) \) measured locally at the minimum section of the neck region of a ductile material depends primarily on the accuracy of the local surface strain measurements along the loading axis by digital image correlation. Besides using a high quality high-pixel density digital imaging system and decorating the tension coupon surface with high contrast speckles, a tensile test may be interrupted (by keeping the grippers at both ends of the test coupon from moving for a short duration) so a digital image can be acquired by averaging multiple frames (Smith et al. 1998). Such an interruption reduces both mechanical vibrations and image noises and thus improves the quality of digital images for surface strain measurements.

3 The finite element analysis

3.1 Finite element models of tension test coupons

An isotropic elastic-plastic material model was used in a nonlinear finite element analysis of the sheet metal tension tests with the commercial program ABAQUS (2003). Details on the pertinent equations and their finite element models in general can be found in Simo and Hughes (2000), Kojic and Bathe (2004). The particular implementations and solutions in the program ABAQUS can be found in Dunne and Petrinic (2005), Fish and Belytschko (2007). Specifically, the nonlinear strain hardening of the plastic deformation of each sheet metal was characterized by its von Mises effective true stress–true strain curve \( \bar \sigma (\bar \varepsilon ^{p} ) \) and a set of discrete data points of \( \bar \sigma \) vs. \( \bar \varepsilon ^{p} \) were used as the input in each finite element analysis (see Chap. 5 in Dunne and Petrinic 2005). Using the general purpose commercial finite element analysis program ABAQUS (version 6.4), full-scale 3D models were built for the five thin sheet metal tension coupons as listed in Table 1. These finite element models with the detailed meshes and some boundary conditions under uniaxial loading are shown in Fig. 3 for the four compact size tension coupons and in Fig. 4 for the miniature square tension bar. A refined mesh was applied at the center of each coupon where necking is expected to occur. All finite element analyses used 3D brick-type element C3D20. The number of nodes and elements are listed in Table 2 for each tensile test coupon. The convergence of computed results in terms of mesh density has been checked to be successfully reached at the level indicated in Table 2. Two linear elastic constants are also listed in Table 2 for each material.

Fig. 4
figure 4

A finite element model of the miniature steel tension bar: (a) a 3D view of the whole tension coupon; (b) an in-plane view; (c) loading and boundary conditions on a ¼ FE model; (d) the FE mesh

Full size image

3.2 The iterative correction procedure

As the effective true stress–true strain curve \( \bar \sigma (\bar \varepsilon ^{p} ) \) beyond diffuse necking is unknown, the entire experimentally measured average axial true stress–true strain curve \( \bar \sigma _{x} (\bar \varepsilon _{x} ) \) without the apparent softening portion at the end was used as an initial guess to be input in the first finite element analysis session of a tension test. Some additional linear extrapolation points up to a very large strain (~200%) were also added to ensure the continuing strain hardening beyond the maximum average surface true strain can be realized in the finite element analyses. Then an iterative procedure was used to carry out the successive corrections on the initially assumed effective true stress–true strain curve. In the following, a superscript “E” will be used to designate the experimentally measured average axial true stress–true strain curve, superscripts “C1”, “C2”, … will be used to designate the computed average axial true stress–true strain curve, and superscript “M1”, “M2”, “M3”, … will be used to designate the initially guessed effective true stress–true strain curve and their subsequent corrected values.

The iterative correction procedure is outlined in the following:

  1. (1)

    The first finite element analysis session: obtain first the experimentally measured average axial true stress–true strain curve \( \bar \sigma _{x}^{E} (\bar \varepsilon _{x} ).\) Use it as an initial guess of the von Mises effective true stress–true strain curve of the material, namely \( \bar \sigma ^{{M1}} (\bar \varepsilon ) = \bar \sigma _{x}^{E} (\bar \varepsilon _{x} ). \) Once the first finite element analysis session of the tension test using \( \bar \sigma ^{{M1}} (\bar \varepsilon ) \) is completed, the average axial true stress–true strain curve at the minimum section of the neck region of the deformed tension coupon can then be computed in the same way given by Eqs. 1 and 2 using the simulation results of the surface true strain \( \varepsilon _{x}^{{C1}} (x,y) \) and axial load \( F_{x}^{{C1}} \) at a preset loading increment in a post-processing routine. The numerically computed average axial true stress–true strain curve is designated here as \( \bar \sigma _{x}^{{C1}} (\bar \varepsilon _{x} ).\)

  2. (2)

    The correction step: take the ratio between experimentally measured and FE-computed average axial true stress–true strain curves as the correction factor \( \alpha ^{{C1}} (\bar \varepsilon ) = \bar \sigma _{x}^{E} (\bar \varepsilon _{x} )/\bar \sigma _{x}^{{C1}} (\bar \varepsilon _{x} ) \) and multiply it to the initial guess of the effective true stress–true strain curve \( \bar \sigma ^{{M1}} (\bar \varepsilon ).\) When the data points in terms of the average axial true strain output from the first finite element analysis session do not coincide exactly with the experimentally measured data points, a linear interpolation is used to obtain the FE-computed true stress at each experimentally measured true strain value. It results in a corrected effective true stress–true strain curve \( \bar \sigma ^{{M2}} (\bar \varepsilon ) = \alpha ^{{C1}} (\bar \varepsilon )\bar \sigma ^{{M1}} (\bar \varepsilon ). \)

  3. (3)

    The subsequent additional finite element analysis sessions and correction steps: repeat the finite element analysis described in 1) using the same meshes and boundary conditions but with the newly corrected effective true stress–true strain curve \( \bar \sigma ^{{M2}} (\bar \varepsilon ).\) Again after the finite element analysis session, the second numerically computed average axial true stress–true strain curve is obtained as \( \bar \sigma _{x}^{{C2}} (\bar \varepsilon _{x} ).\) Similar to the correction step described in (2), another correction factor can be obtained as \( \alpha ^{{C2}} (\bar \varepsilon ) = \bar \sigma _{x}^{E} (\bar \varepsilon _{x} )/\bar \sigma _{x}^{{C2}} (\bar \varepsilon _{x} ). \) It is then used to obtain the further corrected effective true stress–true strain curve \( \bar \sigma ^{{M3}} (\bar \varepsilon ) = \alpha ^{{C2}} (\bar \varepsilon )\bar \sigma ^{{M2}} (\bar \varepsilon ). \) This iterative procedure of both finite element analysis and subsequent correction can continue in the same way until the difference between the successive corrected effective true stress–true strain curves becomes acceptably small (or the correction factor is virtually identical to 1 for all strains).

It is noted that the resulting effective true stress–true strain curve \( \bar \sigma ^{{M(i + 1)}} (\bar \varepsilon ) \) can actually be expressed as (where i is the total number of finite element analysis sessions carried out for each tension coupon)

$$ \bar \sigma (\bar \varepsilon ^{p} ) \approx \bar \sigma ^{{M(i + 1)}} (\bar \varepsilon ) = \frac{{\bar \sigma _{x}^{E} (\bar \varepsilon _{x} )}}{{\bar \sigma _{x}^{{Ci}} (\bar \varepsilon _{x} )}} \cdots \frac{{\bar \sigma _{x}^{E} (\bar \varepsilon _{x} )}}{{\bar \sigma _{x}^{{C2}} (\bar \varepsilon _{x} )}}\frac{{\bar \sigma _{x}^{E} (\bar \varepsilon _{x} )}}{{\bar \sigma _{x}^{{C1}} (\bar \varepsilon _{x} )}}\bar \sigma _{x}^{E} (\bar \varepsilon _{x} ). $$
(4)

The final result depends on the accuracy of both the experimentally measured and successively FE-computed average axial true stress–true strain curves. The final effective true stress–true strain curve obtained was used in one additional finite element analysis in this study with a much denser mesh in order to confirm the convergence of the FE-computed average axial true stress–true strain curves.

4 Results

The average axial true stress–true strain curve computed by Eqs. 1 and 2 with the surface area S of the neck zone so defined in this study is the same as the true stress–true strain curve no. 3 used in our previous works (Tong et al. 2005, 2007; Marya et al. 2006). Both experimentally measured and numerically simulated average axial true stress–true strain curves will thus be explicitly referred also to as “stress–strain curve 3” in the following. Some representative finite element analysis results on the detailed deformation, stress and strain distribution and computed average axial true stress–true strain curves are shown in Fig. 5 for the miniature steel tension bar (see Tables 1, 2). All results shown in Fig. 5a–c are up to a loading point when the computed average axial true strain reached the maximum value of the experimentally measured axial true strain. The neck region with moderate mesh distortion can be seen in Fig. 5a. The von Mises effective true stress and true strain shown in Fig. 5b and c, respectively are clearly non-uniform throughout the gage section of the square tension bar. The effective true stress has a much less variation than the effective true strain both within the neck region and at its minimum section. As described in Sect. 3, an additional finite element analysis with a much denser mesh was usually used to confirm the convergence of the computed average axial true stress–true strain curve and the representative results for the miniature square tension bar are shown in Fig. 5d: little difference is seen between the two FE-computed average axial true stress–true strain curves (one with the number of elements listed in Table 2 and one with up to 8 times more elements) and they both are closely match the experimentally measured one.

Fig. 5
figure 5

Some representative results of the finite element analysis of the GMT77 steel square tension bar up to the maximum measured average axial true strain: (a) the deformed mesh; (b) the distribution of the von Mises effective true stress; (c) the distribution of the von Mises effective true strain; (d) experimentally measured and two computed average axial true stress–true strain curves (one with a coarse mesh and another with a fine mesh)

Full size image

Figure 6 shows a summary of the finite element analysis results on the aluminum sheet metal tension coupon with a tapered gage section (whose digital images acquired during the experiment are shown selectively in Fig. 2). To illustrate the progression and effectiveness of the iterative correction procedure in obtaining the effective true stress–true strain curve \( \bar \sigma (\bar \varepsilon ^{p} ) \)for each material, the experimentally measured average axial true stress–true strain curve (i.e., \( \bar \sigma _{x}^{E} (\bar \varepsilon _{x} ) \) or “experimental SS curve 3”) and the three effective true stress–true strain curves used in the successive analysis sessions (such as \( \bar \sigma ^{{M1}} (\bar \varepsilon ) \) or “material model input 1”, etc.) are shown in Fig. 6a while the experimentally measured and three FE-computed average axial true stress–true strain curves (such as \( \bar \sigma _{x}^{{C1}} (\bar \varepsilon _{x} ) \) or “prediction1 SS curve 3”, etc.) are shown in Fig. 6b. Only two finite element analysis sessions were actually needed to obtain the satisfactory effective true stress–true strain curve according to the results shown in both Fig. 6a and b. The initial guess of the effective true stress–true strain curve \( \bar \sigma ^{{M1}} (\bar \varepsilon ) \) was based on only the initial portion of the stress–strain curve \( \bar \sigma _{x}^{E} (\bar \varepsilon _{x} ) \) before the apparent strain- softening occurs (see Sect. 3.2 for details). The final effective true stress–true strain curve is found to start deviating from \( \bar \sigma _{x}^{E} (\bar \varepsilon _{x} ) \) noticeably at a very small strain of less than 0.02 because the aluminum sheet metal AA1100-H14 is in a work-hardened state. The FE-computed average axial true stress–true strain curve after the third finite element analysis session matches well the experimentally measured one up to the true strain of 0.375. Afterwards, the FE-computed curve shows no or much less softening behavior. The discrepancy between the computed and measured curves was due to the fact that the axial dimension Δx of the neck region area S used in the post-processing of the finite element analysis results to obtain the average axial true strain by Eq. 1 (see Sect. 2) was smaller than the one used in the digital image correlation based strain measurement calculations. The axial dimension Δx of the neck region area S were subsequently adjusted closely to the one used in experimental strain measurement calculations for other four tension coupons in the following.

Fig. 6
figure 6

Summary of the finite element analysis results on the aluminum sheet metal tension coupon: (a) comparison of the experimentally measured average axial true stress–true strain curve and the three effective true stress–true strain curves used in the successive analysis sessions; (b) comparison of the experimentally measured and three computed average axial true stress–true strain curves

Full size image

Similar finite element analysis results on the copper sheet metal tension coupon with a straight gage section are summarized in Fig. 7. Again only two finite element analysis sessions were actually needed to obtain the satisfactory effective true stress–true strain curve as the correction factor \( \alpha ^{{C2}} (\bar \varepsilon ) \) obtained after the second finite element analysis session was found to be nearly a constant of 1. The maximum axial true strain measured in the experiment is rather small (0.35) as the spatial resolution of the digital images acquired for the copper tension coupon was lower. A larger field of view was needed for the digital images acquired in the experiment in order to capture the neck region formed somewhere along the straight gage section of the copper tension coupon after diffuse necking. Results of finite element analyses on the low-carbon steel sheet metal tension coupon with a tapered gage section are summarized in Fig. 8. Here a total of three finite element analysis sessions were needed to reach the final effective true stress–true strain curve. It s noted that the maximum axial true strain from the experiment (1.05) is much higher than that of the copper tension coupon (0.35) as a smaller field of view was able to be used for the tapered steel tension coupon.

Fig. 7
figure 7

Summary of the finite element analysis results on the copper sheet metal tension coupon: (a) comparison of the experimentally measured average axial true stress–true strain curve and the three effective true stress–true strain curves used in the successive analysis sessions; (b) comparison of the experimentally measured and three computed average axial true stress–true strain curves

Full size image
Fig. 8
figure 8

Summary of the finite element analysis results on the steel sheet metal tension coupon: (a) comparison of the experimentally measured average axial true stress–true strain curve and the three effective true stress–true strain curves used in the successive analysis sessions; (b) comparison of the experimentally measured and three computed average axial true stress–true strain curves

Full size image

Results of the finite element analyses on the titanium sheet metal tension coupon and on the miniature square tension bar are shown in Figs. 9 and 10, respectively. The maximum average axial true strains measured in the experiment are similar for these two tests: 0.64 and 0.66, respectively. To check the robustness of the iterative correction procedure used in this study, the initial guess of the effective true stress–true strain curve \( \bar \sigma ^{{M1}} (\bar \varepsilon ) \) was intentionally adjusted to deviate to a certain degree from the experimentally measured average axial true stress–true strain curve beyond diffuse necking: a lower stress–strain curve \( \bar \sigma ^{{M1}} (\bar \varepsilon ) \) was used for the titanium sheet metal and a higher stress–strain curve \( \bar \sigma ^{{M1}} (\bar \varepsilon ) \) was used for the miniature steel square bar. As shown in both Figs. 9 and 10, the final effective true stress–true strain curves were obtained again with just two finite element analysis sessions for the titanium sheet metal tension coupon and three finite element analysis sessions for the miniature steel tension bar.

Fig. 9
figure 9

Summary of the finite element analysis results on the titanium sheet metal tension coupon: (a) comparison of the experimentally measured average axial true stress–true strain curve and the three effective true stress–true strain curves used in the successive analysis sessions; (b) comparison of the experimentally measured and three computed average axial true stress–true strain curves

Full size image
Fig. 10
figure 10

Summary of the finite element analysis results on the miniature steel tension bar: (a) comparison of the experimentally measured average axial true stress–true strain curve and the three effective true stress–true strain curves used in the successive analysis sessions; (b) comparison of the experimentally measured and three computed average axial true stress–true strain curves

Full size image

5 Discussions and conclusion

It is well known that the stress–strain data obtained in a standard tension test of a sheet metal using the conventional extensometer strain measurement technique under-predicts the effective true stress of the material beyond diffuse necking. The average axial true stress–true strain curve \( \bar \sigma _{x}^{E} (\bar \varepsilon _{x} ) \) obtained by the digital image correlation based local strain measurements usually over-predicts the effective true stress, especially at large strains well beyond diffuse necking point (see the results shown in Figs. 6a– 10a). Consequently, the stress–strain curves by the conventional and the DIC-based methods can be used, respectively as the lower and upper bound estimates of the effective true stress–true strain curves (they were designated as stress–strain curves no. 2 and 3, respectively in Tong et al. 2005, 2007; Marya et al. 2006). However, some apparent “strain softening” is often observed on the average axial true stress–true strain curve \( \bar \sigma _{x}^{E} (\bar \varepsilon _{x} ) \) before the final tearing failure of a sheet metal (see especially Figs. 6a, 8a). While some material damages (void nucleation and growth) may occur during the diffuse and localized necking (Duan et al. 2007), one of the major factors contributing to the apparent softening behavior is the limited spatial resolution of the local strain measurements inside the neck by digital image correlation. That is, the plastic deformation becomes so localized in the later part of the neck development only a small portion of the material inside the subset size (which is used in a digital image correlation analysis for computing its average strain) experiences the plastic straining. The apparent softening behavior is thus similar to the one observed in the conventional tension test results due the limited spatial resolution to resolve the non-uniform deformation. It is thus suggested that digital images with high speckle densities and highest possible pixel spatial resolution should be acquired at the necking region of a tension coupon during experiment. This can be accomplished by using a digital imaging system with a large pixel count and using a smaller field of view (a higher magnification).

Both experimental observations and numerical simulations show that the local strain becomes increasingly non-uniform once a diffuse neck develops in a tension test coupon. However, the degree of the strain non-uniformity and the rate of its development are found to depend on the initial aspect ratio of the minimum cross-section of a tension test coupon for a given material. Obviously, both a smaller degree and a slow rate of growth of the strain non-uniformity are preferred so the correction on the experimental measurements would be smaller as well. Inspection of Figs. 6–10 shows that there is a general trend in the experimental measurements: the larger the aspect ratio of the tension coupon cross-section, the smaller the measured maximum value of the axial true strain. To eliminate the possible effect of various strain hardening behavior among the five materials on the measured maximum strain values at a fixed image spatial resolution (a fixed size of S), an additional finite element analysis was carried out for the miniature steel tension coupon with an aspect ratio of its cross-section being 5 (instead of 1 as listed in Table 1). The final effective true stress–true strain curve shown in Fig. 10a was used in the finite element analysis. Fig. 11 shows the comparison of the two FE-calculated average axial true stress–true strain curve (with aspect ratios of 1 and 5, respectively). The experimentally measured stress–strain curve is also shown in Fig. 11, which is nearly identical to the computed one using a tension coupon with an aspect ratio of 1 (see Fig. 10b). Again, the necking area S used in computing the average axial true strain (see Eq. 1) had the same axial dimension Δx (as the same as the size in the axial direction of the subset used in the digital image correlation analysis). When the aspect ratio of the cross-section of the tension coupon was increased from 1 to 5, these two FE-computed curves start to diverge at the average axial true strain of about 0.42, indicating a higher degree of strain localization inside the neck region of the tension coupon with a large aspect ratio (which shows faster apparent softening behavior). So tension coupons with a tapered geometry and a reduced aspect ratio are thus preferred to be used in the experimental measurements and associated numerical simulations for obtaining the effective true stress–true strain curve of a ductile sheet metal at very large strains.

Fig. 11
figure 11

The effect of the aspect ratio of tension coupon cross-section on the computed average axial true stress–true strain curves. The material is the heat-affected zone of a dual-phase steel DPS600 (the same as the miniature steel tension bar)

Full size image

The correction methods with direct finite element analyses used by (Zhang and Li 1994; Ling 1996; Joun et al. 2008) and by us here strike a proper balance between the requirements for accuracy and robustness and the needs for reduced computational cost and complexity by using the reduced experimental data. The hybrid experimental and numerical methods using the whole field displacement measurement data as the target for finite element analysis results such as the one used by Kajberg and Lindkvist (2004) are often too complex and costly as their so-called objective function was based on the entire field of displacement and strain measurements. As the displacement field data outside the actively deforming material inside the neck region become less useful anyway for characterizing the material deformation behavior at large strains, such methods may not obtain improved results with additional complexity and cost. The iterative correction procedure described in this study is however much superior as it uses the locally measured average axial true stress–true strain curve as the target in the iterative correction steps. The global load-displacement commonly used by other correction methods (e.g., Ling 1996) becomes less reliably as the diffuse neck initiates and eventually develops into the localized mode in a sheet metal. On the other hand, the local axial true stress–true strain curve is measured directly off the actively plastic straining material (even inside a localized neck if the spatial resolution of digital images is sufficiently high) and is less affected by any possible irregular boundary loading conditions at the two gripping ends according to the St. Venant’s principle (as the neck is usually furthest away from either gripping end in a tension test). Unlike the proposed methods of using step-by-step iterative corrections inside a single finite element analysis (Zhang and Li 1994; Joun et al. 2008), the current procedure is suitable for use with any general-purpose commercial finite element program as the correction steps are carried out in a post-processing step.

Compared with some simple correction methods recently proposed in the literature (Zhang et al. 1999; Scheider et al. 2004; Yang and Tong 2008), the correction methods of using direct finite element analyses of a tension test are still more complex and costly besides the need for accessing a finite element analysis program. However, within the limit of the experimental measurement and numerical analysis errors and the validity of the assumed material constitutive model, the finite element analysis based methods would always produce more accurate and reliable results. The iterative correction procedure is applicable to tension tests of any coupon geometries and can be easily extended to other types of mechanical tests as well. Once a finite element model is developed for a given tension coupon geometry and the associated hybrid experimental and numerical data analysis procedure is implemented, the current correction method can be used on a routine basis with relative easy and low cost. In fact, one can even combine these two correction approaches to more efficiently obtain the accurate effective true stress–true strain curves of sheet metals: one can first use one of the simple correction methods such as the one suggested by Yang and Tong (2008) to correct the average axial true stress–true strain and then use it as a better initial guess of the effective true stress–true strain curve into a finite element analysis of the tension test. If the initial correction is indeed sufficiently accurate, then the results of the finite element analysis should show no need for further correction and can thus be served as a quality control and assessment tool of the simple correction method. Otherwise, further corrections can be carried out following the iterative procedure described in this study (see Sect. 3.2). As one expects, this improved procedure of the predictor-corrector method may only require no more than a total of two finite element analysis sessions to obtain the accurate effective true stress–true strain curve of a sheet metal. As general-purpose commercial finite element analysis programs become increasingly available in research labs and industrial design firms, the advantages and superior results by the finite element analysis based correction method proposed in this study can be readily realized for improved design applications.

In summary, by using the experimentally measured average axial true stress–true strain curve \( \bar \sigma _{x}^{E} (\bar \varepsilon _{x} ) \) as the initial guess of the effective true stress–true strain curve of a sheet metal material in a finite element analysis of a uniaxial tension test of the material, the accurate effective true stress–true strain curve can be obtained quickly by the iterative correction procedure presented here. The objective of the iterative correction procedure applied to the successively corrected effective true stress–true strain curves is to minimize the difference between the experimentally measured and FE-calculated average axial true stress–true strain curves. In particular, it can be carried out after each finite element analysis session outside the finite element program. The final effective true stress–true strain curve can be determined for arbitrarily general strain hardening behavior of a sheet metal as no specific analytical strain-hardening model is assumed, which is the case in Ling (1996), Kajberg and Lindkvist (2004). Once the final effective true stress–true strain curve is obtained as a set of discrete data points, one can always carry out a curve-fitting routine to find the proper material parameters for one of strain hardening models such as the ones used by Ling (1996), Kajberg and Lindkvist (2004), Dan et al. (2007), Yang and Tong (2008).