Advances in computational contact mechanics

Abstract

Great strides have recently been made in the application of computational mechanics to the design of highly complex engineering systems. It has now become abundantly clear that advanced modelling techniques are central to the competitiveness of the industrialised nations. Excellent examples of this assertion are the computer-integrated design of the recent Boeing 777 aircraft, the collapsible foam-filled structures for the car of the next century and new prosthetic implants for Rheumatoid Arthritis. It is with this in mind that the author focuses his attention to a class of problems where contact mechanics plays a major role in dictating the mechanical integrity of the component/system. Three aspects of the current study are accordingly examined. The first is concerned with the development of the appropriate dynamic variational inequalities expressions, which are capable of the accurate and consistent representation of contact problems. The second is concerned with the development of robust solution algorithms that guarantee the accurate imposition of the kinematic contact constraint and avoid interpenetration. The third is concerned with the application of the developed algorithms to realistic design problems involving intricate mechanical and biomechanical systems.

1 Introduction

Contact problems play an important role in dictating the integrity, performance and safety of many engineering systems/components involved in vehicle design, armament and ballistics, metal forming/cutting, and surface treatments, just to name a few. Despite their importance to the mechanical integrity of the systems examined, contact effects are frequently treated using oversimplifying assumptions, which neglect the main feature of the problem. The reason is that modelling dynamic contact in solids poses mathematical and computational difficulties. With the application of loads to the bodies in contact, the actual surface on which these bodies meet, change with time, and the stresses at the surfaces are generally unknown and complex to determine.

The subject of contact mechanics may be said to have started in 1882 with the pioneering publication of Hertz (Hertz 1882). His theory of contact was developed for elastic smooth frictionless bodies, with the contact region being small compared with the dimensions of the bodies. Hertz formulated the conditions of contact by considering two elastic bodies. In order to obtain expressions for the size of the contact zone and the value of the contact pressure, several simplifications and restrictions were imposed. These include:

• (i) the contacting surfaces must be smooth,

• (ii) the strains and displacements adhere to the small strain theory of elasticity,

• (iii) the stress, in each of the half-space bodies considered, is related to the strain by Hooke’s law,

• (iv) the surfaces of the elastic half-space bodies considered are frictionless, and

• (v) the bodies are in static contact.

Despite its limitations, Hertz’s theory of contact has stood the test of time and has been a landmark in applied mechanics for many decades. More representative analytical solutions of contact problems, mostly developed in the second half of the twentieth century, have been largely associated with the removal of some of these restrictions (see e.g. Johnson 1985, Gladwell 1980). Expressions for contact stresses, size of contact region and displacements at the contact surface were derived for a large number of simplified cases.

In spite of the progress so far made in analytical contact mechanics, the proper treatment of the general dynamic frictional contact problem is still beyond the reach of these analytical solutions. In order to overcome these limitations, most contact problems are currently being treated using computational techniques, with the finite element method being the most appealing.

2 Computational contact mechanics

With the rapid development in the capabilities of digital computers, numerical methods became the prime interest of researchers. Several formulations have been proposed to treat frictional contact problems using the Boundary Element Method (BEM) (Aliabadi and Brebbia 1993) and the Finite Element Method (FEM) (Bathe 1996; Crisfield 1997; Hughes 1987; Zienkiewicz and Taylor 1988; Zhong 1993). However, the FEM is now considered the most favourable, because of its proven success in treating a wide range of engineering problems in areas of mechanics of solids, fluid flow, heat transfer, electromagnetism and coupled field problems. In addition, the BEM becomes computationally inefficient when treating nonlinear problems requiring the calculation of the field variables inside the domain (Aliabadi and Brebbia 1993).

Original FE formulations did not accommodate the treatment of contact and ad hoc techniques were used. In these cases, simplifying assumptions regarding the actual contact surface and the distribution of the contact stress were made. These simplifying assumptions enabled the treatment of each individual body as a separate problem, see for example (Kenny et al. 1991). This ad hoc technique proved inadequate in many cases where neither the contact surface nor the stresses on it could be easily estimated. This has prompted the development of contact elements.

FE methods treat contact problems by extending the variational formulation upon which the FE method is based. Contact elements are formulated and assembled into the original FE code in order to enforce the contact conditions (Böhm 1987). The solution is then obtained by solving the resulting set of nonlinear equations. A large number of contact element formulations has appeared in the literature and has been implemented in a number of commercial FE packages over the last two decades (see for example Chaudhary and Bathe 1985). The solution techniques adopted in these formulations were based upon using either function method or Lagrange multipliers in identifying the contact surface and imposing the contact constraints.

Figure 1 shows a typical example of such contact elements. This particular element is adopted in several FE packages including ANSYS (ANSYS 1999) and MARC (MARC 1993). In this case, the element is based on two stiffness values. They are the normal contact stiffness K_N and the tangential contact stiffness K_T.

Fig. 1

A typical contact element

The normal stiffness K_N is used to penalize interpenetration between the two bodies, while the tangential stiffness K_T is used to approximate the sudden jump in the tangential force, as represented by Coulomb’s friction law when sliding is detected between the two contacting nodes.

Advantages of contact elements

Because of the simplicity of their formulation, contact elements enjoy the following advantages:

• (i) they are simple to formulate,

• (ii) they are easily accommodated into existing FE codes, and

• (iii) they are easy to use.

However, experience with contact elements indicates that they suffer from several difficulties as indicated below.

Disadvantages of contact elements

Figure 2a, b show the variation of the normal and tangential stiffness, K_N and K_T, with displacement. A major problem in the implementation of contact element is the assignment of values to K_N and K_T.

Fig. 2

Variation of contact stiffness with relative nodal displacement: (a) normal stiffness K_N and (b) tangential stiffness K_T

The values of K_N and K_T are required to be very large. However, the use of excessively high values of K_N and K_T results in ill-conditioned global stiffness matrices, leading to numerical errors and divergence. On the other hand, the use of smaller values of K_N and K_T, results in convergence to the wrong solution allowing for interpenetration and wrong estimates of the stick and slip regions. In addition, they lack in mathematical rigor as evidenced by Böhm (1987) as they ignore the non-differentiability of Coulomb’s friction law. Therefore, the difficulties with contact elements can be summarized as follows:

• (i) their performance, in terms of convergence and accuracy, depends on user defined parameters,

• (ii) they increase the size of the problem, and

• (iii) they do not deal with the non-differentiability issue of Coulomb’s friction forces.

In an attempt to overcome some of these difficulties, several formulations combined the method of Lagrange multipliers with that of the penalty function method. In this case, the active contact constraints are first identified by a penalty-type contact element and then the frictional forces are estimated and used with Lagrange multipliers to enforce contact conditions. Although these formulations are better than the above two approaches, they are still dependent upon user defined parameters which govern the convergence and accuracy of the solution. In addition, mathematical inconsistencies associated with the use of Coulomb friction forces are not resolved by combining the two techniques.

Because of the difficulties associated with traditional contact elements, current research efforts on the subject are focused on the formulation and implementation of the newly developed Variational Inequalities (VI) formulations.

2.1 Solution techniques

The exact variational representation of frictional contact problems results in a variational inequality. However, most FE methods treat contact problems by extending the variational formulation, which involve integrals over unknown contact surfaces (e.g., Hughes 1987; Zienkiewicz and Taylor 1988; Zhong 1993). Hughes et al. were the first to provide a detailed analysis of a class of impact frictionless problems (Hughes et al. 1976). In their method, Lagrange multipliers together with Newton-Raphson iterative procedure were utilised to solve the resulting dynamic expressions. Chaudhary and Bathe used Lagrange formulation to solve the static and dynamic contact problems accounting for friction (Chaudhary and Bathe 1986). Wriggers and Simo developed consistently linearised contact formulations for static problems (Wriggers and Simo 1985), while Wriggers et al. (1990) used a penalty formulation to solve these dynamic contact problems. Parisch developed consistent tangent stiffness matrices for treating quasi-static large deformation problems (Parisch 1989). Laursen and Simo developed an approach for treating dynamic frictional contact problems which experience large deformations (Laursen and Simo 1993). In order to impose the kinematic contact conditions, they employed the penalty and augmented Lagrangian regularisation approaches.

The use of the variational method to formulate quasi-static or dynamic contact problems lacks in mathematical rigour, especially when frictional effects are taken into account. This is partly due to the non-differentiability of Coulomb’s friction law, which is not properly addressed in the variational formulations. Furthermore, it usually results in the introduction of user-defined parameters, which influence the accuracy of the solution and the rate of convergence (see e.g., Böhm 1987; Refaat and Meguid 1994).

3 Variational inequalities formulations

The theory of variational inequalities is a relatively young mathematical discipline. It can be considered as an alternative mathematical description of physical problems, which is useful in problems involving constraints. A wide range of applications ranging from network economics to contact mechanics, are ideally formulated using variational inequalities (see e.g., Ferris and Pang 1997). However, the VI approach has not gained popularity in the engineering community because most of the work has appeared in the mathematical literature. The focus of the work was to examine the existence and uniqueness of the resulting inequalities (Adams 1975; Duvaut and Lions 1976; Glowinski et al. 1981; Hlavacek et al. 1988; Rabier et al. 1986; Kinderlehrer and Stampacchia 1980). Only in the last two decades interesting results related to contact have appeared in the engineering literature (see e.g., Kikuchi and Oden 1988; Oden and Martins 1983, 1985; Refaat and Meguid 1996).

The main basis for the development of VI formulations for contact problems was the works of Duvaut (Duvaut and Lions 1976) on the solution of the Signorini problem. Later on, Stampacchia laid the foundation of the theory itself (Kinderlehrer and Stampacchia 1980). Several authors examined the existence and uniqueness of the VI formulation of contact problems (see e.g., Kikuchi and Oden 1988; Klarbring 1988).

However, the literature indicates that little work has been carried out to develop suitable computational techniques to make use of these theoretical results. In this regard, dynamic elastic contact for small deformation was presented by Kikuchi and Oden (Kikuchi and Oden 1988; Oden and Martins 1983, 1985). They devoted their efforts to the mathematical questions concerning existence and uniqueness of the variational inequalities representing different contact problems. They also presented a solution technique based on the use of the penalty method, regularisation, and implicit Newmark time integration. Unfortunately, the resulting solution algorithm suffers from the same disadvantages as those outlined in the traditional penalty approach. A few other publications have devoted attention to the practical implementation of variational inequalities in static contact problems (see e.g., Bogomolny 1984; Bischoff 1984; Qin and He 1995; El-Abbasi 1999).

The current research study overcomes these difficulties by developing and implementing a new variational inequalities methodology to treat dynamic frictional contact in engineering structures.

In the unilateral (Signorini-type) problem, the contact constraints are shown in Fig. 3, and can be expressed as follows:

$$ \hbox{before/after contact } \hbox{u}_{{\rm N}}-\hbox{g} < 0\Rightarrow\sigma_{{\rm N}}=0\,\&\,\dot{\hbox{u}}_{{\rm N}}\hbox{ is unconstrained } $$

(1a)

$$ \hbox{during contact }\hbox{u}_{{\rm N}}-\hbox{g}=0\Rightarrow \sigma_{{\rm N}}\leq 0\,\&\,\dot{\hbox{u}}_{{\rm N}}\le0 $$

(1b)

Fig. 3

Two bodies in contact: (a) unilateral contact model, and (b) schematic of kinematic contact condition

These contact constraints state that: (i) the magnitude of the normal contact stress is less than or equal to zero, and (ii) the displacement of the contacting surfaces must not allow for interpenetration. Note that no constants are required to describe the contacting surfaces in the normal direction.

Coulomb’s friction condition can be expressed as follows:

$$ \hbox{u}_{\rm N} < \hbox{g}\Rightarrow\sigma_{\rm T}=\mathbf{0}$$

(2)

$$ \hbox{u}_{\rm N}=\hbox{g}\Rightarrow\left\{\begin{array}{l} |\sigma_{\rm T}|\le-\mu\sigma_{\rm N}\hfill \\ |\sigma_{\rm T}| < -\mu\sigma_{\rm N}\Rightarrow\dot{{\mathbf{u}}}_{\rm T}={\mathbf{0}},\hfill \\ |\sigma_{\rm T}|=-\mu\sigma_{\rm N}\Rightarrow\exists\lambda\ge0,\quad \dot{{\mathbf{u}}}_{\rm T}=-\lambda\varvec{\sigma}_{\rm T}.\hfill \\ \end{array}\right. $$

(3)

where μ is the coefficient of friction and is assumed to be independent of velocity. This means that tangential stresses are only present if there is contact.

3.1 Dynamic VI formulation for elasto-plastic media

The dynamic contact problem for elastic-plastic media must satisfy the following equations:

• (i) The equation of motion:

  $$ \frac{\partial^{{\rm t}}\sigma_{\rm ij}}{\partial^{{\rm t}}\hbox{x}_{\rm j}}+{}^{\rm t}\hbox{f}_{\rm i}={}^{\rm t}\rho\frac{\partial^{2}({}^{{\rm t}}\hbox{u}_{\rm i})} {\partial\hbox{t}^{2}} $$

  (4)

• (ii) The constitutive law governing the behaviour of the material:

  $$\sigma_{\rm ij}({\mathbf{u}})=\hbox{C}_{\rm ijkl}\varepsilon_{{\rm kl}}({\mathbf{u}}) $$

  (5)

• (iii) The initial conditions:

  $$ {\mathbf{u}}(0)={\mathbf{u}}_{\rm o},\quad \dot{{\mathbf{u}}}(0)=\dot{{\mathbf{u}}}_{\rm o} $$

  (6)

• (iv) The displacement and traction boundary conditions:

  $${\mathbf{u}}_{\rm i}= \bar{{\mathbf{u}}}_{\rm o}\quad \hbox{on }\Upgamma_{\rm D} $$

  (7)
  $$ \sigma_{\rm i}\hbox{n}_{\rm i}= \hbox{t}_{\rm i}\quad \hbox{on }\Upgamma_{\rm F} $$

  (8)

• (v) The kinematic contact and frictional conditions on Γ_C.

Restrictions imposed upon admissible displacement, velocity and stress field are not, in general, equalities but rather inequalities. Accordingly, the variational inequalities approach can be viewed as being the formulation of the principle of rate of virtual work in an inequality form. In the following, we will derive the variational inequality for dynamic frictional contact problems. The basic steps of the derivation are summarised in Fig. 4.

Fig. 4

Basic steps of derivation of dynamic VI formulations for elastic media

The elasto-plastic material considered here is assumed to experience large displacements and large strains. In this case, it is necessary to adopt the Green-Lagrange strain tensor and its energy conjugate, the second Piola-Kirchhoff stress tensor, to account for the necessary kinematic relationships. These formulations are developed in the updated Lagrangian framework. The incremental dynamic variational inequality takes the form:

$$ \langle\rho\ddot{{\mathbf{u}}},\dot{{\mathbf{v}}}- \dot{{\mathbf{u}}}\rangle+A({\mathbf{u}},\dot{{\mathbf{v}}}- \dot{{\mathbf{u}}})+j({\mathbf{u}},\dot{{\mathbf{v}}})-j({\mathbf{u}},\dot{{\mathbf{u}}})\ge R(\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}}),\quad \dot{{\mathbf{v}}} \in {\mathbf{K}} $$

(9)

$${\mathbf{u}}(0)={\mathbf{u}}_{\rm o}\quad \hbox{and}\quad \dot{{\mathbf{u}}}(0)=\dot{{\mathbf{u}}}_{\rm o} $$

where,

• (i) the first term represents the rate of virtual work done by the inertia forces:

  $$ \langle{\rho\ddot{{\mathbf{u}}}},\dot{{\mathbf{v}}}\rangle =\int\limits_{{}^{t+\Updelta t}\Upomega}\rho\ddot{\mathbf{u}}\cdot\dot{\mathbf{v}} d\,{{}^{t+\Updelta t}\Upomega} $$

  (10)

  (ii) the second represents the rate of virtual work done by the internal forces:

  $$ A({\mathbf{u}},\dot{{\mathbf{v}}})= \int\limits_{{}^{t}\Upomega}{}_t C_{ijrs}^{ep}\,{}_t e_{ij}({\mathbf{u}})\,{}_t e_{ij}(\dot{{\mathbf{v}}})d\,{{}^{t}\Upomega} +\int\limits_{{}^t\Upomega}{{}^t\sigma_{ij}({\mathbf{u}})\,{}^t\eta _{ij}}(\dot{{\mathbf{v}}})d\,{{}^{t}\Upomega} $$

  (11)

• (iii) the fourth and fifth terms represent the rate of virtual dissipation by the frictional forces, and can be represented as follows:

  $$ j({\mathbf{u}},\dot{{\mathbf{v}}})=\int\limits_{{}^{t+\Updelta t}\Upgamma_{\rm C}}-\mu^{t+\Updelta t}\,\sigma_{\rm N}({\mathbf{u}})\left|\dot{{\mathbf{v}}}_{\rm T}\right| d\,{{}^{t+\Updelta t}S} $$

  (12)

• (iv) the term on the right-hand-side represents the rate of virtual work done by the residual external forces (unbalance force between the external loading and internal stresses):

  $$ R(\dot{{\mathbf{v}}})=\int\limits_{{}^{t+\Updelta t}\Upomega}{}^{t+\Updelta t}{\mathbf{f}}\cdot(\dot{{\mathbf{v}}})d\,{{}^{t+\Updelta t}\Upomega} +\int\limits_{{}^{t+\Updelta t}\Upgamma_{\rm F}}{{}^{t+\Updelta t}{\mathbf{t}}\cdot(\dot{{\mathbf{v}}})d\,{}^{t+\Updelta t}S}-\int\limits_{{}^t\Upomega} {}^t\sigma_{ij}({\mathbf{u}}(t)){{}_t e_{ij}}(\dot{{\mathbf{v}}})d\,{}^{t}\Upomega $$

  (13)

In addition to the above variational inequality, the elasto-plastic behaviour of the material will be characterised by a yield function F, a strain hardening function ^tκ and the appropriate flow rule. In this case, the constitutive relations take the following form:

$$ \hbox{F}({}^{\rm t}\sigma_{\rm ij},{}^{\rm t}\kappa)=0, \hbox{d}\, {}_{\rm t}\hbox{e}_{\rm ij}^{\rm p}={}^{\rm t}{\hbox {d}}\lambda \frac{\partial {\hbox {F}}}{\partial \,{}^{\rm t}\sigma _{\rm ij}} $$

(14)

$$ \mathop{{}^{\rm t}\sigma_{\rm ij}}\limits^{\nabla}\hbox{dt}={}_{\rm t}\hbox{C}^{\rm e}_{\rm ijrs}(\hbox{d}\,{}_{\rm t}\hbox{e}_{\rm rs}-\hbox{d}\,{}_{\rm t}\hbox{e}_{\rm rs}^{\rm p}) $$

(15)

with C^e _ijrs being the material elastic constitutive tensor.

3.2 Special sub-problems of VI formulations

Currently, there is no direct method available for the solution of the general frictional contact problem of Eq. 9 with all the terms included. In our approach, we divide the general elasto-dynamic variational inequality into two consistent sub-problems. Details are provided below.

3.2.1 Sub-problem I: prescribed tangential stresses

If the tangential stresses $\varvec{\sigma}_{\rm T}$ are assumed to be known everywhere on the boundaries of the two bodies at time t + Δt, then variational inequality (9) reduces to (Fig. 5a):

$$ \langle{\rho\ddot{{\mathbf{u}}}},\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}} \rangle +A({\mathbf{u}},\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}})\ge R_1 (\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}})\quad \dot{\mathbf{v}}\in\mathbf{K}$$

(16)

where

$$R_1 (\dot{{\mathbf{v}}})=R(\dot{{\mathbf{v}}})+\int\limits_{^{{\rm t}+\Updelta{\rm t}}\Upgamma_{\rm C}}{\sigma _{\rm T}\cdot\dot{{\mathbf{v}}}d\,{}^{{\rm t}+\Updelta{\rm t}}S} $$

(17)

Fig. 5

(a) Prescribed tangential contact stresses on the boundaries (sub-problem I), and (b) prescribed normal contact stresses together with the actual contact surface Γ_C (sub-problem II)

The effect of friction is now included in the expression of $\hbox{R}_{1}(\dot{{\mathbf{v}}})$ as known tractions over the boundary Γ_C. Note that for the unilateral contact model, the rate of work done by the normal contact stresses $\langle\hbox{P}({\mathbf{u}}),\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}}\rangle$ is always negative or equal to zero. Therefore, variational inequality Eq. 16 is reduced to:

$$ \langle{\rho\ddot{{\mathbf{u}}}},\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}} \rangle +A({\mathbf{u}},\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}})\ge R_1(\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}}) $$

(18)

3.2.2 Sub-problem II: prescribed normal stresses and contact surface

In sub-problem II, where the normal stresses σ_N together with the actual contact surface Γ_C are known (Fig. 5b), the variational inequality (9) reduces to:

$$ \langle{\rho\ddot{{\mathbf{u}}}},\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}} \rangle+\hbox{A}({\mathbf{u}},\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}})+ \hbox{j}(\dot{{\mathbf{v}}})-\hbox{j}(\dot{{\mathbf{u}}})\ge \hbox{R}_2 (\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}}),\quad \dot{{\mathbf{v}}} \in \mathbf{K} $$

(19)

where

$$ \hbox{j}(\dot{{\mathbf{v}}})=\int\limits_{^{{\rm t}+\Updelta{\rm t}}\Upgamma _{\rm C}} {- ^{{\rm t}+\Updelta{\rm t}}\hat{{\sigma }}_{\rm N} \left| {\dot{{\mathbf{v}}}_{\rm T} } \right| d\, ^{{\rm t}+\Updelta{\rm t}}\hbox {S}} $$

(20a)

$$ \hbox{R}_2 (\dot{{\mathbf{v}}})=\hbox{R}(\dot{{\mathbf{v}}})+\int\limits_{^{{\rm t}+\Updelta{\rm t}}\Upgamma _{\rm C} } {^{{\rm t}+\Updelta{\rm t}}\sigma _{\rm N} \dot{{\mathbf{v}}}_{\rm N} \hbox{d}\, ^{{\rm t}+\Updelta{\rm t}}\hbox{S}} $$

(20b)

The above VI formulation (19) has a non-differentiable frictional term j(·) (Eq. 20a). In order to overcome this difficulty, two approaches, regularisationand nondifferentiable optimisation, were adopted (Czekanski and Meguid 2001).

3.3 Modelling of friction

The above VI formulation (19) has a non-differentiable frictional term j(·) (Eq. 20a). In order to overcome this difficulty, two approaches, regularisationand nondifferentiable optimisation, were adopted (Czekanski and Meguid 2001).

3.3.1 Regularisation technique

In the first method, we adopt the following regularisation approximation and its derivative:

$$|\dot{{\mathbf{u}}}|\rightarrow\psi_{\varepsilon}(\dot{{\mathbf{u}}}) =\left\{\begin{array}{ll} |\dot{{\mathbf{u}}}|-\frac{\varepsilon}{2},&|\dot{{\mathbf{u}}}| > \varepsilon\\ \frac{1}{2\varepsilon}\dot{{\mathbf{u}}}\cdot{\mathbf{u}}, &|\dot{{\mathbf{u}}}|\le\varepsilon \end{array}\right. $$

(21)

$$\phi_{\varepsilon}(\dot{{\mathbf{u}}})=\left\{\begin{array}{ll} \frac{\dot{{\mathbf{u}}}}{|\dot{{\mathbf{u}}}|}, &|\dot{{\mathbf{u}}}| > \varepsilon\\ \frac{\dot{{\mathbf{u}}}}{\varepsilon}, &|\dot{{\mathbf{u}}}|\le\varepsilon \end{array}\right. $$

(22)

In this case, the regularised friction conditions reduce to:

$$ \hbox{u}_{\rm N}\ge \hbox{g}\Rightarrow\varvec{\sigma}_{\rm T}\le \hat{\sigma}_{\rm T}\left\{\begin{array}{ll} \frac{\dot{{\mathbf{u}}}_{\rm T}}{|\dot{{\mathbf{u}}}_{\rm T}|}, &|\dot{{\mathbf{u}}}_{\rm T}| > \varepsilon\\ \frac{\dot{{\mathbf{u}}}_{\rm T}}{\varepsilon}, &|\dot{{\mathbf{u}}}|\le\varepsilon \end{array}\right. $$

(23a)

$$ \hbox{u}_{\rm N} < \hbox{g}\Rightarrow\varvec{\sigma}_{\rm T}=\mathbf{0}$$

(23b)

Accordingly, the regularised form of j(.) can be expressed as:

$$ \hbox{j}_\varepsilon(\dot{{\mathbf{v}}})=\int\limits_{{}^{{\rm t}+\Updelta {\rm t}}\Upgamma_{\rm C}}{{}^{{\rm t}+\Updelta{\rm t}}\hat{\sigma}_{\rm T}\psi_{\varepsilon}(\dot{{\mathbf{v}}})\;\hbox{d}\,{}^{{\rm t}+\Updelta{\rm t}}\hbox{S}} $$

(24)

In this case, the regularised frictional term is convex and differentiable with respect to the second argument (Kikuchi and Oden 1988). The partial derivatives of $\hbox{j}_{\varepsilon}(\dot{{\mathbf{w}}})$ in the direction $\dot{{\mathbf{v}}}$, are given by:

$$ \langle{\hbox{J}_\varepsilon (\dot{{\mathbf{w}}}),\dot{{\mathbf{v}}}} \rangle \equiv\langle\partial \hbox{j}_\varepsilon (\dot{\mathbf{w}}), \dot{\mathbf{v}}\rangle=\int\limits_{{}^{{\rm t}+\Updelta{\rm t}} \Upgamma_{\rm C}}{{}^{{\rm t}+\Updelta{\rm t}}\hat{\sigma}_{\rm N} \phi_\varepsilon(\dot{\mathbf{w}})\dot{{\mathbf{v}}}_{\rm T}\hbox{d}\,{}^{{\rm t}+\Updelta {\rm t}}\hbox{S}} $$

(25)

Based on this regularisation technique, the following formulation is obtained:

$$ \langle {\rho\ddot{{\mathbf{u}}}}, \dot{{\mathbf{v}}}-\dot{{\mathbf{u}}}\rangle +A({\mathbf{u}},\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}})+\langle {J_\varepsilon (\dot{{\mathbf{u}}}),\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}}} \rangle =R_2 (\dot{{\mathbf{v}}}-\dot{{\mathbf{u}}}) $$

(26)

It is appropriate to identify the role of the regularisation parameter ɛ. This parameter determines the region where the tangential component of the relative sliding velocity on the contact surface is small enough to represent sticking. Experimental studies concerning friction between metallic surfaces indicate the existence of a gradual transition from sticking to slipping, which can be represented using the parameter ɛ (Oden and Martins 1985).

3.3.2 Nondifferentiable optimisation

Mathematical formulation and the numerical computations required as well as the accuracy of the solution obtained using the above technique is dependent on the form of the regularisation function employed and the value of the user-defined regularisation parameter. Several NDO algorithms have been proposed (Balinski and Wolfe 1975; Fletcher 1982; Lemarechal 1974; Mifflin 1982; Shimizu et al. 1997; Shor 1985; Wierzbicki 1982). However, they are inappropriate for dealing with the current VI problem. These difficulties have been overcome in the current solution strategy. The solution of variational inequality (19) is equivalent to the minimisation of the following function π:

$$ \pi=\langle{\rho\ddot{{\mathbf{u}}}},\dot{{\mathbf{u}}}\rangle +\frac{1}{2}A({\mathbf{u}},\dot{{\mathbf{u}}})+j(\dot{{\mathbf{u}}}) -R(\dot{{\mathbf{u}}}){\vert} {\mathbf{N\cdot u}}-\hbox{g}\le0\hbox{ on }\Upgamma_{\rm C} $$

(27)

The function π is nondifferentiable, because of the existence of the absolute value function |·| in the frictional term j(·). The frictionless VI formulation is strictly convex and assumes a unique minimum (Hlavacek et al. 1988, Kikuchi and Oden 1988). By considering the frictional formulation, the problem remains convex and quadratic, if the line representing $\dot{{\mathbf{u}}}_{\rm T}={\mathbf{0}}$ is not crossed. In other words, the function is a convex and quadratic on either side of the $\dot{{\mathbf{u}}}_{\rm T}={\mathbf{0}}$ . Therefore, it is necessary to create an artificial cutting line located at vector $\dot{{\mathbf{u}}}_{\rm T}={\mathbf{0}}$ , which we will denote artificial nondifferentiable optimisation (ANDO)constraint. Therefore, the frictional term j(·) represented in Eq. 20, can be described by two complementary sub-problems with additional ANDO constraints (Fig. 6):

$$ \hbox{j}(\dot{{\mathbf{u}}})=\int\limits_{{}^{{\rm t}+\Updelta{\rm t}} \Upgamma_{\rm C}}{{}^{{\rm t}+\Updelta{\rm t}}\hat{\sigma}_{\rm T} \dot{{\mathbf{u}}}_{\rm T}\hbox{d}\,{}^{{\rm t}+\Updelta{\rm t}}\hbox{S}} \vert\dot{{\mathbf{u}}}_{\rm T}\ge{\mathbf{0}}\quad \hbox{on }\Upgamma_{\rm C}$$

(28a)

$$ \hbox{j}(\dot{{\mathbf{u}}})=-\int\limits_{{}^{{\rm t}+\Updelta{\rm t}} \Upgamma_{\rm C}}{{}^{{\rm t}+\Updelta {\rm t}}\hat{\sigma}_{\rm T} \dot{{\mathbf{u}}}_{\rm T} \hbox{d}\,{}^{{\rm t}+\Updelta{\rm t}}\hbox{S}} \vert\dot{{\mathbf{u}}}_{\rm T}\le {\mathbf{0}}\quad \hbox{on } \Upgamma_{\rm C} $$

(28b)

Fig. 6

Solution of nondifferentiable VI function using complementary sub-problems

In this case, each of these complementary two sub-problems is strictly convex and assumes a unique minimum.

The frictional contact problem involves two distinct states: slip and stick. The two complementary NDO sub-problems of Eqs. 27 and 28 lead to two solutions. The ANDO constraint is always active $(\dot{{\mathbf{u}}}_{\rm T}={\mathbf{0}})$ in at least one of the two sub-problems. For the second sub-problem, the ANDO constraint could also be active. In this case, both sub-problems must have the same solution, which represents a state of stick. On the other hand, the constraint in the second sub-problem could be inactive. In this case, the solution of the second sub-problem is always the global minimum, which represents a state of slip.

4 Representation of kinematic contact conditions

The accurate and efficient representation of contact surfaces has received little attention in the scientific literature. Most formulations rely on the use of element interpolation functions to describe the contact surface and to impose the kinematic contact conditions. In most contact algorithms, the contact surfaces are defined as a sequence of lines (or curves) connecting the FE nodes with only C⁰-continuity. In this case, the normal vector is not uniquely defined at element boundaries (Fig. 7).

Fig. 7

Contact surface and normal vector based on spline and traditional element interpolations

Even when higher order elements, such as the 8 and 9 noded 2D elements, are used, the contact surfaces are still non-smooth at the exterior nodes. In fact, higher-order smoothness of the contact surface cannot be achieved through appropriate element selection, since the use of C¹ or higher-order continuous elements in mechanics problems is undesirable (Zienkiewicz and Taylor 1988). On the other hand, only C⁰-continuity of the contact surface violates the assumptions of smoothness, which are essential to the proofs of uniqueness and convexity of contact problems (Kikuchi and Oden 1988). To overcome these inconsistencies, contact problems commonly involve a disproportionately fine mesh at the vicinity of the contact region.

This has motivated the use of splines passing through the FE nodes and possessing at least C¹-continuity. The resulting normal vector is uniquely defined at all point belonging to the selected surface (Fig. 7).

4.1 Cubic spline interpolation of surfaces

Figure 8 shows a smooth cubic spline segment connecting two points in a 2D space. Assuming a parametric representation, the coordinates of any point on this curve can be expressed in terms of an independent variable u, such that:

$$ {\mathbf{x}}\left(\hbox{u}\right)=\left\{\begin{array}{l} {\hbox{x}\left(\hbox{u} \right)}\\ {\hbox{y}\left(\hbox{u} \right)}\\ \end{array}\right\}, \quad 0\le \hbox{u}\le 1 $$

(29)

Fig. 8

Characteristics of a cubic spline segment

For each curve segment α, the interpolation function passes through the end points p ₀ and p ₃, while the intermediate points p ₁ and p ₂ dictate the shape of the curve (Fig. 9). The segment can be described as follows:

$$ {\mathbf{x}}^{\alpha}\left(\hbox{u}\right)=\sum\limits_{\rm i=0}^3 {\hbox{B}_{\rm i}^3\left(\hbox{u}\right)\;{\mathbf{p}}_{\rm i}^{\alpha}} $$

(30)

where

$$ \hbox{B}_{\rm i}^{\rm m}\left(\hbox{u}\right)=\left(\begin{array}{l} \hbox{m}\\ \hbox{i}\\ \end{array}\right)\;\hbox{u}^{{\rm i}}\;(1-\hbox{u})^{{\rm m-i}} $$

(31)

are the Bernstein polynomials.

Fig. 9

Overhauser splines and associated control points

Each spline segment interpolates between two neighbouring points on the contact surface. The end control points p ₀ and p ₃ are located at these points. This guarantees that the interpolated surface passes through all the external points. The intermediate points p ₁ and p ₂ of each segment dictate the shape of the curve and their location is selected based on the specific spline form adopted. In this case, the location of the intermediate control points for all the spline segments are coupled. They can be obtained by solving a predominantly tri-diagonal matrix expressing the C² continuity equations (Hughes et al. 1976).

When the location of the FE nodes changes, the matrix must be solved again for the new location of the intermediate points. The overhead associated with this process does not offset the advantages of second order continuity. Note, however, that if the change in the nodal locations is governed by an affine transformation, such as rigid body translation, rotation or shearing, the modified spline needed not be evaluated again (Hughes et al. 1976). Accordingly, the use of C² cubic splines is only justified for rigid surfaces.

By requiring just C¹ continuity, simpler and faster interpolation functions can be constructed where the intermediate control points can be obtained without resorting to matrix solution. In this case, the location of the intermediate control points of a segment is only governed by a few neighboring nodes. This property is known as local support. A detailed review of C¹-continuous cubic splines is provided in Ref. (Hughes et al. 1976). Interpolation functions can be constructed which satisfy a prescribed tangential vector, a prescribed tangential direction or a prescribed normal direction (Hughes et al. 1976; Wriggers et al. 1990). However, these vectors are generally not available in standard FE meshes. Overhauser splines offer an alternative approach that ensures C¹-continuity without requiring prescribed tangential or normal vectors (Parisch 1989; Laursen and Simo 1993). Accordingly, they are the most suitable interpolation form for the finite element contact problem involving flexible bodies. These splines have also been used to develop smooth boundary elements (Refaat and Meguid 1994) and to evaluate contact between gear teeth (Ferris and Pang 1997). Other cubic spline interpolation schemes possessing the same properties as Overhauser splines were also developed (Duvaut and Lions 1976; Adams 1975). However, not all of them are unique. The Catmull-Rom spline (Duvaut and Lions 1976), for example, is identical to the Overhauser spline.

Each Overhauser curve segment can be considered a linear blend of two parabolas q ^α−1 and q ^α (Fig. 9):

$$ {\mathbf{x}}^{\alpha}\left(\hbox{u}\right)=\left(1-\hbox{u}\right) \;{\mathbf{q}}^{\alpha-1}\left(\hbox{u}+1\right)+\hbox{u}\;{\mathbf{q}} ^{\alpha}\left(\hbox{u}\right),\quad 0\le \hbox{u}\le 1 $$

(32)

Each parabola passes through the two surface nodes ${\mathbf{p}}_{0}^{\alpha}$ and ${\mathbf{p}}_{3}^{\alpha}$ as well as a neighboring surface node (one from each side). Consequently, the Overhauser spline can be expressed directly in terms of the coordinates of the two points defining the segment and their two adjacent points:

$$ {\mathbf{x}}^{\alpha}\left(\hbox{u}\right)=\left[\begin{array}{llll} {{\mathbf{p}}_0^{\alpha -1}}&{{\mathbf{p}}_0^\alpha }& {{\mathbf{p}}_3^\alpha}&{{\mathbf{p}}_3^{\alpha +1}}\\ \end{array}\right]\;\;\left[\begin{array}{l} {-\frac{1}{2}\hbox{u}^{3}+\hbox{u}^{2}-\frac{1}{2}\hbox{u}}\\ {\frac{3}{2}\hbox{u}^{3}-\frac{5}{2}\hbox{u}^{2}+1}\\ {-\frac{3}{2}\hbox{u}^{3}+2\hbox{u}^{2}+\frac{1}{2}\hbox{u}}\\ {\frac{1}{2}\hbox{u}^{3}-\frac{1}{2}\hbox{u}^{2}}\\ \end{array}\right]\;,\quad \quad 0\le \hbox{u}\le1 $$

(33)

It is convenient to use the Bernstein polynomial form of Eq. 30 to represent all forms of cubic splines. In this case, only the location of the four control points should be stored for each spline segment. The first and last control points of each segment coincide with the finite element nodes, while the intermediate control points can generally be obtained using the following relationship:

$$ \begin{array}{l} {\mathbf{p}}_1^\alpha ={\mathbf{p}}_0^\alpha +\frac{1}{3}{\mathbf{m}}^{\alpha}(0)\\ {\mathbf{p}}_2^\alpha ={\mathbf{p}}_3^\alpha -\frac{1}{3}{\mathbf{m}}^{\alpha}(1)\\ \end{array} $$

(34)

where m is the vector tangent to the spline curve such that:

$$ {\mathbf{m}}\left(\hbox{u}\right)=\frac{\hbox{d}}{\hbox{du}} {\mathbf{x}}\left(\hbox{u}\right) $$

(35)

Splines possess several properties which are fundamental to their use for modeling contact surfaces. According to the convex hull property, the spline curve cannot exceed the geometric bounds of the control polygon (Hughes et al. 1976). This polygon is formed from the spline’s control points. This feature is extremely useful for contact detection, since it is much simpler and faster to check interference between a master node and the control polygon rather than the actual spline curve. Most cubic spline interpolation schemes are invariant under affine transformations. This property is generally useful for modeling rigid surfaces. Local support is another important feature that should be present in the splines defining the contact surface. This implies that a change in the location of one of the contact nodes only affects a few neighboring splines and not the entire contact surface. Note, however, that C²-continuous cubic splines do not possess this property.

4.2 Node-to-surface spline slave-master algorithm

In cases involving contact between flexible bodies, analytical surface profiles that describe the initial geometry cannot be used to describe the deformed one. As a result, spline-based surface interpolation should be used.

Based on a master-slave technique, for every point on the master contact surface Γ_m a corresponding closest point on the slave surfaces Γ_s is determined from the kinematics of the deformation (Fig. 10). This is defined for ${\mathbf{x}}\in \Upgamma_{\rm m}$ as being

$$ \Vert{\mathbf{x-y^{\ast}}}({}^{\rm t}{\mathbf{x}})\Vert=\mathop{\hbox{min}}\limits_{{\rm y}\in\Upgamma{\rm_{\rm S}}}\Vert{}^{\rm t}{\mathbf{x}}-{}^{\rm t}{\mathbf{y}}\Vert $$

(36)

The unit normal vector to the slave surface can be defined as:

$$ {}^{\rm t}{\mathbf{N}}=\frac{\partial^{\rm t}{\mathbf{y}}^{\ast}/\partial\xi\times\partial^{\rm t}{\mathbf{y}}^{\ast}/\partial\eta} {\Vert\partial^{\rm t}{\mathbf{y}}^{\ast}/\partial\xi\times\partial^{\rm t}{\mathbf{y}}^{\ast}/\partial\eta\Vert} $$

(37)

where ξ and η are two orthogonal directions tangential to the contact surface. If the contact surfaces are sufficiently smooth, the normal can alternatively be expressed as:

$$ {}^{\rm t}{\mathbf{N}}=\frac{{}^{\rm t}{\mathbf{y}}^{\ast}({}^{\rm t}{\mathbf{x}})-{}^{\rm t}{\mathbf{x}}}{\Vert{}^{\rm t}{\mathbf{y}}^{\ast}({}^{\rm t}{\mathbf{x}})-{}^{\rm t}{\mathbf{x}}\Vert} $$

(38)

Fig. 10

Kinematic contact constraints

The unit outward normal vector for a 2-D spline segment α can be expressed as:

$$ {}^{\rm t}{\mathbf{N}}^{\alpha}\left(\hbox{u}\right)= \frac{[{\begin{array}{ll} {-{}^{\rm t} \hbox{m}_{\rm y}^{\alpha}\left(\hbox{u}\right)}& {{}^{\rm t}\hbox{m}_{\rm x}^{\alpha}\left(\hbox{u}\right)}\\ \end{array}}]^{\rm T}}{\Vert{}^{\rm t}{\mathbf{m}}^{\alpha} \left(\hbox{u}\right)\Vert} $$

(39)

The gap function between two contact surfaces at unknown configuration t + Δt can be expressed as (Fig. 10):

$$ {}^{{\rm t}+\Updelta{\rm t}}\hbox{g}({\mathbf{x}})=\left[{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{y}}^{\ast}({\mathbf{x}})-{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{x}}\right]\cdot{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{N}}\ge0 $$

(40)

This gap function is generally nonlinear. However, for incremental finite element analysis, a linearised form yields:

$$ {}^{{\rm t}+\Updelta{\rm t}}\hbox{g}({\mathbf{x}})={}^{\rm t}\hbox{g}({\mathbf{x}})+\left[\Updelta^{\rm t}{\mathbf{u}}({\mathbf{y}}^{\ast})-\Updelta^{\rm t}{\mathbf{u}}({\mathbf{x}})\right]\cdot{}^{\rm t}{\mathbf{N}}\ge0 $$

(41)

where Δu is the incremental displacement vector.

Contact search

Using nonlinear relationships, such as splines, to represent the contact surface can slow down the contact search procedure. To overcome this, the contact search is divided into two stages. The purpose of the first stage is to obtain a quick estimate of the proximity of a master node to a specific spline segment. In this stage, interference is checked between the master node and the control polygon of the spline segment, as shown in Fig. 11. According to the convex hull property, the spline curve cannot exceed the geometric bounds of the control polygon (Hughes et al. 1976). For rapid penetration problems, it is sometimes useful to search within a wider envelope surrounding the control polygon. If the master node is inside the search region, an accurate iterative contact check is performed in the second stage of the search. In this stage, the exact target point and gap/penetration are determined.

Fig. 11

Control polygon used for preliminary contact search

4.3 Contact constraints

The discretisation of a contact constraint α (Eq. 40 or 41) can be represented as:

$$\left({\mathbf{A}}_{\alpha}\, {\mathbf{\bumpeq}} \, {\varvec{\delta}}_{\alpha}-G_{\alpha}\right)\le 0 $$

(42)

where G_α is the gap and $\varvec{\delta}_{\alpha}$ is the vector of nodal degrees of freedom associated with this constraint.

$$ {\mathbf{\delta}}_{\alpha}=\{{\begin{array}{lllll} {\Updelta{\mathbf{U}}_{\rm M}}&{\Updelta {\mathbf{U}}_{{\rm S}(1)}}& {\Updelta{\mathbf{U}}_{{\rm S}(2)}}&\cdots&{\Updelta {\mathbf{U}}_{{\rm S(L)}}}\\ \end{array}}\}^{\rm T} $$

(43)

where $\Updelta{\mathbf{U}}_{\rm i}$ represents all degrees of freedom associated with node i and L is the number of nodes on the slave surface that affect the displacement of the target node.

Matrix A _α, which represents the contact constraint, can be expressed as follows:

$$ \left\{{{\mathbf{A}}_{\alpha}}\right\}=[\begin{array}{lllll} {{\mathbf{N}}_\alpha^{\rm T}}&{-\phi_{{\rm S}(1)} {\mathbf{N}}_\alpha^{\rm T}}&{-\phi_{{\rm S}(2)}{\mathbf{N}}_\alpha^{\rm T}} &\cdots&{-\Upphi_{{\rm S(L)}}{\mathbf{N}}_\alpha^{\rm T}}\\ \end{array}] $$

(44)

where the weight function ϕ_S(i) is the contribution of each of the surface nodes to the normal displacement at the target point on the slave contact surface. These values are determined based on the contact search and are subject to the following restriction:

$$ \sum\limits_{\rm i=1}^{\rm L}{\phi_{{\rm S(i)}}}=1 $$

(45)

For Overhauser splines, the four weight functions can easily be evaluated based in Eq. 33.

Finally, the assembly of all contact constraints yields a set of inequalities of the form:

$$ {\mathbf{AU}}\le{\mathbf{G}} $$

(46)

where G is the global vector of the gap functions, U is the assembled displacement vector and the A-matrix represents the standard finite element assembly of all individual A _α constraint matrices.

5 Finite element implementation

5.1 Time integration schemes

In order to solve the above VI formulations (Eqs. 16 and 19), the finite difference method is employed in the time domain to establish a relationship between the acceleration, velocity and displacement fields. The Newmark method (Newmark et al. 1959), the most frequently used implicit time integration scheme, allows us to approximate the velocities and displacements at time t + Δt in terms of acceleration at time t + Δt and the field variables at time t, as follows:

$$ {}^{{\rm t}+\Updelta{\rm t}}\dot{{\mathbf{U}}}={}^{{\rm t}}\dot{{\mathbf{U}}}+[(1-\gamma){}^{{\rm t}}\ddot{{\mathbf{U}}}+\gamma\, ^{{\rm t}+\Updelta{\rm t}}\ddot{{\mathbf{U}}}]\Updelta {\hbox{t}} $$

(47a)

$$ {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}={}^{\rm t}{\mathbf{U}}+ {}^{\rm t}\dot{{\mathbf{U}}}\Updelta\hbox{t}+[(0.5-\beta){}^{\rm t} \ddot{{\mathbf{U}}}+\beta\,{}^{{\rm t}+\Updelta{\rm t}}\ddot{{\mathbf{U}}}]\Updelta{\hbox{t}}^{2} $$

(47b)

It has been shown that the use of the trapezoidal rule (γ = 0.5 and β = 0.25) with a fully implicit treatment of the contact constraints produces oscillations, which can be significant as the time steps and spatial discretizations are refined (Chaudhary and Bathe 1986). Recently, the generalized-α method was developed for solving structural dynamics problems with second order accuracy (Chung and Hulbert 1993). In this method, the equation of motion is modified as follows:

$$ {\mathbf{M}}\,{}^{({\rm t}+\Updelta{\rm t})-\alpha_{\rm B}}\ddot{{\mathbf{U}}}+{\mathbf{C}}\,{}^{({\rm t}+\Updelta{\rm t})-\alpha_{\rm H}}\dot{{\mathbf{U}}}+{\mathbf{K}}\,{}^{({\rm t}+\Updelta \hbox{t})-\alpha_{\rm H}}{\mathbf{U}}={}^{({\rm t}+\Updelta{\rm t})-\alpha_{\rm H}}{\mathbf{F}} $$

(48)

where

$$ \begin{array}{l} {}^{({\rm t}+\Updelta{\rm t})-\alpha_{\rm H}}{\mathbf{U}}=\left({1-\alpha_{\rm H}}\right){}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}+ \alpha_{\rm H}{}^{\rm t}{\mathbf{U}}\quad{}^{({\rm t}+\Updelta{\rm t}) -\alpha_{\rm H}}\dot{{\mathbf{U}}}=\left({1-\alpha_{\rm H}}\right) {}^{{\rm t}+\Updelta{\rm t}}\dot{{\mathbf{U}}}+\alpha_{\rm H} {}^{\rm t}\dot{{\mathbf{U}}}\\ {}^{({\rm t}+\Updelta{\rm t})-\alpha_{\rm B}}\ddot{{\mathbf{U}}}=\left({1-\alpha_{\rm B}}\right){}^{{\rm t}+\Updelta{\rm t}} \ddot{{\mathbf{U}}}+\alpha_{\rm B}{}^{\rm t}\ddot{{\mathbf{U}}}\quad {}^{({\rm t}+\Updelta{\rm t})-\alpha_{\rm H}}{\mathbf{F}}=\left({1-\alpha_{\rm H}}\right){}^{{\rm t}+\Updelta{\rm t}}{\mathbf{F}}+ \alpha_{\rm H}{}^{\rm t}{\mathbf{F}} \end{array} $$

(49)

The Newmark time-integration scheme (Eq. 47) is used to solve the above equation of motion.

5.2 General algorithm for dynamic contact problems

The reduced VI sub-problems are integrated into two-step and one-step algorithms to provide the complete solution. For each time increment, the solution algorithm is summarised as follows (Fig. 12a):

• (i) the effective stiffness matrix and load vector are calculated using generalized-α time integration,

• (ii) the reduced VI problem(s) is solved iteratively to obtain the displacement, velocity and acceleration fields as well as the current contact surface, contact forces, and

• (iii) steps (i) and (ii) are repeated until the final time is reached.

Fig. 12

Flow charts of: (a) general algorithm for dynamic contact problems, (b) two-step algorithm, and (c) one-step algorithm

Step (ii) of the above algorithm rely on the decomposition of the physical problem into two and one sub-problem(s). The first two-step approach integrates the two sub-problems in one algorithm to provide the complete solution (Fig. 12b). For each time instant, first, sub-problem I is solved to obtain the current contact surface and normal contact stresses. Then, sub-problem II is solved to obtain the displacement, velocity, acceleration as well as the frictional forces. Those two steps are repeated until convergence is reached. The second one-step approach is based on the iterative solution of sub-problem II (Fig. 12c). It is worth noting that both proposed algorithms are identical in the frictionless cases.

Generally, convergence in contact problems is measured by the change in the contact and frictional states as well as an energy norm. In this study, the solution is deemed converged once the change in the normal and tangential contact forces between two consecutive iterations is less then 0.01%.

5.3 Two step algorithm

The proposed VI algorithm relies on the decomposition of the physical problem into two sub-problems to identify the candidate contact surface and contact stresses.

5.3.1 Solution of sub-problem I

Using expression (18), in conjunction with the generalized-α method, the reduced VI formulation is equivalent to solving the following minimisation problem (Czekanski et al. 2001):

$$ \hbox{min}\left\{{\frac{1}{2}{}^{{\rm t}+\Updelta{\rm t}} {\mathbf{U}}^{{\rm T}}\,\hat{{{\mathbf{K}}}}\,{}^{{\rm t}+\Updelta {\rm t}} {\mathbf{U}}-{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}^{{\rm T}}\,{}^{{\rm t}+\Updelta{\rm t}}\hat{{\mathbf{F}}}}_1\right\}\quad\forall\;{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}|{\mathbf{A}}\,^{{\rm t}+\Updelta{\rm t}} {\mathbf{U}}\le{\mathbf{G}} $$

(50)

where

$$ \hat{{\mathbf{K}}}=\left({1-\alpha_{\rm H}}\right){\mathbf{K}}+\left({1-\alpha_B}\right)\frac{1}{\beta\Updelta t^{2}}{\mathbf{M}} $$

(51a)

$$ \begin{aligned} {}^{{\rm t}+\Updelta{\rm t}}\hat{{\mathbf{F}}}_1=&\left({1-\alpha_{\rm H}} \right){}^{{\rm t}+\Updelta{\rm t}}{\mathbf{F}}+\alpha_{\rm H}{}^{\rm t} {\mathbf{F}}+{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{F}}_{\rm T}-\alpha_{\rm B} {\mathbf{M}}{}^{\rm t}\ddot{{\mathbf{U}}}-\alpha_{\rm H}{\mathbf{K}}{}^{\rm t} {\mathbf{U}}+\\ &\left({1-\alpha_{\rm B}}\right){\mathbf{M}}\left[{\frac{1}{\beta \Updelta t^{2}}{}^{\rm t}{\mathbf{U}}+\frac{1}{\beta\Updelta t}{}^{\rm t} \dot{{\mathbf{U}}}+\left({\frac{1}{2\beta}-1}\right){}^{\rm t}\ddot{{\mathbf{U}}}}\right]\\ \end{aligned} $$

(51b)

where β and γ are Newmark time integration parameters, α_H is the generalized-α time integration parameter which modifies all terms in the equation of motion with the exception of the inertia term. The generalized-α time integration α_B modifies only the inertia term. Selection of those four parameters is crucial to the stability and accuracy of the solution. The details regarding the selection of the time integration scheme and parameters are provided in the chapter five.

F represents the vector of external nodal forces, while vector F_T represents the frictional forces acting on Γ_C. The Hessian matrix $\hat{{\mathbf{K}}}$ in Eq. 50 is the effective stiffness matrix, which is positive definite. Accordingly, expression (50) represents a convex Quadratic Programming problem. The current contact surface is directly defined by the active set of constraints. In this study, we adopt the technique of Quadratic Programming to solve this minimisation problem based on the projected gradients search method. The flow chart for the algorithm of the sub-problem I for unilateral contact model is depicted in Fig. 13.

Fig. 13

Flow chart of algorithm for sub-problem I

5.3.2 Solution of sub-problem II

The solution of sub-problem II is equivalent to the minimisation of the functional ${}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}$ , subject to the equality constraint ${\mathbf{B}}{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}={\mathbf{G}}$ resulting from the known contact surface Γ_C and the prescribed displacements on Γ_D (Czekanski et al. 2001), i.e.,

$$ \hbox{min}(\pi({}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}))\vert {\mathbf{B}}{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}={\mathbf{G}}\quad\hbox{ on }\Upgamma_{\rm C}\cup\Upgamma_{\rm D} $$

(52)

where

$$ \begin{array}{c} \pi\left({{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}}\right)= \frac{1}{2}{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}^{{\rm T}} (1-\alpha_{\rm H}){\mathbf{K}}{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}-{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{F}}_\alpha^{{\rm T}}\,{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}+{}^{{\rm t}+\Updelta{\rm t}} \ddot{{\mathbf{U}}}^{{\rm T}}(1-\alpha_{\rm B}){\mathbf{M}}{}^{{\rm t}+ \Updelta{\rm t}}{\mathbf{U}}+\\ {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{F}}_{\rm T}^{{\rm T}}\,{}^{{\rm t}+\Updelta{\rm t}}\Psi_\varepsilon\\ \end{array} $$

(53)

The modified external force vector is defined as:

$$ {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{F}}_\alpha = (1-\alpha_{\rm H}) {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{F}}+\alpha_{\rm H} {}^{\rm t}{\mathbf{F}}-{}^{\rm t}{\mathbf{U}}^{\rm T} \alpha_{\rm H} {\mathbf{K}}-{}^{\rm t}\ddot{{\mathbf{U}}}^{\rm T} \alpha _{\rm B} {\mathbf{M}} $$

(54)

The last term in Eq. 53 represents the regularised discrete frictional forces. The solution to Eq. 53 can be obtained using Lagrange multipliers. In this case, the equivalent unconstrained functional$\chi\left({}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\mathbf{U},{}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\mathbf{\Uplambda}\right)$ is as follows:

$$\begin{aligned}\chi\left({}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\mathbf{U},{}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\mathbf{\Uplambda}\right)=&\frac{1}{2}{}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\mathbf{U}^{\rm T}(1-\alpha_{\rm H})\mathbf{K}{}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\mathbf{U}+{}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\ddot{\mathbf{U}}^{\rm T}(1-\alpha_{\rm B})\mathbf{M}{}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\mathbf{U}-\\&{}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\mathbf{F}_{\alpha}^{\rm T}\,{}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\mathbf{U}+{}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\mathbf{F}_{\rm T}{}^{\rm T}\Psi_{\varepsilon}+{}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\mathbf{\Uplambda}(\mathbf{B}{}^{{\rm t}+\mathbf{\Updelta}{\rm t}}\mathbf{U}-\mathbf{G})\end{aligned}$$

(55)

which attains its extremum when:

$$ {\mathbf{L}}_1=\frac{\partial\chi({}^{{\rm t}+\Updelta{\rm t}} {\mathbf{U}},{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}})}{\partial{}^{{\rm t} +\Updelta{\rm t}}{\mathbf{U}}}=\mathbf{0}\hbox{ and }{\mathbf{L}}_2=\frac{\partial\chi({}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}},{}^{{\rm t}+\Updelta{\rm t}} {\mathbf{\Uplambda}})}{\partial{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}}}=\mathbf{0} $$

(56)

where L ₁ and L ₂ are defined as:

$$ {\mathbf{L}}_1({}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}, {}^{{\rm t}+\Updelta {\rm t}}{\mathbf{\Uplambda}})=\hat{{\mathbf{K}}}{}^{{\rm t}+\Updelta {\rm t}}{\mathbf{U}}-{}^{{\rm t}+\Updelta{\rm t}}\hat{{\mathbf{F}}}+\Upphi _\varepsilon^{\rm T}\,{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{F}}_{\rm T}+ {\mathbf{B}} {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}}=0$$

(57a)

$${\mathbf{L}}_2({}^{{\rm t}+\Updelta {\rm t}}{\mathbf{U}}, {}^{{\rm t}+\Updelta {\rm t}}{\mathbf{\Uplambda}})={\mathbf{B}}{}^{{\rm t}+\Updelta {\rm t}} {\mathbf{U}}-{\mathbf{G}}=\mathbf{0} $$

(57b)

$\hat{{\mathbf{K}}}$ is the effective stiffness matrix defined in Eq. 51a, ${\mathbf{\Uplambda}}$ represents the vector of nodal normal forces, and $\hat{{\mathbf{F}}}$ is the effective load vector, defined as:

$$ \begin{aligned} {}^{{\rm t}+\Updelta{\rm t}}\hat{{\mathbf{F}}}=\left({1-\alpha_{\rm H}} \right){}^{{\rm t}+\Updelta{\rm t}}{\mathbf{F}}+\alpha_{\rm H}{}^{{\rm t}+ \Updelta{\rm t}}{\mathbf{F}}-\alpha_{\rm B}{\mathbf{M}}{}^{\rm t} \ddot{{\mathbf{U}}}-\alpha_{\rm H}{\mathbf{K}}{}^{\rm t}{\mathbf{U}}-\\ \left({1-\alpha_{\rm B}}\right){\mathbf{M}}\left[{\frac{1}{\beta\Updelta \hbox{t}^{2}}{}^{\rm t}{\mathbf{U}}+\frac{1}{\beta \Updelta \hbox{t}} {}^{\rm t}\dot{{\mathbf{U}}}+\left({\frac{1}{2\beta }-1}\right) {}^{\rm t}\ddot{{\mathbf{U}}}}\right]\\ \end{aligned} $$

(58)

The elements of the matrix $\varvec{\Upphi}_{\varepsilon}$ of Eq. 57 (dimension mxn), which represents the regularisation function $\phi_\varepsilon(\dot{\mathbf{v}})$ , can be calculated as:

$$ \left\{{\Upphi_\varepsilon}\right\}_{\rm ij}=\hbox{T}_{{\rm ij}} \left\{{\begin{array}{ll} 1,& \sum\limits_{{\rm k=1}}^{\rm n}{\hbox{T}_{{\rm ik}}{}^{{\rm t}+\Updelta{\rm t}} \dot{{\mathbf{U}}}_{\rm k}} > \varepsilon\hfill \\ {\frac{1}{\varepsilon}\sum\limits_{{\rm k=1}}^{\rm n} {\hbox{T}_{{\rm ik}}{}^{{\rm t}+\Updelta{\rm t}} \dot{{\mathbf{U}}}_{\rm k}}},&{\left|{\sum\limits_{{\rm k=1}}^{\rm n}{\hbox{T}_{{\rm ik}} {}^{{\rm t}+\Updelta{\rm t}} \dot{{\mathbf{U}}}_{\rm k}}}\right|\le\varepsilon}\hfill \\ {-1},&{\sum\limits_{{\rm k=1}}^{\rm n}{\hbox{T}_{{\rm ik}}{}^{{\rm t}+\Updelta{\rm t}} \dot{{\mathbf{U}}}_{\rm k}} < -\varepsilon}\hfill \\ \end{array}}\right. i=1,\ldots, m, \quad j=1,\ldots, n $$

(59)

where m is the number of active contact constraints and n is the total number of degree of freedom.

In the above expression, the discretised tangential velocity component $\dot{{\mathbf{U}}}_{\rm T}$ is determined by multiplying the global velocity vector $\dot{{\mathbf{U}}}$ with the T matrix, as follows:

$$ {}^{{\rm t}+\Updelta{\rm t}}\dot{{\mathbf{U}}}_{\rm T}= {\mathbf{T}}{}^{{\rm t}+\Updelta{\rm t}}\dot{{\mathbf{U}}}$$

(60)

Equations 57a and 57b can be represented as follows:

$$ \left[{{\begin{array}{l}{{\mathbf{L}}_1 ({}^{{\rm t}+\Updelta {\rm t}}{\mathbf{U}},{}^{{\rm t}+\Updelta {\rm t}}{\mathbf{\Uplambda}})}\\ {{\mathbf{L}}_2 ({}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}},{}^{{\rm t}+\Updelta {\rm t}}{\mathbf{\Uplambda}})} \\ \end{array}}}\right]=\left[\begin{array}{l} {\mathbf{0}}\\ {\mathbf{0}}\\ \end{array}\right] $$

(61)

or in the equivalent compact form ${\mathbf{L}}({}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}, {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}})={\mathbf{0}}$ . The vector functions L ₁ and L ₂ are of dimensions n and m respectively. To solve this system of equations, a Newton–Raphson technique is used. The solution for iteration i is as follows:

$$ \left[ {{\begin{array}{l} {{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}}\\ {{}^{{\rm t}+\Updelta {\rm t}}{\mathbf{\Uplambda}}}\\ \end{array} }} \right]^{{\rm i}}=\left[{{\begin{array}{l} {{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}}\\ {{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}}}\\ \end{array}}}\right]^{{\rm i-1}}-{\mathbf{L^{\prime}}} ({}^{{\rm t}+\Updelta\hbox{t}}{\mathbf{U}}^{\rm i-1}, {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}}^{\rm i-1})^{-1}{\mathbf{L}}({}^{{\rm t}+ \Updelta{\rm t}}{\mathbf{U}}^{\rm i-1},{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}}^{\rm i-1}),\quad i > 1 $$

(62)

The corresponding matrix of first derivatives ${\mathbf{L^{\prime}}}$ can be expressed as:

$$ {\mathbf{L^{\prime}}}({}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}, {}^{{\rm t}+\Updelta {\rm t}}{\mathbf{\Uplambda}})=\left[{{\begin{array}{ll} {\frac{\partial {\mathbf{L}}_1({}^{{\rm t}+\Updelta{\rm t}} {\mathbf{U}}, {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}})} {\partial{}^{{\rm t}+ \Updelta{\rm t}}{\mathbf{U}}}}&{\frac{\partial{\mathbf{L}}_1({}^{{\rm t}+ \Updelta{\rm t}}{\mathbf{U}}, {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}})} {\partial{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}}}}\\ {\frac{\partial {\mathbf{L}}_2 ({}^{{\rm t}+\Updelta{\rm t}} {\mathbf{U}}, {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}})}{\partial {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}}}&{\frac{\partial{\mathbf{L}}_2 ({}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}},{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}})}{\partial{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}}}}\\ \end{array}}}\right]$$

(63)

where

$$ \frac{\partial {\mathbf{L}}_1 ({}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}, {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}})}{\partial{}^{{\rm t}+\Updelta {\rm t}}{\mathbf{U}}}=\hat{{\mathbf{K}}}+\frac{\gamma}{\beta\Updelta{\rm t}}{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{C}}_{\rm T},\quad\frac{\partial {\mathbf{L}}_1 ({}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}},{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}})}{\partial{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}}}={\mathbf{B}}^{{\rm T}} $$

(64a)

$$ \frac{\partial{\mathbf{L}}_2 ({}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}, {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}})}{\partial {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}}={\mathbf{B}},\hbox{ and }\frac{\partial {\mathbf{L}}_2 ({}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}, {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}})}{\partial {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{\Uplambda}}}= {\mathbf{0}} $$

(64b)

Finally, the damping matrix C _T, which results from the regularisation of the frictional term, can be expressed as follow:

$$ \left\{{{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{C}}_{\rm T}}\right\}_{\rm ij}\equiv\sum\limits_{\rm l=1}^{\rm m}{\left\{{{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{F}}_{\rm T}}\right\}_{\rm l}\left\{{\mathbf{T}}\right\} _{{\rm ij}}}\left\{{{\begin{array}{lll} 0&,&{\left|{\sum\limits_{{\rm k=1}}^{\rm n} {\hbox{T}_{{\rm ij}}{}^{{\rm t}+\Updelta{\rm t}}\dot{{\mathbf{U}}}_k } } \right| > \varepsilon}\\ {\frac{\hbox{T}_{{\rm ij}}}{\varepsilon}}&,&{\left|{\sum\limits_{{\rm k=1}}^{\rm n} {\hbox{T}_{\rm ij} {}^{{\rm t}+\Updelta{\rm t}}\dot{{\mathbf{U}}}_{\rm k}}}\right| \le\varepsilon}\\ \end{array}}}\right. $$

(65)

The flow chart for the algorithm for the sub-problem-II for unilateral contact model is depicted in Fig. 14.

Fig. 14

Flow chart of algorithm of sub-problem II

5.4 One-step algorithm using nondifferentiable optimisation

The second approach, which treats the VI formulation in one-step approach, is based on the iterative solution of sub-problem II discussed in chapter three. Using Eqs. 27 and 28, in conjunction with the generalized-α method, the discretised reduced incremental VI formulation is equivalent to solving the following minimisation problem (Czekanski et al. 2001):

$$ \hbox{min}\left\{{\frac{1}{2}{}^{{\rm t}+\Updelta{\rm t}}\Updelta {\mathbf{U}}^{{\rm i+1}{}^{\rm T}}\hat{{\mathbf{K}}}{}^{{\rm t}+ \Updelta{\rm t}}\Updelta{\mathbf{U}}^{\rm i+1}-{}^{{\rm t}+\Updelta{\rm t}}\Updelta {\mathbf{U}}^{{\rm i+1}^{\rm T}}{}^{{\rm t}+\Updelta{\rm t}}\Updelta \hat{{\mathbf{F}}}^{\rm i+1}+{}^{{\rm t}+\Updelta{\rm t}}\Updelta {\mathbf{U}}^{{\rm i+1}^{\rm T}}{\mathbf{T}}{\mathbf{S}}{}^{{\rm t}+\Updelta{\rm t}}{\mathbf{F}}_{\rm T}^{\rm i}}\right\} \forall\;{}^{{\rm t}+\Updelta{\rm t}}\Updelta{\mathbf{U}}^{{\rm i+1}} $$

(66)

subject to the following kinematic contact condition and ANDO constraint:

$$ {\mathbf{A}}{}^{{\rm t}+\Updelta{\rm t}}\Updelta{\mathbf{U}}^{\rm i+1}\le {\mathbf{G}} $$

(67a)

$$ {\mathbf{ST}}{}^{{\rm t}+\Updelta{\rm t}}\Updelta{\mathbf{U}}^{\rm i+1}\le {\mathbf{S}}{\mathbf{T}}\;({}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}^{{\rm i}}-{}^{\rm t}{\mathbf{U}}) $$

(67b)

where

$$ \hat{{\mathbf{K}}}=(1-\alpha_{\rm H}){\mathbf{K}}+\left( {1-\alpha _B } \right)\frac{1}{\beta \Updelta \hbox{t}^{2}}{\mathbf{M}} $$

(68)

$$ \begin{aligned} {}^{{\rm t}+\Updelta{\rm t}}\Updelta \hat{{\mathbf{F}}}^{\rm i+1}&= \left( {1-\alpha_{\rm H}}\right) {}^{{\rm t}+\Updelta{\rm t}} {\mathbf{F}}+\alpha_{\rm H}{}^{\rm t}{\mathbf{F}}-\alpha_{\rm B} {\mathbf{M}}{}^{\rm t}\ddot{{\mathbf{U}}}-\alpha_{\rm H} {\mathbf{K}}{}^t{\mathbf{U}}+\\ &\left({1-\alpha_{\rm B}}\right){\mathbf{M}}\left[{\frac{1}{\beta \Updelta\hbox{t}^{2}}{}^{\rm t}{\mathbf{U}}+\frac{1}{\beta \Updelta t}{}^{\rm t}\dot{{\mathbf{U}}}+\left({\frac{1}{2\beta }-1}\right) {}^{\rm t}\ddot{{\mathbf{U}}}}\right]-{}^{{\rm t}+ \Updelta{\rm t}}{\mathbf{F}}_{{\rm int}}^{\rm i}\\ \end{aligned} $$

(69)

This incremental solution can be represented as follows:

$$ {}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}^{{\rm i+1}}={}^{{\rm t}+\Updelta{\rm t}}{\mathbf{U}}^{{\rm i}}+{}^{{\rm t}+\Updelta{\rm t}}\Updelta {\mathbf{U}}^{\rm i+1}\quad \hbox{for i} > 1 $$

(70)

The first constraint (Eq. 67a) represents the assembly of the kinematic contact conditions of the nodes on the candidate contact surface Γ_C. The second constraint (Eq. 67b) represents the assembly of the ANDO constraint ($\hbox{s}_{\rm k}\, {}^{{\rm t}+\Updelta{\rm t}}\dot{{\mathbf{U}}}_{\rm Tk}\ge 0)$ of the nodes on the candidate contact surface Γ_C. The sign matrix S, which switches between the two complementary sub-problems, is unknown in advance, and is part of the solution. Therefore, the new algorithm employs a sequence of convex Quadratic Programming problems.

The flow chart for the algorithm is depicted in Fig. 15 and can be stated in the following steps:

• (i) Calculate the tangential velocity vector $\dot{{\mathbf{U}}}_{\rm Tk}$ and the signs of each of its terms s_k, for k = 1,..., m, where m is the number of contact constraints. The variable s_k can take only −1 or + 1 for nodes in contact and 0 for nodes not in contact.

• (ii) Create the ANDO constraint set: $\hbox{s}_{\rm k}\dot{{\mathbf{U}}}_{\rm Tk}\ge 0$ for k = 1,..., m.

• (iii) Solve the current Quadratic Programming problem subject to the appropriate kinematic contact condition and ANDO constraints, and then find the minimum of the current objective function.

• (iv) Identify the current active ANDO constraints set ($\dot{{\mathbf{U}}}_{\rm Tk}=0$ for k = 1,..., m). If this set is empty, then we obtain the optimal solution.

• (v) For each active ANDO constraint k reverses the sign of the ANDO constraint, i.e. s_k = −s_k, and solves the resulting complementary Quadratic Programming problem and computes the minimum value of the objective function.

• (vi) If all the elements of the active ANDO constraints are considered and cannot produce an improved value of the objective function, then U is the optimal solution. Exit.

Fig. 15

Details of nondifferentiable optimisation algorithm

The above algorithm is guaranteed to converge in a finite number of steps, because of the condition of strict convexity assumed and because the number of the cutting planes (i.e. the planes given by $\dot{{\mathbf{U}}}_{\rm Tk}=0,$ k = 1,...,m) is finite.

6 Numerical examples

Four examples have been selected to demonstrate the flexibility, robustness and accuracy of the newly developed approach. The first involves dynamic frictionless contact between a cantilever beam and a rigid foundation. In the second example, we analyze contact in gears. The third example is devoted to the analysis of the fir-tree contact in aeroengine turbine disc assembly. Finally, we analyze the residual stress field developed in the shot peening process as a result of inhomogeneous elasto-plastic deformation.

6.1 Contact between a cantilever beam and a flat rigid surface

The first example involves the dynamic frictionless contact between a cantilever beam and a flat rigid surface (Fig. 16). A beam of length l = 0.2 m and height h = 0.02 m is made from aluminum with the following properties: E = 73 GPa, ν = 0.33, and ρ = 2770 kg/m³. A step load of F = 10³ N was applied. The gap between the beam and the rigid foundation was selected to be equal to the maximum static deflection of the beam. A time step of Δt = 5 × 10⁻⁶ s was used. The results were obtained using the new VI approach and compared with the traditional penalty method. The displacements were normalized by the maximum static deflection of the beam, while the user-defined penalty stiffness parameters were normalized by the stiffness of the beam at the point of application of the load.

Fig. 16

Dynamic contact between a cantilever beam and a rigid foundation

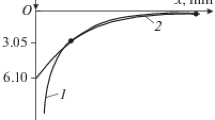
Figure 17 shows the normalized tip displacement predicted using the newly developed algorithm as well as the traditional penalty method. The results show that the VI does not result in any interpenetration. For low values of k_N, the beam experiences excessive unrealistic interpenetration. The penalty-based results approach the VI solution only for k_N/k_beam values approaching 10², or higher.

Fig. 17

Time variation of normalized tip displacement: comparison between VI and penalty based solution

6.2 Analysis of spur gear contact

Gearing is one of the most effective methods of transmitting rotary motion and torque from one shaft to another, with or without a change of speed or direction of motion. The design of efficient and reliable gearing systems is governed, amongst other factors, by their ability to withstand the frictional contact conditions and the high bending stresses experienced at the tooth root.

Whilst the frictional contact conditions govern the pitting and spalling resistance of a given gear, the high stress concentration present at its root determines the root fillet bending stresses and ultimately its fatigue life. Recent advances in turbomachinery have resulted in increasing the load carrying capacity and speeds of gear trains which may, however, make them vulnerable to failure, especially if the designer is unable to accurately and reliably predict the states of contact and root stresses of the mating gears.

Unfortunately, conventional gear strength equations are inaccurate and inadequate to treat modern high speed high load gearing, since they model the gear tooth as a cantilever beam and provide formulae which relate the maximum root bending stress to the design parameters. To overcome the difficulties and limitations associated with the use of these semi-empirical formulae, the newly developed algorithms were use to predict root stresses in gears.

Analysis of a rack-pinion assembly

The present rack-pinion contact problem can be approached from a number of different directions according to the objectives and level of accuracy desired. The gear assembly considered conforms to AGMA standards and is shown schematically in Fig. 18. It comprises a 20 teeth pinion with a rack. Both components have involute teeth profiles of 20° pressure angle, a module of 5 mm, an addendum of one module and dedendum of 1.25 module. The components are assumed to be made of steel with the following elastic properties: Young’s modulus E = 210 GPa and Poisson’s ratio ν = 0.3. Furthermore, the load is represented by an upward force per unit thickness of the rack P₀ = 90 kN/m under the assumptions of plane stress conditions. Several cases were considered in this study, such as: (i) one-pair, (ii) two-pairs, and (iii) three-pairs of teeth in contact.

Fig. 18

Modelling of a pinion-rack problem

The objective of considering two-pairs of contacting teeth are: (i) to predict the effect of load-sharing upon the resulting stresses, (ii) to examine possible interaction effects between the adjacent teeth and (iii) to examine the ability of the proposed method to treat problems involving multiple contact surfaces simultaneously. Figure 19 shows both the coarse and refined mesh of the examined model. In this case, the coarse mesh was used to characterise the overall structural response of the contacting teeth, while the refined mesh was used to evaluate the contact stresses at the desired areas. It is worth pointing out that transferring the boundary conditions from the coarse to the refined model is the most intricate part of using refined mesh modelling. In this work, the boundary conditions were transferred as interpolated displacements, from the initial coarse model, using the appropriate shape functions.

Fig. 19

Coarse and refined mesh for the case of two-pairs of teeth in contact

Both frictionless and frictional contact problems were considered. Figure 20 shows the distribution of the resulting normal contact stress over the contact regions R₁ and R₂. In this case, contact region R₁ represents a pitch point contact position and contact region R₂ represents a point past the start of contact. The results reveal a reduction in the normal contact stress as a result of load sharing between the contacting teeth. In contact region R₂, the contact stress decreases monotonically along the contact length.

Fig. 20

Distribution of normal contact stresses in contact zones: (a) region R₁ and (b) region R₂

6.3 Analysis of fir-tree region in aeroengine turbine discs

Contact stresses, interface conditions (friction, surface roughness, residual stress), and the detailed geometry of the fir-tree joint determine the severity of the resulting stress field. These contact stresses do not remain constant but vary during operation. It is generally accepted that fretting initiated fatigue cracks are due to intermittent high frequency engine resonance and load fluctuations resulting from a change in engine speed or power requirements.

It was therefore the objective of this study to evaluate the contact behaviour of turbine disc assemblies using the finite element method. Specifically, our attention was devoted to examining the effect of the critical geometric features upon the contact stress distribution at the different teeth of a fir-tree joint. These features, shown in Fig. 21, include the number of fir-tree teeth n, flank length l, contact angle α, flank angles β and γ which define the tooth pitch.

Fig. 21

Schematic of (a) disc and (b) fir-tree geometry

The fir-tree models were meshed with four-noded quadrilateral elements (Fig. 22). Plane stress conditions were assumed. No attempt was made to model the blade in details, except insofar as providing the necessary centrifugal loading at the interface. All models were subjected to centrifugal loadings.

Fig. 22

Two-dimensional discretized geometry

The material properties used for modelling the blade and the disc were that of a typical Nickel alloy used in disc design; namely, INCONEL 720. This material is creep and fatigue resistant. In this work, the following values were used: Young’s modulus E = 220 GPa, 0.2% Proof stress σ_0.2 = 635 MPa, Poisson’s ratio ν_0.2 = 0.29, density ρ_0.2 = .8510 kg/m³ and coefficient of friction μ = 0.0, 0.1 and 0.5.

Figure 23a represents a composite image of the photoelastic maximum shear stress contours and the FE predictions. The isochromatic fringe patterns compare well with the maximum shear stress contour plots obtained with FE analysis. In particular, the fringe patterns depict similar contact stresses and stress concentration around the different fillets. The results also reveal that peak stresses occur within the contact region at the bottom and top of each flank. Figure 23b shows the normalised maximum shear stress trajectories along the bottom tooth interface. A maximum discrepancy of about 15% exists between the two-dimensional FE predictions and the photoelastic results.

Fig. 23

(a) Composite image of the photoelastic maximum shear stress contours and FE predictions and (b) normalised maximum shear stress along the bottom contact region

The study also examined the effect of the critical geometrical features, such as the number of teeth, flank length and flank angle upon the stress field in the disc. It was further extended to account for the effect the interfacial friction between the disc and attached blades upon the resulting contact stresses at the interface. The results revealed the following:

• (i) the maximum stress occurs at and just below the lower contact point along the bottom tooth of a turbine disc,

• (ii) the position and magnitude of the maximum stress is dramatically influenced by the number of teeth, the contact angle, the flank length and flank angles,

• (iii) the coefficient of friction influences the peak stress value.

6.4 Residual stress prediction in shot peening

In this case study, we examine the mechanically induced residual stress field developed in the outermost material layers due to the shot peening treatment. A finite element analysis was conducted to study the effect of the mechanical properties of the target material and the shot velocity of peeing media. The following dimensions were selected for the target: width W = 5R and height H = 4R, where R = 0.5 mm is the radius of the shot. These dimensions were carefully selected to ensure that the boundary conditions do not affect the solution. The shot used was assumed to be rigid and modeled with the following properties: modulus of elasticity E = 2 × 10⁴ GPa, Poisson’s ratio ν = 0.3, and mass density ρ = 7800 kg/m³. The following material properties were assumed for the high strength steel target considered: modulus of elasticity E = 200 GPa, Poisson’s ratio ν = 0.3, and mass density ρ = 7800 kg/m³. An elasto-plastic rate independent bilinearly hardening material behavior was assumed with an initial yield stress σ₀ = 600 MPa and strain-hardening coefficient H = 20, 1000 and 2000 MPa (corresponding to H/E = 0.01, 0.5 and 1.0%, respectively). Three different impact velocities were used: v = 50, 75 and 100 m/s. Coulomb’s law, with friction coefficient μ = 0.25, was assumed. The total integration time was t_k = 10 μs with a maximum time step of Δt_max = 2 × 10⁻⁸s. Generalized-α time integration scheme was utilized with the following parameters $\gamma=\sqrt{2}-1/2, \beta=1/2, \alpha_{\rm H}=\sqrt{2}-1,$ and α_B = 0. Four-noded axisymmetric finite elements, with large strain and displacement capabilities, were used to discretize the target (Fig. 24). A fine mesh was used in the impact region where high stress gradients are expected. The rest of the target was discretized using larger elements. Convergence tests were conducted revealing only minor variations.

Fig. 24

Shot-peening problem: (a) geometry and (b) discretized model

Figure 25 shows the time variation of the velocity and total contact force during the entire impact process for an initial shot velocity v = 75 m/s and strain hardening H = 1000 MPa. The results show that contact with the target lasts for 1.70 μs. However, the shot rebound began at about 1.25 μs, at which time the shot approached zero velocity. The terminal shot velocity was 17.3 m/s leading to a coefficient of restitution of 23%. This effectively indicates that approximately 95% of the total initial kinetic energy of the shot was dissipated in plastic work, while the remainder was used in elastic rebound. Figure 25b shows that the maximum contact force is reached when the shot begins its rebound trip.

Fig. 25

Time history of: (a) the shot velocity, and (b) the total contact force

Figure 26a shows the variation of the normalized unloading residual stress σ ^r_r /σ₀, beneath the centre line of the shot for the three selected impact speeds. The results show that a 100% increase in the shot velocity results in: (i) a significant increase in the depth of the compressed layer, and (ii) an insignificant change in the position and the magnitude of the maximum residual stress σ ^r_r . It is interesting to note that the change in the residual stress from compression to tension coincides with the depth of the plastic zone.

Fig. 26

Effect of: (a) shot velocity and (b) strain hardening rate upon normalized transverse residual stress

Figure 26b shows the residual stress variation along the depth of the target for the three values of hardening coefficient and the shot velocity of 75 m/s. The results show that increasing the hardening coefficient of the material results in an increase in the depth of the compressed layer, little change in the magnitude of the maximum subsurface residual stress σ ^r_r , and a decrease in the surface residual stress.

7 Conclusions

In this paper, a new incremental variational inequality-based (VI) formulation is developed in an updated Lagrangian framework for the analysis of elasto-plastic dynamic frictional contact problems involving large deformation. The kinematic contact conditions are developed in a consistent manner based on the use of spline interpolation to represent contact surface. The developed finite element procedures are based on dividing the physical problem into sub-problems. These sub-problems are solved iteratively using Lagrange multipliers and/or mathematical programming in order to identify the candidate contact surface and contact stresses. In order to solve the dynamic expressions, we employ the generalized-α time integration scheme thus ensuring a convergent and accurate results. The newly developed approaches guarantee the accurate imposition of the active kinematic contact constraints.