Supervised representation learning for multi-label classification

Abstract

Representation learning is one of the most important aspects of multi-label learning because of the intricate nature of multi-label data. Current research on representation learning either fails to consider label knowledge or is affected by the lack of labeled data. Moreover, most of them learn the representations and incorporate the label information in a two-step manner. In this paper, due to the success of representation learning by deep learning we propose a novel framework based on neural networks named SERL to learn global feature representation by jointly considering all labels in an effective supervised manner. At its core, a two-encoding-layer autoencoder, which can utilize labeled and unlabeled data, is adopted to learn feature representation in the supervision of softmax regression. Specifically, the softmax regression incorporates label knowledge to improve the performance of both representation learning and multi-label learning by being jointly optimized with the autoencoder. Moreover, the autoencoder is expanded into two encoding layers to share knowledge with the softmax regression by sharing the second encoding weight matrix. We conduct extensive experiments on five real-world datasets to demonstrate the superiority of SERL over other state-of-the-art multi-label learning approaches.

1 Introduction

Multi-label learning, which deals with the problem where one object may be associated with one or more labels, has attracted extensive researches in the past decades (Tsoumakas and Katakis 2006). Different from single-label problem where binary class and multi-class classification hold, multi-label learning could model the world more exactly. Besides, multi-label learning has widespread applications such as news classification and image processing (Boutell et al. 2004). For example, one news may belong to multiple topics such as politics and economy because it reports new policies on bank rate. A scenery picture, as a more familiar example, may contain sky, road, cornfield and so on, where they can be viewed as with multiple labels.

Traditionally in multi-label learning, the problem transformation method transformed the multi-label dataset to a series of single label datasets (Zhang and Zhou 2014), such as the binary relevance method (Tsoumakas et al. 2009) and the label powerset method (Tsoumakas et al. 2011). This kind of methods neglect the fact that some labels are more likely to co-exist in one instance, which is the main focus of many recent multi-label works. Therefore, in order to parameterize the label correlations, Ghamrawi and McCallum (2005) proposed a multi-label classifier in conditional random field by modeling the label co-occurrences explicitly. Zhang and Zhang (2010) utilized a Bayesian network structure to encode the conditional dependencies of the labels and the feature set. Nguyen et al. (2016) proposed a Bayesian nonparametric approach to automatically learn the number of label-feature correlation patterns. However, most existing multi-label methods utilized the raw instance data to formalize the model, which might contain non-helpful feature attributes from the input space prior to training. Hence, learning better feature representation is important for the multi-label learning.

There exist some related works on multi-label learning classifiers based on representative features  (Zhang and Zhou 2008; Read and Perezcruz 2014; Zhang and Wu 2015). MMDM (Zhang and Zhou 2008) discovers a low-dimension feature space which maximizes the dependence between the original features and the corresponding labels. LIFT (Zhang and Wu 2015) uses clustering techniques to construct label-specific features for each label and then solves binary classification problems based on the transformed features. MLFE (Zhang et al. 2018) utilizes the structural information in feature space to enrich the labeling information. However, these works either learn representative features without considering label knowledge or suffer from the lack of labeled data. Recently, deep learning has proven to be able to learn good representation in natural language processing, image classification, and so on. And some effort has been devoted to handling multi-label learning problem to improve the performance. Read and Perezcruz (2014) used restricted Boltzmann machine (RBM) to get a better representation of the original features, and then applied the supervised learning algorithms to training classification models. However, they performed the optimization framework in a two-step manner, while we try to learn the representation and incorporate label knowledge in a joint optimization framework.

To address these issues, we propose a novel framework named SERL (SupErvised Representation Learning for multi-label classification) in this paper. SERL adopts a two-encoding-layer autoencoder to learn better representation of the original features in the supervision of softmax regression. Specially, the softmax regression incorporates label knowledge to improve the performance of both representation learning and multi-label learning by being jointly optimized with the autoencoder, where the autoencoder can sufficiently utilize labeled and unlabeled data to learn nonlinear representation of the original features. In addition, the autoencoder is expanded into two encoding layers to share knowledge with the softmax regression by sharing the second encoding weight matrix. We evaluate the proposed approach on five real-world datasets and observe the effectiveness of SERL that it can outperform the compared state-of-the-art algorithms significantly. The contribution of this paper is summarized as follows.

• We propose an autoencoder based framework (SERL) to discover latent knowledge of the original features by jointly considering all labels in an effective supervised manner.

• The autoencoder learns representation from labeled and unlabeled data in the supervision of the softmax regression. Moreover, the autoencoder shares knowledge with softmax regression by sharing the second encoding weight matrix.

• We conduct extensive experiments on five real-world datasets to demonstrate the superiority of the proposed method over other state-of-the-art algorithms.

The remainder of this paper is organized as follows. Section 2 introduces the preliminary knowledge. The framework and its solution are detailed in Sect. 3. The experimental results are reported in Sect. 4. Section 5 discusses the related work and finally Sect. 6 concludes.

2 Preliminaries

2.1 Softmax regression

Softmax regression which is often used to solve the problem of multi-class classification can be regarded as the generalization of the logistic regression. When given a test input x, softmax regression estimates the probability of each label (label space $y \in \{1,2,\ldots ,k\}$) by the hypothesis function as follows,

$$\begin{aligned} h_{\varvec{\theta }}(\varvec{x}_i)= \left[ \begin{array}{c} p(y_i=1|\varvec{x}_i; \varvec{\theta })\\ p(y_i=2|\varvec{x}_i; \varvec{\theta })\\ \vdots \\ p(y_i=k|\varvec{x}_i; \varvec{\theta })\\ \end{array} \right] =\frac{1}{\sum _{j=1}^{k}e^{\varvec{\theta }_{j}^{\top }\varvec{x}}} \left[ \begin{array}{c} e^{\varvec{\theta }_{1}^{\top }\varvec{x}_i}\\ e^{\varvec{\theta }_{2}^{\top }\varvec{x}_i}\\ \vdots \\ e^{\varvec{\theta }_{k}^{\top }\varvec{x}_i}\\ \end{array} \right] . \end{aligned}$$

(1)

The objective function of softmax regression can be described as follows,

$$\begin{aligned} \min \limits _{\varvec{\theta }} \left( -\frac{1}{n}\sum _{i=1}^{n}\sum _{j=1}^{k}1\{y_i=j\}\log \frac{e^{\varvec{\theta }_{j}^{\top }\varvec{x}_i}}{\sum _{l=1}^{k}e^{\varvec{\theta }_{l}^{\top }\varvec{x}_i}}\right) , \end{aligned}$$

(2)

where the indicator function $1\{\varvec{\cdot }\}$ equals 1 when $x_i$ holds label j and equals 0 otherwise. Given training dataset $\{\varvec{x_i,~y_i}\}_{i=1}^n$ ($y_i \in \{1,2,\ldots ,k\}$), the model parameter $\varvec{\theta }$ can be derived by minimizing Eq. (2). After training, the probability of each label can be computed using Eq. (1), then the predicted label can be assigned as follows,

$$\begin{aligned} y = \max _{j} \frac{e^{\varvec{\theta }_{j}^{\top }\varvec{x}}}{\sum _{l=1}^{k}e^{\varvec{\theta }_{l}^{\top }\varvec{x}}}. \end{aligned}$$

(3)

2.2 Autoencoder

Autoencoder, which is a neural network, uses unsupervised learning method to learn compressed features from original features. A multi-layer autoencoder comprises one input layer, one output layer, and several hidden layers. The aim of the autoencoder is to reconstruct the input signal in the output layer with the least amount of distortion. A simple autoencoder consists of two parts, that is, an encoder including the input layer and hidden layer and a decoder including the hidden layer and output layer. Given an input $\varvec{x_i} \in \mathbb {R}^{d\times 1}$, weight matrix $\varvec{W}_1\in \mathbb {R}^{k\times d}$, $\varvec{W}_1^{'}\in \mathbb {R}^{d\times k}$, and bias vector $\varvec{b}_1\in \mathbb {R}^{k\times 1}$, $\varvec{b}_1^{'}\in \mathbb {R}^{d\times 1}$, a single hidden layer autoencoder encodes it into the hidden layer $\varvec{{\xi }_i} \in \mathbb {R}^{k \times 1}$ and decodes the hidden layer into the output layer ${\hat{\varvec{x_i}}}$ which is as same as possible with the input layer. This process can be described as,

$$\begin{aligned} \varvec{\xi }_i = f(\varvec{W}_1\varvec{x}_i + \varvec{b}_1), \quad {\hat{\varvec{x}_i}} = f(\varvec{W}_1^{'}\varvec{\xi }_i + \varvec{b}_1^{'}). \end{aligned}$$

(4)

Here we use the sigmoid function as the activation function f. Given a set of inputs $\{\varvec{x}_i\}_{i=1}^n$, the goal of autoencoder is to minimize the reconstruction error using L2 regularization as follows,

$$\begin{aligned} \min \limits _{\varvec{W}_1, \varvec{b}_1, \varvec{W}_1^{'}, \varvec{b}_1^{'}}\sum _{i=1}^n\Vert {\hat{\varvec{x}}}_i - \varvec{x}_i\Vert ^{2}. \end{aligned}$$

(5)

3 The SERL framework

In this section, we present our proposed framework in detail and the symbols used are listed in Table 1.

Table 1 Notations and denotations

Fig. 1

The framework of SERL

3.1 Problem formalization

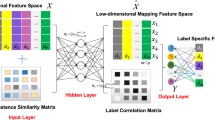
The proposed framework is composed of a two-encoding-layer autoencoder and softmax regression as shown in Fig. 1. The two components are jointly optimized and they share the second encoding weight matrix $\varvec{W}_2$. Given multi-label training dataset ${D_r}=\{(x_i^{(r)},Y_i^{(r)})|1\le i \le n_r\}$ and test dataset ${D_s}=\{(x_i^{(s)},Y_i^{(s)})|1\le i \le n_s\}$, where $x_i^{(r)},x_i^{(s)} \in \mathbb {R}^{d \times 1}$ and $Y_i^{(r)},Y_i^{(s)} \subseteq \mathcal {Y}$ ($\mathcal {Y} = \{1,2\ldots ,c\}$) are sets of relevant labels associated with ${x_i^{(r)}},{x_i^{(s)}}$ respectively. The objective function can be described as follows,

$$\begin{aligned} \mathcal {J} = \sum _{t\in \{r, s\}}J(\varvec{x}^{(t)}, {\hat{\varvec{x}}}^{(t)}) + \alpha \mathcal {L}(\varvec{\theta }, \varvec{\xi }^{(r)}) + \beta \varOmega (\varvec{W}, \varvec{b}, \varvec{W}^{'}, \varvec{b}{'}). \end{aligned}$$

(6)

where J is the loss of autoencoder, $\mathcal {L}$ is the loss of softmax regression, $\varOmega$ is the regularization term, $\alpha$ and $\beta$ are trade-off parameters for the whole framework. $\varvec{W}, \varvec{b}$ include all the parameters for encoding, and $\varvec{W}^{'}, \varvec{b}{'}$ represent the ones for decoding.

There are three terms in Eq. (6). In the first term $J(\varvec{x}^{(t)},{\hat{\varvec{x}}}^{(t)})$, the reconstruction error is calculated for both training and test datasets, and it is defined as follows,

$$\begin{aligned} J(\varvec{x}^{(t)}, {\hat{\varvec{x}}}^{(t)}) = \sum _{t\in \{r, s\}}\sum _{i=1}^{n_t}||\varvec{x}_{i}^{(t)}-{\hat{\varvec{x}}}_{i}^{(t)}||^{2}, \end{aligned}$$

(7)

where

$$\begin{aligned} \varvec{\xi }_{i}^{(t)}= & {} f(\varvec{W}_1\varvec{x}_{i}^{(t)} + \varvec{b}_1), \varvec{z}_{i}^{(t)} = f(\varvec{W}_2\varvec{\xi }_{i}^{(t)} + \varvec{b}_2), \end{aligned}$$

(8)

$$\begin{aligned} {\hat{\varvec{\xi }}}_{i}^{(t)}= & {} f(\varvec{W}_2^{'}\varvec{z}_{i}^{(t)} + \varvec{b}_2^{'}), {\hat{\varvec{x}}}_{i}^{(t)} = f(\varvec{W}_1^{'}{\hat{\varvec{\xi }}}_{i}^{(t)} + \varvec{b}_1^{'}). \end{aligned}$$

(9)

There are three hidden layers in our framework. The first one called the embedding layer has k nodes ($k \le d$) with output $\varvec{\xi }^{(t)}_{i} \in \mathbb {R}^{k\times 1}$, weight matrix $\varvec{W}_1\in \mathbb {R}^{k\times d}$, and bias vector $\varvec{b}_1\in \mathbb {R}^{k\times 1}$. The second one called the label layer has c nodes (equals to the number of labels) with output $\varvec{z}^{(t)}_{i} \in \mathbb {R}^{c\times 1}$, weight matrix $\varvec{W}_2\in \mathbb {R}^{c\times k}$ and bias vector $\varvec{b}_2\in \mathbb {R}^{c\times 1}$. The input of the label layer is also the input of the softmax regression which incorporates label knowledge. The third one is the reconstruction of the embedding layer with output ${\hat{\varvec{\xi }}}^{(t)}_{i}$, weight matrix $\varvec{W}_2^{'} \in \mathbb {R}^{k \times c}$ and bias vector $\varvec{b}_2^{'}\in \mathbb {R}^{k\times 1}$. The output layer is the reconstruction of input $\varvec{x}^{(t)}_{i}$ with output $\varvec{\hat{\varvec{x}}}^{(t)}_{i} \in \mathbb {R}^{d \times 1}$, weight matrix $\varvec{W}_1^{'} \in \mathbb {R}^{d \times k}$ and bias vector $\varvec{b}_1^{'} \in \mathbb {R}^{d \times 1}$.

The second term in the objective Eq. (6) is the optimization of softmax regression, which incorporates the label knowledge from training data. Note here that the autoencoder is expanded into two encoding layers to share the second encoding weight matrix $W_2$ with the softmax regression, which aims to share knowledge with the softmax regression.

Here we try to use the softmax regression to handle multi-label data. The basic idea is to transform the multi-label data to multi-class data. Let $\sigma : (x_i,Y_i) \rightarrow \{(x_i, y_j)|y_j \in Y_i\}$ be the function which converts a (instance, labels) pair into a set of (instance, label) pair where each (instance, label) pair contains only one label. For example, suppose we have one instance $x_i$ with labels $y_1$, $y_2$, $y_4$. $\sigma$ converts $(x_1, \{y_1, y_2, y_4\})$ to $(x_1, y_1)$, $(x_1, y_2)$, $(x_1, y_4)$. In the training phase, we firstly converts the original multi-label training dataset $D_r$ into the following multi-class training dataset $D_r^{\dag }$ by $\sigma$ as follows,

$$\begin{aligned} D_r^{\dag } = \{\sigma (x_i,Y_i)|1 \le i \le n_r\}. \end{aligned}$$

(10)

After that, softmax regression $\mathcal {M}$ is utilized to induce multi-class classifier $g^{\dag }:\mathcal {X} \rightarrow \mathcal {Y}, i.e., g^{\dag } \leftarrow \mathcal {M}(D_r^{\dag })$ ($\mathcal {X} \in \mathbb {R}^{d\times 1}$, $\mathcal {Y} = \{1,2,\ldots ,c\}$). The objective function of softmax regression can be formalized as follows,

$$\begin{aligned} \mathcal {L}(\varvec{\theta }, \varvec{\xi }^{(r)}) = -\frac{1}{n_r}\sum _{i=1}^{n_r}\sum _{j=1}^{c}1\{y_{i}^{(r)}=j\}\log \frac{e^{{\varvec{\theta }_j^{\top }}\varvec{\xi }_{i}^{(r)}}}{\sum _{l=1}^{c}e^{{\varvec{\theta }_l^{\top }}\varvec{\xi }_{i}^{(r)}}}. \end{aligned}$$

In this term, $\varvec{\xi }^{(r)}_i$ is the output of the embedding layer and $\varvec{\theta }_j^{\top } (j \in \{1,\ldots ,c\})$ is the j-th row of $\varvec{W}_2$ which is also the second encoding weight matrix of autoencoder.

Finally, the last term in the objective Eq. (6) is the regularization on model parameters which controls the complexity of the framework to improve its generalization ability. The last term is defined as follows,

$$\begin{aligned} \varOmega (\varvec{W},\varvec{b},\varvec{W}^{'},\varvec{b}{'})= & {} \Vert \varvec{W}_{1}\Vert ^2 + \Vert \varvec{b}_{1}\Vert ^2 + \Vert \varvec{W}_{2}\Vert ^2 \nonumber \\&+\Vert \varvec{b}_{2}\Vert ^2+ \Vert \varvec{W}_1^{'}\Vert ^2 + \Vert \varvec{b}_1^{'}\Vert ^2 + \Vert \varvec{W}_2^{'}\Vert ^2 + \Vert \varvec{b}_2^{'}\Vert ^2. \end{aligned}$$

(11)

3.2 Solution of the proposed framework

The optimization problem of our proposed framework is to minimize $\mathcal {J}$ (seen in Eq. (6)) as a function of $\varvec{W}_1$, $\varvec{b}_1$, $\varvec{W}_2$, $\varvec{b}_2$, $\varvec{W}_2^{'}$, $\varvec{b}_2^{'}$, $\varvec{W}_1^{'}$ and $\varvec{b}_1^{'}$. This is an unconstrained optimization problem and therefore we can adopt the gradient descent method to solve it.

We first introduce some intermediate variables for simplicity as follows,

$$\begin{aligned} A_{i}^{(t)}= & {} \left( {\hat{\varvec{x}}}_{i}^{(t)}-\varvec{x}_{i}^{(t)}\right) \circ {\hat{\varvec{x}}}_{i}^{(t)}\circ \left( 1-{\hat{\varvec{x}}}_{i}^{(t)}\right) , \quad \nonumber \\ B_{i}^{(t)}= & {} {\hat{\varvec{\xi }}}_{i}^{(t)}\circ \left( 1-{\hat{\varvec{\xi }}}_{i}^{(t)}\right) , \nonumber \\ C_{i}^{(t)}= & {} \varvec{z}_{i}^{(t)}\circ \left( 1-\varvec{z}_{i}^{(t)}\right) , \quad D_{i}^{(t)} = \varvec{\xi }_{i}^{(t)}\circ \left( 1-\varvec{\xi }_{i}^{(t)}\right) . \end{aligned}$$

(12)

The partial derivatives of $\varvec{W}_1$, $\varvec{W}_2$, $\varvec{W}_2^{'}$, $\varvec{W}_1^{'}$ are as follows respectively,

$$\begin{aligned} \frac{\partial \mathcal {J}}{\partial {\varvec{W}_{1}}}= & {} \sum _{t \in \{r,s\}} \sum _{i=1}^{n_t}2\varvec{W}_2^{\top }(\varvec{W}_2^{'\top }(\varvec{W}_1^{'\top }A_{i}^{(t)}\circ B_{i}^{(t)})\circ C_{i}^{(t)})\circ D_{i}^{(t)}\varvec{x}_{i}^{(t)\top } \nonumber \\&-\ \frac{\alpha }{n_r}\sum _{i=1}^{n_r}\sum _{j=1}^{c}1\{y_{i}^{(r)}=j\}\left( \varvec{W}_{2j}^{\top }-\frac{\varvec{W}_2^{\top }e^{\varvec{W}_{2}\varvec{\xi }_{i}^{(r)}}}{\sum _{l}e^{\varvec{W}_{2l}\varvec{\xi }_{i}^{(r)}}}\right) \circ D_{i}^{(r)}\varvec{x}_{i}^{(r)\top } \nonumber \\&+\, 2\beta \varvec{W}_1, \nonumber \\ \frac{\partial \mathcal {J}}{\partial {\varvec{W}_{2j}}}= & {} \sum _{t \in \{r,s\}}\sum _{i=1}^{n_t}2\varvec{W}_{2j}^{'\top }(\varvec{W}_1^{'\top }A_{i}^{(t)}\circ B_{i}^{(t)})\circ C_{ij}^{(t)}\varvec{\xi }_{i}^{(t)\top } \nonumber \\&-\, \frac{\alpha }{n_{rj}}\left( \sum _{i=1}^{n_{rj}}\varvec{\xi }_{i}^{(r)\top }-\sum _{i=1}^{n_r}\frac{e^{\varvec{W}_{2j}\varvec{\xi }_{i}^{(r)}}}{\sum _{l}e^{\varvec{W}_{2l}\varvec{\xi }_{i}^{(r)}}}\varvec{\xi }_{i}^{(r)\top }\right) + 2\beta \varvec{W}_{2j}, \end{aligned}$$

(13)

$$\begin{aligned} \frac{\partial \mathcal {J}}{\partial {\varvec{W}_{2}^{'}}}= & {} \sum _{t \in \{r,s\}}\sum _{i=1}^{n_t}2\varvec{W}_1^{'\top }A_{i}^{(t)}\circ B_{i}^{(t)}\varvec{z}_{i}^{(t)\top } + 2\beta \varvec{W}_2^{'}, \end{aligned}$$

(14)

$$\begin{aligned} \frac{\partial \mathcal {J}}{\partial {\varvec{W}_{1}^{'}}}= & {} \sum _{t \in \{r,s\}}\sum _{i=1}^{n_t}2A_{i}^{(t)}{\hat{\varvec{\xi }}}_{i}^{(t)\top } + 2\beta \varvec{W}_1^{'}, \end{aligned}$$

(15)

where $\varvec{W}_{2j}$ is the j-th row of $\varvec{W}_2$ and $n_{rj}$ is the number of instance associated with label j in training dataset. According to the above partial derivatives, we update the parameters by alternatively iterating following those rules,

$$\begin{aligned} \begin{aligned}&\varvec{W}_1 \leftarrow \varvec{W}_1 - \eta \frac{\partial {\mathcal {J}}}{\partial \varvec{W}_1},&\varvec{b}_1 \leftarrow \varvec{b}_1 - \eta \frac{\partial {\mathcal {J}}}{\partial \varvec{b}_1}, \\&\varvec{W}_1^{'} \leftarrow \varvec{W}_1^{'} - \eta \frac{\partial {\mathcal {J}}}{\partial \varvec{W}_1^{'}},&\varvec{b}_1^{'} \leftarrow \varvec{b}_1^{'} - \eta \frac{\partial {\mathcal {J}}}{\partial \varvec{b}_1^{'}}, \\&\varvec{W}_2 \leftarrow \varvec{W}_2 - \eta \frac{\partial {\mathcal {J}}}{\partial \varvec{W}_2},&\varvec{b}_2 \leftarrow \varvec{b}_2 - \eta \frac{\partial {\mathcal {J}}}{\partial \varvec{b}_2}, \\&\varvec{W}_2^{'} \leftarrow \varvec{W}_2^{'} - \eta \frac{\partial {\mathcal {J}}}{\partial \varvec{W}_2^{'}},&\varvec{b}_2^{'} \leftarrow \varvec{b}_2^{'} - \eta \frac{\partial {\mathcal {J}}}{\partial \varvec{b}_2^{'}}. \\ \end{aligned} \end{aligned}$$

(16)

where $\eta$ is step length controlling the learning rate. Finally, the whole algorithm is summarized in “Algorithm 1”.

Although the optimization of the objective function is not convex, we can get a better local optimal solution through appropriate initialization of the weights and biases. Specifically, we use the stacked denosing autoEncoder (SDAE) to initialize the values of $\varvec{W}$ and $\varvec{b}$.

3.3 Prediction

After training, we use the softmax regression to predict the label set of each test instance. Specifically, we can estimate the probability $P(y_i^{(s)}=j| \varvec{x}_i^{(s)})$ of one certain test instance belonging to each label. Then we sort all the label probabilities in descending order and compute the difference between two adjacent label probabilities in this order. Finally we assign the labels, which are in the front of the position of the max difference, as the predicted labels of the instance. This process can be described by Fig. 2, where $P_i$ is the probability of one certain test instance belonging to label i and $\triangle P_j$ is the probability difference between adjacent labels in the ordered list.

Fig. 2

The prediction strategy

4 Experimental evaluation

In this section, we conduct extensive experiments on five benchmark multi-label datasets to evaluate the performance of the proposed framework.

4.1 Datasets and preprocessing

These five datasets include slashdot, corel5k, bibtex, corel16k01 (sample 1) and corel16k02 (sample 2) from MULAN (Tsoumakas et al. 2011) and MEKA (Read et al. 2016) multi-label learning libraries. These datasets can evaluate the proposed framework in different cases including text and image. For all the datasets, we randomly sample $50\%$ of examples without replacement to construct training dataset and the remaining $50\%$ to construct test dataset. We sample each dataset for five times and calculate the average accuracies. The information of all the datasets is detailed in Table 2, #instances represents the number of instances, #features represents the feature dimension, #labels represents the number of labels, and #domains represents the domains of the datasets.

Table 2 Datasets infomration

4.2 Comparison methods

We compare our proposed model with seven multi-label algorithms as follows.

• Binary relevance (BR) (Boutell et al. 2004)   This algorithm learns c independent binary classifiers for each label and queries all the classifiers for prediction.

• Calibrated label ranking (CLR) (Fürnkranz et al. 2008)   This algorithm uses pairwise comparison to decompose the multi-label learning problem into the label ranking problem with calibrated scenario.

• Random k-Labelsets (RAkEL) (Tsoumakas and Vlahavas 2007)   This algorithm applies Label Powerset techniques, which transforms the multi-label learning problem into the multi-class classification problems, on an ensemble of k random label subsets.

• Ensemble of classifier chains (ECC) (Read et al. 2011)   This algorithm is an ensemble of classifier chain algorithm which considers high-order relations among labels represented in an ordered chain and then trains c binary classifiers according to the chain.

• Multi-label learning with Label specIfic FeaTures (LIFT) (Zhang and Wu 2015)   This algorithm conducts clustering analysis on positive and negative instances of each label to construct its specific features, then applies binary relevance algorithm on label-specific features of each label.

• Multi-label learning with stacked denoising autoencoders (SDAE) (Vincent et al. 2010)   Here we use SDAE in a two-step manner to compare with our joint optimization framework. Specially, we first train the autoencoder alone to learn feature representation and then combine the new features with the labels to construct new training dataset. Finally, we use Bayesian Multinomial Regression(BMR) to learn the classifier on the new training dataset.

• Multi-label learning with feature-induced labeling information enrichment (MLFE) (Zhang et al. 2018)   In MLFE, the structural information in feature space is utilized to enrich the labeling information. The sparse reconstruction among the training examples is conducted to characterize the underlying structure of feature space. Then the reconstruction information is conveyed from feature space to label space so as to enrich the labeling information.

4.3 Experimental settings

There are three factors in our proposed framework including trading-off parameters $\alpha$, $\beta$ and the number of nodes k of the embedding layer. After cross-validations on training dataset, we set $\alpha = 15$, $\beta = 0.005$, $k = 100$ for all datasets. LIBSVM with linear kernel (Chang and Lin 2011) is employed as the base classifier for all baselines except SDAE. Bayesian multinomial regression (BMR) (Madigan et al. 2005) is employed as the base classifier for SDAE. Specifically, for RAkEL, the size of label subset k is set as 3 and the size of ensemble is set as 2c (c is the number of labels) as a rule-of-thumb setting. For ECC, the size of ensemble is set 100 to cover the high-order relations among labels sufficiently. For LIFT, the ratio is set to 0.1 as reported in their original paper (Zhang and Wu 2015). For MLFE, the penalty parameters $\beta _1$, $\beta _2$ and $\beta _3$ are set as 2, 10, 1, respectively according to Zhang et al. (2018).

Table 3 Multi-label learning performance comparison on ranking evaluation metrics on five data sets

Table 4 Multi-label learning performance comparison on classification evaluation metrics on five data sets

4.4 Results and discussion

To compare our proposed model with baselines in a more comprehensive way, we adopt two types of evaluation metrics, i.e., ranking metrics and classification metrics. Further more, both types of metrics can be subdivided into example-based and label-based ones. Tables 3 and 4 summarizes the results on all five datasets, and the best results are marked in bold. Next, we analyze the results on all these metrics in detail as follows.

4.4.1 Results on ranking evaluation metrics

Among all ranking evaluation metrics, OneError, Coverage, RankingLoss and AvgPrecision are example-based, while MacroAUC is label-based.

• We can see that SERL performs the best in all five datasets on Coverage and RankingLoss. Even on the metric of OneError, SERL achieves the best performance on datasets corel5k and corel16k01, and gets an comparable performance to CLR and MLFE, which obtain best results on some corresponding datasets.

• For label-based ranking metric MacroAUC, SERL also achieves the best performance in most datasets. According to Table 2, we can see that corel5k has the most labels up to 374 and slashdot has the least labels of 22. The results in all the five datasets show the outstanding performance of SERL in probability estimation over the datasets with high-diversity of label size.

4.4.2 Results on classification evaluation metrics

Among classification evaluation metrics, Accuracy and F1 are example-based and MacroF1 is label-based.

• It is obvious that SERL achieves better performance than the baselines in terms of Accuracy and F1. We can get the following two observations from the results. The first one is that our model performs well for each example, which contributes to high accuracy and F1. And the other one is that some baselines such as BR and RAkEL output empty sets for some examples, failing to predict label information, which makes no sense for classification and leads to unsatisfying results.

• For MacroF1, SERL achieves the best in all data sets, which proves good performance of SERL in classifying the positive and negative examples of each label. The fact that SERL does well in both example-based and label-based classification metrics shows the superior classification performance of our model.

Overall, all the results validate the effectiveness of our framework.

4.5 Parameter sensitivity

For analyzing the influence of the parameters $\alpha$, $\beta$, k, we do a series of sensitivity experiments. We choose RankingLoss as the criterion of sensitivity experiments. All the results are shown in Fig. 3.

• For $\alpha$, RankingLoss has a obvious inflection point when $\alpha$ changes from 0 to 15. Specially, RankingLoss achieves the best value when $\alpha$ gets 15 and 30. In general, the trend of RankingLoss is gentle when $\alpha$ changes, which shows that our proposed framework is not sensitive to $\alpha$ when its value is not too small.

• For $\beta$, RankingLoss gets the best value when $\beta$ is 0.005 and 0.01. When $\beta$ increases after 0.01, RankingLoss gets worse obviously.

• For the number of nodes k of the embedding layer, RankingLoss reduces firstly and then increases slightly. It is interesting that RankingLoss gets its best value when k is relatively small, which guarantees that we can speed up the construction of our model because of the low dimension. Moreover, the trend of RankingLoss is gentle when k changes, which is helpful for the tuning process of k.

As a whole, we set $\alpha = 15$, $\beta = 0.005$, $k = 100$ for all datasets according to the parameter sensitivity experiments.

Fig. 3

The parameter affects

4.6 Effects on supervision information

To study the effectiveness of the proposed model in the case there are different numbers of labeled instances are available, we do a series of experiments in variable ratios of labeled instances. Specifically, the ratio of labeled instances increases from $5\%$ to $50\%$ and the step size is $5\%$. The results are shown in Fig. 4. It is obvious that SERL achieves the best performance in all ratios, which demonstrates the effectiveness of SERL. Moreover, compared to the baselines, the superiority of SERL is higher in small ratios than high ratios, which shows that SERL can make full use of labeled and unlabeled data sufficiently.

Fig. 4

The performance in variable ratios of labeled instances

5 Related work

Multi-label learning has attracted a lot of interest in recent years. There are two kinds of multi-label algorithms, problem transformation and algorithm adaptation methods.

Problem transformation methods transform multi-label learning problem into other problems which have solid theories and well-established solutions. For example, Binary Relevance (Boutell et al. 2004), AdaBoost.MH (Schapire and Singer 2000), Stacked Aggregation (Godbole and Sarawagi 2004) and Classifier Chains (Read et al. 2011) transform multi-label learning problem into binary classification problems. Calibrated Label Ranking transforms multi-label learning problem into label ranking problems with calibrated scenario by pairwise comparison (Fürnkranz et al. 2008). Random k-Labelsets  (Tsoumakas and Vlahavas 2007) transforms multi-label learning problem into multi-class classification problems on an ensemble of k random label subsets.

Algorithm adaptation methods adapt traditional algorithms to multi-label data (Zhang and Zhou 2014). For example, ML-kNN (Zhang and Zhou 2005) adapts traditional k-nearest neighbor algorithm to multi-label data and uses maximum a posteriori(MAP) principle to predict labels for the new instance. ML-DT (Clare and King 2002) calculates information gain based on multi-label entropy. Rank-SVM (Elisseeff and Weston 2002) fits the maximum margin to differentiate the relevant and irrelevant labels of one instance. BP-MLL (Zhang and Zhou 2006) uses feedforward neural network to hold multi-label data where a error function capturing ranking correlation between relevant and irrelevant labels is calculated through backpropagation algorithm. CML (Ghamrawi and McCallum 2005) utilizes conditional random field to model label co-occurrences in multi-label data. Nguyen et al. (2016) proposed a Bayesian nonparametric approach to learn the number of label-feature correlation pat- terns automatically. MLFE (Zhang et al. 2018) utilized the structural information in feature space to enrich the labeling information.

Except these algorithms, representation learning is also one of the most important aspects of multi-label learning (Zhang and Zhou 2008; Read and Perezcruz 2014; Zhang and Wu 2015; Yu et al. 2005; Chen et al. 2008; Sun et al. 2008; Qian and Davidson 2010; Ji et al. 2010; Karalas et al. 2015; Zhou et al. 2017). For example, Read and Perezcruz (2014) utilized restricted Boltzmann machine (RBM) to achieve better representation of the original features to train the classifier. BILC (Zhou et al. 2017) mapped the label relationship into a binary embedded space instead of real-valued to achieve better performance. However, current works about representation learning neglect label knowledge, or suffer from the lack of labeled data, or are limited to linear projection. The most related work (Li and Guo 2014), which proposed a bi-directional representation model for multi-label classification, in which the mid-level representation layer is constructed from both input and output spaces. In essence, their network structure is different from ours. Their framework contained two basic autoencoders, i.e., one for the input features and the other one for output labels, and had to compute the additional parameters of encoding weights from low-dimensional representation of the input features to output labels and prediction model from input features to the low-dimensional representation of the output labels. In this paper, we propose a framework named SERL, which adopts a two-encoding-layer autoencoder to learn feature representation in a supervised manner. The autoencoder can sufficiently utilize labeled and unlabeled data simultaneously under the supervision of softmax regression. The softmax regression incorporates label knowledge to improve the performance of both representation learning and multi-label learning by being jointly optimized with the autoencoder. Extensive experiments on five data sets demonstrate the good performance of our framework.

6 Conclusion

In this paper, we proposed a framework named SERL, which adopts autoencoder to learn feature representation in a supervised manner. In this framework, labeled and unlabeled data can be handled by the autoencoder, meanwhile the softmax regression incorporates label knowledge by being jointly optimized with autoencoder. Moreover, the autoencoder is expanded into two encoding layers to share knowledge with softmax regression by sharing the second encoding weight matrix. Extensive experiments on five real-world datasets demonstrate the superiority of SERL over other state-of-the-art multi-label learning algorithms.