1 Introduction

In traditional supervised learning, there is a one-to-one correspondence between data samples and category labels, that is, a single data sample is only associated with one category label. However, in the reality, objects tend to have multiple semantics. For example, a picture can be annotated as “blue sky”, “white clouds” and “lake” simultaneously, and there may be a strong correlation among labels. Nowadays, multi-label learning has become one of the important research hotspots in data mining and machine learning, and its main task is to assign the corresponding category labels to the objects to be classified. Researchers have enthusiastically proposed many mature multi-label classification algorithms, which have been widely applied in various research areas. For example, text classification [1], image annotation [2, 3], bioinformatics [4, 5] etc.

Multi-label classification algorithms are often classified into the following two categories [6]: problem transformation methods and algorithm adaptive methods. Specifically, the problem transformation approach transforms a multi-label learning problem into one or more traditional single-label learning problems. Its representative algorithm, such as BR [7], the core idea is to decompose the multi-label learning problem into several unrelated single-label learning problems, and then use mature and advanced methods to take effective solutions to these learning subtasks. Algorithm adaptive methods improve the traditional supervised learning algorithms to be applicable to the prediction of multi-label data. The representative algorithm is ML-KNN [8], which classifies the predicted samples based on the Maximum A Posteriori Probability rule using the label information of the sample’s neighboring locations. However, all of them ignore the correlation between labels, which reduces the learning effect of multi-label classification models. Therefore a large number of correlation-based methods have been proposed one after another. Based on the different label correlation strategies, the multi-label classification algorithms can be classified into first-order strategy [7, 8], second-order strategy [9, 10], and higher-order strategy [11, 12] respectively.

Similar to single-label classification, the feature space of multi-label classification is usually high-dimensional, which easily causes the problem of dimensional catastrophe. Recently, many dimensionality reduction methods have been applied to multi-label classification tasks [13, 14]. These methods are mostly based on the fact that each label has the same feature space. In real life, however, each label may be determined by its unique subset of features. For example, in image classification, color-based features are most beneficial to distinguishing between blue sky and white clouds in images. While texture-based features are most helpful to distinguish between desert and hills. To solve the above problems, many new algorithms have been proposed to select a set of feature subsets with good distinguishing characteristics, and effectively eliminate the redundant features in the correlation features [15,16,17], so as to achieve the reduction of feature dimensionality and improve the accuracy of the classification model, while the specific feature subsets extracted are more beneficial to the classification effect of the model.

With the rapid development of deep learning, neural network-based modeling methods have greatly promoted the progress of multi-label classification research. The neural network is formed by connecting many neurons with adjustable connection weights and has good self-organization and self-learning capabilities. Zhang et al. [18] developed a backpropagation algorithm for multi-label learning(BP-MLL), which is an adaptation of traditional multilayer feedforward neural networks for multi-label data. The core idea is to capture the features of multi-label learning by minimizing the global error function. Marilyn et al. [19] proposed a bidirectional neural network structure to learn the correlation among labels. Other CNN and RNN-based neural network algorithms are adapted to solve multi-label prediction problems [20,21,22].

In summary, existing multi-label classification methods have achieved good achievements in capturing information from original data and in establishing correlations between labels. However, the following three challenges exist:

  • Most of the previous research methods mainly used the same feature data set to represent each category label, which not only increased the complexity of calculation but also was not conducive to distinguishing and expressing the attribute information of each label.

  • Existing multi-label learning algorithms are trained and predicted on multi-label datasets in the original feature space. With the explosive growth of feature dimensions, it will become very challenging to capture the internal laws of the instance feature space. Such learning may lead to an over dimensionality of the feature space that is difficult to visualize.

  • Although considering the interrelationship among labels can improve the classification accuracy, as yet the intrinsic correlation among different instance samples is often ignored, and mining the correlation information of the instances can facilitate the training effect of the model and achieve the purpose of improving the classification performance.

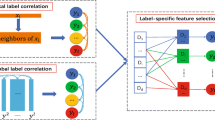
In order to solve the above-mentioned problems, in this paper, we propose an algorithm to learn label-specific features via neural network for multi-label classification(LLFN). First, we represent the original feature space of the input data by a neural network with a low-dimensional mapping:\(X\rightarrow \overset{\wedge }{\mathop {X~}}\), and this nonlinear feature mapping can mine the feature information inside the complex feature space, visualize high-dimensional data and maintain the topology of the input space structure. According to this internal feature space information, we then employ the common squared minimization loss function to model the basic framework for label-specific feature learning. Based on this, we also introduce label correlation and instance similarity to optimize the model. A unified end-to-end multi-label classification framework is finally constructed. The specific model diagram is shown in Fig. 1.

Fig. 1
figure 1

Model framework of LLFN

Full size image

The main contributions of the research in this paper are as follows:

  • Different from the traditional multi-label classification method, this paper uses a single hidden layer neural network to learn the latent representation of the feature and extracts the specific feature of the label in the latent feature space.

  • This is an end-to-end multi-label classifier with a label-specific feature-based joint learning model.

  • Experimental results on 12 widely used datasets show that our proposed method achieves some advantages over the state-of-the-art algorithms.

The rest of the paper is organized as follows. Section 2 provides extensively referenced work, giving an introduction to previous neural network multi-label learning algorithms and multi-label specific feature learning. The LLFN algorithm process is introduced in Sect. 3. Section 4 presents the experimental results and experimental analysis, and finally, the paper is summarized in Sect. 5.

2 Related work

2.1 Neural network multi-label learning

Neural networks have a widespread application in multi-label learning, and many algorithms for neural network multi-label learning have been generated in the past decade or so. Zhang et al. [18] were the first to propose the application of neural networks to multi-label classification and achieved good results compared to traditional machine learning methods. This paper used the backpropagation of multi-label learning(BP-MLL) neural network algorithm, which captures the features of multi-label learning by minimizing the inter-label sorting error. However, for large-scale multi-label text classification, the BP-MLL algorithm shows limitations. Nam et al. [20] proposed a single hidden layer of neural network architecture. The model replaces the ranking loss minimization with a cross-entropy error function on basis of BP-MLL. It demonstrates that a simple network configuration makes the model scale better and is more suitable for large-scale text classification tasks. Subsequently, Zhang [23] also proposed an RBF neural network-based multi-label learning algorithm, in which the k-means clustering analysis of the instances is first performed by the first neural network layer, and the center of mass of the clustering group is used for the prototype vector of the basis function; then the error function is minimized to learn the second ML-RBF layer weights. In this way, we can make full use of prototype vector encoding information to optimize the output neuron weights. Lu et al. [24] propose a method that uses a combination of fuzzy logic technique and DNN. The deep fuzzy hashing network (DFHN) automatically generates more effective image features for accurate prediction and classification of image datasets. In addition, autoencoders can automatically learn features of data samples [25, 26], Based on this mind, Chen et al. [27] proposed a kernel limit learning machine based auto-encoder based multi-label learning algorithm, which improves multi-label classification performance by reconstructing the label space information with auto- encoder networks, and improved generalizability of the model.

Moreover, convolutional neural networks(CNN) [21, 28, 29] and recurrent neural networks(RNN) [20, 30, 31] are increasingly used in the field of multi-label learning. Liao et al. [21] proposed a multi-label learning algorithm based on convolutional neural networks and fully initialized connections. It is a sequence-to-sequence multi-label classification model using encoders and decoders. In this, the encoder is used to encode semantic information using neural networks and attention mechanisms. The decoder combines LSTM and initialized fully connected layers to mine the global correlation and local correlation of the labels. Chen et al. [31] proposed a recurrent neural network-based multi-label classification architecture for images, which introduces the LSMT model and reflects the dependencies between labels through a visual attention mechanism. In [22], the authors propose a unified multi-label learning framework that combines the advantages of CNN and RNN for image/label embedding. The semantic label dependencies and image-label interrelationships can be learned. The semantic features are first extracted from the images by the CNN part, and then the label dependencies and the picture-label interrelationships are modeled using the RNN part to better predict the probability of labels.

2.2 Label-specific features learning

In multi-label learning, most of the existing algorithms deal with datasets with the same features, however, this is not the most ideal way, as each label tends to have its own inherent feature properties. LPLC-LA [32] is a learning method based on extracting label-specific features for obtaining local positive and negative label correlations and addresses the label imbalance problem using perceptual weights between labels. The above algorithm considered the feature-to-feature dependency but failed to reasonably and effectively eliminate the redundant features in the feature space. Bidgoli et al. [33] proposed a new multi-objective optimization method to reduce the complexity of the model by reducing the number of features; meanwhile, based on correlation analysis and redundancy analysis, it can effectively eliminate the redundancy in related features, thereby improving the classification performance.

Also for label space, using the correlation among labels to guide feature selection can greatly improve the classification performance [16, 34,35,36]. Huang et al. [16] argue that the strength of correlation among labels is potentially correlated with the magnitude of similarity among features, based on which label-specific features are learned by a linear regression model. To some extent, the method proves to fully exploit the correlation of the labels, and improve the performance of the multi-label learning algorithm. GLOCAL [36] effectively solves the problem of global labels and missing labels by considering global label correlation and shared local label correlation.

In multi-label learning, besides using the potential relationship between labels to provide additional information for multi-label learning, the samples are also correlated with each other [37, 38], Jie et al. [37] proposed a popular regularization-based multi-task feature selection learning method (MTFS), which considers instance similarity by introducing a popular Laplace-based regularization. Han et al. [38] proposed a multi-label learning algorithm that uses correlation information to learn specific features of labels (LSF-CI). LSF-CI considers that if two instances in feature space have a strong correlation, their corresponding labels will be similar.

In the previous research on multi-label learning methods, neural network algorithms have been widely used, and in recent years, a large number of multi-label classification methods that combine label-specific features, label correlation, and instance similarity have been proposed. However, most algorithms extract label-specific features in the original feature space, which is possibly not the most optimal strategy. Therefore, in this paper, we propose a neural network to map the original feature space into the embedded feature space of labels and then perform label-specific feature extraction in the embedded feature space, and finally, the performance and generalization of the algorithm are improved by introducing label correlation and instance similarity.

3 Proposed approach

3.1 Preliminaries

In multi-label learning, the input feature space is assumed to be represented as \(\varvec{X}={{\left[ {{x}_{1}},\ldots ,{{x}_{n}} \right] }^{\text {T}}}\in {{\mathbb {R}}^{n\times p}}\), and represent the output label matrix space as \(\varvec{Y}={{\left[ {{y}_{1}},\ldots ,{{y}_{n}} \right] }^{\text {T}}}\in {{\mathbb {R}}^{n\times l}}\), and the training dataset with n examples is \(\varvec{D}=\left\{ ({x}_{i},{y}_{i}) \mid {1}\le {i}\le {n}\right\}\). Denote the p-dimensional feature vector by \({{x}_{i}}=\left[ {{x}_{i1}},\ldots , {{x}_{ip}} \right]\), \({{x}_{i}}\in \varvec{X}\), and \({{y}_{i}}=\left[ {{y}_{i1}}, \ldots ,{{y}_{il}} \right]\) is a l-dimensional real-valued label vector. If the label \({y}_{i}\) is associated with \({x}_{i}\), then each element \({y}_{ij}={1}\), otherwise \({y}_{ij}={0}\). The task of MLL involves learning a function \({h}:\varvec{X}\rightarrow {2}^{\varvec{Y}}\) from the multi-label set of training that predicts the confidence of each label by the mapping function \(h(\cdot )\) for any invisible instance \({x}\in \varvec{X}\).

3.2 Learning multi-label specific features based on neural networks

As mentioned above, each category label has its own specific features. However, in previous studies, the specific feature of the label is a subspace filtered from the original feature space, and the subspace is relatively sparse compared to the original feature space. As shown in Fig. 1, we propose a potential mapping representation of instance features obtained by a low-dimensional mapping of the input feature space by a neural network. The neural network structure in Fig. 1 includes an input layer \(\varvec{X}\), an output layer \(\varvec{Y}\), and a hidden layer, where the weight coefficient matrices connected to the hidden layer are \(\varvec{W}_{1}\) and \(\varvec{W}_{2}\), respectively. In this paper, the activation function of the hidden layer is the hyperbolic tangent function \(\tanh \left( \cdot \right)\). Our model can be initially expressed as

$$\begin{aligned} \underset{{\varvec{W}_{1}},{\varvec{W}_{2}}}{\mathop {\min }}\,\frac{1}{2}\left\| \tanh (\varvec{X}{\varvec{W}_{1}}){\varvec{W}_{2}}-\varvec{Y} \right\| _{F}^{2}+\beta {{\left\| {\varvec{W}_{2}} \right\| }_{1}}+\frac{\gamma }{2} \left\| {\varvec{W}_{1}} \right\| _{F}^{2} \end{aligned}$$
(1)

The first term in Eq. 1 is the squared loss term of the combined neural network. where \(\varvec{W}_{1}\in {{\mathbb {R}}^{p\times d}}\) denotes the weight matrix of neuronal connections between the hidden and input layers, and \(\varvec{W}_{2}\in {{\mathbb {R}}^{d\times l}}\) is the weight matrix between the hidden and output layers. The second term is the \({{l}_{1}}\)-norm regularization term that simulates the sparsity of specific features of the label, and \(\beta\) is the parameter that controls its sparsity. The third term is a regularization term that controls the complexity of the model, and \(\gamma\) is its weight coefficient. Moreover, combining Fig. 1 and Eq. 1, it can be found that W1 aims at a low-dimensional data representation of the original feature space with a nonlinear mapping through the activation function. \(\varvec{W}_{2}\) aims to learn label-specific features naturally by reserving non-zero feature elements for each label.

3.3 Combining Label Correlations

In multi-label learning, considering label correlation can improve the classification performance of multiple labels. From the work in [16], if two labels have strong correlations, the features contained in one of the labels should be very close to the features possessed by the other label. That is, if the labels \({y}_{i}\) and \({y}_{j}\) are strongly correlated, the similarity between the coefficient vector \({{w}_{{{2}_{i}}}}\) and \({{w}_{{{2}_{j}}}}\) will be large, otherwise, the similarity will be small. After introducing label correlation, the objective function is obtained as

$$\begin{aligned}&\underset{{\varvec{W}_{1}},{\varvec{W}_{2}}}{\mathop {\min }}\,\frac{1}{2}\left\| \tanh (\varvec{X}{\varvec{W}_{1}}){\varvec{W}_{2}}-\varvec{Y} \right\| _{F}^{2}+\frac{\alpha }{2}tr({\varvec{W}_{2}}\varvec{R}{\varvec{W}_{2}}^{T})\nonumber \\&\quad +\beta {{\left\| {\varvec{W}_{2}} \right\| }_{1}}+\frac{\gamma }{2}\left\| {\varvec{W}_{1}} \right\| _{F}^{2} \end{aligned}$$
(2)

where \(\varvec{R}=1-\varvec{C}\), The element \(\varvec{C}_{ij}\) in \(\varvec{C}\) represents the similarity between the label \({y}_{i}\) and the label \({y}_{j}\). Because the label matrix \(\varvec{Y}\) is a binary variable, and the Hamming distance is a good way to measure the similarity of binary variables [39, 40], the Hamming distance is used to calculate the label correlation.

3.4 Combining instance similarities

Equation 2 only considers the relationship between labels, and the potential relationship between instances is ignored. From [37, 38], Considering the dependency among instances, the distribution information of data samples can be retained to the maximum extent. Introducing the instance similarity regularization term \(\varvec{\varOmega }(\varvec{W}_{1})\), Eq. 2 can be optimized as

$$\begin{aligned}&\underset{{\varvec{W}_{1}},{\varvec{W}_{2}}}{\mathop {\min }}\,\frac{1}{2}\left\| \tanh (\varvec{X}{\varvec{W}_{1}}){\varvec{W}_{2}}-\varvec{Y} \right\| _{F}^{2}+\frac{\alpha }{2}tr({\varvec{W}_{2}}\varvec{R}{\varvec{W}_{2}}^{T})\nonumber \\&\quad +\beta {{\left\| {\varvec{W}_{2}} \right\| }_{1}}+\frac{\lambda }{2}\varvec{\varOmega } ({\varvec{W}_{1}})+\frac{\gamma }{2} \left\| {\varvec{W}_{1}} \right\| _{F}^{2} \end{aligned}$$
(3)

\(\varvec{\varOmega }(\varvec{W}_{1})\) can be defined as

$$\begin{aligned} \varOmega \left( {\varvec{W}_{1}} \right) =\frac{1}{2}\sum \limits _{i,j}{\left\| \varvec{W_{1}}^{T}{{x}_{i}}-\varvec{W_{1}}^{T}{\varvec{x}_{j}} \right\| _{2}^{2}}{\varvec{S}_{ij}} =tr({{(\varvec{X}{\varvec{W}_{1}})}^{T}}\varvec{L}\varvec{X}{\varvec{W}_{1}}) \end{aligned}$$
(4)

where \(\varvec{S}_{ij}\) is the similarity between the i-th and j-th instances, \(\varvec{L}\) is the graph Laplacian matrix of the k-nearest neighbor graph \(\varvec{S}\), \({\varvec{L}=\varvec{D}-\varvec{S}}\), \({\varvec{D}_{ii}}=\sum \nolimits _{j=1}^{n}{{\varvec{S}_{ij}}}\), specifically, can be expressed as

$$\begin{aligned} {\varvec{S}_{ij}}=\left\{ \begin{matrix} exp\left( -\frac{|{{x}_{i}}-{{x}_{j}}{{|}^{2}}}{{{\sigma }^{2}}} \right) ~~\text { }{{x}_{i}}\in {\varvec{N}_{K}}({{x}_{j}})\text { }or\text { }{{x}_{j}}\in {\varvec{N}_{K}}({{x}_{i}}) \\ 0 \qquad \qquad \qquad \qquad otherwise \\ \end{matrix} \right. \end{aligned}$$
(5)

From Eq. 5, if there is a strong similarity between \({x}_{i}\) and \({x}_{j}\), then the distance between them will be smaller, otherwise, the distance between instances will be larger. Therefore, considering the instance similarity regularization term, i.e., minimization \(\varvec{\varOmega }(\varvec{W}_{1})\) can be more accurately solved for the coefficient matrix \(\varvec{W}_{1}\) , Eq. 4 can further be formulated as

$$\begin{aligned} \begin{aligned} f(\varvec{W})&=\underset{{\varvec{W}_{1}},{\varvec{W}_{2}}}{\mathop {\min }}\,\frac{1}{2}\left\| \tanh (\varvec{X}{\varvec{W}_{1}}){\varvec{W}_{2}}-\varvec{Y} \right\| _{F}^{2}+\frac{\alpha }{2}tr({\varvec{W}_{2}}\varvec{R}{\varvec{W}_{2}}^{T})+\beta {{\left\| {\varvec{W}_{2}} \right\| }_{1}}\\&\quad +\frac{\lambda }{2}tr({{(\varvec{X}{\varvec{W}_{1}})}^{T}}\varvec{L}\varvec{X}{\varvec{W}_{1}})+\frac{\gamma }{2} \left\| {\varvec{W}_{1}} \right\| _{F}^{2} \end{aligned} \end{aligned}$$
(6)

where \(\alpha ,\beta ,\lambda\), and \(\gamma\) are all positive constants, and their values are determined by five-fold cross-validation on the training data set.

3.5 Optimization of LLFN model

There are two model coefficients \({\varvec{W}_{1}}\) and \(\varvec{W}_{2}\) to be optimized in Eq. 6. Obviously, it is very difficult to optimize them at the same time. Therefore, we use alternate optimization techniques to optimize \({\varvec{W}_{1}}\) and \(\varvec{W}_{2}\). Specifically, first, fix \({\varvec{W}_{1}}\), use the accelerated proximal gradient method to optimize \(\varvec{W}_{2}\), then fix \(\varvec{W}_{2}\), use the gradient descent algorithm to optimize \({\varvec{W}_{1}}\), and finally obtain the optimal \({\varvec{W}_{1}}\) and \(\varvec{W}_{2}\).

1. Fix \({\varvec{W}_{1}}\), update \(\varvec{W}_{2}\)

When \({\varvec{W}_{1}}\) is fixed, the objective function of optimizing \(\varvec{W}_{2}\) can be further written as

$$\begin{aligned} \begin{aligned}&\underset{{\varvec{W}_{1}},{\varvec{W}_{2}}}{\mathop {\min }}\,\frac{1}{2}\left\| \tanh (\varvec{X}{\varvec{W}_{1}}){\varvec{W}_{2}}-\varvec{Y} \right\| _{F}^{2}\\&\quad +\frac{\alpha }{2}tr({\varvec{W}_{2}}\varvec{R}{\varvec{W}_{2}}^{T})+\beta {{\left\| {\varvec{W}_{2}} \right\| }_{1}} \end{aligned} \end{aligned}$$
(7)

It can be seen that Solving \(\varvec{W}_{2}\) in problem Eq. 7 is a convex optimization problem, but since the learning objective \(\varvec{W}_{2}\) of the model in this paper with \({{l}_{1}}\)-norm regularization term, resulting in \(\varvec{W}_{2}\) is non-smooth and cannot be solved directly by deriving the derivative. Therefore, according to the literature [41], this paper uses Accelerated Proximal Gradient (APG) to solve the model parameters \(\varvec{W}_{2}\).

The convex optimization problem is generally divided into two parts by APG, and the equation is expressed as follows

$$\begin{aligned} \underset{{\varvec{W}_{2}}\in \text {H}}{\mathop {\min }}\,F\left( {\varvec{W}_{2}} \right) =f\left( {\varvec{W}_{2}} \right) +g\left( {\varvec{W}_{2}} \right) \end{aligned}$$
(8)

where H denotes the Hilbert space, \(f({\varvec{W}_{2}})\) is a smooth convex function and \(g({\varvec{W}_{2}})\) is a non-smooth convex function. For \(f({\varvec{W}_{2}})\) satisfying the Lipschitz condition, then for any matrix \({\varvec{W}_{2}}_{_{1}}\) and \({\varvec{W}_{2}}_{_{2}}\) have

$$\begin{aligned} \left\| \nabla f({\varvec{W}_{2}}_{_{1}})-\nabla f(\varvec{{W}_{2}}_{_{2}}) \right\| \le {{L}_{f}}\left\| \varDelta {\varvec{W}_{2}} \right\| \end{aligned}$$
(9)

where \({L}_{f}\) is the Lipschitz constant,\(\varDelta {\varvec{W}_{2}}={\varvec{W}_{{{2}_{1}}}}-{\varvec{W}_{{{2}_{2}}}}\). In accelerated gradient descent it is necessary to introduce \({Q}\left( {\varvec{W}_{2}},\varvec{W}_{2}^{(t)} \right)\) to quadratic approximation \(F\left( {\varvec{W}_{2}} \right)\), instead of direct minimization \(F\left( {\varvec{W}_{2}} \right)\), \({Q}\left( {\varvec{W}_{2}},\varvec{W}_{2}^{(t)} \right)\)defined as

$$\begin{aligned}&Q({\varvec{W}_{2}},\varvec{W_{2}}^{(t)})=f(\varvec{W_{2}}^{(t)})\nonumber \\&\quad +\left\langle \nabla f \right. ({\varvec{W}_{2}}^{(t)}),{\varvec{W}_{2}}-{\varvec{W}_{2}}^{(t)}) +\frac{{{L}_{f}}}{2}\left\| {\varvec{W}_{2}}-{\varvec{W}_{2}}^{(t)} \right\| _{F}^{2} +g({\varvec{W}_{2}}) \end{aligned}$$
(10)

When

$$\begin{aligned} {\varvec{G}^{(t)}}={\varvec{W}_{2}}^{(t)}-\frac{1}{{{L}_{f}}}\nabla f(\varvec{{W}_{2}}^{(t)}) \end{aligned}$$
(11)

Then Eq. 10 can be written as

$$\begin{aligned} {\varvec{W}_{2}}=\underset{{\varvec{W}_{2}}}{\mathop {\arg \min }}\,Q({\varvec{W}_{2}},{\varvec{W}_{2}}^{(t)})=\underset{{\varvec{W}_{2}}}{\mathop {\arg \min }}\,\text {g}({\varvec{W}_{2}})+\frac{{{L}_{f}}}{2}\left\| {\varvec{W}_{2}}-{\varvec{G}^{(t)}} \right\| _{F}^{2} \end{aligned}$$
(12)

From Eqs. 7 and 8, \(f\left( {\varvec{W}_{2}} \right)\) and \(g\left( {\varvec{W}_{2}} \right)\) are further expressed as

$$\begin{aligned} \begin{aligned} f({\varvec{W}_{2}})&=\frac{1}{2}\left\| \tanh (\varvec{X}{\varvec{W}_{1}}){\varvec{W}_{2}}-Y \right\| _{F}^{2}+\frac{\alpha }{2}tr({\varvec{W}_{2}}\varvec{R}{\varvec{W}_{2}}^{T}) \\&\quad +\frac{\lambda }{2}tr({{(\varvec{X}{\varvec{W}_{1}})}^{T}}\varvec{L}\varvec{X}{\varvec{W}_{1}})+\frac{\gamma }{2}\left\| {\varvec{W}_{1}} \right\| _{F}^{2} \end{aligned} \end{aligned}$$
(13)
$$\begin{aligned} g({\varvec{W}_{2}})&=\beta {{\left\| {\varvec{W}_{2}} \right\| }_{1}} \end{aligned}$$
(14)

Then according to Eqs. 12, 13, and 14 coefficient matrix \(\varvec{{W}_{2}}\) can be optimized by

$$\begin{aligned} {\varvec{W}_{2}} = \underset{{\varvec{W}_{2}}}{\mathop {\arg \min }}\,\frac{1}{2}\left\| {\varvec{W}_{2}}-{\varvec{G}^{(t)}} \right\| _{F}^{2}+\frac{\beta }{{{L}_{f}}}{{\left\| {\varvec{W}_{2}} \right\| }_{1}} \end{aligned}$$
(15)

In [42], let \(\varvec{W}_{2}^{(t)}={\varvec{W}_{{{2}_{t}}}}+\frac{{{b}_{t-1}}-1}{{{b}_{t}}}({\varvec{W}_{{{2}_{t}}}}-{\varvec{W}_{{{2}_{t-1}}}})\), \({\varvec{W}_{{{2}_{t}}}}\) and \({\varvec{W}_{{{2}_{t-1}}}}\) here are the coefficient matrices of the t-th and \(t-1\)-th iterations respectively. When the sequence \({{\text {b}}_{t}}\) is satisfied \(b_{t+1}^{2}-{{b}_{t+1}}\le b_{t}^{2}\), the convergence rate of the algorithm can be increased to \(O\left( {{t}^{-2}} \right)\). Since \(g({\varvec{W}_{2}})\) is \({{l}_{1}}\)-norm, the iterative solution for \(\varvec{W}_{2}\) is as follows

$$\begin{aligned} {\varvec{W}_{{{2}_{t+1}}}}={\varvec{S}_{\varepsilon }}\left[ {{\varvec{G}}^{(t)}} \right] =\underset{{\varvec{W}_{2}}}{\mathop {\arg \min }}\,\varepsilon {{\left\| {\varvec{W}_{2}} \right\| }_{1}}+\frac{1}{2}\left\| {\varvec{W}_{2}}-{{\varvec{G}}^{(t)}} \right\| _{F}^{2} \end{aligned}$$
(16)

where \({\varvec{S}_{\varepsilon }}[\cdot ]\) is the soft-threshold operator, for each element \({W}_{ij}\) and \(\varepsilon =\frac{\beta }{{{L}_{f}}}\>0\), the soft-threshold operator is defined as

$$\begin{aligned} {{S}_{\varepsilon }}\left[ {{\varvec{G}}^{(t)}} \right] =\left\{ \begin{matrix} {{w}_{ij}}-\varepsilon &{} \text { if }{{w}_{ij}}>\varepsilon \\ {{w}_{ij}}+\varepsilon &{} \text { if }{{w}_{ij}}<-\varepsilon \\ 0 &{} \text { otherwise } \\ \end{matrix} \right. \end{aligned}$$
(17)

Next, verify the Lipschitz continuity of Eq. 7, and according to Eq. 7, let \(\varvec{M}=\tanh \left( \varvec{X}{\varvec{W}_{1}} \right) , \nabla f\left( {\varvec{W}_{2}} \right)\) is

$$\begin{aligned} \nabla f\left( {\varvec{W}_{2}} \right) \text {=}{\varvec{M}^{\text {T}}}\varvec{M}{\varvec{W}_{2}}-{\varvec{M}^{\text {T}}}\varvec{Y}+\alpha {\varvec{W}_{2}}\varvec{R} \end{aligned}$$
(18)

Given \({\varvec{W}_{{{2}_{1}}}}\) and \({\varvec{W}_{{{2}_{2}}}}\), we obtain

$$\begin{aligned} \begin{aligned} \left\| \nabla f\left( {\varvec{W}_{{{2}_{1}}}} \right) -\nabla f\left( {\varvec{W}_{{{2}_{2}}}} \right) \right\| _{F}^{2}&=\left\| {{\varvec{M}}^{T}}\varvec{M}{\varvec{W}_{2}}-\alpha {\varvec{W}_{2}}\varvec{R} \right\| _{F}^{2}\\&\le 2\left\| {{\varvec{M}}^{T}}\varvec{M}\varDelta {\varvec{W}_{2}} \right\| _{F}^{2}+2\left\| \alpha \varDelta {\varvec{W}_{2}}\varvec{R} \right\| _{F}^{2}\\&\le 2\left\| {{\varvec{M}}^{T}}\varvec{M} \right\| _{2}^{2}\left\| \varDelta {\varvec{W}_{2}} \right\| _{F}^{2}+2\Vert \alpha \varvec{R}\Vert _{2}^{2}\left\| \varDelta {\varvec{W}_{2}} \right\| _{F}^{2}\\&=\left( 2\left\| {{\varvec{M}}^{T}}\varvec{M} \right\| _{2}^{2}+2\Vert \alpha \varvec{R}\Vert _{2}^{2} \right) \left\| \varDelta {\varvec{W}_{2}} \right\| _{F}^{2}\\&=\left( 2\delta _{\max }^{2}\left( {{\varvec{M}}^{T}}\varvec{M} \right) +2\delta _{\max }^{2}(\alpha \varvec{R}) \right) \left\| \varDelta {\varvec{W}_{2}} \right\| _{F}^{2} \end{aligned} \end{aligned}$$
(19)

where \(\varDelta {\varvec{W}_{2}}={\varvec{W}_{{{2}_{1}}}}-{\varvec{W}_{{{2}_{2}}}}\), \({{\delta }_{\max }}(\cdot )\) is the maximum value of singularity of the given matrix. In summary, we can get

$$\begin{aligned}&\left\| \nabla f\left( {\varvec{W}_{{{2}_{1}}}} \right) -\nabla f\left( {\varvec{W}_{{{2}_{2}}}} \right) \right\| _{F}^{2}\le \left( 2\delta _{\max }^{2}\left( {{\varvec{M}}^{T}}\varvec{M} \right) \right. \nonumber \\&\left. \quad +2\delta _{\max }^{2}(\alpha \varvec{R}) \right) \left\| \varDelta {\varvec{W}_{2}} \right\| _{F}^{2} \end{aligned}$$
(20)

In short, the Lipschitz constant is

$$\begin{aligned} {{L}_{f}}=\sqrt{2\delta _{\max }^{2}\left( {{\varvec{M}}^{T}}\varvec{M} \right) +2\delta _{\max }^{2}(\alpha \varvec{R})} \end{aligned}$$
(21)

2. Fix \({\varvec{W}_{2}}\), update \({\varvec{W}_{1}}\)

When \({\varvec{W}_{2}}\) is fixed, the objective function of updating \({\varvec{W}_{1}}\) is written as

$$\begin{aligned}&\underset{{\varvec{W}_{1}},{\varvec{W}_{2}}}{\mathop {\min }}\,\frac{1}{2}\left\| \tanh (\varvec{X}{\varvec{W}_{1}}){\varvec{W}_{2}}-\varvec{Y} \right\| _{F}^{2}+\frac{\lambda }{2}tr({{(\varvec{X}{\varvec{W}_{1}})}^{T}}\varvec{L}\varvec{X}{\varvec{W}_{1}})\nonumber \\&\quad +\frac{\gamma }{2} \left\| {\varvec{W}_{1}} \right\| _{F}^{2} \end{aligned}$$
(22)

The gradient descent algorithm is used to solve for \({\varvec{W}_{1}}\), and the derivative of \({\varvec{W}_{1}}\) for the above equation can be obtained as

$$\begin{aligned}\nabla f\left( {\varvec{W}_{1}} \right)& ={\varvec{X}^{T}}\left( \varvec{1}-\varvec{M}\odot \varvec{M} \right) \left( \varvec{M}{\varvec{W}_{2}}\varvec{W}_{2}^{T}-2\varvec{Y}\varvec{W}_{2}^{T} \right) \nonumber \\&\quad +\lambda {\varvec{X}^{T}}\varvec{L}\varvec{X}{\varvec{W}_{1}}+\gamma {\varvec{W}_{1}} \end{aligned}$$
(23)

Where \(\odot\) is the Hadamard product operator, then the updated \({\varvec{W}_{1}}\) is

$$\begin{aligned} {\varvec{W}_{1}}={\varvec{W}_{1}}-\eta \nabla f({\varvec{W}_{1}}) \end{aligned}$$
(24)

Based on the above iterative optimization process, the specific iterative solution procedure is summarized in Algorithm 1.

figure a
figure b
figure c

The nonzero entities \({{W}_{2{}_{i}}}\) are considered as label-specific features of \({{y}_{i}}\), which are used as inputs to the classification algorithm with multi-labels, and then the binary classifier BSVM is used to achieve multi-label classification. The procedure is summarized in Algorithm 3.

3.6 Complexity analysis

The time complexity of LLFN consists of two main components: the algorithm initialization and the iterative process. The complexity of updating the weight matrix \({\varvec{W}_{{{2}_{0}}}}\) of the model in initialization is \(O(n{{p}^{2}}+npl+{{p}^{3}}+{{p}^{2}}l)\), the complexity of the computing label similarity matrix is \(O(n{{l}^{2}})\), and the graph Laplacian matrix \(\varvec{L}\) requires \(O({{n}^{2}}d)\). During the iteration, the complexity of computing the Lipschitz constant \({{L}_{f}}\) is \(O(npd+n{{d}^{2}}+{{d}^{3}}+n{{l}^{2}}+{{l}^{3}})\), and the focus in the loop process is to compute \(\nabla f(\varvec{{W}_{1}})\). Which is obtained from Eq. 23 as \(O(npd+n{{d}^{2}}+{{d}^{2}}l+ndl+d{{l}^{2}})\). In summary, the complexity of \(\nabla f({\varvec{W}_{1}})\) and \({{L}_{f}}\) is relatively the highest time complexity, and if the time complexity of the initialization process is relatively low, then the overall complexity has to be the higher order of magnitude part of the time complexity. Furthermore, because \({{L}_{f}}\) only needs to be calculated once, so the complexity of the whole algorithm is \(O(npd+n{{d}^{2}}+{{d}^{2}}l+ndl+d{{l}^{2}})\). Meanwhile, we also compare the time complexity of the LLFN algorithm with LLSF, LSML, JLCLS, and BDLS algorithms. From the work in [16, 34, 43, 44], it can be seen that the time complexity of LLSF is \(O\left( {{d}^{2}}+dl+{{l}^{2}}+nd+nl \right)\), the complexity of LSML is \(O\left( \left( n+l \right) {{d}^{2}}+\left( n+d \right) {{l}^{2}}+dnl+{{l}^{3}}+{{d}^{3}} \right)\), the complexity of JLCLS is \(O\left( \left( n+1 \right) \left( {{d}^{2}}{{l}^{2}}+n{{l}^{2}}+n{{d}^{2}}l \right) +{{d}^{3}}+{{l}^{3}} \right)\), and the complexity of BDLS is \(O\left( \left( n+d+l \right) ldt \right)\). The comparison finds that the algorithm proposed in this paper is competitive with other algorithms in terms of time efficiency.

4 Experiment

In this section, to verify the competitiveness and extensiveness of our proposed LLFN, six existing multi-label classification algorithms are used to compare with LLFN, and these methods are experimented on 12 datasets using five multi-label evaluation criteria. The dataset analysis, performance metrics, and comparison algorithms are first briefly introduced to prepare for the analysis of the experimental results.

4.1 Data sets

In this section, the comparison data were selected from 12 multi-label datasets of different domains, and the details of the experimental datasets are described in Table 1. Specifically, These datasets can be downloaded from Mulan,Footnote 1 Yahoo,Footnote 2 and Image.Footnote 3

Table 1 Description of the LLFN datasets
Full size table

4.2 Evaluation metrics

In contrast to single-label learning, multi-label learning is not unique due to the number of labels corresponding to the samples to be classified. The classification complexity leads to the complexity of measuring the performance of multi-label generalization, while the goodness of label prediction can be measured based on certain evaluation metrics. To measure the performance of multi-label classification and feature selection intuitively and numerically, five evaluation metrics [6] commonly used in the multi-label domain are selected in this paper to compare with the algorithms introduced above. Among them, the \(D=\{({{X}_{it}},{{Y}_{il}}|1\le t\le p,1\le i\le n,1\le l\le L)\}\) is the multi-label data set.

  • Hamming Loss (HL \(\downarrow\)) evaluates the variance between the set of true label sets and the predicted label set that is the number of times a sample label pair is misclassified.

    $$\begin{aligned} Hamming\text { }Loss=\frac{1}{n}\sum \limits _{i=1}^{n}{\left( \frac{1}{|Y|}\left| h\left( {{x}_{i}} \right) \varDelta {{Y}_{i}} \right| \right) } \end{aligned}$$
    (25)

  • Average Precision (AP \(\uparrow\)) is used to evaluate the average score of the real labels ranked higher than the non-real labels in the predicted label ranking of the whole sample.

    $$\begin{aligned}&Average\text { }Precision=\frac{1}{n}\sum \limits _{i=1}^{n}{\frac{1}{\left| {{Y}_{i}} \right| }}\cdot \nonumber \\&\quad \sum \limits _{y\in {{Y}_{i}}}{\frac{\left| \left\{ {{y}^{\prime }}\mid {{{\text {rank}}}_{f}}\left( {{x}_{i}},{{y}^{\prime }} \right) \le {{{\text {rank}}}_{f}}\left( {{x}_{i}},y \right) ,{{y}^{\prime }}\in {{Y}_{i}} \right\} \right| }{{{{\text {rank}}}_{f}}\left( {{x}_{i}},y \right) }} \end{aligned}$$
    (26)

  • Ranking Loss (RL \(\downarrow\)) indicates the probability value that the confidence level of the associated labels in the sample prediction result is smaller than the confidence level of the unassociated labels.

    $$\begin{aligned} Ranking\text {}&L\text {oss}=\frac{1}{n}\sum \limits _{i=1}^{n}{\frac{1}{|{{Y}_{i}}||{{\overline{Y}}_{i}}|}}\cdot \left| \{({{y}_{1}},{{y}_{2}})|f({{x}_{i}},{{y}_{1}})\right. \nonumber \\&\quad \left. \le f({{x}_{i}},{{y}_{2}}),({{y}_{1}},{{y}_{2}})\in {{Y}_{i}}\times \overline{{{Y}_{l}}}\} \right| \end{aligned}$$
    (27)

  • One-Error (OE \(\downarrow\)) reflects the probability that the Top-Ranked Label in the prediction result is not in the true set of labels for that sample.

    $$\begin{aligned} One\text { }Error=\frac{1}{n}\sum \limits _{1}^{n}{\left[ \!\left[ \begin{array}{*{35}{l}} {\text {argmax}} \\ y\in Y \\ \end{array}f\left( {{x}_{i}},y \right) \notin {{Y}_{i}} \right] \!\right] } \end{aligned}$$
    (28)

  • Coverage (CV \(\downarrow\)) is used to evaluate the ranking of the marks to be tested for all samples, and how many steps are needed to cover all the marks related to the sample on average.

    $$\begin{aligned} Coverage=\frac{1}{n}\sum \limits _{i=1}^{n}{\underset{y\in {{Y}_{i}}}{\mathop {\max {{{\text {rank}}}_{f}}}}\,}({{x}_{i}},y)-1 \end{aligned}$$
    (29)

4.3 Comparative algorithms

  • ML-kNN [8] It is based on the classical KNN method for multi-label data, which counts the number of occurrences of these neighboring instances to be predicted, and the maximum a posteriori probability (MAP) principle is used to identify the label set of the unknown sample. In our experiments, the parameter k is set to 10.

  • LIFT [15] It uses clustering techniques to study the positive and negative instances of each category label to construct label-specific features. Then the generated label-specific features are then used to generalize a binary classification model for the corresponding category labels. LIFT reduces the dimensionality of the feature space but does not consider label correlation. The ratio parameter r is set to 0.1 for all data sets.

  • LLSF [16] A method of sparse superposition is used to learn related feature subsets for label-specific feature extraction, but does not consider instance correlation. The parameters \(\alpha\), \(\beta\), and \(\gamma\) are set to 0.1, 0.1 and 0.01 respectively. the threshold \(\tau\) is set to 0.5.

  • LSML [34] It handles missing multi-label specific data for classification by learning higher-order label correlation matrix with label feature method. The parameters \({{\lambda }_{\text {1}}, }{{\lambda }_{\text {2}}}, {{\lambda }_{\text {3}}}\), and \({{\lambda }_{\text {4}}}\) are set to \(\text {1}{{\text {0}}^{\text {2}}}, \text {1}{{\text {0}}^{\text {-5}}}, \text {1}{{\text {0}}^{\text {-3}}}\), and \(\text {1}{{\text {0}}^{\text {-5}}}\) respectively.

  • JLCLS [43] It learns jointly by considering the mislabeled tags and tag-specific features. The algorithm uses alternating iterative optimization to obtain the completion matrix and label-specific features with full consideration of label correlation. The parameters \(\alpha , \beta\), and \(\theta\) are searched in \(\{{{2}^{-10}},{{2}^{-9}},\ldots ,{{2}^{9}},{{2}^{10}}\}\), \(\gamma\) selects from \(\left\{ 0.1,1,10 \right\}\).

  • BDLS [44] It considers bidirectional mapping and label causality and thereby learns specific features of the labels. The parameters \(\alpha ,\beta\) and \(\lambda\) are searched in \(\{{{2}^{-7}},{{2}^{-6}},\ldots ,{{2}^{6}},{{2}^{7}}\}\), \(\gamma\) selects from \(\left\{ 0.01,0,1,10 \right\}\).

  • LLFN The method proposed in this paper combines multi-label classification by neural networks after learning multi-label specific features, considering label relevance and instance relevance. The parameters \(\alpha , \beta , \gamma , \lambda\), and \(\eta\) are searched in \(\{{{2}^{-10}},{{2}^{-9}},\ldots ,{{2}^{9}},{{2}^{10}}\}\), \(\tau\) is also set to 0.5.

  • LLFN-BSVM The binary classifier BSVM is added to LLFN, and a data matrix consisting of label-specific features generated by LLFN is set as the training data for BSVM. Where the kernel function is linear and all parameters are set the same as LLFN.

4.4 Experimental results

In order to accurately evaluate the performance of each multi-label classification algorithm, a five-fold cross-validation is applied to the training data of each dataset. The comparison of the values of the five evaluation metrics for each algorithm is shown in Tables 2, 3, 4, 5, 6, and the best results in the table are indicated by bold numbers. The evaluation metrics are followed by the symbols \("\uparrow"\) and \("\downarrow"\) after the evaluation metrics indicate that the larger the value of the evaluation metric is, the better the performance of the algorithm and the smaller the value is, the better the performance of the algorithm, respectively.

Table 2 Experimental results (mean ± std) of the comparison algorithm on HL (\(\downarrow\))
Full size table
Table 3 Experimental results (mean ± std) of the comparison algorithm on AP (\(\uparrow\))
Full size table
Table 4 Experimental results (mean ± std) of the comparison algorithm on OE (\(\downarrow\))
Full size table
Table 5 Experimental results (mean ± std) of the comparison algorithm on RL (\(\downarrow\))
Full size table
Table 6 Experimental results (mean ± std) of the comparison algorithm on CV (\(\downarrow\))
Full size table

In addition, the Friedman test is used in this paper to compare the relative performance among the algorithms, and the corresponding critical values of the Friedman statistic and each evaluation metric are given in Table 7. At the significance level of \(\alpha =0.05\), the hypothesis that all algorithms have the same performance is explicitly rejected. Therefore, we need to use the Nemenyi test to further distinguish the classification performance of LLFN as well as other comparative algorithms on the 12 datasets. Figure 2 presents the CD plots for each algorithm under different evaluation metrics, respectively. In each subplot, if the corresponding mean ordinal values differ by at least the critical value domain (CD): \(CD={{q}_{\alpha }}\sqrt{\frac{K(K+1)}{6N}}\), then it indicates a significant difference in performance between classifiers. For the Nemenyi test, it can be calculated as \(CD=3.031(K=8,N=12)\) at the significance level \(\alpha =0.05\) and the critical difference \({{q}_{\alpha }}=3.031\). As shown in Fig. 2, the algorithm with the red line connected to each subgraph is considered as the algorithm with less significant difference. To summarize the above experimental results, it can be concluded that:

  1. 1.

    Analyzing the optimal comparison experiments shown in Tables 2, 3, 4, 5, 6, it can be observed that LLFN-BSVM significantly outperforms the LLSF, LSML, KNN, JLCSC, and BDLS algorithms on the eight datasets in terms of HL metrics, while showing suboptimal results on art, computers, and emotion. And on AP and OE metrics, LLFN-BSVM presented optimal results on 10 data sets. For RL and CV metrics, LLFN-BSVM had the best experimental results with 6 and 7 datasets, respectively, and LLFN-BSVM slightly outperformed LIFT in RL and CV indicators in general. In addition, it was found from Fig. 2 that when the significance level \(\alpha =0.05\), LLFN-BSVM ranked first in all performance metrics. LLFN ranked higher than LLSF, LSML, KNN, JLCLS, and BDLS algorithms in HL, AP, and OE, but ranked just below JLCLS and BDLS algorithms in RL metrics and below BDLCS in CV algorithms. This verifies the effectiveness of the algorithm proposed in this paper, that is, the introduction of neural networks for label-specific feature learning can improve the performance of multi-label classification.

  2. 2.

    LLFN-BSVM performs better than LLFN in \(\text {85\%}\) of the cases and obtains more stable experimental results in comparison. Additionally, as shown in Tables 5 and 6, LLFN-BSVM and LIFT are close in RL and CV values and perform well. This is because the base classifiers of LLFN-BSVM and LIFT are SVM, and SVM classifiers cannot deal with multi-label problems directly but treat multi-label classification problems as multiple single-label classification problems, so they have superior results in RL and CV. In most cases, LLFN-BSVM has a better presentation on each performance metric compared to LIFT, which is because LIFT does not consider correlation information among labels and similarity among instances, resulting in poor performance on the rest of the performance metrics.

  3. 3.

    We further observed that in most cases, for data sets with a larger number of samples (such as education, science, business, etc.), the neural network has higher accuracy for multi-label classification. For the image, medical, and social data sets (the cardinality of the average value of labels is about 1.2), the labels are relatively sparse compared to other data sets, resulting in insufficient label correlation information obtained from the original label set, so the least square loss model is based on Performance is inferior to SVM. LIFT is better than LLFN-BSVM, which is because LIFT uses various feature sets to distinguish different labels by performing cluster analysis on positive and negative instances.

According to the analysis above, it is possible to obtain that the LLFN algorithm and LLFN-SVM algorithm are competitive with several other algorithms. A great variety of experimental results show the effectiveness of multi-label learning by jointing neural networks with label-specific features.

Fig. 2
figure 2

Nemenyi test results for different evaluation metrics. (at \(\alpha =0.05\))

Full size image
Table 7 Summary of the Friedman statistics \({{F}_{F}}\)(\(K=8\), \(N=12\)) and the critical value in each evaluation metric (K: Comparing Algorithms; N: Data Sets)
Full size table

4.5 Component analysis

To further validate the effectiveness of each module of the LLFN algorithm, component analysis experiments were conducted on 12 multi-label datasets , and the experimental results of three evaluation metrics are shown in Fig. 3. Among them, the algorithm LLFN-Ori only considers the extraction of specific features by the neural network and adds \({{l}_{1}}\)-norm without considering any correlation. The algorithm LLFN-LC only adds label correlation, and the algorithm LLFN-IC adds only instance similarity. The algorithm LLFN in this paper adds label correlation and instance correlation at the same time.

Fig. 3
figure 3

Five evaluation metrics results of LLFN and its variants on all datasets

Full size image

Comparing LLFN-LC, LLFN-IC, and LLFN-Ori, it can be found that LLFN-LC and LLFN-IC outperform LLFN-Ori in all five evaluation metrics on all data sets, which indicates that considering label correlation in label space and instance relevance in feature space alone helps multi-label classification. LLFN is superior to its variant algorithms in most cases. The main reason is that LLFN improves the performance of the algorithm by integrating both label relevance and instance similarity, which confirms the effectiveness of each module of our model.

4.6 Parameter sensitivity analysis

There are 3 basic parameters in the algorithm of this paper \(\alpha , \beta\), and \(\lambda\), which respectively control the label correlation, sparsity of label-specific features after input space mapping, and correlation between instances, respectively. In this paper, experiments are conducted on the emotion dataset to investigate the sensitivity of LLFN. As shown in Fig. 4. First, the sensitivity of \(\alpha\) and \(\lambda\) is analyzed by fixing an optimal parameter \(\beta\). We observed that \(\alpha\) is almost unchanged when \(\lambda\) changes within \(\{{{2}^{-5}},{{2}^{-4}},\ldots ,{{2}^{1}},{{2}^{2}}\}\), finding that the performance index of LLFN is not sensitive to \(\alpha\), and the best performance is when the value of \(\lambda\) is small. We find an interesting phenomenon that the classification performance gradually decreases with the increase of \(\lambda\), intuitively because the instance correlation and feature correlation in the real label set is small, and the \(\alpha\) peak in the feature space, it means that these two instances can share more label subsets, which affects the experimental results to some extent.

Fig. 4
figure 4

Sensitivity analysis of LLFN under different input values of \(\alpha\) and \(\lambda\)

Full size image

The next step is to study the \(\beta\) effect on the classification performance of the algorithm LLFN by setting the other two parameters to their optimal values: \(\alpha ={{\text {2}}^{\text {-1}}},\lambda ={{\text {2}}^{\text {-3}}}\). Figure 5 gives the variation of \(\beta\) under each metric within \(\{{{2}^{-6}},{{2}^{-5}},\ldots ,{{2}^{5}},{{2}^{6}}\}\), and it can be seen that the situation is best when \(\beta ={{\text {2}}^{\text {-1}}}\), and the sparsity constraint for label-specific features cannot be well constrained when \(\beta\) is too small, and the performance drops sharply when \(\beta\) is too large. This is because too large \(\beta\) will cause most elements of the coefficient matrix \(\varvec{W}\) to be zero, and some features will be ignored, which leads to a decrease in classification performance

Fig. 5
figure 5

Sensitivity analysis of \(\beta\), where \(\alpha ={{2}^{-1}}\), \(\lambda ={{2}^{-3}}\) and \(\beta \in \left\{ {{2}^{-6}},{{2}^{-5}},\ldots ,{{2}^{5}},{{2}^{6}} \right\}\)

Full size image

4.7 Convergence analysis

As mentioned earlier, the proposed algorithm LLFN in this paper solves the optimal solution by the accelerated proximal gradient method (APG), and the convergence rate of the APG for a given appropriate step size is \(O\left(t^{-2}\right)\). Figure 6 shows the number of iterations of the objective loss function of LLFN on the two datasets education and emotion, the objective function decreases sharply and stabilizes after 60 iterations.

Fig. 6
figure 6

Convergence trend analysis

Full size image

5 Conclusion

In this paper, we propose a novel neural network-based multi-label specific feature learning algorithm. Different from many multi-label classification methods, this method learns a low-dimensional mapping representation of the original feature space through a neural network, uses the instance feature space as the input layer of the neural network, and eventually obtains the label space as the output layer after the processing of the hidden layer. Meanwhile, the empirical minimization loss function is used to learn the specific features of the labels. Finally, label correlation and instance similarity are introduced for multi-label classification. The experimental results demonstrate that the proposed algorithm is effective in multi-label classification, and compared with many state-of-the-art algorithms, the proposed algorithm has better performance. However, the results of our proposed algorithm are not very satisfactory when dealing with multi-label datasets with a small amount of samples, which is the part that we will optimize and study subsequently. Currently, the research on multi-label classification is widely used. Next, we expect to extend our proposed algorithm to practical application scenarios for related research. Furthermore, We present experimental results of the algorithm in this paper on SVM classifiers, but we are also interested in extending this technique to other classifiers.