Pure Logic of Many-Many Ground

Abstract

A logic of grounding where what is grounded can be a collection of truths is a “many-many” logic of ground. The idea that grounding might be irreducibly many-many has recently been suggested by Dasgupta (2014). In this paper I present a range of novel philosophical and logical reasons for being interested in many-many logics of ground. I then show how Fine’s State-Space semantics for the Pure Logic of Ground (plg) can be extended to the many-many case, giving rise to the Pure Logic of Many-Many Ground (plmmg). In the second, more technical, part of the paper, I do two things. First, I present an alternative formalization of plg; this allows us to simplify Fine’s completeness proof for plg. Second, I formalize plmmg using an infinitary sequent calculus and prove that this formalization is sound and complete.

1 Introduction

The logic of metaphysical grounding has recently taken many steps forward (see e.g., [6, 7, 14, 15, 25]). All presently existing logics of ground, however, have focused on many-one or one-one notions of ground. While one has allowed that a collection of truths can ground a single truth, the idea that what is grounded might itself (irreducibly) be a collection of truths has not been seriously studied.¹ Recently, Dasgupta [10] has suggested that there are metaphysical reasons for wanting a notion of ground where what is grounded is (irreducibly) a collection of truths. The main contribution of this paper lies in satisfying this want: I show how the semantics for the Pure Logic of Ground [15] can be extended to a natural semantics for many-many ground, present a proof theory, and establish soundness and completeness.

The general idea is quite simple. One can see² Fine’s State-Space Semantics as based on two primitive notions. The first primitive is the notion of a metaphysical verifier. For each truth ϕ there are the ways that truth can obtain—its metaphysical verifiers. The second primitive is a notion of equivalence between sets of verifiers. The idea is that two sets of verifiers {f ₀, f ₁,…} and {g ₀, g ₁,…} can be equivalent in the sense that the world is the same way when the verifiers f ₀, f ₁,… all obtain as it is when the verifiers g ₀, g ₁,… all obtain.

With the help of these notions we can characterize the following notion of many-one ground: ϕ ₀, ϕ ₁,… ground ψ iff for any ways f ₀, f ₁,… for ϕ ₀, ϕ ₁,… to be the case, there is a way g for ψ to be the case such that the way the world is when f ₀, f ₁,… all obtain is the same way the world is when g obtains. It is easy to extend this to many-many ground. We say that ϕ ₀, ϕ ₁,… ground ψ ₀, ψ ₁,… iff for any ways f ₀, f ₁,… for ϕ ₀, ϕ ₁,… to be the case there are ways g ₀, g ₁,… for ψ ₀, ψ ₁,… to be the case, such that the way the world is when f ₀, f ₁,… all obtain is the same way the world is when g ₀, g ₁,… all obtain. The many-many logic of ground presented in this paper flows naturally from this idea.³

The paper falls into two parts, the first less technical than the second. (The less technically minded reader can get the essentials by studying just the first part.) We start by providing a range of novel philosophical and logical motivations for the idea of many-many ground (Section 2). The example of how grounding might work in domains with many indiscernibles is of particular interest. In Section 3 we recall the semantics for Fine’s Pure Logic of Ground (plg) and show how it can be extended to the many-many setting in a natural way: the result is the Pure Logic of Many-Many Ground (plmmg). Section 4 gives some examples of how plmmg differs from plg. The first part concludes (Section 5) by considering some objections to the semantics and by considering exactly what notion of ground is captured by plmmg.

The second part is taken up with proving soundness and completeness. We begin (Section 6) by extending the languages we are considering and defining consequence properly. In Section 7 we use the resources of a higher-order sequent calculus⁴ to give an alternative proof-theory for plg and provide a proof-theory for plmmg. We then (Section 8) prove soundness for plmmg. In Sections 9 to 11 we show that the reformalization of plg is complete and we show completeness for plmmg.

2 Many-Many Grounding Introduced

2.1 What is Many-Many Ground?

In order to facilitate the discussion we introduce the language of the logic of ground. Just as in [15] we use sequents to express grounding claims. We have the four sequent signs $<, \leq , \prec$ and ≼ for strict full, weak full, strict partial, and weak partial ground familiar from Fine’s presentation. We also have a sequent sign $\not \preceq$: we might read this as “not a weak partial ground”. When Γ, Δ are some collections of sentences then $\Gamma < \Delta , \Gamma \leq \Delta , \Gamma \prec \Delta$, $\Gamma \preceq \Delta$ and $\Gamma \not \preceq \Delta$ are sequents.⁵ When Γ = {γ ₀, γ ₁,…} and Δ={δ ₀, δ ₁,…} we often write γ ₀, γ ₁,… ≤ δ ₀, δ ₁,… for Γ ≤ Δ. When readability seems to require it we may insert parenthesis, writing, e.g., (γ ₀, γ ₁,…)≤(δ ₀, δ ₁,…). Note that we allow both Γ and Δ to be empty.⁶

Strict full ground is the most familiar notion. If Γ < Δ then Γ provides a full explanation of Δ—nothing needs to be added to Γ in order fully to explain why Δ is the case. The explanation is strict in the sense that Δ cannot in turn be part of an explanation of Γ. Weak full ground is a less familiar notion. Whereas nothing can strictly ground itself, everything weakly fully grounds itself. Γ is a weak partial ground of Δ if there is some Θ such that Γ, Θ is a weak full ground of Δ. Γ is a strict partial ground of Δ if Γ is a weak partial ground of Δ and Δ is not a weak partial ground of Γ.⁷

2.2 Failure of Distributivity: the Wall

The notion of many-many ground we are interested in is collective (non-distributive). It is to be sharply distinguished both from simultaneous many-many ground [14, p. 54] and from distributive many-many ground [14, p. 54]. Those notions can both be characterized in terms of many-one ground. Γ simultaneously grounds δ ₀, δ ₁,… iff Γ grounds each δ _i . Γ distributively grounds {δ _i } _{i ∈ I} iff $\Gamma = \bigcup _{i \in I} \Gamma _{i}$ and Γ _i grounds δ _i for each i ∈ I. If Γ,Δ are two given collections of sentences the claim that Γ distributively grounds Δ can be expressed as a disjunction of conjunctions of claims of many-one ground. The collective (non-distributive) notion of grounding we are interested in differs from the above two in allowing Γ to ground δ ₀, δ ₁,… even when every $\Gamma ^{\prime } \subseteq \Gamma$ is such that for no δ _i does $\Gamma ^{\prime }$ ground δ _i . How can we make sense of distributivity failing?

One way of thinking about grounding is that the grounded “rests on” the grounds; the grounds provide the “support” for the grounded. It is widely accepted that the grounds have to be “relevant” to the grounded. One sees this, e.g., in the widespread acceptance of the claim that mere necessitation is not sufficient for grounding: if mere necessitation sufficed for grounding then any truth would ground that 2+2=4. In terms of the metaphor of “support” the grounds have to be “relevantly” supported by the grounds.

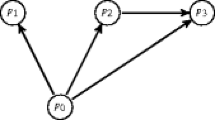
If one approaches grounding via the metaphor of support and insists that the grounds have to be relevant to what they ground, non-distributive many-many grounding is quite natural. The following picture should get the idea across.⁸ Consider Fig. 1. Here we see a wall made out of bricks, the upper row being supported by the lower row. But there is a sense in which no one brick in the top row rests on any collection of bricks from the lower row. Consider, e.g., the bricks a, b, and c depicted in Fig. 1. b and c provide stable support for a, but b, c take up more space than is needed to provide a with stable support: b, c are not (wholly) relevant to a. The upper row as a whole, on the other hand, is relevantly supported by the lower row as a whole. This picture of the wall is very useful for forming the right intuitions about many-many ground.⁹

Fig. 1

Grounds as support

2.3 Non-distributive Explanations

Many philosophers tie grounding closely to a certain kind of explanation (see e.g., [14, pp. 37–40], [12, pp. 3–6], [19, 20]) It is of great interest that many-many grounding arises naturally if we tie grounding closely to explanation.

One central way of expressing explanations is by means of the asking and answering of questions “why?”. One can express grounding-explanations by having the question “why?” take on a particular metaphysical meaning.¹⁰ For instance, one way of expressing that the truth that it is raining or snowing is grounded in the truth that it is raining is by means of the following little (internal) dialogue.

• It is raining or snowing. Why? Because it is raining.

If this is a way of expressing grounding, there is nothing puzzling about the form of claims of many-many grounding: one can easily ask why many truths obtain. This little (internal) dialogue, too, makes perfect sense:

• It is the case that p ₀. It is the case that p ₁. …. Why? Because q ₀, q ₁,….

Another way of expressing claims of ground is by means of inferences that are taken to have a particular explanatory force. Thus one might express a claim of many-many ground by carrying out an inference with many conclusions, for instance:

• q ₀, q ₁,…. Therefore. p ₀, p ₁,….¹¹

A one-step explanatory inference plausibly corresponds to a case of immediate ground. In order to capture the notion of mediate ground the relevant notion is that of an explanatory argument. We can capture that reading by allowing the “therefore” to indicate that there is an explanatory argument from q ₀, q ₁,… to p ₀, p ₁,….¹²

While there is much to be said for tying grounding to explanatory inferences and arguments in the way indicated above it is arguable that the semantics we develop here does not capture the logic of this conception of grounding—what we may call the conception of grounding as explanation. (See Section 5.2 below for more discussion.) The point of bringing up the conception of grounding as explanation is twofold. First, even if this is not the conception of ground that is captured by the semantics developed here, it is a conception of ground that is naturally many-many. Second, it would be of considerable interest if the pure logic governing this notion of ground differed from the pure logic of ground given by the state-space semantics; this would establish some limis to the state-space semantics.

Why are these many-many notions of ground of interest? There are, of course, purely technical reasons for being interested in them; but, as I will argue, there are weighty philosophical reasons for being interested in them as well. While none of the potential applications given below force us to accept many-many grounding—for one thing, the applications are presented in insufficient detail—together they make a strong case that many-many grounding is of considerable philosophical interest.

2.4 Structuralist Motivations

Dasgupta introduced the notion of many-many grounding in the service of “structuralist” metaphysics. He argued that many-many grounding is needed for a proper formulation of qualitativism—the view that, fundamentally, the truths are wholly qualitative—and comparativism about mass—the view that truths about the masses of particular individual objects are grounded in mass-relations. Here we present a novel structuralist motivation for many-many grounding: mathematical structuralism. The following is not intended as a defense of mathematical structuralism, nor is it intended as an argument that a mathematical structuralist has to accept many-many grounding. The point is merely that a mathematical structuralist has some distinctive reasons for wanting a notion of many-many ground.¹³

A natural mathematical structuralist thesis is that truths about individual mathematical objects are grounded in wholly structural truths about the structure in which those mathematical objects live.¹⁴ A standard problem for views of this sort is presented by the complex field.¹⁵

The two square roots of −1, i.e., i and −i, are indiscriminable in the sense that there are automorphisms interchanging them. This makes it difficult to see how the truth that i exists can be grounded in wholly structural truths. To appreciate the problem let us first get clearer on what is meant by a “wholly structural truth”.

It is tempting to identify the wholly structural truths with the truths about the structure that are invariant under all automorphisms; but some care has to be taken here. The truth that 1 is such that i exists is invariant under automorphisms of the complex field in the sense that if we apply an automorphism interchanging i and −i to the truth that 1 is such that i exists what results is a true proposition, viz., the proposition that 1 is such that − i exists. Intuitively, however, this truth is partly about the particular object i and so should not count as “wholly” structural. To get around this problem we take a “structured” view of truths like 1 is such that i exists. One could say that this truth is built up from 1, i, existential quantification, and (something like) λ-abstraction; the truth 1 is such that −i exists, on the other hand, is built up from 1, −i, existential quantification, and (something like) λ-abstraction. If we understand truths in such a structured way the truth that 1 is such that i exists is not invariant under automorphisms: the result of applying an automorphism interchanging i and −i to it gives us the truth 1 is such that −i exists which is a different structured truth. In what follows we take a wholly structural truth to be a truth ϕ such that for all automorphisms π, the result of applying π to ϕ results in the truth ϕ itself.

It is then very plausible that the truth that i exists is not grounded in any wholly structural truths: for there is no wholly structural truth about the complex field that bears on the existence of i (as opposed to the existence of −i). And the wholly structural truths that bear on the existence of both i and −i will contain material that is irrelevant to the existence of i. Similarly, it is very plausible that there is no wholly structural truth about the complex field that grounds the existence of −i; for there is no wholly structural truth about the complex field that bears on the existence of −i (as opposed to the existence of i). Nevertheless, it is very plausible that there is a wholly structural truth about the complex field that grounds the collection of truths: (i exists, −i exists). Since i and −i are the unique square roots of −1, the (unordered) pair of objects 〈i,−i〉 is uniquely characterized in structural terms.¹⁶

By reflecting on this example we see that many-many grounding is of help to the structuralist in two ways: not only does many-many grounding give a new perspective on what is to be grounded—viz., collections of truths—it might also offer a new perspective on what are the ultimate grounds. For if we espouse a thoroughgoing structuralism we would like to say that everything is grounded in the wholly structural, and the question then arises how the wholly structural itself should be stated.

One way out is to concoct a language in which only structural truths can be stated. (This would be the approach of [9].) Once we allow many-many grounding there is, however, a simpler approach. We could allow the wholly structural to be specified using collections of truths concerning particular individuals as long as those collections satisfy two conditions: (i) they are invariant under the structure-preserving transformations; and (ii) they are grounded only in collections that are themselves invariant under the structure-preserving transformations. We might then state how things are in wholly structural terms by making a bunch of assertions none of which individually makes a statement about how things are in wholly structural terms: it would be enough if the collection of statements together amount to a specification of how the world is in wholly structural terms. So the wholly structural feature in which the collection of truths (i exists, −i exists) is grounded might just be the collection of truths (i exists, −i exists) itself.^{17 , 18 , 19}

2.5 Infinite Regress

The idea behind the structuralistic examples is that a collection of truths can be grounded without any of the members of the collection being grounded. But the converse phenomenon is also of interest: each member of a collection of truths could be strictly grounded without the collection of truths itself being strictly grounded. (For the remainder of this subsection we will only be concerned with strict full ground.) The simplest way for this to happen is when we have an infinite regress of ground.²⁰ Thus we can have that ϕ _i is grounded by ϕ _i+1 for all i. Taken individually, then, the ϕ _i are fully grounded.

One might, nevertheless, wonder whether the ϕ _i taken collectively are grounded. If one has a many-many notion of ground one can make sense of each ϕ _i being grounded whilst the collection of the ϕ _i is ungrounded. The idea that each member of a series can be grounded without the series itself being grounded is an idea that occasionally comes up in discussions of the cosmological argument (see e.g., [21]) or the Principle of Sufficient Reason. The point here is not to defend the cosmological argument or the Principle of Sufficient Reason; the point is just to note that the distinction makes perfect sense within a logic of many-many ground.

It is true that this particular application perhaps can be dealt with by relying only on simultaneous many-many ground, but as we will see in (Section 4), there are also more subtle ways in which every member of a collection can be grounded without the collection itself being grounded—and for those applications we need the notion of non-distributive many-many ground.

2.6 The Logic of Ground

One needs a logic of many-many ground in order properly to develop a satisfactory impure ²¹ logic of many-one ground. Suppose we know that Δ strictly grounds a conjunction ϕ∧ψ. If we think—as we should²²—that the conjuncts ϕ, ψ are the unique immediate strict full grounds for the conjunction ϕ∧ψ, then we know that Δ has to weakly fully ground {ϕ, ψ}. In order to state this we require a notion of many-many ground in the object-language. It is true that this application does not require non-distributive many-many ground; but since non-distributive ground is the more general notion of many-many ground this provides an additional reason for studying it.

One similarly needs a logic of many-many ground if one wants properly to develop the pure logic of immediate ground. Suppose we had an operator $\blacktriangleleft$ meant to express immediate strict full ground and that we believe—as we should—that strict full ground is the closure under Cut of strict full immediate ground. Then we need a notion of many-many ground in the object-language in order to express the following principle:

(Closure):

If Γ < ϕ then there are some Δ such that Γ ≤ Δ and $\Delta \blacktriangleleft \phi$.

Finally, many-many grounding might prove useful in giving a proper treatment of negation. Once one has allowed that a collection Δ might be grounded without any one of the δ ∈ Δ being grounded, one can allow for the possibility that some Γ grounds the falsity of the Δ taken collectively, without thereby taking Γ (or indeed: any $\Gamma _{0} \subseteq \Gamma$) to ground the falsity of any particular δ ∈ Δ.²³ In connection with the falsity of conjunctions this might be useful. For there are cases where it is tempting to say that the falsity of a conjunction is grounded without the falsity of either conjunct being grounded. The falsity of the conjunction might, e.g., be grounded in the obtaining of a truth that precludes the joint obtaining of the conjuncts without precluding the obtaining of either conjunct. Plausible cases are instances of the law of non-contradiction²⁴ and cases of color exclusion.

This, by itself, does not force us to accept many-many grounding: one could just claim that there is a p such that p grounds the falsity of a conjunction without grounding the falsity of either conjunct. Where many-many grounding earns its keep is by allowing us to retain a uniform clause for the falsity of conjunctions: one can say that the falsity of a conjunction ϕ∧ψ is grounded in the falsity of ϕ, ψ (taken together).²⁵

The above considerations provide strong reasons for thinking that many-many ground is desirable. But there is a sense in which none of this matters: a pure many-many logic of ground can be developed within Fine’s State-Space Semantics—the many-many logics of ground are there, whether we want them or not. Let us now turn to making good this claim.

3 Semantics

3.1 The Semantics for plg Recalled

We work in Fine’s State Space Semantics (also: “truthmaker semantics”). We take as given a collection F of facts equipped with a function ${\Pi } \colon \mathcal {P}(F) \to F$. This is our fact-frame. Think of π as a fusion operator: it takes facts and fuses them into more complex facts. Note that π is defined even on ∅. We call π(∅) the empty—or null—fact.

We demand that π is associative in the sense that when each X _i is a collection of facts from F and each X _j is a collection of facts from F, then

$${\Pi}\left( \bigcup_{j\in J} X_{j} \cup \bigcup_{i \in I} \{\Pi(X_{i})\}\right) = {\Pi}\left (\bigcup_{k \in I \cup J} X_{k}\right) $$

Intuitively, the order and the number of times one fuses some facts makes no difference. If X = {a ₀, a ₁,…} we often write π(X) as $a_{0} \cdot a_{1} \cdot \dotso$.

Remark 1

The elements f ∈ F of the state space correspond to the metaphysical verifiers mentioned in the introduction. The fusion operator π models the second primitive notion. Two sets of verifiers {f _i :i ∈ I} and {g _j :j ∈ J} are such that the way the world is when the f _i all obtain is the same way the world is when the g _j all obtain iff π({f _i } _{i ∈ I} ) = π({g _j } _{j ∈ J} ).

Let V be a subset of F. We say that V is closed if for all non-empty $V_{0} \subseteq V$, π(V ₀) ∈ V. Let {P _i } _{i ∈ I} be a collection of subsets of F. We define $\bar {\Pi }_{i \in I}(P_{i})$—the fusion of the sets P _i —as the set of pointwise fusions:

$$\bar{\Pi}_{i \in I}(P_{i})=\{\Pi(\{a_{0}, a_{1}, \ldots\}) \colon a_{i} \in P_{i}\} $$

In keeping with the above practice, we often write $P_{0} \cdot P_{1} \cdot \dotso$ for $\bar {\Pi }(P_{i})$.

A generalized fact-frame is a triple $\langle F, {\Pi }, \mathcal {V}\rangle$ where 〈F,π〉 is as before and $\mathcal {V}$ is a collection of closed subsets. A frame is full if $\mathcal {V}$ contains all closed subsets of F. Note that if V is closed and non-empty then V⋅V = V. Note also that if V ₀, V ₁,… are closed then $\bar {\Pi }(V_{i})$ is closed. For plg we will only consider frames where $\mathcal {V}$ is closed under fusion. From now on we abuse notation and use π both for π and for $\bar {\Pi }$.

For the following definition fix a generalized fact frame $\mathcal {F}=\langle F, {\Pi }, \mathcal {V}\rangle$. Assume that P ₀, P ₁,… and Q are all in $\mathcal {V}$.

Definition 1

• (i) $P_{0}, P_{1}, {\ldots } \leq _{\mathcal {F}} Q$ iff $P_{0} \cdot P_{1} \cdot \dotso \subseteq Q$.

• (ii) $P \preceq _{\mathcal {F}} Q$ iff there is R such that $P, R \leq _{\mathcal {F}} Q$.²⁶

• (iii) $P \not \preceq _{\mathcal {F}} Q$ iff it is not the case that $P \preceq _{\mathcal {F}} Q$

• (iv) $P_{0}, P_{1}, {\ldots } <_{\mathcal {F}} Q$ iff $P_{0}, P_{1}, {\ldots } \leq _{\mathcal {F}} Q$ and $Q \not \preceq _{\mathcal {F}} P_{i}$ for each i.

• (v) $P \prec _{\mathcal {F}} Q$ iff $P \preceq _{\mathcal {F}} Q$ and $Q \not \preceq _{\mathcal {F}} P$.

Definition 2

A generalized model is a quadruple $\mathcal {M}=\langle F_{\mathcal {M}}, {\Pi }_{\mathcal {M}}, \mathcal {V}_{\mathcal {M}}, [\phantom {x}]_{\mathcal {M}}\rangle$. Here $\mathcal {F}_{\mathcal {M}}= \langle F_{\mathcal {M}}, {\Pi }_{\mathcal {M}}, \mathcal {V}_{\mathcal {M}}\rangle$ is a generalized frame and $[\phantom {x}]_{\mathcal {M}}$ assigns a set $[p]_{\mathcal {M}} \in \mathcal {V}_{\mathcal {M}}$ to each sentence p. This is the verification set of p. Where no confusion is likely we simply write this [p]. For Γ={p ₀, p ₁,…} a set of atoms we put $[\Gamma ] =\bar {\Pi }([p_{0}], [p_{1}], \ldots )$.

We now define what it is for a sequent α to be true in a model $\mathcal {M}$, writing $\mathcal {M} \models \alpha$ for this notion.²⁷

Definition 3

Let $\mathcal {\mathcal {M}} =\langle F_{\mathcal {M}}, {\Pi }_{\mathcal {M}}, V_{\mathcal {M}}, [\phantom {x}]_{\mathcal {M}}\rangle$ be a model.

• (i) $\mathcal {M} \models p_{0}, p_{1}, {\ldots } \leq q$ iff $[p_{0}], [p_{1}], {\ldots } \leq _{\mathcal {F}} [q]$.

• (ii) $\mathcal {M} \models p \preceq q$ iff $[p] \preceq _{\mathcal {F}} [q]$

• (iii) $\mathcal {M} \models p \not \preceq q$ iff $[p] \not \preceq _{\mathcal {F}} [q]$

• (iv) $\mathcal {M} \models p_{0}, p_{1}, {\ldots } < q$ iff $[p_{0}], [p_{1}], {\ldots } <_{\mathcal {F}} [q]$

• (v) $\mathcal {M} \models p \prec q$ iff $[p] \prec _{\mathcal {F}} [q]$

3.2 Semantics for plmmg

Let a generalized frame $\mathcal {F}= \langle F, {\Pi }, \mathcal {V} \rangle$ be given. For the following definition we assume that P ₀, P ₁,… and Q ₀, Q ₁,… are in $\mathcal {V}$.

Definition 4

• (i) $P_{0}, P_{1}, {\ldots } \leq _{\mathcal {F}} Q_{0}, Q_{1}, \ldots$ iff $P_{0} \cdot P_{1} \cdot \dotso \subseteq Q_{0} \cdot Q_{1} \cdot \dotso$.

• (ii) $P_{0}, P_{1}, {\ldots } \preceq _{\mathcal {F}} Q_{0}, Q_{1}, \ldots$ iff there is R such that $P_{0}, P_{1}, \ldots , R \leq _{\mathcal {F}} Q_{0}, Q_{1}, \ldots$ ²⁸

• (iii) $P_{0}, P_{1}, {\ldots } \not \preceq _{\mathcal {F}} Q_{0}, Q_{1}, \ldots$ iff it is not the case that $P_{0}, P_{1}, {\ldots } \preceq _{\mathcal {F}} Q_{0}, Q_{1}, \ldots$

• (iv) $P_{0}, P_{1}, {\ldots } <_{\mathcal {F}} Q_{1}, Q_{2}, \ldots$ iff $P_{0}, P_{1}, {\ldots } \leq _{\mathcal {F}} Q_{0}, Q_{1}, \ldots$ and $Q_{0}, Q_{1}, {\ldots } \not \preceq _{\mathcal {F}} P_{0}, P_{1}, \ldots$.

• (v) $P_{0}, P_{1}, {\ldots } \prec _{\mathcal {F}} Q_{0}, Q_{1}, \ldots$ iff $P_{0}, P_{1}, P_{2}, {\ldots } \preceq _{\mathcal {F}} Q_{0}, Q_{1}, \ldots$ and $Q_{0}, Q_{1}, {\ldots } \not \preceq _{\mathcal {F}} P_{0}, P_{1}, \ldots$.

A model for plmmg is a quadruple $\mathcal {M} = \langle F_{\mathcal {M}}, {\Pi }_{\mathcal {M}}, \mathcal {V}_{\mathcal {M}}, [\phantom {x}]_{\mathcal {M}}\rangle$, where $[\phantom {x}]_{\mathcal {M}}$ assigns sets in $\mathcal {V}$ to the atoms. We define what it is for a sequent to be true in a model analogously to how we did it for plg.

Definition 5

• (i) $\mathcal {M} \models p_{0}, p_{1}, {\ldots } \leq q_{0}, q_{1}, \ldots$ iff $[p_{0}], [p_{1}], {\ldots } \leq _{\mathcal {F}} [q_{0}], [q_{1}], \ldots$

• (ii) $\mathcal {M} \models p_{0}, p_{1}, {\ldots } \preceq q_{0}, q_{1}, \ldots$ iff $[p_{0}], [p_{1}], {\ldots } \preceq _{\mathcal {F}} [q_{0}], [q_{1}], \ldots$

• (iii) $\mathcal {M} \models p_{0}, p_{1}, {\ldots } \not \preceq q_{0}, q_{1}, \ldots$ iff $[p_{0}], [p_{1}], {\ldots } \not \preceq _{\mathcal {F}} [q_{0}], [q_{1}], \ldots$

• (iv) $\mathcal {M} \models p_{0}, p_{1}, {\ldots } < q_{0}, q_{1}, \ldots$ iff $[p_{0}], [p_{1}], {\ldots } <_{\mathcal {F}} [q_{0}], [q_{1}], \ldots$

• (v) $\mathcal {M} \models p_{0}, p_{1}, {\ldots } \prec q_{0}, q_{1}, \ldots$ iff $[p_{0}], [p_{1}], \ldots \prec _{\mathcal {F}} [q_{0}], [q_{1}], \ldots$

The clause for weak full ground hews closely to the informal characterization given in the introduction. According to the semantics p ₀, p ₁… ≤ q ₀, q ₁,… is true if for all f ₀, f ₁,… such that each f _i ∈[p] _i , there are g ₀, g ₁,… such that g _i ∈[q _i ] and f ₀⋅f ₁⋅… = g ₀⋅g ₁⋅…. Recall (Remark 1) that we may read the identity π _{i ∈ I} {f _i }=π _{j ∈ J} {g _j } as saying that the way the world is when all the f _i obtain is the same way the world is when all the g _i obtain. What the clause for weak full ground expresses is exactly what the informal characterization suggests: a collection of truths p ₀, p ₁,… weakly fully grounds another collection of truths q ₀, q ₁,… when for any ways f ₀, f ₁,… of making all the first truths the case there are some ways g ₀, g ₁,… of making the latter truths the case such that the way the world is when all of f ₀, f ₁,… obtain is the same way the world is when all of g ₀, g ₁,… obtain.

It is worth explaining how and why the clause for strict full ground differs from the clause for many-one ground. To do this we introduce the notion of “explanatory order”. Say that ϕ is below ψ in the explanatory order if ϕ is a strict partial ground for ψ, i.e., if ϕ is a weak partial ground for ψ, but ψ is not a weak partial ground for ϕ. In the many-one setting we can say that p ₀, p ₁,… strictly fully ground p if p ₀, p ₁,… taken together weakly fully ground p and each of the p _i is below p in the explanatory order. (plg has individualistic clauses for < and $\prec$.)

In the many-many setting we understand being below in the explanatory order in a collective way: p ₀, p ₁,… strictly fully ground q ₀, q ₁,… iff p ₀, p ₀,… weakly fully ground q ₀, q ₁,… and q ₀, q ₀,… do not weakly partially ground p ₀, p ₁,…. It does not follow from the q ₀, q ₁,… being above each of them that the q ₀, q ₁,… are above them. (plmmg has collectivist clauses for < and $\prec$.)

The collectivist clauses for < and $\prec$ are forced on us. If we kept the individualistic clauses there would be no guarantee that if Γ ≤ Δ and Δ<Θ then Γ < Θ. Here is a simple example establishing this. Let fusion be union, and let the verification set of p be a, b, and let the verification set for q be a and the verification set for r be b. Then p ≤ (q, r) and (q, r) ≤ p. According to the individualistic clause (q, r)<p, but of course we cannot have p < p. This result is plainly unacceptable: the collectivist clauses for < and $\prec$ are forced on us.

We define consequence in the natural way.²⁹

Definition 6

Let S be a collection of sequents and α a sequent. We say that S⊧α iff for all $\mathcal {M}$ such that $\mathcal {M} \models S$, $\mathcal {M} \models \alpha$.

3.3 A Graphical Illustration

The difference between how (weak full) ground works in plg and plmmg can be illustrated by Figs. 2 and 3. In these graphical presentations the fusion of two regions of logical space is the smallest region containing both regions.

Fig. 2

Grounding in plg

Fig. 3

Grounding in plmmg

In Fig. 2 we see a typical case of grounding in plg. On the left we see sixteen distinct closed sets; on the right we see a single closed set, the fusion of the sixteen sets on the left. Let the verification set of ${p^{1}_{1}}$ be {(1,1)}, the verification set of ${p^{1}_{2}}$ be {(1,2)} etc., and let the verification set of q be the whole rectangle on the right, that is, {(i, j):i, j ≤ 4}. The figure depicts that $\bigcup _{i \leq 4, j \leq 4} \{{p_{i}^{j}}\} \leq \{q\}$, indeed that $\bigcup _{i \leq 4, j \leq 4} \{{p_{i}^{j}\}} < \{q\}$.

In Fig. 3 we see a typical case of grounding in plmmg. While none of the closed sets depicted on the left are contained in a closed set depicted on the right, the region of logical space covered by the rectangles on the left is identical to the space covered by the rectangles on the right. So let the verification set of p _i be {(i, j)|j ≤ 4}. Let the verification set of ${q^{k}_{l}}$ be {(k, l)}. Then the figure depicts that $\bigcup _{i \leq 4} \{p_{i}\} \leq \bigcup _{k,l \leq 4} \{{q_{l}^{k}}\}$. (Imagine putting the right-hand square in Fig. 3 on top of the left-hand square: what results is an instance of “the wall”.)

4 Consequences of the Semantics

4.1 Reverse Subsumption and Amalgamation

Strikingly, the following two valid principles of plg are invalid in plmmg.

$$\frac{\phi_{0}, \phi_{1}, {\ldots} \leq \Delta \qquad \phi_{0} \prec \Delta\quad \phi_{1} \prec \Delta \dotso}{\phi_{0}, \phi_{1} {\ldots} < \Delta}\text{ Reverse Subsumption} $$

$$\frac{\Delta_{0} < \phi \qquad \Delta_{1} < \phi \qquad \ldots}{\Delta_{0}, \Delta_{1}, {\ldots} < \phi}\text{ Strict Amalgamation} $$

The following fact frame witnesses that both principles fail. Put F = {a, b, c, d} and define π by a b = a c = b c = c, where the empty fact is d. Let $\mathcal {V}$ be full. Put [ϕ]={a}, [ψ]={b}, and [θ]={a, b, c}. Then we get ϕ < θ and ψ < θ, but we do not have ϕ, ψ < θ since π(c,[θ]) = c = [ψ, ϕ].

4.2 Non-distributive Grounding

Next we give a simple example of how we might have a collection of truths strictly grounded in some collection of truths without having the collection distributively grounded in that collection of truths.

The following model is intended to capture the following situation. We want to say:

• (i) The truths (i exists or (i exists and 1 exists)) and (−i exists or (−i exists and 1 exists)) are not, taken individually, grounded in wholly structural truths about the complex field; but

• (ii) taken together (i exists or (i exists and 1 exists)) and (−i exists or (−i exists and 1 exists)) are grounded in wholly structural truths about the complex field.

The idea is that while the truth that 1 exists is wholly structural (1 is the unique multiplicative unit of the field), it is “contaminated” with the non-structural truth that i exists (−i exists).

Let a be the fact that i exists, b be the fact that −i exists and c the fact that 1 exists. Say that the facts in the “interior” of Fig. 4 are the structural facts and that the exterior facts are not purely structural. Interpret ϕ as {a, a c} and ψ as {b, b c}. Then ϕ corresponds to the truth that i exists or i and 1 exist while ψ corresponds to the truth that −i exists or −i and 1 exist. Then neither ϕ nor ψ is strictly fully grounded in wholly structural truths, but ϕ, ψ taken together are. For the verification set of {ϕ, ψ} is {a b, a b c}, and ab is a wholly structural fact.

Fig. 4

Complex grounding

4.3 New Principles

The semantics does not just invalidate principles of plg; it also validates some very interesting new principles of grounding. Several of these are established proof-theoretically in Section 7.3 but three of them should be mentioned here: Squeezing, Cancellation and Undercut.

Squeezing is the following principle.

$$\frac{\Gamma \leq \Delta \qquad \Gamma \leq \Delta, {\Sigma}, {\Theta}}{\Gamma \leq \Delta, {\Sigma}}\text{ Squeezing} $$

In words: suppose a collection of facts Δ,Σ is “sandwiched” between the collections Δ and Δ,Σ,Θ. Suppose further that both Δ and Δ,Σ,Θ are (weakly fully) grounded in Γ. Then Squeezing ensures that Δ,Σ is (weakly fully) grounded in Γ.³⁰

We prove Squeezing as follows. Suppose that Γ ≤ Δ. Let a ₀, a ₁,… be some verifiers for Γ. Then there are verifiers b ₀, b ₁,… of Δ such that π(a _i ) = π(b _j ). There are also verifiers $b^{\prime }_{k}, c_{l}, d_{m}$ of Δ,Σ,Θ respectively such that ${\Pi }(a_{i}) = {\Pi }(b^{\prime }_{k}, c_{l}, d_{m})$. The following calculation establishes that π(a ₀, a ₁,…)=π(b _j , c _l ), which suffices to establish Squeezing.

$$\begin{array}{@{}rcl@{}} {\Pi}(a_{0}, a_{1}, \ldots) &=& {\Pi}(b^{\prime}_{k}, c_{l}, d_{m}) = {\Pi}({\Pi}(b^{\prime}_{k}, c_{l}, d_{m}), {\Pi}(c_{l}))\\ &=&{\Pi}({\Pi}(a_{0}, \ldots), {\Pi}(c_{l}))={\Pi}({\Pi}(b_{j}), {\Pi}(c_{l})) ={\Pi}(b_{j}, c_{l}) \end{array} $$

The principle of Cancellation gives us a new way of establishing claims of strict ground.

$$\frac{\Gamma \leq \Delta \qquad \Gamma, {\Sigma}_{1}, {\Sigma}_{0} < {\Sigma}_{0}, \Delta}{\Gamma < \Delta}\text{ Cancellation} $$

In words: if we can transform a weak grounding claim into a strict grounding claim by adding Σ₁,Σ₀ to the grounds and Σ₀ to the grounded then the grounding claim was strict to begin with. This is clearest in the case where Σ₁ = ∅: how could we get a strict grounding claim by adding identical facts to both sides of a weak grounding claim unless the weak grounding claim was strict to begin with?³¹

Undercut is the following principle:

$$\frac{\Gamma \leq \Delta, {\Sigma}}{\Gamma \leq \Gamma, {\Sigma}}\text{ Undercut} $$

We prove Undercut as follows. Suppose that Γ={γ _i } _{i ∈ I} , Δ={δ _j } _{j ∈ J} and Σ is {σ _k } _{k ∈ K} . Then let {a _i } _{i ∈ I} be some verifiers of the γ _i . Then there are verifiers b _j , c _k of the δ _j , σ _k such that

$${\Pi}(a_{i}) \,=\, {\Pi}(b_{j}, c_{k}) \,=\, {\Pi}(b_{j}, c_{k}, c_{k}) \,=\, {\Pi}({\Pi}(b_{j}, c_{k}), c_{k}) \,=\, {\Pi}({\Pi}(a_{i}), c_{k}) \,=\, {\Pi}(a_{i}, c_{k}) $$

This establishes the result.

We conclude the first, less technical, part of the paper by discussing some pressing philosophical issues that are raised by the semantics—and by Squeezing and Undercut in particular. To prefigure: while there are some limitations to what notions of ground can be captured by the state-space semantics this does not mean that the notions of ground that can be captured are not of considerable interest.

5 Ground and Middleground

5.1 Conjunction

It is often assumed that a true conjunction ϕ∧ψ is strictly grounded in the conjuncts ϕ, ψ taken together. And one might think that we could implement this in the semantics simply by means of the following clause:³²

• s⊧ϕ∧ψ iff there are s ₀, s ₁ such that s = s ₀⋅s ₁ with s ₀⊧ϕ and s ₁⊧ψ.

The problem is that if we do this in the many-many setting a conjunction is never strictly grounded in the conjuncts. This, one might think, is a serious problem for the proposed semantics.

To my mind this is a problem with the State-Space Semantics in general, and not just the particular application to many-many ground. For consider that there is no way of making it the case that ϕ, ψ < ϕ∧ψ holds as a matter of logic even in the many-one case. The problem is that logic cannot know that ψ as a matter of fact is not identical to ϕ, and so there is no way of getting ϕ, ψ < ϕ∧ψ logically valid.

One could reply³³ that the problem appears worse in the many-many case: in the many-one case a conjunction is at least sometimes strictly grounded in the conjuncts. I am inclined to think that the opposite is true. There is a natural conception of ground on which a conjunction is always (strictly, immediately) grounded in the conjuncts; and there is a natural conception of ground on which a conjunction is never strictly grounded in the conjuncts. The less natural conception is the one where a conjunction only sometimes is grounded in its conjuncts.

Above (Section 2.3) I mentioned that one could think of grounding in terms of explanatory arguments. If one thinks of grounding in this way it is natural to take conjunction-introduction to result in explanatory arguments: any argument of the form $\frac {\phi \quad \psi }{\phi \wedge \psi }$ is explanatory. On this conception every true conjunction will be grounded in its conjuncts.

We should admit that plmmg does not capture this notion. What it captures, rather, is the notion informally characterized at the beginning of this paper: γ ₀, γ ₁,… weakly fully ground δ ₀, δ ₁,… when for any ways f ₀, f ₁,… of making γ ₀, γ ₁,… the case there are ways g ₀, g ₁,… of making δ ₀, δ ₁,… the case such that the way the world is when all of f ₀, f ₁,… obtain is the same way the world is when all of g ₀, g ₁,… obtain. Let us—to distinguish it from the conception of grounding as explanation—call this notion middleground. (The reason for the name will become clear shortly.)

One may say that on the conception of grounding as explanation grounding turns on the packaging and not on the content of the package. That ϕ, ψ together strictly ground ϕ∧ψ is just a matter of ϕ∧ψ’s being conjunctively packaged. What is inside the truths ϕ, ψ is irrelevant to their grounding ϕ∧ψ; in particular, it is irrelevant whether the truth ϕ in fact is identical to the truth ψ.

Middleground, on the other hand, is all about content. Whether Γ grounds Δ turns on the ultimate ways of making Γ and Δ the case; how those ways are packaged is irrelevant. On this conception it is not surprising that conjunctions never are middlegrounded in their conjuncts. The content of a conjunction is the same as the content of the conjuncts (taken together).

5.2 Middleground and Squeezing

It is important to see that we do not have to consider the impure logic of ground in order to see that plmmg fails to capture a conception of grounding as explanation. plmmg validates principles that are at odds with a conception of grounding as explanation. Consider, e.g., the strict version of Squeezing:

$$\frac{\Gamma < \Delta \qquad \Gamma < \Delta, {\Sigma}, {\Theta}}{\Gamma < \Delta, {\Sigma}} \text{ Strict Squeezing} $$

On the interpretation of grounding in terms of explanatory arguments what this rule tells us is that if there is an explanatory argument from Γ to Δ and also one from Γ to Δ,Σ,Θ, then there is an explanatory argument from Γ to Δ,Σ. But why should this be? What guarantees that there is an explanatory argument from Γ to Δ,Σ?³⁴ In fact, there are, plausibly, counterexamples to Strict Squeezing on a conception of grounding as explanation.

Suppose that the truths are exhaustively divided into three layers: the Low, the Middle, and the High. Suppose that there is an explanatory argument from the low truths taken together to the middle truths taken together. Suppose that there is an explanatory argument from the middle truths taken together to the high truths taken together. (And so, by Composition of explanatory arguments, there is an explanatory argument from the low truths taken together to the high truths taken together.) Crucially, however, distribution fails. For a given middle truth there need be no explanatory argument from some low truths to it. (And similarly for the high truths.) Consider now a collection, called it Mixed, of truths consisting of all the middle truths together with some (but not all) high truths. Squeezing ensures that Mixed is grounded in the low truths. But there does not seem to be any reason to think that there is an explanatory argument from the low truths to the truths in Mixed. If this scenario is possible we have a counterexample to Squeezing for the conception of grounding as explanation.^{35 , 36}

What is the connection between the notion of grounding as explanation and middleground? Since no mathematically precise model theory or proof-theory for a conception of grounding as explanation has yet appeared in print—at least for the many-many setting³⁷—what follows is perforce speculative. With that caveat in mind it is natural to conjecture that the connection is as follows. (The truth of the conjecture would justify the name “middleground”.)³⁸

(Middleground) γ ₀, γ ₁,…middleground δ ₀, δ ₁,… iff for any ultimate grounds f ₀, f ₁,… for γ ₀, γ ₁,… there is an explanatory argument from f ₀, f ₁,… to some $\Delta _{0} \subseteq \{\delta _{0}, \delta _{1}, \ldots \}$ and also an explanatory argument to some $\Delta _{1} \supseteq \{\delta _{0}, \delta _{1}, \ldots \}.$

(As the reader no doubt has noticed (Middleground) is formulated to ensure that Squeezing comes out valid.)

5.3 Is this Really Many-Many Ground?

Finally, one could object that plmmg is not a true logic of many-many ground. Let ⊓Δ be a truth that has as its verifiers exactly the fusions of the verifiers for the Δ. Then one might hold that what we have presented as a many-many sequent Γ ≤ Δ is an eccentric notation for the many-one sequent Γ ≤ ⊓Δ. Far from being a logic of many-many ground plmmg is an impure logic of ground in misleading notation.³⁹

Indeed, given that we require that every frame $\mathcal {F} = \langle F, {\Pi }, \mathcal {V}\rangle$ is such that $\mathcal {V}$ is closed under $\bar {\Pi }$ there will always be truths like ⊓Δ. In other words, the principle of (Unity) holds:⁴⁰

(Unity):

For all ϕ ₀, ϕ ₁,… there is a ψ such that (ϕ ₀, ϕ ₁,…) ≤ ψ and ψ ≤ (ϕ ₀, ϕ ₁,…).

How should we respond to this objection?

First, it is possible is to drop the requirement that $\mathcal {V}$ always be closed under $\bar {\Pi }$; then (Unity) would no longer be valid.⁴¹ While one could respond to the objection in this way, it is preferable not to do so. The worry is not just that one by doing this would complicate the formulation of the logic; what is worrying is that we by making this move would make plmmg’s status as a logic of many-many ground contingent on (Unity)’s failing. (Unity) is an interesting hypothesis; moreover, it is one a defender of many-many ground might well be disposed to accept.⁴²

Secondly, while the above point about (Unity) does not explain what is wrong with the objection it does show that the objection proves too much. If (Unity) is true then any semantics of many-many ground can be recharacterized as a semantics for an impure logic of many-one ground along the lines of the objection. We should not rule out irreducible many-many grounding so easily.

Thirdly, we have explained what it means for many-many sequents γ ₀, γ ₁,… ≤ δ ₀, δ ₁,… to be true. (Any ways f ₀, f ₁,… of making γ ₀, γ ₁,… true are such that there are ways g ₀, g ₁,… of making δ ₀, δ ₁,… true such that π(f ₀, f ₁,…)=π(g ₀, g ₁,…).) It is true—since we demand that $\mathcal {V}$ be closed under fusion—that a sequent Γ ≤ Δ is true in a model $\mathcal {M}$ iff Γ ≤ ⊓Δ is also true in $\mathcal {M}$; but this just shows that two different types of sequents always agree in truth-value. It does not show that sequents of the form Γ ≤ Δ really are sequents of the form Γ ≤ ⊓Δ.

Fourthly, it is not straightforward to develop an impure logic for sequents of the form Γ ≤ ⊓Δ without invoking the resources of many-many ground. The problem is that the interpretation of ⊓Δ has to be specified “from without”: there is no way of expressing, in the language of the logic of many-one ground, that ⊓Δ has as its verifiers exactly the fusions of the verifiers of Δ.⁴³ In the many-many setting, on the other hand, one can easily write down a sequent ensuring that ⊓Δ has as its verifiers exactly the fusions of verifiers of Δ: the one-many sequent ⊓Δ≤Δ will do. Far from (Unity) posing a threat to the many-many logic of ground, a many-many logic of ground provides the ideological resources that allow interesting principles like (Unity) to be stated.

This concludes the more informal part of the paper.

6 Model Theory: Second Pass

To prove soundness and completeness we extend our languages and work with a somewhat unusual consequence relation and proof theory. By doing this we are able to give a uniform treatment of plg and plmmg and greatly simplify the completeness proof for plg.

6.1 The Language of plg

We have the sequent signs $<, \leq , \preceq , \prec$ and $\not \preceq$. Let P be an infinite collection of proper atoms {p} _γ , γ < κ for some cardinal κ. We also have a collection A of auxiliary atoms of cardinality at least κ ⁺, with $\mathbf {P} \cap \mathbf {A}=\emptyset$. We use boldface for the auxiliary atoms, writing p, q,… (possibly with subscripts) for the auxiliary atoms. (Here κ ⁺ is the successor cardinal of κ.) We use ϕ, ψ as meta-linguistic variables ranging over both proper and auxiliary atoms. We use Γ,Δ,Θ,Σ to range over sets of atoms. In what follows, we often take sets to be written in list-form: so if Γ is the set of the ϕ _i , we can write ϕ ₀, ϕ ₁,… for Γ.

If Γ is any set of atoms such that at most κ-many auxiliary atoms occur in Γ and ϕ, ψ are any (proper or auxiliary) atoms, then $\Gamma \leq \phi , \Gamma \leq \mathbin \phi , \phi \preceq \psi$, $\phi \prec \psi$ and $\phi \not \preceq \psi$ are sequents.

We use Γ ₀≪Δ₀,Γ ₁≪Δ₁,… to range over arbitrary sequents. We use S ₀, S ₁,…, T ₀, T ₁,… to range over sets of sequents. (We only consider sets of sequents S such that there are κ ⁺-many auxiliary atoms not occurring in S.)

Remark 2

In the proof theory for plg and plmmg there is an “elimination” rule for weak partial grounding claims. The idea is to mimic an elimination rule for the regular existential quantifier. If we know that ∃x ϕ(x) then we can “let” a witness this, concluding ϕ(a). We can do this if a is an individual constant we have assumed nothing about, that is, that has not been used previously. The elimination rules for ≼ allows us to conclude Γ, p ≤ ϕ from $\Gamma \preceq \phi$ as long as p is an auxiliary atom that has not been used before.

6.2 The Language of plmmg

Just as in plg we have the sequent signs $<, \leq , \preceq , \prec , \not \preceq$ for strict full, weak full, weak partial, strict partial ground, and not weak partial ground. We take as given an infinite collection P = {p _γ } _{γ < κ} of proper atoms, which, again, may be of any cardinality κ. The most convenient way of developing the proof-theory of plmmg requires the set-theoretic assumption that there is a proper class of strongly inaccessible cardinals. If there are κ-many proper atoms let A be a set of auxiliary atoms of cardinality λ where λ is the first strongly inaccessible cardinal larger than κ. We assume that $\mathbf {P} \cap \mathbf {A} = \emptyset$.

In addition to this we introduce a set D of determinates. D is also of cardinality λ. We have $\mathbf {D} \cap \mathbf {P}= \emptyset$ and $\mathbf {D} \cap \mathbf {A} = \emptyset$. If $\langle F, {\Pi }, \mathcal {V} \rangle$ is a frame the idea is that the determinates are to be interpreted as singletons {f}, with f ∈ F: they can only obtain in one way—hence the name. We use a, b, c… to range over determinates.⁴⁴

Whenever Γ,Δ are sets of atoms (proper or auxiliary) and determinates of cardinality γ < λ then Γ < Δ, Γ ≤ Δ, $\Gamma \preceq \Delta$, $\Gamma \prec \Delta$ and $\Gamma \not \preceq \Delta$ are sequents. If Γ,Δ contain only proper atoms, we call them proper sequents. We use S, T, U,…, possibly with subscripts, for sets of sequents. We may write S;T for $S \cup T$.

Remark 3

In plg we only have as many partial sequents as there are atoms; we therefore only need κ ⁺-many auxiliary atoms. In plmmg on the other hand, there are 2^κ-many partial sequents when there are κ-many proper atoms. So we have to have at least (2^κ) auxiliary atoms. The reasons for demanding inaccessibly many auxiliary atoms and determinates will become clear as we proceed with the completeness proof.

6.3 Semantics for plg and plmmg

Let $\mathcal {L}$ be the language of many-one or many-many ground. A model for $\mathcal {L}$ is a tuple $\mathcal {M} =\langle F, {\Pi }, \mathcal {V}, [\phantom {x}]\rangle$ such that

• (i) $\{f\} \in \mathcal {V}$, for each f ∈ F.

• (ii) If λ is the number of determinates in $\mathcal {L}$ then $\mathcal {V}$ is closed under fusions of size <λ.

Here [] is a function from the set of proper atoms into $\mathcal {V}$. Auxiliary atoms and determinates are dealt with separately.

Definition 7

Let $\mathcal {M} = \langle F, {\Pi }, \mathcal {V}, [\phantom {x}] \rangle$ be a model. An $\mathcal {M}$-assignment is a function σ from the set of auxiliary atoms and determinates into $\mathcal {V}$ such that if a is a determinate σ(a)∈{{f}:f ∈ F}. Let S be a collection of sequents and let σ, τ be $\mathcal {M}$-assignments. We say that σ≈ _S τ if σ and τ only differ on what they assign to auxiliaries and determinates not occurring in S.

In what follows we use γ ₀, γ ₁,… for both proper atoms, auxiliaries, and determinates. If γ is an auxiliary or determinate we write [γ] _σ for the value assigned to γ under the assignment σ. If γ is not a determinate then [γ] _σ is [γ]. If $\mathcal {F} = \langle F, {\Pi }, \mathcal {V} \rangle$ is a frame then we define $\leq _{\mathcal {F}}$ for plg and plmmg exactly as in Definitions 1 and 4.

Let $\mathcal {M} =\langle F, {\Pi }, \mathcal {V}, [\phantom {x}]\rangle$ be a model. We define truth relative to a model and an assignment.

Definition 8 (Definition of Truth for plg)

• (i) $\mathcal {M}, \sigma \models \gamma _{0}, \gamma _{1}, {\ldots } \leq \delta$ iff $[\gamma _{0}]_{\sigma }, [\gamma _{1}]_{\sigma }, {\ldots } \leq _{\mathcal {F}} [\delta ]_{\sigma }$

• (ii) $\mathcal {M}, \sigma \models \gamma \preceq \delta$ iff $[\gamma ]_{\sigma } \preceq _{\mathcal {F}} [\delta ]_{\sigma }$.

• (iii) $\mathcal {M},\sigma \models \gamma \not \preceq \delta$ iff $[\gamma ]_{\sigma } \not \preceq _{\mathcal {F}} \delta _{\sigma }$

• (iv) $\mathcal {M},\sigma \models \gamma _{0}, \gamma _{1}, {\ldots } < \delta$ iff $[\gamma _{0}]_{\sigma }, [\gamma _{1}]_{\sigma }, {\ldots } <_{\mathcal {F}} [\delta ]_{\sigma }$

• (v) $\mathcal {M},\sigma \models \gamma \prec \delta$ iff $[\gamma ]_{\sigma } \prec _{\mathcal {F}} [\delta ]_{\sigma }$.

Definition 9 (Definition of Truth for plmmg)

• (i) $\mathcal {M}, \sigma \models \gamma _{0}, \gamma _{1}, {\ldots } \leq \delta _{0}, \delta _{1}, \ldots$ iff $[\gamma _{0}]_{\sigma }, [\gamma _{1}]_{\sigma }, {\ldots } \leq _{\mathcal {F}} [\delta _{0}]_{\sigma }, [\delta _{1}]_{\sigma }, \ldots$

• (ii) $\mathcal {M}, \sigma \models \gamma _{0}, \gamma _{1}, {\ldots } \preceq \delta _{0}, \delta _{1}, \ldots$ iff $[\gamma _{0}]_{\sigma }, [\gamma _{1}]_{\sigma }, {\ldots } \preceq _{\mathcal {F}} [\delta _{0}]_{\sigma }, [\delta _{1}]_{\sigma }, \ldots$

• (iii) $\mathcal {M},\sigma \models \gamma _{0}, \gamma _{1}, {\ldots } \not \preceq \delta _{0}, \delta _{1}, \ldots$ iff $[\gamma _{0}]_{\sigma }, [\gamma _{1}]_{\sigma }, {\ldots } \not \preceq _{\mathcal {F}} [\delta _{0}]_{\sigma }, [\delta _{1}]_{\sigma }, \ldots$

• (iv) $\mathcal {M},\sigma \models \gamma _{0}, \gamma _{1}, {\ldots } < \delta _{0}, \delta _{1}, \ldots$ iff $[\gamma _{0}]_{\sigma }, [\gamma _{1}]_{\sigma }, {\ldots } <_{\mathcal {F}} [\delta _{0}]_{\sigma }, [\delta _{1}]_{\sigma }, \ldots$

• (v) $\mathcal {M},\sigma \models \gamma _{0}, \gamma _{1}, {\ldots } \prec \delta _{0}, \delta _{1}, \ldots$ iff $[\gamma _{0}]_{\sigma }, [\gamma _{1}]_{\sigma }, \ldots \prec _{\mathcal {F}} [\delta _{0}]_{\sigma }, [\delta _{1}]_{\sigma }, \ldots$

We will tacitly invoke the following proposition throughout.

Proposition 1

Let $\mathcal {M}$ be a model and τ be an $\mathcal {M}$ -assignment. If a sequent Γ≪Δ is true in $\mathcal {M}$ with respect to τ, then Γ ≪ Δ is also true in $\mathcal {M}$ with respect to any $\tau ^{\prime }$ , where $\tau ^{\prime } \approx _{\Gamma \ll \Delta } \tau$.

The definition of the consequence relation is the same for plg and plmmg. We define a consequence relation ⊧ holding between a set of sequents S and another set of sequents S ₀ where S ₀ is read conjunctively.

Definition 10

Let S be a collection of sequents and S ₀ a collection of sequents. We say that S ₀ is a consequence of S (S⊧S ₀) iff for all models $\mathcal {M}$ and all $\mathcal {M}$-assignments σ, if $\mathcal {M}, \sigma \models S$ then there is an $\mathcal {M}$-assignment τ such that σ≈ _S τ and $\mathcal {M}, \tau \models S_{0}$. If S is empty we have the following special case: ⊧S ₀ iff for all $\mathcal {M}$ there is an $\mathcal {M}$-assignment σ such that $\mathcal {M}, \sigma \models S_{0}$.

Remark 4

It is this treatment of consequence that allows us to imitate ∀∃-quantification over facts. For consider two sets of sequents S and S ₀. S⊧S ₀ if for any model $\mathcal {M}$ and any assignment σ of values to the auxiliaries and determinates in S such that M, σ⊧S there exists some $\sigma ^{\prime }$ that differs from σ only in what it assigns to auxiliaries and determinates not in S such that $\mathcal {M}, \sigma ^{\prime } \models S_{0}$. In the case where S and S ₀ do not contain any determinates we get the standard account of consequence.

This definition has the following consequence. It is possible for S⊧T ₀ and S⊧T ₁ and yet for S⊮T ₀, T ₁. There is nothing surprising about this: the same phenomenon arises in systems that have a rule of existential instantiation. One can, e.g., infer F c from ∃x F x,∃x¬F x (where c is a fresh constant); one can also infer ¬F c from ∃x F x,∃x¬F x. But one had better not be able to infer F c,¬F c together from ∃x F x,∃x¬F x.

However, if a certain condition is satisfied S⊧T ₁;T ₂ does follow from S⊧T ₁ and S⊧T ₂. For the completeness proofs we need a general version of this condition.

Definition 11

Let {〈R _α , S _α , T _α 〉:α < λ} be a well-ordered set of triples of sequents. {〈R _α , S _α , T _α 〉:α < λ} satisfies the Collection Condition iff:

• (i) for all α, $\bigcup _{\beta < \alpha } R_{\alpha } \subseteq \bigcup _{\beta < \alpha } T_{\alpha }$;

• (ii) for all determinates a and all α: if a occurs in T _α but not S _α then

  • (a) if β≠α then a does not occur in S _β ; and

  • (b) if a occurs in T _β then either α < β and a occurs in $\bigcup _{\beta ^{\prime } < \beta } R_{\beta ^{\prime }}$ or β < α and a occurs in $\bigcup _{\alpha ^{\prime } < \alpha } R_{\alpha ^{\prime }}$ or

Proposition 2

Suppose that for each α<λ we have $S_{\alpha }, \bigcup _{\beta < \alpha } R_{\beta } \models T_{\alpha }$ . Suppose that {〈αR _α ,S _α ,T _α 〉} _α<λ satisfies the Collection Condition. Then $\bigcup _{\alpha < \lambda } S_{\alpha } \models \bigcup _{\alpha < \lambda } T_{\alpha }$.

Proof

Let $\mathcal {M}, \sigma$ be such that $\mathcal {M}, \sigma \models S_{\alpha }$ for each α < λ. Let $S = \bigcup _{\alpha < \lambda } S_{\alpha }$. For each α, let $\widehat {T}_{\alpha }= \bigcup _{\beta < \alpha } T_{\beta }$ and let $\widehat {R}_{\alpha }= \bigcup _{\beta < \alpha } R_{\beta }$. We construct a sequence of assignments σ = τ ₀, τ ₁,…, τ _γ ,… such that $\mathcal {M}, \tau _{\gamma } \models \bigcup _{\beta < \gamma } T_{\beta }$ and such that for all α < γ < λ we have $\tau _{\alpha } \approx _{S; \widehat {T}_{\alpha }} \tau _{\gamma }$.

The case where α = 1 is immediate. Since {R _α :α < 0} = ∅, S ₀⊧T ₀. Since {〈R _α , S _α , T _α 〉} _{α < λ} satisfies the Collection Condition the following is the case. If α ≠ 0, then no determinate a occurring in S _α occurs in T ₀ unless a also occurs in S ₀. It follows that there is τ such that τ≈ _S σ and $\mathcal {M}, \tau \models T_{0}$. Let τ ₁ be any such τ.

Next, let α be a successor ordinal β+1. Let τ _β be the previously constructed assignment. Then $\mathcal {M}, \tau _{\beta } \models \bigcup _{\beta ^{\prime } < \beta } T_{\beta ^{\prime }}$. Since $\bigcup _{\beta ^{\prime } < \beta } R_{\beta ^{\prime }} \subseteq \bigcup _{\beta ^{\prime } < \beta } T_{\beta ^{\prime }}$ we also have that $\mathcal {M}, \tau _{\beta } \models S_{\beta }, \bigcup _{\beta ^{\prime } < \beta } R_{\beta ^{\prime }}$. By assumption $S_{\beta }, \bigcup _{\beta ^{\prime } < \beta } R_{\beta ^{\prime }} \models T_{\beta }$. Let $\rho \approx _{S_{\beta };\widehat {R}_{\beta }} \tau _{\beta }$ be such that $\mathcal {M}, \rho \models T_{\beta }$. We define τ _β+1 as follows:

$$\tau_{\beta+1}(a)=\left\{\begin{array}{ll} \sigma(a) & \text{ if }a\text{ is in } S \\ \tau_{\beta}(a) & \text{ if }a\text{ is in } \bigcup_{\beta^{\prime} < \beta} T_{\beta^{\prime}} \\ \rho(a) & \text{ otherwise} \end{array}\right. $$

Clearly $\tau _{\beta +1} \approx _{S; \widehat {T}_{\beta }} \tau _{\beta }$. Since {〈R _α , S _α , T _α 〉:α < λ} satisfies the Collection Condition it follows that $\mathcal {M}, \tau _{\beta +1} \models T_{\beta }$, which is what we have to show.

Finally, let α be a limit ordinal γ. We define an assignment τ _γ as follows.

$$\tau_{\gamma}(a)\,=\, \left\{\!\! \begin{array}{ll} \sigma(a) & \!\text{if }a\text{ is a determinate that does not occur in any} \bigcup_{\beta^{\prime} < \beta} \!T_{\beta^{\prime}} \text{for any} \beta \!\!<\!\! \gamma \\ \tau_{\beta}(a) & \!\text{if }a\text{ is a determinate that occurs in } \bigcup_{\beta^{\prime} < \beta} T_{\beta^{\prime}}, \text{for some } \beta < \gamma \end{array}\right. $$

This is well defined since the induction hypothesis ensures that if β ₀<β ₁<γ, then $\tau _{\beta _{0}} \approx _{S; \widehat {T}_{\beta _{0}}} \tau _{\beta _{1}}$. It then follows by Proposition 1 that $\mathcal {M}, \tau _{\gamma } \models \bigcup _{\beta <\gamma } T_{\beta }$. □

If each R _α = ∅ we often say that {〈S _α , T _α 〉:α < λ} satisfies the Collection Condition when we mean that {〈R _α , S _α , T _α 〉:α < λ} satisfies the Collection Condition.

We have the following special cases.

Corollary 1

If for each i ∈ I, S⊧T _i and all determinates in T _i occur in S, then $S \models \bigcup _{i \in I }T_{i}$.

Corollary 2

If {〈S _α ,T _α 〉}> _α<λ satisfies the Collection condition and S ₀ ,S ₁ ,…⊮T ₀ ,T ₁ ,… there is some α such that S _α ⊮T _α . In particular, if S ₀ ,S ₁ ,… and T ₀ ,T ₁ ,… do not contain any determinates then if S ₀ ,S ₁ ,…⊮T ₀ ,T ₁ ,… then there is an α such that S _α ⊮T _α .

7 Proof Theory

The proof-systems for plg and plmmg are hypersequent calculi of a distinctive sort. What is distinctive is, first, that we always derive sets of sequents; second, that we read the sets of sequents conjunctively.

Since it is more familiar we begin by giving a new formalization of plg.

7.1 plg Reformalized

The rules of plg are displayed in Fig. 5. A proof in plg is a converse well-founded tree.⁴⁵ The nodes of the trees are labeled with sets of sequents. If S is a set of sequents and Γ≪Δ is a sequent we write S;Γ≪Δ for the set of sequents $S \cup \{\Gamma \ll \Delta \}$. The sets of sequents are to be read conjunctively. The transition between nodes is in accordance with the rules in Fig. 5. We use $\mathcal {D}, \mathcal {E}, \mathcal {F}, \ldots$, possibly with subscripts, as variables ranging over proofs.

Fig. 5

The rules of plg

We take the trees to be equipped with discharge functions. This is understood as follows. An occurrence of a sequent is a sequent occurring in a set of sequents labeling a node. In the rules that discharge sequents, we allow discharge of sequent-occurrences where not all the sequents labeling a node are discharged.

Some features of the formalization have to be explained.

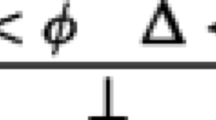
“ ⊥” as it occurs in these rules is not a logical constant. An inference rule written $\frac {\Gamma \ll \Delta }{\bot }$ rather indicates that any set of sequents can be inferred from Γ≪Δ.⁴⁶ For the ≼-E rule we have to impose a condition similar to the eigenvariable conditions on the familiar ∀-I and ∃-E rules. We call this the eigenformula condition. To be precise: In a proof ending with an application of ≼-E like

$$\begin{array}{ll} \frac{\,\, \mathcal{E}}{~\phantom{\frac{@}{@}} S \quad ; \quad \phi \preceq \psi~}\\[-5pt] \frac{}{~\phantom{\frac{@}{@}}S \quad ; \quad \phi, \textbf{p} \leq \psi~}\preceq\!\text{-E} \end{array} $$

we demand that p is an auxiliary atom that does not occur in $\phi \preceq \psi$ or S and that does not occur in the undischarged top-sequents of the proof $\mathcal {E}$.

As noted in Section 6.3 above we cannot conclude that T ₀;T ₁ is a consequence of S ₀;S ₁ even if T ₀ is a consequence of S ₀ and T ₁ a consequence of S ₁. We therefore have to put a restriction on any rules that allow us to “collect together” proofs of S ₀, S ₁, S ₂,… into a proof of S ₀;S ₁;S ₂;…. For convenience the only rule that allows us to collect together different arguments is the rule of Collection; in all the other rules the premiss set labels a single node.

To illustrate this, observe that the following is not an acceptable application of Cut:

$$\frac{\Gamma \leq \phi \quad \phi \leq \psi} {\Gamma \leq \psi} $$

The two premiss sequents Γ ≤ ϕ and ϕ ≤ ψ decorate distinct nodes. To be able to apply Cut we first have to apply Collection, as follows:

$$\begin{array}{l} \frac{~~\Gamma \leq \phi \qquad \phi \leq \psi~~}{}\text{ Collection}\\ \frac{~~\Gamma \leq \phi \quad ; \quad \phi \leq \psi~~}{~~~~~~~~~\Gamma \leq \phi}\text{ Cut} \end{array} $$

While in the the case of plg one can avoid these complications, for plmmg proceeding in this way greatly simplifies the soundness and completeness proofs.

As a further illustration of how Collection works, let us show how we can derive the rule of Reverse Subsumption in this system. In the following derivation we assume that we only deal with proper sequents; this licenses the application of Collection.

$$\begin{array}{cl} \qquad\qquad\qquad\frac{\quad{\ldots} \phi_{i} \prec \phi {\ldots} \quad}{}{\prec}\text{-E}\\[-4pt] \qquad \qquad\qquad\quad\ \ \frac{{\ldots} \phi_{i} \preceq \phi ; \phi \not\preceq \phi_{i} \ldots}{}\text{ Thinning}\\[-4pt] \frac{\phi_{0}, \phi_{1}, {\ldots} \leq \phi \qquad\quad {\ldots} \phi \not\preceq \phi_{i}\ldots}{}\text{ Collection}\\[-4pt] \quad\frac{\phi_{0},\phi_{1},{\ldots} \leq\phi; \ldots\phi\not\preceq \phi_{i}}{{\phi_{0},\phi_{1}, {\ldots} < \phi}}{<\text{-I}} \end{array} $$

Since most of the plmmg-derivations we give carry easily over to their analogues in plg we refrain from carrying out any further derivations in plg.

The reader is encouraged to verify that the other rules of Fine’s formalization of plg are derivable from the rules in Fig. 5.

7.2 Proof Theory for plmmg

The rules of plmmg are depicted in Fig. 6. While most of the rules are quite similar to the rules of plg some of the rules require explanation.

Fig. 6

The Pure Logic of Many-Many Ground

Recall that we use a, b, c,… (with subscripts) for determinates. We will use Γ≈Δ as a meta-linguistic shorthand for Γ ≤ Δ;Δ ≤ Γ. So when we write $\overset {\mathcal {E}} {{\Gamma } {\approx } \Delta }$ this means that $\mathcal {E}$ is a proof ending in Γ ≤ Δ;Δ ≤ Γ.

An eigenformulae condition is imposed in the following rules: ≼-E, Determinization, ≤-I and ≤-E. The ≼-E case is as for plg except that we require that p be an auxiliary atom, and not a determinate. If we know that a is a determinate we know that it cannot serve as an arbitrary proposition—a proposition that can obtain in only one way is hardly arbitrary.

The Determinization rule tells us, in proof theoretic form, that every proposition is weakly fully grounded by a determinate—i.e., by a proposition that has as its verification set the singleton of a fact. If we have concluded some sequents S and those sequents contain some {γ _i } _{i ∈ I} , then we get to assume that there are some determinates {a _i } _{i ∈ I} such that a _i ≤ γ _i for each i ∈ I.

Determinacy expresses that determinates can only obtain in one way: if some fact weakly fully grounds a determinate then the determinate weakly fully grounds that fact.

The ≤-I rule is to be read as follows. Let A be a set of determinates such that S;A ≤ (γ ₀, γ ₁,…). Suppose there are some determinates {b _i } _{i ∈ I} … such that the set of sequents T;{b _i ≤ δ _i :i ∈ I};A≈b ₀, b ₁,…≈c can be derived from S;A ≤ γ ₀, γ ₁,… by means of a proof $\mathcal {E}$. We demand that in this proof the determinates A do not occur in the undischarged assumptions S. (The A represent “arbitrary” verifiers for γ ₀, γ ₁,….) In that case we can conclude S;γ ₀, γ ₁,… ≤ δ ₀, δ ₁,… discharging the assumptions A ≤ γ ₀, γ ₁….

≤-I captures proof-theoretically the right-to-left direction of the semantic clause for ≤ as a special case. For suppose that the determinates a ₀, a ₁,… are such that a ₀ ≤ γ ₀, a ₁ ≤ γ ₁,…. Then a ₀, a ₁,… ≤ γ ₀, γ ₁,…. If we then can find determinates b ₀, b ₁,…, c such that b ₀ ≤ δ ₀, b ₁ ≤ δ ₁,… and such that a ₀, a ₁,…≈b ₀, b ₁,…≈c we can conclude γ ₀, γ ₁,… ≤ δ ₀, δ ₁,….

The left-to-right direction of the semantic clause for ≤ is captured by the ≤-E rule. The idea is the following. Suppose A is a set of determinates such that S;(γ ₀, γ ₁,… ≤ δ ₀, δ ₁,…);A ≤ γ ₀, γ ₁,… is the conclusion of an argument $\mathcal {E}$. Now let b ₀, b ₁,…, c be any determinates not occurring in $\mathcal {E}$. Then we can conclude the set of sequents

$$S ; b_{0}\leq \delta_{0} ; b_{1} \leq \delta_{1} ; {\ldots} ; A \approx b_{0}, b_{1}, {\ldots} \approx c $$

If A = {a ₀, a ₁,…} and f ₀, f ₁,… are the verifiers that interpret a ₀, a ₁,… then since A ≤ γ ₀, γ ₁,… is the case π(f ₀, f ₁,…)∈[γ ₀, γ ₁,…]. Since γ ₀, γ ₁,… ≤ δ ₀, δ ₁,… is the case there has to be some verifiers g ₀, g ₁,… for δ ₀, δ ₁,… such that f ₀, f ₁,… fuse to the same verifier as does g ₀, g ₁,…. Since we have made no prior assumptions about the determinates b ₀, b ₁,…, c we can interpret b ₀, b ₁,… as g ₀, g ₁,… and c as π(g ₀, g ₁,…). It is in order to state this rule that the proof system allows us to draw many conclusions simultaneously.

Remark 5

An important consequence of the ≤-E rule is that if a ≤ γ ₀, γ ₁,… then a can be “apportioned out” into verifiers for γ ₀, γ ₁,….

$$\begin{array}{c} \qquad\quad\qquad\frac{\qquad\qquad a {\leq} \gamma_{0}, \gamma_{1}, {\ldots} \qquad\qquad\qquad\quad}{} \text{ Identity}\\ \frac{\qquad\qquad a {\leq} \gamma_{0}, \gamma_{1}, {\ldots} \quad ; \quad \{\gamma_{0}, \gamma_{1}, \ldots\} {\leq} \{\gamma_{0}, \gamma_{1}, \ldots\}\qquad}{a {\leq} \gamma_{0}, \gamma_{1}, {\ldots} \quad ;\quad b_{0} {\leq} \gamma_{0}; b_{1} {\leq} \gamma_{1} \quad ; \quad{\ldots} a \approx b_{0}, b_{1}, {\ldots} \approx c}{{\leq}- \text{E}} \end{array} $$

In this way the ≤-E rule ensures that any verifier f for a collection Γ={γ ₀, γ ₁,…} is a fusion of verifiers f ₀, f ₁,… for γ ₀, γ ₁,… respectively. (Cf. the discussion in Section 5.3 above.)

Because of the presence of auxiliaries and determinates we have to take some care when defining the provability relation.

Definition 12

If S and T are collections of sequents we say that T is provable from S in plmmg (plg) iff there is a proof $\mathcal {E}$ in plmmg (plg) such that the undischarged nodes of $\mathcal {E}$ are labeled with exactly the sequents in S and the conclusion of $\mathcal {E}$ is labeled with T. We write $\vdash _{\textsc {plmmg}}$ ($\vdash _{\textsc {plg}}$) for provability in plmmg (plg).

7.3 Derived Rules in plmmg

Before we go on to establish soundness and completeness, it is instructive to see that we can establish analogues of the principles of Fine’s plg. In this section $\vdash$ means provability in plmmg. For readability we present most of the proofs so that a single sequent labels a node of a proof tree.

Proposition 3

• (i) $\Gamma < \Delta \vdash \Gamma \leq \Delta$ (Subsumption(</≤))

• (ii) $\Gamma \prec \Delta \vdash \Gamma \preceq \Delta$ (Subsumption($\prec /\preceq$))

• (iii) $\Gamma < \Delta \vdash \Gamma \prec \Delta$ (Subsumption($</\prec$))

• (iv) $\Delta _{0}, \Delta _{1} \preceq \Gamma \vdash \Delta _{0} \preceq \Gamma$ (Subsumption($\preceq /\preceq$))

• (v) $\Delta _{0}, \Delta _{1} \prec \Gamma \vdash \Delta _{0} \prec \Gamma$ (Subsumption($\prec /\prec$))

Proposition 4

• (i) $(\Gamma \preceq \Delta ), (\Delta , \Delta _{0} \preceq {\Theta }) \vdash \Gamma , \Delta _{0} \preceq {\Theta }$ (Transitivity($\preceq /\preceq$))

• (ii) $(\Gamma \preceq \Delta ), (\Delta \prec {\Theta }) \vdash \Gamma \prec {\Theta }$ (Transitivity($\preceq /\prec$))

• (iii) $(\Gamma \prec \Delta ), (\Delta \preceq {\Theta }) \vdash \Gamma \prec {\Theta }$ (Transitivity($\prec /\preceq$))

Proposition 5

• (i) $(\Delta \prec \Delta ) \vdash \bot$

• (ii) $(\Delta _{0} \leq \Gamma _{0}), (\Delta _{1} \leq \Gamma _{1}), \ldots \vdash \Delta _{0}, \Delta _{1}, {\ldots } \leq \Gamma _{0}, \Gamma _{1}, \ldots$ (Amalgamation)

• (iii) $(\Delta _{0} \leq {\Theta }_{1}), (\Delta _{1} \leq {\Theta }_{1}), \ldots , ({\Theta }_{0}, {\Theta }_{1}, \ldots , {\Sigma } < \Gamma ) \vdash \Delta _{0}, \Delta _{1}, \ldots , {\Sigma } < \Gamma$ (Cut(≤/<))

• (iv) $(\Delta \leq \Gamma _{0}, \Gamma _{1}, \ldots ), \Delta \prec \Gamma _{i} \vdash \Delta < \Gamma _{0}, \Gamma _{1}, \ldots$. (Restricted Reverse Subsumption)

Proof

The derivations are all straightforward, but since this type of calculus is unfamiliar we go through some important cases.

The following establishes Subsumption($\preceq /\preceq$).

$$\begin{array}{l} \frac{\,\;\Delta_{0}, \Delta_{1} \preceq \Gamma\,\;}{} {\preceq}\text{-E}\\[-4pt] \frac{\Delta_{0}, \Delta_{1}, \mathbf{p} \leq \Gamma}{\Delta_{0} \preceq \Gamma} {\preceq}\text{-I}\\ \end{array} $$

The following establishes Subsumption($\prec /\prec$).

$$\begin{array}{l} \quad\frac{\,\,\;\Gamma_{0}, \Gamma_{1} \prec \Delta\quad \,\,\,\,\,; \quad\overline{\Delta \preceq \Gamma_{0}}^{1}}{}{\prec}\text{-E}\\ \qquad\frac{\Delta \not\preceq \Gamma_{0}, \Gamma_{1} \quad ; \quad \Delta \preceq \Gamma_{0}\quad}{}{\preceq}\text{-E}\\ \qquad\frac{\Delta \not\preceq \Gamma_{0}, \Gamma_{1}\quad ; \quad\Delta, \mathbf{p} \leq \Gamma_{0}\qquad\qquad\qquad\quad}{}\text{ Identity}\\ \frac{\qquad\Delta \not\preceq \Gamma_{0}, \Gamma_{1}\quad ; \quad\Delta, \mathbf{p} \leq \Gamma_{0}\quad ; \quad \Gamma_{0}, \Gamma_{1} \mathbin{\leq} \Gamma_{0}, \Gamma_{1}}{}\text{ Cut}\\ \frac{\,\;\Delta \mathbin{\not\preceq} \Gamma_{0}, \Gamma_{1} \quad\quad\,\,\,\,\,; \quad \Delta, \mathbf{p},\Gamma_{1} \mathbin{\leq} \Gamma_{0}, \Gamma_{1}}{}{\preceq}\text{-I}\\ \qquad\frac{\Delta \mathbin{\not\preceq} \Gamma_{0}, \Gamma_{1} \quad ; \quad \Delta \mathbin{\preceq} \Gamma_{0}, \Gamma_{1}}{}{\not\preceq}\text{-E}\\ \qquad\frac{\quad\quad\quad\quad{\Sigma} \mathbin{\not\preceq} {\Sigma}\quad\quad}{}1,{\not\preceq}\text{-I}\\ \qquad\frac{\Gamma_{0}, \Gamma_{1} \mathbin{\prec} \Delta \quad ; \quad \Delta \mathbin{\not\preceq} \Gamma_{0}\,\,}{}{\prec}\text{-E}\\ \qquad\frac{\Gamma_{0}, \Gamma_{1} \mathbin{\preceq} \Delta \quad ; \quad \Delta \mathbin{\not\preceq} \Gamma_{0}}{}\text{ Subsumption}(\mathbin{\preceq}/\mathbin{\preceq})\\ \qquad\quad\frac{\Gamma_{0} \mathbin{\preceq} \Delta \quad ; \quad \Delta \mathbin{\not\preceq} \Gamma_{0}}{\quad\Gamma_{0} \mathbin{\prec} \Delta\quad}{\prec}\text{-I}\\ \end{array} $$

The following establishes Transitivity($\mathbin {\preceq }/\mathbin {\preceq }$).

$$\begin{array}{l} \frac{\quad\Gamma \mathbin{\preceq} \Delta\quad ; \quad\Delta \mathbin{\preceq} {\Theta}}{}\mathbin{\preceq}\text{-E}\\ \frac{\,\;\Gamma, \mathbf{p} \mathbin{\leq} \Delta\quad ; \quad\Delta \mathbin{\preceq} {\Theta}}{}\mathbin{\preceq}\text{-E}\\ \frac{\,\,\Gamma, \mathbf{p} \mathbin{\leq} \Delta\quad ; \quad\Delta, \mathbf{q} \mathbin{\leq} {\Theta}\qquad\qquad}{}\text{ Identity}\\ \frac{\Gamma, \mathbf{p} \mathbin{\leq} \Delta\quad ; \quad\mathbf{q} \mathbin{\leq} \mathbf{q} \quad ; \quad \Delta, \mathbf{q} \mathbin{\leq} {\Theta}\,\,\,\;}{}\text{ Cut}\\ \qquad\quad\frac{\Gamma, \mathbf{p}, \mathbf{q} \mathbin{\leq} {\Theta}} {\Gamma \mathbin{\preceq} {\Theta}}\mathbin{\preceq}\text{-I} \end{array} $$

The following derivation establishes Transitivity$(\mathbin {\prec }/\mathbin {\preceq })$.

$$\begin{array}{l} \qquad\frac{\Gamma \mathbin{\prec} \Delta,\quad ;\quad \Delta \mathbin{\preceq} {\Theta} \quad ; \quad \overline{\Theta \mathbin{\preceq} \Gamma}^{1}}{}\mathbin{\prec}\text{-E}\\ \qquad\frac{\;\Delta \mathbin{\not\preceq} \Gamma \quad;\quad \Delta \mathbin{\preceq} {\Theta} \quad ; \quad {\Theta} \mathbin{\preceq} \Gamma}{}\text{ Transitivity}(\mathbin{\preceq}/\mathbin{\preceq})\\ \qquad\frac{\Delta \mathbin{\not\preceq} \Gamma \quad\,\,;\quad \Delta \mathbin{\preceq} \Gamma}{}\mathbin{\not\preceq}\text{-E}\\ \frac{\qquad\quad\quad{\Sigma} \mathbin{\not\preceq} {\Sigma}\qquad\quad\quad}{}\mathbin{\not\preceq}\text{-I}\\ \frac{\Gamma \mathbin{\prec} \Delta \qquad ; \qquad \Delta \mathbin{\preceq} {\Theta} \quad ; \quad {\Theta} \mathbin{\not\preceq} \Gamma}{}\mathbin{\prec}\text{-E}\\ \quad\frac{\Gamma \mathbin{\preceq} \Delta \qquad ; \quad \Delta \mathbin{\preceq} {\Theta} \quad ; \quad {\Theta} \mathbin{\not\preceq} \Gamma}{}\text{ Transitivity}(\mathbin{\preceq}/\mathbin{\preceq})\\ \quad\frac{\Gamma \mathbin{\preceq} {\Theta} \quad ; \quad {\Theta} \mathbin{\not\preceq} \Gamma}{\qquad\Gamma \mathbin{\prec} {\Theta}}\mathbin{\prec}\text{-I}\\ \end{array} $$

The following establishes Restricted Reverse Subsumption:

$$\begin{array}{l} \frac{\Delta \mathbin{\leq} \Gamma_{0}, \Gamma_{1}, {\ldots} \quad ; \quad \Delta \mathbin{\prec} \Gamma_{i} \quad ; \quad \overline{\Gamma_{0}, \Gamma_{1}, \ldots\mathbin{\preceq} \Delta}^{1}}{}\text{ Subsumption}(\mathbin{\preceq}/\mathbin{\preceq})\\ \frac{\Delta \mathbin{\leq} \Gamma_{0}, \Gamma_{1}, {\ldots} \quad ; \quad \Delta \mathbin{\prec} \Gamma_{i} \quad ; \quad \Gamma_{i} \mathbin{\preceq} \Delta}{}\mathbin{\prec}\text{-E}\\ \frac{\Delta \mathbin{\leq} \Gamma_{0}, \Gamma_{1}, {\ldots} \quad ; \quad \Gamma \mathbin{\not\preceq} \Delta \quad ; \quad \Gamma_{i} \mathbin{\preceq} \Delta}{}\text{ Non-Circularity}\\ \quad\frac{\qquad\qquad\quad{\Theta} \mathbin{\not\preceq} {\Theta}\qquad\qquad}{}1, \mathbin{\not\preceq}\text{-I}\\ \quad\frac{\Delta \mathbin{\leq} \Gamma_{0}, \Gamma_{1}, {\ldots} \quad ; \quad \Gamma_{0}, \Gamma_{1}, {\ldots} \mathbin{\not\preceq} \Delta}{\phantom{\frac{@}{@}}\Delta \mathbin{<} \Gamma_{0}, \Gamma_{1}, \ldots}\mathbin{<}\text{-I}\\ \end{array} $$

□

Whereas the previous results were analogues of principles of plg the next results are distinctive of plmmg.

Proposition 6

• (i) $\Gamma \mathbin {\not \preceq } \Delta \vdash \Gamma , \Gamma ^{\prime } \mathbin {\not \preceq } \Delta$ ( $\mathbin {\not \preceq }$ -weakening)

• (ii) $(\Gamma \mathbin {\preceq } \Delta ), (\Gamma , {\Sigma }_{0}, {\Sigma }_{1} \mathbin {\prec } {\Sigma }_{1}, \Delta ) \vdash (\Gamma \mathbin {\prec } \Delta )$ (Partial Cancellation)

• (iii) $(\Gamma \mathbin {\leq } \Delta ), (\Gamma , {\Sigma }_{0}, {\Sigma }_{1} \mathbin {\prec } {\Sigma }_{1}, \Delta ) \vdash \Gamma \mathbin {<} \Delta$ (Full Cancellation)

• (iv) $(\Gamma \mathbin {\leq } \Delta _{0}, \Delta _{1}), (\Delta _{1} \mathbin {\leq } {\Theta }) \vdash \Gamma \mathbin {\leq } \Delta _{0}, {\Theta }$ (Right Cut)

• (v) $(\Gamma \mathbin {<} \Delta _{0}, \Delta _{1}), (\Delta _{1} \mathbin {\leq } {\Theta }) \vdash \Gamma \mathbin {<} \Delta _{0}, {\Theta }$ (Strict Right Cut)

• (vi) $(\Gamma \approx \Delta , {\Sigma }), \Delta \approx \Delta _{0} \vdash \Gamma \approx \Delta _{0}, {\Sigma }$ (Substitution)

• (vii) $\Gamma \mathbin {\leq } \Delta , {\Sigma } \vdash \Gamma \mathbin {\leq } \Gamma , {\Sigma }$ (Undercut)

• (viii) $(\Gamma \mathbin {\leq } \Delta ), (\Gamma \mathbin {\leq } \Delta , {\Theta }, {\Sigma }) \vdash \Gamma \mathbin {\leq } \Delta , {\Theta }$ (Squeezing)

• (ix) $(\Gamma \mathbin {<} \Delta ), (\Gamma \mathbin {\leq } \Delta , {\Theta }, {\Sigma }) \vdash \Gamma \mathbin {<} \Delta , {\Theta }$ (Strict Squeezing)

Proof

In the following proofs we will tacitly use Cut in the form $\frac {\Gamma \mathbin {\leq } \Delta \quad \Delta , {\Sigma } \mathbin {\leq } {\Theta }}{\Gamma , {\Sigma } \mathbin {\leq } {\Theta }}$.

The following establishes $\mathbin {\not \preceq }$-weakening for plmmg.

$$\begin{array}{l} \frac{\Gamma \mathbin{\not\preceq} \Delta \quad ; \quad \overline{\Gamma, \Gamma^{\prime} \mathbin{\preceq} \Delta}^{1}}{}\text{ Subsumption}(\mathbin{\preceq}/\mathbin{\preceq})\\ \frac{\Gamma \mathbin{\not\preceq} \Delta \quad ; \quad \Gamma \mathbin{\preceq} \Delta}{}\mathbin{\not\preceq}\!\text{-E}\\ \quad\frac{\qquad\quad{\Sigma} \mathbin{\not\preceq} {\Sigma}\qquad\quad}{}1, \mathbin{\not\preceq}\text{-I}\\ \quad\frac{\Gamma \mathbin{\not\preceq} \Delta \quad ; \quad \Gamma, \Gamma^{\prime} \mathbin{\not\preceq} \Delta\quad}{\Gamma, \Gamma^{\prime} \mathbin{\not\preceq} \Delta}\text{ Thinning}\\ \end{array} $$

To establish Partial Cancellation it suffices to show that $(\Gamma , {\Sigma }_{0}, {\Sigma }_{1}) \mathbin {\prec } ({\Sigma }_{1}, \Delta ) \vdash \Delta \mathbin {\not \preceq } \Gamma$.

$$\begin{array}{l} \frac{\Gamma, {\Sigma}_{0}, {\Sigma}_{1} \mathbin{\prec} {\Sigma}_{1}, \Delta \quad ; \quad\overline{\Delta \mathbin{\preceq} \Gamma}^{1}}{}\mathbin{\preceq}\text{-E}\\ \frac{\Delta, {\Sigma}_{1} \mathbin{\not\preceq} {\Sigma}_{1}, {\Sigma}_{0}, \Gamma \quad ; \quad \Delta \mathbin{\preceq} \Gamma}{}\mathbin{\preceq}\text{-E}\\ \frac{\Delta, {\Sigma}_{1} \mathbin{\not\preceq} {\Sigma}_{1}, {\Sigma}_{0}, \Gamma \quad ; \quad \Delta, \mathbf{p} \mathbin{\leq} \Gamma\qquad\qquad\qquad\qquad\ \ }{}\text{ Identity}\\ \frac{\Delta, {\Sigma}_{1} \mathbin{\not\preceq} {\Sigma}_{1}, {\Sigma}_{0}, \Gamma \quad ; \quad \Delta, \mathbf{p} \mathbin{\leq} \Gamma \quad ; \quad \Gamma, {\Sigma}_{0}, {\Sigma}_{1} \mathbin{\leq} {\Sigma}_{1}, {\Sigma}_{0}, \Gamma}{}\text{ Cut}\\ \frac{\Delta, {\Sigma}_{1} \mathbin{\not\preceq} {\Sigma}_{1}, {\Sigma}_{0}, \Gamma \quad ; \quad \Delta, \mathbf{p}, {\Sigma}_{0}, {\Sigma}_{1} \mathbin{\leq} {\Sigma}_{1}, {\Sigma}_{0}, \Gamma}{}\mathbin{\preceq}\text{-I}\\ \frac{\Delta, {\Sigma}_{1} \mathbin{\not\preceq} {\Sigma}_{1}, {\Sigma}_{0}, \Gamma \quad ; \quad \Delta, {\Sigma}_{1} \mathbin{\preceq} {\Sigma}_{1}, {\Sigma}_{0}, \Gamma}{}\mathbin{\not\preceq}\text{-I}\\ \qquad\frac{\qquad\qquad{\Theta} \mathbin{\not\preceq} {\Theta}\qquad\qquad}{}\mathbin{\not\preceq}\text{-I}\\ \qquad\frac{\Gamma, {\Sigma}_{0}, {\Sigma}_{1} \mathbin{\prec} {\Sigma}_{1}, \Delta \quad ; \quad \Delta \mathbin{\not\preceq} \Gamma\quad}{\phantom{\frac{@}{@}}\Delta \mathbin{\not\preceq} \Gamma}\text{ Thinning}\\ \end{array} $$

Right Cut follows from Regular Cut as follows.

$$\begin{array}{l} \frac{\qquad\Gamma \mathbin{\leq} \Delta_{0}, \Delta_{1} \quad ; \quad \Delta_{1} \mathbin{\leq} {\Theta}\qquad\qquad\quad}{}\text{ Identity}\\ \frac{\,\,\Gamma \mathbin{\leq} \Delta_{0}, \Delta_{1} \quad ; \quad \Delta_{1} \mathbin{\leq} {\Theta} \quad ; \quad \Delta_{0}, {\Theta} \mathbin{\leq} \Delta_{0}, {\Theta}}{}\text{ Cut}\\ \frac{\,\,\Gamma \mathbin{\leq} \Delta_{0}, \Delta_{1} \quad ; \quad \Delta_{0}, \Delta_{1} \mathbin{\leq} \Delta_{0}, {\Theta}}{\Gamma \mathbin{\leq} \Delta_{0}, {\Theta}}\text{ Cut}\\ \end{array} $$

Strict Right Cut follows from Right Cut by Transitivity($\mathbin {\prec }/\mathbin {\preceq }$) and Restricted Reverse Subsumption.

The following establishes Substitution.

$$\begin{array}{l} \qquad\qquad\frac{\qquad\quad\ \ \quad\Gamma \approx \Delta, {\Sigma} \quad\, ; \quad \Delta \approx \Delta_{0}\qquad\qquad\ \ \ }{}\text{ Definition of}{~\approx}\\ \text{ Right\,Cut}~\frac{\Gamma \mathbin{\leq} \Delta, {\Sigma} \quad ; \quad \Delta \mathbin{\leq} \Delta_{0} \quad ; \quad \Delta_{0} \mathbin{\leq} \Delta \quad ; \quad \Delta,{\Sigma} \mathbin{\leq} \Gamma}{}\\ \qquad\qquad\qquad\qquad\frac{\Gamma \mathbin{\leq} \Delta_{0}, {\Sigma} \quad \,\; ; \quad \Delta_{0} \mathbin{\leq} \Delta \quad ; \quad \Delta,{\Sigma} \mathbin{\leq} \Gamma}{}\text{ Cut}\\ \qquad\qquad\qquad\qquad\frac{\Gamma \mathbin{\leq} \Delta_{0}, {\Sigma} \quad\,\; ; \quad\Delta_{0}, {\Sigma} \mathbin{\leq}\Gamma}{\Gamma \approx \Delta_{0}, {\Sigma}}\text{ Definition of}{~\approx}\\ \end{array} $$

The following establishes Undercut. First we observe that a _i ≈a _i , c _k can be derived from a _i ≈b _j , c _k . The following proof, call it E, witnesses this.

$$\begin{array}{l} \text{ Substitution}\frac{a_{i} \approx b_{j}, c_{k} \quad ; \quad (b_{j}, c_{k}) \approx (b_{j}, c_{k}, c_{k}) \quad ; \quad b_{j}, c_{k} \approx a_{i}}{}\\ \qquad\qquad\quad\frac{a_{i} \approx b_{j}, c_{k}, c_{k} \quad ; \quad b_{j}, c_{k} \approx a_{i}}{a_{i} \approx a_{i}, c_{k}}\text{ Substitution}\\ \end{array} $$

Call this rule Substitution ^∗.

Next, suppose that Γ is γ ₀, γ ₁,…; Δ is δ ₀, δ ₁,…; and Φ is ϕ ₀, ϕ ₁,…. At this point we exploit being able to draw multiple conclusions simultaneously.

$$\begin{array}{l} \frac{\qquad\qquad\gamma_{i} \mathbin{\leq} \delta_{j}, \phi_{k} \quad ; \quad \overline{a_{i} \mathbin{\leq} \gamma_{i}}^{i}\qquad\qquad\qquad}{}\mathbin{\leq}\text{-E}\\ \frac{a_{i} \mathbin{\leq} \gamma_{i} \quad ; \quad (a_{i} \approx b_{j}, c_{k}) \quad ; \quad (b_{j} \mathbin{\leq} \delta_{j}) \quad ; \quad (c_{k} \mathbin{\leq} \phi_{k})}{}\text{ Substitution}^{*}\\ \frac{a_{i} \mathbin{\leq} \gamma_{i} \quad ; \quad (a_{i} \approx a_{i}, c_{k}) \quad ; \quad (b_{j} \mathbin{\leq} \delta_{j}) \quad ; \quad (c_{k} \mathbin{\leq} \phi_{k})}{}\text{ Thinning}\\ \frac{a_{i} \mathbin{\leq} \gamma_{i} \quad ; \quad (a_{i} \approx a_{i}, c_{k}) \quad ; \quad (c_{k} \mathbin{\leq} \phi_{k})}{\qquad\quad\quad\quad\gamma_{i} \mathbin{\leq} \gamma_{i}, \phi_{k}}~i, \mathbin{\leq}\text{-I}\\ \end{array} $$

Note here how we use the fact that we can conclude both a ₀, a ₁,…≈b ₀, b ₁,…, c ₀, c ₁,…and c _k ≤ ϕ _k from γ ₀, γ ₁,… ≤ δ ₀, δ ₁,…, ϕ ₀, ϕ ₁,….

Squeezing is established as follows:

$$\begin{array}{l} \frac{\Gamma \mathbin{\leq} \Delta \quad ; \quad \Gamma \mathbin{\leq} \Delta, {\Theta}, {\Sigma}}{}\text{ Undercut}\\ \frac{\Gamma \mathbin{\leq} \Delta \quad ; \quad \Gamma \mathbin{\leq} \Gamma, {\Sigma}}{\Gamma \mathbin{\leq} \Delta, {\Sigma}}\text{ Right Cut}\\ \end{array} $$

Strict Squeezing follows from Squeezing by Restricted Reverse Subsumption. □

8 Soundness

Theorem 1

The rules in Fig. 5 are sound with respect to the semantics for plg.

Theorem 2

The rules in Fig. 6 are sound with respect to the semantics for plmmg.

We only prove soundness for plmmg. The proof for plg is virtually identical.

Proof

The proof is by induction on the depth of the derivations.

Identity and Thinning. Obvious.

Collection. This follows from Proposition 2.

Cut(≤). Let $\mathcal {M}, \sigma$ be such that S _i ;(Δ _i ≤Θ _i );(Θ₀,Θ₁,… ≤ Γ) is true in $\mathcal {M}$ w.r.t. σ. Say that $\Delta _{i} = {\delta ^{i}_{0}}, {\delta ^{i}_{1}}, \ldots$. Now let ${f^{i}_{0}}, {f^{i}_{1}}, \ldots$ be such that ${f^{i}_{0}} \in [{\delta ^{i}_{0}}]_{\sigma }$, ${f^{i}_{1}} \in [{\delta ^{i}_{1}}]_{\sigma }, \ldots$. Let R be $\bigcup _{i} S_{i} \cup \{\Delta _{0}, \Delta _{1}, {\ldots } {\Theta }_{0}, {\Theta }_{1}, \ldots , \Gamma \}$. We have to show that ${\Pi }(\bigcup _{i,j} {f^{i}_{j}}) \in [\Gamma ]_{\tau }$, for some τ≈ _R σ. We know that ${\Pi }\bigcup _{j}\{{f^{i}_{j}\}} \in [{\Theta }_{i}]_{\sigma }$ for each i. But then ${\Pi } (\bigcup _{i}\{\Pi \bigcup _{j}\{{f^{i}_{j}}\}\}) \in [\Gamma ]_{\sigma }]$, and so ${\Pi }(\bigcup _{i,j} \{{f^{i}_{j}}\} \in [\Gamma ]_{\sigma }$ by the associativity of π. So we may take τ to be σ.

Determinization

Let $\mathcal {E}$ be a proof of S from some sequents T. And let {γ _i } _{i ∈ I} be some atoms (or determinates) that occur in S. Let $\mathcal {M}$ be a model and σ an assignment such that $\mathcal {M}, \sigma \models T$. Then by the induction hypothesis $\mathcal {M}, \sigma ^{\prime } \models S$ for some $\sigma ^{\prime } \approx _{T} \sigma$. Under $\sigma ^{\prime }$ the {γ _i } _{i ∈ I} are interpreted as certain closed sets of facts in $F_{\mathcal {M}}$. For each i pick an f _i ∈[γ _i ]. Then let $\sigma ^{\prime \prime }$ be like $\sigma ^{\prime }$ except that it interprets the {a _i } _{i ∈ I} as the {f _i } _{i ∈ I} . Clearly, $\mathcal {M}, \sigma ^{\prime \prime } \models \bigcup _{i \in I} a_{i} \mathbin {\leq } \gamma _{i}$. Since the a _i satisfy the eigenformulae condition $\sigma ^{\prime \prime } \approx _{T} \sigma$. This establishes the result

Determinacy

Suppose that $\mathcal {M}, \sigma \models a \mathbin {\leq } b$. Then σ interprets a and b as the same f ∈ F. It follows that $\mathcal {M}, \sigma \models b \mathbin {\leq } a$.

≤-I

Suppose that we have a proof $\mathcal {E}$ of the set of sequents T;(b ₀, b ₁,…≈A≈c);b ₀ ≤ δ ₀;b ₁ ≤ δ ₁;… from S and the assumptions A ≤ γ ₀, γ ₁,…. Suppose further that in $\mathcal {E}$ the set of determinates A satisfies the eigenformula condition. Let $\mathcal {M}$ be a model of S w.r.t. to σ. Let f ₀, f ₁,… be any verifiers of [γ ₀] _σ ,[γ ₁] _σ ,…. Since the singleton of any fact is in $\mathcal {V}$ and no determinate in A occurs in S (they are eigenformulae) there is an assignment $\sigma ^{\prime }$ such that $\sigma ^{\prime } \approx _{S} \sigma$ and $\sigma ^{\prime }$ assigns π(f ₀, f ₁,…) to each determinate in A. Then $\mathcal {M}, \sigma ^{\prime } \models S ; (A \mathbin {\leq } \gamma _{0}, \gamma _{1}, \ldots )$. By the induction hypothesis there is some τ such that $\tau \approx _{S ; (A \mathbin {\leq } \gamma _{0}, \gamma _{1}, \ldots )} \sigma ^{\prime }$ and $\mathcal {M}, \tau \models T; (b_{i} \mathbin {\leq } \delta _{i}) ; (A \approx b_{0}, b_{1}, {\ldots } \approx c)$. Hence τ assigns verifiers g ₀, g ₁,… to b ₀, b ₁,… such that π(f ₀, f ₁,…)=π(g ₀, g ₁,…). Since the f _i and σ were arbitrary this establishes that S⊧T;(γ ₀, γ ₁,… ≤ δ ₀, δ ₁,…).

≤-E

Suppose we have an application of ≤-E as follows.

$$\begin{array}{c} \mathcal{E}\\ \frac{\qquad S; (\gamma_{0}, \gamma_{1}, {\ldots} \mathbin{\leq} \delta_{0}, \delta_{1}, \ldots) ; A \mathbin{\leq} \gamma_{0}, \gamma_{1}, \ldots\qquad}{S; A \mathbin{\leq} \gamma_{0}, \gamma_{1}, {\ldots} ; (b_{j} \mathbin{\leq} \delta_{j}) ; (A \approx b_{0}, b_{1}, {\ldots} \approx c)}\mathbin{\leq}\text{-E}\\ \end{array} $$

Let $\mathcal {M}, \sigma$ be such that $\mathcal {M}, \sigma \models S ; (\gamma _{0}, \gamma _{1}, {\ldots } \mathbin {\leq } \delta _{0}, \delta _{1}, \ldots ) ; A \mathbin {\leq } (\gamma _{0}, \gamma _{1}, \ldots )$. Let D be the set of verifiers assigned to A by σ. Since $\mathcal {M}, \sigma \models A \mathbin {\leq } (\gamma _{0}, \gamma _{1}, \ldots )$ there are some verifiers f ₀, f ₁,… such that σ assigns f ₀ to γ ₀, f ₁ to γ ₁ and so on such that π(D) = π(f ₀, f ₁,…). Since $\mathcal {M}, \sigma \models (\gamma _{0}, \gamma _{1}, \ldots ) \mathbin {\leq } (\delta _{0}, \delta _{1}, \ldots )$ it follows that there are verifiers g ₀∈[δ ₀] _σ , g ₁∈[δ ₁] _σ ,… such that π(f ₀, f ₁,…)=π(g ₀, g ₁,…). Since the b ₀, b ₁,… are fresh determinates we can define an assignment τ as follows.

$$\tau(d)= \left\{\begin{array}{ll} \sigma(d) & \text{ if }d\text{ is not one of the determinates }b_{0}, b_{1}, {\ldots} \\ g_{i} & \text{ if }d\text{ is the determinate } b_{i} \in \{b_{0}, b_{1}, \ldots\} \\ {\Pi}(g_{0}, g_{1}, \ldots) & \text{ if }d\text{ is the determinate }c \end{array}\right. $$

It is then clear that $\mathcal {M}, \tau \models b_{i } \mathbin {\leq } \delta _{i}$ for each i and also that $\mathcal {M}, \tau \models (a_{0}, a_{1}, {\ldots } \approx b_{0}, b_{1}, {\ldots } \approx c)$. Since τ≈ _S;A σ we also have $\mathcal {M}, \tau \models S ; A \mathbin {\leq } \gamma _{0}, \gamma _{1}, \ldots$. Since σ was arbitrary this establishes the result.

$\mathbin {\preceq }$-I

Obvious since we demand that $\mathcal {V}$ is closed under fusions of size less than <λ.

$\mathbin {\preceq }$-E

Let $\mathcal {M}, \sigma \models S; (\Gamma \mathbin {\preceq } \Delta )$. Let $V \in \mathcal {V}_{\mathcal {M}}$ be such that $[\Gamma ]_{\sigma }, V \mathbin {\leq }_{\mathcal {M}} [\Delta ]_{\sigma }$. Let τ be exactly like σ except that τ assigns V to p. Since p satisfies the eigenformula condition we have $\sigma \approx _{S; \Gamma \mathbin {\preceq } \Delta }\tau$ and $\mathcal {M}, \tau \models S; (\Gamma , \mathbf {p} \mathbin {\leq } \Delta )$. This establishes the result.

$\mathbin {\not \preceq }$-I

Suppose that ${\Theta } \mathbin {\not \preceq } {\Theta }$ is a consequence of $(\Gamma \mathbin {\preceq } \Delta ); S$. Let $\mathcal {M}, \sigma \models S$. Then $\mathcal {M}, \sigma \models S; \Gamma \mathbin {\not \preceq }\Delta$, since otherwise $\mathcal {M}, \sigma \models {\Theta } \mathbin {\not \preceq } {\Theta }$, which is impossible.

$\mathbin {\not \preceq }$-E

Obvious.

<-I

Obvious.

<-E

Suppose $\mathcal {M}, \sigma$ is such that S;(Γ <Δ) is true in $\mathcal {M}$ w.r.t. σ. By the definition of $\mathbin {<}_{\mathcal {M}}$, [Γ] _σ ≤[Δ] _σ and $[\Delta ]_{\sigma } \mathbin {\not \preceq } [\Gamma ]_{\sigma }$ are both true in $\mathcal {M}$, w.r.t. σ. The result is immediate.

$\mathbin {\prec }$-I

Obvious.

$\mathbin {\prec }$-E

Suppose $S ; (\Gamma \mathbin {\prec } \Delta )$ is true in $\mathcal {M}$ w.r.t. σ. By the definition of $\mathbin {\prec }_{\mathcal {M}}$, $\Gamma \mathbin {\preceq } \Delta$ and $\Delta \mathbin {\not \preceq }\Gamma$ are also true in $\mathcal {M}$, w.r.t. σ. The result is immediate. □

9 Witnessing and Other Extensions

In this section we establish certain proof-theoretic results that are required for the completeness proof.

Definition 13

Let S be a set of sequents in the language of plg (plmmg). S is consistent if there is no derivation from S of a sequent of the form $p \mathbin {\not \preceq } p$ (${\Sigma } \mathbin {\not \preceq } {\Sigma }$) in plg (plmmg).

The idea behind the completeness proofs is to build canonical models from certain consistent collections of sequents. For the construction to work the collections of sequents have to be appropriately witnessed: any partial grounding sequent has to have its truth witnessed by a full grounding sequent. For plg a significant benefit of the present proof theory is how easy it is to show that we can find a witnessed conservative extension; for plmmg I have been unable to find a more standard formalization. It would obviously be of interest to find a more standard formulation for plmmg.

In the following results we use the notation Γ ≪Δ for sequents of plg and plmmg. In the case of plg we make the following two demands.

• (i) Δ has to have cardinality 1.

• (ii) If ≪ is one of the partial sequent signs $\mathbin {\preceq }, \mathbin {\prec }, \mathbin {\not \preceq }$ then Γ, too, has cardinality 1.

Definition 14

Let S be a collection of sequents. S is witnessed iff for every partial sequent $\Gamma \mathbin {\preceq } \Delta \in S$ there is a full sequent Γ,Σ ≤Δ in S.

For S a collection of sequents let S ⁺ be defined as follows. First, for each strict partial sequent $\Gamma \mathbin {\prec } \Delta$ in S, add the weak partial sequent $\Gamma \mathbin {\preceq } \Delta$. In this way we obtain the collection of sequents S ₀. We then introduce new atoms f _i , i ∈ I. For each weak partial sequent $\Gamma \mathbin {\preceq } \Delta$ in S ₀ add a full sequent $\Gamma , f_{\Gamma \mathbin {\preceq } \Delta } \mathbin {\leq } \Delta$ subject to the constraint that if $\Gamma \mathbin {\preceq } \Delta$ is not identical to $\Gamma ^{\prime } \mathbin {\preceq } \Delta ^{\prime }$, then $f_{\Gamma \mathbin {\preceq } \Delta } \neq f_{\Gamma ^{\prime } \mathbin {\not \preceq } \Delta ^{\prime }}$. We call such f witnessing constants.

For the remainder of this section $\vdash$ means provability in either plg or plmmg. $\vdash _{\textsc {plg}}$ means provability in plg and $\vdash _{\textsc {plmmg}}$ means provability in plmmg.

Proposition 7

• (i) Let $\{\Gamma _{i} \mathbin {\preceq } \Delta _{i} \colon i \in I\}$ be some proper weak partial grounding sequents. Let {p _i :i ∈ I} be pairwise distinct auxiliary atoms none of which occur in any of the $\Gamma _{i} \mathbin {\preceq } \Delta _{i}$ . Then $\{\Gamma _{i} \mathbin {\preceq } \Delta _{i} \colon i \in I\} \vdash \{\Gamma _{i}, \mathbf {p}_{i} \mathbin {\leq } \Delta _{i} \colon i \in I\}$.

• (ii) Let $\{\Gamma _{i} \mathbin {\prec } \Delta _{i} \colon i \in I\}$ be some proper strict partial grounding sequents. Then $\{\Gamma _{i} \mathbin {\prec } \Delta _{i} \colon i \in I\} \vdash \{\Gamma _{i} \mathbin {\preceq } \Delta _{i} \colon i \in I\} \cup \{\Delta _{i} \mathbin {\not \preceq } \Gamma _{i} \colon i \in I\}$.

Proof

Let a well-ordering of I be given. The following proof establishes the first claim:

$$\begin{array}{l} \frac{\qquad\Gamma_{0} \mathbin{\preceq} \Delta_{0}\quad}{}\mathbin{\preceq}\text{-E}\quad \frac{\quad\Gamma_{1} \mathbin{\preceq} \Delta_{1} \quad \ldots\quad}{}\mathbin{\preceq}\text{-E}\quad \frac{\quad\Gamma_{y}\mathbin{\preceq}\Delta_{y}\quad \ldots\quad}{}\mathbin{\preceq}\text{-E}\\ \frac{\quad\Gamma_{0}, \mathbf{p}_{0} \mathbin{\leq} \Delta_{0}\qquad\qquad\Gamma_{1}, \mathbf{p}_{1} \mathbin{\leq} \Delta_{1} \quad {\ldots} \qquad\qquad \Gamma_{y},\mathbf{p_{y}\mathbin{\leq}\Delta_{y}\quad\ldots\quad}}{\Gamma_{0}, \mathbf{p}_{0} \mathbin{\leq} \Delta_{0} \quad ; \quad \Gamma_{1}, \mathbf{p}_{1} \mathbin{\leq} \Delta_{1} \quad ; \quad \Gamma_{\gamma}, \mathbf{p}_{\gamma} \mathbin{\leq} \Delta_{\gamma} \quad \ldots}\text{ Collection} \end{array} $$

The second claim is established in the same way. □

Proposition 8

Suppose $S^{+} \vdash U$ where U does not contain any witnessing constants. Then $S \vdash U$.

Proof

Suppose $S^{+} \vdash U$ and let $\mathcal {E}$ be a proof witnessing this. Since the witnessing constants associated with distinct partial sequents are distinct and S;U does not contain any of the witnessing constants, a witnessing constant $f_{\Gamma \mathbin {\precsim } \Delta }$ only occurs undischarged in a top premiss of $\mathcal {E}$ if it occurs in $\Gamma , f_{\Gamma \mathbin {\precsim } \Delta } \mathbin {\leq } \Delta$.

Let F be the set of witnessing constants $f_{\Gamma _{i} \mathbin {\preceq } \Delta _{i}}$ that occur in $\mathcal {E}$. Let $G \subseteq F$ be those witnessing constants of the form $f_{\Gamma \mathbin {\preceq } \Delta }$ where $\Gamma \mathbin {\preceq } \Delta$ is in S ₀∖S. We write $g_{\Gamma \mathbin {\preceq } \Delta }$ for g ∈ G. $\mathcal {E}$ may be taken to have the following form.

$$\begin{array}{c} \text{S} \; ; \; (\Gamma_{0}, f_{\Gamma_{0} \mathbin{\preceq} \Delta_{0}} \mathbin{\leq} \Delta_{0}) \; ; \; (\Gamma_{1}, f_{\Gamma_{1} \mathbin{\preceq} \Delta_{1}} \mathbin{\leq} \Delta_{1}) \dotso \; ; \; ({\Theta}_{0}, g_{{\Theta}_{0} \mathbin{\preceq} {\Sigma}_{0}} \mathbin{\leq} {\Sigma}_{0}) \; ; \; ({\Theta}_{1}, g_{{\Theta}_{1} \mathbin{\preceq} {\Sigma}_{1}} \mathbin{\leq} {\Sigma}_{1}) \dotso\\ \mathcal{E}\\ \text{U} \end{array} $$

We can replace distinct witnessing constants in $\mathcal {E}$ with fresh distinct auxiliary atoms. Write f _i for $f_{\Gamma _{i} \mathbin {\preceq } \Delta _{i}}$; and similarly for $g_{{\Theta }_{j} \mathbin {\preceq } {\Sigma }_{j}}$. Abusing notation, write f _i , g _j ,… for the auxiliary atoms that replace the witnessing constants f _i , g _j ,…. Note that since the witnessing constants for distinct weak partial grounding claims were pairwise distinct and fail to occur in either S (or U for that matter), the f _i and g _j satisfy the eigenformula condition for $\mathbin {\preceq }$-E. The following proof then establishes that $S \vdash U$. (The rules labeled ($\mathbin {\preceq }$-E, Collection) and ($\mathbin {\prec }$-E, Collection) are justified by Proposition 7.)

$$\begin{array}{l} \frac{S \quad ; \quad \Gamma_{i} \mathbin{\preceq} \Delta_{i} \quad ; \quad {\Theta}_{j} \mathbin{\prec} {\Sigma}_{j}}{}\mathbin{\prec}\text{-E}, \text{ Collection}\\ \frac{S \quad ; \quad \Gamma_{i} \mathbin{\preceq} \Delta_{i} \quad ; \quad {\Theta}_{j} \mathbin{\preceq} {\Sigma}_{j}}{S \quad ; \quad \Gamma_{i}, f_{i} \mathbin{\leq} \Delta_{i} \quad ; \quad {\Theta}_{j}, g_{j} \mathbin{\leq} {\Sigma}_{j}}\mathbin{\prec}\text{-E}, \text{ Collection}\\ \qquad\qquad\qquad\qquad\mathcal{E}\\ \qquad\qquad\qquad\qquad\text{U} \end{array} $$

□

Proposition 9

Let S be a set of proper sequents and let ϕ,ψ contain no determinates or auxiliaries.

• (i) Suppose $S \nvdash _{\textsc {plg}} \phi \mathbin {\not \preceq } \psi$ . Then $S \cup \{\phi \mathbin {\preceq } \psi \}$ is consistent in plg.

• (ii) Suppose that $S \vdash _{\textsc {plg}} \phi \mathbin {\preceq } \psi$ , but $S \nvdash _{\textsc {plg}} \phi \mathbin {\prec } \psi$ . Then $S \cup \{\psi \mathbin {\preceq } \phi \}$ is consistent in plg.

• (iii) Suppose that $S \vdash _{\textsc {plg}} \phi _{0}, \phi _{1}, {\ldots } \mathbin {\leq } \phi$ , but that $S \nvdash _{\textsc {plg}} \phi _{0}, \phi _{1}, {\ldots } \mathbin <\phi$ . Then there is an i such that $S \cup \{\phi \mathbin {\preceq } \phi _{i}\}$ is consistent in plg.

Proof

For the first claim, suppose otherwise. There is then a proof $\mathcal {E}$ witnessing that $S \cup \{\phi \mathbin {\preceq } \psi \}$ is inconsistent. The following proof then shows that $S \vdash _{\textsc {plg}} \phi \mathbin {\not \preceq } \psi$.

$$\begin{array}{l} S \quad ; \quad\overline{\phi \mathbin{\preceq} \psi}^{1}\\ \qquad\quad{\mathcal{E}}\\ \frac{\qquad\sigma \mathbin{\not\preceq} \sigma\qquad}{}1, \mathbin{\not\preceq}\text{-I}\\ \frac{\quad S \quad ; \quad \phi \mathbin{\not\preceq} \psi}{\phi \mathbin{\not\preceq} \psi}\text{ Thinning}\\ \end{array} $$

For the second claim, if $S \cup \{\psi \mathbin {\preceq } \phi \}$ is inconsistent then it follows by the first claim that $S \vdash _{\textsc {plg}} \psi \mathbin {\not \preceq } \phi$. So if $S \vdash _{\textsc {plg}} \phi \mathbin {\preceq } \psi$, Collection gives us $S \vdash _{{\textsc {plg}}} (\psi \mathbin {\not \preceq } \phi ) ; (\phi \mathbin {\preceq } \psi )$ and so $S \vdash _{\textsc {plg}} \phi \mathbin {\prec } \psi$ follows by $\mathbin {\prec }$-I. Contradiction.

For the final claim, suppose that $S \vdash _{\textsc {plg}} \phi _{0}, \phi _{1}, {\ldots } \mathbin {\leq } \phi$. Suppose that $S \cup \{\phi \mathbin {\preceq \phi _{i}}\}$ is inconsistent for each i. Then $S \vdash _{\textsc {plg}} \phi _{i} \mathbin {\not \preceq } \phi$ for each i, by the first claim. But then $S \vdash _{\textsc {plg}} (\phi _{0}, \phi _{1}, {\ldots } \mathbin {\leq } \phi ) ; {\ldots } ; \phi _{i} \mathbin {\not \preceq } \phi ; \ldots$ by Collection and so $S \vdash _{\textsc {plg}} \phi _{0}, \phi _{1}, {\ldots } \mathbin {<} \phi$ follows by <-I in plg. □

Remark 6

It is significantly harder to establish these results using Fine’s formulation of plg. It is also notable that we can liberalize the syntax of plg to allow partial sequents of the form $\Delta \mathbin {\preceq } \phi$ and $\Delta \mathbin {\prec } \phi$, where Δ is a set of arbitrary cardinality. The above proofs will still go through. It is not obvious that this can be done using Fine’s techniques. This might be of some significance since it is somewhat artificial to restrict the partial grounding claims to those having a single sentence on the left: if ϕ, ψ, θ are truths, ϕ, ψ together partially ground the conjunction ϕ∧ψ∧θ.

Proposition 10

Let S be a collection of proper sequents and let Γ, Δ be sets that contain no determinates or auxiliaries.

• (i) Suppose $S \nvdash _{\textsc {plmmg}} \Gamma \mathbin {\not \preceq } \Delta$ ; then $S \cup \{\Gamma \mathbin {\preceq } \Delta \}$ is consistent.

• (ii) Suppose that $S \vdash _{\textsc {plmmg}} \Gamma \mathbin {\preceq } \Delta$ , but that $S \nvdash _{\textsc {plmmg}} \Gamma \mathbin {\prec } \Delta$ . Then $S \cup \{\Delta \mathbin {\preceq } \Gamma \}$ is consistent.

• (iii) Suppose that $S \vdash _{\textsc {plmmg}} \Gamma \mathbin {\leq } \Delta$ , but that $S \nvdash _{\textsc {plmmg}} \Gamma \mathbin {<} \Delta$ . Then $S \cup \{\Delta \mathbin {\preceq } \Gamma \}$ is consistent.

Proof

Suppose that $S \cup \{\Gamma \mathbin {\preceq } \Delta \}$ is inconsistent; let $\mathcal {E}$ witness this. Then the following proof witnesses that $S \vdash _{\textsc {plmmg}} \Gamma \mathbin {\not \preceq } \Delta$.

$$\begin{array}{l} S \quad ; \quad \overline{\Gamma \mathbin{\preceq} \Delta}^{1}\\ \qquad\quad\mathcal{E}\\ \frac{\qquad{\Sigma} \mathbin{\not\preceq} {\Sigma}\qquad}{}1, \mathbin{\not\preceq}\text{-I}\\ \frac{\quad S \quad ; \quad\Gamma \mathbin{\not\preceq} \Delta\,\,}{\Gamma \mathbin{\not\preceq} \Delta}\text{ Thinning}\\ \end{array} $$

The two other cases follow straightforwardly from this case as in the proof of Proposition 9. □

Remark 7

Note that in the third case—unlike in the case of plg—we cannot conclude that there is some γ ∈ Γ such that $S \cup \{\Delta \mathbin {\preceq } \gamma \}$ is consistent. We are only entitled to conclude that $S \cup \{\Delta \mathbin {\preceq }\Gamma \}$ is consistent.

The following result on Collection is useful. (It corresponds to Corollary 1 above.)

Proposition 11

If $S \vdash T_{i}$ , for each i∈I and for all i all the determinates in T _i occur in S, then $S \vdash \bigcup _{i\in I} T_{i}$

Proof

For each i, let $\mathcal {E}_{i}$ be a proof of T _i from S. Fix a well-ordering of I. The following proof then establishes that $S \vdash \bigcup _{i \in I} T_{i}$.

$$\frac{\begin{array}{l} S\qquad S\qquad S \quad \ldots\\ \mathcal{E}_{0}\quad\,\,\; \mathcal{E}_{1}\quad\,\,\;\mathcal{E}_{2} \quad \ldots\\ T_{0}\quad\,\,\;T_{1}\quad\,\,\;T_{2} \quad \ldots\qquad \end{array}}{\bigcup_{i \epsilon I} T_{i}}\text{ Collection} $$

This application of Collection is acceptable because any determinates in T _i occur in S. □

10 Completeness of plg

We prove completeness for plg exactly as in [15] but it might be useful to recall this simpler case before tackling the more involved many-many case. The reader who is familiar with that proof should feel free to skip ahead to Section 11.

Let S be a collection of sequents. We define the canonical model $\mathcal {M}_{S}= \langle F, {\Pi }, \mathcal {V}, [\phantom {x}]\rangle$ as follows:

• F = {E:E is a subset of the atoms}

• ${\Pi }(X) = \bigcup X$

• $\mathcal {V}= \{\bigcup X \colon X \subseteq \mathcal {V}_{0}\}$ where $\mathcal {V}_{0} = \{\{\Delta \colon S \vdash \Delta \mathbin {\leq } \phi \}\text { for some } \phi \}$

• $[\phi ] = \{\Delta \colon S \vdash \Delta \mathbin {\leq } \phi \}$

It is easy to verify that $\mathcal {M}_{S}$ is a generalized model. (We define $\mathcal {V}$ in this way because we demand that the collection of closed sets is closed under taking fusions.)

Lemma 1

Let ϕ ₀,ϕ ₁,… ≤ ϕ be a weak full sequent. $S \vdash \phi _{0}, \phi _{1}, {\ldots } \mathbin {\leq } \phi$ iff $\mathcal {M}_{S} \models \phi _{0}, \phi _{1}, {\ldots } \mathbin {\leq } \phi$.

Proof

Suppose first that $S \vdash \phi _{0}, \phi _{1}, {\ldots } \mathbin {\leq } \phi$. Let Δ₀∈[ϕ ₀],Δ₁∈[ϕ ₁],…. Then we have that $S \vdash \Delta _{i} \mathbin {\leq } \phi _{i}$ for each i, and since we have $S \vdash \phi _{0}, \phi _{1}, {\ldots } \mathbin {\leq } \phi$, we have $S \vdash \Delta _{0}, \Delta _{1}, {\ldots } \mathbin {\leq } \phi$ by Cut. But then ${\Pi }(\Delta _{i})=\Delta _{0} \cup \Delta _{1} \cup \dotsb \in [\phi ]$, which is what we have to show.

Conversely, suppose that $S \nvdash \phi _{0}, \phi _{1}, {\ldots } \mathbin {\leq } \phi$. Then by Identity we have {ϕ _i }∈[ϕ _i ] for each i. Hence $[\phi _{0}] \cup [\phi _{1}] {\ldots } = \{\phi _{0}, \phi _{1}, \ldots \} \notin [\phi ]$, which shows that ϕ ₀, ϕ ₁,… ≤ ϕ is not true in $\mathcal {M}_{S}$. □

Lemma 2

Let S be a consistent set of sentences, and let S ⁺ be the witnessed extension. Then every sequent Δ ≪ ϕ ∈ S is true in the canonical model $\mathcal {M}_{S^{+}}$.

Proof

Δ ≪ϕ is Δ ≤ ϕ. Then the result follows by Lemma 1 since Δ ≤ ϕ is derivable from S.

Δ ≪ϕ is Δ < ϕ. By the previous, Δ ≤ ϕ is true in $\mathcal {M}_{S^{+}}$. We have to show that for no ψ ∈ Δ do we have $\phi \mathbin {\preceq } \psi$ true in $\mathcal {M}_{S^{+}}$. Suppose otherwise. Then we have $[{\Theta }], [\phi ] \mathbin {\leq }_{\mathcal {M}_{S^{+}}} [\psi ]$, for some Θ={θ ₀, θ ₁,…}. Then since {θ _i }∈[θ _i ] for i = 0,1,2,… and {ϕ}∈[ϕ], we have that {ϕ, θ ₀, θ ₁,…}∈[ψ]. But then $S^{+} \vdash \phi , \theta _{0}, \theta _{1}, {\ldots } \mathbin {\leq } \psi$, and so $S^{+} \vdash \phi \mathbin {\preceq } \psi$. Since $S^{+} \vdash \Delta \mathbin {<} \phi$, $S^{+} \vdash \psi \mathbin {\prec } \phi$. Hence S ⁺ is inconsistent. By Proposition 8, S is also inconsistent.

Suppose that Δ ≪ϕ is $\psi \mathbin {\preceq } \phi$. Then $S^{+} \vdash \psi , f \mathbin {\leq } \phi$. (Here $f=f_{\psi \mathbin {\preceq } \phi }$.) And so, by Lemma 1, $\mathcal {M}_{S^{+}} \models \psi , f \mathbin {\leq } \phi$. Hence $\psi \mathbin {\preceq } \phi$ is also true in $\mathcal {M}_{S^{+}}$.

Suppose that Δ ≪ϕ is $\psi \mathbin {\not \preceq } \phi$. Suppose, for reductio, that $\psi \mathbin {\preceq } \phi$ is true in $\mathcal {M}_{S^{+}}$. Then we have $[\psi ], [{\Theta }] \mathbin {\leq }_{\mathcal {M}_{S^{+}}} [\phi ]$, for some set of sentences Θ={θ ₀, θ ₁,…}. But then {ψ, θ ₀, θ ₁,…}∈[ϕ], and so we have $S^{+} \vdash \psi , {\Theta } \mathbin {\leq } \phi$, and so $S^{+} \vdash \psi \mathbin {\preceq } \phi$. But then S ⁺ is inconsistent. Contradiction.

If Γ ≪ϕ is $\psi \mathbin {\prec } \phi$, the result follows from the two above cases. □

Lemma 3

Suppose that the sequent Γ ≪ϕ is not derivable from S within plg. Then there is a consistent extension S ₀ of S and a witnessed extension $S_{0}^{+}$ of S ₀ such that Γ≪ϕ is not true in the canonical model $\mathcal {M}_{S^{+}_{0}}$.

Proof

If Γ ≪ϕ is weak full, this follows from Lemma 1, by taking $S^{+}_{0}$ to be S ⁺. (By Proposition 8, S ⁺ is conservative over S.)

If Γ ≪ϕ is weak partial $\psi \mathbin {\preceq } \phi$, let S ₀ be S. Suppose, for contradiction, that there is Θ such that $[{\Theta }], [\psi ] \mathbin {\leq }_{\mathcal {M}_{S^{+}}} [\phi ]$. Then it follows by Lemma 1 that $S^{+} \vdash {\Theta }, \psi \mathbin {\leq } \phi$ and hence that $S^{+} \vdash \psi \mathbin {\preceq } \phi$. But it follows from Proposition 8 that S ⁺ is conservative over S, and so $S \vdash \psi \mathbin {\preceq } \phi$. Contradiction.

If Γ ≪ϕ is strict full Γ <ϕ there are two cases. Suppose first that $S \nvdash \Gamma \mathbin {\leq } \phi$. Then we are done by the first case. So suppose that $S \vdash \Gamma \mathbin {\leq } \phi$. Then we know by Proposition 9 that $\phi \mathbin {\preceq } \psi$ is consistent for some ψ ∈ Γ. Let S ₀ be $S \cup \{\phi \mathbin {\preceq } \psi \}$. Then by Lemma 2 we have that $\phi \mathbin {\preceq } \psi$ is true in $\mathcal {M}_{S^{+}_{0}}$. Hence Γ <ϕ is not true in $\mathcal {M}_{S_{0}^{+}}$.

Γ ≪ϕ is $\psi \mathbin {\prec } \phi$. If $S \nvdash \psi \mathbin {\preceq } \phi$, we are done by the case for $\mathbin {\preceq }$. If $S \vdash \psi \mathbin {\preceq } \phi$ it follows by Proposition 9 that $S \cup \{\phi \mathbin {\preceq } \psi \}$ is consistent. Take this to be S ₀. Then $\phi \mathbin {\preceq } \psi$ is true in $\mathcal {M}_{S_{0}^{+}}$ by Lemma 2, and hence $\psi \mathbin {\prec } \phi$ is not true in $\mathcal {M}_{S^{+}_{0}}$.

Γ ≪ϕ is $\psi \mathbin {\not \preceq } \phi$. Then it follows by Proposition 9 that $S \cup \{\psi \mathbin {\preceq } \phi \}$ is consistent. Take this to be S ₀. Then $\psi \mathbin {\preceq } \phi$ is true in $\mathcal {M}_{S_{0}^{+}}$, and hence $\psi \mathbin {\not \preceq } \phi$ is not true in $\mathcal {M}_{S^{+}_{0}}$. □

From this completeness trivially follows.

Theorem 3 (Completeness of plg)

If Γ ≪ϕ is not derivable from S then Γ ≪ϕ is not a consequence of S.

Proof

By Lemma 3, Γ ≪ϕ is not true in the canonical model $\mathcal {M}_{S^{+}}$ of some witnessed extension of $S^{+}_{0}$ of some extension S ₀ of S. By Lemma 2, every Θ≪ψ ∈ S is true in $\mathcal {M}_{S_{0}^{+}}$. Hence Γ≪ϕ is not a consequence of S. □

11 Completeness of plmmg

Theorem 4

Let S and T be collections of sequents in the language of plmmg such that no determinates occur in S or T. Then if S⊧T then $S \vdash T$.

Remark 8

The proof of Theorem 4 is significantly more involved than the proof of Theorem 3. Before we embark on the completeness proof it is worth getting clear on why this is. The difficulty is that a set of sequents $\{\Gamma \mathbin {\leq } (\delta _{0}, \delta _{1}, \ldots ) \colon S \vdash \Gamma \mathbin {\leq } (\delta _{0}, \delta _{1}, \ldots )\}$ seems not to provide us with enough information to allow us to assign interpretations to the δ _i . The problem is that for (γ ₀, γ ₁,…) ≤(δ ₀, δ ₁,…) to be true is for it to be the case that whenever we have some verifiers f ₀, f ₁,… for γ ₀, γ ₁,… then π(f ₀, f ₁,…) can be “apportioned” out into verifiers g ₀, g ₁,… for δ ₀, δ ₁,…. If we tried to imitate the construction for plg we would get into a position where we know that f ₀, f ₁,… are verifiers for γ ₀, γ ₁,… and that ${\Pi }(f_{0}, f_{1}, \ldots ) \in \bar {\Pi }([\delta _{0}], [\delta _{1}] \ldots )$. But in order to construct a model where the sequent (γ ₀, γ ₁,…) ≤(δ ₀, δ ₁,…) was true we would need to find verifiers g ₀∈[δ ₀], g ₁∈[δ ₁],… such that π(g ₀, g ₁,…)=π(f ₀, f ₁,…).

It is at this point that determinates come into play. For the ≤-E rule allows us to assume that we have found a way of apportioning the fusion of some verifiers for γ ₀, γ ₁,… into verifiers g ₀, g ₁,… for δ ₀, δ ₁,…. This allows us to carry out what is essentially a Henkin construction. Whenever we have a weak grounding claim p ₀, p ₁,… ≤ q ₀, q ₁,… and we think that the determinates A weakly ground p ₀, p ₁,… we throw in some fresh determinates b ₀, b ₁,… representing verifiers for q ₀, q ₁,… together with the assumption that the determinates A fuse to the same fact as b ₀, b ₁,….

We need the following piece of notation. If B is a set of determinates we write B ≤^d{δ ₀, δ ₀,…} to mean that B = {b ₀, b ₁,…} and that we have b ₀ ≤ δ ₀, b ₁ ≤ δ ₁,…. More generally, we write B ≤^dΔ to mean that there is some I such that B = {b _i } _{i ∈ I} , Δ={δ _i } _{i ∈ I} and b _i ≤ δ _i , for each i ∈ I.

This notation allows us to write instances of the ≤-E rule more economically as follows:

$$\begin{array}{l} \frac{\qquad S ; \Gamma \mathbin{\leq} \Delta ; A \mathbin{\leq} \Gamma\qquad}{S; A \mathbin{\leq} \Gamma ; B \mathbin{\leq}^{d} \Delta ; A \approx B \approx c}\mathbin{\leq}\text{-E} \end{array} $$

Definition 15

A diagram is a set of sequents D such that:

• (i) D is witnessed;

• (ii) if p is an atom occurring in a sequent in D then there is some determinate a such that the sequent a ≤ p occurs in D;

• (iii) if a weak full sequent γ ₀, γ ₁,… ≤ δ ₀, δ ₁,… is in D, then for all sets of determinates A such that A ≤{γ ₀, γ ₁,…}∈D there is a set of determinates B such that $B \mathbin {\leq }^{d} \{\delta _{0}, \delta _{1}, \ldots \} \subseteq D$ and such that $A \approx B \approx c \subseteq D$.

The key part of the completeness proof is showing how we can conservatively extend a consistent set of sequents to a diagram.

Let S be a consistent set of sequents. Without loss of generality assume that S is witnessed. If $S \nvdash T$ and S is not witnessed we can always extend S to witnessed S ⁺ with $S^{+} \nvdash T$. We now show how to conservatively extend S to a diagram.

Let κ be the number of proper atoms that occur in S. Let λ be the least strongly inaccessible cardinal larger than κ. Let a collection of fresh determinates c ₀, c ₁,…, c _α ,…, α < λ be given. Let $\mathcal {L}^{+}$ be the language that results from adding the determinates c ₀, c ₁,… to the proper atoms in S. Recall from Section 6.2 that if Γ,Δ are two sets of atoms and determinates of cardinality <λ, then Γ ≪Δ is a sequent of $\mathcal {L}^{+}$, where ≪ is any of the sequent signs $\mathbin {<}, \mathbin {\leq }, \mathbin {\preceq }, \mathbin {\prec }, \mathbin {\not \preceq }$.

For each atom $p \in \mathcal {L}$ such that $S \vdash \sigma$ for some sequent σ in which p occurs, we add a sequent ${c^{p}_{0}} \mathbin {\leq } p$. We make sure that if p≠q, then ${c^{p}_{0}} \neq {c^{q}_{0}}$. We make sure that we have λ-many determinates left over. Call the resulting collection of sequents S ₀.

Next enumerate the weak full sequents of $\mathcal {L}^{+}$ as Γ ⁰ ≤Δ⁰,Γ ¹ ≤Δ¹,…,Γ ^α ≤Δ^α,…, α < λ in such a way that each weak full sequent occurs λ-many times. (Since λ is strongly inaccessible and each sequent only contains β < λ many atoms and determinates there are only λ-many sequents.) We now define a sequence of sets of sequents $S \subseteq S_{0} \subseteq S_{1} \subseteq \ldots , S_{\beta }, \ldots$, β ≤ λ by transfinite recursion.

Let S _β be defined for each β < γ. Say that the γ-th weak full sequent is Γ ^γ ≤Δ^γ. If not all the determinates occurring in Γ ^γ ≤Δ^γ occur in $\bigcup _{\beta < \gamma } S_{\beta }$ just put $S_{\gamma }= \bigcup _{\beta < \gamma } S_{\beta }$. If all the determinates in Γ ^γ ≤Δ^γ do occur in $\bigcup _{\beta < \gamma } S_{\beta }$ but $\bigcup _{\beta < \gamma } S_{\beta } \nvdash \Gamma ^{\gamma } \mathbin {\leq } \Delta ^{\gamma }$ put $S_{\gamma }= \bigcup _{\beta < \gamma } S_{\beta } ; D^{\gamma } \mathbin {\leq }^{d} \Gamma ^{\gamma }$, where D ^γ is a set of pairwise distinct fresh determinates.

Finally, if all the determinates in Γ ^γ ≤Δ^γ occur in $\bigcup _{\beta < \gamma }S_{\beta }$ and $\bigcup _{\beta < \gamma } S_{\beta } \vdash \Gamma ^{\gamma } \mathbin {\leq } \Delta ^{\gamma }$, we proceed as follows. For all sets of determinates $A^{\gamma }_{k}$, k ∈ K ^γ such that $A^{\gamma }_{k} \subseteq \bigcup _{\beta < \gamma } S_{\beta }$ and $\bigcup _{\beta < \gamma } S_{\beta } \vdash A^{\gamma }_{k} \mathbin {\leq } \Gamma ^{\gamma }$ pick a set of pairwise distinct fresh determinates $B^{\gamma }_{k}$ and a fresh determinate $c_{k}^{\gamma }$. Then add the sequents $B^{\gamma }_{k} \mathbin {\leq }^{d} \Delta ^{\gamma }$ and $A^{\gamma }_{k} \approx B^{\gamma }_{k} \approx c^{\gamma }_{k}$. We choose the $B^{\gamma }_{k}$ such that if $A^{\gamma }_{k} \neq A^{\gamma }_{l}$ then $B^{\gamma }_{k} \cap B^{\gamma }_{l}= \emptyset$. Finally, let D ^γ be some pairwise distinct fresh determinates. Add the sequents D ^γ ≤^d Γ ^γ. We can do this in such a way that we have λ-many fresh determinates left over.

Let $S_{\lambda } = \bigcup _{\beta < \lambda } S_{\beta }$. Let D _S = S _λ . We call D _S the canonical diagram over S.

Proposition 12

Suppose that S is witnessed. Then D _S is also witnessed.

Proof

Immediate from the fact that we only add full sequents. □

The canonical diagram over S has the following important feature.

Proposition 13

For all β ₀ <β≤λ, we have $S_{\beta _{0}} \vdash S_{\beta }$ . In particular, $S \vdash D_{S}$.

Proof

We prove the following slightly stronger claim by induction on β ≤ λ: for all β ₀ ≤ β we have $\bigcup _{\beta _{1} < \beta _{0}} S_{\beta _{1}} \vdash S_{\beta }$. Assume that the result holds for all β < α. For each β ₀ ≤ β < α let $\mathcal {E}^{<\beta _{0}}_{\beta }$ witness that $\bigcup _{\beta _{1} < \beta _{0}} S_{\beta _{1}} \vdash S_{\beta }$.

There are three cases. If not all the determinates in Γ ^α ≤Δ^α occur in $\bigcup _{\beta < \alpha }$ then $S_{\alpha } = \bigcup _{\beta < \alpha } S_{\beta }$. Let β < α be given. It suffices to show that $S_{\beta } \vdash S_{\alpha }$. The following argument, call it $\mathcal {E}^{\beta }_{<\alpha }$, establishes this:

$$\begin{array}{l} \quad S_{\beta} \qquad\quad \frac{}{S_{\beta+1}\quad \ldots}{1} \qquad \frac{}{\,\;\bigcup_{\gamma_{0} < \gamma} S_{\gamma_{0}} \quad \ldots}{ \gamma}\\ \,\;\mathcal{E}^{<\beta+1}_{\beta+1}\qquad \mathcal{E}^{<\beta+2}_{\beta+2} \qquad\qquad\quad \mathcal{E}_{\gamma}^{< \gamma}\\ \,\;S_{\beta+1}\qquad S_{\beta+2} \quad {\ldots} \qquad\quad S_{\gamma} \quad \ldots\\ \frac{}{\qquad\qquad\qquad\bigcup_{\beta < \alpha} S_{\beta}\qquad\qquad\qquad}{\gamma < \alpha, \text{ Collection}}\\ \end{array} $$

In the case where all the determinates in Γ ^α ≤Δ^α are in $\bigcup _{\beta < \alpha } S_{\beta }$ but $\bigcup _{\beta < \alpha } S_{\beta } \nvdash \Gamma ^{\alpha } \mathbin {\leq } \Delta ^{\alpha }$, $S_{\alpha }= \bigcup _{\beta < \alpha } S_{\beta } \cup D^{\alpha } \mathbin {\leq }^{d} \Gamma ^{\alpha }$, where D ^α are determinates that do not occur in $\bigcup _{\beta < \alpha } S_{\beta }$. The following proof then establishes that $S_{\beta } \vdash S_{\alpha }$.

$$\begin{array}{l} \quad\quad\quad\mathcal{E}^{\beta}_{< \alpha}\\ \frac{\quad\quad\bigcup_{\beta < \alpha} S_{\beta}\quad\quad}{D^{\alpha} \mathbin{\leq} \Gamma^{\alpha} \quad ; \quad \bigcup_{\beta < \alpha} S_{\beta}}\text{ Determinization} \end{array} $$

The interesting case is when all the determinates in Γ ^α ≤Δ^α are in $\bigcup _{\beta < \alpha } S_{\beta }$ and $\bigcup _{\beta < \alpha } S_{\beta } \vdash \Gamma ^{\alpha } \mathbin {\leq } \Delta ^{\alpha }$. In that case we reason as follows. Let $\{A^{k}\}_{k \in K_{\alpha }}$ enumerate the sets of determinates occurring in $\bigcup _{\beta < \alpha } S_{\beta }$ such that $\bigcup _{\beta < \alpha } S_{\beta } \vdash A^{k} \mathbin {\leq } \Gamma ^{\alpha }$. It then follows by Proposition 11 that

$$\bigcup_{\beta < \alpha} S_{\beta} \vdash \bigcup_{\beta < \alpha} S_{\beta} \quad ; \quad \bigcup_{k \in K^{\alpha}} \{A^{k} \mathbin{\leq} \Gamma^{\alpha}\} \quad ; \quad \Gamma^{\alpha} \mathbin{\leq} \Delta^{\alpha} $$

Let $\mathcal {D}$ be an argument witnessing this.

For each k ₀∈K ^α the following is then a proof witnessing that $S_{\beta } \vdash \bigcup _{\beta < \alpha } S_{\beta } \quad ; \quad \bigcup _{k \in K^{\alpha }} \{A^{k}\mathbin {\leq } \Gamma ^{\alpha }\} \quad ; \quad \Gamma ^{\alpha } \mathbin {\leq } \Delta ^{\alpha } \quad ; \quad B^{k_{0}} \mathbin {\leq }^{d} \Delta ^{\alpha } \quad ;\quad A^{k_{0}} \approx B^{k_{0}} \approx c^{k_{0}}$.

$$\begin{array}{c} S_{\beta}\\ \mathcal{E}_{<\alpha}^{\beta}\\ \bigcup_{\beta < \alpha} S_{\beta}\\ \mathcal{D}\\ \frac{\qquad\quad\bigcup_{\beta < \alpha} S_{\beta} \quad ; \quad \bigcup_{k \in K^{\alpha}} \{A^{k} \mathbin{\leq} \Gamma^{\alpha}\} \quad ; \quad \Gamma^{\alpha} \mathbin{\leq} \Delta^{\alpha}}{\bigcup_{\beta < \alpha} S_{\beta} \quad ; \quad \bigcup_{k \in K^{\alpha}} \{A^{k}\mathbin{\leq} \Gamma^{\alpha}\} \quad ; \quad \Gamma^{\alpha} \mathbin{\leq} \Delta^{\alpha} \quad ; \quad B^{k_{0}} \mathbin{\leq}^{d} \Delta^{\alpha} \quad ;\quad A^{k_{0}} \approx B^{k_{0}} \approx c^{k_{0}}}\mathbin{\leq}\text{-E}\\ \end{array} $$

Call this proof $\mathcal {F}_{k_{0}}$

Since $B^{k} \cap B^{k^{\prime }} =\emptyset$ and $c^{k} \neq c^{k^{\prime }}$ as long as $k \neq k^{\prime }$ it follows that we can apply Collection and Determinization to combine the proofs $\mathcal {F}_{k_{0}}, k_{0} \in K^{\alpha }$ into a proof $\mathcal {E}_{\alpha }^{\beta }$ witnessing that

$$S_{\beta} \!\vdash\! \bigcup_{\beta \!<\! \alpha}\! S_{\beta} ; \!\bigcup_{k \in K^{\alpha}}\! \{A^{k}\mathbin{\leq} \Gamma^{\alpha}\} ;\! \Gamma^{\alpha} \mathbin{\leq} \Delta^{\alpha} ; \bigcup_{k \in K^{\alpha}} \{B^{k} \mathbin{\leq}^{d} \Delta^{\alpha}\} ; \!\bigcup_{k \in K^{\alpha}} \! \{A^{k} \approx B^{k} \!\approx\! c^{k}\} ; D^{\alpha} \mathbin{\leq} \Gamma^{\alpha} $$

Since

$$S_{\alpha} \,=\, \bigcup_{\beta < \alpha} \!S_{\beta} ;\! \bigcup_{k \in K^{\alpha}} \!\{A^{k}\mathbin{\leq} \Gamma^{\alpha}\} ; \!\Gamma^{\alpha} \mathbin{\leq} \Delta^{\alpha} ;\! \bigcup_{k \in K^{\alpha}} \!\{B^{k} \mathbin{\leq}^{d} \Delta^{\alpha}\} ;\! \bigcup_{k \in K^{\alpha}} \!\{A^{k} \approx B^{k} \approx c^{k}\} ; \!D^{\alpha} \mathbin{\leq} \Gamma^{\alpha} $$

this establishes the result. □

We define a relation ≈ on sets of determinates as follows.

Definition 16

Let A, B be two sets of determinates in the language $\mathcal {L}^{+}$. A≈B iff

• (i) $A = \bigcup _{\beta < \lambda } A_{\beta }$, $B= \bigcup _{\beta < \lambda } B_{\beta }$;

• (ii) the cardinality of each A _β is less than λ (and similarly for B _β );

• (iii) {A _β } _{β < λ} is closed under unions of less than λ-many sets. (Similarly for {B _β } _{β < λ} .)

• (iv) $D \vdash A_{\beta } \approx B_{\beta }$ for each β < λ.

Proposition 14

≈ is an equivalence relation.

Proof

That ≈ is reflexive and symmetric is obvious. To see that it is transitive suppose that A≈B and B≈C. Let {A _β } _{β < λ} and {B _β } _{β < λ} witness that A≈B and let $\{B^{\prime }_{\beta }\}_{\beta < \lambda }$ and {C _β } _{β < λ} witness that B≈C.

Let C ∈ {C _β } _{β < λ} be given. Call it $C_{\beta _{0}}$. We can find $B^{\prime }_{\beta _{0}}$ such that $D \vdash B^{\prime }_{\beta _{0}} \approx C_{\beta }$. Then, since {B _β } _{β < λ} is closed under <λ-unions we can find $B_{\alpha _{0}}$ such that $B^{\prime }_{\beta _{0}} \subseteq B_{\alpha _{0}}$. $D \vdash B_{\alpha _{0}} \approx A_{\alpha _{0}}$. Similarly, we can find $B^{\prime }_{\beta _{1}} \supseteq B_{\alpha _{0}}$. In this way we build up the following diagram (here ↪ represents the subset relation):

$\bigcup _{i < \omega } B_{\alpha _{i}} = \bigcup _{i < \omega } B^{\prime }_{\beta _{i}}$. Since $D \vdash \bigcup _{i < \omega } A_{\alpha _{i}} \approx \bigcup _{i < \omega } B_{\alpha _{i}}$ and $D \vdash \bigcup _{i < \omega } B^{\prime }_{\beta _{i}} \approx \bigcup _{i < \omega } C_{\beta _{i}}$ it follows that $D \vdash \bigcup _{i < \omega } A_{\alpha _{i}} \approx \bigcup _{i < \omega } C_{\beta _{i}}$. Both $\bigcup _{i< \omega } A_{\alpha _{i}}$ and $\bigcup _{i < \omega } C_{\beta _{i}}$ have cardinality less than λ.

Since we can do this for each C ∈ {C _β } _{β < λ} we can find $\{A^{\prime }_{\beta }\}_{\beta < \lambda }$ and $\{C^{\prime }_{\beta }\}_{\beta < \lambda }$ such that $D \vdash A^{\prime }_{\beta } \approx C^{\prime }_{\beta }$, for each β < λ. (We may have to close under <λ-sized unions.) This shows that ≈ is an equivalence relation on the sets of determinates in $\mathcal {L}^{+}$. □

If A is a set of determinates in $\mathcal {L}^{+}$ let [A] be the equivalence class of A under ≈.

We define an operation π _D on equivalence classes of sets of determinates as follows.

$${\Pi}_{D}(\{[A]_{i}\}_{i \in I}) = [\bigcup_{i \in I} A_{i}] $$

To show that this is well-defined let B _i ≈A _i , for each i ∈ I. We have to show that $\bigcup _{i \in I} B_{i} \approx \bigcup _{i \in I} A_{i}$. For each i, let $A_{i} = \bigcup _{j \in J_{i}} {A_{j}^{i}}$ and $B_{i}= \bigcup _{j \in J_{i}} {B_{j}^{i}}$ be coverings of A _i , B _i into λ-many pieces of cardinality less than λ such that $D \vdash {A^{i}_{j}} \approx {B^{i}_{j}}$, for each i and j ∈ J _i .

Since $\bigcup _{i \in I} A_{i}$ has size at most λ, $\bigcup _{i \in I} A_{i} = \bigcup _{\beta < \lambda } A^{\prime }_{\beta }$, where each $A^{\prime }_{\beta }$ is an ${A_{j}^{i}}$, for some i ∈ I and j ∈ J _i . For each $A^{\prime }_{\beta }$, let $B^{\prime }_{\beta }$ be some ${B_{j}^{i}}$ such that $D \vdash A^{\prime }_{\beta } \approx {B_{j}^{i}}$. Similarly, $\bigcup _{i \in I} B_{i} = \bigcup _{\beta < \lambda } B^{\prime \prime }_{\beta }$, where each $B^{\prime \prime }_{\beta }$ is some ${B_{j}^{i}}$. For each β let $A^{\prime \prime }_{\beta }$ be an ${A_{j}^{i}}$ such that $D \vdash B^{\prime \prime }_{\beta } \approx A^{\prime \prime }_{\beta }$. By closing $\{A^{\prime }_{\beta }\}_{\beta < \lambda } \cup \{A^{\prime \prime }_{\beta }\}_{\beta < \lambda }$ and $\{B^{\prime }_{\beta }\}_{\beta < \lambda } \cup \{B^{\prime \prime }_{\beta }\}_{\beta < \lambda }$ under unions of size <λ and ordering them appropriately in ordertype λ, we witness that $\bigcup _{i \in I} A_{i} \approx \bigcup _{i \in I } B_{i}$.

For a consistent set of sequents S we now use D = D _S to construct a model $\mathcal {M}_{D} = \langle F_{D}, {\Pi }_{D}, \mathcal {V}_{D}, [\phantom {x}]_{D}\rangle$ as follows.

• $F_{D} = \{[A] \colon A \text { is a set of determinates in } \mathcal {L}^{+}\}$.

• π _D is the operation π _D defined above.

• [p] is { [a]:a is a determinate in the language of D such that $D \vdash a \mathbin {\leq } p$}

$\mathcal {V}_{D}$ is defined as follows: $V \in \mathcal {V}_{D}$ iff there is some Γ in the language of D such that

$$V = \{[c] \colon D \vdash c \mathbin{\leq} \Gamma \}</p><p class="noindent">$$

In words, the closed sets are the verifiers of some or other collection of propositions.

$\mathcal {M}_{D}$ is a state-space model. Clearly, each [p] is non-empty and each $[p] \in \mathcal {V}$. We have to check that $\mathcal {V}_{D}$ is closed under fusions of size less than λ. So let {V _α } _{α < β < λ} be a collection of closed sets from $\mathcal {V}_{D}$. Since $V_{\alpha } \in \mathcal {V}_{\mathcal {D}}$, $V_{\alpha }=\{[c] \colon D \vdash c \mathbin {\leq } \Gamma _{\alpha }\}$, for some Γ _α . So it suffices to show that ${\Pi }_{\alpha < \beta }(V_{\alpha }) = \{[c] \colon D \vdash c \mathbin {\leq } \bigcup _{\alpha < \beta }\Gamma _{\alpha }\}$. The interesting direction is to show that ${\Pi }_{\alpha < \beta }(V_{\alpha }) \supseteq \{[c] \colon D \vdash c \mathbin {\leq } \bigcup _{\alpha < \beta }\Gamma _{\alpha }\}$. So suppose $D \vdash c \mathbin {\leq } \bigcup _{\alpha < \beta } \Gamma _{\alpha }$. Then $S_{\gamma } \vdash c \mathbin {\leq } \bigcup _{\alpha < \beta } \Gamma _{\alpha }$, for some γ < λ. (This follows from Proposition 13.) So by construction of the sets of sequents S _α , there is some γ ₀>γ such that $S_{\gamma _{0}} \vdash c \approx \bigcup _{\alpha < \beta } B_{\alpha } ; \bigcup _{\alpha < \beta } (B_{\alpha } \mathbin {\leq }^{d} \Gamma _{\alpha })$. Since for each a there is some c _a such that $D \vdash B_{\alpha } \approx c_{\alpha }$, we have $D \vdash B_{\alpha } \leq \Gamma c_{\alpha }$ for each α. And so [c]=π({c _α } _{α < β} ) ∈ π({V _α } _{α < β} ).

We can now establish the following lemma.

Lemma 4

Let σ be a weak full sequent such that all the determinates and auxiliaries in σ occur in a S _β , with β<λ. Then if $D \vdash \sigma$ then $\mathcal {M}_{D} \models \sigma$ , and if $D \nvdash \sigma$ then $\mathcal {M}_{D} \not \models \sigma$.

Proof

For the former, suppose that $S_{\lambda } =D \vdash \gamma _{0}, \gamma _{1}, {\ldots } \mathbin {\leq } \delta _{0}, \delta _{1}, \ldots$. Now let [a ₀],[a ₁],… be verifiers for γ ₀, γ ₁,…. Then there is an S _α such that the determinates a ₀, a ₁,… all occur in S _α . Since the sequent γ ₀, γ ₁,… ≤ δ ₀, δ ₁,… occurs λ-many times in the enumeration there is a β>α such that the β’th sequent is γ ₀, γ ₁,… ≤ δ ₀, δ ₁,…. We have constructed S _β+1 so that b _j ≤ δ _j and a ₀, a ₁,…≈b ₀, b ₁,…≈c all occur in S _β+1 for some fresh determinates b ₀, b ₁,… and c. But then π _D ([b ₀],[b ₁],…)=π _D ([a ₀],[a ₁],…)=[c] as required.

Suppose next that $D= S_{\lambda } \nvdash \gamma _{0}, \gamma _{1}, {\ldots } \mathbin {\leq } \delta _{0}, \delta _{1} \ldots$. And suppose that $\mathcal {M}_{D} \models \gamma _{0}, \gamma _{1}, {\ldots } \mathbin {\leq } \delta _{0}, \delta _{1}, \ldots$. Suppose that the determinates in γ ₀, γ ₁,… ≤ δ ₀, δ ₁,… all occur in S _β . Since each sequent γ ₀, γ ₁,… ≤ δ ₀, δ ₁,… occurs λ-many times there is some γ>β and a set of determinates A such that A ≤ γ ₀, γ ₁,… is in S _γ and such that no determinate in A occurs in $\bigcup _{\beta ^{\prime } < \gamma } S_{\beta ^{\prime }}$. Moreover, no other sequents involving A are in S _γ .

By assumption π _D ([A])=π _D ([b ₀],[b ₁],…) for some verifiers [b ₀],[b ₁],… of δ ₀, δ ₁,…. There is, then, a least γ ₀ such that there are representatives b ₀, b ₁,… of [b ₀],[b ₁],… occurring in $S_{\gamma _{0}}$ and such that $S_{\gamma _{0}}$ contains A≈b ₀, b ₁,…≈c; b _j ≤ δ _j .

By Proposition 13 we know that $S_{\gamma } \vdash S_{\gamma _{0}}$; in particular, then, $S_{\gamma } \vdash A \approx b_{0}, b_{1}, {\ldots } \approx c; b_{j} \mathbin {\leq } \delta _{j}$. Let $\mathcal {E}$ be a proof witnessing this. In $\mathcal {E}$, A satisfies the eigenformula condition. We can therefore use ≤-I as follows.

$$\begin{array}{c} \bigcup_{\beta^{\prime} < \gamma} S_{\beta^{\prime}}\quad \frac{}{A \mathbin{\leq} \gamma_{0}, \gamma_{1} \ldots}{0,1,2, \ldots}\\ \qquad\qquad\qquad\mathcal{E}\\ \qquad\qquad\qquad\quad \frac{A \approx b_{0}, b_{1}, {\ldots} \approx c ; \{b_{j} \mathbin{\leq} \delta_{j}\}_{j \in J}}{\bigcup_{\beta^{\prime} < \gamma} S_{\beta^{\prime}} ; \gamma_{0},\gamma_{1}, {\ldots} \mathbin{\leq} \delta_{0}, \delta_{1}, \ldots}{1,2,3, \ldots} \end{array} $$

This shows that $\bigcup _{\beta ^{\prime } < \gamma } S_{\beta ^{\prime }} \vdash \gamma _{0}, \gamma _{1}, {\ldots } \mathbin {\leq } \delta _{0}, \delta _{1}, \ldots$. Since all the determinates and auxiliaries in γ ₀, γ ₁,… ≤ δ ₀, δ ₁,… occur in S _γ and $S_{\gamma } \subseteq D$ it follows that $D \vdash \gamma _{0}, \gamma _{1}, {\ldots } \mathbin {\leq } \delta _{0}, \delta _{1}, \ldots$. Contradiction. □

Proposition 15

Let S be a consistent witnessed collection of sequents. If Γ ≪Δ∈S then Γ ≪Δ is true in $\mathcal {M}_{D}$.

Proof

There are five cases.

Γ ≪Δ is a full weak grounding claim Γ ≤Δ. This follows immediately from Lemma 4.

Γ ≪Δ is a weak partial grounding claim $\Gamma \mathbin {\preceq } \Delta$. Then since S is witnessed $(\Gamma , f_{\Gamma \mathbin {\preceq } \Delta } \mathbin {\leq } \Delta ) \in S$. It follows by Lemma 4 that $\mathcal {M}_{D} \models \Gamma , f_{\Gamma \mathbin {\preceq } \Delta } \mathbin {\leq } \Delta$. Hence $\mathcal {M}_{D} \models \Gamma \mathbin {\preceq } \Delta$.

Γ ≪Δ is $\Gamma \mathbin {\not \preceq } \Delta$. Then since $S \vdash \Gamma \mathbin {\not \preceq } \Delta$, $D \vdash \Gamma \mathbin {\not \preceq } \Delta$. Since D is consistent, we have $D \nvdash \Gamma , {\Theta } \mathbin {\leq } \Delta$ for all Θ in the language $\mathcal {L}^{+}$. By Lemma 4 we know that $\mathcal {M}_{D} \not \models \Gamma , {\Theta } \mathbin {\leq } \Delta$ for all Θ in the language $\mathcal {L}^{+}$. Suppose that $V \in \mathcal {V}$ is such that $[\Gamma ], V \mathbin {\leq }_{F_{D}} [\Delta ]$. By the definition of $\mathcal {V}$ we know that there is Θ such that $V = \{[c] \colon D \vdash c \mathbin {\leq } {\Theta }\}$.

Say that Θ={θ ₀, θ ₁,…}. And let Γ={γ ₀, γ ₁,…} and Δ={δ ₀, δ ₁,…}. Let [a ₀],[a ₁],… be arbitrary verifiers of θ ₀, θ ₁,…; and let [b ₀],[b ₁],… be arbitrary verifiers for γ ₀, γ ₁,…. Since π([a ₀],[a ₁]…)=[c] for some [c]∈V, there has to be [d ₀],[d ₁],… verifiers of δ ₀, δ ₁,… respectively such that π([a ₀],[a ₁],…,[b ₀],[b ₁],…)=π([d ₀],[d ₁],…).

But that means that Γ,Θ ≤Δ is true in $\mathcal {M}_{D}$ and thus by Lemma 4 that $D \vdash \Gamma , {\Theta } \mathbin {\leq } \Delta$ and hence that $D \vdash \Gamma \mathbin {\preceq } \Delta$. But then D is inconsistent. Contradiction.

Γ ≪Δ is Γ <Δ. Then we have $D \vdash \Gamma \mathbin {\leq } \Delta$, and hence $\mathcal {M}_{D} \models \Gamma \mathbin {\leq } \Delta$ by the first case. We also have $D \vdash \Delta \mathbin {\not \preceq } \Gamma$, and hence $\mathcal {M}_{D} \models \Delta \mathbin {\not \preceq } \Gamma$, by the above result about $\mathbin {\not \preceq }$.

The case where Γ ≪Δ is $\Gamma \mathbin {\prec } \Delta$ is dealt with similarly. □

Lemma 5

Let Γ ≪Δ be a sequent that contains no determinates or auxiliaries. Suppose that Γ ≪Δ is not derivable from S within plmmg. Then Γ ≪Δ is not true in the canonical model $\mathcal {M}_{T_{\lambda }}$ for some witnessed extension T of some consistent extension S ₀ of S.

Proof

If Γ ≪Δ is the weak full sequent Γ ≤Δ this follows from Lemma 4, by taking T to be S.

If Γ ≪Δ is the weak partial sequent $\Gamma \mathbin {\preceq } \Delta$, then let $S_{0} = S \cup {\Gamma \mathbin {\not \preceq } \Delta }$. Then it follows by Proposition 15 that $\mathcal {M}_{S_{\lambda }} \models \Gamma \mathbin {\not \preceq } \Delta$, and so $\mathcal {M}_{S_{\lambda }} \not \models \Gamma \mathbin {\preceq } \Delta$.

If Γ ≪Δ is the sequent $\Gamma \mathbin {\not \preceq } \Delta$ it follows by Proposition 10 that $S \cup \{\Gamma \mathbin {\preceq } \Delta \}$ is consistent. Let this be our S ₀ and let T be a witnessed extension of S ₀. Then we know by Proposition 15 that $\Gamma \mathbin {\preceq } \Delta$ is true in $\mathcal {M}_{T_{\lambda }}$.

If Γ ≪Δ is the strict full sequent Γ <Δ then either $S \nvdash \Gamma \mathbin {\leq } \Delta$, in which case the result follows immediately from Lemma 4; or else, by Proposition 10, $S \cup \{\Delta \mathbin {\preceq } \Gamma \}$ is consistent. Let this be our S ₀ and let T be a witnessed extension of S ₀. By Proposition 15 we get that $\Delta \mathbin {\preceq } \Gamma$ is true in $\mathcal {M}_{T_{\lambda }}$, and hence that Γ <Δ is not true in $\mathcal {M}_{T_{\lambda }}$.

If Γ ≪Δ is the sequent $\Gamma \mathbin {\prec } \Delta$ either $S\nvdash \Gamma \mathbin {\preceq } \Delta$ or else $S \vdash \Gamma \mathbin {\preceq } \Delta$. If the former the result follows by the case for $\mathbin {\preceq }$. If the latter, we know by Proposition 10 that $S \cup \{\Delta \mathbin {\preceq } \Gamma \}$ is consistent. Take this to be S ₀ and let T be a witnessed extension of S ₀. Then, by Proposition 15 $\Delta \mathbin {\preceq } \Gamma$ is true in $\mathcal {M}_{T_{\lambda }}$, and hence $\Gamma \mathbin {\prec } \Delta$ is not true in $\mathcal {M}_{T_{\lambda }}$. □

We can finally prove Theorem 4.

Proof

Let S and T be sets of sequents containing no determinates or auxiliaries. Suppose $S \nvdash T$. It follows that there is some Γ ≪Δ∈T such that $S \nvdash \Gamma \mathbin {\ll } \Delta$. Otherwise we would get $S \vdash T$ by Collection. But then S⊮Γ ≪Δ follows from Lemma 5; S⊮T follows. □