Abstract
The system GLS, which is a modal sequent calculus system for the provability logic GL, was introduced by G. Sambin and S. Valentini in Journal of Philosophical Logic, 11(3), 311–342, (1982), and in 12(4), 471–476, (1983), the second author presented a syntactic cut-elimination proof for GLS. In this paper, we will use regress trees (which are related to search trees) in order to present a simpler and more intuitive syntactic cut derivability proof for GLS1, which is a (more connectively and inferentially economical) variant of GLS without the cut rule.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The modal logic GL (for Gödel and Löb) is the logic obtained when we attach to classical propositional logic the two modal axioms
-
A1.
□(A → B) → □A → □B
-
A2.
□(□A → A) → □A
and also the inference rule
(Nec) If A then □A.
Historically, GL was created as an attempt to treat the provability predicate in Peano arithmetic, \(Pr(\ulcorner \cdot \urcorner )\), as a modal operator; and thus the theorems of GL were designed to be provable in Peano arithmetic under any interpretation, ∗, where an interpretation of a propositional formula, A, is a sentence in the language of arithmetic, A ∗, such that (atomic sentence) ∗ is any sentence (except for ⊥∗ which is 0 = 1), ∗ commutes with boolean connectives and \((\Box A)^{*} = Pr(\ulcorner A^{*} \urcorner )\).
Thus, for example, the second axiom, A2, was added due to the fact [4] that \(Pr(\ulcorner Pr(\ulcorner A \urcorner ) \to A \urcorner ) \to Pr(\ulcorner A \urcorner )\) is always provable in Peano arithmetic for every sentence A in the language of arithmetic (where \(\ulcorner A \urcorner \) is the Gödel number of A). Similarly for (Nec) and A1.
The importance of GL lies in the fact that if A is not provable in GL then there exists an interpretation, ∗, such that A ∗ is not provable in Peano arithmetic [7] (thus making GL a provability logic).
In [5], G. Sambin and S. Valentini presented GLS, which (they showed) is a Gentzen-style sequent calculus system corresponding to GL. In the same paper, they proved that, given Γ, Δ, sets of formulas, it is possible to decide whether Γ ⊢ Δ Δ is derivable or not in GLS’ (which is basically equivalent to GLS without the cut rule) by showing that Γ ⊢ Δ must have a finite search tree [3].
In this paper, instead of search trees, we will use similar constructs called regress trees.Footnote 1 A regress tree is, essentially, an attempt to construct a (legal) proof tree for a given sequent; thus, when we want to invert the GLR inference rule then, unlike in search trees, we examine each one of the possible premisses separately—that is, we examine each one in a separate regress tree.
Do note that, for various reasons, the nodes of a regress tree are not sequents but are expressions of the form
 , and are called regressants.Footnote 2
, and are called regressants.Footnote 2
In this paper, we will use regress trees and a regressant-related induction parameter (namely, the height of the regressant’s highest regress tree) in order to present a (complete) syntactic cut-derivability proof for GLS1. This proof, we believe, is simpler and more intuitive than the one presented in [9] or the ones presented in [1] and in [6].Footnote 3
Finally, let us stress that the method of search trees (which can very easily be adapted to regress trees) has been used to obtain decidability and completeness results in numerous logic systems (for example, in [3] and [8]); and indeed, it was used in [5] to show that GL is decidable and complete with respect to finite, transitive and irreflexive Kripke frames. Thus, unlike the methods utilized in the proofs mentioned above, this method is more than just an ad-hoc measure used to obtain a simple cut-derivability result. Moreover, as far as we know, the utilization of regress trees in order to obtain a syntactic cut-derivability proof is a novel approach, which is likely to be helpful in other logics as well.
2 The Systems GLS1 and RGL
First, a few conventions:
-
1.
The formulas in our language (well formed modal formulas) are constructed using ⊥, boolean variables, → and □.
-
2.
Upper case Greek letters such as Γ, Δ, Θ will represent sets of formulas.
-
3.
A formula is called prime if it is atomic or boxed.
-
4.
Γ is atomic (prime) if all the formulas in Γ are atomic (prime).
2.1 The System GLS1
-
(1)
Initial sequents: Γ, ⊥ ⊢ Δ A, Γ ⊢ Δ, A A is prime
-
(2)
\(\to \text {-left}: \frac {\Gamma \vdash {\Delta }, A\phantom {AAAA}B,{\Gamma } \vdash {\Delta }}{\Gamma , A \to B\vdash {\Delta }} \)
-
(3)
\(\to \text {-right}: \frac {\Gamma , A\vdash {\Delta }, B}{\Gamma \vdash {\Delta }, A\to B}\)
-
(4)
\(\perp \text {-right}: \frac {\Gamma , A\vdash {\Delta }}{\Gamma \vdash {\Delta }, A\to \perp } \)
-
(5)
\(\text {-left}: \frac {\Gamma \vdash {\Delta }, A}{\Gamma , A\to \perp \vdash {\Delta }}\)
-
(6)
\(\text {GLR}: \frac {\Gamma , \Box {\Gamma }, \Box A \vdash A}{\Phi , \Box {\Gamma } \vdash \Box A,{\Psi }}\quad \quad \text {(where} {\Phi },{\Psi } \text {are any sets of formulas)}\)
Note:
-
1.
It is straightforward to prove that rules (2)-(5) are invertible; i.e., if the conclusion (denominator) is provable in GLS1 then so is the premiss (numerator).
-
2.
The formulas Φ, Ψ in the GLR rule are called, respectively, the weakening and strengthening formulas of the rule.
-
3.
We can easily prove that weakening and strengthening are derived rules.
-
4.
We do not include a cut rule in our system.
-
5.
Proving cut-derivability for GLS1 is equivalent to proving cut-elimination for GLS.
2.2 The System RGL
Definition 1
-
1.
For any Γ, Δ, we call the expression of the form
 a regressant.
a regressant. -
2.
 is a prime regressant if one of the following applies:
is a prime regressant if one of the following applies:
-
a.
⊥ ∈ Γ.
-
b.
There exists a prime formula, A, such that A ∈ Γ ∩ Δ.
-
c.
Γ is prime and Δ is atomic, ⊥ ∉ Γ and Γ ∩ Δ = ∅.
-
a.
Note that if
 is a prime regressant, then Γ ⊢ Δ is either an initial sequent (cases a. and b.) or it is obviously not derivable in GLS1 since it is not an initial sequent and cannot be the conclusion of any of the inference rules of GLS1 (case c.).
is a prime regressant, then Γ ⊢ Δ is either an initial sequent (cases a. and b.) or it is obviously not derivable in GLS1 since it is not an initial sequent and cannot be the conclusion of any of the inference rules of GLS1 (case c.).
The Rules of Regress:
-
(1)
Primality:
 is a prime regressant
is a prime regressant -
(2)
→ -left:

-
(3)
→ -right:
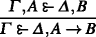
-
(4)
⊥ -right:

-
(5)
⊥-left:

-
(6)
GLR:
 (for all i∈{1,…, n} and such that Φ,Ψ are atomic but the denominator is not a prime regressant). We call □A
i
the p.f. (principle formula) of the rule.
(for all i∈{1,…, n} and such that Φ,Ψ are atomic but the denominator is not a prime regressant). We call □A
i
the p.f. (principle formula) of the rule.
Note that these rules are intended to be applied “upwards” from the denominator to the numerator; thus, for example, we regress
 using rule (3) in order to obtain
using rule (3) in order to obtain
 .
.
Definition 2
A regress tree, T, for a regressant
 is a (graph theoretical) directed rooted tree such that:
is a (graph theoretical) directed rooted tree such that:
-
a).
 is the root of T.
is the root of T. -
b).
If R, a non-prime regressant, is a node in T then it has either exactly one child, R 1, such that \(\frac {R_{1}}{R}\) is a regress rule, or it has exactly two children, R 1, R 2, such that \(\frac {R_{1} \ R_{2}}{R}\) is a regress rule (namely rule (2)).
-
c).
T has no nodes or edges other than those that are required by the previous items.
Thus, for every Γ, Δ we start from the root
 and try to regress it (upwards) until we reach prime regressants, at which point we stop. We call this process the regress process for GLS1.Footnote 4
and try to regress it (upwards) until we reach prime regressants, at which point we stop. We call this process the regress process for GLS1.Footnote 4
This leads us to the following definition:
Definition 3
For every regressant R, we denote by M h (R) as the height of R’s highest regress tree.
The proof in [5] that every search tree in GLS’ is finite can easily be modified to obtain a similar result for search trees in GLS1 (defined analogously). But, since M h (R) is obviously equal to the height of R’s search tree in GLS1, we can immediately deduce that for every regressant R, M h (R)is finite.
The following corollary is readily seen as true:
Corollary 1
If R, R 1 are two regressants such that R 1 is a node in one of R’s regress trees, but not the root, then M h (R 1) < M h (R).
3 Cut Derivability for GLS1
Note that in this section, we will, at times, forgo writing “ Γ ⊢ Δ is derivable in GLS1,” and simply write Γ ⊢ Δ. It will be clear from the context when we use this abbreviation.
Proposition 1
The following two are equivalent for every formula A and any Γ, Δ, Θ, Ω, Φ, Ψ:
-
1.
If Γ ⊢ Δ, A and A, Θ ⊢ Ω then Γ, Θ ⊢ Δ, Ω (cut derivability).
-
2.
If A → A, Φ ⊢ Ψ then Φ ⊢ Ψ.
Proof
The proof is straightforward and therefore is omitted. □
Theorem 1
(Cut-derivability for GLS
1) For any regressant
 and for any formula A, if A → A, Γ ⊢ Δ then Γ ⊢ Δ.
and for any formula A, if A → A, Γ ⊢ Δ then Γ ⊢ Δ.
Proof
By primary induction (P.I.) on the complexity of A and secondary induction (S.I.) on
 .
.
-
Case 1.
A is atomic.
-
I.
 is prime. The only non-immediate case is when Γ is prime and Δ is atomic. By invertibility, we have that Γ ⊢ Δ, A and it must be an initial sequent. Now, if \({\Gamma } \nvdash {\Delta }\) then we must have that A ∈ Γ, but since A, Γ ⊢ Δ we have that Γ ⊢ Δ — contradiction. So Γ ⊢ Δ.
is prime. The only non-immediate case is when Γ is prime and Δ is atomic. By invertibility, we have that Γ ⊢ Δ, A and it must be an initial sequent. Now, if \({\Gamma } \nvdash {\Delta }\) then we must have that A ∈ Γ, but since A, Γ ⊢ Δ we have that Γ ⊢ Δ — contradiction. So Γ ⊢ Δ. -
II.
 is not prime and is the denominator of one of regress rules (2)–(5). For example, let Δ = Δ′, B → C; now, by invertibility, A → A, Γ ⊢ Δ′, B → C implies that A → A, B, Γ ⊢ Δ′, C, and since
is not prime and is the denominator of one of regress rules (2)–(5). For example, let Δ = Δ′, B → C; now, by invertibility, A → A, Γ ⊢ Δ′, B → C implies that A → A, B, Γ ⊢ Δ′, C, and since
 is an application of regress rule (3) we can use the S.I.H. to deduce B, Γ ⊢ Δ′, C. We can now use the (→ -right) inference rule to get Γ ⊢ Δ. The other cases are similar.
is an application of regress rule (3) we can use the S.I.H. to deduce B, Γ ⊢ Δ′, C. We can now use the (→ -right) inference rule to get Γ ⊢ Δ. The other cases are similar. -
III.
The only regress rule applicable is GLR. Then the (derivable) sequent Γ ⊢ Δ, A must be an initial sequent or the conclusion of a GLR inference rule. In the first case it must be because A∈Γ, in the second case A must be a strengthening formula. Both cases imply that Γ ⊢ Δ.
-
I.
-
Case 2.
A = B → C. If (B → C) → (B → C), Γ ⊢ Δ then, by invertibility, we can also derive B → C, Γ ⊢ Δ and Γ ⊢ Δ, B → C; and, again by invertibility, we can derive S 1 = Γ ⊢ Δ, B and S 2 = C, Γ ⊢ Δ and also S 3 = B, Γ ⊢ Δ, C. Now, we can derive S 4 = B → B, Γ ⊢ Δ, C from S 1 and S 3 using the (→ -left) rule;Footnote 5 similarly, we can derive C → C, B → B, Γ ⊢ Δ from S 4 and S 2. We can now apply the P.I.H. twice to get Γ ⊢ Δ.
-
Case 3.
A = □B.
-
I.
 is prime. Again, the only non-immediate case is when Γ is prime and Δ is atomic. Now, □B, Γ ⊢ Δ is derivable and must be an initial sequent, which means that Γ ⊢ Δ is also an initial sequent.
is prime. Again, the only non-immediate case is when Γ is prime and Δ is atomic. Now, □B, Γ ⊢ Δ is derivable and must be an initial sequent, which means that Γ ⊢ Δ is also an initial sequent. -
II.
 is not prime and is the denominator of one of regress rules (2)–(5). Done Similarly to the case where A is atomic.
is not prime and is the denominator of one of regress rules (2)–(5). Done Similarly to the case where A is atomic. -
III.
The only regress rule applicable is GLR. First, we know that Γ, Δ are prime, Δ contains a boxed formula, ⊥ ∉ Γ and Γ ∩ Δ = ∅. We also know that we can prove S = □B, Γ ⊢ Δ and S′ = Γ ⊢ Δ, □B. We can assume that □B ∉ Γ ∪ Δ (otherwise it is immediate). Thus, the only applicable rule in obtaining both S and S′ is GLR.Now, if □B was a weakening or strengthening formula in any one of them we are done. Thus, we may assume we have two proofs ending with: (where Γ = Φ, □ Γ′; Δ = □D, □ Δ′, Ψ and Φ,Ψ are atomic)
$$\frac{{\Gamma}^{\prime},\Box {\Gamma}^{\prime},\Box B \vdash B} {\underbrace{\Phi,\Box{\Gamma}^{\prime} \vdash \Box D,\Box{\Delta}^{\prime},{\Psi},\Box B}\limits_{S^{\prime}}} \quad \frac{B,\Box B,{\Gamma}^{\prime}, \Box {\Gamma}^{\prime}, \Box D \vdash D}{\underbrace{\Box B,{\Phi},\Box{\Gamma}^{\prime} \vdash \Box D,\Box{\Delta}^{\prime},{\Psi}}\limits_{S}} $$Which means we also have proofs ending with:

-
I.
Now, we can obtain S 5 = □B → □B, Γ′, □ Γ′ ⊢ B from S 2 and S 1; we can obtain S 6 = B, □B → □B, Γ′, □ Γ′, □D⊢D from S 2 and S 3, and, finally, we can obtain S 7 = B → B, □B → □B, Γ′, □ Γ′, □D⊢D from S 5 and S 6. We can now apply the P.I.H. to obtain S 8 = □B → □B, Γ′, □Γ′, □D⊢D from S 7.Note that

is an application of the regress rule GLR, thus we can apply the S.I.H. to obtain Γ′, □ Γ′, □D ⊢ D from S 8. Now apply GLR to obtain Γ ⊢ Δ. □
We can now deduce the following:
Corollary 2
The system GLS allows cut-elimination.
Notes
Stemming from one of the meanings of the word “regress,” which is “The reasoning involved when one assumes the conclusion is true and reasons backward to the evidence.”
One reason we use this notation is to avoid confusion with the expression Γ ⊢ Δ which sometimes is a short for “the sequent Γ ⊢ Δ is provable,” which might not be true since Γ,Δ can be any sets of formulas whatsoever. This notation also serves to indicate that the context is of regress trees and not of the (corresponding) Gentzen proof system.
For example, if the root is
 we can use the GLR regress rule to regress it to
we can use the GLR regress rule to regress it to
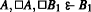 or to regress it to
or to regress it to
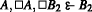 (and therefore
(and therefore
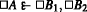 has at least two associated regress trees).
has at least two associated regress trees).Technically, S 1 and S 3 are not in the right form to allow a legal application of the (→ -left) rule; however, they can easily be weakened and strengthened to the right form, thus allowing us to obtain S 4. This remark will apply to all the following instances involving a similar “illegal” use of the (→ -left) rule.
References
Borga, M. (1983). On some proof theoretical properties of the modal logic GL. Studia Logica, 42, 453–459.
Goré, R., & Ramanayake, R. (2008). Valentini’s cut-elimination for provability logic resolved. In Advances in modal logic’08 (pp. 67–86).
Kleene, S.C. (1967). Mathematical Logic. New York: Wiley and Sons.
Löb, M.H. (1955). Solution to a problem of Leon Henkin. Journal of Symbolic Logic, 20, 115–118.
Sambin, G., & Valentini, S. (1982). The modal logic of provability. The sequential approach. Journal of Philosophical Logic, 11(3), 311–342.
Sasaki, K. (2001). Löb’s axiom and cut-elimination theorem. Academia Mathematical Sciences and Information Engineering Nanzan University, 1, 91–98.
Solovay, R. (1976). Provability interpretations of modal logics. Israel Journal of Mathematics, 25, 287–304.
Troelstra, A.S., & Schwichtenberg, H. (2000). Basic proof theory, 2nd Ed. New York, NY, USA: Cambridge University Press.
Valentini, S. (1983). The Modal Logic of Provability: Cut-Elimination. Journal of Philosophical Logic, 12(4), 471–476.
Acknowledgements
I would like to thank David Schwartz for his guidance and great insights.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Brighton, J. Cut Elimination for GLS Using the Terminability of its Regress Process. J Philos Logic 45, 147–153 (2016). https://doi.org/10.1007/s10992-015-9368-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-015-9368-4




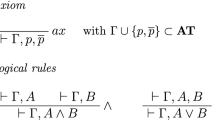
 a regressant.
a regressant. is a prime regressant if one of the following applies:
is a prime regressant if one of the following applies:
 is a prime regressant
is a prime regressant
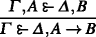


 (for all i∈{1,…, n} and such that Φ,Ψ are atomic but the denominator is not a prime regressant). We call □A
i
the p.f. (principle formula) of the rule.
(for all i∈{1,…, n} and such that Φ,Ψ are atomic but the denominator is not a prime regressant). We call □A
i
the p.f. (principle formula) of the rule. is the root of T.
is the root of T. is prime. The only non-immediate case is when Γ is prime and Δ is atomic. By invertibility, we have that Γ ⊢ Δ, A and it must be an initial sequent. Now, if
is prime. The only non-immediate case is when Γ is prime and Δ is atomic. By invertibility, we have that Γ ⊢ Δ, A and it must be an initial sequent. Now, if  is not prime and is the denominator of one of regress rules (2)–(5). For example, let Δ = Δ′, B → C; now, by invertibility, A → A, Γ ⊢ Δ′, B → C implies that A → A, B, Γ ⊢ Δ′, C, and since
is not prime and is the denominator of one of regress rules (2)–(5). For example, let Δ = Δ′, B → C; now, by invertibility, A → A, Γ ⊢ Δ′, B → C implies that A → A, B, Γ ⊢ Δ′, C, and since
 is an application of regress rule (3) we can use the S.I.H. to deduce B, Γ ⊢ Δ′, C. We can now use the (→ -right) inference rule to get Γ ⊢ Δ. The other cases are similar.
is an application of regress rule (3) we can use the S.I.H. to deduce B, Γ ⊢ Δ′, C. We can now use the (→ -right) inference rule to get Γ ⊢ Δ. The other cases are similar. is prime. Again, the only non-immediate case is when Γ is prime and Δ is atomic. Now, □B, Γ ⊢ Δ is derivable and must be an initial sequent, which means that Γ ⊢ Δ is also an initial sequent.
is prime. Again, the only non-immediate case is when Γ is prime and Δ is atomic. Now, □B, Γ ⊢ Δ is derivable and must be an initial sequent, which means that Γ ⊢ Δ is also an initial sequent. is not prime and is the denominator of one of regress rules (2)–(5). Done Similarly to the case where A is atomic.
is not prime and is the denominator of one of regress rules (2)–(5). Done Similarly to the case where A is atomic.
 we can use the GLR regress rule to regress it to
we can use the GLR regress rule to regress it to
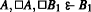 or to regress it to
or to regress it to
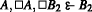 (and therefore
(and therefore
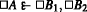 has at least two associated regress trees).
has at least two associated regress trees).