Frailty modelling approaches for semi-competing risks data

Abstract

In the semi-competing risks situation where only a terminal event censors a non-terminal event, observed event times can be correlated. Recently, frailty models with an arbitrary baseline hazard have been studied for the analysis of such semi-competing risks data. However, their maximum likelihood estimator can be substantially biased in the finite samples. In this paper, we propose effective modifications to reduce such bias using the hierarchical likelihood. We also investigate the relationship between marginal and hierarchical likelihood approaches. Simulation results are provided to validate performance of the proposed method. The proposed method is illustrated through analysis of semi-competing risks data from a breast cancer study.

1 Introduction

In clinical studies, we often observe semi-competing risks data (Fine et al. 2001), which involve two-types of events; a non-terminal event (e.g. disease recurrence) and a terminal event (e.g. death). Here, a subject may experience both events that may be dependent (Chen 2012). Thus, several authors have recently studied semi-parametric frailty models for semi-competing risks data (Xu et al. 2010; Zhang et al. 2014; Varadhan et al. 2014; Lee et al. 2015). In particular, Xu et al. (2010) proposed a marginal-likelihood approach under the gamma frailty model. Zhang et al. (2014) and Lee et al. (2015) have proposed Bayesian approaches. However, the marginal likelihood or Bayesian approaches may often involve evaluation of intractable integrals over the frailty distributions, especially for the non-gamma frailties.

Unlike the classical likelihood for fixed parameters only, the hierarchical likelihood (h-likelihood; Lee and Nelder 1996; Lee et al. 2017) is constructed for both fixed parameters and unobserved frailties at the same time. Ha et al. (2001) proposed the h-likelihood for the frailty models where the maximum likelihood (ML) estimator can be substantially biased in the finite samples, particularly for the frailty parameter (Barker and Henderson 2005; Ha et al. 2010). This is because the number of nuisance parameters associated with the baseline hazard function increases with the number of events. In addition, the bias can also occur when the cluster size $n_i$ for subject i is very small such as $n_{i}=1$ or 2 (Ha et al. 2010). Simulation results from Ha et al. (2010) showed that the bias of ML estimator reduces slowly when $n_{i}=1$ or 2 as the sample size (i.e. the number of clusters or subjects) grows.

In this paper, we extend the h-likelihood (Ha et al. 2001) for one shared frailty model to semi-competing risks data. Specifically three shared frailty models are considered to incorporate three states in the semi-competing risks setting; state 0 for on study, state 1 for non-terminal event, and state 2 for terminal event. We treat each subject as a cluster, which would generate realizations of two semi-competing event times. This formulates the semi-competing risks problem into a multivariate survival data setting with cluster size of $n_i=2$. With this small cluster size, therefore, the aforementioned bias problem would still exist when the h-likelihood method is directly applied to this case. To overcome this, we propose a modified estimation procedure of Ha et al. (2001) where the h-likelihoods are constructed to consider the dependency and left-truncation as well as a Markov specification for the terminal event following non-terminal event (multi-state modelling). We also investigate the relationship between marginal likelihood and proposed h-likelihood approaches. In geneal, the h-likelihood method provides efficient statistical inference for various univariate and multivariate survival models (Ha et al. 2017), as well as other statistical models such as generalized linear models with random effects, joint models for different types of responses, and missing or incomplete-data problems, etc. (Lee et al. 2017).

This paper is organized as follows. In Sect. 2 we derive the h-likelihood procedure. We also propose the modifications of likelihoods via the h-likelihood and study their relationships. In Sect. 3, we present simulation studies to assess performance of the proposed method. Section 4 illustrates the proposed method using a real data set from a breast cancer study conducted by the National Surgical Adjuvant Breast and Bowel Project (NSABP) (Fisher et al. 1989, 1996). Section 5 concludes with a discussion. Technical details for the estimation procedures are provided in “Appendix”.

2 Semi-competing risks frailty models and estimation

2.1 The model

Suppose that a subject may experience a terminal event (e.g. death) with or without a non-terminal event (e.g. disease recurrence). Let $T_{i1}$ and $T_{i2}$ be the non-terminal and terminal event times for the ith subject, respectively $(i=1, \ldots , n)$.

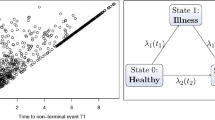
A schematic diagram for semi-competing risks data as shown in Xu et al. (2010) has three states (state 0, on study; state 1, recurrence; state 2, death). To model these three states under semi-competing risks, we consider the following specification of the hazard functions:

$$\begin{aligned} \lambda _{1}(t_1)= & {} \lim _{\Delta t \rightarrow 0} Pr\{t_1 \le T_{1}\le t_1 +\Delta t| T_{1}\ge t_1, T_{2}\ge t_1 \} /{\Delta t},~ t_1>0, \end{aligned}$$

(1)

$$\begin{aligned} \lambda _2(t_2)= & {} \lim _{\Delta t \rightarrow 0} Pr\{t_2 \le T_{2}\le t_2 +\Delta t| T_{1}\ge t_2, T_{2}\ge t_2 \} /{\Delta t},~ t_2>0, \end{aligned}$$

(2)

$$\begin{aligned} \lambda _{12}(t_2|t_1)= & {} \lim _{\Delta t \rightarrow 0} Pr\{t_2 \le T_{2}\le t_2 +\Delta t| T_{1}= t_1, T_{2}\ge t_2 \} /{\Delta t},~ 0<t_1<t_2.\quad \quad \end{aligned}$$

(3)

For $\lambda _{12}(t_2|t_1)$ we assume a Markov process where the transition probability from state 1 to state 2 does not depend on the duration in state 1 (Aalen et al. 2008). That is, we assume

$$\begin{aligned} \lambda _{12}(t_2|t_1)=\lambda _{12}(t_2), 0<t_1<t_2. \end{aligned}$$

(4)

Note that for transition from state 1 to state 2, the left-truncation time is $t_1$, the time at which the recurrence occurred.

Let $x_i$ be a p-dimensional vector of covariates of the ith subject. The classical semi-competing risks model (i.e. illness-death model; Lawless 2003) can be extended to the frailty models which induce the dependency between non-terminal and terminal event times. For simplicity, we consider the semi-competing risks frailty models (Xu et al. 2010) with the common frailty (random effect), denote by $u_i$ for the ith subject. That is, given $u_i$, the conditional hazards functions extended from Eqs. (1)–(3) can be expressed as three shared frailty models

$$\begin{aligned} \lambda _{1i}(t_1|u_i;x_i)= & {} \lambda _{01}(t_1)\exp (x_i^T \beta _1)u_i,~ t_1>0, \end{aligned}$$

(5)

$$\begin{aligned} \lambda _{2i}(t_2|u_i;x_i)= & {} \lambda _{02}(t_2)\exp (x_i^T \beta _2)u_i,~ t_2>0, \end{aligned}$$

(6)

$$\begin{aligned} \lambda _{12i}(t_2|t_1, u_i;x_i)= & {} \lambda _{03}(t_2)\exp (x_i^T \beta _3)u_i,~ 0<t_1<t_2, \end{aligned}$$

(7)

where $\lambda _{01}(\cdot ),\lambda _{02}(\cdot )$ and $\lambda _{03}(\cdot )$ are the unspecified baseline hazard functions and the frailties $u_i$ are assumed to be independent and identically distributed with a density function having a frailty parameter $\alpha$. Recall that from (4) and (7) $\lambda _{12i}(t_2|t_1, u_i;x_i)=\lambda _{12i}(t_2|u_i;x_i)$ depends only on $t_2$ and $u_i$, not $t_{1}$. The common distributions assumed for $u_i$ are gamma and log-normal (Therneau and Grambsch 2000; Ha et al. 2001), where $E(u_i)=1$ and $\mathrm{var}(u_i)=\alpha$ for the gamma frailty model, and $v_i=\log u_i \sim N(0, \alpha )$ for the lognormal one.

2.2 Estimation procedures

Let $C_{i}$ denote the right censoring time for the ith subject $(i=1, \ldots , n)$. If the subject experiences a terminal event before the non-terminal event occurs, we define $T_{i1}=\infty$. Then, for the ith subject we have the following observable data:

$$\begin{aligned} y_{i1}=T_{i1} \wedge y_{i2},~ y_{i2}=T_{i2} \wedge C_{i},~ \delta _{i1}=I(T_{i1} \le y_{i2}) ~\mathrm{and}~ \delta _{i2}=I(T_{i2} \le C_{i}), \end{aligned}$$

where $0 \le y_{i1} \le y_{i2}$.

For the likelihood-based inference, the h-loglikelihood for the semi-competing risks frailty models (5)–(7) is defined by (Ha et al. 2001)

$$\begin{aligned} h=h(\beta , v, \lambda _{0},\alpha )=\sum _{i}\ell _{1i}+\sum _{i}\ell _{2i}, \end{aligned}$$

(8)

where $\ell _{1i}=\ell _{1i}(\beta ,\lambda _{0};y_{i}^{o}|u_{i})$ is the logarithm of the conditional density function for the observed data $y_{i}^{o}=(y_{i1},y_{i2}, \delta _{i1},\delta _{i2})$ given $u_{i}$. Following Xu et al. (2010), we have

$$\begin{aligned} \ell _{1i}= & {} \log \biggl [ \lambda _{1i}(y_{i1}|u_i)^{\delta _{i1}} \lambda _{2i}(y_{i2}|u_i)^{\delta _{i2}(1-\delta _{i1})} \lambda _{12i}(y_{i2}|u_i)^{\delta _{i1} \delta _{i2}} \\&\times \exp \biggl [-\int _0^{y_{i1}} \{\lambda _{1i}(t|u_i) + \lambda _{2i}(t|u_i) \}~ dt \biggl ] \times \exp \biggl \{-\int _{y_{i1}}^{y_{i2}} \lambda _{12i}(t|u_i)~ dt \biggl \} \biggl ] \\= & {} \delta _{i1}\{\log \lambda _{01}(y_{i1})+\eta _{i1}\}+\delta _{i2}(1-\delta _{i1})\{\log \lambda _{02}(y_{i2})+\eta _{i2}\} \\&+\,\delta _{i1}\delta _{i2}\{\log \lambda _{03}(y_{i2})+\eta _{i3}\}\\&-~\{\Lambda _{01}(y_{i1})\exp (\eta _{i1})+\Lambda _{02}(y_{i1})\exp (\eta _{i2})+\Lambda _{03}(y_{i1},y_{i2})\exp (\eta _{i3})\}, \end{aligned}$$

and

$$\begin{aligned} \ell _{2i}=\ell _{2i}(\alpha ; v_{i}) \end{aligned}$$

is the logarithm of the density function of $v_{i}=\log u_i$ with a parameter $\alpha$. Here

$$\begin{aligned} \eta _{i1}=x_i^T \beta _1+v_i, \eta _{i2}=x_i^T \beta _2+v_i ~\mathrm{and}~\eta _{i3}=x_i^T \beta _3+v_i, \end{aligned}$$

$\beta =(\beta _1^T, \beta _2^T, \beta _3^T)^T$ with $\beta _j=(\beta _{j1},\ldots , \beta _{jp})^T$, $v=(v_1,\ldots ,v_n)^T$, and $\lambda _{0}=(\lambda _{01}, \lambda _{02}, \lambda _{03})^T$, and $\Lambda _{03}(s,t)=\Lambda _{03}(t)-\Lambda _{03}(s)$ reflecting the left truncation. We have $\ell _{2i}=\alpha ^{-1}(v_i-u_i)-\log \Gamma (\alpha ^{-1}) -\alpha ^{-1} \log \alpha$ for the gamma frailty, and $\ell _{2i}=-\log (2\pi \alpha )/2-v_{i}^2/(2\alpha )$ for the log-normal frailty. By adding the frailty in the likelihood, the likelihood in (8) can account for the dependency between the non-terminal and terminal events. Unlike a single frailty model studied in Ha et al. (2001), the proposed method focuses on three shared frailty models (5)–(7) for semi-competing risks data.

Note that the functional forms of $\lambda _{0j}~(j=1,2,3)$ from $\sum _{i}\ell _{1i}$ in (8) are unknown. Let $y_{1(1)}, y_{1(2)}, \ldots , y_{1(D_1)}$ be ordered distinct recurrence times with $(\delta _{i1}, \delta _{i2})$=(1, 0) or (1, 1), and $y_{2(1)}, y_{2(2)}, \ldots , y_{2(D_2)}$ be ordered distinct death times without recurrence with $(\delta _{i1}, \delta _{i2})=(0, 1)$, and $y_{3(1)}, y_{3(2)}, \ldots , y_{3(D_3)}$ be ordered distinct death times following recurrence with $(\delta _{i1}, \delta _{i2})=(1, 1)$. Thus, following Fan and Li (2002) and Ha et al. (2011), we approximate the baseline cumulative hazard function $\Lambda _{0j}(t)~(j=1,2,3)$ by a step function with jumps $\lambda _{0jk_j}$ at the observed distinct event times;

$$\begin{aligned} \Lambda _{0j}(t)=\sum _{k_j:y_{j(k_{j})} \le t}\lambda _{0jk_j}~(j=1,2,3), \end{aligned}$$

(9)

where $y_{j(k_{j})}$ is the $k_j$th ($k_j=1,\ldots ,D_j$) smallest distinct event time for each j, and ${\lambda }_{0jk_j}=\lambda _{0j}(y_{j(k_{j})})$. Then $\sum _{i}\ell _{1i}$ in (8) can be rewritten as

$$\begin{aligned} \sum _{i}\ell _{1i}= & {} \sum _{k_1}d_{1(k_1)}\log \lambda _{01k_1}+\sum _{i} \delta _{i1}\eta _{i1}-\sum _{k_1}\lambda _{01k_1} \biggl \{\sum _{~i\in R_{(k_1)}}\exp (\eta _{i1}) \biggl \} \nonumber \\&+ \sum _{k_2}d_{2(k_2)}\log \lambda _{02k_2}+\sum _{i} \delta _{i2}(1-\delta _{i1})\eta _{i2}-\sum _{k_2}\lambda _{02k_2} \biggl \{\sum _{~i\in R_{(k_2)}}\exp (\eta _{i2}) \biggl \} \nonumber \\&+ \sum _{k_3}d_{3(k_3)}\log \lambda _{03k_3}+\sum _{i} \delta _{i1}\delta _{i2}\eta _{i3}-\sum _{k_3}\lambda _{03k_3} \biggl \{\sum _{~i\in R_{(k_3)}}\exp (\eta _{i3}) \biggl \}, \end{aligned}$$

(10)

where $d_{j(k_{j})}$$(j=1,2,3)$ is the number of the events at $y_{j(k_{j})}$, and

$$\begin{aligned} R_{(k_1)}= & {} R(y_{1(k_1)})=\{i:y_{i1}\ge y_{1(k_1)}\}, \\ R_{(k_2)}= & {} R(y_{2(k_2)})=\{i:y_{i1}\ge y_{2(k_2)}\}, {\text{ and }}\\ R_{(k_3)}= & {} R(y_{3(k_3)})=\{i:y_{i1} < y_{3(k_3)}\le y_{i2} \}, \end{aligned}$$

are the risk sets at $y_{1(k_1)}$, $y_{2(k_2)}$ and $y_{3(k_3)}$, respectively. Define $\lambda _{01}=(\lambda _{011}, \ldots , \lambda _{01D_1})^T$, $\lambda _{02}=(\lambda _{021}, \ldots , \lambda _{02D_2})^T$, and $\lambda _{03}=(\lambda _{031}, \ldots , \lambda _{03D_3})^T$. Note that the number of nuisance parameters $\lambda _{0j}$’s can increase with the number of events, which can be viewed as the Neyman-Scott problem (Neyman and Scott 1948; Lee and Nelder 2009). Accordingly, for estimation of $(\beta , v)$, Ha et al. (2001) proposed the use of the profile h-likelihood $h^*=h^*(\beta ,v,\alpha )$, where $\lambda _{0j}$$(j=1,2,3)$ are replaced by their non-parametric estimates as follows:

$$\begin{aligned} h^* = h|_{\lambda _{0j}=\widehat{\lambda }_{0j}}= \sum _{i}\ell ^{*}_{1i}~+~\sum _{i}\ell _{2i}, \end{aligned}$$

where $\ell _{1i}^{*}= \ell _{1i}^{*}(\beta ,v)=\ell _{1i}|_{\lambda _{0j}=\widehat{\lambda }_{0j}}$ and

$$\begin{aligned} \widehat{\lambda }_{0jk_j}(\beta ,v)=\frac{d_{j(k_j)}}{\sum _{~i \in R_{(k_j)}}\exp (\eta _{ij})},~(j=1,2,3) \end{aligned}$$

are the solutions of the estimating equations, $\partial h/\partial \lambda _{0jk_j}=0$, for $k_j=1,\ldots ,D_j$. Now, from (10) we have

$$\begin{aligned} \sum _{i}\ell ^{*}_{1i}= & {} \sum _{k_1}d_{1(k_1)}\log \widehat{\lambda }_{01k_1}+\sum _{i}\delta _{i1}\eta _{i1}-\sum _{k_1}d_{1(k_1)}\\&+\sum _{k_2}d_{2(k_2)}\log \widehat{\lambda }_{02k_2}+\sum _{i} \delta _{i2}(1-\delta _{i1})\eta _{i2}-\sum _{k_2}d_{2(k_2)}\\&+\sum _{k_3}d_{3(k_3)}\log \widehat{\lambda }_{03k_3}+\sum _{i}\delta _{i1} \delta _{i2} \eta _{i3}-\sum _{k_3}d_{3(k_3)}, \end{aligned}$$

which is proportional to the conditional log-partial likelihood $\ell _{p}=\ell _{p}(\beta ,v)$, given by

$$\begin{aligned} \ell _{p}= & {} \sum _{i} \delta _{i1}\eta _{i1} -\sum _{k_1} d_{1(k_1)} \log \biggl \{\sum _{~i \in R_{(k_1)}} \exp (\eta _{i1})\biggl \}\\&+ \sum _{i} \delta _{i2}(1-\delta _{i1})\eta _{i2} -\sum _{k_2} d_{2(k_2)} \log \biggl \{\sum _{~i \in R_{(k_2)}} \exp (\eta _{i2})\biggl \}\\&+ \sum _{i} \delta _{i1} \delta _{i2} \eta _{i3} -\sum _{k_3} d_{3(k_3)} \log \biggl \{\sum _{~i \in R_{(k_3)}} \exp (\eta _{i3})\biggl \} \end{aligned}$$

with the constant terms omitted. This leads to the partial h-likelihood (Ha et al. 2010)

$$\begin{aligned} h_{p}=h_{p}(\beta ,v,\alpha )=\ell _{p}+~\sum _{i}\ell _{2i}, \end{aligned}$$

(11)

which is proportional to the profile h-likelihood $h^{*}$. Thus, once we have $h_{p}$, the h-likelihood method (Ha and Lee 2003; Ha et al. 2010) can be directly extended to the semi-competing risks frailty model. Note that Therneau and Grambsch (2000) and Ripatti and Palmgren (2000) defined a penalized partial likelihood (PPL) by substituting the log-partial likelihood $\ell _{p}$ for $\sum _{i}\ell _{1i}$ in the h-likelihood (8), where $\sum _{i} \ell _{2i}$ was regarded as a penalty term. Our h-likelihood method and their PPL procedure are essentially the same in estimation of $(\beta ,v)$ given $\alpha$, but are different in estimation of $\alpha$ (Ha et al. 2010, 2011).

Specifically, the h-likelihood procedure based on $h_p$ is as follows. Following Ha et al. (2001), given $\alpha$ we estimate $\tau =(\beta ^T, v^T)^T$ by maximizing $h_p$ with respect to $\tau$. The estimating equations for $\tau =(\beta ^T, v^T)^T$ are then in form of

$$\begin{aligned} \partial h_{p}/\partial \tau =(\partial h/\partial \tau )|_{\lambda _0={\widehat{\lambda }}_0}=0, \end{aligned}$$

(12)

where $\lambda _0=(\lambda _{01}^T, \lambda _{02}^T, \lambda _{03}^T)^T$. Note that the asymptotic covariance matrix for ${\widehat{\tau }}-\tau$ is given by the inverse of $H(h_{p}, \tau )=-\partial ^2 h_{p}/\partial \tau ^2$. This asymptotic covariance is constructed along the same lines of work by Lee and Nelder (1996, Section 3.3), which proved that with the h-likelihood h, the inverse of $H(h, \tau )$ is an asymptotic covariance matrix of ${\widehat{\tau }}-\tau$ under the generalized linear models with random effects. By substituting h with $h_p$ given in (11), their asymptotic result can be applied straightforwardly to a class of semiparametric frailty models because the partial h-likelihood $h_p$ does not depend on the nuisance quantities $\lambda _{0}$ (Ha and Lee 2003; Ha et al. 2001, 2017).

Let $\ell =\ell (\theta ,\psi )$ be a likelihood function, either an h-likelihood h or a marginal likelihood m (defined in (15) in Section 2.3), with nuisance parameters $\theta$ and the parameters of interest $\psi$. Here, if $\psi$ is $\alpha$, the nuisance parameters $\theta$ can be either fixed effects $(\beta ,\lambda _{0})$ or random effects v or both. Consider a function $p_{\theta }^{\ell }(\psi )$, defined by

$$\begin{aligned} p_{\theta }^{\ell }(\psi )=\left[ \ell -\frac{1}{2}\log \det \{H(\ell ,\theta )/(2\pi )\}\right] \biggl |_{\theta =\widehat{\theta }}~, \end{aligned}$$

(13)

where $H(\ell ,\theta )=-\partial ^{2}\ell /\partial \theta ^{2}$ is an adjustment term to eliminate $\theta$, and $\widehat{\theta }$ solves $\partial \ell /\partial \theta =0$. The function $p_{\theta }^{\ell }(\psi )$ produces an adjusted profile likelihood for $\psi$ evaluated at $\theta ={\hat{\theta }}$. Following Lee and Nelder (2001) and Ha et al. (2010), we abbreviate $p_{\theta }^{\ell }(\psi )$ in (13) by $p_{\theta }(\ell )$. Next, to estimate the frailty parameter $\alpha$, we use the adjusted profile h-likelihood $p_{\tau }(h_{p})$ (Ha and Lee 2003; Ha et al. 2017), given by

$$\begin{aligned} p_{\tau }(h_{p})=\biggl [h_{p} -\frac{1}{2}\log \det \biggl \{H(h_{p}, \tau )/{(2\pi )} \biggl \} \biggl ] \biggl |_{\tau =\widehat{\tau }}, \end{aligned}$$

where $\widehat{\tau }=\widehat{\tau }(\alpha )=(\widehat{\beta }^T(\alpha ), {\widehat{v}}^T(\alpha ))^T$ and $\widehat{\tau }$ solves $\partial h_{p}/\partial \tau =0$. Thus the estimating equation for $\alpha$ is given by

$$\begin{aligned} \partial p_{\tau }(h_{p})/\partial \alpha =0. \end{aligned}$$

This procedure may work well for the log-normal frailty (Ha et al. 2011), but not for the gamma frailty, so we use the second-order approximation (Lee and Nelder 2001; Lee et al. 2017), defined by

$$\begin{aligned} s_{\beta ,v}(h_p)=p_{\tau }(h_p)-\{F(h_p)/24\}, \end{aligned}$$

where $F(h_p)=\mathrm {tr}[-\{3(\partial ^{4}h_p/\partial v^{4})+ 5(\partial ^{3}h_p/\partial v^{3}) H(h_p,v)^{-1} (\partial ^{3} h_p/\partial v^{3})\}H(h_p; v)^{-2}]|_{v={\widehat{v}}}$. To reduce the computational burden, Ha et al. (2010) used F(h) instead of $F(h_p)$, and Noh and Lee (2007) showed the resulting dispersion-parameter estimators from two restricted likelihoods, $p_{\tau }(h)$ and $p_{v}(h)$, are asymptotically equivalent (Ha et al. 2007). Therefore, we can use

$$\begin{aligned} s_{v}(h_p)= p_{v}(h_p)-\{F(h)/24\}, \end{aligned}$$

(14)

to replace $s_{\beta ,v}(h_p)$ and define

$$\begin{aligned} p_{v}(h_{p})=\left[ h_{p} -\frac{1}{2}\log \det \{H(h_{p},v)/(2\pi )\}\right] \biggl |_{v ={\widehat{v}}}~, \end{aligned}$$

where $H(h_{p},v)=-\partial ^{2} h_{p} /\partial v^{2}$ is an adjustment term to eliminate v and ${\widehat{v}}={\widehat{v}}(\alpha )$ solves $\partial h_{p}/\partial v =0$. In particular, under the gamma frailty F(h) has a simple form,

$$\begin{aligned} F(h)= \sum _i\{-2(\alpha ^{-1}+\delta _{i+})^{-1}\}, \end{aligned}$$

where $\delta _{i+}=\delta _{i1}+\delta _{i2}$.

The classical clustered survival data have a cluster size of $n_{i} \ge 2$, and the bias becomes smaller as $n_i$ increases. In the semi-competing risks setting, however, we consider each cluster contains only two observations for the non-terminal and terminal event times, that is $n_{i}=2$ for all i. Thus, further modifications on the h-likelihood given in the following subsection are necessary for a bias correction.

2.3 Modification of the likelihood

In the standard semi-parametric frailty models, Ha et al. (2010) showed that the ML estimators can be substantially biased in the finite samples. In this section we propose likelihood-based modifications to reduce such biases in the semi-parametric frailty models (5)–(7) under semi-competing risks. We consider a case where parameters of interest are $(\beta ,\alpha )$ and nuisance quantities are $\lambda _{0}$ (fixed parameters) and v (random effects). For inference on $(\beta ,\alpha )$, we need to eliminate the nuisance quantities $(\lambda _{0}, v)$, the dimension of which increase with sample size and number of events. There are typically two ways of eliminating the nuisance parameters using the h-likelihood: one is to integrate v out of the h-likelihood and the other is to profile out $\lambda _{0}$. In this paper, we propose the following two methods to eliminate such nuisance quantities efficiently from the h-likelihood:

Method 1 Eliminate v first and then $\lambda _{0}$,

Method 2 Eliminate $\lambda _{0}$ first and then v.

We now show how to construct the likelihoods depending on the order of the quantities being eliminated. Firstly, in Method 1 we consider the marginal log-likelihood, denoted by m, which can be obtained by integrating out the frailties v from the h-likelihood, i.e.

$$\begin{aligned} m=m(\beta ,\lambda _{0},\alpha )=\sum _{i}\log \biggl \{\int \mathrm {exp} (h_{i})~dv_{i}\biggl \}, \end{aligned}$$

(15)

where $h_{i}=\ell _{1i}~+~\ell _{2i}$ is the contribution of the ith individual to h in (8). Then we construct a profile marginal log-likelihood $m^{*}$ by plugging in the estimates of $\lambda _{0}$, defined by

$$\begin{aligned} m^{*}=m^{*}(\beta ,\alpha ) = m|_{\lambda _{0j}=\widetilde{\lambda }_{0j}}{,} \end{aligned}$$

(16)

where ${\widetilde{\lambda }}_{0jk_j}(\beta ,v),~(j=1,2,3)$ are the solutions of the estimating equations, $\partial m/\partial \lambda _{0jk_j}=0$, for $k_j=1,\ldots ,D_j$. Secondly, in Method 2 we consider the partial h-likelihood $h_p=h_{p}(v,\beta ,\alpha )$ in (11), where $\lambda _{0}$ has been already eliminated by profiling. Thus we can construct a partial marginal log-likelihood $m_p$ (Ha et al. 2010) by integrating out the frailty v from $h_{p}$,

$$\begin{aligned} m_{p}=m_{p}(\beta ,\alpha )=\log \biggl \{\int \mathrm {exp}(h_{p})~dv \biggl \}. \end{aligned}$$

(17)

The marginal log-likelihood m often requires a numerical integration (e.g. for the log-normal frailty) except for the gamma frailty. Note that the resulting ML estimators by maximizing m are equivalent to those by maximizing $m^{*}$. The partial marginal log-likelihood $m_p$ gives a partial ML estimator without finite sample biases (Therneau et al. 2003; Gu et al. 2004) due to an efficient elimination of the nuisance quantities. However, $m_{p}$ is is not easy to use due to intractable integration that does not allow a closed form even with the gamma frailty. Moreover, $m_{p}$ involves high dimensional integration where the dimension increases with the number of frailties (Gu et al. 2004).

As an adequate approximation to $m_{p}$, Ha et al. (2010) proposed to use an adjusted profile marginal likelihood $p_{\omega }(m)$, which was defined as a function of $(\beta ,\alpha )$,

$$\begin{aligned} p_{\omega }(m)=\left[ m-\frac{1}{2}\log \det \{H(m,\omega )/(2\pi )\}\right] \biggl |_{\omega ={\widetilde{\omega }}}~, \end{aligned}$$

(18)

where $\omega =(\omega _{1},\ldots ,\omega _{r})^{T}$ with $\omega _{k}=\log \lambda _{0k}$, $H(m,\omega )=-\partial ^{2}m/\partial \omega ^{2}$ is an adjustment term to eliminate $\lambda _{0}$, and ${\widetilde{\omega }}$ solves $\partial m/\partial \omega =0$. Under the standard gamma frailty models, Ha et al. (2010) showed that as $n^{*}=\mathrm {min}_{1\le i\le q}~{n_{i}}\rightarrow \infty$ for cluster size $n_i$ for subject i,

$$\begin{aligned} p_{\omega }(m) \approx s_{v}(h_p). \end{aligned}$$

Remark 1

For the semi-competing risks models (5)–(7) with gamma frailty, the marginal likelihood has an explicit form. In “Appendix A”, we show that the marginal likelihood procedure is equivalent to that of Xu et al. (2010). In “Appendix B”, we show that given $\alpha$, the h-likelihood and marginal likelihood procedures give the same estimators as in the standard gamma frailty models (Ha et al. 2001; Ha and Lee 2003) and they are compared in terms of the EM, which provides the ML estimators. $\square$

For simplicity, we consider the gamma frailty models for semi-competing risks data where the marginal likelihood m has an explicit form. We have found that $s_{v}(h_p)$ sometimes gives a convergence problem in fitting the semi-competing risks gamma frailty models, particularly for a large $\alpha$ (e.g. $\alpha \ge 1$). To overcome this problem, we further consider a higher-order approximation based on the h-likelihood. Following Tierney and Kadane (1986) and Lee et al. (2017), we can show that with gamma frailty, the fourth-order Laplace approximation (denoted by $m_{v}(h)$) to the marginal likelihood m is given by

$$\begin{aligned} m_{v}(h)=s_{v}(h)-F^{*}(h), \end{aligned}$$

where $s_{v}(h)=p_{v}(h)-F(h)$ is the second-order Laplace approximation to m in (15) and $F^{*}(h) = (1/360)\sum _i (\alpha ^{-1}+\delta _{i+})^{-3}$, which is equivalent to approximating m by the fourth-order Stirling approximation

$$\begin{aligned} \log \Gamma (x)\doteq (x-1/2)\log (x)+\log (2\pi )/2-x+1/(12x)-1/(360x^3). \end{aligned}$$

Accordingly we define a modified h-likelihood based on $h_p$,

$$\begin{aligned} m_{v}(h_p)=s_{v}(h_p)-F^{*}(h), \end{aligned}$$

(19)

where $s_{v}(h_p)$ is a function of $(\beta ,\alpha )$ as is given in (14). The modified h-likelihood $m_{v}(h_p)$ is also a function of $(\beta ,\alpha )$ and is a higher-order approximation to $m_p$ in (17). Note that $s_{v}(h)$ and $s_{v}(h_p)$ are the second-order Laplace approximations to m in (15) and $m_p$ in (17), respectively and that $m_{v}(h)$ and $m_{v}(h_p)$ are the fourth-order Laplace approximations to m and $m_p$, respectively.

The first-order Laplace approximation becomes exact as $n^{*}=\mathrm {min}_{1\le i\le q}~{n_{i}}\rightarrow \infty$. However, it may lead to a serious bias when cluster size $n_{i}$ is small. The second-order approximation generally reduces such bias to some extent (Lee et al. 2017). In the semi-competing risks setting, we suggest an even higher order approximation $m_{v}(h_{p})$ (fourth order) for more effective bias correction.

In summary, we consider four likelihoods for $\psi =(\beta ,\alpha )^T$ constructed by Methods 1 and 2 as follows:

• $m^{*}$ in (16): a profile marginal likelihood by Method 1,

• $p_{\omega }(m)$ in (18) : an adjusted profile marginal likelihood by Method 1,

• $s_{v}(h_{p})$ in (14): the second-order Laplace approximation to $m_p$ by Method 2,

• $m_{v}(h_{p})$ in (19): a modified h-likelihood based on $h_p$ by Method 2,

where the h-likelihood methods have been mainly used in Method 2. Notice that simultaneous eliminations (e.g. $p_{\lambda _{0},v}(h)$) of the nuisance quantities ($\lambda _{0}, v$) may require a heavy computation because the dimension of the corresponding Hessian matrix $H(h, (\lambda _{0}, v))$ increases with sample size and the number of events.

We call the estimators maximizing the marginal likelihoods $m^{*}$ and $p_{\omega }(m)$ the maximum marginal likelihood 1 (MML1) and 2 (MML2) estimators, respectively. It can be shown that with gamma frailty, the MML1 estimator is equivalent to the ML estimator provided by Xu et al. (2010): see “Appendix A” for more details. We also call the estimators maximizing the partial likelihoods $s_{v}(h_{p})$ and $m_{v}(h_{p})$ the maximum partial likelihood 1 (MPL1) and 2 (MPL2) estimators, respectively. Accordingly, the four estimators of $\psi =(\beta ,\alpha )^T$ are summarized as follows:

$$\begin{aligned}&{\mathbf{Method~ 1}}\quad {\hat{\psi }}^{\mathrm{MML1}} =\arg \max _{\psi } m^{*}~~\mathrm{and}~~{\hat{\psi }}^{\mathrm{MML2}} =\arg \max _{\psi } p_{\omega }(m), \\&{\mathbf{Method~ 2}}\quad {\hat{\psi }}^{\mathrm{MPL1}} =\arg \max _{\psi }s_{v}(h_{p})~~\mathrm{and}~~{\hat{\psi }}^{\mathrm{MPL2}} =\arg \max _{\psi } m_{v}(h_{p}). \end{aligned}$$

The fitting algorithm for the four estimation methods is summarized as follows:

• Step 0 Find the initial estimates of $(\beta ,v)$; i.e. take (0,...,0, 0,...,0) as all initial estimates of components of $(\beta ,v)$.

• Step 1 In the inner loop, given $\alpha$, we maximize $h_{p}$ for $\beta$ and v.

• Step 2 In the outer loop, given $\beta$ and v the four likelihoods, $m^{*}$, $p_{\omega }(m)$, $s_{v}(h_p)$ and $m_{v}(h_p)$ are maximized for $\alpha$. A simple grid search method is used to estimate $\alpha$ (Therneau and Grambsch 2000; Ha et al. 2010).

After convergence, we compute the estimated standard errors of ${\hat{\beta }}$ from the inverse of the observed information, $-\partial ^2 h_{p}/\partial \tau ^2$, in (12).

3 Simulation study

We have performed simulation studies to assess the finite sample performance of the proposed estimation methods, MML2, MPL1 and MPL2, in comparison with the MML1 method developed by Xu et al. (2010).

We generated data under the semi-competing risks frailty models (5)–(7) as follows: (i) generate the common frailty $u_i$ from a gamma distribution with mean 1 and variance $\alpha =0.5$ or 1.0, and (ii) given the frailty, generate two event times $t_{i1}$ and $t_{i2}$ independently from the proportional hazards models (5) and (6), i.e.

$$\begin{aligned} \lambda _{1i}(t_1|u_i;x_i)=\lambda _{01}(t_{1})\exp (x_i^{T} \beta _1)u_i ~~\mathrm{and}~~ \lambda _{2i}(t_2|u_i;x_i)=\lambda _{02}(t_{2})\exp (x_i^{T} \beta _2)u_i , \end{aligned}$$

respectively, and (iii) the transition time $t_{i2}^{*}$ is generated based on the transition model from state 1 to state 2 in the form of

$$\begin{aligned} \lambda _{12i}(t_2|u_i;x_i)=\lambda _{03}(t_{2})\exp (x_i^{T} \beta _3)u_i{.} \end{aligned}$$

First, we consider a single covariate case where $x_{i}=x_{i1}$, which follows the standard normal distribution, for $i=1,\ldots , n$. The baseline hazard rates are set to be $\lambda _{01}(t_{1})=\lambda _{02}(t_{2})=1, \lambda _{03}(t_{2})=2$, and the regression coefficients to be $\beta _1=\beta _2=\beta _3=0.5$.

We evaluate the proposed methods under two scenarios with fixed and random censoring times, denoted by $c_i$, as follows:

• (i) Scenario 1$c_{i}$ is fixed as the duration of the follow-up, $c_{i}=3$, yielding a censoring rate ranging from 40% to 60% for the non-terminal event time $y_{i1}$ and 10% to 30% for terminal event time $y_{i2}$, and

• (ii) Scenario 2$c_{i}$ is randomly generated from a 50-50 mixture of a uniform distribution on interval (1.5, 3) and a degenerate distribution concentrated at 3, according to the censoring scheme used in Xu et al. (2010), resulting in the similar ranges of censoring rates for $y_{i1}$ and $y_{i2}$ as in Scenario 1.

Table 1 Simulation results under Scenario 1 with fixed censoring time

We considered various sample sizes of $n=100, 250$ and 500, and implemented 200 replications for each simulation setting. Simulation results from different methods are reported in terms of percentage of relative bias (%rbias) and mean squared error (MSE) for ${\hat{\alpha }}$ and ${\hat{\beta }}=({\hat{\beta }}_1, {\hat{\beta }}_2, {\hat{\beta }}_3)^T$. Based on 200 replications, we also computed the standard deviation (SD) and the mean of the estimated standard errors (SE) for ${\hat{\beta }}$. The SEs were obtained from the inverse of the observed information, $-\partial ^2 h_{p}/\partial \tau ^2$, in (12). The results are presented in Tables 1, 2 for Scenario 1 and Tables 3, 4 for Scenario 2.

From Table 1, we find that the relative biases of the proposed MML2, MPL1 and MPL2 estimates are smaller than those of the MML1 estimates in most of the settings. The MML1 method exhibits non-negligible biases in estimating the parameters, especially for the frailty parameter $\alpha$, which confirms the simulation results in Ha et al. (2010) for the standard gamma frailty models. Table 2 shows that the proposed SEs are generally slightly underestimated as compared to the SDs. The similar findings are observed in Scenario 2 under the random censoring scheme, as shown in Tables 3, 4.

In Tables 1 and 3, the existing MML1 method gives somewhat smaller MSEs compared to other three methods (MML2, MPL1 and MPL2), especially when the frailty parameter $\alpha$ is as small as $\alpha =0.5$, possibly due to underestimation of $\alpha$ by the MML1 method. It is worth noting that the proposed MPL2 estimation outperforms all the other proposed methods in terms of the MSE when the frailty parameter $\alpha$ is as large as $\alpha =1$. This advantage might be from a reduced number of tied observations under Scenario 2 and improvememt in bias correction of the MPL2 estimation using the higher-order approximation (19) to a modified marginal likelihood $m_p$ as described in Sect. 2.

Table 2 Simulation results for comparison between estimated standard error (SE) and sample standard deviation (SD) for $\beta$ under Scenario 1 with fixed censoring

Table 3 Simulation results under Scenario 2 with random censoring

Table 4 Simulation results for comparison between estimated standard error (SE) and sample standard deviation (SD) for $\beta$ under Scenario 2 with random censoring

We have conducted further simulations to assess performance of the proposed estimation methods when there are multiple covariates in each transition model. The simulation scheme is the same as before, except that three additional covariates were considered in each model, that is, $x_i=(x_{i1}, x_{i2}, x_{i3})^T$, where $x_{i1}$ and $x_{i2}$ follow the standard normal distribution, $x_{i3}$ follows a Bernoulli(0.5) distribution, for $i=1,\ldots , n$. The corresponding coefficients were set to be $\beta _1=(\beta _{11},\beta _{12},\beta _{13})=(0.5,0.5,-0.5)$, $\beta _2=(\beta _{21},\beta _{22},\beta _{23})=(0.5,0.5,-0.5)$ and $\beta _3=(\beta _{31}, \beta _{32},\beta _{33})=(1,1,-1)$.

Again, we consider the following two scenarios with fixed and random censoring times $c_i$:

• (i) Scenario 3$c_{i}$ is fixed as the duration of the follow-up, $c_{i}=3$, which yields a censoring rate ranging from 50% to 60% for the non-terminal event time $y_{i1}$ and 20% to 30% for terminal event time $y_{i2}$, and

• (ii) Scenario 4$c_{i}$ is randomly generated from a 50-50 mixture of a uniform distribution on interval (1.5, 3) and a degenerate distribution concentrated at 3, resulting in the similar ranges of censoring rates for $y_{i1}$ and $y_{i2}$ as in Scenario 3.

Simulation results based on 200 replications over different values of $\alpha$ (frailty variance) are presented in the Supplementary Material, where Tables S1-S4 are under Scenario 3 and Tables S5-S8 under Scenario 4. From Tables S1-S2, we can see that the relative biases of the proposed MML2, MPL1 and MPL2 estimates are smaller than those of the MML1 estimates under all settings. The MML1 method exhibits non-negligible biases in the parameter estimates, especially for the frailty parameter $\alpha$. These results confirm the simulation results from Ha et al. (2010) for the standard gamma frailty models. Tables S3-S4 show that the proposed estimated standard errors are closer to their corresponding sample SDs compared to the SEs for the MML1 estimator in most cases, implying that the estimated SEs for the proposed estimators work more effectively than that for MML1 estimator.

The similar observations can be made from Tables S5-S8 under Scenario 4 with a random censoring scheme. From Tables S1, S2, S5 and S6, we find that all of those four methods produce comparable estimation for $\beta$ in terms of the MSEs, while the MPL2 method slightly outperforms the other methods in estimating $\alpha$. Overall, the above findings indicate that the performance of the proposed estimators is sustainable for the semi-competing risks models with multiple covariates.

Remark 2

Our simulation experience indicates all of these four methods may encounter a convergence problem, caused by a monotone likelihood (Heinze and Schemper, 2001) as shown in the Cox’s PH model. For example, the plot of the profile likelihood $m^{*}$ against $\alpha$ shows a monotone function as in Ha et al. (2017, pp. 79). We have observed that the MML1 method ($m^{*}$) has a serious convergence problem for a small sample case (e.g. $n=100$ with $(q,n_i)=(50,2)$), while the other three methods, i.e. MML2, MPL1 and MPL2, generally overcome such problems. In particular, the MPL2 method converges most of the time except for a few cases with a small sample size (e.g. $n=100$ with $(q,n_i)=(50,2)$), leading to a bias reduction.

4 A practical example

For an illustration, we consider a data set from the B-14 phase III breast cancer clinical trial conducted by the National Surgical Adjuvant Breast and Bowel Project (NSABP, Fisher et al. 1989, 1996). Total 2572 eligible patients were followed up for five years since randomization. Patients were randomized to one of two treatment arms, tamoxifen (1278 patients) or placebo (1294 patients). The patients’ median age was 56 (range 25–75) and their average tumor size was about 2.2 cm.

The aim of this analysis is to investigate the effect of a hormonal treatment on a cancer recurrence and/or death, considering three event types. Type 1 is breast cancer recurrence, Type 2 is death without recurrence, and Type 3 is death after recurrence. Table 5 gives the observed numbers of event types in this data set. Here 180 patients (7.00%) experienced Type 1, 535 patients (20.80%) did Type 2, 540 patients (21.00%) did Type 3, and the remaining 1317 patients (51.21%) had no events. Table 5 also shows the numbers of observed event types by treatment arm.

Table 5 Observed event types by two treatment arms ($n=2{,}572$ patients)

In this analysis, we consider three covariates of interest: treatment ($x_{i1}=1$ for tamoxifen and 0 for placebo), tumor size ($x_{i2}$) and age ($x_{i3}$). We first apply the naive transition model (5)–(7) without a frailty and then one with the gamma frailty. For estimation under the gamma frailty model, we use four likelihood methods (MML1, MML2, MPL1 and MPL2) as in the simulation study. The fitted results are listed in Table 6. The results from the naive model and frailty models using the four likelihood methods are very similar because the frailty-parameter estimates are all very small (${\hat{\alpha }}=0.087$ for MPL1, ${\hat{\alpha }}=0.090$ for MPL2, ${\hat{\alpha }}=0.059$ for MML1 and ${\hat{\alpha }}=0.085$ for MML2). Moreover, to test the frailty effect $H_0: \alpha \equiv \mathrm{var}(u_i)=0$ which is on the boundary of the parameter space, an asymptotic null distribution of the likelihood ratio test follows a 50:50 chi-square mixture, denoted by $\chi _{0:1}^2$ (Self and Liang 1987; Stram and Lee 1994; Ha et al. 2011) with its critical value equal to $\chi _{1,0.1}^2 = 2.71$ at a 5% significance level. Let $\ell _{B}$ be the Breslow’s log-likelihood (1974) for the naive model above, i.e. $u_{i}=1$ for all i in the gamma frailty model with (5)–(7), defined by (Lee and Nelder 1996)

$$\begin{aligned} \ell _{B}=\lim _{\alpha \rightarrow 0} s_{v}(h_{p}). \end{aligned}$$

The difference between the likelihood functions from the naive model and frailty model (MPL1) is $2\{s_v(h_{p})-\ell _{B}\}=0.7 (< 2.71)$, indicating that the frailty effect is not significant. The marginal likelihood method (MML1) also gives $2\{m^{*}-\ell _{B}\}=0.4$.

In Table 6, the treatment effect $(x_1)$ is significant for time to recurrence and time to death after recurrence, but not for time to death without recurrence. For time to death without recurrence, the sign of treatment effect is positive, which may be explained from the fact that more patients died without cancer recurrence in the tamoxifen group (293/535) than the placebo group (242/535). We also see that the use of tamoxifen significantly reduces breast cancer recurrence (Type 1), but it is not beneficial in death after recurrence (Type 3). In terms of the other covariates, the age effect $(x_{2})$ is very significant for event types 1 and 2. The effect of tumor size $(x_{3})$ is positively significant for all three event types, implying that the event rate is significantly higher among patients whose tumor sizes were larger at surgery.

Table 6 Fitted results from the semi-competing risks models for NSABP B-14 data

Next we restricted the data analysis only to older patients (1,776 patients with age $\ge 50$). The results are summarized in Table 7. Here we present the results only from three methods (MPL2, MML1 and MML2) because the MPL1 method did not converge. We find that the frailty parameter estimates are all larger compared to those in Table 5. The likelihood difference from the naive model is $2\{m_v(h_{p})-\ell _{B} \}=9.8 > 2.71$, indicating that the frailty effect is significantly large, i.e. $\alpha >0$. The difference between the naive and profile marginal likelihoods also gives $2\{m^{*}-\ell _{B} \}=9.3$, selecting the frailty model again. Thus, the results from the naive and frailty models are expected to be somewhat different. The treatment effects are overall similar to those in Table 6 even though their signs in the frailty model have changed for time to death without recurrence in Table 7. However, for time to death without recurrence and time to death after recurrence, the tumor size effect is not significant in the naive model, whereas it is in the frailty model.

In addition, we also considered older patients only (484 patients with age $\ge 65$). The results are also summarized in Table 7. In particular, we find that the MML1 estimate for $\alpha$$({\hat{\alpha }}=0.482)$ is somewhat smaller compared to other two methods (${\hat{\alpha }}=1.021$ from MPL2 and ${\hat{\alpha }}=1.238$ from MML2), which was also demonstrated in the simulation study. This underestimation is also reflected in the likelihood ratio test for $H_0: \alpha =0$. That is, the likelihood difference is $2\{m^{*}-\ell _{B} \}=1.5 < 2.71$, whereas $2\{m_v(h_{p})-\ell _{B} \}=4.3 > 2.71$ and $2\{p_{\omega }(m)-\ell _{B} \}=4.4 > 2.71$. This implies that the MPL2 and MML2 methods are sensitive enough to detect the significance of the frailty effect, but the MML1 method does not. We also observe that the sign of tumor-size effect is negative from the MML1 method, but becomes positive in the MPL2 and MML2 methods.

Table 7 Fitted results from the semi-competing risks models for older patients in the NSABP B-14 data

5 Discussion

We have shown how to eliminate nuisance quantities from the h-likelihood and thus how to find effective modifications (MML2, MPL1 and MPL2) to reduce the bias of the maximum likelihood estimators (MML1). In general, the adjusted profile marginal likelihood ($p_{\omega }(m)$) is hard to use because an explicit form of the marginal likelihood (m) is not available. For the models such as the lognormal frailty or with correlated frailties, we recommend using the modified likelihoods, $s_{v}(h_{p})$ or $m_{v}(h_{p})$, based on the partial h-likelihood $h_{p}$. This implies that elimination of the nuisance quantities by Method 2 proposed in Sect. 2.3 is practically effective. Based on our experience in numerical studies in the current and previous work for the frailty models, the proposed h-likelihood based methods (i.e. the modified likelihood approaches using $s_{v}(h_{p})$ or $m_{v}(h_{p})$) often provide estimators with smaller biases than that from the marginal likelihood method. Theoretical justification of this property as inquired by a referee would merit future research.

Section 3 presents simulation results for the parameters of interest $(\alpha , \beta )$ only, while the estimates of the nuisance parameters, i.e. three baseline cumulative hazards $\Lambda _{01}(t), \Lambda _{02}(t)$ and $\Lambda _{03}(t)$, are excluded. In fact, even though our simulations also included estimation of those three functions, their estimates from all of the four methods tends to be biased as the time t increases, yet had only minimal impact on the estimation of $(\alpha , \beta )$. It would be worth a further investigation to improve the accuracy of the baseline cumulative hazard estimates.

For modelling the semi-competing risks data, we used a shared frailty in three transition models. Extension to a model, where the transitions are affected by differnt frailties that are correlated, would be an interesting further work. Furthermore, we have assumed a Markov process for such transitions, but comparison with a semi-Markov assumption, i.e. $\lambda _{12}(t_{2}|t_{1})=\lambda _{12}(t_{2} -t_{1})$, may be also interesting. The marginal likelihood may involve evaluation of analytically intractable integrals over the frailty distribution (e.g. log-normal distribution), whereas the h-likelihood obviates such integration. Extension of the proposed h-likelihood method to general frailty distributions including the log-normal distribution would be also an interesting future topic.

Appendix

1.1 Appendix A: Marginal-likelihood estimation procedure

For gamma frailty models with $E(u_{i})=1$ and var$(u_{i})=\alpha$, we have an explicit marginal likelihood as follows. Since the second term of h-likelihood in (8) under the gamma frailty is given by

$$\begin{aligned} \ell _{2i}=\ell _{2i}(\alpha ; v_{i})=\alpha ^{-1}(v_i-u_i) +c(\alpha ), \end{aligned}$$

with $c(\alpha )=-\log \Gamma (\alpha ^{-1}) -\alpha ^{-1} \log \alpha$, from (8) and (15) we have that

$$\begin{aligned} m= & {} \sum _{i} [\delta _{i1} \{\log \lambda _{01}(y_{i1}) + x_{i}^T\beta _1 \} + \delta _{i2} (1-\delta _{i1}) \{\log \lambda _{02}(y_{i2})+ x_i^T\beta _2 \}\nonumber \\&+~ \delta _{i1} \delta _{i2} \{\log \lambda _{03}(y_{i2}) + x_i^T \beta _3\}]\nonumber \\&-\sum _{i}[(\alpha ^{-1}+~\delta _{i+})\log (1+\alpha \mu _{i+}) -\log \{\alpha ^{\delta _{i+}} \Gamma (\alpha ^{-1}+\delta _{i+} )/\Gamma (\alpha ^{-1})\} ]\nonumber \\= & {} \sum _{k_1}d_{1(k_1)}\log \lambda _{01k_1}+\sum _{i} \delta _{i1}(x_i^T\beta _1) + \sum _{k_2}d_{2(k_2)}\log \lambda _{02k_2}\nonumber \\&+\sum _{i} \delta _{i2}(1-\delta _{i1})(x_i^T\beta _2) + \sum _{k_3}d_{3(k_3)}\log \lambda _{03k_3}+\sum _{i} \delta _{i1}\delta _{i2}(x_i^T\beta _3)\nonumber \\&-\sum _{i}[(\alpha ^{-1}+~\delta _{i+})\log (1+\alpha \mu _{i+}) -\delta _{i1}\delta _{i2} \log (1+\alpha )], \end{aligned}$$

(A.1)

where $\delta _{i+}= \delta _{i1} + \delta _{i2}$ and $\mu _{i+}=\sum _{j=1}^{3} \mu _{ij}$ with

$$\begin{aligned} \mu _{i1}= & {} \Lambda _{01}(y_{i1})\exp (x_{i}^T \beta _1)=\sum _{k_1} \lambda _{01k_1} I(y_{1(k_{1})} \le y_{i1}) \exp (x_i^T \beta _1),\\ \mu _{i2}= & {} \Lambda _{02}(y_{i2})\exp (x_{i}^T \beta _2)=\sum _{k_2} \lambda _{02k_2} I(y_{2(k_{2})} \le y_{i1}) \exp (x_i^T \beta _2),\\ \mu _{i3}= & {} \Lambda _{03}(y_{i1}, y_{i2})\exp (x_{i}^T \beta _3) =\sum _{k_3} \lambda _{03k_3} I(y_{i1} < y_{3(k_3)}\le y_{i2} ) \exp (x_i^T \beta _3). \end{aligned}$$

In fact, the marginal likelihood (A.1) is the same as that of Xu et al. (2010).

Under the gamma frailty, the score equations for $\beta$ are given by

$$\begin{aligned} \frac{\partial m}{\partial \beta _1}= & {} \sum _i \biggl \{ \delta _{i1}- \biggl (\frac{\alpha ^{-1} + \delta _{i+}}{\alpha ^{-1} + \mu _{i+}} \biggl ) \mu _{i1} \biggl \} x_i, \end{aligned}$$

(A.2)

$$\begin{aligned} \frac{\partial m}{\partial \beta _2}= & {} \sum _i \biggl \{ \delta _{i2}(1-\delta _{i1})- \biggl (\frac{\alpha ^{-1} + \delta _{i+}}{\alpha ^{-1} + \mu _{i+}} \biggl ) \mu _{i2} \biggl \} x_i, \end{aligned}$$

(A.3)

$$\begin{aligned} \frac{\partial m}{\partial \beta _3}= & {} \sum _i \biggl \{ \delta _{i1}\delta _{i2}- \biggl (\frac{\alpha ^{-1} + \delta _{i+}}{\alpha ^{-1} + \mu _{i+}} \biggl ) \mu _{i3} \biggl \} x_i. \end{aligned}$$

(A.4)

In particular, the solutions of $\partial m/\partial \lambda _{0jk_j}=0~(j=1,2,3)$ lead to closed forms:

$$\begin{aligned} {\widetilde{\lambda }}_{0jk_j}(\beta ,\alpha )=\frac{d_{j(k_j)}}{\sum _{~i \in R_{(k_j)}}\exp (x_i^T \beta _j){\tilde{u}}_i}, \end{aligned}$$

(A.5)

where ${\tilde{u}}_i=(\alpha ^{-1}+\delta _{i+})/(\alpha ^{-1}+\mu _{i+})$. We see that the score equations of $(\beta , \lambda _{0j})$ in (A.2)–(A.4) and (A.5) are extensions of those in the shared gamma frailty models (Andersen et al. 1997). Finally, the score equation for the frailty parameter $\alpha$ is given by

$$\begin{aligned} \frac{\partial m}{\partial \alpha }=\sum _i \biggl \{ \delta _{i1}\delta _{i2} (1+\alpha )^{-1} +\alpha ^{-2}\log (1+\alpha \mu _{i+}) -(\alpha ^{-1} +\delta _{i+})\mu _{i+} (1+\alpha \mu _{i+})^{-1} \biggl \}. \end{aligned}$$

Then the estimates of fixed parameters $(\beta ,\alpha , \lambda _{0})$ can be obtained using a numerical iterative method such as the Newton-Raphson method. Note that the maximum likelihood estimating equations, $\partial m/\partial (\beta ,\alpha , \lambda _{0})=0$, by Xu et al. (2010) are equivalent to $\partial m^{*}/\partial (\beta ,\alpha )=0$, where $m^{*}$ is the profile marginal likelihood in (16).

1.2 Appendix B: Comparison of h-likelihood with marginal likelihood

We assume that $\alpha$ is known. Recall that given $(\beta , v)$, the score equations $\partial h/\partial \lambda _{0jk_j}=0~(j=1,2,3)$ provide the non-parametric maximum h-likelihood estimators in Sect. 2.2, i.e.

$$\begin{aligned} \widehat{\lambda }_{0jk_j}(\beta ,v)=\frac{d_{j(k_j)}}{\sum _{~i \in R_{(k_j)}}\exp (x_i^T \beta _j)u_i}. \end{aligned}$$

The maximum h-likelihood estimating equations for $\beta$, under the gamma frailty, become

$$\begin{aligned} \frac{\partial h}{\partial \beta _1} \left| _{{\lambda _{01}={\widehat{\lambda }}_{01}} }\frac{}{} \right.= & {} \sum _i \biggl \{ \delta _{i1}- \mu _{i1}u_i \biggl \} x_i \left| _{{\lambda _{01}={\widehat{\lambda }}_{01}} }=0\frac{}{} \right. , \end{aligned}$$

(B.1)

$$\begin{aligned} \frac{\partial h}{\partial \beta _2}\left| _{{\lambda _{02}={\widehat{\lambda }}_{02}} }\frac{}{} \right.= & {} \sum _i \biggl \{ \delta _{i2}(1-\delta _{i1})-\mu _{i2} u_i \biggl \} x_i \left| _{{\lambda _{02}={\widehat{\lambda }}_{02}} }=0\frac{}{} \right. , \end{aligned}$$

(B.2)

$$\begin{aligned} \frac{\partial h}{\partial \beta _3}\left| _{{\lambda _{03}={\widehat{\lambda }}_{03}} }\frac{}{} \right.= & {} \sum _i \biggl \{ \delta _{i1}\delta _{i2}- \mu _{i3}u_i \biggl \} x_i \left| _{{\lambda _{03}={\widehat{\lambda }}_{03}} }=0\frac{}{} \right. . \end{aligned}$$

(B.3)

From

$$\begin{aligned} \frac{\partial h}{\partial v_i}= (\delta _{i+}-\mu _{i+}u_i) +\alpha ^{-1} -\alpha ^{-1}u_i=0, \end{aligned}$$

we have that

$$\begin{aligned} {\hat{u}}_i=\frac{\alpha ^{-1}+\delta _{i+}}{\alpha ^{-1}+\mu _{i+}}, \end{aligned}$$

(B.4)

which also becomes $E(u_i|y_i^o)$ because the conditional distribution of $u_i$ given the observed data $y_i^o=(y_{i1}, y_{i2}, \delta _{i1}, \delta _{i2})$ is gamma. Here $\delta _{i+}=\delta _{i1}+\delta _{i2}$ and $\mu _{i+}=\mu _{i1} +\mu _{i2}+\mu _{i3}$. From (12) we see that the estimating Eqs. (B.1)–(B.3) with (B.4) are equivalent to the estimating Eqs. (A.2)–(A.4) with (A.5), given by

$$\begin{aligned} \frac{\partial m}{\partial \beta _1} \left| _{{\lambda _{01}={{\widetilde{\lambda }}}_{01}} }\frac{}{} \right.= & {} \sum _i \biggl \{ \delta _{i1}- \mu _{i1} \biggl (\frac{\alpha ^{-1} + \delta _{i+}}{\alpha ^{-1} + \mu _{i+}} \biggl ) \biggl \} x_i,\left| _{{\lambda _{01}={{\widetilde{\lambda }}}_{01}} }=0\frac{}{} \right. \end{aligned}$$

(B.5)

$$\begin{aligned} \frac{\partial m}{\partial \beta _2} \left| _{{\lambda _{02}={{\widetilde{\lambda }}}_{02}} }\frac{}{} \right.= & {} \sum _i \biggl \{ \delta _{i2}(1-\delta _{i1})- \mu _{i2} \biggl (\frac{\alpha ^{-1} + \delta _{i+}}{\alpha ^{-1} + \mu _{i+}} \biggl ) \biggl \} x_i,\left| _{{\lambda _{02}={{\widetilde{\lambda }}}_{02}} }=0\frac{}{} \right. \quad \quad \end{aligned}$$

(B.6)

$$\begin{aligned} \frac{\partial m}{\partial \beta _3} \left| _{{\lambda _{03}={{\widetilde{\lambda }}}_{03}} }\frac{}{} \right.= & {} \sum _i \biggl \{ \delta _{i1}\delta _{i2}- \mu _{i3} \biggl (\frac{\alpha ^{-1} + \delta _{i+}}{\alpha ^{-1} + \mu _{i+}} \biggl ) \biggl \} x_i,\left| _{{\lambda _{03}={{\widetilde{\lambda }}}_{03}} }=0\frac{}{} \right. . \end{aligned}$$

(B.7)

Accordingly, the maximum h-likelihood (MHL) estimator for $\beta$ given $\alpha$ is the same as the marginal maximum likelihood (ML) estimator as shown in the standard gamma frailty models (Ha et al. 2001; Ha and Lee 2003). Note, however, that both methods give different estimators for $\alpha$.

The marginal likelihood does not often have an analytic form (e.g. log-normal frailty model), so that the natural approach to the maximum likelihood estimator (MLE) is to use the EM treating the random effects as missing data. Below we present the comparison of the proposed h-likelihood method with the EM method for obtaining the MLE. The EM equations for fixed parameters $\theta$ can be expressed via the h-likelihood as follows:

$$\begin{aligned} E(\partial h/\partial \theta \vert \mathrm{data})=0, \end{aligned}$$

which is equivalent to the ML equations, i.e. $\partial m/\partial \theta =0$ (Lee and Nelder 1996; Engel and Keen 1996; Ha et al. 2001).

In the semi-competing risks frailty models (5)–(7), the EM equations for $(\beta ,\alpha )$ are given by

$$\begin{aligned} E\left( \partial h/\partial (\beta ,\alpha ) \vert ~y_i^{o},{{\widetilde{\lambda }}}_{0jk_j}^{*} \right) =0. \end{aligned}$$

Here, the EM equations of the baseline hazards $\lambda _{0jk_j}$ are given by

$$\begin{aligned} E(\partial h/\partial \lambda _{0jk_j} |~y_i^{o} )=0, \end{aligned}$$

which lead to

$$\begin{aligned} {\widetilde{\lambda }}_{0jk_j}^{*}(\beta ,v)=\frac{d_{j(k_j)}}{\sum _{~i \in R_{(k_j)}}\exp (x_i^T \beta _j) E(u_{i} |y_i^{o}) }. \end{aligned}$$

Following Ha et al. (2001), in the gamma frailty models, given $\alpha$ the MHL equations for $\beta$

$$\begin{aligned} \partial h_{p}/\partial \beta =(\partial h/\partial \beta )|_{\lambda _0={\widehat{\lambda }}_0}=0{,} \end{aligned}$$

with (B.4) are equivalent to the EM equations

$$\begin{aligned} E(\partial h/\partial \beta \vert ~y_i^{o},{{\widetilde{\lambda }}}_{0jk_j}^{*} )=0{,} \end{aligned}$$

since $E(u_{i} |y_i^{o})$ becomes ${\tilde{u}}_{i}$ in (A.5) and thus ${{\widetilde{\lambda }}}_{0jk_j}^{*}$ is identical to ${\tilde{\lambda }}_{0jk_j}$ in (A.5) as well as to ${\widehat{\lambda }}_{0jk_j}$. However, in general the EM may be difficult to apply because the conditional distribution of $u_{i}$ given $y_i^{o}$ is not trivial to be evaluated. For example, in the log-normal frailty with $v_{i}=\log u_{i} \sim N(0, \alpha )$, the EM equation for $\beta _1$ is given by

$$\begin{aligned} E\left( \partial h/\partial \beta _{1} \vert ~y_i^{o},{{\widetilde{\lambda }}}_{0jk_j}^{*}\right) = \sum _i \biggl \{ \delta _{i1}- {{\widetilde{\mu }}}_{i1}^{*} E(u_i|y_{i}^{o}) \biggl \} x_i =0, \end{aligned}$$

where

$$\begin{aligned} {\widetilde{\mu }}_{i1}^{*}={\widetilde{\Lambda }}_{01}^{*}(y_{i1})\exp (x_{i}^T \beta _1)=\sum _{k_1} {\widetilde{\lambda }}_{01k_1}^{*} I(y_{1(k_{1})} \le y_{i1}) \exp (x_i^T \beta _1). \end{aligned}$$

Note here that the computation of $E(u_i|y_{i}^{o})$ requires a numerical integration.