1 Introduction

In survival data, the goal is to model the time until the occurrence of an event of interest. In the general theory, it is assumed that an element is always susceptible to a certain event of interest that will eventually occur. However, such an assumption is often invalid because many databases have what we call immune elements. For immune elements, the event will never occur because they are not susceptible to the event of interest.

Thus, the study of the proportion of this population, or rather, the cure fraction, became one of the major subfields of survival analysis. To solve such problems (Berkson and Gage 1952), based on the work of (Boag 1949), a standard mixture model was proposed. The survival function is adjusted to

$$\begin{aligned} \displaystyle S(t)=p+(1-p) S_0(t) \end{aligned}$$

such that \( S_0(t) \) is a proper survival function. In this way, \( S(t) \) converges to \( p \) as the time goes by. Berkson and Gage (1952) analyzed a stomach cancer data set using the standard mixture model. Since then many other data sets have been analyzed using the standard mixture model. The most common choices for \( S_0 (t) \) have been the Weibull, log-logistic and lognormal distributions. Recently, different distributions have been proposed for this purpose, see Yakovlev and Tsodikov (1996), Chen et al. (1999) and Ibrahim et al. (2005).

However, here we use an alternative methodology based on defective models, a concept introduced by Balka et al. (2009). In these models it is possible to estimate a cure rate with the use of a naturally improper distribution. Instead of estimating the proportion \(p\) directly as a mixture model, we use a distribution by changing the domain of its parameters. It becomes a model with long-term duration. The integral of the density function does not result in \(1\), but in a value \( p \in (0,1) \). This is because the parameters of the distribution are no longer in their original domains. The cumulative distribution function no longer approaches to \(1\), but to \( p \) and, therefore, the survival function approaches to \( 1-p \). Models that have this characteristic are called defective.

Obviously, the defective distribution is not proper. When used as a model for cure fraction, the proportion of the population that is immune is obtained by calculating the limit of the survival function with the estimated parameters. In the literature, there are two known distributions that can be used for this purpose: the inverse Gaussian and Gompertz distributions. The Gompertz distribution has two parameters, both positive. For negative values of the shape parameter, the distribution becomes defective. Haybittle (1959) fitted the Gompertz distribution to a breast cancer data set. Cantor and Shuster (1992) fitted a modified version of the same distribution to a pediatric cancer data set. Gieser et al. (1998) extended the distribution to include covariates.

The inverse Gaussian distribution is another distribution which can take a defective form. The inverse Gaussian distribution was derived by Schrödinger (1915) by calculating the probability of the first time passage of a one-dimensional Brownian process (also called Wiener process). A deeper study was made by Tweedie (1945). It is also where the name inverse Gaussian arose (Balka et al. 2009).

Application of survival models in terms of stochastic processes can be found in Whitmore et al. (1998), Lee and Whitmore (2004) and Lee and Whitmore (2006). Aalen and Gjessing (2001) suggested that more attention be given to these type of models. Whitmore (1979) used the inverse Gaussian distribution in its defective form. More concise studies from the point of view of survival analysis were presented in Balka et al. (2009) and Balka et al. (2011). Several scenarios involving the inverse Gaussian distribution as a cure fraction model were presented. Balka et al. (2011) presented real data applications with classical and Bayesian inferences.

The great advantage of the defective models compared to the standard mixture model is that the former have one less parameter to be estimated in the likelihood function, which can be quite relevant in terms of estimation, especially when the chosen models already have various parameters.

The aim of this paper is to propose two new defective distributions based on the Marshall–Olkin family of distributions (Marshall and Olkin 1997). This family is obtained by adding an extra parameter to a known distribution. Suppose \(S(t)\) is a known survival function. Then, the extended survival function by the Marshall–Olkin family, \(S^*(t) \), is

$$\begin{aligned} \displaystyle S^*(t)=\frac{\displaystyle rS(t)}{\displaystyle 1-(1-r)S(t)} \end{aligned}$$

for \( r>0 \) and \( t\in {\mathbb {R}}\). Simple algebraic manipulations determine the density function of the extended distribution:

$$\begin{aligned} \displaystyle f^*(t)=\frac{\displaystyle rf(t)}{\displaystyle \left[ 1 - (1-r)S(t) \right] ^2}. \end{aligned}$$
(1)

The Marshall–Olkin extension for particular choices of \(S (t)\) has been investigated by several authors, see Alice and Jose (2003), Alice and Jose (2005), Jose and Krishna (2011) and Cordeiro and Lemonte (2013). Barreto-Souza et al. (2013) investigated mathematical properties of the Marshall–Olkin family.

The main purpose of this paper is to propose two new defective distributions, extending the Gompertz and inverse Gaussian distributions through the Marshall–Olkin family. The details of these extensions including maximum likelihood estimation and the fact that \(S^*\) is defective if \(S\) is defective are shown in Sect. 2. Section 3 is a simulation study to assess the performance of the maximum likelihood estimators. Section 4 illustrates the proposed distributions using three real data sets.

2 Methodology

The Gompertz distribution is used for modeling survival data in various areas of knowledge (Gieser et al. 1998), especially where there is a suspicion of exponential hazard. The Gompertz density function is

$$\begin{aligned} \displaystyle f(t)=be^{at}e^{-\frac{b}{a} \left( e^{at}-1\right) } \end{aligned}$$
(2)

for \(a>0, b>0\) and \(t>0\). In this parameterization, \(a \) is the shape parameter and \( b \) is the location parameter. The survival function is

$$\begin{aligned} \displaystyle S(t)=e^{-\frac{b}{a} \left( e^{at}-1\right) }. \end{aligned}$$
(3)

The defective Gompertz distribution is the distribution that allows for negative values for the parameter \( a \). The proportion of immunity in the population is calculated as the limit of the survival function when \( a <0 \):

$$\begin{aligned} \displaystyle p=\lim _{t\rightarrow \infty }S(t)=\lim _{t\rightarrow \infty }e^{-\frac{b}{a} \left( e^{at}-1\right) }=e^\frac{b}{a} \in (0,1). \end{aligned}$$
Fig. 1
figure 1

Density, survival and hazard functions of the defective Gompertz distribution

Full size image

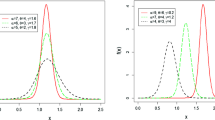
Once the parameter values are estimated, one can easily compute the fraction of cure \(p\). Figure 1 illustrates various scenarios for the density, survival and hazard functions of the Gompertz distribution.

The inverse Gaussian distribution arises as the first passage time of a Wiener process (Balka et al. 2009). Lee and Whitmore (2006) noted its potential as models for cure rate. Its density function is

$$\begin{aligned} \displaystyle f(t)=\frac{\displaystyle 1}{\displaystyle \sqrt{2b\pi t^3}}\exp \left\{ -\frac{1}{2b t}\left( 1-at\right) ^2\right\} \end{aligned}$$
(4)

for \(a>0, b>0\) and \( t>0 \). The inverse Gaussian distribution has survival function given by

$$\begin{aligned} \displaystyle S(t)=1-\left[ \varPhi \left( \frac{\displaystyle -1+a t}{\displaystyle \sqrt{b t}} \right) + e^{2a/b}\varPhi \left( \frac{\displaystyle -1-a t}{\displaystyle \sqrt{b t}} \right) \right] , \end{aligned}$$
(5)

where \(\varPhi (\cdot )\) denotes the cumulative distribution function of a standard normal random variable.

The inverse Gaussian distribution can be defective when \( a<0\). The fraction of cure, or the survival function limit, is

$$\begin{aligned} \displaystyle p=\lim _{t\rightarrow \infty } S(t)= & {} \lim _{t\rightarrow \infty } 1-\left[ \varPhi \left( \frac{\displaystyle -1+a t}{\displaystyle \sqrt{b t}} \right) + e^{2a/b}\varPhi \left( \frac{\displaystyle -1-a t}{\displaystyle \sqrt{b t}} \right) \right] \\= & {} 1-e^{2a/b}\in (0,1). \end{aligned}$$
Fig. 2
figure 2

Density, survival and hazard functions of the defective inverse Gaussian distribution

Full size image

We estimate the cure fraction using the estimated parameters \( a \) and \( b \). Figure 2 illustrates various scenarios for the density, survival and hazard functions of the inverse Gaussian distribution.

The great advantage of these distributions is that the proportion of cured is always estimated using a model with one parameter less than the standard mixture model, which brings plenty of benefits in terms of estimation.

We have been able to find only these two distributions (Gompertz and inverse Gaussian) that can be adapted to being defective. This does not mean there are not others. In order to construct other distributions of this kind, we propose the use of the Marshall–Olkin class (Marshall and Olkin 1997) to generalize a given distribution by adding an extra parameter.

The main result of this paper is that if a given distribution is defective, then its extension under the Marshall–Olkin family will be defective as well.

Theorem 1

If \(S (t)\) is defective then \(S^{*}(t)\) is also defective.

Proof

Suppose the limit of \( S (t) \) is equal to \(p_0 \in (0, 1)\). Then

$$\begin{aligned} \displaystyle \lim _{t\rightarrow \infty }S^*(t)=\lim _{t\rightarrow \infty } \frac{\displaystyle r S(t)}{\displaystyle 1-(1-r)S(t)}= \frac{\displaystyle r p_0}{\displaystyle 1-(1-r)p_0}=\frac{\displaystyle rp_0}{\displaystyle rp_0+1-p_0}. \end{aligned}$$
(6)

Since \(1-p_0\) is positive, it is easy to see that the last expression in (6) takes a value in \( (0,1) \). The proof is complete. \(\square \)

We propose now two new defective distributions: the Marshall–Olkin Gompertz and Marshall–Olkin inverse Gaussian distributions.

2.1 The Marshall–Olkin Gompertz distribution

Using (1) with density function in (2) and survival function in (3), we obtain the Marshall–Olkin Gompertz density function

$$\begin{aligned} \displaystyle f(t)=\frac{\displaystyle b\cdot r\cdot \exp \left( {\frac{b-b \exp (a t)}{a}+a t}\right) }{\displaystyle \left[ r-(r-1) \exp \left( {\frac{b-b \exp (at)}{a}}\right) \right] ^2} \end{aligned}$$
(7)

for \( a>0 , b>0 , r>0 \) and \( t>0 \). The corresponding survival function is

$$\begin{aligned} \displaystyle S(t)=\frac{\displaystyle r \exp \left[ {-\frac{b}{a} \left( \exp (at)-1\right) }\right] }{\displaystyle 1-(1-r) \exp \left[ {-\frac{b}{a} \left( \exp (at)-1\right) }\right] }. \end{aligned}$$
(8)
Fig. 3
figure 3

Density, survival and hazard functions of the defective Marshall–Olkin Gompertz distribution

Full size image

Figure 3 illustrates various scenarios for the density, survival and hazard functions of the Marshall–Olkin Gompertz distribution. As in the Gompertz distribution, if \(a <0\) then the Marshall–Olkin Gompertz distribution is defective. Its cure fraction is

$$\begin{aligned} \displaystyle \lim _{t\rightarrow \infty }S(t)=\lim _{t\rightarrow \infty } 1-\frac{\displaystyle 1}{\displaystyle r e^{\frac{b \left( e^{a t}-1\right) }{a}}-r+1}= \frac{\displaystyle r p_0}{\displaystyle 1-(1-r)p_0} =\frac{\displaystyle rp_0}{\displaystyle rp_0+1-p_0} =p, \end{aligned}$$

where \( p_0 \) is the cure fraction of the defective Gompertz distribution.

2.2 The Marshall–Olkin inverse Gaussian distribution

Using (1) with density and survival functions of the inverse Gaussian distribution given by (4) and (5), respectively, we obtain the density function of the Marshall–Olkin inverse Gaussian distribution as

$$\begin{aligned} \displaystyle f(t)=\frac{\displaystyle r \exp \left( {-\frac{(a t-1)^2}{2 b t}}\right) }{\displaystyle \sqrt{2 \pi } \sqrt{b t^3} \left[ (r-1) \varPhi \left( \frac{a t-1}{\sqrt{b t}}\right) + (r-1) e^{\frac{2 a}{b}} \varPhi \left( -\frac{a t+1}{\displaystyle \sqrt{b t}}\right) -r\right] ^2}\quad \quad \quad \end{aligned}$$
(9)

for \( a>0 , b>0 \) and \( r>0 \). The corresponding survival function is

$$\begin{aligned} \displaystyle S(t)=\frac{r\left[ 1- \varPhi \left( \frac{\displaystyle -1+a t}{\displaystyle \sqrt{b t}} \right) - e^{2a/b}\varPhi \left( \frac{\displaystyle -1-a t}{\displaystyle \sqrt{b t}} \right) \right] }{1-(1-r)\left[ 1- \varPhi \left( \frac{\displaystyle -1+a t}{\displaystyle \sqrt{b t}} \right) - e^{2a/b}\varPhi \left( \frac{\displaystyle -1-a t}{\displaystyle \sqrt{b t}} \right) \right] }. \end{aligned}$$
(10)
Fig. 4
figure 4

Density, survival and hazard functions of the defective Marshall–Olkin inverse Gaussian distribution

Full size image

Figure 4 illustrates various scenarios for the density, survival and hazard functions of the Marshall–Olkin inverse Gaussian distribution. As in the inverse Gaussian distribution, if \( a <0\) then the Marshall–Olkin inverse Gaussian distribution is also defective. Its cure fraction is

$$\begin{aligned} \displaystyle \lim _{t\rightarrow \infty }S(t)=\frac{\displaystyle rp_0}{\displaystyle rp_0 + 1-p_0}=p, \end{aligned}$$

where \( p_0 \) is the cure fraction of the defective inverse Gaussian distribution.

2.3 Inference

Consider a data set \(\mathbf{D} = \left( \mathbf{t}, {\varvec{\delta }} \right) \), where \(\mathbf{t} = \left( t_1, \ldots , t_n \right) ^T \) are the observed failure times and \({\varvec{\delta }} = \left( \delta _1, \ldots , \delta _n \right) ^T \) are the censored failure times. The \(\delta _i\) is equal to \(1\) if a failure is observed and \(0\) otherwise.

Suppose that the data are independently and identically distributed and come from a distribution with density and survival functions specified by \(f \left( \cdot , {\varvec{\theta }} \right) \) and \(S \left( \cdot , {\varvec{\theta }} \right) \), respectively, where \({\varvec{\theta }} = \left( \theta _1, \ldots , \theta _q \right) ^T\) denotes a vector of parameters. The likelihood function of \({\varvec{\theta }}\) can be written as (see Klein and Moeschberger 2003)

$$\begin{aligned} \displaystyle L \left( {\varvec{\theta }}, \mathbf{D} \right) \propto \prod _{i=1}^n \left[ f \left( t_i, {\varvec{\theta }} \right) ^{\delta _i} S \left( t_i, {\varvec{\theta }} \right) ^{1 - \delta _i} \right] . \end{aligned}$$

The corresponding log-likelihood function is

$$\begin{aligned} \displaystyle \log L \left( {\varvec{\theta }}, \mathbf{D} \right) = \mathrm{const } + \sum _{i=1}^n \delta _i \log f \left( t_i, {\varvec{\theta }} \right) + \sum _{i = 1}^n \left( 1 - \delta _i \right) \log S \left( t_i, {\varvec{\theta }} \right) . \end{aligned}$$

For the Marshall–Olkin Gompertz distribution given by (7) and (8),

$$\begin{aligned} \displaystyle \log L \left( {\varvec{\theta }}, \mathbf{D} \right)= & {} \displaystyle \mathrm{const } + \sum ^n_{i=1}\delta _i\left[ \log \left( b r \exp \left( {\frac{b-b \exp (a t)}{a}+a t}\right) \right) \right] \nonumber \\&-\sum ^n_{i=1}\delta _i\left[ \log \left( \left[ r-(r-1) \exp \left( {\frac{b-b \exp (at)}{a}}\right) \right] ^2 \right) \right] \nonumber \\&\displaystyle +\sum ^n_{i=1} \left( 1 - \delta _i \right) \left[ \log \left( r \exp \left[ {-\frac{b}{a} \left( \exp (at)-1\right) }\right] \right) \right] \nonumber \\&-\sum ^n_{i=1} \left( 1 - \delta _i \right) \left[ \log \left( 1-(1-r) \exp \left[ {-\frac{b}{a} \left( \exp (at)-1\right) }\right] \right) \right] .\quad \quad \quad \end{aligned}$$
(11)

For the Marshall–Olkin inverse Gaussian distribution given by (9) and (10),

$$\begin{aligned} \displaystyle \log L \left( {\varvec{\theta }}, \mathbf{D} \right)= & {} \displaystyle \mathrm{const } + \sum ^n_{i=1} \delta _i \log \left( r \exp \left( -\frac{(a t-1)^2}{2 b t} \right) \right) \nonumber \\&\displaystyle -\sum ^n_{i=1}\delta _i \log \left( \sqrt{b t^3} \left[ (r-1) \varPhi \left( \frac{a t-1}{\sqrt{b t}}\right) \right. \right. \nonumber \\&\left. \left. +(r-1) e^{\frac{2 a}{b}} \varPhi \left( -\frac{a t+1}{\displaystyle \sqrt{b t}}\right) -r\right] ^2 \right) \nonumber \\&\displaystyle +\sum ^n_{i=1} \left( 1 - \delta _i \right) \log \left( r \left[ \varPhi \left( \frac{a t-1}{\sqrt{b t}}\right) +e^{\frac{2 a}{b}} \varPhi \left( -\frac{a t+1}{\sqrt{b t}}\right) -1\right] \right) \nonumber \\&\displaystyle -\sum ^n_{i=1} \left( 1 - \delta _i \right) \log \left( -(r-1) \varPhi \left( \frac{a t-1}{\sqrt{b t}}\right) \right. \nonumber \\&+(r-1) e^{\frac{2 a}{b}} \left. \left( \varPhi \left( \frac{a t+1}{\sqrt{b t}}\right) +1\right) -1 \right) . \end{aligned}$$
(12)

The log likelihoods, (11) and (12), can be maximized numerically to obtain the maximum likelihood estimates. There are various routines available for numerical maximization. We used the routine optim in the R software (R Core Team 2014). Numerical calculations not reported here showed that the surfaces of (11) and (12) were smooth. The routine optim was able to locate the maximum for a wide range of starting values. The solution for the maximum was unique for all starting values. In the simulations and real data applications presented in Sects. 3 and 4, the routine optim converged all the time, giving unique maximum likelihood estimates. In all cases considered, optim did not take more than five seconds for convergence.

Confidence intervals for the parameters were based on asymptotic normality. If \(\widehat{\varvec{\theta }}\) denotes the maximum likelihood estimator of \({\varvec{\theta }}\) then it is well known that the distribution of \(\widehat{\varvec{\theta }} - {\varvec{\theta }}\) can be approximated by a \(q\)-variate normal distribution (where \(q\) denotes the length of the vector \({\varvec{\theta }}\) as defined above) with zero means and covariance matrix \(\mathbf{I} \left( \widehat{\varvec{\theta }} \right) \), where \(\mathbf{I} \left( {\varvec{\theta }} \right) \) denotes the observed information matrix defined by

$$\begin{aligned} \displaystyle \mathbf{I} \left( {\varvec{\theta }} \right) = -\left( \begin{array}{llll} \displaystyle \frac{\displaystyle \partial ^2 \log L}{\displaystyle \partial \theta _1^2} &{} \quad \displaystyle \frac{\displaystyle \partial ^2 \log L}{\displaystyle \partial \theta _1 \partial \theta _2} &{} \quad \cdots &{} \quad \displaystyle \frac{\displaystyle \partial ^2 \log L}{\displaystyle \partial \theta _1 \partial \theta _q}\\ \displaystyle \frac{\displaystyle \partial ^2 \log L}{\displaystyle \partial \theta _2 \partial \theta _1} &{} \quad \displaystyle \frac{\displaystyle \partial ^2 \log L}{\displaystyle \partial \theta _2^2} &{} \quad \cdots &{} \quad \displaystyle \frac{\displaystyle \partial ^2 \log L}{\displaystyle \partial \theta _2 \partial \theta _q}\\ \displaystyle \vdots &{} \quad \vdots &{} \quad \ddots &{} \quad \vdots \\ \displaystyle \frac{\displaystyle \partial ^2 \log L}{\displaystyle \partial \theta _q \partial \theta _1} &{} \quad \displaystyle \frac{\displaystyle \partial ^2 \log L}{\displaystyle \partial \theta _q \partial \theta _2} &{} \quad \cdots &{} \quad \displaystyle \frac{\displaystyle \partial ^2 \log L}{\displaystyle \partial \theta _q^2} \end{array} \right) . \end{aligned}$$

So, an approximate \(100 (1 - \alpha )\) percent confidence interval for \(\theta _i\) is \(\left( \widehat{\theta _i} - z_{\alpha / 2} \sqrt{I^{ii}}, \widehat{\theta _i} + z_{\alpha / 2} \sqrt{I^{ii}} \right) \), where \(I^{ii}\) denotes the \(i\)th diagonal element of the inverse of \(\mathbf{I}\) and \(z_a\) denotes the \(100 (1 - a)\) percentile of a standard normal random variable.

We have supposed the usual asymptotes of the maximum likelihood estimates hold. However, defective distributions like the mixture model are not proper distributions. The checking of regularity conditions for the asymptotes by analytical means is not easy. Such conditions have not been checked even for the standard mixture model. We suggest analytical checking of the regularity conditions as a possible future work.

In the next section, we perform an extensive simulation study partly to check the asymptotes of the maximum likelihood estimates. Simulations have been used in many papers to assess the behavior of maximum likelihood estimates, especially when an analytical investigation is intractable.

3 Simulation study

Here, we perform three simulation experiments. The first one is to assess the performance of the maximum likelihood estimates with respect to sample size. The second one is a comparison of defective and mixture models in terms of AIC and cure rate estimates when the data were generated from a defective model. The third one is the same as the second one, but the data were generated from a mixture model. All computations were performed in R Core Team (2014).

Consider that the time of occurrence of an event of interest has cumulative distribution function \(F(t)\). Suppose we want to simulate a random sample of size \(n\) containing real times, censored times and a cure fraction of \(p\). An algorithm to generate data from the defective model is:

  1. 1.

    Determine the desired parameter values, as well as the value of the cure fraction \(p\);

  2. 2.

    Generate \( M_i \sim \) Bernoulli \((1 - p)\);

  3. 3.

    If \( M_i=0 \) set \( t'_i=\infty \). If \( M_i=1 \) take \( t'_i \) as the root of \(F(t) = u\), where \(u \sim \) uniform \((0, 1 - p)\);

  4. 4.

    Generate \(u'_i \sim \) uniform\(\left( 0, \max \left( t_i \right) \right) \), considering only the finite \( t_i\);

  5. 5.

    Calculate \(t_i = \min \left( t'_i, u'_i \right) \). If \( t_i<u'_i \) set \(\delta _i = 1\), otherwise set \(\delta _i=0\).

In this first experiment, we simulated one thousand random samples each of size \(n = 20, 40, \ldots , 1000\). The random samples were taken to come from (i) the Marshall–Olkin Gompertz distribution with \((a, b, r, p) = (-3, 4, 2, 0.4172)\); (ii) the Marshall–Olkin inverse Gaussian distribution with \((a, b, r, p) = (-2, 10, 2, 0.4958)\). We computed the maximum likelihood estimates, \(\widehat{a}, \widehat{b}, \widehat{r}\) and \(\widehat{p}\), and their standard errors for each sample. These were used to compute the bias, the mean squared error, the coverage probability and the coverage length of \(\widehat{a}, \widehat{b}, \widehat{r}\) and \(\widehat{p}\) for each \(n\).

Figures 5 and 6 show the plots of the mean squared errors, the biases, the coverage probabilities and the coverage lengths of \(\left( \widehat{a}, \widehat{b}, \widehat{r}, \widehat{p} \right) \) versus \(n\) for simulated data from the Marshall–Olkin Gompertz and Marshall–Olkin inverse Gaussian distributions.

Fig. 5
figure 5

Mean squared errors, biases, coverage probabilities and coverage lengths of \(\left( \widehat{a}, \widehat{b}, \widehat{r}, \widehat{p} \right) \) versus \(n\) for simulated data from the Marshall–Olkin Gompertz distribution with \((a,b,r,p) = (-3, 4, 2, 0.4172)\)

Full size image
Fig. 6
figure 6

Mean squared errors, biases, coverage probabilities and coverage lengths of \(\left( \widehat{a}, \widehat{b}, \widehat{r}, \widehat{p} \right) \) versus \(n\) for simulated data from the Marshall–Olkin inverse Gaussian distribution with \((a,b,r,p) = (-2, 10, 2, 0.4958)\)

Full size image

We can observe the following from the figures: (i) the mean squared errors for all parameters generally decrease to zero with increasing \(n\); (ii) the mean squared errors for all parameters appear reasonably close to zero for all \(n \ge 600\); (iii) the mean squared errors appear smallest for the parameter, \(p\); (iv) the mean squared errors appear largest for the parameters, \(b\) and \(r\); (v) the biases for all parameters generally approach zero with increasing \(n\); (vi) the biases for all parameters appear reasonably close to zero for all \(n \ge 600\); (vii) the biases appear generally negative for the parameter, \(a\); (viii) the biases appear generally positive for the parameter, \(r\); (ix) the biases appear smallest for the parameter, \(p\); (x) the coverage probabilities for all parameters generally approach the nominal level with increasing \(n\); (xi) the coverage probabilities for all parameters appear reasonably close to the nominal level for all \(n \ge 800\); (xii) the coverage probabilities appear furthest from the nominal level for the parameter, \(r\); (xiii) the coverage lengths for all parameters generally decrease with increasing \(n\); (xiv) the coverage lengths appear smallest for the parameter, \(p\); (xv) the coverage lengths appear largest for the parameters, \(b\) and \(r\).

These observations are for the Marshall–Olkin Gompertz distribution with \((a, b, r, p) = (-3, 4, 2, 0.4172)\) and for the Marshall–Olkin inverse Gaussian distribution with \((a, b, r, p) = (-2, 10, 2, 0.4958)\). But many of the observations were the same when the simulations were repeated for a wide range other values of \((a, b, r, p)\) for both the Marshall–Olkin Gompertz and Marshall–Olkin inverse Gaussian distributions.

We also noted that the decrease in coverage lengths with increasing \(n\) was slow. Indeed, some of the coverage lengths in Figs. 5 and 6 do appear large even for a sample of size \(200\). Some of the confidence intervals reported in Sect. 4 appear large too. This suggests a very large sample size may be needed in order to have reliable interval estimates. It is comforting however two of the three real data sets considered in Sect. 4 have sizes over one thousand.

Fig. 7
figure 7

In the left, the plotted line represents the difference between the AIC values obtained under the Marshall–Olkin Gompertz mixture and defective models, when the data were generated from a defective model. In the right, the corresponding estimates of \(p\)

Full size image
Fig. 8
figure 8

In the left, the plotted line represents the difference between the AIC values obtained under the Marshall–Olkin inverse Gaussian mixture and defective models, when the data were generated from a defective model. In the right, the corresponding estimates of \(p\)

Full size image

The second experiment is to compare the performance of the defective models versus their respective mixture models when the data were generated from defective models. The Marshall–Olkin Gompertz and Marshall–Olkin inverse Gaussian defective distributions were simulated using \((a, b, r, p) = (-3, 4, 2, 0.4172)\) and \((a, b, r, p) = (-2, 10, 2, 0.4958)\), respectively. They were compared to the corresponding mixture versions. Figures 7 and 8 (left) provide a comparison in terms of the AIC. The black line represents the difference between the AIC of the mixture model and that of the defective model. The difference is positive for all samples sizes, meaning that the AIC of the defective model is always smaller. On average, the AIC of the defective model is 1.7704 smaller than the AIC of the mixture model for the Marshall–Olkin Gompertz distribution. On average, the AIC of the defective model is 1.0865 smaller for the Marshall–Olkin inverse Gaussian distribution.

Figures 7 and 8 (right) compare the cure rate estimates for mixture and defective models. We have not compared other parameters since they do not directly relate to the proposed distributions. The estimates of \(p\) under both models appear good for the Marshall–Olkin Gompertz distribution, see Fig. 7. The quadratic error sum for the defective model is 0.00130 and that for the mixture model is 0.00049. This gives a slight advantage for the mixture model. The estimates of \(p\) under the defective and mixture models appear good also for the Marshall–Olkin inverse Gaussian distribution, see Fig. 8. The quadratic error sum for the defective model is 0.00256 and that for the mixture model is 0.00727. Again a small difference but now in favour of the defective model.

Fig. 9
figure 9

In the left, the plotted line represents the difference between the AIC values obtained under the Marshall–Olkin Gompertz mixture and defective models, when the data were generated from a mixture model. In the right, the corresponding estimates of \(p\)

Full size image
Fig. 10
figure 10

In the left, the plotted line represents the difference between the AIC values obtained under the Marshall–Olkin inverse Gaussian mixture and defective models, when the data were generated from a mixture model. In the right, the corresponding estimates of \(p\)

Full size image

The third and the last experiment is to compare the performance of the defective models versus their respective mixture models when the data were generated from mixture models. Mixture versions of the Marshall–Olkin Gompertz and Marshall–Olkin inverse Gaussian distributions were simulated using \( (a,b,r,p)=(0.2,0.2,0.2,0.5) \) and \( (a,b,r,p)=(2,2,0.5,0.5) \), respectively. They were compared to the corresponding defective versions. Figures 9 and 10 (left) compare the models in terms of the AIC. The black line again represents the difference between the AIC of the mixture model and that of the defective model. The differences decrease as \(n\) increases for the Marshall–Olkin Gompertz distribution and become less than zero only when \(n > 960\), see Fig. 9. The differences appear positive for all sample sizes for the Marshall–Olkin inverse Gaussian distribution, see Fig. 10. On average, the AIC of the defective model is 0.8196 smaller than the AIC of the mixture model for the Marshall–Olkin Gompertz distribution. On average, the AIC of the defective model is 0.7511 smaller for the Marshall–Olkin inverse Gaussian distribution.

Figures 9 and 10 (right) compare the cure rate estimates for mixture and defective models. The estimates of \(p\) under both models appear good for both Marshall–Olkin Gompertz and Marshall–Olkin inverse Gaussian distributions. The quadratic error sums for the defective and mixture models are 0.00715 and 0.00782, respectively, for the Marshall–Olkin Gompertz distribution. The quadratic error sums for the defective and mixture models are 0.00288 and 0.00302, respectively, for the Marshall–Olkin inverse Gaussian distribution.

The differences found in the second and third experiments are small, but they show clearly that the defective model is better. The results remained the same for a wide range of other parameter choices. That is, the AIC values and the quadratic error sums were smaller for the defective model most of the time for a wide range of parameter choices and for the two distributions. Hence, the defective model can be considered a viable alternative for the mixture model.

Section 4 presents three real data applications. The sample size for the first data set is forty four. The sample size for the second data set is over one thousand. The sample size for the third data set is over one thousand eight hundred. Hence, the given point as well as interval estimates for the second and third data sets can be considered accurate enough. But those for the first data set must be treated conservatively.

4 Applications

To illustrate the distributions presented we are going to use three data sets. The first one relates to a study of recurrence of leukemia in patients who were submitted to a certain kind of transplantation. Leukemia is a type of cancer that affects the white blood cells produced by the bone marrow and can take several forms. The data set has forty four observations with \(20.45\) percent censoring (nine in total). The maximum observation time was approximately five years. For details of this data set, see Kersey et al. (1987).

The second data set relates to the time of birth of a second child for a couple and is based on medical records of births in Norway in 1997. The observed time is the gap between the birth of the first child and the birth of the second child for the same couple. The data set consists of \(53543\) women who had their first child between 1983 and 1997. The censoring indicates whether the woman had a second child, the event of interest, or if she did not before the end of the study. The data set was previously analyzed by Aalen et al. (2008). For illustrative purposes, we took a random sample accounting for \(2\) percent of the data set, totalling \(1071\) observations with \(69.74\) percent censoring (\(747\) in total).

The third data set arises from one of the first successful trials of adjuvant chemotherapy for colon cancer. The event of interest here is the recurrence or death for the individual under the proposed treatment. The data set has \(1858\) observations and \(50.58\) percent censoring (\(938\) in total). The data set is available in R Core Team (2014) in the survival package. Details of this data set can be found in Laurie et al. (1989).

The three data sets represent three different real scenarios (see the Kaplan–Meier curves later). They were chosen carefully to test the flexibility of the proposed distributions under different conditions. The first and third data sets are about the recurrence of a type of cancer. For these data sets, it is fair to assume that there are individuals who will never have the cancer again, implying a cure rate. For the second data set, the presence of a cure rate is even more obvious: the immune elements are simply those couples who do not plan to have a second child.

The Gompertz, the Marshall–Olkin Gompertz, the inverse Gaussian and the Marshall–Olkin inverse Gaussian distributions were fitted to the data set via maximum likelihood. The variance of the cure fraction was estimated by using the delta method. Software packages in the R Core Team (2014) environment were used for optimization of functions of interest and other computations. The summary of the fitted Gompertz and Marshall–Olkin Gompertz distributions is shown in Tables 1, 2 and 3. The summary of the fitted inverse Gaussian and Marshall–Olkin inverse Gaussian distributions is shown in Tables 4, 5 and 6.

Table 1 MLEs for the fits of the Gompertz and Marshall–Olkin Gompertz distributions for the leukemia data set
Full size table
Table 2 MLEs for the fits of the Gompertz and Marshall–Olkin Gompertz distributions for the birth data set
Full size table
Table 3 MLEs for the fits of the Gompertz and Marshall–Olkin Gompertz distributions for the colon data set
Full size table
Table 4 MLEs for the fit of the Marshall–Olkin inverse Gaussian distribution for the leukemia data set
Full size table
Table 5 MLEs for the fit of the Marshall–Olkin inverse Gaussian distribution for the birth data set
Full size table
Table 6 MLEs for the fit of the Marshall–Olkin inverse Gaussian distribution for the colon data set
Full size table

The fitted survival curves of the proposed distributions for the leukemia data set are shown in Fig. 11. Those for the birth data set are shown in Fig. 12. Those for the colon data set are shown in Fig. 13. Table 7 presents the AIC values for all four of the fitted distributions. Figure 14 plots the Kaplan–Meier estimates of the survival function versus the predicted values from the proposed distributions. There is a diagonal line in each plot. The closer the points to this line the better the fit.

Table 7 AIC values for the fitted defective distributions compared with their respective mixture models
Full size table
Fig. 11
figure 11

Survival curves for the fitted Gompertz, Marshall–Olkin Gompertz, inverse Gaussian and Marshall–Olkin inverse Gaussian distributions for the leukemia data set

Full size image
Fig. 12
figure 12

Survival curves for the fitted Gompertz, Marshall–Olkin Gompertz, inverse Gaussian and Marshall–Olkin inverse Gaussian distributions for the birth data set

Full size image
Fig. 13
figure 13

Survival curves for the fitted Gompertz, Marshall–Olkin Gompertz, inverse Gaussian and Marshall–Olkin inverse Gaussian distributions for the colon data set

Full size image
Fig. 14
figure 14

Plots of the Kaplan–Meier estimates of the survival function versus the predicted values from the proposed distributions. The top four plots are for the birth data set. The middle four plots are for the leukemia data set. The bottom four plots are for the colon data set

Full size image

The Marshall–Olkin Gompertz distribution is a clear improvement over the Gompertz distribution for all three data sets. The fitted survival curve for the former captures the Kaplan–Meier curve much better, see Figs. 11, 12, 13 and 14. For all data sets, the Marshall–Olkin Gompertz distribution estimates \(a\) by a negative value with a negative confidence interval. The Gompertz distribution gives a negative interval for \(a\) for the leukemia and colon data sets but estimates \(a\) by a positive value for the birth data set. So, the birth data set is an example, where the baseline distribution does not yield a defective model, while the Marshall–Olkin extension gives a much better fit as a defective model. All but the Marshall–Olkin inverse Gaussian distribution appear to estimate the cure fraction in the expected range in relation to the Kaplan–Meier curve. The Marshall–Olkin inverse Gaussian distribution appears to underestimate the cure fraction for the birth and colon data sets.

The Marshall–Olkin inverse Gaussian distribution is a clear improvement over the inverse Gaussian distribution for all data sets, especially for the leukemia data set. The fitted survival curve for the former captures the Kaplan–Meier curve much better. For the birth data set, both distributions appear to perform equally well at first, but as time increases the tail of the inverse Gaussian distribution gets distanced from the Kaplan–Meier curve while that of the Marshall–Olkin inverse Gaussian distribution keeps close. For the leukemia data set, the inverse Gaussian distribution estimates \(a\) by a very small negative value, giving a very small estimate of the cure fraction not significantly different from zero. For the leukemia and birth data sets, the Marshall–Olkin inverse Gaussian distribution estimates \(a\) by a negative value with a negative confidence interval. The estimate of \(a\) for the colon data set is close to zero, leading to a very small cure fraction.

The estimate of \(r\) for Marshall–Olkin distributions is significantly different from \(1\), meaning that those distributions provide better fits. This can also be checked in Fig. 14. The Marshall–Olkin distributions have points closer to the diagonal line than the baseline distributions.

Table 7 shows there is a big reduction in AIC values when the Marshall–Olkin Gompertz and Gompertz distributions are compared and when the Marshall–Olkin inverse Gaussian and inverse Gaussian distributions are compared.

For the leukemia and birth data sets, the best fitting defective model is the Marshall–Olkin inverse Gaussian distribution, the second best fitting model is the Marshall–Olkin Gompertz distribution, the third best fitting model is the inverse Gaussian distribution and the worst fitting model is the Gompertz distribution. For the colon data set, the best fitting defective model is the Marshall–Olkin Gompertz distribution, the second best fitting model is the Gompertz distribution, the third best fitting model is the Marshall–Olkin inverse Gaussian distribution and the worst fitting model is the inverse Gaussian distribution.

Table 7 also compares the AIC values between the defective and mixture models based on the Gompertz, Marshall–Olkin Gompertz, inverse Gaussian and Marshall–Olkin inverse Gaussian distributions. The bold value represents the smaller value in the comparison. The defective model performs better for the leukemia data set when based on the Marshall–Olkin Gompertz and Marshall–Olkin inverse Gaussian distributions. The defective model is better for the birth data set when based on all but the Gompertz distribution. The defective model is better for the colon data set when based on all but the Marshall–Olkin Gompertz distribution.

5 Conclusions

We have proposed two new distributions by using an idea due to Marshall and Olkin. These distributions can assume a defective form. In this way, the cure rate can be estimated by models having one less parameter than the usual standard mixture models.

Three real data applications have shown that Marshall–Olkin distributions perform much better than known defection distributions in terms of likelihood values, proximity to the Kaplan–Meier curve and AIC values. Further investigations are needed to verify the potential of such distributions as cure fraction models.