Rectifying I: three point and continuous fit of the spatial autocorrelation metric, Moran’s I, to ideal form

Abstract

Context

Interpreting spatial autocorrelation is complicated by differences in data type, spatial conformation, and contiguity definitions. Though lacking consistent meaning, Moran’s I is commonly reported, compared, and interpreted based on conceptual ideals. To provide consistent, logical, and intuitive meaning and enable broader synthetic work, a new approach to I is needed.

Objectives

We sought to standardize I and true it to conceptual ideals and existing intuition regarding regular correlations. We also wished to test performance of transformed metrics over a diversity of designed and empirical datasets.

Methods

We developed two means to rectify I. Both fit null distributions from data permutation to a target frame of [− 1, 0, 1], followed by projection of original I into this conformation. One method used three-point registration employing the distribution median and select tail percentiles. The other directly projected all I based on theory or cumulative frequencies reflecting the distribution of regular correlations. Repeatability and sensitivity of results were examined for varied permutation replication and framing parameter choices. Empirical and designed datasets were used to compare rectified to traditional metrics.

Results

Both rectification methods improved distributional characteristics of I. Three-point registration produced overly broad distributions with discontinuous peaks. Continuous projection fit the distribution for regular correlations precisely. Diverse case studies demonstrated failings of I and the clarity gained by rectification.

Conclusions

Rectified I enabled meaningful comparisons of spatial patterns for diverse data and landscape conditions. Preserving the intuitive value of Moran’s I while providing a theoretically sound and consistent approach for standardizing its values should foster sustained use.

Introduction

Measurements made in proximity to each other tend to be similar (Moran 1947; Durbin and Watson 1950; Tobler 1970; Cliff and Ord 1981). A traditional measure of such spatial autocorrelation is Moran’s I (Moran 1947, 1950). I is conceptually elegant for its basic and intuitive nature, although it is often idealized beyond its actual character. Several authors have detailed I’s systematic properties, biases, and limitations (Cliff and Ord 1973; Sen 1976; de Jong et al. 1984; Waldhör 1996; Fortin and Dale 2005). Yet presumptions and mistaken perceptions of I’s character persist.

I is often presented in idealized terms wherein it is said to range between − 1 and 1, with perfect interspersion at − 1, random dispersion at 0, and perfect clumping or gradient conformation at 1 (Fig. 1). It is often interpreted as analogous or homologous to a regular (Pearson) correlation coefficient r. Values of I considered small for r are regularly treated as respectively weak autocorrelation. Analogy with r suggests an oppositive scale (± I indicate the same magnitude of pattern). These properties if realized would facilitate interpretation within and comparisons across studies. The intuitive, pedagogical, and potential comparative value of this ideal are important to protect if I can be modified to achieve its reputed or assumed qualities. A list of assumed or desirable characteristics for an autocorrelation metric is given in Table 1.

Fig. 1

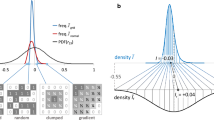
Spatial patterns and assessment metric values expected and observed. a Spatial data arrays illustrating over-dispersed, random, or positively autocorrelated (clumped or gradient) landscape patterns. A common expectation is that I for these caricatured patterns should be at or near − 1, 0, or 1. Actual values for the four patterns are given above each array. b Probability density functions (PDFs) for Pearson r and χ² are given for comparison. The χ² PDFs were scaled to the data breadth observed in simulation using uniform grid spatial conformation (blue line) versus random normal coordinate values (red line). c Distributions of $\tilde{I}$ realized through 3 × 10⁴ random permutations of binomial data in grid conformation as in panel A (blue line) and in a random bivariate normal location matrix (red line). Mathematically derived range limits (eigenvalue extremes of the n-sum weights matrix, nW₁) for each distribution are given as horizontal bars. Observed ranges of Ĩ are given as distribution stop points on the abscissa. I values for the conformations in panel A are given in the context of their null distribution. Calculations are archived in Supplementary file ESM_1

Table 1 Qualities expected, assumed, or desireable for an autocorrelation metric

In reality, I is negatively biased and variably so based on sample size. Its null distribution—the distribution of values from replicated random data permutations—is right skewed and excessively narrow compared to other statistical metrics such as t or r. Its extrema are not limited to − 1 and 1 and its scale is not oppositive (de Jong et al. 1984). For example, I of 0.2 in one neighborhood may represent stronger or weaker autocorrelation than − 0.2 in another (Anselin 1995). Theory suggests the actual bounds of I are the minimum and maximum eigenvalues of the normalized (unit sum) hollow matrix of inverse-distances (de Jong et al. 1984, Griffith 1996, Chen 2013). Yet these eigenvalues provide little indication of actual null distribution position or breadth (Fig. 1c). I varies with the geometric conformation of measurement locations (Tiefelsdorf 1998), the means of representing sample proximity, and the quantitative nature of the measured variables (extensively reviewed in Cliff and Ord 1973). These problems render I incomparable among or even within studies for different variables.

Despite the well documented reality that I has no consistent meaning beyond singular contexts, the metric is still commonly reported, compared, and often interpreted based on its conceptual ideals. Even when reported in context with its theoretical mathematical limits, which is rarely done by empiricists, values of I are still difficult or even misleading to interpret. To provide consistent, logical, and intuitive meaning beyond individual contexts, and hence to enable conceptual and analytical syntheses such as meta-analyses (Rosenthal and Rubin 1986) or expansion to multi-domain use (Kim et al. 2015; Ritters 2019), an improved standard for I and similarly plagued spatial pattern metrics is needed.

Given the perceptions, potential, and problems described for Moran’s I, taken with the long history in spatial analysis, instead of continuing efforts to reframe its narrative, it may be better to reframe the metric itself to require fewer or no qualifications. Two methods of reframing I were developed and herein are described. The first method used a dichotomous Procrustes approach, anisometric three-point registration, to fit the null distribution based on its median and values at select tail percentages, to a target frame of [− 1, 0, 1], followed by projection of the original I into this conformation. The second method projected I in a continuous manner, using its cumulative percentage in the null distribution, to the theoretical distribution of regular (Pearson) correlations. We referred to these projections as ‘rectification’ because they scaled alternative regions of the distribution of I differently such that the collective distribution fit a designated target frame. Differential scaling to geometric fit is eponymously termed ‘Procrustes’ methodology by analogy with the character in Greek mythology who variously contorted victims to fit a specific (bed) frame (Hurley and Cattell 1962). Whereas the first method used two independent scaling operations, each homogeneous on a given side of the median, the second used continuous but inhomogeneous scaling. Our goal in both cases was to register the original metric in a frame that obviates many or all the problems of the original (Table 1), so it has consistent and intuitive meaning and sustainable impact in the field of spatial analysis.

Background

Nomenclature in this article was summarized in Table 2. The original metric, I, was developed by Moran (1947, 1950). The expected mean, variance, and z and χ² test statistics to assess significance of I are well known (e.g., Cliff and Ord 1973; Goodchild 1988; Rogerson 1999; Getis 2010). I is χ² distributed commensurate with its derivation from inverse distances (Thirey and Hickman 2015; e.g., Fig. 1c).

Table 2 Nomenclature used in this paper

We use Chen’s (2013) formulation of Moran’s I as

$$ I = {\mathbf{z}}^{\prime}{\mathbf{W}}_{1} {\mathbf{z}} $$

(1)

where z is a standardized data vector for n measurements from known locations and W₁ is the spatial weights matrix scaled to unit sum. In this formulation, local indicators of spatial autocorrelation, ‘LISA’ (sensu Anselin 1995), are diagonal elements of zz′ W₁ (Chen 2013). Because local I are additive, global I can also be defined as the trace of zz′ W₁. Range limits of I are expected to be the signed minimum and maximum eigenvalues of n·W₁ (de Jong et al. 1984, Griffith 1996). These limits are highly sensitive to proximity definitions and their values give no practical guidance to actual distributions within them (Fig. 1c). These limits and even empirical values of I often exceed 1 (de Jong et al. 1984; Tiefelsdorf 1998). The nature of I in practice, therefore, bears little resemblance to what is widely presumed and taught regarding the metric.

W can be rendered from variously composed physical distance or contiguity mappings among sample sites (well presented in Getis 2010). Distance matrices, D, may be defined linearly (without exponentiation) or nonlinearly (exponentiated by > 1). For example, squared distances are often used to enhance down-weighting of increasingly distant neighboring samples to reduce their influence on the magnitude of I. Contiguity matrices, C, are generally binary definitions of sampling plot edge adjacencies in regular or irregular polygonal grids and may include or exclude vertex adjacency. C is row-standardized to compensate differences in neighbor numbers by site as in cases where edge sites have fewer neighbors. If appropriate and desired, contiguity and distance matrices may be combined (Cliff and Ord 1969). Distance and contiguity elements are converted to inverses and can be regarded as proximities composing a matrix P. Perfect proximity, the proximity of a datum’s location to its own location, P_ii, and distances beyond a selected limit if desired, are set to zero so those cases drop out of subsequent calculations. P can be calculated to ensure diagonal elements are 0 as P = 1/(I_n + D)—I_n, where I_n is an n × n unit (identity) matrix where diagI_n = 1. W is a scaled version of P, such as the unit-sum W₁ = P/∑P_ij. The type of distance and contiguity representations used to derive W should be based on the logic of the spatial arrangement and functional logic of the process being studied (Anselin 1988). Exploratory investigation of weighting schemes based on model performance and validation may be a useful compliment to the logical and functional approach.

Expectations and interpretations of I may reflect those of regular correlations (Fig. 1b) due to similar nomenclature: ‘index of autocorrelation’ and ‘correlation coefficient’ or the widely repeated notion that I was developed from Pearson’s r (e.g., Getis 2010) which implies mathematical homology. Yet Pearson’s r is a cross product between two similarly (n × 1) dimensioned, similarly (unit-variance) scaled, and similarly (normally) distributed variables. In contrast, I is a cross product between a normally distributed n × 1 data vector and and inverse elements of a variably dimensioned, χ²-distributed n × n matrix scaled to unit sum. For example, the distance matrix for the example in Fig. 1 has one dimension but as a proximity or weights matrix it has six (see eigenvalue counts in Supplementary file ESM_1). Thus, compared to r, I is dimensionally, volumetrically, and distributionally convoluted (Tiefelsdorf 1998, in part).

Expected I under a null hypothesis of no spatial pattern, E(I), is − 1/(n−1) with expected variance and a z test statistic as given in Cliff and Ord (1973) or a χ² statistic as given in Rogerson (1999). Significance of I metrics is better assessed by permutation analysis than by inference from a test statistic because the distribution of I can be unpredictably skewed based on spatial arrangement of the sample sites, varied distributional properties of measured variables, and other characteristics that violate parametric assumptions (Upton and Fingleton 1985; Goodchild 1988; Tiefelsdorf and Boots 1997; Li et al. 2007). $\tilde{P}$ values from Monte Carlo simulations are determined as the proportion of permutation results more extreme than the observed I as appropriate to the null hypothesis. For example, the probability of unbiased processes underlying an I equal or smaller than that observed is the cumulative percentage of data up to I. For extremely patterned data, I will often exceed the maximum or minimum of values obtained in even large numbers of permutations. As probability estimates are limited by permutation number, the logical limit must be imposed that it be not less than 1/(k + 1) for k permutations (Griffith 1987) or half that for two-tailed tests. Permutations also produce an explicit null distribution that can be scaled, as demonstrated herein, to fit a specific frame or desired density function.

Methods

3-point registration

This method to rectify I used dichotomous scaling of null distributions of Ĩ obtained by Monte Carlo simulation using replicated random data permutations. Based on the ideology described in the Sect. “Introduction” and Table 1, null distributions were median centered, and each half of the distributions was separately scaled, homogeneously on a given side, so that the bounds of chosen distribution tail percentages occurred at − 1 and 1. Use of the median to center null distributions guaranteed that half of the values obtained by randomly permuting the data were positive and half were negative. This criterion for centrality did not rely on specific expectations for the geometry of central tendency. Obvious choices for extremes to serve as the ± 1 limits for the null distribution were the minimum and maximum values, Ĩ₀ and Ĩ ₁₀₀. If all possible n! permutations or an infinite number of random permutations were conducted, this choice of distributional limits would ensure that no conformation of data could yield |I_3P|> 1, making an absolutely bounded distribution frame. In practice, we attempted to approach the absolute frame with stringent definitions of tail percentages and high permutation effort. In theory, this could also be achieved by using the nW₁ eigenvalue limits. But in practice these extrema are far and variably removed from the bulk of the realizable distribution, so that frame would result in greatly contorted transformed distributions. Because the repeatability and proximity to a reasonable frame could have depended on permutation number, choice of tail percentages for the reference frame, and possibly their interaction, as well as unique system-specific properties, sensitivity analyses as described below Sect. (“Survey of published datasets”) were performed. Our methods were intended to identify combinations of frame definitions and number of permutations that balanced accuracy and effort to provide an acceptably repeatable standard for diverse datasets.

We calculated I following Chen (2013; Eq. 1). Then, either the standardized data vector z or the location matrix L was permuted (shuffled case wise) k times and Ĩ was recalculated each time to yield a ‘null’ distribution of frequencies. Null distributions were therefore those for values of Ĩ calculated from datasets with no covariation, on average, between z and D, which is the matrix of pairwise distances calculated from L. Ĩ values at designated cumulative percentages of the null distribution were then used to enact median centering and the separate scaling of the positive and negative sides of the centered distribution. I values obtained by permutation were denoted with a tilde in super-position, Ĩ, median-centered values with a circumflex in sub-position, , and fully rectified (centered and scaled) values were denoted for the 3-point registration method with subscript, as in Ĩ_3P. These conventions apply hereafter for any parameter obtained through permutation. The cumulative percentage of values ≤ Ĩ was designated with numerical subscript. For example, the null distribution minimum was denoted Ĩ₀, the maximum as Ĩ₁₀₀, and the median as Ĩ₅₀. Tail percentages defining frame boundaries were mirrored as in Ĩ_x and Ĩ_1-x (Table 2).

After median-centering, each half of the null distributions was scaled by the distance from the median to each respective frame boundary:

$$ \tilde{I}_{{3{\text{P}}}} \left( {\tilde{I}} \right) = \left\{ { \begin{array}{*{20}c} {\frac{{\tilde{I} - \tilde{I}_{50} }}{{\tilde{I}_{50} - \tilde{I}_{{\text{x}}} }}} \\ 0 \\ {\frac{{\tilde{I} - \tilde{I}_{50} }}{{\tilde{I}_{{1 - {\text{x}}}} - \tilde{I}_{50} }}} \\ \end{array} \begin{array}{*{20}c} {{\text{if }}\tilde{I} < \tilde{I}_{50} } \\ {{\text{if }}\tilde{I} = \tilde{I}_{50} } \\ {{\text{if }}\tilde{I} > \tilde{I}_{50} .} \\ \end{array} } \right. $$

(2)

Scaling was applied similarly for the observed I. This scaling method set all values on a given side of the centered null distribution to their proportional position between the median and the respective tail boundary. For example, I of +0.2 in a null distribution having median 0 and Ĩ_1-x of 0.4, yields an I_3P of +0.5 (= ^0.2/_0.4). In this manner, any original null distribution frame [Ĩ_x, Ĩ₅₀, Ĩ_1-x] was anisometrically scaled about the median to [−1, 0, 1].

Values of |Ĩ_3P|> 1 were expected to occur at frequency 2xn (frequency xn on each side of the null distribution). As well, empirical datasets with strong autocorrelation would often yield |I_3P| ≫ 1. Values of |I_3P| and |Ĩ_3P| in excess of 1 were set based on their signs to ±1:

$$ |I_{{3{\text{P}}}} | > 1 = \left\{ {\begin{array}{*{20}c} { - 1 \, {\text{if }} \tilde{I}_{{3{\text{P}}}} < - 1} \\ { 1 \, {\text{if }} \, \tilde{I}_{{3{\text{P}}}} > 1.} \\ \end{array} } \right. $$

(3)

P-values for hypothesis tests and analysis were obtained directly from cumulative proportions at I or I_3P in their respective null distributions. For example, a directional hypothesis of overdispersion is supported when the cumulative proportion of I_3P in its null distribution is less than or equal to α, where α is the established minimum probability of making a statistical type-I inferential error. A hypothesis of any systematic spatial structure is supported if the cumulative proportion of negative I ≤ α/2 or that for positive I ≥ 1-α/2. Calculation of $\tilde{P}$ values for null hypothesis tests by frequencies are:

$$ \tilde{P}\left( {H_{0} } \right) = \left\{ {\begin{array}{*{20}l} {A = \frac{{\sum\nolimits_{{ - 1}}^{I} f req.\left( {\tilde{I}} \right)}}{k}} \hfill & {H_{0} :{\text{ no over dispersion}}} \hfill \\ {B = \frac{{\sum\nolimits_{I}^{1} f req.\left( {\tilde{I}} \right)}}{k}} \hfill & {H_{0} :{\text{ no clumping or gradients}}} \hfill \\ {\frac{{2 \cdot {\text{min}}\left( {A,B} \right)}}{k}} \hfill & {H_{0} :{\text{ no autocorrelation}}.} \hfill \\ \end{array} } \right. $$

(4)

Parametric P values for some specific demonstrations were also calculated using z statistics per Cliff and Ord (1973).

Fit to Pearson’s r

Our second method of rectification also made use of permutations as described above. However, since our goal was to register the null distribution to a theoretically known distribution, there was no need to define target frame boundaries. I values were fit to r using inverse distribution functions based on their cumulative proportions in null distributions. The probability distribution of correlation coefficients from random bivariate normal or uniform data is

$$ {\text{prob}}.\left( r \right) = \frac{{\left( {1 - r^{2} } \right)^{{\frac{n - 4}{2}}} }}{\sqrt \pi } \cdot \frac{{\Gamma \left( {\frac{n - 1}{2}} \right)}}{{\Gamma \left( {\frac{n - 2}{2}} \right)}} $$

(5)

(Hotelling 1953). This function can be integrated from − 1 to that r having the same cumulative proportion as I in its null distribution, which r is then deemed I_r.

$$ I_{{\text{r}}} : = r\left| {\int\limits_{ - 1}^{r} {prob.\left( r \right)dr = CP_{{\text{I}}} } } \right. $$

(6)

In practice it was simpler to invoke the inverse t distribution as it is widely available in software packages such as R, MATLAB, Stata, and Excel. The expected t-distribution of Pearson correlations for bivariate normal or uniform random variables is given by

$$ t\left( r \right) = r\sqrt {\left( {n - 2} \right)/(1 - r^{2} } ) $$

(7)

(Rahman 1968), where n−2 is the degrees of freedom. To map I values to this distribution, their cumulative proportion in the null distribution was used to calculate a t_n−2 statistic using the inverse t distribution as

$$ t\left( {CP_{{\text{I}}} } \right) = \left\{ {\begin{array}{*{20}l} {t.inv\left( {\frac{1}{{k + 1}}/2,~n - 2} \right)} \hfill & {CP_{{\text{I}}} = 0} \hfill \\ {t.inv(I_{R} ,{\text{n}} - 2)} \hfill & {0 < CP_{{\text{I}}} < 1} \hfill \\ {t.inv\left( {(1 - \frac{1}{{k + 1}})/2,n - 2} \right)} \hfill & {CP_{{\text{I}}} = 1} \hfill \\ \end{array} } \right. $$

(8)

then t was converted to r as

$$ r\left( t \right) = t/\sqrt {n - 2 + t^{2} } : = I_{r} $$

(9)

with I_r given to equal r. Where t was undefined at the distribution limits, CP = 0 and 1, I_r was set to the respective limits of r given the constraint of P ≥  ± 1/(k + 1) (Griffith 1987). Thus Eqs. 5, 8 and 9 functioned to prevent I_r from being set to a value with greater significance than the limit imposed by permutation number.

Mapping from cumulative proportions to r was used both to rectify empirical I values but also to convert permutation results to I_r. I_r was graphically illustrated by denoting its position within either the theoretical distribution function (Eqs. 5, 9) or the empirical histogram of all Ĩ obtained through permutation. The latter was used for intuitive value and contrast with the original null distribution histogram.

Both rectification methods are available as options in the R package Irescale (Fuentes et al. 2020).

Focal case: autocorrelation of major Chinese city population sizes

Both rectification procedures were applied to data from Chen (2013; Fig. 2a) on population sizes of and rail distances among 29 major Chinese cities. This dataset is referred to hereafter as Cities. I was calculated following Chen (2013; Eq. 1), whose result we wished to replicate. The rail distance matrix, D, was non-positive definite due to rail paths being variously indirect (Dokmanic et al. 2015). Therefore, D could not have been used to derive an L matrix to be permuted and still replicate Chen’s results. Therefore, we permuted only the standardized data vector z. The Cities example was examined using the original data, a natural logarithm (log_e) transformed version, and a designed dataset composed to have extremely high autocorrelation (Fig. 2b). The latter two data vectors were included to assess the responsiveness of I and its rectified metrics to variable transformation and inform on the positive metric limit. Each of the three data vectors were used to calculate I for each of 10⁴ permutations. From these results we calculated (i.e., $\tilde{I}$ −  $\tilde{I}$₅₀), I_3P using x = 0 and 0.1 tail percentages as frame boundaries, and I_r. As a control measure to test for permutation bias, a Pearson correlation was calculated between the original data vector and each permuted version. The null distribution of these correlations was examined to ensure r̄₂₇ ≈ 0. Calculations for this case analysis are provided in an Excel file (Supplementary file ESM_2). All calculations cited, except the random r, can be performed with the R package Irescale (Fuentes et al. 2020).

Fig. 2

Focal data to illustrate rectification methods. a Original data on populations of major Chinese cities (from Chen 2013). b Designed data created to have high spatial autocorrelation due to data gradients and clumping. Marker diameter corresponds to population size

Sensitivity analysis

Sensitivity and repeatability of null distribution parameters were explored for both rectification methods using replicated sets of permutations. All datasets were used for this purpose. We focused on the Cities dataset for presentation of detailed dynamics (“Sensitivity analysis” sect.). Summary statistics and exceptional behaviors noted for the broader survey described in “Survey of published datasets” sect. were also assessed and reported in “Survey of published datasets” sect. For the Cities analysis, we used the rail D matrix where possible to align with the analysis by Chen (2013) but could not do so for spatial regressions, in which case we used geographic D. The geographic and rail distance matrices were highly correlated (matrix r₄₀₄ = 0.93). Simulations were carried out for 10 replicates of each combination of six permutation numbers (k = 10¹, 10², … 10⁶). From simulation results, average and standard error, which in this paper is considered to be the obverse of repeatability, were calculated for all I, , rectified metrics, and 3-point registration frame boundaries (I_x, I_1-x) defined by tail percentiles x = 0, 10^–3, 10^–2, 10^–1, and 10⁰.

To resolve how I tracked with other autocorrelation metrics, we calculated the matrix correlation between D and the matrix of Euclidian distances among elements of z. This ‘matrix’ correlation is a Pearson correlation of the corresponding elements taken in pairs from the two distance matrices (Mantel 1967). We also calculated a multiple correlation from a spatial multiple regression of the form

$$ {\hat{\mathbf{z}}} = b_{{0}} + b_{{1}} \cdot{\text{latitude }} + b_{{2}} \cdot{\text{longitude }} + b_{{3}} \cdot{\text{latitude}}\cdot{\text{longitude}} $$

(10)

The square of multiple r is the proportion of variance in z explained by gradient effects (Sokal and Rohlf 1995). This measure of gradient effect size was used with I_r², a dimensionally comparable metric of non-dispersion, to create complementary indices that differentially capture aspects of spatial pattern due to clumping versus gradient effects as

$$ I_{{\text{C}}}^{{2}} = I_{{\text{r}}}^{{2}} / \, (I_{{\text{r}}}^{{2}} + {\text{ multiple}}\,r^{{2}} ) \, = { 1 } - I_{{\text{G}}}^{{2}} $$

(11)

To enable the last three calculations (Eqs. 9, 10 and 11) for Cities, we used an L matrix composed of GPS coordinates obtained from Google Earth. We also applied the gradient and clumping metrics to the ‘number fledged’ data vector of Marrot et al. (2015), three designed versions of that vector, and an array of patterns from the 25-plot grid illustrated in Fig. 1. Designed data vectors from Cities, Marrot et al. (2015), and targeted simulations of gradient, random, clumped, and ‘clumpy-gradient’ data were used to assess sensitivity of I_C² and I_G² to cases with known magnitude patterns.

Sensitivity results were compared within and between studies with emphasis on repeatability and magnitude of I_r metrics and correlations between I, I_3P, I_r, matrix r, and multiple r from regression. The sensitivity analysis for Cities as implemented in Excel is available in Supplemental file ESM_3. Irescale (v. 2.3.0; Fuentes et al. 2020) was used to confirm the Cities result and calculate sensitivity analyses for the case studies described in the following section.

Survey of published datasets

To achieve a broad view of how rectified I compared to traditional I and related metrics, we identified and examined four published datasets in addition to Cities. The additional data were identified by searching the phrase “Moran’s I” in Google Scholar (in mid-2019) and examining recent publications returned to find a subset of 12 in which the authors openly archived data. The 12 datasets were further examined and four were selected by qualitative review for having diverse variable types within studies and diverse sample size and spatial structures among studies. The four datasets identified were Cozzarolo et al. (2018), Goldsmith et al. (2019), L’Herpiniere et al. (2019), and Marrot et al. (2015). These datasets collectively included 24 variables as accounted in detail in the “Results” sect. For each dataset, we conducted rectification and companion procedures, including the sensitivity analysis described above (“Sensitivity analysis” sect.). Results for sensitivity dynamics and correlations of spatial pattern metrics within and among studies were reported.

Summation regarding metric ideals

Results of the varied methods described above were scrutinized for congruence or dissonance with the characteristics given in Table 1 as regards I and comparator metrics. These inferences were drawn primarily from mathematical definitions and null distribution shapes as presented below and confirmed with broader explorations archived in the supplementary files.

Results

Three-point registration

General results are recounted here and specific case study detail and procedural assessments are reported in sections that follow. Null distributions rectified by 3-point registration resulted in the frame [Ĩ_x, Ĩ₅₀, Ĩ_1-x] = [− 1, 0, 1]. The mean of 3P-rectified distributions was generally mismatched with the median, most often in a direction opposite that for the unrectified null distribution. Empirical I from strongly patterned datasets when projected into their rectified null distributions in several cases exceeded 1 and were subjected to capping (Eq. 3). Selecting smaller distribution tails for target frame references reduced I_3P and the frequency of times limits were necessary to invoke. Even when using maximum and minimum values of $\tilde{I}$ as the target frame, the caps were still necessary because some empirical patterns represented a degree of patterning not discovered with limited permutation. For I observed to be significant by permutation, rectification by 3-point registration generally resulted in |I_3P| ≫|I| and .

Rectification by 3-point registration greatly increased similarity of null distribution tail shapes relative to the unrectified distribution (Fig. 3a, b). However, separate scaling of the upper and lower distribution halves resulted in strong leverage in the skewed side of distributions, such that the long tail contracted toward the bound at the median. Tail contraction resulted in pushing up the area (distribution density) near the median in that half of the distribution. In opposite manner, the short-tailed half of the distribution drew out the tail and density near the median decreased, producing a slumping effect. The result of the opposing shifts in density created a shape discontinuity at the median (Fig. 3b). Despite creating an odd distribution shape around the median, skewness was most often considerably reduced and sometimes was reversed (changed in sign). $\tilde{P}$ values for I, I_3P, and I_r were equivalent when calculated from frequencies. P values calculated from z tests per Cliff and Ord (1973) differed among the metrics and frequently fell below the practical limit of $\tilde{P}$ from frequencies.

Fig. 3

Null distribution of I from 10⁴ permutations of the Cities data. a Moran’s $\tilde{I}$. b $\tilde{I}$ rectified using 3-point registration. c $\tilde{I}$ fit to the distribution of Pearson’s r. The position of unrectified and rectified I on the abscissa are indicated in red with the respective medians in blue. Distribution tail boundaries for x = 0.1 and skewness is given in each panel. Calculations were archived in Supplementary file ESM_4

Fit to distribution of Pearson’s r

The distribution-fitting method produced null distributions fully contained in the interval [− 1, 1] without applying caps (Fig. 3c), although distributional extrema [I ₀, I₁₀₀] where t is undefined had to be limited to that having $\tilde{P}$ = 1/(k + 1) per Eq. 8. The mean and median were coincident at 0. By definition, the rectified null distribution, being fit to a t-distribution, was neither appreciably skewed nor asymmetric about the median, although it was subject to moderate platykurtism for sample sizes below 10. Left and right tail percentiles were oppositive; that is, tail areas were of the same magnitude at ±  $\tilde{I}$_r. $\tilde{P}$-values were functionally equivalent when calculated from simulation frequencies (Eq. 4) or by t statistics derived from I_r (Eq. 7).

Focal case: autocorrelation of major Chinese city population sizes

The Cities population and rail distance data yielded I of − 0.031 in concurrence with Chen (2013; z₂₇ = 0.11, one tailed P = 0.46; $\tilde{P}$ = 0.42). Null distributions for the original, log and designed data from simulations with 10⁴ permutations yielded mean I within a few ten-thousandths of the expected mean. Medians were approximately 9% more negatively biased than the means for all three data vectors and all were right skewed (Table 3). Null distributions from untransformed data were most skewed and log-transformed data were least skewed. Simulation results in this analysis never produced median-centered I in excess of 0.27, suggesting a limit. However, based on I for the designed dataset (= 0.28) and sensitivity analyses, the limit appeared to be ≈ 0.33 (“Survey of published datasets” sect.). This limit from simulation contradicts the theoretical limit of the maximum eigenvalue of nW₁ which was 1.09. $\tilde{P}$ was similar to that from parametric z-tests except where P < 1/(k + 1). The limit imposed by Eq. 4 prevents assigning I_r any higher value than that which can be resolved as significant given any fixed k. (Table 3). These calculations are archived in Supplementary file ESM_2.

Table 3 SpaSpatial autocorrelation metrics and right tailed P-values for the Cities dataset

I statistics differed markedly in this analysis, most strongly among data vectors but also among modes of rectification (Table 3). For the original data vector and its log version, was 0.01 and 0.06. The latter value was marginally significant by one-tailed test against a null hypothesis of no positive autocorrelation ($\tilde{P}$ = 0.09). The rectified metrics produced similarly low values for the untransformed data (0.03–0.04) but rose for the log data to values that would be moderate as regular correlations (0.26–0.39). Finally, the designed positive autocorrelative dataset yielded I = 0.28, though the values for the rectified metric were much greater (I_r = 0.64, both I_3P = 1). Both I_3P in this case were constrained by the cap set at 1 (Eq. 3). I_r was limited due to permutation replication because t_n-2, part of the conversion procedure from I to I_r, was limited to that having probability 1/(k + 1)—in this case t₂₇ = 4.3, which translates to r₂₇ = I_r = 0.64.

Overall pattern strength was much greater for the designed dataset at I_r = 0.64 compared to 0.26 for the log data. However, the autocorrelation partitioning indices I_G² and I_C² demonstrated similar patterns between the log data and the designed dataset. For both datasets, the cluster metrics I²_C were approximately 0.3; thus the gradient metrics I²_G were approximately 0.7. The joint presence of clumping per se and gradient effects for the designed data was visually apparent from Fig. 2b as datum magnitudes were clumped at one scale but the clumps were arrayed as a north–south gradient. The pattern partitioning indices were not calculated for untransformed data due to lack of evidence for any spatial pattern to be characterized ($\tilde{P}$ > 0.4 for both I and multiple r, Table 3).

Figure 3a illustrates a focal null distribution of $\tilde{I}$ from 10⁴ random permutations of the Cities data. The distribution was negatively biased to the expected level and in this case was particularly right skewed. Over 83% of $\tilde{I}$ values from permutation were negative and the skew was highly significant based on D’agostino et al.’s (1990) test for excess skewness (z₂₇ = 27.6, P < 10^–20). The range of median-centered values extended 1.3-fold as far to the right as they did on the left, but this range was still far less than was suggested given the 3.2-fold difference in theoretical limits imposed by eigenvalues of nW₁. The null distribution mean of Pearson correlations between the original data vector and its permuted version was near 0 (r̄₂₇ = 0.002) with no noteworthy skewness (= 0.01). Matrix correlations of geographical distance and Euclidean distance among permuted measurements were not notably biased for any Cities datasets (matrix r̄ = ≤|0.002|), but these distributions were strongly skewed (= 0.97, 0.46, and 0.80 for actual, log transformed, and designed datasets). Null distributions of multiple r from the spatial regressions averaged 0.30–0.31 and were moderately skewed (= 0.55, 0.27, 0.25).

Figure 4 gives the null distributions of I, its transforms, matrix r, and Pearson’s r for the untransformed Cities data vector. The only null distribution that was oppositive (symmetric about the mean/median) was that for I_r, which was fitted to and therefore represented the theoretical function for Pearson’s r. Null distributions of I_3P at some frame definitions were found to have similar properties to those of Pearson’s r but presented the characteristically strong shape discontinuity about the median (Fig. 4b). Plotting null distributions in log space enhanced the apparency of null distribution tail shapes (Fig. 4c). Extremal probability decays for I_3P were similar in nature to, but broader than the theoretical expectation for Pearson’s r.

Fig. 4

Null distribution shapes for 3 × 10⁴ permutations of the untransformed Cities data. a Moran’s I, I_r, and matrix and multiple r. b I_3P for two frame definitions. c I metric null distributions in log space to emphasize tail conformations relevant for hypothesis testing (Supplementary file ESM_5)

Sensitivity analysis

Permutation with different numbers of iterations demonstrated the repeatability of rectified metrics and in the case of I_3P in particular the ultimate values obtained. Since the natures of the two rectification methods were different, they were considered separately.

3-point registration

Regardless of the tail percentiles selected as a frame of reference to scale I, increased permutation replication increased the range of extreme values discovered. This was especially so in the skewed end of the distribution. The greater extrema revealed through higher permutation replication had the effect of widening reference frames (Fig. 5a). Wider frames entailed frame boundaries more distant from the median. Since I was scaled by these distances (Eq. 2), greater permutation replication resulted in smaller |I_3P|. This relationship between more permutation and reduced |I_3P| was asymptotic at accessible levels of permutation (Fig. 5b). For example, the maximum frame width using 1% tails as frame boundaries was evident and highly repeatable with a total of 10⁴ permutations (10 replicates of 10³ permutations). In general, as asymptotes became evident with sufficient replication, error became trivial. Thus, asymptotic values being so identified by sensitivity analysis demonstrated the levels of sufficient replication needed to attain I_3P nearly invariant to increased permutation effort.

Fig. 5

Sensitivity analysis for 3-point rectification of $\tilde{I}$ from the Cities dataset. Values are from 10 replicate simulations at various permutation numbers and target frame percentiles. a Frame boundaries expanded with increased permutation replication and reduced target frame percentiles. Repeatability (~ se ⁻¹) of frame boundaries increased with permutation replication and more stringent tail percentiles. b Dependency of I_3P on permutation replication and frame criteria. I_3P decreased with increasing permutation replication to asymptotes unique for each frame designation. Asymptotic values for alternative frames were reached at different permutation replications. c Summary of tradeoffs among illustrated parameters. Increasingly diminished tail area (arrow train from red to purple symbols) led to a stable limit for the frame definition (0.29 on the abscissa) but also increased error (ordinate; Supplementary file ESM_3)

Despite the repeatability and stable limit for frame boundaries, and hence stability of I_3P for a given frame definition, alternative frame definitions had different asymptotes and different errors. For example, while the right frame boundary using 1% tails to define the frame resolved an average frame bound of 0.12 in 10⁴ permutations (red symbol, Fig. 5c), the 0.01% tail at that replication averaged twice that (0.24; green symbol, Fig. 5c), with tenfold increased error. Error was mitigable with more permutation, yet higher permutation widened the reference frame further and reduced I_3P. Therefore, a basic finding of this sensitivity analysis involves complex tradeoffs mitigable only by joint optimization of frame definitions and replication, the dynamics and appreciable balance of which could only be discerned through explicit analysis.

Fit to Pearson’s r

This method of rectification was highly repeatable even at modest permutation replication (Fig. 6). For example, I_r calculated from the Cities data using 10 replicate null distributions of 10⁴–10⁶ permutations, all reached the asymptotic value (0.04) with no noteworthy error. Thus, the original I of − 0.03 would be solidly + 0.04 on the expected scale for regular correlation. Even with lower replication by an order of magnitude, the asymptotic value was met but with concern-worthy (11.7% of the mean) error. The two lowest replication levels resulted in exponentially greater error and inflation of I_r. This sensitivity analysis and that for the 3-point registration method are archived in Supplementary file ESM_3.

Fig. 6

I_r average and standard error of 10 replicate simulations plotted in log space (ordinate) as a function of 6 magnitudes of permutation (abscissa) of the Cities data

Table 4 gives correlations of the three spatial pattern metrics ($\tilde{I_\text{r}}$, matrix $\tilde{r}$, and multiple $\tilde{r}$) over 2 × 10⁴ permutations both with each other (for a given data vector) and across data vectors (for a given metric). These correlations reflect the co-sensitive nature of the metrics to spatial data patterns in the Monte Carlo simulation. In general, there were strong relationships for values of a given metric calculated for the untransformed and log data vectors (0.79 ≤  $\tilde{r}$ ≤ 0.85; blue shading in Table 4). The strongest relationships among metrics for a given data vector were between matrix $\tilde{r}$ and multiple $\tilde{r}$ (0.54 ≤  $\tilde{r}$ < 0.66; yellow shading in Table 3). Of the two $\tilde{r}$ metrics, multiple $\tilde{r}$ was more closely correlated with $\tilde{I}$ (0.42 ≤  $\tilde{r}$ < 0.43; green shading in Table 3) than matrix r (0.24 ≤   $\tilde{r}$ ≤ 0.29; orange shading in Table 4). There was no reason to expect correlation between the designed dataset and the empirical data vectors so metric correlations for these are not given in the table. These calculations are archived in Supplementary file ESM_2.

Table 4 Correlations among spatial pattern metrics from permutations of Cities data vectors

Survey of published datasets

I varied considerably among variables and studies (Table 5). Few (4 of 29) empirical I in the survey were below the null distribution median and none were less than − 0.03. Of the 25 I values above the median, 13 were significant. The range of median-centered values was 0.034–1.17. Rectified values ranged from − 0.36 to 1. The positive cap (Eq. 3) was invoked in five cases exclusive of designed data vectors. Summary metrics for the 29 variables from five studies plus three designed and one log transformed data vector were collected in Table 5. Both rectified metrics were highly correlated with original I scores. In general, I_r was a more conservative metric than I_3P; larger magnitude values occurred especially less frequently for I_r. relative to I_3P. Scaling of both rectified metrics attenuated for larger uncentered I; however, centered I and the rectified metrics exibited a strongly linear relationship. The average within-study correlation between I and the rectified metrics was ≈ 0.9. Example correlations are illustrated in Fig. 7.

Table 5 Spatial pattern metrics from five published studies

Fig. 7

Relationship between I values. a I_3P calculated with null distribution extrema and b I_r plotted relative to raw I. c I_3P,0 and d I_r plotted with median-centered I. Shown are the data for six variables from the 2006 data series of Cozzarolo et al. (2018)

The pattern partitioning metrics, I_C² and I_G², for the data vector based on the replication and spatial structure of Marrot et al. (2015), but designed for strong gradient, clumping, or mixed patterns, acted in accord with our intent (Fig. 8). The gradient, clumped data, and clumpy gradient had equivalent I_r of 0.29, which is the maximum correlation that can be achieved with 229 cases and 10⁵ permutations with this spatial array. That is, $\tilde{I}$ from none of 10⁵ permutations exceeded the observed I for any of the designed arrays (all $\tilde{P}$ = 10^–5). Median-centered , however, suggested a weaker signal for clumping (Fig. 8d, row 1). Spatial regression demonstrated strong signal for the two cases with gradient patterns with no appreciable signal for the clumped-only data conformations.

Fig. 8

a–c Designed data vectors (ordinate) as a function of transect position (abscissa). d Autocorrelation metrics for the designed data including the pattern-partitioning metrics I_G² and I_C² (Supplementary file ESM 6)

The partitioning metric I_G² strongly signaled both pure and ‘clumpy gradient’ effects (Fig. 8a, c). I_C² strongly signaled only the pure clumping effect (Fig. 8b) with weak to modest indications of pattern in the other two conformations (Fig. 8d, row 6). A broader view of the behavior of I_C² emerged from permutations of the data illustrated in Fig. 1a. Figure 9 demonstrates the response of I_C² over the range of dispersion observed in random permutations and selected designed data in 5 × 5 grid conformations (Supplementary file ESM 7). For negative I_r, greater magnitude (neglecting sign) indicated greater dispersion. The negative extreme represented perfect interspersion. Conversely, the positive extreme of I_r indicated pure gradient conformation which by definition entails clumping of data with progressive but collective monotonic increase in data values over a spatial vector. However, the metric I_C² for increasingly positive I_r was particularly sensitive to non-gradient clumping (Fig. 9). I_C²’s complement, I_G², was concomitantly more sensitive to gradients.

Fig. 9

Covariation of the spatial pattern partitioning metric I_C² with the nondispersion metric I_r. Overdispersion was gaged in this space by increasingly negative I_r which also compelled concomitant increase in I_C². The gradient term (multiple r) in the denominator for I_C² attenuated the rise of I_C². Nondispersion (clumping and gradients) was indexed by increasingly positive I_r and either an accelerated or attenuated increase in I_C² for patterning that was due to gradients. Thus, I_C² rose faster as a function of nongradient clumping over the space of I_r. The differential response of I_C² to the two data structures therefore created a means to partition influences of the two structuring mechanisms on overall pattern

Recalling that I_C² = I_r² / (I_r² + multiple r²), increasing multiple r as it increases with gradient conformation could only increase the denominator and constrain I_C² to smaller values. These effects were evident in Fig. 9 as positive autocorrelation due to pure clumping drove I_C² upward to the limit of 1 while wholly graded conformations constrained I_C² to its lower limit. These effects were visually fit with an inverted χ² function of appropriate dimensionality for the clumping effect and with linear demarcation of the covariance limit fit to its apparency in the plot (Fig. 9; Supplementary file ESM_7).

Sensitivity analyses for the 29 empirical data vectors most often demonstrated the same pattern found for the Cities data (Fig. 5). Wider frames, hence lesser I_3P, generally arose from increasing replication which resulted in differential increase in absolute values of frame boundaries, especially for more stringent tail frame designations (Fig. 10a). However, in several instances in the broader survey, increased replication resulted in a decrease in frame boundaries for more liberal tail frame designations (Fig. 10b).

Fig. 10

Sensitivity of frame boundary definitions by permutation number for two data vectors from L’Herpiniere et al. (2019). Three point rectification demonstrated two patterns in which greater permutation replication resulted in either wider (a) or constricted (b) reference frames. Widening of frame boundaries with greater permutation effort was more commonly observed within and across studies

Summation regarding metric ideals

Table 6 summarizes performance of each metric of autocorrelation with respect to ideals framed in the Introduction and Background. The cardinal results of these evaluations were: (1) Moran’s I met only 2 of 14 ideal (desired) criteria, failing even those it is reputed to fit. (2) No metric alone met the ability to distinguish pure clumping and gradient data conformations. (3) The ratio I_C² = I_r² / (I_r² + multiple r²) was differentially sensitive to nongradient clumping and gradient effects.

Table 6 Qualities expected, assumed, or desireable for autocorrelation metrics

Discussion

Through diverse case studies and simulations, we found that Moran’s I varied with spatial pattern but also with several aspects of data structure that distort metrical representations of pattern. I, its transforms, and the other spatial pattern metrics examined, including matrix correlation and spatial regression, demonstrated a diverse mixture of qualities populating the ‘ideals’ table (Table 1). A reprise of these qualities and performance of the metrics for each is given in Table 6.

The original metric, I, failed to provide a consistent standard for comparing autocorrelation within or among studies (see also Sen 1976; de Jong et al. 1984; Waldhör 1996; Tiefelsdorf and Boots 1997). Our goal was to ‘unwarp’ I—to morph it into an intuitive metric that fit conceptual expectations for both I and for correlations in general. We believe that both rectification methods presented, 3-point registration and fitting to the distribution of r, did this. However, analysis revealed that the 3-point method had a diversity of caveats that made it advisable to conduct sensitivity analyses in each application. Although we provided software for doing the analyses (Fuentes et al. 2020), the sensitivities we felt made 3-point rectification, though preferable to no rectification, less desirable than fitting to the distribution for r. The latter method appeared apt for all the goals described in the “Introduction” sect. and Table 1, except for distinguishing non-gradient clumping from gradient effects. No single metric would be able to distinguish three unique states (overdispersion and two types of exception) which is a two-dimensional issue. But a ratio of I_r and multiple r provided a measure of distinction by indexing contributions of the two non-exclusive patterns (Figs. 8d, 9).

All of the I metrics rendered identical $\tilde{P}$-values from Monte Carlo simulation, evincing preservation of type I error despite centering and the two scaling methods. Scaling I was not intended to change inferential outcomes regarding autocorrelation. Our intention was to project the well-recognized traditional metric to a quantitative and conceptual space concordant with the inertia of existing ideals and intuition. Such inertias have been termed ‘apperception’, meaning mental anticipation based on the sum of prior experience (Greenwood 2015). Apperception regarding I mirrors that for regular correlation per Pearson (1924). Correlations are expected to be t-distributed and to span the oppositive frame [− 1,0,1] with 0 indicating absence of pattern (Sokal and Rohlf 1995). A given value of correlation implies the same effect strength for variable relationships from similarly replicated studies, though qualitative interpretation of the effect strength varies by discipline (e.g., Möller and Jennions 2002; Mukaka 2012). Rectification by 3-point registration eliminated bias (i.e. the median null value was 0), greatly reduced skewness, and generally expanded the scale of the null distribution of I to a semblance of that for correlation (Fig. 4). However, the scale and null distribution of I_r was fit by definition to that for regular correlation. Thus, I_r registered precisely with apperception for correlation.

Moran’s I is often cited as derivative of Pearson’s correlation coefficient, implying a homology and hence theoretical basis for I that is entirely false. An I metric that is dimensionally, volumetrically, and distributionally homologous to r may not be possible to derive theoretically given the multifarious disparities that emerge due to factors such as alternative data types and patterns of site proximities. Suspending doubt, if such a direct, mathematically homologous version of I were possible, with dimensionality, scale, and variable distributions homologous to r, then it follows that the distribution of said metric would match that for r. In substitution for that derivation, we can be true to the Pearsonesque theoretical basis for a new I derived directly from probability theory.

The approach of converting other statistics to r is increasingly used in meta-analysis to enable the sorts of comparisons we have described (Rosenthal and Rubin 1986; Möller and Jennions 2002). Although the conversion to r in the approach illustrated herein is conceptually related, it is free from parametric assumptions. Instead of calculating r from test statistics, effect sizes, or P-values based on them, fitting uses null distributions created directly from empirical data. Therefore, this fitting method makes no assumptions about the specific geometry of residual or null distribution shapes, or the scale of data matrices. While not being wedded to assumptions of parametric test statistics, I_r relied on permutation and its improbable null extrema were limited by replication effort. Minimum $\tilde{P}$ depended on permutation number and hence maximum I_r was limited through Eqs. 8 and 9. For example, maximum I_r from 20-case datasets with a true I_r of 0.9, assuming that is known, by using 10⁴, 10⁵, or 10⁶ replicates yields I_r estimates of 0.76, 0.82, and 0.86 respectively. In our frequentist approach, $\tilde{P}$ did not change if I_r exceeded the null distribution maximum by 1 unit or 100. In parametric statistics, it is common for P to short $\tilde{P}$ by many orders of magnitude where $\tilde{P}$ is limited by permutation replication. This limit to I_r only occurred when an observed dataset was extremely (very improbably if randomly) patterned. So for most empirical cases the issue may not be relevant, but at least two solutions may obviate the limit. First, for cases in which $\tilde{P}$ equals the lower limit of 1/(n + 1), one could increase replication effort until a threshold number of Ĩ in excess of I are returned. If replication had to be incremented enough to overtax computing resources, I_r from the simulations conducted to that point could be plotted as in our sensitivity analyses and an asymptotic value would likely be evident. Second, rather than the try-and-try-again procedure just outlined, one could use a parametric test to get an initial estimate for k (= 1/P−1) sufficient to yield an unconstrained I_r or the next order of magnitude higher to ensure adequacy. This assures that I_r is not capped and therefore is comparable to an empirical parametric r.

Although the ‘exact distribution of I’ has been derived with assumptions standard for parametric statistical inference (Tiefelsdorf 1998), the multifarious nature of real-world applications may limit its utility. For example, dimensionality of null distributions varies based on geometry of sample locations, measurement distributions, and procedural aspects of calculating I such as contiguity definitions. Although positive definite distance matrices have singular dimensionality, inversion of its values produces proximities with unpredictable dimensionality. The 5 × 5 uniform grid pattern of Fig. 1 had 6 dimensions (positive eigenvalues) yet that for 25 sampling sites in unconstrained (normally distributed) conformation had 7–9 dimensions for alternative permutations (Supplementary file ESM_1). Similarly problematic is the z parameter frequently used as a test statistic for I (Cliff and Ord 1969). Its values are χ²-distributed with various dimensionality, so it should perhaps always be paired with significance tests by simulations. Rectifying I to an alternative distribution would seem suspect for subverting ‘the exact distribution’ and its probability architecture. Though the values of I are rescaled in our correlation-fitting method, the probability structure among values (differences in CP among any pair of I) is unaltered by rectification.

Projecting I based on its null distribution to the theoretical distribution for r also eliminates the need to scale data inputs. Calculation of I_r requires neither scaling the proximity matrix to unit sum nor scaling of the centered data vector to unit variance per Moran (1950). It is only necessary to create a cross product by pre- and post-multiplying the unscaled proximity matrix by the centered data vector, ${\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\cdot}$}}{v} }}$′P${\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\cdot}$}}{v} }}$ and then converting this to I_r using its cumulative probability within its null distribution. Supplementary file ESM_8 demonstrates the equivalence of using scaled or unscaled data arrays.

The only caveats we conceived for rectifying I to the ideals frequently assumed or desired relate to the ease it grants to pass over consideration of the potentially informative if messy reality of raw null distributions. The tidied view offered by I_r may prevent insights that could flow from observing the original null distribution shape, such as the utility of data transformation. Worse, a ‘normalized’ frame of view may prevent recognition of functional inferences regarding the system or discovery of higher order phenomena (see DeWitt 2016, for ‘bell curve’ biases in evolutionary biology). To prevent such a disconnect between the original and rectified distributions, it is advised to visualize both and perhaps the geometric mapping between them as in Fig. 11 (Supplementary file ESM_9).

Fig. 11

Mapping of a null distribution of I to that of I_r

The ability to compare I among variables and studies is essential if the metric is to be useful beyond solitary instances and to facilitate its expansion to multiple domains (Kim et al. 2015). Presently, empirical values and null distributions typical of I appear as varied contortions that fit neither each other nor a theoretical or idealized standard. Examples of such contortions can be readily observed among our empirical survey results (Table 5). Two data vectors from Goldsmith et al. (2019) yield I = 0.02 and − 0.04, yet the former is highly significant and the latter is not ($\tilde{P}$ = 0.007 and 0.12) in dissonance with the expectation of oppositivity. In terms of scale, an I from L’Herpiniere et al. (2019) was inordinate at 1.2 while an I from Marrot et al. (2015) was miniscule at 0.01 and both were significant. Results so misfit to each other and to the scale of regular correlations are difficult to reconcile with intuition. The inscrutible nature of I thereby also precludes comparisons among studies. Rectification trues I to a standard that meets the apperceptive mass of ideals thought, taught, and wrought in the statistical and geospatial literature. We can continue to qualify every I statistic for each of its idiosyncrasies or we can present it in a manner that does not require those labors.