Introduction

Thermal damage to the skin is the most common damage to civilians and military people. In medical treatment, by heat transmitted to damage the cancerous tissue without affecting the normal tissue, hyperthermia treatment under a control temperature distribution should have a cancer cell distorted. For medical treatment, it is necessary to detect heat distribution in biological tissue. There is also thermal damage to the skin in a hot (like Desert) and cold (like Mountain) climate. Many researchers use different forms of bioheat models (Pennes [1], Weinbaum and Jiji [2], Nakayama and Kuwahara [3]) to study the thermal behavior in skin tissue. In Pennes model, the temperature gradient in organic tissue is obtained by classical Fourier’s law which is

$$\begin{aligned} q(r,t)\,=-k{\triangledown} T(r,t), \end{aligned}$$
(1)

where heat flux q(r, t) and the temperature gradient \({\triangledown} T(r,t)\) are at the arbitrary point of tissue.

The Pennes bioheat model [1] is a commonly used model to simulate the study of the thermal behavior of body tissues, which includes metabolic heat and blood perfusion. Shen et al [4] considered the heat and mass transfers in skin models with the diffusion of water and vaporization, but Ming stated that it is different for each layer, which is not considered in the Shen model. Analysis of the numerical skin model was defined for multi-layer (i.e., solder, epidermis, dermis, and fatty tissue), using laser coupled on human skin [5]. The layer of each skin is assigned to the properties of initial optical, thermal, and water density, and the water content in each layer is calculated from diffusion, where water loss occurs by evaporation. The blood perfusion, the diffusion of water, and the heat of metabolism remain in all three layers except the perfusion of blood are not present in the epidermis layer. The dynamic temperature and distribution for the multi-layer have been defined. Physical parameters affect burning injuries, i.e., thickness of epidermis and dermis tissue, the thermal conductivity of the dermis and subcutaneous tissue. The capacity of heat, blood perfusion rate, and the diffusion of water have very little effect on epidermis and dermis layer. To analyze skin burn at high temperatures, Ming [6, 7] introduces a one dimension multi-layer skin model and obtained temperature distribution using a finite volume method which is found to be good with experimental. The results show very little effect of temperature distribution with variation of blood perfusion and initial temperature on multi-layer skin models. Metabolic heat in the skin model was considered to be zero by Ming et. al. [6, 7], but it is experimental that it has a significant effect on skin.

A mathematical model is considered for measuring the blood perfusion rate in local tissue by using Pennes equation [8]. Two parameters are difficult to know, i.e., \(T_{\mathrm{a}}\) is arterial blood temperature and \(Q_\mathrm{m}\) is the metabolic heat generation rate has been eliminated for evaluating \(W_{\mathrm{b}}\) is the local perfusion rate in the tissue. In the novel, a noninvasive method for laser Lipolysis and the heating and cooling behavior occurring in laser Lipolysis was studied [9]. In the theoretical model, laser Lipolysis that helped by cooling the skin was investigated by establishing a homogeneous multi-layer skin model that included the epidermis, dermis, and subcutaneous layer.

In biological tissue, a classical Fourier law describes a mathematical model for the study of heat transfer. In this model, during the thermal therapy of electromagnetic radiation, a separate coordination system and various boundary conditions are studied [10]. Galerkin’s method is used to solve the problem with Bernstein polynomial as a basis function [11]. They discussed the effect of the parameters \(P_{\mathrm{f}}, P_\mathrm{m}, P_\mathrm{r}, K_{\mathrm{i}}\) and \(B_{\mathrm{i}}\) on the tissue and found that the condition of the boundary and internal heat in the human body during thermal therapy is not equal, that is, changes in organ from one organ to another.

The classical Fourier law is not good for heat transfer in biological tissue. Heat always promotes with biological tissue at the time of relaxation with finite speed. A thermal wave model approach has been introduced based on relaxation time known as the non-classical Fourier bioheat model. After removing, the paradox Cattaneo [12] and Vernotte [13] introduced SPL bioheat model as follows:

$$\begin{aligned} q(r,t+\tau _{\mathrm{q}})=-k{\triangledown} T(r,t). \end{aligned}$$
(2)

This theoretically examines the thermal behavior in the living tissue of the thermal wave model, which is under continuous, sinusoidal, or phase surface heating. The heat mainly spreads in the direction of the skin vertically. The effects of thermal physical properties were discussed on wave model heat transfer. The problem has been solved using a modified discretization scheme based on the Laplace transform [14].

A mathematical model is considered for non-Fourier (SPL) heat transfer in tumor or cancer tissue [15] and a non-Fourier (SPL) heat mass transfer within the food items under generalized boundary conditions [16]. In these mathematical models, a finite difference technique is used for discretization in space, and the non-dimensional boundary value problem has been solved by the Legendre Wavelet basis function and compared to the results obtained by the Legendre Galerkin Wavelet method, with exact solutions and found in good agreement \((\tau _{\mathrm{q}}=0)\). They discussed the variability of time, the location of tumors or cancer, relaxation time, temperature distribution, etc.

This mathematical model [17] is based on the implementation of Cattaneo Christov heat flux for single and multi-walled-type carbon nanotubes with considering water as based fluid. The effect of thermal Biot numbers on fluid temperature is discussed and found a higher value of thermal relaxation parameter results in gradual retardation in the temperature profile.

The delay between the heat flux and temperature gradient is known as thermal relaxation time. However, due to microscale responses from time to time, the thermal wave model of bioheat transfer has not captured the microscale reactions in space. Due to this, it produces some unusual behavior of thermal diffusion. To consider the effect of rapid transient effects along with the effect of microstructural interaction, a phase interval for the temperature gradient has introduced another relaxation time \(\tau _{\mathrm{t}}\) [18, 19],

$$\begin{aligned} q(r,t+\tau _{\mathrm{q}})=-k{\triangledown} T(r,t+\tau _{\mathrm{t}}), \end{aligned}$$
(3)

and the respective model is called the dual-phase lagging (DPL) model. A DPL model is applied to the principle of porous media and non-balance heat transfer in organic tissues by Zhang [20]. In this work, phase lag times have been expressed as coupling factors, porosity, thermal conductivity of tissues and blood, and capacity of heat. If \(\tau _{\mathrm{t}}=0\), then DPL model changed in SPL model and if \(\tau _{\mathrm{q}}=0,\tau _{\mathrm{t}}=0\), then DPL model changed in classical Fourier model.

A mathematical model is considered as a DPL model of bioheat transfer, under generalized boundary condition, and hyperthermia treatment is studied by using the term Gaussian distribution source [21]. During the treatment of hyperthermia, the Gaussian distribution source helps in controlling the temperature, which makes this study more useful in the field of clinical therapeutic for prediction and control of temperature.

During theoretical thermal therapy, thermal behavior is examined under various non-Fourier boundary condition in living biological tissue with the DPL bioheat transfer model. The properties of the Legendre wavelet are utilized to obtain an estimated analytical solution to the problem, together with a finite difference scheme. It has been observed that when it is used with a spherical symmetrical coordination system, the second and third kinds of boundary condition are less affected to the surrounding tissues [22].

The time-fractional nonlinear dispersive partial differential equations in the sense of conformable fractional derivative are proposed. The solitary pattern solution to the problem is based on the residual fractional power series and homotopy asymptotic method. The results show that the algorithm is based on Taylor series approximations of the nonlinear equations in a rapid convergence series leading to ideal solutions [23, 24].

A comparative study of the Newell–Whitehead–Segel and nonlinear Kaup–Kupershmidt equations, this equation is solved by a modified analytical technique based on auxiliary parameters, residual power series method, and numerical approximations with the integral recursive scheme [25, 26]. A coupled nonlinear partial differential equations for momentum and conservation of energy are transformed into coupled nonlinear ordinary differential equations using exact similarity transformations, which are known as Cattaneo–Christov heat flux model for third-grade viscoelastic power-law non-Newtonian fluid [27]. A systematic analysis of boundary-layer flow depends on various parameters including Prandtl number, power index, and temperature variation coefficient and shows the effect of these parameters on the velocity and temperature profiles.

Theoretical analysis and a comprehensive experimental investigation of thermal and fire properties were performed in the work using thermogravimetric analysis, cone calorimeters, limiting oxygen index, vertical/horizontal burning tests, and scanning electron microscope tests [28]. Kleilton et al. [29] analysis concluded that the films fit the biological system. Thermal, physical, chemical, and mechanical stability are the same, and instability of the material is caused by the addition of charges in the chitosan polymer matrix.

Henze et al. [30] have analyzed the effect of thermal barrier coating for separation from hot gas. They explained the general behavior of the effect of the thermal barrier coating Biot number on the effective heat transfer coefficient. Biot number increases with increase in the Reynolds number, and the ratio between the pure hot gas and the effective heat transfer coefficient is increased. The conduction and convection heat transfer mechanisms were studied by [31] and also considering the importance of heat transfer parameters, i.e., Rayleigh number, Stefan number, Biot number, etc.

In the present study, we discussed the thermal behavior of the DPL model to skin tissues under the most generalized non-Fourier boundary condition. Using the discretization in space coordination, the problem with the initial condition is changed into the system of O.D.E’s. The unknown variables in the system of O.D.E’s are resolved using FELWGM, which converts the system into a Sylvester equation. Solving this Sylvester’s equation by using MATLAB software, the solution obtained is used for non-dimensional temperature distribution and various effects on the skin layer are analyzed.

Description of physical problem

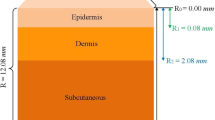
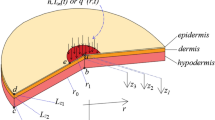
A multi-layer model on the skin is established including lagging behavior and the thermal behaviors of the skin during simulating. The skin made of three layers, i.e., epidermis, dermis, and subcutaneous tissue, is shown in Fig. 1. Every layer assumes to be homogeneous and considers the heat transfer in the skin with metabolic heat \(Q_\mathrm{m}\), water diffusion \(Q_\mathrm{d}\), and vaporization \(Q_\mathrm{v}\). Metabolic heat is generated in the skin tissues due to various physical processes occurring in the body [15]. Blood perfusion is a convection term produced by the flow of blood [15]. All three-layer contain metabolic heat and diffusion of water. Blood perfusion occurs in three layers except the epidermis layer. Water present inside the skin tissue could be vaporized due to temperature, but vaporization occurs only outer surface, i.e., epidermis layer [5].

Fig. 1
figure 1

Multi-layer of human skin

Full size image

Formulation of problem

The Fourier heat transfer model of multi-layer of tissue is given below [6, 7]:


Epidermis layer:

$$\begin{aligned}&\rho c_{{\uprho}}\,\frac{{\partial}T(r,t)}{{\partial} t}=k{\triangledown^{2}} T(r,t)+ Q_{\rm m}-Q_{\rm v}-Q_{\rm d}, \end{aligned}$$
(4)

Dermis layer:

$$ \begin{aligned} & \rho c_{\uprho } \frac{{\partial T(r,t)}}{{\partial t}} = k{\triangledown }^{2} T(r,t) + Q_{{\text{m}}} - Q_{{\text{d}}} \\ & \quad + \rho _{{\text{b}}} c_{{\uprho {\text{b}}}} w_{{\text{b}}} (T_{{\text{b}}} - T(r,t)), \\ \end{aligned} $$
(5)

Subcutaneous layer:

$$\begin{aligned}&\rho \,c_{\uprho }\,\frac{\partial T(r,t)}{\partial t}=\,k\,\triangledown ^{2} T(r,t)\,+Q_\mathrm{m}\,-Q_\mathrm{d}\nonumber \\&\quad +\rho _{\mathrm{b}}\,c_{{\uprho}{\rm b}}w_{\mathrm{b}}\,(T_{\mathrm{b}}\,-T(r,t)). \end{aligned}$$
(6)

After applying lagging in both space and time in the Fourier model of multi-layer, i.e., also called a DPL model of multi-layer, which is given below:


Epidermis layer:

$$\begin{aligned} \begin{aligned}&\tau _{\mathrm{q}}\rho c_{\uprho }\frac{\partial ^{2}T(r,t)}{\partial t^2}-\tau _{\mathrm{q}}\frac{\partial Q_\mathrm{m}}{\partial t}+\tau _{\mathrm{q}}\frac{\partial Q_\mathrm{d}}{\partial t}+\rho c_{\uprho }\frac{\partial T(r,t)}{\partial t}\\&\quad =k\triangledown ^{2} \left[ T(r,t)+\tau _{\mathrm{t}}\frac{\partial T(r,t)}{\partial t}\right] + Q_\mathrm{m}-Q_\mathrm{v}-Q_\mathrm{d}, \end{aligned} \end{aligned}$$
(7)

Dermis layer:

$$ \begin{aligned} & \tau _{{\text{q}}} \rho c_{\uprho } \frac{{\partial ^{2} T(r,t)}}{{\partial t^{2} }} - \tau _{{\text{q}}} \frac{{\partial Q_{{\text{m}}} }}{{\partial t}} + \tau _{{\text{q}}} \frac{{\partial Q_{{\text{d}}} }}{{\partial t}} + \rho c_{\uprho } \frac{{\partial T(r,t)}}{{\partial t}} \\ & \quad + \tau _{{\text{q}}} \rho _{{\text{b}}} c_{{\rho {\text{b}}}} w_{{\text{b}}} \frac{{\partial T(r,t)}}{{\partial t}} = k{\triangledown }^{2} \left[ {T(r,t) + \tau _{{\text{t}}} \frac{{\partial T(r,t)}}{{\partial t}}} \right] \\ & \quad + Q_{{\text{m}}} - Q_{{\text{d}}} + \rho _{{\text{b}}} c_{{\uprho {\text{b}}}} w_{{\text{b}}} (T_{{\text{b}}} - T(r,t)), \\ \end{aligned} $$
(8)

Subcutaneous layer:

$$ \begin{aligned} & \tau _{{\text{q}}} \rho c_{\uprho } \frac{{\partial ^{2} T(r,t)}}{{\partial t^{2} }} - \tau _{{\text{q}}} \frac{{\partial Q_{{\text{m}}} }}{{\partial t}} + \tau _{{\text{q}}} \frac{{\partial Q_{{\text{d}}} }}{{\partial t}} + \rho c_{\uprho } \frac{{\partial T(r,t)}}{{\partial t}} \\ & \quad + \tau _{{\text{q}}} \rho _{{\text{b}}} c_{{\rho {\text{b}}}} w_{{\text{b}}} \frac{{\partial T(r,t)}}{{\partial t}} = k{\triangledown }^{2} \left[ {T(r,t) + \tau _{{\text{t}}} \frac{{\partial T(r,t)}}{{\partial t}}} \right] \\ & \quad + Q_{{\text{m}}} - Q_{{\text{d}}} + \rho _{{\text{b}}} c_{{\uprho {\text{b}}}} w_{{\text{b}}} (T_{{\text{b}}} - T(r,t)), \\ \end{aligned} $$
(9)
$$\begin{aligned}&Q_\mathrm{m}\,= Q_{\mathrm{mo}}\,\begin{Bmatrix} 1+\frac{(T(r,t)\,-T_{0})}{10} \end{Bmatrix}, \end{aligned}$$
(10)
$$\begin{aligned}&Q_\mathrm{d}=\frac{D_{{f}}c_{{\uprho} {\rm W}}\,(\rho_\mathrm{s}\,-\rho _{\mathrm{c}})}{(\Delta r)^2}(T(r,t)\,-T_{\mathrm{0}}), \end{aligned}$$
(11)
$$\begin{aligned}&Q_{\mathrm{v}}=\frac{{\bigtriangleup} m{\bigtriangleup} H_{\mathrm{vap}}}{\delta c}, \end{aligned}$$
(12)
$$\begin{aligned}&{\Delta}m=\frac{D_{{v}}M_{\mathrm{W}}}{R_{\mathrm{a}}\delta c} \Big [\Big (\frac{P_{\mathrm{W}}}{T_{\mathrm{W}}}\Big )_\mathrm{s}-\Big (\frac{P_{\mathrm{W}}}{T_{\mathrm{W}}}\Big )_{{a}}RH\Big ], \end{aligned}$$
(13)

where the term \(Q_{\mathrm{mo}}\) is constant metabolic heat, blood perfusion rate \(w_{\mathrm{b}}\), blood density \(\rho _{\mathrm{b}}\) is taken as 1060 kg m\(^{-3}\), blood specific heat \(c_{{\uprho}{\rm b}}\) is taken as 3770 J kg\(^{-1}\,\) °C\(^{-1}\) [33] and blood temperature \(T_{\mathrm{b}}\) is taken as equal to core temperature \(T_{\mathrm{0}}\,(37\,^{\circ }\text {C})\). The average water vapor diffusivity and specific heat of water are \(D_\mathrm{v}\) and \(c_{{\uprho}{\rm W}}\) respectively. The water content in the core body and skin layer are \(\rho _{\mathrm{c}}\) and \(\rho _\mathrm{s}\), respectively. The thermal physical properties of three skin layer are shown in Table 1 [6, 7].

Table 1 Physical and thermal properties of the skin layer [6, 7]
Full size table

The associated initial conditions for DPL skin model are

$$\begin{aligned} T(r,0)&= T_{0}, \end{aligned}$$
(14)
$$\begin{aligned} \frac{\partial T(r,0)}{\partial t}&= 0, \end{aligned}$$
(15)

generalized non-Fourier boundary condition

$$\begin{aligned} A'\,\frac{\partial }{\partial r}\left[ T(0,t)+\tau _{\mathrm{t}}\,\frac{\partial T(0,t)}{\partial t}\,\right] \,+B'\,T(0,t)=f(t), \end{aligned}$$
(16)

for the first kind non-Fourier boundary condition: \( A'\,=0,\,B'\,=1,\,f(t)\,=T_{\mathrm{w}},\)

for the second kind non-Fourier boundary condition: \( A'\,=\,-k,\,B'\,=0,\,f(t)\,=q_{\mathrm{w}},\) for the third kind non-Fourier boundary condition: \( A'\,=\,-k,\,B'\,=H,\,f(t)\,=H\,T_\mathrm{s},\)

and non-Fourier symmetric condition

$$\begin{aligned} \frac{\partial }{\partial r}\left[ T(R,t)+\tau _{\mathrm{t}}\,\frac{\partial T(R,t)}{\partial t}\,\right] \,=0. \end{aligned}$$
(17)

Skin burn of model

The temperature of the epidermis or dermis or subcutaneous will cause damage to the skin reaches \(44^{o}C\) [36]. According to the first-order process of a chemical reaction,

$$\begin{aligned} \frac{{\text{d}}\Omega }{{\text{d}}t}=\left\{ \begin{array}{ll} 0 &{}\quad T(r,t)<44^{\text{o}}\text {C}, \;\text {i.e.}\, \text {no~ burn},\\ Pe^{\frac{\Delta {\text E}}{\text{RT}}}&{}\quad T(r,t)\ge 44^{\text{o}}\text {C},\;\text {i.e.}\, \text {burn}. \end{array}\right. \end{aligned}$$

First, second, and third-degree burn occurred, if damage function \(\Omega \) reaches values of 0.53, 1.0 and \(10^{4}\), respectively [37]. P and \(\Delta E\) [38] values are selected according to the prediction of skin burning [6, 7].

Non-dimensional quantities

Introducing the non-dimensional parameter and similarity criteria \(\theta (x,F_{\mathrm{o}})=\frac{T(r,t)\,-T_{0}}{T_{0}}, F_{\mathrm{o}}=\frac{k\,t}{\rho \,c_{\uprho }\,R^2},x=\frac{r}{R},\)\(\theta _{\mathrm{b}}=\frac{T_{\mathrm{b}}\,-T_{0}}{T_{0}}, \theta_{\mathrm{w}}\,=\frac{T_{\mathrm{w}}\,-T_{0}}{T_{0}}, \theta_\mathrm{s}\,=\frac{T_\mathrm{s}\,-T_{0}}{T_{0}},F_\mathrm{oq}\,=\frac{k\,\tau _{\mathrm{q}}}{\rho \,c_{\uprho }\,R^2},\) \(F_{\mathrm{o t}}=\frac{k\,\tau _{\mathrm{t}}}{\rho \,c_{\uprho} R^2}, P_{\mathrm{f}}=\sqrt{\frac{w_{\mathrm{b}}\,c_{{\uprho}{\rm b}}\,\rho _{\mathrm{b}}}{k}}R, P_{\mathrm{mo}}=\frac{Q_{\mathrm{mo}}\,R^2}{k\,T_{0}}, \alpha \,=0.1 \times T_{0}\),\(Q_{\mathrm{vo}}=\frac{\Delta m\,.\Delta H_\mathrm{vap}}{\delta c}\,\frac{R^2}{k T_{0}},Q_{\mathrm{do}}=\frac{D_{f}\,c_{{\uprho}{\rm W}}\,(\rho _\mathrm{s}\,-\rho _{\mathrm{c}})}{(\Delta r)^2}\,\frac{R^2}{k},\) \(f(F_{\mathrm{o}})\,=\frac{f(t)\,-B'\,T_{0}}{T_{0}},A\,=\frac{A'}{R}, B\,=B',K_{\mathrm{i}}=\frac{q_{\mathrm{w}}R}{T_{0}k},B_{\mathrm{i}}=\frac{H R}{k}.\) Equations (7–17) are converted into non-dimensional form as follows: Epidermis layer:

$$\begin{aligned} \begin{aligned}&F_{\mathrm{oq}}\,\frac{\partial ^{2}\theta (x,F_{\mathrm{o}})}{\partial F_{\mathrm{o}}^2}\,+(1\,-F_{\mathrm{oq}}\,\alpha \,P_{\mathrm{mo}}\,+F_{\mathrm{oq}}\,\,Q_{\mathrm{do}})\frac{\partial \theta (x,F_{\mathrm{o}})}{\partial F_{\mathrm{o}}}\,\\&\quad =\frac{\partial ^{2}}{\partial x^2}\left[ \theta (x,F_{\mathrm{o}})+F_{\mathrm{ot}}\frac{\partial \theta (x,F_{\mathrm{o}})}{\partial F_{\mathrm{o}}}\right] \\&\quad\quad + \,(\alpha \,P_{\mathrm{mo}} -Q_{\mathrm{do}})\,\theta (x,F_{\mathrm{o}})\,+P_{\mathrm{mo}}\,-Q_{\mathrm{vo}}, \end{aligned} \end{aligned}$$
(18)

Dermis layer:

$$\begin{aligned} \begin{aligned}&F_{\mathrm{oq}}\,\frac{\partial ^{2}\theta (x,F_{\mathrm{o}})}{\partial F_{\mathrm{o}}^2}\, +(1\,-F_{\mathrm{oq}}\,\alpha \,P_{\mathrm{mo}}\,+F_{\mathrm{oq}}\,\,Q_{\mathrm{do}}\,+F_{\mathrm{oq}}\,P_{\mathrm{f}}^2)\\&\quad \frac{\partial \theta (x,F_{\mathrm{o}})}{\partial F_{\mathrm{o}}} =\frac{\partial ^{2}}{\partial x^2}\left[ \theta (x,F_{\mathrm{o}})+F_{\mathrm{ot}}\frac{\partial \theta (x,F_{\mathrm{o}})}{\partial F_{\mathrm{o}}}\right] \,\\&\quad +(\alpha \,P_{\mathrm{mo}}\,-Q_{\mathrm{do}}\,-P_{\mathrm{f}}^2)\,\theta (x,F_{\mathrm{o}})\,+(P_{\mathrm{mo}}\,+P_{\mathrm{f}}^2\, \theta _{\mathrm{b}}), \end{aligned} \end{aligned}$$
(19)

Subcutaneous layer:

$$\begin{aligned} \begin{aligned}&F_{\mathrm{oq}}\,\frac{\partial ^{2}\theta (x,F_{\mathrm{o}})}{\partial F_{\mathrm{o}}^2}\,+(1\,-F_{\mathrm{oq}}\,\alpha \,P_{\mathrm{mo}}\,+F_{\mathrm{oq}}\,\,Q_{\mathrm{do}}\,+F_{\mathrm{oq}}\,P_{\mathrm{f}}^2)\\&\quad \frac{\partial \theta (x,F_{\mathrm{o}})}{\partial F_{\mathrm{o}}}=\frac{\partial ^{2}}{\partial x^2}\left[ \theta (x,F_{\mathrm{o}})+F_{\mathrm{ot}}\frac{\partial \theta (x,F_{\mathrm{o}})}{\partial F_{\mathrm{o}}}\right] \,\\&\quad +(\alpha \,P_{\mathrm{mo}}\,-Q_{\mathrm{do}}\,-P_{\mathrm{f}}^2)\,\theta (x,F_{\mathrm{o}})\,+(P_{\mathrm{mo}}\,+P_{\mathrm{f}}^2\, \theta _{\mathrm{b}}). \end{aligned} \end{aligned}$$
(20)

Initial conditions

$$\begin{aligned} \theta (x,0)&= 0, \end{aligned}$$
(21)
$$\begin{aligned} \frac{\partial \theta (x,0)}{\partial F_{\mathrm{o}}}&= 0, \end{aligned}$$
(22)

generalized non-Fourier boundary condition

$$\begin{aligned} A\,\frac{\partial }{\partial x}\left[ \theta (0,F_{\mathrm{o}})+F_{\mathrm{ot}}\frac{\partial \theta (0,F_{\mathrm{o}})}{\partial F_{\mathrm{o}}}\right] \,+B\,\theta (0,F_{\mathrm{o}})=f(F_{\mathrm{o}}), \end{aligned}$$
(23)

for the first kind non-Fourier boundary condition: \( A\,=0,\,B\,=1,\,f(F_{\mathrm{o}})\,=\theta _{\mathrm{w}},\)

$$\begin{aligned} \theta (0,F_{\mathrm{o}})=F(F_{\mathrm{o}})=\theta _{\mathrm{w}}, \end{aligned}$$
(24)

for the second kind non-Fourier boundary condition: \( A\,=\,1,\,B\,=0,\,f(F_{\mathrm{o}})\,=\,-K_{\mathrm{i}},\)

$$\begin{aligned} \frac{\partial \theta (0,F_{\mathrm{o}})}{\partial x}=F(F_{\mathrm{o}})= -K_{\mathrm{i}}(1-e^{\frac{-F_{\mathrm{o}}}{F_{\mathrm{ot}}}}), \end{aligned}$$
(25)

(see Appendix “Second kind non-Fourier boundary condition”),


for the third kind non-Fourier boundary condition: \( A\,=\,1,\,B\,=\,-B_{\mathrm{i}},\,f(F_{\mathrm{o}})\,=\,-B_{\mathrm{i}}\,\theta _\mathrm{s},\)

$$\begin{aligned} \frac{\partial \theta (0,F_{\mathrm{o}})}{\partial x}=F(F_{\mathrm{o}})= -B_{\mathrm{i}}(\theta _\mathrm{s}-\theta (0,F_{\mathrm{o}}))(1-e^{\frac{-F_{\mathrm{o}}}{F_{\mathrm{ot}}}}), \end{aligned}$$
(26)

(see Appendix “Third kind non-Fourier boundary condition”),


and non-Fourier symmetric condition

$$\begin{aligned} \frac{\partial }{\partial x}\left[ \theta (1,F_{\mathrm{o}})+F_{\mathrm{ot}}\frac{\partial \theta (1,F_{\mathrm{o}})}{\partial F_{\mathrm{o}}}\right] \,=0, \end{aligned}$$
(27)

(see Appendix “Non-Fourier symmetric condition”).

Numerical solution of the problem

By finite difference scheme, we discretized the domain in space variable x. Let the grid size, \(x = h = 1 /{\text{k}}\,\ge \,0\) and grid points are taken in the space interval [0, 1] are the numbers \(x_\mathrm{j} = jh, j = 1 , 2 , \ldots , {\text{k}} .\) The non-dimensional temperature \(\theta \) at points \(x_\mathrm{j}\) is indicated by \(\theta _\mathrm{j}(F_{\mathrm{o}})\,= \theta (x_\mathrm{j},F_{\mathrm{o}})\), for \(F_{\mathrm{o}}\,\ge \,0.\) We used central difference scheme for second order derivative.

After simple algebraic computation, Eqs. (18–27) change the system into vector matrix as follows:


Epidermis layer:

$$\begin{aligned} \begin{aligned}&F_{\mathrm{oq}}\,\frac{{\text{d}}^{2}\theta _\mathrm{j}(F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}^2}\,+(1\,-F_{\mathrm{oq}}\,\alpha \,P_{\mathrm{mo}}\,+F_{\mathrm{oq}}\,\,Q_{\mathrm{do}})\frac{{\text{d}} \theta _\mathrm{j}(F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}} \\&\quad =\frac{1}{h^2} \left[ \theta _\mathrm{j+1}(F_{\mathrm{o}})\,-2\,\theta _\mathrm{j}(F_{\mathrm{o}})\,+\theta _\mathrm{j-1}(F_{\mathrm{o}})\right] \\&\quad \quad +F_{\mathrm{ot}}\frac{{\text{d}}}{{\text{d}} F_{\mathrm{o}}}\left[ \frac{1}{h^2} \{\theta _\mathrm{j+1}(F_{\mathrm{o}})\,-2\,\theta _\mathrm{j}(F_{\mathrm{o}})\,+\theta _\mathrm{j-1}(F_{\mathrm{o}})\}\right] \\&\quad \quad +(\alpha \,P_{\mathrm{mo}}\,-Q_{\mathrm{do}})\,\theta _\mathrm{j}(F_{\mathrm{o}})\,+N_\mathrm{1j}, \end{aligned} \end{aligned}$$
(28)

Dermis layer:

$$\begin{aligned} \begin{aligned}&F_{\mathrm{oq}}\,\frac{{\text{d}}^{2}\theta _\mathrm{j}(F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}^2}\,+(1\,-F_{\mathrm{oq}}\,\alpha \,P_{\mathrm{mo}}\, +F_{\mathrm{oq}}\,\,Q_{\mathrm{do}}\,+F_{\mathrm{oq}}\,P_{\mathrm{f}}^2)\\&\quad \frac{{\text{d}} \theta _\mathrm{j}(F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}} =\frac{1}{h^2} \left[ \theta _\mathrm{j+1}(F_{\mathrm{o}})\,-2\,\theta _\mathrm{j}(F_{\mathrm{o}})\,+\theta _\mathrm{j-1} (F_{\mathrm{o}})\right] \,\\&\quad +F_{\mathrm{ot}}\frac{{\text{d}}}{{\text{d}} F_{\mathrm{o}}}\left[ \frac{1}{h^2} (\theta _\mathrm{j+1}(F_{\mathrm{o}})\,-2\,\theta _\mathrm{j}(F_{\mathrm{o}})\,+\theta _\mathrm{j-1}(F_{\mathrm{o}}))\right] \\&\quad +(\alpha \,P_{\mathrm{mo}}\, -Q_{\mathrm{do}}\,-P_{\mathrm{f}}^2)\,\theta _\mathrm{j}(F_{\mathrm{o}})\,+N_\mathrm{2j}, \end{aligned} \end{aligned}$$
(29)

Subcutaneous layer:

$$\begin{aligned} \begin{aligned}&F_{\mathrm{oq}}\,\frac{{\text{d}}^{2}\theta _\mathrm{j}(F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}^2}\,+(1\,-F_{\mathrm{oq}}\,\alpha \,P_{\mathrm{mo}}\,+F_{\mathrm{oq}}\,\,Q_{\mathrm{do}}\,+F_{\mathrm{oq}}\,P_{\mathrm{f}}^2)\\&\quad \frac{{\text{d}} \theta _\mathrm{j}(F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}}=\frac{1}{h^2} \left[ \theta _\mathrm{j+1}(F_{\mathrm{o}})\,-2\,\theta _\mathrm{j}(F_{\mathrm{o}})\,+\theta _\mathrm{j-1}(F_{\mathrm{o}})\right] \,\\&\quad +F_{\mathrm{ot}}\frac{{\text{d}}}{{\text{d}} F_{\mathrm{o}}}\left[ \frac{1}{h^2} (\theta _\mathrm{j+1}(F_{\mathrm{o}})\,-2\,\theta _\mathrm{j}(F_{\mathrm{o}})\,+\theta _\mathrm{j-1}(F_{\mathrm{o}}))\right] \\&\quad +(\alpha \,P_{\mathrm{mo}}\,-Q_{\mathrm{do}}\,-P_{\mathrm{f}}^2)\,\theta _\mathrm{j}(F_{\mathrm{o}})\,+N_\mathrm{3j}, \end{aligned} \end{aligned}$$
(30)

with initial conditions

$$\begin{aligned} \theta _\mathrm{j}(0)\,=0,\,\frac{{\text{d}} \theta _\mathrm{j}(0)}{{\text{d}} F_{\mathrm{o}}}\,=0. \end{aligned}$$
(31)

Using four-point formula [39], boundary points given as

$$\begin{aligned}&\frac{\partial \theta }{\partial x}\mid _{x\,=0}\,=\frac{1}{20\,h}\,\left[ -21\,\theta _{0}\, +13\,\theta _\mathrm{1}\,+17\,\theta _\mathrm{2}\,-9\,\theta _\mathrm{3}\right] , \end{aligned}$$
(32)
$$\begin{aligned}&\frac{\partial \theta }{\partial x}\mid _{x\,=1}\,=\frac{1}{20\,h}\,\left[ 21\,\theta _\mathrm{k\,+1}\,-13\,\theta _\mathrm{k}\,-17\, \theta _\mathrm{k\,-1}\,+9\,\theta _\mathrm{k\,-2}\right] . \end{aligned}$$
(33)

Using vector-matrix notation, Eqs. (28–30) can be written in the more compact form

Epidermis layer:

$$\begin{aligned} \begin{aligned}&F_{\mathrm{oq}}\,\frac{{\text{d}}^{2}\theta (F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}^2}\,+(1\,-F_{\mathrm{oq}}\,\alpha \,P_{\mathrm{mo}}\,+F_{\mathrm{oq}}\,\,Q_{\mathrm{do}})\frac{{\text{d}} \theta (F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}}\,\\&\quad =M\,\theta (F_{\mathrm{o}})\,+F_{\mathrm{ot}}\frac{{\text{d}} \,(M\,\theta (F_{\mathrm{o}}))}{{\text{d}} F_{\mathrm{o}}}\\&\quad\quad +\,(\alpha \,P_{\mathrm{mo}}-Q_{\mathrm{do}})\,\theta (F_{\mathrm{o}})+ N_\mathrm{1}, \end{aligned} \end{aligned}$$
(34)

Dermis layer:

$$\begin{aligned} \begin{aligned}&F_{\mathrm{oq}}\,\frac{{\text{d}}^{2}\theta \,(F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}^2}+(1-F_{\mathrm{oq}}\,\alpha \,P_{\mathrm{mo}}+F_{\mathrm{oq}}\,Q_{\mathrm{do}}+F_{\mathrm{oq}}\,P_{\mathrm{f}}^2)\frac{{\text{d}} \theta (F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}}\,\\&\quad =M\,\theta (F_{\mathrm{o}})\,+F_{\mathrm{ot}}\frac{{\text{d}} \,(M\,\theta (F_{\mathrm{o}}))}{{\text{d}} F_{\mathrm{o}}}\\&\quad \quad +\,(\alpha \,P_{\mathrm{mo}}\,-Q_{\mathrm{do}}\,-P_{\mathrm{f}}^2)\,\theta (F_{\mathrm{o}})\,+N_\mathrm{2}, \end{aligned} \end{aligned}$$
(35)

Subcutaneous layer:

$$\begin{aligned} \begin{aligned}&F_{\mathrm{oq}}\,\frac{{\text{d}}^{2}\theta \,(F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}^2}\,\\&\quad +(1\,-F_{\mathrm{oq}}\,\alpha \,P_{\mathrm{mo}}\,+F_{\mathrm{oq}}\,\,Q_{\mathrm{do}}\,+F_{\mathrm{oq}}\,P_{\mathrm{f}}^2)\frac{{\text{d}} \theta (F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}}\,\\&=M\,\theta (F_{\mathrm{o}})\,+F_{\mathrm{ot}}\frac{{\text{d}} \,(M\,\theta (F_{\mathrm{o}}))}{{\text{d}} F_{\mathrm{o}}}\\&\quad +\,(\alpha \,P_{\mathrm{mo}}\,-Q_{\mathrm{do}}\,-P_{\mathrm{f}}^2)\,\theta (F_{\mathrm{o}})\,+N_\mathrm{3}, \end{aligned} \end{aligned}$$
(36)

where

$$\begin{aligned} \theta \,=[\theta _\mathrm{1}\theta _\mathrm{2}\cdots \theta _\mathrm{k}]^\mathrm{T}, \end{aligned}$$
(37)

with initial condition

$$\begin{aligned} \theta (0)\,=[\theta _\mathrm{1}(0)\theta _\mathrm{2}(0)\;\cdots \;\theta _\mathrm{k}(0)]^\mathrm{T}\, =[0\;0\;\cdots \;0]^\mathrm{T}, \end{aligned}$$
(38)

and

$$\begin{aligned} \frac{{\text{d}}\theta (0)}{{\text{d}}F_{\mathrm{o}}}\,=\begin{bmatrix} \frac{{\text{d}}\theta _\mathrm{1}(0)}{{\text{d}}F_{\mathrm{o}}}\;\frac{{\text{d}}\theta _\mathrm{2}(0}{{\text{d}}F_{\mathrm{o}}}\;\cdots \; \frac{{\text{d}}\theta _\mathrm{k}(0)}{{\text{d}}F_{\mathrm{o}}} \end{bmatrix}^\mathrm{T}\,=[0\;0\;\cdots \;0]^\mathrm{T}, \end{aligned}$$
(39)

order of matrix M is \({\text{k}}\times {\text{k}}\) and order of matrix \(\theta , N_\mathrm{1}, N_\mathrm{2}\), and \(N_\mathrm{3}\) are \({\text{k}}\times 1\), where

$$\begin{aligned}&M=M_{l}\left\{ \begin{array}{ll} l=1& \quad {{\text{for}}\quad{\text{first}}\quad{\text{kind}}\quad{\text{non-Fourier}}\quad{\text{boundary}}\quad{\text{condition}} },\\ l=2&\quad {{\text{for}}\quad{\text{second}}\quad{\text{kind}}\quad{\text{non-Fourier}}\quad{\text{boundary}}\quad{\text{condition}},}\\ l=3& \quad {{\text{for}}\quad{\text{third}}\quad{\text{kind}}\quad{\text{non-Fourier}}\quad{\text{boundary}}\quad{\text{condition}}.} \end{array}\right. \end{aligned}$$
(40)
$$\begin{aligned}&F_{l}(F_{\mathrm{o}})=\left\{ \begin{array}{ll} \theta _{\mathrm{w}}&{}\quad l=1,\,\hbox {for first kind non-Fourier boundary condition,}\\ \frac{20\,h\,K_{\mathrm{i}}(1-e^{\frac{-F_{\mathrm{o}}}{F_{\mathrm{ot}}}})}{21}&{}\quad l=2,\,\hbox {for second kind non-Fourier boundary condition,}\\ \frac{20\,h\,B_{\mathrm{i}}(\theta _\mathrm{s}-\theta (0,F_{\mathrm{o}}))(1-e^{\frac{-F_{\mathrm{o}}}{F_{\mathrm{ot}}}})}{21}&{}\quad l=3,\,\hbox {for third kind non-Fourier boundary condition. } \end{array}\right. \end{aligned}$$
(41)
$$\begin{aligned}&\quad&\quad M_\mathrm{1}=\frac{1}{h^2}\begin{bmatrix} -2 &{}\quad 1 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad -2 &{}\quad 1 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad -2 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0\\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 1 &{}\quad -2 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad \frac{-9}{21} &{}\quad \frac{38}{21} &{}\quad \frac{-29}{21} \end{bmatrix}, \end{aligned}$$
(42)
$$\begin{aligned}&\quad&\quad M_\mathrm{2}=\frac{1}{h^2}\begin{bmatrix} \frac{-29}{21} &{}\quad \frac{38}{21} &{}\quad \frac{-9}{21} &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad -2 &{}\quad 1 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad -2 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0\\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 1 &{}\quad -2 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad \frac{-9}{21} &{}\quad \frac{38}{21} &{}\quad \frac{-29}{21} \end{bmatrix}, \end{aligned}$$
(43)
$$\begin{aligned}&\quad&\quad M_\mathrm{3}=\frac{1}{h^2}\begin{bmatrix} \frac{-29}{21} &{}\quad \frac{38}{21} &{}\quad \frac{-9}{21} &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad -2 &{}\quad 1 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad -2 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0\\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 1 &{}\quad -2 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad \frac{-9}{21} &{}\quad \frac{38}{21} &{}\quad \frac{-29}{21} \end{bmatrix}, \end{aligned}$$
(44)
$$\begin{aligned}&N_{1}=\begin{bmatrix} P_{\mathrm{mo}}-Q_{\mathrm{vo}}+\frac{F_{l}(F_{\mathrm{o}})}{h^2}&P_{\mathrm{mo}}-Q_{\mathrm{vo}}&\cdots&P_{\mathrm{mo}}-Q_{\mathrm{vo}} \end{bmatrix}^\mathrm{T}, \end{aligned}$$
(45)
$$\begin{aligned}&N_\mathrm{2}=\begin{bmatrix} P_{\mathrm{mo}}+P_{\mathrm{f}}^2 \theta _{\mathrm{b}}+\frac{F_{l}(F_{\mathrm{o}})}{h^2}&P_{\mathrm{mo}}+P_{\mathrm{f}}^2 \theta _{\mathrm{b}}&\cdots&P_{\mathrm{mo}}+P_{\mathrm{f}}^2 \theta _{\mathrm{b}} \end{bmatrix}^\mathrm{T}, \end{aligned}$$
(46)
$$\begin{aligned}&N_\mathrm{3}=\begin{bmatrix} P_{\mathrm{mo}}+P_{\mathrm{f}}^2 \theta _{\mathrm{b}}+\frac{F_{l}(F_{\mathrm{o}})}{h^2}&P_{\mathrm{mo}}+P_{\mathrm{f}}^2 \theta _{\mathrm{b}}&\cdots&P_{\mathrm{mo}}+P_{\mathrm{f}}^2 \theta _{\mathrm{b}} \end{bmatrix}^\mathrm{T}. \end{aligned}$$
(47)

Finite element Legendre wavelet Galerkin method

To solve the system of ordinary differential Eqs. (34–39), let us consider

$$\begin{aligned} \frac{{\text{d}}^{2}\theta \,(F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}^2}\,=C_{\mathrm{y}}^\mathrm{T}\,\psi (F_{\mathrm{o}}), \end{aligned}$$
(48)

where \({\text{y}}=1, 2,\) and 3 for epidermis, dermis, and subcutaneous layer, respectively, \(C_{\mathrm{y}}^\mathrm{T}\) is unknown coefficient matrix of order \(2^{{\text{k}}-1} M'\times 2^{{\text{k}}-1} M'\), and \(\psi (F_{\mathrm{o}})\) is a column vector of \(2^{{\text{k}}-1} M'\times 1\),

$$ \psi (F_{{\text{o}}} ) = \left[ {\begin{array}{*{20}c} {\psi _{{10}} } & {\psi _{{11}} } & \cdots & {\psi _{{1{{M'}} - 1}} } & {\psi _{{20}} } & {\psi _{{21}} } & \cdots & {\psi _{{2{{M'}} - 1}} } & {\psi _{{2^{{{\text{k}} - {1}}} 0}} } \\ {} & {\psi _{{2^{{{\text{k}} - {1}}} 1}} } & \cdots & {\psi _{{{\text{2}}^{{{\text{k}} - {\text{1}}}} {{M'}} - {1}}} } & {} & {} & {} & {} & {} \\ \end{array} } \right]^{{\text{T}}} $$
(49)

Legendre Wavelets  \(\psi _{nm}(F_{\mathrm{o}})=\psi (\text{k},{\hat{n}},m,F_{\mathrm{o}})\) by Razzaghi and Yousefi [40] in [0,1) have four arguments, \({\text{k}}=2,3,\cdots, \, {\hat{n}}=2n-1; \,n=1,2,\cdots ,2^{{\text{k}}-1};\, m=0,1,\cdots, \,M'-1;\) \(F_{\mathrm{o}}\) is the normalized time. The Legendre polynomial of order m with mass function \(w(F_{o})=1;\,F_{\mathrm{o}}\in [0,1]\) formed orthogonal set.

$$\begin{aligned} \psi _{nm}(F_{\mathrm{o}})= {\left\{ \begin{array}{ll} \sqrt{({m}+\frac{1}{2})} 2^\frac{\text{k}}{2} P_{m}(2^{\text{k}}F_{\mathrm{o}}-{\hat{n}}),& \quad \frac{{\hat{n}}-1}{2^{\text{k}}}\le F_{\mathrm{o}}\le \frac{{\hat{n}}+1}{2^{\text{k}}},\\ 0&\quad \text{otherwise}, \end{array}\right. } \end{aligned}$$
(50)

where \(P_{0}(F_{\mathrm{o}})=1, P_\mathrm{1}(F_{\mathrm{o}})=F_{\mathrm{o}}, P_{m+1}(F_{\mathrm{o}})=\frac{2 m+1}{m+1}F_{\mathrm{o}} P_{m}(F_{\mathrm{o}})-\frac{m}{m+1}P_{m-1}(F_{\mathrm{o}})\). Integrating Eq. (48) with respect to \(F_{\mathrm{o}}\), we get

$$\begin{aligned} \frac{{\text{d}}\theta \,(F_{\mathrm{o}})}{{\text{d}} F_{\mathrm{o}}}\,=C_{\mathrm{y}}^\mathrm{T}\,P\,\psi (F_{\mathrm{o}}), \end{aligned}$$
(51)

where P is an operational matrix of order \(2^{{\text{k}}-1} M'\times 2^{{\text{k}}-1} M'\). The operational matrix of integration [40] is defined as

$$\begin{aligned}&\int _{0}^{F_{\mathrm{o}}} \psi (s)\,ds =P\, \psi (F_{\mathrm{o}}), F_{\mathrm{o}}\in [0,1], \end{aligned}$$
(52)
$$\begin{aligned}&P=\frac{1}{2^{\text{k}}}\begin{bmatrix} L &{} \quad O &{} \quad O &{} \quad \cdots &{} \quad O &{} \quad O &{} \quad O \\ 0 &{} \quad L &{}\quad O &{}\quad \cdots &{}\quad O &{}\quad O &{}\quad O \\ 0 &{}\quad 0 &{}\quad L &{}\quad \cdots &{}\quad O &{}\quad O &{}\quad O\\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad L &{}\quad O \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad L \end{bmatrix}, \end{aligned}$$
(53)

where O and L are the matrix of order \(M'-1\times M'-1\) defined as

$$\begin{aligned} O=\begin{bmatrix} 2 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0\\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ . &{}\quad . &{}\quad . &{}\quad \cdots &{}\quad . &{}\quad . &{}\quad . \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{bmatrix},\end{aligned}$$
(54)

and

$$\begin{aligned} L =\begin{bmatrix} {1} &{}\quad \frac{1}{ \sqrt{3}} &{}\quad 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ -\frac{1}{\sqrt{3}} &{}\quad 0 &{}\quad \frac{1}{\sqrt{15}} &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -\frac{1}{\sqrt{15}} &{}\quad 0 &{}\quad \frac{1}{\sqrt{35}} &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -\frac{1}{\sqrt{35}} &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \dots &{}\quad \dots &{}\quad \dots &{}\quad \dots &{}\quad \dots &{}\quad \dots &{}\quad \dots \\ \dots &{}\quad \dots &{}\quad \dots &{}\quad \dots &{}\quad \dots &{}\quad \dots &{}\quad \dots \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \frac{1}{\sqrt{(2M'-3)(2M'-1)}} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \dots &{}\quad -\frac{1}{\sqrt{(2M'-1)(2M'-3)}} &{}\quad 0 \\ \end{bmatrix}. \end{aligned}$$
(55)

Again integration Eq. (51) with respect to \(F_{\mathrm{o}}\), we get

$$\begin{aligned} \theta \,(F_{\mathrm{o}})\,=C_{\mathrm{y}}^\mathrm{T}\,P^2\,\psi (F_{\mathrm{o}}). \end{aligned}$$
(56)

Replace the value of \(\theta (F_{\mathrm{o}}), \frac{d\theta \,(F_{\mathrm{o}})}{d F_{\mathrm{o}}}\) and \(\frac{d^{2}\theta \,(F_{\mathrm{o}})}{d F_{\mathrm{o}}^2}\) in Eqs. (34–36) respectively, we get


Epidermis layer:

$$\begin{aligned} C_\mathrm{1}^\mathrm{T}-M_{l} C_\mathrm{1}^\mathrm{T} X_\mathrm{1}-Z_\mathrm{1}=0, \end{aligned}$$
(57)

Dermis layer:

$$\begin{aligned} C_\mathrm{2}^\mathrm{T}-{M}_{{l}} C_\mathrm{2}^\mathrm{T} X_\mathrm{2}-Z_\mathrm{2}=0, \end{aligned}$$
(58)

Subcutaneous layer:

$$\begin{aligned} C_\mathrm{3}^\mathrm{T}-M_{l} C_\mathrm{3}^\mathrm{T} X_\mathrm{3}-Z_\mathrm{3}=0, \end{aligned}$$
(59)

where \(X_\mathrm{1}=(P^2+F_{\mathrm{ot}}P)[(F_{\mathrm{oq}}I +(1-F_{\mathrm{oq}}\alpha P_{\mathrm{mo}}+F_{\mathrm{oq}} Q_{\mathrm{do}})P -(\alpha P_{\mathrm{mo}}-Q_{\mathrm{do}})P^2)]^{-1}, Z_\mathrm{1}=N_\mathrm{1}d^{T}[(F_{\mathrm{oq}}I +(1-F_{\mathrm{oq}}\alpha P_{\mathrm{mo}}+F_{\mathrm{oq}} Q_{\mathrm{do}})P -(\alpha P_{\mathrm{mo}}-Q_{\mathrm{do}})P^2)]^{-1}, X_\mathrm{2}=(P^2+F_{\mathrm{ot}}P)[(F_{\mathrm{oq}}I +(1-F_{\mathrm{oq}}\alpha P_{\mathrm{mo}}+F_{\mathrm{oq}} Q_{\mathrm{do}}+F_{\mathrm{oq}}P_{\mathrm{f}}^2)P -(\alpha P_{\mathrm{mo}}-Q_{\mathrm{do}}-P_{\mathrm{f}}^2)P^2)]^{-1}, Z_\mathrm{2}=N_\mathrm{2}d^{T}[(F_{\mathrm{oq}}I +(1-F_{\mathrm{oq}}\alpha P_{\mathrm{mo}}+F_{\mathrm{oq}} Q_{\mathrm{do}}+F_{\mathrm{oq}}P_{\mathrm{f}}^2)P -(\alpha P_{\mathrm{mo}}-Q_{\mathrm{do}}-P_{\mathrm{f}}^2)P^2)]^{-1}, \) \(X_\mathrm{3}=(P^2+F_{\mathrm{ot}}P)[(F_{\mathrm{oq}}I +(1-F_{\mathrm{oq}}\alpha P_{\mathrm{mo}}+F_{\mathrm{oq}} Q_{\mathrm{do}}+F_{\mathrm{oq}}P_{\mathrm{f}}^2)P -(\alpha P_{\mathrm{mo}}-Q_{\mathrm{do}}-P_{\mathrm{f}}^2)P^2)]^{-1}, \) and \(Z_\mathrm{3}=N_\mathrm{3}d^{T}[(F_{\mathrm{oq}}I +(1-F_{\mathrm{oq}}\alpha P_{\mathrm{mo}}+F_{\mathrm{oq}} Q_{\mathrm{do}}+F_{\mathrm{oq}}P_{\mathrm{f}}^2)P -(\alpha P_{\mathrm{mo}}-Q_{\mathrm{do}}-P_{\mathrm{f}}^2)P^2)]^{-1}.\) Equations (57–59) are Sylvester equations. After solving these Sylvester equations, we get the unknown value of the coefficient vector \(C_{\mathrm{y}}^\mathrm{T}\) and substituting these values of \(C_{\mathrm{y}}^\mathrm{T}\) in Eq. (56). We now obtain required non-dimensional temperature \((\theta (x,F_{\mathrm{o}}))\) in each layer of skin. Mathematica [41] and MATLAB [42] software has been used for computational analysis.

Results and discussion

To analyze the effect of different parameters and non-Fourier boundary conditions on multi-layer of skin injuries, we select reference value including content properties and parameters as mentioned in Table 1 and some other parameters vary as shown inside the figures.

Comparison with an exact solution

To verify the validity of the method, the solution obtained from FELWGM is compared with the exact solution, which was obtained by using a Laplace transformation technique for a particular case (setting \(F_{\mathrm{oq}}=F_{\mathrm{ot}}=0\) in Eqs. (18–20) with first kind boundary condition). Using the Laplace transform technique, we obtain the exact solution as follows:

Epidermis layer:

$$\begin{aligned} \begin{aligned}&\theta (x,\,F_{\mathrm{o}})=\,\frac{1}{U_\mathrm{1,1}(U_\mathrm{1,2}+1)V_\mathrm{1}}\left[ -(U_\mathrm{1,2}+U_\mathrm{1,3})\,Q_{\mathrm{do}}\,\theta _{\mathrm{w}}\right. \\&\quad \left. + \,P_{\mathrm{mo}}(\alpha (U_\mathrm{1,2}+U_\mathrm{1,3})\,\theta _{\mathrm{w}}+(U_\mathrm{1,1}-1)(U_\mathrm{1,1}-U_\mathrm{1,2}))\right. \\&\quad \left. +\,(U_\mathrm{1,2}-U_\mathrm{1,1})(U_\mathrm{1,1}-1)\,Q_{\mathrm{vo}}\right] \\&\quad +\,\sum _\mathrm{n=0}^{\infty }\left( \frac{1}{U_\mathrm{1,4}\,V_\mathrm{1,n}}\right) \left[ e^{{\text{F}}_{\mathrm{o}}\,{{V}}_\mathrm{1,n}-{{U}}_\mathrm{1,4}({{x}}+2)}\left( \left( e^{2\,{{U}}_\mathrm{1,4}\,{{x}}} +e^{2\,{{U}}_\mathrm{1,4}\,}\right) \theta _{\mathrm{w}}(Q_{\mathrm{do}}+V_{1,\text{n}})\right. \right. \\&\quad \left. \left. +\,P_{\mathrm{mo}}\left( \left( e^{2\,{{U}}_\mathrm{1,4}}-e^{{{U}}_\mathrm{1,4}\,{{x}}}\right) \;(e^{{{U}}_\mathrm{1,4}\,{{x}}}-1) -\alpha (e^{2\,{{U}}_\mathrm{1,4}\,{{x}}}+e^{2\,U_\mathrm{1,4}})\theta _{\mathrm{w}}\right) \right. \right. \\&\quad \left. \left. +\,Q_{\mathrm{vo}}\left( -\left( e^{2\,{{U}}_{1,4}} -e^{{{U}}_{1,4}\,{{x}}}\right) \right) \left( e^{{{U}}_{1,4}\,{{x}}}-1\right) \right) \right] , \end{aligned} \end{aligned}$$
(60)

Dermis layer:

$$\begin{aligned} \begin{aligned}&\theta (x,\,F_{\mathrm{o}})=\,-\frac{1}{U_{2,1}(U_{2,2}+1)V_{2}} \left[ \left( U_{2,2}+U_{2,3}\right) \,Q_{\mathrm{do}}\,\theta _{\mathrm{w}}\right. \\&\quad \left. +\,P_{\mathrm{f}}^2\left( \left( U_{2,2}-U_{2,1}\right) \left( -1+U_{2,1}\right) \theta _{\mathrm{b}}+\left( U_{2,2}+U_{2,3}\right) \theta _{\mathrm{w}}\right) \right. \\&\quad \left. +\,P_{\mathrm{mo}}\left( \left( U_{2,2}-U_{2,1}\right) \left( -1+U_{2,1}\right) -\left( U_{2,2}+U_{2,3}\right) \alpha \,\theta {w}\right) \right] \\&\quad +\,\sum _\mathrm{n=0}^{\infty }\frac{1}{U_{2,4}\,V_{2,n}}\left[ e^{{\text{F}}_{\mathrm{o}}\,{{V}}_{2,{\text{n}}}-{{U}}_{2,4}({{x}}+2)}\left( \left( e^{2\,{{U}}_{2,4}\,{{x}}} +e^{2\,{{U}}_{2,4}\,}\right) \right. \right. \\&\quad \left. \left. \theta _{\mathrm{w}}\left( Q_{\mathrm{do}}+V_{2,\text{n}}\right) +P_{\mathrm{f}}^{2}\left( \left( e^{2\,{{U}}_{2,4}} -e^{{{U}}_{2,4}\,{{x}}}\right) \left( e^{{{U}}_{2,4}\,{{x}}}-1\right) \theta _{\mathrm{b}}\right. \right. \right. \\&\quad \left. \left. \left. +\,\left( e^{2\,{{U}}_{2,4}\,{{x}}}+e^{2\,{{U}}_{2,4}}\right) \theta _{\mathrm{w}}\right) +P_{\mathrm{mo}}\left( \left( e^{2\,{{U}}_{2,4}}-e^{{{U}}_{2,4}\,{{x}}}\right) \right. \right. \right. \\&\quad \left. \left. \left. \left( e^{{{U}}_{2,4}\,{{x}}}-1\right) -(e^{2\,{{U}}_{2,4}\,{{x}}} +e^{2\,{{U}}_{2,4}\,}\right) \alpha \theta _{\mathrm{w}})\right) \right] , \end{aligned} \end{aligned}$$
(61)

Subcutaneous layer:

$$\begin{aligned} \begin{aligned}&\theta (x,\,F_{\mathrm{o}})=\,-\frac{1}{U_\mathrm{3,1}(U_\mathrm{3,2}+1)V_\mathrm{3}}\\&\quad \left[ \left( U_\mathrm{3,2}+U_\mathrm{3,3}\right) \,Q_{\mathrm{do}}\,\theta _{\mathrm{w}}+P_{\mathrm{f}}^2\left( \left( U_\mathrm{3,2}-U_\mathrm{3,1}\right) (-1+U_\mathrm{3,1})\theta _{\mathrm{b}} \right. \right. \\&\quad \left. \left. +\,\left( U_\mathrm{3,2} +U_\mathrm{3,3}\right) \theta _{\mathrm{w}}\right) \right. \\&\quad \left. +\,P_{\mathrm{mo}}\left( \left( U_\mathrm{3,2}-U_\mathrm{3,1}\right) \left( -1+U_\mathrm{3,1}\right) -\left( U_\mathrm{3,2} +U_\mathrm{3,3}\right) \alpha \,\theta {w}\right) \right] \\&\quad +\,\sum _\mathrm{n=0}^{\infty }\frac{1}{U_\mathrm{3,4}\,V_\mathrm{3,n}} \left[ e^{{\text{F}}_{\mathrm{o}}\,{\text{V}}_\mathrm{3,{\text{n}}}-{{U}}_\mathrm{3,4}({{x}}+2)}\left( \left( e^{2\,{{U}}_\mathrm{3,4}\,{{x}}}+e^{2\,{{U}}_\mathrm{3,4}\,}\right) \right. \right. \\&\quad \left. \left. \theta _{\mathrm{w}}\left( Q_{\mathrm{do}}+V_{3,\text{n}}\right) +P_{\mathrm{f}}^{2} \left( \left( e^{\,{{2U}}_\mathrm{3,4}}-{\text{e}}^{{{U}}_\mathrm{3,4}\,{{x}}}\right) (e^{{{U}}_\mathrm{3,4}\,{{x}}}-1)\theta _{\mathrm{b}}\right. \right. \right. \\&\quad \left. \left. \left. +\,\left( e^{2\,{{U}}_\mathrm{3,4}\,{{x}}} +e^{2\,{{U}}_\mathrm{3,4}}\right) \theta _{\mathrm{w}}\right) \right. \right. \\&\quad \left. \left. +\,P_{\mathrm{mo}}\left( \left( e^{2\,{{U}}_\mathrm{3,4}}-e^{{{U}}_\mathrm{3,4}\,{{x}}}\right) \left( e^{{{U}}_\mathrm{3,4}\,{{x}}}-1\right) \right. \right. \right. \\&\quad \left. \left. \left. -\,\left( e^{2\,{{U}}_\mathrm{3,4}\,{{x}}}+e^{2\,{{U}}_\mathrm{3,4}\,}\right) \alpha \theta _{\mathrm{w}}\right) \right) \right] , \end{aligned} \end{aligned}$$
(62)

where \(U_\mathrm{y,1}\,=e^{{\text{x}}\,\sqrt{-{\text{V}}_{\mathrm{y}}}},\;U_\mathrm{y,2}\,=e^{2\sqrt{-{\text{V}}_{\mathrm{y}}}},\,U_\mathrm{y,3}\,=e^{2\,{\text{x}}\,\sqrt{-{\text{V}}_{\mathrm{y}}}},\, U_\mathrm{y,4}=\sqrt{-V_{\mathrm{y}}+V_\mathrm{y,n}}\,,\; V_\mathrm{1}\,=\alpha \,P_{\mathrm{mo}}-Q_{\mathrm{do}},\,V_\mathrm{2}=-(P_{\mathrm{f}}^{2}-\alpha P_{\mathrm{mo}}+Q_{\mathrm{do}}),\,V_\mathrm{3}=-(P_{\mathrm{f}}^{2}-\alpha P_{\mathrm{mo}}+Q_{\mathrm{do}}),\,V_\mathrm{y,n}=\frac{-1}{4}\,(1+2\,n)^{2}\,\pi ^{2}+V_{\mathrm{y}}\,;\;y=1\) for epidermis, \({\text{y}}=2\)  for dermis, and  \({\text{y}}=3\) for subcutaneous layers. A comparison of the exact and obtained solution is shown in Figs. 2–4 and found in good agreement.

Lagging behavior on skin layer for first kind non-Fourier boundary condition

Epidermis layer: If \(F_{\mathrm{oq}}=0,0.00696379\) and \(F_{\mathrm{ot}}=0,0.00696379\), we observed that the skin temperature decreases continuously. As time decreased, we observed that the temperature of the skin layer in the DPL model is decreased more than both classical Fourier and SPL models as shown in Figs. 5 , 8 and 11.

If \(\theta _{\mathrm{w}}=0.229189=45.48^{o}C\), the skin layer thickness burns up to \(x=0.3\), here in classical Fourier and SPL models burning are slightly greater than the DPL model. If \(\theta _{\mathrm{w}}\geq0.3=48.1^{\text{o}}{\text{C}}\), then skin layer burned almost completely. If \(\theta _{\mathrm{w}}\) increases, we observed that the burning of the skin layer in the DPL model is slightly less than to SPL and classical Fourier model as shown in Fig. 14.

If \(F_{\mathrm{oq}}=0.00696379\) be fixed, we observed that damage to skin thickness decreases as \(F_{\mathrm{ot}}\) increases. If \(F_{\mathrm{ot}}=0.00696379\) be fixed, we observed that damage of skin thickness increases as \(F_{\mathrm{oq}}\) increases as shown in Fig. 32.

Dermis layer: If \(F_{\mathrm{oq}}=0,0.0140766\) and \(F_{\mathrm{ot}}=0,0.0140766\), we observed that the skin temperature decreases continuously. As time decreases, we observed that the temperature of the skin layer in the DPL model is decreased more than both classical Fourier and SPL models. It also observed that initially, (\(x=0.0-0.25\)) temperature on the skin layer in the DPL model is slowly decreased than both classical Fourier and SPL models, after that skin temperature in the DPL model is below than the both classical Fourier model and SPL model as shown in Figs. 6 , 9 and 12.

If \(\theta _{\mathrm{w}}=0.240541=45.9^{o}C\), the skin layer thickness burns almost up to \(x=0.4\) in the DPL model with a slight change in classical Fourier and SPL models. If \(\theta _{\mathrm{w}}\geq0.302703=48.2^{o}C\), the skin layer burned almost completely. If \(\theta _{\mathrm{w}}\) increases, we observed that the burning of the skin layer in the DPL model is slightly less than classical Fourier and SPL models as shown in Fig. 15 .

If \(F_{\mathrm{oq}}=0.0140766\) is fixed, we observed that damage to skin thickness decreases as \(F_{\mathrm{ot}}\) increases. If \(F_{\mathrm{ot}}=0.0140766\) is fixed, in this case, we observed that damage of skin thickness increases as \(F_{\mathrm{oq}}\) increases as shown in Fig. 33.

Subcutaneous layer: If \(F_{\mathrm{oq}}=0,0.00791667\) and \(F_{\mathrm{ot}}=0,0.00791667\), we observed that the skin temperature decreases continuously. As time decreases, we observed that temperature of the skin layer in the DPL model is decreased more than both classical Fourier and SPL models. It also observed that initially, (\(x=0.0-0.3\)) skin temperature of the DPL model slight changed with respect to classical Fourier and SPL models, after that skin temperature in DPL model is below than the both classical Fourier and SPL models as shown in Figs. 7 , 10 and 13.

If \(\theta _{\mathrm{w}}=0.259459=46.6^{o}C\), the skin layer thickness burns almost up to \(x=0.2\) in the DPL model with a slight change in SPL and classical models. If \(\theta _{\mathrm{w}}\geq0.545946=57.2^{o}C\), the skin layer burned almost completely. If \(\theta _{\mathrm{w}}\) increases, we observed that the burning of skin layer in the DPL model is slightly less than classical Fourier and SPL model as shown in Fig. 16 .

If \(F_{\mathrm{oq}}=0.00791667\) is fixed, we observed that damage to skin thickness increases as \(F_{\mathrm{ot}}\) increases. If \(F_{\mathrm{ot}}=0.00791667\) be fixed, in this case, we observed that damage of skin thickness decreases as \(F_{\mathrm{oq}}\) increases as shown in Fig. 34.

Effect of temperature on the skin layer thickness for first kind non-Fourier boundary condition

Epidermis, Dermis, and Subcutaneous layers: We found the effect on skin layer thickness for \(\theta {w}=0.0540541(\,< \theta =0.189189\,(44\,^{o}C))\), the temperature in the skin layer is constantly increased as time increased and also observed that the temperature rise is less in DPL model than classical Fourier model at the initial time. It has been observed that if the thickness of the skin layer increases, then its temperature decreases as shown in Figs. 17–19 respectively.

Analysis of lagging on skin during hot and cold surface temperature with the first kind non-Fourier boundary condition at \(F_{\mathrm{o}}=0.5\)

Epidermis, Dermis, and Subcutaneous layers: If \(\theta _{\mathrm{w}}=0.0810811=40^{o}C(>\) body temperature), we observed that the skin temperature decreases continuously and also found that the skin temperature in the DPL model decreases slightly more than classical Fourier and SPL models. If \(\theta _{\mathrm{w}}(=\) body temperature), we found that the temperature has a negligible effect on the skin layer. But if \(\theta _{\mathrm{w}}=-0.324324\), we observed that the skin temperature increases continuously because the layer temperature reaches to normal body temperature and also found that the skin temperature in the DPL model increases slightly more than classical Fourier and SPL models as shown in Figs. 20–22, respectively.

Effect of Kirchhoff number \((K_{\mathrm{i}})\) and Biot number \((B_{\mathrm{i}})\) on skin layer at \(F_{\mathrm{o}}=0.5\)

The non-dimensional quantity \(K_{\mathrm{i}}\) is defined by the reference heat flux on the temperature profile that is demonstrated in the second kind boundary condition. We observed that as the value of the \(K_{\mathrm{i}}\) increased at fixed \(F_{\mathrm{o}}=0.5\), then the temperature of the skin increases at the initial boundary position, i.e., \(x=0\). At a fixed Kirchhoff number, we observed that the skin temperature is decreasing continuously as \(x>0\) which is shown in Figs. 23–25.

The non-dimensional quantity \(B_{\mathrm{i}}\) is defined by the reference heat transfer coefficient which is demonstrated in the third kind boundary condition. We observed that as the value of the \(B_{\mathrm{i}}\) increased at fixed \(F_{\mathrm{o}}=0.5\), then the temperature of the skin increases at the initial boundary position, i.e., \(x=0\). At a fixed Biot number, we observed that the skin temperature is decreasing continuously as \(x>0\) which is shown in Figs. 26–28.

The effect of generalized non-Fourier boundary condition on three layers of skin at \(F_{\mathrm{o}}=0.5\)

Epidermis, Dermis, and Subcutaneous layer: In the first, second, and third kind non-Fourier boundary conditions, we observed that skin temperature is continuously decreased. The skin layer temperature in the second and third kind non-Fourier boundary conditions decreases fast in comparison with the first kind non-Fourier boundary condition as shown in Figs. 29–31, respectively.

Conclusions

In this work, a detailed description of skin burns on different types of non-Fourier boundary condition is considered. The Legendre wavelet properties are applied to calculate the approximate analytical solution of the DPL model of multi-layer of skin.

In the first kind non-Fourier boundary condition, the burning of the skin layers depends on its thickness. As skin layer thickness increases, then burning reduces.

The burning time for skin layers varies with temperatures. As time increases, burning of the skin layers thickness also increases.

The temperature on skin layers decreases continuously in non-Fourier generalized boundary condition. In epidermis and dermis layers, the first kind non-Fourier boundary condition has more difference in the burning of skin layer thickness in comparison with the second and third kind non-Fourier boundary conditions. In subcutaneous layer, the first kind non-Fourier boundary condition has little difference in the burning of skin layer thickness in comparison with the second and third kind non-Fourier boundary conditions.

The skin layer thickness in the DPL model is less damaged than both classical Fourier and SPL models. If \(\theta _{\mathrm{w}}>\) body temperature, we observed that skin temperature in the DPL model is significantly decreased in comparison with classical Fourier and SPL models. If \(\theta _{\mathrm{w}}<\) body temperature, we observed that skin temperature in the DPL model is significantly increased in comparison with classical Fourier and SPL models because the layer temperature reaches to normal body temperature.

At time \(F_{\mathrm{o}}=0.5\), the multi-layer of skin thickness is completely burned if surface temperature \(\theta _{\mathrm{w}}\) is greater than \(\theta _{\mathrm{B}}\) where \(\theta _{\mathrm{B}}=\left\{ \begin{array}{ll} 0.3=48.1^{\circ}\text{C} &{}\quad \hbox {For~Epidermis~layer.~i.e.~First~Kind~Burn},\\ 0.302703=48.2^{\circ}\text{C}&{}\quad \hbox {For~Dermis~layer.~i.e.~Second~Kind~Burn},\\ 0.545946=57.2^{\circ}\text{C}&{} \quad \hbox {For~Subcutaneous~layer.~i.e.~Third~Kind~Burn}. \end{array}\right. \)

The burning of skin thickness decreases if \(\left\{ \begin{array}{ll} F_{\mathrm{oq}}<F_{\mathrm{ot}} &{}\quad \hbox {For\,Epidermis\,layer},\\ F_{\mathrm{oq}}<F_{\mathrm{ot}} &{}\quad \hbox {For\,Dermis\,layer, and}\\ F_{\mathrm{oq}}>F_{\mathrm{ot}} &{}\quad \hbox {For\,Subcutaneous\,layer}. \end{array}\right. \)

The burning of skin thickness increases if \(\left\{ \begin{array}{ll} F_{\mathrm{oq}}>F_{\mathrm{ot}} &{}\quad \hbox {For\,Epidermis\,layer},\\ F_{\mathrm{oq}}>F_{\mathrm{ot}} &{}\quad \hbox {For\,Dermis\,layer, and}\\ F_{\mathrm{oq}}<F_{\mathrm{ot}}&{}\quad \hbox { For\,Subcutaneous\,layer}. \end{array}\right. \)

The present work demonstrates the study of the DPL model of multi-layer of skin based on heat transfer and FELWGM as a solution method helps in the precise prediction of temperature. So, it makes this study more useful for the prediction and control of temperature for medical doctors in the clinical field. The entire analysis is presented in non-dimensional form. Therefore, these results provide a more comprehensive and better insight for understanding the behavior of skin burn injuries during temperature distribution of different types of boundary condition.