Introduction

Nowadays, due to the increase in energy saving demand in many engineering fields of the modern industry such as heating ventilation air conditioning and powertrain cooling and waste heat recovery, heat exchangers that are more efficient, smaller size and lower cost, heat transfer enhancement have been introduced to improve the overall thermohydraulic performance. There are several methods to increase heat transfer in the category of active, passive and combined mechanism. Passive technique uses special surface geometries, or fluid additives. Active technique due to external power source requirement has attracted relatively little attention in real practical applications, and passive technique through the use of various surface geometries such as corrugated tubes to be desired. Corrugated tubes can be made known as one of the coarsening surface methods. The thermal boundary layer developed on its walls is periodically interfered by flow recirculation, separation and reattachment and thereby increase of convective heat transfer coefficient. However, such achievements in heat transfer are perpetually followed by increased pressure drop penalty. Shell and helically coiled tube heat exchanger is one of the most applicable types of heat exchanger that its thermal performance can be investigated by replacing the corrugated coiled tubes instead of plain coiled tube. The use of internal helical plain tubes in heat exchangers is studied by a substantial number of researchers in thermal engineering systems. In what follows, the most relevant ones are mentioned. Rabienataj et al. [1] performed an empirical study to evaluate the alumina nanoparticles effects on the hydrothermal performance of a shell and helical tube heat exchanger. They found that lower pitches and higher heights of the groove of the heat exchanger lead to the highest efficiency. Moreover, these researchers proved that using a shell and helical tube heat exchanger results in better thermal performance in comparison with using nanofluid. Vicente et al. [2, 3] analyzed the geometrical effects of a shell and helical tube heat exchanger in different flow regimes on nine different models. Their obtained results revealed that employing a helical coil decreases the transient Reynolds number to lower than 1400. They also deduced that in the laminar flow regime, groove geometrical efficacy on Nusselt number is subtle; however in the turbulent flow regime, augmenting the helical height and reducing the helical pitch cause higher thermal performance. Naphon et al. [4] investigated an experimental work to examine the effects of the height-to-pitch ratio of a helical tube inside the shell of a heat exchanger on its hydrothermal performance. They deduced that the helical tube height can be effect on heat transfer and friction coefficient more than its pitch. Later, Hassanpour et al. [5] evaluated three configurations of V-shaped helical, U-shaped and perforated strips benefiting from use of both helical coils and strips. They concluded that each helical strip configuration enhances both heat transfer and pressure drop. Afterward, Han et al. [6] performed a numerical study to inquire the efficacies of flow direction on the helical strip tubes side on the thermal performance of a shell and tube heat exchanger. These researchers stated the optimum magnitude for the geometrical parameters as equal to 0.6. Thereafter, Liu et al. [7] investigated a numerical study of helical shell and tube heat exchanger. They found that the model of one-pas helical tube results in the highest heat exchanger hydrothermal performance. Han et al. [8] by use of the surface response technique and multi-objective method optimization studied four geometrical parameters of a two-pipe heat exchanger with helical tubes. Sadeghi et al. [9] assessed the various shapes of flow effects in a helical double-pipe heat exchanger empirically to optimize six different shape configurations. Salimpour et al. [10] examined the pitch, depth and width of a helical tube at various geometries employing titanium oxide nanofluid experimentally. These researchers stated that the helical tube use in higher Reynolds number values is more effective. Kareem et al. [11] performed a numerical and empirical study of a one-way helical coil in low magnitudes of Reynolds number. They showed 2.4 to 3.7 times heat transfer enhancement 1.7 to 2.4 times friction coefficient augmentation by use of the helical tube comparing to a plain tube. Then, Han et al. [12] studied the thermal performance of corrugated tubes utilizing the different turbulent methods. Afterward, Panahi and Zamzamian [13] used a wire turbulator to improve the performance of a double-pipe helically coiled heat exchanger flowing gas and water to the coil side and water to the shell side. They showed that on the coil side in all models both heat transfer and friction coefficient enhance. An energy and exergy study using the Taguchi’s method was performed by Etghani and Baboli [14] who revealed that the most effective parameters on the heat exchanger thermal performance include the flow rate of cold flow and the diameter of coil. Mirgolbabaei [15] analyzed the effects of mass flow rate and geometrical parameters of a shell and helical tube heat exchanger on its hydrothermal performance with annular cylindrical shell. Mashoofi et al. [16] represented a model to produce a double-pipe helically coiled heat exchanger employing a turbulator which caused the Nusselt number to enhance as about 81%. Alimoradi and Maghareh [17] optimized a ring-shaped fin in a shell and helically coiled tube heat exchanger by investigating its geometrical parameters which results in 44% enhancement in heat transfer. Milani and et al. proposed a novel experimentally study on the heat transfer characteristics in a shell and tube heat exchanger with wavy cosine corrugated wall in structure of tube bundle. They use of response surface methodology to obtain maximum effectiveness and the overall heat transfer coefficient. The results show that the effectiveness and the overall heat transfer coefficient increase with the cold water flow rates [18]. Hosseinnezhad et al. numerically investigated the turbulent flow of water/Al2O3 nanofluid in a tubular heat exchanger with two twisted-tape inserts. The parameters of their investigation are Reynolds numbers, the effect of twist ratio of twisted-tape inserts, co-swirl flow and counter-swirl flow of two twisted-tapes inside the tube and volume fractions of nanofluid. The results show that, by decreasing the twist ratio, the counter-swirl flow twisted-tape and the enhancement of volume fraction of Al2O3 nanoparticles in the base fluid, the amount of average Nusselt number increases [19]. Multiphase flows in microfluidic devices are usually used as an effective way to improve the cooling process, since phase change process can provide high heat transfer coefficient in comparison with single-phase flows. On the other hand, high surface-to-volume ratio of micro heat exchangers can intensify the overall heat rejection from the system. Asadollahi et al. investigated three models, namely (a) the formation of interior and exterior phase, (b) hydrodynamics of droplets during condensation process in a diffusive oblique fin (mini-channel) with hydrophilic walls and (c) liquid evacuation from the channel, by means of a novel perspective of pseudo-potential lattice Boltzmann model. The results show that the channel slope angle plays an important role at the rate of droplet nucleation and on evacuation time [20]. Milani et al. with use of two phase mixture model and response surface methodology (RSM) investigated the sensitivity analysis of heat transfer and heat exchanger effectiveness in a double-pipe heat exchanger filled with Al2O3 nanofluid [21]. Karimipour et al. [22,23,24,25,26,27,28,29,30] studied the improvement of heat transfer in different flow patterns and nanoparticle volume fractions for different geometries.

In another study, Alimoradi and Veysi [31] with use of empirical and numerical study examine the thermal performance of a shell and helical tube heat exchanger. These researchers’ results revealed that enhancing the pitch of helical coil as about twice on the shell side augments the Nusselt number, but the this number enhances as just 0.8% on the coil side. Later, Alimoradi [32] proposed a correlation for a double-pipe helically coiled heat exchanger effectiveness as a function of the number of heat transfer units (NTU). Later, a similar study performed by Alimoradi [33] on exergy analysis to evaluate the geometrical parameters of the same heat exchanger. These researchers concluded that the heat exchanger thermal performance enhancement reaches as the coil rounds number augments and the coil diameter reduces. Numerical study and sensitivity analysis are carried out on turbulent heat transfer and heat exchanger effectiveness enhancement in a double-pipe heat exchanger filled with porous media by Milani et al. They found that the mean Nusselt number increases by increase in the values of Reynolds number and dwindling of the Darcy number and porous substrate thickness [34]. Mamourian et al. used Taguchi method for finding optimum conditions (the maximum Nusselt number) of the mixed convection heat transfer in a wavy surface square cavity filled with Cu–water nanofluid [35].

The above literature review demonstrates that although many studies have been performed to improve the shell and helical tube heat exchangers hydrothermal performance, investigation on heat transfer and flow performance (Nusselt number, pressure drop and exergy loss) in shell and helically corrugated coiled tube heat exchanger has rarely been reported. The lack of data about this research has provoked the current study. Then, optimizing these types of heat exchangers by use of energy and exergy analysis is a technological gap. Hence, this paper aims to bridge it by examining the geometrical parameters and operating conditions on the heat exchanger hydrothermal performance by employing Taguchi’s empirical method. Numerical simulations and analysis of parameters such as the corrugation depth, corrugation pitch or number of rounds, inlet fluid flow rate on the coil and shell sides on the proposed heat exchanger have been conducted by Taguchi optimization.

Model descriptions

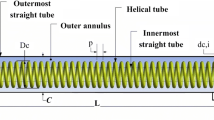
The shell and helically corrugated coiled tube heat exchanger has been investigated in the present study. The helical tube and the two important parameters including corrugation depth (e) and number of rounds or corrugation pitch (p) and also the heat exchanger which are designed in the current study are shown in Fig. 1.

Fig. 1
figure 1

Display of shell and helically corrugated coiled tube heat exchanger

Full size image

Figure 2 displays the correlated hydraulic diameter to each helically coiled tube corrugation depth with its cross-sectional image.

Fig. 2
figure 2

Correlated hydraulic diameter to each helically coiled tube corrugation depth

Full size image

Governing equations

The numerical simulation is performed with a three-dimensional steady-state turbulent flow system on both sides of the helical shell and tube heat exchanger. The governing equations (i.e., continuity, momentum and energy) are, respectively as follows [17]:

$$\frac{{\partial (\rho u_{\text{j}} )}}{{\partial x_{\text{j}} }} = 0$$
(1)
$$\frac{{\partial \left( {\rho u_{\text{i}} u_{\text{j}} } \right)}}{{\partial x_{\text{j}} }} = - \frac{\partial p}{{\partial x_{\text{i}} }} + \frac{\partial }{{\partial x_{\text{j}} }}\left( {\mu \left( {\frac{{\partial u_{\text{i}} }}{{\partial x_{\text{j}} }} + \frac{{\partial u_{\text{j}} }}{{\partial x_{\text{i}} }}} \right)} \right)$$
(2)
$$\frac{{\partial \left( {u_{\text{j}} T} \right)}}{{\partial x_{\text{j}} }} = \frac{\partial }{{\partial x_{\text{j}} }}\left( {\frac{\lambda }{{\rho c_{\text{p}} }}\frac{\partial T}{{\partial x_{\text{j}} }}} \right)$$
(3)

The turbulent flow is considered for the both shell and tube sides; thus, a model should be selected for the consideration of the turbulence effects in addition to the other governing equation. In comparison with standard \(k - \varepsilon\) model, the realizable \(k - \varepsilon\) turbulence model can present better performance for flows involving rotation, boundary layer under strong adverse pressure gradients, separation and recirculation. Consequently, realizable \(k - \varepsilon\) is selected for the simulation of the turbulence effects. The transfer equations for this model are as follows [17]:

$$\frac{{\partial \left( {\rho ku_{\text{j}} } \right)}}{{\partial x_{\text{j}} }} = \frac{\partial }{{\partial x_{\text{j}} }}\left[ {\left( {\mu + \frac{{\mu_{\text{t}} }}{{\sigma_{\text{k}} }}} \right)\frac{\partial k}{{\partial x_{\text{j}} }}} \right] + G_{\text{k}} - \rho \varepsilon$$
(4)
$$\frac{{\partial \left( {\rho \varepsilon u_{\text{j}} } \right)}}{{\partial x_{\text{j}} }} = \frac{\partial }{{\partial x_{\text{j}} }}\left[ {\left( {\mu + \frac{{\mu_{\text{t}} }}{{\sigma_{\upvarepsilon} }}} \right)\frac{\partial \varepsilon }{{\partial x_{\text{j}} }}} \right] + \rho C_{1} S\varepsilon - \rho C_{2} \frac{{\varepsilon^{2} }}{{k + \sqrt {\upsilon \varepsilon } }}$$
(5)

where \(C_{1}\) and \(C_{2}\) are the model coefficients; \(\sigma_{\text{k}}\) and \(\sigma_{\upvarepsilon}\) are the turbulence Prandtl numbers for the \(k\) and \(\varepsilon\), respectively; \(G_{\text{k}}\) represents the generation of turbulence kinetic energy due to the mean velocity gradients, and it can be calculated as follows [17]:

$$G_{\text{k}} = 2\mu_{\text{t}} S_{\text{ij}} S_{\text{ij}}$$
(6)

\(S_{\text{ij}}\) is the strain rate tensor which is

$$S_{\text{ij}} = \frac{1}{2}\left( {\frac{{\partial u_{\text{j}} }}{{\partial x_{\text{i}} }} + \frac{{\partial u_{\text{i}} }}{{\partial x_{\text{j}} }}} \right)$$
(7)

and the eddy viscosity is computed from

$$\mu_{\text{t}} = \rho C_{\upmu} \frac{{k^{2} }}{\varepsilon }$$
(8)

.

The difference between the realizable \(k - \varepsilon\) model and the standard and RNG \(k - \varepsilon\) models is that \(C_{\upmu}\) is no longer constant. It is computed from.

$$C_{\upmu} = \frac{1}{{4.04 + \frac{k}{\varepsilon }\sqrt 6 \cos \left[ {\frac{1}{3}\cos^{ - 1} \left( {\sqrt 6 \frac{{S_{\text{ij}} S_{\text{jk}} S_{\text{ki}} }}{{(S_{\text{ij}} S_{\text{ij}} )^{{\frac{2}{3}}} }}} \right)} \right]}}$$
(9)

and

$$C_{1} = \hbox{max} \left[ {0.43,\frac{{S\frac{k}{\varepsilon }}}{{S\frac{k}{\varepsilon } + 5}}} \right]$$
(10)
$$S = \sqrt {2S_{\text{ij}} S_{\text{ij}} }$$
(11)

with constant values of:

$$C_{2} = 1.9,\;\sigma_{\text{k}} = 1.0,\;\sigma_{\upvarepsilon} = 1.2$$

Boundary conditions

The fluid flows through both shell and tube sides are water. Due to the low-temperature range, the physical properties of the water were assumed to be constant. The hot fluid with temperature of 50 °C is on the tube side, and the cold fluid with temperature of 20 °C is on the shell side. Different corrugation depth and pitch of the helical tube, the flow rates of cold and hot fluids will be investigated based on the Taguchi’s proposed models discussed as follows.

Numerical modeling

In this study, the steady-state governing equations are solved, numerically, by using the finite volume method with double-precision and pressure-based segregated algorithm named SIMPLE [36,37,38,39,40,41]. Presto algorithm is used to couple the velocity and pressure. Furthermore, the second-order upwind scheme was adopted for the momentum, energy, kinetic turbulence and its dissipation rate. All the solutions were considered fully converged when sum of scaled residuals of the continuity, momentum, energy and realizable \(k - \varepsilon\) equations are smaller than 10−6, 10−6, 10−7 and 10−3, respectively. To simplify the numerical simulation, the following assumptions are made: the fluids are incompressible, continuous, Newtonian and isotropic; thermal radiation and viscous heating are negligible; the non-slip conditions are adopted on all solid surfaces; and buoyancy force and heat dissipation from the outer surfaces of the shell are negligible.

Taguchi’s method

The experimental design of Taguchi is employed in this paper to optimize the hydrothermal and geometrical performance of the shell and helically corrugated coiled tube heat exchanger. This empirical design is composed of some techniques that maximize the efficiency and minimize the cost and time. This method aims to reduce the number of experiments, and also the use of the SN factor, and to represent the experiments and interactions optimal levels. The design is organized based on the number of possible tests, time and the minimum resources. The advantages of this method to be useful for the researchers are: minimizing the number of test, the possibility to evaluate the investigated parameters effects, providing the SN analysis, defining the optimal levels (Table 1).

Table 1 Based geometrical dimensions derived from the optimum case of the study of Jamshidi et al. [42]
Full size table

Taguchi uses the orthogonal arrays for assigning the selected parameters in which L8, L16 and L18 are among the most common ones. In engineering problems, this model applies to the statistical methods. The design of an experiment involves the following main steps:

  • Introducing independent variables

  • Introducing of number of level settings for each independent variable

  • Selection of orthogonal array

  • Assigning the independent variables to each column

  • Conducting the experiments

  • Analyzing the data and inference

Before selecting the orthogonal array, the minimum number of experiments to be conducted shall be fixed based on the total number of degrees of freedom (as shown in Eq. 12) present in the study [37],

$${\text{DF}} = {\text{Factors}} \times \left( {{\text{Levels}} - 1} \right)$$
(12)

To analyze quality of the experiments design by Taguchi method, SN ratio is used. Following equations are presented, namely for SN ratio, larger-the-better (LB), smaller-the-better (SB) and nominal-the-better (NB) [37]:

$${\text{SB}} = \frac{1}{n}\sum \left( {y_{\text{i}} } \right)^{2}$$
(13)
$${\text{LB}} = \frac{1}{n}\sum \left( {\frac{1}{{y_{\text{i}} }}} \right)^{2}$$
(14)
$${\text{NB}} = \frac{1}{n}\sum \left( {y_{\text{i}} - y_{\text{o}} } \right)^{2}$$
(15)

where N and y show the number of iterations and the measured output, respectively. The SN value is computed after computing the magnitude of the loss function for each output by the following equation [37].

$${\text{SN}} = - 10{\text{Log}}\left( {L_{\text{i}} } \right)$$
(16)

Taguchi’s proposed models

The basic geometry and proper geometrical dimensions need to be represented first before using the Taguchi-designed tests. In this study, the basic geometrical parameters are derived from the optimum case of the study of Jamshidi et al. [42] and represented in Table 2. In this study, two geometrical parameters for the helical coil are considered including the corrugation depth and pitch of the helical tube and also two parameters for the operating conditions are considered including hot and cold fluid flow rates. As a result, four parameters are chosen which by considering three levels for each parameter and due to Eq. 7, L9 orthogonal arrays is selected. L9 orthogonal arrays are shown in Table 2.

Table 2 Designed experiments using Taguchi method (L9 orthogonal arrays)
Full size table

Grid study

An irregular mesh with tetrahedron grids is applied to the current geometry due to its complexity. Different meshing sizes are investigated to study the mesh independence of the results shown in Table 3. This table reveals that by choosing 3,600,000 numbers of elements the solution does not depend on the mesh and it could be a suitable grid for the following simulations. For more accuracy, the boundary layer mesh with five layers and growth rate 1.2 was applied in three different areas including the inner and outer sides of the helical tube and the inner side of the shell with the first layer thickness of 0.1, 0.3 and 1 mm, respectively. To show the quality of the generated mesh, Figs. 3 and 4 are provided.

Table 3 Mesh independency check
Full size table
Fig. 3
figure 3

The generated mesh on a the coil and b the shell of the heat exchanger

Full size image
Fig. 4
figure 4

The generated mesh at the a cross and b longitudinal sections of the heat exchanger

Full size image

Validation

The numerical results are validated by the study of Jamshidi et al. [42] with the coil diameter of 0.1041 m and pitch of 0.013 m. The comparison between the numerical results and experimental data is presented in Fig. 5 in which the maximum error 5% occurs in the largest Reynolds. Consequently, the present numerical simulation is valid.

Fig. 5
figure 5

Comparison of the current numerical study with the experimental data of Jamshidi et al. [42]

Full size image

Results and discussion

Hydrothermal performance of heat exchanger

In this section, the hydrothermal performance of the shell and helically corrugated coiled tube heat exchanger for nine Taguchi-designed experiments (Table 2) is investigated by numerical modeling. The thermal performance results including parameters such as Nusselt number, heat transfer coefficient, heat transfer rate, coil outlet temperature and shell outlet temperature in the nine models are presented in Table 4. This results show that increasing inlet fluid flow rate on the coil side, corrugation depth and number of rounds increases the heat transfer coefficient, Nusselt number and as a result heat transfer, but it is different for the heat transfer rate. Increasing the heat transfer by increasing the inlet Reynolds number is because of the improvement of the advection phenomenon, and enhancing the heat transfer by augmenting the corrugation depth and number of rounds is because of the improvement of mixing flow effects. The highest and lowest Nusselt number values correspond to models of 7 and 6, respectively. On the other hand, the highest and lowest heat transfer rate corresponds to models of 3 and 1, respectively. This is because of the fluid flow rates on the coil and shell sides, which in model 3, the fluid flow rates on the coil and shell sides are equal to 3 and these are equal to 1 for model 1.

Table 4 The hydrothermal performance of the heat exchanger for nine Taguchi-designed experiments (numerical modeling results)
Full size table

The hydrodynamic results including coil and shell sides pressure drop for nine models are presented in Table 4. The results shows that the variations of pressure drop on the shell side are insignificant in comparison with that on the coil side as the geometrical parameters vary, but variations in the shell pressure drop with fluid flow rate are considerable. On the other hand, the geometrical parameters affect the pressure drop on the coil side significantly as it varies in the range of 1 to 6 kPa. Moreover, it is visible that increasing the inlet fluid flow rate on the coil side, corrugation depth and number of rounds increases the coil pressure drop.

Figure 6 displays the temperature contours of shell and helically plain coiled tube heat exchanger and models of 1 and 3 in cross and longitudinal sections. In fact, models 1 and 3 are different at corrugation depth with equal corrugation pitch. The more uniform temperature distribution on the coil side by using helically corrugated coiled tube in comparison with helically plain coiled tube is visible which means a higher heat transfer. It is also observable that increasing the corrugation depth causes the temperature distribution on the coil side to be more uniform. For shell and helically corrugated coiled tube heat exchanger, the corrugated tube of the helical coil improves the mixing effect of the fluid flowing over the coil on the shell side and as a result its heat transfer will be enhanced.

Fig. 6
figure 6

The temperature contours of a longitudinal and b cross sections of plain shell and tube heat exchanger, c longitudinal and d cross sections of model 1, e longitudinal and f cross sections of model 3

Full size image

Taguchi analysis

Taguchi analysis is used to examine the effect of the investigated parameters on the heat exchanger performance. This method analyzes the hydrothermal parameters by considering the interaction effects of them. The Taguchi analysis is shown in Fig. 7 by considering the Nusselt number as the target parameter and as the parameter that the highest value is the best. In this figure, the higher the diagram slope the higher the effectiveness of the parameter. As a result, this figure shows that the most effective parameter on the thermal performance of the heat exchanger is the fluid flow rate on the coil side, followed by the corrugation depth. However, the parameters of corrugation pitch and fluid flow rate on the shell side have insignificant effect on the thermal performance of the heat exchanger.

Fig. 7
figure 7

The effects of design parameters of n, e, q1 and q2 on Nusselt number

Full size image

The Taguchi analysis is demonstrated in Fig. 8 by considering the pressure drop as the target parameter and as the parameter that the lowest value is the best. It shows that the most effective parameter on the hydrodynamic performance of the heat exchanger is fluid flow rate on the coil side, followed by corrugation pitch and corrugation depth. In addition, it is visible that increasing both corrugation depth and pitch enhances the pressure drop.

Fig. 8
figure 8

The effects of design parameters of n, e, q1 and q2 on pressure drop

Full size image

Exergy analysis

The models were examined in the previous section using the numerical method. In what follows, the various models efficiency will be examined by means of exergy analysis. In a steady-state open system, the exergy equilibrium is defined as below [37]:

$$\sum {\dot{\text{E}}\text{x}}_{\text{i}} - \sum {\dot{\text{E}}\text{x}}_{\text{o}} + \sum {\dot{\text{E}}\text{x}}_{\text{product}} = 0$$
(17)

The difference between actual and maximum work is defined by lost work or exergy [37]:

$${\dot{\text{E}}\text{x}}_{\text{loss}} = \sum \dot{m}_{\text{i}} \left( {h_{\text{i}} - T_{\text{e}} S_{\text{i}} } \right) - \sum \dot{m}_{\text{o}} \left( {h_{\text{o}} - T_{\text{e}} S_{\text{o}} } \right) + \sum \dot{Q}_{\text{i}} \left( {1 - \frac{{T_{\text{e}} }}{{T_{\text{i}} }}} \right) - \dot{W}_{\text{cv}}$$
(18)

In an open system heat exchanger, the exergy dissipation rate is determined as below [37]:

$${\dot{\text{E}}\text{x}}_{\text{loss}} = \dot{m}_{\text{c}} \left( {h_{\text{ci}} - T_{\text{e}} S_{\text{ci}} } \right) + \dot{m}_{\text{h}} \left( {h_{\text{hi}} - T_{\text{e}} S_{\text{hi}} } \right) - \dot{m}_{\text{c}} \left( {h_{\text{co}} - T_{\text{e}} S_{\text{co}} } \right) - \dot{m}_{\text{h}} \left( {h_{\text{ho}} - T_{\text{e}} S_{\text{ho}} } \right)$$
(19)

By substituting in Eq. (19):

$${\dot{\text{E}}\text{x}}_{\text{loss}} = \dot{m}_{\text{c}} \left( {h_{\text{ci}} - h_{\text{co}} } \right) + \dot{m}_{\text{h}} \left( {h_{\text{hi}} - h_{\text{ho}} } \right) + T_{\text{e}} \left[ {\dot{m}_{\text{c}} \left( {S_{\text{co}} - S_{\text{ci}} } \right) + \dot{m}_{\text{h}} \left( {S_{\text{ho}} - S_{\text{hi}} } \right)} \right]$$
(20)

The heat transfer by hot fluid is equal to the cold fluid if the heat loss is neglected in the heat exchanger.

$$\dot{Q} = \dot{m}_{\text{h}} \left( {h_{\text{hi}} - h_{\text{ho}} } \right) = \dot{m}_{\text{c}} \left( {h_{\text{ci}} - h_{\text{co}} } \right)$$
(21)

Considering Eq. (20), flowing correlation is obtained:

$${\dot{\text{E}}\text{x}}_{\text{loss}} = T_{\text{e}} \left[ {\dot{m}_{\text{c}} \left( {S_{\text{co}} - S_{\text{ci}} } \right) + \dot{m}_{\text{h}} \left( {S_{\text{ho}} - S_{\text{hi}} } \right)} \right]$$
(22)

If the entropy variation of hot and cold fluid in constant temperature is expressed by specific heat [37]:

$$\begin{aligned} & S_{\text{co}} - S_{\text{ci}} = C_{\text{p}} { \ln }\left( {\frac{{T_{\text{co}} }}{{T_{\text{ci}} }}} \right) \\ & S_{\text{ho}} - S_{\text{hi}} = C_{\text{p}} { \ln }\left( {\frac{{T_{\text{ho}} }}{{T_{\text{hi}} }}} \right) \\ \end{aligned}$$
(23)

By substituting the above equation, following equation is obtained [37]:

$${\dot{\text{E}}\text{x}}_{\text{loss}} = T_{\text{e}} \left[ {\dot{m}_{\text{c}} C_{\text{p}} \ln \left( {\frac{{T_{\text{co}} }}{{T_{\text{ci}} }}} \right) + \dot{m}_{\text{h}} C_{\text{p}} \ln \left( {\frac{{T_{\text{ho}} }}{{T_{\text{hi}} }}} \right)} \right]$$
(24)

Exergy loss calculation

In this section, the exergy losses in the investigated models are calculated using the equations presented in the previous section as shown in Table 5. In this table, test numbers 1 to 9 are introduced in Table 2, but test numbers 10 and 11 represent the numerical simulation results for the shell and helically plain coiled tube heat exchanger for low and high flow rates, respectively. This table reveals that comparing models 1 with 11 and 7 with 10 results in a reduction in exergy loss by using helically corrugated coiled tube which 24.6% and 12.67% decrease in exergy loss is obtained, respectively. Consequently, using helically corrugated coiled tube in the heat exchangers in low Reynolds numbers has higher effectiveness.

Table 5 Exergy losses calculation
Full size table

Taguchi analysis results of the investigated parameters and sensitivity analysis are shown in Table 6. This table represents the effects of level change for the four investigated parameters in this study. According to the ranking, the most effective parameters are in order of priority: cold fluid flow rate (on the coil side), hot fluid flow rate (on the shell side), number of rounds and corrugation depth. The reason for the small effect of corrugation depth on the performance of the heat exchanger is attributed to the change in hydraulic diameter and increase in diameter equivalent to increasing corrugation depth because by increasing the equivalent diameter in flow rate the local flow velocity in the coil decreases and reduces the heat transfer coefficient and Nusselt number.

Table 6 Taguchi analysis results of the parameters and sensitivity analysis
Full size table

Figure 9 demonstrates the Taguchi analysis of the investigated parameters based on their exergy loss. The slope of the graph in the two parameters of flow rate on the coil and shell sides indicates the greater sensitivity of the exergy loss to these two parameters. Since exergy loss values are used in this analysis, optimization and analysis of the data based on the lowest value are the best.

Fig. 9
figure 9

Taguchi analysis based on the exergy losses

Full size image

Conclusions

In this study, the energy and exergy analysis of a shell and helically corrugated coiled tube heat exchanger was numerically investigated. The SIMPLE algorithm was applied for the pressure and velocity coupling scheme. Furthermore, the second-order upwind was used as discretization scheme for all governing equations and realizable \(k - \varepsilon\) was selected as the turbulence model. Various design parameters and operating conditions such as corrugation pitch, corrugation depth, inlet fluid flow rate on the coil and shell sides are investigated to examine the hydrothermal performance of the heat exchanger. Taguchi method has been used for design the experiments (L9 orthogonal arrays) and analyze the hydrothermal parameters by considering the interaction effects of them. The obtained results showed that increasing inlet fluid flow rate on the coil side, corrugation depth and number of rounds increases pressure drop, the heat transfer coefficient, Nusselt number and as a result heat transfer, but it is different for the heat transfer rate. It is also found that the most effective parameter on the thermal performance of the heat exchanger is the fluid flow rate on the coil side, followed by the corrugation depth and the most effective parameter on the hydrodynamic performance of the heat exchanger is fluid flow rate on the coil side, followed by corrugation pitch and corrugation depth. Based on the exergy analysis, using helically corrugated coiled tube instead of helically plain coiled tube in the heat exchangers can decrease the exergy loss up to 24.6%, and this is higher effectiveness for the cases of low Reynolds numbers. The Taguchi analysis based on the exergy revealed that the most effective parameters are in order of priority: cold fluid flow rate (coil side), hot fluid flow rate (shell side), number of rounds and corrugation depth.