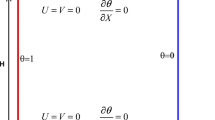Introduction

Mixed convection heat transfer occurs when forced and free convection mechanisms contribute to heat transfer simultaneously. Convective flows in porous media have been a focal point in fundamental heat transfer analyses over the past few decades. Convective flow in porous media is extensively covered in the works by Nield and Bejan [1], Ingham and Pop [2], Vafai [3, 4], and Pop and Ingham [5].

Mixed convection heat transfer and fluid flow in lid-driven cavities filled with porous media are important subjects of investigation with wide-ranging applications in engineering and geophysical systems such as electronic equipment cooling [6], thermal-hydraulics of nuclear reactors [7], flow and heat transfer in solar ponds [8], and dynamics of lakes [9]. There are some industrial applications such as float glass production [10] and heating and drying processes [11]. These problems are used as benchmark configurations for evaluating numerical solutions of Navier–Stokes equations [12, 13]. In a trapezoidal container with the change in temperature in the sinusoidal bottom wall, mixed convection flow has recently been studied, according to ref. [14]. It highlights the impacts of three leading parameters, including sinusoidal function amplitude m, the Hartmann number (Ha), and the Richardson number (Ri), while maintaining the Reynolds number and Prandtl number constant at 100 and 6.2, respectively. Basak et al. [15] conducted a computational analysis of mixed convection flows in a square hollow with porous media and a lid-driven surface. Specifically, they examined the case of a uniformly heated bottom surface with either linearly heated side walls or a cooled right wall. The analysis was carried out using the penalty finite element method. On the other hand, Al-Salem et al. [16] focused on a study on the results of changing the direction of the lid on magnetohydrodynamic mixed convection within a square-shaped enclosure with adiabatic vertical walls, one linearly heated bottom surface, and a constant-temperature top sliding wall. Kamel et al. [17] experimented with mixed convection heat transfer within a vented square container with base fluid inside and a magnetic field outside. They discovered that the Hartmann number and the rate of heat transport have an inverse relationship, meaning that as the Hartmann number rises, the heat transport rate declines. Pirmohammadi and Ghassemi [18] did quite similar work as well but they worked with a tilted square cavity instead of ventilated. They observed that the properties of the flow of fluid and the heat transfer process are significantly influenced by the existing magnetic field and inclination angle. Additionally, Bakar et al. [19] examined how the magnetic field affected the streamlines and contours of the vortices that were generated in the container. Moreover, [20] focuses on the consequences of mixed convection in a square-shaped enclosure that is driven by a differentially heated lid about the problem of heat transmission for a porous fluid. Results were computed using several scenarios for the Prandtl number, porosity values, Darcy number, and Richardson number. The research paper [21] investigates the mixed convection of MHD in a lid-driven enclosure that features a wavy shape top wall and rectangular heaters located on the bottom wall. Geridonmez and Oztop [22] utilized a polyharmonic spine radial basis function-based pseudospectral approach to investigate the mixed convection flow in a lid-driven enclosure subjected to a uniform partial magnetic field. To examine the flow and heat transmission effects, the mixed convection flow within a square chamber with moving walls that had partial slide was numerically analyzed by Ismael et al. [23]. It has been observed that when partial slip is present, the rate of heat transfer increases with an increase in the value of the Richardson number. However, the isotherms remain unaffected by the Richardson number in the absence of a partial slip. In their study, Nasrin and Parvin [24] utilized a finite element formulation to analyze mixed convection flow in a lid-driven cavity that featured a sinusoidal wavy surface. They also observed how reversed magnetic effects influenced the flow. Their findings indicated that the highest Reynolds number and lowest Hartmann number resulted in the optimal average Nusselt number. A study referenced as Ref. [25] delved into the flow pattern and temperature changes that occur during mixed convection in a trapezoidal chamber with a lid-driven mechanism. This chamber features a cold top moving wall and a heated bottom wall that is either isothermal or non-isothermal. It was found that in the heat transport regime (\(\Pr \, \times\, {\text{Re}} \, {>\sim}\, 1\)) dominated by convection, the non-isothermal bottom floor creates multiple stable states in both the regime dominated by natural convection (\(\frac{Gr}{{{\text{Re}}^{2} }}\,>>\,1\)) and the mixed convection regime (\(\frac{Gr}{{{\text{Re}}^{2} }}\,{\sim}\,O(1)\)). Ali et al. [26] conducted a study on the mixed convection flow and heat transfer in a hexagonal cavity using magnetohydrodynamics (MHD). They found that the flow configuration and temperature distribution were affected by the governing parameters. The computational modeling of mixed convection of MHD flow with the joule effect in a two-dimensional lid-driven chamber featuring a corner heater was examined by Oztop et al. [27]. The article [28] examines mixed convection in a trapezoidal cavity with a lid that is open and driven by a channel. It explores four scenarios based on the movement of the cavity’s sidewalls. Javed et al. [29] conducted a study on mixed convection in a trapezoidal cavity field with a lid, where the bottom surface was heated both uniformly and non-uniformly, while a magnetic field was present. The finite element method’s Galerkin weighted residual methodology is used to solve the reduced equations in this study, following the solution of governing equations through the penalty method. Aparna and Seetharamu [30] conducted a study in a porous trapezoidal chamber with a bottom wall that was heated uniformly and non-uniformly, using a finite element computational approach. They found that the average Nusselt number increases consistently with increasing Ra for both top and bottom walls. Additionally, the average Nusselt number is higher for the uniform bottom wall case than the linearly and sinusoidally varying temperature cases at the hot and cold walls. The study presented in Ref. [31] investigated the impact of a magnetic field on double-diffusive mixed convection in a wavy porous cavity filled with a hybrid nanofluid with a rotating cylindrical heat source at the center. The results show that a rotating heat source significantly influences flow circulation, isotherms, and heat transfer, with rates increasing by 682.07% and 45.62% for varying Darcy numbers and cavity porosity, respectively, in the absence of a magnetic field (Ha = 0) and declining to 504.02% and 22.83% in the presence of a magnetic field (Ha = 100). In Ref. [32], researchers numerically studied mixed convective hybrid-nanofluid flow in a partially heated square cavity with two rotating rough cylinders under an external magnetic field. The findings showed heat transfer enhancement of up to 261.29% at the highest rotating speed of the rough cylinders, while the heat transfer rate decreased with increasing magnetic field strength. At the highest magnetic field impact (Ha = 50), the lowest heat transfer rate was observed, 144.62% less than that in the absence of a magnetic field (Ha = 0). Ali et al. [33] used the finite element method to analyze mixed convection in a horizontal channel with alternating baffles and an external magnetic field. They found that optimal heat transfer occurred with the appropriate orientation of baffles and observed a 22.14% reduction in heat transfer augmentation at Ha = 50 compared to Ha = 0. In [34], researchers used the finite difference method to analyze the mixing of convection and entropy generation in a trapezoidal cavity, considering various positions of a solid cylinder filled with nanofluid. The study examined the effects of parameters such as Reynolds number, Richardson number, nanoparticles volume fraction, dimensionless radius, and location of the solid cylinder on the streamlines, isotherms, and isentropic. The results show that the size and location of the solid cylinder are significant control parameters for optimizing heat transfer and the Bejan number inside the trapezoidal cavity.

It is essential to study the heat transfer characteristics in complex geometries to obtain the optimal container design for various industrial applications. Thus, it is important to study the energy flow within trapezoidal enclosures. Although there have been many research studies on trapezoidal cavities, there is still a shortage of information on how fluid flow and heat transfer can be improved in trapezoidal enclosures that are porous, linearly heated, and exposed to a magnetic field. Based on our review of existing literature, we have chosen to conduct a numerical study on convective heat transfer in a trapezoidal enclosure filled with porous material, which is linearly heated while exposed to a magnetic field. This research aims to enhance our comprehension of heat transfer, flow field modifications, and temperature distribution, which are all crucial in various engineering disciplines. The primary objective of this project is to investigate how a magnetic field affects the convective heat flow within a porous trapezoidal cavity that is heated linearly. The focus is to analyse how the Darcy, Hartmann, Prandtl, Grashof, and Reynold numbers impact the fluid flow and thermal fields within the cavity. The numerical results are illustrated through graphical representations of streamlines, isotherms, and the average Nusselt number. The analysis of heat transfer rates and the flow field has been fully conducted using the finite element approach.

Physical Model

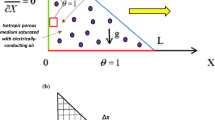
Steady and two-dimensional convective heat flow within a trapezoidal space of height \(H\) is considered. A porous material with uniform porosity that is saturated with an incompressible fluid fills the cavity. The porous bed is considered to be hydrodynamically and thermally isotropic. Figure 1 shows the schematic representation of the physical model under consideration. The inclination angle of the side walls concerning the vertical line is taken as 30°. The top wall is moving in the positive x-direction with velocity \(U_{0}\) at a constant cooled temperature \(T_{c}\), whereas the bottom wall of length \(L\) moving with an identical velocity \(U_{0}\) in the opposite direction of the x-axis, is maintained linear temperature \(T = T_{h} - (T_{h} - T_{c} )\frac{x}{2}\). The inclined side walls are kept adiabatic maintaining no slip condition. The force due to gravity works vertically downward, while a magnetic field of uniform strength \(B_{0}\) is provided in the opposite direction of the x-axis.

Fig. 1
figure 1

Schematic representation of the physical model

Full size image

Mathematical Formulation

The continuity, momentum, and energy equations are basic principles for dealing with problems involving fluid flow and heat transmission. These three laws develop a family of combined, nonlinear partial differential equations. The effects of viscosity, radiation, and Joule heating are disregarded, and physical characteristics of fluids, such as thermal conductivity, specific heats, and thermal expansion coefficient, are taken for constants except for the variation in density in the body force element of the momentum equation. The temperature-dependent density variations are considered using the Boussinesq approximation, which also links the temperature field and flow field.

According to the presumption given above, the governing equations founded on the balance laws of energy, momentum, and mass can be expressed in dimensional form as [14,15,16,17, 19, 21, 22, 29, 35, 36]:

$$ \frac{\partial u}{{\partial x}}\,\,\, + \,\,\,\frac{\partial v}{{\partial y}}\,\,\, = \,\,\,0 $$
(1)
$$ u\frac{\partial u}{{\partial x}}\,\,\, + \,\,\,v\frac{\partial u}{{\partial y}} = \, - \,\,\,\frac{1}{\rho }\frac{\partial p}{{\partial x}}\,\,\, + \,\,\,\nu \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }}\,\,\, + \,\,\,\frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)\,\,\, - \,\,\,\frac{\nu }{\kappa }u $$
(2)
$$ u\frac{\partial v}{{\partial x}}\,\, + \,\,v\frac{\partial v}{{\partial y}} = - \,\,\frac{1}{\rho }\frac{\partial p}{{\partial y}}\,\, + \,\,\,\nu \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }}\,\,\, + \,\,\,\frac{{\partial^{2} v}}{{\partial y^{2} }}} \right)\,\, + \,\,\,g\beta \left( {T - T_{c} } \right) - \,\,\,\frac{\nu }{\kappa }v - \,\,\,\frac{{\sigma B_{0}^{2} }}{\rho }v $$
(3)
$$ u\frac{\partial T}{{\partial x}}\,\,\, + \,\,\,v\frac{\partial T}{{\partial y}}\,\,\, = \,\,\,\alpha \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }}\,\,\, + \,\,\,\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) $$
(4)

In light of the geometry in Fig. 1, the boundary conditions of the aforementioned system of equations are outlined below [37, 38]:

At the top surface:

$$ u = U_{0} \,\,,\,\,\,\,\,\,v = 0\,\,,\,\,\,\,\,\,T = T_{c} \, $$
(5a)

At the left and right inclined side surfaces:

$$ u = v = 0\,\,,\,\,\,\,\frac{\partial T}{{\partial x}}\,\,\, = \,\,\,0\, $$
(5b)

At the bottom surface:

$$ u = - \,U_{0} \,\,\,,\,\,v = 0\,\,\,\,,\,\,T\,\,\, = \,\,\,T_{h} \,\,\, - \,\,\,\left( {T_{h} - T_{c} } \right)\frac{x}{2}\, $$
(5c)

The equations in this study can be transformed into their non-dimensional form using the following non-dimensional variables:

$$ \begin{gathered} X\,\,\, = \,\,\,\frac{x}{L},\,\,\,\,\,Y\,\,\, = \,\,\,\frac{y}{L},\,\,\,\,\,U\,\,\, = \,\,\,\frac{u}{{U_{0} }},\,\,\,\,\,V\,\,\, = \,\,\,\frac{v}{{U_{0} }}\,,\,\,\,\,\theta \,\,\, = \,\,\,\frac{{T - T_{c} }}{{T_{h} - T_{c} }},\,\,\,\,P\,\,\, = \,\,\,\frac{p}{{\rho U_{0}^{2} }}\,,\,\,\,\,\Pr \,\,\, = \,\,\,\frac{\nu }{\alpha },\,\,\,\, \hfill \\ \hfill \\ Gr\,\,\, = \,\,\,\frac{{g\rho \left( {T_{h} - T_{c} } \right)L^{3} }}{{\nu^{2} }},\,\,\,\,\,\,\,{\text{Re}} \,\,\, = \,\,\,\frac{{U_{0} L}}{\nu },\,\,\,\,\,\,\,Da\,\,\, = \,\,\,\frac{\kappa }{{L^{2} }},\,\,\,\,\,\,\,Ha\,\,\, = \,\,\,\sqrt {\frac{{\sigma B_{0}^{2} L^{2} }}{\mu }} \,\,,\,\,\,\,\,\alpha = \frac{k}{{c_{p} \rho }} \hfill \\ \end{gathered} $$
(6)

Therefore, the non-dimensional equations are:

$$ \frac{\partial U}{{\partial X}}\,\,\, + \,\,\,\frac{\partial V}{{\partial Y}}\,\,\, = \,\,\,0 $$
(7)
$$ U\frac{\partial U}{{\partial X}}\,\,\, + \,\,\,V\frac{\partial U}{{\partial Y}}\,\,\, = \,\,\, - \,\,\,\frac{\partial P}{{\partial X}}\,\,\, + \,\,\,\frac{1}{{\text{Re}}}\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }}\,\,\, + \,\,\,\frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right)\,\,\, - \,\,\,\frac{1}{{{\text{Re}} Da}}U $$
(8)
$$ U\frac{\partial V}{{\partial X}}\,\,\, + \,\,\,V\frac{\partial V}{{\partial Y}}\,\,\, = \,\,\, - \frac{\partial P}{{\partial Y}}\,\,\, + \,\,\,\frac{1}{{\text{Re}}}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }}\,\,\, + \,\,\,\frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right)\,\,\, + \,\,\,\frac{Gr}{{{\text{Re}}^{2} }}\theta \,\,\, - \,\,\,\frac{1}{{{\text{Re}} Da}}V\,\,\, - \,\,\,\frac{{Ha^{2} }}{{\text{Re}}}V $$
(9)
$$ U\frac{\partial \theta }{{\partial X}}\,\,\, + \,\,\,V\frac{\partial \theta }{{\partial Y}}\,\,\, = \,\,\,\frac{1}{{{\text{Re}} \Pr }}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }}\,\,\, + \,\,\,\frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right) $$
(10)

These are the possible expressions for the non-dimensional boundary conditions considered:

At top wall:

$$ U = 1\,\,,\,\,\,\,\,V = 0\,\,,\,\,\,\,\,\theta = 0 $$
(11a)

At left and right inclined side surfaces:

$$ U = V = 0\,\,,\,\,\,\,\,\,\frac{\partial \theta }{{\partial X}} = 0 $$
(11b)

At bottom wall:

$$ U = \,\, - 1\,\,,\,\,\,\,\,V = \,\,\,0\,\,,\,\,\,\,\,\theta \,\,\, = \,\,\,1\,\, - X\, $$
(11c)

Using the finite element method, the resultant non-dimensional governing equations linked to the boundary conditions have been resolved numerically.

Heat Transfer

To reckon the rate of heat transmission, it is necessary to assess the local and the average Nusselt number. These are described as follows [19, 27]:

$$ Nu_{local} \,\,\, = \,\,\, - \left( {\frac{\partial \theta }{{\partial Y}}} \right)_{Y = \,\,0} $$
(12a)
$$ Nu_{avg} \,\,\, = \,\,\,\frac{1}{L}\int_{0}^{L} {\,\,\,Nu_{local} \,\,\,\,dX} $$
(12b)

Computation Technique

The modeled governing equations Eqs. (7–10) and their related boundary conditions Eqs. (11a–11c) are simulated by implementing Galerkin’s weighted finite element method. In this simulation procedure, Galerkin weighted residual method [40] is implemented to convert the governing partial differential equations into integral equations. The integral equations are:

$$ \int_{A} {N_{\alpha } \,\,\left( {\frac{\partial U}{{\partial X}} + \frac{\partial V}{{\partial Y}}} \right)} \,\,dA = 0 $$
(13)
$$ \begin{gathered} \int_{A} {N_{\alpha } \,\,\left( {U\,\,\frac{\partial \,U}{{\partial X}} + V\,\,\frac{\partial \,U}{{\partial Y}}} \right)} \,\,dA = - \,\,\,\int_{A} {H_{\lambda } \,\,\frac{\partial P}{{\partial X}}} dA\,\,\, + \frac{1}{{\text{Re}}}\,\,\int_{A} {N_{\alpha } \left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right)\,\,dA} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \,\,\,\,\frac{1}{{{\text{Re}} Da}}\,\,\,\int_{A} {N_{\alpha } \,U\,dA} \hfill \\ \end{gathered} $$
(14)
$$ \begin{gathered} \int_{A} {N_{\alpha } } \left( {U\frac{\partial V}{{\partial X}} + V\frac{\partial V}{{\partial Y}}} \right)\,\,dA = - \,\,\int_{A} {H_{\lambda } \left( {\frac{\partial P}{{\partial Y}}} \right)} \,dA\,\, + \,\,\,\frac{1}{{\text{Re}}}\int_{A} {N_{\alpha } } \left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right)\,dA \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \,\,\,\frac{1}{{{\text{Re}} Da}}\int_{A} {N_{\alpha } } V\,dA\,\,\, - \,\,\,\frac{{Ha^{2} }}{{\text{Re}}}\int_{A} {N_{\alpha } } V\,dA\,\,\, + \,\,\,\frac{Gr}{{{\text{Re}}^{2} }}\int_{A} {N_{\alpha } \theta \,dA\,} \hfill \\ \hfill \\ \end{gathered} $$
(15)
$$ \int_{A} {N_{\alpha } \left( {U\frac{\partial \theta }{{\partial X}} + V\frac{\partial \theta }{{\partial Y}}} \right)} \,\,dA = \frac{1}{{\Pr {\text{Re}} }}\int_{A} {N_{\alpha } \left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right)dA} $$
(16)

Here A represents the element area, \(N_{\alpha } (\alpha = 1,\,\,2,...,6)\) and \(H_{\lambda } (\lambda = 1,2,3)\) represent the element shape functions for velocity component and temperature, and pressure. Now, the following boundary integral equations associated with the surface tractions (\(A_{x} \,\,,\,\,A_{y}\)) and heat flux (\(q_{w}\)) have been obtained using Gaussian divergence theorem:

$$ \int_{\,A} {\,N_{\alpha } \,\,\left( {\frac{\partial \,U}{{\partial X}}\, + \,\,\frac{\partial \,V}{{\partial Y}}} \right)} \,dA\, = \,0 $$
(17)
$$ \begin{gathered} \int_{A} {N_{\alpha } \,\,\left( {U\frac{\partial U}{{\partial X}} + V\frac{\partial U}{{\partial Y}}} \right)} \,\,dA + \int_{A} {H_{\lambda } \left( {\frac{\partial P}{{\partial X}}} \right)} dA - \frac{1}{{\text{Re}}}\int_{A} {\left( {\frac{{\partial N_{\alpha } }}{\partial X}\frac{\partial U}{{\partial X}} + \frac{{\partial N_{\alpha } }}{\partial Y}\frac{\partial U}{{\partial Y}}} \right)\,\,dA} \hfill \\ + \,\,\,\,\frac{1}{{{\text{Re}} Da}}\int_{A} {N_{\alpha } U\,dA} \,\, = \,\,\int_{{A_{0} }} {N_{\alpha } \,A_{x} \,dA_{0} } \hfill \\ \end{gathered} $$
(18)
$$ \begin{gathered} \int_{A} {\,N_{\alpha } \left( {U\frac{\partial V}{{\partial X}} + V\frac{\partial V}{{\partial Y}}} \right)\,\,} dA + \int_{A} {\,H_{\lambda } \left( {\frac{\partial P}{{\partial Y}}} \right)} dA\,\,\, - \frac{1}{{\text{Re}}}\,\,\int_{A} {\left( {\frac{{\partial N_{\alpha } }}{\partial X}\frac{\partial V}{{\partial X}} + \frac{{\partial N_{\alpha } }}{\partial Y}\frac{\partial V}{{\partial Y}}} \right)\,\,dA} \hfill \\ - \frac{Gr}{{{\text{Re}}^{2} }}\,\,\int_{A} {\,N_{\alpha } \theta \,dA + \,\,\,\,\frac{1}{{{\text{Re}} Da}}\,\,\,\int_{A} {\,N_{\alpha } V\,dA} \,\,\, + \,\,\,\,\frac{{Ha^{2} }}{{\text{Re}}}\,\,\int_{A} {\,N_{\alpha } V\,dA} } = \,\,\,\int_{{A_{0} }} {N_{\alpha } A_{y} dA_{0} } \hfill \\ \end{gathered} $$
(19)
$$ \int_{A} {\,N_{\alpha } \left( {U\frac{\partial \theta }{{\partial X}} + V\frac{\partial \theta }{{\partial Y}}} \right)} \,\,\,dA - \frac{1}{{\Pr {\text{Re}} }}\int_{A} {\left( {\frac{{\partial N_{\alpha } }}{\partial X}\frac{\partial \theta }{{\partial X}} + \frac{{\partial N_{\alpha } }}{\partial Y}\frac{\partial \theta }{{\partial Y}}} \right)\,\,\,dA} = \int_{{A_{w} }} {N_{\alpha } q_{w} \,dA_{w} } $$
(20)

For the development of the finite element equations, the six-node triangular element is used in this work. All six nodes are associated with velocities as well as temperature, only the three corner nodes are linked with pressure. This means that a lower-order polynomial is chosen for pressure, which is satisfied through a continuity equation. The velocity components, temperature profiles, and linear interpolation for the pressure distribution according to their highest derivative orders for the differential Eqs. (7–10) are as:

$$ U(X\,,\,\,Y) = N_{\beta } U_{\beta } $$
(21)
$$ V\,(X\,,\,\,Y) = N_{\beta } V_{\beta } $$
(22)
$$ \theta (X\,,\,\,Y) = N_{\beta } \theta_{\beta } $$
(23)
$$ P(X\,,\,\,Y) = H_{\lambda } P_{\lambda } $$
(24)

Here \(\beta = 1,\,\,2, \ldots \,\, \ldots ,6\) and \(\lambda = 1,\,\,2,\,\,3\). With the help of Eqs. (21–24), the finite element equations can be obtained from Eqs. (17–20) in the following form:

$$ U_{\beta } \int_{\,A} {N_{\alpha } \,N_{\beta ,\,\,x} } \,dA + V_{\beta } \int_{\,A} {N_{\alpha } \,N_{\beta ,\,\,y} } \,dA\, = \,0 $$
(25)
$$ \begin{gathered} U_{{_{\beta } }} U_{{_{\gamma } }} \int_{A} {N_{\alpha } N_{\beta } N_{\gamma ,x} } dA + V_{{_{\beta } }} U_{{_{\gamma } }} \int_{A} {N_{\alpha } N_{\beta } N_{\gamma ,y} } dA\,\,\, + P_{\mu } \int_{A} {H_{\lambda } H_{\mu ,x} } dA - \frac{1}{{\text{Re}}}U_{\beta } \,\int_{A} {\left( {N_{\alpha ,x} N_{\beta ,x} + N_{\alpha ,y} N_{\beta ,y} } \right)\,\,dA} \hfill \\ + \,\,\,\frac{1}{{{\text{Re}} Da}}\,\,\,U_{\beta } \,\int_{A} {N_{\alpha } N_{\beta } \,\,dA} = \int_{{A_{0} }} {N_{\alpha } A_{x} dA_{0} } \hfill \\ \end{gathered} $$
(26)
$$ \begin{gathered} U_{{_{\beta } }} V_{{_{\gamma } }} \int_{A} {N_{\alpha } N_{\beta } N_{\gamma ,x} } dA + \,\,V_{{_{\beta } }} V_{{_{\gamma } }} \int_{A} {N_{\alpha } N_{\beta } N_{\gamma ,y} } \,dA + P_{\mu } \,\int_{A} {H_{\lambda } H_{\mu ,y} } \,dA\,\,\, - \frac{1}{{\text{Re}}}V_{\beta } \,\int_{A} {\,\left( {N_{\alpha ,x} N_{\beta ,x} + N_{\alpha ,y} N_{\beta ,y} } \right)\,\,dA} \hfill \\ - \,\,\,\frac{Gr}{{{\text{Re}}^{2} }}\,\,\theta_{\beta } \int_{A} {N_{\alpha } N_{\beta } \,dA\,\,\, + \,\,\,\frac{1}{{{\text{Re}} Da}}\,\,V_{\beta } \,\int_{A} {N_{\alpha } N_{\beta } \,\,\,dA} \,\,\, + \,\,\,\frac{{Ha^{2} }}{{\text{Re}}}\,\,V_{\beta } \int_{A} {N_{\alpha } N_{\beta } \,dA} } \,\,\, = \,\,\,\int_{{A_{0} }} {N_{\alpha } A_{y} \,dA_{0} } \hfill \\ \end{gathered} $$
(27)
$$ \begin{gathered} U_{\beta } \theta_{\gamma } \int_{A} {\,N_{\alpha } N_{\beta } N_{\gamma ,\,\,x} dA + V_{\beta } \theta_{\gamma } \int_{A} {\,N_{\alpha } N_{\beta } N_{\gamma \,,\,\,y} dA} } \hfill \\ - \frac{1}{{\Pr {\text{Re}} }}\,\,\theta_{\beta } \int_{A} {\,\left( {N_{\alpha ,x} N_{\beta ,x} + N_{\alpha ,y} N_{\beta ,y} } \right)\,\,dA} = \int_{{A_{w} }} {N_{\alpha } \,q_{w} \,\,dA_{w} } \hfill \\ \end{gathered} $$
(28)

Now we consider the coefficients in the above governing equations are as follows:

\(K_{{\alpha \,\beta^{x} }} \, = \,\int_{\,A} {N_{\alpha } \,N_{\beta ,\,\,x} } \,dA\), \(K_{{\alpha \,\beta^{y} }} \, = \,\int_{\,A} {N_{\alpha } \,N_{\beta ,\,\,y} } \,dA\), \(K_{{\alpha \,\beta \,\gamma^{x} }} \, = \,\int_{\,A} {\,N_{\alpha } \,N_{\beta } \,N_{\gamma ,\,x\,} \,} \,dA\).

\(K_{{\alpha \,\beta \,\gamma^{y} }} \, = \,\int_{\,A} {\,N_{\alpha } \,N_{\beta } \,N_{\gamma ,\,y\,} \,} \,dA\), \(K_{\alpha \,\beta } \, = \,\int_{\,A} {N_{\alpha } \,N_{\beta } } \,dA\),

\(S_{{\alpha \,\beta^{xx} }} \, = \,\int_{\,A} {N_{\alpha ,x} \,N_{\beta ,x} } \,dA\), \(S_{{\alpha \,\beta^{yy} }} \, = \,\int_{\,A} {N_{\alpha ,y} \,N_{\beta ,y} } \,dA\), \(M_{{\lambda \,\mu^{x} \,}} = \,\int_{\,A} {\,H_{\lambda } \,H_{\mu \,,\,\,x} \,} dA\), \(M_{{\lambda \,\mu^{y} \,}} = \,\int_{\,A} {\,H_{\lambda } \,H_{\mu \,,\,\,y} \,} dA\).

\(Q_{{\alpha^{u} }} = \,\int_{{\,A_{0} }} {N_{\alpha } \,A_{x} \,dA_{0} }\), \(Q_{{\alpha^{v} }} = \,\int_{{\,A_{0} }} {N_{\alpha } \,A_{y} \,dA_{0} }\),\(Q_{{\alpha^{\theta } }} = \int_{{A_{w} }} {N_{\alpha } \,q_{w} \,dA_{w} }\).

These element matrices are evaluated in closed form for numerical simulation. Details of the derivation for these element matrices are omitted for brevity.

With the help of the above coefficients, the finite element equations can be written in the following type:

$$ K_{{\alpha \beta^{x} }} \,U_{\beta } \, + \,K_{{\alpha \beta^{y} }} \,V_{\beta } \, = \,0 $$
(29)
$$ \begin{gathered} K_{{\alpha \beta \gamma^{x} }} \,U_{\beta } U_{\gamma } + \,\,\,K_{{\alpha \beta \gamma^{y} }} \,V_{\beta } U_{\gamma } \, + M_{{\lambda \mu^{x} }} P_{\mu } \,\, - \frac{1}{{\text{Re}}}U_{\beta } \left( {S_{{\alpha \beta^{xx} }} + S_{{\alpha \beta^{yy} }} } \right) \hfill \\ + \,\,\,\frac{1}{{{\text{Re}} Da}}\,\,U_{\beta } = Q_{{\alpha^{u} }} \hfill \\ \end{gathered} $$
(30)
$$ \begin{gathered} K_{{\alpha \beta \gamma^{x} }} U_{\beta } \,V_{\gamma } + K_{{\alpha \beta \gamma^{y} }} V_{\beta } \,V_{\gamma } + M_{{\lambda \mu^{y} }} P_{\mu } \,\, - \frac{1}{{\text{Re}}}\,\,V_{\beta } \left( {S_{{\alpha \beta^{xx} }} + S_{{\alpha \beta^{yy} }} } \right) - \,\,\,\frac{Gr}{{{\text{Re}}^{2} }}K_{\alpha \beta } \,\theta_{\beta } \hfill \\ + \,\,\,\frac{1}{{{\text{Re}} Da}}V_{\beta } \,\, + \,\,\,\frac{{Ha^{2} }}{{\text{Re}}}K_{\alpha \beta } \,V_{\beta } = Q_{{\alpha^{V} }} \hfill \\ \end{gathered} $$
(31)
$$ K_{{\alpha \beta \gamma^{x} }} \,U_{\beta } \theta_{\gamma } + K_{{\alpha \beta \gamma^{y} }} \,V_{\beta } \theta_{\gamma } - \frac{1}{{\Pr {\text{Re}} }}\theta_{\beta } \left( {S_{{\alpha \beta^{xx} }} + S_{{\alpha \beta^{yy} }} } \right) = Q_{{\alpha^{\theta } }} $$
(32)

The above nonlinear Eqs. (29–32) are converted into linear algebraic equations using the Newton–Raphson method [41] and then solved by implementing the Triangular Factorization method [42] and also the reduced integration method explained by Zeinkiewicz et al. [43]. The convergence criterion of the simulation along with error estimation has been set to \(\left| {\varphi^{m + 1} - \varphi^{m} } \right| \le 10^{ - 5}\), where m is the number of iterations and \(\phi\) is a function of U, V, and θ. The detailed computational procedure was well described in Refs. [44, 45].

Grid independency test and mesh generation

To estimate the ideal number of grids, grid function accuracy tests have been conducted.

A grid refinement study was executed systematically to choose the grid size for the current study appropriately. A grid refinement test was surveyed using six different types of meshes, where Pr = 7, Ha = 10, Da = 10−3, Re = 100, and Gr = 104; this is represented in Table 1. The average heat transfer rate at the linearly heated surface with grid elements is seen to be converging in Fig. 2. For the grid refinement tests, six several non-uniform grids with a chosen number of nodes and elements were taken into consideration. The value of Nuavg on the linearly heated bottom surface was calculated to evaluate the grid independence of the current code. 15,759 nodes and 30,578 elements are satisfactory grid sizes for ensuring the grid independence of the solution for the current inquiry when compared to the acquired numerical values of the average Nusselt number. Thus, this grid resolution can be used throughout the simulation (Fig. 3).

Table 1 Check for grid independence at Pr = 7, Ha = 10, Da = 10−3, Re = 100 and Gr = 104
Full size table
Fig. 2
figure 2

Convergency of average Nusselt number (Nuavg) with grid independency for Ha = 10, Pr = 7, Re = 100, Gr = 104 and Da = 10.−3

Full size image
Fig. 3
figure 3

Finite element mesh generation inside the computational domain of porous trapezoidal enclosure

Full size image

Validation of the Code

Code Validation Through Data

After establishing grid independence, the created code is checked against studies on convective heat flow in lid-driven enclosures by M. Bhattacharya et al. [25] and Iwatsu et al. [39] that have been published. These comparisons are performed for the Nusselt number at the moving top wall in case of mixed convection within a similar enclosure with alike boundary conditions. Table 2 shows excellent alignment among the respective results, demonstrating the veracity of the current simulation.

Table 2 Comparison of current solution with the literature data by M. Bhattacharya et al. [25] and Iwatsu et al. [39] in terms of Nusselt number at the moving top wall in case of mixed convection within a lid-driven square enclosure with hot top wall, a cold bottom wall, and adiabatic side walls
Full size table

Code Validation Through Streamlines and Isotherms

The results of the current analytical code were compared to those derived by Bhattacharya et al. [25] for mixed convection and the role of multiple solutions in lid-driven trapezoidal-shaped space. In Fig. 4, where the first row holds the outcomes of Bhattacharya et al. [25] and the last row carries the solutions acquired by the present study, streamlines, as well as isothermal lines for Pr = 0.015, Gr = 105 and Re = 1, are compared between our results and the numerical data of Bhattacharya et al. [25]. Both of the outcomes in this comparison are in excellent agreement with one another and are nearly identical. These verifications increase the trust in the numerical code to continue the inquiry.

Fig. 4
figure 4

Comparison of streamlines and isotherms between current results and that of Bhattacharya et al. [25] using Pr = 0.015, Re = 1, and Gr = 105 for the isothermally hot bottom wall

Full size image

Results and Discussion

In current work, the transfer of convective heat in a porous trapezoidal space with a bottom wall that is heated linearly while being subjected to a magnetic field has been numerically explored. To examine the current study focuses on how three regulating parameters—the Darcy number (Da), Hartmann number (Ha), and Prandtl number (Pr)—affect flow patterns, isothermal lines, and heat transfer rate. A broad range of Da (10–2 ≤ Da ≤ 10–5), Ha (0 ≤ Ha ≤ 100), Pr (7 ≤ Pr ≤ 50), Gr (103 ≤ Gr ≤ 106), and Re (10 ≤ Re ≤ 200) were used in the numerical computation, respectively. Throughout the study, \(\frac{Gr}{{{\text{Re}}^{2} }}\left( { = Ri} \right)\) is fixed at 1 which refers to pure mixed convection. Furthermore, the results have been portrayed in two sections. The initial one has concentrated on flow patterns and temperature contours based on streamlines and isotherms for several phenomena. The final one discussed the heat transfer rate regarding the average Nusselt number (Nuavg) at the heated wall.

Impact of Darcy Number on Flow Pattern and Temperature

Figure 5 shows how the Darcy number (Da), for four distinct values of Da, affects the flow trends and temperature lines while maintaining the values of the other parameters at Pr = 7 and Ha = 10. Starting from the ascending order of the value, the strength of the flow circulation is perceived to be quite poor at Da = 10−5 in Fig. 5a. The drag force generated by the movement of the upper wall causes a pinch of fluid to be dragged toward the left and right corners. The same incident happens for the motion of lower walls. In Fig. 5a, it is also observed that there are some almost triangle-shaped eddies near both upper and lower horizontal walls which are also affected by drag force. As Da increases to 10−4 (Fig. 5b), the impact of buoyancy is enhanced, and the intensity of circulations increases, as well as the lid-driven effect reduces near both the upper and lower walls. The triangle-shaped eddies become more prominent than before and there also a smaller elliptical eddy is found inside the triangular-shaped eddies. As we step forward to the value of Da = 10−3, in Fig. 5c, it is noticed that the intensity of the flow becomes stronger, and the circulation cells occupy most of the enclosure. The shape of the circulations has changed, they become symmetric and the effect of drag force is further reduced. For Da = 10−2 in Fig. 5d, it is remarked that the flow pattern becomes more intense than the previous figure and occupies almost the entire cavity. The cells of circulation are noted to be nearly symmetrical in nature which is evidence that buoyant force makes the flow primarily dominated rather than the lid-driven force. Thus, the porous cavity creates a force that opposes the flow direction and resists it. It is commonly observed that the flow intensity is lower for small Darcy numbers (Da), as the Darcy number is either directly proportional to permeability or inversely proportional to flow resistance inside a porous bed. As a result, with reduced values of Da, the intensity of flow is slightly lower. On the contrary, Fig. 5a represents that isothermal lines are symmetric and occupy a wide portion of the encloser at the value of Da = 10−5. In Fig. 5b, it is seen that isotherms tend to be steeper and become more condensed and diagonally symmetrical at Da = 10−4. Then at Da = 10−3, it is remarked that isotherms become more steeper than before, and vertically symmetric and distributed towards the right-sided inclined surface. It is noticeable that the pattern of the temperature profile has remarkably changed at Da = 10−2 (see Fig. 5d). It becomes semi-elliptically symmetric going beyond the sequence that the previous figures (Fig. 5a–c) are maintaining and the isotherms occupy almost the entire cavity in Fig. 5d.

Fig. 5
figure 5

Streamlines and isotherms for linearly heated bottom wall with Pr = 7, Ha = 10, Gr = 104, Re = 100 for: a Da = 10−5, b Da = 10−4, c Da = 10−3, d Da = 10.−2

Full size image

Impact of Hartmann Number on Flow Pattern and Temperature

The effect of Hartmann number (Ha) on streamlines and temperature profile is depicted in Fig. 6 at Pr = 7 and Da = 10−3. In general, the magnetic field tends to influence the convective flow, and this leads to retard fluid flows. As illustrated in Fig. 6a, there produced symmetrical circulation cells with two triangular-shaped eddies inside them at Ha = 0, proving that there is no magnetic field. The maximum strength of the flow circulation can be observed here. By applying a magnetic field and increasing the Hartmann number, it acts like a barrier against the flow, which prompts a change in the distribution of streamlines inside the enclosure, and two inner triangular-shaped eddies have vanished. For various higher values of Ha (Ha = 10, 50, 100), it is evident from Fig. 6b–d that the sizes and shapes of the interior circulation cells have changed significantly. In addition, the numerical values of the velocity magnitude signify that the flow movement decreases with rising Ha. In other words, flow strength reduces with the progressive value of Hartmann number (Ha). This means that the existence of a magnetic zone has a strong influence on the flow field. Without a magnetic field (Ha = 0) isothermal lines look semi-elliptically symmetric and occupy almost the entire cavity (see Fig. 6a). In Fig. 6b, for Ha = 10, isotherms are vertically symmetric and also become denser than before. While the value of Ha = 50 (in Fig. 6c) the isotherms have bent to the left wall and tend to become non-symmetric. Then in Fig. 6d, by increasing the value of Ha to the maximum (Ha = 100), the isothermal lines stoop down to the maximum heated segment of the linearly heated bottom wall and turn into non-symmetric.

Fig. 6
figure 6

Streamlines and isotherms for a linearly heated bottom wall at Pr = 7, Da = 10−3, Gr = 104, Re = 100 for: (a) Ha = 0, (b) Ha = 10, (c) Ha = 50, (d) Ha = 100

Full size image

Impact of Prandtl Number on Fluid Flow and Temperature

Keeping the other regulating parameters constant at Da = 10−3 and Ha = 10, the impact of Prandtl number (Pr) on flow fields and isothermal lines for the linearly heated bottom wall is represented in Fig. 7. It can be noticed in Fig. 7 that Pr affects the flow pattern. The measurement of the circulation cells and flow velocity is decreased with the increasing value of Pr. In other words, flow strength declines as Pr increases. That is because with increasing Pr, the specific heat and viscosity of fluid increases while thermal conductivity decreases. As a result, though the heat absorption power of the fluid increases, viscosity slows down the fluid and the heat transfer rate decreases. A maximum temperature is experienced at the bottom wall’s left side as the temperature there changes linearly. The isothermal lines in Fig. 7a are symmetric. As Pr increases to 10 (see Fig. 7b), isotherms tend to become non-symmetric and distributed towards the right-sided inclined wall. The temperature profile is non-symmetric about a central inclined line which signifies a convection dominant mode of heat transport, for linearly varying temperature, with the value of Pr = 15. Figure 7d shows a drastic change in isothermal lines. The lines are condensed to the boundary walls creating a hollow inside. When the bottom surface is linearly heated, the isothermal lines are crammed towards the bottom left corner for a higher value of Pr. The compression of isothermal lines towards the left bottom corner indicates a greater heat transmission rate through the bottom wall.

Fig. 7
figure 7

Streamlines and isotherms for linearly heated bottom wall with Ha = 10, Da = 10−3, Gr = 10.4, Re = 100 for: a Pr = 7, b Pr = 10, c Pr = 15, d Pr = 50

Full size image

Impact of Grashof Number on Flow Pattern and Temperature

Figure 8 illustrates streamline and temperature contours (on left and right columns, respectively) at Da = 10–3, Ha = 10, Re = 100, Pr = 7, and Gr = 103 to 105 for the linearly hot bottom wall. It is noticed that the flow field is influenced by the Grashof number as seen from streamlines. In this case, the flow circulation cells are symmetrically in an hourglass shape having two triangular-shaped eddies inside them at Gr = 103 and the circulation cells occupy almost the whole space. As Gr increases to Gr = 104 and 105 it is seen that flow circulation and intensity of contour increases. For the higher value of Gr = 106, the intensity of flow circulation becomes stronger, and red colored area indicates the higher velocity. On the other hand, the temperature profile has experienced significant change for variation in the value of Gr. For lower value of Gr (Gr = 103), thermal contour lines are seen to be symmetric. With the increasing value of Gr, the temperature profile becomes to be asymmetric. At Gr = 106 (see Fig. 8d), thermal contour lines bent like a S-shape in the middle of the cavity.

Fig. 8
figure 8

Streamlines and isotherms for a linearly heated bottom wall at Pr = 7, Da = 10−3, Ha = 10, Re = 100 for: a Gr = 103, b Gr = 104, c Gr = 105, d Gr = 10.6

Full size image

Impact of Reynold Number on Flow Pattern and Temperature

The impact of Reynolds number in streamlines and thermal profile is described in Fig. 9 for Re = 10 to 200 while the remaining parameters are kept constant at Da = 10−3, Ha = 10, Pr = 7, and Gr = 104. Reynolds number has a significant impact on streamlines and isothermal lines. For a lower value of Re = 10, the circulation cells are symmetric having an oval-shaped cell inside. While for Re = 50 and 100, the cells become intense having square-like and hourglass-shaped cells respectively. In Fig. 9d, there are two triangular-shaped eddies inside the circulation cell, and the strength of circulation increases. On the other hand, the temperature contour lines are symmetric. With the increasing value of Re the isothermal lines tend to become asymmetric. At Re = 100, the thermal contour lines are vertically distributed towards the right wall. The temperature profile becomes asymmetric and occupies the whole cavity.

Fig. 9
figure 9

Streamlines and isotherms for a linearly heated bottom wall at Pr = 7, Da = 10−3, Ha = 10, Gr = 104 for: a Re = 10, b Re = 50, c Re = 100, d Re = 200

Full size image

Heat Transfer Rates

Figure 10a represents how the value of the average Nusselt number along the bottom surface which is linearly heated changes under the influence of Pr with four distinct values of Da, keeping the remaining parameters constant. The average Nusselt number (Nuavg) has been shown to grow with an increase in the value of Pr for a particular value of Da. It can be remarked from Fig. 10a that there is a parallelism in the behavior of two heat lines, indicating Da = 10−2 and Da = 10−3. It is noticed that initially, the lines indicating the heat transfer rate are almost vertical, i.e., the heat transfer rate grows rapidly for Pr, ranging from 7 to 10 but when the value 10 has been crossed, the rate of heat transfer slows down slightly and becomes moderate. However, the heat transfer rate has dropped dramatically at Da = 10−4 and become modest. It is worth noticing that at the lowest Da value, Da = 10−5, there is almost a small variation in the value of Nuavg for the Pr = 7 to 10 values. Specifically, at Pr = 10 The heat transfer rate demonstrates an increase of 208.95% at a Darcy (Da) number of 10−4, 577.16% at Da = 10−3, and 622.78% at Da = 10−2 in comparison to the minimum Da value of 10–5. After this value of Pr, Nuavg tends to go up minimally compared to other values of Pr. Thus, the growing heat transfer rate decreases at a higher value of Da, i.e., it rises with the escalating value of Pr and Da.

Fig. 10
figure 10

Effects of a Darcy number (Da), b Hartmann number (Ha), c Reynolds number (Re), and d Grashof number (Gr) on Average Nusselt number (Nuavg) at the linearly heated bottom surface while Pr = 7–50

Full size image

In Fig. 10b, the impact of the magnetic field on the average Nusselt number (Nuavg) is shown for an enclosure with the same heating conditions as previously mentioned. The graph displays how Nuavg changes with the Prandtl number (Pr). It is noticed that for some specific values of Ha, Nuavg enhances with the larger values of Pr, and it is found to be upper as well for the smaller value of Ha, signifying that uppermost heat transfer occurs for the minimum value of Ha (Ha = 0). In Fig. 10b, it is remarked that the line, indicating the rate of heat transport at Ha = 0 and Ha = 10 respectively, shows a similar trend. There is a sharp growth in heat transfer rate from Pr = 7 to 10; after that, the rate declines slightly. Particularly, the heat transfer rate diminishes by 2.102% upon the application of a magnetic field at Ha = 10, by 12.8% at Ha = 50, and by 55.44% at Ha = 100 in contrast to the absence of a magnetic field (Ha = 0) at Pr = 10. Moreover, the heat transmission rate has moderately decreased at Ha = 50 but shows a parallel behavior with the former. However, it is perceived that there is a drastic fall in the rate of heat transfer at Ha = 100, which is the highest value of Ha. The line, representing heat transfer, is an inclined straight line indicating that the heat transmission rate is consistent. To sum up, the flow velocity decreases more for higher values of Ha, which raises the temperature and reduces heat transmission.

Figure 10c demonstrates the effect of Reynolds number (Re) on the average Nusselt number (Nuavg) under similar heating conditions. The heat transfer indicating lines show an upward trend. For a definite value of Pr, Nuavg increases with an increasing value of Re. For Pr values between 7 and 10, the value of Nuavg increases quickly. It can be seen that the lines representing heat transmission are rising at a sharp angle at Re = 200 and progressively becoming less acute as Re declines. The augmentation of heat transfer rate decreases slightly for Pr values between 10 and 15, yet it still increases. The enhancement of the heat transfer rate increases slightly with additional Pr values. For any specific value of Pr, the average Nusselt number reaches its maximum at Re = 200 and its minimum at Re = 10. Overall, the heat transfer rate increases with increasing values of Re and Pr.

Figure 10d illustrates the relationship between the average Nusselt number and the Grashof number (Gr) for the same heating settings as well as for other parameters. The graph reveals that for Pr = 7 to 10, the heat transfer lines for four different values of Gr overlap, and the lines are steep. This indicates a significant change in Nuavg, and the rate of change in heat transfer rate is similar. For Pr = 10 to 15, the heat transfer rate slightly decreases, and it is slightly different for different values of Gr as the lines tend to separate from each other. For values of Pr above 15, the enhancement of the heat transfer rate moderately increases. Notably, the heat transfer rate is maximum for the minimum value of Gr (Gr = 103) and minimum for the maximum value of Gr (Gr = 106) for a particular value of Pr. Overall, it is evident that the rate of heat transfer increases with decreasing Gr values and increasing Pr values.

Conclusions

The current inquiry examined how a linearly heated bottom wall affected the flow and heat transfer characteristics resulting from convective heat flow in a trapezoidal cavity containing porous media in a magnetic field setting. While keeping the value of \(\frac{Gr}{{{\text{Re}}^{2} }}\) constant at 1 (pure mixed convection), the finite element approach is used to create smooth solutions in the form of streamlines, isotherm contours, and average Nusselt numbers to investigate the effects of various dimensionless parameters like Da, Ha, Pr, Gr, and Re. Comparisons with prior studies published on particular situations of the problem were performed, and it was found that they were in good accord. The outcomes may be advantageous to analyze several heating processes, such as material processing in a linearly heated chamber or heating functions for geophysical systems. Based on the discussion above, noteworthy conclusions can be drawn as follows:

  • The flow field inside the cavity depends magnificently on the impact of Darcy number. Flow circulation becomes stronger by increasing the value of Da. The temperature profile is also noticeably affected by Darcy number.

  • The flow circulation strength reduces with the escalating effect of the magnetic field. The isothermal lines become more bent due to the increment of Ha.

  • The overall flow behavior is significant due to variation of Pr. The thermal contour lines are initially dragged toward the bottom heated wall as the convection dominating mode begins.

  • The strength of flow circulation increases with the increasing value of Gr and Re. The temperature contour lines are significantly affected by the Grashof number and Reynolds number.

  • Hartmann number has a negative impact on the average Nusselt number (Nuavg). At Pr = 10, the heat transfer rate decreases by 2.102% with Ha = 10, 12.8% with Ha = 50, and 55.44% with Ha = 100 compared to the absence of magnetic field is present (Ha = 0). It is observed that heat transmission decreases as the Hartmann number (Ha) value increases.

  • Darcy number has a positive influence on the average Nusselt number. The heat transfer rate increases by 208.95% at Da = 10–4, by 577.16% at Da = 10–3, and by 622.78% at Da = 10–2 compared to the lowest value of Da = 10–5 at Pr = 10. The rate of heat transmission significantly increases as Da gets elevated.

  • Prandtl number also has a favorable impact on the average Nusselt number. When Da and Ha have certain values, increasing Pr boosts the heat transmission rate.

  • The Grashof number has an inverse relation with the average Nusselt number. Increasing the value of Gr decreases the heat transfer rate.

  • Increasing the Reynolds number positively impacts the average Nusselt number, resulting in a higher rate of heat transfer.