Axisymmetric flow by a rotating disk with Cattaneo–Christov heat flux

Abstract

Here, axisymmetric flow of Jeffrey fluid by a rotating disk with variable thicked surface is studied. Heat transfer is discussed through Cattaneo–Christov heat flux model. Transformation procedure has been adopted in obtaining ordinary differential systems. Convergent series solutions are obtained. Flow, temperature and skin friction coefficient for various parameters of interest are graphically illustrated. The radial and tangential velocities are increasing functions of Deborah number.

1 Introduction

Non-Newtonian fluid has significant applications in industrial and technological processes. It plays a great role in food processing, suspensions, certain oils, lubrications, nourishment preparing, polymer, biomechanics, manufacturing of paints and emulsions, etc. Non-Newtonian fluids are much complex because of additional rheological parameters in constitutive relationship. Materials like soap solutions, ketchup, blood, apple sauce are common examples of non-Newtonian fluids. Classifications of non-Newtonian fluids are through integral, rate and differential types. Jeffrey fluid describes the phenomenon of relaxation and retardation times. Narayana and Babu [1] investigated stretched flow of Jeffrey fluid with magnetohydrodynamics and thermal radiation. Turkyilmazoglu [2] described magnetic field and slip effects on the flow and heat transfer of stagnation point Jeffrey fluid over deformable surfaces. Abbasi et al. [3] presented convective flow of Jeffrey fluid in the presence of thermal radiation and magnetohydrodynamics (MHD). Shehzad et al. [4] scrutinized MHD radiative flow of Jeffrey fluid. Heat transfer in MHD flow of Jeffrey fluid over a stretching sheet is inspected by Zeeshan and Majeed [5]. Dalir [6] focused on stretched flow of Jeffrey fluid with entropy generation. Turkyilmazoglu and Pop [7] analyzed stagnation point flow of Jeffrey fluid. Hayat et al. [8] described three-dimensional flow of Jeffrey fluid due to a stretching surface.

Flow due to rotating surfaces has promising applications in engineering and industrial sectors such as lubrication, air cleaning machine, electric power generating system, turbo machinery, gas turbine, food processing technology and centrifugal machinery. Flow due to rotating disk is initially studied by Karman [9]. He provided von Karman transformations to convert Navier–Stokes equations into ordinary differential equations. Ming et al. [10] worked on steady flow and heat transfer of the power law fluid over a rotating disk. Rotating flow of nanofluid with heat transfer is illustrated by Turkyilmazoglu [11]. Bayat et al. [12] investigated magneto-thermo-mechanical response in a functionally graded annular over a rotating disk. Sheikholeslami et al. [13] analyzed nanofluid flow due to a rotating disk. Rotating flow of Jeffrey fluid with magnetohydrodynamics is done by Hayat et al. [14]. Turkyilmazoglu [15] studied flow and heat transfer due to a rotating disk. Hayat et al. [16] presented influence of Cattaneo–Christov heat flux in flow of Jeffrey fluid due to a rotating disk. Saidi and Tamim [17] examined unsteady flow of nanofluid between two rotating disks. Flow of Ostwald–de Waele fluid with heat transfer analysis by a rotating disk is studied by Xun et al. [18].

The phenomenon of heat transfer has numerous applications in industry and engineering processes, e.g., nuclear reactor cooling, energy production, cooling of electronic devices, transportations, micro electronics and fuel cells, etc. Heat transfer phenomenon was successfully presented by Fourier heat conduction law [19]. This model has some limitations that whole medium is sensed instantly by the initial disturbance (main drawback of this model). This unrealistic argument is named as “paradox of heat conduction”. In order to resolve this problem, Cattaneo [20] proposed Fourier law of heat conduction by adding a thermal relaxation time. Christov [21] further worked on Cattaneo’s model by introducing Oldroyd upper convectived derivative. Impact of Cattaneo–Christov heat flux model in the flow of viscoelastic fluid is illustrated by Tibullo and Zampoli [22]. Han et al. [23] described flow of viscoelastic fluid in the existence of Cattaneo–Christov heat flux model. Hayat et al. [24] examined effects of magnetohydrodynamic in the flow of Oldroyd-B fluid with Cattaneo–Christov heat flux model. Analysis of heat transfer through Cattaneo–Christov heat flux model in nanofluid flow by a stretched surface is studied by Sui et al. [25]. Mustafa [26] discussed rotating flow of Maxwell fluid in the presence of Cattaneo–Christov heat flux model. Li et al. [27] presented influence of Cattaneo–Christov heat flux model in viscoelastic fluid flow due to a stretching sheet.

Present analysis examines the axisymmetric three-dimensional flow of Jeffrey fluid due to a rotating disk with variable thickness. Heat transfer analysis is examined by Cattaneo–Christov heat flux. Solution expressions of nonlinear problem are obtained by homotopy analysis method [28,29,30,31,32,33,34,35]. Influence of various involved parameters on axial, radial and tangential velocities, temperature and surface drag force is discussed graphically.

Fig. 1

Flow geometry

2 Model development

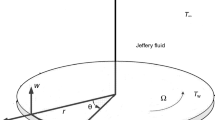
Here, we have an interest to examine flow of Jeffrey fluid by a disk with variable thickness. Disk rotates with constant angular velocity $\Omega$. Temperatures at disk and away from it are denoted by $T_{w}$ and $T_{\infty }$ (see Fig. 1). The resulting equations for flow and thermal fields [18] are

$$\begin{aligned}&\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0, \end{aligned}$$

(1)

$$\begin{aligned}&\left( u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}-\frac{ {{v}}^{2}}{r}\right) =\frac{\nu }{1+\lambda _{1}}\frac{\partial ^{2}u}{ \partial z^{2}}+\frac{\lambda _{2}\nu }{1+\lambda _{1}}\left( 2u\frac{ \partial ^{3}u}{\partial r\partial z^{2}}+2w\frac{\partial ^{3}u}{\partial z^{3}}+\frac{\partial u}{\partial z}\frac{\partial ^{2}u}{\partial r\partial z}+\frac{\partial w}{\partial z}\frac{\partial ^{2}u}{\partial z^{2}}\right) , \end{aligned}$$

(2)

$$\begin{aligned}&\left( u\frac{\partial {{v}}}{\partial r}+w\frac{\partial {{v}}}{ \partial z}+\frac{u{{v}}}{r}\right) =\frac{\nu }{1+\lambda _{1}}\frac{ \partial ^{2}{{v}}}{\partial z^{2}}+\frac{\lambda _{2}\nu }{1+\lambda _{1} }\left( 2u\frac{\partial ^{3}{{v}}}{\partial r\partial z^{2}}+2w\frac{ \partial ^{3}{{v}}}{\partial z^{3}}+\frac{\partial u}{\partial z}\frac{ \partial ^{2}{{v}}}{\partial r\partial z}+\frac{\partial w}{\partial z} \frac{\partial ^{2}{{v}}}{\partial z^{2}}\right) , \end{aligned}$$

(3)

$$\begin{aligned}&\rho C_{p}\left( u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z }\right) =-{{\varvec{\nabla }} }.{\mathbf {q}}, \end{aligned}$$

(4)

with

$$\begin{aligned}&u=0,{\text { v}}=\Omega r,w=0,T=T_{w} \ \, {\text { at }}\,z=a\left( \frac{r}{R_{0}}+1\right) ^{-m}, \nonumber \\&u=0,{\text { v}}=0,~ T=T_{\infty }\ {\text { when }}\,z\rightarrow \infty , \end{aligned}$$

(5)

where $u(r,\theta ,z),$ v$(r,\theta ,z)$ and $w(r,\theta ,z)$ are components of velocity ${\mathbf {V}}$, $\nu$ denotes the kinematic viscosity, $\mu$ the dynamic viscosity, $\rho$ the density of fluid, m the disk thickness index, $R_{0}$ the dimensional constant, $C_{p}$ the specific heat, a the thickness coefficient of disk, $\lambda _{1}$ the ratio of relaxation to retardation times and $\lambda _{2}$ the retardation time. Here, heat flux ${\mathbf {q}}$ obeys

$$\begin{aligned} {\mathbf {q}}+\lambda \left( \frac{\partial {\mathbf {q}}}{\partial t}+{\mathbf {V}} .\nabla {{\mathbf {q-q.}}}\nabla {\mathbf {V}}+(\nabla .{\mathbf {V}})\mathbf {q}\right) =-\,k\nabla T, \end{aligned}$$

(6)

in which k and $\lambda$ elucidate the thermal conductivity and relaxation time. Incompressible situation leads to

$$\begin{aligned} {\mathbf {q}}+\lambda \left( \frac{\partial {\mathbf {q}}}{\partial t}+{\mathbf {V}} .\nabla {\mathbf {q-q.}}\nabla {\mathbf {V}}\right) =-\,k\nabla T, \end{aligned}$$

(7)

Expressions (4) and (7) give

$$\begin{aligned} u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}&= {} \frac{k}{ \rho C_{p}}\frac{\partial ^{2}T}{\partial z^{2}}-\lambda \left[ u^{2}\frac{ \partial ^{2}T}{\partial r^{2}}+w^{2}\frac{\partial ^{2}T}{\partial z^{2}} +\,2uw\frac{\partial ^{2}T}{\partial r\partial z}+\left( u\frac{\partial u}{ \partial r}+w\frac{\partial u}{\partial z}\right) \frac{\partial T}{\partial r}\right. \nonumber \\&\left. \left. +\left( u\frac{\partial w}{\partial r}+w\frac{\partial w}{ \partial z}\right) \frac{\partial T}{\partial z}\right] .\right. \end{aligned}$$

(8)

Following transformations

$$\begin{aligned} u&= {} r\Omega F(\eta ),{\text { v}}=r\Omega G(\eta ),w=-R_{0}\Omega \left( 1+\frac{r}{R_{0}}\right) ^{-m}\left( \frac{\Omega R_{0}^{2}\rho }{\mu }\right) ^{-\frac{1}{n+1}}J(\eta ),\nonumber \\ \eta&= {} \frac{z}{R_{0}}\left( \frac{\Omega R_{0}^{2}\rho }{\mu }\right) ^{ \frac{1}{n+1}}\left( 1+\frac{r}{R_{0}}\right) ^{m},\Theta =\frac{ T-T_{\infty }}{T_{w}-T_{\infty }}. \end{aligned}$$

(9)

Using Eq. (9), Eqs. (1–3) and (8) become

$$\begin{aligned}&J^{\prime }+2F+m\eta \epsilon F^{\prime }=0, \end{aligned}$$

(10)

$$\begin{aligned}&{\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}F^{\prime \prime }+\beta {\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\left( 2FF^{\prime \prime }+4m\epsilon FF^{\prime \prime }+2m\epsilon \eta FF^{\prime \prime \prime }-2JF^{\prime \prime \prime }\right. \nonumber \\&\quad \left. \left. +F^{\prime 2}+\epsilon F^{\prime 2}+m\eta \epsilon F^{\prime }F^{\prime \prime }-J^{\prime }F^{\prime \prime }\right) -(1+\lambda _{1})(F^{2}-G^{2}+JF^{\prime }+m\eta \epsilon FF^{\prime })=0,\right. \end{aligned}$$

(11)

$$\begin{aligned}&{\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}G^{\prime \prime }+\beta {\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\left( 2FG^{\prime \prime }+4m\epsilon FG^{\prime \prime }+2m\epsilon \eta FG^{\prime \prime \prime }-2JG^{\prime \prime \prime }\right. \nonumber \\&\quad \left. \left. +F^{\prime }G^{\prime }+m\epsilon F^{\prime }G^{\prime }+m\eta \epsilon F^{\prime }G^{\prime \prime }-J^{\prime }G^{\prime \prime }\right) -(1+\lambda _{1})(2FG+JG^{\prime }+m\eta \epsilon FG^{\prime })=0,\right. \end{aligned}$$

(12)

$$\begin{aligned}&\frac{1}{\Pr }{\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\Theta ^{\prime \prime }-\gamma \left( m(m-1)\eta \epsilon ^{2}F^{2}\Theta ^{\prime \prime }+J^{2}\Theta ^{\prime \prime }+m\epsilon JF\Theta ^{\prime }+m\eta \epsilon F^{2}\Theta ^{\prime }\right. \nonumber \\&\quad \left. \left. +\,m^{2}\eta ^{2}\epsilon ^{2}FF^{\prime }\Theta ^{\prime }+m\eta \epsilon JF^{\prime }\Theta ^{\prime }+m\eta r^{*}FJ^{\prime }\Theta ^{\prime }+JJ^{\prime }\Theta \right) -m\eta \epsilon F\Theta ^{\prime }-J\Theta ^{\prime }=0,\right. \end{aligned}$$

(13)

$$\begin{aligned}&F(\alpha ) =0,G(\alpha )=1,J(\alpha )=0,\Theta (\alpha )=1, \nonumber \\&F(\infty ) =0,G(\infty )=0,\Theta (\infty )=0. \end{aligned}$$

(14)

Letting

$$\begin{aligned} j(\xi )&= {} j(\eta -\alpha )=J(\eta ),f(\xi )=f(\eta -\alpha )=F(\eta ) \nonumber \\ g(\xi )&= {} g(\eta -\alpha )=G(\eta ),\theta (\xi )=\theta (\eta -\alpha )=\Theta (\eta ), \end{aligned}$$

(15)

we have

$$\begin{aligned}&j^{\prime }+2f+m(\xi +\alpha )\epsilon f^{\prime }=0, \end{aligned}$$

(16)

$$\begin{aligned}&{\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}f^{\prime \prime }+\beta {\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\left( 2ff^{\prime \prime }+4m\epsilon ff^{\prime \prime }\right. \nonumber \\&\quad \left. +\,2m\epsilon (\xi +\alpha )ff^{\prime \prime \prime }-2jf^{\prime \prime \prime }+f^{\prime 2}+\epsilon f^{\prime 2}+m(\xi +\alpha )\epsilon f^{\prime }f^{\prime \prime }\right. \nonumber \\&\quad \left. \left. -\,j^{\prime }f^{\prime \prime }\right) -(1+\lambda _{1})(f^{2}-g^{2}+jf^{\prime }+m(\xi +\alpha )\epsilon ff^{\prime })=0,\right. \end{aligned}$$

(17)

$$\begin{aligned}&{\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}g^{\prime \prime }+\beta {\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\left( 2fg^{\prime \prime }+4m\epsilon fg^{\prime \prime }\right. \nonumber \\&\quad \left. +\,2m\epsilon (\xi +\alpha )fg^{\prime \prime \prime }-2jg^{\prime \prime \prime }+f^{\prime }g^{\prime }+m\epsilon f^{\prime }g^{\prime }+m(\xi +\alpha )\epsilon f^{\prime }g^{\prime \prime }\right. \nonumber \\&\quad \left. \left. -\,j^{\prime }g^{\prime \prime }\right) -(1+\lambda _{1})(2fg+jg^{\prime }+m(\xi +\alpha )\epsilon fg^{\prime })=0,\right. \end{aligned}$$

(18)

$$\begin{aligned}&\frac{1}{\Pr }{\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\theta ^{\prime \prime }-\gamma \left( m(m-1)(\xi +\alpha )\epsilon ^{2}f^{2}\theta ^{\prime \prime }+j^{2}\theta ^{\prime \prime }+m\epsilon jf\theta ^{\prime }\right. \nonumber \\&\quad \left. +\,m(\xi +\alpha )\epsilon f^{2}\theta ^{\prime }+m^{2}(\xi +\alpha )^{2}\epsilon ^{2}ff^{\prime }\theta ^{\prime }+m(\xi +\alpha )\epsilon jf^{\prime }\theta ^{\prime }+m(\xi +\alpha )\right. \nonumber \\&\quad \quad \left. \left. r^{*}fj^{\prime }\theta ^{\prime }+jj^{\prime }\theta \right) -m(\xi +\alpha )\epsilon f\theta ^{\prime }-j\theta ^{\prime }=0,\right. \end{aligned}$$

(19)

$$\begin{aligned}&f(0) =0,g(0)=1,j(0)=0,\theta (0)=1, \nonumber \\&f(\infty ) =0,g(\infty )=0,\theta (\infty )=0, \end{aligned}$$

(20)

with

$$\begin{aligned} {\text {Re}}=\frac{\Omega R_{0}^{2}\rho }{\mu },\alpha =\frac{a}{R_{0}} \left( \frac{\Omega R_{0}^{2}\rho }{\mu }\right) ^{\frac{1}{n+1}}, \epsilon =\frac{r}{R_{0}+r},r^{*}=\frac{r}{R_{0}},\Pr = \frac{c_{p}\mu }{k},\gamma =\lambda \Omega ,\beta =\lambda _{2}\Omega . \end{aligned}$$

(21)

Here, ${\text {Re}}$ depicts the Reynolds number, $\alpha$ the dimensionless coefficient of disk, $\epsilon$ the dimensionless constant, $r^{*}$ the radius parameter, $\Pr$ the Prandtl number, $\gamma$ the nondimensional thermal relaxation parameter, $\beta$ the Deborah number and n the power law exponent of fluid. Also, (f, g,  j and $\theta )$ are dimensionless (radial, tangential and axial) velocities and temperature.

Skin friction coefficient in radial and axial directions are

$$\begin{aligned} C_{f_{r}}&= {} \tau _{wr}/\rho (\Omega R_{0})^{2}, \nonumber \\ C_{f_{\theta }}&= {} \tau _{w\theta }/\rho (\Omega R_{0})^{2}, \end{aligned}$$

(22)

in which radial shear stress $(\tau _{wr})$ and tangential shear stress $(\tau _{w\theta })$ satisfy

$$\begin{aligned} \tau _{w\theta }=\frac{\mu }{1+\lambda _{1}}\left[ \frac{\partial {{v}}}{ \partial z}+\lambda _{2}\left( u\frac{\partial }{\partial r}+w\frac{\partial }{\partial z}\right) \frac{\partial {{v}}}{\partial z}\right] |_{z=a\left( \frac{r}{R_{0}}+1\right) ^{-m}}. \end{aligned}$$

(23)

Radial and tangential skin friction coefficients are

$$\begin{aligned} {\text {Re}}^{\frac{n}{n+1}}C_{f_{r}}&= {} \frac{(1+r^{*})^{m}}{r^{*}(1+\lambda _{1})}\left[ f^{\prime }(0)+\beta (f(0)f^{\prime }(0)+m\epsilon f(0)f^{\prime }(0)\right. \nonumber \\&\left. +\,m\eta \epsilon f(0)f^{\prime \prime }(0)-h(0)f^{\prime \prime }(0)) \right] , \nonumber \\ {\text {Re}}^{\frac{n}{n+1}}C_{f_{\theta }}&= {} \frac{(1+r^{*})^{m}}{r^{*}(1+\lambda _{1})}\left[ g^{\prime }(0)+\beta (f(0)g^{\prime }(0)+m\epsilon f(0)g^{\prime }(0)\right. \nonumber \\&\left. +\,m\eta \epsilon h(0)g^{\prime \prime }(0)-h(0)g^{\prime \prime }(0)) \right] . \end{aligned}$$

(24)

3 Solutions procedure

Initial guesses $j_{0}(\xi ),$ $f_{0}(\xi ),$ $g_{0}(\xi )$ and $\theta _{0}(\xi )$ are

$$\begin{aligned} j_{0}(\xi )=0,f_{0}(\xi )=0,g_{0}(\xi )=e^{-\xi }, \theta _{0}(\eta )=e^{-\xi }, \end{aligned}$$

(25)

where linear operators ${\mathcal {L}}_{j}$, ${\mathcal {L}}_{f}$, ${\mathcal {L}} _{g}$ and ${\mathcal {L}}_{\theta }$ are

$$\begin{aligned} {\mathcal {L}}_{j}=j^{\prime },{\mathcal {L}}_{f}=f^{\prime \prime }-f, {\mathcal {L}}_{g}=g^{\prime \prime }-g,{\mathcal {L}}_{\theta }=\theta ^{\prime \prime }-\theta . \end{aligned}$$

(26)

with

$$\begin{aligned} {\mathcal {L}}_{j}[c_{1}]&= {} 0, \nonumber \\ {\mathcal {L}}_{f}\left[ c_{2}e^{\xi }+c_{3}e^{-\xi }\right]&= {} 0, \nonumber \\ {\mathcal {L}}_{g}[c_{4}e^{\xi }+c_{5}e^{-\xi }]&= {} 0, \nonumber \\ {\mathcal {L}}_{\theta }\left[ c_{6}e^{\xi }+c_{7}e^{-\xi }\right]&= {} 0, \end{aligned}$$

(27)

in which $c_{i}$ $(i=1-7)$ denote the constants.

3.1 Zeroth-order deformation problems

Considering $p\in [0,1]$ as embedding and ($\hbar _{j},$ $\hbar _{f},$ $\hbar _{g}$ and $\hbar _{\theta })$ the nonzero auxiliary parameters, then zeroth-order deformation problems are

$$\begin{aligned}&(1-p){\mathcal {L}}_{j}\left[ \hat{\jmath }(\xi ,p)-j_{0}(\xi )\right] =p\hbar _{j}{\mathcal {N}}_{j}[\hat{\jmath }(\xi ,p),\hat{f}(\xi ,p)], \end{aligned}$$

(28)

$$\begin{aligned}&(1-p){\mathcal {L}}_{f}\left[ \hat{f}(\xi ,p)-f_{0}(\xi )\right] =p\hbar _{f} {\mathcal {N}}_{f}[\hat{f}(\xi ,p),\hat{g}(\xi ,p)], \end{aligned}$$

(29)

$$\begin{aligned}&(1-p){\mathcal {L}}_{g}\left[ \hat{g}(\xi ,p)-g_{0}(\xi )\right] =p\hbar _{g} {\mathcal {N}}_{g}[\hat{f}(\xi ,p),\hat{g}(\xi ,p)], \end{aligned}$$

(30)

$$\begin{aligned}&(1-p){\mathcal {L}}_{{\theta }}\left[ \hat{\theta }(\xi ,p)-\theta _{0}(\xi )\right] =p\hbar _{\theta }{\mathcal {N}}_{\theta }[\hat{\theta }(\xi ,p),\hat{f}(\xi ,p),\hat{\jmath }(\xi ,p)], \end{aligned}$$

(31)

$$\begin{aligned}&{\mathcal {N}}_{j}\left[ \hat{\jmath }(\xi ,p),\hat{f}(\xi ,p)\right] = \frac{\partial \hat{\jmath }(\xi ,p)}{\partial \xi }+2\hat{f}(\xi ,p)+m(\xi +\alpha )\epsilon \frac{\partial \hat{f}(\xi ,p)}{\partial \xi }, \end{aligned}$$

(32)

$$\begin{aligned} {\mathcal {N}}_{f}\left[ \hat{f}(\xi ,p),\hat{g}(\xi ,p)\right]&= {} {\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\frac{\partial ^{2}\hat{f}(\xi ,p)}{\partial \xi ^{2}}+\beta {\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\left( 2\hat{f}(\xi ,p)\frac{\partial ^{2}\hat{f}(\xi ,p)}{\partial \xi ^{2}}\right. \nonumber \\&\left. +\,4m\epsilon \hat{f}(\xi ,p)\frac{\partial ^{2}\hat{f}(\xi ,p)}{ \partial \xi ^{2}}+2m\epsilon (\xi +\alpha )\hat{f}(\xi ,p)\frac{\partial ^{3}\hat{f}(\xi ,p)}{\partial \xi ^{3}}-2\hat{\jmath }(\xi ,p)\frac{\partial ^{3}\hat{f}(\xi ,p)}{\partial \xi ^{3}}\right. \nonumber \\&\left. +\left( \frac{\partial \hat{f}(\xi ,p)}{\partial \xi }\right) ^{2}+\epsilon \left( \frac{\partial \hat{f}(\xi ,p)}{\partial \xi }\right) ^{2}+m(\xi +\alpha )\epsilon \frac{\partial \hat{f}(\xi ,p)}{\partial \xi } \frac{\partial ^{2}\hat{f}(\xi ,p)}{\partial \xi ^{2}}\right. \nonumber \\&\left. - \frac{\partial \hat{\jmath }(\xi ,p)}{\partial \xi }\frac{\partial ^{2}\hat{f}(\xi ,p)}{\partial \xi ^{2}}\right) -\left( 1+\lambda _{1}\right) \left( \left( \frac{\partial \hat{f}(\xi ,p)}{\partial \xi }\right) ^{2}-\left( \frac{\partial \hat{g}(\xi ,p)}{\partial \xi }\right) ^{2}\right. \nonumber \\&\left. +\hat{\jmath }(\xi ,p)\frac{\partial \hat{f}(\xi ,p)}{\partial \xi } +m(\xi +\alpha )\epsilon \hat{f}(\xi ,p)\frac{\partial \hat{f}(\xi ,p)}{ \partial \xi }\right) , \end{aligned}$$

(33)

$$\begin{aligned} {\mathcal {N}}_{g}\left[ \hat{f}(\xi ,p),\hat{g}(\xi ,p)\right]&= {} {\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\frac{\partial ^{2}\hat{g}(\xi ,p)}{\partial \xi ^{2}}+\beta {\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\left( 2\hat{f}(\xi ,p)\frac{\partial ^{2}\hat{g}(\xi ,p)}{\partial \xi ^{2}}\right. \nonumber \\&\left. +\,4m\epsilon \hat{f}(\xi ,p)\frac{\partial ^{2}\hat{g}(\xi ,p)}{ \partial \xi ^{2}}+2m\epsilon (\xi +\alpha )\hat{f}(\xi ,p)\frac{\partial ^{3}\hat{g}(\xi ,p)}{\partial \xi ^{3}}-2\hat{\jmath }(\xi ,p)\frac{\partial ^{3}\hat{g}(\xi ,p)}{\partial \xi ^{3}}\right. \nonumber \\&\left. +\frac{\partial \hat{f}(\xi ,p)}{\partial \xi }\frac{\partial \hat{g }(\xi ,p)}{\partial \xi }+\epsilon \frac{\partial \hat{f}(\xi ,p)}{\partial \xi }\frac{\partial \hat{g}(\xi ,p)}{\partial \xi }+m(\xi +\alpha )\epsilon \frac{\partial \hat{f}(\xi ,p)}{\partial \xi }\frac{\partial ^{2}\hat{g}(\xi ,p)}{\partial \xi ^{2}}\right. \nonumber \\&\left. -\frac{\partial \hat{\jmath }(\xi ,p)}{\partial \xi }\frac{\partial ^{2}\hat{g}(\xi ,p)}{\partial \xi ^{2}}\right) -\left( 1+\lambda _{1}\right) \left( 2\hat{f}(\xi ,p)\hat{g}(\xi ,p)+\hat{\jmath }(\xi ,p)\frac{\partial \hat{g}(\xi ,p)}{\partial \xi }\right. \nonumber \\&\left. +\,m(\xi +\alpha )\epsilon \hat{f}(\xi ,q)\frac{\partial \hat{g}(\xi ,p)}{\partial \xi }\right) , \end{aligned}$$

(34)

$$\begin{aligned} {\mathcal {N}}_{\theta }\left[ \hat{\theta }(\xi ,p),\hat{f}(\xi ,p),\hat{\jmath } (\xi ,p)\right]&= {} \frac{1}{\Pr }{\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\frac{\partial ^{2}\hat{\theta }(\xi ,p)}{\partial \xi ^{2}}-\gamma \left( m(m-1)(\xi +\alpha )\epsilon ^{2}\left( \hat{f}(\xi ,q)\right) ^{2} \frac{\partial ^{2}\hat{\theta }(\xi ,p)}{\partial \xi ^{2}}\right. \nonumber \\&\left. \left. +\left( \hat{\jmath }(\xi ,p)\right) ^{2}\frac{\partial ^{2} \hat{\theta }(\xi ,p)}{\partial \xi ^{2}}+m\epsilon \hat{\jmath }(\xi ,p)\hat{f }(\xi ,p)\frac{\partial \hat{\theta }(\xi ,p)}{\partial \xi }+m(\xi +\alpha )\epsilon \left( \hat{f}(\xi ,q)\right) ^{2}\right. \right. \nonumber \\&\quad \left. \frac{\partial \hat{\theta }(\xi ,p)}{\partial \xi }+m^{2}(\xi +\alpha )\epsilon ^{2}\hat{f}(\xi ,q)\frac{\partial \hat{f}(\xi ,p)}{ \partial \xi }\frac{\partial \hat{\theta }(\xi ,p)}{\partial \xi }+m(\xi +\alpha )\epsilon \hat{\jmath }(\xi ,p)\frac{\partial \hat{f}(\xi ,p)}{ \partial \xi }\right. \nonumber \\&\quad \left. \frac{\partial \hat{\theta }(\xi ,p)}{\partial \xi }+m(\xi +\alpha )r^{*}\hat{f}(\xi ,q)\frac{\partial \hat{\jmath }(\xi ,p)}{\partial \xi } \frac{\partial \hat{\theta }(\xi ,p)}{\partial \xi }+\hat{\jmath }(\xi ,p) \frac{\partial \hat{\jmath }(\xi ,p)}{\partial \xi }\hat{\theta }(\xi ,p)\right) \nonumber \\&-m(\xi +\alpha )\epsilon \hat{f}(\xi ,q)\frac{\partial \hat{\theta }(\xi ,p) }{\partial \xi }-\hat{\jmath }(\xi ,p)\frac{\partial \hat{\theta }(\xi ,p)}{ \partial \xi }, \end{aligned}$$

(35)

$$\begin{aligned} \hat{\jmath }(0,p)&= {} 0,\hat{f}(0,p)=0,\hat{g}(0,p)=1, \hat{\theta }(0,p)=1,\nonumber \\ \hat{f}(\infty ,p)&= {} 0,\hat{g}(\infty ,p)=0,\hat{\theta } (\infty ,p)=0. \end{aligned}$$

(36)

3.2 mth order deformation problems

The corresponding problem statements are

$$\begin{aligned}&{\mathcal {L}}_{f}\left[ j_{m}(\xi )-\chi _{m}j_{m-1}(\xi )\right] =\hbar _{j} {\mathcal {R}}_{j,m}(\xi ), \end{aligned}$$

(37)

$$\begin{aligned}&{\mathcal {L}}_{f}\left[ f_{m}(\xi )-\chi _{m}f_{m-1}(\xi )\right] =\hbar _{f} {\mathcal {R}}_{f,m}(\xi ), \end{aligned}$$

(38)

$$\begin{aligned}&{\mathcal {L}}_{g}\left[ g_{m}(\xi )-\chi _{m}g_{m-1}(\xi )\right] =\hbar _{g} {\mathcal {R}}_{g,m}(\xi ), \end{aligned}$$

(39)

$$\begin{aligned}&{\mathcal {L}}_{\theta }\left[ \theta _{m}(\xi )-\chi _{m}\theta _{m-1}(\xi ) \right] =\hbar _{\theta }{\mathcal {R}}_{\theta ,m}(\xi ), \end{aligned}$$

(40)

$$\begin{aligned}&{\mathcal {R}}_{j,m}\left( \xi \right) =j_{m-1}^{\prime }+2f_{m-1}+m(\xi +\alpha )\epsilon f_{m-1}^{\prime }, \end{aligned}$$

(41)

$$\begin{aligned} {\mathcal {R}}_{f,m}\left( \xi \right)&= {} {\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}f_{m-1}^{\prime \prime }+\beta {\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\sum \limits _{k=0}^{m-1}\left[ 2f_{m-1-k}f_{k}^{^{\prime \prime }}+4m\epsilon f_{m-1-k}f_{k}^{^{\prime \prime }}\right. \nonumber \\&\left. +\,2m\eta \epsilon f_{m-1-k}f_{k}^{^{^{\prime \prime \prime }}}-2j_{m-1-k}f_{k}^{\prime \prime \prime }+f_{m-1-k}^{\prime }f_{k}^{\prime }+\epsilon f_{m-1-k}^{\prime }f_{k}^{\prime }+m\epsilon \eta f_{m-1-k}^{\prime }f_{k}^{\prime \prime }\right. \nonumber \\&\left. -\,j_{m-1-k}^{\prime }f_{k}^{\prime \prime }\right] +\left( 1+\lambda _{1}\right) \sum \limits _{k=0}^{m-1}\left[ -f_{m-1-k}^{\prime }f_{k}^{\prime }+g_{m-1-k}^{\prime }g_{k}^{\prime }-j_{m-1-k}f_{k}^{\prime }\right] \nonumber \\&-m(\xi +\alpha )\left( 1+\lambda _{1}\right) \epsilon \sum \limits _{k=0}^{m-1}\left[ f_{m-1-k}f_{k}^{\prime }\right] , \end{aligned}$$

(42)

$$\begin{aligned} {\mathcal {R}}_{g,m}(\xi )&= {} {\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}g_{m-1}^{\prime \prime }+\beta {\text {Re}}^{\frac{1-n}{1+n}}(1+r^{*})^{2m}\sum \limits _{k=0}^{m-1}\left[ 2f_{m-1-k}g_{k}^{\prime \prime }+4m\epsilon f_{m-1-k}g_{k}^{\prime \prime }\right. \nonumber \\&\left. +\,2m\eta \epsilon f_{m-1-k}g_{k}^{\prime \prime \prime }-2j_{m-1-k}g_{k}^{\prime \prime \prime }+f_{m-1-k}^{\prime }g_{k}^{\prime }+m\epsilon f_{m-1-k}^{\prime }g_{k}^{\prime }+m\epsilon \eta f_{m-1-k}^{\prime }g_{k}^{\prime \prime }\right. \nonumber \\&\left. -\,j_{m-1-k}^{\prime }g_{k}^{\prime \prime }\right] +\left( 1+\lambda _{1}\right) +\sum \limits _{k=0}^{m-1}\left[ -2f_{m-1-k}g_{k}+j_{m-1-k}g_{k}^{\prime }\right] \nonumber \\&-m(\xi +\alpha )\epsilon \sum \limits _{k=0}^{m-1}\left[ f_{m-1-k}g_{k}^{ \prime }\right] , \end{aligned}$$

(43)

$$\begin{aligned} {\mathcal {R}}_{\theta ,m}(\xi )&= {} \frac{1}{\Pr }{\text {Re}}^{\frac{1-n}{1+n} }(1+r^{*})^{2m}\theta _{m-1}^{\prime \prime }-m(\xi +\alpha )\epsilon \sum \limits _{k=0}^{m-1}\theta _{m-1-k}^{\prime }f_{k}-\sum \limits _{k=0}^{m-1}\theta _{m-1-k}^{\prime }j_{k} \nonumber \\&-\gamma \left( \theta _{m-1-l}^{\prime \prime }\sum \limits _{h=0}^{l}[m(m-1)(\xi +\alpha )\epsilon ^{2}f_{l-h}f_{h}+j_{l-h}j_{h}]+\theta _{m-1-l}^{^{\prime }}\sum \limits _{h=0}^{l}[m\epsilon j_{l-h}f_{h}\right. \nonumber \\&\left. +\,m(\xi +\alpha )\epsilon f_{l-h}f_{h}m^{2}(\xi +\alpha )\epsilon ^{2}f_{l-h}f_{h}^{\prime }+m(\xi +\alpha )\epsilon j_{l-h}f_{h}^{\prime }+m(\xi +\alpha )r^{*}f_{l-h}j_{h}^{\prime }\right] \nonumber \\&\left. +\,\theta _{m-1-l}\sum \limits _{h=0}^{l}j_{l-h}j_{h}^{\prime }\right) , \end{aligned}$$

(44)

$$\begin{aligned} f_{m}(0)&= {} f_{m}(\infty )=g_{m}(0)=g_{m}(\infty )=j_{m}(0)=\theta _{m}(0)=\theta _{m}(\infty )=0, \end{aligned}$$

(45)

$$\begin{aligned} \chi _{m}&= {} \left\{ \begin{array}{ll} 0,&{} m\le 1 \\ 1,&{} m>1 \end{array} \right. . \end{aligned}$$

(46)

The general solutions $(j_{m},$ $f_{m},$ $g_{m},$ $\theta _{m})$ with particular values $(j_{m}^{*},$ $f_{m}^{*},$ $g_{m}^{*},$ $\theta _{m}^{*})$ are

$$\begin{aligned} j_{m}(\xi )&= {} j_{m}^{*}(\xi )+c_{1}, \end{aligned}$$

(47)

$$\begin{aligned} f_{m}(\xi )&= {} f_{m}^{*}(\xi )+c_{2}e^{-\xi }+c_{3}e^{\xi }, \end{aligned}$$

(48)

$$\begin{aligned} g_{m}(\xi )&= {} g_{m}^{*}(\xi )+c_{4}e^{-\xi }+c_{5}e^{\xi }, \end{aligned}$$

(49)

$$\begin{aligned} \theta _{m}(\xi )&= {} \theta _{m}^{*}(\xi )+c_{6}e^{-\xi }+c_{7}e^{\xi }. \end{aligned}$$

(50)

4 Analysis

4.1 Convergence of derived series solutions

The region of convergence of series solutions can be adjusted with the help of auxiliary parameters $\hbar _{j},$ $\hbar _{f},$ $\hbar _{g}$ and $\hbar _{\theta }$. For this reason, we have plotted $\hbar$-curves (see Figs. 2, 3, 4 and 5 ) of $j^{\prime }(0),$ $f^{\prime \prime }(0),$ $g^{\prime }(0)$ and $\theta ^{\prime }(0)$. Appropriate ranges of auxiliary parameters $\hbar _{j}$, $\hbar _{f},$ $\hbar _{g}$ and $\hbar _{\theta }$ are $[-\,1.49,-\,0.3],$ $[-\,1.15,-\,0.4]$, $[-\,1.3,-\,0.65]$ and $[-\,0.9,-\,0.4],$ respectively. Convergence of HAM solutions for different order of approximations is given in Table 1. Table 2 is constructed to compare our results with the previous published Refs. [10, 18], and the results are found in excellent agreement

Fig. 2

$\hbar$-curve for $j^{\prime }(0)$ when $m=1.0,$ $\alpha =0.15$, ${\text {Re}}=1.0,$ $n=1.1,$ $\epsilon =0.4,$ $r^{*}=0.2,$ $\Pr =1.5$, $\gamma =0.6,$ $\lambda _{1}=0.5$ and $\beta =0.25$

Fig. 3

$\hbar$-curve for $f^{\prime \prime }(0)$ when $m=1.0,$ $\alpha =0.15$, ${\text {Re}}=1.0,$ $n=1.1,$ $\epsilon =0.4,$ $r^{*}=0.2,$ $\Pr =1.5$, $\gamma =0.6$ $\lambda _{1}=0.5$ and $\beta =0.25$

Fig. 4

$\hbar$-curve for $g^{\prime }(0)$ when $m=1.0,$ $\alpha =0.15$, ${\text {Re}}=1.0,$ $n=1.1,$ $\epsilon =0.4,$ $r^{*}=0.2,$ $\Pr =1.5$, $\gamma =0.6$ $\lambda _{1}=0.5$ and $\beta =0.25$

Fig. 5

$\hbar$-curve for $\theta ^{\prime }(0)$ when $m=1.0,$ $\alpha =0.15$, ${\text {Re}}=1.0,$ $n=1.1,$ $\epsilon =0.4,$ $r^{*}=0.2,$ $\Pr =1.5$, $\gamma =0.6$ $\lambda _{1}=0.5$ and $\beta =0.25$

Table 1 Convergence of HAM solutions for different order of approximations when $m=1.0,$ $\alpha =0.15$, ${\text {Re}}=1.0,$ $n=1.1,$ $\epsilon =0.4,$ $r^{*}=0.2,$ $\Pr =1.5$, $\gamma =0.6,$ $\lambda _{1}=0.5$ and $\beta =0.25$

Table 2 Comparison of the present solutions with the results in Refs. [10, 18] for $n=Pr=1$, $m=\alpha =\gamma =\lambda _{1}=\beta =0$

4.2 Discussion

4.2.1 Axial velocity profile

Figure 6 analyzes the impact of disk thickness index m on axial velocity profile. Here, magnitude of velocity field decreases for rising values of m . Influence of thickness coefficient of disk $\alpha$ on axial velocity profile is shown in Fig. 7. Here, magnitude of velocity profile increases for increasing values of $\alpha .$ Figure 8 is plotted to show the impact of $\epsilon$ on axial velocity profile. Here, axial velocity decays for higher values of $\epsilon$.

Fig. 6

Impact of m on axial velocity

Fig. 7

Impact of $\alpha$ on axial velocity

Fig. 8

Impact of $\epsilon$ on axial velocity

4.2.2 Radial velocity profile

Influence of power law exponent of fluid n on radial velocity is sketched in Fig. 9. Radial velocity increases for ascending values of n. Thickness of disk decreases for increasing values of n which enhances the fluid velocity. Figure 10 demonstrates the impact of thickness index parameter m on radial velocity field. Here, radial velocity profile enhances for ascending values of m. Variations of $\alpha$ and $\epsilon$ on radial velocity are plotted in Figs. 11 and 12. It is seen that velocity rises for increasing values of $\alpha$ and $\epsilon .$ Figure 13 depicts the behavior of ${\text {Re}}$ on radial velocity profile. Velocity profile shows increasing behavior of ${\text {Re}}.$ It is due to the fact that viscosity decays for larger values of ${\text {Re}}$ which enhances the fluid velocity. Figure 14 analyzes the increasing behavior of $\lambda _{1}$ on radial velocity profile. It is observed that boundary layer thickness rises when $\lambda _{1}$ is enhanced. It is seen from Fig. 15 that radial velocity has direct relation with Deborah number $\beta$. Boundary layer thickness and velocity profile enhance for larger $\beta$. As expected, increasing values of retardation time enhance the elasticity.

Fig. 9

Impact of n on radial velocity

Fig. 10

Impact of m on radial velocity

Fig. 11

Impact of $\alpha$ on radial velocity

Fig. 12

Impact of $\epsilon$ on radial velocity

Fig. 13

Impact of ${\text {Re}}$ on radial velocity

Fig. 14

Impact of $\lambda _{1}$ on radial velocity

Fig. 15

Impact of $\beta$ on radial velocity

4.2.3 Tangential velocity profile

Figures 16 and 17 show distribution of tangential velocity profile $g(\xi )$ for larger values of thickness index parameter m and constant $\epsilon$. It is observed that tangential velocity enhances for ascending values of m and constant $\epsilon$. Figure 18 is plotted to demonstrate the impact of ${\text {Re}}$ on tangential velocity. Here, tangential velocity field rises when ${\text {Re}}$ is enlarged. Higher values of ${\text {Re}}$ decrease the viscosity, and thus, fluid velocity enhances. Variation in tangential velocity for larger values of $\lambda _{1}$ is characterized in Fig. 19. We observed that tangential velocity declines for increasing values of $\lambda _{1}.$ Since relaxation time increases corresponding to larger $\lambda _{1},$particles need more time to come back to equilibrium system from perturbed system. As a consequence fluid velocity decreases. Increment in tangential velocity profile for increasing values of Deborah number $\beta$ is displayed in Fig. 20. Tangential velocity increases for rising values of $\beta$. Fluid velocity and boundary layer thickness are enhanced for increasing values of $\beta$.

Fig. 16

Impact of m on tangential velocity

Fig. 17

Impact of $\epsilon$ on tangential velocity

Fig. 18

Impact of ${\text {Re}}$ on tangential velocity

Fig. 19

Impact of $\lambda _{1}$ on tangential velocity

4.2.4 Dimensionless temperature profile

Figure 21 discloses the behavior of power law exponent n on temperature field. Temperature of fluid enhances for larger values of n. Figure 22 reveals the variation of index parameter m on temperature. Here, increase in m enlarges temperature distribution. Influence of thickness coefficient of disk $\alpha$ on temperature is indicated in Fig. 23. Temperature distribution rises corresponding to higher values of $\alpha$. Figure 24 illustrates the variation of $\epsilon$ on temperature field. It is seen that temperature is increasing function of $\epsilon .$ Figures 25 and 26 analyze the increasing behavior of ${\text {Re}}$ and $r^{*}$ on temperature distribution. Impact of Prandtl number $\Pr$ on temperature distribution is presented in Fig. 27. Here, temperature profile reduces when $\Pr$ is enhanced. Prandtl number is ratio of momentum diffusivity to thermal diffusivity. Larger values of Prandtl number reduce the thermal diffusivity, and so, temperature distribution decreases. Figure 28 portrays the influence of thermal relaxation parameter on temperature profile. For higher values of $\gamma$ the temperature and thermal layer thickness reduced. In fact, particles require more time to transfer heat which decreases the temperature distribution.

Fig. 20

Impact of $\beta$ on tangential velocity

Fig. 21

Impact of n on $\theta (\xi )$

Fig. 22

Impact of m on $\theta (\xi )$

Fig. 23

Impact of $\alpha$ on $\theta (\xi )$

4.2.5 Radial skin friction coefficient

Behavior of thickness index parameter m (via n) on radial skin friction coefficient is examined in Fig. 29. Surface drag force enhances for larger m. Figure 30 illustrates the impact of $\lambda _{1}$ on radial skin friction coefficient against ${\text {Re}}$. Here, surface drag force rises for ascending values of $\lambda _{1}.$

Fig. 24

Impact of $\epsilon$ on $\theta (\xi )$

Fig. 25

Impact of ${\text {Re}}$ on $\theta (\xi )$

Fig. 26

Impact of $r^{*}$ on $\theta (\xi )$

4.2.6 Tangential skin friction coefficient

Figures 31 and 32 reveal the impact of $\beta$ and $\epsilon$ on tangential skin friction coefficient. Here, we noticed that magnitude of skin surface drag force decreases for ascending values of $\beta$ and $\epsilon$.

Fig. 27

Impact of $\Pr$ on $\theta (\xi )$

Fig. 28

Impact of $\gamma$ on $\theta (\xi )$

Fig. 29

Behavior of m on ${\text {Re}}^{\frac{n}{n+1}}C_{f_{r}}$

5 Concluding remarks

Axisymmetric flow of Jeffrey fluid by a rotating disk with variable thicked surface is studied. Heat transfer is discussed through Cattaneo–Christov heat flux model. HAM is used to obtain analytical solutions. It is observed that for larger values of the ratio of relaxation to retardation times $\lambda _{1},$ the velocity along radial direction increases, while it reduces along tangential direction. Radial and tangential velocities have direct relation with Deborah number $\beta .$ An increase in retardation time enhances elasticity. Since elasticity and viscosity effects are inversely proportional to each other, decrease in viscosity enhances the fluid velocity. For larger thermal relaxation time parameter, particles require more time to transfer heat which decreases the temperature distribution. Higher thickness index of disk m implies an enhancement in the skin friction coefficient in redial direction.

Fig. 30

Behavior of $\lambda _{1}$ on ${\text {Re}}^{\frac{n}{n+1} }C_{f_{r}}$

Fig. 31

Behavior of $\beta$ on ${\text {Re}}^{\frac{n}{n+1}}C_{f_{\theta }}$

Fig. 32

Behavior of $\epsilon$ on ${\text {Re}}^{\frac{n}{n+1}}C_{f_{\theta }}$