Introduction

Recently, the applications of nanofluids have been widely accepted by many scholars in numerous engineering problems like mechanical, chemical, and electrical engineering, due to their favorable properties compared to the conventional fluids, such as lubricating efficiency, cooling capacity, thermal characteristics, and viscosity behavior [1,2,3,4,5].

The viscosity augmentation can be achieved with the help of adding nanoparticles to the base fluid [6,7,8]. The nanofluids’ viscosity affects the convective heat transfer coefficient, pressure drop, pumping power, its workability in industrial application, and thereby the pressure reduction must be compensated by using higher quantity of power [9]. The addition of micrometer-sized particles to the base fluids causes vast changes in the properties of the operating fluid [10, 11]. In this way, it can be concluded that nanofluids express higher convective heat transfer and viscosity by comparison of nanofluids with liquids which conventionally utilized [12,13,14]. Thus, the optimization of heat transfer process can be obtained by applying nanotechnology. The examples of nanoparticles that are suspended in the fluids are metals, oxides, ceramics, and nanotubes [15,16,17,18,19]. Additionally, the range contributed to the nanoparticles’ size is approximately between 1 and 100 nm. As suspended particles have the characteristics of higher viscosity and thermal performance, auspicious properties associated with nanofluids can be achieved by adding these particles. In this way, some experimental investigations on the viscosity of nanofluids have been performed by many researchers [4]. Therefore, the influence of various parameters on nanofluids viscosity has been studied by many scholars [20,21,22,23,24]. The effects of temperature [9, 21, 22, 25,26,27,28,29,30,31,32,33], volumetric concentration of nanoparticle [1, 20, 21, 23, 27,28,29, 34,35,36,37,38,39], aggregation radius [40, 41], particle shape [42], thickness of nanolayers [43, 44], and packing fraction [45] have been widely provided in these studies.

The flow characteristic and thermal performance of TiO2/distilled water flowing through a vertical pipe in an upward direction have been investigated by He et al. [46]. The operation conditions can be stated as a constant heat flux boundary condition in turbulent and laminar flow regimes. In the investigation, the average diameter of 95 nm was utilized for TiO2 nanoparticles. As indicated in the results, the estimated quantity of the Einstein equation is considerably lower than the calculated viscosity of nanofluids [28]; the viscosity of TiO2/water nanofluid in the temperature range of 15–35 °C and volume concentration range of 0.2–2 vol% has been studied by Duangthongsuk et al. [28]. According to the experiments, the nanofluids’ viscosity reduced by increasing the temperature and particle concentrations. As stated in the results, the comparison of the experimental viscosity of nanofluids with estimated quantities from the previous correlations showed these two values were distinct. Therefore, new correlations were performed in order to predict the nanofluids’ viscosity [47].

In addition to the experimental investigations, vast variety of efforts were done to model the experimental results by proposing different correlations or by utilizing artificial neural networks. Various studies in different fields have recommended applying artificial intelligence like support vector machines, fuzzy inference systems, and the artificial neural networks (ANNs), which commonly lead to accurate results [48,49,50,51,52,53].

Radial basis function neural networks (RBF-NN) have been applied by Zhao et al. [34] for the aim of predicting the viscosity of CuO/water and Al2O3/water nanofluids. In this way, 721 experimental data contributed to the mentioned nanofluids were utilized. Also, for predicting the viscosity of nine various nanofluids with the help of hybrid self-organizing polynomial neural network based on GMDH, nine models have been developed by Atashrouz et al. [54].

Derakhshanfard and Mehralizadeh in 2018 published a paper on the impact of the efficiency of radial basis function method. They investigated the viscosity of crude oil under different ranges of temperatures and various mass fractions of five types of nanofluids. Increase in the concentration of TiO2, ZnO, and FeO3 nanoparticles led to decrease in the viscosity of their corresponding nanofluids; by contrast, any raise in the mass fraction of WO3 and NiO will result in higher viscosities [55].

Additionally, LSSVM approach has been employed by Meybodi et al. [56] for predicting the viscosity of water-based SiO2, CuO, TiO2, and Al2O3 nanofluids. For the aim of estimating the viscosity of TiO2/water nanofluid, an ANN has been developed by Esfe et al. [40] with considering volume fraction and temperature as input data. As stated in the results, the ANN model can precisely and reliably estimate the viscosity of TiO2/water nanofluid. Baghban et al. [57] used least square support vector machine algorithm (LSSVM) to examine the properties of 29 various nanofluids.

Furthermore, or the aim of predicting the viscosity of non-Newtonian EG–water/Fe3O4 nanofluids as a function of shear rate, volume fraction, and temperature, GMDH approach has been utilized by Atashrouz et al. [58]. According to the results, the GMDH approach can estimate the viscosity accurately. Heidari et al. [59] and Barati-Harooni et al. [60] proposed two distinct methods utilizing a similar data bank for predicting the viscosity based on MLP-ANN and RBF-ANN, respectively. Based on their results, both models have the ability to predict the nanofluids’ viscosity accurately [61].

Additionally, the ANN model has been used by Longo et al. [62] for estimating the thermal conductivity of Al2O3/water and TiO2/water nanofluids. Moreover, different investigations with the help of ANN approach for estimating the thermophysical properties of nanofluids containing various kinds of nanoparticles (Fe, Cu, Mg(OH)2, TiO2, MgO, Al2O3) and base fluids (ethylene glycol, water, and their mixture) have been stated by Esfe et al. [63,64,65,66,67]. Also, another study has been carried out by Aminian [68] which focused on the development of an ANN model for predicting the water-based nanofluid’s effective viscosity for an extensive group of experimental data [47]. In addition to the ANN approaches, Tafarroj et al. [69] utilized the computational fluid dynamics and predicted the efficiency of the absorption of nanofluids. The impact of concentration of nanofluid and the operating temperature was investigated through CFD and ANN approaches. They drew a comparison between these methods and discussed their benefits and disadvantages. In spite of the CFD approach, they proposed that MLP network is not able to either analyze the trends or predict anything beyond its training domain [70].

In the present study, we utilize various neural networks (ANFIS, MLP-ANN, LSSVM, and RBF-ANN) to model the experimentally obtained data of viscosity of TiO2–water nanofluid and develop four various models to predict the viscosity precisely, rapidly, and cost-effectively.

Theory

Multilayer perceptron artificial neural network (MLP-ANN)

A type of computational intelligence which is originated from biological nervous systems like the human brain is named artificial neural networks (ANNs). Complicated relations between outputs and inputs of a system can be found with the help of ANNs. Interconnections or links and processing elements are mentioned as two major elements for each ANN. In this way, interconnections and masses provide connections between neurons; however, nodes or neurons and the processing elements process the information [71, 72]. Radial basis function (RBF) and multilayer perceptron (MLP) are considered as the most prevailing ANNs. The mentioned networks differ fundamentally based on the approach in which the neurons process the information. Various layers are included in an MLP neural network, in which the input layer proportionate to the input data and the output layer proportionate to the output of the model are the first and the last layers, respectively. Additionally, the middle layers between the output and input layers are called hidden layers [73]. In general, hidden layers have an obligation for the internal appearance of the relation between the model’s inputs and the favorable output. The neurons’ number and input variables are equal; on the other hand, the outputs’ number is typically the one that is the appealing property/parameter. The numbers of neurons and hidden layers must be decided based on empirical approaches. A one-hidden-layer MLP is favorable in many problems [74]. Nonetheless, mainly two hidden layers are utilized for complex systems. Also, the whole neurons in the next and previous layer are connected to each neuron in the hidden layer [61]. In turn, the hidden neurons’ outputs perform as inputs to the output neuron where they undergo another transformation. The following equation describes the output of MLP neural network:

$$\gamma_{\text{jk}} = F_{\text{k}} \left( {\sum\limits_{i = 1}^{{N_{{{\text{k}} - 1}} }} {\omega_{\text{ijk}} \gamma_{{{\text{i}}({\text{k}} - 1)}} + \beta_{\text{jk}} } } \right){ ,}$$
(1)

in which \(\beta_{\text{jk}}\) and \(\gamma_{\text{jk}}\) express bias mass for neuron j in layer k and the neuron j’s output from k’s layer, respectively. \(\omega_{\text{ijk}}\) indicates the model-fitting parameters, which are the link masses. These parameters have been chosen indiscriminately in the start of network training process. Additionally, \(F_{\text{k}}\) signifies the nonlinear activation transfer functions that are regarded in various forms like linear functions, Gaussian, bipolar sigmoid, binary sigmoid, binary step function, and identity function [75].

Adaptive neuro-fuzzy inference system (ANFIS)

The combination of multilayer artificial neural network and Sugeno fuzzy inference model (SFIM) is named ANFIS. Synaptic masses are not utilized in ANFIS approach; however, it applies nonadaptive and adaptive nodes in its different layers. The performing principle of ANFIS and SFIM is relatively identical [76]. In the initial phase of ANFIS, least square method and gradient descent with backpropagation algorithm identify model parameters and fuzzy membership function [77]. The analysis of viscosity values is performed with the help of using the fuzzy membership functions. Generally, a set of degrees and objects of membership is considered as a fuzzy set, which its values vary between 0 and 1. The analysis of ambiguous and subjective judgments is mentioned as the crucial role of the fuzzy logic. It is presumed that the ANFIS approach includes two inputs x and y, as well as one output f. For generating two if–then rules, the first-order Sugeno kind should be utilized as follows:

$$\begin{aligned} {\text{Rule}}\;1\;{\text{if}}\;x\;{\text{is}}\;U_{1} \;{\text{and}}\;y\;{\text{is}}\;V_{1} ,{\text{then}}\;f_{1} = p_{1} x + q_{1} y + r_{1} \hfill \\ {\text{Rule}}\;2\;{\text{if}}\;x\;{\text{is}}\;U_{2} \;{\text{and}}\;y\;{\text{is}}\;V_{2} ,{\text{then}}\;f_{2} = p_{2} x + q_{2} y + r_{2} , \hfill \\ \end{aligned}$$

in which x and y express the input variables, and U1, U2, V1, and V2 indicate small, medium, and large fuzzy sets. Also, different design parameters like p1, q1, r1, p2, q2, and r2 define the linguistic labels in the training phase. A typical schematic of the ANSIS model is provided in Fig. 1.

Fig. 1
figure 1

Typical structure of the ANFIS [4]

Full size image

Least squares support vector machine (LSSVM)

A machine learning technique utilized in regression pattern recognition, classification, and analysis amid input data is named support vector machine (SVM). Least square support vector machine (LSSVM) is considered as a novel version of SVM, which was proposed to obviate the prevailing problems of SVM approach. In this approach, regression error is added to the constraints associated with the optimization. To be clear, regression error is mathematically determined and solved in LSSVM approaches; nonetheless, it is optimized in the learning phase of SVM methods. Equation 2 defines the penalized function in this method as follows [78]:

$$Q_{\text{LSSVM}} = \frac{1}{2}w^{{\text{T}}} w + \gamma \sum\limits_{k = 1}^{N} {e_{\text{k}}^{2} } ,$$
(2)

in which T and γ indicate transpose matrix and regression errors’ summation. The succeeding constraints subject to the above equation:

$$y_{\text{k}} = w^{{\text{T}}} \phi (x_{\text{k}} ) + b + e_{\text{k}} \quad k = 1,2, \ldots ,N,$$
(3)

in which, ek, T, y, b, and w express the N training objects’ regression error, the transpose matrix, the output vector contributed to the model, the bias or the intercept of linear regression, and the regression mass (the linear regression slope), respectively. Additionally, the following equation regularly expresses the mass coefficient (w):

$$w = \sum\limits_{k = 1}^{N} {a_{\text{k}} x_{\text{k}} } \quad {\text{where}}\;a_{\text{k}} = 2\gamma e_{\text{k}} \, .$$
(4)

By reformulating Eq. (4) with the help of LSSVM method, the succeeding equation is obtained [78]:

$$w = \sum\limits_{k = 1}^{N} {a_{\text{k}} x_{\text{k}}^{{\text{T}}} x} + b \, .$$
(5)

Therefore, the Lagrange multipliers can be described as follows:

$$a_{k} = \frac{{(y_{\text{k}} - b)}}{{x_{\text{k}}^{{\text{T}}} x + (2\gamma )^{ - 1} }} \, .$$
(6)

By utilizing the succeeding Kernel function, the mentioned linear regression equation is reformulated:

$$f(x) = \sum\limits_{k = 1}^{N} {a_{\text{k}} K(x,x) + b \, } .$$
(7)

Also, K(x, xk) indicates the Kernel function that is the result of dot product of x and xk vectors. Actually, the dot product of Φ(xk) and Φ(x)T is K(x, xk) like the succeeding expression [78]:

$$K(x,x_{\text{k}} ) = \phi (x)^{{\text{T}}} \times \phi (x_{\text{k}} ) \, .$$
(8)

Radial basis Kernel function is considered as one of the most eminent Kernel function which has been applied in this investigation as follows:

$$K(x,x_{\text{k}} ) = \exp \left( { - \left\| {x_{\text{k}} - x} \right\|^{2} /\sigma^{2} } \right) \, .$$
(9)

This paper uses a PSO algorithm for the aim of optimizing the LSSVM approach. A schematic illustration of the PSO-LSSVM method is demonstrated in Fig. 2.

Fig. 2
figure 2

A schematic illustration of PSO-LSSVM

Full size image

RBF-ANN

Radial basis function neural networks are referred as one of the firm-proved neural networks, which are applied in regression and classification. In fact, the theory of function approximation is the basis of the concept associated with RBF-ANN. The introduction of this method was rendered by Broomhead, which was a sort of feed-forward neural networks. Furthermore, numerous numerical and mathematical investigations have been carried out with the help of using these networks [79]. Generally, a three-layer feed-forward structure is included in a RBF neural network, that is, an input layer is connected to the output layer with the help of a hidden layer. In reality, p is the input nodes in the input layer which is similar to the input variables’ number of the model. The major part of RBF-ANN which transmits the data from input space to a hidden space is the hidden layer. Every point contributed to the hidden layer is centered at an exact radius. The distance between the input vector and its own center is measured in every neuron [80].

The configuration of an RBF-ANN system is similar to the structure of MLP-ANN, but a complex RBF function is applied to the hidden layers. The result of RBF-ANN is:

$$y_{\text{ik}} (x) = \sum\limits_{i = 1}^{n} {w_{\text{i}} \varPhi_{\text{ki}} \left( {\left\| {x_{\text{k}} - c_{\text{i}} } \right\|} \right)} ,\quad i = 1,2, \ldots N\;{\text{and}}\;k = 1,2, \ldots ,M{ ,}$$
(10)

where x is an input pattern, yi (x) is ith output, and wki is the mass of connection from the kth interior element to the ith element of outcome layer. The || || symbol represents the Euclidean norm, and ck is the archetype of the middle of the kth interior element. Conventionally, the RBF (φ) is picked out as the Gaussian operator which is presented below:

$$h(x) = \exp \left( { - \frac{{(x - c)^{2} }}{{r^{2} }}} \right).$$
(11)

The radius (r) and center (c) are parameters of Gaussian RBF. Away from the center, it decreases uniformly.

Methodology

Pre-analysis phase

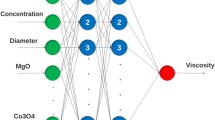
The data used for modeling are extracted from the experimental studies [81,82,83,84,85]. There are 56 sets of data points in this study for predicting viscosity of TiO2-based water nanofluid as a function of temperature, volume fraction, and average diameter. The temperature ranges between 15 and 50 °C, while the volume fraction, average diameter, and viscosity range between 0.2 and 3, 21 and 25 nm, and 0.00057 and 0.00122 kg (mS)−1, respectively. In the current paper, four model-building procedures and five different statistical approaches were used in order to estimate and validate the viscosity of nanofluid. The resulted data from the experimental section of the study at the first step are used to train the models. In order to evaluate the globalization of models, we used dataset of nanofluid with a diameter of 21 nm for testing phase and other data points with a diameter of 25 nm were used for training stage. The suggested models can predict viscosity of TiO2 nanofluids with great accuracy for different inputs. Equation 12 shows the normalization procedure of every data:

$$D_{\text{k}} = 2\frac{{x - x_{\hbox{min} } }}{{x_{\hbox{max} } - x_{\hbox{min} } }} - 1{ ,}$$
(12)

where x is the value of the nth parameter. The absolute value of \(D_{\text{k}}\) will be less than unity. The other values are fed to the neural network systems, and the models are built to predict the viscosity as the main output.

Outlier detection

On the condition of implementing statistical approaches or training machine learning algorithms, outliers or anomalies could be mentioned as a severe concern. They are generally made due to the measurements’ errors or excellent systems conditions, as the result cannot illustrate the prevailing functioning of the underlying system. Certainly, applying an outlier removal phase before proceeding with additional investigation can be stated as the exceptional practice. The leverage value procedure is applied as an outlier detection method in this study. The Hat and the residual values of any input were calculated. This method’s principles are provided in Refs. [86, 87]. The succeeding equation is applied to calculate the Hat matrix:

$$H = X(X^{{\text{T}}} X)^{ - 1} X^{{\text{T}}} .$$
(13)

X is a matrix of size N × P, in which N represents the data points’ total number and P denotes the input parameters’ number. T and − l are transposed and inverse operators, respectively. A warning leverage value is also defined using the following expression:

$$H^{*} = \frac{3(p + 1)}{N} \, .$$
(14)

A rectangular area restricted to R = ± 3 and 0 ≤ H ≤ H* is considered as the feasible region.

Model development and verification methodology

As an essential step in developing a model, the validation of model must be carried out. This step aims to check the accuracy of the proposed models and see if they produce valid results [88]. To derive the representative models, outstanding approaches of MLP-ANN, LSSVM, ANFIS, and RBF-ANN were utilized. The accuracy of models was examined by Eqs. 15–19:

$${\text{MSE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {(X_{\text{i}}^{\exp } - X_{\text{i}}^{\text{simul}} ) \, }$$
(15)
$${\text{ARD}}\;(\% ) = \frac{100}{N} \times \sum\limits_{i = 1}^{N} {\frac{{\left| {X_{\text{i}}^{\exp } - X_{\text{i}}^{\text{simul}} } \right|}}{{X_{\text{i}}^{\text{simul}} }}} \,$$
(16)
$${\text{STD}} = \left( {\frac{1}{N - 1} \times \sum\limits_{i = 1}^{N} {(X_{\text{i}}^{\exp } - X_{\text{i}}^{\text{simul}} )^{2} } } \right)^{0.5}$$
(17)
$${\text{RMSE}} = \left( {\frac{1}{N}\sum\limits_{i = 1}^{N} {(X_{\text{i}}^{\exp } - X_{\text{i}}^{\text{simul}} )^{2} } } \right)^{0.5}$$
(18)
$$R^{2} = 1 - \frac{{\sum\nolimits_{i = 1}^{N} {(X_{\text{i}}^{\exp } - X_{\text{i}}^{\text{simul}} )^{2} } }}{{\sum\nolimits_{i = 1}^{N} {(X_{\text{i}}^{\exp } - X_{\text{i}}^{\text{avg}} )^{2} } }}{ ,}$$
(19)

where output property is denoted by X, N represents the figure of total data points, ‘exp’ illustrates the experimental values and ‘simul’ is a notation for modeled values. \(X_{\text{i}}^{\text{avg}}\) is the average of experimentally obtained viscosities.

Results and discussion

The proposed MLP-ANN, RBF-ANN, ANFIS, and LSSVM strategies were associated with common optimization algorithms including Levenberg–Marquardt and particle swarm optimization (PSO). Figure 3 shows the bubble curve of viscosity versus the volume fraction and temperature in which the size of each bubble is dependent on the size of particles. The detailed information of MLP-ANN including the number of neurons in hidden and output layers is listed in Table 1. In this table, the amount of mass parameter for different inputs (temperature, volume fraction, and diameter of TiO2) and also the bias numbers for the interior and the output layers are presented. It is worth mentioning that several structures were evaluated and then the best one with four neurons in hidden layer was selected as good structure with minimum parameters. Based on the above procedure for MLP-ANN model, we tried several times to find the best structure of RBF-ANN with minimum parameters. The optimization algorithm to find the optimized RBF-ANN parameters was Levenberg–Marquardt.

Fig. 3
figure 3

Bubble curves of suggested experimental data set

Full size image
Table 1 Optimal mass and bias values for the MLP-ANN method
Full size table

In association with ANFIS strategy, the particle swarm optimization (PSO) method is utilized for the aim of determining optimum parameters. Training results of membership functions for different parameters and various clusters are demonstrated in Fig. 4, where the plot of degree of membership versus average diameter of particles, percentage of volume fraction, and temperature is illustrated. Detailed information about the proposed models such as used membership and activation functions, number of clusters, interior and exterior layers, and the optimization methods is reported in Table 2. Two kinds of tuning parameters (γ and σ2) were used in the LSSVM machine. The optimized values for γ and σ2 are 5745.3831 and 2.0486028, respectively.

Fig. 4
figure 4

Trained membership functions for different input parameters

Full size image
Table 2 More details of trained models for the prediction of viscosity of TiO2/water nanofluid
Full size table

Model validation results

We applied both graphical and statistical approaches to evaluate the models’ performances regarding the estimation of the viscosity. Figure 5 illustrates the MSE error for the LM algorithm. Increasing the number of iterations results in the decrease in MSE error until it touches a final value of 4 × 10−4 after about 40 iterations. Figure 6 shows information about the performance of ANFIS method evaluated by PSO approach; it was seen that the corresponding root-mean-squared error was decreased rapidly in the first 100 iterations. Figure 7 shows the plot of the resulted viscosities obtained from the proposed models. In this figure, the results of prediction are plotted versus data index and shows the training and testing procedure results. From this figure, it can be seen that the LSSVM and RBF-ANN had a better prediction capability and led to a more precise results. The coefficient of determination (R2) indicates how close predicted values are to experimental values. This parameter usually lies between 0 and 1.0. Closer values to unity indicate more accurate predictions. Near-unity coefficients of determination for the proposed models represent their capability in predicting the viscosity. As is demonstrated in different parts of Fig. 8, the regression diagram of experimental and estimated values shows an R2 coefficient of 0.995 and 0.993 for training and testing sections of the ANFIS method in part a, and in the b, c and d parts of the diagram; the coefficients of determination were 0.998 and 0.999, 0.995 and 0.997, 0.997 and 1.000 for training and testing part of MLP-ANN, RBF-ANN, and LSSVM models. The majority of data points for both training and testing datasets are concentrated around the Y = X line which implies the accurate predictions of the proposed models. In addition to the conclusion derived from Fig. 7, Fig. 8 also verifies the accurateness and the prediction capability of LSSVM and the MLP-ANN approaches. Detailed information about the results of the evaluation methods is summarized in Table 3. Based on the acquired values, LSSVM showed an absolutely brilliant accurateness; it has had minimum MRE%, while having the maximum R-squared quantitates. Different parts of Fig. 9 illustrate the percentage of the relative deviation for the developed models. It was observed that the LSSVM model had the best accuracy than the others and its relative deviation does not exceed from 1.5% band. The relative deviation of MLP-ANN also lies between + 1.5 and − 1.5%.

Fig. 5
figure 5

Performance of the LM algorithm according to MSE in different iterations for the MLP-ANN

Full size image
Fig. 6
figure 6

ANFIS performance during training stage using PSO approach

Full size image
Fig. 7
figure 7

Estimated viscosity values compared to experimental data using different models; a ANFIS, b MLP-ANN, c RBF-ANN, d LSSVM

Full size image
Fig. 8
figure 8

Regression diagram to predict viscosity using different models in the training and testing steps; a ANFIS, b MLP-ANN, c RBF-ANN, d LSSVM

Full size image
Table 3 Evaluation of the performance of the proposed models using statistical analysis
Full size table
Fig. 9
figure 9

Relative deviation (%) of testing and training data using different models; a ANFIS, b MLP-ANN, c RBF-ANN, d LSSVM

Full size image

Detection of suspicious dataset for different models was done based on the pre-mentioned strategy of outlier detection, and the results are illustrated in Fig. 10. According to these analyses, based on various plots of standard residual versus Hat values, in ANFIS, MLP-ANN, RBF-ANN, and LSSVM no data were considered as outlier.

Fig. 10
figure 10

Detection of suspicious dataset for different models; a ANFIS, b MLP-ANN, c RBF-ANN, d LSSVM

Full size image

Sensitivity analysis

A bunch of sensitivity analyses were carried out to find out how each input parameter affects the target variable, namely the viscosity. Quantitative effect of each parameter calculated using a relevancy factor is defined by the following expression:

$$r = \frac{{\sum\nolimits_{i = 1}^{N} {(X_{\text{k,i}}^{\exp } - X_{\text{k}}^{\text{avg}} )(y_{\text{i}} - \bar{y})} }}{{\sum\nolimits_{i = 1}^{N} {(X_{\text{k,i}}^{\exp } - \bar{X}_{\text{k}} )^{2} \times \sum\limits_{i = 1}^{N} {(y_{\text{i}} - \bar{y})^{2} } } }},$$
(20)

where N, Xk,i, Yi, \(\bar{X}_{\text{k}}\), and \(\bar{Y}\) are the total number of data points, ith input value of the kth parameter, ith output value, average value of the kth input parameter, and mean value of the output parameter, respectively. The relevancy factor lies between − 1 and + 1, in which higher absolute values represent the higher effect of the corresponding parameter. The positive effect reflects the target variable’s increment as a specific input parameter increases, while the negative effect reflects the target variable’s decrement as a specific input parameter increases. From three main input parameters, all parameters showed direct impact on the results, which means any increase in anyone of the input parameters leads to increase in viscosity. Figure 11 illustrates the sensitivity analysis results, in which the average diameter had the highest positive effects with relevancy factor of 0.9922. The second most affecting parameter was temperature and showed a positive effect of 0.9722. It was seen that volume fraction also had a great impact on the viscosity of the nanofluid with relevancy factor of 0.9320.

Fig. 11
figure 11

Sensitivity analysis to determine the effect of inputs on viscosity

Full size image

Conclusions

Enhancement of heat transfer rates with the lowest utilization of energy attracted a lot of attention during recent decades. Carbon nanotubes (TiO2) are considered as promising nanomaterials and have been in the center of attention. In the present study, four soft computing-based approaches including MLP-ANN, ANFIS, LSSVM, and RBF-ANN were used in order to model the amount of viscosity of TiO2–water nanofluid system. Among MLP-ANN, ANFIS, LSSVM, and RBF-ANN methods, it was found that the LSSVM produced better results with the lowest deviation factor and reflected the most accurate responses. The regression diagram of experimental and estimated values shows the R2 coefficient of 0.9982 and 0.9969 for training and testing. The coefficients of determination were 0.9993 and 0.9989, 0.9975 and 0.9963, 0.9996 and 0.9993 for training and testing part of MLP-ANN, RBF-ANN, and LSSVM models. Furthermore, LSSVM model had the best accuracy than the others and its relative deviation does not exceed from 1.5% band. The relative deviation of MLP-ANN also lies between + 1.5 and − 1.5%. Results from the sensitivity analysis revealed that all parameters had direct impact on the viscosity which means increase in every parameter will increase the viscosity of TiO2–water nanofluid. The present study can be worthy to reach a better understanding of nanofluids and their applications in heat transfer phenomenon, especially when a high level of performance is needed.