Investigation of convective nanomaterial flow and exergy drop considering CVFEM within a porous tank

Abstract

In the current research, ferrofluid migration and exergy destroyed became the main goal. Demonstration of characteristics impact of permeability, buoyancy and Hartmann numbers on variation of nanomaterial movement as well as irreversibility was examined. CVFEM with triangular element is utilized to calculate the solution of formulated equations. An increment in magnetic field results in greater exergy drop which is not beneficial in view of convective mode. An increase in permeability demonstrates a growth of nanomaterial convective flow. Augmenting Da causes a reduction in Bejan number while it makes Nu_ave to augment.

Introduction

Nanofluid can be offered as an efficient carrier fluid because of its capability to enhance thermal feature [1,2,3,4,5,6,7,8]. Two important issues including extra stream resistance and possible erosion should not be ignored because the particles are not stable in the suspension phase. For these reasons, there has not any effort to commercialize such fluids including particles which are interspersed and coarse-grained [9,10,11,12,13,14,15,16,17]. Modern nanotechnology gives us the opportunity to generate and to process substances including crystallite scale which are less than 50 nm. General definition of nanofluid is fluids with suspended nanoparticles [17,18,19,20]. Therefore, basis fluids flowing with certain heat transfer features can pursue different patterns of behavior when nanoparticles are suspended in them [21,22,23,24]. Several new techniques were suggested to augment performance [25,26,27,28,29,30,31]. Mixture of H₂O and MWCNT was employed by Hussien et al. [32] within a mini duct, and friction factor was analyzed numerically. They reported Nu improvement as a consequence of dispersing nanomaterial.

Multi-louvered fins have been mounted by Kumar et al. [33] inside a duct filled with alumina. Performance of unit augmented about 80% with 0.2% nanomaterial fraction. Wu et al. [34] employed copper powder to expedite the charging of paraffin and reported 32% reduction in melting time for 1% fraction. Variable magnetic impact for controlling forced convection was investigated by Mehrez and Cafsi [35], and they concluded that impact of nanoparticles fraction is function of Hartmann number. There exist various passive ways for augmentation of efficiency like inserting fins, etc. [36,37,38,39,40,41,42,43,44,45,46,47]. Beryllium oxide has been mixed with deionized water by Selvaraj et al. [48] to generate new carrier fluid for saving energy. TiO₂ nanomaterial for cooling of sinusoidal duct was employed by Sajid et al. [49], and they achieved the highest performance with 0.012% fraction of powder. Among various numerical approaches which are offered by various researchers [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85], there is very accurate method which combined two powerful approaches and its name is CVFEM which was employed in various applications [86,87,88,89,90,91,92,93,94,95,96,97,98,99,100] and proved the high power of this technique. As mentioned in [101], CNT nanoparticles can be utilized corrugated cavity in existence of rotational heat source inside the domain. They showed that geometric variable has greater impact than fraction of nanomaterial. Parabolic collector performance was analyzed by Bellos and Tzivanidis [102]. They tried to improve the efficiency with mounting fins and dispersing CuO.

In this article, variations of entropy of nanomaterial by imposing Lorentz forces were illustrated. Behaviors of nanofluid through a permeable media were examined. CVFEM was utilized to illustrate the impacts Da, Ra and Ha.

Geometry and mathematical model

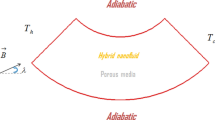
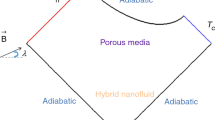
A permeable tank with circular hot inner cylinder is illustrated in Fig. 1. The testing fluid is iron oxide–water nanomaterial. To inform about the amount of properties of nanomaterial components, Ref. [103] can be reviewed. It should be noticed that formulation for nanomaterial is as same as that paper, too. The outer wall is maintained at T_c, and domain was affected by magnetic effect in one direction. For macroscopic simulation, non-Darcy law was involved with considering single-phase model. To gain the accurate solution, we utilized CVFEM which was suggested by Sheikholeslami [104] in last seven years. He combined the benefits of FVM and FEM to achieve more accurate approach. The formulations for our model are:

Fig. 1

Related domain of the current article

$$\frac{\partial v}{\partial y} + \frac{\partial u}{\partial x} = 0$$

(1)

$$\begin{aligned} & \left( {\rho_{\text{nf}} } \right)\left( {\frac{\partial u}{\partial y}v + u\frac{\partial u}{\partial x}} \right) = \left[ { + \sigma_{\text{nf}} B_{\text{x}} B_{\text{y}} v - \sigma_{\text{nf}} B_{\text{y}}^{2} u + \left( {\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial x^{2} }}} \right)\mu_{\text{nf}} - \frac{\partial P}{\partial x} - \frac{{\mu_{\text{nf}} }}{K}u} \right], \\ & \left( {B_{\text{y}} ,B_{\text{x}} } \right) = B_{o} \left( {\sin \gamma ,\cos \gamma } \right) \\ \end{aligned}$$

(2)

$$\begin{aligned} & \rho_{\text{nf}} \left( {v\frac{\partial v}{\partial y} + \frac{\partial v}{\partial x}u} \right) = - \frac{\partial P}{\partial y} + \mu_{\text{nf}} \left( {\frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{{\partial^{2} v}}{{\partial x^{2} }}} \right) - \frac{{\mu_{\text{nf}} }}{K}v + g\left( {T - T_{\text{c}} } \right)\rho_{\text{nf}} \beta_{\text{nf}} \\ & - B_{\text{x}} vB_{\text{x}} \sigma_{\text{nf}} + B_{\text{x}} u\sigma_{\text{nf}} B_{\text{y}} , \\ \end{aligned}$$

(3)

$$\left( {\rho C_{\text{p}} } \right)_{\text{nf}} \left( {u\frac{\partial T}{\partial x} + \frac{\partial T}{\partial y}v} \right) = k_{\text{nf}} \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right)$$

(4)

To inform about the amount of properties of nanomaterial components, Ref. [103] can be reviewed. It should be noticed that formulation for nanomaterial is as same as that paper, too. In addition, to gain simpler formulation, pressure terms were discarding by introducing given equation as follows:

$$\begin{aligned} & - \frac{\partial \psi }{\partial x} = v, \\ & \frac{\partial \psi }{\partial y} = u, \\ & \frac{\partial u}{\partial y} - \frac{\partial v}{\partial x} = - \omega , \\ \end{aligned}$$

(5)

Considering Eq. (6), the final formulation can be summarized as:

$$\begin{aligned} &\Theta = \left( {q^{\prime \prime } L /k_{\text{f}} } \right)^{ - 1} \left[ {T - T} \right],\;V = \frac{vL}{{\alpha_{\text{f}} }}, \\ & \left( {X,Y} \right) = \frac{{\left( {x,y} \right)}}{L},\;U = \frac{uL}{{\alpha_{\text{f}} }} \\ \end{aligned}$$

(6)

$$\frac{{\partial^{2}\Psi }}{{\partial Y^{2} }} + \frac{{\partial^{2}\Psi }}{{\partial X^{2} }} = -\Omega$$

(7)

$$\left( {\frac{{\partial^{2}\Theta }}{{\partial X^{2} }} + \frac{{\partial^{2}\Theta }}{{\partial Y^{2} }}} \right) = V\frac{{\partial\Theta }}{\partial Y} + U\frac{{\partial\Theta }}{\partial X}$$

(8)

$$\begin{aligned} & Pr\left( {\frac{{A_{5} A_{2} }}{{A_{1} A_{4} }}} \right)\left( {\frac{{\partial^{2} \varOmega }}{{\partial Y^{2} }} + \frac{{\partial^{2} \varOmega }}{{\partial X^{2} }}} \right) + Ra\,Pr\left( {\frac{\partial \varTheta }{\partial X}} \right)\left( {\frac{{A_{3} A_{2}^{2} }}{{A_{1} A_{4}^{2} }}} \right) \\ & \quad \quad + Ha^{2} \,Pr\left[ {\frac{{A_{6} A_{2} }}{{A_{1} A_{4} }}} \right]\left( { - \frac{\partial V}{\partial X}\left( {\cos \gamma } \right)^{2} + \left( {\cos \gamma } \right)\frac{\partial U}{\partial X}\left( {\sin \gamma } \right)} \right) \\ & \quad \quad - \frac{Pr}{Da}\left( {\frac{{A_{5} A_{2} }}{{A_{1} A_{4} }}} \right)\Omega \\ & \quad \quad + Ha^{2} \,Pr\left[ {\frac{{A_{6} A_{2} }}{{A_{1} A_{4} }}} \right]\left[ { - \left( {\sin \gamma } \right)\left( {\cos \gamma } \right)\frac{\partial V}{\partial Y} + \frac{\partial U}{\partial Y}\left( {\sin \gamma } \right)^{2} } \right] \\ & \quad = U\frac{\partial \varOmega }{\partial X} + \frac{\partial \varOmega }{\partial Y}V \\ \end{aligned}$$

(9)

$$\begin{aligned} & A_{3} = \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }},\;A_{5} = \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }},\;Ra = g\beta_{\text{f}} q^{\prime \prime } L^{4} /\left( {k_{\text{f}} \upsilon_{\text{f}} \alpha_{\text{f}} } \right), \\ & A_{2} = \frac{{\left( {\rho C_{\text{P}} } \right)_{\text{nf}} }}{{\left( {\rho C_{\text{P}} } \right)_{\text{f}} }},\;Da = \frac{K}{{L^{2} }}, \\ & A_{1} = \frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }},\;Pr = \upsilon_{\text{f}} /\alpha_{\text{f}} , \\ & A_{4} = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }},\;A_{6} = \frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }},\;Ha = LB_{0} \sqrt {\sigma_{\text{f}} /\mu_{\text{f}} } , \\ \end{aligned}$$

(10)

$Nu_{\text{loc}}$ and $Nu_{\text{ave}}$ and other parameters are determined from:

$$Nu_{\text{loc}} = \frac{1}{\theta }\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right)$$

(11)

$$Nu_{\text{ave}} = \frac{1}{S}\int\limits_{0}^{s} {Nu_{\text{loc}} } \,{\text{d}}s$$

(12)

$$\begin{aligned} Be & = S_{\text{gen,th}} /S_{\text{gen,total}} , \\ S_{\text{gen,total}} & = \underbrace {{\frac{{k_{\text{nf}} }}{{T^{2} }}\left[ {\left( {\frac{\partial T}{\partial x}} \right)^{2} + \left( {\frac{\partial T}{\partial y}} \right)^{2} } \right]}}_{{S_{\text{gen,th}} }} \\ & \quad + \underbrace {{\frac{{\mu_{\text{nf}} }}{{T^{2} }}\left[ {2\left( {\left( {\frac{\partial v}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial x}} \right)^{2} } \right) + \left( {\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}} \right)^{2} } \right]}}_{{S_{\text{gen,f}} }} \\ & \quad + \underbrace {{\frac{{\sigma_{\text{nf}} }}{{T^{2} }}B_{0}^{2} v^{2} }}_{{S_{\text{gen,M}} }} + \underbrace {{\frac{{\mu_{\text{nf}} }}{KT}\left( {u^{2} + v^{2} } \right)}}_{{{\text{S}}_{\text{gen,P}} }} \\ \end{aligned}$$

(13)

$$X_{\text{d}} = T_{0} S_{\text{gen,total}}$$

(14)

Results and discussion

This article investigates the nanomaterial irreversibility and thermal behavior through a porous region. Medium with various values of permeability is under the impact of magnetic force. Mesh analysis example is given in Table 1, and validation was performed as shown in Fig. 2 [105]. This graph indicates the good accuracy. Contour plots of various outcomes are demonstrated in Figs. 3, 4, 5 and 6. More fluctuation in contour of magnetic irreversibility can be appeared with the increase in buoyancy effect. This is attributed to domination of convection. Isolines of stream have no significant changes with the increase in Da when Ra has its lowest value. Lorentz forces can increase the resistance against the nanofluid movement, so convective flow reduces. Changing the patterns of isothermal decreases with applying magnetic force, and thermal plume vanishes with augment of Ha. In contrast, exergy drop amount reduces with the increase in Da and Ra. So, to gain the design with minimum irreversibility, lowest values of Da and Ra should be selected.

Table 1 Variation of outputs with changing mesh when $\phi = 0.04,\;Da = 100,\;Ha = 20$ and $Ra = 10^{4}$

Fig. 2

Outputs of Khanafer et al. [105] versus present data

Fig. 3

Impact of buoyancy forces on outcomes at $\phi = 0.04,\;Ha = 1,\;Da = 0.01$

Fig. 4

Impact of buoyancy forces on outcomes at $\phi = 0.04,\;Ha = 20,\;Da = 0.01$

Fig. 5

Impact of buoyancy forces on outcomes at $\phi = 0.04,\;Ha = 1,\;Da = 100$

Fig. 6

Impact of buoyancy forces on outcomes at $\phi = 0.04,\;Ha = 20,\;Da = 100$

Figures 7, 8 and 9 present the changes of the Nu_ave, X_d and Bejan number. Feasible way to reach lower exergy drop is selecting greater permeability and stronger buoyancy force. As Da rises, Nu_ave improves which can be attributed to reduction in resistance against the nanofluid flow. Be increases with augment of Lorenz forces, so to reduce the irreversibility, magnetic effect should be weaken. An augment in permeability of porous region results in augmentation in convective flow and in turn makes Nu_ave to increase. It can be determined that X_d and Ha have direct relationship. At greater Da, changes of exergy drop with Ha increase. Permeability has negligible effect on variation of Be when buoyancy force is very low. Hartmann number does not expressively affect the Bejan number at low Ra. Below formulations belong to above functions:

Fig. 7

Various $Ra,\,Ha,\,Da$ and obtained Nuave at $\phi = 0.04$

Fig. 8

Various $Ra,\,Ha,\,Da$ and obtained Be at $\phi = 0.04$

Fig. 9

Various $Ra,\,Ha,\,Da$ and obtained X_d at $\phi = 0.04$

$$\begin{aligned} Nu_{\text{ave}} & = 2.22 + 0.07Da + 0.13\log \left( {Ra} \right) - 0.099Ha \\ & \quad + 0.058Da\,\log \left( {Ra} \right) - 0.058Da\,Ha - 0.085\log \left( {Ra} \right)Ha \\ \end{aligned}$$

(15)

$$\begin{aligned} Be & = 0.96 - 0.036\log \left( {Ra} \right) + 8.27 \times 10^{ - 3} Ha\log \left( {Ra} \right) + 9.34 \times 10^{ - 3} Ha \\ & \quad - 5.05 \times 10^{ - 3} \,\log \left( {Ra} \right)Da + 2.12 \times 10^{ - 3} Ha\,Da - 6.07 \times 10^{ - 3} Da \\ \end{aligned}$$

(16)

$$\begin{aligned} X_{\text{d}} & = 58.77 - 1.44Da + 2.22Ha + 1.21Da\,Ha \\ & \quad - 1.08Da\,\log \left( {Ra} \right) - 2.22\log \left( {Ra} \right) + 1.6\log \left( {Ra} \right)Ha \\ \end{aligned}$$

(17)

Conclusions

A numerical modeling based on CVFEM was utilized for illustration of nanomaterial movement inside a cavity. Increasing buoyancy force results in greater nanofluid diffusion which guaranteed the higher Nu_ave. Permeability augments the power of nanofluid flow which is result in higher Nu_ave. Increasing Ha makes the X_d to decline. In contrast, higher values of Da result in lower X_d. Exergy loss declines as a consequence of greater buoyancy forces. Augment of the circulation intensity occurs with augment of Da while streamlines become weaker with augment of Ha.