Introduction

Nanofluid is comparatively a newly recognized class of fluids containing carrier liquid with particles of nano-size. Basically some materials like oil, ethylene glycol, propylene glycol etc. in view of their weaker thermal conductivity have poor heat transfer properties. Thus, inclusion of nanoparticles in such type of carrier liquids is a quite charismatic way to enhance the thermal efficiency of such liquids. These nanoparticles are especially made of metals, oxide ceramics, carbide ceramics, non-metals and various other composite materials. Such nanoparticles have distinctive physical and chemical features and have thermal efficiencies magnificently higher than carrier liquids. These nanoparticles are utilized in development and structural process of fiber production in textile, MHD power generators, petroleum reservoirs, cooling of nuclear reactors, cancer therapy, vehicle transformer, geothermal energy, safer surgery processes and many others. Recent inspections on nanofluid reveal that the carrier liquid has absolutely different features with the nanoparticle mixture because the thermal efficiency of carrier liquid is smaller than the nanoparticle’s thermal efficiency. Appropriate storage of thermal energy and higher convective heat transfer coefficients are the main features of nanofluid. Nanofluids have various common applications in industrial and vehicle cooling, heat control systems, sensing, food industry, chemical industry, cooling towers, power production and efficiency of hybrid-powered engines etc. Initially, the idea of nanofluid was devised by Choi [1]. He concluded that the nanoparticles dramatically increase the thermal efficiency of carrier liquids. Buongiorno [2] developed the two-phase model of nanoparticles by considering the thermophoretic and Brownian motion aspects. Here we employed the Buongiorno model to study the convective heat transfer characteristics in nanofluids. This model determined that the homogeneous-flow models are in conflict with the experimental results and tend to underpredict the heat transfer coefficient of nanofluid. While the dispersion effect is totally negligible as a result of nanoparticle size. Thus, Buongiorno proposed an alternative model that ignores the shortcomings of homogeneous and dispersion models. He affirmed that the abnormal heat transfer appears due to particle migration in the fluid. Exploring the nanoparticle migration, he considered the seven slip mechanisms that can produce a parallel velocity between the nanoparticles and base fluid. These are inertia, thermophoresis, Brownian diffusion, diffusiophoresis, Magnus effect, fluid drainage and gravity. He concluded that, of these seven, only Brownian diffusion and thermophoresis are important slip mechanisms in nanofluids. Based on such findings, he established a two-component four-equation nonhomogeneous equilibrium model for mass, momentum and heat transport in nanofluids. Tiwari and Das [3] also discussed the heat transfer experimentally of nanoliquids in a two-sided lid-driven heated square cavity. Pantzali et al. [4] discussed importance of CuO-water nanomaterials on the surface of heat exchangers experimentally. Review of thermal convective enhancement in nanofluids is reported by Kakac and Pramuanjaroenkij [5]. Abu-Nada and Oztop [6] explored effects of inclination angle in natural convective Cu-water nanofluid flow in enclosures. Few interesting studies about nanofluids can be seen via refs. [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36].

The study of fluid flow and heat transport process in a porous media has achieved much attention of researchers due to its ample applications in technological, industrial, chemical and manufacturing processes. Such applications include crude oil production, nuclear-based repositories, casting and welding in manufacturing processes, nuclear waste disposal, units of the energy storage, fermentation processes and drying of a porous solid etc. The modification of classical Darcy’s theory results in the non-Darcian porous space which involves inertial and boundary effects. The classical Darcy’s law is applicable for a finite range of low velocity and smaller porosity. Forchheimer [37] considered inertia effects through the inclusion of a square velocity term in momentum equation. Muskat [38] entitled this contribution as Forchheimer factor. Mixed convective flow in a porous medium has been developed by Seddeek [39]. Jha and Kaurangini [40] presented approximate solutions for nonlinear Brinkman-Forchheimer-extended Darcy flow. Darcy–Forchheimer porous space in hydromagnetic convective flow with non-uniform heat source/sink is studied by Pal and Mondal [41]. Darcy–Forchheimer flow of Maxwell material due to convectively heated sheet has been investigated by Sadiq and Hayat [42]. Shehzad et al. [43] employed Cattaneo–Christov heat flux model for Darcy–Forchheimer flow of an Oldroyd-B fluid with variable conductivity and nonlinear convection. Forced convection stagnation-point flow with Darcy–Forchheimer expression is examined by Bakar et al. [44]. Hayat et al. [45] analyzed Darcy–Forchheimer flow with variable thermal conductivity and Cattaneo–Christov heat flux. A comparative study for Darcy–Forchheimer flow of viscoelastic nanofluids is studied by Hayat et al. [46]. Umavathi et al. [47] used Darcy–Forchheimer-Brinkman model in order to present a numerical study for natural convective flow of nanofluids. Darcy–Forchheimer flow of Maxwell nanofluid with convective boundary condition has been studied by Muhammad et al. [48]. Sheikholeslami [49] discussed the impact of Lorentz forces on nanofluid flow in a porous cavity by means of non-Darcy model. A revised model for Darcy–Forchheimer three-dimensional flow of nanofluid subject to convective boundary condition is investigated by Muhammad et al. [50]. Darcy–Forchheimer three-dimensional flow of Williamson nanofluid induced by a convectively heated nonlinear stretching sheet is reported by Hayat et al. [51]. Recently Hayat et al. [52] present an optimal analysis for Darcy–Forchheimer 3D flow of Carreau nanofluid with convectively heated surface.

The investigators at present are engaged in analyzing the fluid flow and heat transport problem in rotating frame. It is because of their numerous applications in gas turbine rotors, rotating machinery, thermal power generation, electronic devices, aeronautics, air-cleaning machine and several others. Analytical solutions for viscous fluid flow over a stretched sheet in rotating frame are computed by Wang [53]. Takhar et al. [54] analyzed magnetohydrodynamics in rotating flow past a stretched sheet. Time-dependent rotating flow induced by an impulsively deforming surface is addressed by Nazar et al. [55]. Javed et al. [56] constructed local similar solutions for rotating flow induced by an exponentially deforming sheet. Zaimi et al. [57] investigated rotating flow of viscoelastic fluid by an impermeable stretchable sheet. Rosali et al. [58] numerically investigated rotating flow caused by an exponentially permeable sheet. Shafique et al. [59] studied simultaneous effects of activation energy and binary chemical reactions in rotating flow of Maxwell fluid. Mustafa et al. [60] discussed rotating flow of Maxwell fluid with variable thermal conductivity. Three-dimensional rotating flow of Maxwell nanoliquid is reported by Hayat et al. [61]. Darcy–Forchheimer three-dimensional rotating flow of water-based carbon nanotubes is explored by Hayat et al. [62]. Maqsood et al. [63] numerically investigated viscoelastic fluid flow subject to homogeneous–heterogeneous reactions in rotating frame. Mustafa et al. [64] computed analytical solutions of three-dimensional rotating flow of an Oldroyd-B liquid by considering Cattaneo–Christov theory. Turkyilmazoglu [65] discussed the fluid flow and heat transfer over a rotating and vertically moving disk. Very recently Mustafa et al. [66] computed numerical solutions of rotating flow of nanofluid over an exponentially deforming sheet.

The prime interest in present study is to illustrate Darcy–Forchheimer three-dimensional flow of nanoliquid induced by an exponentially stretchable surface in rotating frame. Thermophoretic diffusion and random motion aspects are retained. Prescribed surface heat and mass fluxes are implemented at stretchable surface. The governing systems are solved numerically by NDSolve technique. Moreover temperature, concentration, surface drag coefficients and local Nusselt and Sherwood numbers are graphically illustrated.

Statement

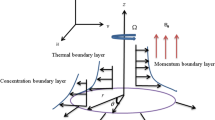
Here we intend to illustrate steady 3D rotating flow of nanoliquid induced by an exponentially stretchable surface. Darcy–Forchheimer porous space is considered. Buongiorno model is implemented for nanoliquid transport process. Cartesian coordinate system is employed. The sheet stretches with velocity \(u_{\text{w}} (x) = U_{0} {\text{e}}^{\rm {x/L}}\) where \(U_{0}\) being positive constant. In addition fluid rotates about \(z\)-direction with constant angular velocity \(\omega\). The boundary layer expressions governing the three-dimensional (3D) rotating flow of viscous nanofluid in the absence of viscous dissipation and thermal radiation are [52, 66]:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0,$$
(1)
$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} - 2\omega v = \nu \frac{{\partial^{2} u}}{{\partial z^{2} }} - \frac{\nu }{{k^{*} }}u - Fu^{2} ,$$
(2)
$$u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} + 2\omega u = \nu \frac{{\partial^{2} v}}{{\partial z^{2} }} - \frac{\nu }{{k^{*} }}v - Fv^{2} ,$$
(3)
$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + w\frac{\partial T}{\partial z} = \alpha^{*} \frac{{\partial^{2} T}}{{\partial z^{2} }} + \frac{{(\rho c)_{\text{p}} }}{{\left( {\rho c} \right)_{\text{f}} }}\left( {D_{\text{B}} \left( {\frac{\partial T}{\partial z}\frac{\partial C}{\partial z}} \right) + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial z}} \right)^{2} } \right),$$
(4)
$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} + w\frac{\partial C}{\partial z} = D_{\text{B}} \left( {\frac{{\partial^{2} C}}{{\partial z^{2} }}} \right) + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{{\partial^{2} T}}{{\partial z^{2} }}} \right).$$
(5)

Here one has the following conditions [23, 66]:

$$\left. {\begin{array}{*{20}c} {u = u_{w} (x) = U_{0} {\text{e}}^{\rm {x/L}} ,\,v = 0,\,w = 0,\, - \;k\left( {\tfrac{\partial T}{\partial z}} \right)_{\text{w}} = T_{0} {\text{e}}^{{\tfrac{({\text{A}} + 1) {\text{x}}}{2{\text{L}}}}} ,} \\ { - D_{\text{B}} \left( {\tfrac{\partial C}{\partial z}} \right)_{\text{w}} = C_{0} {\text{e}}^{{\tfrac{({\text{B}} + 1){\text{x}}}{2{\text{L}}}}} \;{\text{at}}\;z = 0,} \\ \end{array} } \right\}$$
(6)
$$u \to 0,\quad v \to 0,\quad T \to T_{\infty } ,\quad C \to C_{\infty } \quad {\text{when}}\;z \to \infty .$$
(7)

Note that \(u,\;v\) and \(w\) represent the velocity components in \(x\)-, \(y\)-, and \(z\)-directions while \(\nu \left( { = \mu /\rho_{\text{f}} } \right)\), \(\mu\) and \(\rho_{\text{f}}\) stands for kinematic viscosity, dynamic viscosity and density of base liquid, \(k^{{^{ * } }}\) for permeability of porous medium, \(F = C_{\text{b}} /xk^{{^{{^{ * 1/2} }} }}\) for non-uniform inertia coefficient of porous space, \(C_{\text{b}}\) for drag coefficient, \(\alpha^{{^{ * } }} = k/(\rho c)_{\text{f}}\), \(k\), \((\rho c)_{\text{f}}\) and \((\rho c)_{\text{p}}\) for thermal diffusivity, thermal efficiency, heat capacity of liquid and effective heat capacity of nanomaterials, respectively, \(T\) for temperature, \(D_{\text{B}}\) for Brownian diffusivity, \(C\) for concentration, \(D_{\text T}\) for thermophoretic diffusion coefficient, \(U_{0}\), \(T_{0}\) and \(C_{0}\) for positive constants, \(L\) for reference length, \(A\), \(B\), \(T_{\infty }\) and \(C_{\infty }\) for temperature exponent, concentration exponent, ambient fluid temperature and ambient fluid concentration, respectively. Considering

$$\left. {\begin{array}{*{20}c} {u = U_{0} {\text{e}}^{\rm {x/L}} f^{\prime}(\zeta ),\, \, v = U_{0} {\text{e}}^{\rm {x/L}} g(\zeta ),\, \, w = - \left( {\tfrac{{\nu U_{0} }}{2L}} \right)^{1/2} {\text{e}}^{\rm {x/2L}} \left( {f(\zeta ) + \zeta f^{\prime}(\zeta )} \right),} \\ {T = T_{\infty } + \tfrac{{T_{0} }}{k}\sqrt {\tfrac{2\nu L}{{U_{0} }}} {\text{e}}^{\rm {Ax/2L}} \theta (\zeta ),\,C = C_{\infty } + \tfrac{{C_{0} }}{{D_{\text{B}} }}\sqrt {\tfrac{2\nu L}{{U_{0} }}} {\text{e}}^{\rm {Bx/2L}} \varphi (\zeta ),\,\zeta = \left( {\tfrac{{U_{0} }}{2\nu L}} \right)^{1/2} {\text{e}}^{\rm {x/2L}} z,} \\ \end{array} } \right\}\,$$
(8)

Equation (1) is identically verified while Eqs. (2)–(7) yield

$$f^{\prime\prime\prime} + ff^{\prime\prime} - 2f^{\prime 2} + 4\varOmega g - 2\lambda f^{\prime} - 2Frf^{\prime 2} = 0,$$
(9)
$$g^{\prime\prime} + fg^{\prime} - 2f^{\prime}g - 4\varOmega f^{\prime} - 2\lambda g - 2Frg^{2} = 0,$$
(10)
$$\theta^{\prime\prime} + \mathop {\Pr }\limits \left( {f\theta^{\prime} - Af^{\prime}\theta + N_{\text{b}} \theta^{\prime}\varphi^{\prime} + N_{t} \theta^{{\prime^{2} }} } \right) = 0,\,$$
(11)
$$\varphi^{\prime\prime} + Sc\left( {f\varphi^{\prime} - Bf^{\prime}\varphi } \right) + \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\theta^{\prime\prime} = 0,$$
(12)
$$f(0) = g(0) = 0,\, \, f^{\prime}(0) = 1,\, \, \theta^{\prime}(0) = - 1,\, \, \varphi^{\prime}(0) = - \;1,$$
(13)
$$f^{\prime}(\infty ) \to 0,\, \, g(\infty ) \to 0,\, \, \theta (\infty ) \to 0,\, \, \varphi (\infty ) \to 0.$$
(14)

Here rotation parameter, porosity parameter, Forchheimer number, Prandtl number, thermophoresis parameter, Schmidt number and Brownian motion parameter are symbolized by \(\varOmega\), \(\lambda\), \(Fr\), \(Pr\), \(N_{\text{t}}\), \(Sc\) and \(N_{\text{b}}\), respectively. Nondimensional forms of these parameters are given below:

$$\left. {\begin{array}{*{20}c} {\lambda = \tfrac{\nu L}{{k^{{^{ * } }} u_{\text{w}} }},\, \, Fr = \tfrac{{C_{b} }}{{k^{{^{ * 1/2} }} }},\, \, \varOmega = \tfrac{\omega L}{{u_{\text{w}} }},\,Pr = \tfrac{\nu }{{\alpha^{ * } }},\, \, Sc = \tfrac{\nu }{{D_{\text{B}} }},} \\ { \, N_{\text{b}} = \tfrac{{\left( {\rho c} \right)_{\text{p}} D_{\text{B}} (C_{\text{w}} - C_{\infty } )}}{{\left( {\rho c} \right)_{\text{f}} \nu }},\, \, N_{\text{t}} = \tfrac{{\left( {\rho c} \right)_{\text{p}} D_{\text{T}} \left( {T_{\text{w}} - T_{\infty } } \right)}}{{\left( {\rho c} \right)_{\text{f}} \nu T_{\infty } }}.} \\ \end{array} } \right\}\,$$
(15)

The nondimensional forms of coefficients of skin friction and local Nusselt and Sherwood numbers are

$$\left. {\begin{array}{*{20}c} {\left( {\tfrac{{Re_{x} }}{2}} \right)^{1/2} C_{fx} = f^{\prime\prime}(0),} \\ {\left( {\tfrac{{Re_{x} }}{2}} \right)^{1/2} C_{fy} = g^{\prime}(0),} \\ {\tfrac{L}{x}\left( {\tfrac{{Re_{x} }}{2}} \right)^{ - 1/2} Nu_{x} = \tfrac{1}{\theta (0)},} \\ {\tfrac{L}{x}\left( {\tfrac{{Re_{x} }}{2}} \right)^{ - 1/2} Sh_{x} = \tfrac{1}{\varphi (0)}.} \\ \end{array} } \right\}\,$$
(16)

In above expressions \(Re_{\text x} = u_{\text w} x/\nu\) represents the local Reynolds number.

Discussion

This section addresses the contributions of local porosity parameter \(\lambda\), Brownian motion parameter \(N_{\text{b}}\), Forchheimer number \(Fr\), Schmidt number \(Sc\), temperature exponent \(A\), local rotational parameter \(\varOmega\), Prandtl number \(Pr\), thermophoresis parameter \(N_{\text{t}}\) and concentration exponent \(B\) on nondimensional temperature \(\theta \left( \zeta \right)\) and concentration \(\varphi (\zeta )\) fields. Figure 1 displays variation of temperature field \(\theta (\zeta )\) for various local porosity parameter \(\lambda\). An increment in porosity parameter \(\lambda\) causes stronger temperature field \(\theta (\zeta )\) and related layer thickness. Physically existence of porous space generates resistance in fluid motion and ultimate it decays in velocity of fluid. Hence an increment is noticed for temperature \(\theta \left( \zeta \right)\) and associated thermal layer thickness. Figure 2 is plotted to explore impact of Forchheimer number \(Fr\) on temperature field \(\theta (\zeta )\). Larger \(Fr\) correspond to increasing trend in temperature field \(\theta (\zeta )\). Figure 3 presents influence of \(\varOmega\) on temperature field \(\theta (\zeta )\). Higher local rotational parameter \(\varOmega\) enhance temperature field \(\theta (\zeta )\) and associated layer thickness. Figure 4 elucidates that temperature field \(\theta (\zeta )\) shows decreasing trend for higher values of temperature exponent \(A\). Figure 5 shows temperature field \(\theta \left( \zeta \right)\) for varying Prandtl number \(Pr\). Temperature field \(\theta \left( \zeta \right)\) decayed for higher \(Pr\). Figure 6 is sketched to examine that how temperature field \(\theta \left( \zeta \right)\) gets affected with the variation of Brownian motion parameter \(N_{\text{b}}\). By increasing \(N_{\text{b}}\), the temperature field \(\theta \left( \zeta \right)\) shows increasing trend. Physically the random motion of nanoparticles enhances by increasing Brownian motion parameter \(N_{\text{b}}\) due to which collision of particles occurs. As a result kinetic energy is converted into heat energy which causes an enhancement in temperature and related layer thickness. Figure 7 elaborates the influence of thermophoresis parameter \(N_{\text{t}}\) on temperature \(\theta \left( \zeta \right)\). Clearly, temperature field is enhanced via larger \(N_{\text{t}}\). Figure 8 illustrates that concentration field \(\varphi (\zeta )\) shows increasing trend via local porosity parameter \(\lambda\). From Fig. 9 it is noted that Forchheimer number \(Fr\) yields higher concentration field \(\varphi (\zeta )\). Figure 10 elaborates that how the concentration field \(\varphi (\zeta )\) is affected by higher values of local rotational parameter \(\varOmega\). Here both temperature field and related layer thickness are elevated by increasing \(\varOmega\). Figure 11 illustrates the variation in concentration field \(\varphi (\zeta )\) for concentration exponent \(C\). Larger concentration exponent yields lower concentration field \(\varphi (\zeta )\) and related layer thickness. Effect of Schmidt number \(Sc\) on \(\varphi (\zeta )\) is sketched in Fig. 12. Here concentration field \(\varphi (\zeta )\) exhibits decreasing trend via larger Schmidt number \(Sc\). Figure 13 is portrayed to deliberate the variation in concentration field under the influence of Brownian motion parameter \(N_{\text{b}}\). An increment in \(N_{\text{b}}\) causes a decay in concentration. Here an enhancement in thermophoresis means that the nanoparticles are migrated from warm zone to cold zone. Therefore higher number of nanoparticles is dragged away from the warm zone due to which nanoliquid concentration decays. Figure 14 presents the outcome of thermophoresis parameter \(N_{\text{t}}\) for concentration field \(\varphi (\zeta )\). Larger thermophoresis parameter \(N_{\text{t}}\) give an enhancement in \(\varphi (\zeta )\) and related layer thickness. Table 1 is calculated in order to investigate the numerical computations of skin-friction coefficients \(- \;f^{\prime\prime}(0)\) and \(- \;g^{\prime}(0)\) for several estimations of porosity parameter \(\lambda\), Forchheimer number \(Fr\) and rotation parameter \(\varOmega\). Surface drag coefficients are increasing functions of \(\varOmega\) while reverse behavior is noticed for larger \(\lambda\) and \(Fr\). Table 2 shows the numerical computations of local Nusselt number \(\tfrac{1}{\theta \left( 0 \right)}\) and local Sherwood number \(\tfrac{1}{\varphi \left( 0 \right)}\) for different values of \(\lambda\), \(Fr\), \(\varOmega\), \(Sc\), \(Pr\), \(N_{\text{t}}\) and \(N_{\text{b}}\) when \(A = B = 0.5\). Heat transfer rate (local Nusselt number) decays via \(\lambda\), \(Fr\), \(\varOmega\), \(N_{\text{t}}\) and \(N_{\text{b}}\). Effects of \(Sc\) and \(Pr\) on heat transfer rate are quite similar. It is also observed that mass transfer rate (local Sherwood number) has lower and higher values for larger (\(\lambda\), \(Fr\), \(\varOmega\), \(Pr\), \(N_{\text{t}}\), \(N_{\text{b}}\)) and (\(Sc\)), respectively.

Fig. 1
figure 1

θ(ζ) variation for λ

Full size image
Fig. 2
figure 2

θ(ζ) variation for Fr

Full size image
Fig. 3
figure 3

θ(ζ) variation for Ω

Full size image
Fig. 4
figure 4

θ(ζ) variation for A

Full size image
Fig. 5
figure 5

θ(ζ) variation for Pr

Full size image
Fig. 6
figure 6

θ(ζ) variation for Nb

Full size image
Fig. 7
figure 7

θ(ζ)variation for Nt

Full size image
Fig. 8
figure 8

ϕ(ζ) variation for λ

Full size image
Fig. 9
figure 9

ϕ(ζ) variation for Fr

Full size image
Fig. 10
figure 10

ϕ(ζ) variation for Ω

Full size image
Fig. 11
figure 11

ϕ(ζ) variation for B

Full size image
Fig. 12
figure 12

ϕ(ζ) variation for Sc

Full size image
Fig. 13
figure 13

ϕ(ζ) variation for Nb

Full size image
Fig. 14
figure 14

ϕ(ζ) variation for Nt

Full size image
Table 1 Numerical data of surface drag coefficients \(- \;f^{\prime\prime}(0)\) and \(- \;g^{\prime}(0)\) for distinct estimations of \(\lambda\), \(Fr\) and \(\varOmega\)
Full size table
Table 2 Numerical computations of local Nusselt number \(\tfrac{1}{\theta \left( 0 \right)}\) and local Sherwood number \(\tfrac{1}{\varphi \left( 0 \right)}\) for various values of \(\lambda\), \(Fr\), \(\varOmega\), \(N_{\text{t}}\), \(Sc\), \(N_{\text{b}}\) and \(Pr\) when \(A = B = 0.5.\)
Full size table

Conclusions

Darcy–Forchheimer three-dimensional (3D) rotating flow of nanoliquid due to stretchable surface with constant heat and mass flux conditions is discussed. The prime findings of present study have been structured as follows:

  • Higher porosity parameter \(\lambda\) and Forchheimer number \(Fr\) exhibit similar trend for both temperature \(\theta (\zeta )\) and concentration \(\varphi (\zeta )\) fields.

  • Both temperature \(\theta (\zeta )\) and concentration \(\varphi (\zeta )\) fields represent increasing behavior for higher local rotational parameter \(\varOmega\).

  • An increment in temperature exponent \(A\) and concentration exponent \(B\) leads to reduce temperature \(\theta (\zeta )\) and concentration \(\varphi (\zeta )\) fields.

  • Larger Prandtl \(Pr\) and Schmidt \(Sc\) numbers correspond to lower temperature and concentration fields.

  • Brownian motion parameter \(N_{\text{b}}\) for temperature and concentration has reverse effects.

  • Both temperature and concentration profiles are increased via thermophoresis parameter \(N_{\text{t}}\).