Introduction

Laser sintering is an additive manufacturing process that enables the generation of complex, three-dimensional components layer by layer from polymer powders based on CAD data. The advantages of additive manufacturing are discussed widely, and the fields of application grow continuously [1, 2]. The cyclic process consists of the following steps: decline of the building platform by the amount of a layer, spread of a new layer of powder and selective exposure by a laser [3]. During the process, the powder’s temperature is controlled by several heaters, which are located at the top, bottom and sidewalls of the building chamber. Unlike laser beam melting of metals, parts are not fixed to the baseplate by support structures and only embedded in the powder bed. Polymers for laser sintering are amorphous or semicrystalline, which ones prevailed. Onside semicrystalline polymers, polyamide 12 (PA 12) is widely used. The main difference in molecular scale is the arrangement of semicrystalline materials to a state of regular structure during cooling from melt. In consequence, the specific volume exhibits a jump during the crystallization. The phase transition itself depends on the cooling conditions. Crystallization plays a major role in structure development of polymers, though on final properties of the parts [4]. It has been observed that several process conditions affect the part’s bed temperature variation as it has been monitored by thermal imaging [5]. In conjunction with the different heating mechanisms, a non-uniform cooling of the parts within the building chamber can be expected [6]. This leads to unequal crystallization kinetics of different sections in the components [7]. In consequence, inhomogeneous shrinkage induces deviations between resulting and desired geometry [8] and causes location-dependent part warpage [9].

Concerning the cooling rates within the process, Diller et al. [10] reported temperatures measured at the powder surface by thermal imaging. A cooling of about 130 °C in 1000 min has been observed at the surface. Measurements of Yuan and Bourell [11] have indicated a slightly higher cooling of a few Kelvin per minute in the first stages of the cooling phase. Temperature measurements inside the powder are very limited until now. First approaches using thermocouples placed in fiberglass-reinforced plastic tubes have been conducted by Josupeit and Schmid [6, 12]. From the results, an average cooling rate in the region of 0.7 °C min−1 can be estimated.

Aiming the simulation-based prediction of warpage and therefore the crystallization kinetics in laser sintering, an effective model for crystallization needs to be calibrated. A method to analyze the crystallization behavior experimentally is differential scanning calorimetry (DSC). It is based on the measurement of enthalpy changes, which are linked to phase transitions. A detailed description is given in [13].

As powder of different suppliers may have different properties [14], it is not feasible to adopt parameters from other investigations. Therefore, aim of this paper is to present the results of isothermal and non-isothermal DSC measurements of a polyamide 12 delivered by company EOS, called PA2200, and the parameters of the Nakamura crystallization model that were obtained, for the first time. The parameters have already been used but not presented in a numerical simulation model for calculation of temperature [15] in laser sintering.

The paper is organized as follows: Subsequent to a short introduction into the theory of crystallization (following [16]) and application examples, material’s specifications and experimental procedures are presented. Afterward, the results of isothermal and non-isothermal DSC measurements are given and discussed in the context of Avrami and Nakamura.

Crystallization kinetics of polymers

The degree of crystallization α(t), which is the ratio of the crystalized volume to the ultimate crystallizable volume [16], is a function of time and temperature. In case of quiescent isothermal conditions, the degree of crystallization can be calculated using following analytical expression that results from the theory of Avrami [17].

$$ \alpha (t) = 1 - { \exp }\left( { - k(T)t^{\text {n}} } \right) $$
(1)

The parameters n and k(T) of Eq. (1) are the Avrami exponent, which is linked to the nucleation mechanisms and growth direction [18], and the crystallization rate, respectively. The parameters n and k can be obtained through linearization of Eq. (1) by twofold application of the logarithm and plot of \( { \log }\left( { - \log (1 - \alpha )} \right) \) against \( \log (t) \) as long as the curvature of the plot is limited. For cases of greater curvature, Smith [19] has presented a method to determine the Avrami parameters directly from isothermal calorimetry data. The analysis of isothermal crystallization kinetics based on the theory of Avrami has been widely used for different materials, recently, for example, Trogamid [20], pigments containing polyamide 6 [21], polylactic acid [22] and isotactic polypropylene nanocomposites [23].

In non-isothermal conditions, the crystallization rate k(T) changes with time. In case of constant cooling rates, an extension of the Avrami model has been developed by Ozawa [24]. It has been tested among others on nylon 6 [25] and polypropylene [26, 27]. Anyhow, when polypropylene/ethylene–octene has been used [28], the model has not been found suitable. As secondary crystallization is not included in the Ozawa model, McFerran et al. [29] have successfully modeled non-isothermal crystallization kinetics of Nylon 12 using a combination of the Avrami and Ozawa model by Liu et al. [30]. That proposed combination led to reasonable results for nylon 11 [31] as well as isotactic polypropylene [32].

However, as constant cooling is not given in polymer processing, this model is not suitable for simulation of crystallization in laser sintering. For purpose of modeling crystallization in more general non-isothermal conditions, Nakamura [33, 34] has developed a more general model based on Avrami that is written

$$ \alpha \left( t \right) = 1 - { \exp }( - \left( {\mathop \int \limits_{0}^{t} K\left( T \right) {\text{d}}\tau )^{\text {n}} } \right) $$
(2)

in integral and

$$ \frac{\partial \alpha }{\partial t} = nK\left( T \right)\left( {1 - \alpha } \right)\left[ {\log \left( {\frac{1}{1 - \alpha }} \right)} \right]^{{\frac{\text{n} - 1}{\text {n}}}} $$
(3)

in differential form. The parameter n in the Nakamura model is equal to the Avrami exponent, and K(T) is a modification of the isothermal crystallization rate of the Avrami rate k(T). Both rates can be linked by the following equation:

$$ K\left( T \right) = k\left( T \right)^{{\frac{1}{\text {n}}}} = \log \left( 2 \right)^{{\frac{1}{\text {n}}}} \left( {\frac{1}{{t_{{\frac{1}{2}}} }}} \right) $$
(4)

The half crystallization time \( t_{{\frac{1}{2}}} \) can be expressed by the Hoffman–Lauritzen theory [35].

$$ \left( {\frac{1}{{t_{{\frac{1}{2}}} }}} \right) = K_{0} \cdot \exp \left( { - \frac{U}{{R\left( {T - T_{\infty } } \right)}}} \right) \cdot { \exp }\left( { - \frac{{K_{G} \left( {T + T_{0} } \right)}}{{2T^{2} \Delta T}}} \right) $$
(5)

Within this, U = 6270 J mol−1 [35] is the activation energy for crystallization, R is the universal gas constant, and \( T_{\infty } = T_{\text {g}} - 30 {\text{K}} \) is the temperature limit below which the crystallization stops. T g is the glass transition temperature and ΔT = T 0 − T wherein T 0 is the equilibrium melting temperature that can be obtained by the Hoffman–Weeks plot [36]. To obtain the parameters K G and K 0, Eq. (5) can be arranged to

$$ \log \left( {\frac{1}{{\frac{{t_{1} }}{2}}}} \right) + \frac{U}{{R\left( {T - T_{\infty } } \right)}} = \log \left( {K_{0} } \right) - \frac{{K_{\rm {G}} \left( {T + T_{0} } \right)}}{{2 {\cdot} T^{2} \Delta T}} $$
(6)

so constituted that a linear fit delivers slope \( - K_{\text {G}} \) and offset \( {\text{log(}}K_{0} ). \)

An analysis of available methods for modeling of polymer crystallization has been presented by Patel et al. [37]. Isothermal and non-isothermal crystallization of nylon 6 has been considered for cooling rates in range of 2 and 40 °C min−1. The integral and differential versions of the Nakamura model have been used and found to give substantially better results than the empirical integral model by Kamal and Chu [38]. Furthermore, it has been found to perform well in a study on PET and nylon 6 [39].

The mentioned modeling approaches are only an excerpt of the developed ones. Additionally, it should be mentioned that in terms of rising computational power other numerical methods have been developed, like a pixel coloring method to capture the morphology evolution [40, 41] and Monte Carlo methods to simulate non-isothermal crystallization of isotactic polypropylene [42]. Boutaous et al. [43] have developed a model for computation of the crystallization based on a birth and growth algorithm and Avrami theory. They have verified the model on different isothermal and non-isothermal crystallization experimental data and simulated the non-isothermal crystallization morphology evolution in injection molding. Considering the application in the injection molding process, a finite element model to calculate the connection of temperature and crystallization in a simplified one-dimensional system of a polypropylene plate has been developed [43]. Good agreements have been obtained in controlled temperature conditions as well as non-isothermal situations. Le Goff et al. [44] studied the coupling between heat transfer and solidification in self-designed apparatuses at low and high cooling rates. The effects of crystallization and temperature on material properties have been included as well.

Considering explicitly the crystallization kinetics of polyamides that are used in laser sintering, isothermal DSC measurements have been taken of PA2200 in range from 168 to 173 °C and discussed in the context of Avrami [45]. These measurements have been extended by Amado et al. [16], where isothermal and non-isothermal crystallization of Duraform PA® and a co-polypropylene has been investigated. The Nakamura model has been used in conjunction with calculation of temperature in laser sintering of ten layers. In principle, good accordance of measured data and model predictions has been obtained.

Material and measurements

Investigated material of this study was a polyamide 12-based powder by EOS called PA2200 (EOS GmbH Electro Optical Systems, Krailling/München, Germany). A mixture of 50 % used and 50 % fresh powder was used in line with common industrial applications. Quality assurance was controlled by measurement of the melt volume-flow rate (MVR) according to DIN EN ISO 1133-1 and DIN EN ISO 1133-2 with a MeltFlow @on by Karg (Emmeram Karg Industrietechnik, Krailling, Germany). Three measurements revealed a mean value from 33.33 cm3 10 min−1 with a standard deviation of 2.59 cm3 10 min−1.

For the non-isothermal measurements, the following procedure was applied following [16, 46]: At first, all samples were heated from 25 to 120 °C where they were held for 15 min. Afterward, the samples were heated to a level of 174 °C where the temperature was kept constant for 2 min. To emulate the laser exposure in the laser sintering process, first the material was heated to 240 °C with a subsequent cooling down back to 174 °C, both at rates of 40 °C min−1. From this temperature, the material was cooled down to 25 °C with cooling rates of 0.1, 0.5, 2.5, 5, 10 and 20 °C min−1.

The basic settings for the isothermal measurements were performed identical to the non-isothermal until the material was heated to 240 °C. Hereinafter, the cooling at 40 °C min−1 was stopped at the respective target temperature. The measurements were taken with an isothermal holding temperature of 170 °C for 300 min and 168 °C for 240 min, respectively, 180 min at 166, 164, 162, 160 and 158 °C. The data were logged as endo up.

All DSC measurements were taken on a Mettler-Toledo DSC 1/700 (Mettler-Toledo AG, Schwerzenbach, Switzerland).

Data processing

There are several parameters, which influence the analysis of a DSC signal, namely reaction start, reaction end and the virtual baseline in between. The virtual baseline is an imaginary line in the range of the reaction that would be recorded if no reaction or transformation enthalpy is present. Various types of baselines have established whereby they need to fulfill several criteria [13].

Commonly, reaction start and end are determined visually what is insufficient in terms of variations brought in by the operator. Foubert et al. [47] have shown this with a study, where they asked eight persons to determine starting and ending point on each three different samples. In particular, the endpoint and the total reaction heat were subject to strong variations.

In order to be independent of unknown algorithms of commercial analyzing software, all data were processed using a self-designed, half-automated software written in MATLAB®. Inputs for the analysis were blind curve corrected values of the heat flow (S(t)) in dependency of time t. For calculation of the virtual baseline (B(t)), the method of integral tangential baseline was chosen as there were small, nonlinear changes in the heat flow with temperature detectable and a straight line would have intersected the signal. In an iterative process, this type of baseline and the degree of crystallization are calculated simultaneously using the following calculation.

$$ \alpha (t) = \frac{{\mathop \smallint \nolimits_{{t_{0} }}^{t} \left[ {S(t) - B(t)} \right]{\text{d}}t }}{{\mathop \smallint \nolimits_{{t_{0} }}^{{t_{\text {e}} }} \left[ {S(t) - B(t)} \right]{\text{d}}t }} $$
(6)

Therein, the tangential area-proportional baseline is described by

$$ B(t) = \left( {1 - \alpha (t)} \right) \tilde{T}_{0} (t) + \alpha (t)\tilde{T}_{\text {e}} (t) $$
(7)

with \( \tilde{T}_{0} (t) = a_{0} + m_{0} t \) and \( \tilde{T}_{\text {e}} (t) = a_{\text {e}} + m_{\text {e}} t \) the tangentials at beginning t 0 and end t e of the crystallization signal. The integrals were calculated using MATLAB’s inbuilt integration scheme based on trapezoidal numerical integration. The iterative process of crystallization and baseline calculation was stopped if the maximal change of B(t) was <10−11.

The major problem for an algorithm that is used for determination of t 0 and t e is to work for all temperatures properly even if the heat flow signals have different strength. On the one hand, for small signals as obtained at high temperatures, the endpoint must not be underestimated. On the other hand, it must not overestimate well-pronounced signals. Within the investigation, many tested algorithms failed one or the other of these two criteria.

In the ideal case, the endpoint of crystallization is at a point at which the extrapolated baseline is a horizontal line again. In the measured samples of this study, there was a small, increasing heat flow even after the obvious visible crystallization had finished. Moreover, the recorded signal had measurement errors resulting in fluctuations, which disturbed the signal. As the progression of the phase transition depends strongly on the ending point, an algorithm was used to obtain it automatically, which is similar to that of the one proposed in [47].

For determination of the endpoint at isothermal crystallization, first the numerical derivative of the smoothed heat flow was calculated. As it is a constant at advanced times (about last 700 s at isothermal temperatures), the absolute value of the difference between the derivative and a reference line with the corresponding mean value was calculated. The first time at which this difference was <1 % of its maximal value for 5 succeeding data points was chosen to be the endpoint. The consideration of more than one value below or above the threshold was chosen as the algorithm became more stable against fluctuations. Thus, the endpoint is the point at which the derivative of the heat flux changes. As this is the same case for the crystallization onset, the algorithm can be used for determination of the starting point as well, as long as there is a baseline before the crystallization starts.

Results

Isothermal measurements

In Fig. 1, the isolated heat flows of crystallization for the different isothermal temperatures are depicted together. With increased isothermal temperature, the maximum of heat flow decreased, and coincidentally the maximum was shifted toward longer times. In Table 1, the times of maximal heat flow are listed for the isothermal temperatures. The times varied between about 2 min at 158 °C and 41 min at 168 °C. The whole time of crystallization differs between about 5 min at 158 °C and 100 min at 168 °C. The measurement at 170 °C had to be withdrawn from the analysis as the crystallization had not finished within the experimental time of 5 h.

Fig. 1
figure 1

Heat flow for isothermal DSC measurements at temperatures between 158 and 168 °C

Full size image
Table 1 Isothermal temperatures T and times t peak of maximal heat flow
Full size table

The analysis showed small differences at 158, 160, 162 and 164 °C in height of the heat flow at crystallization onset and the baseline afterward that might be appeared because the crystallization had already started during the cooling from the melt to the isothermal temperature [48]. As the lags are small (≤5 %) compared to the maximal difference in baseline and signal, the starting point for crystallization was set manually to the time point of these local maximum in heat flow. In consequence, at these temperatures the tangential at the onset of crystallization was chosen a horizontal line. At 166 and 168 °C, there was a short period between onset of crystallization and the time when the isothermal temperature was reached. This period had a length of about 100 s at 166 °C and 200 s at 168 °C, and the starting points of crystallization were set to the end of this period.

According to the theory of Avrami, parameters n and k(T) can be obtained by linearization of Eq. 1 by twofold application of the logarithmic function. It has been reported that a good linearization (R 2 ≥ 0.99) has been possible within 3 and 95 % of relative degree of crystallization and that values outside these limits have not been taken into account for linearization [49]. Elsewhere [48], it has been proposed to choose α higher than 0.9990. In consequence, the range for the linear interpolation has been limited to 3–20 %. Based on these considerations, linear fits were performed first on values in a small interval around 50 % crystallization. The fitting range was enlarged successively, first to the lower limit and afterward to the upper one. Additional data for the fit were taken into account as long as R 2 > 0.995 and α > 0.03. The resulting ranges for the linearization were at least 0.03 ≤ α ≤ 0.91. The linearized plots are shown in Fig. 2. The respective values of n, k, R 2 and the half crystallization times that were calculated from the data and using the Avrami model are listed in Table 2. The Avrami exponent varies between n = 2.57 and n = 3.05. The calculated curves of the degree of crystallization are depicted in Fig. 3 together with the experimental values.

Fig. 2
figure 2

Linearized plots of the isothermal measurements according to the theory of Avrami for calculation of the Avrami exponent and rate

Full size image
Table 2 Isothermal temperatures T, Avrami exponent n, Avrami rate constant k, coefficient of determination for the linear fits R 2, half crystallization times from the measurements \( {t}_{1/2}^{{\text {m}}} \) and half crystallization time from the Avrami model \({ t}_{1/2}^{{\text {A}}} \)
Full size table
Fig. 3
figure 3

Degree of crystallization for different isothermal measurements and calculated curves according to the theory of Avrami (dashed lines)

Full size image

Non-isothermal measurements

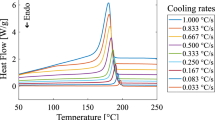
In Fig. 4, the heat flow curves of the non-isothermal measurements are depicted. Comparable to the isothermal case, slower cooling led to a decrease in maximal heat flow and shifted the peaks toward longer times. In contrast to the isothermal case, the crystallization began after the starting temperature for cooling was reached and a clear baseline was given before the onset of crystallization for all measurements. Beneath that, the maximal amplitude of heat flow was larger during crystallization compared to isothermal measurements. Crystallization at 20 °C min−1 was finished in less than 2 minutes. In the slowest cooling of 0.1 °C min−1, crystallization took at about 70 min.

Fig. 4
figure 4

Measured heat flow for non-isothermal DSC measurements at different cooling rates between 0.1 and 20 °C min−1

Full size image

For calibration of the Nakamura model, the obtained half crystallization times were used to fit the parameters K G and K 0. The linearized form according to Eq. 6 is plotted in Fig. 5. In the evaluated range of temperatures, the measurements fit quite well to the theory (R 2 = 0.992). As necessary input for this calculation, the glass transition temperature was determined from the data to T G = 60 °C. The equilibrium melting temperature was estimated from the literature and set to 190 °C [14]. At this point, it can be admitted that small deviations of the true T 0 do not have a substantial influence on the solution of the differential equation. In addition, the theoretical progression of the half crystallization time (Fig. 6) and the Nakamura rate (Fig. 7) are shown. In Table 3, the parameters K 0 and K G are listed for the half crystallization times obtained from the measurement and the Avrami model. Additionally, the values reported by Amado et al. [16] are listed. Though polyamide 12 was used in both investigations, K 0 differs about one order of magnitude.

Fig. 5
figure 5

Linearized representation according to Eq. 6 and fitted linear curve for calculation of parameters K 0 and K G used in the Hoffmann–Lauritzen theory

Full size image
Fig. 6
figure 6

Measured isothermal half crystallization times and model prediction according to Eq. 5 as function of temperature

Full size image
Fig. 7
figure 7

Calculated Nakamura rate according to Eq. 4 using the measured and calculated half crystallization times as function of temperature

Full size image
Table 3 Calculated parameters K 0 and K G of the Hoffmann–Lauritzen theory using the half crystallization times from the theoretical values obtained from the Avrami model and the measurements in comparison with [16]
Full size table

The fitted Nakamura model was used to calculate both the isothermal (Fig. 8) and non-isothermal (Fig. 9) crystallization in dependency of the time (isothermal) and temperature (non-isothermal). The Avrami exponent for all calculations was set to the mean value of \( \bar{n} = 2.82 \).

Fig. 8
figure 8

Degree of crystallization for the isothermal measurements and calculated values using the model of Nakamura (dashed lines)

Full size image
Fig. 9
figure 9

Degree of crystallization for the non-isothermal measurements and calculated values using the model of Nakamura (dashed lines)

Full size image

Discussion

Aim of this study was to investigate the crystallization kinetics of polyamide 12 (PA 2200) that is used in laser sintering. For that purpose, isothermal DSC measurements at temperatures in the range of 158 and 170 °C and non-isothermal ones at cooling rates of 0.1, 0.5, 2.5, 5, 10 and 20 °C min−1 were taken. In order to calculate the crystallization end point, an algorithm following [47] was used, which is based on the change in the derivative of the heat flow. As the change in the absolute value of the derivative is taken, the algorithm can be used for determination of the crystallization onset as well, as long as there is a clear baseline before the onset. It should be noted that the numerical derivative if computed in fine resolved data may be subject to strong variations and the algorithm may determine incorrect start and end points. In these cases, it might be useful to compute the derivative based on larger time steps to smooth the fluctuations.

Despite from minor deviations, the isothermal crystallization can be well described by the theory of Avrami in the evaluated temperature range. In conjunction with results of Amado et al. [16], the data suggested a maximum of the Avrami exponent at 164 °C as Amado et al. investigated the crystallization between 166 and 170 °C and found a decrease in the exponent as the temperature increased. However, the values at 168 °C seem to be an exception of this as n is close to its maximum whereby the algorithm found best coefficient of determination. Anyhow, the drying conditions, humidity or manufacturing of the powder influence the results.

The measured half crystallization times were used to calibrate the parameters of the crystallization model by Nakamura. Despite the good accordance of measured half crystallization times and predictions by the Hoffmann–Lauritzen theory, a deficit of this modeling approach is the lag of data over the full temperature range. However, crystallization will be even faster at lower temperatures and conventional DSC apparatus react too slowly to conduct valid experiments. In the investigated temperature range, the deviations of the estimated parameters K 0 and K G from the true parameter set that would be obtained if the half crystallization times could be measured for the whole temperature range, do not have a strong impact. Anyhow, it might cause variations of the maximal rate at lower temperatures, which can influence the results of non-isothermal simulations.

Comparing the parameters of the given study with those of Amado et al. [16], the factor K 0 differs about one order of magnitude, which may have several reasons. The measured half crystallization times at 166 and 168 °C are about 33 and 28 % larger than those reported [16]. That differences might be because of unequal crystalline structures due to different manufacturers [14] and the additional step in the heat circle at 120 °C that has been chosen according to Drummer et al. [46]. In conjunction with the calculation of the product of two exponential functions in Eq. (5), the variations will be nonlinearly increased.

The calibrated model was used to simulate both the isothermal and non-isothermal experiment. Beside minor deviations due to the utilization of the mean Avrami exponent for the calculations, both conditions are well reproduced. The deviation at 168 °C seems to be highest; however, as discussed, the crystallization took longest, and due to the exponential parameters within the formula of the rate, small deviations become larger. As observed elsewhere [37] as well, the model performs better in the non-isothermal case. Therefore, it can be used for the simulation of laser sintering as the process always exhibits slow temperature variations.

Conclusions

In this study, the isothermal and non-isothermal crystallization kinetics of a polyamide 12-based powder that is used in laser sintering was analyzed. The results of the isothermal measurements were analyzed in conjunction with the Avrami model. Nearly perfect agreement was obtained for all temperatures. Aiming the inclusion of a crystallization model in calculation of temperature and warpage of laser sintering, non-isothermal experiments were conducted as well. The isothermal half crystallization times were used to calibrate the parameters of the Nakamura model, and isothermal and non-isothermal crystallization was simulated. For that purpose, the mean of the Avrami exponent was used for the simulation. Good accordance was obtained for both cases, anyhow the non-isothermal case performed better. Future work should focus the application of the simulation model to analyze the crystallization kinetics in laser sintering in dependency of process conditions as well as to extend the model in terms of calculation of warpage.