1 Introduction

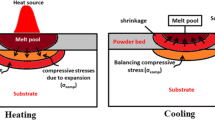
Selective laser sintering (SLS), a powder-based additive manufacturing technique, uses a high-intensity laser to fabricate parts with complex geometry by selectively fusing polymer powder in a layer-by-layer manner [1,2,3,4]. It mainly involves the sintering and cooling processes. Powder particles are rapidly melted under laser irradiation, and a melt pool is formed along the laser scanning track. After sintering, the melted polymer cools down to room temperature. During the cooling process, the polymer first experiences a phase transition from the liquid state to the solid state. The solid-state polymer further undergoes non-uniform thermal contraction. Moreover, parts of molecular chains fold together in an orderly arrangement to form a crystalline phase for semicrystalline polymers. This crystallization process causes a significant shrinkage of polymer volume. All these behaviors affect the dimensional accuracy, surface roughness, porosity, microstructure, and mechanical behavior of SLS-printed parts.

Extensive investigations have been conducted to evaluate the material properties of polymers and polymeric composites for determining the processability of SLS. Verbelen et al. [5] studied the powder properties, melt rheology, crystallization, and solidification behavior of four commercial polyamide (PA) powder used in SLS. Laumer et al. [6] measured the laser energy consumed by reflection, absorption, and transmission of polyamide 12 (PA12) and polyethylene powder under laser irradiation. On the basis of the information of material properties, more research focused on the influence study of SLS process parameters (laser power, scanning speed, scanning pattern, hatching space, layer thickness, and building orientation) on the quality of built parts. Caulfield et al. [7] studied the effect of laser energy density determined by the laser power, scanning speed, and laser beam radius on the mechanical behavior of SLS-printed PA components. Peyre et al. [8] developed a combined numerical and experimental method to study the effect of laser power and scanning speed on the maximum temperature of PA12 and PEKK samples. Yuan et al. [9, 10] conducted material evaluation and process optimization of multi-walled carbon nanotubes (CNT)-coated PA12 powder for SLS. According to these experimental results, various methods including variance analysis [11, 12], artificial neural network [13, 14], and finite element modeling [15] have been developed to optimize SLS process parameters for the excellent mechanical behavior of printed parts. However, experimental investigations of the SLS process could not shed light on the underlying mechanisms of the melting and cooling processes, especially the relationships among the process parameters, temperature distribution, melt pool dimensions, thermal and mechanical deformation, crystallization, and residual stress.

Numerical modeling has intrinsic advantages to reproduce the melting and cooling processes of SLS. The temperature distribution, melt pool dimensions, and crystallization process can be considered in the modeling of SLS. Dong et al. [16] conducted a finite element analysis to evaluate the temperature distribution and evolution during the sintering process of polycarbonate. Riedlbauer et al. [17] used the finite element method to predict the temperature field and dimensions of the melt pool. Recently, Balemansd et al. [18] developed a finite element-based model to reveal the temperature and crystallization kinetics of PA12 powder. In addition to macroscopic modeling approaches, mesoscopic approaches considering particles and their interactions have been developed to provide a more realistic prediction of the melting process [19,20,21,22]. In these approaches, a transient heat transfer model with a specified laser heat source was used to predict the temperature distribution and evolution as a laser beam scanned a powder bed. The temperature-dependent thermal properties of polymers under powder, solid, and liquid states were included in the modeling. However, these modeling approaches mainly concerned the temperature field and related crystallization behavior in SLS, while the thermal deformation, mechanical deformation, and residual stress were not considered. In addition to the physics-based modeling of the actual physical process of 3D printing such as finite element analysis, the data-driven approaches used the existing machine learning strategies based on extensive experimental data to efficiently predict the thermal–mechanical field in 3D printing processes [23,24,25]. Recently, the data-driven approach without training from a large data set has also been developed to evaluate the thermal distortion in additive manufacturing [26]. These approaches greatly enrich the modeling methods in additive manufacturing. However, the data-driven approaches are not in the scope of the present study.

Molten polymers experience thermal contraction as the temperature decreases in the cooling process. It causes mechanical deformation of polymer materials. Manshoori Yeganeh et al. [27] conducted a simple numerical simulation on the thermal stresses and part warping of PA12 in SLS. The elastic deformation of the printed material was included in the modeling. Semicrystalline polymers commonly exhibit elastic- (or viscoelastic-) viscoplastic deformation at moderate strain and hardening behavior at large strain. Several micromechanics and phenomenological constitutive models have been developed to reproduce the stress–strain behavior of polymers with the dependency of temperature and time [15, 28,29,30,31]. For polymers under elevated temperature, the yield stress is relatively low, and thus viscoplastic flow can easily occur in the cooling process. Therefore, the viscoplastic deformation of polymers should be considered in the modeling of the SLS process. Another aspect is the crystallization of semicrystalline polymers. A part of molecular chains arranges themselves regularly during the cooling process and forms a crystalline state in a certain temperature range. The volume shrinkage caused by crystallization is strongly dependent on the degree of crystallinity. Experimental investigations revealed that the crystallization-induced volume shrinkage was about 4.7% for the PA12 polymer [5, 32], which is comparable to that caused by thermal contraction. The volume shrinkage for polymers with high crystallinity such as high-density polyethylene can reach 13% [5]. The crystallization process is also affected by the temperature history during the cooling process. A high cooling rate usually causes incomplete crystallization due to limited time for chain folding [33]. For the SLS process, the cooling rate of a polymer on sintered tracks is non-uniform. Therefore, it is of significance to consider the crystallization process and its effect on residual stress in the modeling of SLS.

This study developed a macroscopic thermomechanical model to predict temperature, strain, and stress fields in the SLS process of PA12. A laser heat source model considering the laser penetration and energy decay in a powder bed is used with a transient heat transfer model to evaluate the temperature distribution and evolution. An elastic–viscoplastic constitutive model is developed to describe the temperature- and time-dependent stress–strain response of PA12. The thermal strain is also included in the constitutive model. A non-isothermal crystallization model is used to consider the crystallization process and the resultant strain during cooling. The finite element implementation of these models is conducted to evaluate the temperature, elastic strain, viscoplastic strain, stress, and degree of crystallization in the sintering and cooling processes. The predicted deformation of the printed parts during the SLS process is validated by experimental results.

2 Theoretic models

2.1 Transient heat transfer model

The SLS process of polymer powder involves a powder melting process under laser irradiation and a subsequent cooling process to form printed parts. Polymer powder is preheated to a desired temperature (also called the bed temperature) before laser sintering. As the laser scans selectively on the powder bed, powder particles are rapidly heated to their melting temperature. A melt pool is formed along the laser scanning track. During the cooling process, the melted polymer gradually cools down at a relatively slow rate to room temperature. The crystallization phenomenon is also involved in this process.

A transient heat transfer model is developed to predict the temperature evolution in the SLS process. The layer to be sintered on the powder bed is treated as a homogeneous and continuous media with equivalent material properties. The transient heat transfer model considers the laser as a body heat source:

$$\rho_{\text{h}} C_{\text{h}} \frac{\partial T}{{\partial t}} = \nabla \cdot (k_{\text{h}} \nabla T) + Q,$$
(1)

where \(\rho_{{\text{h}}}\), \(C_{{\text{h}}}\), and \(k_{{\text{h}}}\) are the temperature-dependent density, specific heat capacity, and thermal conductivity during the heating process, respectively. It is noted that the variations in the material phases are different between the heating process and the cooling process. Therefore, the temperature-dependent thermal properties during the two processes are different as introduced in Sect. 3.2. As the laser irradiates on the powder bed, laser energy can transmit into a certain depth beneath the powder top surface because of the porosity of the powder bed. It was reported that the laser energy experienced an exponential decay along the depth direction [8]. The laser energy on the top surface of the powder bed, i.e., the x–y plane, is assumed to have a normal distribution over the irradiated area with a laser beam radius \(r_{{{\text{laser}}}}\) [16]. Therefore, the laser heat source is modeled as [15]

$$Q = \frac{2AP}{{\pi r_{{{\text{laser}}}}^{2} }}\exp \left( { - 2\frac{{x^{2} + y^{2} }}{{r_{{{\text{laser}}}}^{2} }}} \right)\eta \exp ( - \eta z),$$
(2)

where \(P\) is the laser power and \(A\) is the energy absorption coefficient of the powder bed. The parameter \(\eta\) is the extinction coefficient, which indicates the decay rate of laser energy along the depth direction. To model the moving laser beam, the position of the laser beam center on the top surface of the powder bed, i.e., the x and y in Eq. (2), changes according to the scanning strategy.

The initial temperature condition is given as follows:

$$T(x,y,z,0) = T_{{\text{b}}},$$
(3)

where \(T_{{\text{b}}}\) is the powder bed temperature. Since the maximum temperature during the polymer SLS process is much lower than that during the metal melting process, the thermal radiation is not considered in the modeling of thermal boundary conditions. The thermal convection condition is expressed as

$$- {\mathbf{n}} \cdot k_{{\text{h}}} \nabla T = h_{{\text{h}}} (T - T_{{\text{b}}} ),$$
(4)

where \({\mathbf{n}}\) is the surface normal direction and \(h_{{\text{h}}}\) is the convection coefficient in the heating process.

During the cooling process, there is no laser heat source and the heat transfer model is changed as

$$\rho_{\text{c}} C_{\text{c}} \frac{\partial T}{{\partial t}} = \nabla \cdot (k_{\text{c}} \nabla T),$$
(5)

where the subscript ‘c’ of the thermal properties indicates the cooling process. Since the crystallization during the cooling process is considered, the crystallization-induced enthalpy variation is described as the bump in the specific heat capacity during the cooling process. The chamber temperature gradually decreases to room temperature. The thermal boundary condition is changed as follows:

$$- {\mathbf{n}} \cdot k_{{\text{c}}} \nabla T = h_{{\text{c}}} (T - T_{{{\text{rt}}}} ),$$
(6)

where \(T_{{{\text{rt}}}}\) represents room temperature and \(h_{{\text{c}}}\) is the convection coefficient in the cooling process.

2.2 Thermo-elasto-viscoplastic constitutive model

The polymer experiences thermal expansion and contraction in the sintering and cooling process, respectively. Mechanical deformation is also involved because of the internal stress caused by non-uniform temperature distribution. All molecular chains are randomly distributed after powder melting. However, parts of chains begin to crystallize from a molten state to a crystalline state as the temperature reaches the crystallization point during the cooling process. It results in a significant reduction in polymer volume [5, 32, 34]. Therefore, the total strain can be written as the summation of three strain components under the small strain assumption:

$${{\varvec{\upvarepsilon}}} = {{\varvec{\upvarepsilon}}}_{{{\text{me}}}} + {{\varvec{\upvarepsilon}}}_{{{\text{th}}}} + {{\varvec{\upvarepsilon}}}_{{{\text{re}}}},$$
(7)

where \({{\varvec{\upvarepsilon}}}_{{{\text{me}}}}\), \({{\varvec{\upvarepsilon}}}_{{{\text{th}}}}\), and \({{\varvec{\upvarepsilon}}}_{{{\text{re}}}}\) are the mechanical strain, thermal strain, and crystallization-induced strain, respectively.

Typical stress–strain curve of semicrystalline polymers under tension includes three distinct stages: the nearly elastic behavior at small strain, the nonlinear yielding behavior at moderate strain, and strain hardening at large strain [35, 36]. These three stages have both temperature and strain-rate dependency. As there is no external mechanical loading applied on the printed part in the SLS process, only the linear elastic and nonlinear yielding behavior of the polymer is considered in the modeling. The last strain-hardening stage is not included in this study. A thermo-elasto-viscoplastic constitutive model is developed to describe the evolutions of stress, mechanical strain, and thermal strain during the SLS process. The mechanical strain \({{\varvec{\upvarepsilon}}}_{{{\text{me}}}}\) is divided into elastic strain \({{\varvec{\upvarepsilon}}}_{{\text{e}}}\) and viscoplastic strain \({{\varvec{\upvarepsilon}}}_{{{\text{vp}}}}\):

$${{\varvec{\upvarepsilon}}}_{{{\text{me}}}} = {{\varvec{\upvarepsilon}}}_{{\text{e}}} + {{\varvec{\upvarepsilon}}}_{{{\text{vp}}}}.$$
(8)

The stress is determined by the elastic strain \({{\varvec{\upvarepsilon}}}_{{\text{e}}}\) and temperature-dependent fourth-order elastic tensor \({\mathbf{C}}\) as

$${{\varvec{\upsigma}}} = {\mathbf{C}}\left( T \right):{{\varvec{\upvarepsilon}}}_{{\text{e}}},$$
(9)

where the elastic tensor \({\mathbf{C}}\) can be calculated by the temperature-dependent elastic modulus \(E(T)\) and Poisson’s ratio \(\nu\). The viscoplastic strain rate with respect to time is defined as

$${\boldsymbol{\dot{\varepsilon }}}_{{{\text{vp}}}} = \dot{\lambda }_{{{\text{vp}}}} \frac{\partial f}{{\partial {{\varvec{\upsigma}}}}},$$
(10)

where \(\dot{\lambda }_{{{\text{vp}}}}\) is the viscoplastic multiplier, \(f\) the yield function, and \(\partial f/\partial {{\varvec{\upsigma}}}\) the direction of the viscoplastic flow. The Mises yield function is used here, i.e., \(f = \sqrt {3{\mathbf{s}}:{\mathbf{s}}/2} - \sigma_{{\text{y}}} (T)\), where \({\mathbf{s}}\) is the deviatoric component of \({{\varvec{\upsigma}}}\) and \(\sigma_{{\text{y}}}\) is temperature-dependent yield stress. The effect of the volumetric component on the viscoplastic flow [37,38,39] is not considered since the plastic deformation in SLS is not significant. Therefore, Eq. (10) is rewritten as

$${\boldsymbol{\dot{\varepsilon }}}_{{{\text{vp}}}} = \dot{\lambda }_{{{\text{vp}}}} \frac{{3{\mathbf{s}}}}{{2\sqrt {3{\mathbf{s}}:{\mathbf{s}}/2} }}.$$
(11)

The equivalent viscoplastic strain is thus defined based on Eq. (11):

$$p = \sqrt {2{{\varvec{\upvarepsilon}}}_{{{\text{vp}}}} :{{\varvec{\upvarepsilon}}}_{{{\text{vp}}}} {/3}}.$$
(12)

The viscoplastic multiplier \(\dot{\lambda }_{{{\text{vp}}}}\) is a function of von Mises stress, yield stress, and equivalent viscoplastic strain [35] and written as

$$\dot{\lambda }_{{{\text{vp}}}} = \dot{\lambda }_{{0}} \left( {\frac{{\sqrt {3{\mathbf{s}}:{\mathbf{s}}/2} }}{{\sigma_{{\text{y}}} (T)\left( {1 + \delta - \delta \exp ( - p/p_{{\text{y}}} )} \right)}}} \right)^{m},$$
(13)

where \(\dot{\lambda }_{{0}}\), \(\delta\), \(p_{{\text{y}}}\), and \(m\) are material parameters. The term \(1 + \delta - \delta \exp ( - p/p_{{\text{y}}} )\) increases from the initial value (1) and approaches to the maximum value (\(1 + \delta\)) with an increase of the equivalent viscoplastic strain. It is used to reproduce a smooth increase process of the stress beyond the yield stress on the stress–strain curve.

The thermal strain increment \(\Delta {{\varvec{\upvarepsilon}}}_{{{\text{th}}}}\) is determined by the temperature variation:

$$\Delta {{\varvec{\upvarepsilon}}}_{{{\text{th}}}} = \alpha (T)\Delta T \cdot {\mathbf{I}},$$
(14)

where \(\alpha\) is the temperature-dependent coefficient of thermal expansion (CTE) and \({\mathbf{I}}\) is the second-order unit tensor.

The model to consider the crystallization-induced strain is explained in the following subsection.

2.3 Crystallization model

The crystallization phenomenon is considered in the modeling. It mainly occurs in the cooling process as the polymer temperature is lower than the onset temperature of crystallization. It is noted that the crystallization also occurs in the heating process [40]. In this study, only the crystallization in the cooling process is considered using a non-isothermal model [34, 41, 42]:

$$\chi (t) = 1 - \exp \left( - \left(\int\limits_{0}^{t} {K(T){\text{d}}\tau }\right )^{n}\right ),$$
(15)

where \(\chi\) is the relative degree of crystallization, \(n\) the Avrami exponent, and \(K(T)\) the non-isothermal crystallization rate expressed as \(K(T) = \ln (2)^{1/n} /t_{1/2}\) in which \(t_{1/2}\) is the half crystallization time written as [43]

$$\frac{1}{{t_{1/2} }} = K_{0} \exp \left( - \frac{U}{{R\left(T - T_{\infty } \right)}}\right)\exp \left( - \frac{{K_{g} \left(T + T_{{\text{m}}}^{0} \right)}}{{2T^{2} \left(T_{{\text{m}}}^{0} - T\right)}}\right),$$
(16)

where \(K_{0}\) is the growth rate, \(U\) the activation energy, \(R\) the universal gas constant, \(T_{\infty } = T_{g} - 30K\) the temperature limit below which the crystallization stops, \(T_{g}\) the glass transition temperature, \(K_{g}\) the nucleation rate constant, and \(T_{{\text{m}}}^{0}\) the equilibrium melting temperature. The time differential form of Eq. (15) is used for the calculation:

$$\dot{\chi } = n\frac{{\ln (2)^{1/n} }}{{t_{1/2} }}(1 - \chi )\left( {\ln \frac{1}{1 - \chi }} \right)^{(n - 1)/n}.$$
(17)

The relative degree of crystallization grows from 0 to 1 as the crystallization time increases. It is noted that the relative degree of crystallization is different from the crystallinity of the polymer. The relative degree of crystallization is a ratio of the actual crystallinity to the maximum crystallinity of the polymer achieved at a constant cooling rate. Zhao et al. [34] conducted experimental and theoretic investigation on the crystallization kinetics of PA12. It was found that the crystallization model can provide reasonable prediction of the crystallization kinetics under different cooling rates. Furthermore, the model was able to predict the variation of the onset temperature of the crystallization under different conditions.

The crystallization-induced strain relates to the relative degree of crystallization. As the relative crystallization degree grows, the strain \({{\varvec{\upvarepsilon}}}_{{{\text{re}}}}\) also increases and follows the equation

$${{\varvec{\upvarepsilon}}}_{{{\text{re}}}} = - \varepsilon_{{{\text{ref}}}} \chi \cdot {\mathbf{I}},$$
(18)

where \(\varepsilon_{{{\text{ref}}}}\) is the strain under the full crystallization, i.e., the relative degree of crystallization equals 1. The minus symbol indicates it is a contraction strain. It is noted that the isotropic shrinkage assumption is used here for SLS modeling.

3 Computation method

3.1 Implicit implementation of theoretic models

The developed thermomechanical model is implemented in the commercial finite element code ABAQUS. A full thermomechanical coupling method is adopted, i.e., the temperature field and the stress and strain fields are computed simultaneously. The equilibrium equations in the thermal and mechanical analysis are handled by the code. There are two main tasks left for the code user, i.e., to provide the laser heat source and to calculate the stress, several strain components, and relative degree of crystallization. Two user subroutines, DFLUX and UMAT, are used to complete the two tasks, respectively. The moving laser heat source with a given energy distribution is defined in the DFLUX subroutine according to Eq. (2). The temperature field is calculated by combing the heat transfer model and the heat source model.

The UMAT subroutine is used for the implicit mechanical analysis. The incremental form of the developed thermo-elasto-viscoplastic model is used to calculate the strain components and stress at each time increment. It is assumed the stress, strain components, equivalent viscoplastic strain, and temperature at the ith increment are known. The results at the (i + 1)th increment are needed to be calculated. It is noted that the temperature at the (i + 1)th increment \(T_{i + 1}\) has been calculated. Moreover, the total strain increment \(\Delta {{\varvec{\upvarepsilon}}}\) has been calculated by using the Jacobian matrix \({\mathbf{C}}_{{{\text{alg}},i}}\). Therefore, the stress and strain results at the (i + 1)th increment are written as

$$\Delta {{\varvec{\upvarepsilon}}} = \Delta {{\varvec{\upvarepsilon}}}_{{\text{e}}} + \Delta {{\varvec{\upvarepsilon}}}_{{{\text{vp}}}} + \Delta {{\varvec{\upvarepsilon}}}_{{{\text{th}}}} + \Delta {{\varvec{\upvarepsilon}}}_{{{\text{re}}}},$$
(19)
$${{\varvec{\upvarepsilon}}}_{{{\text{e}},i + 1}} = {{\varvec{\upvarepsilon}}}_{{{\text{e}},i}} + \Delta {{\varvec{\upvarepsilon}}}_{{\text{e}}},$$
(20)
$${{\varvec{\upsigma}}}_{i + 1} = {\mathbf{C}}(T_{{i{ + 1}}} ):{{\varvec{\upvarepsilon}}}_{{{\text{e}},i + 1}} ,\;{\text{and}}$$
(21)
$${{\varvec{\upvarepsilon}}}_{{{\text{vp}},i + 1}} = {{\varvec{\upvarepsilon}}}_{{{\text{vp}},i}} + {\boldsymbol{\dot{\varepsilon }}}_{{{\text{vp}},i + 1}} \Delta t,$$
(22)

where \(\Delta t\) is the time increment. Since the term \({\boldsymbol{\dot{\varepsilon }}}_{{{\text{vp}},i + 1}}\) relates to the deviatoric stress \({\mathbf{s}}_{i + 1}\) according to Eq. (11), the elastic strain and the viscoplastic strain are coupled together in Eq. (22). To solve both mechanical strain components, the thermal strain increment and the crystallization-induced strain increment should be calculated in advance.

The thermal strain increment \(\Delta {{\varvec{\upvarepsilon}}}_{{{\text{th}}}}\) is determined by the temperature increment and the CTE:

$$\Delta {{\varvec{\upvarepsilon}}}_{{{\text{th}}}} = \alpha (T_{i + 1} )(T_{i + 1} - T_{i} ) \cdot {\mathbf{I}}.$$
(23)

The CTE at temperature \(T_{i + 1}\) is used here. The evolution of the relative crystallization degree is calculated according to the temperature information and Eq. (17). The Newton iteration method is used to solve the following equation:

$$\chi_{i + 1} - \chi_{i} = \dot{\chi }_{i + 1} \Delta t.$$
(24)

The parameters \(n\) and \(t_{1/2}\) are determined by the two temperature terms \(T_{i}\) and \(T_{i + 1}\) before the calculation of \(\chi_{i + 1}\). Therefore, the increment of crystallization-induced strain \(\Delta {{\varvec{\upvarepsilon}}}_{{{\text{re}}}}\) is written as

$$\Delta {{\varvec{\upvarepsilon}}}_{{{\text{re}}}} = - \varepsilon_{{{\text{ref}}}} (\chi_{i + 1} - \chi_{i} ) \cdot {\mathbf{I}}.$$
(25)

After the calculation of \(\Delta {{\varvec{\upvarepsilon}}}_{{{\text{th}}}}\) and \(\Delta {{\varvec{\upvarepsilon}}}_{{{\text{re}}}}\), Eqs. (19)–(22) can be solved by the Newton iteration method. The four strain components, equivalent viscoplastic strain, and stress at the (i + 1)th increment are obtained.

The Jacobian matrix should be updated after the calculation of the stress and strain, which is used to predict the total strain increment at the next increment. The differential forms of Eqs. (7), (21), (22), (23), and (25) are expressed as

$${\text{d}}{{\varvec{\upvarepsilon}}} = {\text{d}}{{\varvec{\upvarepsilon}}}_{{\text{e}}} + {\text{d}}{{\varvec{\upvarepsilon}}}_{{{\text{vp}}}} + {\text{d}}{{\varvec{\upvarepsilon}}}_{{{\text{th}}}} + {\text{d}}{{\varvec{\upvarepsilon}}}_{{{\text{re}}}},$$
(26)
$${\text{d}}{{\varvec{\upsigma}}} = \frac{{\partial {\mathbf{C}}}}{\partial T}{\text{d}}T:{{\varvec{\upvarepsilon}}}_{{\text{e}}} + {\mathbf{C}}:{\text{d}}{{\varvec{\upvarepsilon}}}_{{\text{e}}},$$
(27)
$${\text{d}}{{\varvec{\upvarepsilon}}}_{{{\text{vp}}}} = \frac{{\partial {\dot{\boldsymbol{\varepsilon }}}_{{{\text{vp}}}} }}{{\partial {{\varvec{\upsigma}}}}}{\text{:d}}{{\varvec{\upsigma}}}\Delta t + \frac{{\partial {\dot{\boldsymbol{\varepsilon }}}_{{{\text{vp}}}} }}{\partial T}{\text{d}}T\Delta t,$$
(28)
$${\text{d}}{{\varvec{\upvarepsilon}}}_{{{\text{th}}}} = (\alpha {\text{d}}T + \frac{\partial \alpha }{{\partial T}}{\text{d}}T(T_{i + 1} - T_{i} )) \cdot {\mathbf{I}},\;{\text{and}}$$
(29)
$${\text{d}}{{\varvec{\upvarepsilon}}}_{{{\text{re}}}} = - \varepsilon_{{{\text{ref}}}} \frac{\partial \chi }{{\partial T}}{\text{d}}T \cdot {\mathbf{I}},$$
(30)

where the subscript ‘i + 1’ is omitted for clarity. The new Jacobian matrix at the (i + 1)th increment \({\mathbf{C}}_{a\lg ,i + 1}\) is obtained as

$${\mathbf{C}}_{a\lg ,i + 1} = \frac{{\partial {{\varvec{\upsigma}}}}}{{\partial {{\varvec{\upvarepsilon}}}}} = \left[ {{\mathbf{C}}^{ - 1} + \frac{{\partial {\dot{\boldsymbol{\varepsilon }}}_{{{\text{vp}}}} }}{{\partial {{\varvec{\upsigma}}}}}\Delta t} \right]^{ - 1},$$
(31)

where the superscript ‘-1’ indicates the inverse of the fourth-order tensor. The variation of stress with respect to the temperature is also derived as

$$\frac{{\partial {{\varvec{\upsigma}}}}}{\partial T} = - \left[ {{\mathbf{C}}^{ - 1} + \frac{{\partial {\dot{\boldsymbol{\varepsilon }}}_{{{\text{vp}}}} }}{{\partial {{\varvec{\upsigma}}}}}\Delta t} \right]^{ - 1} :\left( { - {\mathbf{C}}^{ - 1} \frac{{\partial {\mathbf{C}}}}{\partial T}:{{\varvec{\upvarepsilon}}}_{{\text{e}}} + \frac{{\partial {\dot{\boldsymbol{\varepsilon }}}_{{{\text{vp}}}} }}{\partial T}\Delta t + \alpha {\mathbf{I}} + \frac{\partial \alpha }{{\partial T}}(T_{i + 1} - T_{i} ){\mathbf{I}} - \varepsilon_{{{\text{ref}}}} \frac{\partial \chi }{{\partial T}}{\mathbf{I}}} \right).$$
(32)

The above-mentioned updating methods of the stress and the Jacobian matrix are coded into the UMAT subroutine.

3.2 Material properties

The SLS process for PA12 powder (PA2200 from EOS GmbH, Munich, Germany) is simulated in this study. The thermal and mechanical properties of PA12 are required for the modeling. For the thermal properties, the differential scanning calorimetry (DSC) analysis is conducted using a DSC Q200 calorimeter from TA Instruments to evaluate the melting and solidification behavior of PA12. Figure 1a shows the evolution of the specific heat capacity with respect to temperature during the heating process. The peak melting temperature \(T_{{\text{m}}}\) is 186 ℃. A significant bump takes place at the phase transition from the solid state to the liquid state, indicating the latent heat of melting. During the cooling process, the cooling rate significantly affects the onset temperature of crystallization and the crystallization time as reported by Zhao et al. [34]. Under a cooling rate of 20 ℃/min, the onset temperature of crystallization is 156.4 ℃, which is smaller than that (170 ℃) under a cooling rate of 0.2 ℃/min. The half crystallization time \(t_{1/2}\) under a cooling rate of 20 ℃/min is 27.6 s, which is much smaller than that (1387.2 s) under a cooling rate of 0.2 ℃/min. Because the focus of this study is to predict the thermal and mechanical behavior of SLS-printed PA12 during the cooling process, the thermal properties under a reasonable cooling rate are critical for the modeling. The common cooling rate of SLS for PA12 is about 0.5 ℃/min. Figure 1b shows the specific heat capacity during the cooling process. The onset temperature for the crystallization \(T_{{\text{re,s}}}\) is 168 ℃. A small bump of the specific heat capacity occurs during the crystallization process, indicating the release of heat energy due to the crystallization. Figures 1c and d show the density evolution of PA12 during the heating and cooling process, respectively. The material state changes from the powder phase to the liquid phase during the heating process and then to the solid phase during the cooling process. As the porosity of PA12 powder is about 0.44 [9], the density of the powder phase treated as a homogeneous and continuous media is about 56% of the solid density. Therefore, a rapid increase of the density occurs as the polymer changes from the powder phase to the liquid phase during the heating process. During the cooling process, a small change of the density occurs during the phase transition. Figure 1e shows the evolution of thermal conductivity. The thermal conductivities before the melting of the polymer powder are obtained through the transient plane source method (TPS2500S, Sweden). The data after the melting are from the literature [17]. As shown in the figure, the thermal conductivity increases from about 0.1 W/m/°C at the powder state to 0.31 W/m/°C at the liquid state. During the cooling process, a constant thermal conductivity of 0.31 W/m/°C is used. The temperature-dependent CTE of PA12 was seldom reported in the published literature. We obtained the CTE data from the PA12 manufacturer [44]. A small increase of the CTE before the melting is assumed. A linear relationship between the CTE of PA12 and the temperature is used here:

$$\alpha = 1.4 \times 10^{ - 4} + 2.48 \times 10^{ - 7} (T - 25).$$
(33)
Fig. 1
figure 1

Temperature-dependent thermal properties of PA12 under the heating and cooling processes: (a) and (b) the heat capacity, (c) and (d) the density, and (e) the thermal conductivity

Full size image

The thermal properties and the CTE are used as the inputs in the finite element model.

The parameters in the thermo-elasto-viscoplastic model are calibrated through two steps. The first step is to determine the temperature-dependent elastic modulus. According to the stress–strain curves of PA12 under various temperatures [44], the elastic moduli are obtained by measuring the slope of the initial linear stage. An exponential decay function of the temperature is used to model the elastic modulus [35]:

$$E(T) = 167.4 + 1799\exp \left( - \frac{T}{33.6}\right).$$
(34)

The constant Poisson’s ratio \(\nu = 0.4\) is used in this study. The second step is to determine the viscoplastic behavior-related material parameters. The yield stress is the stress first beyond the initial linear stage of the stress–strain curve. An exponential decay function of temperature is used here [35]:

$$\sigma_{{\text{y}}} (T) = 4.66 + 40.0\exp \left( - \frac{T}{27.5}\right).$$
(35)

For the calibration of material parameters \(\dot{\lambda }_{{0}}\), \(\delta\), \(p_{{\text{y}}}\), and \(m\), a numerical method is used here [35]. A cube with one element is built in the finite element code. The stress–strain responses under tension at different temperatures are predicted. The calibration of the four parameters is based on the comparison between the numerical stress–strain curves and the experimental results [44]. Figure 2 shows the comparison between both results under three different temperatures. The determined material parameters \(\dot{\lambda }_{{0}}\), \(\delta\), \(p_{{\text{y}}}\), and \(m\) are listed in Table 1.

Fig. 2
figure 2

Numerical and experimental results [44] of the stress–strain responses of PA12 under different temperatures

Full size image
Table 1 Parameters used for modeling of SLS process for PA 12
Full size table

The crystallization-related material parameters are the Avrami exponent and the strain under full crystallization. A constant value \(n = 2.6\) is used for the modeling of the non-isothermal crystallization process. Verbelen et al. [5] investigated the powder characteristics, melt flow, and solidification behavior of PA12. The strain caused by the full crystallization under a cooling rate of 0.5 ℃/min is determined by the volumetric shrinkage percentage, i.e., \(\varepsilon_{{{\text{ref}}}} = 0.01567\). Furthermore, the parameters in Eq. (16) for PA12 are determined in [34], which are listed in Table 1. The parameters in the thermo-elasto-viscoplastic model and the crystallization model are used in the UMAT subroutine.

3.3 Finite element model

The simulation domain is set as a block with the dimensions of 5 mm × 1 mm × 1 mm. The block is composed of an upper powder layer with a thickness of 0.12 mm and several printed layers beneath the powder layer. The reciprocating scanning pattern is used in the simulation, as shown in Fig. 3. The element size of the powder layer is set as 0.03 mm after the check of the mesh convergence, which is able to capture the high temperature gradient in the laser irradiated zone. The sintered layers are meshed by relatively coarse elements to save computational cost. The eight-node temperature-displacement element C3D8T is used in the modeling. The displacements along the three directions at the bottom of the model are fixed throughout the simulation. The initial temperature or the preheating temperature of PA12 \(T_{{\text{b}}}\) is set as 174 ℃. The thermal boundary conditions are applied on the surfaces except the bottom surface. The SLS process parameters including the laser power \(P\), scanning speed \(s\), and hatching space \(h\) are used in the DFLUX subroutine. The radius of the laser beam \(r_{{{\text{laser}}}}\) is 0.21 mm so that each laser irradiated zone includes about 50 elements. The energy absorption coefficient of PA12 powder \(A\) is set as 0.96 and the extinction coefficient \(\eta\) is set as 9000 m−1 [8, 15].

Fig. 3
figure 3

Simulation model and finite element model of the SLS process for PA12 powder

Full size image

4 Results and discussion

4.1 Validation

Two experiments are conducted to obtain the necessary data for model validation. The first experiment is to prepare a specimen fabricated by one-layer printing under the process parameters of \(P = 40\) W, \(s = 4000\) mm/s, and \(h = 0.25\) mm, as shown in Fig. 4a. The SLS machine (EOS P395 model from EOS GmbH, Munich, Germany) is used in this study. The length and width of the specimen are both 15 mm. The thicknesses of this specimen at different positions are measured to calculate an average value of 0.27 mm, which is more than two times the powder layer thickness. The specimen thickness is compared with the predicted melt pool depth. In the simulation, one track sintering on the powder bed is modeled and the temperature field is obtained, as shown in Fig. 4b. The zone with temperature higher than the melting point is marked with gray color, which indicates the melt pool. The depth of the melt pool is about 0.24 mm as shown in Fig. 4c, which is close to the experimental result. The experimental value of the depth is larger than the numerical result. The main reason is that the non-fusion powder particles are wrapped around the printed specimen. The specimen thickness should be larger than the melt pool depth.

Fig. 4
figure 4

(a) Printed one-layer specimen of PA12, (b) schematic of the simulation, and (c) melt pool depth under the process parameters of \(P = 40\) W and \(s = 4000\) mm/s

Full size image

The second experiment is to prepare cuboid specimens under the process parameters of \(P = 35\) W, \(s = 4000\) mm/s, and \(h = 0.25\) mm, as shown in Fig. 5. The length and width of the printed specimens are measured and compared with the design values. The dimension error is defined as the ratio of the difference between the actual dimension value and the design dimension value to the design dimension value. It can be used to indicate the dimension accuracy of the SLS process. In the simulation, the length and width of the predicted specimen are also obtained under the process parameters of \(P = 35\) W, \(s = 4000\) mm/s, and \(h = 0.25\) mm and the dimension errors are calculated and listed in Table 2. The average value of the three calculated errors along the length direction is − 2.32%. The minus sign indicates that the length of the printed part is smaller than the design length. The predicted dimension error under the same process parameters is − 2.43%, which is close to the experimental data. However, the predicted dimension error along the width direction has a larger variation from the experimental results. Nonetheless, the developed model can provide a reasonable prediction of the melt pool depth and the dimension accuracy of the printed specimens.

Fig. 5
figure 5

Specimens printed under the process parameters of \(P = 35\) W, \(s = 4000\) mm/s, and \(h = 0.25\) mm. The dimension error is defined as the ratio of the difference between the actual dimension and the design dimension to the design dimension, i.e., \(\lambda_{L} = (L - L_{0} )/L_{0}\) and \(\lambda_{W} = (W - W_{0} )/W_{0}\) for the length and width directions, respectively

Full size image
Table 2 Experimental and predicted dimension errors of printed parts under the process parameters of \(P = 35\) W, \(s = 4000\) mm/s, and \(h = 0.25\) mm
Full size table

4.2 Temperature distribution and crystallization results

The simulation case with \(P = 35\) W, \(s = 4000\) mm/s, and \(h = 0.25\) mm is used to illustrate the temperature results in the heating and cooling processes of PA12. Figure 6a shows the temperature distribution at the end of one-layer laser scanning. The maximum temperature is about 272 ℃ and occurs on the last scanning track. The middle sections along the x- and y-direction are defined as the C–D section and A–B section, respectively. The temperature distribution on the A–B section is also illustrated in Fig. 6b. The gray zone represents the melt pool, in which the temperature is higher than the material melting point. The depth of the melt pool is around 0.2 mm larger than the powder thickness. Parts of the previously sintered layer are melted; thus, the adjacent two layers have strong bonds after the sintering. Figure 7 shows the temperature distributions along the top lines of the A–B and C–D section. The temperature on previous tracks is lower than that on the last track. Furthermore, the center of each scanning track has a higher temperature. The difference between the minimum and maximum temperature on the top line of the A–B section is 17 ℃. The temperature on the top line of the C–D section is steady except at the starting and ending points.

Fig. 6
figure 6

(a) Temperature distribution for the simulation case with \(P = 35\) W, \(s = 4000\) mm/s, and \(h = 0.25\) mm. (b) Melt pool on the A–B section. The gray zone represents the melt pool

Full size image
Fig. 7
figure 7

Temperature distributions on the top lines of the A–B section and C–D section

Full size image

Figure 8 shows the temperature evolution at point E (shown in Fig. 6a) in the heating and cooling processes. The initial temperature is the bed temperature. It has a slight increase during the scanning of the second track. As the laser beam irradiates on point E, the temperature dramatically increases up to about 270 ℃. The temperature further increases during the scanning of the fourth track, indicating the laser energy in the two adjacent tracks (Track 2 and 4) affect the temperature of point E. In the cooling process, the temperature decreases from 184 to 30 ℃ within 15,000 s. The average cooling rate is about 0.6 ℃/min. It is noted that there is a region with a relatively low rate of temperature decrease, which is attributed to the heat generation by the polymer crystallization occurring in the temperature range of \(160 \le T \le 168\) ℃. The low decreasing rate lasts for about 700 s. Figure 9 illustrates the evolution of the relative degree of crystallization at point E in the cooling process. As the temperature reaches the critical point for crystallization, the relative degree of crystallization increases from 0 to 1 within about 700 s. After that, the relative crystallization degree remains unchanged. The maximum relative degree of crystallization reaches 1 because the cooling rate is very low.

Fig. 8
figure 8

Temperature evolution at point E in the heating and cooling processes

Full size image
Fig. 9
figure 9

Evolution of the relative degree of crystallization at point E in the cooling process

Full size image

4.3 Evolutions of strain and residual stress

The thermal strain, crystallization-induced strain, elastic strain, and viscoplastic strain are calculated in the simulation. Figure 10a shows the distribution of equivalent viscoplastic strain after cooling for the simulation case with \(P = 35\) W, \(s = 4000\) mm/s, and \(h = 0.25\) mm. The value in the middle of the top surface is about 0.035, which is the largest one on the top line of the A–B section shown in Figs. 10b and c illustrates the evolution of crystallization-induced strain and equivalent viscoplastic strain at point E. The crystallization-induced strain is controlled by the relative degree of crystallization; thus, its evolution curve is similar to that in Fig. 9. The total crystallization-induced strain is 0.0157. The equivalent viscoplastic strain also has a significant increase in the crystallization region. It is noted that the temperature change in this region is only 8 ℃ and the resultant thermal strain is about 0.00096. Therefore, the crystallization-induced strain is dominant and accommodated through the elastic deformation and viscoplastic deformation. After this region, the thermal strain becomes dominant and is accommodated by both mechanical strain components. The equivalent viscoplastic strain still increases, but at a slower rate.

Fig. 10
figure 10

(a) Distribution of the equivalent viscoplastic strain after cooling, (b) distribution of the equivalent viscoplastic strain on the top line of the A–B section, and (c) evolutions of the crystallization-induced strain and equivalent viscoplastic strain at point E

Full size image

Figure 11 shows the distributions of the Mises stress and other two stress components after cooling. The maximum Mises stress is about 5.9 MPa. The stress along the scanning direction is much larger than that in the transverse direction. During the cooling process, the polymer material experiences thermal contraction and crystallization-induced contraction. The material at the side surfaces is free to deform without constraints. For the material inside the model, the surrounding material restricts the contraction of the material point. As a result, the residual stress is tensile stress with its maximum value occurring at the middle point of the top surface.

Fig. 11
figure 11

Distributions of the Mises stress and other two stress components along the x- and y-direction in the scanning plane

Full size image

Figure 12 shows the evolution of the Mises stress at point E. After the temperature is lower than the melting point, the stress begins to increase from zero. Before the start of crystallization, the thermal contraction is the main source of deformation. There is no viscoplastic strain in this region as shown in Fig. 10c and thus the thermal contraction only causes elastic strain. The stress increases up to about 0.6 MPa. In the crystallization region, the crystallization process causes rapid and large volumetric contraction, resulting in a significant increase of the stress. The stress increment in this region is about 2 MPa. However, the stress evolution curve has a drop after the crystallization region. It has two main reasons: (a) there is no more strain decrement caused by crystallization and (b) the strain decrement caused by temperature decrease is small. After the drop, the stress continues to increase. Even though the thermal strain is small compared to the crystallization-induced strain, the stress increment after the crystallization region is about 3.5 MPa, which is larger than that in the crystallization region. It is because that the material properties including the elastic modulus increase with the decreasing temperature. At the end of the simulation, the Mises stress begins to decrease due to stress relaxation since the temperature variation is very small as shown in Fig. 8.

Fig. 12
figure 12

Evolution of the Mises stress at point E during the cooling process

Full size image

4.4 Effect of cooling rate on the strain and residual stress

The above-mentioned results are obtained under a cooling rate of 0.6 ℃/min. In this section, the effect of the cooling rate on the strain and residual stress is studied. The thermal and mechanical behavior under a higher cooling rate of 8 ℃/min is predicted using the developed model. It is noted that this high cooling rate is not used for the practical SLS process. In the modeling, the specific heat capacity during the cooling process under the cooling rate of 8 ℃/min is different from that in Fig. 1b. At a higher cooling rate, the onset temperature of the crystallization is lower. The evolutions of the temperature, Mises stress, crystallization-induced strain, and equivalent viscoplastic strain at point E under both cooling rates are compared. Figure 13 shows the comparison of the two temperature evolution curves. The simulation time under the cooing rate of 8 ℃/min is about 1800 s. The crystallization region lasts for about 120 s as shown in the inset, which is insufficient for the polymer material at point E to complete the full crystallization. The relative degree of crystallization after cooling is about 0.7.

Fig. 13
figure 13

Temperature evolutions at point E under different cooling rates. The inset shows the temperature decrease in the first 800 s under the cooling rate of 8 ℃/min. The crystallization region is included in this time period

Full size image

Figure 14 illustrates the comparisons of the crystallization-induced strain and equivalent viscoplastic strain. Since the relative degree of crystallization under a cooling rate of 8 ℃/min cooling rate is smaller than that under a cooling rate of 0.6 ℃/min, the crystallization-induced strain, i.e., 0.011, is smaller. The equivalent viscoplastic strain under the cooling rate of 8 ℃/min is also smaller. Figure 15 shows the comparison of Mises stress results. The maximum stress under the cooling rate of 8 ℃/min cooling rate is about 8.5 MPa, which is larger than that under the cooling rate of 0.6 ℃/min. The larger maximum stress is attributed to the more rapid cooling rate. The thermal strain values under the two cooling rates are the same, i.e., 0.0343. The sum of the thermal strain and crystallization-induced strain is 0.0443 under the cooling rate of 8 ℃/min and 0.0486 under the cooling rate of 0.6 ℃/min. The difference in the total strain values is insignificant. However, the simulation time for the two cooling rates has a large variance. The higher strain rate under the cooling rate of 8 ℃/min causes the larger stress.

Fig. 14
figure 14

Evolutions of the crystallization-induced strain and equivalent viscoplastic strain at point E under different cooling rates

Full size image
Fig. 15
figure 15

Mises stress evolutions at point E under different cooling rates

Full size image

5 Conclusions

A thermo-mechanical model is proposed to evaluate the temperature, crystallization, strain, and stress of PA12 during heating and cooling processes. This model considers the temperature-dependent material properties, elastic and viscoplastic deformation of polymeric material, polymer crystallization, and crystallization-induced strain. Through an implicit numerical implementation, the model is used together with a finite element method to simulate the thermal and mechanical behavior of PA12 during the heating and cooling processes. The distribution and evolution results of the temperature, relative degree of crystallization, crystallization-induced strain, equivalent viscoplastic strain, and stress are evaluated by the numerical approach. The proposed model can provide a reasonable prediction of the melt pool depth and the deformation of printed parts during the SLS process.

The temperature increases up to the melting point in less than 2 ms as the laser beam scans the polymeric powder. The depth of the melt pool for the simulation case with \(P = 35\) W, \(s = 4000\) mm/s, and \(h = 0.25\) mm is larger than the powder layer thickness. During the cooling process, the polymer crystallization occurs in a narrow temperature range from 168 to 160 ℃ under a cooling rate of 0.6 ℃/min. The heat generation due to the polymer crystallization causes a slower temperature decrease in the crystallization region. The crystallization-induced strain and equivalent viscoplastic strain significantly increase in the crystallization region. The cooling rate affects the duration of the crystallization. Under a high cooling rate, the crystallization-induced strain is small due to the short time of crystallization. However, a high cooling rate causes a large strain rate, which results in high residual stress of SLS-printed PA12 parts.