Measurement testing of heat transfer coefficients in the evaporator and condenser of heat pumps

Abstract

In our earlier studies, it has been stated that the validity and limits of correlations developed for the calculation of heat transfer processes in the evaporator and condenser of heat pumps are not published in general. The values yielded for model structures and process characteristics indicate extreme ranges of standard deviation. While the description and physical and mathematical modeling of phenomena occurring in heat pump components have developed really much and the mathematical accuracy of solutions can be increased at one’s own discretion, descriptions of changes in heat transfer and heat transfer coefficients in the course of refrigerant flow are quite uncertain. At the same time, these factors highly influence the accuracy of the solution. Our study presents the measurements and the new proposed heat transfer correlations, developed on the basis of such measurements, which can be used for calculating heat transfer in heat pump evaporators and condensers with higher accuracy than existing correlations in the literature.

Introduction

In the 2008 UN Summit, the European Commission adopted a future-oriented proposal on the application of renewable energy resources. The proposal package (Renewable Energy Technology Roadmap) is intended for the European Union to realize a 20 % reduction in greenhouse gases compared to the 2007 baseline by 2020, at the same time, to increase the proportion of renewable energy resources to 20 % within the total of energy use [1]. The application of the renewable energy sources offers excellent potential for the usage of heat pumps. Heat pumps replace fossil fuels by the utilization of renewable and waste energies. Nowadays, heat pumps are one of the most efficient means of saving energy and reducing carbon dioxide emissions. Heat pump systems are usually used in energetics for heating or production of domestic hot water (DHW).

In recent years, the application has expanded to reversed process as cooling systems for cooling the buildings. Further, heat pumps can be used as part of other technological processes, as well. Heat pumps are expected to become indispensable in building engineering equipment in the near future, as a result of heating technology modernization. Improvement of the output factor and the operational optimization of heat pumps has become a priority issue. The physical and mathematical modeling of heat pump cycles is an issue settled by today [2]. Based on our investigations, the accuracy of the results yielded is determined by the accuracy of input data. The issue of the accuracy of heat transfer coefficients should be mentioned in the first place among these. Our study is intended to describe heat transfer processes in the evaporator and condenser of heat pumps more accurately than before, which can be achieved by the specification of heat transfer coefficients based on measurements, specially by measurements performed on the refrigerant applied in the heat pump, by the precise definition of measurement conditions, and by determining the error limits and reliability of the formulas obtained. A number of researchers have discussed the determination of the heat transfer coefficient [3–5], but their results show high standard deviation [6]. In general, the reliability and limits of applicability of formulas are not published.

Experimental

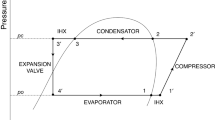
As regards structure, the heat exchangers examined are horizontal, reverse current, and coaxial shell and tube type heat exchangers. The tubes are made of copper and have a staggered layout. In the current case, the refrigerant R134a flows through in finned tube bundle of heat exchangers, while primary and secondary fluid flow in the shell across the tube bundle. In the shell side of heat exchangers, baffles were applied primarily used for supporting the tubes and for inducing cross flow over the tubes, resulting in improved heat transfer performance. The examined heat exchangers have segmental baffles. The segment baffles force the (main stream) primary and secondary fluid to change direction. Measuring instruments were placed along the shell and tube evaporator and the condenser; the length of which was 3 m. Measuring points were installed at 10 discrete points in the heat exchangers. The distance between measuring points was 30 cm. At the measuring points thus installed, the temperature and pressure of the refrigerant as well as of the cooled and the heated fluid were to be measured. Meters were applied to measure the volumetric flow of the primary and secondary fluids, and a mass flow meter was used for measuring the mass flow of the refrigerant. The measurement arrangement is shown in Fig. 1 below, and the accuracy of measuring instruments is specified in Table 1.

Fig. 1

Installation and arrangement of measuring points

Table 1 Measuring instruments

Results in the evaporator

Heat transfer coefficient between the refrigerant and the tube wall

Figure 2 shows changes by Δz steps in the temperature of the primary fluid (cooled water) and the refrigerant along the tube in the evaporator. Heat transfer coefficient values were determined on the basis of temperature measurements, by stating heat balances.

Fig. 2

Flow directions and measuring points of the working fluids in the shell and tube evaporator

The measurement performed was intended to obtain this new proposed correlation for the calculation of the heat transfer coefficient of the two-phase refrigerant flowing in the tubes of the evaporator, which are more accurate and more generally applicable than the results to be obtained by the existing correlations in the literature. The Chen correlation—most generally applied in the literature to determine the heat transfer coefficient of two-phase refrigerants—was taken as a basis to analyze measurement results. The correlation developed by Chen [7]

$$ \alpha_{\text{tp}} = F \cdot \alpha_{\text{f}} + S \cdot \alpha_{\text{nb}} $$

(1)

was further specified on the basis of our measurements, and more precise calculation formulas were determined for the values of F and S:

The two-phase correction multiplier for convective boiling:

$$ F = b \cdot \frac{{Co^{\text{c}} }}{{X_{\text{tt}}^{\text{d}} }}. $$

(2)

The two-phase correction multiplier factor for bubble boiling:

$$ S = a \cdot \left( {1 - x} \right). $$

(3)

Based on our measurements, the expected values and confidence intervals of the constants are as follows at a reliability level of 95 %:

$$ a = 0.431 \pm 0.2527,\,\, b = 12.6 \pm 9.5, \,\,c = 4.14 \pm 1.2 \,\, {\text{and }}\,\,d = 4.80 \pm 1.35. $$

The confidence interval of the heat transfer coefficient calculated by constants and defined by Eq. (1) is

$$ \alpha_{\text{tp}} \pm 289 \,{\text{Wm}}^{ - 2}\, {\text{K}}^{ - 1}. $$

The auxiliary functions and dimensionless numbers included in calculation Eq. (1) are the following:

Martinelli parameter:

$$ X_{\text{tt}} = \left( {\frac{{\mu_{\text{f}} }}{{\mu_{\text{g}} }}} \right)^{1/8} \cdot \left( {\frac{1 - x}{x}} \right)^{7/8} \cdot \left( {\frac{{\rho_{\text{g}} }}{{\rho_{\text{f}} }}} \right)^{0.5}. $$

(4)

Convective number:

$$ Co = \left( {\frac{1}{x} - 1} \right)^{0.8} \cdot \left( {\frac{{\rho_{\text{g}} }}{{\rho_{\text{f}} }}} \right)^{0.5} . $$

(5)

The liquid-phase convective heat transfer coefficient is given by the Dittus-Boelter [8] correlation:

$$ \alpha_{\text{f}} = 0.023 \cdot {\text{Re}}_{\text{f}}^{0.8} \cdot {\text{Pr}}_{\text{f}}^{0.4} \cdot \frac{\lambda }{{{\text{d}}_{\text{in}} }}, $$

(6)

where the liquid Reynolds number is

$$ {\text{Re}}_{\text{f}} = \frac{{\left( {1 - x} \right) \cdot G \cdot {\text{d}}_{\text{in}} }}{{\mu_{\text{f}} }}. $$

(7)

The Cooper [9] correlation gives the nucleate pool boiling coefficient is

$$ \alpha_{\text{nb}} = 55 \cdot {\text{Pr}}^{0.12} \left( { - 0.4343 \cdot {\text{ln}}\left( {\text{Pr}} \right)} \right)^{ - 0.55} \cdot M^{ - 0.5} \cdot \dot{q}^{0.67}. $$

(8)

The Eqs. (2) and (3) presented were defined in the following measurement conditions and subject to the following criteria:

Refrigerant	R134a
Mass velocity	$G = 106, 114, 135 \,{\text{kg\,m}}^{ - 2} \,{\text{s}}^{ - 1}$
Reynolds number	Re = 2,461−3,155
Input temperature	$t_{\text{ref,i}} = 4.6, \;4.7, \;5.4$ °C
Steam content	x = 0.09÷0.98
Tube diameter	$d_{\text{in}} = 6 \,{\text{mm}}$
Number of tubes	$n = 5 \,{\text{pcs}}$
Heating capacity	$\dot{q} = 7,961 \,{\text{W}}{\text{m}}^{ - 2}$
Length of evaporator	$z = 3\, {\text{m}}$

Error analysis of measurement results: confidence interval, error range

On the basis of measurements, constants in the heat transfer correlation can be considered as stochastic variables whose expected values were specified; however, they are also with errors. The confidence interval was determined by Student’s t-distribution. Student’s t-distribution plays a highly important role in the estimation of average values and confidence intervals in cases when both the standard deviation and the expected values of the multitude examined are estimated from the sample. The t-distribution is basically applied in case of small samples.

Heat transfer coefficient in the shell side between the primary fluid and the outer walls of tubes

Values calculated by the existing correlations in the literature do not represent such a high standard deviation as the heat transfer correlations for two-phase refrigerants. Nevertheless, it was deemed reasonable to verify their generalizability. Measurement results were used for the proposed new heat transfer correlation to determine the value of the shell-side heat transfer coefficient. The starting point of the new correlation was the general form of the equation to determine the heat transfer coefficient [10]:

$$ \alpha = E_{1} \cdot {\text{Re}}^{{{\text{E}}_{2} }} \cdot {\text{Pr}}^{{{\text{E}}_{3} }} \cdot \frac{\lambda }{d}. $$

(9)

The new heat transfer correlation based on measurement results can be seen below, applying Re and Pr numbers:

$$ \alpha_{\text{w}} = a \cdot {\text{Re}}^{\text{b}} \cdot {\text{Pr}}^{\text{c}} \cdot \frac{\lambda }{{D_{\text{e}} }}, $$

(10)

where the expected values and confidence intervals of constants are as follows, at a reliability level of 95 % and based on t-distribution:

$$ a = 1.66 \pm 0.66, \,\,b = 0.432 \pm 0.171 \,\,{\text{and}}\,\, c = 0.0382 \pm 0.0151. $$

Confidence interval of Eq. (10): $\alpha_{\text{w}} \pm 83 \,\text{Wm}^{ - 2} \text{K}^{ - 1} .$

The Eq. (10) presented was defined in the following measurement conditions:

Working fluid	Water
Volumetric flow	$\dot{V} = 1, 1.5\, {\text{and}} \; 2 \,{\text{m}}^{3}\, {\text{h}}^{ - 1}$
Reynolds number	3,800 < Re < 8,000
Input temperature	$t_{\text{w,i}}$ = 13 °C
Shell internal diameter	$D_{\text{in}} = 32\,{\text{mm}}$
Tube outside diameter	$d_{\text{out}} = 8\, {\text{mm}}$
Number of tubes	$n = 5 \,{\text{pcs}}$
Tube pitch	Triangular
Baffle spacing	$L = 75 \,{\text{mm}}$
Baffle cut percentage	$k = 50\,\%$
Length of evaporator	$z = 3 \,{\text{m}}.$

Results in the condenser

Heat transfer coefficient between the refrigerant and the tube wall

Figure 3 presents changes by Δz steps in the temperature of the secondary fluid (heated water) and the refrigerant along the tube in the condenser.

Fig. 3

Directions of flow and measuring points of the working fluids in the shell and tube condenser

The measurement performed was intended to obtain the new proposed correlation Eq. (11) for the calculation of the heat transfer coefficient of the two-phase refrigerant flowing in the tubes of the condenser, which are more accurate and more generally applicable than the results to be obtained by the existing correlations in the literature in respect of the refrigerant R134a. Upon the evaluation of results, the following correlation was yielded for determining the heat transfer coefficient of the two-phase refrigerant flowing in the condenser tubes:

$$ \alpha_{\text{tp}} = a \cdot e^{{\text{b}} \cdot {\text{Re}}_{\text{e}}} \cdot {\text{Pr}}^{\text{c}} \cdot \left( {\frac{\lambda }{{d_{\text{in}} }}} \right), $$

(11)

Expected values and confidence intervals of constants at 95 % reliability level are as follows, based on t-distribution:

$$ a = 28.6 \pm 5.16, \,\,\, b = 3.15 \cdot 10^{ - 5} \pm 4.48 \cdot 10^{ - 6} ,\,\,\, c = 1.11 \pm 0.88. $$

Confidence interval of Eq. (11): $\alpha_{\text{tp}} \pm 78 \,{\text{Wm}}^{ - 2}\, {\text{K}}^{ - 1}.$

The new proposed heat transfer coefficient of condensation was partly based on the Akers correlation [11] modified by the authors, namely e, Euler’s base of natural logarithm, was introduced in the Akers correlation and the Re number was placed in the exponent thereof. In the measurement conditions described and within the Re number range specified, this solution yields more accurate values than the original Akers correlation. The Eq. (11) presented was defined in the following measurement conditions and subject to the following criteria:

Refrigerant	R134a
Mass velocity	$G = 106, 114, 135 \,{\text{kg\,m}}^{ - 2}\, {\text{s}}^{ - 1}$
Reynolds number	Re = 3,500 ÷ 4,950
Input temperature	$t_{\text{ref,i}} = 34.5, 35.4, 38.9$ °C
Steam content	x = 0.99 ÷ 0.09
Tube diameter	$d_{\text{in}} = 6 \,{\text{mm}}$
Number of tubes	$n = 5 \,{\text{pcs}}$
Length of condenser	$z = 3 \,{\text{m}}$

Heat transfer coefficient in the shell side between the secondary fluid and the outer wall of tubes

Determination of the heat transfer coefficient of the secondary fluid flowing in the condenser shell side completely coincides with the calculation Eq. (10) to determine the heat transfer coefficient of the primary (cooled) fluid, as both fluids flow in the shell side of heat exchangers and the physical dimensions of heat exchangers are also completely identical.

Comparison of results

Comparison of two-phase heat transfer correlations with experimental data in the evaporator

Figures 4–7 show the experimental heat transfer coefficient for R134a compared to the heat transfer coefficient evaluated with the correlations of Chen [7], Bertsh [12], Kattan [13], and Kwang [14]. Figure 8 shows the comparison between the new correlations and measured data.

Fig. 4

Comparison of experimental heat transfer coefficient with Chen`s correlation [7]

Fig. 5

Comparison of experimental heat transfer coefficient with Bertsh’s correlation [12]

Fig. 6

Comparison of experimental heat transfer coefficient with Kattan`s correlation [13]

Fig. 7

Comparison of experimental heat transfer coefficient with Kwang`s correlation [14]

Fig. 8

Comparison of experimental heat transfer coefficient with new proposed correlation Eq. (1)

The average discrepancy of calculated and measured values was defined as follows:

$$ \bar{e} = \frac{1}{N} \cdot \sum\nolimits_{i = 1}^{N} {} \frac{{y(i)_{\text{cal}} - y(i)_{\text{exp}} }}{{y(i)_{\text{exp}} }}, $$

(12)

where y_cal is the calculated value, y_exp is experimental value, and N is the number of the data points.

Figure 8 above shows that the maximum discrepancy of the values yielded by the model set up by us is $\varepsilon_{\text{max}} =$ 22.21 % , while the average discrepancy is only $\bar{e} =$ 9.45 %.

The comparison results are shown in Table 2.

Table 2 Comparison of heat transfer coefficients of evaporation based on different correlations

It can be observed that the best values are yielded by the new proposed correlation Eq. (1).

Comparison of two-phase heat transfer correlations with experimental data in the condenser

Comparisons of the experimental data with the predicted heat transfer coefficients are shown in Figs. 9–12. The existing correlations proposed by Akers [11], Shah [15], Tang [16], and Thome [17] are selected for comparison with the experimental data. The comparison of the experimental heat transfer coefficient with the predicted heat transfer coefficients calculated from the new proposed correlation is presented in Fig. 13. Comparisons were made under the following conditions: $G = 106,\,114\;{\text{and}}\,135 \,{\text{kg\,m}}^{ - 2}\, {\text{s}}^{ - 1}$, $t_{\text{ref,c}} = 34.5,\;35.4 \,{\text{and}} \,38.9$ °C, x = 0.09 ÷ 0.99.

Fig. 9

Comparison of experimental heat transfer coefficient with Akers`s correlation [11]

Fig. 10

Comparison of experimental heat transfer coefficient with Shah’s correlation [15]

Fig. 11

Comparison of experimental heat transfer coefficient with Tang`s correlation [16]

Fig. 12

Comparison of experimental heat transfer coefficient with Thome`s correlation [17]

Fig. 13

Comparison of experimental heat transfer coefficient with new proposed correlation Eq. (11)

Figure 13 above shows that the maximum discrepancy—from measurement values—of the values yielded by the correlation as set up by us is $\varepsilon_{\text{max}} =$ 9.34 %, while the average discrepancy is only $\bar{e} =$ 4.15 %. The deviations of the comparisons between the experimental data and predicted values are summarized in Table 3.

Table 3 Comparison of heat transfer coefficients of condensation based on different correlations

Comparison of shell-side heat transfer correlations with experimental data in the condenser

This chapter presents the standard deviation of calculations using correlations by various authors—Kern [18], Bell-Delaware [19], and Taborek [20]—as compared to laboratory measurement results. The following conditions of measurement and simulation were applied:

Volumetric flow of water: $\dot{V} = 1, 1.5 \,{\text{and}} \,2 \,{\text{m}}^{3} {\text{h}}^{ - 1}.$

Temperature of water entering the evaporator: t _w = 13 °C.

Figures 14, 15, 16, and 17 show the results calculated using formulas by various authors.

Fig. 14

Comparison of experimental heat transfer coefficient with Kern`s correlation [18]

Fig. 15

Comparison of experimental heat transfer coefficient with Bell-Delaware`s correlation [19]

Fig. 16

Comparison of experimental heat transfer coefficient with Taborek`s correlation [20]

Fig. 17

Comparison of experimental heat transfer coefficient with new proposed correlation Eq. (10)

Figure 17 shows that the maximum discrepancy of the values yielded by the shell-side heat transfer coefficient established by us is $\varepsilon_{\text{max}} =$6.4 %, while the average discrepancy from measurement values is $\bar{e} =$  2.87 %, representing the best value among the models presented.

Table 4 below provides a summary of discrepancies of heat transfer coefficient values by different correlations from measurement results in the shell side of heat exchangers.

Table 4 Comparison of single-phase heat transfer coefficients in the shell side of heat exchangers

It can be observed that the best values are yielded by the new proposed correlation Eq. (10).

Conclusions

Our study specified more precisely the heat transfer coefficients for shell and tube heat exchangers in the evaporator and condenser of heat pumps on the basis of measurements. The measurements were conducted in various operating points of the heat pump, which formed the basis for the new correlations. Limits of applicability and reliability levels of the new correlations were stated together with the confidence intervals of coefficients in the formulas. The new proposed heat transfer correlations presented in this work describe heat transfer using dimensionless numbers for a refrigerant R134a and within the specified range of Re numbers. In each case, the correlations clearly approximated measurement results at lower error rates than the existing correlations in the literature. Measurements were performed using high-precision instruments. The new heat transfer correlations presented here can be used to model the refrigeration cycle by distributed parameter mathematical models more precisely than before. Thus, the coefficients of performance (COP) of heat pumps can be optimized and heat pump operation economy can be improved.