Introduction

During the last few decades, increased interest has been paid to amorphous chalcogenide semiconductors. The continually rising interest in these materials is caused by their unique physical, optical, and electrical properties that make them ideal materials for numerous hi-tech applications, e.g., switching, electrophotography, infrared optics, or memory devices. Even the archetype of this group of materials, pure amorphous selenium (a-Se), still finds use in a number of modern technologies such as solar cells (as a Se rectifier), xerography (as a photographic toner) or most recently in digital radiology (as a photosensor in HARP technology) [1–4]. Nevertheless, even though the first industry usage of amorphous selenium dates back to the 1960s, certain physical processes vital for these applications are still not fully and satisfactorily explained. Namely, crystallization from the glassy matrix may be a limiting factor for the quality and stability of prepared materials. This is especially true in the case of a-Se, where the thermal degradation of glassy layers or powders begins at very low temperatures (due to the lack of stabilizing dopants, e.g., Ge).

The kinetics of crystallization from glassy matrices is (apart from still rather rare “TA” instrumental techniques, e.g., conductivity measurements or dilatometry) commonly studied by differential thermal analysis (DTA) or differential scanning calorimetry (DSC). However, although the methodology and kinetic calculations for the these techniques have been developed over recent decades, even recent kinetic studies on such a fundamental and often also considered “model” material as amorphous selenium still contain questions and discrepancies. Moreover, no general consensus regarding the values of kinetic parameters has been reached [5–10].

In this study, the advantages of a novel approach in the evaluation of crystallization kinetics, namely the interpretation of characteristic kinetic functions [11, 12], will be introduced. It will be shown that the characteristic kinetic functions contain an extensive amount of so-far neglected information about the complexity of the involved processes. Furthermore, it will be shown that in the case when this approach is applied to a set of samples differing in particle size, the nature of the proceeding crystallization mechanisms can be revealed. As such, the “advanced interpretation approach” then has the potential to serve as a preliminary step for the recently developed modified deconvolution procedure [13].

Theory

Crystallization in glasses (i.e., the process when glass is heated high enough for its structure to be able to “de-freeze” and transform into a thermodynamically stable crystalline phase) is commonly studied by DSC. The kinetic equation of DSC curve can be described [14] as follows:

$$ \Upphi = \Updelta H \, A \, {\text{e}}^{{ - {{\text{E}} \mathord{\left/ {\vphantom {\text{E} {\text{RT}}}} \right. \kern-0pt} {\text{RT}}}}} \, f\left( \alpha \right), $$
(1)

where Φ is the measured heat flow, ΔH is the crystallization enthalpy, A is the pre-exponential factor, E is the apparent activation energy of the process, R is the universal gas constant, T is temperature and f(α) stands for the expression of a kinetic model with α being conversion. The primary objective of kinetic analysis is then to determine all these quantities.

In the first step of kinetic analysis, usually the apparent activation energy E is calculated. There are a number of methods suitable for this task; the most commonly used equations for two basic approaches, isoconversional and non-isoconversional, are listed in [15]. In our work, the original Kissinger method and isoconversional Friedman method are discussed. The Kissinger equation [16] is based on an assumption that the conversion degree α corresponding to the maximum crystallization rate is constant and does not depend on experimental conditions. The apparent activation energy of the crystallization process is proportional to the slope of the dependence of the temperature corresponding to the maximum of the crystallization peak T p (i.e., the point of the maximum conversion rate) on the applied heating rate q +:

$$ \ln \left( {\frac{{T_{\text{p}}^{2} }}{{q^{ + } }}} \right) = - \frac{E}{{RT_{\text{p}} }} + {\text{const}} . $$
(2)

Contrary to the isoconversional methods, which are based solely on an artificially determined conversion degree, the original Kissinger method utilizes the maximum rate of conversion, i.e., a physically driven action independent of most peak-distortion effects [11], which is the main advantage of this method.

The second mentioned evaluation method is that developed by Friedman [17], where the activation energy is calculated for various chosen degrees of conversion and then averaged (usually for the interval of α = 0.3–0.7 where the influence of experimental conditions is minimized, in contrast to the peak tails). The main advantage of isoconversional methods is that a continuous dependence of activation energy on the conversion degree is obtained. Moreover, in the case of complex or overlapping processes, such dependence can suggest/indicate the interval (onset and/or endset) of the actual overlapping. Nevertheless, on the other hand, the discussed isoconversional dependence may also be misleading as it is extremely sensitive to all kinds of deformations and distortions of the evaluated kinetic peaks [11] (produced by, e.g., thermal gradients or inaccurate subtraction of the process background).

In the second step of kinetic analysis, an appropriate kinetic model needs to be determined. Málek [18, 19] introduced a method to test the applicability of various kinetic models to experimental data. The kinetic file data (T–Φ–α) are for non-isothermal conditions transformed according to Eqs. (3) and (4) and displayed as the z(α) or y(α) functions versus α.

$$ y\left( \alpha \right) = \Upphi \cdot {\text{e}}^{{{{\text{E}} \mathord{\left/ {\vphantom {{\text {E}} {RT}}} \right. \kern-0pt} {{\text{RT}}}}}} $$
(3)
$$ z\left( \alpha \right) = \Upphi \cdot T^{2} $$
(4)

In order to determine an appropriate kinetic model from the y(α) and z(α) functions, the conversion rates corresponding to their maxima, α max,y and α max,z , have to be found. Characteristic maxima for several of the most typical kinetic models can be found in Ref. [19]. One of the most widely used kinetic models for the description of crystallization processes in glasses is the nucleation-growth Johnson–Mehl–Avrami model, JMA (m) [20–23]:

$$ f\left( \alpha \right) = m\left( {1 - \alpha } \right)\left[ { - \ln \left( {1 - \alpha } \right)} \right]^{{1 - \left( {{1 \mathord{\left/ {\vphantom {\text{1 m}}} \right. \kern-0pt} {\text{m}}}} \right)}} , $$
(5)

where m is the parameter reflecting the nucleation and crystal growth mechanisms, as well as the crystal morphology. Málek [18] showed that, for the JMA model to be applicable, the α max,z has to be equal to 0.632, which is a characteristic “fingerprint” of the JMA model. In our recent studies, however, it has been shown that the range for α max,z values is relatively large in order for the JMA model to be still applicable and describe data with high precision [11, 12, 24].

The JMA kinetic parameter m can be determined according to one of the two following equations [25, 26]:

$$ m = \frac{1}{{1 + \ln \left( {1 - \alpha_{\hbox{Max} ,y} } \right)}} $$
(6)
$$ \frac{{{\text{d}}\ln \left[ { - \ln \left( {1 - \alpha } \right)} \right]}}{{{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}} = - \frac{m \, E}{R} $$
(7)

In addition, the actual shape of the dependence represented by Eq. 7 may, under certain circumstances, reveal various effects influencing the experimental data or help to identify the source of complexity for the studied process [11]. Advantages and disadvantages of both these methods have been discussed in detail in Ref. [12].

In the last step of enumerating the quantities in Eq. 1, the pre-exponential factor A is determined, e.g., by means of curve-fitting.

Experimental

Selenium glass was prepared by a melt-quenching technique from the pure element. Approximately 10 g of selenium pellets (5 N, Sigma Aldrich) were inserted into a fused silica ampoule; the ampoule was degassed and sealed afterward. The batched ampoule was annealed in a rocking furnace at 650 °C for 24 h and then quenched in water. The amorphous nature of the glass was checked by X-ray diffraction. The prepared glass was ground, and the obtained powder was sieved and distributed according to particle size into the following fractions: 0–20, 20–50, 50–125, 125–180, 180–250, 250–300, and 300–500 μm. In addition, bulk samples were also prepared by cracking a layer of the as-prepared bulk glass right after it was removed from the ampoule. It was shown recently [11] that shape-adjusting operations (grinding, polishing, etc.) may introduce a large number of defects or mechanical strains and stresses into the bulk material, considerably influencing and changing the resulting kinetics compared to that expected for a true untreated bulk glass (this will be further referred to in the Discussion section). Bulk samples were for reasons of comparison assigned the average particle size d aver = 1 mm. Each fraction was studied separately and the kinetic analysis was performed independently.

The crystallization processes in the prepared powder fractions were studied by a conventional DSC 822e differential scanning calorimeter (Mettler, Toledo) equipped with a cooling accessory. Dry nitrogen was used as the purge gas at a rate of 20 cm3 min−1. Temperature, heat flow, and τ-lag calibrations of the calorimeter were performed based on the melting of In, Zn, and Ga. The baseline was checked daily. A thin layer of the powder was always spread on the bottom of the aluminum pans to improve thermal contact, and at the same time to minimize the variety of heat transfer processes (i.e., crucible-to-glass, glass-to-glass, air-to-glass, with the first being the ideal and desired one). By a very careful manipulation of the sealed crucibles during their transfer to the DSC, it was assured that an evenly distributed thin layer of particles was truly measured and no irreproducible thermal gradients were produced by, e.g., cumulating or piling of the powder on the crucible wall. Masses of the powder samples varied from 8 to 10 mg; in the case of bulk samples, the masses were approximately 20 mg.

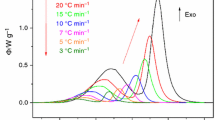
Regarding the applied temperature program, in the case of selenium glass, the crystallization process is jeopardized from both sides. On the low temperature side, the glass transition tends to interfere with crystallization; on the high temperature side, melting of the crystalline phase may overlap with the end of the crystallization peak. The influence of the glass transition in our work was eliminated by the suppression of relaxation effects; the sample was first subjected to a 5 min isotherm at 50 °C, where the material reached the thermal and structural equilibrium state of an undercooled liquid (thus, the entire previous thermal history was erased and the corresponding relaxation effects were eliminated); this short period of time also served as a pre-nucleation step. In the second step, the sample was cooled to 10 °C at rate of 10 K min−1; finally, a heating step to 250 °C was applied. The cooling step was inserted in order for the linear heating rate to be established before reaching the temperatures critical for nucleation and crystal growth even for the highest heating rates. Concerning the intervention of the melting process, in the case of the highest heating rates and coarsest powder fractions, the crystallization peak end-tail started to turn directly into melting, which may slightly affect the ΔH cry value for these samples (the kinetics follow the trend given by lower heating rates and therefore do not seem to be influenced at all). The applied heating rates were 1, 2, 3, 5, 7, 10, 15, 20, and 30 K min−1.

Prior to the evaluation of kinetic analysis, the data corresponding directly to the heat evolved during the crystallization needed to be acquired. As the difference between the undercooled liquid and the crystal heat capacities is not negligible, a simple linear baseline approximation could not be used. In our recent studies [11, 12, 27], where more detailed discussions on this topic were conducted, it was found that spline-type baselines imitate very well with various thermodynamic backgrounds. This was confirmed also for the glass studied within the framework of this article.

Following all the abovementioned procedures and conditions, nearly perfect reproducibility of the experimental data was achieved. This was confirmed when a completely new selenium glass was prepared, similar particle size fractions were made and the entire kinetic analysis was performed once again on this new set of samples; the characteristic kinetic functions as well as the shape of the actual fitted experimental data remained absolutely unchanged.

Results and discussion

The advanced interpretations of characteristic kinetic functions are based on the evolution of these functions with various experimental conditions, most importantly with changing particle size and heating rate. Therefore, this approach is in fact similar to conventional kinetic analysis regarding the mathematical side; what differs is an added derivation of supplemental information resulting from measurements under a specific set of experimental conditions.

This section will be divided into two parts. In the first part, the common procedure of kinetic analysis will be applied to the data, i.e., the activation energy and kinetic model will be determined. In the second part, the advanced interpretation of the characteristic kinetic functions z(α) and y(α) will be applied in order to demonstrate the extent of information accessible by following this approach in the case of a study involving particle size distribution division.

Basic kinetic analysis

In order to evaluate the crystallization kinetics, the apparent activation energy E needs to be determined first. As is mentioned in the Theoretical section, for this reason, a number of methods were derived; in our work, the Kissinger and Friedman methods were employed in this task. The evaluation according to the Kissinger equation (Eq. 2) is for all the studied particle size fractions displayed in Fig. 1. It can be very clearly seen that with increasing particle size, the dependencies gain a convex curvature, i.e., the peak maxima are for high heating rates shifted to temperatures higher than would correspond to the linearity observed for fine powders. This phenomenon usually corresponds to either a change in the crystallization mechanism or a shift resulting from thermal gradients in the sample or DSC cell. As the DSC instrument time constant was properly calibrated, the thermal contacts were maximized (see “Experimental” part). Also, as similar materials (alike chemical structure and thermal properties including thermal conductivity and heat capacity) were measured under similar conditions (same heating rates, similar sample masses) as in our earlier experiments (e.g., [12]) and did not show this curvature, it can be safely assumed that the thermal gradients were eliminated and the dependence curvatures were a true response of the measured material. However, in such cases, a problem arises for the following kinetic analysis, where ideally a uniform value of activation energy needs to be assigned to the studied process. Bearing in mind that an apparent activation energy is being evaluated, a possible solution might be to determine E for each heating rate separately from the slope of the corresponding tangent line. On the other hand, such a solution would not correctly represent the fact that the temperature corresponding to the maximum of the crystallization peak is a very robust value that is invariable under most experimental conditions (thus reflecting the true response of the material), which, in most cases, corresponds to the dominant crystallization mechanism. Therefore, without deeper knowledge of the relationship between the involved mechanisms, we have decided to consider in the first approximation a uniform value of E corresponding to the leading process (in this case, that manifested at low heating rates) over introducing an additional parameter of varying activation energy in the consequent interpretation of the characteristic kinetic functions. This choice is later taken into account during interpretation of kinetic parameters.

Fig. 1
figure 1

Determination of apparent activation energy of the crystallization process according to the Kissinger method for all studied selenium particle size fractions

Full size image

The Kissinger plots depicted in Fig. 1 were used to determine the apparent activation energy E according to Eq. 2. The data corresponding to low heating rates (approx. 1–5 K min−1) were taken for the reasons explained in the previous paragraph. Resulting values of E are depicted in Fig. 2 (circles) as a function of average particle size. Nevertheless, for further comparison, the activation energies corresponding to the high heating rates data (approx. 15–30 K min−1) were also evaluated, shown as squares in Fig. 2. It can be seen that the difference is significant. For the reasons of the kinetic analysis and advanced interpretations, the activation energies determined from low q + data were used—the exact values are also listed in Table 1. On a related topic, the authors would like to remark that in the case of unknown thermal properties of a material or DSC cell, low heating rates should always be used to evaluate the activation energy E due to the unknown possible influence of thermal gradients present at higher heating rates (which was, however, not the case with our data).

Fig. 2
figure 2

Comparison of apparent activation energies determined for glassy selenium according to Kissinger equation in dependence on average particle size in particular fractions. Bulk samples were assigned d aver = 1 mm. Evaluations based on data corresponding to the low/high heating rates are shown as two respective separate dependencies

Full size image
Table 1 Activation energy evaluated by Kissinger method and values of kinetic parameter m JMA determined according to Málek (Eq. 6) and Šesták (Eq. 7) for all particle size fractions of the studied selenium glass
Full size table

In addition to the Kissinger equation, the isoconversional Friedman method was also applied to our data. For the two lowest particle size fractions, the Friedman plots of ln(Φ α ) versus T −1 α were perfectly linear and the determined activation energies agreed within the experimental error with the values obtained from the Kissinger plots. Moreover, the activation energy was perfectly uniform over the entire examined range of conversion degrees α = (0.1–0.9). In the case of coarser powders, all the dependencies corresponding to the particular degrees of conversion α started to show curvatures similar to those observed in the case of the Kissinger plots. However, the dependencies were almost similar for all examined values of α (evaluated energies from both methods would be similar, showing similar dependencies on heating rate). The independence of E on α then means either that the two involved crystallization processes fully overlap over the entire range (the same mean activation energy applies for the entire α range) or that the activation energies of the two mechanism are very close (so that the partial overlapping in a certain range of α still results in a similar activation energy). In addition, the similar curvature observed at high heating rates for all examined degrees of conversion suggests either an influence on the overall crystallization process by an external effect arising from the experimental conditions or a phenomenon resulting from the mutual interaction of the two involved processes. In conclusion, despite the disadvantages of the isoconversional methods mentioned in the Experimental part, there is still valuable information that these methods can provide.

Apart from the determination of activation energy, one more important piece of information can be derived from the Kissinger plot shown in Fig. 1, namely, the answer to the question as to which crystallization mechanism (surface or volume) prevails/dominates in the observed process. Recently, a new method for the estimation of the dominating crystallization mechanism was introduced [11]. This method is based on the very essence of the idea of joint influence of bulk and surface crystallization mechanisms. The influence of the prevailing mechanism drives the crystallization process and takes control over it with moderate amounts of either surface defects or dislocations (in the case of surface crystallization) or bulk nuclei (in the case of volume crystallization). On the other hand, correspondingly, the number of preferred crystallization centers has to be very small in order for the secondary crystallization mechanism to dominate. Therefore, in the extreme cases of either the surface or bulk crystallization mechanism being entirely dominant, the properties of the system tend to “limit” toward the situation with maximal opportunity for this mechanism to manifest itself (fine powders for surface crystallization and bulk glass for volume crystallization). Several criteria were established based on this fact in a paper by Ray and Day [28]. However, as was shown in Refs. [11, 12, 27], our new method utilizes a more robust quantity (temperature of the maximum of the crystallization peak T p) compared to those used by Ray and Day, which in consequence leads to a more reliable estimate of the dominant mechanism.

The determination of the dominant crystallization mechanism is shown in Fig. 3, where T p is depicted in dependence on the logarithm of average particle size for three chosen heating rates. It is obvious that the dependence is not limited to either of the two extreme cases; hence, the manifestation of both crystallization mechanisms is of considerable importance. Nevertheless, as can be seen, a small plateau is created around the 180–250, 250–300, and 300–500 μm particle size fractions. In our opinion, the plateau corresponds to the optimum ratio between the two processes (and, by implication, also an optimum ratio between the numbers of the respective crystallization centers, whether surface defects and volume nuclei), for which the averaged manifestation is maximum and most reproducible. Similar conclusions can also be derived following the criteria of Ray and Day.

Fig. 3
figure 3

Normalized crystallization mechanism plot constructed to determine the dominating crystallization mechanism. Results for three chosen heating rates are displayed, see text for details

Full size image

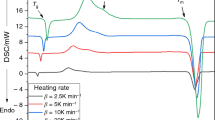
In a continuation of the evaluation of crystallization kinetics, the proper reaction model needs to be determined. As was mentioned in the Theoretical section, the characteristic kinetic functions introduced by Málek [18] will be employed in this task. In Fig. 4, the normalized characteristic kinetic functions z(α) and y(α) are depicted for several chosen particle size fractions, and the curves corresponding to all applied heating rates are always shown. A complete set of the kinetic functions graphs for all studied particle size fractions can be found in Supplementary Appendix 1. For the kinetic model to be determined, the value of the degree of conversion corresponding to the maximum of the z(α) function is critical. Values of α max,z characteristic for the most typical kinetic models can be found in Ref. [19]: Málek showed that for the most common kinetic model—Johnson–Mehl–Avrami (JMA)—to be applicable, the α max,z has to be equal to 0.632, which is a characteristic “fingerprint” of the JMA model. Nonetheless, it was shown [11, 12] that, in certain cases, the JMA model can provide a very good description of the experimental data even when the α max,z value is outside the limits of 0.62–0.64 originally suggested by Málek. Looking at the graphs in Fig. 4 and Supplementary Appendix 1, it is apparent that the maxima of all z(α) functions are very close to the value α max,z = 0.632, suggesting the applicability of the JMA model.

Fig. 4
figure 4

Normalized y(α) and z(α) functions corresponding to non-isothermal measurements of chosen particle size fractions of the selenium glass. Particular rows match the individual studied fractions

Full size image

The JMA model parameter m can then be easily determined following one of the two procedures introduced in the Theory section, i.e., Eqs. 6 and 7. The results of both evaluation types are listed in Table 1. A relatively good agreement was found for the m JMA values provided by the two employed methods; details on the advantages and disadvantages of these evaluation methods can be found in Refs. [11, 12]. For a single process, the values of the kinetic parameter m JMA can be associated with crystal morphology; information about the eventual proceeding nucleation can be also deduced. Nevertheless, in the case of a complex crystallization process, the m JMA values should not be overrated as significant distortions of the crystallization peak as well as shifts in the α max,y value usually occur. This inconvenience may be overcome by employing the novel approach of interpretation of the kinetic functions z(α) and y(α).

Advanced interpretation of characteristic kinetic functions

Apart from the determination of an appropriate kinetic model, the characteristic kinetic functions are, however, still a source of a large amount of supplemental information. This information is then accessible by the so-called advanced interpretation approach which, as a matter of fact, stands for interpretations of the changing shape of the functions calculated for measurements performed under various experimental conditions. In our previous studies, it was shown that a change in the studied material grain size together with a change in the heating rate provides a very suitable combination of factors allowing a number of interesting effects and dependencies to be recognized.

The first aspect to consider is the reproducibility of the characteristic kinetic functions within the framework of each particle size fraction with respect to the changing heating rate. The changing shape of the z(α) function or the position of α max,z is generally undesirable and may be associated with either a change in the kinetic model or a pronounced influence of thermal gradients and lagging. In the case of a significant change in the kinetic model with heating rate, an overlapping of two mutually interacting unrelated processes is the most probable option; nevertheless, this interaction will also manifest in a change in the y(α) function shape, which can make subsequent conclusions regarding the change in the process mechanism unreliable. Similarly, the influence of thermal gradients may distort the crystallization peaks and make the kinetic analysis provide incorrect and biased results. In the case of significant thermal gradients being present, identification of their origin is crucial for either their elimination or accounting for them in at least a qualitative interpretation of the kinetics. In any case, both of the abovementioned situations should be recognized and carefully accounted for in subsequent interpretations or process separations. In the case of the data obtained for a-Se studied in our work, it can be seen that all the z(α) functions are perfectly consistent for each particle size fraction, with the only exception being an occasional slight shift in the curve corresponding to the highest heating rates, where some small distortions due to insufficient thermal contact or transport are acceptable.

On the other hand, the inconsistency of the shape of the y(α) function with heating rate for a single studied fraction is not unusual and provides information about the overall crystallization mechanism change due to differing representation intensity of overlapping crystallization processes/mechanisms as a consequence of different values of their apparent activation energy E and pre-exponential factor A. With regard to the data shown in this article, it can be seen that for the 0–20 μm and bulk fractions, the shape of the y(α) function is relatively consistent, which implies strong domination of a single crystallization mechanism (surface crystallization in the case of the 0–20 μm fraction, volume crystallization in the case of the bulk sample). On the other hand, in the case of all other studied fractions, the curves systematically change with heating rate, indicating a significant representation of both discussed mechanisms.

In the second considered aspect of advanced interpretations of characteristic kinetic functions, the variability of the y(α) function with particle size is explored. For this reason, the values of α max,y and α max,z can either be plotted in dependence on average particle size or a combined kinetic plot similar to that shown in Fig. 5 can be created. In Fig. 5, it can be clearly seen that the “averaged” overall mechanism shifts with particle size toward higher values of α max,y, i.e., the crystallization dimensionality increases. This again corresponds with the concept of surface crystallization being dominant for fine powders (a large portion of the material includes surface defects and crystallization centers typical for surface crystallization) and volume crystallization manifests dominantly in case of coarse powders, where the major part of the glass grain is in the bulk form with minimal mechanical defects or stresses being present. One exception from this generally assumed concept is the data for the finest particle size fraction (0–20 μm) that shows slightly higher dimensionality than corresponds to the other fine powders. A similar observation was, however, made in our earlier work for the Se70Te30 glass, where this phenomenon was explained on the basis of steric restrictions forcing the individual crystallites to grow throughout the entire grain, hence showing virtually higher dimensionality [11]. In addition, it is further apparent from the figure that all data including their error bars lie in close vicinity to the original narrow JMA model applicability interval suggested by Málek, i.e., the Johnson–Mehl–Avrami model should provide a reasonable description of the crystallization data.

Fig. 5
figure 5

So called “kinetic plot” evaluated for the selenium glass. Theoretical applicability of the JMA model as suggested by Málek [18] is displayed. The solid curve guides eyes in direction of the increasing particle sizes in particular fractions

Full size image

Within the framework of the third, most important considered aspect, the overall trends in crystallization responses are identified and the involved mechanisms are qualitatively described for the complex crystallization process. Based on the y(α) and z(α) functions shown in Supplementary Appendix 1, the following interpretations can be made. In the case of amorphous selenium, both basic crystallization mechanisms—surface and bulk—are significantly represented in the overall devitrification transformation. Their proportion is driven by the initial ratio between the numbers of crystallization centers corresponding to the particular mechanisms. In case of the finest fraction (0–20 μm), there are no signs of the bulk crystallization mechanism being present, and the glass grains are so small that the entire particle is composed of a material containing a high number of mechanical defects, which are in addition subjected to large amounts of strain and stress. This type of mixed “surface” crystallization behavior in addition seems to lead to the typical rounded shape of the z(α) function (similar behavior was observed for Ge2Sb2Se5 glass [27]). For all the other particle size fractions, there is the apparent simultaneous presence of the bulk crystallization process, the manifestation of which increases with increasing particle size (higher amounts of true “bulk” material containing nuclei). It is further apparent that the heating rate plays a crucial role in the relative representation of the two proceeding types of crystallization—for low heating rates, the bulk crystallization mechanism is more pronounced and vice versa. In order to explain this phenomenon, the difference in activation energies of the two involved processes will be employed.

It is apparent from Fig. 1 that surface crystallization appears to have slightly but still significantly higher activation energy than the bulk process. In addition, the three-dimensional kinetics are axiomatically slower and can be further decelerated, for example due to steric reasons. As can be seen in Fig. 4, the first process that corresponds to the earliest heat evolution is always surface crystallization. Therefore, during rapid heating, the starting primary surface crystallization mechanism takes control over the larger partition of the complex crystallization process (with more than enough energy being provided by the faster heating and thermal gradients causing the entire process to be allocated to higher temperatures), while the slower bulk mechanism does not have enough time to fully develop (in accordance with the concept of competing processes). Correspondingly, at low heating rates, it is the difference in activation energies that determines the outcome. Although it is still surface crystallization that initiates complex crystallization, the energy input (caused by the factual temperature increase plus the heat evolved during crystallization) is relatively low and an actual competition based on the difference in energy barriers (represented by the apparent activation energy E A) takes place, causing the bulk process to be more pronounced while “consuming” a larger part of the provided energy.

Furthermore, information about the relative position of the peaks representing the respective involved processes can be extracted from the shape of the y(α) function. In particular, it is the dominant crystallization mechanism with respect to the degree of conversion α which is identified. This effect is most apparent for the 30 K min−1 heating rate and coarse powders, where independence of the surface and bulk crystallization processes can be assumed. In such cases, even partial separation of the two processes (with respect to their mutual position on the temperature axis) results in a characteristic shape of the y(α) function. This characteristic shape is caused by and corresponds to the extent of separation rather than the ratio between the actual intensities of the processes. Nonetheless, it has to be borne in mind that this characteristic shape corresponding to partially separated/shifted processes appears only when the mechanisms significantly differ in their kinetics. The opposite case (only partially overlapping peaks of comparable areas but corresponding to processes with very similar kinetics) is seen in our data represented by the two finest powder fractions, 0–20 and 20–50 μm. This information can be, however, obtained only once deconvolution is performed, i.e., it was not derived by means of advanced interpretation of the characteristic kinetic functions.

In the final step of kinetic analysis performed within the advanced z(α) and y(α) interpretation approach, the experimental data were fitted by the JMA model. The fit was performed in a standard way, as if a single process reaction was treated; the fitted data for all studied particle size fractions and applied heating rates can be found in Supplementary Appendix 2. As can be seen, in cases when both mechanisms manifest significantly without mutual interaction of their kinetics (higher heating rates of fine and medium-sized powders), the JMA fit is very poor even though the maxima of the z(α) function may be close to the theoretical value of 0.632. This important finding has several implications: for a true verification of JMA model applicability, it is not only the value of α max,z that counts, but the actual shape of the characteristic kinetic functions (reflecting the shape of the crystallization peak) is also very important; on the contrary, the inability of the JMA model to provide an accurate description even though α max,z ~0.632 may for the studied process suggest a specific type of complexity appearing in this case. In addition, the quality of the “single process JMA fit” may in this situation give at least approximate information about the magnitude of deviation from ideality and, consequently, suggest important input parameters for the eventual deconvolution procedure.

Conclusions

Crystallization kinetics in amorphous selenium were studied under non-isothermal conditions using DSC. Concerning the basic kinetic information, an extensive investigation of the influence of particle size on apparent activation energy was made. For the purposes of interpreting the influence of sample form, both thermal gradients and the effect of grinding procedures were considered. A recently developed criterion for a quick determination of the dominating crystallization mechanism—surface or bulk—was introduced. The complete kinetic analysis was performed in terms of the Johnson–Mehl–Avrami model. The complexity of the competing surface and bulk mechanisms was explained. The obtained DSC data allowed an explanation of the mutual interaction of the processes as well as of the origin of their sequentiality. A discussion of the observed effects, shifts in temperature and deviations from ideal model behavior was conducted on the basis of thermal gradients, surface crystallization centers arising from sample preparation and the amount of volume nuclei originating from the combination of the pre-nucleation period and the actual glass preparation phase.

The main aim of the study was to demonstrate the current level of information obtainable by one of the recently developed approaches to crystallization kinetics—the advanced interpretation of characteristic kinetic functions z(α) and y(α). It was shown that by employing the introduced approach, a very good picture of crystallization kinetics in a given material can be obtained, even in the case of complex overlapping processes.