Introduction

In the past, several significant explosion incidents in Taiwanese industries have been related to the thermal instability of organic peroxides (OPs). OPs, having the peroxy oxygen bond (–O–O–), can easily be broken down due to their highly active characteristics. OPs also react with external materials, such as may be kept nearby in storage facilities, in various ways resulting in large discharges of energy [1–5]. Di-tert-butyl peroxide (DTBP) is one commonly used industrial OP, widely employed as a radical initiator for polymerization, as a source for alkoxyl radicals, as a hardener, as a linking agent, and as a fuel combustion additive or used in reforming operations. Because of this variety of uses, it is necessary to understand the various potential exothermic reactions of DTBP. Due to its reactivity and instability, the National Fire Protection Association (NFPA) of USA has recognized DTBP as one of its class III OPs [6, 7].

In this study, the initial stage was to acquire fundamental thermokinetic data and the essential safety parameters of DTBP by differential scanning calorimetry (DSC) and vent sizing package 2 (VSP2). The second stage was to employ that data, specifically the onset temperature of reaction (T o), heat of decomposition reaction (ΔH d), activation energy (E a), maximum temperature of reaction (T p ), maximum increase in temperature ((dT dt −1)max), and maximum increase in pressure ((dP dt −1)max), to evaluate the thermokinetic parameters of the decomposition reactions of DTBP. Measuring the thermal parameters can be employed by using experimental methods involving isothermal reaction temperature varying removal heat, and the reaction temperature and heat change throughout the reaction time [8–11]. The third stage was to evaluate the critical temperature of DTBP through numerical simulation according to Semenov’s thermal explosion theory [12–15]. Finally, we tried to clearly identify the criterion of critical temperature incurred by the gassy system containing DTBP during undesirable situations.

Experimental setup

Experimental samples

Ninety-eight mass% of DTBP was purchased from Aldrich Co., and then stored in a refrigerator at 4 °C. Its density was 0.796 g cm−3. Furthermore, 25 mass% of DTBP was prepared in toluene solution for use in our VSP2 experiments.

Experimental apparatus and procedures

DSC

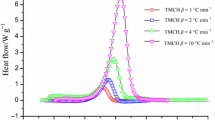
The DSC is considered as an useful tool for evaluating thermal hazards and investigating decomposition heat of reactive chemicals. Non-isothermal programmed screening experiments were performed on a Mettler TA8000 system DSC 821e apparatus. Each sample was put into a high pressure gold-plated crucible (ME-26732), which was then manually brought to a hermetic seal by use of a special tool equipped with the Mettler DSC and could withstand a high pressure, up to 15 MPa. STARe software was used to acquire thermal curves and to assess the thermokinetics [16, 17]. The heating rates chosen for the temperature-programmed ramps were 1, 4, 6, and 10 °C min−1 from 30 to 300 °C to give the reaction processes better thermal equilibrium. In each case, a 4–8 mg test sample of DTBP was prepared.

VSP2

The VSP2, a PC-controlled adiabatic calorimeter manufactured by Fauske & Associates, Inc., was used to obtain thermokinetic and thermal hazard data for DTBP, such as temperature and pressure traces versus time. The heat-wait-search (H-W-S) method for detecting the self-heating rate was employed. If the self-heating rate was greater than 0.1 °C min−1, the H-W-S and main heater would be immediately terminated to measure the phenomenon of self-exothermicity. The low heat capacity of the cell ensured that any reaction heat released remained within the tested sample. Thermokinetic data and pressure behavior in the same test cell (112 mL) could usually be tested without any difficult extrapolation to the process scale due to the low phi factor (Φ) of about 1.05–1.32. This low Φ allows for bench-scale simulation of worst-case scenarios, such as incorrect dosing, cooling failure, or external fire conditions [18, 19].

Results and discussion

Thermal decomposition analysis of DTBP by DSC

Table 1 summarizes the thermokinetic data from the DSC STARe program for runaway assessment. The thermal curve of the DSC tests is also shown in Fig. 1 and the decomposition data is listed in Table 1. According to various heating rates, the decomposition temperature of DTBP began at about 98–109 °C, and the overall released heat (△H total) is ca. 1,100 J g−1.

Table 1 Thermal decomposition data for DTBP at various heating rates by DSC
Full size table
Fig. 1
figure 1

Thermal decomposition of DTBP at various heating rates by DSC

Full size image

Adiabatic analysis of DTBP by VSP2

The VSP2 is capable of showing temperature and pressure rise under adiabatic conditions. The VSP2 test of DTBP is shown in Fig. 2, where the maximal temperature (T p ) and pressure (P max) were 302 °C and 59.8 bar, respectively.

Fig. 2
figure 2

Measured transitional temperature and pressure of the decomposition reaction of 25 mass% DTBP by means of VSP2

Full size image

Evaluation of thermokinetic parameters

Several important numerical assumptions were employed to derive the thermokinetic parameters of an exothermic reaction from experimental data on the rate of self-heating under adiabatic conditions:

  1. (1)

    The reaction mechanism was assumed to be independent of temperature, which allowed the temperature and concentration dependencies to be dealt separately. The total heat generated was considered to be directly from the adiabatic temperature increase, assuming constant heat capacity.

  2. (2)

    Heat generated in the reaction vessel was assumed to correspond to changes in concentration, such that the rate of change of concentration and the rate of heat generation are directly proportional to the rate of temperature increase under adiabatic conditions, where the extent of the reaction equals the temperature increase expressed as a fraction of the total adiabatic temperature increase. The temperature dependence of the reaction rate constant was assumed to obey the Arrhenius equation.

  3. (3)

    The dependence of reaction rate on concentration was represented by first order reactions with fractional values applied such that complex mechanisms can be represented by simple overall kinetic expressions.

In an adiabatic reaction system, the fractional conversion (X A ) and reaction temperature (T) at any reaction time (t) can be correlated with the assumption of constant specific heat capacity by the ratio value of △H t to △H total from initiation to end as follows:

$$ X_{A} = \Updelta H_{\text{t}} /\Updelta H_{\text{total}} = [mC_{p} (T - T_{\text{o}} )]/[mC_{p} (T_{p} - T_{\text{o}} )] = (T - T_{\text{o}} )/(T_{p} - T_{\text{o}} ), $$
(1)

where T o and T p are the initial and maximal temperatures for the overall decomposition reaction of DTBP, respectively. ∆H t and ∆H total are the heat of reaction at temperature T and T p , respectively.

Reaction concentration can be correlated as follows:

$$ C = C_{0} (1 - X_{A} ) = C_{0} (T_{p} - T)/(T_{p} - T_{o} ) = C_{0} (T_{p} - T)/\Updelta T_{p} , $$
(2)

where C 0 is the initial concentration, C is the concentration at any time t, and ΔT p equals T p  − T o.

An nth-order rate equation of decomposition reaction for DTBP can be expressed as:

$$ - r_{\text{b}} = - {\text{d}}C/{\text{d}}t = kC^{n} . $$
(3)

Substituting Eq. 2 into Eq. 3 and combining with the Arrhenius equation yields

$$ k^{*} = C_{0}^{n - 1} A{ \exp }\left( { - E_{\text{a}} /RT} \right) = ({\text{d}}T/{\text{d}}t)/\left[ {(T_{p} - T)/\Updelta T_{p} } \right]^{n} \Updelta T_{p} . $$
(4)

Taking the natural logarithms on both sides of Eq. 4 gives the following:

$$ {\text{ln}}k^{ * } = { \ln }\left\{ {({\text{d}}T/{\text{d}}t)/\left[ {(T_{p} - T)/\Updelta T_{p} } \right]^{n} \Updelta T_{p} } \right\} = { \ln }(C_{0}^{n - 1} A) - E_{\text{a}} /RT, $$
(5)

where dT dt −1 is the rate of temperature increase between the onset temperature (T o) and the maximum temperature (T p ) in an adiabatic reaction system. The Arrhenius kinetic parameters for the overall reaction can thenceforth be determined from Eq. 5.

Heat evolved during the VSP2 experiment was absorbed by the sample and sample container. This would be expected to the adiabatic temperature increase and the rate of temperature increase, and must be taken into account during data analysis. The Φ (Phi) factor, or thermal inertia, is defined as Φ = 1 + M b C p,b /M s C p,s, where M b, M s, and C p represent the mass of the container, the mass of the sample, and the heat capacity of the sample. The Φ value was used to adjust the self-heating rate as well as the observed adiabatic temperature increase. Further, the initial data obtained by H-W-S processes were experimentally and mathematically insignificant, and were therefore excluded in the derivation of the kinetic parameters. The data from runaway conditions were also excluded due to the instability of the reaction system.

Substituting the modified experimental data from VSP2 into Eq. 5 and assuming n = 1, we can plot lnk versus −1,000 T −1 and derive truly significant linear correlations, as illustrated in Fig. 3. As such, the assumption of n = 1 for reaction order is reasonable. The activation energy (E a) and pre-exponential factor (A) of the Arrhenius equation can be obtained from the slope and intersection of the line at the vertical axis. In this way, the measured and evaluated thermokinetic parameters of decomposition reactions for DTBP were acquired.

Fig. 3
figure 3

lnk* versus 1,000 T−1 for reactive rate prediction of 25 mass% DTBP at n = 1

Full size image

Stability criteria and critical runaway temperature for the decomposition reaction of DTBP

Semenov model assumes an uniform temperature distribution within the reaction system. This assumption is very close to the case of a homogeneous system in a container [20]. The general formula for heat generation rate due to volume of reactant (V) is expressed as:

$$ q_{\text{g}} = qV( - r_{\text{b}} ), $$
(6)

where q is exothermic heat of reaction (q) and chemical reaction rate is −r b. Expressing the reaction rate by Arrhenius’ method and substituting it into Eq. 6, the heat generation rate can be expressed as:

$$ q_{\text{g}} = qVAC^{n} { \exp }( - E_{\text{a}} /RT). $$
(7)

Similarly, the heat removal rate from the reaction container to the ambient cooling medium is expressed as:

$$ q_{\text{r}} = hS(T - T_{\text{a}} ), $$
(8)

where the overall heat transfer coefficient of the ambient medium is h, and the external surface area of the container is S. T and T a are the temperatures inside the reaction container and of the ambient medium under cooling system, respectively.

The overall energy balance in the control sample volume is that the rate of heat accumulation is equivalent to the rate of heat generation minus the rate of heat removal:

$$ \rho VC_{P} ({\text{d}}T/{\text{d}}t) = q_{\text{g}} - q_{\text{r}} . $$
(9)

The first term on the right-hand side, q g, represents the heat generation rate for an exothermic reaction and the second term, q r, is the heat removal rate from this reaction system. Inserting Eqs. 7 and 8 into Eq. 9, the overall energy balance can be expressed as:

$$ \rho VC_{P} ({\text{d}}T/{\text{d}}t) = qV{\text{A}}C^{n} { \exp }( - E_{\text{a}} /RT) - hS(T - T_{\text{a}} ). $$
(10)

As mentioned above, it is assumed that the overall reaction order of a decomposition reaction of DTBP, n, is tantamount to unity. Thus, substituting Eq. 2 into Eq. 10 with n = 1, this process can be rewritten as:

$$ \rho VC_{P} ({\text{d}}T/{\text{d}}t) = qVAC_{0} [(T_{p} - T)/(T_{p} - T_{\text{o}} )]{ \exp }( - E_{\text{a}} /RT) - hS(T - T_{\text{a}} ). $$
(11)

Under a steady state, i.e., (dT/dt) = 0, Semenov’s sufficient and necessary conditions for a “critical situation of the reaction system” are

$$ q_{\text{g}} \left| {_{{T = T_{\text{c}} }} } \right. = q_{\text{r}} \left| {_{{T = T_{\text{c}} }} } \right. $$
(12)

and

$$ \left. {{\frac{{{\text{d}}q_{\text{g}} }}{{{\text{d}}T}}}} \right|_{{T = T_{\text{c}} }} = \left. {{\frac{{{\text{d}}q_{\text{r}} }}{{{\text{d}}T}}}} \right|_{{T = T_{\text{c}} }} . $$
(13)

Equation 11 also denotes the reaction system under the conditions of a steady state, i.e., (dT/dt) = 0, when the rate of heat generation of the system is equal to the rate of heat removal. If q g is greater than q r, then (dT/dt) > 0. In such a situation, heat accumulation can lead to runaway reactions. Equation 11 can also be written as:

$$ qVAC_{0} [(T_{{_{p} }} - T_{\text{c}} )/(T_{{_{p} }} - T_{\text{o}} )]{ \exp }( - E_{\text{a}} /RT_{\text{c}} ) = hS(T_{\text{c}} - T_{\text{a}} ). $$
(14)

Applying the conditions of Eqs. 12 and 13 gives:

$$ {\frac{{qVAC_{0} { \exp }( - E_{\text{a}} /RT_{\text{c}} )[ - 1 + E_{\text{a}} (T_{p} - T_{\text{c}} )/RT_{\text{c}}^{2} ]}}{{(T_{p} - T_{\text{o}} )}}} = hS. $$
(15)

After dividing Eq. 14 by 15, and some rearranging, the temperature in the reaction system can be acquired by Eq. 16:

$$ {\frac{{E_{\text{a}} }}{{RT_{\text{c}}^{2} }}} = {\frac{1}{{(T_{\text{c}} - T_{\text{a}} )}}} + {\frac{1}{{(T_{p} - T_{\text{c}} )}}}. $$
(16)

Critical temperature (T c) can be solved as:

$$ T_{\text{c}} = {\frac{{(T_{p} + T_{\text{a}} ) \pm \sqrt {(T_{p} + T_{\text{a}} )^{2} - 4[1 + R(T_{p} - T_{\text{a}} )/E_{\text{a}} ]T_{p} T_{\text{a}} } }}{{2[1 + R(T_{p} - T_{\text{a}} )/E_{\text{a}} ]}}}. $$
(17)

Equation 17 indicates that the critical temperature (T c) is a function of the activation energy (E a), the ambient temperature under cooling system (T a), and the maximum temperature of reaction (T p ) under adiabatic conditions. Figure 4 shows an example of calculating critical temperatures for the decomposition of DTBP. T a was set at 363.15 K and the values of E a were listed, respectively. Two critical temperature points of T c can be obtained from the diagram of heat generation rate and theoretical critical heat removal rate versus temperature. One was the critical extinction temperature T CE = 442.13 K and the other was the critical ignition temperature T CI = 373.63 K, which were calculated from Eq. 17. Substituting these two values of T c into Eq. 15, the values of hS can be obtained, which were the overall heat transfer coefficient multiplied by the external surface of the container. The calculated values of hS from this equation were equal to 13.38 and 1.086 kJ min−1 K−1, which correspond to T CE and T CI, respectively. By substituting the values of hS into Eq. 14 and iterating, one can obtain another set of temperatures, denoted as T SE and T SI. These T SE and T SI values were the intersection points of the curve q g with curves q r1 and q r3 instead of tangent points, respectively. These two points, T SE and T SI, can also be obtained graphically from the intersection points of q g and q r when the values of hS are equal to 13.38 and 1.086 kJ min−1 K−1, individually.

Fig. 4
figure 4

Balance diagram of heat generation rate q g, and heat removal rate q r, for the decomposition reaction of DTBP

Full size image

We found that the value of T SI was 457.27 K and the value of T SE was 363.46 K in this case. As hS = 13.38 kJ min−1 K−1 and the temperature in the reaction system was greater than 442.13 K, i.e., T > T CE, the heat removal rate q r1 was greater than the heat generation rate q g. Therefore, the temperature in the reaction system decreases continually and moves toward point T CE. Finally, it ceases at this point, when the temperature in the reaction system was in the range of T SE < T < T CE. Similarly, the heat removal rate q r1 was again greater than the heat generation rate q g. As such, the temperature of the reaction system approached and terminated at point T SE. When the reaction system temperature was lower than T SE, the heat removal rate q r1 became less than the heat generation rate q g. As a result, the temperature of the reaction system increases and goes back to point T SE at the end. Points T CE and T SE were the critical extinction temperature and the final stable extinction temperature, respectively. These two points also represent the temperature that never increased and the temperature that never decreased at hS = 13.38 kJ min−1 K−1, respectively.

Equations 15 and 17 gave values of T CI and hS equal to 373.63 K and 1.086 kJ min−1 K−1, respectively. The intersection point of curves q g and q r3 at this calculation was T SI = 457.27 K. When the temperature in the reaction system was less than 373.63 K, i.e., T < T CI, the heat removal rate q r3, was less than the heat generation rate q g. From this we can see that the temperature in the reaction system increases and moves toward T CI. When the temperature of the reaction system was in the range of T CI < T < T SI, the heat removal rate q r3, was again lower than the heat generation rate q g, which leads us to see the temperature of the reaction system increasing from point T CI moving toward to point T SI. Once the temperature was greater than T SI, the heat removal rate q r3 was higher than the heat generation rate q g, which leads us to the temperature of the reaction system moving back to point T SI. Points T CI and T SI were the critical ignition temperature and the final stable ignition temperature, respectively. These two points also represent the temperature that never decreased and the temperature of no return at hS = 1.086 kJ min−1 K−1, respectively. When the value of hS is located in the range of 1.086 < hS < 13.38 kJ min−1 K−1, three intersection points can be obtained between curves q r2 and q g. These three points, denoted as T SL, T M, and T SH, individually represent the steady-state temperatures at the low, intermediate, and high points. The curve q r2 is shown as a dashed line.

As in previous analysis, it was difficult to arrive at the intermediate point T M because of the instability of this point during chemical reaction. We assumed that it was appropriate to start this reaction system exactly at the temperature T M; in this way, if some tiny perturbation in the operating conditions was to take the reaction system away from its steady state, it would not move back to T M but rather would finish up either at the low or the high temperature in a steady state, either T SL or T SH, respectively. Thus, a slight increase in temperature would produce a net heat generation that could boost the temperature even higher and conversely a minute drop in temperature would induce a net heat removal, which would cause the temperature to fall even further. In this case, the intermediate steady-state temperature T M was unstable. By contrast, the steady-state temperatures T SL and T SH were stable, such that if the situation were perturbed in any way, it would return there naturally.

Figure 5 shows the correlation of evaluated temperatures T CI, T CE, T SI, and T SE versus ambient temperature T a using the above calculation technique for the decomposition reactions of DTBP. These temperatures were in the order T SI > T CE > T CI > T SE. Both T SI and T CE decreased, and both T CI and T SE rose gradually with increasing T a. As soon as the ambient temperature T a increased to the transitional point T a(tp), all four of these temperature curves coincide at a transitional point, T c(tp). The temperatures of this transitional point can be deduced from the following equations:

$$ T_{\text{a(tp)}} = {\frac{{E_{\text{a}} T_{p} }}{{(E_{\text{a}} + 4RT_{p} )}}} $$
(18)

and

$$ T_{\text{c(tp)}} = {\frac{{E_{\text{a}} T_{p} }}{{(E_{\text{a}} + 2RT_{p} )}}}. $$
(19)
Fig. 5
figure 5

Correlation of evaluated temperatures T CI, T CE, T SI, and T SE versus T a and the temperature of transitional point for the decomposition reaction of DTBP

Full size image

With respect to the criteria for stability or instability in a reaction system, the heat generation and removal diagrams do not permit us to conclude stability when

$$ {\frac{{{\text{d}}q_{\text{g}} }}{{{\text{d}}T}}} < {\frac{{{\text{d}}q_{\text{r}} }}{{{\text{d}}T}}}. $$
(20)

This equation is necessary, but by itself is not sufficient condition for stability. Even still, it does allow us to validate that the state will be unstable when

$$ {\frac{{{\text{d}}q_{\text{g}} }}{{{\text{d}}T}}} > {\frac{{{\text{d}}q_{\text{r}} }}{{{\text{d}}T}}}. $$
(21)

If T s is defined as a stable temperature in a reaction system at the state of q g = q r and a small temperature perturbation as δT = T − T S in this state, the reaction system is stable under the following conditions:

$$ {\rm if}\; \delta T > 0,\,q_{\text{g}} < q_{\text{r}} {\rm or}\;{\rm if} \delta T < 0,\,q_{\text{g}} > q_{\text{r}} . $$
(22)

Equation 22 gives both the sufficient and necessary conditions for a stable reaction system. This criterion for stability has been evaluated by Lu et al. [21, 22].

From the above definitions and energy–mass balance equations, the stable and unstable criteria of DTBP decomposition reactions can be determined. As long as the temperature of the reaction system occurred over the curve for T SI or under the curve for T SE, the system was stable: the temperature in the reaction system would return to either of these two curves eventually. When the reaction temperature fell between the curves for T CI and T CE, the system was unstable. Furthermore, there were two stable areas, T SL and T SH, located between two narrow areas, where T SE < T SL < T CI and T CE < T SH < T SI, respectively. As the value of T a increased, the values for the T SI and T CE temperature curves decreased, but the values for the T CI and T SE temperature curves increased at the same time. Thus, when the value of T a increases, these four temperature curves move closer and closer. As soon as the value of T a exceeded 407.92 K, the phenomenon of criticality vanished. These temperature curves coincide with the transitional point. Here, the value of transitional point T c(tp) was 431.40 K.

The required values for hS at critical runaway and stable temperatures could be evaluated by using either Eq. 14 or 15 after the value of T c was determined from Eq. 17. The calculated result of T a versus hS at the critical runaway and stable temperatures for the decomposition reaction of DTBP s is shown in Fig. 6, where we see a boomerang-shaped area. The solid curve of hS signifies the critical extinction temperature, T CE, and the final stable extinction temperature, T SE, while the other solid curve with dot points inside denotes the curve of hS at critical ignition temperature, T CI, and the final stable ignition temperature, T SI. Between these two curves is a boomerang-shaped area which contains one unstable temperature, T M, and two stable temperatures, T SL and T SH (Fig. 7). When the temperatures T CE, T SE, T CI, and T SI were equivalent, the value of hS is expressed as hS (tp). The value of hS (tp) was equal to 32.66 kJ min−1 K−1. The values of hS (tp) can be calculated by a rearrangement Eq. 15, which was obtained by combining Eqs. 18 and 19.

$$ hS_{{({\text{tp}})}} = {\frac{{qVAC_{0} (1 + 4RT_{p} /E_{\text{a}} ){ \exp }[ - (2 + E_{\text{a}} /RT_{p} )]}}{{(T_{p} - T_{\text{o}} )}}}. $$
(23)
Fig. 6
figure 6

Relationship between T a and hS at critical ignition and extinction temperatures for the decomposition reaction of DTBP

Full size image
Fig. 7
figure 7

Correlation of evaluated temperatures T CI, T CE versus T a and hS for the decomposition reaction of DTBP

Full size image

Above this boomerang-shaped area in the diagram, the area contains the temperatures T SL and T SH, which were distributed both above and below this zone. From this diagram, we see that the required value of hS in the decomposition reaction of DTBP was strongly affected by variation of T a. Once the value of T a was gathered, the value of T CI, T CE, and hS could all be estimated from the reaction thermokinetic parameters and Eqs. 15–17 mentioned before (Fig. 8).

Fig. 8
figure 8

Correlation of evaluated temperatures T c versus T s and hS for the decomposition reaction of DTBP

Full size image

Conclusions

The heat of the decomposition reaction of 98 mass% DTBP was approximately 1,100 J g−1, as measured by DSC. The thermokinetic parameters of the decomposition reaction, listed in Table 2, were determined from the experimental result of VSP2. The unstable temperature area of the decomposition reaction of DTBP was shown to be enclosed by the curves T CI/T SI and T CE/T SE in Fig. 6. With the exception of this unstable area, the reaction system was otherwise stable.

Table 2 Thermokinetic parameters of 25 mass% DTBP by VSP2
Full size table