1 Introduction

Recent interests are focused on the topic on basic results related to affine functions on Riemannian manifolds; see, e.g., [1–3]. In particular, fixing a point \(x_0\) in a Hadamard manifold and a nonzero vector \(u_0\) in the tangent space at \(x_0\), one considers the special function \(f_0\), generated by the inner product between vector \(u_0\) and the inverse of the exponential map at point \(x_0\), and the associated parallel vector field \(X_0\), formed by the parallel transportation of the given vector \(u_0\) (see (5) and (6) in Sect. 3, respectively). Assertions (i) and (ii) below were claimed in [2, Proposition 3.4] (without the proof for assertion (ii)).

(i) The gradient of \(f_0\) is the associated parallel vector field \(X_0\);

(ii) \(f_0\) is linear affine.

Assertions (i) and (ii) have been used in [2, 4] to study the proximal point algorithm for quasi-convex/convex functions with Bregman distances on Hadamard manifolds, while assertion (ii) was also used in [5, 6] to establish some existence results of solutions for equilibrium problems and vector optimization problems on Hadamard manifolds, respectively. However, assertion (ii) is clearly not true in general because, by [1, p. 299, Theorem 2.1]), any twice differentiable linear affine function on Poincaré plane \({\mathbb {H}}\) (a two-dimensional Hadamard manifold of constant curvature \(-1\)) is constant. Indeed, it has been further shown in [3, Theorem 2.1] that assertion (ii) is true for all points \(x_0\) in the Hadamard manifold and vectors \(u_0\) in the corresponding tangent space if and only if the manifold is isometric to the Euclidean space \({\mathbb {R}}^n\). Furthermore, one can easily check that the function \(f_0\) is even not convex, in general, because, otherwise, one has that both \(f_0\) and \(-f_0\) are convex (and so linear affine). This motivates us to consider the following problems:

Problem 1

Is \(f_0\) quasi-convex?

Problem 2

Is assertion (i) true?

The first purpose of this paper is to present a characterization for linear affine functions on Hadamard manifolds in terms of assertion (i) and parallel transports, and to provide a counterexample on Poincaré plane to illustrate that the answer to each problem is negative. In particular for Problem 2, we show that the vector field \(X_0\) is even not a gradient field.

Our second purpose in the present paper is, in spirit of the negative answer to Problem 1, to study the convexity issue of sub-level sets of the function \(f_0\) mentioned above in Riemannian manifolds with constant sectional curvatures. Our main results provide the exact estimate of the constant c such that the sub-level set \(L_{c,f_0}\), consisting of all points x with value \(f_0(x)\) being no more than c, is strongly convex, which in particular improves and extends the corresponding result in [7, Corollary 3.1].

The paper is organized as follows. We review, in Sect. 2, some basic notions, notations, and some classical results of Riemannian geometry that will be needed afterward. The characterization for linear affine functions on Hadamard manifolds and the counterexample on Poincaré plane are presented in Sect. 3. Finally, in Sect. 4, the convexity properties of the sub-level sets of the function \(f_0\) in Riemannian manifolds with constant sectional curvatures are discussed.

2 Notations, Notions, and Preliminaries

In the present section, we present some basic notations, definitions, and properties of Riemannian manifolds. The readers are referred to some textbooks for details, for example [1, 8, 9].

Let M be a complete, simply connected n-dimensional Riemannian manifold with the Levi-Civita connection \(\nabla \) on M. We denote the tangent space at \(x\in M\) by \(T_{x}M\), and Let \(\mathcal {X}(M)\) denote all (\(C^\infty \)) vector fields on M. By \(\langle \cdot ,\cdot \rangle _{x}\) and \(\Vert \cdot \Vert _x\), we mean the corresponding Riemannian inner product and the norm on \(T_{x}M\), respectively (where the subscript x is sometimes omitted). For \(x,y\in {M}\), let \(\gamma :[0,1]\rightarrow M\) be a piecewise smooth curve joining x to y. Then, the arc-length of \(\gamma \) is defined by \(l(\gamma ):=\int _{0}^{1}\Vert \dot{\gamma }(t)\Vert \mathrm{d}t\), while the Riemannian distance from x to y is defined by \(\mathrm{d}(x,y):=\inf _{\gamma }l(\gamma )\), where the infimum is taken over all piecewise smooth curves \(\gamma :[0,1]\rightarrow M\) joining x to y. We use \({\mathbb {B}}(x,r)\) to denote the open metric ball at x with radius r, that is,

$$\begin{aligned} {\mathbb {B}}(x,r):=\{y\in M:\mathrm{d}(x, y)<r\}. \end{aligned}$$

For a smooth curve \(\gamma \), if \(\dot{\gamma }\) is parallel along itself, then \(\gamma \) is called a geodesic, that is, a smooth curve \(\gamma \) is a geodesic if and only if \(\nabla _{\dot{\gamma }}{\dot{\gamma }}=0\). A geodesic \(\gamma :[0,1]\rightarrow M\) joining x to y is minimal if its arc-length equals its Riemannian distance between x and y. By the Hopf–Rinow theorem [8], \((M,\mathrm{d})\) is a complete metric space, and there is at least one minimal geodesic joining x to y. The set of all geodesics \(\gamma :[0,1]\rightarrow M\) with \(\gamma (0)=x\) and \(\gamma (1)=y\) is denoted by \({\varGamma }_{xy}\), that is,

$$\begin{aligned} {\varGamma }_{xy}:=\{\gamma :[0,1]\rightarrow M:\;\gamma (0)=x,\, \gamma (1)=y \text{ and } \nabla _{\dot{\gamma }}\dot{\gamma }=0\}. \end{aligned}$$

We use \(\gamma _{xy}:[0,1]\rightarrow M\) to denote the minimal geodesic satisfying \(\gamma _{xy}(0)=x\) and \(\gamma _{xy}(1)=y\) if it is unique.

Let \(\gamma \) be a geodesic. We use \(P_{\gamma ,\cdot ,\cdot }\) to denote the parallel transport on the tangent bundle TM (defined below) along \(\gamma \) with respect to \(\nabla \), which is defined by

$$\begin{aligned} P_{\gamma ,\gamma (b),\gamma (a)}v=X(\gamma (b))\quad \text{ for } \text{ all } a,b\in {\mathbb {R}} \text{ and } v\in T_{\gamma (a)}M, \end{aligned}$$
(1)

where X is the unique vector field satisfying

$$\begin{aligned} X(\gamma (a))=v\quad \text{ and }\quad \nabla _{\dot{\gamma }}X=0. \end{aligned}$$
(2)

Then, for any \(a,b\in {\mathbb {R}}\), \(P_{\gamma ,\gamma (b),\gamma (a)}\) is an isometry from \(T_{\gamma (a)}M\) to \(T_{\gamma (b)}M\). We will write \(P_{y,x}\) instead of \(P_{\gamma ,y,x}\) in the case when \(\gamma \) is a minimal geodesic joining x to y and no confusion arises.

The exponential map of M at \(x\in M\) is denoted by \(\exp _x(\cdot ):T_xM\rightarrow M\). For a \(C^\infty \) function \(f:M\rightarrow {\mathbb {R}}\), \(\mathrm{grad}\,f\) and \(\mathrm{Hess}\, f\) denote its gradient vector and Hessian, respectively. Let \(X,Y\in \mathcal {X}(M)\). The Riemannian connection has the expression in terms of parallel transportation, that is,

$$\begin{aligned} (\nabla _XY)(x)=\lim _{t\rightarrow 0}\frac{1}{t}\left\{ P_{\gamma ,\gamma (0),\gamma (t)}Y(\gamma (t))-Y(x)\right\} \quad \text{ for } \text{ any } x\in M, \end{aligned}$$
(3)

where the curve \(\gamma \) with \(\gamma (0)=x\) and \(\dot{\gamma }(0)=X(x)\) (see, e.g., [9, p. 29 Exercise 5]).

A complete simply connected Riemannian manifold of non-positive sectional curvature is called a Hadamard manifold. The following proposition is well known about the Hadamard manifolds; see, e.g, [9, p. 221].

Proposition 2.1

Suppose that M is a Hadamard manifold. Let \(p\in M\). Then, \(\exp _p:T_pM\rightarrow M\) is a diffeomorphism, and for any two points \(p,q\in M\), there exists a unique normal geodesic joining p to q, which is in fact a minimal geodesic.

The following definition presents the notions of different convexities, where item (a) and (b) are known in [10]; see also [11–13].

Definition 2.1

Let Q be a non-empty subset of the Riemannian manifold M. Then, Q is said to be

(a) Weakly convex if, for any \(x,y\in Q\), there is a minimal geodesic of M joining x to y and it is in Q;

(b) Strongly convex if, for any \(x,y\in Q\), there is just one minimal geodesic of M joining x to y, and it is in Q.

All convexities in a Hadamard manifold coincide and are simply called the convexity. Let \(f:M\rightarrow \overline{{\mathbb {R}}}\) be a proper function, and let \(\mathrm{dom}\,f\) denote its domain, that is, \(\mathrm{dom}\,f:=\{x\in M:f(x)\ne \infty \}\). We use \({\varGamma }^f_{xy}\) to denote the set of all \(\gamma \in {\varGamma }_{xy}\) such that \(\gamma \subseteq \mathrm{dom}\,f\). In the following definition, item (a) is known in [14, 15] and item (b) is an extension of the one in [1, p. 59], which is introduced for the case when \(\mathrm{dom}\,f\) is totally convex.

Definition 2.2

Let \(f:M\rightarrow \overline{{\mathbb {R}}}\) be a proper function and suppose that \(\mathrm{dom}\,f\) is weakly convex. Then, f is said to be

(a) convex if

$$\begin{aligned} f\circ \gamma (t)\le (1-t)f(x)+tf(y)\quad \text{ for } \text{ all } x,y\in \mathrm{dom}\,f,\;\gamma \in {\varGamma }_{xy}^f,\;t\in [0,1]; \end{aligned}$$

(b) quasi-convex if

$$\begin{aligned} f\circ \gamma (t)\le \max \{f(x),f(y)\}\quad \text{ for } \text{ all } x,y\in \mathrm{dom}\,f,\;\gamma \in {\varGamma }_{xy}^f,\;t\in [0,1]. \end{aligned}$$

Clearly, for a proper function f with a weakly convex domain, the convexity implies the quasi-convexity. Fixing \(c\in {\mathbb {R}}\), we use \(L_{c,f}\) to denote the sub-level set of f defined by

$$\begin{aligned} L_{c,f}:=\{x\in M:f(x)\le c\}. \end{aligned}$$

The following proposition describes the relationship between the convexities of a function f and its sub-level sets.

Proposition 2.2

Let \(f:M\rightarrow \overline{{\mathbb {R}}}\) be a proper function with weakly convex domain \(\mathrm{dom}\,f\). Then, f is quasi-convex if and only if, for each \(c\in {\mathbb {R}}\), the sub-level set \(L_{c,f}\) is totally convex with restricted to \(\mathrm{dom}\,f\) in the sense that for any \(x,y\in L_{c,f}\), if \(\gamma \in {\varGamma }^f_{xy}\) then \(\gamma \subseteq L_{c,f}\). In particular, f is quasi-convex if and only if \(L_{c,f}\) is strongly convex for each \(c\in {\mathbb {R}}\) in the case when \(\mathrm{dom}\,f\) is strongly convex.

Proof

We only consider the case when \(\mathrm{dom}\,f\) is weakly convex (otherwise when \(\mathrm{dom}\,f\) is strongly convex, the result is immediate by definition).

Suppose that f is quasi-convex. Take \(c\in {\mathbb {R}}\). Let \(x,y\in L_{c,f}\subseteq \mathrm{dom}\,f\) and let \(\gamma \in {\varGamma }_{xy}^f\). Then, \(f(x)\le c\) and \(f(y)\le c\). Noting that f is quasi-convex, it follows that

$$\begin{aligned} f\circ \gamma (t)\le \max \{f(x),f(y)\}\le c\quad \text{ for } \text{ all } \quad t\in [0,1]. \end{aligned}$$

This implies that \(\gamma \subseteq L_{c,f}\) and so \(L_{c,f}\) is totally convex restricted to \(\mathrm{dom}\,f\) since \(x,y\in L_{c,f}\) and \(\gamma \in {\varGamma }_{xy}^f\) are arbitrary.

Conversely, suppose that \(L_{c,f}\) is totally convex restricted to \(\mathrm{dom}\,f\) for each \(c\in {\mathbb {R}}\). Let \(x,y\in \mathrm{dom}\,f\) and let \(\gamma \in {\varGamma }_{xy}^f\). Set \(c_0:=\max \{f(x),f(y)\}\). Then, by assumption, \(\gamma \subseteq L_{c_0,f}\), that is,

$$\begin{aligned} f\circ \gamma (t)\le c_0=\max \{f(x),f(y)\}\quad \text{ for } \text{ all } t\in [0,1]. \end{aligned}$$

This implies that f is quasi-convex since \(x,y\in \mathrm{dom}\,f\) and \(\gamma \in {\varGamma }_{xy}^f\) are arbitrary. The proof is complete. \(\square \)

3 Linear Affine Functions and Counterexampls on Hadamard Manifolds

For the whole section, we assume that M is a Hadamard manifold. Consider a proper convex function \(f:M\rightarrow \overline{{\mathbb {R}}}\) on M. The subdifferential of f at \(x\in \mathrm{dom}\,f\) is defined by

$$\begin{aligned} \partial f(x):=\left\{ v\in T_{x}M:\; f(y)\ge f(x)+\langle v,\dot{\gamma }_{xy}(0)\rangle \;\; \text{ for } \text{ all } y\in \mathrm{dom}\,f.\right\} \end{aligned}$$

By [1, p. 74] (see also [15, Proposition 6.2]), \(\partial f(x)\) is a non-empty, compact and convex set for any \(x\in \mathrm{int}(\mathrm{dom}\,f)\), where \(\mathrm{int}Q\) denotes the topological interior of a subset Q of M. Let \(f:M\rightarrow \overline{{\mathbb {R}}}\) be a proper function with convex domain. Recall that f is linear affine if both f and \(-f\) are convex. Furthermore, if f is of \(C^2\) and \(\mathrm{dom}\,f\) is open, its \(\mathrm{Hess}\,f\) is defined by

$$\begin{aligned} \mathrm{Hess}\,f(X,Y)=\langle \nabla _{X}\mathrm{grad}\,f,Y\rangle \quad \text{ for } \text{ any } X,Y\in \mathcal {X}(M). \end{aligned}$$

Then, by [1, p. 83, remark 6], we have that

$$\begin{aligned} f \text{ is } \text{ linear } \text{ affine } \Longleftrightarrow \nabla _X\mathrm{grad}\,f=0\quad \text{ for } \text{ any } X\in \mathcal {X}(M). \end{aligned}$$
(4)

Let \(x_0\in M\), and let \(u_0\in T_{x_0}M\). Then, the function \(f_0\) and the vector field \(X_0\) considered in the introduction can be formulated as

$$\begin{aligned} f_0(x):=\langle u_0,\exp _{x_0}^{-1}x\rangle \quad \text{ for } \text{ any } \quad x\in M \end{aligned}$$
(5)

and

$$\begin{aligned} X_0(x):=P_{x,x_0}u_0\quad \quad \text{ for } \text{ any } \quad x\in M, \end{aligned}$$
(6)

respectively. Thus, assertions (i) and (ii) in [2, Proposition 3.4] can be restated as follows:

(i) \(\mathrm{Grad}\,f_0=X_0\).

(ii) \(f_0\) is linear affine on M.

The following theorem presents, in particular, a characterization in Hadamard manifolds for assertion (ii) to be true in terms of assertion (i) and the parallel transports.

Theorem 3.1

Let \(f:M\rightarrow \overline{{\mathbb {R}}}\) be a proper function and suppose that \(\mathrm{dom}\,f\) is a non-empty open convex subset. If function f is linear affine, then, for any \(x_0\in \mathrm{dom}\,f\), there exists \(u_0\in T_{x_0}M\) such that

$$\begin{aligned} P_{x,x_0}u_0= & {} P_{x,z} \circ P_{z,x_0}u_0 \quad \text{ for } \text{ any } (z,x)\in \mathrm{dom}\,f\times \mathrm{dom}\,f, \end{aligned}$$
(7)
$$\begin{aligned} \mathrm{grad}\, f(x)= & {} P_{x,x_0}u_0\quad \text{ for } \text{ any } x\in \mathrm{dom}\,f \end{aligned}$$
(8)

and

$$\begin{aligned} f(x)=f(x_0)+\langle u_0,\exp _{x_0}^{-1}x\rangle \quad \text{ for } \text{ any } x\in \mathrm{dom}\,f. \end{aligned}$$
(9)

Conversely, if there exist \(x_0\in \mathrm{dom}\,f\) and \(u_0\in T_{x_0}M\) such that (7) and (8) hold, then f is linear affine.

Proof

Assume that f is linear affine. Then, both f and \(-f\) are convex. Take \(x_0\in \mathrm{dom}\,f\) and note that \( \mathrm{dom}\,f\) is open. It follows that both \(\partial f(x_0)\) and \(\partial (-f(x_0))\) are non-empty. Thus, one can chose \(u_0\in \partial f(x_0)\) and \(u_0'\in \partial (-f(x_0))\), respectively. Then, by definition, we have that, for any \(x\in \mathrm{dom}\,f\),

$$\begin{aligned} \begin{array}{ll} f(x)\ge f(x_0)+\left\langle u_0,\exp _{x_0}^{-1}x\right\rangle \;\;\text{ and }\;\;-f(x)\ge -f(x_0)+\left\langle u_0',\exp _{x_0}^{-1}x\right\rangle ; \end{array} \end{aligned}$$
(10)

hence \( \langle u_0+u_0^{\prime },\exp _{x_0}^{-1}x\rangle _{x_0}\le 0 \) for any \(x\in \mathrm{dom}\,f\). This implies that \(u_0+u_0'=0\), that is \(u_0^{\prime }=-u_0\) (as \( \mathrm{dom}\,f\) is open). Thus, (9) follows from (10). Furthermore, noting that f is of class \(C^\infty \) by (9), one then has that \(\mathrm{Hess}\,f=0\) on \(\mathrm{dom}\,f\), that is,

$$\begin{aligned}\mathrm{Hess}\,f(X,Y)=\langle \nabla _X\mathrm{grad}\, f,Y\rangle =0\;\; \text{ for } \text{ any } X,Y\in \mathcal {X}(\mathrm{dom}\,f).\end{aligned}$$

In particular, one has that

$$\begin{aligned} \nabla _{\dot{\gamma }_{xz}}\mathrm{grad}\, f =0 \quad \text{ for } \text{ any } x,z\in \mathrm{dom}\,f, \end{aligned}$$

where \({\gamma }_{xz}\) is the geodesic joining x and z, which lies in \(\mathrm{dom}\,f\). This, together with the definition of parallel transport (e.g., (1)), implies that

$$\begin{aligned} \mathrm{grad}\, f(x)=P_{x,z}\mathrm{grad}\, f(z)\quad \text{ for } \text{ any } x,z\in \mathrm{dom}\,f. \end{aligned}$$
(11)

Note further that, for any \(u\in T_{x_0}M\), one has

$$\begin{aligned} \langle \mathrm{grad}\,f(x_0),u\rangle _{x_0}=\frac{\mathrm{d}}{\mathrm{d}t}f\circ \exp _{x_0}t u\mid _{t=0}=\langle u_0,u\rangle _{x_0}. \end{aligned}$$

It follows that \(\mathrm{grad}\,f(x_0)=u_0\). This, together with (11), implies that (7) and (8) hold.

Now, suppose that (7) and (8) hold for some \(x_0\in \mathrm{dom}\,f\) and \(u_0\in T_{x_0}M\). Let \(x\in \mathrm{dom}f\) and \(X\in \mathcal {X}(\mathrm{dom}\,f)\). Let \(\gamma :[-\varepsilon ,\varepsilon ]\rightarrow \mathrm{dom}\,f\) be the geodesic contained in \(\mathrm{dom}\,f\) with \(\gamma (0)=x\) and \(\dot{\gamma }(0)=X(x)\). Let \(t\in [-\varepsilon ,\varepsilon ]\). We see from (8) that

$$\begin{aligned} \mathrm{grad}\, f(x)=P_{x,x_0}u_0,\;\mathrm{grad}\, f(\gamma (t))=P_{\gamma (t),x_0}u_0. \end{aligned}$$

In light of (7), it follows that

$$\begin{aligned} P_{x,\gamma (t)}\mathrm{grad}\, f(\gamma (t))=P_{x,\gamma (t)}\circ P_{\gamma (t),x_0}u_0=P_{x,x_0}u_0=\mathrm{grad}\, f(x). \end{aligned}$$

Noting that \(P_{x,\gamma (t)}=P_{\gamma ,x,\gamma (t)}\), one gets by (3) that

$$\begin{aligned} (\nabla _X\mathrm{grad}\, f)(x)=\lim _{t\rightarrow 0}\frac{1}{t}\{P_{x,\gamma (t)}\mathrm{grad}\, f(\gamma (t))-\mathrm{grad}\, f(x)\}=0. \end{aligned}$$

Since \(X\in \mathcal {X}(\mathrm{dom}\,f)\) and \(x\in \mathrm{dom}\,f\) are arbitrary, we conclude that \(\mathrm{Hess}\,f=0\) on \(\mathrm{dom}\,f\), and so f is linear affine. The proof is complete. \(\square \)

Before considering Problems 1–2 proposed in the introduction which are related to the function \(f_0\) defined by (5), we make a remark regarding the quasi-convexity properties about composite functions. To this end, we have the following theorem, which is due to Udriste [1, p. 101, Theorem 10.9] in the special case when \(M=\tilde{M}\). The idea of the proof is the same as that for [1, p. 101, Theorem 10.9] (although the arguments presented there are not completely clear), and so we omit the proof here.

Theorem 3.2

Let \((\tilde{M},\tilde{\nabla })\) be a Riemannian manifold with Levi-Civita connection \(\tilde{\nabla }\) and \(D\subseteq \tilde{M}\) be a totally convex subset. If \(\varphi :D\rightarrow \mathbb {R}\) is a quasi-convex function on \((\tilde{M},\tilde{\nabla })\) and \(F:\tilde{M}\rightarrow M\) is a diffeomorphism, then \(\varphi \circ F^{-1}\) is a quasi-convex function on \((M,F_*\tilde{\nabla })\).

Remark 3.1

Recall that M is with the Levi-Civita connection \(\nabla \) and \(x_0\in M\), \(u_0\in T_{x_0}M\). Set \(\tilde{M}:=T_{x_0}M\), and let \(\tilde{M}\) be endowed with the Riemannian metric \(\tilde{g}\) given by \(\tilde{g}_x(\cdot ,\cdot ):=\langle \cdot ,\cdot \rangle _{x_0}\) for each \(x\in \tilde{M}\) (i.e., \(\tilde{M}\) is an n-dimensional Hilbert space). Let \(\tilde{\nabla }\) be the Levi-Civita connection compatible with the metric. Then, \(f_0\) (defined by (5)) can be written as \(f_0=\varphi \circ F^{-1}\), where \(F:\tilde{M} \rightarrow M\) and \(\varphi :\tilde{M}\rightarrow {\mathbb {R}}\) are defined by \(F(\cdot ):=\exp _{x_0}(\cdot )\) and

$$\begin{aligned} \varphi (v):=\langle u_0,v\rangle _{x_0}\quad \text{ for } \text{ any } v\in \tilde{M}, \end{aligned}$$

respectively. It is evident that \(\varphi \) is linear affine on \(\tilde{M}\) and F is a diffeomorphism by Proposition 2.1. Thus, one could apply Theorem 3.2 to conclude that the function \(f_0\) is quasi-convex on M with the connection \(F_*\tilde{\nabla }\) but not the Levi-Civita connection \(\nabla \). Indeed, we shall see from Example 3.1 below that \(f_0\) is not quasi-convex.

Recalling the equivalence (4), the following problem related to Problems 1-2 is also natural:

Problem 3

Does the vector field \(X_0\) satisfy

$$\begin{aligned} \nabla _XX_0=0\quad \text{ for } \text{ any } X\in \mathcal {X}(M)? \end{aligned}$$

The remainder of this section is to construct a counterexample on Poincaré plane to show that the answer to each of Problems 1–3 is negative. To do this, let

$$\begin{aligned} M={\mathbb {H}}=:\{(t_1,t_2)\in \mathbb {R}^{2}:\ t_2>0\}, \end{aligned}$$

be the Poincaré plane endowed with the Riemannian metric, in terms of the natural coordinate system, defined by

$$\begin{aligned} g_{11}=g_{22}:=\frac{1}{t_2^2},\ g_{12}:=0\text { for each } (t_1,t_2)\in {\mathbb {H}}. \end{aligned}$$
(12)

The sectional curvature of \({\mathbb {H}}\) is equal to \(-1\) (see, e.g., [8, p. 160]), and the geodesics on \({\mathbb {H}}\) are the semilines \(\gamma (a;\cdot ):=(\gamma ^1(a;\cdot ),\gamma ^2(a;\cdot ))\) (through (a, 1)), and the semicircles \(\gamma (b,r;\cdot ):=(\gamma ^1(b,r;\cdot ),\gamma ^2(b,r;\cdot ))\) with center at (b, r) and radius r), which admit the following natural parameterizations:

$$\begin{aligned} \left\{ \begin{array}{l} \gamma ^1(a;s)=a\\ \gamma ^2(a;s)=e^{s}\\ \end{array} \right. \quad \text{ and } \quad \left\{ \begin{array}{l} \gamma ^1(b,r;s)=b-r\tanh s\\ \gamma ^2(b,r;s)=\frac{r}{\cosh s}\\ \end{array} \right. \quad \text{ for } \text{ any } s\in {\mathbb {R}}, \end{aligned}$$
(13)

respectively; see, e.g., [1, p. 298].

By [1, p. 297], the Riemannian connection \(\nabla \) on \({\mathbb {H}}\) (in terms of the natural coordinate system) has the components:

$$\begin{aligned} {\varGamma }_{11}^1={\varGamma }_{22}^1={\varGamma }_{12}^2={\varGamma }_{21}^2=0,\;\; {\varGamma }_{12}^1={\varGamma }_{21}^1={\varGamma }_{22}^2=-\frac{1}{t_2} \;\;\text{ and }\;\; {\varGamma }_{11}^2=\frac{1}{t_2}. \end{aligned}$$

Hence, noting the expression of the connection \(\nabla \) given in [8, p. 51], one has the following formula for the connection \(\nabla _{(\cdot )}(\cdot ):=\left( \nabla ^1_{(\cdot )}(\cdot ),\nabla ^2_{(\cdot )}(\cdot )\right) \) on \({\mathbb {H}}\) with

$$\begin{aligned} \nabla ^1_YX=Y^1\frac{\partial X^1}{\partial t_1}+Y^2\frac{\partial X^1}{\partial t_2}-\frac{1}{t_2}X^1Y^2-\frac{1}{t_2}X^2Y^1 \end{aligned}$$
(14)

and

$$\begin{aligned} \nabla ^2_YX=Y^1\frac{\partial X^2}{\partial t_1}+Y^2\frac{\partial X^2}{\partial t_2}+\frac{1}{t_2}X^1Y^1-\frac{1}{t_2}X^2Y^2 \end{aligned}$$
(15)

for any \(X:=(X^1,X^2),Y:=(Y^1,Y^2)\in \mathcal {X}({\mathbb {H}})\), where and in sequel, for a differential function \(\phi \) on \({\mathbb {H}}\), \(\frac{\partial \phi }{\partial t_1}\) and \(\frac{\partial \phi }{\partial t_2}\) denote the classical partial derivatives of \(\phi \) in \({\mathbb {R}}^2\) with respect to the first variable \(t_1\) and the second variable \(t_2\), respectively. Consider a differentiable function \(f:{\mathbb {H}}\rightarrow {\mathbb {R}}\). Then, using (12), one concludes that the gradient vector \(\mathrm{grad}\, f\) and the differential \(\mathrm{d}f\) of f are, respectively, given by

$$\begin{aligned} \mathrm{grad}\, f{(x)}=t_2^2\left( \frac{\partial f{(x)}}{\partial t_1}\frac{\partial }{\partial t_1}+\frac{\partial f{(x)}}{\partial t_1}\frac{\partial }{\partial t_2}\right) \end{aligned}$$
(16)

and

$$\begin{aligned} \mathrm{d}f(x)=\frac{\partial f(x)}{\partial t_1}\mathrm{d}t_1+\frac{\partial f(x)}{\partial t_2}\mathrm{d}t_2 \end{aligned}$$
(17)

for any \(x=(t_1,t_2)\in {\mathbb {H}}\); see, e.g., [1, p. 8].

For convenience, we also need the expressions of the exponential map \(\exp _{x}^{-1}y\) and the geodesic \(\gamma _{xy}\) joining x to y, which can be found in [16]. To this end, let \(x:=(t_1,t_2)\) and \(y:=(s_1,s_2)\) be in \( {\mathbb {H}}\), and set for any x, y with \(t_1\ne s_1\),

$$\begin{aligned} b_{xy}:=\frac{(s_1)^2+(s_2)^2-((t_1)^2+(t_2)^2)}{2(s_1-t_1)} \end{aligned}$$
(18)

and

$$\begin{aligned} r_{xy}:=\sqrt{(s_1-b_{xy})^2+(s_2)^2}. \end{aligned}$$
(19)

For saving of printing space, we use \(\omega \) to denote the inverse function of the hyperbolic tangent function \(\mathrm{tanh}\), that is,

$$\begin{aligned} \mathrm{\omega }(t):=\mathrm{tanh}^{-1}t\quad \text{ for } \text{ all } t\in {\mathbb {R}}. \end{aligned}$$

Then, one has

$$\begin{aligned} \exp _{y}^{-1}x=\left\{ \begin{array}{ll} \left( 0,s_2\ln \frac{t_2}{s_2}\right) ,&{}\text { if }\,\, t_1=s_1,\\ \frac{s_2}{r_{xy}}\left( \mathrm{\omega }\left( \frac{{b_{xy}-s_1}}{r_{xy}}\right) -\mathrm{\omega }\left( \frac{{b_{xy}-t_1}}{r_{xy}}\right) \right) (s_2,b_{xy}-s_1),&{}\text { if }\,\, t_1\ne s_1. \end{array} \right. \end{aligned}$$
(20)

and \(\gamma _{xy}:=\left( \gamma _{xy}^1,\gamma _{xy}^2\right) \) with \(\gamma _{xy}^1\) and \(\gamma _{xy}^2\) defined, respectively, by

$$\begin{aligned} \gamma _{xy}^1(s):=\left\{ \begin{array}{ll} t_1,&{}\text { if }\,\, t_1=s_1,\\ b_{xy}-r_{xy}\tanh \left( (1-s)\;\mathrm{\omega }\left( \frac{{b_{xy}-t_1}}{r_{xy}}\right) +s\;\mathrm{\omega }\left( \frac{{b_{xy}-s_1}}{r_{xy}}\right) \right) ,&{}\text { if }\,\, t_1\ne s_1, \end{array}\right. \end{aligned}$$
(21)

and

$$\begin{aligned} \gamma _{xy}^2(s):=\left\{ \begin{array}{ll} e^{(1-s)\cdot \ln t_2+s\cdot \ln s_2},&{}\text { if } t_1=s_1,\\ \frac{r_{xy}}{\cosh \left( (1-s)\;\mathrm{\omega }(\frac{{b_{xy}-t_1}}{r_{xy}})+s\;\mathrm{\omega }(\frac{{b_{xy}-s_1}}{r_{xy}})\right) },\quad &{}\text { if } t_1\ne s_1 , \end{array}\right. \end{aligned}$$
(22)

for any \(s\in [0,1]\). Now, we are ready to present the counterexample.

Example 3.1

Let \(x_0:=(0,1)\), and let \(u_0:=(0,1)\in T_{x_0}{\mathbb {H}}\) be a unit vector. Let \(f_0:{\mathbb {H}}\rightarrow {\mathbb {R}}\) and \(X_0:{\mathbb {H}}\rightarrow T{\mathbb {H}}\) be the function and the vector field defined by

$$\begin{aligned} f_0(x):=\langle u_0,\exp _{x_0}^{-1}x\rangle \quad \text{ for } \text{ any } x\in M \end{aligned}$$
(23)

and

$$\begin{aligned} X_0(x):=P_{x,x_0}u_0\quad \quad \text{ for } \text{ any } x\in M, \end{aligned}$$
(24)

respectively. We claim that, for each \(x=(t_1,t_2)\in {\mathbb {H}}\),

$$\begin{aligned} f_0(x)=\left\{ \begin{array}{ll} \ln {t_2},&{}\text { if } t_1=0,\\ \frac{b_x}{r_x}\left( \mathrm{\omega }(\frac{b_x}{r_x})-\mathrm{\omega }(\frac{b_x-t_1}{r_x})\right) ,&{}\text { if } t_1\ne 0, \end{array} \right. \end{aligned}$$
(25)

and

$$\begin{aligned} X_0(x)=\left\{ \begin{array}{ll} (0,t_2),&{}\text { if } t_1=0,\\ \left( \frac{b_xt_2^2-t_2(b_x-t_1)}{b_x^2+1},\frac{b_xt_2(b_x-t_1)+t_2^2}{b_x^2+1}\right) ,&{}\text { if } t_1\ne 0, \end{array} \right. \end{aligned}$$
(26)

where, for any x with \(t_1\ne 0\),

$$\begin{aligned} b_x:=b_{xx_0}=\frac{t_1^2+t_2^2-1}{2t_1}\quad \text{ and }\quad r_x:=r_{xx_0}=\sqrt{b_x^2+1}. \end{aligned}$$
(27)

Indeed, let \(x=(t_1,t_2)\in {\mathbb {H}}\). Then, by (20), we get that

$$\begin{aligned} \exp _{x_0}^{-1}x=\left\{ \begin{array}{ll} (0,\ln {t_2}),&{}\text { if } t_1=0,\\ \frac{1}{r_x}\left( \mathrm{\omega }\left( \frac{{b_x}}{r_x}\right) -\mathrm{\omega }\left( \frac{{b_x-t_1}}{r_x}\right) \right) (1,b_x),&{}\text { if } t_1\ne 0; \end{array} \right. \end{aligned}$$

thus (25) follows immediately from definition. To check (26), let \(\gamma \) be the geodesic through x and \(x_0\). By the definition of \(X_0\) and thanks to (2), we have to show \(\nabla _{\dot{\gamma }}X_0=0\). To do this, write \(X_0:=(X^1_0,X^2_0)\) and \(\gamma :=(\gamma ^1,\gamma ^2)\). Then,

$$\begin{aligned} X_0^1(x)=\left\{ \begin{array}{ll} 0,&{}\text { if } t_1=0,\\ \frac{b_xt_2^2-t_2(b_x-t_1)}{b_x^2+1},&{}\text { if } t_1\ne 0, \end{array} \right. \end{aligned}$$
(28)

and

$$\begin{aligned} X_0^2(x)=\left\{ \begin{array}{ll} t_2,&{}\text { if } t_1=0,\\ \frac{b_xt_2(b_x-t_1)+t_2^2}{b_x^2+1},&{}\text { if } t_1\ne 0. \end{array} \right. \end{aligned}$$
(29)

In expression of the differential equations (see, e.g., [8, p. 53]), we only need to verify that \(X_0\) and \(\gamma \) satisfy

$$\begin{aligned} \frac{\mathrm{d}\left( X_0^1\circ \gamma \right) }{\mathrm{d}s}-\frac{X_0^1\circ \gamma }{\gamma ^2}\frac{\mathrm{d}\gamma ^2}{\mathrm{d}s}-\frac{X_0^2\circ \gamma }{\gamma ^2}\frac{\mathrm{d}\gamma ^1}{\mathrm{d}s}= & {} 0,\nonumber \\ \frac{\mathrm{d}\left( X_0^2\circ \gamma \right) }{\mathrm{d}s}+\frac{X_0^1\circ \gamma }{\gamma ^2}\frac{\mathrm{d}\gamma ^1}{\mathrm{d}s}-\frac{X_0^2\circ \gamma }{\gamma ^2}\frac{\mathrm{d}\gamma ^2}{\mathrm{d}s}= & {} 0. \end{aligned}$$
(30)

Without loss of generality, we assume that \(t_1\ne 0\) and adopt the expression (13) of the geodesic, that is, \((\gamma ^1(\cdot ),\gamma ^2(\cdot )) = (\gamma ^1(b_x,r_x;\cdot ),\gamma ^2(b_x,r_x;\cdot ))\) with

$$\begin{aligned} \gamma ^1(b_x,r_x;s)=b_x-r_x\tanh s\quad \text{ and }\quad \gamma ^2(b_x,r_x;s)=\frac{r_x}{\cosh s} \end{aligned}$$
(31)

for any \(s\in {\mathbb {R}}\left( \hbox {noting } x_0=\gamma \left( b_x,r_x;\mathrm{\omega }(\frac{b_x}{r_x})\right) \hbox {and } x=\gamma \left( b_x,r_x;\mathrm{\omega }(\frac{b_x-t_1}{r_x})\right) \right) \), where \(b_x\) and \(r_x\) are defined by (27). Thus, using (31), one conclude that, for each \(s\in {\mathbb {R}}\),

$$\begin{aligned}&X_0^1\circ \gamma (b_x,r_x;s)=\frac{1}{b_x^2+1}\left( \frac{b_xr_x^2}{\cosh ^2s}-\frac{r_x^2\sinh s}{\cosh ^2s}\right) ,\\&X_0^2\circ \gamma (b_x,r_x;s)=\frac{1}{b_x^2+1}\left( \frac{b_xr_x^2\sinh s}{\cosh ^2s}+\frac{r_x^2}{\cosh ^2s}\right) , \end{aligned}$$

and so

$$\begin{aligned}&\frac{\mathrm{d}X_0^1\circ \gamma (b_x,r_x;s)}{\mathrm{d}s}=\frac{1}{b_x^2+1}\left( -\frac{2b_xr_x^2\sinh s}{\cosh ^3s}-\frac{r_x^2(1-\sinh ^2s)}{\cosh ^3s}\right) ,\\&\frac{\mathrm{d}X_0^2\circ \gamma (b_x,r_x;s)}{\mathrm{d}s}=\frac{1}{b_x^2+1}\left( \frac{b_xr_x^2(1-\sinh ^2s)}{\cosh ^3s}-\frac{2r_x^2\sinh s}{\cosh ^3s}\right) . \end{aligned}$$

Moreover, we also have that

$$\begin{aligned} \frac{\mathrm{d}\gamma ^1(b_x,r_x;s)}{\mathrm{d}s}=-\frac{r_x}{\cosh ^2s} \quad \text{ and } \quad \frac{\mathrm{d}\gamma ^2(b_x,r_x;s)}{\mathrm{d}s}=-\frac{r_x\sinh s}{\cosh ^2s} \end{aligned}$$

for any \(s\in {\mathbb {R}}\). Thus, (30) is seen to hold. Hence, \(\nabla _{\dot{\gamma }}X_0=0\), and (26) is checked.

Below we show the following assertions:

(i) \(f_0\) is not quasi-convex.

(ii) \(\mathrm{Grad}\,f_0\ne X_0\).

(iii) \(\nabla _{\frac{\partial }{\partial t_1}}X_0\ne 0\).

(iv) \(X_0\) is not a gradient vector field.

To show assertion (i), take \(x=(\frac{1}{2},\frac{1}{2}),\ y=(-\frac{1}{2},\frac{1}{2})\in {\mathbb {H}}\), and let \(c_0:=-0.4\). Then, \(x,y\in L_{c_0,f_0}\) because, by (25) and (27),

$$\begin{aligned} f_0(x)=f_0(y)=\frac{1}{\sqrt{5}}\left( \mathrm{\omega }\left( \frac{2}{\sqrt{5}}\right) -\mathrm{\omega }\left( \frac{1}{\sqrt{5}}\right) \right) =-0.4304\cdots <-0.4. \end{aligned}$$

Let \(\gamma _{xy}=(\gamma ^1_{xy},\gamma ^2_{xy})\) be the geodesic segment joining x to y. Then, for any \(s\in [0,1]\),

$$\begin{aligned} \gamma ^1_{xy}(s):=-\frac{1}{\sqrt{2}}\tanh \left( (2s-1)\mathrm{\omega }\left( \frac{1}{\sqrt{2}}\right) \right) \end{aligned}$$

and

$$\begin{aligned} \gamma ^2_{xy}(s):=\frac{1}{\sqrt{2}\cosh \left( (2s-1)\mathrm{\omega }\left( \frac{1}{\sqrt{2}}\right) \right) } \end{aligned}$$

thanks to (18), (19), (21), and (22). Hence, \(\gamma _{xy}(\frac{1}{2})=(0,\frac{1}{\sqrt{2}})\), and

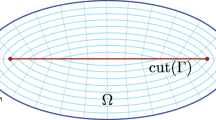
$$\begin{aligned} f_0\left( \gamma _{xy}\left( \frac{1}{2}\right) \right) =\ln \frac{1}{\sqrt{2}}=-0.3465\cdots >-0.4 \end{aligned}$$

by (25). This means that \(\gamma _{xy}(\frac{1}{2})\not \in L_{c,f_0}\), and so \(L_{c,f_0}\) is not convex; see Fig. 1. In view of Proposition 2.2, we see that \(f_0\) is not quasi-convex, and assertion (i) holds.

To show assertion (ii), take \(z:=(2,1)\). Then,

$$\begin{aligned} b_{z}=1\quad \text{ and }\quad r_z=\sqrt{2} \end{aligned}$$
(32)

(see (27)). Therefore, we have by (26) that \(X_0(z)=(1,0)\). On the other hand, we get from (16) that

$$\begin{aligned} \mathrm{grad}\,f_0(z)=\left( \frac{\partial f_0}{\partial t_1},\frac{\partial f_0}{\partial t_2}\right) \end{aligned}$$

where \(\frac{\partial f_0}{\partial t_1}\) and \(\frac{\partial f_0}{\partial t_2}\) are classical partial derivatives in \({\mathbb {R}}^2\). Then, using (25) and (27), one calculates

$$\begin{aligned} \mathrm{grad}\,f_0(z)=\left( \frac{\sqrt{2}}{8}\ln (3+2\sqrt{2})+\frac{1}{2},\frac{\sqrt{2}}{8}\ln (3+2\sqrt{2})-\frac{1}{2}\right) . \end{aligned}$$

Therefore, \(\mathrm{grad}\,f_0(z)\ne X_0(z)\), and assertion (ii) is checked. We further have that

$$\begin{aligned} \nabla _{\frac{\partial }{\partial t_1}}X_0(z)\ne 0. \end{aligned}$$
(33)

Granting this, assertion (iii) is also checked. To show (33), we get from (14) and (15) that

$$\begin{aligned} \nabla _{\frac{\partial }{\partial t_1}}X_0=\left( \frac{\partial X_0^1}{\partial t_1}-\frac{1}{t_2}X_0^2,\frac{\partial X_0^2}{\partial t_1}+\frac{1}{t_2}X_0^1\right) . \end{aligned}$$
(34)

(noting that \({\frac{\partial }{\partial t_1}} =(1,0)\) for any \(x\in {\mathbb {H}}\)). Recalling that \(X_0^1\) and \(X_0^2\) are given by (28), (29), and \(z:=(2,1)\), we have that \(X_0^1(z)=1\) and \(X_0^2(z)=0\) (noting (32)). Furthermore, by elemental calculus, we can calculate the partial derivatives

$$\begin{aligned} \frac{\partial X_0^1}{\partial t_1}\mid _{z}=0\quad \text{ and }\quad \frac{\partial X_0^2}{\partial t_1}\mid _{z}=-\frac{1}{2} . \end{aligned}$$

Thus, we conclude from (34) that \(\nabla _{\frac{\partial }{\partial t_1}}X_0\mid _{z}=(0,\frac{1}{2})\ne 0\), as desired to show.

For assertion (iv), we suppose on the contrary that there exists a \(C^\infty \) function f such that \(X_0=\mathrm{grad}\,f\). Then, \(\mathrm{d}\circ \mathrm{d}f =0\) by the fundamental property (see, e.g., [9, p. 17]). To proceed, note that \(X_0=X_0^1\frac{\partial }{\partial t_1}+X_0^2\frac{\partial }{\partial t_2}\), where \(X_0^1\) and \(X_0^2\) are defined by (28) and(29), respectively. Then, we calculate by elementary calculus that

$$\begin{aligned} \left. \left( \frac{\partial \left( \frac{1}{t_2^2}X_0^1\right) }{\partial t_2}-\frac{\partial \left( \frac{1}{t_2^2}X_0^2\right) }{\partial t_1}\right) \right| _{x=(2,1)}=\frac{1}{2}\ne 0. \end{aligned}$$
(35)

Furthermore, by (16) and (17), one has that

$$\begin{aligned} \mathrm{d}f=\frac{1}{t_2^2}X_0^1\mathrm{d}t_1+\frac{1}{t_2^2}X_0^2\mathrm{d}t_2, \end{aligned}$$

and so the exterior differentiation

$$\begin{aligned} \mathrm{d}\circ \mathrm{d}f=\left( \frac{\partial \left( \frac{1}{t_2^2}X_0^2\right) }{\partial t_1}-\frac{\partial \left( \frac{1}{t_2^2}X_0^1\right) }{\partial t_2}\right) \mathrm{d}t_1\wedge \mathrm{d}t_2, \end{aligned}$$

where \(\wedge \) is the exterior product; see, e.g., [9, p. 17]. This, together with (35), means that \(\mathrm{d}\circ \mathrm{d}f\not =0\), and so assertion (iv) is shown.

Fig. 1
figure 1

Non-convexity of the sub-level set \(L_{-0.4,f}\)

Full size image

4 Convexity Properties of Sub-Level Sets on Riemannian Manifolds

Throughout this section, let \(\kappa \in {\mathbb {R}}\) and assume that M is a n-dimensional complete, simply connected Riemannian manifold of constant sectional curvature \(\kappa \). Let \({\mathbb {R}}^n\) be the n-dimensional Euclidean space, \(\mathbb {S}_\rho ^n\) be the n-dimensional sphere of radius \(\frac{1}{\sqrt{\rho }}\) in \({\mathbb {R}}^{n+1}\) and \({\mathbb {H}}_\rho ^n\) be the manifold obtained from the hyperbolic space \({\mathbb {H}}^n\) by multiplying the Riemannian metric by the positive constant \(\frac{1}{\rho }>0\). Then, M is isometric to

(a) \({\mathbb {H}}_\kappa ^n\), if \(\kappa <0\),

(b) \(\mathbb {S}_\kappa ^n\), if \(\kappa >0\),

(c) \({\mathbb {R}}^n\), if \(\kappa =0\);

see, e.g., [9, p. 135]. As usual, define \(D_\kappa :=\frac{\pi }{\sqrt{\kappa }}\) if \(\kappa >0\) and \(D_\kappa :=+\infty \) otherwise. The proposition below is a direct consequence of [17, Propositions 1.4 and 1.7]; see also [15, Proposition 4.1].

Proposition 4.1

Let \(x,y\in M\). We have the following assertions:

(i) If \(\mathrm{d}(x,y)<D_\kappa \), then \({\varGamma }_{xy}\) contains a unique minimal geodesic \(\gamma _{xy}\).

(ii) Any open ball \({\mathbb {B}}(x,r)\) with \(r\le \frac{D_\kappa }{2}\) is strongly convex.

Let \(x_0\in M\) and \(u_0\in T_{x_0}M\setminus \{0\}\). Consider the following function \(f_0:M\rightarrow \overline{{\mathbb {R}}}\) defined by

$$\begin{aligned} f_0(x)=\left\{ \begin{array}{ll} \langle u_0,\dot{\gamma }_{x_0x}(0)\rangle ,&{}\text { if } x\in {\mathbb {B}}(x_0,\frac{D_\kappa }{2}),\\ +\infty ,&{}\text { otherwise}, \end{array} \right. \end{aligned}$$
(36)

where \({\gamma }_{x_0x}(0)\in {{\varGamma }}_{x_0x}\) is the unique minimal geodesic lying in \({\mathbb {B}}(x_0,\frac{D_\kappa }{2})\). It is clear that \(\mathrm{dom}\,f_0={\mathbb {B}}(x_0,\frac{D_\kappa }{2})\) is strongly convex. If M is a Hadamard manifold, function (36) is reduced to the function defined by (23), that is,

$$\begin{aligned} f_0(x):=\left\langle u_0,\exp _{x_0}^{-1}x\right\rangle \quad \text{ for } \text{ any } \quad x\in M. \end{aligned}$$
(37)

For any \(c\in {\mathbb {R}}\), the sub-level set of \(f_0\) is denoted by \(L_{c,f_0}(c\in {\mathbb {R}})\) and defined by

$$\begin{aligned} L_{c,f_0}:=\{x\in M:f_0(x)\le c\}. \end{aligned}$$

Note by Example 3.1 that \(L_{c,f_0}\) is not strongly convex in general. This section is devoted to estimating the constant c such that the sub-level set \(L_{c,f_0}\) is strongly convex. For this purpose, we first recall that a geodesic triangle \(\triangle (p_{1}p_{2}p_{3})\) in M is a figure consisting of three points \(p_{1},p_{2},p_{3}\) (the vertices of \(\triangle (p_{1}p_{2}p_{3})\)) and three minimal geodesic segments \(\gamma _{i}\) (the edges of \(\triangle (p_{1}p_{2}p_{3})\)) such that \(\gamma _i(0)=p_{i-1}\) and \(\gamma _i(1)=p_{i+1}\) with \(i=1,2,3\) ( mod3). For each \(i=1,2,3\) ( mod3), the inner angle of \(\triangle (p_{1}p_{2}p_{3})\) at \(p_{i}\) is denoted by \(\angle p_{i}\), which equals the angle between the tangent vectors \(\dot{\gamma }_{i+1}(0)\) and \(-\dot{\gamma }_{i-1}(1)\). The following proposition (i.e., comparison theorem for triangles) follows immediately from [9, p.161 Theorem 4.2 (ii), p. 138 Low of Cosines and p. 167 Remark 4.6].

Proposition 4.2

Let \(\triangle (p_{1}p_{2}p_{3})\) be a geodesic triangle in M of the perimeter less than \(2D_{\kappa }\). Set \(l_i=\mathrm{d}(p_{i+1},p_{i-1})\) for each \(i=1,2,3\). Then, the following relations hold:

$$\begin{aligned} l_i^2< l_{i-1}^2+l_{i+1}^2-2l_{i-1}l_{i+1}\cos \angle p_i\quad \text{ if } \kappa >0, \end{aligned}$$
(38)

and

$$\begin{aligned} l_i^2> l_{i-1}^2+l_{i+1}^2-2l_{i-1}l_{i+1}\cos \angle p_i\quad \text{ if } \kappa <0. \end{aligned}$$
(39)

Recall from [18, p. 104] that a k-dimensional submanifold \(N\subset M\) is totally geodesic if any geodesic in N is also a geodesic in M. Another property for a complete, simply connected Riemannian manifolds of constant curvature, which will be used in sequel, is the axiom of plane described as follows: (see, e.g., [9, p. 137]):

Proposition 4.3

Let \(x\in M\), and let W be a m-dimensional subspace of \(T_xM\) (\(m\ge 2\)). Then, the submanifold \(N:=\exp _xW\) is a m-dimensional totally geodesic and complete simply connected Riemannian manifold of constant curvature \(\kappa \), that is, N is isometric to \({\mathbb {H}}_{\kappa }^m\) if \(\kappa <0\) and to \(\mathbb {S}_{\kappa }^m\) if \(\kappa >0\).

The following lemma, taken from [19, Theorem 3.1 and Remark 3.6], plays a very key role in our study afterward.

Lemma 4.1

Let \(\triangle (ypq)\) be a geodesic triangle in M of the perimeter less than \(2D_\kappa \). Let \(\triangle (\tilde{y}\tilde{p}\tilde{q})\) be a triangle in \({\mathbb {R}}^2\) such that

$$\begin{aligned} \mathrm{d}(y,p)=\Vert \overrightarrow{\tilde{y}\tilde{p}}\Vert ,\quad \mathrm{d}(y,q)=\Vert \overrightarrow{\tilde{y}\tilde{q}}\Vert \quad \text{ and }\quad \angle pyq=\angle \tilde{p}\tilde{y}\tilde{q}. \end{aligned}$$
(40)

Let x be in the minimal geodesic joining p to q, and \(\tilde{x}\) be the corresponding point in the interval \([\tilde{p},\tilde{q}]\) satisfying

$$\begin{aligned} \angle pyx=\angle \tilde{p}\tilde{y}\tilde{x} \quad \text{ and }\quad \angle qyx=\angle \tilde{q}\tilde{y}\tilde{x} \end{aligned}$$
(41)

(see Fig. 2). Then, the following assertions hold:

$$\begin{aligned} \mathrm{d}(y,x)\ge \Vert \overrightarrow{\tilde{y}\tilde{x}}\Vert \; \text{ if } \kappa \ge 0 \quad \text{ and }\quad \mathrm{d}(y,x)\le \Vert \overrightarrow{\tilde{y}\tilde{x}}\Vert \; \text{ if } \kappa \le 0. \end{aligned}$$
(42)
Fig. 2
figure 2

Geodesic triangle \(\triangle ypq\) in M and its comparison triangle \(\triangle \tilde{y}\tilde{p}\tilde{q}\) in \({\mathbb {R}}^2\) in Lemma 4.1 and 4.2

Full size image

Recall that \(\gamma _{xy}\) is the unique minimal geodesic joining x to y for any \(x,y\in M\) with \(\mathrm{d}(x,y)<D_\kappa \) (see Proposition 4.1(i)).

Lemma 4.2

Let \(\triangle (ypq)\) be a geodesic triangle in M of the perimeter less than \(2D_\kappa \). Let \(\gamma :=\gamma _{pq}:[0,1]\rightarrow M\) be the unique minimal geodesic joining p to q. Then, for each \(t\in ]0,1[\), there exist two positive numbers \(a_t\) and \(b_t\) satisfying

$$\begin{aligned} a_t+b_t\;\left\{ \begin{array}{ll} \ge 1, &{}\quad \text{ if } \,\,\kappa \ge 0,\\ \le 1, &{}\quad \text{ if } \,\,\kappa \le 0,\\ \end{array} \right. \end{aligned}$$
(43)

such that

$$\begin{aligned} \dot{\gamma }_{y\gamma (t)}(0)=a_t\dot{\gamma }_{yp}(0)+b_t\dot{\gamma }_{yq}(0). \end{aligned}$$
(44)

Proof

Set \(N:=\exp _y\{\mathrm{span}\{\dot{\gamma }_{yp}(0),\dot{\gamma }_{yq}(0)\}\}\). By assumption, we see from Proposition 4.3 that \(\gamma \subset N\), and so

$$\begin{aligned} \dot{\gamma }_{y\gamma (t)}(0)\in T_{y}N=\mathrm{span}\{\dot{\gamma }_{yp}(0),\dot{\gamma }_{yq}(0)\}\quad \text{ for } \text{ any } \quad t\in [0,1]. \end{aligned}$$
(45)

Thus, there exist some \(a_t,b_t\in {\mathbb {R}}\) such that (44) holds (see Fig. 2).

Below, we show that \(a_t,b_t\) are positive and satisfy (43). To this end, as in Lemma 4.1 (see Fig. 2), set \(x=\gamma (t)\), and let \(\triangle (\tilde{y}\tilde{p}\tilde{q})\) be the corresponding triangle of \(\triangle (ypq)\) in \({\mathbb {R}}^2\) satisfying (40) and \(\tilde{x}\) be the corresponding point in the interval \([\tilde{p},\tilde{q}]\) satisfying (41). Without loss of generality, we may assume by (40) that \(\overrightarrow{\tilde{y}\tilde{p}}=\dot{\gamma }_{yp}(0)\) and \(\overrightarrow{\tilde{y}\tilde{q}}=\dot{\gamma }_{yq}(0)\). Note, by (45), that the vectors \(\overrightarrow{\tilde{y}\tilde{x}}\) and \(\dot{\gamma }_{yx}(0)\) are in the same 2-dimensional Euclidean plane. It follows from (41), together with (44), that there exists some \(\lambda >0\) such that

$$\begin{aligned} \lambda \overrightarrow{\tilde{y}\tilde{x}}=\dot{\gamma }_{yx}(0)=a_t\dot{\gamma }_{yp}(0)+b_t\dot{\gamma }_{yq}(0). \end{aligned}$$
(46)

Note that \(\tilde{x}\) lies actually in the open interval \((\tilde{p},\tilde{q})\) in \({\mathbb {R}}^2\) (as \(0<t<1\) and so \( \angle \tilde{p}\tilde{y}\tilde{x}>0,\; \angle \tilde{q}\tilde{y}\tilde{x}>0\) by (41)). It follows from (46) that

$$\begin{aligned} a_t>0,\quad b_t>\quad \text{ and }\quad \frac{a_t+b_t}{\lambda }=1. \end{aligned}$$
(47)

Furthermore, in view of (42), we see that \(\lambda \le 1\) if \( \kappa \ge 0\) and \(\lambda \ge 1\) if \(\kappa \le 0\). This, together with (47), implies that (43) holds and the proof is complete. \(\square \)

Recall that M is assumed to be of constant sectional curvature \(\kappa \). Now, we are ready to verify the first theorem in the present section.

Theorem 4.1

Suppose \(\kappa >0\), and let \(f_0\) be the function defined by (36). Then, the sub-level set \(L_{c,f_0}\) is strongly convex if and only if either \(c\le 0\) or \(c\ge \frac{\Vert u_0\Vert D_\kappa }{2}\).

Proof

We first show the sufficiency part. To do this, suppose that \(c\le 0\) or \(c\ge \frac{\Vert u_0\Vert D_\kappa }{2}\). Note that if \(c\ge \frac{\Vert u_0\Vert D_\kappa }{2}\), then \(L_{c,f_0}={\mathbb {B}}(x_0,\frac{D_\kappa }{2})\) is strongly convex because

$$\begin{aligned} f_0(x)=\langle u_0,\dot{\gamma }_{x_0x}(0)\rangle \le \Vert u_0\Vert \cdot \Vert \dot{\gamma }_{x_0x}(0)\Vert \le \frac{\Vert u_0\Vert D_\kappa }{2}\le c. \end{aligned}$$

holds for all \(x\in {\mathbb {B}}(x_0,\frac{D_\kappa }{2})\). Thus, we need only to consider the case when \(c\le 0\). To proceed, fix \(c\le 0\), and let \(p,q\in L_{c,f_0}\), that is,

$$\begin{aligned} \langle u_0,\dot{\gamma }_{x_0p}(0)\rangle \le c\quad \text{ and }\quad \langle u_0,\dot{\gamma }_{x_0q}(0)\rangle \le c. \end{aligned}$$
(48)

Then, \(p,q\in {\mathbb {B}}(x_0,\frac{D_\kappa }{2})\) and the geodesic triangle \(\triangle (x_0pq)\) is well defined with perimeter less than \(2D_\kappa \). Let \(t\in [0,1]\). By assumption, Lemma 4.2 is applicable to concluding that there exist two positive numbers \(a_t\) and \(b_t\) satisfying with \(a_t+b_t\ge 1\) such that

$$\begin{aligned} \dot{\gamma }_{x_0\gamma (t)}(0)=a_t\dot{\gamma }_{x_0p}(0)+b_t\dot{\gamma }_{x_0q}(0), \end{aligned}$$

where \(\gamma :=\gamma _{pq}:[0,1]\rightarrow M\) is the unique minimal geodesic joining p and q. It follows from (36) and (48) that

$$\begin{aligned} f_0(\gamma (t)) =a_t\langle u_0,\dot{\gamma }_{x_0p}(0)\rangle +b_t\langle u_0,\dot{\gamma }_{x_0q}(0)\rangle \le c(a_t+b_t)\le c \end{aligned}$$

(note that \(c<0\)). This means that \(\gamma _{p,q}(t)=\gamma (t)\in L_{c,f_0}\) for all \(t\in [0,1]\), and so \(L_{c,f_0}\) is strongly convex as desired to show. The proof for the sufficiency part is complete.

To show the necessity part, without loss of generality, we may assume that \(\Vert u_0\Vert =1\). Let \(0<c<\frac{D_\kappa }{2}\). It suffices to verify that \(L_{c,f_0}\) is not strongly convex, or equivalently, to construct two points \(p,\,q\) and a number \(\bar{t}\in ]0,1[\) such that

$$\begin{aligned} p, q\in L_{c,f_0}\quad \text{ and }\quad \bar{z}:=\gamma _{pq}(\bar{t})\notin L_{c,f_0}. \end{aligned}$$
(49)

To do this, consider the geodesic \(\gamma :[0, \frac{D_\kappa }{2})\rightarrow M\) defined by

$$\begin{aligned} \gamma (t):=\exp _{x_0}tu_0\quad \text{ for } \text{ each } \quad t\in \bigg [0,\frac{D_\kappa }{2}\bigg [. \end{aligned}$$
(50)

Clearly, it is contained in \({\mathbb {B}}\left( x_0,\frac{D_\kappa }{2}\right) \). Since \({\mathbb {B}}\left( x_0,\frac{D_\kappa }{2}\right) \) is strongly convex, we see that, for each \( t\in [0, \frac{D_\kappa }{2}[\), the unique minimal geodesic joining \(x_0\) and \(\gamma (t)\) can be expressed as

$$\begin{aligned} \gamma _{x_0\gamma (t)}(s)=\exp _{x_0}s(tu_0) \quad \text{ for } \text{ each } s\in [0,1]. \end{aligned}$$

This in particular implies that, for each \( t\in [0, \frac{D_\kappa }{2}[\), \(\dot{\gamma }_{x_0\gamma (t)}(0)=tu_0\) and so

$$\begin{aligned} f_0(\gamma (t))=\langle u_0,\dot{\gamma }_{x_0\gamma (t)}(0)\rangle =\langle u_0,tu_0\rangle =t. \end{aligned}$$

Hence,

$$\begin{aligned} \gamma (t) \in L_{c,f_0} \text{ for } \text{ all } t\in [0,c]\quad \text{ and }\quad \gamma (t)\not \in L_{c,f_0} \text{ for } \text{ all } t\in \quad \left]c,\frac{D_\kappa }{2}\right[ \end{aligned}$$
(51)

In particular, \(z:=\gamma (c) \in L_{c,f_0}\) with

$$\begin{aligned} \mathrm{d}({x_0},z)=c<\frac{D_\kappa }{2} \end{aligned}$$
(52)

by the choice of c. Take \(u\in T_zM\) such that \(u\perp \dot{\gamma }(c)\). Then, by (52), there exists some \(\varepsilon >0\) such that the geodesic \(\tau :[-\varepsilon ,\varepsilon ]\rightarrow M\), determined by

$$\begin{aligned} \tau (0)=z\quad \text{ and }\quad \dot{\tau }(0)=u, \end{aligned}$$
(53)

is contained in \({\mathbb {B}}\left( x_0,\frac{D_\kappa }{2}\right) \cap {\mathbb {B}}\left( z,\frac{D_\kappa }{2}\right) \). Set \(p_{\varepsilon }:=\tau (\varepsilon )\) and \(q_{\varepsilon }:=\tau (-\varepsilon )\). Then,

$$\begin{aligned} p_{\varepsilon },\;q_{\varepsilon }\in {\mathbb {B}}\left( x_0,\frac{D_\kappa }{2}\right) \cap {\mathbb {B}}\left( z,\frac{D_\kappa }{2}\right) . \end{aligned}$$
(54)

Below, we shall show that

$$\begin{aligned} p_\varepsilon ,\;q_\varepsilon \in L_{c,f_0} \text{ with } f_0(p_\varepsilon )<c \text{ and } f_0(q_\varepsilon )<c. \end{aligned}$$
(55)

Consider the geodesic triangle \(\triangle (x_0zp_\varepsilon )\). Then, its perimeter is less than \(2D_\kappa \) thanks to (52) and (54). Thus, Proposition 4.2 is applicable, and using (39), we have that

$$\begin{aligned} \begin{array}{ll} \mathrm{d}^2(x_0,p_\varepsilon )&{}<\mathrm{d}^2(x_0,z)+\mathrm{d}^2(z,p_\varepsilon )-2\mathrm{d}(x_0,z)\mathrm{d}(z,p_\varepsilon )\cos \angle p_\varepsilon zx_0\\ &{}=\mathrm{d}^2(x_0,z)+\mathrm{d}^2(z,p_\varepsilon ) \end{array} \end{aligned}$$

(noting that \(\angle p_\varepsilon zx_0=\frac{\pi }{2}\) as \(\dot{\tau }(0)\perp \dot{\gamma }(c)\)), and

$$\begin{aligned} \mathrm{d}^2(z,p_\varepsilon )<\mathrm{d}^2(x_0,z)+\mathrm{d}^2(x_0,p_\varepsilon )-2\mathrm{d}(x_0,z)\mathrm{d}(x_0,p_\varepsilon )\cos \angle p_\varepsilon x_0z. \end{aligned}$$

Combining these two inequalities, we get that

$$\begin{aligned} \mathrm{d}(x_0,p_\varepsilon )\cos \angle p_\varepsilon x_0z<\mathrm{d}(x_0,z). \end{aligned}$$

Thus,

$$\begin{aligned} f_0(p_\varepsilon )=\mathrm{d}(x_0,p_\varepsilon )\cdot \Vert u_0\Vert \cdot \cos \angle p_\varepsilon x_0z=\mathrm{d}(x_0,p_\varepsilon )\cos \angle p_\varepsilon x_0z<\mathrm{d}(x_0,z)=c, \end{aligned}$$

where the last equality holds because of (52). Similarly, we have \(f_0(q_\varepsilon )<c\) and (55) is shown.

Let \(\gamma _{x_0}:[0,\infty )\rightarrow M\) be the geodesic satisfying \(\gamma _{x_0}\mid _{[0,1]}=\gamma _{x_0p_\varepsilon }\). In light of (54) and (55), we get by the continuity of \(f_0\) that there exists \(t_0>1\) such that \(\gamma _{x_0}\mid _{[0,t_0]}\) is the minimal geodesic joining \(x_0\) and \(\gamma _{x_0}(t_0)\) and \(\gamma _{x_0}(t_0)\in L_{c,f_0}\). Set \(p :=\gamma _{x_0}(t_0)\) and \(q:=q_{\varepsilon }\). Then, \(p,\; q\in L_{c,f_0}\) \(\left( \text {and so } p,q\in {\mathbb {B}}\left( x_0,\frac{D_\kappa }{2}\right) \right) \). Since \({\mathbb {B}}\left( x_0,\frac{D_\kappa }{2}\right) \) is strongly convex by Proposition 4.1(ii), it follows that \(\gamma _{pq}\subset {\mathbb {B}}(x_0,\frac{D_\kappa }{2})\). We further show that

$$\begin{aligned} \bar{z}:=\gamma _{pq}(\bar{t})\notin L_{c,f_0} \; \text{ for } \text{ some } \bar{t}\in ]0,1[. \end{aligned}$$
(56)

Granting this, (49) is established. To show (56), write

$$\begin{aligned} N:=\exp _z\{\mathrm{span}\{\dot{\gamma }(c),\dot{\tau }(0)\}\} \end{aligned}$$

where \(\tau \) and \(\gamma \) are geodesics defined by (53) and (50), respectively. Then, N is isometric to \(\mathbb {S}_{\kappa }^2\) by Proposition 4.3, and we assume that \(N=\mathbb {S}_{\kappa }^2\) without loss of generality. Noting that \(x_0=\gamma (0)\), \(z=\gamma (c)=\tau (0)\), \(p_\varepsilon =\tau (\varepsilon )\) and \(q=\tau (-\varepsilon )\), we have that \(x_0,q,p_\varepsilon ,z\) lie in \(\mathbb {S}_{\kappa }^2\). Recall that \(\gamma _{x_0}\) is the geodesic passing through \(x_0\) and \(p_\varepsilon \). It follows that \(p=\gamma _{x_0}(t_0)\) is also in \(\mathbb {S}_{\kappa }^2\). By the definition of the geodesic \(\gamma \) and the choice of the points \(p,\,q\) in the two-dimensional sphere \(\mathbb {S}_{\kappa }^2\), one checks that \(\gamma _{pq}\) must meet \(\gamma \) at some point \(\bar{z}:=\gamma _{pq}(\bar{t})=\gamma (c_0)\) with \(\bar{t}\in (0,1)\) and \(c_0>c\) (see Fig. 3). Hence, \(\bar{z}\not \in L_{c,f_0}\) thanks to(51). Thus, (56) is shown, and the proof is complete. \(\square \)

Fig. 3
figure 3

Non-convexity of the sub-level set \(L_{c,f}\) for some \(0<c<\frac{D_\kappa }{2}\) in Theorem 4.1

Full size image

Our second theorem in this section is Theorem 4.2 below, which is an analogue of Theorem 4.1 on Hadamard manifold of constant sectional curvature. In particular, Theorem 4.2 improves and extends the corresponding result in [7, Corollary 3.1], where it was shown that the sub-level sets \(L_{c,f_0}\) are convex in the special case when \(c=0\). The proof of Theorem 4.2 is quite similar to that we did for Theorem 4.1 and so we omit it here.

Theorem 4.2

Suppose \(\kappa <0\), and let \(f_0\) be the function defined by (37). Then, \(L_{c,f_0}\) is convex if and only if \(c\ge 0\).

As a direct consequence of Theorems 4.1 and 4.2, together with Proposition 2.2, we have the following corollary which shows that the function defined by (36) is not quasi-convex in general.

Corollary 4.1

Suppose that M is of nonzero constant sectional curvature. Let \(x_0\in M\) and \(u_0\in T_{x_0}M\setminus \{0\}\). Then, the functions defined by (36) are not quasi-convex.

5 Conclusions

The function \(f_0:M\rightarrow {\mathbb {R}}\) defined by (36) is widely used in equilibrium problems, vector optimization problems, and the proximal point algorithm in Riemannian manifolds. Such class of functions is clearly linear affine in Euclidean spaces; we obtain some basic results related to the function \(f_0\), and our results show that it is not quasi-convex even in Poincaré plane. Moreover, we estimate the constant c such that the sub-level set \(L_{c,f_0}\) is strongly convex in Riemannian manifolds of constant curvatures. The results could be used to study some existence results in equilibrium problems and vector optimization problems in Riemannian manifolds of constant curvatures. However, it remains open to estimate the constant c such that the sub-level set \(L_{c,f_0}\) is strongly convex in general Riemannian manifolds, or in Riemannian manifolds of bounded constant curvatures, and this is one possible direction for our future work.