Abstract
This paper gives new existence results for elliptic and evolutionary variational and quasi-variational inequalities. Specifically, we give an existence theorem for evolutionary variational inequalities involving different types of pseudo-monotone operators. Another existence result embarks on elliptic variational inequalities driven by maximal monotone operators. We propose a new recessivity assumption that extends all the classical coercivity conditions. We also obtain criteria for solvability of general quasi-variational inequalities treating in a unifying way elliptic and evolutionary problems. Two of the given existence results for evolutionary quasi-variational inequalities rely on Mosco-type continuity properties and Kluge’s fixed point theorem for set-valued maps. We also focus on the case of compact constraints in the evolutionary quasi-variational inequalities. Here a relevant feature is that the underlying space is the domain of a linear, maximal monotone operator endowed with the graph norm. Applications are also given.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, the theory of quasi-variational inequalities has emerged as one of the most promising domains of applied mathematics. Quasi-variational inequalities not only subsume variational inequalities and nonlinear partial differential inequations, they also provide a unified framework for studying general boundary value problems with complicated, possibly unilateral, boundary conditions. This field offers us a powerful mathematical apparatus for investigating a wide range of problems arising in diverse domains such as mechanics, economics, finance, optimization, optimal control, and others, see [1–30]. The existence and the approximation theories for quasi-variational inequalities require that a variational inequality and a fixed point problem be solved simultaneously. As a result, many solution techniques which are readily available for variational inequalities cannot be extended for quasi-variational inequalities in a straightforward manner. In this paper, our primary objective is to give new existence results for elliptic and evolutionary quasi-variational inequalities. This work on quasi-variational inequalities subsumes many known results and presents new ones for elliptic and evolutionary quasi-variational inequalities, as well as elliptic and evolutionary variational and hemivariational inequalities, and numerous boundary value problems.
The rest of the paper is organized as follows. Section 2 describes the problem formulation. Section 3 contains preliminaries that are needed in the sequel. Section 4 is devoted to variational inequalities. Section 5 sets forth the results on quasi-variational inequalities. Section 6 presents applications of the abstract results.
2 Problem Formulation
Given a Banach space \({\mathcal {Z}}\) with the topological dual \({\mathcal {Z}}^*\), the duality pairing between \({\mathcal {Z}}\) and \({\mathcal {Z}}^*\) will be denoted by \(\langle \cdot ,\cdot \rangle _{{\mathcal {Z}}}\). By \(\displaystyle \Vert \cdot \Vert _{{\mathcal {Z}}}\) we denote the norm on \({\mathcal {Z}}\). The domain and the graph of a multi-valued map \({\mathcal {F}}:{\mathcal {Z}}\rightrightarrows {\mathcal {Z}}^*\) are given by \(D({\mathcal {F}}):=\{x\in {\mathcal {Z}}|\ {\mathcal {F}}(x)\ne \emptyset \}\), and \(G({\mathcal {F}}):=\{(x,w)|\ x\in D({\mathcal {F}}), \ w\in {\mathcal {F}}(x)\}\), respectively. We denote the (effective) domain of a functional \(\varPhi :{\mathcal {Z}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\), which is \(\not \equiv +\infty \), by \( D(\varPhi ):=\{x\in {\mathcal {Z}}|\ \varPhi (x)<+\infty \}\). The strong convergence and the weak convergence are specified by \(\rightarrow \) and \(\rightharpoonup ,\) respectively.
To define the quasi-variational inequality that is the focus of this study, we first introduce the data. Let \({\mathcal {X}}\) and \({\mathcal {Y}}\) be reflexive Banach spaces with a compact linear map \(i:{\mathcal {X}}\rightarrow {\mathcal {Y}}\), and let \({\mathcal {L}}:D({\mathcal {L}})\subseteq {\mathcal {X}}\rightarrow {\mathcal {X}}^*\) be a linear, maximal monotone map. Let \({\mathcal {A}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) and \({\mathcal {B}}:{\mathcal {Y}}\rightrightarrows {\mathcal {Y}}^*\) be multi-valued maps, let \({\mathcal {K}}\) be a nonempty, closed, and convex subset of \({\mathcal {X}}\), let \(\varPhi :{\mathcal {X}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) be a functional \(\not \equiv +\infty \), and let \({\mathcal {C}}:{\mathcal {K}}\rightrightarrows {\mathcal {K}}\) be a multi-valued map such that for any \(z\in {\mathcal {K}}\), \({\mathcal {C}}(z)\) is a nonempty, closed, and convex subset of \({\mathcal {K}}\), and let \(f\in {\mathcal {X}}^*\). With these data, we formulate the following quasi-variational inequality: find \(x\in {\mathcal {C}}(x)\cap D({\mathcal {L}})\cap D(\varPhi )\) such that for some \(a\in {\mathcal {A}}(x)\) and \(b\in {\mathcal {B}}(ix),\) we have
The statement of (1) incorporates evolutionary inequality problems thanks to the presence of the possibly unbounded operator \({\mathcal {L}}\) whose prototype is the time derivative \({\mathcal {L}}(x)=x'\) on a space as \({\mathcal {X}}=L^p(0,\tau ,{\mathcal {V}})\), with \(1<p<+\infty \), \(\tau >0\), and a reflexive Banach space \({\mathcal {V}}\). A detailed study of this setting can be found in Zeidler [30] (see also [7]). We emphasize that the constraint set \({\mathcal {C}}(x)\) in (1) depends on the solution x. This dependence poses serious challenges and is the main reason that a majority of techniques which are available for variational inequalities have not yet been fully extended to quasi-variational inequalities.
Quasi-variational inequality (1) is quite general covering both elliptic and evolutionary problems and conveniently includes many important situations and applications of interest as special cases. In this direction we mention just a simple but relevant example, namely that if the map \({\mathcal {A}}\) is single-valued with \(D({\mathcal {A}})={\mathcal {X}}\), \(\varPhi =0\), \({\mathcal {B}}=0\), and \({\mathcal {L}}=0\), then (1) reduces to the quasi-variational inequality given by Bensoussan and Lions [6]: find \(x\in {\mathcal {C}}(x)\) such that
If additionally \({\mathcal {C}}(x)={\mathcal {K}}\) for every \(x\in {\mathcal {K}},\) then it recovers the standard statement of variational inequality (see [10, 20]): find \(x\in {\mathcal {K}}\) such that
A powerful technique for solving quasi-variational inequalities is by finding fixed points of the associated variational selection which is defined below. For any \(w\in {\mathcal {K}}\), we consider the following parametric evolutionary variational inequality: find \(x\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\cap D(\varPhi )\) such that for some \(a\in {\mathcal {A}}(x)\) and \(b\in {\mathcal {B}}(ix)\) and for all \(z\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\), we have
This permits us to define a set-valued map, commonly termed as variational selection,
by the condition that for each \(y\in {\mathcal {K}}\), the image \({\mathcal {S}}(y)\) is the set of all solutions of (2). Note that if x is a fixed point of the set-valued map \({\mathcal {S}}\) in (3), that is, \(x\in {\mathcal {S}}(x),\) then x solves the evolutionary quasi-variational inequality (1).
One of the primary objectives of this work is to study a quite general class of variational inequalities. Our first result is Theorem 4.1, which deals with evolutionary variational inequalities involving different types of pseudo-monotone operators. In Theorem 4.2 we give a new existence result for elliptic variational inequalities with generalized pseudo-monotone maps. Moreover, in Theorem 4.3 we give another new existence result for variational inequalities for pseudo-monotone maps. Another existence result, which is stated as Theorem 4.4, embarks on elliptic variational inequalities driven by maximal monotone operators. Our results cover new situations. For example, the recessivity assumption \((H_2)\) (see below) extends all the classical coercivity conditions. Another trait of interest of our results is that the imposed assumptions exploit the interplay between the properties of the operators involved in the problem and the geometry of the sets of constraints, for instance their exterior normal cones.
Another major goal of our work is to obtain criteria for solvability of general quasi-variational inequalities as stated in problem (1) treating in a unifying way elliptic and evolutionary problems. Here our first main result is Theorem 5.1, which is based on Mosco-type continuity properties and Kluge’s fixed point theorem for set-valued maps. In Theorem 5.3 we give an existence result for quasi-variational inequalities where the focus is on maximal monotone maps. As a tool to prove this existence result, we also give the Minty formulation for evolutionary variational inequalities. Finally, in Theorem 5.4 we focus on the case of compact constraints in the evolutionary quasi-variational inequalities. A relevant feature is that the underlying space is the domain of the linear, maximal operator \({\mathcal {L}}\) endowed with the graph norm. Examples and applications of abstract results, specifically of Theorem 5.1, are given in Theorems 6.1 and 6.2.
3 Preliminaries
In this section, we collect a few notions and results to be used later in the paper. For this, we first recall the basic classes of functions that will be dealt with in the present work.
Definition 3.1
Given a Banach space \({\mathcal {X}}\), let \({\mathcal {F}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) be a set-valued map.
-
\({\mathcal {F}}\) is called monotone, iff \(\langle u-v,x-y\rangle _{\mathcal {X}} \ge 0\) for every \((x,u),(y,v)\in G({\mathcal {F}})\).
-
\({\mathcal {F}}\) is called maximal monotone, iff \({\mathcal {F}}\) is monotone and \(G({\mathcal {F}})\) is not included in the graph of any other monotone map with the same domain.
-
\({\mathcal {F}}\) is called generalized pseudo-monotone iff for any sequence \(\{(x_n,w_n)\}\subset G({\mathcal {F}})\) with \(x_n\rightharpoonup x\) and \(w_n\rightharpoonup w\) such that \(\displaystyle \limsup _{n\rightarrow \infty }\langle w_n,x_n-x\rangle _{\mathcal {X}}\le 0 ,\) we have \(w\in {\mathcal {F}}(x)\) and \(\langle w_n,x_n\rangle _{\mathcal {X}}\rightarrow \langle w,x\rangle _{\mathcal {X}}.\)
Definition 3.2
The set-valued map \({\mathcal {F}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) on a Banach space \({\mathcal {X}}\) is called pseudo-monotone iff it satisfies the conditions:
-
(PM1)
For each \(x\in {\mathcal {X}},\) the set \({\mathcal {F}}(x)\) is nonempty, closed, and convex in \({\mathcal {X}}^*\).
-
(PM2)
For any sequence \(\{(x_n,w_n)\}\subset G({\mathcal {F}})\) such that \(x_n\rightharpoonup x\) and \(\displaystyle \limsup _{n\rightarrow \infty }\langle w_n,x_n-x\rangle _{\mathcal {X}}\le 0 ,\) then for each \(y\in {\mathcal {X}}\) there exists \(w(y)\in {\mathcal {F}}(x)\) satisfying \(\displaystyle \liminf _{n\rightarrow \infty }\langle w_n,x_n-y\rangle _{\mathcal {X}}\ge \langle w(y),x-y \rangle _{\mathcal {X}}.\)
-
(PM3)
The map \({\mathcal {F}}\) is upper semicontinuous from each finite-dimensional subspace of \({\mathcal {X}}\) to the weak-topology of \({\mathcal {X}}^*\).
Remark 3.1
Kenmochi [16] showed that a set-valued map \({\mathcal {F}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) with \(D({\mathcal {F}})={\mathcal {X}}\) on a reflexive Banach space \({\mathcal {X}}\) verifying (PM1), (PM2) of Definition 3.2 is pseudo-monotone if it satisfies the condition:
-
(PM4)
For each \(x\in {\mathcal {X}}\) and for each bounded subset B of \({\mathcal {X}}\), there exists a constant c(B, x) such that for every \((z,u)\in G({\mathcal {F}})\) with \(z\in B\), it holds \(\langle u,z-x\rangle _{\mathcal {X}} \ge c(B,x).\)
The above condition is fulfilled by any monotone map \({\mathcal {F}}\) with \(D({\mathcal {F}})={\mathcal {X}}\) as well as by bounded maps.
Remark 3.2
A pseudo-monotone map \({\mathcal {F}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) on a reflexive Banach space \({\mathcal {X}}\) is a generalized pseudo-monotone. Conversely, a generalized pseudo-monotone and bounded map \({\mathcal {F}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) on a reflexive Banach space \({\mathcal {X}}\) satisfying (PM1) is pseudo-monotone (see [7]).
We quote from Kenmochi [16, Proposition 4.1] the following result:
Theorem 3.1
Let \(F:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) be a set-valued map on a reflexive Banach space \({\mathcal {X}}\) satisfying (PM1), (PM2), and (PM4), let C be a nonempty, closed, convex, and bounded subset of \({\mathcal {X}}\), let \(\varPhi :{\mathcal {X}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) be lower semicontinuous, convex, with \(C\cap D(\varPhi )\not =\emptyset \), and let \(f\in {\mathcal {X}}^*\). Then there exists \(x\in C\cap D(\varPhi )\) such that for some \(w\in F(x)\) we have
Next we quote the following result from Lunsford [26, Theorem 3.1].
Theorem 3.2
Let X be a separable Banach space with its topological dual \(X^*\) and let K be a nonempty, compact, convex subset of X. Let the set-valued maps \(F:K\rightrightarrows X^*\) and \(G:K\rightrightarrows K\) satisfy the conditions:
-
(i)
The map \(M:K\rightrightarrows K\) defined by
$$\begin{aligned} M(x):=\left\{ z\in K|\inf _{w\in F(x)}\langle w,x-z \rangle _X\le 0\right\} \end{aligned}$$has a closed graph.
-
(ii)
G is lower semicontinuous and has closed graph and nonempty convex values.
Then there exists a fixed point \(x\in G(x)\) such that
If, in addition, F(x) is weakly compact, then there exists \(w\in F(x)\) such that
We also recall the continuity property introduced by Mosco [27, 28].
Definition 3.3
Given a nonempty, closed, and convex subset \({\mathcal {K}}\) of a reflexive Banach space \({\mathcal {X}}\), a map \({\mathcal {C}}:{\mathcal {K}}\rightrightarrows {\mathcal {K}}\) is called M-continuous iff the following conditions hold:
-
(M1)
For any sequence \(\{x_n\}\subset {\mathcal {K}}\) with \(x_n\rightharpoonup x,\) and for each \(y\in {\mathcal {C}}(x),\) there exists \(\{y_n\}\) such that \(y_n\in {\mathcal {C}}(x_n)\) and \(y_n\rightarrow y\).
-
(M2)
For \(y_n\in {\mathcal {C}}(x_n)\) with \(x_n\rightharpoonup x\) and \(y_n\rightharpoonup y,\) we have \(y\in {\mathcal {C}}(x).\)
Remark 3.3
We will make use in Theorem 5.1 below of an M-continuity property of a map \({\mathcal {C}}:{\mathcal {K}}\rightrightarrows {\mathcal {K}}\) relative to a function \(\varPhi :{\mathcal {X}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) which is \(\not \equiv +\infty \) (see condition \((A_8)\)).
The following estimate by Alber and Notik [2] will also be useful:
Lemma 3.1
Let Z be a reflexive Banach space with \(Z^*\) as its dual. Let \({\mathcal {A}}:Z\rightrightarrows Z^*\) be a monotone map with \(\bar{x}\in int(D({\mathcal {A}})).\) Then there exists a constant \(r=r(\bar{x})>0\) such that for every \((x,w)\in G({\mathcal {A}})\) and corresponding \(c:=\sup \{\Vert w'\Vert |\ \Vert x'-\bar{x}\Vert \le r,\ \ \text {and}\ \ w'\in {\mathcal {A}}(x')\}<\infty ,\) we have
We conclude this section by stating for easy reference the fixed point theorem of Kluge [21]:
Theorem 3.3
Let \({\mathcal {Z}}\) be a real reflexive Banach space and let \({\mathcal {D}}\subset {\mathcal {Z}}\) be nonempty, convex, bounded, and closed. Assume that \(P:{\mathcal {D}}\rightrightarrows {\mathcal {D}}\) is a set-valued map such that for every \(u\in {\mathcal {D}}\), the set P(u) is nonempty, closed, and convex, and its graph G(P) is weakly closed. Then P has a fixed point.
Remark 3.4
In Theorem 3.3, the hypothesis on the set \({\mathcal {D}}\) to be bounded in \({\mathcal {Z}}\) can be replaced by requiring that the image \(P({\mathcal {D}})\) be bounded. For this it is sufficient to apply Theorem 3.3 to the closed convex hull \(\overline{\mathrm{co}}(P({\mathcal {D}}))\) of \(P({\mathcal {D}})\) in place of \({\mathcal {D}}\).
4 Existence Results for Variational Inequalities
The first step toward developing an existence theory for quasi-variational inequalities is to ensure that for every parameter \(w\in {\mathcal {K}}\), the corresponding parametric variational inequality (2) is solvable. Our aim in this section is to give general existence results for elliptic and evolutionary variational inequalities to be applied later on to quasi-variational inequalities.
Theorem 4.1
Given the reflexive Banach spaces \({\mathcal {X}}\) and \({\mathcal {Y}}\) with a compact linear map \(i:{\mathcal {X}}\rightarrow {\mathcal {Y}}\), and a closed convex subset \({\mathcal {K}}\) of \({\mathcal {X}}\) with nonempty interior \(\mathrm{int}{\mathcal {K}}\), assume that:
-
(\(A_1\)) \({\mathcal {L}}:D({\mathcal {L}})\subseteq {\mathcal {X}}\rightarrow {\mathcal {X}}^*\) is linear, maximal monotone.
-
(\(A_2\)) \({\mathcal {A}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) is bounded, pseudo-monotone.
-
(\(A_3\)) \({\mathcal {B}}:{\mathcal {Y}}\rightrightarrows {\mathcal {Y}}^*\) is bounded, sequentially strongly-weakly graph closed (i.e., if \((y_n,b_n)\in G({\mathcal {B}})\) with \(y_n\rightarrow y\) in \({\mathcal {Y}}\) and \(b_n\rightharpoonup b\) in \({\mathcal {Y}}^*\), then \((y,b)\in G({\mathcal {B}})\)), and has nonempty, convex, closed values.
-
(\(A_4\)) \(\varPhi :{\mathcal {K}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) is convex, lower semicontinuous, and
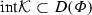 .
. -
(\(A_5\)) \(f\in {\mathcal {X}}^*\), and when the set \({\mathcal {K}}\) is unbounded in \({\mathcal {X}}\) there exist
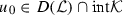 and an \(r>0\) satisfying $$\begin{aligned} \langle a,v-u_0\rangle _{{\mathcal {X}}}+\langle b,iv-iu_0\rangle _{{\mathcal {Y}}}>\langle f,v-u_0 \rangle _{{\mathcal {X}}} \end{aligned}$$
and an \(r>0\) satisfying $$\begin{aligned} \langle a,v-u_0\rangle _{{\mathcal {X}}}+\langle b,iv-iu_0\rangle _{{\mathcal {Y}}}>\langle f,v-u_0 \rangle _{{\mathcal {X}}} \end{aligned}$$for all \(a\in {\mathcal {A}}(v)\), \(b\in {\mathcal {B}}(iv)\), \(v\in {\mathcal {X}}\) with \(\Vert v\Vert _{\mathcal {X}}>r\).
Then there exists a solution of the following variational inequality: find \(u\in {\mathcal {K}}\cap D({\mathcal {L}})\cap D(\varPhi )\) such that for some \(a\in {\mathcal {A}}(u)\) and \(b\in {\mathcal {B}}(iu)\) we have
Proof
Define \(\varPsi :{\mathcal {X}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) by
From assumption \((A_4)\), it follows that \(\varPsi \) is convex, lower semicontinuous and \(\not \equiv +\infty \). We note that problem (5) is equivalent to the following statement: find \(u\in D({\mathcal {L}})\cap D(\varPsi )\) such that for some \(a\in {\mathcal {A}}(u)\) and \(b\in {\mathcal {B}}(iu)\) it holds
In turn, (6) is equivalent to the inclusion problem: find \(u\in D({\mathcal {L}})\cap D(\partial \varPsi )\) such that
where the notation \(\partial \varPsi \) stands for the subdifferential of \(\varPsi \) in the sense of convex analysis (see [18]). Indeed, admitting (6) we have
thus (7) ensues. Conversely, if (7) holds, then (6) follows by definition of the convex subdifferential \(\partial \varPsi (u)\). Therefore, in order to complete the proof, it suffices to show the solvability of (7).
Since  as known from hypothesis (\(A_4\)), it turns out that
as known from hypothesis (\(A_4\)), it turns out that

On the other hand, hypothesis (\(A_1\)) implies that
(see, e.g., [30, Theorem 32.L]). Then (9) yields

Due to (8) and (10), we are in a position to apply the sum theorem for maximal monotone operators obtaining
We claim that
Indeed, in view of the last part of assumption (\(A_3\)), the values of the operator \(i^*{\mathcal {B}}i\) are nonempty and convex. Let \(x\in {\mathcal {X}}\) and \(\{b_n\}\subset {\mathcal {B}}(ix)\) with \(i^*b_n\rightarrow z\) in \({\mathcal {X}}^*\). By (\(A_3\)), \(\{b_n\}\) is bounded in \({\mathcal {Y}}^*\), so along a relabeled subsequence we have \(b_n\rightharpoonup b\) in \({\mathcal {Y}}^*\) with \(b\in {\mathcal {B}}(ix)\), so \(z=i^*b\) showing that the set-valued mapping \(i^*{\mathcal {B}}i\) is closed valued. Furthermore, we note that if \(x_n\rightharpoonup x\) in \({\mathcal {X}}\) and \(w_n\rightharpoonup w\) in \({\mathcal {X}}^*\), with \(w_n\in i^*{\mathcal {B}}(ix_n)\), then \(ix_n\rightarrow ix\) in \({\mathcal {Y}}\) (because \(i:{\mathcal {X}}\rightarrow {\mathcal {Y}}\) is compact) and \(w_n=i^*b_n\) with \(b_n\in {\mathcal {B}}(ix_n)\). Since by assumption (\(A_3\)), \({\mathcal {B}}\) is bounded, along a relabeled subsequence there holds \(b_n\rightharpoonup b\) in \({\mathcal {Y}}^*\). Using once again (\(A_3\)), this results in \(b\in {\mathcal {B}}(ix)\). We infer that \(i^*b_n\rightarrow i^*b\) in \({\mathcal {Y}}^*\) because \(i^*\) is compact, thus we can conclude that \(w_n\rightarrow w=i^*b\in i^*{\mathcal {B}}(ix)\). From this, taking into account Definition 3.2, it is straightforward to derive (12).
Since the sum of pseudo-monotone operators is pseudo-monotone, from (\(A_2\)) and (12) it follows that
Now on the basis of (11), (13) and assumption (\(A_5\)), the main theorem on pseudo-monotone perturbations of maximal monotone mappings (see [30, Theorem 32.A and problem 32.4*]) implies that inclusion (7) holds true for some \(u\in D({\mathcal {L}})\cap D(\partial \varPsi )\). The second inclusion in (8) ensures \(u\in {\mathcal {K}}\). The equivalence between problems (5) and (7) completes the proof. \(\square \)
Remark 4.1
Theorem 4.1 extends different existence results for variational inequalities as well as variational-hemivariational inequalities as for instance [16, Theorem 4.1] and [25, Theorem 3.1] (see also [24]). Specifically, for variational-hemivariational inequalities, if \(g:{\mathcal {Y}}\rightarrow {\mathbb {R}}\) is a locally Lipschitz function, denoting its generalized gradient by \(\partial g:{\mathcal {Y}}\rightrightarrows {\mathcal {Y}}^*\), we can choose \({\mathcal {B}}=\partial g\). If the function g is convex, the generalized gradient \(\partial g\) becomes the subdifferential of g in the sense of convex analysis.
In the next result, we give a new existence result for multi-valued elliptic variational inequalities where the constraint set \({\mathcal {K}}\) could have an empty interior. The proof of this result relies on a novel asymptotic recessivity condition (see (\(H_2\))) and cannot be derived from the proof of Theorem 4.1.
Theorem 4.2
Given the reflexive Banach spaces \({\mathcal {X}}\) and \({\mathcal {Y}}\) with a compact linear map \(i:{\mathcal {X}}\rightarrow {\mathcal {Y}}\), and a nonempty closed convex subset \({\mathcal {K}}\) of \({\mathcal {X}},\) and \(f\in {\mathcal {X}}^*\), assume the conditions (\(A_2\)), (\(A_3\)), and
-
(\(H_1\)) \(\varPhi :{\mathcal {X}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) is convex, and lower semicontinuous and \(x_0\in {\mathcal {K}}\cap D(\varPhi )\).
-
(\(H_2\)) If K is unbounded, then for every \(\{x_n\}\subset {\mathcal {K}}\cap D(\varPhi )\) with \(\Vert x_n\Vert _{{\mathcal {X}}}\rightarrow \infty \) and \(\frac{x_n}{\Vert x_n\Vert _{{\mathcal {X}}}}\rightharpoonup x\) in \({\mathcal {X}}\), for every \(a_n\in {\mathcal {A}}(x_n)\), and for every \(b_n\in {\mathcal {B}}(ix_n),\) we have
$$\begin{aligned} \liminf _{n\rightarrow \infty }\frac{1}{\Vert x_n\Vert _{{\mathcal {X}}}}\left[ \langle a_n+i^*b_n,x_n-x_0\rangle _{{\mathcal {X}}}+\varPhi (x_n)\right] >\langle f,x\rangle _{{\mathcal {X}}}. \end{aligned}$$(14)
Then there exists a solution of the following variational inequality: find \(x\in {\mathcal {K}}\cap D(\varPhi )\) such that for some \(a\in {\mathcal {A}}(x)\) and for some \(b\in {\mathcal {B}}(ix)\) we have
Proof
For every integer n, we define \({\mathcal {K}}_n:={\mathcal {K}}\cap B_{{\mathcal {X}}}(x_0,n)\), where \(B_{{\mathcal {X}}}(x_0,n)\) stands for the closed ball in \({\mathcal {X}}\) of center \(x_0\) and of radius n. Here \(x_0\in {\mathcal {K}}\cap D(\varPhi )\) is the point given in assumption \((H_1)\). Note that \({\mathcal {K}}_n\) is closed, convex, and bounded in \({\mathcal {X}}\) with \(x_0\in {\mathcal {K}}_n.\) By virtue of (\(A_2\)), (\(A_3\)), as shown in the proof of Theorem 4.1, the map \(A+i^*{\mathcal {B}}i:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) is bounded and pseudo-monotone.
On the basis of the previous claim and of hypothesis \((H_1)\), we can apply Theorem 3.1, which ensures that there exists \(x_n\in {\mathcal {K}}_n\cap D(\varPhi )\) such that for some \(a_n\in {\mathcal {A}}(x_n)\) and for some \(b_n\in {\mathcal {B}}(ix_n)\) we have
Now we claim that there exists an integer \(k>0\) such that
Arguing by contradiction, assume that for every integer \(n>0\) it holds
Due to the reflexivity of \({\mathcal {X}}\), passing to a subsequence we can admit that \(\frac{x_n}{\Vert x_n\Vert _{{\mathcal {X}}}}\rightharpoonup x\) in \({\mathcal {X}}\) for some \(x\in {\mathcal {X}}\). By setting \(z=x_0\) in (16), we obtain
Passing to the limit as \(n\rightarrow \infty \) yields
contradicting (14). Therefore the sequence \(\{x_n\}\) is bounded in \({\mathcal {X}}\).
Let \(y\in {\mathcal {K}}\) be arbitrary. By (17), for sufficiently small \(t>0,\) we know that
Inserting \(z=x_{k}+t(y-x_{k})\), with a sufficiently small \(t>0,\) in (16) for \(n=k\) and using the convexity of \(\varPhi \), we deduce
where \(a_{k}\in {\mathcal {A}}(x_{k})\) and \(b_{k}\in {\mathcal {B}}(ix_{k})\) are independent of y. We conclude that \(x_{k}\) solves (15). The proof is thus complete.\(\square \)
The following new existence result for variational inequalities with pseudo-monotone maps can be proven by following the arguments used in the above result with \({\mathcal {B}}=0\) and by means of Remark 3.1.
Theorem 4.3
Given the reflexive Banach space \({\mathcal {X}}\) and a nonempty closed convex subset \({\mathcal {K}}\) of \({\mathcal {X}},\) and \(f\in {\mathcal {X}}^*\), assume (\(H_1\)), and
-
(\(C_1\)) \({\mathcal {A}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) is a set-valued map satisfying (PM1), (PM2), and (PM4).
-
(\(C_2\)) If K is unbounded, then for every \(\{x_n\}\subset {\mathcal {K}}\cap D(\varPhi )\) with \(\Vert x_n\Vert _{{\mathcal {X}}}\rightarrow \infty \) and \(\frac{x_n}{\Vert x_n\Vert _{{\mathcal {X}}}}\rightharpoonup x\) in \({\mathcal {X}}\), for every \(a_n\in {\mathcal {A}}(x_n)\), we have
$$\begin{aligned} \liminf _{n\rightarrow \infty }\frac{1}{\Vert x_n\Vert _{{\mathcal {X}}}}\left[ \langle a_n,x_n-x_0\rangle _{{\mathcal {X}}}+\varPhi (x_n)\right] >\langle f,x\rangle _{{\mathcal {X}}}. \end{aligned}$$(20)
Then there exists a solution of the following variational inequality: find \(x\in {\mathcal {K}}\cap D(\varPhi )\) such that for some \(a\in {\mathcal {A}}(x)\) we have
Now we present an existence theorem for variational inequalities targeting the case where the operator \({\mathcal {A}}\) is maximal monotone. Generally, in this situation we can have \(D({\mathcal {A}})\not ={\mathcal {X}},\) so none of the above theorems is applicable. For the sake of simplicity, we suppose that \({\mathcal {L}}=0\) and \({\mathcal {B}}=0\).
Theorem 4.4
Let \({\mathcal {K}}\) be a nonempty, closed, and convex subset of a reflexive Banach space \({\mathcal {X}}\), let \(f\in {\mathcal {X}}^*\) and let \(\varPhi :{\mathcal {X}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) be convex, lower semicontinuous. Assume the following conditions:
-
\((S_1)\) \({\mathcal {A}}:D({\mathcal {A}})\subseteq {\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) is a maximal monotone map, with \(0\in {\mathcal {K}}\cap int(D({\mathcal {A}}))\cap int(D(\partial \varPhi ))\), \(0\in {\mathcal {A}}(0)\), and the weak closure in \({\mathcal {X}}\) of \({\mathcal {K}}\cap D({\mathcal {A}})\cap D(\partial \varPhi )\) is contained in \(D({\mathcal {A}})\).
-
\((S_2)\) For every sequence \(\{x_n\}\subset {\mathcal {K}}\cap D({\mathcal {A}})\cap D(\partial \varPhi )\) with \(\Vert x_n\Vert _{{\mathcal {X}}}\rightarrow \infty \) and \(\frac{x_n}{\Vert x_n\Vert _{{\mathcal {X}}}}\rightharpoonup z\) in \({\mathcal {X}}\), we have
$$\begin{aligned} \liminf _{n\rightarrow \infty }\frac{\varPhi (x_n)}{\Vert x_n\Vert _{{\mathcal {X}}}}>\langle f,z\rangle _{{\mathcal {X}}}. \end{aligned}$$(22) -
\((S_3)\) For every \(x\in {\mathcal {K}}\cap D({\mathcal {A}})\cap D(\varPhi )\) there exists \(a=a(x)\in {\mathcal {A}}(x)\) such that if \(z\in {\mathcal {K}}\cap D(\varPhi )\) there are a sequence \(t_n\downarrow 0\) as \(n\rightarrow \infty \) with \(x+t_n(z-x)\in D({\mathcal {A}})\) and a sequence \(\xi _n\in {\mathcal {A}}((1-t_n)x+t_nz)\) satisfying
$$\begin{aligned} \liminf _{n\rightarrow \infty }\langle \xi _n,z-x\rangle _{{\mathcal {X}}}\le \langle a,z-x\rangle _{{\mathcal {X}}}. \end{aligned}$$
Then there exists \(x\in {\mathcal {K}}\cap D({\mathcal {A}})\cap D(\varPhi )\) such that for \(a=a(x)\in {\mathcal {A}}(x)\) given in (\(S_3\)), we have
Proof
Since \({\mathcal {X}}\) is reflexive, we can renorm it so that \({\mathcal {X}}\) and \({\mathcal {X}}^*\) become strictly convex. Define the set-valued map \({\mathcal {T}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) by \({\mathcal {T}}:={\mathcal {A}}+N_{{\mathcal {K}}}+\partial \varPhi \), where \(N_{{\mathcal {K}}}\) denotes the subdifferential of the indicator function of \({\mathcal {K}}\) (equivalently, \(N_{{\mathcal {K}}}(x)\) is the cone of exterior normals to \({\mathcal {K}}\) at \(x\in {\mathcal {K}}\)). Due to assumption (\(S_1\)), we know that \({\mathcal {T}}\) is a maximal monotone map (see, e.g., [30, Theorem 32.I]). By a classical surjectivity result, there exists \(x_n\in D({\mathcal {T}})={\mathcal {K}}\cap D({\mathcal {A}})\cap D(\partial \varPhi )\) such that \(f\in {\mathcal {T}}(x_n)+\epsilon _n J(x_n)\), where \(J:{\mathcal {X}}\rightarrow {\mathcal {X}}^*\) stands for the duality mapping of \({\mathcal {X}}\) and the sequence \(\{\epsilon _n\}\) satisfies \(\epsilon _n\downarrow 0\). Therefore, for every \(n\in {\mathbb {N}},\) there exist \(w_n\in {\mathcal {A}}(x_n)\), \(v_n\in N_{{\mathcal {K}}}(x_n),\) and \(u_n\in \partial \varPhi (x_n)\) such that
Thanks to the inequalities \(\langle v_n,y-x_n\rangle _{\mathcal {X}}\le 0\) and \(\varPhi (y)-\varPhi (x_n)\ge \langle u_n,y-x_n\rangle _{\mathcal {X}}\) whenever \(y\in {\mathcal {K}},\) it turns out
From this and the monotonicity of \({\mathcal {A}}\), we infer that
We claim that \(\{x_n\}\) is bounded. Arguing by contradiction, assume that there exists a relabeled subsequence such that \(\Vert x_n\Vert _{\mathcal {X}}\rightarrow \infty \) as \(n\rightarrow \infty \). In view of the reflexivity of \({\mathcal {X}}\), we can find \(z\in {\mathcal {X}}\) such that up to a subsequence it holds
Setting \(y=0\) and \(w=0\) in (24), which is possible according to assumption (\(S_1\)), and then dividing by \(\Vert x_n\Vert _{\mathcal {X}}\) and letting \(n\rightarrow \infty \) give
This contradicts assumption (\(S_2\)), which proves the claim.
The reflexivity of \({\mathcal {X}}\) enables us to pass to a subsequence still denoted \(\{x_n\}\) converging weakly in \({\mathcal {X}}\) to some \(x\in {\mathcal {K}}\). Letting \(n\rightarrow \infty \) in (24) yields
Setting \(y=0\) and \(w=0\) in (25) shows that \(x\in D(\varPhi )\), whereas from the last part of assumption (\(S_1\)) we know that \(x\in D({\mathcal {A}})\).
By virtue of hypothesis (\(S_3\)), to \(x\in {\mathcal {K}}\cap D({\mathcal {A}})\cap D(\varPhi )\) there corresponds an \(a\in {\mathcal {A}}(x)\) as stated therein. Let \(z\in {\mathcal {K}}\cap D(\varPhi )\). Then we can find \(t_n\downarrow 0\) as \(n\rightarrow \infty \) with \(x+t_n(z-x)\in D({\mathcal {A}})\) and a sequence \(\xi _n\in {\mathcal {A}}((1-t_n)x+t_nz)\) that fulfills
Since \((1-t_n)x+t_nz\in {\mathcal {K}}\cap D({\mathcal {A}})\), we can insert \(y=(1-t_n)x+t_nz\) in (25), which renders through the convexity of \(\varPhi \) that
In particular, we obtain
Then on the basis of (26) we get (23). Observe that (23) is valid for any \(z\in {\mathcal {K}}\) with \(\varPhi (z)=+\infty \), which completes the proof. \(\square \)
Remark 4.2
Condition (\(S_3\)) in the statement of Theorem 4.4 represents a multi-valued version of Minty technique for variational inequalities driven by single-valued monotone and hemicontinuous operators. Nonetheless, Theorem 5.2 gives a Minty formulation for evolutionary variational inequalities where it is shown that by assuming that \({\mathcal {K}}\subset int(D({\mathcal {A}}))\cap int(D(\partial \varPhi ))\), condition (\(S_3\)) can be dropped. We also note that the asymptotic recessivity (22) which played the central role in Theorem 4.4 is a condition that does not involve \({\mathcal {A}}\); in particular, it does not require any coercivity for \({\mathcal {A}}\) and is supposed through the data \(\varPhi \) and f. However, it is evident from the above proof that the classical coercivity can be imposed on \({\mathcal {A}}\) to reach the conclusion.
5 Quasi-Variational Inequalities
In this section, we focus on the evolutionary quasi-variational inequality (1). We proceed through a parametric approach by means of evolutionary variational inequalities of type (5). The notation is that indicated in the statement of (1). Let us suppose that for every \(w\in {\mathcal {K}}\), \({\mathcal {C}}(w)\) is a closed convex subset of \({\mathcal {K}}\) with nonempty interior in \({\mathcal {X}}\) (see also (27) below).
Using the data in problem (1) we formulate the conditions:
-
(\(A_5'\)) \(f\in {\mathcal {X}}^*\), and if the set \({\mathcal {K}}\) is unbounded in \({\mathcal {X}}\), there exist an \(r>0\) and a point
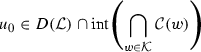 (27)
(27)satisfying
$$\begin{aligned} \langle a,v-u_0\rangle _{{\mathcal {X}}}+\langle b,iv-iu_0\rangle _{{\mathcal {Y}}}>\max \left\{ \langle f,v-u_0 \rangle _{{\mathcal {X}}},\langle f-{\mathcal {L}}(u_0),v-u_0 \rangle _{{\mathcal {X}}}\right\} \end{aligned}$$for all \(a\in {\mathcal {A}}(v)\), \(b\in {\mathcal {B}}(iv)\), \(v\in {\mathcal {X}}\) with \(\Vert v\Vert _{\mathcal {X}}>r\).
-
(\(A_6\)) The operator \({\mathcal {A}}+i^*{\mathcal {B}}i\) is monotone on \({\mathcal {C}}(w)\), that is,
$$\begin{aligned} \langle a_v-a_u,v-u\rangle _{\mathcal {X}}+\langle b_v-b_u,iv-iu\rangle _{{\mathcal {Y}}}\ge 0\quad \text {for all}\ u,v\in {\mathcal {C}}(w), \end{aligned}$$\(a_u\in {\mathcal {A}}(u)\), \(a_v\in {\mathcal {A}}(v)\), \(b_u\in {\mathcal {B}}(iu)\), \(b_v\in {\mathcal {B}}(iv)\), \(w\in {\mathcal {K}}\).
-
(\(A_7\)) For every \(x\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\cap D(\varPhi )\), there exist \(A_x\in {\mathcal {A}}(x)\) and \(B_x\in {\mathcal {B}}(ix)\) such that
$$\begin{aligned} \limsup _{t\downarrow 0}[\langle a_t,z-x\rangle _{{\mathcal {X}}}+\langle b_t,iz-ix\rangle _{{\mathcal {Y}}}]\le \langle A_x,z-x\rangle _{{\mathcal {X}}}+\langle B_x,iz-ix\rangle _{{\mathcal {Y}}} \end{aligned}$$whenever \(z\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\), \(a_t\in {\mathcal {A}}(x+t(z-x))\), \(b_t\in {\mathcal {B}}(ix+t(iz-ix))\).
-
(\(A_8\)) The map \({\mathcal {C}}:{\mathcal {K}}\rightrightarrows {\mathcal {K}}\) has the following Mosco-type continuity properties:
-
(i)
If \(\{w_n\}\subset {\mathcal {K}}\) and \(u_n\in {\mathcal {C}}(w_n)\cap D({\mathcal {L}})\cap D(\varPhi )\) satisfy \(w_n\rightharpoonup w\) in \({\mathcal {X}}\) and \(u_n\rightharpoonup u\) in \({\mathcal {X}}\), with \(u\in D({\mathcal {L}})\) and \({\mathcal {L}}(u_n)\rightharpoonup {\mathcal {L}}(u)\) in \({\mathcal {X}}^*\), then \(u\in {\mathcal {C}}(w)\).
-
(ii)
For every sequence \(\{w_n\}\subset {\mathcal {K}}\cap D({\mathcal {L}})\) with \(w_n\rightharpoonup w\) in \({\mathcal {X}}\) and for every \(v\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\), there exist a subsequence \(\{w_{n_k}\}\) of \(\{w_n\}\) and a sequence \(v_k\in {\mathcal {C}}(w_{n_k})\cap D({\mathcal {L}})\) with \(v_k\rightarrow v\) in \({\mathcal {X}}\) and \(\varPhi (v_k)\rightarrow \varPhi (v)\).
-
(i)
Theorem 5.1
Assume that conditions \((A_1)\)–\((A_4)\), \((A_5')\), \((A_6)\)–\((A_8)\) hold. Then there exists a solution of the quasi-variational inequality (1).
Proof
Conditions \((A_1)\)–\((A_5)\) are verified with \({\mathcal {C}}(w)\) in place of \({\mathcal {K}}\) for each \(w\in {\mathcal {K}}\). Therefore Theorem 4.1 with \({\mathcal {C}}(w)\) in place of \({\mathcal {K}}\) can be applied. In particular, this ensures that the parametric problem (2) is solvable for every \(w\in {\mathcal {K}}\). Consequently, the variational selection \({\mathcal {S}}:{\mathcal {K}}\rightrightarrows {\mathcal {K}}\) introduced in (3) has nonempty values. Toward proving the existence of a fixed point of \({\mathcal {S}}\), we split the proof in several parts.
Step 1: For every \(w\in {\mathcal {K}}\), problem (2) is equivalent to the following one: find \(x\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\cap D(\varPhi )\) such that for every \(z\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\), and for every \(a\in {\mathcal {A}}(z)\) and \(b\in {\mathcal {B}}(iz)\), we have
The fact that if \(x\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\cap D(\varPhi )\) is a solution of (2), then it solves (28) follows from \((A_1)\) and \((A_6)\).
Conversely, suppose that \(x\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\cap D(\varPhi )\) is a solution of (28) and let \(z\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\). Since \({\mathcal {C}}(w)\cap D({\mathcal {L}})\) is a convex set, it follows that \(z_t :=(1-t)x+tz\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\) for all \(t\in ]0,1]\). Then (28) yields
whenever \(a_t\in {\mathcal {A}}(z_t)\) and \(b_t\in {\mathcal {B}}(iz_t)\). The linearity of \({\mathcal {L}}\) and the convexity of \(\varPhi \) as postulated in \((A_4)\) imply
Letting \(t\rightarrow 0\) in (29), by hypothesis \((A_7)\) we find that x solves problem (2).
Step 2: The set \({\mathcal {S}}(w)\) is convex and closed in \({\mathcal {X}}\) whenever \(w\in {\mathcal {K}}\).
On the basis of Step 1, we first check that the solution set of (28) is convex in \({\mathcal {X}}\). To this end, fix \(w\in {\mathcal {K}}\). Let u and v solve (28), so \(u,v\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\cap D(\varPhi )\) such that for every \(z\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\) and for every \(a\in {\mathcal {A}}(z)\) and \(b\in {\mathcal {B}}(iz)\) we have
Let \(t\in [0,1]\). From the convexity of \(\varPhi \), it is seen that
which in view of Step 1 entails the convexity assertion.
Now we consider \(\{u_n\}\subset {\mathcal {S}}(w)\) with \(u_n\rightarrow u\) in \({\mathcal {X}}\). Since \(u_n\in {\mathcal {S}}(w)\), we deduce at once that \(u_n\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\cap D(\varPhi )\), and for some \(a_n\in {\mathcal {A}}(u_n)\) and \(b_n\in {\mathcal {B}}(iu_n)\) we have
Using that \({\mathcal {C}}(w)\) is a closed subset of \({\mathcal {K}}\), we get that \(u\in {\mathcal {C}}(w)\). By hypotheses \((A_2)\) and \((A_3)\), the sequences \(\{a_n\}\) and \(\{b_n\}\) are bounded in \({\mathcal {X}}^*\) and \({\mathcal {Y}}^*\), respectively. Consequently, along relabeled subsequences there hold \(a_n\rightharpoonup a\) in \({\mathcal {X}}^*\) and \(b_n\rightharpoonup b\) in \({\mathcal {Y}}^*\). Observing that \(\lim _{n\rightarrow \infty }\langle a_n,u_n-u\rangle _{\mathcal {X}}=0\), we obtain from (\(A_2\)) that \(a\in {\mathcal {A}}(u)\) because then \({\mathcal {A}}\) is generalized pseudo-monotone (see Remark 3.2). Similarly, in view of (12), we derive that \(b\in {\mathcal {B}}(iu)\).
Recalling that  is nonempty, we can choose a ball B in \({\mathcal {X}}\) such that \(B\subset {\mathcal {C}}(w)\). Then (30), in conjunction with the density of \(D({\mathcal {L}})\) in \({\mathcal {X}}\), guarantees that the sequence \(\{{\mathcal {L}}(u_n)\}\) is uniformly bounded from below on the ball B, which ensures that \(\{{\mathcal {L}}(u_n)\}\) is bounded in \({\mathcal {X}}^*\). Since \({\mathcal {L}}\) is linear, maximal monotone, so weakly graph closed, we have that \(u\in D({\mathcal {L}})\) and \({\mathcal {L}}(u_n)\rightharpoonup {\mathcal {L}}(u)\) in \({\mathcal {X}}^*\). We also observed from (30) that \(u\in D(\varPhi )\) thanks to the lower semicontinuity of \(\varPhi \) as required in \((A_4)\), Altogether, we can pass to the limit in (30) as \(n\rightarrow \infty \) proving that \(u\in {\mathcal {S}}(w)\).
is nonempty, we can choose a ball B in \({\mathcal {X}}\) such that \(B\subset {\mathcal {C}}(w)\). Then (30), in conjunction with the density of \(D({\mathcal {L}})\) in \({\mathcal {X}}\), guarantees that the sequence \(\{{\mathcal {L}}(u_n)\}\) is uniformly bounded from below on the ball B, which ensures that \(\{{\mathcal {L}}(u_n)\}\) is bounded in \({\mathcal {X}}^*\). Since \({\mathcal {L}}\) is linear, maximal monotone, so weakly graph closed, we have that \(u\in D({\mathcal {L}})\) and \({\mathcal {L}}(u_n)\rightharpoonup {\mathcal {L}}(u)\) in \({\mathcal {X}}^*\). We also observed from (30) that \(u\in D(\varPhi )\) thanks to the lower semicontinuity of \(\varPhi \) as required in \((A_4)\), Altogether, we can pass to the limit in (30) as \(n\rightarrow \infty \) proving that \(u\in {\mathcal {S}}(w)\).
Step 3: The image \({\mathcal {S}}({\mathcal {K}})\) of \({\mathcal {S}}\) is bounded in \({\mathcal {X}}\).
Arguing by contradiction, we assume that there exists a sequence \(\{u_n\}\subset {\mathcal {S}}({\mathcal {K}})\) satisfying
Necessarily, (31) requires that \({\mathcal {K}}\) is unbounded. Let \(w_n\in {\mathcal {K}}\) be such that \(u_n\in {\mathcal {S}}(w_n)\). Consequently, \(u_n\in {\mathcal {C}}(w_n)\cap D({\mathcal {L}})\cap D(\varPhi )\) and there exist \(a_n\in {\mathcal {A}}(u_n)\) and \(b_n\in {\mathcal {B}}(iu_n)\) satisfying (30). Due to \((A_5')\) we can insert \(v=u_0\) in (30), which by the monotonicity of \({\mathcal {L}}\) reads as
Taking into account (31), we reach a contradiction to the inequality demanded in hypothesis \((A_5')\). In view of this contradiction, we have thus checked that Step 3 is valid.
Step 4: The graph \(G({\mathcal {S}})\) of \({\mathcal {S}}\) is sequentially weakly closed in \({\mathcal {X}}\times {\mathcal {X}}\).
Let \(\{(w_n,u_n)\}\subset G({\mathcal {S}})\) converge weakly to (w, u) in \({\mathcal {X}}\times {\mathcal {X}}\). The fact that \(u_n\in {\mathcal {S}}(w_n)\) means that \(w_n\in {\mathcal {K}}\), \(u_n\in {\mathcal {C}}(w_n)\cap D({\mathcal {L}})\cap D(\varPhi )\) and for some \(a_n\in {\mathcal {A}}(u_n)\) and \(b_n\in {\mathcal {B}}(iu_n)\), inequality (30) is fulfilled. We note that \(w\in {\mathcal {K}}\).
Owing to (27) in \((A_5')\), we can choose a ball B in \({\mathcal {X}}\) such that \(B\subset {\mathcal {C}}(w_n)\) for all n. Then (30) and the density of \(D({\mathcal {L}})\) in \({\mathcal {X}}\) ensure that the sequence \(\{{\mathcal {L}}(u_n)\}\) is uniformly bounded from below on the ball B, which guarantees that \(\{{\mathcal {L}}(u_n)\}\) is bounded in \({\mathcal {X}}^*\). Since \({\mathcal {L}}\) being linear, maximal monotone, is weakly graph closed, we obtain that \(u\in D({\mathcal {L}})\) and \({\mathcal {L}}(u_n)\rightharpoonup {\mathcal {L}}(u)\) in \({\mathcal {X}}^*\). Then according to assumption \((A_8)\) (i) we have that \(u\in {\mathcal {C}}(w)\). Moreover, by \((A_4)\) and (30) we derive that \(u\in D(\varPhi )\).
Since \(u\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\cap D(\varPhi )\), we can invoke assumption \((A_8)\) (ii) obtaining a subsequence of \(\{w_n\}\), denoted again \(\{w_n\}\), corresponding to which there exists a sequence \(\{z_n\}\) with \(z_n\in {\mathcal {C}}(w_n)\cap D({\mathcal {L}})\), \(z_n\rightarrow u\) in \({\mathcal {X}}\) and \(\varPhi (z_n)\rightarrow \varPhi (u)\). It is thus permitted to insert \(v=z_n\) in (30) resulting in
which reads as
The monotonicity of \({\mathcal {L}}\), in conjunction with \(u_{n_k}\rightharpoonup u\) in \({\mathcal {X}}\) and \({\mathcal {L}}(u_{n_k})\rightharpoonup {\mathcal {L}}(u)\) in \({\mathcal {X}}^*\), implies
Because the map \(i:{\mathcal {X}}\rightarrow {\mathcal {Y}}\) is compact, we have that \(iu_n\rightarrow iu\) in \({\mathcal {Y}}\). We also note that from hypothesis \((A_3)\) and property (12) it turns out that along a relabeled sequence it holds \(b_n\rightharpoonup b\) in \({\mathcal {Y}}^*\) with \(b\in {\mathcal {B}}(iu)\). Thanks to the boundedness of the map \({\mathcal {A}}\), up to a subsequence, we have \(a_n\rightharpoonup a\) in \({\mathcal {X}}^*\). So (32), (33) and \((A_4)\) yield
Due to this, assumption \((A_2)\) and Remark 3.2 entail that
Now let an arbitrary \(v\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\). On the basis of assumption \((A_8)\) (ii), there exists \(v_k\in {\mathcal {C}}(w_{n_k})\cap D({\mathcal {L}})\) such that \(v_k\rightarrow v\) in \({\mathcal {X}}\) and \(\varPhi (v_k)\rightarrow \varPhi (v)\). By testing (30) with \(v=v_k\) when \(n=n_k\), we get
Letting \(k\rightarrow \infty \) in (35) and taking into account (33) and (34) give
which proves that \((w,u)\in G({\mathcal {S}})\). This confirms that \(G({\mathcal {S}})\) is sequentially weakly closed in \({\mathcal {X}}\times {\mathcal {X}}\).
At this point let us apply Theorem 3.3 by taking \({\mathcal {D}}\) to be the closed convex hull of \({\mathcal {S}}({\mathcal {K}})\) in \({\mathcal {X}}\) and let P be the restriction of \({\mathcal {S}}\) to this \({\mathcal {D}}\) (see Remark 3.4). Steps 2–4 show that all the hypotheses are verified. Consequently, through Theorem 3.3 we obtain a fixed point of \({\mathcal {S}}\), which represents a solution of the quasi-variational inequality (1). This completes the proof. \(\square \)
Remark 5.1
The part regarding the closeness of \({\mathcal {S}}(w)\) in Step 2 cannot be handled on the basis of Step 1 as done for the convexity of \({\mathcal {S}}(w)\) because we must show that the limit u belongs to \(D({\mathcal {L}})\). Actually, this assertion is also the consequence of Step 4.
We now consider the following evolutionary quasi-variational inequality where the focus is on maximal monotone maps \({\mathcal {A}}\): find \(x\in {\mathcal {C}}(x)\cap D({\mathcal {L}})\cap D(\varPhi )\) such that for some \(a\in {\mathcal {A}}(x)\) we have
As before, we proceed through the use of the variational selection. For this, for any \(w\in {\mathcal {K}}\), we consider the parametric evolutionary variational inequality: find \(x\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\cap D(\varPhi )\) such that for some \(a\in {\mathcal {A}}(x)\) we have
We first give the following Minty formulation for evolutionary variational inequality:
Theorem 5.2
Let \({\mathcal {K}}\) be a nonempty, closed, and convex subset of a reflexive Banach space \({\mathcal {X}},\) let \({\mathcal {L}}:D({\mathcal {L}})\subseteq {\mathcal {X}}\rightarrow {\mathcal {X}}^*\) be linear, maximal monotone, let \({\mathcal {A}}:D({\mathcal {A}})\subseteq {\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) be a maximal monotone map, let \(\varPhi :{\mathcal {X}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) be a convex, lower semicontinuous functional \(\not \equiv +\infty \), let \(f\in {\mathcal {X}}^*,\) and let \({\mathcal {K}}\subset int(D({\mathcal {A}}))\cap int(D(\partial \varPhi )).\) Assume that there exists an element \(x\in {\mathcal {K}}\cap D({\mathcal {L}})\) such that for every \(z\in {\mathcal {K}}\cap D({\mathcal {L}})\) and for every \(a_{z}\in {\mathcal {A}}(z),\) we have
Then there exists \(a\in {\mathcal {A}}(x)\) such that
Proof
Since for every \(z\in {\mathcal {K}}\subset D(\partial \varPhi ),\) for every \(z^*\in \partial \varPhi (z),\) and for every \(y\in {\mathcal {X}},\) we have
it follows from (38) by setting \(y=x\) that for any \(z\in {\mathcal {K}}\cap D({\mathcal {L}}),\) for any \(z^*\in \varPhi (z),\) and for any \(a_z\in {\mathcal {A}}(z),\) we have
We define the set-valued map \({\mathcal {T}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) by \({\mathcal {T}}:={\mathcal {L}}+{\mathcal {A}}+N_{{\mathcal {K}}}+\partial \varPhi \), where \(N_{{\mathcal {K}}}\) denotes the subdifferential of the indicator function of \({\mathcal {K}}\). We know that \({\mathcal {T}}\) is a maximal monotone map with \(D({\mathcal {T}})={\mathcal {K}}\cap D({\mathcal {L}})\) (see, e.g., [30, Theorem 32.1]).
Therefore, for any \(u_z\in N_{K}(z)\) and for any \(z\in {\mathcal {K}}\cap D({\mathcal {L}}),\) we note from (40) that
implying by the maximal monotonicity of \({\mathcal {T}}\) that \(f\in ({\mathcal {L}}+{\mathcal {A}}+\partial \varPhi +N_{{\mathcal {K}}})(x).\)
Consequently, there exist \(a\in {\mathcal {A}}(x)\), \(u\in N_{{\mathcal {K}}}(x),\) and \(x^*\in \partial \varPhi (x)\) such that
which by using the inequalities \(\langle u,z-x\rangle _{\mathcal {X}}\le 0\) and \(\varPhi (z)-\varPhi (x)\ge \langle x^*,z-x\rangle _{\mathcal {X}}\) whenever \(z\in {\mathcal {K}}\cap D({\mathcal {L}}),\) confirms that (39) holds, and the proof is complete. \(\square \)
We have the following existence result with focus on maximal monotone maps:
Theorem 5.3
Let \({\mathcal {K}}\) be a nonempty, closed and convex subset of a reflexive Banach space \({\mathcal {X}}\), let \(f\in {\mathcal {X}}^*\) and let \(\varPhi :{\mathcal {X}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) convex, lower semicontinuous. Assume \((A_1)\), \((A_8)\), and the conditions:
-
\((T_1)\) \({\mathcal {A}}:D({\mathcal {A}})\subseteq {\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) is a maximal monotone map, with
$$\begin{aligned} 0\in int(\bigcap _{w\in {\mathcal {K}}}{\mathcal {C}}(w))\subset {\mathcal {K}}\subset int(D({\mathcal {A}}))\cap int(D(\varPhi )) \end{aligned}$$and \(0\in {\mathcal {A}}(0)\).
-
\((T_2)\) For every sequence \(\{x_n\}\subset {\mathcal {K}}\) with \(\Vert x_n\Vert _{{\mathcal {X}}}\rightarrow \infty ,\) and \(\frac{x_n}{\Vert x_n\Vert _{{\mathcal {X}}}}\rightharpoonup z\) in \({\mathcal {X}}\), we have
$$\begin{aligned} \liminf _{n\rightarrow \infty }\frac{\varPhi (x_n)}{\Vert x_n\Vert _{{\mathcal {X}}}}>\langle f,z\rangle _{{\mathcal {X}}}. \end{aligned}$$(41)
Then the evolutionary quasi-variational inequality (36) has a nonempty solution set.
Proof
It is straightforward to check that the assumptions of Theorem 4.4 are fulfilled for every \({\mathcal {C}}(w)\) in place of \({\mathcal {K}}\). Specifically, condition \((S_3)\) is true because \({\mathcal {A}}\) is hemicontinuous on \({\mathcal {K}}\) due to \((T_1)\), whereas \((T_1)\) and \((T_2)\) imply \((S_1)\) and \((S_2)\), respectively. Then Theorem 4.4 ensures that the parametric evolutionary variational inequality (37) is solvable for every \(w\in {\mathcal {K}}\). Therefore, the associated variational selection \({\mathcal {S}}:{\mathcal {K}}\rightrightarrows {\mathcal {K}}\) has nonempty values for every \(w\in {\mathcal {K}}\).
We are going to show the existence of a fixed point of \({\mathcal {S}}\). Using Theorem 5.2, it is seen that (37) is equivalent to the following evolutionary variational inequality: find \(x\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\) such that for every \(a\in {\mathcal {A}}(z)\), we have
This at once proves that the solution set \({\mathcal {S}}(w)\) is convex. It is also closed, which can be established through a reasoning like in Step 2 of Theorem 5.1. Here the essential fact is that \({\mathcal {A}}\) is locally bounded on \({\mathcal {K}}\) as guaranteed by assumption \((T_1)\).
Our next objective is to show that the image \({\mathcal {S}}({\mathcal {K}})\) is bounded in \({\mathcal {X}}\). This corresponds to Step 3 in the proof of Theorem 5.1. By contradiction, suppose that there exists a sequence \(\{u_n\}\subset {\mathcal {S}}({\mathcal {K}})\) satisfying (31). Let \(w_n\in {\mathcal {K}}\) be such that \(u_n\in {\mathcal {S}}(w_n)\), that is \(u_n\in {\mathcal {C}}(w_n)\cap D({\mathcal {L}})\) and there exists \(a_n\in {\mathcal {A}}(u_n)\) such that
Setting \(v=0\) in (43), which is permitted in view of assumption \((T_1)\), and using the monotonicity of \({\mathcal {L}}\) and \({\mathcal {A}}\) we arrive at
From here it is clear that we reach a contradiction to (41) in assumption \((T_2)\). Therefore \({\mathcal {S}}({\mathcal {K}})\) is bounded in \({\mathcal {X}}\).
Let us prove that the graph \(G({\mathcal {S}})\) of \({\mathcal {S}}\) is sequentially weakly closed in \({\mathcal {X}}\times {\mathcal {X}}\). In this respect, let \(\{(w_n,u_n)\}\subset G({\mathcal {S}})\) converge weakly to (w, u) in \({\mathcal {X}}\times {\mathcal {X}}\). We know that \(w_n\in {\mathcal {K}}\) and \(u_n\in {\mathcal {C}}(w_n)\cap D({\mathcal {L}})\) satisfies for some \(a_n\in {\mathcal {A}}(u_n)\) that
By (\(T_1\)), we can choose a ball B in \({\mathcal {X}}\) such that \(B\subset {\mathcal {C}}(w_n)\) for all n. Then (44), the local boundedness of the monotone map \({\mathcal {A}}\) on \({\mathcal {K}}\) (see (\(T_1\))) and the density of \(D({\mathcal {L}})\) in \({\mathcal {X}}\) ensure that the sequence \(\{{\mathcal {L}}(u_n)\}\) is bounded in \({\mathcal {X}}^*\). Since \({\mathcal {L}}\) is weakly graph closed, it turns out that \(u\in D({\mathcal {L}})\) and \({\mathcal {L}}(u_n)\rightharpoonup {\mathcal {L}}(u)\) in \({\mathcal {X}}^*\). Then assumption \((A_8)\) (i) yields that \(u\in {\mathcal {C}}(w)\).
We claim that \(\{a_n\}\) is bounded. Since \(u\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\), we can obtain through assumption \((A_8)\) (ii) a relabeled subsequence of \(\{w_n\}\) and a sequence \(\{z_n\}\) with \(z_n\in {\mathcal {C}}(w_n)\cap D({\mathcal {L}})\), \(z_n\rightarrow u\) in \({\mathcal {X}}\) and \(\varPhi (z_n)\rightarrow \varPhi (u)\). This allows us to insert \(v=z_n\) in (44) getting
Lemma 3.1 applied for \({\mathcal {A}} - f\) implies that there are constants \(c>0\) and \(r>0\) such that
and consequently,
Since \(z_n\rightarrow u\) and the right-hand side of the above inequality remains bounded, we deduce the boundedness of \(\{a_n\}\) as claimed.
Let \(v\in {\mathcal {C}}(w)\cap D({\mathcal {L}})\). By assumption \((A_8)\) (ii), there exists \(v_k\in {\mathcal {C}}(w_{n_k})\cap D({\mathcal {L}})\) such that \(v_k\rightarrow v\) in \({\mathcal {X}}\) and \(\varPhi (v_k)\rightarrow \varPhi (v)\). From (44) with \(v=v_k\) and \(a_{n_k}\in {\mathcal {A}}(u_{n_k})\) we infer that
Then, for any \(a_v\in {\mathcal {A}}(v),\) (46) enables us to find
where we used the monotonicity of \({\mathcal {L}}\) and \({\mathcal {A}}.\) In the limit we obtain
We now apply Theorem 3.3 with \({\mathcal {D}}\) being the closed convex hull of \({\mathcal {S}}({\mathcal {K}})\) in \({\mathcal {X}}\) and P the restriction of \({\mathcal {S}}\) to this \({\mathcal {D}}\). The discussion before ensures that this fulfills all the requirements in Theorem 3.3. So, Theorem 3.3 provides a fixed point of \({\mathcal {S}}\), thus a solution of the quasi-variational inequality (36). This completes the proof. \(\square \)
Finally, we study evolutionary quasi-variational inequalities (1) with compact constraints \({\mathcal {C}}(w)\), but allowing more flexibility for other data. Suppose that \({\mathcal {X}}\) and \({\mathcal {Y}}\) are reflexive Banach spaces and it is given a continuous linear map \(i:{\mathcal {X}}\rightarrow {\mathcal {Y}}\). Consider the maps \({\mathcal {L}}:{\mathcal {W}}:=D({\mathcal {L}})\subseteq {\mathcal {X}}\rightarrow {\mathcal {X}}^*\), \({\mathcal {A}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\), and \({\mathcal {B}}:{\mathcal {Y}}\rightrightarrows {\mathcal {Y}}^*\) such that conditions \((A_1)\), \((A_2)\), \((A_3)\) are satisfied.
We notice that \({\mathcal {W}}\) endowed with the graph norm
is a reflexive Banach space, and further assume that \({\mathcal {W}}\) is separable. Let \({\mathcal {K}}\) be a nonempty compact convex subset of \({\mathcal {W}},\) let \(\varPhi :{\mathcal {X}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) be a convex and lower semicontinuous function with \({\mathcal {K}}\subset D(\partial \varPhi )\), let \({\mathcal {C}}:{\mathcal {K}}\rightrightarrows {\mathcal {K}}\) be a multi-valued map, and let \(f\in {\mathcal {X}}^*\). With these data, the quasi-variational inequality (1) reads: find \(x\in {\mathcal {C}}(x)\cap D({\mathcal {L}})\) such that for some \(a\in {\mathcal {A}}(x)\) and \(b\in {\mathcal {B}}(ix)\) we have
We formulate the following statement:
Theorem 5.4
Under assumptions \((A_1)\), \((A_2)\), \((A_3)\), if \(\partial \varPhi \) is bounded on \({\mathcal {K}}\) and the multi-valued map \({\mathcal {C}}:{\mathcal {K}}\rightrightarrows {\mathcal {K}}\) is lower semicontinuous with closed graph and nonempty convex values, then the evolutionary quasi-variational inequality (48) has a nonempty solution set.
Proof
By the definition of the convex subdifferential \(\partial \varPhi \), it is sufficient to find \(x\in {\mathcal {C}}(x)\) such that for some \(a\in {\mathcal {A}}(x)\), \(b\in {\mathcal {B}}(ix)\), and \(c\in \partial \varPhi (x)\) we have
Since \({\mathcal {K}}\subset D(\partial \varPhi )\), we can introduce for every \(x\in {\mathcal {K}}\) the set
Notice that \(x\in M(x)\) for every \(x\in {\mathcal {K}}\).
We claim that the multi-valued map \(M:{\mathcal {K}}\rightrightarrows {\mathcal {K}}\) defined in (50) has closed graph in the \({\mathcal {W}}\) topology. To justify this, let \((x_n,z_n)\in G(M)\) be a sequence such that \(x_n\rightarrow x\) and \(z_n\rightarrow z\) in \({\mathcal {W}}\). It is seen from (50) that \((x_n,z_n)\in G(M)\) means that there exist \(a_n\in {\mathcal {A}}(x_n)\), \(b_n\in {\mathcal {B}}(ix_n)\), \(c_n\in \partial \varPhi (x_n)\) such that
We note that \(x_n\rightarrow x\) in \({\mathcal {X}}\), \(z_n\rightarrow z\) in \({\mathcal {X}}\), and \({\mathcal {L}}(x_n)\rightarrow {\mathcal {L}}(x)\) in \({\mathcal {X}}^*\), which ensures that
On the other hand, it turns out from assumptions (\(A_2\)) and (\(A_3\)) that along relabeled subsequences one has \(a_n\rightharpoonup a\) in \({\mathcal {X}}^*\) and \(b_n\rightharpoonup b\) in \({\mathcal {Y}}^*\) for some \(a\in {\mathcal {A}}(x)\) and \(b\in {\mathcal {B}}(ix).\) Moreover, the boundedness of \(\partial \varPhi \) on \({\mathcal {K}}\) renders that along a relabeled subsequence one has \(c_n\rightharpoonup c\) in \({\mathcal {X}}^*\), with \(c\in \partial \varPhi (x)\) because \(\partial \varPhi \) is maximal monotone. Then, taking into account (51) and (52), we infer that
which entails \(z\in M(x)\), so our claim holds true. Hence hypothesis (i) in Theorem 3.2 is verified.
Since we assumed that \({\mathcal {C}}:{\mathcal {K}}\rightrightarrows {\mathcal {K}}\) is lower semicontinuous with closed graph and nonempty convex values, hypothesis (ii) in Theorem 3.2 holds also true. Therefore we are able to apply Theorem 3.2 for \(X={\mathcal {W}}\), \(K={\mathcal {K}}\), \(F=({\mathcal {L}}+{\mathcal {A}}+i^*{\mathcal {B}}i+\partial \varPhi )|_{\mathcal {K}}-f\) and \(G={\mathcal {C}}\). Notice that our hypotheses ensure that the set F(x) is bounded, convex, and closed in \({\mathcal {X}}^*\), and so weakly compact in \({\mathcal {W}}^*\). Therefore, the final assertion of Theorem 3.2 enables us to complete the proof. \(\square \)
Remark 5.2
Sufficient conditions to have the properties required for the multi-valued map \({\mathcal {C}}:{\mathcal {K}}\rightrightarrows {\mathcal {K}}\) in Theorem 5.4 can be found in [26].
6 Examples and Applications
Here we present two applications of Theorem 5.1. In order to emphasize the main ideas by avoiding technicalities, we regard situations less general than the abstract result permits. For instance, we take the set \({\mathcal {K}}\) to be the whole space.
The first application deals with an elliptic quasi-variational inequality in the form of a hemivariational inequality. Given a bounded domain \(\varOmega \) in \({\mathbb {R}}^N\) and a number \(p\in [2,+\infty )\), we consider the reflexive Banach spaces \(W^{1,p}_0(\varOmega )\) and \(L^p(\varOmega )\) endowed with their usual norms. Notice that the inclusion \(W^{1,p}_0(\varOmega )\subset L^p(\varOmega )\) is a dense compact embedding. Recall that the negative (Dirichlet) p-Laplacian \(-\Delta _p:W^{1,p}_0(\varOmega )\rightarrow W^{-1,p'}(\varOmega )\), with \(1{/}p+1{/}p'=1\), defined by \(\Delta _pu=\mathrm{div}(|\nabla u|^{p-2}\nabla u)\), satisfies
with a constant \(c(p)>0\), and has a positive first eigenvalue \(\lambda _1\).
Let \(f\in W^{-1,p'}(\varOmega )\) and let a convex and continuous function \(\varPhi :W^{1,p}_0(\varOmega )\rightarrow {\mathbb {R}}\). Next we fix a function \(J:L^p(\varOmega )\rightarrow {\mathbb {R}}\) which is Lipschitz continuous on the bounded sets in \(L^p(\varOmega )\) and whose generalized gradient \(\partial J:L^p(\varOmega )\rightrightarrows L^{p'}(\varOmega )\) satisfies \(0\in \partial J(0)\) and
with a constant \(c_0<\lambda _1c(p)\).
At this point, we formulate the following quasi-variational inequality: given \(\rho >0\), find \(u\in W^{1,p}_0(\varOmega )\) provided
such that for some \(b\in \partial J(u)\) we have
for all \(v\in W^{1,p}_0(\varOmega )\) with \(\Vert v\Vert _{W^{1,p}_0(\varOmega )}\le \rho +\Vert u\Vert _{L^p(\varOmega )}\).
Theorem 6.1
If the locally Lipschitz function \(J:L^p(\varOmega )\rightarrow {\mathbb {R}}\) fulfills (54), then for any \(\rho >0\), problem (55), (56) possesses at least a solution.
Proof
Fix a number \(\rho >0\) and set \({\mathcal {X}}=W^{1,p}_0(\varOmega )\) and \({\mathcal {Y}}=L^p(\varOmega )\). Our goal is to apply Theorem 5.1 for \({\mathcal {K}}=W^{1,p}_0(\varOmega )\), \({\mathcal {L}}=0\), \({\mathcal {A}}=-\Delta _p\), \({\mathcal {B}}=\partial J\), and a convex, lower semicontinuous function \(\varPhi :W^{1,p}_0(\varOmega )\rightarrow {\mathbb {R}}\). It is clear that requirements (\(A_1\)) and (\(A_4\)) are true. It is known that \(-\Delta _p\) is continuous, bounded, uniformly monotone (see (53)), so it is pseudo-monotone. Therefore assumption (\(A_2\)) is verified.
In order to check assumption (\(A_3\)), let \(b_n\in \partial J(y_n)\) with \(y_n\rightarrow y\) in \(L^p(\varOmega )\) and \(b_n\rightharpoonup b\) in \(L^{p'}(\varOmega )\). Then [7, Proposition 2.171] ensures that \(b\in \partial J(y)\). Furthermore, \(\partial J\) has nonempty, convex, closed values, and it is a bounded operator because J is supposed to be Lipschitz continuous on the bounded sets. Altogether, we can conclude that assumption (\(A_3\)) is fulfilled.
We define the multi-valued map \({\mathcal {C}}:W^{1,p}_0(\varOmega )\rightrightarrows W^{1,p}_0(\varOmega )\) by
By (53) and (54), the following estimate is valid
for every \(u\in W^{1,p}_0(\varOmega )\) and \(b\in \partial J(u)\). Since \(c_0<\lambda _1c(p)\), we derive that hypothesis (\(A_5'\)) is satisfied with \(u_0=0\). Through an estimate of the same type based on (53) and (54), we arrive at the conclusion that hypothesis (\(A_6\)) holds true.
Given \(u, z\in {\mathcal {C}}(w)\) with \(w\in W^{1,p}_0(\varOmega )\), from [7, Proposition 2.171] it turns out that
whenever \(b_t\in \partial J(ix+t(z-x))\) with \(t\downarrow 0\). This enables us to obtain
for some \(B_u\in \partial J(u))\), because the generalized gradient \(\partial J(u))\) is weak*-compact in \(L^{p'}(\varOmega )\). Combining with the continuity of \(-\Delta _p\), this proves assertion (\(A_7\)).
We now pass to the proof of assertion (\(A_8\)). Let \(\{w_n\}\subset W^{1,p}_0(\varOmega )\) and \(u_n\in {\mathcal {C}}(w_n)\) satisfy \(w_n\rightharpoonup w\) and \(u_n\rightharpoonup u\) in \(W^{1,p}_0(\varOmega )\). It is thus known that \(\Vert u_n\Vert _{W^{1,p}_0(\varOmega )}\le \rho +\Vert w_n\Vert _{L^p(\varOmega )}\) and along a relabeled subsequence \(w_n\rightarrow w\) in \(L^p(\varOmega )\). Therefore in the limit we get \(\Vert u\Vert _{W^{1,p}_0(\varOmega )}\le \rho +\Vert w\Vert _{L^p(\varOmega )}\), so \(u\in {\mathcal {C}}(w)\), which ensues condition (\(A_8\)) (i).
Let \(\{w_n\}\subset W^{1,p}_0(\varOmega )\) with \(w_n\rightharpoonup w\) in \(W^{1,p}_0(\varOmega )\) and \(v\in {\mathcal {C}}(w)\). We set
Along a relabeled subsequence, we have \(v_n\rightarrow v\) in \(W^{1,p}_0(\varOmega )\) and \(v_n\in {\mathcal {C}}(w_n)\) because \(v\in {\mathcal {C}}(w)\) and thus
Hence condition (\(A_8\)) (ii) holds, too.
Since all the hypotheses of Theorem 5.1 are verified, we are in a position to apply this result to problem (55), (56), which leads to the desired conclusion. \(\square \)
Our second application concerns an evolutionary quasi-variational inequality. Let a bounded domain \(\varOmega \) in \({\mathbb {R}}^N\) and numbers \(p\in [2,+\infty )\) and \(\tau >0\). As before we denote \(p'\) the number satisfying \(1{/}p+1{/}p'=1\). For simplicity, we set \({\mathcal {X}}:=L^p(0,\tau ;W^{1,p}_0(\varOmega ))\), which is a reflexive Banach space under the usual norm and has the dual space \({\mathcal {X}}^*=L^{p'}(0,\tau ;W^{-1,p'}(\varOmega ))\). Let \(f\in {\mathcal {X}}^*\), and let a convex, continuous function \(\varPhi :{\mathcal {X}}\rightarrow {\mathbb {R}}\). We also introduce the map \({\mathcal {A}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) by
Fix a (possibly nonlinear) compact operator \(T:{\mathcal {X}}\rightarrow {\mathcal {X}}\). We state the following evolutionary quasi-variational inequality: given a number \(\rho >0\), find \(u\in {\mathcal {X}}\) with \(u'=\frac{du}{dt}\in {\mathcal {X}}^*\) and \(u(0)=0\) such that
and
for all \(v\in {\mathcal {X}}\) with \(\Vert v\Vert _{{\mathcal {X}}}\le \rho +\Vert Tu\Vert _{{\mathcal {X}}}\).
Theorem 6.2
For any \(\rho >0\), problem (58), (59) possesses at least a solution.
Proof
Fix a \(\rho >0\). Recall that the (time) derivative on \({\mathcal {X}}:=L^p(0,\tau ;W^{1,p}_0(\varOmega ))\) is an operator \({\mathcal {L}}:D({\mathcal {L}})\subseteq {\mathcal {X}}\rightarrow {\mathcal {X}}^*\) defined as follows: \({\mathcal {L}}(u)=u'\) for all \(u\in D({\mathcal {L}})\), where
It is a linear, maximal monotone operator (see e.g., [7, Lemma 2.149]), so assumption (\(A_{1}\)) is satisfied. The map \({\mathcal {A}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}^*\) introduced in (57) is monotone, hemicontinuous, and bounded (see e.g., [30, p. 878]), which implies assumption (\(A_{2}\)). Hypothesis (\(A_{3}\)) is verified by taking \({\mathcal {B}}=0\).
Choose \({\mathcal {K}}:={\mathcal {X}}\). Then hypothesis (\(A_{4}\)) is automatically satisfied. Let us define the multi-valued map \({\mathcal {C}}:{\mathcal {X}}\rightrightarrows {\mathcal {X}}\) by
By (53), the operator \({\mathcal {A}}\) introduced in (57) is coercive, which renders true assumption (\(A_5'\)) for instance with \(u_0=0\). Since the operator \({\mathcal {A}}\) is monotone, whereas \({\mathcal {B}}=0\), condition (\(A_{6}\)) is valid. Condition (\(A_{7}\)) holds because the operator \({\mathcal {A}}\) is hemicontinuous.
In order to check condition (\(A_8\)) (i), we consider sequences \(\{w_n\}\subset {\mathcal {X}}\) and \(u_n\in {\mathcal {C}}(w_n)\) satisfying \(w_n\rightharpoonup w\) and \(u_n\rightharpoonup u\) in \({\mathcal {X}}\). We have that \(\Vert u_n\Vert _{{\mathcal {X}}}\le \rho +\Vert Tw_n\Vert _{{\mathcal {X}}}\) and, thanks to the compactness of the mapping T, we can pass to a relabeled subsequence such that \(Tw_n\rightarrow Tw\) in \({\mathcal {X}}\). Taking the limit results in \(\Vert u\Vert _{{\mathcal {X}}}\le \rho +\Vert Tw\Vert _{{\mathcal {X}}}\), that is \(u\in {\mathcal {C}}(w)\), thus (\(A_8\)) (i) holds.
In order to establish condition (\(A_8\)) (ii), we consider \(\{w_n\}\subset {\mathcal {X}}\) with \(w_n\rightharpoonup w\) in \({\mathcal {X}}\) and \(v\in {\mathcal {C}}(w)\). Set
Using that the map T is compact and \(v\in {\mathcal {C}}(w)\), it is straightforward to show that along a relabeled subsequence \(v_n\rightarrow v\) in \({\mathcal {X}}\) and \(v_n\in {\mathcal {C}}(w_n)\). Since the function \(\varPhi \) is continuous, condition (\(A_8\)) (ii) is satisfied.
We have proven that all the hypotheses of Theorem 5.1 hold true. Through Theorem 5.1, we can infer the solvability of problem (58), (59), which completes the proof. \(\square \)
7 Conclusions
We presented very general existence results for evolutionary and elliptic variational and quasi-variational inequalities. Motivated by diverse applications, numerous constraint sets enjoying Mosco-type convergence properties have been studied (see [3, 15]). Evidently our general theorems can conveniently be coupled with such constraint sets to give new existences results. Moreover, the notion of generalized solutions for quasi-variational inequalities can be used to relax some of the monotonicity conditions from our results (see [13, 14]). It is also natural to explore issues such as regularization, penalization, and control for the evolution quasi-variational inequalities studied in this work (see [1, 9, 17, 19]).
References
Alber, Y.I., Butnariu, D., Ryazantseva, I.: Regularization of monotone variational inequalities with Mosco approximations of the constraint sets. Set Valued Anal. 13, 265–290 (2005)
Alber, Y.I., Notik, A.I.: Perturbed unstable variational inequalities with unbounded operators on approximately given sets. Set Valued Anal. 1, 393–402 (1993)
Azevedo, A., Miranda, F., Santos, L.: Variational and quasivariational inequalities with first order constraints. J. Math. Anal. Appl. 397, 738–756 (2013)
Baiocchi, C., Capelo, A.: Variational and Quasivariational Inequalities. Applications to Free Boundary Problems. Wiley, New York (1984)
Barrett, J.W., Prigozhin, L.: Lakes and rivers in the landscape: a quasi-variational inequality approach. Interfaces Free Bound. 16(2), 269–296 (2014)
Bensoussan, A., Lions, J.L.: Nouvelles méthodes en contrôle impulsionnel, Appl. Math. Optim., 1, 289–312 (1974/75)
Carl, S., Le, V.K., Motreanu, D.: Nonsmooth Variational Problems and Their Inequalities. Comparison Principles and Applications. Springer, New York (2007)
Giannessi, F.: Separation of sets and gap functions for quasi-variational inequalities. Variational Inequalities and Network Equilibrium Problems (Erice, 1994), pp. 101–121. Plenum, New York (1995)
Giannessi, F., Khan, A.A.: Regularization of non-coercive quasi-variational inequalities. Control Cybern. 29, 91–110 (2000)
Giannessi, F., Khan, A.A.: On the envelope of a variational inequality. Nonlinear Anal. Var. Probl. 35, 285–293 (2010)
Goeleven, D., Motreanu, D., Dumont, Y., Rochdi, M.: Variational and Hemivariational Inequalities: Theory, Methods and Applications, vol. I. Unilateral Analysis and Unilateral Mechanics, Nonconvex Optimization and its Applications, 69, Kluwer Academic Publishers, Boston (2003)
Goeleven, D., Motreanu, D.: Variational and Hemivariational Inequalities: Theory, Methods and Applications, vol. II. Unilateral Problems. Nonconvex Optimization and its Applications, 70, Kluwer Academic Publishers, Boston (2003)
Jadamba, B., Khan, A.A., Raciti, F., Rouhani, D.B.: Generalized solutions of multi-valued monotone quasi-variational inequalities. Optim. optim. control 39, 227–240 (2010)
Jadamba, B., Khan, A.A., Sama, M.: Generalized solutions of quasi-variational inequalities. Optim. Lett. 6(7), 1221–1231 (2012)
Kano, R., Kenmochi, N., Murase, Y.: Existence theorems for elliptic quasi-variational inequalities in Banach spaces. In Recent Advances in Nonlinear Analysis, pp. 149–169. World Scientific Publishing, New Jersey (2008)
Kenmochi, N.: Nonlinear operators of monotone type in reflexive Banach spaces and nonlinear perturbations. Hiroshima Math. J. 4, 229–263 (1974)
Khan, A.A., Sama, M.: Optimal control of multivalued quasi-variational inequalities. Nonlinear Anal. 75(3), 1419–1428 (2012)
Khan, A.A., Tammer, C., Zalinescu, C.: Set-Valued Optimization. An Introduction with Applications. Springer, Berlin (2015)
Khan, A.A., Tammer, C., Zalinescu, C.: Regularization of quasi-variational inequalities. Optimization 64, 1703–1724 (2015)
Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and Their Applications. SIAM, Philadelphia (1987)
Kluge, R.: On some parameter determination problems and quasi-variational inequalities, Theory of nonlinear operators. In: Proc. Fifth Internat. Summer School, Central Inst. Math. Mech. Acad. Sci. GDR, Berlin, 1977, pp. 129-139. Akademie-Verlag, Berlin (1978)
Kravchuk, A.S., Neittaanmäki, P.J.: Variational and Quasi-Variational Inequalities in Mechanics. Springer, Dordrecht (2007)
Lenzen, F., Lellmann, J., Becker, F., Schnorr, C.: Solving quasi-variational inequalities for image restoration with adaptive constraint sets. SIAM J. Imaging Sci. 7(4), 2139–2174 (2014)
Liu, Z.: Generalized quasi-variational hemi-variational inequalities. Appl. Math. Lett. 17, 741–745 (2004)
Liu, Z.: Existence results for evolution noncoercive hemivariational inequalities. J. Optim. Theory Appl. 120, 417–427 (2004)
Lunsford, M.L.: Generalized variational and quasi-variational inequalities with discontinuous operators. J. Math. Anal. Appl. 214, 245–263 (1997)
Mosco, U.: Convergence of convex sets and of solutions of variational inequalities. Adv. Math. 3, 512–585 (1969)
Mosco, U.: Implicit variational problems and quasi-variational inequalities. In: Nonlinear Operators and the Calculus of Variations, Lecture Notes in Mathematics, vol. 543, pp. 83–156. Springer, Berlin (1976)
Motreanu, V.V.: Existence results for constrained quasivariational inequalities. In Abstract and Applied Analysis, Art. ID 427908 (2013)
Zeidler, E.: Nonlinear Functional Analysis and its Applications. II/B. Nonlinear Monotone Operators. Springer, New York (1990)
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Prof. Franco Giannessi on his 80th birthday.
Rights and permissions
About this article
Cite this article
Khan, A.A., Motreanu, D. Existence Theorems for Elliptic and Evolutionary Variational and Quasi-Variational Inequalities. J Optim Theory Appl 167, 1136–1161 (2015). https://doi.org/10.1007/s10957-015-0825-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-015-0825-6
Keywords
- Quasi-variational inequalities
- Variational inequalities
- Hemivariational inequalities
- Monotone
- Pseudo-monotone
- Generalized pseudo-monotone
- Coercivity
- Asymptotic recessivity



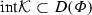 .
.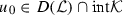 and an
and an