1 Introduction

Fractional differential calculus [1, 2], an old mathematical topic from the 17th century, has recently attracted a rapid growth in the number of applications. It was found that many systems in interdisciplinary fields could be elegantly described with the help of fractional derivatives and integrals [3, 4]. Also, fractional-order controllers have so far been implemented to enhance the robustness and the performance of the control systems [5–7].

Iterative learning control (ILC) is an approach for improving the transient performance of systems that operate repetitively over a fixed time interval [8, 9]. Owing to its simplicity and effectiveness, ILC has been found to be a good alternative in many areas and applications (see, for instance, [10, 11] and the referenced therein). In recent years, the application of ILC to the fractional-order systems has become a new topic [4, 12–14]. The authors in [12] were the first to propose the \(\mathcal{D}^{\alpha}\)-type ILC algorithm in frequency domain. For fractional-order linear systems described in the state space form, the convergence conditions are derived in [5]. In [13], the asymptotic stability of P\(\mathcal{D}^{\alpha}\)-type ILC for a fractional-order linear time invariant (LTI) system was investigated. The convergence condition of open-loop P-type ILC for fractional-order nonlinear system was studied in [14].

It should be noted that the higher-order learning algorithms are the ones in which the information from past cycles, not just from the last cycle, is taken advantage of. As a result, developing higher-order learning algorithms can lead to better performance in terms of both robustness and convergence rate [11, 15, 16]. The key idea of the presented method was to use past information of more than one to update the current adaptation learning law.

In this paper, we investigated a high-order \(\mathcal{D}^{\alpha}\)-type ILC updating law design method for a class of fractional-order nonlinear time-delay systems. The rest of this paper is organized as follows. In Sect. 2, the fractional derivative and some preliminaries are presented. The high-order \(\mathcal{D}^{\alpha}\)-type ILC scheme as well as the convergence condition for fractional-order systems is discussed in Sect. 3. MATLAB/SIMULINK results are shown in Sect. 4. Finally, some conclusions are drawn in Sect. 5.

2 Fractional Derivative and Preliminaries

In this section, some basic definitions and properties (for more details see [1]) are introduced, which will be used in the following sections.

Definition 2.1

The definition of fractional integral is described by

where Γ(⋅) is the well-known Gamma function.

Definition 2.2

The Riemann–Liouville derivative is defined as

and the Caputo derivative is

where m∈ℤ+, D m is the classical m-order derivative.

Definition 2.3

[1]

The two-parameter Mittag–Leffler function is defined by

Property 2.1

[1]

The fractional-order differentiation or integral of Mittag–Leffler function is

$$ _{t_0}\mathcal{D}_t^{\rho}\bigl[t^{\beta-1}E_{\alpha,\beta} \bigl(\lambda t^\alpha\bigr)\bigr] =t^{\beta-\rho-1}E_{\alpha,\beta-\rho}\bigl( \lambda t^\alpha\bigr), $$

where ρ<β, \(\mathcal{D}\) denotes either the Riemann–Liouville or Caputo fractional-order operator.

Lemma 2.1

If the function f(t,x) is continuous, then the initial value problem

$$ \left \{ \begin{array}{l} {}^C_{t_0}\mathcal{D}_t^{\alpha}x (t)=f(t,x(t)),\quad0<\alpha<1,\\[3pt] x(t_0)=x(0) \end{array} \right . $$

is equivalent to the following nonlinear Volterra integral equation:

and its solutions are continuous [17]. The initial value problem:

$$ \left \{ \begin{array}{l} {}^{\mathit{RL}}_{t_0}\mathcal{D}_t^{\alpha}x (t)=f(t,x(t)),\quad0<\alpha<1,\\[5pt] {}^{\mathit{RL}}_{t_0}\mathcal{D}_t^{\alpha-1} x(t_0)=x(0) \end{array} \right . $$

is equivalent to the following nonlinear Volterra integral equation [18]:

Lemma 2.2

(Generalized Gronwall Inequality, [14])

Let u(t) be a continuous function on t∈[0,T] and let v(t−τ) be continuous and nonnegative on the triangle 0≤τ≤T. Moreover, let w(t) be a positive continuous and non-decreasing function on t∈[0,T]. If

$$ u(t)\leq h(t)+\int^t_0v(t-\tau)u(\tau)\,d \tau,\quad t\in [0,T], $$

then

$$ u(t)\leq w(t)e^{\int^t_0v(t-\tau)\,d\tau}, \quad t\in [0,T], $$

Throughout this paper, the 2-norm for the n-dimensional vector w=(w 1,w 2,…,w n ) and the matrix A n×n is defined as \(\|w\|:=\sqrt{\sum^{n}_{i=1}w^{2}_{i}}\), \(\|A\|:=\sqrt{\lambda_{\max}(A^{T}A)}\), respectively. The λ-norm for n-vector-valued function h(t):[0,T]→ℝn is defined as

$$\big\|h(t)\big\|_\lambda: =\sup_{t\in[0, T]}\bigl\{e^{-\lambda t}\big\|h(t)\big\| \bigr\},\quad \lambda>0, $$

while the (λ,ξ)-norm for m-vector-valued function g k (t):[0,T]→ℝm, k∈{0,1,2,…} is defined as

$$\big\|g_k(t)\big\|_{(\lambda,\xi)}:=\sup_{t\in[0, T]} \bigl\{e^{-\lambda t}\big\|g_k(t)\big\|\xi^k\bigr\}, \quad \lambda>0, $$

where ∥⋅∥ can be chosen as any kind of norm.

3 High-Order \(\mathcal{D}^{\alpha}\)-Type ILC for Fractional-Order Nonlinear Time-Delay Systems

Consider the following fractional-order nonlinear time-delay system:

$$ \left \{ \begin{array}{l} \mathcal{D}_t^{\alpha}x_k (t)=f( x_k(t),x_k(t-\tau),t)+Bu_k(t), \\[3pt] y_k(t)=C x_k(t)+D \mathcal{D}_t^{-\alpha}u_k(t), \end{array} \right . $$
(1)

where k∈{0,1,2,…},t∈[0,T],0<α<1.

x k (t)∈ℝn is the state of the plant, and u k (t)∈ℝm and y k (t)∈ℝm are the control input and output, respectively. A,A 1,B,C and D are constant system matrices with appropriate dimensions, τ is a pure delay and with the associated function of the initial state: x k (t)=ψ(t),−τ≤t≤0. ψ(t) is a given continuous function on [−τ,0]. \(\mathcal{D}_{t}^{\alpha}\) denotes either Caputo derivative or Riemann–Liouville derivative of order α. (If one denotes the Riemann–Liouville derivative, the additional condition \(\mathcal{D}_{t}^{\alpha-1}x_{k} (0)=x(0)\) is needed.)

In this paper, the following high-order \(\mathcal{D}^{\alpha}\)-type ILC updating law is considered:

$$ u_{k+1}(t)=\varLambda u_{k}(t)+ u_{kh}(t)+ \varGamma \mathcal{D}^\alpha_t e_k(t), \quad k\in \{1, 2, \ldots\}, $$
(2)

where

and t∈[0,T],0<α<1, e k (t)=y d (t)−y k (t) denotes the tracking error, Γ, Λ i and Λ are unknown gain matrices to be determined.

For fractional-order nonlinear time-delay system (1) under the \(\mathcal{D}^{\alpha}\)-type ILC updating law (2), we have the following Lemmas.

Lemma 3.1

Let Δu k (t):=u k (t)−u k−1(t),Δx k (t):=x k (t)−x k−1(t), Δf k (t):=f k (⋅)−f k−1(⋅) and

then

(3)

Proof

It follows from (2) that, for k≥N,

$$ u_{k+1}(t)=\varLambda u_{k}(t)+ \sum _{i=1}^N \varLambda_i u_{k-i}(t)+\varGamma\mathcal{D}^\alpha_t e_k(t). $$
(4)

Noting that \(\sum_{i=1}^{N} \varLambda_{i}= I-\varLambda\), it can easily be shown that

(5)

Since e k+1(t)−e k (t)=−(y k+1(t)−y k (t)), then, from (1), one has

(6)

Taking into account (5), it yields

(7)

Therefore, from (5) and (7), one gets

(8)

The proof is complete. □

Lemma 3.2

Denote that b:=∥B∥,c:=∥C∥, and \(M_{1}:= e^{\frac{a T^{\alpha}+a_{1}[(T-\tau)^{\alpha}+\tau^{\alpha}]}{\varGamma(\alpha+1)}}\), M 2:=(∥Γ∥+∥Λ−I∥), \(h:= (\frac{a+a_{1}e^{-\lambda \tau}}{\lambda^{\alpha}} )bcM_{1}\), then

(9)

Proof

It follows the definition of F k (t) that

(10)

On the other hand, from Lemma 2.1 and in accordance with the property of the fractional-order 0<α<1, we have

(11)

Therefore, if t∈[0,τ], then

(12)

If t∈[τ,T], then

(13)

After combining (12) and (13), it yields, for any t∈[0,T],

(14)

Noting that

$$ \frac{b}{\varGamma(\alpha)}\int_0^t(t-s)^{\alpha-1}e^{\lambda s} \,ds=bt^\alpha E_{1,1+\alpha}(\lambda t), $$

it follows from the Property 2.1 that, for λ>0,

$$ \frac{dt^\alpha E_{1,1+\alpha}(\lambda t)}{dt}=t^{\alpha-1}E_{1,\alpha}(\lambda t)>0. $$

Therefore,

is an increasing function. Setting

it can be proved that, for all t∈[0,T],

(15)

Taking into account (15) and applying Lemma 2.2 to (14), one obtains

(16)

and

(17)

From (10), (16) and (17), it yields

(18)

Multiplying both sides of (18) by e −λt and taking the λ-norm, one has

(19)

Note that

(20)

and

(21)

From (19)–(21), it yields, for any t∈[0,T],

(22)

Moreover, it follows from (5) that

(23)

As a result, one obtains from (22) and (23) that

(24)

Applying the (λ,ξ)-norm to (24) yields (9), which completes the proof. □

Theorem 3.1

For the fractional-order nonlinear time-delay system (1) and a given reference y d (t), suppose that y d (0)=y k (0) and

(25)
(26)

where ρ{G(t)} is the spectral radius of G, \(\bar{\rho}\) is a constant, then, for all t∈[0,T], and arbitrary initial input satisfying u −i (t)=0,i=1,2,…,N, the high-order \(\mathcal{D}^{\alpha}\)-type ILC updating law (2) guarantees that {u k (t)} is uniformly convergent, and

$$ \lim_{k\rightarrow\infty} y_k(t)=y_d(t). $$
(27)

Proof

It follows from (3) that, for k>N,

$$ Q_k(t)= G^{k-N}Q_N(t)+\sum _{i=N}^{k-1}G^{k-i-1}F_i(t). $$
(28)

Therefore, for k>N,

(29)

Noting that \(0\leq\bar{\rho}<1\) and c 1<1 by assumption, there exist a constant ξ>1 and a sufficiently large λ such that \(\bar{\rho}\xi<1\), and

$$ 0<\hat{h}=\frac{1}{1-\bar{\rho}\xi}\bigl[N\xi^{N+1}(c_1+c_2h)+ \xi h M_2\bigr]<1, $$
(30)

where \(c_{2}= \sum_{j=1}^{N} \|\varLambda_{j}\|\), M 2 and h as defined in Lemma 3.2.

For the above λ and ξ, multiplying both sides of (29) by e −λt ξ k and taking the (λ,ξ)-norm, it yields

(31)

Now, it follows from (9) that (31) gives

(32)

Therefore,

(33)

Hence,

(34)

Note that

(35)

Consequently, one obtains from (34) and (35)

(36)

where \(r= \frac{\rho^{-N} e^{\lambda T} }{1-\hat{h}}\|Q_{N}(t)\|_{\lambda}\). It follows from ξ>1 and (36) that

(37)

Therefore, for all t∈[0,T], we have

(38)

Furthermore, it follows from the initial conditions that {u k (t)} is uniformly robust convergent, and lim k→∞ y k (t)=y d (t). The proof is complete. □

Corollary 3.1

For fractional-order linear time-delay system

$$ \left \{ \begin{array}{l} \mathcal{D}_t^{\alpha}x_k (t)=A x_k(t)+A_1 x_k(t-\tau)+Bu_k(t), \\[3pt] y_k(t)=C x_k(t)+D \mathcal{D}_t^{-\alpha}u_k(t), \end{array} \right . $$
(39)

where k∈{0,1,2,…},t∈[0,T],α∈(0,1), and a given reference y d (t), suppose that y d (0)=y k (0) and \(\rho\{G(t)\}\leq\bar{ \rho}<1\), then, for all t∈[0,T], and arbitrary initial input satisfying u −1(t)=u 0(t), the second-order \(\mathcal{D}^{\alpha}\)-type ILC updating law

$$ u_{k+1}(t)=\varLambda u_{k}(t)+(1-\varLambda) u_{k-1}(t)+\varGamma \mathcal{D}^\alpha_t e_k(t), $$
(40)

guarantees that {u k (t)} is uniformly convergent, and lim k→∞ y k (t)=y d (t).

Corollary 3.2

For the fractional-order linear system

$$ \left \{ \begin{array}{l} \mathcal{D}_t^{\alpha}x_k (t)=A x_k(t)+Bu_k(t), \\[3pt] y_k(t)=C x_k(t)+D \mathcal{D}_t^{-\alpha}u_k(t), \end{array} \right . $$
(41)

and a given reference y d (t), suppose that y d (0)=y k (0) and

$$ \rho\bigl(I-(CB+D)\varLambda \bigr)<1, $$
(42)

then, for all t∈[0,T], and arbitrary initial input satisfying u 0(t), \(\mathcal{D}^{\alpha}\)-type ILC updating law

$$ u_{k+1}(t)=u_{k}(t)+\varLambda\mathcal{D}^\alpha_t e_k(t), $$
(43)

guarantees that {u k (t)} is uniformly convergent, and lim k→∞ y k (t)=y d (t).

Remark 3.1

Note that the convergence analysis of ILC updating law (43) for fractional-order linear system (41) has been investigated in [4], in which the convergence condition is

$$ \big\|I-(CB+D)\varLambda \big\|<1. $$
(44)

Since ρ(I−(CB+D)Λ)≤∥I−(CB+D)Λ∥, the convergence condition (42) is less conservative than the condition (44).

4 Numerical Example

Consider the fractional-order linear time-delay system (39) with the Caputo derivative (fractional order α=0.85),

$$ \left \{ \begin{array}{l@{\quad}l} A= \left [ \begin{array}{c@{\quad}c} -3 &1 \\[2pt] 2&-1 \end{array} \right ], & A_1= \left [ \begin{array}{c@{\quad}c} 1& -1\\[2pt]0& 0.5 \end{array} \right ], \\[12pt] B= \left [ \begin{array}{c@{\quad}c} 0 & 1 \\[2pt]-1& 0 \end{array} \right ], & C=\left [ \begin{array}{c@{\quad}c} 1 & 0\\[2pt]0& 1 \end{array} \right ], \quad D=0, \end{array} \right . $$
(45)

t∈[0,1],τ=0.5 and ψ(t)=[0 1]T,−0.5≤t<0. Let the reference and external disturbance be

$$y_d(t)=\left [ \begin{array}{c} 12t^2(1-t)\\[3pt] \sin(3\pi t) \end{array} \right ], \quad \quad w_k(t)=[0.1\sin t\quad 0.2\cos t]^T, \quad t \in[0,1], $$

respectively. We apply the second-order \(\mathcal{D}^{\alpha}\)-type ILC updating law

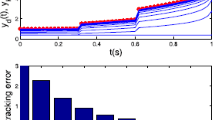
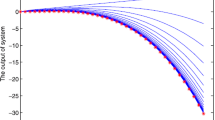
$$ u_{k+1}(t)=0.9u_{k}(t)+0.1u_{k-1}(t)+(CB)^{-1} \mathcal{D}^\alpha_t e_k(t). $$

with the initial control be u −1(t)=u 0(t)=0. In this case, it can be calculated that ρ(G)=0.3702<1. The simulation results are shown in Figs. 1, 2, and 3. Figures 1 and 2 show the system output y k (t) (solid) of the first five iterations and the referenced trajectory y d (t) (dotted), while Fig. 3 shows the 2-norm of the tracking errors in the first eight iterations. It can be seen that the output is capable of approaching the desired trajectory accurately within few iterations.

Fig. 1
figure 1

The tracking performance of the system output (\(y^{k}_{1}(t)\): solid, \(y_{1}^{d}(t)\): dotted)

Full size image
Fig. 2
figure 2

The tracking performance of the system output (\(y^{k}_{2}(t)\): solid, \(y_{2}^{d}(t)\): dotted)

Full size image
Fig. 3
figure 3

The 2-norm of the tracking errors in each iteration

Full size image

5 Concluding Remarks

In this paper, a high-order \(\mathcal{D}^{\alpha}\)-type ILC scheme for fractional-order nonlinear time-delay systems was investigated. By using the generalized Gronwall–Bellman Lemma, the convergence condition was derived. The validity of the proposed method was verified by a numerical example.