1 Introduction

1.1 Rare Events, Instantons and Sub-exponential Prefactors

Many systems in physics, chemistry, economics or biology can be described by stochastic differential equations with small noise. In such cases many statistical quantities, for instance the invariant distribution, first exit times, mean first passage times or transition probabilities have asymptotic exponential behavior \(C^\epsilon \exp (-I/\epsilon )\), where I is the exponential rate, \(\epsilon \) is the noise amplitude, and \(C^\epsilon \) is a sub-exponential prefactor (see below for a more precise definition).

This mathematical remark has profound consequences in physics. The most classical examples of such exponential rates are the Arrhenius law, or thermodynamic potentials.Footnote 1 Besides static properties, from a dynamical perspective, when conditioned on the occurence of a rare event, path probabilities often concentrate close to a predictable path, called instanton. This is a key and fascinating property for the dynamics of rare events and of their impact, which was first observed in statistical physics, for the nucleation of a classical supersaturated vapor [26]. Soon after, a similar concentration of path probabilities has been studied in gauge field theories [10, 41], for instance for the Yang–Mills theory. Instantons continue to have number of applications in modern statistical physics, for instance to describe excitation chains at the glass transition [27], reaction paths in chemistry [24], escape of Brownian particles in soft matter [40].

The computation of the rate I is the subject of classical techniques using Laplace asymptotics, for instance in classical or path integrals [10, 22, 41]. At the mathematical level, this is the subject of large deviation theory, see for instance the Freidlin–Wentzell theory for small noise large deviations [17]. However, for most genuine applications, computing the rate I is not sufficient and a proper estimation of the sub-exponential prefactor \(C^\epsilon \), or of its asymptotic behavior in the limit of small noise \(\epsilon \downarrow 0\), is required. From a field theory perspective, such computations require the estimation of the path integrals at next to leading order. Such computations are very classical in the field theory context and involve the estimation of expectations over Gaussian processes, for which solutions of Riccati equations are needed. Several classical tools and approaches have been devised in quantum field theory and for equilibrium problems, often on a case by case basis (see for instance [8, 41] as examples among many others).

Recently, rare events, instantons, transitions rates, have been studied in far from equilibrium systems and non-equilibrium steady states, were one starts from dynamics without detailed balance. The statistical mechanics approaches have then be extended to scientific fields so far unexpected. For instance rare events, instantons, and related concepts have been used in turbulence [6, 11, 19, 20, 28], atmosphere dynamics [6, 37], climate dynamics [34], astronomy [1, 39], among many other examples. Moreover, a large effort has been pursued to develop dedicated numerical approches to compute the related instantons [18].

For all of these cases, it is essential to go beyond the computation of the exponential rates and to compute the sub-exponential prefactors. Then, although formally classical ideas still apply, several simplifications related to equilibrium dynamics no more occur. Often, the extent of possible analytic simplifications is limited, and one has to rely more on numerical simulations for actual computations. The aim of this paper is to develop the theoretical analysis at a level were it will be useful for devising numerical algorithms. We will thus consider stochastic differential equations with small noise, and develop the formalism and show the potential for numerical computations. The numerical computation will be illustrated on a simple example.

At a technical level, we will derive the needed matrix Riccati equations, discuss their initial conditions which are not trivial, for instance in the case of statistically stationary quantities, and explain the relation between the matrix Riccati equations and the quantities of interest.

1.2 Setting

In this article, we consider systems described by the stochastic differential equation

$$\begin{aligned} \mathrm {d}X^{\epsilon }_s = b\left( X^{\epsilon }_s\right) \mathrm {d}s + \sqrt{2\epsilon } \mathrm {d}W_s, \quad s \ge 0, \end{aligned}$$
(1)

in \(\mathbb {R}^d\), where \(b : \mathbb {R}^d \rightarrow \mathbb {R}^d\) is a smooth vector field, W is a d-dimensional Brownian motion, and \(\epsilon > 0\) can be interpreted as a temperature parameter. In general, the diffusion process \(X^\epsilon \) defined by (1) is not reversible, so that it serves as a model for physical systems driven out of equilibrium. In particular, when the process possesses a stationary distribution \(P^\epsilon \)-called the non-equilibrium steady state, the latter may not be explicit. Still, the Freidlin–Wentzell theory [17] asserts that in the \(\epsilon \downarrow 0\) limit and under suitable assumptions which we shall detail in Sect. 2 below, \(P^\epsilon \) satisfies a large deviation principle, with a rate function V called the quasipotential and defined in (6). We shall formally denote by

$$\begin{aligned} \lim _{\epsilon \downarrow 0} -\epsilon \log P^{\epsilon }(x) = V(x) \end{aligned}$$
(2)

this large deviation principle, and we refer to [12] for standard material on large deviation theory. The quasipotential is known to play the role of an entropy function for non-equilibrium models [3, 17, 22].

Let us define the large deviation prefactor \(C^\epsilon (x)\) to the non-equilibrium steady state \(P^\epsilon \) by the identity

$$\begin{aligned} P^{\epsilon }(x) = C^\epsilon (x)\exp \left( -\frac{V(x)}{\epsilon }\right) . \end{aligned}$$
(3)

An equivalent formulation of (2) is the assertion that \(\lim _{\epsilon \downarrow 0} \epsilon \log C^\epsilon (x) = 0\), so that no precise information on the prefactor can be obtained merely from large deviation theory. However, combining notions from this theory with a WKB approximation, we derived an asymptotic equivalent of the prefactor in [4], recalled in Eq. (18) below.

The purpose of the present article is to continue our study of the prefactor, by proposing an alternative method to obtain (18), based on the path integral formulation, and presenting a numerical method to effectively compute the terms appearing in this formula. Both tasks rely on the study of matrix-valued Riccati equations satisfied by quantities related to the fluctuations of the diffusion process \(X^\epsilon \) around given deterministic paths.

1.3 Organization of the Paper

In Sect. 2, we state the asymptotic equivalent of the prefactor obtained in [4] and recall the notions of large deviation theory involved in this formula. In Sect. 3, we describe an alternative method leading to the same formula, which is based on the path integral formulation of the non-equilibrium steady state and establishes a connection between the prefactor and the fluctuations of the process \(X^\epsilon \) around its most probable path. The relation with sharp asymptotics for mean exit times is discussed in Sect. 4. Section 5 is dedicated to the numerical computation of the asymptotic equivalent of the prefactor, which we apply on an illustrative example in Sect. 6. The conclusive Sect. 7 summarizes the main contribution of the paper and discusses their relation with other recent works.

1.4 Notations

The Euclidian norm and inner product of \(\mathbb {R}^d\) are respectively denoted by \(\Vert \cdot \Vert \) and \(\langle \cdot , \cdot \rangle \). We write \(I_d\) for the identity matrix of size \(d \times d\). Given a smooth function \(f : \mathbb {R}^d \rightarrow \mathbb {R}\) (typically, V or \(b_k\), \(\ell _k\)), we denote by \(\nabla f\) and \(\nabla ^2 f\) the gradient and Hessian matrix of f. Similarly, given a smooth vector field \(F : \mathbb {R}^d \rightarrow \mathbb {R}^d\) (typically b or \(\ell \)), \(\nabla F(x)\) refers to the matrix with coefficient \(\partial _j F_i(x)\) at the i-th row and j-th column (that is to say, \(\nabla F\) is the Jacobian matrix of F), and \(\nabla ^2F(x)(y,y)\) refers to the vector whose i-th coordinate is \(\langle y, \nabla ^2 F_i(x) y\rangle \). The symbols \(\Delta \) and \(\text {div}\) refer to the usual Laplacian and divergence operators of scalar functions. The closure of an open set \(D \subset \mathbb {R}^d\) is denoted by \(\bar{D}\). For two positive quantities \(u_\epsilon \), \(v_\epsilon \) indexed by \(\epsilon >0\), the notation \(u_\epsilon \mathop {\sim }\limits _{\epsilon \downarrow 0} v_\epsilon \) means that the ratio \(u_\epsilon /v_\epsilon \) converges to 1 when \(\epsilon \downarrow 0\).

2 Prefactor for the Stationary Distribution

In this section, we first precise the assumptions under which we shall work. We then provide a very brief summary of the main notions from the Freidlin–Wentzell theory on which we shall rely. Finally, we provide an asymptotic equivalent for the prefactor \(C^\epsilon (x)\), obtained in [4] through a WKB approximation.

2.1 Assumptions on the Vector Field b

Throughout this section, we make the following assumptions:

  1. (A1)

    the deterministic system \(\dot{x}=b(x)\) possesses a unique equilibrium point \(\bar{x} \in \mathbb {R}^d\), which attracts all the trajectories,

  2. (A2)

    for all \(\epsilon >0\), the SDE (1) possesses a unique stationary measure \(P^{\epsilon }\).

Remark 1

Assumption (A1) allows to streamline the exposition of our results. In the more general case where the deterministic system \(\dot{x}=b(x)\) possesses several (isolated) equilibrium points, our arguments can be adapted and produce statements that are valid in the neighborhood of the equilibrium points.

2.2 Action Functional, Quasipotential and Hamilton–Jacobi Equation

We recall a few notions from the Freidlin–Wentzell theory [17, Chapter 4] that will be useful in the paper.

The action functional for the stochastic differential equation (1) is defined for a trajectory \(\phi = (\phi _s)_{t_1 \le s \le t_2}\) on the time interval \([t_1,t_2]\) by

$$\begin{aligned} \mathcal {A}_{t_1,t_2}[\phi ] = {\left\{ \begin{array}{ll} \int _{s=t_1}^{t_2} \mathcal {L}(\phi _s, \dot{\phi }_s) \mathrm {d}s &{}\quad \text {if}\,\phi \hbox { is absolutely continuous},\\ +\infty &{}\quad \text {otherwise}, \end{array}\right. } \end{aligned}$$
(4)

where the Lagrangian \(\mathcal {L}\) writes

$$\begin{aligned} \forall (x,v) \in \mathbb {R}^d \times \mathbb {R}^d, \quad \mathcal {L}(x,v) = \frac{1}{4}\Vert v-b(x)\Vert ^2. \end{aligned}$$
(5)

It describes the large deviations of the trajectory \((X^{\epsilon }_s)_{s \in [t_1,t_2]}\) when \(\epsilon \downarrow 0\) [17, Theorem 1.1, p. 86].

The quasipotential with respect to \(\bar{x}\) is defined by the variational formula

$$\begin{aligned} V(x) = \inf \{\mathcal {A}_{t_1,t_2}[\phi ], \phi _{t_1} = \bar{x}, \phi _{t_2} = x, t_1 < t_2\}, \end{aligned}$$
(6)

where the infimum runs over all finite time intervals \([t_1,t_2]\) and trajectories \(\phi = (\phi _s)_{t_1 \le s \le t_2}\). The quasipotential is nonnegative. Besides, it is known that if it is smooth, then it solves the Hamilton–Jacobi equation

$$\begin{aligned} \langle \nabla V(x), \nabla V(x)\rangle + \langle b(x), \nabla V(x)\rangle = 0, \end{aligned}$$
(7)

in domains of \(\mathbb {R}^d\) in which, in particular, \(\bar{x}\) is the only critical point of V. We refer to the discussion in [17, pp. 100–101] for details. In this work, we shall assume that this property actually holds globally:

  1. (A3)

    the quasipotential V is \(C^2\) on \(\mathbb {R}^d\), \(\nabla V(x) \not =0\) for any \(x \not = \bar{x}\), and the Hamilton–Jacobi equation (7) holds on \(\mathbb {R}^d\).

Equivalently, the vector field \(\ell \) defined by

$$\begin{aligned} b(x) = -\nabla V(x) + \ell (x) \end{aligned}$$
(8)

satisfies

$$\begin{aligned} \forall x \in \mathbb {R}^d, \qquad \langle \nabla V(x), \ell (x)\rangle = 0. \end{aligned}$$
(9)

Assumption (A3) then implies that the quasipotential satisfies the identity

$$\begin{aligned} V(x) = \int \limits _{s=-\infty }^0 \mathcal {L}(\varphi ^x_s,\dot{\varphi }^x_s)\mathrm {d}s = \mathcal {A}_{-\infty ,0}[\varphi ^x], \end{aligned}$$
(10)

where \(\varphi ^x = (\varphi ^x_s)_{s \le 0}\) is the minimum action path joining \(\bar{x}\) to x, defined as the unique solution to the backward Cauchy problem

$$\begin{aligned} \left\{ \begin{aligned}&\dot{\varphi }^x_s = \nabla V(\varphi ^x_s) + \ell (\varphi ^x_s), \quad s \le 0,\\&\varphi ^x_0 = x, \quad \lim _{s \rightarrow -\infty } \varphi ^x_s = \bar{x}. \end{aligned}\right. \end{aligned}$$
(11)

The identity (10) shows in particular that in (6), the quantity V(x) could be equivalently defined as \(\inf \{\mathcal {A}_{-\infty ,0}[\phi ], \lim _{t \rightarrow -\infty } \phi _t = \bar{x}, \phi _0 = x\}\). In the sequel of the paper, we shall call \(\varphi ^x\) the fluctuation path, as it describes the most probable path followed by a fluctuation of the diffusion process \(X^\epsilon \) joining \(\bar{x}\) to x.

Remark 2

Under Assumption (A3), differentiating the equality \(\langle \nabla V, \ell \rangle = 0\) twice, we get the identity

$$\begin{aligned} \sum _{k=1}^d (\partial _k \nabla ^2 V) \ell _k + \nabla ^2 V \nabla \ell + \nabla \ell ^{\top } \nabla ^2 V + \sum _{k=1}^d (\partial _k V) \nabla ^2 \ell _k = 0, \end{aligned}$$
(12)

which shall be useful in the course of the paper. We recall here that the notation \(\nabla ^2\) refers to the Hessian matrix, see Sect. 1.4.

Remark 3

Putting (8) and (11) together shows that the fluctuation path, the quasipotential and the drift b satisfy the identity

$$\begin{aligned} \nabla V(\varphi ^x_s) = \frac{1}{2}\left( \dot{\varphi }^x_s-b(\varphi ^x_s)\right) , \end{aligned}$$
(13)

which will be used in the sequel of the paper.

Remark 4

Assumption (A3) is satisfied in particular if the vector field b is known to possess an explicit transverse decomposition of the form \(b = -\nabla V + \ell \), for some smooth function \(V : \mathbb {R}^d \rightarrow \mathbb {R}\) which is such that \(\langle \nabla V, \ell \rangle = 0\) on \(\mathbb {R}^d\), and \(\nabla V(x) \not = 0\) if \(x \not = \bar{x}\). In this case, V can be then shown to coincide with the quasipotential with respect to \(\bar{x}\), defined by the right-hand side of the identity (6). However, even if the vector field b is smooth, it is in general difficult to prove directly that the quasipotential, defined by the right-hand side of (6), is smooth.

2.3 WKB Derivation of the Formula for the Prefactor

Injecting both the decomposition (8) of the vector field b and the ansatz (3) in the stationary Fokker–Planck equation

$$\begin{aligned} \epsilon \Delta P^\epsilon - \text {div}(b P^\epsilon ) = 0 \end{aligned}$$
(14)

shows that \(P^\epsilon \) is equal to the Gibbs measure

$$\begin{aligned} P^\epsilon _{\mathrm {Gibbs}}(x) = \frac{1}{Z^\epsilon } \exp \left( -\frac{V(x)}{\epsilon }\right) , \quad Z^\epsilon = \int \limits _{x \in \mathbb {R}^d} \exp \left( -\frac{V(x)}{\epsilon }\right) \mathrm {d}x, \end{aligned}$$
(15)

if and only if the condition

$$\begin{aligned} \forall x \in \mathbb {R}^d, \qquad \text {div}\ell (x) = 0 \end{aligned}$$
(16)

holds. In this case, the prefactor \(C^\epsilon \) does not depend on x and the Laplace approximation for \(Z^\epsilon \) provides the asymptotic equivalence

$$\begin{aligned} C^\epsilon \mathop {\sim }\limits _{\epsilon \downarrow 0} \sqrt{\frac{\det \nabla ^2 V(\bar{x})}{(2\pi \epsilon )^d}}, \end{aligned}$$
(17)

as soon as the following assumption holds:

  1. (A4)

    the matrix \(\nabla ^2 V(\bar{x})\) is positive-definite.

If the condition (16) does not hold, an expansion in powers of \(\epsilon \) can be performed in (14), following the usual WKB approximation method. This leads to the prefactor equivalent

$$\begin{aligned} C^\epsilon (x) \mathop {\sim }\limits _{\epsilon \downarrow 0} \sqrt{\frac{\det \nabla ^2 V(\bar{x})}{(2\pi \epsilon )^d}}\exp \left( -\int \limits _{s=-\infty }^0 \text {div}\ell (\varphi ^x_s)\mathrm {d}s\right) , \end{aligned}$$
(18)

which was derived in [4, Sect. 3], see also previous results in [9, 31, 32, 36]. The supplementary exponential term appearing in the right-hand side of (18) depends on the value of \(\text {div}\ell \) along the whole trajectory of the fluctuation path \(\varphi ^x\). Therefore, we shall call it the nonlocal contribution to the prefactor.

3 Derivation of the Formula from the Path Integral Formulation

In this section, we still work under Assumptions (A1–4), and describe an alternative method to the WKB approximation in order to derive the formula (18) for the prefactor to the stationary distribution \(P^\epsilon \). The method is based on the path integral formulation of \(P^\epsilon \), in which a Laplace approximation is performed, leading to the computation of an infinite-dimensional Gaussian integral. The latter involves the fluctuations of the process \(X^\epsilon \) around the path \(\varphi ^x\), and thanks to the Feynman–Kac formula, it is computed by solving a backward matrix Riccati equation.

Our derivation is rather formal; in particular, the Laplace approximation in the path integral formulation is not rigorously justified. However, and although it is certainly less straightforward than the direct WKB approximation sketched in the previous section (which is also nonrigorous), the method presented here has the conceptual advantage to establish a connection between the prefactor, written under the form of a functional determinant, and the process of fluctuations of \(X^\epsilon \) around the path \(\varphi ^x\). The latter process was recently studied in the mathematical literature [30, 35].

3.1 Laplace Approximation in the Path Integral Formulation

In this subsection, we fix \(X^{\epsilon }_0 = \bar{x}\). Then, observables of the trajectory \((X^\epsilon _s)_{s \in [0,t]}\) write in the path integral formalism

$$\begin{aligned} \mathbb {E}\left[ F\left( (X^\epsilon _s)_{s \in [0,t]}\right) \right] = \int \limits _{\phi _0=\bar{x}} F[\phi ] \mathrm {e}^{-\frac{1}{\epsilon }\mathcal {A}_{0,t}[\phi ]} \mathcal {D}[\phi ], \end{aligned}$$
(19)

where the integral is taken over all absolutely continuous, \(\mathbb {R}^d\)-valued trajectories \(\phi =(\phi _s)_{s \in [0,t]}\) such that \(\phi _0=\bar{x}\). This fact can be obtained following the standard time-discretization construction of path integrals, using Ito’s convention for the discretization. Alternatively, with a more probabilistic point of view, it may be derived from the Girsanov theorem, once one takes the convention to denote by \(\mathrm {e}^{-\frac{1}{4\epsilon }\int _{s=0}^t \Vert \dot{\phi }_s\Vert ^2 \mathrm {d}s}\mathcal {D}[\phi ]\) the law of the Brownian trajectory \((\bar{x}+\sqrt{2\epsilon }W_s)_{s \in [0,t]}\).

In this formalism, we deduce that the density of the random variable \(X^\epsilon _t\) writes

$$\begin{aligned} P^\epsilon _t(x) = \int \limits _{\phi _0=\bar{x}} \delta _0(\phi _t-x) \mathrm {e}^{-\frac{1}{\epsilon }\mathcal {A}_{0,t}[\phi ]} \mathcal {D}[\phi ], \end{aligned}$$
(20)

for any \(x \in \mathbb {R}^d\), where \(\delta _0\) is the Dirac distribution at 0. In the sequel, it is more convenient to consider trajectories defined on [t, 0], \(t<0\), rather than on [0, t], \(t>0\). Therefore we introduce the notation

$$\begin{aligned} \bar{P}^\epsilon _t(x) = P^\epsilon _{-t}(x) = \int \limits _{\phi _t=\bar{x}} \delta _0(\phi _0-x) \mathrm {e}^{-\frac{1}{\epsilon }\mathcal {A}_{t,0}[\phi ]} \mathcal {D}[\phi ], \end{aligned}$$
(21)

for \(t<0\). As a consequence, the stationary distribution \(P^{\epsilon }\) writes

$$\begin{aligned} P^{\epsilon }(x) = \lim _{t \rightarrow +\infty } P^\epsilon _t(x) = \lim _{t \rightarrow -\infty } \bar{P}^\epsilon _t(x). \end{aligned}$$
(22)

The second-order expansion of the action functional on [t, 0] around the fluctuation path defined by (11) writes

$$\begin{aligned} \mathcal {A}_{t,0}[\phi ] \simeq \mathcal {A}_{t,0}[\varphi ^x] + \frac{\delta \mathcal {A}_{t,0}}{\delta \phi }[\varphi ^x](\phi -\varphi ^x) + \frac{1}{2}\frac{\delta ^2 \mathcal {A}_{t,0}}{\delta \phi ^2}[\varphi ^x](\phi -\varphi ^x, \phi -\varphi ^x). \end{aligned}$$
(23)

In the \(t \rightarrow -\infty \) limit, the first-order term vanishes because of the optimality condition on \(\varphi ^x\). The second-order term rewrites

$$\begin{aligned} \begin{aligned}&\frac{1}{2}\frac{\delta ^2 \mathcal {A}_{t,0}}{\delta \phi ^2}[\varphi ^x](\delta \phi , \delta \phi )\\&= \frac{1}{4} \int \limits _{s=t}^0 \left( \Vert \delta \dot{\phi }_s - \nabla b(\varphi ^x_s) \delta \phi _s\Vert ^2 - \langle \dot{\varphi }^x_s - b(\varphi ^x_s), \nabla ^2 b(\varphi ^x_s)(\delta \phi _s, \delta \phi _s)\rangle \right) \mathrm {d}s\\&= \frac{1}{4} \int \limits _{s=t}^0 \left( \Vert \delta \dot{\phi }_s + Q^x_s \delta \phi _s\Vert ^2 + 2\langle \delta \phi _s, R^x_s\delta \phi _s\rangle \right) \mathrm {d}s, \end{aligned} \end{aligned}$$
(24)

where the matrices \(Q^x_s\) and \(R^x_s\) are defined, for \(s \le 0\), by

$$\begin{aligned} Q^x_s = -\nabla b(\varphi ^x_s), \quad R^x_s = -\sum _{k=1}^d \partial _k V(\varphi ^x_s) \nabla ^2 b_k(\varphi ^x_s). \end{aligned}$$
(25)

At this stage, let us anticipate on the numerical discussion of Sect. 5, and point out that the identity (13) shows that the matrices \(Q^x_s\) and \(R^x_s\) can be computed from the mere knowledge of the vector field b with its space derivatives, and the fluctuation path \(\varphi ^x\) together with its time derivative. In particular, it is not necessary to compute neither the quasipotential nor its space derivatives along the fluctuation path.

As a consequence of the second-order expansion of the action functional, the Laplace approximation yields, for \(\epsilon > 0\) small but fixed,

$$\begin{aligned} \bar{P}^{\epsilon }_t(x) \simeq \mathrm {e}^{-\frac{1}{\epsilon }\mathcal {A}_{t,0}[\varphi ^x]} \int \limits _{\delta \phi _t=\bar{x}-\varphi ^x_t} \delta _0(\delta \phi _0) \mathrm {e}^{-\frac{1}{4\epsilon }\int _{s=t}^0 \left( \Vert \delta \dot{\phi }_s + Q^x_s \delta \phi _s\Vert ^2 + 2\langle \delta \phi _s, R^x_s\delta \phi _s\rangle \right) \mathrm {d}s} \mathcal {D}[\delta \phi ]. \end{aligned}$$
(26)

By (10), in the \(t \rightarrow -\infty \) limit, \(\mathcal {A}_{t,0}[\varphi ^x]\) converges to the quasipotential V(x), while (11) shows that \(\bar{x}-\varphi ^x_t\) vanishes. Therefore the prefactor \(C^{\epsilon }(x)\) defined by (3) is equivalent, when \(\epsilon \downarrow 0\), to the \(t \rightarrow -\infty \) limit of the path integral

$$\begin{aligned} \begin{aligned}&\int \limits _{\delta \phi _t=0} \delta _0(\delta \phi _0) \mathrm {e}^{-\frac{1}{4\epsilon }\int _{s=t}^0 \left( \Vert \delta \dot{\phi }_s + Q^x_s \delta \phi _s\Vert ^2 + 2\langle \delta \phi _s, R^x_s\delta \phi _s\rangle \right) \mathrm {d}s} \mathcal {D}[\delta \phi ]\\&= \frac{1}{\epsilon ^{d/2}} \int \limits _{\delta \phi _t=0} \delta _0(\delta \phi _0) \mathrm {e}^{-\frac{1}{4}\int _{s=t}^0 \left( \Vert \delta \dot{\phi }_s + Q^x_s \delta \phi _s\Vert ^2 + 2\langle \delta \phi _s, R^x_s\delta \phi _s\rangle \right) \mathrm {d}s} \mathcal {D}[\delta \phi ] \end{aligned} \end{aligned}$$
(27)

after rescaling \(\delta \phi \) by the factor \(\sqrt{\epsilon }\) and using the fact that \(\delta _0(\sqrt{\epsilon }y) = \epsilon ^{-d/2}\delta _0(y)\). Since the term appearing in the time integral above is quadratic in \(\delta \phi \), the path integral is an infinite-dimensional Gaussian integral, the computation of which usually reduces to the computation of a functional determinant. In the next paragraph, we adopt a different strategy to compute its value, based on the use of the Feynman–Kac formula.

3.2 Feynman–Kac Formula and Backward Matrix Riccati Equation

Let us define, for all \(t \le 0\) and \(x,y \in \mathbb {R}^d\),

$$\begin{aligned} u(x;t,y) = \int \limits _{\delta \phi _t=y} \delta _0(\delta \phi _0) \mathrm {e}^{-\frac{1}{4}\int _{s=t}^0 \left( \Vert \delta \dot{\phi }_s + Q^x_s \delta \phi _s\Vert ^2 + 2\langle \delta \phi _s, R^x_s\delta \phi _s\rangle \right) \mathrm {d}s} \mathcal {D}[\delta \phi ], \end{aligned}$$
(28)

where the path integral is taken over trajectories \(\delta \phi \) on [t, 0] such that \(\delta \phi _t=y\), so that by (26–27),

$$\begin{aligned} C^{\epsilon }(x) \mathop {\sim }\limits _{\epsilon \downarrow 0} \frac{1}{\epsilon ^{d/2}} \lim _{t \rightarrow -\infty } u(x;t,0). \end{aligned}$$
(29)

The introduction of this notation allows to provide a probabilistic interpretation to the right-hand side of (28). Indeed, the path integral there writes as the expectation

$$\begin{aligned} u(x;t,y) = \mathbb {E}_{t,y}\left[ \exp \left( -\frac{1}{2}\int \limits _{s=t}^0 \langle Y^x_s, R^x_sY^x_s\rangle \mathrm {d}s\right) \delta _0(Y^{\epsilon }_0)\right] , \end{aligned}$$
(30)

where \((Y^x_s)_{s \le 0}\) is the diffusion process defined by

$$\begin{aligned} \mathrm {d}Y^x_s = - Q^x_s Y^x_s \mathrm {d}s + \sqrt{2} \mathrm {d}W_s, \quad s \le 0, \end{aligned}$$
(31)

and \(\mathbb {E}_{t,y}[\cdot ]\) refers to the expectation under which \(Y^x_t=y\) while \(\delta _0\) still denotes the Dirac distribution in 0. The linear process \((Y^x_s)_{s \le 0}\) describes the scaled Gaussian fluctuations of the original process around \((\varphi ^x_s)_{s \le 0}\).

By the Feynman–Kac formula, the function u(x; t, y) is the solution to the backward parabolic problem

$$\begin{aligned} \left\{ \begin{aligned}&-\partial _t u(x;t,y) = \Delta _y u(x;t,y) - \langle Q^x_t y, \nabla _y u(x;t,y)\rangle - \frac{1}{2} \langle y, R^x_t y\rangle u(x;t,y), \quad t < 0,\\&u(x;0,y) = \delta _0(y). \end{aligned}\right. \end{aligned}$$
(32)

Since the diffusion process \((Y^x_s)_{s \le 0}\) describes Gaussian fluctuations around the fluctuation path, we shall look for a solution to (32) with the Gaussian ansatz

$$\begin{aligned} u(x;t,y) = \frac{1}{\sqrt{(4\pi )^d \eta ^x_t}} \exp \left( -\frac{\langle y, K^x_t y\rangle }{4}\right) , \end{aligned}$$
(33)

where, for all \(t<0\), \(\eta ^x_t>0\) and the matrix \(K^x_t\) is symmetric. This is a natural ansatz since (30) shows that \(u(x;t,\cdot )\) is the marginal distribution at time \(s=0\) of the Gaussian process \((Y^\epsilon _s)_{s \in [t,0]}\), under an (unnormalized) exponential tilting by a quadratic functional of this process. Since such changes of measure are known to preserve Gaussian distributions, the resulting density may be expected to remain Gaussian. Furthermore, the condition \(u(x;0,y) = \delta _0(y)\) implies the limit behavior

$$\begin{aligned} \lim _{t \uparrow 0} (K^x_t)^{-1} = 0, \quad \lim _{t \uparrow 0} \eta ^x_t = 0, \quad \lim _{t \uparrow 0} \eta ^x_t \det K^x_t = 1. \end{aligned}$$
(34)

Injecting the ansatz (33) into the problem (32), we get the system of ordinary differential equations

$$\begin{aligned} \forall t < 0, \qquad \left\{ \begin{aligned}&\dot{\eta }^x_t = - \eta ^x_t \text {tr}K^x_t,\\&\dot{K}^x_t = (K^x_t)^2 + {Q^x_t}^{\top }K^x_t + K^x_t Q^x_t - 2R^x_t. \end{aligned}\right. \end{aligned}$$
(35)

The second equation is a backward matrix Riccati equation, it is solved in Appendix 2. We obtain the explicit result

$$\begin{aligned} \forall t < 0, \quad K^x_t = -2\nabla ^2 V\left( \varphi ^x_t\right) + \left( Z^x_t\right) ^{-1}, \end{aligned}$$
(36)

with

$$\begin{aligned} \begin{aligned}&Z^x_t = \int \limits _{s=t}^0 \left\lfloor \exp \left( \int \limits _{r=s}^t A^x_r \mathrm {d}r\right) \right\rfloor \left\lfloor \exp \left( \int \limits _{r=s}^t A^x_r \mathrm {d}r\right) \right\rfloor ^{\top }\mathrm {d}s,\\&A^x_r = \nabla ^2 V(\varphi ^x_r) + \nabla \ell (\varphi ^x_r), \end{aligned} \end{aligned}$$
(37)

and \(\lfloor \exp (\cdot )\rfloor \) denotes the time ordered exponential of matrices, the definition and a few properties of which are recalled in Appendix 1. From (36) we deduce in Appendix 3 that

$$\begin{aligned} \lim _{t \rightarrow -\infty } \eta ^x_t = \frac{1}{2^d \det (\nabla ^2 V(\bar{x}))}\exp \left( 2\int \limits _{s=-\infty }^0 \text {div}\ell (\varphi ^x_s)\mathrm {d}s\right) . \end{aligned}$$
(38)

Combining this result with the identities (29) and (33) allows to recover the formula (18). As a conclusive statement, we write the asymptotic equivalence for the non-equilibrium steady state

$$\begin{aligned} P^\epsilon (x) \mathop {\sim }\limits _{\epsilon \downarrow 0} \sqrt{\frac{\det \nabla ^2 V(\bar{x})}{(2\pi \epsilon )^d}}\exp \left( -\frac{V(x)}{\epsilon }-\int \limits _{s=-\infty }^0 \text {div}\ell (\varphi ^x_s)\mathrm {d}s\right) . \end{aligned}$$
(39)

The computation of the solution (36) to the system (35), together with the proof of the identity (38), make our derivation of the final asymptotics (39) for the non-equilibrium steady state definitely different from the WKB approximation from Sect. 2. This chain of arguments may be considered as the main conceptual result from this article.

4 Application to Mean Exit Times

Let \(D \subset \mathbb {R}^d\) be a domain containing an equilibrium point \(\bar{x}\) of the deterministic system \(\dot{x}=b(x)\). Let us define the exit time from D by

$$\begin{aligned} \tau ^\epsilon _D = \inf \{s \ge 0 : X^\epsilon _s \not \in D\}. \end{aligned}$$
(40)

Under suitable assumptions on D, the Freidlin–Wentzell theory asserts that

$$\begin{aligned} \lim _{\epsilon \downarrow 0} \epsilon \log \mathbb {E}_{\bar{x}}[\tau ^\epsilon _D] = \inf _{y \in \partial D} V(y), \end{aligned}$$
(41)

where the subscript \(\bar{x}\) indicates that \(X^\epsilon _0 = \bar{x}\), and V still refers to the quasipotential with respect to \(\bar{x}\) defined by (6).

When the deterministic system \(\dot{x}=b(x)\) possesses several stable equilibrium points and D denotes the basin of attraction of one of these points \(\bar{x}\), then the diffusion process \((X^\epsilon _s)_{s \ge 0}\) is called metastable, and the logarithmic equivalent (41) is called the Arrhenius law.

In any case, the associated prefactor \(L^\epsilon _D\) to the mean exit time from D is defined by

$$\begin{aligned} \mathbb {E}_{\bar{x}}[\tau ^\epsilon _D] = L^\epsilon _D \exp \left( \frac{1}{\epsilon } \inf _{y \in \partial D} V(y)\right) . \end{aligned}$$
(42)

In this section, we express this prefactor in terms of the function \(C^\epsilon (x)\) computed in (18).

4.1 Domain with a Noncharacteristic Boundary

In this subsection, we assume that D is an open, smooth and connected subset of \(\mathbb {R}^d\) satisfying the following conditions, where we denote by n(y) the exterior normal vector at \(y \in \partial D\).

  1. (B1)

    The deterministic system \(\dot{x}=b(x)\) possesses a unique equilibrium point \(\bar{x}\) in D, which attracts all the trajectories started from D, and \(\langle b(y), n(y) \rangle < 0\) for all \(y \in \partial D\).

  2. (B2)

    The function V is \(C^1\) in D; for any \(x \in \bar{D}\), the fluctuation path \(\varphi ^x_s\) goes to \(\bar{x}\) when \(s \rightarrow -\infty \); and \(\langle \nabla V(y), n(y)\rangle > 0\) for all \(y \in \partial D\).

Under these assumptions, we proceed as in Sect. 2.2 and define the vector field \(\ell : \bar{D} \rightarrow \mathbb {R}^d\) by the identity \(b=-\nabla V+\ell \). Then \(\ell \) still satisfies the orthogonality relation (9).

  1. (B3)

    The minimum of V over \(\partial D\) is reached at a single point \(y^*\), at which

    $$\begin{aligned} \mu ^* = \langle \nabla V(y^*) + \ell (y^*), n(y^*) \rangle > 0, \end{aligned}$$
    (43)

    and the quadratic form \(h^*: \xi \mapsto \langle \xi , \nabla ^2 V(y^*) \xi \rangle \) has positive eigenvalues on the hyperplane \(n(y^*)^\perp = \{\xi \in \mathbb {R}^d: \langle \xi , n(y^*)\rangle = 0\}\).

By Assumption (B1), [17, Theorem 4.1, p. 106] applies and yields (41). In [4, Eq. (4.25)], the integral formula

$$\begin{aligned} \lambda ^\epsilon _D = \int \limits _{y \in \partial D} \langle \nabla V(y) + \ell (y), n(y)\rangle C^\epsilon (y) \exp \left( -\frac{V(y)}{\epsilon }\right) \mathrm {d}y \end{aligned}$$
(44)

was derived for the exit rate \(\lambda ^\epsilon _D = \mathbb {E}_{\bar{x}}[\tau ^\epsilon _D]^{-1}\). Using the second-order expansion of V in the neighborhood of \(y^*\) in this formula, we obtain the equivalent

$$\begin{aligned} \begin{aligned} L^\epsilon _D&\mathop {\sim }\limits _{\epsilon \downarrow 0} \frac{1}{C^\epsilon (y^*) \mu ^*} \sqrt{\frac{\det h^*}{(2\pi \epsilon )^{d-1}}}\\&\mathop {\sim }\limits _{\epsilon \downarrow 0} \frac{1}{\mu ^*}\sqrt{\frac{2\pi \epsilon \det h^*}{\det \nabla ^2 V(\bar{x})}}\exp \left( \int \limits _{s=-\infty }^0 \text {div}\ell \left( \varphi ^{y^*}_s\right) \mathrm {d}s\right) \end{aligned} \end{aligned}$$
(45)

for the prefactor to the mean exit time from D.

4.2 The Eyring–Kramers Formula for Metastable States

In this subsection, we assume that the deterministic system \(\dot{x}=b(x)\) possesses two stable equilibrium points \(\bar{x}_1\) and \(\bar{x}_2\), whose basins of attractions are separated by a smooth hypersurface S.

We call D the basin of attraction of \(\bar{x}_1\) and formulate the following set of assumptions.

  1. (C1)

    All the trajectories of the deterministic system \(\dot{x}=b(x)\) started on S remain in S and converge to a single equilibrium point \(x^* \in S\); besides, the matrix \(\nabla b(x^*)\) possesses \(d-1\) eigenvalues with negative real part and a single positive eigenvalue \(\lambda ^*\).

  2. (C2)

    Denoting by V the quasipotential with respect to \(\bar{x}_1\) still defined by (6), there exists a unique (up to time shift) trajectory \(\rho = (\rho _t)_{t \in \mathbb {R}} \subset D\) such that

    $$\begin{aligned} \lim _{t \rightarrow -\infty } \rho _t = \bar{x}_1, \quad \lim _{t \rightarrow +\infty } \rho _t = x^*, \quad \text {and} \quad V(x^*) = \mathcal {A}_{-\infty ,+\infty }[\rho ]. \end{aligned}$$
    (46)
  3. (C3)

    V is smooth in the neighborhood of \((\rho _t)_{t \in \mathbb {R}}\), and the vector field \(\ell \) defined by the identity \(b=-\nabla V+\ell \) satisfies the orthogonality relation (9).

In this context, V reaches its minimum on S at the point \(x^*\), and we refer to [2] for a proof of the Arrhenius law (41) based on the Freidlin–Wentzell theory. Furthermore, the path \(\rho \) is called the instanton and it satisfies

$$\begin{aligned} \forall t \in \mathbb {R}, \quad \dot{\rho }_t = \nabla V(\rho _t) + \ell (\rho _t). \end{aligned}$$
(47)

As a consequence, for any \(t \in \mathbb {R}\), the fluctuation path \((\varphi ^x_s)_{s \le 0}\) joining \(\bar{x}\) to \(x=\rho _t\) coincides with the instanton, in the sense that

$$\begin{aligned} \forall s \le 0, \quad \varphi ^x_s = \rho _{s+t}. \end{aligned}$$
(48)

In order to describe the prefactor \(L^\epsilon _D\) in this case, we formulate the following supplementary assumption.

  1. (C4)

    The matrix \(H^* = \lim _{t \rightarrow +\infty } \nabla ^2 V(\rho _t)\) exists and has \(d-1\) positive eigenvalues and 1 negative eigenvalue.

Under Assumptions (C1–4), a formula was obtained in [4, Eq. (1.10)] to describe the sharp asymptotics of the expected time taken by the process to reach the neighborhood of \(\bar{x}_2\), which is the contents of the so-called Eyring–Kramers formula in the context of reversible diffusion processes [7]. Large deviation theory shows that with overwhelming probability, the path taken by the process to reach \(\bar{x}_2\) passes close to \(x^*\). At this point, since \(b(x^*)=0\), the process has a probability close to 1/2 to turn back into D and a probability close to 1/2 to reach the neighbourood of \(\bar{x}_2\). Therefore, the expected time taken by the process to exit D is half the time described by the Eyring–Kramers formula. As a consequence, dividing the right-hand side of [4, Eq. (1.10)] by 2, we get the estimate

$$\begin{aligned} L^\epsilon _D \mathop {\sim }\limits _{\epsilon \downarrow 0} \frac{\pi }{\lambda ^*}\sqrt{\frac{|\det H^*|}{\det \nabla ^2 V(\bar{x}_1)}}\exp \left( \int \limits _{t=-\infty }^{+\infty } \text {div}\ell (\rho _t)\mathrm {d}t\right) \end{aligned}$$
(49)

for the prefactor to the mean exit time from D.

Remark 5

Notice that in the case addressed in Sect. 4.1, \(L^\epsilon _D\) is proportional to \(\sqrt{\epsilon }\), while in the present case, \(L^\epsilon _D\) does not depend on \(\epsilon \).

4.3 Comments on the Nonlocal Contribution

In the formula obtained for \(L^\epsilon _D\) in the cases of both Sects. 4.1 and 4.2, the nonlocal contribution discussed at the end of Sect. 2 appears. In particular for the Eyring–Kramers formula, the identity (48) allows to relate the integral term of (49) to fluctuation paths by the remark that

$$\begin{aligned} \int \limits _{t=-\infty }^{+\infty } \text {div}\ell (\rho _t)\mathrm {d}t = \lim _{t \rightarrow +\infty } \int \limits _{s=-\infty }^0 \text {div}\ell (\varphi ^{\rho _t}_s)\mathrm {d}s. \end{aligned}$$
(50)

As a consequence, in the sequel of this paper, we focus on the numerical evaluation of this term.

Recent rigorous derivations of the Eyring–Kramers formula for nonreversible diffusion processes have been obtained in [25, 29], but to our knowledge, they are restricted to the case of processes whose invariant distribution is given by the measure (15) and therefore do not include the nonlocal contribution.

5 Effective Computation of the Prefactor \(C^\epsilon \)

In Sect. 4, we showed that sharp asymptotics for mean exit times essentially follow from an accurate computation of the prefactor \(C^\epsilon \) to the stationary distribution, which was the object of Sects. 2 and 3. In this section, we therefore come back to the framework of Assumptions (A1–4) and focus on the numerical evaluation of this prefactor, whose equivalent is given by (18).

For a given \(x \in \mathbb {R}^d\), the evaluation of the right-hand side of (18) requires the computation of the following quantities:

  • the fluctuation path \((\varphi ^x_s)_{s \le 0}\),

  • the divergence of \(\ell \) along the fluctuation path,

  • the determinant of \(\nabla ^2 V(\bar{x})\).

The main difficulty to access these quantities is that in general, the transverse decomposition (8) of the vector field b is not explicit, and therefore neither \(\nabla V\) nor \(\ell \) are straightforward to obtain.

As a first step, one can remark that thanks to (8),

$$\begin{aligned} \forall s \le 0, \quad \text {div}\ell (\varphi ^x_s) = \text {div}b(\varphi ^x_s) + \Delta V(\varphi ^x_s), \end{aligned}$$
(51)

so that computing the Hessian matrix \(\nabla ^2 V(\varphi ^x_s)\) of the quasipotential along the fluctuation path is sufficient to obtain \(\text {div}\ell (\varphi ^x_s)\) and \(\det \nabla ^2 V(\bar{x})\).

Motivated by the large deviation principle (2), specific methods have been developed in the computational physics community to evaluate the quasipotential V (we provide more context in Remark 7 below). The geometric Minimum Action Method (gMAM) [23, 38] is a numerical procedure which computes the fluctuation path \(\varphi ^x\) and returns the value of V(x) given by (10). Once we are supplied with \(\varphi ^x\), we could virtually iterate the method described above in order to compute the values of V in the neighborhood of the fluctuation path, and hence approximate \(\nabla ^2 V(\varphi ^x_s)\) for selected points s on a time grid. However, computing a fluctuation path for each evaluation of V is too costly and we shall look for an algorithm that avoids doing so. Our method relies on the fact that \(\nabla ^2 V(\varphi _t^x)\) satisfies a forward matrix Riccati equation, which was already observed in [31, 32].

Proposition 1

Let \(x \in \mathbb {R}^d\). Under Assumption (A3), the family of matrices \((H^x_t)_{t \le 0}\) defined by

$$\begin{aligned} H^x_t = \nabla ^2 V\left( \varphi _t^x\right) \end{aligned}$$
(52)

satisfies the forward matrix Riccati equation

$$\begin{aligned} \dot{H}^x_t = -2\left( H^x_t\right) ^2 + {Q_t^x}^{\top } H^x_t + H^x_tQ_t^x + R_t^x, \end{aligned}$$
(53)

complemented with the limit condition

$$\begin{aligned} \lim _{t \rightarrow -\infty } H^x_t = \nabla ^2 V(\bar{x}). \end{aligned}$$
(54)

Proof

By (11), the time derivative of \(H^x_t\) writes

$$\begin{aligned} \dot{H}^x_t = \sum _{k=1}^d \left( \partial _k V\left( \varphi ^x_t\right) + \ell _k\left( \varphi ^x_t\right) \right) \partial _k \nabla ^2 V\left( \varphi ^x_t\right) . \end{aligned}$$
(55)

On the one hand, using (8) and (25) yields

$$\begin{aligned} \begin{aligned} \sum _{k=1}^d \partial _k V(\varphi ^x_t)\partial _k \nabla ^2 V(\varphi ^x_t)&= \sum _{k=1}^d \partial _k V(\varphi ^x_t)\nabla ^2 (-b_k(\varphi ^x_t)+\ell _k(\varphi ^x_t))\\&= R_t^x + \sum _{k=1}^d \partial _k V(\varphi ^x_t)\nabla ^2 \ell _k(\varphi ^x_t), \end{aligned} \end{aligned}$$
(56)

while on the other hand, the identity (12) yields

$$\begin{aligned} \begin{aligned}&\sum _{k=1}^d \ell _k(\varphi ^x_t)\partial _k \nabla ^2 V(\varphi ^x_t)\\&\quad = -\nabla ^2 V(\varphi ^x_t) \nabla \ell (\varphi ^x_t) - \nabla \ell (\varphi ^x_t)^{\top } \nabla ^2 V(\varphi ^x_t) - \sum _{k=1}^d \partial _k V(\varphi ^x_t)\nabla ^2 \ell _k(\varphi ^x_t), \end{aligned} \end{aligned}$$
(57)

so that

$$\begin{aligned} \dot{H}^x_t = -\nabla ^2 V(\varphi ^x_t) \nabla \ell (\varphi ^x_t) - \nabla \ell (\varphi ^x_t)^{\top } \nabla ^2 V(\varphi ^x_t) + R_t^x. \end{aligned}$$
(58)

We now compute

$$\begin{aligned} {Q_t^x}^{\top } H^x_t + H^x_tQ_t^x = 2(H^x_t)^2 - \nabla ^2 V(\varphi ^x_t) \nabla \ell (\varphi ^x_t) - \nabla \ell (\varphi ^x_t)^{\top } \nabla ^2 V(\varphi ^x_t), \end{aligned}$$
(59)

which yields (53) and completes the proof.

Remark 6

The backward matrix Riccati equation (35) and the forward Riccati equation (53) are related by the fact that if \(H_t\) is a solution to (53), then \(K_t = -2H_t\) is a solution to (35). This remark is employed in Appendix 2 to solve (35) by quadrature.

As was already noted in Sect. 3.1, the coefficients \(Q^x_t\) and \(R^x_t\) of the forward matrix Riccati equation (53) can be computed from the mere knowledge of b and \(\varphi ^x\), thanks to the identity (13). As a consequence, \(\nabla ^2 V(\varphi ^x_t)\) can be obtained by numerical integration of (53). Therefore we are left with two tasks: computing the limit condition \(\nabla ^2 V(\bar{x})\) for (53), and integrating this equation on \((-\infty ,0]\). These tasks are discussed in the respective Sects. 5.1 and 5.2. The whole method is then summarized in Sect. 5.3.

Remark 7

The numerical evaluation of large deviation quantities, such as quasipotentials or prefactors, is known to be a difficult question, even in low-dimensional cases. Indeed, the presence of a small term \(\epsilon \) in the second-order part of the infinitesimal generator \(\epsilon \Delta + \langle b, \nabla \rangle \) of (1) may make standard discretization schemes for Fokker–Planck or Kolmogorov equations ill-conditioned and unstable. Therefore, dedicated methods need to be developed. Roughly speaking, two classes of such methods exist: path-based methods, such as the gMAM employed in this section, which rely on the computation of minimum action paths, and mesh-based solvers which compute the value of the quasipotential V on a predetermined grid. We refer for instance to the recent work by Paskal and Cameron [33] for an example of the latter class of methods, which has the advantage to also provide an approximation of \(\nabla V\) on the grid, but crucially suffers from the curse of dimensionality.

5.1 Determination of the Limit Condition

The \(t \rightarrow -\infty \) limit condition for \(H^x_t\) is given by

$$\begin{aligned} \bar{H} = \nabla ^2 V(\bar{x}), \end{aligned}$$
(60)

which we assume to be positive-definite. This matrix satisfies the stationary version of (53), which writes

$$\begin{aligned} 2\bar{H}^2 = \bar{Q}^\top \bar{H} + \bar{H}\bar{Q}, \end{aligned}$$
(61)

with \(\bar{Q} = -\nabla b(\bar{x})\). In the context of optimal control, this equation is referred to as a continuous time algebraic Riccati equation (CARE). Alternatively, since \(\bar{x}\) is a stable equilibrium point of the dynamical system \(\dot{x}=b(x)\), the eigenvalues of \(\bar{Q}\) have nonnegative real parts. Let us assume that these eigenvalues have positive real parts. Then \(\bar{H}^{-1}\) solves the continuous Lyapunov equation

$$\begin{aligned} 2I_d = \bar{H}^{-1}\bar{Q}^\top + \bar{Q}\bar{H}^{-1}, \end{aligned}$$
(62)

so that

$$\begin{aligned} \bar{H}^{-1} = 2 \int \limits _{t=0}^{+\infty } \exp (-t\bar{Q})\exp (-t\bar{Q}^\top )\mathrm {d}t. \end{aligned}$$
(63)

5.2 Reparametrization and Integration of the System

The system (53-54) is defined on the time interval \((-\infty ,0]\), with a limit condition in \(t=-\infty \). To facilitate its numerical integration, we first introduce a reparametrization of time by the length of the fluctuation path, in the spirit of gMAM [23, 38].

The length of the fluctuation path is defined by

$$\begin{aligned} L^x = \int \limits _{s=-\infty }^0 \Vert \dot{\varphi }^x_s\Vert \mathrm {d}s = \int \limits _{s=-\infty }^0 \Vert b(\varphi ^x_s)\Vert \mathrm {d}s, \end{aligned}$$
(64)

where the second identity follows from the orthogonality relation (9). For all \(t \le 0\), we denote

$$\begin{aligned} \sigma _t = \int \limits _{s=-\infty }^t \Vert \dot{\varphi }^x_s\Vert \mathrm {d}s = \int \limits _{s=-\infty }^t \Vert b(\varphi ^x_s)\Vert \mathrm {d}s \in (0,L^x]. \end{aligned}$$
(65)

The reparametrized fluctuation path is the trajectory \((\tilde{\varphi }^x_{\sigma })_{\sigma \in [0,L^x]}\) defined by the identity

$$\begin{aligned} \forall t \le 0, \quad \varphi ^x_t = \tilde{\varphi }^x_{\sigma _t}, \end{aligned}$$
(66)

and the continuous extension \(\tilde{\varphi }^x_0 = \bar{x}\). It is easily observed that, for all \(\sigma \in (0,L^x]\),

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}\sigma } \tilde{\varphi }^x_{\sigma } = \frac{\nabla V(\tilde{\varphi }^x_{\sigma }) + \ell (\tilde{\varphi }^x_{\sigma })}{\Vert b(\tilde{\varphi }^x_{\sigma })\Vert }. \end{aligned}$$
(67)

We now define

$$\begin{aligned} \tilde{H}^x_\sigma = \nabla ^2 V(\tilde{\varphi }^x_{\sigma }), \end{aligned}$$
(68)

so that \(\tilde{H}^x_{\sigma _t} = H^x_t\) for all \(t \le 0\). Then the family \((\tilde{H}^x_\sigma )_{\sigma \in [0,L^x]}\) satisfies the problem

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm {d}}{\mathrm {d}\sigma } \tilde{H}^x_\sigma = \Vert b(\tilde{\varphi }^x_{\sigma })\Vert ^{-1}\left( -2(\tilde{H}^x_\sigma )^2 + (\tilde{Q}_\sigma ^x)^\top \tilde{H}^x_\sigma + \tilde{H}^x_\sigma \tilde{Q}_\sigma ^x + \tilde{R}_\sigma ^x\right) , \qquad \sigma \in (0,L^x],\\&\tilde{H}^x_0 = \bar{H}, \end{aligned}\right. \end{aligned}$$
(69)

with

$$\begin{aligned} \tilde{Q}_{\sigma _t}^x = Q^x_t, \quad \tilde{R}_{\sigma _t}^x = R^x_t. \end{aligned}$$
(70)

Notice that when \(\sigma \downarrow 0\), both \(\Vert b(\tilde{\varphi }^x_{\sigma })\Vert \) and \(-2(\tilde{H}^x_\sigma )^2 + (\tilde{Q}_\sigma ^x)^\top \tilde{H}^x_\sigma + \tilde{H}^x_\sigma \tilde{Q}_\sigma ^x + \tilde{R}_\sigma ^x\) vanish. Therefore in order to integrate this system starting from \(\sigma =0\), we have to provide an a priori estimate of the \(\sigma \downarrow 0\) limit of

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}\sigma } \tilde{H}^x_\sigma = \sum _{l=1}^d \frac{\mathrm {d}}{\mathrm {d}\sigma } \tilde{\varphi }^x_{l,\sigma } \partial _l \nabla ^2 V(\tilde{\varphi }^x_{\sigma }). \end{aligned}$$
(71)

First, a first-order expansion in (67) yields, in the \(\sigma \downarrow 0\) regime,

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}\sigma } \tilde{\varphi }^x_\sigma \simeq \frac{\left( \nabla ^2 V(\bar{x}) + \nabla \ell (\bar{x})\right) \left( \tilde{\varphi }^x_\sigma -\bar{x}\right) }{\left\| \nabla b(\bar{x})\left( \tilde{\varphi }^x_\sigma -\bar{x}\right) \right\| } = \frac{\left( 2\bar{H} + \nabla b(\bar{x})\right) \left( \tilde{\varphi }^x_\sigma -\bar{x}\right) }{\left\| \nabla b(\bar{x})\left( \tilde{\varphi }^x_\sigma -\bar{x}\right) \right\| } \end{aligned}$$
(72)

thanks to (8). Each individual term in the right-hand side is computable, so that one can evaluate the quantities \({\frac{\mathrm {d}}{\mathrm {d}\sigma } \tilde{\varphi }^x_{l,\sigma }}_{|\sigma =0}\) for all \(l \in \{1, \ldots , d\}\).

It remains to compute the third derivatives of V at \(\bar{x}\) in order to evaluate the matrices \(\partial _l \nabla ^2 V(\bar{x})\), \(l \in \{1, \ldots , d\}\). To this aim, we take the derivative of (12) with respect to the l-th coordinate, and evaluate the result at \(\bar{x}\). Using the fact that \(\ell (\bar{x})\) and \(\nabla V(\bar{x})\) vanish, we get the matrix identity

$$\begin{aligned} \begin{aligned} 0&= \sum _{k=1}^d \left( \partial _k \nabla ^2 V(\bar{x})\right) \left( \partial _l \ell _k(\bar{x})\right) + \left( \partial _l \nabla ^2 V(\bar{x})\right) \left( \nabla \ell (\bar{x})\right) + \left( \nabla ^2 V(\bar{x})\right) \left( \partial _l \nabla \ell (\bar{x})\right) \\&\quad + \left( \partial _l \nabla \ell (\bar{x})\right) ^\top \left( \nabla ^2 V(\bar{x})\right) + \left( \nabla \ell (\bar{x})\right) ^\top \left( \partial _l \nabla ^2 V(\bar{x})\right) + \sum _{k=1}^d \left( \partial _{kl}V(\bar{x})\right) \left( \nabla ^2 \ell _k(\bar{x})\right) . \end{aligned} \end{aligned}$$
(73)

Substituting the derivatives of \(\ell \) with those of \(b+\nabla V\), and introducing the notations

$$\begin{aligned} v_{ijl} = \partial _{ijl} V(\bar{x}), \quad h_{ij} = \partial _{ij} V(\bar{x}), \quad \beta _{i,j} = \partial _j b_i(\bar{x}), \quad \gamma _{i,jl} = \partial _{jl} b_i(\bar{x}), \end{aligned}$$
(74)

we finally obtain that, for all \(i,j,l \in \{1, \ldots , d\}\),

$$\begin{aligned} \begin{aligned} 0&= \sum _{k=1}^d v_{ijk}(\beta _{k,l}+h_{kl}) + v_{ikl}(\beta _{k,j}+h_{jk}) + h_{ik}(\gamma _{k,jl}+v_{jkl})\\&\quad + (\gamma _{k,il}+v_{ikl})h_{jk} + (\beta _{k,i}+h_{ik})v_{jkl} + h_{kl}(\gamma _{k,ij}+v_{ijk}). \end{aligned} \end{aligned}$$
(75)

Since the coefficients \(h_{ij}\), \(\beta _{i,j}\) and \(\gamma _{i,jl}\) are known, the system of equations above induces \(d^3\) linear relations between the \(d^3\) unknown coefficients \(v_{ijl}\) –- more precisely, since both the left-hand side of (75) and the value of \(v_{ijl}\) are invariant by permutation of the indices i, j and l, the number of independent linear relations and unknown coefficients is reduced to \(d(d+1)(d+2)/6\). The resolution of this system allows to reconstruct the matrices \(\partial _l \nabla ^2 V(\bar{x})\) and completes the computation of (71). Notice that these matrices also possess an explicit formulation as an integral along the fluctuation path associated with the linearized stochastic differential equation

$$\begin{aligned} \mathrm {d}\tilde{X}^{\epsilon }_s = \nabla b(\bar{x})\left( \tilde{X}^{\epsilon }_s-\bar{x}\right) \mathrm {d}s + \sqrt{2\epsilon } \mathrm {d}W_s, \quad s \ge 0, \end{aligned}$$
(76)

see [5, Sect. 3.3 and Eq. (3.39)].

5.3 Conclusion

Given \(x \in \mathbb {R}^d\) and \(\epsilon > 0\), the numerical procedure sketched above to compute the right-hand side of (18) can be summarized in the following steps.

  1. 1.

    Compute the fluctuation path \(\varphi ^x\), for example using gMAM [23, 38]. From this step, the value of V(x) along the fluctuation path can be deduced thanks to (10), which allows to evaluate the right-hand side of (2).

  2. 2.

    Solve the stationary matrix Riccati equation (61) to get \(\bar{H} = \nabla ^2 V(\bar{x})\). This can be done either:

  • by computing the integral (63), which solves the Lyapunov equation (62), and inverting the result;

  • or by using a numerical solver for the CARE (61) directly.

  1. 3.

    Compute \(L^x\) and for a given number of time steps \(N \gg 1\), compute times \(0 = t_N> t_{N-1}> \cdots> t_1 > t_0 = -\infty \) such that

    $$\begin{aligned} \forall n \in \{1, \ldots , N-1\}, \quad \int \limits _{s=t_n}^{t_{n+1}} \Vert b(\varphi ^x_s)\Vert \mathrm {d}s = \theta , \end{aligned}$$
    (77)

    with \(\theta = L^x/N\).

  2. 4.

    Using (72), compute

    $$\begin{aligned} {\frac{\mathrm {d}}{\mathrm {d}\sigma } \tilde{\varphi }^x_\sigma }_{|\sigma =0} \simeq \frac{\left( 2\bar{H} + \nabla b(\bar{x})\right) \left( \varphi ^x_{t_1}-\bar{x}\right) }{\left\| \nabla b(\bar{x})\left( \varphi ^x_{t_1}-\bar{x}\right) \right\| }, \end{aligned}$$
    (78)

    and solve (75) to get the matrices \(\partial _l \nabla ^2 V(\bar{x})\), \(l \in \{1, \ldots , d\}\).

  3. 5.

    Compute the approximation \(\tilde{H}^{[n]}\) of \(\tilde{H}^x_{n\theta } = H_{t_n}\) by integrating the matrix-valued differential equation

    $$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}\sigma } \tilde{H}^x_\sigma = \frac{-2(\tilde{H}^x_\sigma )^2 + (\tilde{Q}_\sigma ^x)^\top \tilde{H}^x_\sigma + \tilde{H}^x_\sigma \tilde{Q}_\sigma ^x + \tilde{R}_\sigma ^x}{\Vert b(\tilde{\varphi }^x_{\sigma })\Vert } \end{aligned}$$
    (79)

    on the grid \(\sigma \in \{\theta , 2\theta , \ldots , N\theta \}\), with initial conditions

    $$\begin{aligned} \left\{ \begin{aligned}&\tilde{H}^{[0]} = \bar{H},\\&\tilde{H}^{[1]} = \tilde{H}^{[0]} + \theta \sum _{l=1}^d {\frac{\mathrm {d}}{\mathrm {d}\sigma } \tilde{\varphi }^x_{l,\sigma }}_{|\sigma =0}\partial _l \nabla ^2 V(\bar{x}). \end{aligned}\right. \end{aligned}$$
    (80)

    Many schemes can be employed for this numerical integration; in the example of Sect. 6, we use a first-order implicit Euler scheme, which is observed to have satisfying stability properties.

  4. 6.

    Deduce from (51) that

    $$\begin{aligned} \int \limits _{s=-\infty }^0 \text {div}\ell (\varphi ^x_s)\mathrm {d}s \simeq \sum _{n=0}^{N-1} (t_{n+1}-t_n)\left( \text {div}b(\varphi ^x_{t_n}) + \text {tr}\tilde{H}^{[n]}\right) , \end{aligned}$$
    (81)

    where we recall that the times \(t_0, \ldots , t_N\) are chosen so that the length of the instanton on each time interval \((t_n,t_{n+1})\) be equal to \(\theta \).

6 Numerical Illustration

In this section, we apply the method devised in Sect. 5 to a two-dimensional process which exhibits bistability, in the sense that the associated vector field \(b : \mathbb {R}^2 \rightarrow \mathbb {R}^2\) possesses two stable equilibrium points. We are therefore in the context of Sect. 4.2 and our purpose is to numerically approximate the various quantities appearing in the right-hand side of (49).

We shall fix one equilibrium point \(\bar{x}\) and first compute the instanton \((\rho _t)_{t \in \mathbb {R}}\). By (48), the integral term involved in the computation of the prefactor \(C^\epsilon (x)\) to the stationary distribution at the point x writes

$$\begin{aligned} \int \limits _{s=-\infty }^0 \text {div}\ell (\varphi ^x_s)\mathrm {d}s = \int \limits _{s=-\infty }^t \text {div}\ell (\rho _s)\mathrm {d}s. \end{aligned}$$
(82)

For notational convenience, we denote this quantity by J(t). Hence, computing J(t) for any \(t \in \mathbb {R}\) amounts to computing a whole family of prefactors \(C^\epsilon \), at points \(x=\rho _t\). In the \(t \rightarrow +\infty \) limit, we shall finally obtain the value of the prefactor \(L^\epsilon _D\) to the mean exit time from the basin of attraction of \(\bar{x}_1\), as is described in Sect. 4.2.

In the present section, we follow the steps of the procedure detailed in Sect. 5.3. Step 1, which corresponds to the computation of the fluctuation path, is addressed in Sect. 6.1, where we first present the example. The computation of \(\bar{H}\) (Step 2) is performed in Sect. 6.2. Anticipating on Step 4, we compute the third derivatives of V at \(\bar{x}\) in Sect. 6.3. Steps 3, 4 and 5 are then addressed in Sect. 6.4, which yields \(\tilde{H}^{[n]}\). Since we are considering fluctuation paths which finally reach the saddle-point (that is to say, the instanton), the reparametrization by the arclength of the instanton display a singularity when approaching this point, so that the computation of \(\tilde{H}^{[n]}\) becomes unstable. This point is treated in Sect. 6.5. Last, the overall value of J(t) is computed in Sect. 6.6, which corresponds to Step 6 of the procedure.

6.1 Presentation of the Example

For \(\alpha > 0\), we consider the potential function on \(\mathbb {R}^2\) defined by

$$\begin{aligned} V(x_1,x_2) = v_1(x_1) + v_2(x_2), \quad v_1(x_1) = \frac{x_1^4}{4} - \frac{x_1^2}{2}, \quad v_2(x_2) = \alpha \frac{x_2^2}{2}, \end{aligned}$$
(83)

the critical points of which are \((-1,0)\), (0, 0) and (1, 0). It is easily checked that the first and third points are stable equilibria of the dynamical system \(\dot{x}=-\nabla V(x)\), while the second point is stable in the direction of \(x_2\) but unstable in the direction of \(x_1\).

For a smooth scalar field \(c : \mathbb {R}^2 \rightarrow \mathbb {R}\) to be chosen below, let us define the vector field b by

$$\begin{aligned} b = -\nabla V + \ell , \qquad \ell (x_1,x_2) = c(x_1,x_2)\left( \begin{matrix} -v'_2(x_2)\\ v'_1(x_1) \end{matrix}\right) . \end{aligned}$$
(84)

For any choice of c, the Hamilton–Jacobi equation (7) is satisfied, the vector field b vanishes at the same points as \(-\nabla V\), and the points \((-1,0)\) and (1, 0) are stable equilibria of the dynamical system \(\dot{x}=b(x)\). The saddle-point (0, 0) is stable in one direction and unstable in one direction, but these directions may differ from the canonical vectors of \(\mathbb {R}^2\).

Let us denote \(\bar{x} = (-1,0)\) and \(x^* = (0,0)\). The instanton \((\rho _t)_{t \in \mathbb {R}}\) is the heteroclinic orbit of the dynamical system

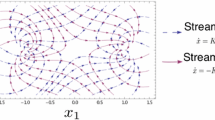
$$\begin{aligned} \dot{x} = \nabla V(x) + \ell (x) \end{aligned}$$
(85)

joining \(\bar{x}\) in \(t=-\infty \) to \(x^*\) in \(t=+\infty \). The instanton, the level lines of V and the field lines of b are plotted on Fig. 1 for the choice

$$\begin{aligned} c(x_1,x_2) = \beta x_1, \quad \beta > 0. \end{aligned}$$
(86)

The numerical illustrations of this section are plotted for \(\alpha =0.5\) and \(\beta =3\).

Fig. 1
figure 1

The level lines of V (pale blue), some field lines associated with b (red) and the instanton (thick blue) joining \(\bar{x}=(-1,0)\) to \(x^*=(0,0)\)

Full size image

6.2 Stationary Matrix Riccati Equation

With our definition of the vector field b and the choice (86) for the scalar field c, the matrix \(\bar{Q} = -\nabla b(\bar{x})\) appearing in (61) writes

$$\begin{aligned} \bar{Q} = \left( \begin{matrix} v''_1(\bar{x}_1) &{}\quad c(\bar{x})v''_2(\bar{x}_2)\\ -c(\bar{x})v''_1(\bar{x}_1) &{}\quad v''_2(\bar{x}_2) \end{matrix}\right) = \left( \begin{matrix} 2 &{} -\beta \alpha \\ 2\beta &{} \alpha \end{matrix}\right) , \end{aligned}$$
(87)

where we have used the fact that \(\nabla V(\bar{x})=0\) for the first identity. The numerical resolution of (61) yields the expected result

$$\begin{aligned} \bar{H} = \left( \begin{matrix} 2 &{}\quad 0\\ 0 &{}\quad \alpha \end{matrix}\right) . \end{aligned}$$
(88)

6.3 Third Derivatives of V at \(\bar{x}\)

In order to determine the initial condition for the computation of \(\tilde{H}^{[n]}\), we write the coefficients appearing in (75):

  • the computation of \(\bar{H}\) performed above yields

    $$\begin{aligned} h_{11}=2, \quad h_{12}=0, \quad h_{22}=\alpha ; \end{aligned}$$
    (89)

  • the computation of \(\nabla b(\bar{x})\) yields

    $$\begin{aligned} \beta _{1,1}=-2, \quad \beta _{1,2}=\beta \alpha , \quad \beta _{2,1}=-\beta , \quad \beta _{2,2}=-\alpha ; \end{aligned}$$
    (90)

  • the computation of the second derivatives of b yields

    $$\begin{aligned} \left\{ \begin{aligned}&\gamma _{1,11} = 6, \quad \gamma _{1,12} = -\beta \alpha , \quad \gamma _{1,22} = 0,\\&\gamma _{2,11} = 10 \beta , \quad \gamma _{2,12} = 0, \quad \gamma _{2,22} = 0. \end{aligned}\right. \end{aligned}$$
    (91)

The system of linear equations (75) contains 4 equations, corresponding to the choices \(\{i,j,l\} = \{1,1,1\}, \{1,1,2\}, \{1,2,2\}, \{2,2,2\}\), which write

$$\begin{aligned} \left\{ \begin{aligned} 0&= 36 + 6v_{111} -3\beta v_{112},\\ 0&= 6\beta \alpha +\beta \alpha v_{111} + (4+\alpha )v_{112} - 2\beta v_{122},\\ 0&= 2\beta \alpha v_{112} + 2(1+\alpha )v_{122} - \beta v_{222},\\ 0&= 3\beta \alpha v_{122} + 3\alpha v_{222}. \end{aligned}\right. \end{aligned}$$
(92)

The unique solution of this system is

$$\begin{aligned} v_{111} = -6, \quad v_{112} = v_{122} = v_{222} = 0, \end{aligned}$$
(93)

therefore we recover

$$\begin{aligned} \partial _1 \nabla ^2 V(\bar{x}) = \left( \begin{matrix} -6 &{}\quad 0\\ 0 &{}\quad 0 \end{matrix}\right) , \qquad \partial _2 \nabla ^2 V(\bar{x}) = \left( \begin{matrix} 0 &{}\quad 0\\ 0 &{}\quad 0 \end{matrix}\right) , \end{aligned}$$
(94)

as expected from the analytical expression of V.

6.4 Computation of \(\tilde{H}^{[n]}\)

The instanton on Fig. 1 is computed for times t ranging from \(t_\mathrm {min}\) such that \(\Vert \rho _{t_\mathrm {min}}-\bar{x}\Vert \ll 1\) to \(t_\mathrm {max}\) such that \(\Vert \rho _{t_\mathrm {max}}-x^*\Vert \ll 1\). The length of the instanton is thus

$$\begin{aligned} L = \int \limits _{t=-\infty }^{+\infty } \Vert b(\rho _t)\Vert \mathrm {d}t \simeq \int \limits _{t=t_\mathrm {min}}^{t_\mathrm {max}} \Vert b(\rho _t)\Vert \mathrm {d}t. \end{aligned}$$
(95)

For the example which we are studying, \(L \simeq 2.15\).

The parametrization of the instanton by its length is defined by

$$\begin{aligned} \sigma _t = \int \limits _{s=-\infty }^t \Vert b(\rho _s)\Vert \mathrm {d}s \simeq \int \limits _{s=t_\mathrm {min}}^t \Vert b(\rho _s)\Vert \mathrm {d}s, \end{aligned}$$
(96)

and we denote

$$\begin{aligned} \tilde{\rho }_{\sigma _t} = \rho _t, \qquad \tilde{Q}_\sigma = -\nabla b(\tilde{\rho }_\sigma ), \qquad \tilde{R}_\sigma = -\sum _{k=1}^d \partial _k V(\tilde{\rho }_\sigma ) \nabla ^2 b(\tilde{\rho }_\sigma ). \end{aligned}$$
(97)

In order to integrate the differential equation

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}\sigma } \tilde{H}_\sigma = \frac{-2(\tilde{H}_\sigma )^2 + (\tilde{Q}_\sigma )^\top \tilde{H}_\sigma + \tilde{H}_\sigma \tilde{Q}_\sigma + \tilde{R}_\sigma }{\Vert b(\tilde{\rho }_\sigma )\Vert }, \end{aligned}$$
(98)

we use standard, first-order Euler schemes. The explicit scheme

$$\begin{aligned} \frac{\tilde{H}^{[n+1]}-\tilde{H}^{[n]}}{\theta } = \frac{-2(\tilde{H}^{[n]})^2 + (\tilde{Q}_{n\theta })^\top \tilde{H}^{[n]} + \tilde{H}^{[n]} \tilde{Q}_{n\theta } + \tilde{R}_{n\theta }}{\Vert b(\tilde{\rho }_{n\theta })\Vert } \end{aligned}$$
(99)

is observed to be unstable. A semi-implicit scheme is presented in [15]; in the present case, it is also observed to be unstable. Following ideas introduced in [13, 14], we finally consider the implicit scheme

$$\begin{aligned} \frac{\tilde{H}^{[n+1]}-\tilde{H}^{[n]}}{\theta } = \frac{-2(\tilde{H}^{[n+1]})^2 + (\tilde{Q}_{n\theta })^\top \tilde{H}^{[n+1]} + \tilde{H}^{[n+1]} \tilde{Q}_{n\theta } + \tilde{R}_{n\theta }}{\Vert b(\tilde{\rho }_{n\theta })\Vert } \end{aligned}$$
(100)

which requires to solve the CARE

$$\begin{aligned} 2\tilde{\theta }_n(\tilde{H}^{[n+1]})^2 + \left( \frac{I_2}{2}-\tilde{\theta }_n\tilde{Q}_{n\theta }\right) ^\top \tilde{H}^{[n+1]} + \tilde{H}^{[n+1]}\left( \frac{I_2}{2}-\tilde{\theta }_n\tilde{Q}_{n\theta }\right) = \tilde{H}^{[n]} + \tilde{\theta }_n\tilde{R}_{n\theta }, \end{aligned}$$
(101)

with \(\tilde{\theta }_n = \theta /\Vert b(\tilde{\rho }_{n\theta })\Vert \), at each step. This scheme is observed to be stable and convergent.

We point out the fact that, to our knowledge, the theoretical results regarding the numerical analysis of the matrix Riccati equation (98), such as [13,14,15], assume that the matrix \(\tilde{R}_\sigma \) remains nonnegative, which then ensures the nonnegativity of the solution \(\tilde{H}_\sigma \). In our situation, the matrix \(\tilde{H}_\sigma \) is clearly not nonnegative in general, except at the initial point \(\sigma =0\). Therefore, the result of our numerical simulations are purely empirical, and are not backed up by some rigorous stability or convergence result.

Figure 2 represents the value of the coefficient \(\tilde{H}^{[n]}_{11}\) for \(n=0, \ldots , N\), for several choices of the mesh size \(\theta \). The actual values of the first coefficient of \(\nabla ^2 V(\rho _{t_n})\), computed from the analytical expression of V, are provided as a benchmark. We observe that the convergence is slow in the neighborhood of the saddle-point \(x^*\), which is discussed in the next subsection.

Fig. 2
figure 2

Comparison between the computed value of \(\tilde{H}^{[n]}_{11}\) (blue curves) and the actual value of \(\partial _{11}V(\rho _{t_n})\) (red), parametrized by the arclength of the instanton \(\sigma \in [0,L]\). The smaller the mesh size \(\theta \), the better the convergence at the saddle-point. The different choices of \(\theta \) correspond to the values 2000, 4000, 8000, 16,000 and 40,000 for the number of steps \(N=L/\theta \)

Full size image

When the dimension d is large, solving the CARE (101) at each step of the algorithm may turn out to be costly and lessen the interest of the implicit scheme. In such cases, alternative approaches such as the ‘fundamental solution method’ from [13] can be employed. The latter method also allows to implement higher-order schemes.

6.5 Singularity at the Saddle-Point

When \(\sigma \) approaches L, the instanton becomes close to the saddle-point \(x^*\) and the value of \(\Vert b(\tilde{\rho }_\sigma )\Vert \) goes to 0. Therefore the integration of (98) becomes sensitive to the fact that the denominator in the right-hand side takes small values, which causes the singularity observed on Fig. 2. In order to overcome this issue, we note that, similarly to the initial value \(\bar{H} = \tilde{H}_0\), the terminal value

$$\begin{aligned} \tilde{H}_L = \lim _{t \rightarrow +\infty } H_t = \nabla V(x^*) = H^* \end{aligned}$$
(102)

can be computed by solving the stationary matrix Riccati equation

$$\begin{aligned} 2H^* = (Q^*)^\top H^* + H^* Q^*, \quad Q^* = -\nabla b(x^*). \end{aligned}$$
(103)

This remark allows us to implement the following interpolation procedure.

  1. 1.

    Fix a threshold \(\delta \) such that \(\theta \ll \delta \ll L\).

  2. 2.

    Among the indices n such that \(n\theta \ge L-\delta \), select the index \(n^*\) for which the linear continuation

    $$\begin{aligned} \tilde{H}^{[n]} + \frac{\tilde{H}^{[n+1]}-\tilde{H}^{[n]}}{\theta }(L-n\theta ) \end{aligned}$$
    (104)

    is the closest to the terminal value \(H^*\), for a given matrix norm.

  3. 3.

    For n between \(n^*\) and the total number of steps N, replace the estimation \(\tilde{H}^{[n]}\) of \(\tilde{H}_{n \theta }\) with the linear interpolation

    $$\begin{aligned} \tilde{H}'^{[n]} = \frac{N-n}{N-n^*} \tilde{H}^{[n^*]} + \frac{n-n^*}{N-n^*} H^*. \end{aligned}$$
    (105)

This procedure allows to alleviate the singularity at the saddle-point, as is shown on Fig. 3. We observe that the computed value of the first coefficient of \(\tilde{H}_\sigma \) is correct up to an error of the order of magnitude \(5\%\) (respectively \(1\%\)) for the coarsest mesh size \(\theta = L/2000\) (respectively the finest mesh size \(\theta = L/40,000\)), localized in the area close to the critical point, for distances of order \(10\%\) of L or less.

Fig. 3
figure 3

A zoom on the numerical computation of the first coefficient of \(\tilde{H}_\sigma \) when \(\sigma \uparrow L\). The red curve is the actual value. The blue curves are the values of \(\tilde{H}^{[n]}_{11}\) already shown on Fig. 2. The green curves are the values of \(\tilde{H}'^{[n]}_{11}\) obtained by the interpolation procedure. Here, \(\delta =0.2\) (Color figure online)

Full size image

6.6 Evaluation of J(t)

From the quantity J(t), defined by (82), let us define \(\tilde{J}(\sigma )\) for \(\sigma \in [0,L]\) by

$$\begin{aligned} \tilde{J}(\sigma _t) = J(t). \end{aligned}$$
(106)

The quantity \(\tilde{J}(\sigma )\) is the value of the prefactor at the point with arclength \(\sigma \) on the instanton. These values, computed from the numerical resolution of the matrix Riccati equation for \((H_t)_{t \in \mathbb {R}}\), are plotted on Fig. 4 (the interpolation procedure at the saddle-point discussed in the previous subsection is employed), for several choices of the mesh size \(\theta \). The actual values of \(\tilde{J}(\sigma )\), computed from the analytical expression of V, are provided as a benchmark. We observe a good agreement, up to an error of the order of magnitude \(1\%\) localized in the area close to the critical point, for distances of order \(10\%\) of L or less, which supports the efficiency of our method. The evolution of the discretization error on \(\tilde{J}(L)\) as a function of \(\theta \) is plotted on Fig. 5, it is observed to be proportional to \(\sqrt{\theta }\).

Fig. 4
figure 4

Comparison between the computed value of \(\tilde{J}(\sigma )\) (blue curves) and its actual value (red curve), for \(\sigma \in [0,L]\). The closer the curve, the smaller \(\theta \). The different choices of \(\theta \) correspond to the values 2000, 4000, 8000, 16,000 and 40,000 for the number of steps \(N=L/\theta \) (Color figure online)

Full size image
Fig. 5
figure 5

Log–log plot of the discretization error on \(\tilde{J}(L)\) as a function of \(\theta \), with linear fit of slope 0.50

Full size image

7 Summary and Relation to Recent Works

In this conclusive section, we summarize the main contributions of the article, on both theoretical and numerical aspects. We also compare these results with other recent works, in particular [21] which was released during the last stages of our work and contains several related ideas and results.

7.1 Theoretical Contributions

At the conceptual level, the main original contribution of the article is the derivation in Sect. 3 of a sharp equivalent, when \(\epsilon \downarrow 0\), to the prefactor \(C^\epsilon \) of the stationary distribution \(P^\epsilon \). It is done in two steps.

  1. (i)

    We perform an asymptotic expansion in the path integral formulation of \(P^\epsilon \) (see Eq. (26)) in order to relate the prefactor \(C^\epsilon \) with the process of scaled fluctuations \(Y^x\) defined by (31), through the identity (30).

  2. (ii)

    We express \(C^\epsilon \) in terms of two quantities \(\eta ^x_t\) and \(K^x_t\), which are related by the matrix Riccati equation (35). We then solve explicitly this equation in the Appendix by a quadrature method, which finally allows to recover a sharp equivalent for \(C^\epsilon \).

As is recalled in Sect. 2, the expression of the sharp equivalent for \(C^\epsilon \) is not new and was already derived by a WKB approximation in [4]. Therefore the real novelty here is the sketch of the argument, and in particular the resolution of the matrix Riccati equation.

The fact that large deviation prefactors induced by Gaussian fluctuations around action minimizing paths can be described in terms of solutions to matrix Riccati equations has already been observed in various contexts [16, 31, 32]. It was put forth in the recent work [21] by Grafke, Schäfer and Vanden-Eijnden, who conducted a thorough derivation of expressions of large deviation prefactors in terms of solutions to matrix Riccati equations, both for finite-time observables and quantities related to stationary distribution. Their work includes many illustrative examples and generalization towards nongaussian noises and infinite-dimensional systems.

Some fundamental ideas in [21] are similar to the present paper; for instance, the use of the Girsanov transform in Proposition 2.2 there makes the scaled fluctuation process \(Y^x\) appear in the prefactor \(C^\epsilon \) in an equivalent way to our use of the path integral formalism. However, both works differ on several methodological aspects. In particular, both the formulation of matrix Riccati equations and the expression of prefactor asymptotics in [21] involve the fact that the fluctuation path \(\varphi ^x\) is defined by the forward-backward Hamiltonian system

$$\begin{aligned} \dot{\varphi }^x_s = b(\varphi ^x_s) + 2 \theta ^x_s, \quad \dot{\theta }^x_s = -(\nabla b(\varphi ^x_s))^\top \theta ^x_s, \quad s \in [0,t], \end{aligned}$$
(107)

with suitable limit conditions on \(\varphi ^x_0\) and \(\theta ^x_t\) depending on the large deviation quantity on which prefactors are computed. In contrast, in the present article, the definition (11) of fluctuation paths relies on the transverse decomposition (8) of b. As is noted in [21, Sect. 3.2], this is due to the fact that we are merely interested in quantities related with infinite time horizon. Still, this allows us to then derive prefactor asymptotics from the explicit resolution of the matrix Riccati equation (35) by quadrature, which as is argued above is the main theoretical contribution of our article and is inherent to the use of the transverse decomposition.

7.2 Numerical Contributions

The second main contribution of the paper is the formalization in Sect. 5 of a complete numerical method to compute all quantities involved in the prefactor \(C^\epsilon \). In fact, based on the connections recalled in Sect. 4 between this prefactor and mean exit times, our numerical procedure enables one to evaluate prefactors to transition times between metastable sets, as is illustrated in Sect. 6.

Numerical schemes, based on the resolution of matrix Riccati equations, are also discussed in [21] (but the study of metastable settings is not covered there). A common feature of both works is the preliminary reparametrization of these equations by the arclength of the fluctuation path, which allows to address their long-time behavior. The singularity at \(\sigma =0\) induced by this reparametrization, which is addressed in Sect. 5.2, is also discussed in Remark 3.4 and Appendix A of [21], and solved with similar arguments.

On the other hand, Paskal and Cameron [33] recently devised a mesh-based method dubbed ‘Efficient Jet Marcher’ which allows to compute the values of V and \(\nabla V\) on a grid (see Remark 7). In Sect. 6.2 of their article, they applied this method to evaluate the prefactor \(L^\epsilon _D\) from (49) of the mean transition time in a two-dimensional metastable setting. This method, which radically differs from the path-inspired approaches from the present article and [21], is however currently limited to low-dimensional situations.