1 Introduction

Open quantum walks were defined in [5]. They are extensions of (discrete-time) Markov chains, where the process retains some amount of memory, and this memory is encoded by a quantum state. Open quantum walks are a simple model, which has stirred interest because of its various possible applications (see [36] and references therein for models based on open quantum walks, and [38] on the general topic of control of quantum trajectories) and interesting features and extensions (see [6, 7, 33]). They have therefore given rise to various theoretical studies, investigating e.g. ergodic properties, central limit theorems and large deviations properties (see [4, 9,10,11, 29]). The approach of [10] was to give analogues for open quantum walks of notions usually associated with Markov chains, such as irreducibility and period, and to investigate their consequences. In this article, we continue this program of studying open quantum walks in analogy with Markov chains, and investigate other notions: the probability of visiting a given site in finite time, the expected number of visits, the expected return time, and their relation with the Dirichlet problem. Some of these notions were discussed in e.g. [11, 17], but our study is the first systematic exploration of these concepts and their behavior for irreducible open quantum walks.

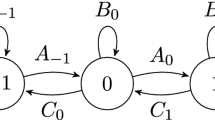
The first standard question one may ask about Markov chains treats recurrence problems. Let \((x_n)_n\) be a Markov chain on a discrete set V. For any i in V we define

$$\begin{aligned} t_i = \inf \{n\ge 1\, |\, x_n=i\}, \qquad n_i = \mathrm {card}\{n\ge 1\, |\, x_n=i\}, \end{aligned}$$

The classical results (see e.g. [18, 32]) concerning return times \((t_i)_{i\in V}\) and number of visits \((n_i)_{i\in V}\) imply that for any i in V

$$\begin{aligned} {\mathbb {P}}_i(t_i<\infty )=1 \Leftrightarrow {\mathbb {E}}_i( n_i)=\infty . \end{aligned}$$
(1)

Therefore, this equivalence allows to define the notion of recurrence using either quantity \({\mathbb {P}}_i(t_i<\infty )\) or \({\mathbb {E}}_i( n_i)\). In addition, if the Markov chain is irreducible,

$$\begin{aligned} {\mathbb {P}}_i(t_i<\infty )<1 \quad \text{ for } \text{ all } \quad i\in V, \text{ or } {\mathbb {P}}_i(t_i<\infty )=1 \quad \text{ for } \text{ all } \quad i\in V, \end{aligned}$$
(2)
$$\begin{aligned} {\mathbb {E}}_i(n_i)<\infty \quad \text{ for } \text{ all } \quad i\in V, \text{ or } {\mathbb {E}}_i(n_i)=\infty \quad \text{ for } \text{ all } \quad i\in V. \end{aligned}$$
(3)

Similarly, for an irreducible Markov chain,

$$\begin{aligned} {\mathbb {E}}_i(t_i)<\infty \quad \text{ for } \text{ all } \quad i\in V, \text{ or } {\mathbb {E}}_i(t_i)=\infty \quad \text{ for } \text{ any } \quad i\in V. \end{aligned}$$
(4)

In addition, if the Markov chain admits an invariant probability measure \((\pi _i)_{i\in V}\), then

$$\begin{aligned} {\mathbb {E}}_i(t_i)=\pi _i^{-1}<\infty \quad \text{ for } \text{ any } \quad i\in V. \end{aligned}$$
(5)

The second standard question concerns exit times and exit probabilities. If D is a finite subset of V, we define \(t_{{\partial \! D}}\) as its exit time

$$\begin{aligned} t_{\partial \! D}=\inf \{n\ge 1\,|\, x_n\in {\partial \! D}\} \end{aligned}$$

where \({\partial \! D}\) is the boundary of D (we give a precise definition later on), and for \(i\in D\), \(j\in {\partial \! D}\) define the harmonic measure at i relative to j by

$$\begin{aligned} \begin{aligned} \mu _{i}^D(j)={\mathbb {P}}_{i}(x_{t_{{\partial \! D}}}=j)\ \end{aligned} \end{aligned}$$
(6)

which represents the probability of exiting D through j when starting from i. It is known that the map \(i\mapsto \mu _{i}^{D}(j)\) is harmonic on D for any \(j\in {\partial \! D}\), and is an important tool in solving Dirichlet problems. In addition, the solution of a Dirichlet problem can be characterized as the minimizer of some functional, related to a Dirichlet form.

In this article we investigate similar relations to (1)–(5), and study an analogue of Dirichlet problems for open quantum walks. We also look at the notion of harmonic measures for open quantum walks. These measures, as well as the Dirichlet problems for open quantum walks, provide simple examples of non-commutative extensions of standard geometrical structures.

This article is organized as follows: in Sect. 2 we recall the definitions of open quantum walks and various notions, including irreducibility and harmonicity. In Sect. 3 we study the relation between return times and number of visits and in particular analogues for OQW of (1), (2) and (3), and discuss the literature on the subject of recurrence for open quantum walks. In Sect. 4 we study the expected values of return times, prove an analogue of (4), and relate these expected values to invariant measures, similar to (5). In Sect. 5 we describe various examples that serve in particular as counterexamples to various possible conjectures. In Sect. 6 we define Dirichlet problems for open quantum walks and characterize their solutions. In Sect. 7 we discuss extensions of various results to reducible open quantum walks. In Sect. 8 we introduce Dirichlet forms for open quantum walks and use them to characterize solutions of Dirichlet problems. In every section, a non-optimal but nevertheless satisfactory result is given early in the introductory part, and the intermediate results necessary for the proof (most of which have weaker assumptions than necessary for the results stated earlier) are detailed in the rest of the section. The proofs are given in the Appendix, unless they contain elements necessary to the comprehension of the text.

2 Open Quantum Walks: Definitions and Notation

We start this section with a short presentation of open quantum walks and the associated notion of irreducibility. We follow the notation of [10] and refer the reader to that article for more details.

We consider a Hilbert space \({\mathcal H}\) of the form \({\mathcal H}= \bigoplus _{i\in V}\mathfrak h_i\) where V is a countable set of vertices, and each \(\mathfrak h_i\) is a separable Hilbert space. We view \({\mathcal H}\) as describing the degrees of freedom of a particle constrained to move on V: the “V-component” describes the spatial degrees of freedom (the position of the particle) while \(\mathfrak h_i\) describes the internal degrees of freedom of the particle, when it is located at site \(i\in V\).

For book-keeping purposes we denote the subspace \(\mathfrak h_i\) of \({\mathcal H}\) by \(\mathfrak h_i \otimes |i\rangle \). Therefore, whenever a vector \(\varphi \in {\mathcal H}\) belongs to the subspace \(\mathfrak h_i\), we will denote it by \(\varphi \otimes |i\rangle \) and drop the (implicit) assumption that \(\varphi \in \mathfrak h_i\). Similarly, when an operator A on \({\mathcal H}\) satisfies \(\mathfrak h_j^\perp \subset \mathrm {Ker}\, A\) and \(\mathrm {Ran}\, A\subset \mathfrak h_i\), we denote it by \(A=L_{i,j}\otimes |i\rangle \langle j|\) where \(L_{i,j}\) is viewed as an operator from \(\mathfrak h_j\) to \(\mathfrak h_i\). This will allow us to use the same notation as in e.g. [4, 5, 26, 28, 33]. Consistently with this notation, for W a subset of V we denote

$$\begin{aligned} \mathcal H_W=\bigoplus _{i\in W} {\mathfrak h}_i\otimes |i\rangle . \end{aligned}$$

and \(\mathrm {Id}_W=\sum _{i\in W} \mathrm {Id}_{{\mathfrak h}_i}\otimes |i\rangle \langle i|\). We identify \(\mathcal H_W\) (respectively \(\mathcal B(\mathcal H_W)\)) with a subspace of \(\mathcal H\) (respectively \(\mathcal B(\mathcal H)\)).

An open quantum walk (or OQW) is a map on the Banach space \(\mathcal I _1({\mathcal H})\) of trace-class operators on \({\mathcal H}\), given by

$$\begin{aligned} \mathfrak M \, : \, \tau \mapsto \sum _{i,j\in V}A_{i,j}\, \tau \,A_{i,j}^* \end{aligned}$$
(7)

where, for any i, j in V, the operator \(A_{i,j}\) is of the form \(L_{i,j}\otimes |i\rangle \langle j|\) and the operators \(L_{i,j}\) satisfy

$$\begin{aligned} \forall j\in V,\quad \sum _{i\in V}L_{i,j}^* L_{i,j}=\mathrm {Id}_{{\mathfrak h}_j}, \end{aligned}$$
(8)

(this series is meant in the strong convergence sense). The operators \(L_{i,j}\) represent the effect of a transition from site j to site i, encoding both the probability of that transition and its effect on the internal degrees of freedom. Equation (8) therefore encodes the “stochasticity” of the transitions \(L_{i,j}\), and immediately implies that \(\mathrm {Tr}\,\mathfrak M(\tau ) = \mathrm {Tr}\, \tau \) for any \(\tau \) in \(\mathcal I _1({\mathcal H})\).

Recall that an operator X on \({\mathcal H}\) is called positive (respectively definite positive) if \(\langle \varphi , X\varphi \rangle \ge 0\) (respectively \(\langle \varphi , X\varphi \rangle > 0\)) for any \(\varphi \in {\mathcal H}\setminus \{0\}\). We define a state on \({\mathcal H}\) to be a positive operator in \(\mathcal I_1({\mathcal H})\) with trace one, and call a state faithful if it is definite positive. We denote the set of states on \({\mathcal H}\) (respectively \({\mathfrak h}_i\)) by \(\mathcal S({\mathcal H})\) (respectively \(\mathcal S({\mathfrak h}_i)\)). The map defined by (7) maps a state to a state. It actually has the stronger property of being trace-preserving and completely positive, i.e. for any \(n\in \mathbb {N}\), \(\mathfrak M\otimes \mathrm {Id}_{\mathcal B(\mathbb {C}^n)}\) acting on \(\mathcal I_1(\mathcal H)\otimes \mathcal B(\mathbb {C}^n)\) is positive; such an operator is commonly called a quantum channel, see e.g. [37]. In addition, the topological dual \(\mathcal I_1({\mathcal H})^*\) can be identified with \({\mathcal B}({\mathcal H})\) through the linear form

$$\begin{aligned} (\tau ,X)\mapsto \mathrm {Tr}(\tau X), \end{aligned}$$

so that the dual \(\mathfrak M^*\) of \(\mathfrak M\) acts on \(\mathcal B(\mathcal H)\). By the Russo–Dye Theorem (see [34]), we have the relationFootnote 1 \(\Vert \mathfrak M^*\Vert =\Vert \mathfrak M^*(\mathrm {Id}_{\mathcal H})\Vert \), so that relation (8) implies that \(\Vert \mathfrak M\Vert =1\) as an operator on \(\mathcal I_1({\mathcal H})\).

A crucial remark is that the range of \(\mathfrak M\) is a subset of the class of “diagonal” states, i.e. states of the form

$$\begin{aligned} \sum _{i\in V}\tau (i)\otimes |i\rangle \langle i|, \end{aligned}$$
(9)

where each \(\tau (i)\) is in \(\mathcal I_1({\mathfrak h}_i)\). In addition, even if \(\tau \) is not diagonal, i.e. is of the form \(\tau = \sum _{i,j\in V} \tau (i,j)\otimes |i\rangle \langle j|\), then \(\mathfrak M(\tau )\) depends only on its diagonal elements \(\tau (i,i)\). Therefore, from now on, we will only consider states of the form (9). The action of \(\mathfrak M\) on such states takes the form

$$\begin{aligned} \mathfrak M(\tau )=\sum _{i\in V}\big (\sum _{j\in V} L_{i,j}\, \tau (j)\, L_{i,j}^*\big ) \otimes |i\rangle \langle i|. \end{aligned}$$
(10)

As argued in [10] (see in particular section 8), a natural extension of the above framework is to encode the transition from site j to site i not by \(\tau (j)\mapsto L_{i,j}\, \tau (j) \, L_{i,j}^*\), but by a more general completely positive map \(\tau (j)\mapsto \Phi _{i,j}\big (\tau (j)\big )\). We will not discuss this extension any further. Note, however, that all our results hold for these generalized open quantum walks (except for the explicit formulas involving operators \(L_{i,j}\), which need to be amended). The adaptation of the proofs is straightforward.

We now describe a family of classical random processes associated with \(\mathfrak M\). Let \(\Omega =V^{\mathbb {N}}\) and for any state \(\rho \) on \({\mathcal H}\) of the form (9), define on \(\Omega \) a probability by defining its restrictions to \(V^{n+1}\) for \(n\ge 0\):

$$\begin{aligned} {\mathbb {P}}_\tau (i_0,\ldots ,i_n)=\mathrm {Tr}\big (L_{i_n,i_{n-1}}\ldots L_{i_1,i_0} \,\tau (i_0)\, L_{i_1,i_0}^* \ldots L_{i_n,i_{n-1}}^* \big ). \end{aligned}$$
(11)

Relation 8 ensures the consistency of these restrictions, and the Daniell–Kolmogorov extension Theorem implies that \({\mathbb {P}}_\tau \) defines a unique probability on \(\Omega \). We will mostly consider initial states \(\tau \) of the form \(\rho \otimes |i\rangle \langle i|\) with \(\rho \in \mathcal S({\mathfrak h}_i)\), i.e. with initial position i and initial internal state \(\rho \); for notational simplicity, the corresponding probability \({\mathbb {P}}_\tau \) will then be denoted by \({\mathbb {P}}_{i,\rho }\).

We will consider two random processes \((x_n)_n\) and \((\rho _n)_n\) defined for \(\omega =(i_0,i_1,\ldots ) \in \Omega \) by

$$\begin{aligned} x_n(\omega )= & {} i_n,\nonumber \\ \rho _n(\omega )= & {} \frac{L_{i_n,i_{n-1}}\ldots L_{i_1,i_0} \,\tau (i_0)\, L_{i_1,i_0}^* \ldots L_{i_n,i_{n-1}}^* }{\mathrm {Tr}\big (L_{i_n,i_{n-1}}\ldots L_{i_1,i_0} \,\tau (i_0)\, L_{i_1,i_0}^* \ldots L_{i_n,i_{n-1}}^* \big )}\,. \end{aligned}$$
(12)

Note that the variable \(\rho _n\) is a state on \(\mathfrak h_{x_n}\). Besides, the process \((x_n,\rho _n)_n\) is Markov, corresponding to the transitions defined loosely as follows: conditionally on \((x_n=j,\rho _n=\rho )\), one has

$$\begin{aligned} (x_{n+1},\rho _{n+1})= \big (i, \frac{L_{i,j} \rho L_{i,j}^*}{\mathrm {Tr}(L_{i,j} \rho \,L_{i,j}^*)}\big ) \quad \text{ with } \text{ probability } \,\mathrm {Tr}(L_{i,j} \rho \,L_{i,j}^*). \end{aligned}$$
(13)

Remark that \((x_n)_n\) or \((\rho _n)_n\) considered separately are not Markov processes.

Note that open quantum walks include classical Markov chains. More precisely, consider a Markov chain \((M_n)_n\) on the vertex set V, with probability \(t_{i,j}\) of transition from j to i and initial distribution \((p_i)_{i\in V}\). Define an open quantum walk \(\mathfrak M\) with \(\mathfrak h_i \equiv \mathbb {C}\) and \(L_{i,j}=\sqrt{t_{i,j}}\). If the initial state is \(\tau =\sum _{i\in V} p_i \otimes |i\rangle \langle i|\) then \(\mathfrak M(\tau )\) is of the form

$$\begin{aligned} \mathfrak M(\tau )=\sum _{i\in V} \big (\sum _{j\in V} t_{i,j}\,p_j\big )\otimes |i\rangle \langle i|. \end{aligned}$$

Therefore, \(x_0\) has the same law as \(M_0\) and \(x_1\) has the same law as \(M_1\), etc. This open quantum walk will be called the minimal dilation of the Markov chain (because it is an OQW implementation of the Markov chain with minimal spaces \({\mathfrak h}_i\), see [10] for more details).

We now introduce the notion of irreducibility for open quantum walks. For i, j in V we call a path from i to j any finite sequence \(i_0,\ldots ,i_\ell \) in V with \(\ell \ge 1\), such that \(i_0=i\) and \(i_\ell =j\). Such a path is said to be of length \(\ell \), and we denote the length of a path \(\pi \) by \(\ell (\pi )\). We denote by \({\mathcal P}_\ell (i,j)\) the set of paths from i to j of length \(\ell \), and let

$$\begin{aligned} {{\mathcal P}}(i,j)=\cup _{\ell \ge 1} {\mathcal P}_\ell (i,j). \end{aligned}$$

For a fixed OQW \(\mathfrak M\) and \(\pi =(i_0,\ldots ,i_\ell )\) in \({\mathcal P}(i,j)\) we denote by \(L_\pi \) the operator from \(\mathfrak h_i\) to \(\mathfrak h_j\) defined by:

$$\begin{aligned} L_\pi =L_{i_\ell ,i_{\ell -1}}\ldots L_{i_1,i_0}=L_{j,i_{\ell -1}}\ldots L_{i_1,i}. \end{aligned}$$

Definition 2.1

An open quantum random walk \(\mathfrak M\) as above is irreducible if for any i, j in V and for any \(\varphi \) in \(\mathfrak h_i\setminus \{0\}\), the set

$$\begin{aligned} \big \{L_\pi \varphi \, |\, \pi \in {\mathcal P}(i,j)\big \} \end{aligned}$$
(14)

is total in \(\mathfrak h_j\).

This definition (which is a special case of Davies irreducibility as defined in [14]) and its consequences were introduced in [10]. The main consequence is that for \(\mathfrak M\) an irreducible open quantum walk, the set of solutions of \(\mathfrak M(\tau )=\tau \) is a space of dimension at most one, and one solution is a faithful state.

Remark 2.2

There was a slight ambiguity in the definition of irreducibility as given in [9, 10], where the path “of length zero” \(\pi =\{i\}\) with associated transition \(L_{\{i\}}=\mathrm {Id}_{{\mathfrak h}_i}\) was allowed in (14). In other words, irreducibility was defined by the fact that for any i, j in V and \(\varphi \) in \(\mathfrak h_i\setminus \{0\}\), the set

$$\begin{aligned} \big \{\varphi \big \}\cup \big \{L_\pi \varphi \, |\, \pi \in {\mathcal P}(i,j)\big \} \end{aligned}$$
(15)

(with \(\pi \) of length at least one) is total. It is easy, however, to see that this second definition is equivalent to Definition 2.1. Therefore, even though we define irreducibility by Definition 2.1, we can still apply the results of [10].

The following class of open quantum walks will be relevant, and in particular will have properties closer to those of (classical) Markov chains.

Definition 2.3

We say that an open quantum walk \(\mathfrak M\) is semifinite if for any i in V, \(\dim \mathfrak h _i< \infty \). We say that it is finite if it is semifinite and V is a finite set.

Non-semifinite open quantum walks, i.e. those that can have an infinite number of degrees of freedom at a given site \(i\in V\), can exhibit local degeneracies that will make them less interesting to us.

One of the topics of interest in the present paper is that of quantum harmonic operators:

Definition 2.4

An operator \(A=\sum _{i\in V} A_i \otimes |i\rangle \langle i|\) with \(A_i \in {\mathcal B}(\mathfrak h_i)\) for each \(i\in ~V\) is called quantum harmonic if it satisfies \(\mathfrak M^*(A)=A\), or equivalently if

$$\begin{aligned} \text{ for } \text{ any } j\in V, \text{ one } \text{ has } A_j= \sum _{i\in V} L_{i,j}^* A_i L_{i,j}. \end{aligned}$$

Remark that any operator \(\lambda \mathrm {Id}_{\mathcal H}\), \(\lambda \) in \(\mathbb {C}\), is quantum harmonic. In the case of a minimal dilation of a classical Markov chain, this definition is equivalent to the classical definition of harmonicity. An immediate property of quantum harmonic operators is the following:

Lemma 2.5

Let \(\mathfrak M\) be an open quantum walk and A a quantum harmonic operator for \(\mathfrak M\). Then for any initial \((x_0,\rho _0)\), the Markov chain \((x_n,\rho _n)_n\), with transition probabilities given by Equation (13), is such that \(m_n=\big (\mathrm {Tr}(\rho _n A_{x_n})\big )_n\) is a \({\mathbb {P}}_{x_0,\rho _0}\)-martingale.

Before we move on to the next section, it will be convenient to introduce some additional notation for specific paths. For any i and j in V, and for W a subset of V, we define \({\mathcal P}^{W}(i,j)\) to be the set of paths in \({\mathcal P}(i,j)\) that remain in W except possibly for their start- and endpoint. More precisely:

$$\begin{aligned} (i_0,\ldots ,i_\ell )\in {\mathcal P}^{W} \Leftrightarrow (i_0,\ldots ,i_\ell )\in {\mathcal P} \text{ with } i_1,\ldots ,i_{\ell -1}\in W. \end{aligned}$$

We denote for any \(\ell \ge 1\) by e.g. \({\mathcal P}_\ell ^{W}\) the subset of \({\mathcal P}^{W}\) consisting of paths of length \(\ell \), etc.

3 Passage Times and Number of Visits

In this section we consider the passage times \(t_j\) to a given point \(j\in V\) and the number of visits \(n_j\) to that point. We define

$$\begin{aligned} t_j = \inf \{n\ge 1\, |\, x_n=j\}, \qquad n_j = \mathrm {card}\{n\ge 1\, |\, x_n=j\}. \end{aligned}$$

Recall the standard results (1), (2), (3) in the case where the OQW is a minimal dilation of a Markov chain. The equivalence (1) follows from the markovianity of the process \((x_n)_n\). However, in the general OQW case, the process \((x_n)_n\) alone is not markovian and at least some of the above relations will fail. Indeed, Example 5.1 below with \(i=0\) and \(\rho \ne |e_1\rangle \langle e_1|, |e_2\rangle \langle e_2|\) is such that \({\mathbb {P}}_{i,\rho }(t_i<\infty )<1\) and \({\mathbb {E}}_{i,\rho }(n_i)=\infty \), showing that the analogue of (1) does not hold. Example 5.2, which displays an irreducible OQW, is such that \({\mathbb {P}}_{i,\rho }(t_i<\infty )=1\) and \({\mathbb {E}}_{i,\rho }(t_i)<\infty \) for \(p<1/2\) and \(i=0\), \(\rho =|e_2\rangle \langle e_2|\). Consequently it shows that this analogue (1) may not even hold for irreducible OQWs.

We therefore have to work some more in order to obtain nontrivial connections between \({\mathbb {P}}_i(t_i<\infty )\) and \({\mathbb {E}}_i(n_i)\), and to obtain universality results in the irreducible case. This will be done in the next two subsections. As a corollary of our investigation, a clear conclusion can be drawn for semifinite irreducible open quantum walks, which we give in Theorem 3.1 below. Its proof, however, relies on all results given in those two subsections. We will finish this section with a discussion of the notion of recurrence for open quantum walks.

Theorem 3.1

Let \(\mathfrak M\) be a semifinite irreducible open quantum walk. We are in one (and only one) of the following situations:

  1. 1.

    for any i, j in V,  \(\rho \) in \(\mathcal S({\mathfrak h}_i)\), one has \({\mathbb {E}}_{i,\rho }(n_j)=\infty \) and \({\mathbb {P}}_{i,\rho }(t_j<\infty )=1\);

  2. 2.

    for any i, j in V,  \(\rho \) in \(\mathcal S({\mathfrak h}_i)\), one has \({\mathbb {E}}_{i,\rho }(n_j)<\infty \) and \({\mathbb {P}}_{i,\rho }(t_j<\infty )~<~1\);

  3. 3.

    for any i, j in V,  \(\rho \) in \(\mathcal S({\mathfrak h}_i)\), one has \({\mathbb {E}}_{i,\rho }(n_j)<\infty \), but there exist i in V, \(\rho , \rho '\) in \(\mathcal S({\mathfrak h}_i)\) (\(\rho \) necessarily non-faithful) with \({\mathbb {P}}_{i,\rho }(t_i<\infty )~=~1\) and \({\mathbb {P}}_{i,\rho '}(t_i<\infty )~<~1\).

Remark 3.2

  1. 1.

    Situation 1 is illustrated by any finite irreducible OQW, or by a \((\mathbb {Z},\mathbb {C}^2)\)-simple OQW (see Example 5.5) with \(L_+^*L_+=L_-^* L_-=\frac{1}{2}\,\mathrm {Id}_{\mathbb {C}^2}\).

  2. 2.

    Situation 2 is illustrated by e.g. the minimal dilation of a transient classical Markov chain, or a \((\mathbb {Z},\mathbb {C}^2)\)-simple OQW with, \(L_+^*L_+>\frac{1}{2}\mathrm {Id}_{\mathbb {C}^2}\).

  3. 3.

    Situation 3, which of course is the most surprising in comparison with the case of classical Markov chains, is illustrated by Example 5.2.

3.1 Passage Time vs. Number of Visits: General Results

In this section we investigate the quantities \({\mathbb {P}}_{i,\rho }(t_j<\infty )\) and \({\mathbb {E}}_{i,\rho }(n_j)\), and the relation between them. The proofs relating the two quantities \({\mathbb {P}}_{i,\rho }(t_j<\infty ) \) and \({\mathbb {E}}_{i,\rho }(n_j)\) in the classical case are based on the fact that any path \(\pi \in {\mathcal P}(j,j)\) can be written uniquely as a concatenation of paths \(\pi \in {\mathcal P}^{V\setminus \{j\}}(j,j)\). We will use this simple idea in the present case. This is summarized in Proposition 3.3:

Proposition 3.3

There exists a family \(({\mathfrak P}_{j,i})_{i,j\in V}\), where \({\mathfrak P}_{j,i}\) is a completely positive linear contraction from \(\mathcal I_1({\mathfrak h}_i)\) to \(\mathcal I_1({\mathfrak h}_j)\), such that for any i, j in V and any \(\rho \) in \(\mathcal S({\mathfrak h}_i)\),

$$\begin{aligned} {\mathbb {P}}_{i,\rho }(t_j<\infty )=\mathrm {Tr}\big ({\mathfrak P}_{j,i}(\rho )\big ),\qquad {\mathbb {E}}_{i,\rho }(n_j)= \sum _{k\ge 0} \mathrm {Tr}\big ({\mathfrak P}_{j,j}^k\circ {\mathfrak P}_{j,i} ( \rho )\big ), \end{aligned}$$

(where the second expression is possibly \(\infty \)).

Remark 3.4

 

  1. 1.

    The map \({\mathfrak P}_{j,i}\) can be expressed by:

    $$\begin{aligned} {\mathfrak P}_{j,i}(\rho )= \sum _{\pi \in {\mathcal P}^{V\setminus \{j\}}(i,j)} L_\pi \rho L_\pi ^* \end{aligned}$$

    (see the proof of Proposition 3.3 to see that this expression is meaningful).

  2. 2.

    An immediate consequence of Proposition 3.3 is that

    $$\begin{aligned} \Vert {\mathfrak P}_{j,i}\Vert =\sup _{\rho \in \mathcal S({\mathfrak h}_i)}{\mathbb {P}}_{i,\rho }(t_j<\infty ), \end{aligned}$$

    where the norm is the operator norm on \(\mathcal I_1({\mathcal H})\).

  3. 3.

    It is immediate from the proof that

    $$\begin{aligned} {\mathbb {E}}_{i,\rho }\left( \rho _{t_j}\,|\, t_j<\infty \right) = \frac{{\mathfrak P}_{j,i}(\rho )}{\mathrm {Tr}\left( {\mathfrak P}_{j,i}(\rho )\right) }. \end{aligned}$$
    (16)

We have the following corollary:

Corollary 3.5

Let i, j be in V.

  1. 1.

    One has \({\mathbb {P}}_{i,\rho }(t_j<\infty )=1\) if and only if \({\mathfrak P}_{j,i}^*(\mathrm {Id}_{{\mathfrak h}_j})\) has the form \(\begin{pmatrix} \mathrm {Id}&{} 0 \\ 0 &{} *\end{pmatrix}\) in the decomposition \({\mathfrak h}_i=\mathrm {Ran}\,\rho \oplus (\mathrm {Ran}\,\rho )^\perp \). In particular, if there exists a faithful \(\rho \) in \(\mathcal {S}({\mathfrak h}_i)\) such that \({\mathbb {P}}_{i,\rho }(t_j<\infty )=1\), then \({\mathbb {P}}_{i,\rho '}(t_j<\infty )=1\) for any \(\rho '\in \mathcal S({\mathfrak h}_i)\).

  2. 2.

    If there exists a faithful \(\rho \) in \(\mathcal {S}({\mathfrak h}_i)\) such that \({\mathbb {P}}_{i,\rho }(t_i<\infty )=1\), then one has \({\mathbb {E}}_{i,\rho '}(n_i)=\infty \) for any \(\rho '\in \mathcal S({\mathfrak h}_i)\).

  3. 3.

    If there exists a faithful \(\rho \) in \(\mathcal {S}({\mathfrak h}_i)\) such that \({\mathbb {E}}_{i,\rho }(n_j)<\infty \) and \({\mathfrak h}_i\) is finite-dimensional, then one has \({\mathbb {E}}_{i,\rho '}(n_j)<\infty \) for any \(\rho '\) in \(\mathcal S({\mathfrak h}_i)\).

  4. 4.

    If  \({\mathbb {E}}_{i,\rho }(n_j)<\infty \) for every \(\rho \) in \(\mathcal S({\mathfrak h}_i)\), then there exists a completely positive linear bounded map \({\mathfrak N}_{j,i}\) from \(\mathcal I_1({\mathfrak h}_i)\) to \(\mathcal I_1({\mathfrak h}_j)\) such that

    $$\begin{aligned} {\mathbb {E}}_{i,\rho }(n_j)=\mathrm {Tr}\big ({\mathfrak N}_{j,i}(\rho )\big ), \end{aligned}$$
    (17)

    and one has the expression

    $$\begin{aligned} {\mathfrak N}_{j,i}(\rho )=\sum _{\pi \in {\mathcal P}(i,j)}L_\pi \rho L_\pi ^*. \end{aligned}$$
    (18)

Remark 3.6

 

  1. 1.

    The second part of the first statement, and the second statement, do not hold without the faithfulness assumption, as shown by Examples 5.1 and 5.2.

  2. 2.

    Since \({\mathfrak P}_{j,i}\) is a completely positive contraction, one has \({\mathfrak P}^*_{j,i}(\mathrm {Id}_{{\mathfrak h}_j})\le \mathrm {Id}_{{\mathfrak h}_i}\). In addition, by the Russo–Dye Theorem [34], \(\Vert {\mathfrak P}^*_{j,j}\Vert =\Vert {\mathfrak P}^*_{j,j}(\mathrm {Id}_{{\mathfrak h}_j})\Vert \) so that if \(\Vert {\mathfrak P}^*_{j,j}(\mathrm {Id}_{{\mathfrak h}_j})\Vert <1\), then \({\mathbb {E}}_{i,\rho }(n_j)<\infty \) for every \(\rho \) in \(\mathcal S({\mathfrak h}_i)\) and:

    $$\begin{aligned} {\mathfrak N}_{j,i}=\left( \mathrm {Id}-{\mathfrak P}_{j,j}\right) ^{-1}\circ {\mathfrak P}_{j,i}. \end{aligned}$$
  3. 3.

    Again, under the assumptions of point 4, an immediate consequence is

    $$\begin{aligned} \Vert {\mathfrak N}_{j,i}\Vert =\sup _{\rho \in \mathcal S({\mathfrak h}_i)}{\mathbb {E}}_{i,\rho }(n_j), \end{aligned}$$

    and \({\mathfrak N}_{j,i}^{(\alpha )}\) introduced in Sect. 1 satisfies \({\mathfrak N}_{j,i}=\lim _{\alpha \rightarrow 1}{\mathfrak N}_{j,i}^{(\alpha )}\).

  4. 4.

    If \({\mathbb {E}}_{i,|\varphi \rangle \langle \varphi |}(n_j)<\infty \) for a total set of unit vectors \(\varphi \) of an infinite-dimensional \({\mathfrak h}_i\), then \({\mathfrak N}_{j,i}\) can still be constructed as a densely defined (a priori unbounded) selfadjoint operator, thanks to the representation theory for closed quadratic forms (see e.g. [25, Theorem VIII.3.13a]).

We have an easy partial converse to the third statement of Corollary 3.5 (a stronger result will be given under the additional assumption of irreducibility).

Proposition 3.7

Let i be in V and assume that \({\mathfrak h}_i\) is finite-dimensional. If \({\mathbb {P}}_{i,\rho }(t_i<\infty )<1\) for every \(\rho \) in \(\mathcal S({\mathfrak h}_i)\), then \({\mathbb {E}}_{i,\rho '}(n_i) <\infty \) for every \(\rho '\) in \(\mathcal S({\mathfrak h}_i)\).

Remark 3.8

Proposition 3.7 implies in particular that, if \({\mathfrak h}_i\) is finite-dimensional and there exists \(\rho \) in \(\mathcal S({\mathfrak h}_i)\) such that \({\mathbb {E}}_{i,\rho }(n_i)=\infty \), then there exists \(\rho '\) in \(\mathcal S({\mathfrak h}_i)\) such that \({\mathbb {P}}_{i,\rho '}(t_i<\infty )=1\). Note that this does not necessarily hold with \(\rho '=\rho \), as Examples 5.1 and 5.5 show.

3.2 The Irreducible Case

We now turn to the “universality” properties analogous to (2) and (3) that are expected in the irreducible case. We will prove the following:

Proposition 3.9

Let \(\mathfrak M\) be an irreducible open quantum walk and let j be in V. We are in one (and only one) of the following situations:

  1. 1.

    for every i in V there exists a domain \({\mathfrak d}^n_{j,i}\), dense in \({\mathfrak h}_i\), such that the quantity \({\mathbb {E}}_{i,\rho }(n_j)\) is finite for any \(\rho \) that has finite range contained in \({\mathfrak d}^n_{j,i}\),

  2. 2.

    for every i in V, for any \(\rho \) in \(\mathcal S({\mathfrak h}_i)\), the quantity \({\mathbb {E}}_{i,\rho }(n_j)\) is infinite.

For semifinite OQW, the picture is simpler. We have the following corollary:

Corollary 3.10

Let \(\mathfrak M\) be a semifinite irreducible open quantum walk. We are in one (and only one) of the following situations:

  1. 1.

    the quantity \({\mathbb {E}}_{i,\rho }(n_j)\) is finite for any i, j in V and any \(\rho \) in \(\mathcal S({\mathfrak h}_i)\),

  2. 2.

    the quantity \({\mathbb {E}}_{i,\rho }(n_j)\) is infinite for any i, j in V and any \(\rho \) in \(\mathcal S({\mathfrak h}_i)\).

Remark 3.11

  1. 1.

    Example 5.1 shows that the above statements do not hold without the irreducibility assumption.

  2. 2.

    Example 5.3 shows that any irreducible open quantum walk that admits an invariant state (and in particular a finite OQW) is in case 2 of Corollary 3.10.

The next proposition is the last ingredient to prove Theorem 3.1.

Proposition 3.12

Let \(\mathfrak M\) be an irreducible open quantum walk. Assume that there exists i, j in V with \(\mathrm {dim}\, {\mathfrak h}_i <\infty \), \(\mathrm {dim}\, {\mathfrak h}_j <\infty \) and \({\mathbb {E}}_{i,\rho }(n_j)=\infty \) for some \(\rho \) in \(\mathcal S({\mathfrak h}_i)\). Then \({\mathbb {P}}_{j,\rho '}(t_j<\infty )=1\) for every \(\rho '\) in \(\mathcal S({\mathfrak h}_j)\).

The proof of Theorem 3.1 follows immediately from Corollary 3.5, Proposition 3.7, Corollary 3.10 and Proposition 3.12.

3.3 Notions of Recurrence for Open Quantum Walks

In view of Corollary 3.10, we propose the following terminology:

Definition 3.13

A semifinite irreducible open quantum walk \(\mathfrak M\) is called transient if it satisfies property 1. of Corollary 3.10, and recurrent if it satisfies property 2.

In other words, our classification depends on the quantity \({\mathbb {E}}_{i,\rho }(n_i)\) being finite or infinite. Thanks to Corollary 3.10, for a semifinite irreducible open quantum walk this quantity is universal in the sense that it is either finite for all i and \(\rho \), or infinite for all i and \(\rho \). We now compare this with existing definitions of recurrence for open quantum walks and related objects.

First of all, if the open quantum walk \(\mathfrak M\) is the minimal dilation of a classical Markov chain, then \(\mathfrak M\) is recurrent in our sense if and only if the Markov chain is recurrent in the classical sense.

Fagnola and Rebolledo defined in [20] a notion of recurrence for (continuous-time) quantum dynamical semigroups. When applied to the (discrete-time) quantum dynamical semigroup \((\mathfrak M^n)_n\), this definition of recurrence is that for any operator A of \(\mathcal B(\mathcal H)\) that satisfies \(\langle \varphi , A\varphi \rangle >0\) for any \(\varphi \in \mathcal H\setminus \{0\}\), the set

$$\begin{aligned} D(\mathfrak U(A)) =\big \{\varphi =\sum _{i\in V}\varphi _i\otimes |i\rangle \ \text{ s.t. } \sum _{k\ge 0}\langle \varphi , (\mathfrak M^*)^k(A)\, \varphi \rangle < \infty \big \}. \end{aligned}$$

equals \(\{0\}\). We call this notion FR-recurrence. Our definition of a recurrent OQW, as can be seen from Sect. 1, is equivalent to the fact that for any \(j\in V\), \(D\big (\mathfrak U(A_j)\big )=\{0\}\) for \(A_j=\mathrm {Id}_{{\mathfrak h}_j}\otimes |j\rangle \langle j|\). It is clear that if the OQW is FR-recurrent, then it is recurrent in our sense. If the OQW is not FR-recurrent, then there exists A as above such that \( \sum _{k\ge 0}\langle \varphi , (\mathfrak M^*)^k(A)\, \varphi \rangle < \infty \), and if the OQW is semifinite, then for any j in V there exists \(\lambda _j>0\) such that \(\lambda _j \mathrm {Id}_{{\mathfrak h}_j}\otimes |j\rangle \langle j|\le A\) and the OQW is not recurrent. Therefore, for semifinite OQWs, our notion of recurrence and FR-recurrence are equivalent.

A series of results investigating recurrence of open quantum walks can be found in [11, 28, 29]. In particular, in these references, a site \(i\in V\) is called (LS)-recurrent if (in our terms) one has \({\mathbb {P}}_{i,\rho }(t_i<\infty )=1\) for any \(\rho \) in \(\mathcal S({\mathfrak h}_i)\). The OQW is called (LS)-site-recurrent if every site i in V is LS-recurrent. In other words, LS-recurrence classifies sites depending on the quantity

$$\begin{aligned} \inf _{\rho \in \mathcal S({\mathfrak h}_i)}{\mathbb {P}}_{i,\rho }(t_i<\infty ) \end{aligned}$$
(19)

being equal to 1 or not. Corollary 3.10 shows that, for a semifinite irreducible open quantum walk, \( \inf _{\rho \in \mathcal S({\mathfrak h}_i)}{\mathbb {P}}_{i,\rho }(t_i<\infty ) =1\) for some i if and only if it is true for all i (a fact which is not proved in [11, 28, 29]), and also that this is equivalent with recurrence in the sense of Definition 3.13. Therefore, an irreducible semifinite OQW is LS-site-recurrent if and only if it is recurrent in our sense. Without the irreducibility assumption, point 2 of Corollary 3.5 shows that if i is LS-recurrent then \({\mathbb {E}}_{i,\rho }(n_i)=\infty \) for any \(\rho \) in \(\mathcal S({\mathfrak h}_i)\); the converse does not hold, as shown by Example 5.4. Note, however, that the quantity \({\mathbb {E}}_{i,\rho }(n_i)\) has the advantage of being universal in i and \(\rho \), in the sense that (for a semifinite irreducible OQW) it is either finite for every i and \(\rho \), or infinite for every i and \(\rho \). This is not true of \({\mathbb {P}}_{i,\rho }(t_i<\infty )=1\), as Examples 5.2 and 5.5 show. The reason can be traced back to the fact that the set of “diagonal” \(\varphi =\sum _{i\in V} \varphi _i \otimes |i\rangle \) such that \({\mathbb {P}}_{|\varphi \rangle \langle \varphi |}(t_j <\infty )=1\), even though it is stable by any \(L_\pi \otimes |j\rangle \langle i|\) with \(\pi \in \mathcal P(i,j)\), is not a vector space, and therefore cannot be an enclosure (see the proof of Proposition 3.9 in Sect. 1).

Recently, Dhahri and Mukhamedov discussed a notion of recurrence in [17]. That notion actually concerns quantum Markov chains (objects that originate in [1, 2]), and was defined in [3]. The connection with open quantum walks is established by associating a quantum Markov chain to an open quantum walk. This can be done, however, in different ways, and the property of recurrence depends on the choice of the associated quantum Markov chain. In addition, it is not clear what this notion of recurrence has to do with the properties of the random variables \((x_n)_n\). A major setback, making the associated quantum Markov chains non-canonical, is that they are constructed over the algebra \(\big (\mathcal B(\bigoplus _{i\in V} {\mathfrak h}_i)\big )^{\otimes \mathbb {N}}\); a more direct connection could probably be obtained, at least when \({\mathfrak h}_i\equiv {\mathfrak h}\), by a construction over \(\mathcal B({\mathfrak h})\otimes \big (\mathcal B(\mathbb {C}^V)\big )^{\otimes \mathbb {N}}\), as can be done using the theory of finitely correlated states (see [21]).

Last, remark that, inspired by [24], the authors of [11] discuss an alternate notion of recurrence to a site \(i\in V\). In that new notion, physically speaking, the observer does not at every time n measure the position \(x_n\) of the particle, but measures only whether the particle has returned to i or not. Mathematically, this amounts to considering the probability space defined by \(\tilde{\Omega }=\{0,1\}^\mathbb {N}\), and probability

$$\begin{aligned} \tilde{{\mathbb {P}}}_{i,\rho }(\tilde{\imath }_1,\ldots ,\tilde{\imath }_n)=\mathrm {Tr}\left( \Phi _{\tilde{\imath }_n,\tilde{\imath }_{n-1}}\circ \ldots \circ \Phi _{\tilde{\imath }_1,1}(\rho \otimes |i\rangle \langle i|)\right) \end{aligned}$$

where we have, for \(\tau \) a state on \(\mathcal H\), and with \(A_{i,j}\) as in (7)

$$\begin{aligned} \Phi _{1,1}(\tau )= A_{i,i}\tau A_{i,i}^*,\quad \Phi _{1,0}(\tau )=\sum _{j\ne i} A_{i,j}\tau A_{i,j}^*, \\ \Phi _{0,1}(\tau )=\sum _{j\ne i} A_{j,i}\tau A_{j,i}^*, \quad \Phi _{0,0}(\tau )=\sum _{j,k\ne i} A_{j,k}\tau A_{j,k}^*. \end{aligned}$$

The new notion of recurrence is then related to the first time \(\tilde{t}_i\ge 1\) for which the process defined by \(\tilde{x}_n(\tilde{\omega })=\tilde{\imath }_n\) takes the value 1. It is easy to verify, however, that this \(\tilde{t}_i\) has the same law under \(\tilde{\mathbb {P}}_{i,\rho }\) as \(t_i\) under \({\mathbb {P}}_{i,\rho }\), so that this alternate notion of recurrence is identical to LS-recurrence, as was noted in [11].

4 Expectation of Return Times

We now turn to results analogous to (4). Our first statement is a representation result.

Proposition 4.1

For any i, j in V and \(\rho \) in \(\mathcal S({\mathfrak h}_i)\), we have

$$\begin{aligned} {\mathbb {E}}_{i,\rho }(t_j)=\left\{ \begin{array}{ll} \sum \limits _{\pi \in {\mathcal {P}}^{V \setminus \{ j \} } (i,j)} \ell (\pi ) \,\mathrm {Tr}\, L_\pi \rho L_\pi ^{*} &{} \text{ if } {\mathbb {P}}_{i,\rho }(t_j< \infty )=1,\\ +\infty &{} \text{ if } {\mathbb {P}}_{i,\rho }(t_j<\infty )<1. \end{array} \right. \end{aligned}$$
(20)

If \({\mathbb {E}}_{i,\rho }(t_j)<\infty \) for every \(\rho \in \mathcal S({\mathfrak h}_i)\), then there exists a bounded operator \({\mathfrak T}_{j,i}\) from \(\mathcal I_1({\mathfrak h}_i)\) to \(\mathcal I_1({\mathfrak h}_j)\) such that

$$\begin{aligned} {\mathbb {E}}_{i,\rho }(t_j)=\mathrm {Tr}\big ({\mathfrak T}_{j,i}(\rho )\big ). \end{aligned}$$
(21)

Remark 4.2

  1. 1.

    In the case where \({\mathbb {E}}_{i,\rho }(t_j)<\infty \) for every \(\rho \in \mathcal S({\mathfrak h}_i)\) we have the expression

    $$\begin{aligned} {\mathfrak T}_{j,i}(\rho )=\sum _{\pi \in \mathcal P^{V\setminus \{j\}}(i,j)} \ell (\pi ) \,L_\pi \rho L_\pi ^* \end{aligned}$$
  2. 2.

    We have in addition the identity (with both sides possibly \(\infty \))

    $$\begin{aligned} {\mathbb {E}}_{i,\rho }(t_i)=\frac{\mathrm d}{\mathrm d \alpha } \mathrm {Tr}\big ({\mathfrak P}_{i,i}^{(\alpha )}(\rho )\big )\big |_{\alpha =1}. \end{aligned}$$

    The operators \({\mathfrak P}_{i,i}^{(\alpha )}\) are defined in Sect. 1.

Our first relevant theorem is a universality result in the irreducible case:

Theorem 4.3

Let \(\mathfrak M\) be a semifinite irreducible open quantum walk. We are in one (and only one) of the following situations:

  1. 1.

    for any i in V and \(\rho \) in \(\mathcal S({\mathfrak h}_i)\), one has \({\mathbb {E}}_{i,\rho }(t_i)<\infty \),

  2. 2.

    for any i in V and \(\rho \) in \(\mathcal S({\mathfrak h}_i)\), one has \({\mathbb {E}}_{i,\rho }(t_i)=\infty \).

Our proof uses the following intermediate universality result, similar to Proposition 3.9 and which can be useful in a wider setting:

Proposition 4.4

Let \(\mathfrak M\) be an irreducible open quantum walk and let j be in V. We are in one (and only one) of the following situations:

  1. 1.

    for every i in V, there exists a domain \({\mathfrak d}^t_{j,i}\), dense in \({\mathfrak h}_i\), such that the quantity \({\mathbb {E}}_{i,\rho }(t_j)\) is finite for any \(\rho \) in \(\mathcal {S}({\mathfrak h}_i)\) that has finite range contained in \({\mathfrak d}^t_{j,i}\);

  2. 2.

    for every i in V and \(\rho \) in \(\mathcal S({\mathfrak h}_i)\), the quantity \({\mathbb {E}}_{i,\rho }(t_j)\) is infinite.

Our second result relates the invariant state with the expectation of return times. To state it, for \(j\in V\), we define by induction for \(k\in \mathbb {N}\) the k-th return time

$$\begin{aligned} t_j^{(k)}=\inf \big \{n>t_j^{(k-1)}\, |\, x_n=j\big \}. \end{aligned}$$

Theorem 4.5

Let \(\mathfrak M\) be a semifinite irreducible open quantum walk with an invariant state \({\tau ^{\mathrm {inv}}}=\sum _{i\in V}{\tau ^{\mathrm {inv}}}(i)\otimes |i\rangle \langle i|\). Then we are in situation 1 of Theorem 4.3, and for any i, j in V and \(\rho \) in \(\mathcal S({\mathfrak h}_i)\), the sequence \((t_j^{(k)}/k)_{k}\) converges, with respect to \({\mathbb {P}}_{i,\rho }\), both almost-surely and in the \(\mathrm L^1\) sense, to

$$\begin{aligned} {\mathbb {E}}_{j,\frac{{\tau ^{\mathrm {inv}}}(j)}{\mathrm {Tr}\,{\tau ^{\mathrm {inv}}}(j)}}(t_j)= \big (\mathrm {Tr}\,{\tau ^{\mathrm {inv}}}(j)\big )^{-1}. \end{aligned}$$
(22)

The proof is based on the Kümmerer-Maassen ergodic Theorem and Birkhoff’s ergodic Theorem. Note that Theorem 1.6 in [11] shows a result of the same type, but with less explicit assumptions.

5 Examples

Example 5.1

Consider the open quantum walk defined by \(V=\{0,1,2\}\), with \({\mathfrak h}_i=\mathbb {C}^2\) for \(i=0,1,2\) and

$$\begin{aligned} L_{1,0}=\begin{pmatrix} 1&{} 0 \\ 0 &{} 0 \end{pmatrix} \qquad L_{2,0}=\begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix} \qquad L_{0,1}=\begin{pmatrix} 1&{} 0 \\ 0 &{} 1 \end{pmatrix} \qquad L_{2,2}=\begin{pmatrix} 1&{} 0 \\ 0 &{} 1 \end{pmatrix} , \end{aligned}$$

all other transitions being zero. This OQW is obviously not irreducible. Denote by \(e_1\), \(e_2\) the canonical basis of \(\mathbb {C}^2\). For \(\rho =\begin{pmatrix}1-r &{} s\\ \overline{s}&{}r\end{pmatrix}\) (with \(r\in [0,1]\) and \(|s|^2\le r(1-r)\), so that \(r=1\) if and only if \(\rho =|e_2\rangle \langle e_2|\)) one has \({\mathbb {P}}_{0,\rho }(t_0<\infty )=1-r\), and \({\mathbb {E}}_{0,\rho }(n_0)= 0\) if \(r=1\), and \(\infty \) otherwise. One therefore has

In this case, it is easy to compute the operator \({\mathfrak P}_{0,0}\):

$$\begin{aligned} {\mathfrak P}_{0,0}(\rho )=\begin{pmatrix} 1&{} 0 \\ 0 &{} 0 \end{pmatrix} \rho \begin{pmatrix} 1&{} 0 \\ 0 &{} 0 \end{pmatrix}. \end{aligned}$$

Therefore, \({\mathfrak P}_{0,0}^{*\,k}(\mathrm {Id}_{{\mathfrak h}_0})=\begin{pmatrix} 1&{} 0 \\ 0 &{} 0 \end{pmatrix}\) for any \(k\ge 1\), so that loosely speaking, one has \(\sum _{k\ge 0}{\mathfrak P}_{0,0}^{*\,k}(\mathrm {Id}_{{\mathfrak h}_0})=\begin{pmatrix} \infty &{} 0 \\ 0 &{} 0 \end{pmatrix}\), consistently with Proposition 3.3.

Example 5.2

Consider the open quantum walk defined by \(V=\{0,1,2,\ldots \}\) with \({\mathfrak h}_0=\mathbb {C}^2\) and \({\mathfrak h}_i=\mathbb {C}\) for \(i>0\), and transition operators

$$\begin{aligned} L_{0,0}=\begin{pmatrix} 0&{} 1 \\ 0 &{} 0 \end{pmatrix} \qquad L_{1,0}=\begin{pmatrix} 1&0 \end{pmatrix} \qquad L_{0,1}=\sqrt{p/2\,}\begin{pmatrix} 1 \\ 1 \end{pmatrix} \end{aligned}$$

and \(L_{i,i+1}=\sqrt{p}\), \(L_{i+1,i}=\sqrt{q}\) for \(i\ge 1\), with \(p+q=1\) (all other transitions being zero). This OQW is semifinite and irreducible, independently of the value of p. However, it is a simple exercise (using classical results about the gambler’s ruin, see [22]) to see that, depending on the value of p, one has different behaviors for \({\mathbb {P}}_{0,\rho }(t_0<\infty )\) and \({\mathbb {E}}_{0,\rho }(n_0)\):

  • for \(p\ge 1/2\) one has

    $$\begin{aligned} {\mathbb {P}}_{0,\rho }(t_0<\infty )&=1&\quad \forall \rho \in \mathcal S({\mathfrak h}_0),\\ {\mathbb {E}}_{0,\rho }(n_0)&=\infty&\quad \forall \rho \in \mathcal S({\mathfrak h}_0),\\ {\mathbb {E}}_{0,\rho }(t_0)&=\frac{2p-r}{2p-1} &\quad \text{ for } \rho =\begin{pmatrix}1-r &{} s\\ \overline{s}&{}r\end{pmatrix}. \end{aligned}$$

  • for \(p<1/2\) one has

    $$\begin{aligned} {\mathbb {P}}_{0,\rho }(t_0<\infty )=1 \text{ and } {\mathbb {E}}_{0,\rho }(t_0)=1&\quad \text{ if } \rho =|e_2\rangle \langle e_2|,\\ {\mathbb {P}}_{0,\rho }(t_0<\infty )<1 \quad \text{ and } \ {\mathbb {E}}_{0,\rho }(t_0)=\infty&\quad \text{ if } \rho \ne |e_2\rangle \langle e_2|,\\ {\mathbb {E}}_{0,\rho }(n_0)<\infty&\quad \forall \rho \in \mathcal S({\mathfrak h}_0). \end{aligned}$$

Here again it is easy to compute the operator \({\mathfrak P}_{0,0}\): for any \(\rho \) in \(\mathcal I_1({\mathfrak h}_0)\) we have

$$\begin{aligned} {\mathfrak P}_{0,0}(\rho )=\begin{pmatrix} 0&{}1\\ 0 &{}0\end{pmatrix} \rho \begin{pmatrix} 0&{}0\\ 1 &{}0\end{pmatrix}+ \frac{1}{2} \inf (p/q,1) \begin{pmatrix} 1&{}0\\ 1 &{}0\end{pmatrix} \rho \begin{pmatrix} 1&{}1\\ 0 &{}0\end{pmatrix}. \end{aligned}$$

In particular, for \(p\ge 1/2\), one has \({\mathfrak P}_{0,0}^{*k}(\mathrm {Id}_{{\mathfrak h}_0})=\mathrm {Id}_{{\mathfrak h}_0}\), and for \(p<1/2\) one has \({\mathfrak P}_{0,0}^{*k}(\mathrm {Id}_{{\mathfrak h}_0})= \begin{pmatrix} u_{k+1} &{} 0 \\ 0 &{} u_k\end{pmatrix}\) with \(u_k\rightarrow 0\) exponentially fast, so that \({\mathfrak P}_{0,0}^{*k}(\mathrm {Id}_{{\mathfrak h}_0})\) is summable. This is consistent with Corollary 3.5. In addition, for \(p\ge 1/2\) one has

$$\begin{aligned} {\mathfrak T}_{0,0}(\rho )= \begin{pmatrix} 0&{}1\\ 0 &{}0\end{pmatrix} \rho \begin{pmatrix} 0&{}0\\ 1 &{}0\end{pmatrix} + \frac{p}{2p-1} \begin{pmatrix} 1&{}0\\ 1 &{}0\end{pmatrix} \rho \begin{pmatrix} 1&{}1\\ 0 &{}0\end{pmatrix}. \end{aligned}$$

Example 5.3

In the case of an irreducible open quantum walk which admits a faithful invariant state (for example a finite irreducible open quantum walk), the Kümmerer–Maassen ergodic Theorem (proved originally in [27], see [31] for an infinite-dimensional extension and [10] for an application to the case of open quantum walks) immediately implies that, for any initial position i in V and any state \(\rho \) in \(\mathcal S(\mathfrak h_i)\), any point j is almost-surely visited infinitely often:

$$\begin{aligned} {\mathbb {P}}_{i,\rho }(n_j=\infty )=1. \end{aligned}$$

A fortiori, one has \({\mathbb {P}}_{i,\rho }(t_j<\infty )=1\) and \({\mathbb {E}}_{i,\rho }(n_j)=\infty \), and therefore the OQW is always recurrent. This is the same as in the classical case, where an irreducible Markov chain on a finite set is always recurrent.

Example 5.4

Consider the open quantum walk with \(V=\{0,1,2,3\}\), \({\mathfrak h}_{0}=\mathbb {C}\) and \({\mathfrak h}_i=\mathbb {C}^2\) for \(i=1, 2, 3\), and

$$\begin{aligned} L_{0,0}=1 \qquad L_{0,1}=\begin{pmatrix}1/2&0 \end{pmatrix}\\ L_{2,1}=\begin{pmatrix} \sqrt{3} /2 &{} 0 \\ 0 &{} 1 \end{pmatrix} \qquad L_{1,2}=\begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix}\\ L_{3,2}=\begin{pmatrix} 1 &{} 0 \\ 0 &{} 0 \end{pmatrix} \qquad L_{2,3}=\begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}, \end{aligned}$$

all other transitions \(L_{i,j}\) being zero. One checks by examination that, starting from \(i=1\) and \(\rho =\begin{pmatrix}1-r &{} s\\ \overline{s}&{}r\end{pmatrix}\): with probability \((1-r)/4\) the first step goes to 0 and then the walk stays there and, with probability \((3+r)/4\) the first step goes to 2 and then, after a finite number of steps, goes back and forth between 1 and 2. Therefore, for any \(\rho \), one has \({\mathbb {P}}_{1,\rho }(t_0<\infty )=(1-r)/4\) but \({\mathbb {E}}_{1,\rho }(n_0)=\infty \). Again it is easy to compute \({\mathfrak P}_{1,1}\):

$$\begin{aligned} {\mathfrak P}_{1,1}(\rho )=\begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix} \rho \begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix} + \begin{pmatrix} 0 &{} 0 \\ \sqrt{3} /2 &{} 0 \end{pmatrix} \rho \begin{pmatrix} 0 &{} \sqrt{3} /2\\ 0 &{} 0 \end{pmatrix}. \end{aligned}$$

One then has \({\mathfrak P}_{1,1}^{*\,k}(\mathrm {Id}_{{\mathfrak h}_0})=\begin{pmatrix} (3/4)^k &{} 0 \\ 0 &{} 1 \end{pmatrix}\), so that loosely speaking, \(\sum _k {\mathfrak P}_{1,1}^{*\,k}(\mathrm {Id}_{{\mathfrak h}_0})= \begin{pmatrix} 4 &{} 0 \\ 0 &{} \infty \end{pmatrix}\), consistently with Corollary 3.5.

Example 5.5

We consider now the case of (space) homogeneous nearest-neighbor random walks on \(V=\mathbb {Z}\) with \({\mathfrak h}_i\equiv {\mathfrak h}=\mathbb {C}^2\) for all \(i\in \mathbb {Z}\). This OQW is entirely determined by two operators \(L_+\) and \(L_-\) on \(\mathbb {C}^2\) satisfying \(L_+^* L_+ + L_-^* L_-=\mathrm {Id}_{{\mathfrak h}}\). We call such an open quantum walk a \((\mathbb {Z},\mathbb {C}^2)\)-simple OQW. It is proven in [11] that:

  1. 1.

    if \(L_{+}^{*} L_+=L_{-}^{*}L_-=\{1/2\}\) then \({\mathbb {P}}_{i,\rho }(t_i<\infty )~=~1\) for any i and \(\rho \),

  2. 2.

    if \({\mathbb {P}}_{i,\rho }(t_i<\infty )=1\) for any i and \(\rho \) with \(L_+\), \(L_-\) normal, then \(L_{+}^{*}L_+=L_{-}^{*}L_-=\{1/2\}\).

With the tools developed in this section, we can recover the first point and make the second more precise. First, if \(L_{+}^{*}L_+=L_{-}^{*}L_-=\{1/2\}\) then

$$\begin{aligned} {\mathfrak P}^*_{i,i}(\mathrm {Id}_{{\mathfrak h}})= \sum _{\pi \in {\mathcal P}^{V\setminus \{i\}}(i,i)} \left( \frac{1}{2}\right) ^{\ell (\pi )} \,\mathrm {Id}_{{\mathfrak h}} \end{aligned}$$

which, by the results on (classical) simple random walks, is just \(\mathrm {Id}_{\mathfrak h}\), and by Corollary 3.5, \({\mathbb {P}}_{i,\rho }(t_i<\infty )=1\) for any \(\rho \). Second, assume that \(L_+\) and \(L_-\) are normal, and consider a diagonal basis for \(L_+^* L_+\) (and therefore for \(L_-^* L_-\)). In this basis, one has

$$\begin{aligned} L_+^* L_+ = \begin{pmatrix} p_1 &{} 0 \\ 0 &{} p_2 \end{pmatrix}\qquad L_-^* L_- = \begin{pmatrix} q_1 &{} 0 \\ 0 &{} q_2 \end{pmatrix} \end{aligned}$$
(23)

with \(p_k+q_k=1\), \(k=1,2\). It is then easy to show that if a path \(\pi \) is made of \(n_+(\pi )\) “up” steps, and \(n_-(\pi )\) “down” steps, then

$$\begin{aligned} L_\pi ^* L_\pi = (L_+^* L_+)^{n_+(\pi )} (L_-^* L_-)^{n_-(\pi )}= \begin{pmatrix} p_1^{n_+(\pi )}q_1^{n_-(\pi )} &{} 0 \\ 0 &{} p_2^{n_+(\pi )}q_2^{n_-(\pi )}\end{pmatrix}, \end{aligned}$$

and using again standard results on simple random walks we have

$$\begin{aligned} {\mathfrak P}^*_{0,0}(\mathrm {Id}_{{\mathfrak h}})=\begin{pmatrix} \inf (2p_1,2q_1) &{} 0 \\ 0 &{} \inf (2p_2,2q_2) \end{pmatrix}. \end{aligned}$$

Therefore, if \(L_+\) and \(L_-\) are normal, then:

  • if \(p_1=p_2=1/2\), then \({\mathbb {P}}_{i,\rho }(t_i<\infty )=1\) for any i and \(\rho \), and therefore \({\mathbb {E}}_{i,\rho }(n_i)=\infty \);

  • if \(p_1\) and \(p_2\) are both \(\ne 1/2\), then \({\mathbb {P}}_{i,\rho }(t_i<\infty )<1\) for any i and \(\rho \), and therefore \({\mathbb {E}}_{i,\rho }(n_i)<\infty \);

  • if e.g. \(p_1=1/2\) and \(p_2\ne 1/2\) then \({\mathbb {P}}_{i,\rho }(t_i<\infty )=1\) for \(\rho =|e_1\rangle \langle e_1|\) and \(<1\) otherwise. If furthermore the OQW is irreducible (see [9, Proposition 6.12] for a necessary and sufficient condition), then by Theorem 3.1 one has \({\mathbb {E}}_{i,\rho }(n_i)=\infty \) for any i and \(\rho \).

A natural question is what happens when we drop the assumption of normality for \(L_+\) and \(L_-\). We can still assume the form (23); if \(\sup (p_1,p_2)<1/2\) or \(\inf (p_1,p_2)>1/2\) and \(L_+\), \(L_-\) do not have an eigenvector in common, then [9, Theorem 5.4] implies that the process satisfies a law of large numbers \(x_n/n \rightarrow m\ne 0\) almost-surely, and satisfies a large deviations principle with respect to any \({\mathbb {P}}_{i,\rho }\). This is enough to show that \({\mathbb {E}}_{i,\rho }(n_i)<\infty \) for any i and \(\rho \). On the other hand, if e.g. \(p_1>1/2\) and \(p_2<1/2\) then we can still have \({\mathbb {P}}_{i,\rho }(t_i<\infty )=1\) for any i and \(\rho \): consider (as suggested by [11]) the case

$$\begin{aligned} L_+=\frac{1}{\sqrt{2}}\begin{pmatrix} 1 &{} 1 \\ 0 &{} 0 \end{pmatrix} \qquad L_-=\frac{1}{\sqrt{2}}\begin{pmatrix} 0&{} 0 \\ 1 &{} -1 \end{pmatrix} \end{aligned}$$

where \(L_{+}^{*}L_+ = L_{-}^{*} L_-=\{0,1\}\). By [9, Proposition 6.12], this open quantum walk is irreducible. In addition, for any \(\pi =(i_0,\ldots ,i_\ell )\), denoting \(\varepsilon =i_1-i_0\), one shows that \(2^{\ell (\pi )/2}\,L_\pi \) equals

$$\begin{aligned} \pm \begin{pmatrix} 1 &{} \varepsilon \\ 0 &{} 0 \end{pmatrix} \text{ if } i_\ell -i_{\ell -1}=+1, \qquad \pm \begin{pmatrix} 0 &{} 0\\ 1 &{} \varepsilon \end{pmatrix} \text{ if } i_\ell -i_{\ell -1}=-1. \end{aligned}$$

We can therefore compute, again using results for simple random walks,

$$\begin{aligned} {\mathfrak P}_{0,0}(\rho ) = \frac{1}{2} \begin{pmatrix}1 &{} -1 \\ 0 &{} 0\end{pmatrix} \rho \begin{pmatrix} 1 &{} 0 \\ -1 &{} 0\end{pmatrix} + \frac{1}{2} \begin{pmatrix} 0 &{} 0 \\ 1 &{} 1\end{pmatrix} \rho \begin{pmatrix} 0 &{} 1 \\ 0 &{} 1\end{pmatrix}. \end{aligned}$$

We therefore have \({\mathfrak P}^*_{0,0}(\mathrm {Id}_{{\mathfrak h}_0})=\mathrm {Id}_{{\mathfrak h}_0}\), so that \({\mathbb {P}}_{i,\rho }(t_j<\infty )=1\) and \({\mathbb {E}}_{i,\rho }(n_j)=\infty \) for any i, j and \(\rho \). In addition, \({\mathbb {E}}_{i,\rho }(t_i)=\infty \) for any i and \(\rho \).

6 Exit Times and Dirichlet Problems on Finite Domains

In this section, we consider a finite subset D of V and study whether, conditionally on starting with \(x_0\) in D, the position process \((x_n)_n\) reaches the boundary \({\partial \! D}\) of D (which we define below) in finite time. We then study the related problem of solving Dirichlet problems of the type \(\big ((\mathrm {Id}-\mathfrak M^*)(Z)\big )_i=A_i\) for every i in D, with a boundary condition \(Z_j=B_j\) for \(j\in {\partial \! D}\). Before we start, however, let us discuss shortly the Dirichlet problem on V. We consider an irreducible open quantum walk \(\mathfrak M\), fix \(A=\sum _{i\in V} A_i\otimes |i\rangle \langle i|\) with \(A_i\) in \(\mathcal {B}({\mathfrak h}_i)\) for all i, and look for a solution Z of the equation \((\mathrm {Id}-\mathfrak M^*)(Z)=A.\) As in the classical case (see e.g. [30]), the form of the solution differs, depending on the recurrence or transience of the OQW. We give here only a simple result in the transient case. We define the Dirichlet problem on V with data A as the following equation with unknown Z:

$$\begin{aligned} (\mathrm {Id}-\mathfrak M^*)(Z)=A. \end{aligned}$$
(24)

The operators \({\mathfrak N}_{j,i}\) as defined in (18) play a central role in this section.

Proposition 6.1

Let \(\mathfrak M\) be an open quantum walk such that \({\mathbb {E}}_{i,\rho }(n_j)<\infty \) for any i, j in V and \(\rho \) in \(\mathcal S({\mathfrak h}_i)\). If we assume that \(A=\sum _{i\in V} A_i\otimes |i\rangle \langle i|\) is such that for any i in V, \(\sum _{j\in V}\Vert {\mathfrak N}_{j,i}^*\big (A_j\big )\Vert <\infty \), then the operator

$$\begin{aligned} Z=A+\sum _{i\in V} \big (\sum _{j\in V}{\mathfrak N}_{j,i}^*(A_j)\big )\otimes |i\rangle \langle i| \end{aligned}$$
(25)

satisfies (24). If in addition \(\mathfrak M\) is irreducible, then any two solutions of (24) differ only by an operator \(\lambda \mathrm {Id}_{\mathcal H}\).

The form of Z can be guessed by analogy with the classical case, so that this result is obtained by direct computation.

We will give analogous results for the Dirichlet problem on a bounded domain. We start by defining precisely the boundary \({\partial \! D}\) of D relative to an open quantum walk \(\mathfrak M\):

$$\begin{aligned} {\partial \! D}&= \{i\in V\setminus D \, |\, \exists j\in D \ \ \hbox {with} \quad L_{i,j}\ne 0\}. \end{aligned}$$

We say that \(Z=\sum _{i\in V} Z_i\otimes |i\rangle \langle i|\) is a solution to the Dirichlet problem on D with data A and boundary condition B if

(26)

A key step in order to solve explicitly this equation will be to prove that the exit time for D, defined as

$$\begin{aligned} t_{{\partial \! D}} = \inf \{n\in \mathbb {N}\, |\, x_n\in {\partial \! D}\}, \end{aligned}$$

is \({\mathbb {P}}_{i,\rho }\)-almost-surely finite for any i in D and \(\rho \) in \(\mathcal S({\mathfrak h}_i)\). Our main results are summarized in the following statement:

Theorem 6.2

Let \(\mathfrak M\) be a semifinite irreducible open quantum walk and let D be a finite subset of V such that \({\partial \! D}\ne \emptyset \). Then for any i in D and any state \(\rho \) on \(\mathfrak h_i\),

$$\begin{aligned} {\mathbb {P}}_{i,\rho }( t_{{\partial \! D}} < +\infty )=1. \end{aligned}$$

In addition, for any \(A=\sum _{i\in D} A_i\otimes |i\rangle \langle i|\) and \(B=\sum _{j\in {\partial \! D}} B_j\otimes |j\rangle \langle j|\), the Dirichlet problem (26) has a solution, and any two solutions of (26) differ by an operator with support in \(\mathcal H_{V\setminus (D\cup {\partial \! D})}\).

The steps in order to prove this, and related results, are described in Subsects. 6.1 and 6.2.

6.1 Exit Times: The Irreducible Case

We now focus on the particular case where the OQW is irreducible. Our first technical result, which plays an analogous role to Proposition 3.3, is the following:

Proposition 6.3

Let \(\mathfrak M\) be an open quantum walk and let D be a finite subset of V such that \({\partial \! D}\ne \emptyset \). Then there exists a family \(({\mathfrak P}^D_{j,i})_{i\in D,j\in D\cup {\partial \! D}}\), where \({\mathfrak P}^D_{j,i}\) is a completely positive linear contraction from \(\mathcal I_1({\mathfrak h}_i)\) to \(\mathcal I_1({\mathfrak h}_j)\), such that each

$$\begin{aligned} {\mathfrak P}^D_{i}=\sum _{j\in {\partial \! D}}{\mathfrak P}^D_{j,i} \end{aligned}$$

is again a completely positive linear contraction from \(\mathcal I_1({\mathfrak h}_i)\) to \(\mathcal I_1({\mathfrak h}_{\partial \! D})\). Moreover, for any i in D, j in \(D\cup {\partial \! D}\) and any \(\rho \) in \(\mathcal S({\mathfrak h}_i)\), one has

$$\begin{aligned} {\mathbb {P}}_{i,\rho }(t_j\le t_{\partial \! D}<\infty )=\mathrm {Tr}\big ({\mathfrak P}^D_{j,i}(\rho )\big ), \qquad {\mathbb {P}}_{i,\rho }(t_{\partial \! D}<\infty )=\mathrm {Tr}\big ({\mathfrak P}^D_{i}(\rho )\big ). \end{aligned}$$

Remark 6.4

Again, a byproduct of our proof will be the expression

$$\begin{aligned} {\mathfrak P}_{j,i}^D(\rho )= \sum _{\pi \in {\mathcal P}^{D\setminus \{j\}}(i,j)} L_\pi \rho L_\pi ^*. \end{aligned}$$
(27)

We also obtain the relations

$$\begin{aligned} {\mathbb {E}}_{i,\rho }(\rho _{t_j}\,|\, {t_j \le t_{\partial \!D}}< \infty )=\frac{{\mathfrak P}^D_{j,i}(\rho )}{\mathrm {Tr}\big ({\mathfrak P}^D_{j,i}(\rho )\big )} \end{aligned}$$
(28)
$$\begin{aligned} {\mathbb {E}}_{i,\rho }(\rho _{t_{\partial \! D}}< \infty )=\frac{{\mathfrak P}^D_{i}(\rho )}{\mathrm {Tr}\big ({\mathfrak P}^D_{i}(\rho )\big )}. \end{aligned}$$
(29)

The first part of Theorem 6.2 is shown in the following proposition. Apart from having its own interest, it will be a key step in solving the Dirichlet problem:

Proposition 6.5

Let \(\mathfrak M\) be an irreducible open quantum walk and let D be a finite subset of V such that \({\partial \! D}\ne \emptyset \). Then, for any i in D such that \(\mathrm {dim}\,{\mathfrak h}_i<\infty \) and any state \(\rho \) on \(\mathfrak h_i\), one has

$$\begin{aligned} {\mathbb {P}}_{i,\rho }( t_{{\partial \! D}} < +\infty )=1. \end{aligned}$$

The main consequence of Proposition 6.5 is the following:

Lemma 6.6

Under the assumptions of Proposition 6.5, for any j in D such that \(\mathrm {dim}\,{\mathfrak h}_j<\infty \), the map \({\mathfrak P}^D_{j,j}\) has norm \(\Vert {\mathfrak P}^D_{j,j}\Vert <1\). For any i in D one can define \({\mathfrak N}^D_{j,i}=(\mathrm {Id}- {\mathfrak P}^D_{j,j})^{-1}\circ {\mathfrak P}^D_{j,i}\). Then, defining

$$\begin{aligned} n_j^D= \mathrm {card}\{n \le t_{\partial \! D}\, |\, x_n=j\}, \end{aligned}$$

one has for any \(\rho \) in \(\mathcal S({\mathfrak h}_i)\) the identity

$$\begin{aligned} {\mathbb {E}}_{i,\rho }(n_j^D)=\mathrm {Tr}\big ({\mathfrak N}^D_{j,i}(\rho )\big ). \end{aligned}$$
(30)

Remark 6.7

Under the assumptions of Lemma 6.6, the operator \({\mathfrak N}^D\) satisfies

$$\begin{aligned} {\mathfrak N}^D_{j,i}(\rho )= \sum _{\pi \in \mathcal P^D(i,j)} L_\pi \rho L_\pi ^*, \end{aligned}$$
(31)

which shows in particular the obvious relation \({\mathfrak N}^D_{j,i}={\mathfrak P}^D_{j,i}\) for \(i\in D\), \(j\in {\partial \! D}\).

6.2 Dirichlet Problems on D: The Irreducible Case

We now turn to the Dirichlet problem on a finite domain D. Recall that \(Z=\sum _{i\in V} Z_i\otimes |i\rangle \langle i|\) is said to be a solution to the Dirichlet problem on D with data A and boundary condition B if it is a solution of Equation (26), which we recall:

The solution to these equations has a very simple form, now that we have introduced the operators \({\mathfrak N}^D_{j,i}\) and \({\mathfrak P}^D_{j,i}\).

Proposition 6.8

Let \(\mathfrak M\) be an irreducible, semifinite open quantum walk and let D be a finite subset of V such that \({\partial \! D}\ne \emptyset \). For any

$$\begin{aligned} A=\sum _{i\in D} A_i\otimes |i\rangle \langle i|\quad \text{ and } \quad B=\sum _{j\in {\partial \! D}} B_j\otimes |j\rangle \langle j|, \end{aligned}$$

the operator

$$\begin{aligned} Z= A+B+\sum _{i\in D}\Big (\sum _{j\in D} {\mathfrak N}^{D\,*}_{j,i}(A_j)+\sum _{j\in {\partial \! D}} {\mathfrak P}^{D\,*}_{j,i}(B_j)\Big )\otimes |i\rangle \langle i| \end{aligned}$$

is well-defined, and is a solution to the Dirichlet problem (26). Any two solutions of (26) differ by an operator with support in \(\mathcal H_{V\setminus (D\cup {\partial \! D})}\).

6.3 Harmonic Measures: The Irreducible Case

Given a finite subdomain D of V, the harmonic measure quantifies the probability for an OQW starting in D to escape from D by a given point of its boundary \({\partial \! D}\). It is intimately related to the Dirichlet problem.

Definition 6.9

Let D be a finite subset of V such that \({\partial \! D}\ne \emptyset \). Let \(\mathfrak M\) be an irreducible and semifinite open quantum walk, conditioned to start at i in D with initial state \(\rho \) in \(\mathcal {S}({\mathfrak h}_i)\). Let j be in \({\partial \! D}\). Recall the definition of the stopping time \(t_{{\partial \! D}}=\mathrm {inf}\{n\in \mathbb {N}\,|\,x_n\in {\partial \! D}\}\). The harmonic measure at j relative to i and \(\rho \) is defined as

$$\begin{aligned} \mu ^D_{i,\rho }(j)= \mathbb {P}_{i,\rho }\left( x_{t_{{\partial \! D}}}=j\right) . \end{aligned}$$

Recall that for an irreducible and semifinite OQW, the escape time \(t_{{\partial \! D}}\) is finite with probability 1. The previous propositions directly imply the following:

Proposition 6.10

The harmonic measure is linear in \(\rho \). More precisely, for \(i\in D\), \(j\in {\partial \! D}\), \(\rho \in \mathcal S({\mathfrak h}_i)\),

$$\begin{aligned} \mu ^D_{i,\rho }(j) = \mathrm {Tr}\big ({\mathfrak P}^D_{j,i}(\rho )\big ), \end{aligned}$$
(32)

with \({\mathfrak P}^D_{j,i}(\rho )=\sum _{\pi \in \mathcal {P}^D(i,j)} L_\pi \rho L^*_\pi \) (consistently with (27)). Moreover,

$$\begin{aligned} \mathbb {E}_{i,\rho }\big (\rho _{t_{{\partial \! D}}}| x_{t_{{\partial \! D}}}=j\big ) = \frac{{\mathfrak P}^D_{j,i}(\rho )}{\mathrm {Tr}\big ( {\mathfrak P}^D_{j,i}(\rho ) \big )}. \end{aligned}$$

Of course by Proposition 6.5, \(\sum _{j\in {\partial \! D}} \mu ^D_{i,\rho }(j) =1\), as we assume the OQW to be irreducible.

Remark 6.11

The connection with the Dirichlet problem is twofold, as usual. First, by linearity in \(\rho \) let us write the harmonic measure as :

$$\begin{aligned} \mu ^D_{i,\rho }(j) = \mathrm {Tr}(\mathfrak {I}^D_{j,i}\, \rho ), \end{aligned}$$

with \(\mathfrak {I}^D_{j,i}= {{\mathfrak P}^D_{j,i}}^*(\mathrm {Id}_{\mathfrak {h}_j})=\sum _{\pi \in \mathcal {P}^D(i,j)} L^*_\pi L_\pi \). Let \(I^D_j\in \mathcal {B}(\mathcal {H})\) be defined by

$$\begin{aligned} I^D_j=\sum _{i \in D} \mathfrak {I}^D_{j,i}\otimes |i\rangle \langle i| + \mathrm {Id}_{\mathfrak {h}_j}\otimes |j\rangle \langle j|. \end{aligned}$$
(33)

Then \(I^D_j\) is quantum harmonic in D (i.e \(\big ((\mathrm {Id}-\mathfrak M^*)(I^D_j)\big )_k=0\) for \(k\in D\)) with boundary condition \(\mathrm {Id}_{\mathfrak {h}_j}\otimes |j\rangle \langle j|\) on \({\partial \! D}\). Furthermore, one has \(\sum _{j\in {\partial \! D}} I^D_j = \mathrm {Id}_{D \cup {\partial \! D}}\), so that \(I^D_j\) may be viewed as a non-commutative quantum analogue of a harmonic measure.

This link with the Dirichlet problem potentially gives an alternative way to evaluate the harmonic measure. Indeed, assuming the harmonic measure to be linear in \(\rho \) (as expected from quantum mechanics), it is then fully determined by solving a Dirichlet problem. Suppose (as we actually proved) that \(\mu ^D_{i,\rho }(j)\) is linear in \(\rho \), and let us write \(\mu ^D_{i,\rho }(j) = \mathrm {Tr}(\mathfrak {I}^D_{j,i}\, \rho )\) (without knowing the explicit expression of \(\mathfrak {I}^D_{j,i}\)). Then conditioning on the first step of the OQW proves that \(I^D_j=\sum _{i \in D} \mathfrak {I}^D_{j,i}\otimes |i\rangle \langle i| + \mathrm {Id}_{\mathfrak {h}_j}\otimes |j\rangle \langle j|\) is quantum harmonic in D with the appropriate boundary conditions. Furthermore, if \(I_j^D\) is quantum harmonic in D with boundary condition \(\mathrm {Id}_{\mathfrak {h}_j}\otimes |j\rangle \langle j|\) then, by Lemma 2.5, \((m_j^D)_n=\mathrm {Tr}((I_j^D)_{x_n}\rho _n)\) stopped at \(n=t_{{\partial \! D}}\) is a \(\mathbb {P}_{i,\rho }\)-martingale. The optional sampling Theorem then yields

$$\begin{aligned} \mathrm {Tr}(\mathfrak {I}^D_{j,i}\rho )= \mathbb {E}_{i,\rho }\big ((m_j^D)_{t_{{\partial \! D}}}\big )= \mathbb {P}_{i,\rho }\big (x_{{\partial \! D}}=j\big ). \end{aligned}$$

7 Results for Reducible Open Quantum Walks

In this section, we collect some properties regarding passage times, number of visits and exit times for reducible open quantum walks. We begin by recalling some results regarding decompositions of reducible open quantum walks from [10].

We fix an open quantum walk \(\mathfrak M\). By [10, Proposition 7.11], there exists an orthogonal decomposition of \({\mathcal H}\)

$$\begin{aligned} {\mathcal H}= \mathcal D \oplus \bigoplus _{\kappa \in K} {\mathcal H}^\kappa \end{aligned}$$
(34)

where we have

$$\begin{aligned} \bigoplus _{\kappa \in K} {\mathcal H}^\kappa = \sup \{\mathrm {supp}\,\rho \, |\, \rho \text{ a } \mathfrak M\text{-invariant } \text{ state }\}. \end{aligned}$$
(35)

We denote the space (35) by \(\mathcal {R}\); we also let \(\mathcal D = \mathcal R^\perp \). The restriction \(\mathfrak M^\kappa \) of \(\mathfrak M\) to \(\mathcal I_1({\mathcal H}^{\kappa })\) is an irreducible OQW, and \(\mathcal {D}=\{0\}\) if and only if \(\mathfrak M\) has a faithful invariant state. In addition, each \({\mathcal H}^\kappa \) is an enclosure, i.e. has a decomposition

$$\begin{aligned} {\mathcal H}^\kappa = \bigoplus _{i\in V} \mathfrak h^\kappa _i \end{aligned}$$

where every \(\mathfrak h^\kappa _i\) is a subspace of \(\mathfrak h_i\), and for any i, j in V one has \( L_{i,j}\,\mathfrak h^\kappa _j \subset \mathfrak h^\kappa _i\). The decomposition (34) is non-unique, as is discussed in [10, Sects. 6 and 7]; we fix, however, one such decomposition, and denote by \(\mathfrak M^\kappa \) the open quantum walk induced by \(\mathfrak M\) on \(\mathcal I_1({\mathcal H}^\kappa )\). We define for every \(\kappa \) in K the set \(V^\kappa = \big \{i\in V\, |\, \mathfrak h^\kappa _i \ne \{0\} \big \}.\)

For any i in V, \(\mathfrak h_i\) has a decomposition \(\mathfrak h^{\mathcal D}\oplus \bigoplus _{\kappa \in K} \mathfrak h^\kappa _i\). Then, any state \(\rho _i\) on \(\mathfrak h_i\) can be written in block matrix form \(\rho =(\rho _i^{\kappa ,\kappa '})_{\kappa ,\kappa '\in K\cup \{0\}}\), where the index 0 corresponds to \(\mathcal D\). We denote by \(\rho _i^{\kappa }\) the diagonal blocks: \(\rho _i^{\kappa } = \rho _i^{\kappa ,\kappa }\). The main tool in this section is a simple observation: for any path \(\pi \in {\mathcal P}_\ell (i,j)\) starting at i, the probability of observing, as \(\ell \) first steps, the trajectory \(\pi =(i_0,\ldots ,i_\ell )\) with initial conditions \((i,\rho )\) satisfies

$$\begin{aligned} \mathbb P_{i,\rho }(i_0,\ldots ,i_\ell ) \ge \sum _{\kappa \in K} \mathrm {Tr}\big ((L_\pi \rho L_\pi ^*)^{\kappa }\big ) \ge \sum _{\kappa \in K} \mathrm {Tr}(L_\pi \rho ^{\kappa } L_\pi ^*). \end{aligned}$$
(36)

In addition, if \(\rho \) has support in \(\mathcal R\), then inequalities in (36) become an equality. If we denote by e.g. \({\mathfrak P}_{j,i}^{\kappa }\) the operator \({\mathfrak P}_{j,i}\) associated with the OQW \(\mathfrak M^*\), etc. then we have the following result:

Proposition 7.1

Assume that the open quantum walk \(\mathfrak M\) admits a decomposition (34). Then, for any \(\rho \) in \(\mathcal S({\mathcal H})\),

$$\begin{aligned} {\mathbb {P}}_{i,\rho }(t_j<\infty )&\ge \sum _{\kappa \in K} \mathrm {Tr}\,\rho ^{\kappa }\times \mathrm {Tr}\Big ( {\mathfrak P}_{j,i}^{\kappa }\big (\frac{\rho ^{\kappa }}{\mathrm {Tr}\,\rho ^{\kappa }}\big )\Big ) \, \mathbbm {1}_{i,j \in V^{\kappa }},\\ {\mathbb {E}}_{i,\rho }(n_j)&\ge \sum _{\kappa \in K} \mathrm {Tr}\,\rho ^{\kappa }\times \mathrm {Tr}\Big ( {\mathfrak N}_{j,i}^{\kappa }\big (\frac{\rho ^{\kappa }}{\mathrm {Tr}\,\rho ^{\kappa }}\big )\Big ) \, \mathbbm {1}_{i,j \in V^{\kappa }},\\ {\mathbb {E}}_{i,\rho }(t_j)&\ge \sum _{\kappa \in K} \mathrm {Tr}\,\rho ^{\kappa }\times \mathrm {Tr}\Big ( {\mathfrak T}_{j,i}^{\kappa }\big (\frac{\rho ^{\kappa }}{\mathrm {Tr}\,\rho ^{\kappa }}\big )\Big ) \, \mathbbm {1}_{i,j \in V^{\kappa }},\\ {\mathbb {P}}_{i,\rho }(t_{\partial \! D})&\ge \sum _{\kappa \in K} \mathrm {Tr}\,\rho ^{\kappa }\times \mathrm {Tr}\Big ( {\mathfrak P}^{D{\kappa }}_{j,i}\big (\frac{\rho ^{\kappa }}{\mathrm {Tr}\,\rho ^{\kappa }}\big ) \Big )\, \mathbbm {1}_{i \in V^{\kappa }, \,{\partial \! D}\cap V^{\kappa }\ne \emptyset }. \end{aligned}$$

(where as before we assume that D is a finite domain such that \({\partial \! D}\ne \emptyset \)), and each of these inequalities becomes an equality if we assume that \(\rho \) has support in \(\mathcal R\).

If the support of \(\rho \) is contained in \(\mathcal R\) (in particular if \(\mathcal D=\{0\}\)) then since \(\sum _{\kappa \in K} \mathrm {Tr}\,\rho ^{\kappa }=1\), it is easy to characterize e.g. the equality \({\mathbb {P}}_{i,\rho }(t_j<\infty )=1\), or the finiteness of \({\mathbb {E}}_{i,\rho }(n_j)\), in terms of the sub-open quantum walks \(\mathfrak M^{\kappa }\) (to which our various results for irreducible open quantum walks apply).

8 Variational Approach to the Dirichlet Problem

We assume throughout this section that \({\tau ^{\mathrm {inv}}}=\sum _{i\in V}{{\tau ^{\mathrm {inv}}}(i)\otimes |i\rangle \langle i|}\) is an invariant state for the OQW \(\mathfrak M\), which furthermore is faithful. In all of this section we write \(\tau _\diamond \) instead of \({\tau ^{\mathrm {inv}}}\), i.e. we let

$$\begin{aligned} \tau _\diamond ={\tau ^{\mathrm {inv}}}. \end{aligned}$$

Our goal in this section is to characterize the solutions of the Dirichlet problem given by Equation (26) as minimizers of a certain functional, involving the Dirichlet form associated to the OQW. The present Dirichlet forms are simple, discrete-time versions of the non-commutative extensions of classical Dirichlet forms (such extensions were studied first by Davies and Lindsay in [15], see also [12, 13, 16]).

We first focus on the definition of the Dirichlet form and its properties. Define on \({\mathcal B}({\mathcal H})\) the scalar product

$$\begin{aligned} \langle X ,Y\rangle _{\diamond } =\mathrm {Tr}\big (\tau _\diamond ^{1/2}X^*\tau _\diamond ^{1/2}Y\big ). \end{aligned}$$
(37)

Definition 8.1

The Dirichlet form associated to the open quantum walk \(\mathfrak M\) is the quadratic form

$$\begin{aligned} {\mathcal E}(X,Y) = \langle X ,\left( I-\mathfrak M^*\right) (Y)\rangle _{\diamond } \end{aligned}$$
(38)

We also denote \( {\mathcal E}(X)= {\mathcal E}(X,X)\), for \(X\in {\mathcal B}(\mathcal {H})\).

The central hypothesis in the following is the detailed balance condition.

Definition 8.2

We say that the open quantum walk \(\mathfrak M\) satisfies the detailed balance condition with respect to \(\tau _\diamond \) if \(\mathfrak M^*\) is selfadjoint with respect to the scalar product \(\langle {\,\cdot \,},{\,\cdot \,}\rangle _\diamond \).

Note that we reserve the notation \(\mathfrak M^*\) for the adjoint of \(\mathfrak M\) with respect to the duality between \(\mathcal I^1(\mathcal H)\) and \(\mathcal B(\mathcal H)\). The detailed balance condition is satisfied, in particular, if

$$\begin{aligned} \tau _\diamond (i)^{1/2} L_{j,i}^*= L_{i,j}\,\tau _\diamond (j)^{1/2} \ \text{ for } \text{ all } i,j\in V. \end{aligned}$$

It has two immediate consequences:

Lemma 8.3

If the open quantum walk \(\mathfrak M\) satisfies the detailed balance condition, then \(\mathcal {E}(X)\ge 0\) for any \(X\in \mathcal B(\mathcal H)\). If in addition \(\mathfrak M\) is irreducible, then \(\mathcal {E}(X)=0\) if and only if \(X\in \mathbb {C}\mathrm {Id}_{\mathcal H}\).

8.1 Dirichlet Problem on the Whole Domain

Quantum harmonic operators are easily characterized as minimizers of the Dirichlet form. Indeed, the detailed balance condition implies that \({\mathcal E}(X)\ge 0\), with equality if and only if \((I-\mathfrak M^*)(X)=0\), that is, if X is harmonic.

Proposition 8.4

Suppose that \(\mathfrak M\) satisfies the detailed balance condition. Then X is a quantum harmonic observable if and only if \({\mathcal E}(X)\) is minimal, if and only if \({\mathcal E}(X)=0\).

8.2 Dirichlet Problem on a Sub-domain

We now focus on the Dirichlet problem on a finite domain \(D\subset V\), that we suppose to be non-empty. Recall the definition of the inner data A and the outer data B as

$$\begin{aligned} A= \sum _{i\in D} A_i\otimes |i\rangle \langle i| \qquad B=\sum _{j\in {\partial \! D}} B_j\otimes |j\rangle \langle j|, \end{aligned}$$

where \(A_j,B_j\in \mathcal B({\mathfrak h}_j)\) for all j.

Our theorem is the following. An analogue of this result can be found in [12] for more general non-commutative Dirichlet forms.

Theorem 8.5

Let \(\mathfrak M\) be an irreducible open quantum walk with detailed balance condition and D a finite domain of V such that \({\partial \! D}\ne \emptyset \). Then any solution of the Dirichlet problem

is of the form \(X_0+B+ Y\), where Y has support in \(\mathcal H_{V\setminus (D\cup {\partial \! D})}\) and \(X_0\) is the unique minimizer over the set \(\mathcal {B}\left( \mathcal {H}_D\right) \) of the functional

$$\begin{aligned} E(X)=\frac{1}{2}\,{\mathcal E}(X)+\mathcal {E}(X,B)-\langle A ,X\rangle _\diamond . \end{aligned}$$
(39)

8.3 The Case of Doubly Stochastic Open Quantum Walks

In this last section we point out that the Dirichlet form can alternatively be written in terms of first order discrete derivatives (to be defined below) in the special case of doubly stochastic OQW, i.e. for open quantum walks that satisfy \(\mathfrak {M}^*=\mathfrak {M}\).

Proposition 8.6

Let \(\mathfrak {M}\) be a doubly stochastic open quantum walk satisfying \(\mathfrak {M}^*=\mathfrak {M}\). Then \(\mathcal {E}(X)\) equals

$$\begin{aligned} \frac{1}{2} \sum _{i,j\in V} \mathrm {Tr}\big ((\nabla X)_{i,j}(\nabla X)_{i,j}^*\big )=: \frac{1}{2} \Vert (\nabla X)\Vert _V^2 \end{aligned}$$
(40)

where \((\nabla X)_{i,j}= X_iL_{i,j}-L_{i,j}X_j\) for \(X=\sum _{j\in V} X_j\otimes |j\rangle \langle j| \in \mathcal {B}(\mathcal {H})\).

Positivity of the Dirichlet form is then manifest in (40). Notice that the passage from the definition of the Dirichlet form in (38) to the formula (40) amounts to an integration by part. This presentation of the Dirichlet form in terms of first order difference operators can easily be extended to finite sub-domains if one includes appropriate boundary terms arising from the discrete integration by part.