Abstract
We study a class of finite dimensional quantum dynamical semigroups \(\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq0}\) whose generators \(\mathcal{L}\) are sums of Lindbladians satisfying the detailed balance condition. Such semigroups arise in the weak coupling (van Hove) limit of Hamiltonian dynamical systems describing open quantum systems out of equilibrium. We prove a general entropic fluctuation theorem for this class of semigroups by relating the cumulant generating function of entropy transport to the spectrum of a family of deformations of the generator \({\mathcal{L}}\). We show that, besides the celebrated Evans-Searles symmetry, this cumulant generating function also satisfies the translation symmetry recently discovered by Andrieux et al., and that in the linear regime near equilibrium these two symmetries yield Kubo’s and Onsager’s linear response relations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Markov semigroups are widely used to model non-equilibrium phenomena in classical statistical physics. Their non-commutative counterparts—quantum dynamical semigroups—play the same role in quantum statistical physics (see, e.g., [4, 55] for pedagogical introductions to the subject). The development of the mathematical theory of QDS started in 1974 with the seminal works of Brian Davies [10–12] where he showed that QDS emerge as effective dynamics of open systems weakly coupled to extended reservoirs. These groundbreaking works were followed by the celebrated 1976 papers of Lindblad [46, 47] and Gorini, Kossakowski and Sudarshan [35] on the structure of the generator of QDS (see also [7]). Herbert made several fundamental contributions at this early stage of development. In [58, 59] he gave efficient criteria for the existence and uniqueness of a stationary state and approach to equilibrium. Together with Joel Lebowitz, in [48] he developed a comprehensive picture of the nonequilibrium thermodynamics of weakly coupled open systems. This work remains a standard reference and has been a source of inspiration for many later developments on the subject, including the present one. Among other things, in [48] Herbert and Joel introduced the central concept of entropy production, which was further discussed in [60], and developed the linear response theory for thermodynamical forces. The closely related linear response theory for weakly coupled open systems under mechanical drive was developed by Herbert in a joint paper with Brian Davies [23]. In another enlightening work, Herbert and R. Dümcke [24] showed that some of the generators that were (and sometimes still are) used to describe the weak coupling limit lead to negative probabilities. Years later, Herbert came back to the subject and, with Walter Aschbacher, showed that when properly applied to nonequilibrium situations, the algebraic criterion of [59] also ensures the strict positivity of entropy production [5].
In 1993/4, using a new scheme to construct nonequilibrium statistical ensembles of interacting particle systems, Evans, Cohen and Morriss discovered some universal features of the fluctuations of entropy production in transient regimes of deterministic classical systems out of thermal equilibrium [26, 30]. One year later, Gallavotti and Cohen proved that some steady states of highly chaotic dynamical systems (SRB measures of transitive Anosov systems) display the same features [33, 34]. These discoveries, nowadays called fluctuation relations or fluctuation theorems, triggered a large amount of works during the last two decades (see [40, 56] and references therein). In particular, Kurchan showed that the fluctuation relations hold for a Brownian particle in a force field [43]. Subsequently, Herbert and Joel formulated and proved fluctuation relations for general Markov processes [49] while Maes derived a local version of the fluctuation relations from the Gibbsian nature of the path space measure associated to such processes [50] (see also [52]). As shown by Gallavotti [32], the fluctuation relations can be seen as a far from equilibrium generalization of the familiar near equilibrium fluctuation-dissipation relations (Green-Kubo formulae, Onsager reciprocity relations).
The attempts to extend fluctuation relations to quantum domain have led to a number of surprises. The naive quantization of the classical transient fluctuation relations fails and there is no obvious way to implement the steady state fluctuation relations. These problems have attracted a lot of interest and generated a huge literature which we will not try to review here. We shall only mention a few works which, in our opinion, are relevant to the development of a mathematical understanding of the subject. The interested reader can consult [27] for an exhaustive review and an extended list of references to the physics literature and [36, 39] for recent mathematical developments.
To our knowledge, a (transient) quantum fluctuation relation based on operationally defined counting statistics was first derived by Kurchan in 2000 [44]. Shortly afterwards, Matsui and Tasaki obtained an apparently unrelated abstract fluctuation relation for open quantum systems in terms of the spectral measure of a relative modular operator [53]. The connection between their result and the counting statistics of entropic transport was established in [36].
Within the framework of QDS, de Roeck and Maes [22] used the unraveling technique to obtain the first complete transient fluctuation theorem (see Sect. 6). The relation between this Markovian approach to fluctuations and the Hamiltonian description of the dynamics of a small system weakly coupled to an extended environment was discussed by de Roeck in [18] and by Dereziński, de Roeck and Maes [14] (see also Sect. 5). The works [14, 18, 22] complete the program of [48] regarding nonequilibrium thermodynamics of weakly coupled open systems. The first proof of the transient fluctuation theorem for a fully Hamiltonian system (the spin-boson model) was given by de Roeck in the important paper [19] (see also [20, 21, 41]).
Among the non-rigorous works let us mention the important observation of Andrieux, Gaspard, Monnai and Tasaki [2] that global conservation laws (energy and charge) induce translation symmetries in the cumulant generating function of (energy and charge) fluxes. Translation symmetries and entropic fluctuation relation lead to fluctuation relations for individual fluxes and, following the arguments of [32, 49], to Green-Kubo and Onsager relations near thermal equilibrium. We also mention the recent work by Chetrite and Mallik [8] where finite time fluctuation relations (similar to the classical transient Evans-Searles relations) for time-reversible quantum dynamical semigroups are derived.
This work is of a review nature and we do not prove any specific new results. The purpose of the paper is to provide an abstract general setup for the non-equilibrium statistical mechanics of QDS and to generalize and streamline the proof of the full fluctuation theorem of [14, 18, 22] emphasizing (in the spirit of [60]) the minimal mathematical structure behind the result. The fluctuation theorem we discuss includes large deviation bounds and the central limit theorem for individual entropic fluxes, as well as linear response formulae and the fluctuation-dissipation relations near equilibrium, and applies to the weakly coupled quantum systems studied in [48]. Although the paper is mathematically self-contained, it is intended for readers familiar with the works [48, 58–60]. This paper can be also viewed as an introduction to [41] where we discuss fluctuation relations and non-equilibrium statistical mechanics of the fully Hamiltonian Pauli-Fierz systems.
The paper is organized as follows. In Sect. 2 we recall basic definitions and facts about positive maps and QDS. In Sect. 3 we introduce the setup of QDS out of equilibrium, and state our main results. In Sect. 4 we show that open systems weakly coupled to thermal reservoirs fit into our general setup. In Sects. 5 and 6 we relate our results to the full counting statistics of entropic transport and the unraveling of quantum dynamical semigroups. Finally, Sect. 7 is devoted to the proofs.
2 Preliminaries
Let \(\mathcal{H}\) be a finite dimensional Hilbert space and \(\mathcal{O}=\mathcal{B}(\mathcal{H})\) the C
∗-algebra of all linear operators on \(\mathcal{H}\) (the identity operator will be always denoted by  ). Equipped with the inner product 〈X|Y〉=tr(X
∗
Y), \(\mathcal{O}\) is a Hilbert space. The adjoint and the spectrum of a linear map \(\varPhi:\mathcal{O}\rightarrow \mathcal{O}\) are denoted by Φ
∗ and sp(Φ). Id denotes the identity of \(\mathcal{B}(\mathcal{O})\). A subset \(\mathcal{A}\subset\mathcal{O}\) is called self-adjoint if \(X\in\mathcal{A} \Rightarrow X^{\ast}\in\mathcal{A}\). The commutant of a subset \(\mathcal{A}\subset \mathcal{O}\) is \(\mathcal{A}^{\prime}=\{B\in \mathcal{O}\,|\,AB=BA\ \mathrm{for\ all}\ A\in\mathcal{A}\}\).
). Equipped with the inner product 〈X|Y〉=tr(X
∗
Y), \(\mathcal{O}\) is a Hilbert space. The adjoint and the spectrum of a linear map \(\varPhi:\mathcal{O}\rightarrow \mathcal{O}\) are denoted by Φ
∗ and sp(Φ). Id denotes the identity of \(\mathcal{B}(\mathcal{O})\). A subset \(\mathcal{A}\subset\mathcal{O}\) is called self-adjoint if \(X\in\mathcal{A} \Rightarrow X^{\ast}\in\mathcal{A}\). The commutant of a subset \(\mathcal{A}\subset \mathcal{O}\) is \(\mathcal{A}^{\prime}=\{B\in \mathcal{O}\,|\,AB=BA\ \mathrm{for\ all}\ A\in\mathcal{A}\}\).
We denote by \(\mathcal{O}_{+}=\{X\,|\, X\geq0\}\) the cone of positive elements of \(\mathcal{O}\). A linear map Φ from \(\mathcal{O}\) to another unital C
∗-algebra \(\mathcal{B}\) is called unital if  , positive if \(\varPhi(\mathcal{O}_{+})\subset \mathcal{B}_{+}\), and positivity improving if Φ(X)>0 for all non-zero \(X\in \mathcal{O}_{+}\). A positive linear map is automatically a ∗-map, i.e., it satisfies Φ(X
∗)=Φ(X)∗. A positive linear map \(\varPhi: \mathcal{O}\rightarrow \mathcal{O}\) is called Schwartz if
, positive if \(\varPhi(\mathcal{O}_{+})\subset \mathcal{B}_{+}\), and positivity improving if Φ(X)>0 for all non-zero \(X\in \mathcal{O}_{+}\). A positive linear map is automatically a ∗-map, i.e., it satisfies Φ(X
∗)=Φ(X)∗. A positive linear map \(\varPhi: \mathcal{O}\rightarrow \mathcal{O}\) is called Schwartz if
for all \(X\in \mathcal{O}\). Note that if Φ is Schwartz, then  .
.
A state on \(\mathcal{O}\) is a positive and unital linear map \(\rho: \mathcal{O}\rightarrow {\mathbb{C}}\). Any state ρ has the form ρ(X)=tr(DX) for some \(D\in \mathcal{O}_{+}\) satisfying tr(D)=1. Such an operator D is called a density matrix. In the following, we shall use the same symbol to denote a density matrix and the state it induces on \(\mathcal{O}\) (hence, ρ(X)=tr(ρX), etc.). With this convention, the set of states on \(\mathcal{O}\), which we denote by \({\mathfrak{S}}\), is a closed convex subset of \(\mathcal{O}_{+}\). A state ρ is called faithful if ρ>0, and we denote by \({\mathfrak{S}}_{\mathrm{f}}\) the set of faithful states. \({\mathfrak{S}}_{\mathrm{f}}\) is an open convex and dense subset of \({\mathfrak{S}}\).
A linear map \(\varPhi: \mathcal{O}\rightarrow \mathcal{O}\) is called completely positive (CP) if \(\sum_{i, j}B_{i}^{\ast}\varPhi(A_{i}^{\ast}A_{j})B_{j}\geq0\) for any finite families \(\{A_{1}, \ldots, A_{N}\}, \{B_{1}, \ldots, B_{N}\} \subset \mathcal{O}\). Equivalently, Φ is CP if Φ⊗Id is a positive map on \(\mathcal{O}\otimes \mathcal{B}({\mathbb{C}}^{N})\) for all N≥1. A CP map is automatically Schwartz. We denote by \(\mathrm{CP}(\mathcal{O})\) the monoid of completely positive maps, and by \(\mathrm{CP}_{1}(\mathcal{O})\) the sub-monoid of unital maps. \(\mathrm{CP}(\mathcal{O})\) is a convex cone and \(\mathrm{CP}_{1}(\mathcal{O})\) is a convex set. Stinespring’s theorem [61] asserts that \(\varPhi\in \mathrm{CP}(\mathcal{O})\) iff there exists a finite family {V j } j∈J in \(\mathcal{O}\) such that
for all \(X\in \mathcal{O}\). The formula (1) is called a Kraus representation of Φ. Such representation is in general not unique.
Unital CP maps naturally arise in the quantum mechanics of open systems. Indeed, assume that the quantum system \(\mathcal{S}\) with Hilbert space \(\mathcal{H}\) interacts with some environment described by the Hilbert space \(\mathcal{H}_{\mathrm{env}}\). According to the general structure of quantum mechanics, the evolution of the joint system over some time interval is given by a unitary U on \(\mathcal{H}\otimes \mathcal{H}_{\mathrm{env}}\). Thus, if X is an observable of the system \(\mathcal{S}\), then its Heisenberg evolution over the considered time interval is given by the map

where \(\mathrm{tr}_{\mathcal{H}_{\mathrm{env}}}(\,\cdot\,)\) denotes the partial trace over the environment Hilbert space and ρ env is the initial state of the environment. One easily checks that Φ is a unital CP map such that, for any state ρ of \(\mathcal{S}\),

A positive linear map Φ is called irreducible (in the sense of Davies [9]) if the inequality Φ(P)≤λP, where P is a projection and λ>0, holds only for P=0 or  . If Φ is positivity improving, then obviously Φ is irreducible. In terms of a Kraus decomposition, irreducibility can be characterized as follows (see, e.g., [57]):
. If Φ is positivity improving, then obviously Φ is irreducible. In terms of a Kraus decomposition, irreducibility can be characterized as follows (see, e.g., [57]):
Theorem 2.1
Let
Φ
be a
\(\mathrm{CP}(\mathcal{O})\)
map with a Kraus decomposition (1) and let
\(\mathcal{A}\)
be the subalgebra of
\(\mathcal{O}\)
generated by {V
j
| j∈J} and
 . Then
Φ
is irreducible iff
\(\mathcal{A}\psi=\mathcal{H}\)
for any non-zero vector
\(\psi\in \mathcal{H}\).
. Then
Φ
is irreducible iff
\(\mathcal{A}\psi=\mathcal{H}\)
for any non-zero vector
\(\psi\in \mathcal{H}\).
For reader’s convenience, we shall prove Theorem 2.1 in Sect. 7.2.
The adjoint Φ ∗ of a linear map Φ is positive/positivity improving/CP/irreducible iff Φ is. Φ ∗ is trace preserving, i.e., tr(Φ ∗(X))=tr(X) for all \(X\in \mathcal{O}\), iff Φ is unital. In particular, Φ ∗ maps \({\mathfrak{S}}\) into itself iff Φ is positive and unital. A state \(\rho\in{\mathfrak{S}}\) is called Φ-invariant if Φ ∗(ρ)=ρ, which is equivalent to ρ(Φ(X))=ρ(X) for all \(X\in \mathcal{O}\).
Let \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) be a continuous semigroup of linear maps on \(\mathcal{O}\) generated by a linear map \(\mathcal{L}\). This semigroup is called unital/positive/positivity improving/\(\mathrm{CP}(\mathcal{O})\)/\(\mathrm{CP}_{1}(\mathcal{O})\) iff \(\mathrm {e}^{t \mathcal{L}}\) is for all t>0. A \(\mathrm{CP}_{1}(\mathcal{O})\) semigroup is called quantum dynamical semigroup (QDS).Footnote 1
Let \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) be a positive unital semigroup. A state ρ is called steady (or stationary) if \(\rho(\mathrm {e}^{t\mathcal{L}}(X))=\rho(X)\) for all t≥0 and \(X\in \mathcal{O}\). Clearly, ρ is steady iff \(\mathcal{L}^{\ast}(\rho)=0\).
A positive unital semigroup \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) is said to be relaxing to a steady state ρ + if
for all \(\rho\in{\mathfrak{S}}\). The relaxation is exponentially fast if there exists γ>0 such that for all states ρ,
as t→∞. The relaxation to a steady state is an ergodic property that plays a fundamental role in the statistical mechanics of QDS.
Our study of the large deviation theory of QDS will be based on the following result.
Theorem 2.2
Let \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) be a positivity improving \(\mathrm{CP}(\mathcal{O})\) semigroup and
Then ℓ is a simple eigenvalue of \(\mathcal{L}\) and is the only eigenvalue of \(\mathcal{L}\) on the line Re z=ℓ. For any state ρ on \(\mathcal{O}\), one has
for all non-zero \(X\in \mathcal{O}_{+}\). If in addition the semigroup \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) is unital, then ℓ=0 and the semigroup is relaxing exponentially fast to a faithful steady state ρ +.
The proof of this theorem is based on the Perron-Frobenius theory of positive maps developed in [28] and is given in Sect. 7.2.
It is a fundamental result of Lindblad [46, 47], Gorini, Kossakowski and Sudarshan [35], and Christensen and Evans [7], that \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) is a \(\mathrm{CP}(\mathcal{O})\) semigroup iff there are \(K\in \mathcal{O}\) and \(\varPhi\in \mathrm{CP}(\mathcal{O})\) such that
for all \(X\in \mathcal{O}\). For short, we shall call the generator of a \(\mathrm{CP}(\mathcal{O})\) semigroup a Lindbladian, and the r.h.s. of Eq. (4) a Lindblad decomposition of \(\mathcal{L}\). Although the Lindblad decomposition is not unique, it can be effectively used to characterize some important properties of the semigroup. In particular, we have:
Theorem 2.3
Let \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) be a \(\mathrm{CP}(\mathcal{O})\) semigroup and \(\mathcal{L}(X)= K^{\ast}X + XK +\varPhi(X)\) a Lindblad decomposition. If Φ is irreducible, then the semigroup is positivity improving.
We shall prove this theorem in Sect. 7.2. Theorems 2.1 and 2.3 provide an effective criterion for verifying the positivity improving assumption of Theorem 2.2 (see Sect. 4).
If \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) is a QDS, then  , and it follows from (4) that
, and it follows from (4) that

where T is a self-adjoint element of \(\mathcal{O}\) and \(\varPhi\in \mathrm{CP}(\mathcal{O})\). We shall also refer to the r.h.s. of Eq. (5) as a Lindblad decomposition of \(\mathcal{L}\).
The dissipation function of a QDS \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) is the sesquilinear map \(D: \mathcal{O}\times \mathcal{O}\rightarrow \mathcal{O}\) defined by
If (5) is the Lindblad decomposition of \(\mathcal{L}\) and (1) a Kraus decomposition of Φ, then
Hence, D(X,X)≥0 and D(X,X)=0 iff X∈{V j | j∈J}′. The dissipation function of a QDS was introduced by Lindblad in [46] and has played an important role in many subsequent works on the subject.
The detailed balance condition and time-reversal invariance will play an important role in our work. Both properties refer to a pair \((\rho, \mathcal{L})\), where ρ is a faithful state and \(\mathcal{L}\) is the generator of a QDS. Note that any faithful state induces an inner product 〈X|Y〉 ρ =〈Xρ 1/2|Yρ 1/2〉=tr(ρX ∗ Y) on \(\mathcal{O}\). We call the ρ-adjoint of a linear map Φ its adjoint Φ ρ w.r.t. this inner product. In particular, we say that a linear map Φ is ρ-self-adjoint if Φ ρ=Φ.
Definition 2.4
Consider a pair \((\rho, \mathcal{L})\), where ρ is a faithful state and \(\mathcal{L}\) is a Lindbladian generating a QDS.
-
(a)
The pair \((\rho, \mathcal{L})\) is said satisfy the detailed balance condition if \(\mathcal{L}^{\ast}(\rho)=0\) and there exists Lindblad decomposition
 such that Φ is ρ-self-adjoint.
such that Φ is ρ-self-adjoint. -
(b)
The pair \((\rho, \mathcal{L})\) is said to be time-reversal invariant (TRI) if there exists an involutive anti-linear ∗-automorphism \(\varTheta: \mathcal{O}\rightarrow \mathcal{O}\), called the time-reversal, such that \(\mathcal{L}^{\rho}\circ\varTheta=\varTheta\circ \mathcal{L}\) and Θ(ρ)=ρ.
Definition 2.4(a) is equivalent to the definition of detailed balance given by Kossakowski, Frigerio, Gorini, and Verri [42] (see Theorem 7.2 below). The above definition, however, is technically and conceptually more suitable for our purposes.Footnote 2 The detailed balance condition is characteristic of QDS describing the interaction of a system \(\mathcal{S}\) with an environment at equilibrium (see [42, 48]).
For the motivation regarding the definition of time-reversal we refer the reader to Sect. 4 and [31, 51]. We recall that \(\varTheta: \mathcal{O}\rightarrow \mathcal{O}\) is an involutive anti-linear ∗-automorphism iff there exists an anti-unitary involution \(\theta: \mathcal{H}\rightarrow \mathcal{H}\) such that Θ(X)=θXθ (see Exercise 4.36 in [36]), and that Θ(ρ)=ρ iff ρ(Θ(X))=ρ(X ∗) for all \(X\in \mathcal{O}\).
3 Quantum Dynamical Semigroups Out of Equilibrium
3.1 The Setup
We shall study QDS \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) on \(\mathcal{O}=\mathcal{B}(\mathcal{H})\), \(\dim \mathcal{H}<\infty\), satisfying the following ergodicity condition
(ER) The QDS \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) is positivity improving.
Furthermore, we shall focus on semigroups whose generator \(\mathcal{L}\) has the special structure given by
(DB) There are M pairs \((\rho_{j}, \mathcal{L}_{j})\) satisfying the detailed balance condition such that
$$\mathcal{L}=\sum_{j=1}^M \mathcal{L}_j. $$
We shall interpret each of the M sub-Lindbladians \(\mathcal{L}_{j}\) as describing the interaction of a quantum system \(\mathcal{S}\) with some reservoir \(\mathcal{R}_{j}\). A QDS is out of equilibrium if Hypothesis (DB) holds and \(\rho_{j}\not =\rho_{k}\) for some pair j,k (such a QDS describes the interaction of the system \(\mathcal{S}\) with an environment \(\sum_{j} \mathcal{R}_{j}\) out of equilibrium).
A QDS satisfying (DB) is called time-reversible if
(TR) All the pairs \((\rho_{j}, \mathcal{L}_{j})\) are time-reversal invariant with the same time-reversal map Θ.
Finally, we shall investigate more closely the special case where the states ρ j are thermal equilibrium states at inverse temperature β j >0 for the same Hamiltonian.
(KMS β ) \(\beta=(\beta_{1},\ldots,\beta_{M})\in {\mathbb{R}}_{+}^{M}\) and there exists a self-adjoint element \(H_{\mathcal{S}}\in \mathcal{O}\) such that
$$\rho_j=\frac{\mathrm {e}^{-\beta_jH_\mathcal{S}}}{\mathrm{tr}(\mathrm {e}^{-\beta_jH_\mathcal{S}})}, $$for j=1,…,M.
As we shall see in Sect. 4, Hypotheses (ER), (DB) and (KMS β ) are naturally satisfied by the QDS describing the weak coupling (van Hove) limit dynamics of an open quantum system \(\mathcal{S}\) with Hilbert space \(\mathcal{H}\) interacting with an environment made of M thermal reservoirs. In this case, the Lindbladian \(\mathcal{L}_{j}\) pertains to the interaction of \(\mathcal{S}\) with the jth reservoir and the state ρ j is a steady state of the system coupled only to this reservoir. If the joint dynamics of the system and reservoirs is time-reversal invariant, then Hypothesis (TR) is also satisfied.
3.2 Main Result
Suppose that a QDS \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) satisfies Hypothesis (DB). Our main technical result concerns the properties of the deformations of this QDS generated by
where \(\alpha=(\alpha_{1},\ldots,\alpha_{M})\in {\mathbb{R}}^{M}\). We will use the notation 1=(1,…,1) wherever the meaning is clear within the context, e.g., 1−α=(1−α 1,…,1−α M ). Let
Theorem 3.1
Suppose that Hypothesis (DB) holds. Then:
-
(1)
\(\{\mathrm {e}^{t\mathcal{L}_{(\alpha)}}\}_{t\geq0}\) is a \(\mathrm{CP}(\mathcal{O})\) semigroup for all \(\alpha\in {\mathbb{R}}^{M}\).
-
(2)
For any state ρ on \(\mathcal{O}\), there is a Borel probability measure \(P_{\rho}^{t}\) on \({\mathbb{R}}^{M}\) such that

We denote by 〈 ⋅ 〉 ρ,t the expectation w.r.t. this measure.
In the remaining statements we assume that Hypothesis (ER) is satisfied.
-
(3)
For all \(\alpha\in {\mathbb{R}}^{M}\) the \(\mathrm{CP}(\mathcal{O})\) semigroup \(\{\mathrm {e}^{t\mathcal{L}_{(\alpha)}}\}_{t\geq0}\) is positivity improving. In particular, the QDS \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) is relaxing exponentially fast to a steady state ρ +.
-
(4)
For all \(\alpha\in {\mathbb{R}}^{M}\), e(α) is a simple eigenvalue of \(\mathcal{L}_{(\alpha)}\) and this operator has no other eigenvalues on the line Re z=e(α). Moreover, for any state ρ and all \(\alpha\in {\mathbb{R}}^{M}\),
$$ \lim_{t\to\infty}\frac{1}{t}\log \bigl \langle \mathrm {e}^{-t\alpha\cdot\varsigma}\bigr \rangle _{\rho,t}=e(\alpha). $$(7) -
(5)
The function \({\mathbb{R}}^{M}\ni\alpha\mapsto e(\alpha)\) is real analytic and convex.
-
(6)
Relation (7) holds for α in an open neighborhood of \({\mathbb{R}}^{M}\) in \({\mathbb{C}}^{M}\).
-
(7)
If Hypothesis (TR) is satisfied, then
$$ e(1-\alpha)=e(\alpha), $$(8)for all \(\alpha\in {\mathbb{R}}^{M}\).
-
(8)
If Hypothesis (KMS β ) is satisfied, then
$$e\bigl(\alpha+\lambda\beta^{-1}\bigr)=e(\alpha), $$for all \(\alpha\in {\mathbb{R}}^{M}\) and all \(\lambda\in {\mathbb{R}}\) with \(\beta^{-1}=(\beta _{1}^{-1},\ldots,\beta_{M}^{-1})\).
Remark 1
The identity (8) is the QDS analog of the generalized Evans-Searles symmetry of time-reversal invariant classical dynamical systems (see [26, 30, 40]). However, contrary to the classical case, we do not expect that the function

satisfies this symmetry for fixed finite time t. A notable exception is provided by the very special “chaotic state”  . Indeed, it follows from the fact that \(\varTheta\circ \mathcal{L}_{(\alpha)}^{\ast}=\mathcal{L}_{(1-\alpha)}\circ\varTheta\) (see the proof of Theorem 3.1) that \(e_{\rho_{\mathrm{ch}},t}(1-\alpha)=e_{\rho_{\mathrm{ch}},t}(\alpha)\) for all \(\alpha\in {\mathbb{R}}^{M}\) and all t≥0.
. Indeed, it follows from the fact that \(\varTheta\circ \mathcal{L}_{(\alpha)}^{\ast}=\mathcal{L}_{(1-\alpha)}\circ\varTheta\) (see the proof of Theorem 3.1) that \(e_{\rho_{\mathrm{ch}},t}(1-\alpha)=e_{\rho_{\mathrm{ch}},t}(\alpha)\) for all \(\alpha\in {\mathbb{R}}^{M}\) and all t≥0.
Remark 2
Property (8) is a consequence of energy conservation. It was first proposed by Andrieux et al. in the framework of Hamiltonian dynamics on the basis of a formal calculation [2].
We shall call the probability measure \(P_{\rho}^{t}\) the entropic full counting statistics (EFCS) of the QDS generated by \(\mathcal{L}\) (w.r.t. the specific decomposition \(\mathcal{L}=\sum_{j}\mathcal{L}_{j}\)). As explained in Sect. 5, in cases where this QDS arises as a weak coupling limit of the dynamics of a system \(\mathcal{S}\) coupled to M thermal reservoirs, the EFCS is the scaling limit of a measure \(\mathbb{P}_{\rho}^{t}\) which describes the mean rate of entropy exchange between the system and the M reservoirs during the time interval [0,t] (see Eq. (38) below).
An alternative interpretation of the measures \(P_{\rho}^{t}\) is based on the well-known unraveling technique. In other words, these measures can be understood in terms of a classical stochastic process which provides a coarse grained description of the dynamics of the system by so called quantum trajectories. Within this framework, \(P_{\rho}^{t}\) is the joint distribution of M random variables which describe the exchange of entropy between the system and the M reservoirs (see Sect. 6).
3.3 Entropic Fluctuations
As a direct consequence of Theorem 3.1 and the Gärtner-Ellis theorem (see, e.g., [25, 29]), we have
Corollary 3.2
Assume that Hypotheses (DB) and (ER) hold and let
I(ς) is the Fenchel-Legendre transform of e(−α). Then:
-
(1)
I(ς) takes values in [0,∞] and is a convex lower-semicontinuous function with compact level sets.Footnote 3
-
(2)
I(ς)=0 iff \(\varsigma=\overline {\varsigma}\), where \(\overline{\varsigma}=-\nabla e(0)\). Moreover, for any ϵ>0 there exists a positive constant a(ϵ) such that
$$P_\rho^t\bigl(\bigl\{\varsigma\in {\mathbb{R}}^M\,|\,| \varsigma-\overline {\varsigma}|\ge\epsilon\bigr\} \bigr)\le \mathrm {e}^{-t a(\epsilon)}, $$for all t>0.
-
(3)
The family of measures \(\{P_{\rho}^{t}\}_{t\ge0}\) satisfies the large deviation principle with rate function I. More precisely, for any Borel set \(G\subset {\mathbb{R}}^{M}\) we have
$$ -\inf_{\varsigma\in\mathrm{int}(G)} I(\varsigma) \leq\liminf_{t \rightarrow\infty} \frac{1}{t} \log P_\rho^t (G ) \leq\limsup_{t \rightarrow\infty} \frac{1}{t} \log P_\rho^t (G ) \leq -\inf_{\varsigma\in\mathrm{cl}(G)} I(\varsigma), $$(9)where int(G) and cl(G) denote the interior and the closure of the set G.
-
(4)
If Hypothesis (TR) is satisfied, then the rate function satisfies
$$ I(-\varsigma)=1\cdot\varsigma+ I(\varsigma). $$(10) -
(5)
If Hypothesis (KMS β ) is satisfied, then I(ς)=+∞ for any \(\varsigma\in {\mathbb{R}}^{M}\) such that \(\beta^{-1}\cdot\varsigma\not=0\).
Remark 1
The components of \(\overline {\varsigma}=(\overline {\varsigma}_{1}, \ldots, \overline {\varsigma}_{M})\) describe the asymptotic rates of entropy transport between the system \(\mathcal{S}\) and the M reservoirs constituting its environment. The non-negative number
is the steady state entropy production rate of a QDS satisfying Hypotheses (ER) and (DB) (see the next section for additional information about this important concept). If (TR) holds, then Relation (10) implies \(I(-\overline {\varsigma})=\sigma_{+}\) and σ +>0 iff \(\overline {\varsigma}\not=0\).
Remark 2
The large deviation principle (9) quantifies the exponential rate of decay of the measures \(P_{\rho}^{t}\) away from the asymptotic mean value \(\overline {\varsigma}\) and describes the statistics of the fluctuations of the rates of entropy transport over large but finite periods of time. In particular, (9) implies that
for large t. Combining Parts (2) and (3) we derive that for large t,
and in particular that
The identities (8) and (10), together with the resulting asymptotics (11) and (12), constitute fluctuation relations for a QDS out of equilibrium. One important feature of the fluctuation relations is universality (independence of the model).
Theorem 3.1 and Bryc’s theorem (see Proposition 1 in [6] and Appendix A in [36]) imply the Central Limit Theorem for the family of measures \(\{P_{\rho}^{t}\}_{t\geq0}\).
Corollary 3.3
Assume that Hypotheses (ER) and (DB) hold. Then for any Borel set \(G\subset {\mathbb{R}}^{M}\),
where μ D denotes the centered Gaussian measure on \({\mathbb{R}}^{M}\) with covariance D given by
Note that if Hypothesis (KMS β ) holds, then Theorem 3.1 (8) implies that the Gaussian measure μ D has its support on the hyperplane β −1⋅ς=0. This is of course related to Part (5) of Corollary 3.2 and to energy conservation.
3.4 Thermodynamics
The von Neumann entropy of a state ρ is Ent(ρ)=−tr(ρlogρ) and we shall call S=−logρ the entropy observable associated to ρ. The relative entropy of a state ν w.r.t. to another state μ is
We refer the reader to the monograph of Ohya and Petz [54] for further information on these fundamental concepts. Following Lebowitz and Spohn [48, 60], we define the entropy production in the state ρ of a QDS \(\{\mathrm {e}^{t\mathcal{L}}\}_{t\ge0}\) satisfying Hypothesis (DB) byFootnote 4
We recall basic properties of the entropy production established in [48, 60].
-
(a)
Since ρ j is a steady state of the QDS generated by \(\mathcal{L}_{j}\), we have
$$\mathrm{Ent}\bigl(\mathrm {e}^{t\mathcal{L}_j^\ast}(\rho)\big|\rho_j\bigr)=\mathrm{Ent}\bigl( \mathrm {e}^{t\mathcal{L}_j^\ast}(\rho)\big|\mathrm {e}^{t\mathcal{L}_j^\ast}(\rho_j)\bigr), $$and Uhlman’s monotonicity theorem ([62], see also [36, 54]) implies that the r.h.s. of this identity is a non-decreasing function of t. Hence,
$$\sigma(\rho)\geq0. $$ -
(b)
An application of a theorem of Lieb [45] gives that the map \({\mathfrak{S}} \ni\rho\mapsto\sigma(\rho)\) is convex (see Theorem 3 in [60]).
-
(c)
Set S j =−logρ j and \(\mathcal{I}_{j}=\mathcal{L}_{j}(S_{j})\). An immediate consequence of (14) is the entropy balance equation:
$$ \frac{\mathrm {d}\ }{\mathrm {d}t}\mathrm{Ent}\bigl(\mathrm {e}^{t\mathcal{L}^\ast}(\rho)\bigr) \big|_{t=0}=\sigma( \rho) +\sum_{j=1}^M\rho(\mathcal{I}_j). $$(15)The second term on the r.h.s. of Eq. (15) describes the flux of entropy entering the system. Thus, we can interpret the observable \(\mathcal{I}_{j}\) as the entropy flux out of the jth reservoir. Note that if ρ is a steady state, then the l.h.s. of (15) vanishes, and the entropy balance equation takes the form
$$ \sigma(\rho)=-\sum_{j=1}^M \rho(\mathcal{I}_j). $$(16)
Our next result links the function e(α) to the observables S j and \(\mathcal{I}_{j}\).
Theorem 3.4
Let \(\{\mathrm {e}^{t\mathcal{L}}\}_{t\ge0}\) be a QDS satisfying Hypotheses (ER) and (DB). Set \(\mathcal{J}_{j}= \mathcal{I}_{j}-\rho_{+}(\mathcal{I}_{j})\). Then the following holds:
-
(1)
$$\frac{\partial e(\alpha)}{\partial\alpha_j}\bigg\vert _{\alpha=0}=\rho _+(\mathcal{I}_j). $$
In particular,
$$\rho_+(\mathcal{I}_j)=-\lim_{t\to\infty}\langle \varsigma_j\rangle_{\rho,t}=-\overline{\varsigma}_j, $$and \(\sigma(\rho_{+})=\sum_{j} \overline {\varsigma}_{j}\).
-
(2)
$$\begin{aligned} \frac{\partial^2 e(\alpha)}{\partial\alpha_j\partial\alpha _k}\bigg\vert _{\alpha=0} =& -\int_0^\infty \rho_+ \bigl( \mathrm {e}^{t\mathcal{L}}(\mathcal{J}_j)\mathcal{J}_k^++ \mathrm {e}^{t\mathcal{L}}(\mathcal{J}_k)\mathcal{J}_j^+ \bigr)\mathrm {d}t \\ &{}+\int_0^\infty\rho_+ \bigl(\mathcal{L}_k \bigl(\mathrm {e}^{t\mathcal{L}}(\mathcal{J}_j)S_k\bigr)+ \mathcal{L}_j\bigl(\mathrm {e}^{t\mathcal{L}}(\mathcal{J}_k)S_j \bigr) \bigr)\mathrm {d}t +\delta_{jk}\rho_+\bigl(D_j(S_j,S_j) \bigr) \\ =&\lim_{t\to\infty}t \bigl\langle\bigl(\varsigma_j- \langle\varsigma_j\rangle_{\rho ,t}\bigr) \bigl( \varsigma_k-\langle\varsigma_k\rangle_{\rho,t} \bigr)\bigr\rangle_{\rho,t}, \end{aligned}$$
where \(\mathcal{J}_{j}^{+}=\mathcal{L}_{j}^{\rho_{+}}(S_{j})=\mathcal{L}_{j}^{\ast}(S_{j}\rho_{+})\rho_{+}^{-1}\) and \(D_{j}(A,B)=\mathcal{L}_{j}(A^{\ast}B)-\mathcal{L}_{j}(A^{\ast})B-A^{\ast} \mathcal{L}_{j}(B)\) is the dissipation function of the jth Lindbladian.
Remark 1
Under the assumptions of the theorem the semigroup \({\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq 0}}\) is relaxing exponentially fast to ρ +. Since \(\rho_{+}(\mathcal{J}_{j})=0\), this implies that the operators \(\mathrm {e}^{t\mathcal{L}}(\mathcal{J}_{j})\) are exponentially decaying as t→∞, and so the time integrals in Part (2) are absolutely convergent.
Remark 2
We shall make use of Part (2) in Sect. 3.6 where we discuss linear response theory.
3.5 Energy Fluxes
The Hypothesis (KMS β ) allows us to relate entropy fluxes to energy fluxes by simple rescaling and to restate our main results in terms of energy transport. As a preparation for the discussion of the linear response theory, in this section we briefly discuss how this restating is carried out. Until the end of this section we shall assume that Hypotheses (ER), (DB), and (KMS β ) hold.
The observable describing the energy flux out of the jth reservoir is \(\mathcal{F}_{j}=\mathcal{L}_{j}(H_{\mathcal{S}})\) (see [48]). Note that \(\mathcal{I}_{j}=\beta _{j} \mathcal{F}_{j}\). If in addition (TR) holds, then \(\varTheta(H_{\mathcal{S}})=H_{\mathcal{S}}\) and it follows from Parts (1) and (2) of Theorem 7.1 that \(\mathcal{L}_{j}^{\rho_{j}}(H_{\mathcal{S}})= \mathcal{L}_{j}(H_{\mathcal{S}})\). Hence,
The steady state energy fluxes are
Obviously, \(\overline {\varsigma}_{j} =-\beta_{j} \overline {\phi}_{j}\), and Eq. (16) takes the form
This relation expresses the second law of thermodynamics for QDS satisfying our assumptions. The relation \(\mathcal{L}^{\ast}(\rho_{+})=0\) yields the first law (conservation of energy):
The energetic full counting statistics of the system is the probability measure \(Q_{\rho}^{t}\) on \({\mathbb{R}}^{M}\) given by
where βϕ=(β 1 ϕ 1,…,β M ϕ M ). In particular,

where α/β=(α 1/β 1,…,α M /β M ). Hence, for \(\alpha\in {\mathbb{R}}^{M}\),
and in particular,
Note that the translation symmetry of e(α) (described in Part (8) of Theorem 3.1) implies that
for all \(\alpha\in {\mathbb{R}}^{M}\), \(\lambda\in {\mathbb{R}}\). If (TRI) holds, then the Evans-Searles symmetry takes the form
The large t fluctuations of \(Q_{\rho}^{t}\) are described by obvious reformulations of Corollaries 3.2 and 3.3.
Finally, we discuss briefly the equilibrium case where β j =β 0 for j=1,…,M. In this case
and \(\mathcal{L}_{j}^{\ast}(\rho_{0})=0\) for all j. It follows that \(\mathcal{L}^{\ast}(\rho _{0})=0\) and hence that ρ +=ρ 0 and \(\overline {\phi}_{j}=0\) for all j. Combining Parts (1) and (2) of Theorem 7.1 with Theorem 3.4 (2) one easily derives that \(\mathcal{J}_{j}^{+}= \mathcal{J}_{j}=\mathcal{I}_{j}=\beta_{0}\mathcal{F}_{j}\), and that
If the pair \((\rho_{0}, \mathcal{L})\) is TRI, then
3.6 Linear Response Theory
Our last result concerns linear response to thermodynamical forces. We consider a small system \(\mathcal{S}\) coupled to M thermal reservoirs \(\mathcal{R}_{j}\) in equilibrium at inverse temperatures β j where each β j is close to some common equilibrium value β 0>0. The purpose of linear response theory is to study the behavior of various physical quantities to first order in the thermodynamical forces ζ j =β 0−β j . It is therefore natural to parametrize β=(β 1,…,β M ) by ζ=(ζ 1,…,ζ M ) so that ζ=0 corresponds to the equilibrium situation β=β eq=(β 0,…,β 0). The precise setup is as follows.
Let \((\mathcal{L}_{\zeta})_{\zeta\in\mathcal{U}}\) be a family of Lindbladians indexed by an open neighborhood \(\mathcal{U}\) of 0 in \({\mathbb{R}}^{M}\) and such that each \(\mathcal{L}_{\zeta}\) satisfies Hypotheses (ER) and (TR). Moreover, we assume Hypotheses (DB) and (KMS β ) in the following form: for each \(\zeta\in\mathcal{U}\),
where \(\mathcal{L}_{\zeta,j}\) depends only on ζ j and satisfies the detailed balance condition w.r.t. the state
for some ζ-independent self-adjoint \(H_{\mathcal{S}}\in \mathcal{O}\). We shall also assume the following regularity in ζ:
(RE) The map \(\zeta\mapsto \mathcal{L}_{\zeta}\) is continuously differentiable at ζ=0.
In what follows we shall indicate explicitly the dependence on ζ by writing \(\mathcal{L}_{\zeta, (\alpha)}\), e(ζ,α), χ(ζ,α), \(\mathcal{F}_{\zeta,j}\), \(\overline{\phi}_{\zeta, j}\), etc. Our assumptions imply that all partial derivatives of \(\mathcal{L}_{\zeta, (\alpha)}\) w.r.t. α are continuously differentiable w.r.t. ζ at ζ=0.
For all \(\alpha\in {\mathbb{R}}^{M}\) and \(\zeta\in \mathcal{U}\), e(ζ,α) is a simple eigenvalue of \(\mathcal{L}_{\zeta,(\alpha)}\). The perturbation theory of isolated eigenvalues (see the proof of Theorem 3.4) implies that all partial derivatives of e(ζ,α) w.r.t. α are also continuously differentiable w.r.t. ζ at ζ=0 and the same holds for the function χ(ζ,α). In particular, the maps \(\zeta\mapsto \overline {\phi}_{\zeta, j}\) are continuously differentiable at ζ=0.
Combining (17) and (18) yields the following expressions of the first and second laws of thermodynamics
The kinetic transport coefficients are defined by
It follows from the first law that
while the second law implies that the real quadratic form determined by the matrix [L jk ] is positive definite.Footnote 5 It further follows from the first relation in (19) that
In terms of the variable ζ, the Evans-Searles symmetry (21) takes the form χ(ζ,α)=χ(ζ,−β eq+ζ−α), while the translation symmetry (20) reads χ(ζ,α)=χ(ζ,α+λ1). Since β eq=β 01, combining these two symmetries we derive
This relation and the chain rule (see Lemma 4.4 in [40]) yield
The equality of mixed partial derivatives \(\partial_{\alpha_{k}}\partial_{\alpha_{j}}\chi=\partial_{\alpha_{j}}\partial _{\alpha_{k}}\chi\) implies the Onsager reciprocity relations L jk =L kj . Relations (22), (23), and Corollary 3.3 complete the linear response theory. We summarize:
Theorem 3.5
Under the Hypotheses formulated at the beginning of this section the following statements hold.
-
(1)
The Green-Kubo formulae:
$$L_{jk}=\int_0^\infty \rho_0\bigl(\mathrm {e}^{t \mathcal{L}_0}(\mathcal{F}_{0, j}) \mathcal{F}_{0, k}\bigr)\mathrm {d}t - \frac{1}{2} \delta_{jk} \rho_0\bigl(D_{0,j}(H_\mathcal{S}, H_\mathcal{S}) \bigr), $$where D 0,j denotes the dissipation function of \(\mathcal{L}_{0,j}\).
-
(2)
The Onsager reciprocity relations:
$$L_{jk}=L_{kj}. $$ -
(3)
The Fluctuation-Dissipation Theorem: for a state ρ on \(\mathcal{O}\) let \(Q_{\mathrm{eq},\rho}^{t}\) be the energetic full counting statistics of the equilibrium system, i.e.,

and let 〈 ⋅ 〉eq,ρ,t denote the expectation w.r.t. the measure \(Q_{\mathrm{eq},\rho}^{t}\). For any Borel set \(G\subset {\mathbb{R}}^{M}\),
$$\lim_{t\rightarrow\infty} Q_{\mathrm{eq},\rho}^t \bigl( \bigl\{ \phi\in {\mathbb{R}}^M\, |\, \sqrt{t}\bigl(\phi-\langle\phi\rangle_{\mathrm{eq},\rho ,t} \bigr)\in G \bigr\} \bigr)=\mu_D(G), $$where μ D is the centered Gaussian measure on \({\mathbb{R}}^{M}\) with covariance D given by
$$D_{jk}=2L_{jk}. $$
Remark 1
Concerning the diagonal transport coefficients L jj , the terms \(\rho_{0}(D_{0,j}(H_{\mathcal{S}}, H_{\mathcal{S}}))\) are non-negative, and are strictly positive if \(\mathcal{S}\) is effectively coupled to the jth-reservoir (see Sect. 4). Parts (1)–(2) of Theorem 7.1 imply that \(\rho_{0}(D_{0,j}(H_{\mathcal{S}}, H_{\mathcal{S}}))=-2\rho_{0}(H_{\mathcal{S}}\mathcal{F}_{0,j})\).
Remark 2
In the absence of time-reversal, Part (3) holds with
Remark 3
Parts (1) and (2) of Theorem 3.5 were first proven in [48] by a different method. For comparison purposes we sketch the proof of [48]. Since \(\mathcal{L}_{\zeta,k}^{\ast}(\rho_{\zeta_{k}})=0\),
where the last equality follows from Parts (1) and (2) of Theorem 7.1. Hypotheses (ER) and (RE) imply that the map ζ↦ρ ζ,+ is continuously differentiable at ζ=0. Differentiating \(\mathcal{L}_{\zeta}^{\ast}(\rho _{\zeta, +})=0\) w.r.t. ζ k at ζ=0, we get
The last two relations give
Since
the operators \(\mathrm {e}^{t\mathcal{L}_{0}^{\ast}}(\mathcal{F}_{0, k}\rho_{0})\) are exponentially decaying as t→∞, and we deduce from (27) that there is a constant c such that
If \(j\not=k\) then \(\mathcal{F}_{\zeta,j}=\mathcal{L}_{\zeta,j}(H_{\mathcal{S}})\) does not depend on ζ k and it follows that
The conservation law (24), the limit (28) and the last formula in Remark 1 yield
Note that the above argument did not make use of Hypothesis (TR) and so Part (1) of Theorem 3.5 holds without time-reversal assumption (in fact, Lebowitz and Spohn do not discuss time-reversal at all in [48]). However, if the pair \((\rho_{0}, \mathcal{L}_{0})\) is time-reversal invariant, then Part (1) and Relation (23) yield the Onsager reciprocity relations.
In contrast to the direct argument of [48], the proof described in this section exploits fundamentally the symmetry (25). The advantage of this derivation in context of a QDS out of equilibrium is conceptual. The fluctuation relations are structural model independent features of non-equilibrium statistical mechanics. As observed by Gallavotti [32], in the linear regime near equilibrium the fluctuation relations reduce to familiar fluctuation-dissipation formulae, and this structural model independent view of linear response theory is of fundamental conceptual importance (see [36, 40, 49] for a pedagogical discussion of this point). Our proof shows how a QDS out of equilibrium fit into this general picture and complements the derivation of [48] from the conceptual point of view.
4 Weakly Coupled Open Quantum Systems
We consider a small quantum system \(\mathcal{S}\), described by the Hamiltonian \(H_{\mathcal{S}}\) acting on the finite dimensional Hilbert space \(\mathcal{H}_{\mathcal{S}}\). To induce a dissipative dynamics on \(\mathcal{S}\), we couple this system to several infinitely extended thermal reservoirs \(\mathcal{R}_{1},\ldots,\mathcal{R}_{M}\). Each reservoir \(\mathcal{R}_{j}\) is initially in a thermal equilibrium state at inverse temperature β j >0.Footnote 6 By passing to the GNS representations induced by these states, each \(\mathcal{R}_{j}\) is described by a Hilbert space \(\mathcal{H}_{j}\), a W ∗-algebra \(\mathcal{O}_{j}\subset \mathcal{B}(\mathcal{H}_{j})\) of observables, and a self-adjoint operator L j (the Liouvillean) acting on \(\mathcal{H}_{j}\), such that the Heisenberg dynamics \(\tau_{j}^{t}(A)=\mathrm {e}^{\mathrm {i}tL_{j}}A\mathrm {e}^{-\mathrm {i}tL_{j}}\) leaves \(\mathcal{O}_{j}\) invariant. The initial state of \(\mathcal{R}_{j}\) is given by \(\mathcal{O}_{j}\ni A\mapsto\omega_{j}(A)=\langle\xi_{j}|A\xi_{j}\rangle\), where \(\xi_{j}\in \mathcal{H}_{j}\) is a unit vector such that L j ξ j =0. Moreover, the state ω j satisfies the KMS boundary condition: for all \(A, B \in \mathcal{O}_{j}\),
The Hilbert space of the joint system \(\mathcal{S}+\mathcal{R}_{1}+\cdots+\mathcal{R}_{M}\) is \(\mathcal{H}=\mathcal{H}_{\mathcal{S}}\otimes \mathcal{H}_{1}\otimes\cdots\otimes \mathcal{H}_{M}\) and we shall denote  ,
,  simply by \(H_{\mathcal{S}}\), H
1,…
simply by \(H_{\mathcal{S}}\), H
1,…
The interaction between the system \(\mathcal{S}\) and the reservoir \(\mathcal{R}_{j}\) is described by the Hamiltonian
where each \(Q^{(k)}_{j}\) is a self-adjoint operator on \(\mathcal{H}_{\mathcal{S}}\) and each \(R^{(k)}_{j}\) is a self-adjoint element of \(\mathcal{O}_{j}\) such that \(\omega_{j}(R^{(k)}_{j})=0\).Footnote 7 The full Hamiltonian (more precisely the semi-standard Liouvillean in the terminology of [17]) of the coupled system is
where λ is a coupling constant. The effective dynamics of the system \(\mathcal{S}\) is then defined by the family of linear map \(\{\mathcal{T}_{\lambda}^{t}\}_{t\in {\mathbb{R}}}\) on \(\mathcal{B}(\mathcal{H}_{\mathcal{S}})\) determined by

where \(X\in \mathcal{B}(\mathcal{H}_{\mathcal{S}})\), \(\psi\in \mathcal{H}_{\mathcal{S}}\), and ξ=ξ 1⊗⋯⊗ξ M .
Except in trivial cases, \(\{\mathcal{T}_{\lambda}^{t}\}_{t\geq0}\) is not a semigroup. However, under appropriate conditions on the decay of the multi-time correlation functions \(\omega_{j}(\tau_{j}^{t_{1}}(R^{(k_{1})}_{j})\cdots\tau_{j}^{t_{n}}(R^{(k_{n})}_{j}))\), Davies has shown (see Theorem 2.3 in [10]) that there exists a Lindbladian \(\mathcal{L}\) generating a QDS such that \(\mathcal{L}\) commutes with \(\mathcal{L}_{\mathcal{S}}(X)=\mathrm {i}[H_{\mathcal{S}},X]\), and
holds for any compact interval \(I=[0,\tau]\subset {\mathbb{R}}\). In other words, in the limit of small coupling λ→0 and for times of the order λ −2 the effective dynamics of \(\mathcal{S}\) is well approximated by the quantum dynamical semigroup generated by \(\mathcal{L}_{\mathcal{S}}+\lambda^{2}\mathcal{L}\). This theory is well-known and we refer the reader to the in depth exposition of [15, 48] for further details. To write down the explicit form of the generator \(\mathcal{L}\), we introduce the functions
and their Hilbert transforms
where \(\mathcal{P}\) denotes Cauchy’s principal value (the hypotheses of the above mentioned theorem of Davies ensure the existence of these integrals). Note that the n j ×n j -matrices
are respectively positive and self-adjoint and that the KMS condition (29) implies the relation
We denote by P μ the spectral projection of \(H_{\mathcal{S}}\) associated to the eigenvalue \(\mu\in \mathrm{sp}(H_{\mathcal{S}})\), and for
we define
Obviously,
for all \(\alpha\in {\mathbb{C}}\).
The generator \(\mathcal{L}\) has the Lindblad form (5), with the self-adjoint operator T given by
and the CP map Φ given by
A Kraus decomposition of Φ j is constructed as follows. Denote by \(u_{j}(\omega)=[u_{j}^{(kl)}(\omega)]\) a unitary matrix which diagonalize the positive matrix h j (ω),
Setting \(W_{j}^{(k)}(\omega)=\sqrt{g_{j}^{(k)}(\omega)}\sum_{l}u_{j}^{(kl)}(\omega)V_{j}^{(l)}(\omega)\), we obtain
Note that \(\mathcal{L}\) can be written as the sum of the Lindbladians

where \(\mathcal{L}_{j}\) describes the interaction of the small system \(\mathcal{S}\) with a single reservoir \(\mathcal{R}_{j}\). Using (30) and (32) one easily verifies that \(\mathcal{L}_{j}\) satisfies the detailed balance condition w.r.t. the faithful state
Thus, Hypotheses (DB) and (KMS β ) are automatically satisfied by the weak coupling Lindbladian \(\mathcal{L}\).
Regarding time-reversibility, assuming that
-
(a)
each reservoir is time-reversal invariant, i.e., there exists antiunitary involution θ j acting on \(\mathcal{H}_{j}\) such that L j θ j =θ j L j and θ j ξ j =ξ j ;
-
(b)
the small system \(\mathcal{S}\) is time-reversal invariant, i.e., there is an antiunitary involution \(\theta_{\mathcal{S}}\) on \(\mathcal{H}_{\mathcal{S}}\) such that \(\theta_{\mathcal{S}}H_{\mathcal{S}}=H_{\mathcal{S}}\theta_{\mathcal{S}}\);
-
(c)
\(\theta_{j}R_{j}^{(k)}=R_{j}^{(k)}\theta_{j}\) and \(\theta_{\mathcal{S}}Q_{j}^{(k)}=Q_{j}^{(k)}\theta_{\mathcal{S}}\) for all j,k,
we easily conclude that \(h_{j}^{(kl)}(\omega)=\overline{h_{j}^{(lk)}(\omega)}\), \(s_{j}^{(kl)}(\omega )=\overline{s_{j}^{(lk)}(\omega)}\), and \(\theta_{\mathcal{S}}V_{j}^{(k)}(\omega)=V_{j}^{(k)}(\omega)\theta_{\mathcal{S}}\). It immediately follows that \(\theta_{\mathcal{S}}T_{j}=T_{j}\theta_{\mathcal{S}}\) and \(\varPhi_{j}(\theta_{\mathcal{S}}X\theta_{\mathcal{S}})=\theta_{\mathcal{S}}\varPhi_{j}(X)\theta_{\mathcal{S}}\). Hence, Hypothesis (TR) is satisfied with \(\varTheta(X)=\theta_{\mathcal{S}}X\theta_{\mathcal{S}}\).
We now turn to the ergodicity Hypothesis (ER). Clearly, \(\{Q_{j}^{(k)}\} _{j,k}^{\prime}\cap\{H_{\mathcal{S}}\}^{\prime}\subset \mathrm{Ker}\,\mathcal{L}\) and the condition

is obviously necessary for (ER) to hold. On the other hand, assuming that the matrices h j (ω) are strictly positive for all 1≤j≤M and ω∈Ω, the construction of the Kraus family \(\{W_{j}^{(k)}(\omega)\}_{j,k,\omega}\) shows that its linear span coincides with the linear span of the family \(\mathcal{V}=\{V_{j}^{(k)}(\omega)\}_{j,k,\omega}\). By Eq. (31), the family \(\mathcal{V}\) is self-adjoint, and von Neumann’s bicommutant theorem implies that the smallest subalgebra of \(\mathcal{O}\) containing \(\mathcal{V}\) is the bicommutant \(\mathcal{V}^{\prime\prime}\). As shown by Spohn (see Theorem 3 in [59]), the condition \(\mathcal{V}^{\prime\prime}=\mathcal{O}\) is equivalent to (34). Hence, assuming strict positivity of the matrices h j (ω) for all j and ω, Theorems 2.1 and 2.3 imply that the Spohn condition (34) is also sufficient for Hypothesis (ER) to hold.
Note that
where σ j (ρ) is the entropy production of the system \(\mathcal{S}\) interacting only with the reservoir \(\mathcal{R}_{j}\) via the Lindbladian \(\mathcal{L}_{j}\). If the matrix h j (ω) is strictly positive and

then, as discussed above, the QDS \(\{\mathrm {e}^{t \mathcal{L}_{j}}\}_{t\geq0}\) is positivity improving. Moreover, \(\mathcal{L}_{j}^{\ast}(\rho)=0\) iff \(\rho=\mathrm {e}^{-\beta_{j} H_{\mathcal{S}}}/\mathrm{tr}(\mathrm {e}^{-\beta_{j} H_{\mathcal{S}}})\).Footnote 8 Hence, we arrive at the following elegant condition (see [5, 48]) which ensures that σ(ρ)>0 for all states ρ: there exists a pair j 1,j 2 such that \(\beta_{j_{1}}\not=\beta_{j_{2}}\), the relation (35) holds for j=j 1,j 2, and the matrix h j (ω) is strictly positive for all ω and j=j 1,j 2.
In conclusion, under very general and natural conditions the class of weak coupling limit QDS introduced in [48] satisfies Hypotheses (ER), (DB), (TR), (KMS β ), and has strictly positive entropy production.Footnote 9 Starting with the seminal paper [48], such semigroups have been one of the basic paradigms of non-equilibrium quantum statistical mechanics.
5 Full Counting Statistics
In this section, we elucidate the physical meaning of the measure \(P_{\rho}^{t}\) introduced in Theorem 3.1 in cases where the Lindbladian \(\mathcal{L}\) describes a weakly coupled open quantum system as discussed in the preceding section. We shall keep our presentation at a formal level; the interested reader should consult Sect. 5 of [36] for a more detailed discussion as well as [14, 20, 21, 41] for a mathematically rigorous treatment of some specific models.
We start with the open system described in Sect. 4, but we assume now that the reservoirs \(\mathcal{R}_{j}\) are confined to finite boxes. More precisely, working in the Schrödinger representation, we assume that the reservoir Hamiltonians H j have purely discrete spectrum and that the operators \(\mathrm {e}^{-\beta H_{j}}\) are trace class for all β>0. The initial state of the combined system is \(\rho=\rho_{\mathcal{S}}\otimes\rho_{\mathcal{R}}\), where
and \(\rho_{\mathcal{S}}\) is the initial state of the small system \(\mathcal{S}\).
The full counting statistics of the entropy fluxes across the system \(\mathcal{S}\) is defined as follows. Set S=(S 1,…,S M ) with S j =β j H j . The observables S j commute and hence can be simultaneously measured. Let Π s denote the joint spectral projection of S associated to the eigenvalue s∈sp(S). Two successive measurements of S at time t 0 and at time t 0+t are described by the positive map valued measure (PMVM) (see, e.g., [13]) which, to any subset A∈sp(S)×sp(S), associate the CP map
Indeed, if \(\rho_{t_{0}}\) denotes the state of the system at time t 0, one easily checks that, according to the usual rules of projective measurements,
is the joint probability for the first measurement to yield the result s and for the second one to yield the result s′. Hence, the probability distribution of ς=(s′−s)/t, the mean rate of entropy transport from the system \(\mathcal{S}\) to the M reservoirs over the time interval [0,t], is given in terms of the initial state \(\rho_{\mathcal{S}}\) by the formula
The atomic probability measure \({\mathbb{P}}^{t}_{\rho_{\mathcal{S}}}\) on \({\mathbb{R}}^{M}\) is the full counting statistics of the energy/entropy flow. An elementary calculation shows that the Laplace transform of this measure is given by
where, for \(\alpha=(\alpha_{1},\ldots,\alpha_{M})\in {\mathbb{R}}^{M}\), we have set

Assuming that the operators
are entire analytic functions of s, we can define the deformed Hamiltonian
and write

At this point, one can pass to the GNS representation of the reservoirs and perform a thermodynamic limit, letting the size of the confining boxes become infinite. If the deformed operators \(\tau_{j}^{\mathrm {i}\alpha_{j}\beta_{j}/2}(R_{j}^{(k)})\) remain well defined elements of the W ∗-algebras \(\mathcal{O}_{j}\) in this limit, then we can define the effective deformed dynamics of the open system with infinitely extended reservoirs

with the deformed semi-standard Liouvillean
Assuming that the thermodynamic limit

exists for any \(\psi\in \mathcal{H}_{\mathcal{S}}\), \(X\in \mathcal{B}(\mathcal{H}_{\mathcal{S}})\), and \(\alpha\in {\mathbb{R}}^{M}\), we conclude that the Laplace transform \(\ell^{t}_{\rho_{\mathcal{S}}}(\alpha)\) of the full counting statistics \(\mathbb{P}^{t}_{\rho_{\mathcal{S}}}\) has a well defined thermodynamic limit

for all \(\alpha\in {\mathbb{R}}^{M}\). Then one can show that, as the size of the reservoir increases, the full counting statistics \(\mathbb{P}^{t}_{\rho_{\mathcal{S}}}\) converges weakly to a Borel probability measure which we again denote by \(\mathbb{P}^{t}_{\rho_{\mathcal{S}}}\) which satisfies

(see Proposition 4.1 in [37]). We call the limiting measure \(\mathbb{P}^{t}_{\rho_{\mathcal{S}}}\) the full counting statistics of the open system \(\mathcal{S}\) coupled to the infinitely extended reservoirs \(\mathcal{R}_{1},\ldots,\mathcal{R}_{M}\). Note that since infinitely extended reservoirs have an infinite energy, it is not possible to implement directly the successive measurement procedure we have described to this model, and that one is forced to invoke the thermodynamic limit to construct its full counting statistics.
Applying the Davies procedure to extract the weak coupling limit of the deformed effective dynamics leads to
where \(\mathcal{K}_{(\alpha)}\) is a deformed generator commuting with \(\mathcal{L}_{\mathcal{S}}\). An explicit calculation shows that the only difference between \(\mathcal{K}_{(\alpha)}\) and the undeformed Lindbladian \(\mathcal{L}=\mathcal{K}_{0}\) is that the functions \(h_{j}^{(kl)}\) are replaced with (recall that L j ξ j =0),
Using Eq. (32), one finally concludes that, with the ρ j defined in Eq. (33),
and so \(\mathcal{K}_{(\alpha)}\) coincides with the deformed Lindbladian \(\mathcal{L}_{(\alpha)}\). We conclude that if \([H_{\mathcal{S}}, \rho_{\mathcal{S}}]=0\), then the measure \(P_{\rho}^{t}\) introduced in Theorem 3.1 is related to the full counting statistics \(\mathbb{P}^{t}_{\rho_{\mathcal{S}}}\) through the scaling limit
We note that in the weak coupling regime, the energy/entropy fluxes are of order λ 2 so the scaling λ −2 ς which appears on the left hand side of the last identity is natural. The measure \(P^{t}_{\rho_{\mathcal{S}}}\) thus describes the rescaled mean energy/entropy fluxes at the Van Hove time scale t/λ 2. To the best of our knowledge, this observation is due to de Roeck [18].
For some specific models it is possible to show that
(see [19–21, 41]), and in such cases one can relate the large deviation principle of Corollary 3.2 to the large deviation principle of the full counting statistics \({\mathbb{P}}_{\rho_{\mathcal{S}}}^{t}\).
The link between full counting statistics and deformations of the semi-standard Liouvillean (relations (36) and (37)) goes back to [18]. The link between full counting statistics and deformations of the standard Liouvillean can be traced back to [16, 38, 53], was fully elaborated in [36], and plays the key role in the work [41]. The second link relates full counting statistics to modular theory of operator algebras and deformed Lindbladians \(\mathcal{L}_{(\alpha)}\) to Fermi Golden Rule for spectral resonances of the deformed standard Liouvilleans. This point is discussed in detail in [41] and we refer the reader to this work for additional information.
6 Unraveling of the Deformed Semigroup \(\mathrm {e}^{t\mathcal{L}_{(\alpha)}}\)
In this section we follow [22] and present an alternative and more general interpretation of the measure \(P^{t}_{\rho}\) based on the standard unraveling technique. As a byproduct of this construction, we shall get a proof of Parts (1) and (2) of Theorem 3.1. We shall assume that Hypothesis (DB) holds throughout the section and use the elementary properties of Lindbladians summarized in Theorem 7.1.
Let  denote a Lindblad decomposition of \(\mathcal{L}_{j}\) and set
denote a Lindblad decomposition of \(\mathcal{L}_{j}\) and set

By Theorem 7.1, K j commutes with ρ j and Φ j admits a decomposition
where Ω j ={μ−ν | μ,ν∈sp(logρ j )} and \(\varPhi _{j,\omega}\in \mathrm{CP}(\mathcal{O})\) satisfies \(\varPhi_{j,\omega}(X\rho_{j}^{-\alpha_{j}})\rho_{j}^{\alpha_{j}}=\mathrm {e}^{-\alpha_{j}\omega}\varPhi_{j,\omega}(X)\). It follows that
is of the Lindblad form (4) for \(\alpha\in {\mathbb{R}}^{M}\), which proves Part (1) of Theorem 3.1. Using the Dyson expansion of the cocycle \(\varGamma^{t}_{\alpha}=\mathrm {e}^{-t\mathcal{K}}\circ \mathrm {e}^{t\mathcal{L}_{(\alpha)}}\), we obtain the representation

where \(\rho_{t}=\mathrm {e}^{t\mathcal{K}^{\ast}}(\rho)\) and \(\varPhi_{j,\omega,s}=\mathrm {e}^{-s\mathcal{K}}\circ\varPhi_{j,\omega}\circ \mathrm {e}^{s\mathcal{K}}\).
Unraveling consists of rewriting this expression in terms of a probability measure \(\mu^{t}_{\rho}\) on a set Ξ t of quantum trajectories defined as follows. For N≥1, let
and set \(\varXi^{t}_{0}=\{\emptyset\}\). On the disjoint union
one defines the positive measure \(\mu^{t}_{\rho}\) by

Comparison with Eq. (40) shows that

and hence \(\mu^{t}_{\rho}\) is a probability measure. An element ξ∈Ξ t is a quantum trajectory which represent the history of the system during the time interval [0,t]. Observe that the system can exchange entropy with the reservoir \(\mathcal{R}_{j}\) only in quanta of the form ω∈sp(S j )−sp(S j )=Ω j where S j =−logρ j . An element ξ=[ξ 1,…,ξ N ] of Ξ t is a chronologically ordered list of elementary events ξ k =(j k ,ω k ,s k ) which we interpret in the following way: at time s k the system has exchanged an entropy quantum ω k with reservoir \(\mathcal{R}_{j_{k}}\). According to this interpretation, the random variable
represents the mean rate of entropy exchange of the system with reservoir \(\mathcal{R}_{j}\) during the time interval [0,t]. It follows that one can rewrite the expansion (40) as

This proves Part (2) of Theorem 3.1 and identifies the measure \(P_{\rho}^{t}\) as the law of the random variable ς(ξ)=(ς 1(ξ),…,ς M (ξ)) induced by the measure \(\mu^{t}_{\rho}\).
7 Proofs
7.1 Detailed Balance
To a faithful state ρ, we associate two groups of transformations of \(\mathcal{O}\), the modular group \(\varDelta_{\rho}^{z}(X)=\rho^{z}X\rho^{-z}\), and the group \(\mathcal{R}_{\rho}^{z}(X)=\rho ^{z} X\rho^{z}\), \(z\in {\mathbb{C}}\). \(\varDelta_{\rho}^{1}=\varDelta_{\rho}\) is the modular operator of the state ρ. Note that \(\varDelta_{\rho}^{\mathrm {i}\alpha}\in \mathrm{CP}_{1}(\mathcal{O})\) and \(\mathcal{R}_{\rho}^{\alpha}\in \mathrm{CP}(\mathcal{O})\) for \(\alpha\in {\mathbb{R}}\).
Theorem 7.1
Let
ρ
be a faithful state on
\(\mathcal{O}\)
and
 a Lindbladian generating a QDS. Suppose that
\(\mathcal{L}^{\ast}(\rho)=0\)
and
Φ
ρ=Φ. Then:
a Lindbladian generating a QDS. Suppose that
\(\mathcal{L}^{\ast}(\rho)=0\)
and
Φ
ρ=Φ. Then:
-
(1)
The Hermitian and anti-Hermitian parts of \(\mathcal{L}\) w.r.t. the inner product induced by ρ are given by

They are also called dissipative and Hamiltonian parts of \(\mathcal{L}\).
-
(2)
\(\mathcal{L}\), \(\mathcal{L}^{(h)}\), \(\mathcal{L}^{(d)}\) and Φ commute with the modular operator Δ ρ . In particular, T and
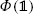 commute with
ρ
and
\(\mathcal{L}^{(d)\ast}(\rho)=\mathcal{L}^{(h)\ast}(\rho)=0\).
commute with
ρ
and
\(\mathcal{L}^{(d)\ast}(\rho)=\mathcal{L}^{(h)\ast}(\rho)=0\). -
(3)
The CP map Φ admits a decomposition
$$\varPhi=\sum_{\omega\in \mathrm{sp}(\log\varDelta_\rho)}\varPhi_\omega, $$where \(\varPhi_{\omega}\in \mathrm{CP}(\mathcal{O})\) satisfies Φ ω (Xρ −α)ρ α=e−αω Φ ω (X), \(\varPhi_{\omega}^{\rho}=\varPhi_{-\omega}\) and \(\varPhi_{\omega}^{\ast}=\mathrm {e}^{\omega}\varPhi _{-\omega}\).
-
(4)
For \(\alpha\in {\mathbb{C}}\) define \(\mathcal{L}_{\alpha}=\mathcal{R}_{\rho}^{\alpha/2}\circ \mathcal{L}\circ \mathcal{R}_{\rho}^{-\alpha/2}\). Then
 (41)
(41)holds for all \(X\in \mathcal{O}\). Moreover, \(\{\mathrm {e}^{t\mathcal{L}_{\alpha}}\}_{t\geq0}\) is a \(\mathrm{CP}(\mathcal{O})\) semigroup for \(\alpha\in {\mathbb{R}}\).
-
(5)
If the pair \((\rho, \mathcal{L})\) is time-reversible with time-reversal Θ, then for all \(\alpha\in {\mathbb{R}}\)
$$\varTheta\circ \mathcal{L}_\alpha^\ast=\mathcal{L}_{1-\alpha}\circ \varTheta. $$
Remark
The proofs of Parts (1)–(3) can be found in [3, 42]. For the readers convenience we provide a complete proof below.
Proof
We start with the simple remarks that  and that \(\mathcal{M}^{\rho}(X)=\mathcal{M}^{\ast}(X\rho)\rho^{-1}\) for any linear map \(\mathcal{M}\) on \(\mathcal{O}\). We recall that \(\mathcal{M}\) is a ∗-map if \(\mathcal{M}(X^{\ast})=\mathcal{M}(X)^{\ast}\) for all \(X\in \mathcal{O}\). The maps \(\mathcal{L}\) and \(\mathcal{L}^{\ast}\), as generators of positive semigroups, and Φ as a positive map, are all ∗-maps.
and that \(\mathcal{M}^{\rho}(X)=\mathcal{M}^{\ast}(X\rho)\rho^{-1}\) for any linear map \(\mathcal{M}\) on \(\mathcal{O}\). We recall that \(\mathcal{M}\) is a ∗-map if \(\mathcal{M}(X^{\ast})=\mathcal{M}(X)^{\ast}\) for all \(X\in \mathcal{O}\). The maps \(\mathcal{L}\) and \(\mathcal{L}^{\ast}\), as generators of positive semigroups, and Φ as a positive map, are all ∗-maps.
The fact that Φ is ρ-self-adjoint implies Φ
∗(Xρ)=Φ(X)ρ for all \(X\in \mathcal{O}\) and in particular that  . Thus, since T,
. Thus, since T,  and ρ are self-adjoint, it follows from
and ρ are self-adjoint, it follows from

that ρ commutes with T and  . A simple calculation yields
. A simple calculation yields

and Part (1) follows.
The formula (42) implies that \(\mathcal{L}^{\rho}\) is a ∗-map. Thus, one can write
It follows that \([\mathcal{L}^{\rho},\varDelta_{\rho}]=0\) and, since Δ ρ is ρ-self-adjoint, that \([\mathcal{L},\varDelta_{\rho}]=0\). Clearly, [T,ρ]=0 implies that \([\mathcal{L}^{(h)},\varDelta_{\rho}]=0\) and \(\mathcal{L}^{(h)\ast}(\rho)=0\). Thus, one also has \([\mathcal{L}^{(d)},\varDelta_{\rho}]=0\) and
Finally,  implies [Φ,Δ
ρ
]=0, which concludes the proof of Part (2).
implies [Φ,Δ
ρ
]=0, which concludes the proof of Part (2).
Denote by logρ=∑ λ λP λ the spectral representation of logρ. The operator logΔ ρ =[logρ, ⋅ ] is self-adjoint on \(\mathcal{O}\), with spectrum sp(logΔ ρ )=sp(logρ)−sp(logρ). Its spectral representation is given by
Since Φ commutes with Δ ρ , it commutes with each of the spectral projection \(\mathcal{P}_{\omega}\), and in particular one has \(\mathcal{P}_{\omega}\circ\varPhi\circ \mathcal{P}_{\omega}=\mathcal{P}_{\omega}\circ\varPhi\). Thus, setting

we have
Moreover, since Φ is completely positive, it follows from the identity
where A i,λ =A i P λ and B i,λ =P λ−ω B i , that Φ ω is completely positive. Next, note that the identity
implies
The identity Φ ∗(X)=Φ(Xρ −1)ρ and a simple calculation yield

The last identity combined with Eq. (44) gives
and Part (3) follows.
To prove Part (4), note that since \(\mathcal{L}\) commutes with Δ ρ , one has
The formula (41) follows from the relation \(\mathcal{L}_{\alpha}(X)=\mathcal{L}(X\rho^{-\alpha})\rho^{\alpha}\), the fact that ρ commutes with T and  and Eq. (44). Since \(\mathrm {e}^{t\mathcal{L}_{\alpha}}=\mathcal{R}_{\rho}^{\alpha/2}\circ \mathrm {e}^{t\mathcal{L}}\circ \mathcal{R}_{\rho}^{-\alpha/2}\), \(\{\mathrm {e}^{t\mathcal{L}_{\alpha}}\}_{t\geq0}\) is a \(\mathrm{CP}(\mathcal{O})\) semigroup for all \(\alpha\in {\mathbb{R}}\), and Part (4) follows.
and Eq. (44). Since \(\mathrm {e}^{t\mathcal{L}_{\alpha}}=\mathcal{R}_{\rho}^{\alpha/2}\circ \mathrm {e}^{t\mathcal{L}}\circ \mathcal{R}_{\rho}^{-\alpha/2}\), \(\{\mathrm {e}^{t\mathcal{L}_{\alpha}}\}_{t\geq0}\) is a \(\mathrm{CP}(\mathcal{O})\) semigroup for all \(\alpha\in {\mathbb{R}}\), and Part (4) follows.
It remains to prove Part (5). Define \(\mathcal{L}_{\alpha}^{(d)}(X)=\mathcal{L}^{(d)}(X\rho^{-\alpha})\rho^{\alpha}\). A simple calculation gives
and Part (1) implies
Hence,
Since Θ is involutive, the relation \(\mathcal{L}^{\rho}\circ\varTheta=\varTheta \circ \mathcal{L}\) implies \(\mathcal{L}\circ\varTheta=\varTheta\circ \mathcal{L}^{\rho}\). It follows from Part (1) that \(\mathcal{L}^{(h)}\circ\varTheta=-\varTheta\circ \mathcal{L}^{(h)}\) and \(\mathcal{L}^{(d)}\circ\varTheta =\varTheta\circ \mathcal{L}^{(d)}\). Moreover, Θ(ρ α)=ρ α implies \(\mathcal{L}_{\alpha}^{(d)}\circ\varTheta=\varTheta\circ \mathcal{L}_{\alpha}^{(d)}\). Thus, one has
and
□
We finish this section with:
Theorem 7.2
Let ρ be a faithful state and \(\mathcal{L}\) a Lindbladian on \(\mathcal{O}\) generating a QDS. Suppose that \(\mathcal{L}^{\ast}(\rho)=0\). Then the following statements are equivalent:
-
(1)
There exist a self-adjoint \(T\in \mathcal{O}\) such that the Hermitian part of \(\mathcal{L}\) w.r.t. the inner product induced by ρ has the form
$$\mathcal{L}^{(h)}(X)=\frac{1}{2}\bigl(\mathcal{L}- \mathcal{L}^\rho\bigr) (X)=\mathrm {i}[T, X]. $$ -
(2)
There exists a Lindblad decomposition
 such that
Φ
ρ=Φ.
such that
Φ
ρ=Φ.
Remark
This theorem establishes that Definition 2.4 (a) is equivalent to the definition of detailed balance given in [42] (see also Sect. IV in [48]). Although we shall not make use of this result in the sequel, we include the proof for reader’s convenience.
Proof
The implication (2) ⇒ (1) follows from Part (1) of Theorem 7.1. To prove the implication (1) ⇒ (2), note first that (1) implies that
is a Lindbladian generating a QDS. Since \(\mathcal{L}^{(d)}\) is ρ-self-adjoint, arguing as in (43) one deduces that \([\varDelta_{\rho}, \mathcal{L}^{(d)}]=0\). Let now  be a Lindblad decomposition. Since
be a Lindblad decomposition. Since
setting
we deduce that

is also a Lindblad decomposition. Clearly, [Δ
ρ
,Ξ]=0, [M,ρ]=0,  . Hence,
. Hence,

and we derive that  . Setting
. Setting
we get

where Φ is CP and Φ
ρ=Φ. Hence,  is a Lindblad decomposition of \(\mathcal{L}\) with Φ
ρ=Φ. □
is a Lindblad decomposition of \(\mathcal{L}\) with Φ
ρ=Φ. □
7.2 Irreducibility and Positivity Improving
We start with the following observation of [57]:
Proposition 7.3
A positive linear map \(\varPhi: \mathcal{O}\rightarrow \mathcal{O}\) is irreducible iff etΦ is positivity improving for some (and hence all) t>0.
Proof
If Φ is irreducible, then it follows from Lemma 2.1 in [28] that
is positivity improving, and so etΦ is positivity improving for all t>0. To prove the converse, suppose that etΦ is positivity improving and that Φ(P)≤λP, where λ>0 and \(P\not=0\) is a projection. Then Φ
n(P)≤λ
n
P for all n, and so 0<etΦ(P)≤eλt
P. The last relation implies that  . □
. □
Proof of Theorem 2.1
We follow [57]. Let \(\varphi,\psi\in \mathcal{H}\) be non-zero vectors and t>0. Expanding \(\mathrm {e}^{t\varPhi^{\ast}}\) into a power series, we get
Hence, \(\langle\varphi|\mathrm {e}^{t\varPhi^{\ast}}(|\psi\rangle\langle\psi|)\varphi \rangle=0\) iff \(\varphi\perp\mathcal{A}\psi\), and we deduce that \(\mathrm {e}^{t\varPhi^{\ast}}\) is positivity improving iff \(\mathcal{A}\psi=\mathcal{H}\) for all non-zero vectors \(\psi\in \mathcal{H}\). Since \(\mathrm {e}^{t\varPhi^{\ast}}\) is positivity improving iff etΦ is, the result follows from Proposition 7.3. □
Proof of Theorem 2.2
The proof of based on Perron-Frobenius theory of positive maps developed in [28]. Let t>0 be given. The map \(\mathrm {e}^{t \mathcal{L}}\) is positive and its spectral radius is etℓ. It follows from Theorem 2.5 in [28] that etℓ is an eigenvalue of \(\mathrm {e}^{t \mathcal{L}}\), and that there exists a non-zero \(M\in \mathcal{O}_{+}\) such that
Since the map \(\mathrm {e}^{t \mathcal{L}}\) is positivity improving, M>0. Define
The map Ψ is unital, completely positive (hence Schwartz), and positivity improving (hence irreducible). The same holds for Ψ n , n≥1, and it follows from Theorem 4.2 in [28] that 1 is a simple eigenvalue of Ψ and that Ψ has no other eigenvalues on the unit circle |z|=1. Hence, \(\mathcal{L}\) has a simple eigenvalue at ℓ and no other eigenvalues on the line Re z=ℓ.
Denote by μ the eigenvector of \(\mathcal{L}^{\ast}\) associated to the eigenvalue ℓ. Since \(\mathrm {e}^{t\mathcal{L}^{\ast}}\) is positivity improving by duality, one can chose μ>0 and normalize it by 〈μ|M〉=1. Let δ>0 be the distance from \(\mathrm{sp}(\mathcal{L})\setminus\{\ell\}\) to the line Re z=ℓ. Then, for any ϵ>0,
holds for all states ρ and all \(X\in \mathcal{O}\). Since 〈ρ|M〉>0 and 〈μ|X〉>0 for non-zero \(X\in \mathcal{O}_{+}\), Eq. (3) follows.
If  , then
, then  and since
and since  , it follows that ℓ=0 and
, it follows that ℓ=0 and  . By duality, (45) yields
. By duality, (45) yields
and the semigroup \(\{\mathrm {e}^{t \mathcal{L}}\}_{t\geq0}\) is relaxing exponentially fast to the faithful state ρ +=μ. □
Proof of Theorem 2.3
Note that \(\mathcal{K}_{0}\colon X\mapsto K^{\ast}X+XK\) generates a continuous group of completely positive maps on \(\mathcal{O}\), namely \(\mathrm {e}^{t\mathcal{K}_{0}}(X)=\mathrm {e}^{tK^{\ast}}X \mathrm {e}^{tK}\). Denoting \(\varGamma^{t}=\mathrm {e}^{-t\mathcal{K}_{0}}\circ \mathrm {e}^{t\mathcal{K}}\), it is sufficient to show that 〈φ|Γ t(|ψ〉〈ψ|)φ〉>0 for any non-zero vectors \(\varphi,\psi\in \mathcal{H}\) and all t>0. To prove this claim, let us assume that \(\langle\varphi|\varGamma^{t_{0}}(|\psi\rangle\langle\psi|)\varphi\rangle=0\) for some t 0>0. The Dyson expansion for \(\varGamma^{t_{0}}\) gives
where
\(\varPhi_{s}=\mathrm {e}^{-s\mathcal{K}_{0}}\circ\varPhi\circ \mathrm {e}^{s\mathcal{K}_{0}}\) for \(s\in {\mathbb{R}}\), and \(\varPhi^{n}_{s}=\varPhi_{s_{1}}\circ\varPhi_{s_{2}}\circ\cdots\circ\varPhi_{s_{n}}\) for s∈Δ n . It follows that
Since the functions \(s\mapsto\langle\varphi|\varPhi^{n}_{s}(|\psi\rangle \langle\psi|)\varphi\rangle\) are continuous and non-negative, we infer that \(\langle\varphi|\varPhi^{n}_{s}(|\psi\rangle\langle \psi|)\varphi\rangle=0\) for all n and all s∈Δ n , and in particular that 〈φ|Φ n(|ψ〉〈ψ|)φ〉=0 for all n. Hence, 〈φ|etΦ(|ψ〉〈ψ|)φ〉=0 for all t≥0, and Proposition 7.3 implies that φ=0 or ψ=0. □
For later reference, we mention the following simple fact:
Proposition 7.4
Let Φ j , j=1,…,n, be positive linear maps such that ∑ j Φ j is irreducible. If λ 1,…,λ n are strictly positive then ∑ j λ j Φ j is irreducible.
Proof
The result follows from the obvious inequality
□
7.3 Proof of Theorem 3.1
(1)–(2) were already proven in Sect. 6.
(3)–(4) By Eq. (39), Proposition 7.4, and Theorem 2.3, the CP semigroup \(\{\mathrm {e}^{t\mathcal{L}_{(\alpha)}}\}_{t\geq0}\) is positivity improving for all \(\alpha\in {\mathbb{R}}^{M}\), and the statement follows from Theorem 2.2.
(5) Note that the map \({\mathbb{C}}^{M}\ni\alpha\mapsto \mathcal{L}_{(\alpha)}\) is entire analytic. Since e(α) is a simple eigenvalue of \(\mathcal{L}_{(\alpha)}\) for all \(\alpha\in {\mathbb{R}}^{M}\), the regular perturbation theory implies that e(α) is a real analytic function of α. Property (2) and Hölder’s inequality yield that e(α) is a convex function of α.
(6) This part also follows from regular perturbation theory. Fix \(\alpha _{0}\in {\mathbb{R}}^{M}\) and set
If ϵ is small enough and \(\alpha\in D_{\epsilon}=\{z\in {\mathbb{C}}^{M}\,|\, |\alpha-\alpha_{0}|<\epsilon\}\), one has

where e(α), M
α
and μ
α
are analytic functions of α such that  and
and  . It follows that there exists ϵ>0 such that for α∈D
ϵ
,
. It follows that there exists ϵ>0 such that for α∈D
ϵ
,

(7) Let Θ be the time-reversal map. By Property (5) of Theorem 7.1 one has
for all \(\alpha\in {\mathbb{R}}^{M}\). It follows that \(\mathrm{sp}(\mathcal{L}_{(\alpha)})=\mathrm{sp}(\mathcal{L}_{(1-\alpha)})\) and hence e(α)=e(1−α).
(8) If Hypothesis (KMS β ) is satisfied, then \(\rho_{j}=Z_{j}^{-1}\nu^{\beta _{j}}\) with \(\nu=\mathrm {e}^{-H_{\mathcal{S}}}\) and \(Z_{j}=\mathrm{tr}(\nu^{\beta_{j}})\). Hence, \(\mathcal{R}_{\rho_{j}}^{\alpha_{j}}=Z_{j}^{-2\alpha_{j}}\mathcal{R}_{\nu}^{\alpha_{j}\beta_{j}}\) and Part (4) of Theorem 7.1 yields
It follows that
and so \(\mathrm{sp}(\mathcal{L}_{(\alpha+\lambda\beta^{-1})})=\mathrm{sp}(\mathcal{L}_{(\alpha)})\). In particular, e(α+λβ −1)=e(α).
7.4 Proof of Theorem 3.4
(1) At α=0, the spectral projection of \(\mathcal{L}_{(\alpha)}=\mathcal{L}\) associated to its dominant eigenvalue 1 is  . Thus, for α sufficiently close to \(0\in {\mathbb{R}}^{M}\), e(α)=E
1(α)/E
0(α) where
. Thus, for α sufficiently close to \(0\in {\mathbb{R}}^{M}\), e(α)=E
1(α)/E
0(α) where

and Γ is a small circle centred at 1 such that no other point of \(\mathrm{sp}(\mathcal{L})\) is on or inside Γ. Since  , one has E
1(0)=0 and E
0(0)=1 and hence \((\partial_{\alpha_{j}}e)(0)=(\partial_{\alpha_{j}}E_{1})(0)\). An elementary calculation yields
, one has E
1(0)=0 and E
0(0)=1 and hence \((\partial_{\alpha_{j}}e)(0)=(\partial_{\alpha_{j}}E_{1})(0)\). An elementary calculation yields

where
The identities

yield
and the statement follows.
(2) From the previous calculation, we easily infer

where

Theorem 7.1 (2) implies
and hence \(\mathcal{L}_{j}([S_{j},X])=[S_{j},\mathcal{L}_{j}(X)]\). It follows that \([S_{j},\mathcal{L}_{j}(S_{j})]=0\) and  . Using the fact that
. Using the fact that
we can replace \(\mathcal{I}_{j/k}\) with \(\mathcal{J}_{j/k}=\mathcal{I}_{j/k}-\rho_{+}(\mathcal{I}_{j/k})\) in Eq. (47). Since \(\rho_{+}(\mathcal{J}_{j})=0\), the meromorphic function \((z-\mathcal{L})^{-1}(\mathcal{J}_{j})\) is regular at z=0 and one has
the integral on the r.h.s. being absolutely convergent. We therefore have
The relation
now follows from Eq. (46) and the identity
Finally, an application of Vitali’s convergence theorem (see Appendix B in [36]) gives
Notes
The name quantum Markov semigroup is also used in the literature.
The level sets of I are {ς | I(ς)≤l} where l∈[0,∞[.
The derivative exists for all \(\rho\in \mathfrak{S}\), see Theorem 3 in [60].
This does not imply that L jk =L kj .
Here, we could also consider conserved charges and introduce associated chemical potentials. We refrain to do so in order to keep notation as simple as possible.
In some models (like the spin-boson system) the operators \(R^{(k)}_{j}\) are unbounded and only affiliated to the W ∗-algebra \(\mathcal{O}_{j}\). With some additional technicalities the discussions of this and the next three section easily extend to such cases, see any of the references [15, 17, 19, 41, 48].
The same conditions ensure that the terms \(\rho_{\beta_{0}}(D_{j}(H_{\mathcal{S}}, H_{\mathcal{S}}))\) in Theorem 3.5(1) are strictly positive, providing of course that
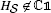 .
.At the current level of generality, the verification of Hypothesis (RE) requires supplementing Davies’ conditions with additional regularity assumptions which we shall not discuss for reasons of space. In practice, i.e. in the context of concrete models, the verification of (RE) is typically an easy exercise.
References
Agarwal, G.S.: Open quantum markovian systems and the microreversibility. Z. Physik 258, 409–422 (1973)
Andrieux, D., Gaspard, P., Monnai, T., Tasaki, S.: The fluctuation theorem for currents in open quantum systems. New J. Phys. 11, 043014 (2009)
Alicki, R.: On the detailed balance condition for non-Hamiltonian systems. Rep. Math. Phys. 10, 249–258 (1976)
Alicki, R., Lendi, K.: Quantum Dynamical Semigroups and Applications. Springer, Berlin (2007)
Aschbacher, W., Spohn, H.: A remark on the strict positivity of the entropy production. Lett. Math. Phys. 75, 17–23 (2006)
Bryc, W.: A remark on the connection between the large deviation principle and the central limit theorem. Stat. Prob. Lett. 18, 253–256 (1993)
Christensen, E., Evans, D.E.: Cohomology of operator algebras and quantum dynamical semigroups. J. London Math. Soc. 20, 358–368 (1979)
Chetrite, R., Mallick, K.: Quantum fluctuation relations for the Lindblad master equation. J. Stat. Phys. 148, 480–501 (2012)
Davies, E.B.: Quantum stochastic processes II. Commun. Math. Phys. 19, 83–105 (1970)
Davies, E.B.: Markovian master equations. Commun. Math. Phys. 39, 91–110 (1974)
Davies, E.B.: Markovian master equations. II. Math. Ann. 219, 147–158 (1976)
Davies, E.B.: Markovian master equations. III. Ann. Inst. H. Poincaré, section B 11, 265–273 (1975)
Davies, E.B.: Quantum Theory of Open Systems. Academic Press, London (1976)
Dereziński, J., de Roeck, W., Maes, C.: Fluctuations of quantum currents and unravelings of master equations. J. Stat. Phys. 131, 341–356 (2008)
Dereziński, J., Früboes, R.: Fermi golden rule and open quantum systems. In: Attal, S., Joye, A., Pillet, C.-A. (eds.) Open Quantum Systems III. The Markovian Approach. Lecture Notes in Mathematics, vol. 1882. Springer, Berlin (2006)
Dereziński, J., Jakšić, V.: On the nature of Fermi Golden Rule for open quantum systems. J. Stat. Phys. 116, 411–423 (2004)
Dereziński, J., Jakšić, V., Pillet, C.-A.: Perturbation theory of W ∗-dynamics, Liouvilleans and KMS-states. Rev. Math. Phys. 15, 447–489 (2003)
de Roeck, W.: Quantum fluctuation theorem: Can we go from micro to meso? Comptes Rendus Phys. 8, 674–683 (2007)
de Roeck, W.: Large deviation generating function for currents in the Pauli-Fierz model. Rev. Math. Phys. 21, 549–585 (2009)
de Roeck, W., Kupianien, A.: ‘Return to Equilibrium’ for weakly coupled quantum systems: a simple polymer expansion. Commun. Math. Phys. 305, 797–826 (2011)
de Roeck, W., Kupianien, A.: Approach to ground state and time-independent photon bound for massless spin-boson models. Ann. H. Poincaré 14, 253–311 (2013)
de Roeck, W., Maes, C.: Steady state fluctuations of the dissipated heat for a quantum stochastic model. Rev. Math. Phys. 18, 619–653 (2006)
Davies, E.B., Spohn, H.: Open quantum systems with time-dependent Hamiltonians and their linear response. J. Stat. Phys. 19, 511–523 (1978)
Dümcke, R., Spohn, H.: The proper form of the generator in the weak coupling limit. Z. Physik B 34, 419–422 (1979)
Dembo, A., Zeitouni, O.: Large Deviations Techniques and Applications, 2nd edn. Applications of Mathematics, vol. 38. Springer, New York (1998)
Evans, D.J., Cohen, E.G.D., Morriss, G.P.: Probability of second law violation in shearing steady flows. Phys. Rev. Lett. 71, 2401–2404 (1993)
Esposito, M., Harbola, U., Mukamel, S.: Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 81, 1665–1702 (2009)
Evans, D.E., Høegh-Krohn, R.: Spectral properties of positive maps on C ∗-algebras. J. London. Math. Soc. 17, 345–355 (1978)
Ellis, R.S.: Entropy, Large Deviations, and Statistical Mechanics. Classics of Mathematics. Springer, Berlin (1985). Reprinted in the series, 2006
Evans, D.J., Searles, D.J.: Equilibrium microstates which generate second law violating steady states. Phys Rev. E 50, 1645–1648 (1994)
Fagnola, F., Umanità, V.: Detailed balance, time reversal, and generators of quantum Markov semigroups. Mathematical Notes 84, 108–115 (2008)
Gallavotti, G.: Extension of Onsager’s reciprocity to large fields and the chaotic hypothesis. Phys. Rev. Lett. 77, 4334–4337 (1996)
Gallavotti, G., Cohen, E.G.D.: Dynamical ensembles in nonequilibrium statistical mechanics. Phys. Rev. Lett. 74, 2694–2697 (1995)
Gallavotti, G., Cohen, E.G.D.: Dynamical ensembles in stationary states. J. Stat. Phys. 80, 931–970 (1995)
Gorini, V., Kossakowski, A., Sudarshan, E.C.G.: Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 17, 821–825 (1976)
Jakšić, V., Ogata, Y., Pautrat, Y., Pillet, C.-A.: Entropic fluctuations in quantum statistical mechanics—an introduction. In: Fröhlich, J., Salmhofer, M., de Roeck, W., Mastropietro, V., Cugliandolo, L.F. (eds.) Quantum Theory from Small to Large Scales. Oxford University Press, Oxford (2012)
Jakšić, V., Ogata, Y., Pillet, C.-A., Seiringer, R.: Quantum hypothesis testing and non-equilibrium statistical mechanics. Rev. Math. Phys. 24, 1230002 (2012)
Jakšić, V., Pillet, C.-A.: Non-equilibrium steady states of finite quantum systems coupled to thermal reservoirs. Commun. Math. Phys. 226, 131–162 (2002)
Jakšić, V., Pillet, C.-A.: Entropic functionals in quantum statistical mechanics. In: Proceedings of the XVIIth International Congress of Mathematical Physics. Aalborg, Denmark (2012), to appear
Jakšić, V., Pillet, C.-A., Rey-Bellet, L.: Entropic fluctuations in statistical mechanics I. Classical dynamical systems. Nonlinearity 24, 699 (2011)
Jakšić, V., Panati, A., Pillet, C.-A., Westrich, M.: Non-equilibrium statistical mechanics of Pauli-Fierz systems. In preparation
Kossakowski, A., Frigerio, A., Gorini, V., Verri, M.: Quantum detailed balance and KMS condition. Commun. Math. Phys. 57, 91–110 (1977)
Kurchan, J.: Fluctuation theorem for stochastic dynamics. J. Phys. A 31, 3719–3729 (1998)
Kurchan, J.: 2000, A quantum fluctuation theorem. Preprint. arXiv:cond-mat/0007360
Lieb, E.H.: Convex trace functions and the Wigner-Yanase-Dyson conjecture. Adv. in Math. 11, 267–288 (1973)
Lindblad, G.: On the generators of quantum dynamical semigroups. Commun. Math. Phys. 48, 119–130 (1976)
Lindblad, G.: Dissipative operators and cohomology of operator algebras. Lett. Math. Phys. 1, 219–224 (1976)
Lebowitz, J.L., Spohn, H.: Irreversible thermodynamics for quantum systems weakly coupled to thermal reservoirs. Adv. Chem. Phys. 38, 109–142 (1978)
Lebowitz, J.L., Spohn, H.: A Gallavotti-Cohen-type symmetry in the large deviation functional for stochastic dynamics. J. Stat. Phys. 95, 333–365 (1999)
Maes, C.: The fluctuation theorem as a Gibbs property. J. Stat. Phys. 95, 367–392 (1999)
Majewski, W.A.: The detailed balance condition in quantum statistical mechanics. J. Math. Phys. 25, 614–616 (1984)
Maes, C., Redig, F., Verschuere, M.: From global to local fluctuation theorems. Mosc. Math. J. 1, 421–438 (2001)
Matsui, T., Tasaki, S.: Fluctuation theorem, nonequilibrium steady states and MacLennan-Zubarev ensembles of a class of large quantum systems. In: Accardi, L., Tasaki, S. (eds.) Fundamental Aspects of Quantum Physics. World Scientific, Singapore (2003)
Ohya, M., Petz, D.: Quantum Entropy and its Use, 2nd edn. Springer, Berlin (2004)
Rebolledo, R.: Complete positivity and the Markov structure of open quantum systems. In: Attal, S., Joye, A., Pillet, C.-A. (eds.) Open Quantum Systems II. The Markovian Approach. Lecture Notes in Mathematics, vol. 1882. Springer, Berlin (2006)
Rondoni, L., Mejía-Monasterio, C.: Fluctuations in non-equilibrium statistical mechanics: models, mathematical theory, physical mechanisms. Nonlinearity 20, 1–37 (2007)
Schrader, R.: Perron-Frobenius theory for positive maps on trazce ideals. In: Mathematical Physics in Mathematics and Physics, Siena, 2000. Fields Inst. Commun., vol. 30, pp. 361–378. AMS, Providence (2001)
Spohn, H.: Approach to equilibrium for completely positive dynamical semigroups of N-level systems. Rep. Math. Phys. 10, 189–194 (1976)
Spohn, H.: An algebraic condition for the approach to equilibrium of an open N-level system. Lett. Math. Phys. 2, 33–38 (1977)
Spohn, H.: Entropy production for quantum dynamical semigroups. J. Math. Phys. 19, 1227–1230 (1978)
Stinespring, W.F.: Positive functions on C ∗-algebras. Proceedings of the American Mathematical Society 6, 211–216 (1955)
Uhlmann, A.: Relative entropy and the Wigner-Yanase-Dyson-Lieb concavity in an interpolation theory. Comm. Math. Phys. 54, 21–32 (1977)
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Herbert Spohn on the occasion of his 65th birthday.
The research of V.J. was partly supported by NSERC. The research of C.-A.P. was partly supported by ANR (grant 09-BLAN-0098). C.-A.P. is also grateful to the Department of Mathematics and Statistics at McGill University and to CRM (CNRS–UMI 3457) for hospitality and generous support during his stay in Montreal where most of this work was done. We are grateful to J. Dereziński, B. Landon, and A. Panati for useful comments. We also thank C. Maes and W. de Roeck for interesting related discussions.
Rights and permissions
About this article
Cite this article
Jakšić, V., Pillet, CA. & Westrich, M. Entropic Fluctuations of Quantum Dynamical Semigroups. J Stat Phys 154, 153–187 (2014). https://doi.org/10.1007/s10955-013-0826-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-013-0826-5



 such that Φ is ρ-self-adjoint.
such that Φ is ρ-self-adjoint.


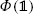 commute with
ρ
and
commute with
ρ
and

 such that
Φ
ρ=Φ.
such that
Φ
ρ=Φ.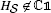 .
.