The Signed Loop Approach to the Ising Model: Foundations and Critical Point

Abstract

The signed loop approach is a beautiful way to rigorously study the two-dimensional Ising model with no external field. In this paper, we explore the foundations of the method, including details that have so far been neglected or overlooked in the literature. We demonstrate how the method can be applied to the Ising model on the square lattice to derive explicit formal expressions for the free energy density and two-point functions in terms of sums over loops, valid all the way up to the self-dual point. As a corollary, it follows that the self-dual point is critical both for the behaviour of the free energy density, and for the decay of the two-point functions.

1 Introduction and Main Results

The Ising model [14] was introduced to explain certain properties of ferromagnets, in particular, the phenomenon of spontaneous magnetization. In 1952, Kac and Ward [15] proposed a method for approaching the Ising model on $\mathbb{Z}^{2}$, based on studying configurations of signed loops. In this self-contained paper, we explore this method in detail and with mathematical rigour. This leads to new explicit formal expressions for the free energy density and two-point functions in terms of sums over signed loops, which in turn allow us to rederive several classical results about the Ising model.

We consider the Ising model on finite rectangles in $\mathbb{Z}^{2}$, by which we mean graphs G=(V,E) whose vertex sets V consist of all points of $\mathbb{Z}^{2}$ contained in a rectangle [a,b]×[c,d] in $\mathbb{R}^{2}$, and whose edge sets E consist of all unordered pairs {u,v} with u,v∈V such that their L ₁ distance ∥u−v∥ is 1. For brevity, we will also write uv instead of {u,v} for the edge between u and v (note that uv=vu). The boundary ∂G of G is the set of those vertices u in V for which there is a $v\in\mathbb{Z}^{2}\setminus V$ with ∥u−v∥=1.

We associate to G a space of spin configurations Ω _G ={−1,+1}^V. For σ∈Ω _G , σ _v denotes the spin at v. Sometimes we impose positive boundary conditions, meaning that we restrict ourselves to the set of configurations

$$\varOmega_G^+ = \{\sigma\in\varOmega_G \colon \sigma_u = +1\ \text{if}\ u\in{\partial G}\}. $$

In contrast, when we speak of free boundary conditions, we work with the unrestricted set of spin configurations $\varOmega_{G}^{\text {free}}= \varOmega_{G}$.

The Ising model defines a (Gibbs–Boltzmann) probability distribution on the set of spin configurations. At inverse temperature β, it is given by

$$ P^\Box_{G,\beta}(\sigma) = \frac{1}{Z^\Box_{G,\beta}} \prod_{uv\in E} e^{\beta\sigma_u\sigma_v}, \quad\sigma\in\varOmega_G^\Box, $$

(1.1)

where □∈{free,+} stands for the imposed boundary condition, and $Z^{\Box}_{G,\beta}$ is the partition function of the model, defined as

$$ Z^\Box_{G,\beta} = \sum _{\sigma\in\varOmega^\Box} \prod_{uv\in E} e^{\beta\sigma _u\sigma_v}. $$

(1.2)

To simplify the notation, and following the physics literature, we will write

$$ \langle{\,\cdot\,}\rangle^\Box_{G,\beta} = E^\Box_{G,\beta}(\, \cdot\,) $$

(1.3)

for expectations with respect to $P^{\Box}_{G,\beta}$. Important functions are the Helmholtz free energy

$$F^\Box_{G,\beta} = -\beta^{-1} \ln Z^\Box_{G,\beta} $$

and the free energy density f(β), obtained as the infinite-volume limit

$$\lim_{G\to\mathbb{Z}^2} \frac{1}{\lvert{V}\rvert} F^\Box_{G,\beta} = \lim_{G\to\mathbb{Z}^2} -\frac{1}{\beta\lvert{V}\rvert} \ln Z^\Box_{G,\beta} =: f(\beta). $$

It is well known that this limit exists, and also not difficult to show that the limit is the same for all boundary conditions, see for example [26, Sect. II.3] (as we shall see, existence of the limit actually also follows from the signed loop approach for non-critical β). The formalism of statistical mechanics predicts that phase transitions coincide with discontinuities or other singularities in derivatives of the free energy density.

In the case of the Ising model on $\mathbb{Z}^{2}$, the classical arguments of Peierls [23] and Fisher [9] (see also [6, 11, 12]) established that it does undergo a phase transition, which can be characterized in terms of a change in behaviour of the infinite-volume limits $\langle{\sigma_{u} \sigma_{v} }\rangle ^{\Box}_{\mathbb{Z}^{2}, \beta}$ of the two-point functions $\langle{\sigma_{u}\sigma _{v} }\rangle^{\Box}_{G, \beta}$. Peierls’ argument implies that as ∥u−v∥→∞, these infinite-volume two-point functions stay bounded away from 0 for large enough β. In contrast, Fisher’s argument yields exponential decay to 0 of these two-point functions as ∥u−v∥→∞, for sufficiently small β. However, there is a gap between the two ranges of β for which these arguments work, so they are not strong enough to conclude that the phase transition is sharp. As we shall see, the signed loop method studied here does lead to a proof of this fact.

To be more specific, a signed loop is essentially a closed, non-backtracking walk, with a positive or negative weight assigned to it; see Sect. 1.1 for a precise definition. In this paper, we demonstrate how the free energy and two-point functions can be expressed as (infinite) sums over signed loops in $\mathbb{Z}^{2}$, and moreover, how the rate of convergence of these sums can be controlled. For instance, Theorem 1.2 below expresses the free energy density f(β) as an explicit formal sum of the weights of all loops for which the origin is the “smallest” vertex visited (in lexicographic order). Likewise, Theorems 1.4 and 1.6 express the two-point functions $\langle{\sigma_{u} \sigma_{v} }\rangle ^{\Box}_{\mathbb{Z}^{2},\beta}$ as infinite sums over explicitly defined classes of signed loops.

In all cases, we first derive the corresponding loop expressions for finite rectangles G. These were also obtained simultaneously and independently by Helmuth [13] via the theory of heaps of pieces, but we in addition give explicit bounds on the rates of convergence to take the infinite-volume limit. As corollaries, without requiring any external results, we rederive several classical results about the Ising model, which can be summarized as follows:

Corollary 1.1

(Sharpness of phase transition)

The free energy density f(β) is analytic for all β>0 except at the self-dual point β=β _c given by

$$ \exp(-2\beta_c) = \tanh \beta_c = \sqrt{2}-1. $$

(1.4)

Moreover, as ∥u−v∥→∞, $\langle {\sigma_{u} \sigma_{v} }\rangle^{\mathrm{free}}_{\mathbb{Z}^{2}, \beta}$ decays to 0 exponentially fast when β∈(0,β _c ), while $\langle\sigma_{u}\sigma_{v} \rangle^{+}_{\mathbb {Z}^{2}, \beta}$ stays bounded away from 0 when β∈(β _c ,∞).

Of course, various other approaches to the Ising model have been developed and explored in the past. Most famous are the original algebraic methods of Onsager and Kaufman [17, 18, 21], used by them to compute the free energy and study correlations (see also [22]). We also mention the approach of Aizenman, Barsky and Fernández [1], who prove sharpness of the phase transition using differential inequalities (this approach actually applies to a large class of ferromagnetic spin models in any dimension). More recently, in [2], the fermionic observables, originally introduced by Smirnov [27] to study the Ising model at criticality, have been used in an interesting way for yet another derivation of the value of the critical point.

The method considered here (based on the proposition of Kac and Ward) is combinatorial in nature, and as such often referred to as the combinatorial method, but there are other approaches which include combinatorial aspects, such as the dimer approach exposed in [20]. We therefore prefer to refer to the method considered here as the signed loop approach.

Over the years, a number of articles developing the signed loop approach have appeared in the physics literature, of which the most relevant are [3, 5, 10, 24, 25, 28]. However, from a mathematical point of view, these papers leave a lot to be desired in terms of rigour and technical details. Moreover, doubts have been cast on the very validity of the whole method to begin with, not only in the years following the Kac–Ward paper, but still recently by Dolbilin et al. [7], who rightly pointed out an error in Vdovichenko’s article [28] (reproduced in [19, §151]) on the signed loop method.

With the present paper, we aim to remove these doubts and deficiencies once and for all. To this end, we provide complete, rigorous and detailed proofs of the combinatorial identities central to the signed loop method, all in a geometric manner. Our proofs of these identities essentially follow the same steps as Vdovichenko’s paper. A key feature of this particular approach is that each configuration of s loops is assigned a signed weight which is simply the product of the signed weights of the individual loops, divided by s!. This factorization of weights is a crucial aspect of the method, which we believe could well be the key to further results beyond this paper. We show here that the desired factorization can be made to work if one defines the weight of a loop in the right way. Specifically, the error of Vdovichenko was that she did not include a loop’s multiplicity into its weight, as we do in equation (1.7) below. In addition to clarifying the signed loop approach and correcting Vdovichenko’s error in this way, we also apply the results to the Ising model on $\mathbb{Z}^{2}$ in ways not considered before to derive both new and classical results about the Ising model, as was already mentioned above.

The paper is organized as follows. A precise definition of signed loops and the formulation of our main results follows in Sects. 1.1–1.4, with our results for the Ising model in Sect. 1.2, and our key combinatorial identities in Sect. 1.4. A brief discussion of the history and status of the combinatorial identities is included at the end of Sect. 1.4. The proofs of these identities are given in Sect. 2, and the proofs of our results about the Ising model are in Sect. 3.

1.1 Signed Loops

Although our applications are in $\mathbb{Z}^{2}$, it will be both necessary for this paper and of interest for future applications to study signed loops on a more general class of graphs. Our starting point is a (finite or infinite) graph G=(V,E) embedded in the plane, with vertex set V and edge set E. We identify G with its embedding. We assume G does not have multiple edges, but we do not assume that G is planar. For convenience (although this is not strictly necessary), we require that edges are straight line segments in the embedding, and that except for the vertices at the two endpoints, no other vertices lie on an edge. As before, we write uv or vu for the (undirected) edge between u and v.

A path of n steps in G is a sequence (v ₀,v ₁,…,v _n−1)∈V ⁿ such that v _i v _i+1∈E for i=0,1,…,n−2, and v _i+2≠v _i for i=0,1,…,n−3 (paths are non-backtracking). If all rotations of the sequence (v ₀,…,v _n−1) are also paths (so that in particular, v ₀ v _n−1∈E), then we call the path closed. We now order the vertices of G lexicographically by their coordinates in the plane, and define a loop as a closed path (v ₀,…,v _n−1) which is the lexicographically smallest element in the collection consisting of all rotations of (v ₀,…,v _n−1) and all rotations of the reverse sequence (v _n−1,…,v ₀) (note that these are all in a way closed paths traversing the same loop).

If ℓ=(v ₀,…,v _n−1) is a loop or a closed path, we shall make the identification v _j ≡v _jmodn for all $j\in\mathbb {Z}$. We say that a loop ℓ is edge-disjoint if v _i v _i+1≠v _j v _j+1 for all i,j∈{0,…,n−1} with i≠j. If ℓ is not edge-disjoint, it might be the case that the sequence (v ₀,…,v _n−1) is periodic, in which case we call ℓ a periodic loop. The multiplicity of ℓ, denoted by m(ℓ), is its number of steps divided by its smallest period. In particular, the multiplicity of every nonperiodic loop is 1.

Given two distinct edges uv and vw, we define ∠(v−u,w−v)∈(−π,π) as the turning angle in the plane from the vector v−u to w−v, see Fig. 1 (left). The winding angle α(ℓ) of a loop ℓ=(v ₀,…,v _n−1) is simply the sum of all turning angles along the loop, that is,

$$ \alpha(\ell) = \sum_{i=0}^{n-1} \angle(v_{i+1}-v_i,v_{i+2}-v_{i+1}). $$

(1.5)

We now define the sign $\operatorname{sgn}(\ell)$ of ℓ as

$$ \operatorname{sgn}(\ell) = - \exp\biggl( \frac{i}{2} \alpha(\ell) \biggr). $$

(1.6)

Observe that the winding angle of every loop is a multiple of 2π (here we use the fact that the edges of G are straight line segments), hence the sign of a loop is either +1 or −1.

Fig. 1

The turning angle from the vector v−u to the vector w−v (left). The loop (v ₁,v ₂,v ₃,v ₄,v ₅,v ₆) on the right has sign −1, the loop (v ₁,v ₂,v ₃,v ₅,v ₄,v ₆) has sign +1

To define the signed weight of a loop, we require a vector x=(x _uv ) _uv∈E of edge weights $x_{uv}\in\mathbb{R}$ (or $\mathbb{C}$). Given these edge weights x _uv , the signed weight of a loop ℓ=(v ₀,…,v _n−1) in G is defined as

$$ w(\ell; x) = \frac{\operatorname{sgn}(\ell )}{m(\ell)} \prod _{i=0}^{n-1} x_{v_iv_{i+1}}. $$

(1.7)

Remark

If a loop is edge-disjoint, it follows from Whitney’s formula [29] that the sign of the loop is −1 if and only if the loop crosses itself an odd number of times (see Fig. 1). For loops that are not edge-disjoint, it may not be so clear what is meant by a “crossing”, but definition (1.6) makes sense for both kinds of loop. However, if one draws loops in such a way that each visit to an edge is drawn slightly apart from a previous visit, the number of crossings one is forced to draw will always be odd for a loop of sign −1, and even for a loop of sign +1 (see for instance Fig. 5 below).

1.2 Main Results for the Ising Model

We now return to the Ising model on $\mathbb{Z}^{2}$. In this section we will formulate our main theorems for the Ising model, which express the free energy density and two-point functions in terms of sums over signed loops. Each of our theorems will be accompanied by a corollary, which taken together constitute Corollary 1.1. Similar results as the ones presented here can be obtained for the hexagonal and triangular lattices using the same methods. In fact, the method applies to the Ising model on even more general graphs, and also allows one to study general k-point functions. We intend to go into these issues in a subsequent paper.

We start with the free energy density f(β). As we shall prove, f(β) can be expressed as a sum over those loops in $\mathbb {Z}^{2}$ for which the origin o=(0,0) is the lexicographically smallest vertex traversed. To be more specific, we define $\mathcal{L}^{\circ}_{r} (\mathbb{Z}^{2})$ as the collection of all loops ℓ=(v ₀,…,v _r−1) of r steps in $\mathbb{Z}^{2}$ such that v ₀=o. We take all edges of $\mathbb{Z}^{2}$ to have the same edge weight x. The weights w(ℓ;x) of all loops $\ell\in\mathcal{L}^{\circ}_{r} (\mathbb {Z}^{2})$ are now defined by (1.7), where by slight abuse of notation, we let x denote both the weight of a single edge, and the vector of all edge weights. Write

$$f^\circ_r(x) = \sum_{\ell\in\mathcal{L}^\circ_r (\mathbb{Z}^2)} w( \ell;x). $$

Theorem 1.2

The free energy density satisfies

$$ -\beta f(\beta) = \begin{cases} \ln(2\cosh^2\beta) + \sum_{r=1}^\infty f^\circ_r ( \tanh \beta ) &\text{\textit{if} }\beta\in(0,\beta_c), \\ \noalign{\vspace{3pt}} 2\beta+ \sum_{r=1}^\infty f^\circ_r ( \exp(-2\beta) ) &\text{\textit{if} }\beta\in(\beta_c,\infty). \end{cases} $$

(1.8)

Note that since $f^{\circ}_{r}(x) = f^{\circ}_{r}(1) \, x^{r}$, $\sum_{r} f^{\circ}_{r}(x)$ is really a power series in the variable x. The power series expressions (1.8) show directly that the free energy density is an analytic function of β on (0,β _c )∪(β _c ,∞). Thus, in terms of the behaviour of the free energy density, the Ising model can only be critical at the self-dual point β _c . That f(β) is not analytic at β _c follows from Onsager’s formula, which we will obtain as a corollary to Theorem 1.2:

Corollary 1.3

(Onsager’s formula)

For β∈(0,β _c ) and for β∈(β _c ,∞), the free energy density f(β) is given by the formula

$$-\frac{1}{\beta}\frac{1}{8\pi^2} \int_0^{2\pi} \int_0^{2\pi} \ln\bigl[ 4 \cosh^22\beta- 4\sinh2\beta(\cos\omega_1 + \cos \omega_2) \bigr] \, d\omega_1\,d\omega_2. $$

The functions f and u=∂(βf)/∂β, which is the internal energy density of the system, are both continuous functions of β. However, in [21] Onsager has shown that the specific heat, which is the derivative of u with respect to temperature, diverges as β approaches β _c . This shows that β _c is indeed critical for the behaviour of the free energy.

Next, we look at the magnetic behaviour of the model by considering the one-point and two-point functions above and below β _c . We start with the case β∈(β _c ,∞). What we will show is that for fixed $u,v\in \mathbb{Z}^{2}$, the functions $\langle{\sigma_{u} }\rangle^{+}_{G, \beta }$ and $\langle{\sigma_{u} \sigma_{v} }\rangle^{+}_{G,\beta}$ have infinite-volume limits along rectangles G, where the limits can be identified in terms of sums over certain classes of loops in $\mathbb{Z}^{2*}$, the dual graph of $\mathbb{Z}^{2}$, defined as follows. Given $u,v\in\mathbb{Z}^{2}$, let γ be a self-avoiding path in $\mathbb{Z}^{2}$ from u to v (see Fig. 2, left). We call a loop in $\mathbb{Z}^{2*}$ uv-odd if it crosses γ an odd number of times. Similarly, we call a loop in $\mathbb{Z}^{2*}$ u-odd if it crosses a self-avoiding path γ in $\mathbb{Z}^{2}$ from u to ∞ an odd number of times. It is not difficult to see that neither of these definitions depends on the particular choice of γ. We write $\mathcal{L}^{u}_{r} (\mathbb{Z}^{2*})$ and $\mathcal{L}^{uv}_{r} (\mathbb{Z}^{2*})$ for the sets of u-odd and uv-odd loops in $\mathbb{Z}^{2*}$ of r steps, respectively.

Fig. 2

The paths γ (with bold edges), that we use to study the 2-point functions $\langle{\sigma_{u} \sigma_{v}}\rangle^{\Box}_{G,\beta }$. The low-temperature case is on the left (spins are −1 in the gray squares, +1 in the white regions), the high-temperature case on the right

Let x be the vector of edge weights on $\mathbb{Z}^{2*}$ such that every edge has the weight exp(−2β), and define the weights of loops in $\mathbb{Z}^{2*}$ by (1.7). Set

$$f^u_r(x) = \sum_{ \ell\in\mathcal{L}^u_r (Z^{2*}) } w( \ell; x); \qquad f^{uv}_r(x) = \sum _{ \ell\in\mathcal{L}^{uv}_r (\mathbb{Z}^{2*}) } w(\ell; x). $$

Theorem 1.4

For all β∈(β _c ,∞) and fixed $u,v\in\mathbb{Z}^{2}$ (u≠v),

As a corollary to the proof of this theorem, we will obtain that for β∈(β _c ,∞), the two-point functions in the infinite-volume limit stay bounded away from 0 as ∥u−v∥→∞:

Corollary 1.5

(Positive two-point functions above β _c )

For all β∈(β _c ,∞),

$$\lim_{\|{u-v}\|\to\infty} \langle{\sigma_u\sigma _v}\rangle^+_{\mathbb{Z}^2,\beta} = \bigl[ \langle\sigma_o \rangle^+_{\mathbb{Z}^2,\beta} \bigr]^2 > 0. $$

We now turn to the two-point functions for β∈(0,β _c ). Fix $u,v\in \mathbb{Z}^{2}$, and choose dual vertices u ^∗ and v ^∗ of $\mathbb {Z}^{2*}$ such that ∥u−u ^∗∥=∥v−v ^∗∥=1. This choice is not unique, but every choice of u ^∗ and v ^∗ will do. Next, choose a self-avoiding path γ in $\mathbb{Z}^{2*}$ from u ^∗ to v ^∗ (see Fig. 2, right). Let V _γ denote the set of vertices in γ, and let E _γ denote the union of {uu ^∗,vv ^∗} with the set of edges traversed by γ. Write $\mathbb{Z}^{2}_{\gamma}$ for the graph obtained from $\mathbb{Z}^{2}$ by adding the vertices and edges from V _γ and E _γ to it.

We define $\mathcal{L}^{uu^{*}}_{r} (\mathbb{Z}^{2}_{\gamma})$ as the collection of loops in $\mathbb{Z}^{2}_{\gamma}$ that visit the edge uu ^∗ exactly once and have r−|E _γ | steps. Note that by definition, if $\ell \in \mathcal{L}^{uu^{*}}_{r} (\mathbb{Z}^{2}_{\gamma})$, r only counts the number of steps taken by ℓ along edges of $\mathbb{Z}^{2}$, that is, the steps along the edges in E _γ are excluded. As our edge weight vector on $\mathbb {Z}^{2}_{\gamma}$ we take the vector $x'_{\gamma}$ such that the weight of every edge in E _γ is 1, the weight of every edge in $\mathbb{Z}^{2}$ which intersects γ is −tanhβ, and the weight of all other edges is tanhβ. Set

$$f^{uu^*}_r\bigl(x'_\gamma\bigr) = \sum_{ \ell\in\mathcal{L}^{uu^*}_r (\mathbb{Z}^2_\gamma) } w\bigl (\ell; x'_\gamma \bigr), $$

with $w(\ell; x'_{\gamma})$ defined by (1.7). Let β ^∗ denote the inverse temperature which is dual to β, i.e. such that exp(−2β ^∗)=tanhβ.

Theorem 1.6

For all β∈(0,β _c ) and fixed $u,v\in\mathbb{Z}^{2}$ (u≠v),

$$\lim_{G\to\mathbb{Z}^2} \langle\sigma_u \sigma_v \rangle^{\mathrm{free}}_{G,\beta} = \Biggl( \sum_{r=1}^\infty f^{uu^*}_r \bigl(x'_\gamma\bigr) \Biggr) \langle\sigma_{u^*} \sigma_{v^*} \rangle^+_{ \mathbb{Z}^{2*}, \beta^* } =: \langle{\sigma_u \sigma_v} \rangle^{\mathrm{free}}_{\mathbb {Z}^2,\beta}. $$

The term $\langle{\sigma_{u^{*}} \sigma_{v^{*}}}\rangle^{+}_{ \mathbb{Z}^{2*}, \beta^{*} }$ appearing here is the infinite-volume limit of a two-point function for an Ising model on the dual square lattice $\mathbb{Z}^{2*}$ at the dual inverse temperature β ^∗ with positive boundary conditions. It can be expressed in terms of signed loops by means of Theorem 1.4. As an aside, we note that the result in Theorem 1.6 simplifies when u and v are on the same face of $\mathbb{Z}^{2}$ (i.e. ∥u−v∥=1), since then we can take u ^∗=v ^∗, so that $\sigma_{u^{*}} \sigma_{v^{*}} = 1$. Moreover, since the path γ is void in this case, none of the edge weights will be equal to −tanhβ.

As a corollary to Theorem 1.6 we will obtain that the two-point functions decay exponentially to 0 with the distance ∥u−v∥ for β∈(0,β _c ), which together with Corollaries 1.3 and 1.5 implies Corollary 1.1:

Corollary 1.7

(Decaying two-point functions below β _c )

For all β∈(0,β _c ) and fixed $u,v\in\mathbb{Z}^{2}$, we have that

$$0\leq\langle{\sigma_u \sigma_v}\rangle^{\mathrm{free}}_{\mathbb {Z}^2,\beta} \leq16 \sum_{r\geq \|{u-v}\|} \biggl( \frac{\tanh\beta}{\tanh\beta_c} \biggr)^r. $$

Note that Corollaries 1.5 and 1.7 show contrasting behaviour of the two-point functions above and below β _c : at low temperatures they stay bounded away from 0, while for high temperatures they decay to 0. However, we have used different boundary conditions above and below the critical point. Ideally, we would like to use the signed loop method to show that for all β≠β _c , the infinite-volume limit of the two-point functions is the same for both boundary conditions. We leave this issue for a subsequent paper.

1.3 Additional Edges and Loop Length

The set of edges E _γ that we introduced above to formulate our Theorem 1.6 is an example of what we call additional edges. As this example shows, we occasionally need these additional edges in our applications. They act as “shortcuts” that our loops can follow, and in general, just as we did above, we do not want to count the steps taken by our loops along these shortcuts.

Another example of the use of additional edges is in our proofs leading to Corollary 1.3, in which we compare loops in $\mathbb {Z}^{2}$ with loops on a torus. Here we face a problem, because our methods and theorems about signed loops (to be presented below) require that the graph we work on is embedded in the plane. As a solution, we will not work on the torus directly, but on a representation of it in the plane. As our representation, we take a rectangle in $\mathbb{Z}^{2}$ with opposite sides connected by additional edges, as illustrated in Fig. 3. In this example, the additional edges do not correspond to edges that can be traversed by a loop on the torus, and this is the reason why steps taken along the additional edges again should not be counted.

Fig. 3

A square lattice wrapped around a torus (right) and a representation of it in the plane (left). The gray square corresponds to the torus, the dotted lines and open circles are the additional edges and vertices

In general, these considerations lead us to allow the edge set E of the graph G=(V,E) we work on to be divided into a set E _A of additional edges and a set E∖E _A of edges that we call representative. For reasons that will become clear, we must impose that the set E _A is such that the graph (V,E _A ) is free of cycles, but otherwise, the edge set can in principle be any subset of edges. We now define the length r(ℓ) of a loop ℓ=(v ₀,…,v _n−1) as the number of i in {0,…,n−1} such that v _i v _i+1∈E∖E _A . Note the distinction between the length of a loop and its number of steps.

1.4 The Combinatorial Identities

We next formulate our combinatorial identities about signed loops for a fixed finite graph G=(V,E) embedded in the plane, satisfying the same assumptions as in Sect. 1.1. In particular, recall that edges are straight line segments, and that we do not assume G is planar, which implies that two edges can intersect in a point which is not a vertex. In this case, we say that the two edges cross each other.

We call a subset F of E even if every vertex in the subgraph (V,F) of G has even degree (the empty set is also even). By C _F we denote the total number of unordered pairs of edges in F that cross each other. Given a vector x=(x _uv ) _uv∈E of edge weights on G, we now define the generating function Z(x) of even subgraphs of G as

$$ Z(x) = \sum_{\text{even}\ F\subset E} (-1)^{C_F} \prod_{uv \in F} x_{uv}. $$

(1.9)

If the graph G is planar, we can embed it in such a way that no edges cross each other, so that C _F =0 for all F, but in general, an even F⊂E may give a negative contribution to the right-hand side of (1.9). This makes our generating function different from the one usually studied in the literature. Note as a consequence that different embeddings of the same (abstract) graph can lead to different functions Z(x). Since we identify G with its embedding, this last fact does not concern us here.

Our combinatorial identities express the generating function Z(x) in terms of sums over the signed loops in G, with their weights defined by (1.7). This is what allows us to study the Ising model in terms of signed loops, since the free energy and the two-point functions of the Ising model can be expressed in terms of graph generating functions, as we shall see. Our first identity:

Theorem 1.8

For uv∈E, let d _uv denote the maximum of the degrees of u and v in the graph G. If |x _uv |<(d _uv −1)⁻¹ for all uv∈E, then

$$ Z(x) = \exp\biggl( \sum _{\ell\ \text{\textit{in}}\ G} w(\ell; x) \biggr). $$

(1.10)

We will show that under the condition of Theorem 1.8, the loop weights are absolutely summable, so that the order of summation does not matter. In particular, let $\mathcal{L}_{r}$ be the collection of all loops of length r in G, and let

$$ f_r(x) = \sum_{\ell\in\mathcal{L}_r} w(\ell; x). $$

(1.11)

Then Theorem 1.8 implies that Z(x) equals exp(∑ _r f _r (x)), but we claim that this latter equality already holds under a significantly weaker condition.

This condition can be formulated in terms of the transition matrix Λ(x), which we now introduce. If uv is an edge of G, then by $\overrightarrow{uv}$ we will denote the directed edge from u to v. The matrix Λ(x) will be indexed by the directed representative edges of G. Given two directed representative edges $\overrightarrow{uv}$ and $\overrightarrow{wz}$, we say that v is linked to w if either v=w, or there exists a sequence of distinct additional edges v ₁ v ₂,v ₂ v ₃,…,v _n−1 v _n such that v=v ₁ and v _n =w. In the former case, if v=w and u≠z, we write

$$\angle(\overrightarrow{uv}, \overrightarrow{wz}) = \angle(v-u, z-w) $$

for the turning angle from $\overrightarrow{uv}$ to $\overrightarrow {wz}$. In the latter case, the sequence (v ₁,…,v _n ) is a path (the chain) linking v to w, passing through additional edges only, and we say that “v⇝w via (v ₁,…,v _n )”. By our assumption that the additional edges form no cycles, there can be at most one such path. Hence, without ambiguity, if v is linked to w in this way, we can define

The transition matrix Λ(x) is now defined as follows. Write $\varLambda_{\overrightarrow{uv}, \overrightarrow{wz}}(x)$ for the entry of the matrix with row index $\overrightarrow{uv}$ and column index $\overrightarrow{wz}$. Then

$$ \varLambda_{\overrightarrow {uv},\overrightarrow{wz}}(x) = \everymath{\displaystyle}\begin{cases} x_{uv} e^{i\angle(\overrightarrow{uv},\overrightarrow{wz})/2} &\text{if}\ v = w\ \mbox{and}\ u\neq z; \\ \noalign{\vspace{6pt}} x_{uv} \prod_{i=1}^{n-1} x_{v_iv_{i+1}} e^{i\angle(\overrightarrow{uv},\overrightarrow{wz})/2} &\text{if}\ v \leadsto w\ \mbox{via}\ (v_1,\dots,v_n); \\ \noalign{\vspace{6pt}} 0 &\text{otherwise}. \end{cases} $$

(1.12)

Let λ _i (x), i=1,2,…,2|E∖E _A |, denote the eigenvalues of Λ(x), and let ρ(x)=max _i |λ _i (x)| be its spectral radius. We will show that if ρ(x)<1, then the f _r (x) are absolutely summable. This leads to our second identity, which forms the core of the signed loop approach:

Theorem 1.9

If ρ(x)<1, then

$$ Z(x) = \exp\Biggl( \sum_{r=1}^\infty f_r(x) \Biggr) = \sqrt{\det\bigl( \mathrm{I}- \varLambda(x) \bigr)}. $$

(1.13)

Clearly, to apply Theorem 1.9 to the Ising model on $\mathbb{Z}^{2}$, we will need a bound on the spectral radius ρ(x). Since ρ(x) is bounded from above by the operator norm ∥Λ(x)∥ of Λ(x) induced by the Euclidean metric, the desired bound is provided by the next theorem:

Theorem 1.10

For a finite rectangle G in  $\mathbb{Z}^{2}$ with no additional edges,

If we take all edge weights to be 1, Theorem 1.10 says that the “number” of signed loops of n steps, counted with signs and multiplicities included, grows (in absolute value) like $(\sqrt{2} + 1)^{n}$. Contrast this with the number of unsigned non-backtracking loops in $\mathbb{Z}^{2}$, which grows like 3ⁿ. It is this reduction in growth rate which allows us to go all the way to the critical point, while the classical Peierls and Fisher arguments stay far from it. Indeed, in Sect. 1.2 we have seen that we will take our edge weights to be either exp(−2β) or tanhβ, so by Theorem 1.10 and (1.4), the spectral radius will be smaller than 1 for all β∈(β _c ,∞) or all β∈(0,β _c ), respectively.

We conclude this introduction with a few remarks about the history and status of the combinatorial identities presented above. Kac and Ward observed in their paper [15] that the Onsager–Kaufman formula for the partition function Z _G,β of the Ising model on $\mathbb{Z}^{2}$ (or rather its square) appears to be proportional to the determinant of a matrix A _G , which for rectangles in $\mathbb{Z}^{2}$ is equivalent to our matrix I−Λ(x). Various attempts were subsequently undertaken to justify the formula $Z^{2}_{G,\beta} \propto\det A_{G}$, and to rederive the Onsager–Kaufman formula in this way. These attempts involved expanding the partition function into a formal infinite product over signed loops [3, 24, 25], or a formal infinite sum over signed loop configurations [28]. In either case, the correct interpretation and convergence of the obtained formal expressions are serious mathematical issues.

These issues were circumvented by Dolbilin et al. [8] by directly comparing the coefficients of the finite polynomials $Z^{2}_{G, \beta }$ and detA _G , thus rigorously proving the formula $Z^{2}_{G,\beta} \propto\det A_{G}$ for finite planar graphs G. The same method was then employed by Cimasoni to generalize this Kac–Ward formula to graphs embedded in surfaces of higher genus [4]. He also exposed a direct relation between the Kac–Ward determinant and the adjacency matrix arising in the dimer approach.

Historically then, the main focus appears to have been on the equality between the extreme left-hand and right-hand sides of equation (1.13), in cases where Z(x) is proportional to the Ising partition function and A _G =I−Λ(x). For the applications to the Ising model presented in this paper, however, the first equality in (1.13) is the more important and relevant one. Therefore, our proof proceeds along the lines of the Vdovichenko paper, which is targeted at directly expressing Z(x) as an infinite sum over configurations of signed loops. As we go along, we carefully address the issues of interpretation and convergence of this sum, mentioned above. In particular, Theorem 1.10, the key to the convergence issue, is to the best of our knowledge a new result.

Moreover, for our applications of the combinatorial results to the Ising model, it turns out to be necessary to allow crossing edges. This means that our function Z(x) (and hence also Theorem 1.9) is not quite the same as the one considered in the literature so far. In particular, our Z(x) need not be proportional to the Ising partition function for the graph G.

2 Proofs of the Combinatorial Identities

We now turn to the proof of our main Theorems 1.8 and 1.9. Recall that here G=(V,E) is a general finite graph embedded in the plane, potentially containing crossing edges or additional edges. The proof proceeds in a number of steps. In the first step, detailed in Sect. 2.1, we will identify each even subgraph (V,F) of G with a number of edge-disjoint collections of loops, and show that the sum of their weights yields precisely the contribution of F to the generating function Z(x). In the second step, in Sect. 2.2, we will explain the conditions under which we can express Z(x) in terms of ∑ _r f _r (x) and det(I−Λ(x)), under the assumption that the weights of all remaining configurations of loops in G of total length r cancel each other. The proof of this assumption, the last step, is carried out in Sect. 2.3.

2.1 Expansion into Collections of Edge-Disjoint Loops

We will be concerned with crossings of loops and paths, and we need to carefully establish the relevant definitions first. More specifically, we will consider collections {ℓ ₁,…,ℓ _s } of loops with the properties that all loops ℓ ₁,…,ℓ _s are edge-disjoint, and no two loops in the collection visit a common edge. We call these edge-disjoint collections of loops. Intuitively it may be clear what we mean by a crossing of such edge-disjoint loops, but some care is needed, so we will now give the precise definitions.

First, consider two paths (u,v,w) and (x,y,z) in G, and let A be the union of the two half-lines {v+t(u−v):t≥0} and {v+t(w−v):t≥0}. We say that (u,v,w) and (x,y,z) cross each other at the vertex v if v=y and the vertices x and z do not lie in the same infinite component of the complement of A in the plane.

Now let ℓ ₁=(u ₀,…,u _n−1) and ℓ ₂=(v ₀,…,v _m−1) be two loops that form an edge-disjoint pair {ℓ ₁,ℓ ₂}. By C _V (ℓ ₁,ℓ ₂) we denote the number of pairs (i,j), where 0≤i<n and 0≤j<m, such that the paths (u _i−1,u _i ,u _i+1) and (v _j−1,v _j ,v _j+1) cross each other at u _i . We call C _V (ℓ ₁,ℓ ₂) the number of vertex crossings between ℓ ₁ and ℓ ₂. Similarly, we define the number of edge crossings between ℓ ₁ and ℓ ₂, denoted C _E (ℓ ₁,ℓ ₂), as the number of pairs (i,j) such that 0≤i<n and 0≤j<m, and the edges u _i u _i+1 and v _j v _j+1 cross each other in G.

We also need to formally define the number of times a loop crosses itself, so consider an edge-disjoint loop ℓ=(v ₀,…,v _n−1). We define the number of vertex self-crossings of ℓ, denoted C _V (ℓ), as the number of pairs (i,j), where 0≤i<j<n, such that (v _i−1,v _i ,v _i+1) and (v _j−1,v _j ,v _j+1) cross each other at the vertex v _i . The number of edge self-crossings of ℓ, denoted C _E (ℓ), is defined as the number of pairs (i,j) such that 0≤i<j<n, and the edges v _i v _i+1 and v _j v _j+1 cross each other in the graph G.

As was already mentioned in the introduction, Whitney’s formula [29] says that the sign of an edge-disjoint loop is −1 if the loop crosses itself an odd number of times, and +1 otherwise. In other words, we have

$$\operatorname{sgn}(\ell) = (-1)^{C_V(\ell) + C_E(\ell)} $$

if ℓ is edge-disjoint. We now simply define the sign of an edge-disjoint collection of loops {ℓ ₁,…,ℓ _s } as

$$ \operatorname{sgn}\{\ell_1,\dots, \ell_s\} = \prod_{i=1}^s \operatorname{sgn}(\ell_i) = (-1)^{ \sum_{i=1}^s \{C_V(\ell_i) + C_E(\ell_i)\} }. $$

(2.1)

If F⊂E is even, we can decompose F into an edge-disjoint collection of loops in such a way, that the union of all edges traversed by the loops is F (one way to find such a decomposition is given in the proof of Proposition 2.1 below). This decomposition is in general not unique. We write $\mathcal{D}(F)$ for the set of all possible edge-disjoint decompositions of F, and recall that C _F denotes the number of unordered pairs of edges in F that cross each other.

Proposition 2.1

For all even subsets F of E we have that

$$\sum_{\{\ell_1,\dots,\ell_s\} \in\mathcal{D}(F)} \operatorname {sgn}\{\ell_1, \dots,\ell_s\} = (-1)^{C_F}. $$

Proof

Let {ℓ ₁,…,ℓ _s } be an edge-disjoint collection of loops. Since ℓ ₁,…,ℓ _s are all closed loops in the plane, any two distinct loops ℓ _i and ℓ _j from the collection necessarily cross each other an even number of times. That is, C _V (ℓ _i ,ℓ _j )+C _E (ℓ _i ,ℓ _j ) is even for all i≠j. Therefore,

$$\operatorname{sgn}\{\ell_1,\dots,\ell_s\} = (-1)^{ \sum_{1\leq i\leq s}\{ C_V(\ell_i) + C_E(\ell_i)\} + \sum_{1\leq i<j\leq s} \{ C_V(\ell_i,\ell_j) + C_E(\ell_i,\ell_j)\} }. $$

Furthermore, if $\{\ell_{1},\dots,\ell_{s}\} \in\mathcal{D}(F)$, then clearly the total number of edge crossings occurring among the loops must coincide with C _F , that is,

$$C_F = \sum_{1\leq i\leq s} C_E( \ell_i) + \sum_{1\leq i<j\leq s} C_E( \ell_i,\ell_j). $$

Hence, it suffices to prove that

$$ \sum_{\{\ell_1,\dots,\ell_s\} \in \mathcal{D}(F)} (-1)^{\sum _{1\leq i\leq s} C_V(\ell_i) + \sum_{1\leq i<j\leq s} C_V(\ell_i,\ell_j)} = 1. $$

(2.2)

Let V _F denote the set of vertices in V whose degree in the subgraph (V,F) is nonzero, and let deg(v,F) denote the degree of v in (V,F). For v∈V _F of degree 2k, write v ₁,…,v _2k for the endpoints of the edges in F that are incident to v. Assume that these vertices are ordered in a clockwise manner around v, starting from the lexicographically smallest one (see Fig. 4). Denote by $\mathcal{P}_{v}(F)$ the collection of partitions of the vertices v ₁,…,v _2k into sets of size 2. We call these partitions pairings at the vertex v. We write

$$\mathcal{P}(F) = \prod_{v\in V_F} \mathcal{P}_v(F), $$

and call an element of $\mathcal{P}(F)$ a pairing associated with the subgraph (V,F).

Fig. 4

The neighbours v ₁,v ₂,… of a vertex v in an even subgraph (V,F) are ordered in a clockwise fashion around v. Two neighbours that are connected by edges drawn in the same line style are paired to each other (see the text)

We have a natural 1–1 correspondence between $\mathcal{P}(F)$ and $\mathcal{D}(F)$. Indeed, starting from any vertex v∈V _F and any i∈{1,…,deg(v,F)}, the pairing $\pi\in\mathcal{P}(F)$ defines a unique closed path (u ₀,…,u _n−1) with the properties that u ₀=v _i , u ₁=v, and for all j, u _j−1 is paired with u _j+1 at the vertex u _j . Continuing this way, and replacing each closed path obtained by the corresponding loop, yields an edge-disjoint collection $\{\ell_{1}, \dots, \ell_{s}\}\in\mathcal{D}(F)$. It is easy to see that this defines a bijective relation between $\mathcal{P}(F)$ and $\mathcal{D}(F)$.

Using this bijection, we can express the sum in (2.2) equally well as a sum over all pairings. More precisely, for $\pi\in\mathcal{P}(F)$ let π _v denote the pairing it induces at the vertex v∈V _F , and write C _v (π _v ) for the number of crossings at the vertex v introduced by this pairing. We call π _v even (odd) if C _v (π _v ) is even (odd). Note that (2.2) is equivalent to

$$\sum_{\pi\in\mathcal{P}(F)} (-1)^{\sum_{v\in V_F} C_v(\pi_v)} = \prod _{v\in V_F} \sum_{\pi_v\in\mathcal{P}_v(F)} (-1)^{C_v(\pi_v)} = 1, $$

from which we see that it suffices to prove that for all v∈V _F , the number of even pairings π _v exceeds the number of odd pairings π _v by 1.

We prove this by induction on the degree 2k of v. Write $N^{+}_{k}$ and $N^{-}_{k}$ for the numbers of even, resp. odd, pairings for v of degree 2k. For k=1 we clearly have $N^{+}_{k} = 1$ and $N^{-}_{k} = 0$. Now let k>1, and suppose that we pair the vertex v ₁ with v _i at v. Next pair the remaining 2k−2 neighbours v _j of v in all possible ways. For even i, there is an even number of j in between 1 and i, and therefore the pairing we obtain will be even if and only if the pairing of the remaining 2k−2 vertices is even (see Fig. 4). Likewise, for odd i, the obtained pairing will be even if and only if the pairing of the remaining vertices is odd. Since we have k even values for i, and k−1 odd values, this gives $N^{+}_{k} = kN^{+}_{k-1} + (k-1)N^{-}_{k-1}$ and $N^{-}_{k} = kN^{-}_{k-1} + (k-1)N^{+}_{k-1}$. Hence by the induction hypothesis, $N^{+}_{k}-N^{-}_{k} = 1$. □

From Proposition 2.1 we will now obtain our first main result. Recall that

$$Z(x) = \sum_{\text{even}\ F\subset E} (-1)^{C_F} \prod _{uv\in F} x_{uv}. $$

The case F=∅ is treated separately: by convention it contributes 1 to the sum. Hence, Proposition 2.1 implies that

Recall that the multiplicity m(ℓ) of an edge-disjoint loop ℓ is 1. Therefore, using (2.1) and the definition (1.7) of the weight of a loop, we can write

Since this is a finite sum, we do not need to worry about the order of summation, so we have

If we now denote by $\mathcal{D}_{r}$ the set consisting of all those edge-disjoint collections of loops {ℓ ₁,…,ℓ _s } for which the total length $\sum_{i=1}^{s} r(\ell_{i})$ is r, we see that we have established the following theorem:

Theorem 2.2

$$Z(x) = 1 + \sum_{r=1}^{\infty} \sum _{\{\ell_1, \dots, \ell_s\} \in \mathcal{D}_r} \prod_{i=1}^s w(\ell_i; x). $$

2.2 Extension to All Loop Configurations

In Theorem 2.2, we have expressed the generating function Z(x) as a sum over all edge-disjoint collections of loops in G. In this section, we will see that if the edge weights are sufficiently small, we can drop the condition that the loops have to be edge-disjoint, and sum instead over all possible loop configurations in G. Here, a loop configuration is simply an ordered sequence (ℓ ₁,…,ℓ _s ) of loops; there is no condition that loops have to be edge-disjoint, nor that two loops in the configuration have to be distinct (i.e. it is allowed that ℓ _i =ℓ _j for some i≠j, which is why we work with ordered sequences of loops now).

Write $\mathcal{C}_{r}$ for the collection of all loop configurations (ℓ ₁,…,ℓ _s ) satisfying r(ℓ ₁)+⋯+r(ℓ _s )=r. Some of these loop configurations will consist of distinct loops that together form an edge-disjoint collection of loops. Let $\mathcal{C}^{*}_{r}$ denote the subset of $\mathcal{C}_{r}$ containing only these edge-disjoint loop configurations. Observe that if {ℓ ₁,…,ℓ _s } is an edge-disjoint collection of loops, then the corresponding loop configuration (ℓ ₁,…,ℓ _s ) has s! permutations. Therefore, by Theorem 2.2 we already have that

$$Z(x) = 1 + \sum_{r=1}^\infty\sum _{s=1}^\infty\sum_{ (\ell_1, \dots, \ell_s) \in\mathcal{C}^*_r} \frac{1}{s!} \prod_{i=1}^s w( \ell_i; x), $$

but we claim that here we may sum over $\mathcal{C}_{r}$ instead of $\mathcal{C}^{*}_{r}$:

Theorem 2.3

$$Z(x) = 1 + \sum_{r=1}^\infty\sum _{s=1}^\infty\sum_{(\ell_1,\dots,\ell_s) \in\mathcal{C}_r} \frac{1}{s!} \prod_{i=1}^s w( \ell_i; x). $$

Clearly, since $\mathcal{C}_{r}$ is a finite set for every fixed r, this result is an immediate consequence of the following proposition:

Proposition 2.4

For all r>0,

$$\sum_{s=1}^\infty\sum _{ (\ell_1, \dots, \ell_s) \in\mathcal{C}_r \setminus\mathcal{C}^*_r} \frac{1}{s!} \prod_{i=1}^s w(\ell_i; x) = 0. $$

The proof of Proposition 2.4 is involved, and we postpone it to Sect. 2.3. For now, we assume that Proposition 2.4 and hence Theorem 2.3 hold, and explain how Theorems 1.8 and 1.9 follow from this.

Proof of Theorem 1.8

By splitting the sum over the set of loop configurations $\mathcal {C}_{r}$ in Theorem 2.3 according to the lengths of the individual loops, using (1.11) we can write

(2.3)

Now suppose that, given x, there exist γ∈(0,1) and C<∞ such that

$$ \bigl|{f_r(x)}\bigr|\leq C \gamma^r \quad\text{for all}\ r. $$

(2.4)

For future reference, we note that this condition is implied by the stronger condition that

$$ \sum_{\ell\in\mathcal{L}_r} \bigl| {w(\ell; x)}\bigr|\leq C\gamma^r \quad\text{for all}\ r. $$

(2.5)

Under condition (2.4), if we write h(r,s) for the summand in (2.3), we have

$$\bigl|h(r,s)\bigr|= \Biggl| \frac{1}{s!} \sum_{r_1+\cdots+r_s = r} \prod_{i=1}^s f_{r_i}(x) \Biggr| \leq\frac{C^s}{s!} \binom{r-1}{s-1} \gamma^r, $$

and thus

$$\sum_{s=1}^\infty\sum _{r=1}^\infty\bigl|h(r,s)\bigr|\leq\sum _{s=1}^\infty\frac{C^s}{s!} \sum _{r=s}^\infty\binom{r-1}{s-1} \gamma^r = \exp\biggl( \frac{C\gamma}{1-\gamma} \biggr)-1. $$

Hence, we can apply Fubini’s theorem to interchange the order of summation over r and s in (2.3), which yields

$$Z(x) = 1 + \sum_{s=1}^\infty\frac{1}{s!} \sum _{r=1}^\infty\sum _{r_1+\cdots+r_s = r} \prod_{i=1}^s f_{r_i}(x). $$

Note that under condition (2.4), ∑ _r f _r (x) is absolutely convergent. We now apply Mertens’ theorem, which says that if a series ∑ _r a _r converges absolutely, and the series ∑ _r b _r converges, then their Cauchy product converges to (∑ _r a _r )(∑ _r b _r ). In particular, by induction, the s-fold Cauchy product of the series ∑ _r a _r with itself, which is $\sum_{r} \sum_{r_{1}+\cdots +r_{s} = r} a_{r_{1}} a_{r_{2}} \ldots\allowbreak a_{r_{s}}$, converges to (∑ _r a _r )^s. Applying this with a _r =f _r (x), we obtain

$$ Z(x) = 1 + \sum_{s=1}^\infty \frac{1}{s!} \Biggl( \sum_{r=1}^\infty f_r(x) \Biggr)^s = \exp\Biggl( \sum _{r=1}^\infty f_r(x) \Biggr). $$

(2.6)

Observe that this result holds already under the weaker of the two conditions (2.4) and (2.5), but that under the stronger condition (2.5), the loop weights can in fact be summed in any order. We will now show that the condition of Theorem 1.8 implies (2.5). Indeed, under the condition of Theorem 1.8, there exists γ∈(0,1) such that (d _uv −1)|x _uv |≤γ for all edges uv∈E. Observing that if a loop takes a step along uv, then there are at most d _uv −1 possibilities for the next step, this implies that the sum of |w(ℓ;x)| over all loops ℓ of n steps is bounded by |V|γ ⁿ. Since a loop of length r takes at least r steps, summing over n≥r yields (2.5). □

Proof of Theorem 1.9

Recall definition (1.12) of the entries of Λ(x), which are indexed by the directed representative edges of G. We can interpret this matrix as a transition matrix for non-backtracking paths on the graph G′ which is represented by G. This represented graph G′ can be obtained from G by removing every chain of additional edges from G, and identifying the two vertices at the ends of this chain (see Fig. 3 for an example).

Indeed, consider two directed representative edges $\overrightarrow {uv}$ and $\overrightarrow{wz}\neq\overrightarrow{vu}$ in G, and write $\overrightarrow{uv}'$ and $\overrightarrow{wz}'$ for the corresponding directed edges in the represented graph G′. By construction, a non-backtracking path in G′ can make a step from $\overrightarrow{uv}'$ to $\overrightarrow{wz}'$ if and only if v is linked to w in the graph G, since only then will v be identified with w in G′. This step corresponds to either a direct step from $\overrightarrow{uv}$ to $\overrightarrow{wz}$ in G (if v=w), or to a sequence of steps along the chain linking v to w. In either case, the matrix entry $\varLambda_{\overrightarrow {uv}, \overrightarrow{wz}} (x)$ picks up all edge weights and turning angles associated with these steps in G.

We can now interpret this entry as describing the weight picked up by a non-backtracking walk in G′ when it steps from $\overrightarrow{uv}'$ to $\overrightarrow{wz}'$. Viewed in this way, the entry of the matrix Λ ^r(x) indexed by $\overrightarrow{uv}$ and $\overrightarrow{wz}$ is equal to the sum of the weights of all non-backtracking paths in G′ of r steps starting from $\overrightarrow{uv}'$ and ending on $\overrightarrow{wz}'$. In particular, the sum of the diagonal entries of Λ ^r(x) is equal to the sum of the weights of all non-backtracking paths in G′ of r steps starting and ending on the same directed edge.

Now consider a loop ℓ of length r in G. Note that it is possible to start traversing this loop from each step it takes along a representative edge in two directions. Mapping the paths thus obtained to the represented graph G′ yields precisely 2r/m(ℓ) different non-backtracking paths of r steps in G′ that start and end on the same directed edge. By (1.7), (1.6) and (1.11), it now follows that

$$\operatorname{tr}\varLambda^r(x) = -2r f_r(x), $$

where the minus sign comes from the minus sign in the definition (1.6) of the sign of a loop in terms of its winding angle. Expressed in the eigenvalues λ _i (x) of Λ(x), we therefore have that

$$ f_r(x) = -\frac{1}{2r} \sum _i \lambda_i^r(x). $$

(2.7)

In particular, condition (2.4) is satisfied if ρ(x)=max _i |λ _i (x)|<1, so in this case the same argument as in the proof of Theorem 1.8 yields (2.6). Moreover, if ρ(x)<1, then using (2.7) we can write

$$Z(x) = \exp\Biggl( -\frac{1}{2} \sum_{r=1}^\infty \sum_i \frac{\lambda_i^r(x)}{r} \Biggr) = \exp\Biggl( - \frac{1}{2} \sum_i \sum_{r=1}^\infty \frac{\lambda_i^r(x)}{r} \Biggr), $$

and since $\sum_{r=1}^{\infty}u^{r}/r = -\ln(1-u)$ if |u|<1, we conclude that

$$Z(x) = \prod_i \bigl( 1-\lambda_i(x) \bigr)^{1/2} = \sqrt{\det\bigl( \mathrm{I}- \varLambda(x) \bigr)}. $$

 □

2.3 Cancellation of Non-edge-disjoint Loop Configurations

We now turn to the missing step in the proofs of Theorems 1.8 and 1.9, which is the proof of Proposition 2.4. That is, we must show that the weights of all loop configurations (ℓ ₁,…,ℓ _s ) which are not edge-disjoint and satisfy r(ℓ ₁)+⋯+r(ℓ _s )=r for a given r, cancel each other. What complicates matters here, is the fact that these loop configurations do not cancel each other one by one, see for example Fig. 5.¹ Our strategy of the proof is to map loop configurations to so-called labelled loop configurations, which do cancel each other one by one, and show that this implies cancellation of the unlabelled loop configurations for combinatorial reasons.

Fig. 5

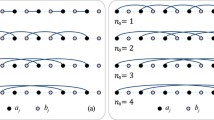
Four loop configurations on the same vertices and edges, where the traversals of the same edge have been drawn slightly apart to make them discernible. The factors $\frac{1}{s!} \prod_{i=1}^{s} \operatorname {sgn}(\ell _{i}) / m(\ell_{i})$ are spelled out below each loop configuration to show that the sum of their signed weights is 0

We will therefore start by introducing the notion of a labelled loop, and work our way from there towards the notion of a labelled loop configuration, and the proof of their cancellation. In words, a labelled loop is a loop with a label attached to each step it takes, where the labels are distinct positive integers. For periodic loops, the first step is repeated after completing a period, and we require that the label of the first step of the loop is smaller than the label associated with each of these repetitions.

Formally, a labelled loop ℓ ^♢ is a sequence (v ₀,a ₀,v ₁,a ₁,…,v _n−1,a _n−1) satisfying the following conditions:

L1 :

ℓ=(v ₀,…,v _n−1) is a loop;

L2 :

(a ₀,a ₁,…,a _n−1) is a sequence of distinct positive integers, called the labelling of the loop;

L3 :

if ℓ is periodic, i.e. m(ℓ)>1, then a ₀ is smaller than a _kn/m(ℓ) for all k∈{1,2,…,m(ℓ)−1}.

We call the number a _i the label on step i+1 of the loop ℓ; we also regard it as a label assigned to the edge v _i v _i+1. We will use the superscript ♢ for labelled loops, and the unlabelled loop corresponding to a labelled loop will consistently be denoted by dropping this superscript: if ℓ ^♢ is a labelled loop, then ℓ is the corresponding unlabelled loop, and so on.

Observe that one of the effects of labelling loops is that it breaks the periodicity of periodic loops: sequences representing labelled loops cannot be periodic. Therefore, if ℓ is periodic, we do not assign to the labelled loop ℓ ^♢=(v ₀,a ₀,…,v _n−1,a _n−1) the same weight as to its unlabelled counterpart. Instead, we define the weights of labelled loops in general by

$$ w\bigl(\ell^\diamondsuit; x\bigr) = \operatorname{sgn}(\ell) \prod_{i=0}^{n-1} x_{v_iv_{i+1}}, $$

(2.8)

where the sign is defined in terms of the winding angle of ℓ by (1.6), as before. Note that this weight is actually independent of the particular labelling of the loop, and that w(ℓ ^♢;x)=m(ℓ)w(ℓ;x).

We write n(ℓ) for the number of steps of a loop ℓ (recall that this is not necessarily the same as the length r(ℓ) of the loop). By a labelled loop configuration we mean a collection $\{\ell ^{\diamondsuit}_{1}, \dots, \ell^{\diamondsuit}_{s}\}$ of labelled loops, in which all labels are distinct and take values from the set $\{ 1, 2, \dots, \sum_{i=1}^{s} n(\ell_{i}) \}$. In particular, any loop configuration (ℓ ₁,…,ℓ _s ) can be turned into a labelled loop configuration by attaching a label to every step of every loop in such a way, that condition L3 above is fulfilled for every labelled loop obtained, and all labels $1, 2, \dots, \sum_{i=1}^{s} n(\ell_{i})$ are used.

Now fix r and n, and consider a loop configuration (ℓ ₁,…,ℓ _s ) which is not edge-disjoint and satisfies $\sum_{i=1}^{s} r(\ell_{i}) = r$ and $\sum_{i=1}^{s} n(\ell_{i}) = n$. Let t denote the number of distinct loops in (ℓ ₁,…,ℓ _s ), and write k ₁,…,k _t for the respective number of times each of them occurs, so that k ₁+⋯+k _t =s. Consider the collection of all labelled loop configurations $\{\ell ^{\diamondsuit}_{1}, \dots, \ell^{\diamondsuit}_{s}\}$ that can be obtained from (ℓ ₁,…,ℓ _s ) by labelling the loops, as described above. For a periodic loop ℓ _i , only one of the rotations of its labelling, rotated over a multiple of the smallest period, satisfies condition L3. Furthermore, interchanging the labellings of two identical loops ℓ _i and ℓ _j (ℓ _i =ℓ _j but i≠j) yields the same labelled loop configuration. Therefore, the number of labelled loop configurations we obtain from (ℓ ₁,…,ℓ _s ) is precisely

$$\frac{n!}{\prod_{i=1}^s m(\ell_i) \prod_{i=1}^t k_i!}. $$

We assign to each of these labelled loop configurations the same weight $\prod_{i=1}^{s} w(\ell^{\diamondsuit}_{i}; x)$, where we use the fact that according to the definition (2.8), $w(\ell^{\diamondsuit}_{i}; x)$ does not depend on the actual labelling. Then the total weight of all labelled loop configurations associated with (ℓ ₁,…,ℓ _s ) is

$$\frac{n!}{\prod_{i=1}^s m(\ell_i) \prod_{i=1}^t k_i!} \prod _{i=1}^s w\bigl( \ell^\diamondsuit_i; x\bigr) = \frac{n!}{\prod_{i=1}^t k_i!} \prod _{i=1}^s w(\ell_i; x). $$

We claim that this is exactly n! times the total weight that all the permutations of the loop configuration (ℓ ₁,…,ℓ _s ) contribute to the sum in Proposition 2.4. Indeed, there are precisely

$$\frac{s!}{\prod_{i=1}^s k_i!} $$

such permutations, and the weight each of them contributes to the sum is

$$\frac{1}{s!} \prod_{i=1}^s w( \ell_i; x). $$

We conclude that to prove Proposition 2.4, it suffices to show that for given n and r, the weights of all labelled loop configurations $\{\ell^{\diamondsuit}_{1}, \dots, \ell^{\diamondsuit}_{s}\}$ such that $\sum_{i=1}^{s} n(\ell_{i}) = n$, $\sum_{i=1}^{s} r(\ell_{i}) = r$ and (ℓ ₁,…,ℓ _s ) is not edge-disjoint, sum to 0. Write $\mathcal{C}^{\diamondsuit}_{n,r}$ for this collection of labelled loop configurations. We will now prove the desired cancellation of weights, and hence Proposition 2.4, by finding a bijection $g\colon\mathcal{C}^{\diamondsuit}_{n,r} \to\mathcal {C}^{\diamondsuit}_{n,r}$ which maps each labelled loop configuration to a labelled loop configuration which has a weight of the opposite sign, but with the same absolute value.

Proof of Proposition 2.4

Before we go into the formal details of the bijection, let us give an informal description of how it will work. Consider a labelled loop configuration $\{\ell^{\diamondsuit}_{1}, \dots, \ell^{\diamondsuit}_{s}\} \in\mathcal{C}^{\diamondsuit}_{n,r}$, and let E ^♢ be the set of edges in G that are assigned more than 1 label in this configuration. Find the smallest of all the labels that are assigned to the edges in E ^♢, let a be this label, and let uv be the edge to which this label is assigned. Next, find the second smallest label b which is assigned to the edge uv.

The label a labels a step of one of the loops ℓ _i . The label b either labels another step of the same loop ℓ _i , or it labels a step of a second loop ℓ _j , i≠j. The bijection involves interchanging the “connections” on one side of the two steps marked a and b (either at the vertex u or at the vertex v), as illustrated in Fig. 6. It is clear that this operation does not change the absolute value of the weight of the configuration, since the total number of steps that go through a given edge does not change. But Fig. 6 also suggests that the operation corresponds to increasing or decreasing the number of “crossings” in the configuration by 1, which should indeed lead to a change in sign.

Fig. 6

All cases that occur in the cancellation of labelled loop diagrams, as explained in the text. The curves ℘₁ and ℘₂ represent arbitrary paths connected to the vertices u and v

However, signs were formally defined in terms of winding angles, not numbers of crossings, since it is more difficult to make sense of the latter when loops are not edge-disjoint. Furthermore, we must still formally define the mapping g. We will now deal with these technical issues.

For the formal treatment of the bijection, we need to introduce some additional notation. Given a sequence a=(a ₀,…,a _n ) of arbitrary elements, we write a ⁻¹ for its reversion a ⁻¹=(a _n ,a _n−1,…,a ₀). If b=(b ₀,…,b _m ) is another sequence of arbitrary elements, we write a⊕b for the concatenation of a with b, that is,

$$a \oplus b = (a_0, \dots, a_n, b_0, \dots, b_m). $$

The weight of a labelled loop configuration $\{\ell^{\diamondsuit}_{1}, \dots, \ell^{\diamondsuit}_{s}\}$ is defined as the product of the signs of the loops ℓ ₁,…,ℓ _s , times the product of all the edge weights picked up by all the loops. As was anticipated above, the product of edge weights will not change under the bijection, so we will only be concerned with the product of the signs of the loops. We recall from (1.5) and (1.6) that the sign of a loop ℓ=(v ₀,…,v _n−1) is defined in terms of its winding angle as

$$ \operatorname{sgn}(\ell) = - \exp\biggl( \frac{i}{2} \alpha(\ell) \biggr), $$

(2.9)

where the winding angle α(ℓ) is given by

$$ \alpha(\ell) = \sum_{i=0}^{n-1} \angle(v_{i+1}-v_i, v_{i+2}-v_{i+1}). $$

(2.10)

We now define the winding angle and sign of a closed path (v ₀,…,v _n−1) by the exact same formulas. In particular, all rotations of a loop ℓ have the same winding angle and sign. On the other hand, the reversion ℓ ⁻¹ of ℓ and all its rotations are traversed in the opposite direction, and therefore they all have winding angle α(ℓ ⁻¹)=−α(ℓ). However, since the winding angle of a loop is a multiple of 2π, we do have that

$$ \operatorname{sgn}\bigl(\ell^{-1}\bigr) = \operatorname{sgn}(\ell) \quad\text{for all closed paths}\ \ell. $$

(2.11)

We call all the rotations of a loop ℓ, and all rotations of its reversion ℓ ⁻¹, alternative representations of ℓ. All these representations have the same sign. Likewise, the rotations of a labelled loop ℓ ^♢ and its reversion (ℓ ^♢)⁻¹ will be called representations of this labelled loop.

We also need to define the winding angle for paths in G which are not loops. Note that a path ℘=(v ₀,…,v _n−1) is not a loop if v ₀ v _n−1∉E, v ₀=v _n−2, or v ₁=v _n−1. If we follow such a path from v ₀ to v _n−1, we turn through n−2 angles, and it is natural to define the winding angle of ℘ by

$$\alpha(\wp) = \sum_{i=0}^{n-3} \angle(v_{i+1}-v_i, v_{i+2}-v_{i+1}). $$

We now have all the notation we need to define and analyse the bijection formally. So consider a labelled loop configuration $\{\ell ^{\diamondsuit}_{1}, \dots, \ell^{\diamondsuit}_{s}\} \in\mathcal{C}^{\diamondsuit}_{n,r}$, and define E ^♢, a, b and uv as above. We will now explain to which labelled loop configuration our configuration $\{\ell^{\diamondsuit}_{1}, \dots, \ell^{\diamondsuit}_{s}\}$ is mapped by the bijection, and prove that the image has the opposite sign, and hence the opposite weight. There are three possible cases to consider, which are illustrated in Fig. 6.

Case 1: The labels a and b belong to different labelled loops. Let $\ell^{\diamondsuit}_{i}$ be the labelled loop containing label a, and let $\ell^{\diamondsuit}_{j}$ be the labelled loop containing label b. Then these labelled loops have representations of the form ${\hat{\ell}}^{\diamondsuit}_{i} = (u,a,v) \oplus\wp^{\diamondsuit}_{1}$ and ${\hat{\ell}}^{\diamondsuit}_{j} = (u,b,v) \oplus\wp^{\diamondsuit}_{2}$, respectively, where $\wp^{\diamondsuit}_{1}$ and $\wp^{\diamondsuit}_{2}$ are paths interspersed with labels. We can now form the combined representation

$${\hat{\ell}}^\diamondsuit_{ij} = (u,a,v) \oplus\wp^\diamondsuit_1 \oplus(u,b,v) \oplus\wp^\diamondsuit_2 $$

of a new labelled loop $\ell^{\diamondsuit}_{ij}$. Our bijection maps $\{\ell^{\diamondsuit}_{1}, \dots, \ell^{\diamondsuit}_{s}\}$ to the labelled loop configuration

$$\bigl\{\ell^\diamondsuit_1, \dots, \ell^\diamondsuit_s, \ell^\diamondsuit_{ij}\bigr\} \setminus\bigl\{\ell^\diamondsuit_i, \ell^\diamondsuit_j\bigr\}. $$

To see that this labelled loop configuration has the opposite sign of its pre-image $\{\ell^{\diamondsuit}_{1}, \dots, \ell^{\diamondsuit}_{s}\}$, note that by (2.9)–(2.11),

Case 2: The labels a and b are on steps of the same labelled loop taken in the same direction. This case is the reverse of Case 1. The labels a and b are in a labelled loop $\ell ^{\diamondsuit}_{i}$ which has a representation of the form

$${\hat{\ell}}^\diamondsuit_i = (u,a,v) \oplus\wp^\diamondsuit_1 \oplus(u,b,v) \oplus\wp^\diamondsuit_2. $$

From this we obtain the representations $(u,a,v) \oplus\wp ^{\diamondsuit}_{1}$ and $(u,b,v) \oplus\wp^{\diamondsuit}_{2}$ of two new labelled loops $\ell ^{\diamondsuit}_{i1}$ and $\ell^{\diamondsuit}_{i2}$. The bijection maps $\{\ell ^{\diamondsuit}_{1}, \dots, \ell^{\diamondsuit}_{s}\}$ to the labelled loop configuration

$$\bigl\{\ell^\diamondsuit_1, \dots, \ell^\diamondsuit_s, \ell^\diamondsuit_{i1}, \ell^\diamondsuit_{i2}\bigr\} \setminus\bigl\{\ell^\diamondsuit_i\bigr\}. $$

The same argument as in Case 1 shows that $\operatorname{sgn}(\ell_{i1}) \operatorname{sgn}(\ell_{i2}) = - \operatorname{sgn}(\ell_{i})$.

Case 3: The labels a and b are on steps of the same labelled loop taken in opposite directions. In this case the labels a and b are in a labelled loop $\ell^{\diamondsuit}_{i}$ which has a representation of the form

$${\hat{\ell}}^\diamondsuit_i = (u,a,v) \oplus\wp^\diamondsuit_1 \oplus(v,b,u) \oplus\wp^\diamondsuit_2. $$

From this we can construct the representation

$${\hat{\ell}}^\diamondsuit= (u,a,v) \oplus\bigl(\wp ^\diamondsuit_1 \bigr)^{-1} \oplus(v,b,u) \oplus\wp^\diamondsuit_2 $$

of a new labelled loop ℓ ^♢. The bijection maps $\{ \ell^{\diamondsuit}_{1}, \dots, \ell^{\diamondsuit}_{s}\}$ to the labelled loop configuration

$$\bigl\{\ell^\diamondsuit_1, \dots, \ell^\diamondsuit_s, \ell^\diamondsuit\bigr\} \setminus\bigl\{\ell^\diamondsuit_i \bigr\}. $$

To verify that these loop configurations have opposite signs, observe that

$$ \alpha({\hat{\ell}}_i) = \alpha\bigl( (u,v) \oplus\wp_1 \oplus(v,u) \bigr) + \alpha\bigl( (v,u) \oplus \wp_2 \oplus(u,v) \bigr), $$

(2.12)

and likewise

$$ \alpha({\hat{\ell}}) = \alpha\bigl( (u,v) \oplus \wp_1^{-1} \oplus(v,u) \bigr) + \alpha\bigl( (v,u) \oplus \wp_2 \oplus(u,v) \bigr), $$

(2.13)

where ℘₁ and ℘₂ are the paths obtained from $\wp ^{\diamondsuit}_{1}$ and $\wp^{\diamondsuit}_{2}$ by dropping the labels. Now notice that upon reversion,

$$ \alpha\bigl( (u,v) \oplus\wp_1 \oplus(v,u) \bigr) = -\alpha\bigl( (u,v) \oplus\wp_1^{-1} \oplus(v,u) \bigr). $$

(2.14)

Furthermore, it is not difficult to see that

$$\alpha\bigl( (u,v) \oplus\wp_1 \oplus(v,u) \bigr) = 2m\pi+ \pi \quad\text{for some}\ m\in\mathbb{Z}. $$

Together with (2.12), (2.13) and (2.14), this implies

$$\frac{\operatorname{sgn}(\ell_i)}{\operatorname{sgn}(\ell)} = \frac{\operatorname{sgn}({\hat{\ell}}_i)}{\operatorname{sgn}({\hat{\ell}})} = \exp\biggl( \frac{i}{2} \alpha({\hat{\ell}}_i) - \frac{i}{2} \alpha({\hat{\ell}}) \biggr) = -1. $$

We conclude that in all cases, the labelled loop configuration $\{\ell^{\diamondsuit}_{1}, \dots, \ell^{\diamondsuit}_{s}\}$ is mapped to a labelled loop configuration of opposite weight. From the explicit descriptions given above, it is not difficult to see that the mapping is bijective. As we have explained above, this implies Proposition 2.4. □

3 Proofs of Our Results for the Ising Model

In this section, we will apply Theorem 1.9 to the Ising model on the square lattice $\mathbb{Z}^{2}$. This will lead to explicit expressions for the free energy density and two-point functions in terms of sums over loops in $\mathbb{Z}^{2}$ or its dual $\mathbb{Z}^{2*}$, valid all the way up to the critical point. We start with a brief review of the low- and high-temperature expansions in Sect. 3.1. The bound on the operator norm in Theorem 1.10 will be derived in Sect. 3.2. Then we will study the free energy density in Sect. 3.3, and finally the two-point functions at low and high temperatures in Sects. 3.4 and 3.5, respectively.

3.1 Low- and High-Temperature Expansions

The partition function of the Ising model is closely related to the graph generating function Z(x) from Sect. 1.4. This can be seen from the low- and high-temperature expansions considered in this section. More details on these expansions and the related duality of the Ising model can be found in [26, Sect. II.7].

Let G=(V,E) be a finite rectangle in $\mathbb{Z}^{2}$. By G ^∗=(V ^∗,E ^∗) we shall denote the weak dual graph of G, i.e. the rectangle in $\mathbb{Z}^{2*}$ whose vertices are the centres of the faces of G (see Fig. 7, left). For our purposes, the low-temperature expansion is best considered in the case of positive boundary conditions. It is not difficult to see that in this case, there is a 1–1 correspondence between the even subgraphs of the weak dual G ^∗ and the spin configurations in Ω ⁺: given σ∈Ω ⁺, one obtains the corresponding even subset F(σ) of E ^∗ by including the edge dual to uv in F(σ) if and only if σ _u ≠σ _v , for every uv∈E. See Fig. 7 (left) for an illustration.

Fig. 7

Left: the graph G and its weak dual G ^∗, with an even subgraph of G ^∗ marked by bold dashed edges. The spins in the gray squares have value −1, the rest have value +1. Right: the subgraph of G drawn with bold edges contributes $\sigma_{x}^{2} \sigma_{y}^{2} \sigma_{z}^{3} \sigma_{u}^{2} \sigma_{v} (\tanh\beta)^{5}$ in the high-temperature expansion

Note that by this correspondence, if F⊂E ^∗ is even, then every edge in F separates two spins that have opposite sign. This means that adding an edge uv to F decreases σ _u σ _v from +1 to −1, and hence has a “cost” exp(−2β) in the probability distribution (1.1). It follows that we can write

$$ P^+_{G,\beta}(\sigma) = \frac{\exp(\beta \lvert{E}\rvert)}{Z^+_{G,\beta}} \prod _{uv\in F(\sigma)} x_{uv}, \quad\sigma\in \varOmega_G^+, $$

(3.1)

where x _uv =exp(−2β) for every uv∈E ^∗, and

$$ Z^+_{G,\beta} = \exp(\beta| E|) \sum _{\text{even}\ F\subset E^*} \prod_{uv\in F} x_{uv}. $$

(3.2)

This is the low-temperature expansion of the partition function for positive boundary conditions. Observe that up to the factor exp(β|E|), this expansion takes exactly the form (1.9) of the graph generating function Z(x) for the dual graph G ^∗ (in which no edges cross each other), if we set the edge weights of all dual edges uv∈E ^∗ equal to x _uv =exp(−2β).

We now turn to the high-temperature expansion, for which we impose free boundary conditions. The expansion will be over even subgraphs of the graph G, rather than of the dual G ^∗. Unlike in the low-temperature expansion, these subgraphs do not have a clear geometric interpretation, so we will take some time to explain how they arise.

The high-temperature expansion starts from equation (1.2) and the observation that σ _u σ _v can only take the values −1 or +1. Since exp(±β)=coshβ±sinhβ, we see that

$$Z^{\mathrm{free}}_{G,\beta} = (\cosh\beta)^{\lvert{E}\rvert} \sum _{\sigma\in\varOmega _G^{\mathrm{free}}} \prod_{uv\in E} (1 + \sigma_u\sigma_v \tanh\beta). $$

The next step is to expand the product over uv∈E. Each term in the expansion will be a product of factors obtained by choosing for each edge uv whether 1 is taken as a factor, or σ _u σ _v tanhβ, so that the expansion becomes a sum over all choices of factors for each edge uv. We can represent each choice graphically by removing the edge uv if we choose the factor 1 for this edge, and keeping uv if we choose the factor σ _u σ _v tanhβ. This gives a 1–1 correspondence between all terms in the expansion, and all F⊂E (not just the even ones). See also Fig. 7 (right).

Using this correspondence, and then interchanging the order of summation over σ and F, we may now write the partition function as

$$Z^{\mathrm{free}}_{G,\beta} = (\cosh\beta)^{\lvert{E}\rvert} \sum _{F\subset E} \sum_{\sigma \in\varOmega_G^{\mathrm{free}}} \prod _{u\in V} \sigma_u^{\deg(u,F)} \prod _{uv\in F} x_{uv}, $$

where x _uv =tanhβ for all uv∈E and deg(u,F) denotes the degree of u in the graph (V,F). Note that the sum over σ vanishes unless deg(u,F) is even for all u∈V, in which case the sum yields simply 2^|V|. Therefore,

$$ Z^{\mathrm{free}}_{G,\beta} = 2^{|V|} ( \cosh\beta)^{|E|} \sum_{\text {even}\ F\subset E} \prod _{uv\in F} x_{uv}. $$

(3.3)

Again, up to a multiplicative constant, the expansion takes exactly the form (1.9) of the graph generating function Z(x), this time for the graph G, if we set the edge weights equal to x _uv =tanhβ.

3.2 Bound on the Operator Norm

Let G=(V,E) be a fixed finite rectangle in $\mathbb{Z}^{2}$ with no additional edges (i.e. E _A =∅). Without loss of generality, we may assume that the vertex set is

$$ V = \{0,1,\dots,M-1\} \times\{0,1,\dots,N-1\}. $$

(3.4)

Since we are on the square lattice, directed edges can point in only 4 directions, and we now introduce some convenient notation for this specific case. We write v↑, v↓, v→ and v← for the directed edges from v to, respectively, v+(0,1), v−(0,1), v+(1,0) and v−(1,0). We also write ↑v for the directed edge pointing from v−(0,1) to v, and define ↓v, →v, ←v analogously.

Given a vector of edge weights x=(x _uv ) _uv∈E on E, Λ(x) is the transition matrix indexed by the directed edges of G, defined by (1.12). For a vertex v not on the boundary of G, the row of Λ(x) indexed by →v, for instance, has exactly 3 nonzero entries, corresponding to the 3 possible steps that a loop can take from →v. To be precise, with u=v−(1,0), these 3 entries are

$$\varLambda_{\rightarrow v,v\rightarrow}(x) = x_{uv}, \qquad \varLambda_{\rightarrow v,v{\uparrow}}(x) = x_{uv} e^{i\pi/4}, \qquad\varLambda_{\rightarrow v,v{\downarrow }}(x) = x_{uv} e^{-i\pi/4}. $$

Observe that most rows of Λ(x) have exactly 3 nonzero entries. The only exceptions are the rows indexed by directed edges pointing to a vertex in ∂G. These exceptional rows make it impossible to compute the eigenvalues of Λ(x) directly. We will therefore make the graph periodic by connecting opposite sides, as described in Sect. 1.3, so that all vertices can be treated alike, and then bound the eigenvalues of Λ(x) in terms of those of the periodic graph (or equivalently, a graph wrapped on a torus).

To be precise, we first extend our graph G to a graph G ^⊚ (⊚ stands for “torus”), by adding edges and vertices as shown in Fig. 3 (left). Note that this adds directed representative edges v→ and ←v for every vertex v on the right boundary of G, and v↑ and ↓v for v on the top boundary. All other edges that are added are considered as additional edges in the graph G ^⊚. Henceforth, when we work on the graph G ^⊚, computations will be performed modulo M and N in the two respective lattice directions.

We define Λ ^⊚ as the transition matrix for the graph G ^⊚, with specific edge weights chosen as follows: all representative edges of G ^⊚ have edge weight 1; for the additional edges, we choose the edge weights in such a way, that the product of the edge weights along every chain of additional edges linking opposite sides of the rectangle to each other is −1. Note that by this choice, the factor −1 will exactly compensate the sign picked up by a path which follows the chain, because of the 4 quarter-turns it makes.

Proof of Theorem 1.10

We first prove that the operator norm of the matrix Λ ^⊚ is $\sqrt{2}+1$. To this end, assume that the rows of Λ ^⊚ are arranged in such a way, that for every vertex v∈V, the 4 rows indexed by →v, ↑v, ←v and ↓v immediately succeed each other in this order. Let Π be the permutation matrix which permutes the columns of Λ ^⊚ so that column vd maps to column dv, for all v∈V and d∈{↑,↓,→,←}.

By construction, the matrix Λ ^⊚ Π with the permuted columns is now a block-diagonal matrix, since the 4 rows indexed by the directed edges pointing to v are matched along the diagonal with the 4 columns indexed by the directed edges pointing out from v. By considering the turning angles, it is easy to see that each 4×4 block is equal to the Hermitian matrix

which has eigenvalues $\sqrt{2}+1$ and $\sqrt{2}-1$, both of multiplicity 2.

Since A is Hermitian, its spectral radius is equal to its operator norm ∥A∥. It follows that the operator norm of Λ ^⊚ Π is given by $\|{A}\| = \sqrt{2}+1$, and since permuting columns does not change the operator norm of a matrix, we conclude that $\|{\varLambda^{\circledcirc}}\| = \sqrt{2}+1$.

We will now use this fact, together with the sub-multiplicativity of the operator norm, to bound ∥Λ(x)∥. To this end, let D(x) be the diagonal matrix of the same dimensions as Λ ^⊚, defined as follows. For vertices v on the right boundary of G, the diagonal entries of D(x) on the rows v→ and ←v are 0, and so are the diagonal entries on the rows v↑ and ↓v for v on the top boundary of G. For all other directed edges $\overrightarrow {uv}$ in the graph G ^⊚, the diagonal entry of D(x) on row $\overrightarrow{uv}$ is equal to the edge weight x _uv .

Now consider the matrix D(x)Λ ^⊚ D(1), where 1 denotes the edge weight vector on G ^⊚ with constant weight 1 on every edge. The multiplication by D(x) multiplies all rows of Λ ^⊚ corresponding to directed edges $\overrightarrow{uv}$ in the graph G by x _uv , and zeroes out all rows corresponding to directed edges which are in the graph G ^⊚, but not in the graph G. The multiplication by D(1) then zeroes out all columns of Λ ^⊚ corresponding to directed edges which are in G ^⊚ but not in G. In other words, D(x)Λ ^⊚ D(1) is just the matrix Λ(x) with rows and columns of zeros added to it for every directed edge which is in G ^⊚ but not in G. Therefore,

$$\bigl\|{\varLambda(x)}\bigr\|= \bigl\|D(x) \varLambda^\circledcirc D(1)\bigr\|\leq\bigl\|D(x)\bigr\| \cdot\bigl\|{\varLambda^\circledcirc}\bigr\|\cdot\bigl\| {D(1)}\bigr\|= (\sqrt{2}+1) \|{x}\|_{\infty}. $$

The desired bound on |f _r (x)| now follows from (2.7) and the facts that ρ(x)≤∥Λ(x)∥ and the number of directed edges in G is bounded by 4|V|. □

Remark

Using Fourier transforms, we can actually compute all eigenvalues of Λ ^⊚, and show that its spectral radius is $\sqrt{2}+1$. Also, with some extra effort, it is possible to show that for all finite rectangles, the spectral radius of Λ(x) is strictly less than $(\sqrt{2}+1) \|{x}\|_{\infty}$.

3.3 Free Energy Density

We are now going to use the bound obtained in Theorem 1.10 to prove Theorem 1.2 and it’s Corollary 1.3.

Proof of Theorem 1.2

We start with the high-temperature case, so fix β∈(0,β _c ) and set x=tanhβ. Let G be a rectangle in $\mathbb{Z}^{2}$, and take the set of additional edges to be empty. Note that by (1.4), $x\in(0,\sqrt{2}-1)$. By (3.3),

$$ \ln Z^{\mathrm{free}}_{G,\beta} = |V| \ln2 + \lvert{E}\rvert\ln(\cosh\beta) + \ln Z_G(x), $$

(3.5)

where Z _G (x) is the generating function for the graph G with edge weights equal to x. By Theorems 1.9 and 1.10, lnZ _G (x) equals ∑ _r f _G,r (x), where f _G,r (x) denotes the sum of the weights of all loops of length r in G.

Consider these loops of length r in G. For each vertex v∈V, let $\mathcal{L}^{v}_{r}(G)$ denote the collection of loops in G of length r for which v is the smallest vertex traversed. Observe that if v has distance at least r to the boundary of G, then $\mathcal {L}^{v}_{r}(G)$ can be mapped bijectively to $\mathcal{L}^{\circ}_{r} (\mathbb{Z}^{2})$ by a translation on $\mathbb{Z}^{2}$, hence $\sum_{\ell\in\mathcal{L}^{v}_{r}(G)} w(\ell;x) = f^{\circ}_{r}(x)$. There are at most |∂G|r vertices at a distance less than r from ∂G, and since |x|<1, for such a vertex v we have $\sum_{\ell\in\mathcal{L}^{v}_{r}(G)} |w(\ell;x)| \leq 3^{r}$ (by counting non-backtracking paths). From these observations and the fact that $\lim_{G\to\mathbb{Z}^{2}} |{\partial G}|/ |V|= 0$, it follows that

$$\lim_{G\to\mathbb{Z}^2} \frac{1}{|V|} f_{G,r}(x) = \lim _{G\to\mathbb{Z}^2} \frac{1}{|V|} \sum _{v\in V} \sum_{\ell\in \mathcal{L}^v_r(G)} w(\ell;x) = f^\circ_r(x) \quad\text{for all} \ r\geq1. $$

Furthermore, Theorem 1.10 says that $|{f_{G,r}(x)}| \leq 2\lvert{V}\rvert r^{-1} (\sqrt{2}+1)^{r} x^{r}$. Therefore, by dominated convergence and Theorem 1.9,

$$\lim_{G\to\mathbb{Z}^2} \frac{1}{\lvert{V}\rvert} \ln Z_G(x) = \lim_{G\to\mathbb{Z}^2} \sum_{r=1}^\infty \frac{1}{\lvert{V}\rvert} f_{G,r}(x) = \sum_{r=1}^\infty f^\circ_r(x). $$

We now combine this with (3.5), and use $\lim_{G\to \mathbb{Z}^{2}} |E|/ |V|= 2$ to obtain

$$-\beta f(\beta) = \lim_{G\to\mathbb{Z}^2} \frac{1}{|V| } \ln Z^{\text {free}}_{G,\beta} = \ln\bigl(2\cosh^2\beta\bigr) + \sum _{r=1}^\infty f^\circ_r(x). $$

The low-temperature case can be treated in a similar manner, except that one must work on the dual graphs G ^∗ with edge weights x=exp(−2β) on the dual edges, and use (3.2) instead of (3.3). □

Proof of Corollary 1.3

We will now show that Onsager’s formula follows from the expressions for f(β) derived above. First, we claim that with x=tanhβ for β∈(0,β _c ) and x=exp(−2β) for β∈(β _c ,∞), we have

$$ -\beta f(\beta) = \ln\biggl[ \frac{2\cosh 2\beta}{1+x^2} \biggr] + \sum_{r=1}^\infty f^\circ_r(x) $$

(3.6)

for all these β. This follows from (1.8) and the equality cosh² β+sinh² β=cosh² β(1+x ²)=cosh2β for β∈(0,β _c ), and from (1.8) together with the logarithm of the equality 2cosh2β=e ^2β(1+x ²) for β∈(β _c ,∞).

In the proof of Theorem 1.2, we have obtained $\sum_{r} f^{\circ}_{r}(x)$ as the limit of |V|⁻¹∑ _r f _G,r (x). It is clear from the proof that here we may as well replace f _G,r (x) by the corresponding sum of loop weights for the periodic graph G ^⊚ from Sect. 3.2. In fact, the argument becomes even simpler on G ^⊚, since we no longer have to treat vertices near the boundary separately. The transition matrix generating the loops in G ^⊚ with the desired edge weights x is xΛ ^⊚. Hence, by Theorem 1.9 and the proof of Theorem 1.10 in Sect. 3.2, which gives $\|{x\varLambda ^{\circledcirc}}\| \leq x(\sqrt{2}+1)$, we see that for $x\in(0,\sqrt{2}-1)$,

$$ \sum_{r=1}^\infty f^\circ_r(x) = \lim_{G\to\mathbb{Z}^2} \frac{1}{\lvert{V} \rvert} \sum_{r=1}^\infty f_{G^\circledcirc,r}(x) = \lim_{G\to\mathbb{Z}^2} \frac{1}{\lvert{V}\rvert} \frac{1}{2} \ln \det\bigl( \mathrm{I}-x\varLambda^\circledcirc\bigr). $$

(3.7)

We can compute det(I−xΛ ^⊚) by taking the Fourier transform of Λ ^⊚. This computation has appeared in the literature before, see for instance [10, 24, 28], but we also present it in brief form here for completeness.

Without loss of generality, we may assume that V is the set (3.4), in which case the Fourier transform of Λ ^⊚ is defined as

$$\widetilde{\varLambda}^\circledcirc_{(p,q)d,(p',q')d'} = \frac{1}{MN} \sum _{k,k'=0}^{M-1} \sum_{l,l'=0}^{N-1} e^{-\frac{2\pi i}{M}(pk-p'k')-\frac{2\pi i}{N}(ql-q'l')} \varLambda ^\circledcirc_{(k,l)d,(k',l')d'}, $$

where d,d′∈{↑,↓,→,←}. The calculation of this Fourier transform is made straightforward by the periodicity of Λ ^⊚, and reveals that the only entries surviving the summations are those for which p′=p and q′=q. Hence, $\widetilde{\varLambda}^{\circledcirc}$ is a block-diagonal matrix of 4×4 blocks. To be precise, writing ω _p =2πp/M, ω _q =2πq/N, the 4×4 block for given p and q is

Since $\det(\mathrm{I}-x\varLambda^{\circledcirc}) = \det(\mathrm {I}-x\widetilde{\varLambda}^{\circledcirc})$, from this Fourier transform we obtain

Using (3.7), we conclude that

(3.8)

To finish the computation, note that by (3.6), we have

$$-\beta f(\beta) = \frac{1}{8\pi^2} \int_0^{2\pi} \int_0^{2\pi} \ln\biggl[ \frac{4\cosh^2 2\beta}{(1+x^2)^2} \biggr] \, d\omega_1\, d\omega_2 + \sum _{r=1}^\infty f^\circ_r(x). $$

Combining this with (3.8), and then using the identity

$$\frac{2x(1-x^2)}{(1+x^2)^2} = \frac{\sinh2\beta}{\cosh^22\beta}, $$

which holds both for x=exp(−2β) and for x=tanhβ, we obtain

$$-\beta f(\beta) = \frac{1}{8\pi^2} \int_0^{2\pi} \!\! \int_0^{2\pi} \ln\bigl[ 4 \cosh^22\beta- 4\sinh2\beta(\cos\omega_1 + \cos \omega_2) \bigr] \,d\omega_1\,d\omega_2. $$

This is Onsager’s formula for the isotropic Ising model on $\mathbb{Z}^{2}$. □

3.4 Low-Temperature Correlations

In this section, we discuss the Ising model with positive boundary conditions. We consider rectangles G=(V,E) in $\mathbb{Z}^{2}$ (which later tend to $\mathbb{Z}^{2}$) and denote by G ^∗ the weak dual of G. Recall that every spin configuration $\sigma\in\varOmega_{G}^{+}$ on G corresponds bijectively to an even subgraph of G ^∗, that is, a graph in which all vertices in V ^∗ have even degree. For given σ, we denote the corresponding even subset of E ^∗ by F(σ); for given even F⊂E ^∗, we denote the corresponding spin configuration by σ(F).

Setting x _e =e ^−2β for every edge e in $\mathbb{Z}^{2*}$, by (3.1) and (3.2) we have

$$ P_{G,\beta}^+(\sigma) = \frac{1}{Z_{G^*}(x)} \prod_{e\in F(\sigma)} x_e, \quad\sigma\in \varOmega_G^+, $$

(3.9)

where $Z_{G^{*}}(x)$ is the generating function for G ^∗ with edge weight vector $x = (x_{e})_{e\in E^{*}}$. Note that here we implicitly restrict the edge weight vector x on $\mathbb{Z}^{2*}$ to the edges of the graph G ^∗ we work on. Such implicit restrictions to the relevant edges will occur throughout this and the following section.

Proof of Theorem 1.4

Fix $u,v \in\mathbb{Z}^{2}$, u≠v, and let γ be a self-avoiding path in $\mathbb{Z}^{2}$ from u to v. We may assume that G is large enough so that u, v and γ are all contained in the area spanned by G, see Fig. 2. We will express the two-point function $\langle{\sigma_{u} \sigma_{v}}\rangle^{+}_{G, \beta}$ as the quotient of two generating functions. To this end, we define new edge weights $x'_{e}$ on the edges of $\mathbb{Z}^{2*}$ such that $x'_{e} = -x_{e}$ if e crosses γ, and $x_{e}' = x_{e}$ otherwise. The reason for defining the weights $x_{e}'$ in this way is the crucial fact that for all $\sigma\in\varOmega_{G}^{+}$,

$$ \sigma_u \sigma_v \prod _{e \in F(\sigma)} x_e = \prod _{e \in F(\sigma)} x_e'. $$

(3.10)

To see this, recall that the edges in F(σ), by their very definition, cross edges xy∈E for which σ _x ≠σ _y . If σ _u =σ _v , then following γ from u to v, we necessarily cross an even number of such edges. If σ _u ≠σ _v , then we cross an odd number. In either case, (3.10) holds.

With the help of (3.9), we can write

$$\langle{\sigma_u\sigma_v}\rangle^+_{G,\beta} = \sum_{\sigma\in\varOmega_G^+} \sigma_u\sigma_v P^+_{G,\beta }(\sigma) = \frac{1}{Z_{G^*}(x)} \sum _{\sigma\in\varOmega_G^+} \sigma_u\sigma_v \prod _{e\in F(\sigma)} x_e, $$

and using (3.10) and the bijection between even F and $\varOmega_{G}^{+}$, we obtain

$$ \langle{\sigma_u\sigma_v} \rangle^+_{G,\beta} = \frac{1}{Z_{G^*}(x)} \sum _{\text{even}\ F\subset E^*} \prod_{e\in F} x_e' = \frac{Z_{G^*}(x')}{Z_{G^*}(x)}. $$

(3.11)

The idea that correlations in the Ising model can be studied by means of ratios of generating functions with changed edge weights (or equivalently, changed spin-spin interactions) has arisen before in the physics literature, see [16]. It now follows from Theorems 1.9 and 1.10 that for β>β _c , we have

$$\langle{\sigma_u \sigma_v }\rangle^+_{G,\beta} = \exp\Biggl( \sum_{r=1}^\infty\sum _{\ell\in\mathcal{L}_r(G^*)} \bigl[ w\bigl(\ell; x'\bigr)-w(\ell ; x) \bigr] \Biggr), $$

where $\mathcal{L}_{r}(G^{*})$ is the collection of loops of length r in the graph G ^∗.

Recall that we call a loop in G ^∗ uv-odd if it crosses γ an odd number of times. Observe that for uv-odd loops ℓ, w(ℓ;x′)=−w(ℓ;x), while for loops ℓ that are not uv-odd, w(ℓ;x′)=w(ℓ;x). It follows that

$$ \langle{\sigma_u \sigma_v } \rangle^+_{G,\beta} = \exp\Biggl( -2\sum_{r=1}^\infty \sum_{\ell\in\mathcal{L}^{uv}_r(G^*)} w(\ell; x) \Biggr), $$

(3.12)

where $\mathcal{L}^{uv}_{r}(G^{*})$ is the collection of uv-odd loops of length r in the graph G ^∗.

Note that a uv-odd loop of length r cannot travel far from u and v. To be precise, these loops must be contained in $B^{u}_{r} \cup B^{v}_{r}$, where $B^{u}_{r}$ is a square in the plane of side length r centred at u, and $B^{v}_{r}$ is defined similarly. To study the convergence of (3.12) as $G\to\mathbb{Z}^{2}$, for arbitrary rectangles R in $\mathbb{Z}^{2}$ that can be finite or infinite, and even equal to $\mathbb{Z}^{2}$, we now define

$$a_r\bigl(R^*;x\bigr) := \sum_{\ell\in\mathcal{L}^{uv}_r(R^*)} w ( \ell; x). $$

This definition makes sense both for finite and infinite R, since the loops contributing to the sum must be contained in $B^{u}_{r} \cup B^{v}_{r}$.

Let $B^{uv}_{r}$ denote the smallest rectangle in $\mathbb{R}^{2}$ containing both $B^{u}_{r}$ and $B^{v}_{r}$, and write $R^{*}\cap B^{uv}_{r}$ for the largest subgraph of R ^∗ which is a rectangle in $\mathbb{Z}^{2*}$ entirely contained in $B^{uv}_{r}$. Then for all R,

$$ a_r\bigl(R^*;x\bigr) = a_r\bigl(R^* \cap B^{uv}_r;x\bigr) = \frac{1}{2} \sum _{\ell\in\mathcal{L}_r(R^*\cap B^{uv}_r)} \bigl[ w(\ell; x) - w\bigl(\ell; x'\bigr) \bigr]. $$

(3.13)

Now, since the volume of $B^{uv}_{r}$ is bounded from above by (∥u−v∥+r)², and $\exp(2\beta_{c}) = \sqrt{2}+1$ by (1.4), Theorem 1.10 yields the uniform bound

$$ \bigl|a_r\bigl(R^*;x\bigr)\bigr| \leq2\bigl(\|u-v\|+r\bigr)^2 r^{-1} \exp \bigl( -2(\beta-\beta_c)r \bigr) \quad\text{for all}\ R. $$

(3.14)

We now return to (3.12). Since eventually, $G^{*}\cap B^{uv}_{r} = \mathbb{Z}^{2*}\cap B^{uv}_{r}$ when $G\to\mathbb{Z}^{2}$, from (3.13) we conclude that

$$a_r\bigl(G^*; x\bigr) \to a_r \bigl( \mathbb{Z}^{2*}; x \bigr) \quad\text{for all}\ r\geq1. $$

Moreover, the a _r (G ^∗;x) are uniformly bounded in G by the right-hand side of (3.14), which is summable over r. Therefore, by dominated convergence,

$$\lim_{G\to\mathbb{Z}^2} \sum_{r=1}^\infty a_r\bigl(G^*; x\bigr) = \sum_{r=1}^\infty a_r \bigl( \mathbb{Z}^{2*}; x \bigr), $$

where the series on the right is absolutely summable. Using (3.12), this proves the convergence of $\langle{\sigma_{u}\sigma_{v} }\rangle^{+}_{G,\beta}$ in Theorem 1.4.

Next, we consider $\langle{\sigma_{u} }\rangle^{+}_{G,\beta}$ for u∈G∖∂G. We can treat this like $\langle{\sigma_{u}\sigma_{v} }\rangle^{+}_{G, \beta}$ by taking v on the boundary of G, since then σ _v =+1. We now call a loop which crosses γ an odd number of times u-odd, since this depends only on u, not v. The box $B^{uv}_{r}$ can be replaced by $B^{u}_{r}$ in the argument, which replaces (∥u−v∥+r)² by r ² in (3.14). This completes the proof of Theorem 1.4. □

Proof of Corollary 1.5

The limit $\langle{\sigma_{u} }\rangle^{+}_{\mathbb{Z}^{2},\beta}$ in Theorem 1.4 is easily seen to be independent of the choice of u, and we take u=o as the canonical choice. We now consider what happens to the two-point function when we take u and v further and further apart. When r<∥u−v∥/2, the boxes $B_{r}^{u}$ and $B_{r}^{v}$ in the proof of Theorem 1.4 above are disjoint. If this is the case, a uv-odd loop of length r in $\mathbb{Z}^{2*}$ must be contained in either $B_{r}^{u}$ or $B_{r}^{v}$. Hence,

When ∥u−v∥→∞, the first factor converges to 1 exponentially fast, since the uniform bound in (3.14) applies to $a_{r} ( \mathbb{Z}^{2*}; x )$. In the second factor, the first term in the sum is a sum over the u-odd loops of length r, and the second term is a sum over the v-odd loops. Hence the second factor factorizes and converges (exponentially fast) to $[\langle{\sigma_{o}}\rangle ^{+}_{\mathbb{Z}^{2},\beta}]^{2}$. □

3.5 High-Temperature Correlations

In this section, we discuss the Ising model on rectangles G=(V,E) in $\mathbb{Z}^{2}$ (which will again tend to $\mathbb{Z}^{2}$) with free boundary conditions. From the definitions (1.1), (1.2) and (1.3), we have

$$\langle{\sigma_u \sigma_v}\rangle^{{\mathrm{free}}}_{G, \beta} = \sum_{\sigma\in\varOmega_G^{\mathrm{free}}} \sigma_u \sigma_v P^{\mathrm{free}}_{G,\beta}(\sigma) = \frac{1}{Z^{\mathrm{free}}_{G,\beta}} \sum_{\sigma\in\varOmega _G^{\mathrm{free}}} \sigma_u\sigma_v \prod _{xy\in E} e^{\beta\sigma_x\sigma_y}. $$

Performing the high-temperature expansion on the right-hand side of this expression, in the way explained in Sect. 3.1, leads to

where x _e =tanhβ for every edge e in $\mathbb{Z}^{2}$, and δF denotes the set of all vertices that have odd degree in (V,F). Using (3.3), we conclude that

(3.15)

where Z _G (x) is the graph generating function for the graph G with edge weight vector x=(x _e ) _e∈E .

Proof of Theorem 1.6

Fix $u,v\in\mathbb{Z}^{2}$, u≠v, and recall the definitions of u ^∗, v ^∗, the path γ and the additional edges E _γ and vertices V _γ from Sect. 1.2 (see Fig. 2, right). For an arbitrary rectangle R in $\mathbb{Z}^{2}$ (either finite or infinite) containing u and v, we denote by R _γ the graph obtained from R by adding all vertices in V _γ to its vertex set, and all edges in E _γ to its edge set. In R _γ , all edges added from the set E _γ are considered as additional, and the edges from R are considered as representative.

As in the low-temperature case, we now define weights $x'_{e}$ on the edge set of $\mathbb{Z}^{2}$ such that $x_{e}' = -x_{e}$ if e crosses γ, and $x_{e}' = x_{e}$ otherwise. We also define edge weights $x'_{\gamma}(t)_{e}$ on the edge set of $\mathbb{Z}^{2}_{\gamma}$, as follows:

$$x'_\gamma(t)_e = \begin{cases} x'_e &\text{if $e$ is an edge of~$\mathbb{Z}^{2}$}; \\ 1 &\text{if $e \in E_{\gamma}\setminus\{uu^{*}\}$}; \\ t &\text{if $e = uu^{*}$}. \end{cases} $$

To motivate this definition, consider a given rectangle G=(V,E) in $\mathbb{Z}^{2}$, large enough so that u,v∈V. We claim that

(3.16)

To see this, note that we can bijectively map every F contributing to the first sum to a subgraph in the second sum, by taking the union F∪E _γ . Doing this may introduce edge crossings, whence the factor $(-1)^{C_{F}}$, but these are compensated by switching from the edge weight vector x to $x_{\gamma}'(1)$.

The crucial step is now to recognize the last expression as the derivative of a graph generating function. Indeed, a simple consideration shows that

evaluated at any t, since any even F⊂E _γ contributes at most one factor t to the product of edge weights on the right. In particular, we are allowed to evaluate the derivative at t=0. By (3.15) and (3.16), this establishes that

$$ Z_G(x) \cdot\langle\sigma_u \sigma_v\rangle^{\text {free}}_{G,\beta} = \frac{\partial}{\partial t} Z_{G_\gamma} \bigl( x_\gamma'(t) \bigr) \bigr|_{t=0}. $$

(3.17)

We now fix β∈(0,β _c ), so that by (1.4), $x_{e}\in (0,\sqrt{2}-1)$ for every e∈E, and by Theorem 1.10, the spectral radius of Λ(x′) is strictly less than 1. We now need a similar bound on the spectral radius of the matrix $\varLambda_{\gamma}( x'_{\gamma}(t) )$, which is the transition matrix for the modified graph G _γ with edge weight vector $x'_{\gamma}(t)$. The difference between these two matrices is that $\varLambda_{\gamma}( x'_{\gamma}(t) )$ allows transitions between u and v along the chain of additional edges in E _γ . This means that the 32 matrix entries from du to vd′ and from dv to ud′, with d,d′∈{↑,↓,→,←}, are nonzero in $\varLambda_{\gamma}( x'_{\gamma}(t) )$ for t≠0, while they are 0 in Λ(x′); all other entries of the two matrices are the same.

The 32 deviating matrix entries are all of the form te ^iϕ/2, where ϕ is a sum of turning angles. Here, t will be treated as a complex variable. For t=0, $\varLambda_{\gamma}( x'_{\gamma}(t) ) = \varLambda(x')$. Since the eigenvalues vary continuously with t, we conclude that there exists ε>0 such that for all t satisfying |t|<ε, the spectral radius of $\varLambda _{\gamma}( x'_{\gamma}(t) )$ is bounded from above by some α∈(0,1).

Hence, if |t|<ε, Theorem 1.9 applies, and we obtain

$$Z_{G_\gamma} \bigl( x_\gamma'(t) \bigr) = \exp \Biggl( \sum_{r=1}^\infty f_{\gamma r}(t) \Biggr), $$

where

$$f_{\gamma r}(t) = \sum_{\ell\in\mathcal{L}_r(G_\gamma)} w \bigl( \ell; x_\gamma'(t) \bigr). $$

Note that, this last sum being finite, the f _γr (t) are polynomials in t. Also, from (2.7) it follows that |f _γr (t)|≤2|V|α ^r. Therefore, the partial sums of the series ∑ _r f _γr (t) are uniformly convergent for |t|<ε, and the sum of the series is an analytic function of t. Moreover, the derivatives of the partial sums also converge uniformly to the derivative of the sum of the series.

From all this, it follows that the right-hand side of (3.17) is equal to

$$\Biggl( \sum_{r=1}^\infty\frac{\partial}{\partial t} \sum_{\ell \in \mathcal{L}_r(G_\gamma)} w \bigl( \ell; x_{\gamma}'(t) \bigr) \Bigg|_{t=0} \Biggr) \exp\Biggl( \sum_{r=1}^\infty \sum_{\ell\in \mathcal{L}_r(G_\gamma)} w \bigl( \ell; x_{\gamma}'(0) \bigr) \Biggr). $$

In the first factor, the only loops that survive the differentiation are those that visit the edge uu ^∗, since only they contribute a factor t to the weight. Taking the derivative at t=0, we are only left with those loops that visit the edge uu ^∗ exactly once. In the second factor, because we set t=0, the only loops that contribute are those that do not visit uu ^∗. This leaves precisely all loops in the graph G. The right-hand side of (3.17) therefore becomes

$$\Biggl( \sum_{r=1}^\infty\sum _{\ell\in\mathcal {L}^{uu^*}_r(G_\gamma)} w \bigl( \ell; x_\gamma'(1) \bigr) \Biggr) \exp\Biggl( \sum_{r=1}^\infty \sum_{\ell\in\mathcal{L}_r(G)} w\bigl(\ell; x'\bigr) \Biggr), $$

where $\mathcal{L}^{uu^{*}}_{r}(G_{\gamma})$ is the set of loops of length r in G _γ that visit uu ^∗ once. From this, applying Theorem 1.9 again to the second factor, we find that

$$ \langle{\sigma_u \sigma_v} \rangle^{\mathrm{free}}_{G,\beta} = \Biggl( \sum_{r=1}^\infty \sum_{\ell\in\mathcal {L}^{uu^*}_r(G_\gamma)} w \bigl( \ell; x_{\gamma}'(1) \bigr) \Biggr) \frac{Z_G(x')}{Z_G(x)}. $$

(3.18)

Note the ratio of graph generating functions in (3.18). Recall that we have seen such a ratio of graph generating functions before in the low-temperature case, namely in (3.11). Thus, this ratio can be interpreted as a two-point function between the spins at u ^∗ and v ^∗ in a dual Ising model with positive boundary conditions at the dual low temperature β ^∗, given by exp(−2β ^∗)=tanhβ. Using (3.12), we can express this ratio in terms of a sum over all u ^∗ v ^∗-odd loops in the graph G, if we like.

Next, we want to consider the limit as $G\to\mathbb{Z}^{2}$. By the argument given in Sect. 3.4, we already know that the ratio of graph generating functions in (3.18) converges to $\langle{\sigma_{u^{*}} \sigma_{v^{*}}}\rangle^{+}_{ \mathbb{Z}^{2*}, \beta^{*} }$. It remains to consider what happens to the sum over the loops that visit uu ^∗ once. To this end, for a general finite or infinite rectangle R in $\mathbb{Z}^{2}$ containing u and v, we define

$$ a_r\bigl(R_\gamma; x'_\gamma \bigr) := \sum_{\ell\in\mathcal {L}^{uu^*}_r(R_\gamma)} w\bigl(\ell; x'_\gamma\bigr), $$

(3.19)

where we have simplified the notation by letting $x'_{\gamma}\equiv x'_{\gamma}(1)$.

As in the low-temperature case, the loops that contribute to $a_{r}(R_{\gamma}; x'_{\gamma})$ must be confined to the box $B^{uv}_{r}$, defined in the same way as before, except possibly for the steps taken along the additional edges in E _γ , which are not counted in the length of the loop, and are allowed to go outside $B^{uv}_{r}$. Hence,

$$ a_r\bigl(R_\gamma; x'_\gamma\bigr) = a_r \bigl( \bigl(R \cap B^{uv}_r\bigr)_\gamma; x'_\gamma \bigr), $$

(3.20)

where $R \cap B^{uv}_{r}$ is the largest subgraph of R contained in $B^{uv}_{r}$, as before. It follows that $a_{r}(G_{\gamma}; x'_{\gamma}) \to a_{r} ( \mathbb{Z}^{2}_{\gamma}; x'_{\gamma})$ for all r≥1. As before, we now want to use dominated convergence to prove that

$$ \lim_{G\to\mathbb{Z}^2} \sum _{r=1}^\infty a_r\bigl(G_\gamma; x'_\gamma\bigr) = \sum_{r=1}^\infty a_r \bigl( \mathbb{Z}^2_\gamma; x'_\gamma\bigr), $$

(3.21)

and that the right-hand side is absolutely summable. This requires an appropriate uniform bound (in R) on the right-hand side of (3.19).

To obtain this bound, by (3.20) it is sufficient to consider an arbitrary finite rectangle R in $\mathbb{Z}^{2}$ containing u and v, and such that R is contained in $B^{uv}_{r}$. Note that every loop of length r in R _γ which visits the edge uu ^∗ once, has a representation of the form ℘⊕γ, where ℘ is a path of length r in R from v to u. Here, we use the facts that the part ℘ of the loop never visits uu ^∗, and that the steps taken along γ from u to v do not contribute towards the length of the loop, since they are along additional edges.

Let Λ _R (x′) be the transition matrix for the graph R with edge weights $x'_{e}$. Note that the sum of the weights of all paths ℘ of length r from v→ to ↑u, for instance, is given by the entry of the matrix $\varLambda_{R}^{r}(x')$ in row v→ and column ↑u. To compute the sum of the weights of the corresponding loops ℘⊕γ, we only need to multiply this entry by the factor e ^iϕ/2, where ϕ is the sum of the turning angles encountered in the path from ↑u to v→ along the edges in E _γ . From these observations, we can conclude that

$$a_r\bigl(R_\gamma; x'_\gamma\bigr) \leq16\, \bigl\|{\varLambda_R^r \bigl(x'\bigr)}\bigr\|_{\max}, $$

where ∥⋅∥_max denotes the maximum-entry norm, and the factor 16 comes from the fact that there are 4 directed (representative) edges pointing out from v, and 4 pointing to u. By Theorem 1.10 and the fact that the maximum-entry norm of a matrix is bounded by the operator norm, and using that $(\tanh\beta_{c})^{-1} = \sqrt{2}+1$ by (1.4), we obtain

$$ a_r \bigl( R_\gamma; x'_\gamma\bigr) \leq16\, \bigl\| \varLambda_R^r\bigl(x'\bigr)\bigr\| \leq16\, \bigl\|\varLambda_R\bigl(x'\bigr)\bigr \|^r \leq16\, \biggl( \frac{\tanh\beta}{\tanh\beta_c} \biggr)^r. $$

(3.22)

We emphasize that this bound holds uniformly for all finite and infinite rectangles R containing u and v. Hence, (3.21) holds by dominated convergence, and this completes the proof of Theorem 1.6. □

Proof of Corollary 1.7

We now consider what happens to the two-point function studied above when we let ∥u−v∥ tend to infinity. Since the loops that visit uu ^∗ necessarily have length at least ∥u−v∥, we can write

$$\langle\sigma_u \sigma_v\rangle^{\mathrm{free}}_{\mathbb {Z}^2,\beta} = \biggl( \sum_{r\geq\|{u-v}\|} a_r \bigl( \mathbb {Z}^2_\gamma; x'_\gamma\bigr) \biggr) \langle\sigma_{u^*} \sigma_{v^*}\rangle ^+_{\mathbb{Z}^{2*}, \beta^*}. $$

By Theorem 1.4, the two-point function on the right is bounded between 0 and 1. Alternatively, at this stage we could also observe that the ratio of graph generating functions in (3.18) is always between −1 and +1, since the same even subgraphs contribute to both generating functions, but only in the numerator, some of them come with a negative sign. Furthermore, the bound in (3.22) holds for $a_{r} ( \mathbb {Z}^{2}_{\gamma}; x'_{\gamma})$. This gives the desired upper bound. That the two-point function is nonnegative follows directly from (3.15). □