Abstract
Chemical thermodynamics is of central importance in chemistry, physics, the biosciences and engineering. It is a highly formalized scientific discipline of enormous generality, providing a mathematical framework of equations (and a few inequalities), which yields exact relations between macroscopically observable thermodynamic equilibrium properties of matter and restricts the course of any natural process. While these aspects alone are already of the greatest value for practical applications, in conjunction with judicially selected molecular-based models of material behavior, that is to say by using concepts from statistical mechanics, experimentally determined thermodynamic quantities contribute decisively towards a better understanding of molecular interactions and hence of real macroscopic systems. A plenary lecture affords the lecturer an opportunity to survey a few reasonably large sub-areas of the fields he works/worked in and to reflect on them from the perspective of many years of research. The general subject I selected for this review, i.e. chemical thermodynamics of liquid nonelectrolytes (pure or mixed), is vast. Over the last decades, the field’s impressive growth has been stimulated by the continuously increasing need for thermophysical property data and phase equilibrium data in the applied sciences, and it has greatly profited by advances in experimental techniques, by advances in the theory of liquids in general, and by advances in computer simulations of reasonably realistic model systems in particular. Specifically, I shall focus on just three topics of increasing complexity: (1) heat capacities and related quantities of fairly simple molecular liquids, predominantly at or near orthobaric conditions; (2) chemical thermodynamics of binary liquid mixtures containing one strongly dipolar aprotic component; (3) caloric properties of dilute solutions of nonelectrolytes, with emphasis on properties of aqueous solutions at infinite dilution (which are of importance in biophysical chemistry).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Every novel is a debtor to Homer. Every carpenter who shaves with a fore-plane borrows the genius of a forgotten inventor.
Ralph Waldo Emerson in: Representative Men. Seven Lectures: I. Uses of Great Men, pp. 7–38, The Riverside Press, Cambridge, Mass., U.S.A. (1893)
1 Introduction
Taking advantage of being a plenary lecturer at the 20th Ulm-Freiberger Calorimetry Conference in Freiberg, Saxony, the German analogue to the Calorimetry Conference Series in the USA, I will present some areas of chemical thermodynamics of liquid nonelectrolyte systems (either pure or mixed) which are representative of my long-time research interests in liquid state physical chemistry. In fact, “back to the roots!” and “forwards to new frontiers!” will be the leading mottos. While the title of this lecture is intentionally quite general, the focus will be on just three topics:
-
Heat capacities and related properties of fairly simple molecular liquids, predominantly at, or near, saturation conditions [1–9].
-
Caloric properties of binary liquid mixtures containing one strongly polar aprotic component [10–17].
-
Caloric properties of dilute solutions of nonelectrolytes, with emphasis on high-dilution properties of aqueous solutions [18–34].
All three topics are more complex and less understood than might be supposed. In order to keep the review to a reasonable size, the coverage throughout is necessarily brief. For the omission of many interesting papers I would like to offer my apologies in advance: my choices for references are illustrative and not comprehensive.
Thermodynamics rests on an experiment-based axiomatic fundament. Experiments, together with theory and computer simulation, are the pillars of science, and Fig. 1 (the “knowledge triangle” [35]) indicates what may be learned from a comparison of respective results under idealized conditions. It may be used to illustrate the process of inductive reasoning in science, also known informally as bottom-up reasoning, which amplifies and generalizes our experimental observations, eventually leading to theories and new knowledge. In contradistinction, deduction, informally known as top-down reasoning, orders and explicates already existing knowledge, thereby leading to predictions which may be corroborated by experiment, or falsified (see Popper [36]). As pointed out by Dyson [37], “Science is not a collection of truths. It is a continuing exploration of mysteries…an unending argument between a great multitude of voices.” The most popular heuristic principle to guide our hypothesis testing in these arguments is known as Occam’s Razor, named after the Franciscan friar William of Ockham (England, ca. 1285–1349). Also called the principle of parsimony or the principle of the economy of thought, it states that the number of assumptions to be incorporated into an adequate model should be kept minimal. While this is the preferred approach, the model with the fewest assumptions may turn out to be wrong. More elaborate versions of Occam’s razor have been introduced by modern scientists, and for in-depth philosophical discussions see, for instance, Mach [38], Popper [36], Swinburne [39], Katz [40], and Sober [41].
In the three topics I shall present in this review, the formal framework of chemical thermodynamics has been augmented by simple ideas from molecular theory, effectively anchoring them in the field of molecular thermodynamics. This term was coined by Prausnitz [42, 43] more than four decades ago. It is a field of great academic fascination, an indispensable part of physical chemistry as well as of chemical engineering. The impressive growth of molecular thermodynamics has been stimulated by the continuously increasing need for thermodynamic property data and phase equilibrium data [44–62] in the applied sciences, and has greatly profited by unprecedented advances in experimental techniques [63–71], by advances in the theory of liquids in general [72–91], and by advances in computer simulations of reasonably realistic model systems [92–102].
2 Heat Capacities and Related Properties of Pure Liquids
Heat capacities belong to the most important thermodynamic/thermophysical properties, this fact has been amply documented [6, 7, 9, 71, 103, 104]. For PVT systems, where P denotes the pressure, V the molar volume, and T the thermodynamic temperature, there are three liquid-state heat capacities in common use (in the following, for the sake of brevity and whenever unambiguously possible, the descriptive superscript L for liquid, the superscript V for vapor, and the superscript asterisk (*) indicating a pure-substance property will be omitted). The molar heat capacity at constant volume C V , also known as the molar isochoric heat capacity, is defined by
the molar heat capacity at constant pressure C P , also known as the molar isobaric heat capacity, is defined by
and the molar heat capacity at saturation \( C_{\upsigma} \) of a liquid maintained at all temperatures in equilibrium with an infinitesimally small amount of vapor at the corresponding vapor pressure \( P_{\upsigma} \left( T \right) \) is defined by [76]
This heat capacity is more closely related to conventional adiabatic calorimetry, where measurements are performed on samples consisting of saturated liquid in equilibrium with a small amount of its vapor enclosed in a constant-volume vessel [76, 103, 105]. Here, all the symbols have their usual significance, i.e. U is the molar internal energy, H is the molar enthalpy, S is the molar entropy, F is the molar Helmholtz energy, and G is the molar Gibbs energy. The corresponding extensive quantities are obtained through multiplication with the total amount of substance \( n = {m \mathord{\left/ {\vphantom {m {M_{\text{m}} }}} \right. \kern-0pt} {M_{\text{m}} }} \), where m is the mass of the liquid, and \( M_{\text{m}} \) is its molar mass [106, 107]. Note that henceforward derivatives along the saturation (or orthobaric) curve will be indicated by the subscript \( \upsigma \).
C P and \( C_{\upsigma} \) are related as follows [9, 76, 103, 104]:
Here, \( V = V^{\text{L}} \left( {T,P_{\upsigma} \left( T \right)} \right) \) is the molar volume of the liquid at saturation, \( \gamma_{\upsigma} \equiv \left( {{{\partial P} \mathord{\left/ {\vphantom {{\partial P} {\partial T}}} \right. \kern-0pt} {\partial T}}} \right)_{\upsigma} \) denotes the slope of the vapor–pressure curve, i.e. \( {{{\text{d}}P_{\upsigma} } \mathord{\left/ {\vphantom {{{\text{d}}P_{\upsigma} } {{\text{d}}T}}} \right. \kern-0pt} {{\text{d}}T}} \), and
is the isobaric expansivity of the liquid, with \( \rho \equiv M_{\text{m}} /V \) being the mass density. For the expansivity \( \alpha_{\upsigma} \) of a liquid remaining in contact with its vapor equilibrium phase we obtain
where
denotes the isothermal compressibility, and
is the isochoric thermal pressure coefficient. Below the normal boiling point the difference \( \alpha_{P}^{\text{L}} - \alpha_{\upsigma}^{\text{L}} \) is usually very small.
and at the critical point, which is characterized by the critical temperature \( T_{\text{c}} \), the critical pressure \( P_{\text{c}} \), and the critical molar volume \( V_{{\text{c}}} \)
remain finite. Here, the superscript V indicates the vapor phase. Equation 6 is obtained with the help of the exact Clapeyron equation
where \( \Delta_{\text{vap}} H \) is the molar enthalpy of vaporization, and \( {{\Delta }}_{{{\text{vap}}}} V \equiv V^{{\text{V}}} \left( {T,P_{{{\sigma }}} \left( T \right)} \right) - V^{{\text{L}}} \left( {T,P_{{{\sigma }}} \left( T \right)} \right) \) is the volume change on vaporization, with \( V^{\text{V}} \left( {T,P_{\upsigma} \left( T \right)} \right) \) denoting the molar volume of the vapor at saturation.
Neither C P nor \( C_{\upsigma} \) is equal to the change of the enthalpy of the liquid with temperature along the saturation curve, which quantity is given by [9, 76, 103, 104]
Since U = H − PV,
Thus, for the saturated liquid at temperatures well below the critical temperature, where usually 0 < \( T\alpha_{P}^{\text{L}} \) < 1, the following sequence is obtained:
The differences between the first four quantities are generally much smaller than the difference between \( \left( {{{\partial U^{\text{L}} } \mathord{\left/ {\vphantom {{\partial U^{\text{L}} } {\partial T}}} \right. \kern-0pt} {\partial T}}} \right)_{\upsigma} \) and \( C_{V}^{\text{L}} \). At low vapor pressures, the difference between \( C_{\upsigma}^{\text{L}} \) and \( C_{P}^{\text{L}} \) is frequently negligible (see above), but at higher vapor pressures corrections in the spirit of Eq. 4 have to be applied. The general form of the equations derived above may also be applied to the saturated vapor [76, 103], where, however, the difference \( C_{\upsigma}^{\text{V}} - C_{P}^{\text{V}} \) is always significant since \( \alpha_{P}^{\text{V}} V^{\text{V}} \) is always large. In fact, for vapors of substances consisting of small molecules, such as argon, carbon dioxide, ammonia and water (steam), \( \alpha_{P}^{\text{V}} V^{\text{V}} \) may be large enough to make \( C_{\upsigma}^{\text{V}} \) even negative. Finally we note that the difference between the isobaric heat capacities in the vapor phase and the liquid phase at equilibrium may be expressed as
Equation 21 is known as the Planck equation. At temperatures well below the critical temperature, where \( \gamma_{\upsigma} \) is small, the frequently used approximate relation
is obtained.
The difference between the heat capacities C P and C V may be derived as follows. Since
and
one obtains
or, with Eq. 11,
and
respectively. With the compression factor Z ≡ PV/RT, alternatively the difference is given by [9]
where R is the gas constant. Note that it is fully expressed in terms of PVT quantities.
The ratio of the heat capacities, κ ≡ C P /C V , is accessible via Eqs. 1 and 2:
With
and
we obtain
At this juncture it is convenient to introduce, by definition, another auxiliary quantity, the isentropic compressibility β S , often loosely called the adiabatic compressibility:
Substituting 1/(Vβ S ) for −(∂P/∂V) S in Eq. 32 yields
At low frequencies and small amplitudes, to an excellent approximation (i.e. neglecting dissipative processes, such as those associated with shear and bulk viscosity and thermal conductivity) the speed of ultrasound ν 0 is related to β S by [108, 109]
Using Eq. 34, the speed of ultrasound may also be expressed as
Within the constraints indicated above [9], ν 0 may be treated as a thermodynamic equilibrium property. However, at higher frequencies many liquids show sound speed dispersion due to thermal molecular relaxation and structural relaxation [108–112], i.e. the experimental sound speed is larger than the speed v 0 appearing in Eqs. 35 and 36. Thus, care must always be exercised in deciding whether the measured speed of ultrasound is indeed the quantity to be subsequently used in a thermodynamic analysis. In passing we note that β S of liquids has also been determined by purely mechanical methods, i.e. by directly measuring the volume increase on sudden decompression [113–117], though this method is considerably less common and less accurate than that based on ultrasonics, Eq. 35.
Using Eq. 26 in conjunction with Eq. 36, the ratio of the heat capacities (or the ratio of the compressibilities) may now be calculated from
This is one of the most important equations in thermophysics, since at low temperatures, where γ V of liquids is very large, the direct calorimetric determination of C V of liquids is not easy and requires sophisticated instrumentation, as evidenced by the careful work of Magee at NIST [118–123]. It becomes more practicable near the critical point where γ V is much smaller. Most of the isochoric heat capacity data for liquids reported in the literature have been obtained indirectly through use of Eq. 37 from
that is to say, from experimentally determined isobaric heat capacities, isobaric expansivities and ultrasonic speeds at sufficiently low frequencies. With modern equipment, these three quantities may be measured accurately and speedily, thereby making the indirect method for determining C V of liquids quite attractive.
In addition, Eq. 37 provides also a valuable alternative to the direct determination of β T via PVT measurements, since
Combining Eqs. 26 and 34, we obtain for the difference between the compressibilities
or
while
Evidently, the most important use of liquid-state β S data obtained via speed-of-sound measurements is the calculation of C V and/or β T using the appropriate equations given above. The indirect approaches for determining the isochoric heat capacity and the isothermal compressibility of liquids usually yield highly accurate results [3, 124, 125].
According to Eqs. 10, 34, 36 and 37, the isothermal pressure dependence of the density may be expressed as
which gives upon integration at constant temperature [126–130]
where \( P_{\text{ref}} \) is a conveniently selected reference pressure, usually 0.1 MPa. Thus, by measuring the thermodynamic speed of ultrasound v 0(T, P) as a function of temperature and pressure [131], and combining these results with data at ordinary pressure, that is \( \rho \left( {T,P_{{{\text{ref}}}} } \right) \) and \( C_{P} \left( {T,P_{{{\text{ref}}}} } \right) \), Eq. 43 provides a versatile alternative route to high-pressure PVT data and high-pressure heat capacity data. The first integral on the right-hand side may be evaluated directly by fitting the isothermal ultrasonic speed data v 0(T, P) with suitably selected polynomials or Padé approximants, and for the second integral several successive integration algorithms have been devised, taking into account
and
Equation 45 follows from
which in turn is obtained by differentiating the Gibbs–Helmholtz equation H = G − T(∂G/∂T) P . The simplicity, rapidity and precision of this method makes it highly attractive for the determination of the density, isobaric expansivity, isothermal compressibility, isochoric thermal pressure coefficient, isobaric heat capacity and isochoric heat capacity of liquids at high pressures [132–138]. The most interesting results of these wide-temperature range/wide-pressure range investigations of hydrocarbons, say, of heptane and toluene [133], are the proof of the existence of (shallow) minima of the isotherms C P = C P (P) at elevated pressures, and of a substance-specific crossing “point” (or small crossing region?) of the isotherms α P = α P (P). These two effects are closely related. For heptane, this crossing “point” is found at ca. 120 MPa, at which pressure (∂α P /∂T) P ≈ 0. Thus, for any given pressure lower than 120 MPa α P of heptane increases with temperature, while at any given pressure higher than 120 MPa α P decreases with temperature. For liquid water, recent high-precision measurements of the speed of sound over large temperature and pressure ranges have been communicated by Lin and Trusler [139] and by Baltasar et al. [140].
Note that
which follows from
In turn, Eq. 48 is obtained by differentiating the Gibbs–Helmholtz equation U = F − T(∂F/∂T) V . Using Eqs. 35 and 37 yields the alternative expression
(∂U/∂V) T is called the internal pressure and is frequently given the symbol Π(T, P). It is closely related to liquid structure and thus plays an important role in liquid-state physical chemistry [141–146]. Assuming the intermolecular pair potential energy u(r) for a simple fluid to be spherically symmetric, as is the case, for instance, with a Mie (n,m)-type potential energy function (introduced in 1903 [147, 148]),
and pairwise additive, the molar configurational internal energy U c, which is equal to the molar residual internal energy \( U^{\text{r}} = U - U^{\text{pg}} \), is related to the pair distribution function \( g\left( {r,T,\rho_{\text{n}} } \right) \) by [78, 87],
Here, r is the distance between the molecules, n and m are positive constants associated with repulsion and attraction, respectively (n > m), ɛ is an intermolecular energy parameter characterizing the well-depth of the interaction energy function, i.e. \( u\left( {r_{ \hbox{min} } } \right) = - \varepsilon \), σ is an intermolecular distance parameter characterized by u(σ) = 0, \( \rho_{\text{n}} = {{N_{\text{A}} } \mathord{\left/ {\vphantom {{N_{\text{A}} } V}} \right. \kern-0pt} V} \) is the number density, N A is the Avogadro constant, k B = R/N A is the Boltzmann constant, and the superscript pg indicates the perfect-gas state (ideal-gas state), i.e. the real limiting state as P → 0. Special cases of the Mie (n,m) function were introduced by Jones in 1924 and connected with gas viscosities [149], the equations of state of real gases [150], X-ray measurements on crystals [151], and quantum mechanics [152]. The most common form of the Lennard-Jones (12,6) function is [152]
where \( \sigma = 2^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 6}} \right. \kern-\nulldelimiterspace} 6}}} r_{{{\text{min}}}} .\)
By using a chorostat (constant volume piezometer), the internal pressure may be determined directly, according to Eq. 48, as the difference between the thermal (or kinetic) pressure Tγ V and the total external pressure P, or indirectly, via Eqs. 49 or 50, respectively. Interestingly, isochoric thermal pressure coefficients γ V of liquids have been measured far less frequently [153–163] than the other mechanical coefficients α P and β T , though direct determinations with a piezometer can be carried out with high accuracy. For normal liquids below the boiling point, P ≪ Tγ V .
The solubility parameter δ [42, 43, 55, 72, 75, 141, 164–173] is a versatile quantity introduced by Hildebrand and by Scatchard. It is generally defined as the square-root of the cohesive energy density of a liquid and thus reflects the intermolecular interactions. While several definitions of the molar cohesive energy may be found in the literature, the most appropriate is
Thus, the solubility parameter is given by
For \( P = P_{\upsigma} \), the molar cohesive energy is directly connected with the molar enthalpy of vaporization [46]:
The PVT behavior of the vapor phase at moderate pressures, say, at less than 0.3 MPa, is reasonably well approximated by a two-term virial equation in pressure,
which has practical advantages. Here, B(T) is the second virial coefficient [44]. Insertion of this volume-explicit equation of state into Eq. 56 yields
At sufficiently low vapor pressures and with the approximation of ideal-gas behavior of the vapor, Eq. 58 may be further simplified to
and correspondingly the solubility parameter at saturation condition is
The majority of the solubility parameters found in the literature is based on Eq. 60 and refers to 298.15 K. If the cohesive energy of a liquid is needed for \( P > P_{\upsigma} \), one has to integrate along the desired isotherm,
Concomitantly, the pressure dependence of \( V^{\text{L}} \) must be accounted for, for instance via the modified Tait equation (MTE), a versatile liquid-phase equation of state which is usually satisfactory for pressures up to about 100 MPa [26, 174, 175]:
Here, \( \beta_{T}^{\text{L}} \left( {T,P_{\upsigma} } \right) \) is the isothermal compressibility of pure saturated liquid, and \( m_{\text{MTE}} \) is a pressure-independent parameter. For many liquid nonelectrolytes, experimental values cluster around \( m_{\text{MTE}} \) = 10, with only a weak temperature dependence. For recent work on the pressure dependence of the solubility parameter see Verdier and Andersen [176], and Rai et al. [177].
Based on ideas introduced by van Laar [178–180], for binary mixtures of essentially nonpolar molecules Hildebrand and Scatchard showed that the symmetrically normalized activity coefficients (Lewis–Randall convention, see below in Sect. 3) γ i , i = 1,2, can be expressed as
and
where \( V_{1}^{{{\text{L}} * }} \) is the molar volume of pure liquid component 1, \( V_{2}^{{{\text{L}} * }} \) is the molar volume of pure liquid component 2, and the corresponding volume fractions Φ i are defined by
with x i being the mole fraction of component i. The cohesive energy densities of the pure liquids are denoted by
where \( U_{{{\text{coh,}}i}}^{{{\text{L}} * }} \) is the cohesive energy of pure liquid component i, and c 12 reflects the interaction between unlike molecules. Formally, this key quantity may be related to the cohesive energy densities of the pure liquids by
where k 12 is a binary interaction parameter. As a first approximation, Scatchard and Hildebrand assume k 12 = 0, whence with
the activity coefficients may be estimated using pure-component properties only:
and
yielding
for the excess molar Gibbs energy. Only positive deviations from Raoult’s law are predicted. The regular-solution equations Eqs. 68a and 68b may readily be generalized to multicomponent mixtures. For many solutions containing nonpolar components the regular-solution equations provide reasonable estimates provided that the temperature range of application is not large and that it is well below critical conditions.
For liquids, the graph P against T at constant volume is generally close to a straight line, i.e. the curvature of the isochores is very small, whence the density dependence of the isochoric heat capacity is very small (cf. Eq. 47), and its determination requires precision experiments. Starting with the pioneering work of Bridgman [181, 182] and, in particular, of Gibson and colleagues [183–187], we know that for organic solvents at ordinary temperatures (∂γ V /∂T) V , and hence (∂C V /∂V) T , is negative, which fact will be discussed below in another context.
In classical, direct high-pressure PVT measurements on fluids, isothermal compression is achieved by applying hydrostatic pressure and measuring the resulting volume changes. The value of β T at saturation pressure, i.e. β T (T, P σ (T)), is then obtained through appropriate extrapolation of the (mean) experimental values over a fairly large pressure range, which needs careful attention to detail [188, 189]. On the other hand, vibrating-tube flow densimeters for the determination of ρ(T, P) are widely used because they combine high precision and simple operation in the flow mode (involving fairly small samples). In addition, they allow a problem-oriented selection of the incremental pressure steps, which may be kept quite small. Based on the work of Kratky et al. [190] in the late 1960s and of Picker et al. [191] in 1974, Albert and Wood [192] presented a versatile high-pressure, high-temperature flow densimeter, and since then many new, improved designs have been introduced [193–199].
Equation 45 suggests still another method for obtaining heat capacities of fluids at elevated pressures. At constant T
with
Here, the isobaric expansivity is the main experimental property to be measured as a function of T and P. The other experimental properties are the molar volume \( V\left( {T_{\text{ref}} ,P} \right) \) as a function of pressure at a convenient low reference temperature T ref and the molar isobaric heat capacity \( C_{P} (T,P_{\text{ref}} ) \) as a function of temperature at a convenient low reference pressure P ref. With a scanning transitiometer [200–203] it is possible to measure α P (T, P) over wide ranges of temperature and pressure with an uncertainty of about 1–3 %, the reference volume isotherm with an uncertainty of about 0.6 %, and the reference heat capacity isobar with an uncertainty of about 0.3 %. Thus, the overall uncertainty of the heat capacities of liquids at high pressures obtained by scanning transitiometry is estimated to be about 2 %. Again, perhaps the most interesting results are (i) the confirmation, for some organic liquids, of the existence of (shallow) minima of the isotherms of the isobaric heat capacity at elevated pressures, and (ii) the confirmation, for some organic liquids, of the existence of a crossing “point” (a crossing region?) of the isotherms α P = α P (P) at elevated pressures. As concerns the experimental results for the isobaric expansivity obtained with this technique, we note that, say for liquid hexane [201], the isotherms α P = α P (P) show a crossing “point” (a crossing region?) at about (65 ± 2) MPa, where (∂α P /∂T) P ≈ 0. However, the α P isotherms of liquid hexan-1-ol [202] indicates a possible crossing region only at much higher pressure, i.e. around 280 MPa, whence the C P isotherms of this hydrogen-bonded liquid do not show any minima at the conditions investigated. Closely related work has been reported by Romaní’s group [204–207] in Spain.
The resolution of the variation of \( C_{V}^{\text{L}} \) of liquids along the orthobaric curve, i.e. along states with \( V^{\text{L}} \left( {T,P_{\upsigma} \left( T \right)} \right) \), into contributions due to the increase of temperature and due to the increase of volume, respectively, is a highly interesting problem [1, 3, 7, 73, 104, 114–116]. It is important to realize that because of the close packing of molecules in a liquid, even a rather small change of the average volume available for their motion may have a considerable impact on the molecular dynamics: volume effects may become more important in influencing molecular motion in the liquid state than temperature changes. Since
in the absence of calorimetrically measured values of \( \left( {{{\partial C_{V}^{\text{L}} } \mathord{\left/ {\vphantom {{\partial C_{V}^{\text{L}} } {\partial T}}} \right. \kern-0pt} {\partial T}}} \right)_{V} \), evaluation of this quantity requires knowledge of the second term of the right-hand-side of Eq. 72. At temperatures below the normal boiling point, the saturation expansivity \( \alpha_{\upsigma}^{\text{L}} \) is practically equal to \( \alpha_{P}^{\text{L}} \) of the liquid (see Eqs. 8 or 9), and is frequently used instead. In principle, \( \left( {{{\partial C_{V}^{\text{L}} } \mathord{\left/ {\vphantom {{\partial C_{V}^{\text{L}} } {\partial V}}} \right. \kern-0pt} {\partial V}}} \right)_{T} \) is accessible via precise PVT measurements, see Eq. 47, but measurements of (∂2 P/∂T 2) V are also not plentiful. As indicated above, for simple organic liquids at ordinary temperatures, available data indicate that this quantity is small and negative, that is to say, at constant temperature \( C_{V}^{\text{L}} \) decreases with increasing volume. Alternatively, one may use [1, 3, 7, 73, 104]
The last term in parenthesis on the right-hand side can be evaluated by means of a modified Tait equation [1, 3, 7, 26, 73, 104, 116, 174, 175, 208], see Eq. 62. Specifically,
which relation holds remarkably well up to pressures of about 100 MPa (see above). For example, for liquid tetrachloromethane [3] at 298.15 K and corresponding \( V^{\text{L}} \left( {T,P_{\upsigma} } \right) \), the calculated value of \( \left( {{{\partial C_{V}^{\text{L}} } \mathord{\left/ {\vphantom {{\partial C_{V}^{\text{L}} } {\partial V}}} \right. \kern-0pt} {\partial V}}} \right)_{T} \) amounts to −0.48 J·K−1·cm−3, for cyclohexane −0.57 J·K−1·cm−3 is obtained, and for 1,2-dichloroethane [4] \( \left( {{{\partial C_{V}^{\text{L}} } \mathord{\left/ {\vphantom {{\partial C_{V}^{\text{L}} } {\partial V}}} \right. \kern-0pt} {\partial V}}} \right)_{T} \) = −0.60 J·K−1·cm−3. These results indicate a substantial contribution of \( \left( {{{\partial C_{V}^{\text{L}} } \mathord{\left/ {\vphantom {{\partial C_{V}^{\text{L}} } {\partial V}}} \right. \kern-0pt} {\partial V}}} \right)_{T} V^{\text{L}} \alpha_{\upsigma}^{\text{L}} \) to the change of \( C_{V}^{\text{L}} \) along the orthobaric curve (as well as to the corresponding change of the residual heat capacity, see below).
Equation 37 is a suitable starting point for a discussion of the temperature dependence of \( \kappa^{\text{L}} \equiv C_{P}^{\text{L}} /C_{V}^{\text{L}} = {{\beta_{T}^{\text{L}} } \mathord{\left/ {\vphantom {{\beta_{T}^{\text{L}} } {\beta_{S}^{\text{L}} }}} \right. \kern-0pt} {\beta_{S}^{\text{L}} }} \) along the orthobaric curve [1, 3, 104]:
Usually, the second term in parenthesis on the right-hand-side of Eq. 75 is positive and the third term is negative [209]; the fourth term may contribute positively or negatively. Thus \( \kappa^{\text{L}} \left( {T,P_{\upsigma} \left( T \right)} \right) \) of a liquid may increase or decrease with temperature.
From experimental heat capacities \( C_{V}^{{\text{L}}} \) of liquids, relatively simple approximate models may be used to extract information on the type of motion executed by molecules in the liquid state compared to the perfect or ideal gas state (pg). In general, they are based on the separability of contributions due to translation, rotation, vibration and so forth. Though none of the models is completely satisfactory, they have provided eminently useful insights and have thereby furthered theoretical advances. By following the pioneering work of Eucken [210, 211], Bernal [212], Eyring [213], Staveley [114, 115], Moelwyn-Hughes [116], Kohler [1, 214, 215], Bondi [216] and their collaborators, one may resolve the total molar heat capacity at constant volume of polyatomic non-associated liquids as follows [3, 7, 104]:
The translational contribution \( C_{{{\text{tr}}}}^{{\text{L}}} \) arises from the motion of the centers of gravity of the molecules under the influence of all the other molecules in the system (movement within the respective free volumes). It is of the order 3R/2 + R, R (the gas constant) being roughly the excess over the molar translational heat capacity associated with the perfect gas state. \( C_{{{\text{rot}}}}^{{\text{L}}} \) represents the contribution from the rotational movement of the molecules as a whole (over-all molecular rotation). For nonlinear molecules, due to hindered rotation (often called libration), its value may be appreciably higher than its perfect-gas phase value of 3R/2 (free rotation). The contribution from internal degrees of freedom, \( C_{{{\text{int}}}}^{{\text{L}}} \), can be subdivided advantageously into a part \( C_{{{\text{vib}}}}^{{\text{L}}} , \) resulting from internal molecular vibrations which are not appreciably influenced by density changes (say, by going from the liquid to the perfect gas state), and another part, \( C_{{{\text{conf}}}}^{{\text{L}}} \), resulting from internal rotations, i.e. conformational equilibria, which depend on changes in the surroundings of the molecules and hence on density [1, 4, 214–219]. Lastly, for polar substances there is a further contribution \( C_{{{\text{or}}}}^{{\text{L}}} \) from the change of the dipole–dipole orientational energy with temperature, which may become quite important [1, 4, 215, 219]. Here, the focus will be on liquids composed of quasi-rigid and not too anisotropic molecules, possessing no or only a small permanent dipole moment, of which tetrachloromethane, benzene and toluene are representatives. Preferably, all these contributions to \( C_{V}^{{\text{L}}} \) are discussed in terms of residual quantities in (T,V)-space [9], as elaborated in Refs. [3] and [7]. They provide the most direct measure of the contributions due to intermolecular interactions at any given state condition [76]. Note that when there is no risk of ambiguity, again for convenience quantities referring to the liquid will appear without a superscript L. The residual molar heat capacity \( C_{V}^{{\text{r}}} \left( {T,V} \right) \) at constant volume of the liquid is directly obtained from experimentally determined isochoric liquid state heat capacities and subtracting the corresponding heat capacity for the substance in the perfect gas state:
For fairly simple molecules, \( C_{V}^{{{\text{pg}}}} \left( T \right) \) may be calculated using the frequencies of their normal modes of vibration [220–222], and extensive data compilations are available [45, 62, 223]. With the separability assumption
is obtained. For the class of liquids indicated above (i.e. quasi-rigid nonpolar or weakly polar non-associated molecules), to an excellent approximation
whence Eq. 78 may be recast into
Here,
and for nonlinear molecules
which quantity represents the excess over the (classical) perfect gas phase value due to hindered rotation in the liquid of the molecules as a whole. Using corresponding states arguments and focusing on orthobaric states, \( C_{\text{tr}}^{\text{r}} \left( {T,V_{\upsigma} } \right) \) may be approximated by the orthobaric \( C_{V}^{\text{r}} \left( {\text{Ar}} \right) \) of liquid argon [3, 73, 224] (where, of course, \( C_{\text{int}}^{\text{r}} = 0 \) as well as \( C_{\text{rot}}^{\text{r}} = 0 \)) at the same reduced temperature \( T_{\text{r}} = {T \mathord{\left/ {\vphantom {T {T_{\text{c}} }}} \right. \kern-0pt} {T_{\text{c}} }} \), where \( T_{\text{c}} \) denotes the critical temperature. Thus, semiquantitative estimates of the residual molar rotational heat capacity may be conveniently obtained from
and subsequently discussed in terms of any suitable model for restricted molecular overall rotation (hindered external rotation) in the liquid phase. An alternative scaling has been suggested by Harrison and Moelwyn-Hughes [116], who use the experimental value of \( C_{V}^{\text{L}} \) for mercury as giving \( C_{\text{tr}}^{\text{L}} \) for the polyatomic molecules at any “reduced” temperature Θ, which is defined in terms of the temperature of interest, the melting temperature \( T_{\text{mp}} \) and the normal boiling temperature \( T_{\text{bp}} \):
Focusing on the entire orthobaric liquid range, from the triple point (tr) temperature to the critical temperature, one may use instead
Figure 2 shows the residual molar rotational heat capacity \( C_{\text{rot}}^{\text{r}} \left( {T,V_{\upsigma} } \right) \) of the liquid quasi-spherical molecules tetrachloromethane, tetrachlorosilane, and tin tetrachloride as a function of temperature. Specifically, these three liquids were selected [3] to corroborate and quantify Sackmann’s geometry-based cogwheel model [225], in which interlocking of the tetrahalide molecules hinders free rotation. Whereas the results for CCl4 and SiCl4 are quite similar, amounting to \( C_{\text{rot}}^{\text{r}} \left( {T,V_{\upsigma} } \right) \approx {{3R} \mathord{\left/ {\vphantom {{3R} 4}} \right. \kern-0pt} 4} \) at 298.15 K, \( C_{{{\text{rot}}}}^{{\text{r}}} \left( {T,V_{{{\sigma }}} } \right) \) for liquid SnCl4 is distinctly larger, i.e. about 5R/4: this is a clear indication of significantly more hindered external molecular rotation in tin tetrachloride. Though originally developed by Pitzer and Gwinn [226] for molecules with restricted internal rotation, their model may be adopted to deal qualitatively with restricted external rotation (subscript rr) [3]. The resulting contributions \( C_{\text{rr}} \) depend on the barrier height U 0 hindering free rotation and on temperature. The available experimental data [3] suggest that at 298.15 K all the tetrahalides are already on the high-temperature decline, i.e. past the maximum of the Pitzer–Gwinn curve \( C_{\text{rr}} \) versus T.
Residual molar rotational heat capacity \( C_{\text{rot}}^{\text{r}} \left( {T,V_{\upsigma} } \right) \) as a function of temperature \( {t \mathord{\left/ {\vphantom {t {^\circ {\text{C}} = {T \mathord{\left/ {\vphantom {T {{\text{K}} - 273.15}}} \right. \kern-0pt} {{\text{K}} - 273.15}}}}} \right. \kern-0pt} {^\circ {\text{C}} = {T \mathord{\left/ {\vphantom {T {{\text{K}} - 273.15}}} \right. \kern-0pt} {{\text{K}} - 273.15}}}} \) of the liquid quasi-spherical molecules tetrachloromethane (CCl4), tetrachlorosilane (SiCl4), tin tetrachloride (SnCl4), and cyclohexane (c-C6H12, not discussed in this review) for orthobaric conditions: \( V_{\upsigma} = V\left( {T,P_{\upsigma} \left( T \right)} \right) \) [3]
For SnCl4, the experimental residual molar rotational heat capacity (see Fig. 2) at 298.15 K for one degree of freedom amounts to \( {{C_{\text{rot}}^{\text{r}} } \mathord{\left/ {\vphantom {{C_{\text{rot}}^{\text{r}} } {3R \approx 0.4}}} \right. \kern-0pt} {3R \approx 0.4}} \). Approximating this value with \( {{C_{\text{rr}}^{\text{r}} } \mathord{\left/ {\vphantom {{C_{\text{rr}}^{\text{r}} } R}} \right. \kern-0pt} R} \) calculated via the Pitzer–Gwinn model indicates a barrier height of ca. U 0 = 5.5 kJ·mol−1. For the other two tetrahalides where molecular rotation is less hindered, the experimental value (Fig. 2) at 298.15 K for one degree of freedom is \( {{C_{\text{rot}}^{\text{r}} } \mathord{\left/ {\vphantom {{C_{\text{rot}}^{\text{r}} } {3R \approx 0.25}}} \right. \kern-0pt} {3R \approx 0.25}} \), which corresponds to a barrier height of ca. U 0 = 4.0 kJ·mol−1 [3]. For the volume dependence of U 0 of, say, CCl4 at 298.15 K, \( \left( {{{\partial U_{0} } \mathord{\left/ {\vphantom {{\partial U_{0} } {\partial V}}} \right. \kern-\nulldelimiterspace} {\partial V}}} \right)_{T} \approx - 100{\text{ J}} \cdot {\text{cm}}^{{ - 3}} \) is obtained: increasing the molar volume by 1 cm3·mol−1 results in the decrease of the barrier height responsible for hindered rotation by about 100 J·mol−1. In liquids, the nuclear spin relaxation rate via quadrupolar interaction is related to the rotational correlation time. From its temperature dependence in liquid CCl4, O’Reilly and Schacher [227] derived the rotational activation energy of (5.4 ± 0.4) kJ·mol−1. Relaxation times of 119Sn in liquid SnCl4 have been measured as a function of temperature by Sharp [228], yielding a distinctly higher activation energy of 7.8 kJ·mol−1, in satisfactory accord with our results.
Over the past four decades, liquids consisting of tetrahedral molecules in general, and liquid tetrachloromethane in particular, have been extensively studied by X-ray and neutron diffraction [229–240]. These studies indicate some common orientational order, as do computer simulations [236, 238, 241–246] and theoretical approaches [247–249] based on the reference interaction site model (RISM), though there are important differences in the details. For instance, it is found that the CCl4 molecules form interlocking structures which give rise to significant orientational correlations between molecules in the dense liquid phase, extending up to the limit of the second solvation shell, i.e. up to about 14 Å (Å = 10−10 m). According to Rey [244], of the configurations within the first solvation shell (which at ambient temperature reaches up to ca. 8 Å and contains about 12 molecules) approximately 5 molecules belong to the edge-to-edge (2:2) configuration, approximately 3 molecules belong to the edge-to-face (2:3) configuration, at least 2 to corner-to-edge (1:2), and at most 1 to corner-to-face (1:3). Face-to face (3:3) and corner-to-corner (1:1) configurations share the remaining molecule. It is important to emphasize that this (or similar) pictures will be heavily influenced by the decrease of density when going along the saturation curve towards elevated temperatures [233, 234].
Combining the detailed analysis of molecular dynamics simulation results and the interpretation of neutron diffraction measurements using the reverse Monte Carlo method [250], it appears that the corner-to-face (1:3) type near-neighbor configuration (Sackmann’s arrangement II [225], also known as the Apollo model [230]), which has been favored for the interpretation of structure in liquid CCl4 for more than three decades, is quite rare, the occurrence being around 5 % [245]. We note, however, that at very short distances (<5.8 Å), where four molecules interlock directly with the central molecule [247], the face-to-face (3:3) configuration (Sackmann’s arrangement I) becomes more important. Evidently, the orientational order in the liquid phase of tetrahedral molecules of type XCl4 is much more complex and long ranged than previously thought.
3 Caloric Properties of Binary Liquid Mixtures Containing One Strongly Polar Aprotic Component
Mixtures/solutions of practical interest for the chemist, chemical engineer or biophysicist are usually quite complex, that is to say, the intermolecular potential energy functions characterizing the pure components differ strongly, and frequently cause pronounced nonideal thermodynamic behavior. At this juncture, perhaps a few words are in order to indicate the three main reasons for the enormous efforts invested into experimental, theoretical and computer-based work on properties of mixtures/solutions in general, and on liquid-phase nonelectrolyte systems in particular. First and foremost, by systematically studying mixture/solution properties our knowledge of intermolecular interaction between different species in bulk liquid phases will improve. Second, the appearance of new physical phenomena in multicomponent systems is scientifically fascinating as well as challenging, and adds a new dimension to physico-chemical research. And third, the scientific insight gained allows the practitioner to deal efficiently (and pragmatically) with technologically important systems and processes.
Experiments are the fundament of science, yet the huge number of potentially interesting and useful mixture/solubility data connected with binary, ternary, quaternary, etc. systems at different temperatures and pressures effectively precludes their experimental determination for all but a few representative key systems of physico-chemical/technological interest. This is best illustrated by calculating the number of different multicomponent systems containing r components which can be formed out of, say, n = 1000 important chemicals. This r-combination is given by
whence \( {\text{C}}\left( {1000,2} \right) = 4.995 \times 10^{5} \) different binaries may be formed, \( {\text{C}}\left( {1000,3} \right) = 1.66167 \times 10^{8} \) different ternary systems, \( {\text{C}}\left( {1000,4} \right) = 4.141712475 \times 10^{10} \) different quaternary systems, and so forth. Reliable and effective prediction methods for mixture/solution properties are thus indispensable tools of the trade, which are provided, for instance, by group contribution methods such as UNIFAC or DISQUAC [251–260], or the new MOQUAC model [261], in which the effect of molecular orientation on molecular interaction is explicitly taken into account. While they work reasonably well for excess molar Gibbs energies \( G^{\text{E}} \) and excess molar enthalpies \( H^{\text{E}} \) over not too large temperature ranges, predicted results for activity coefficients at infinite dilution, aqueous solubilities of hydrocarbons and excess molar heat capacities at constant pressure, \( C_{P}^{\text{E}} \), are frequently not satisfactory [262]. Similar comments apply to the COSMO-RS and related models [263–272]. This is not really surprising since mixture models are usually constructed at the free-energy level. If T, P and x i are selected as independent canonical variables, \( G^{\text{E}} = H^{\text{E}} - TS^{\text{E}} \) becomes a generating function for all the other excess molar quantities and the activity coefficients γ i (T, P, x i ) based on the Lewis–Randall rule (symmetric convention). This is perhaps best seen from the fundamental property relation
whence,
and
The excess heat capacity is related to the second derivative of G E with respect to temperature, thus making it a very important discriminatory property for model evaluation:
Here, \( S^{\text{E}} \) denotes the excess molar entropy, \( V^{\text{E}} \) is the excess molar volume, x i = n i /n is the mole fraction of component i in a multicomponent system, n i is the amount of substance of component i, the total amount of substance is given by \( { n\,=\,\sum_{{i}} {n_{i}}} \), and \( { \sum_{{i}} {x_{i}}}\,=\,1 \). Note, that
The partial molar excess Gibbs energy \( G_{i}^{\text{E}} \) of component i is the excess chemical potential, that is \( G_{i}^{\text{E}} = \mu_{i}^{\text{E}} \), and since \( RT{ \ln }\gamma_{i} \) is a partial molar property with respect to G E,
see also Eq. 69. Derivation of useful relations for other excess partial molar properties in a constant-composition solution is straightforward.
In order to overcome their inherent difficulties, G E-models may be combined with equations of state (EOS), such as the Soave–Redlich–Kwong (SRK) EOS or the Volume-Translated Peng–Robinson (VTPR) EOS, to yield predictive group contribution equations of state [268, 273–279]. A survey of many popular models used to describe phase equilibria was recently prepared by Lei et al. [280].
For the practically and theoretically important global thermodynamic description of liquid mixtures of nonelectrolytes [9], the excess molar isobaric heat capacities are pivotal quantities, and one can take advantage of the exact thermodynamic relations contained in Eq. 91 to effect a considerable economy in experimental effort. Given \( H^{\text{E}} \) and \( G^{\text{E}} \) at one suitably selected temperature \( T_{\text{ref}} \) and \( C_{P}^{\text{E}} \) as a function of temperature, integration at constant pressure of the relevant equations yields \( H^{\text{E}} \), \( S^{\text{E}} \) and \( G^{\text{E}} \) over the temperature range of the heat capacity measurements. Well below the vapor–liquid critical region, \( C_{P}^{\text{E}} \) of a mixture of given composition and at constant pressure usually shows a simple functional dependence on temperature, for instance [9, 252]
where \( \tau \equiv {{T_{\text{ref}} } \mathord{\left/ {\vphantom {{T_{\text{ref}} } T}} \right. \kern-0pt} T}, \). Starting from the differential equations of Eq. 91, integration over temperature at constant pressure and composition yields
and
The dimensionless coefficients a j = a j (P, {x i }) are related to the corresponding excess quantities at \( T_{\text{ref}} ,P,\left\{ {x_{i} } \right\} \) by
Analogous expressions may be derived if \( C_{P}^{\text{E}} \), at constant pressure and composition, is given by a polynomial in T instead of T −1 (see also Sect. 4 of this review). Global studies of this kind are, however, quite rare, with some of the most careful and extensive investigations being those of Ziegler and colleagues [281, 282].
Heuristically, a discussion of mixtures/solutions may be conducted in terms of differences in molecular size, shape anisotropy, dispersion energy, polarity, molecular polarizability, flexibility, and so forth. Figure 3 presents an overview of the most important aspects at the molecular level as well as the bulk level [7, 12, 43, 76, 87, 101, 283, 284]. In fact, in many liquid mixtures/solutions dipolar (and quadrupolar) interactions contribute significantly to the thermodynamic properties and may involve cooperative phenomena. The principal obstacles for a comprehensive discussion of complex liquid mixtures/solutions are:
-
Uncertainty concerning the intermolecular potential energy functions of the components, and insufficient knowledge about the potential energy functions characterizing unlike interaction, i.e. of combining rules [43, 87, 285–288];
-
Difficulties encountered when two or more of the above-mentioned molecular aspects, say, shape anisotropy and a permanent electric dipole moment, are present simultaneously [43, 76, 87, 289–295];
-
Meager knowledge of many-body effects [76, 78, 296–298], exemplified, for instance, by the correlation of molecular orientation and medium effects on conformational equilibria [1, 2, 4, 15, 214, 215, 217, 219, 299–305].
Additional aspects include molecular association via hydrogen bonds [306–308], or charge transfer interaction [309, 310], and if aqueous solutions are involved, hydrophobic and hydrophilic effects [311–317].
A dipolar substance is characterized by its permanent molecular electric dipole moment p, though this quantity by itself is not sufficiently helpful in guiding the discussion of the impact of polarity on thermodynamic properties of pure liquids and liquid mixtures. For characterizing the effective polarity of a molecule, one may define a reduced dipole moment [7, 12, 76] according to
where ɛ 0 is the permittivity of the vacuum, σ is an appropriate molecular size parameter, say, of a Mie-type intermolecular potential energy function, and ɛ is the corresponding interaction energy parameter (see Eqs. 51 and 53). Equivalently, by virtue of the corresponding states principle, we may use
Evidently, a small dipole moment in a small molecule may cause as large a contribution to the interaction free energy as a large dipole moment in a large molecule [76]. However, even this quantity does not fully reflect the increase in effective polarity which results from an unsymmetrical disposition of the polar group within the molecule, i.e. from dipole moments exposed on the molecular periphery [7].
Here, I will only consider binary liquid systems of type [a polar aprotic component (1) + an aliphatic or alicyclic hydrocarbon (2)], where the focus is on dipolar orientational effects (caused by an appreciable dipole moment \( \varvec{p}_{1} \)) and increasing non-randomness in the mixtures when the temperature is lowered. Following Pople’s treatment [318] of the thermodynamic effects of orientational forces in liquids, which includes, but is not restricted to, dipolar interactions, the total molar Helmholtz energy can be expressed as the sum of spherically symmetric central-force (cf) contributions and additional orientational (or) contributions:
Assuming a lattice model, the extra molar Helmholtz energy in a pure liquid due to the contribution of dipole–dipole interactions is given by [7]
where \( V_{\text{r}}^{{{\text{L}} * }} = {{V^{{{\text{L}} * }} } \mathord{\left/ {\vphantom {{V^{{{\text{L}} * }} } {V_{\text{c}} }}} \right. \kern-0pt} {V_{\text{c}} }} \) is the reduced molar volume, \( T_{\text{r}} = {T \mathord{\left/ {\vphantom {T {T_{\text{c}} }}} \right. \kern-0pt} {T_{\text{c}} }} \) is the reduced temperature, and l depends on the lattice selected. For a face-centered cubic lattice, including also interactions beyond the first coordination sphere, l = 1.2045. We note that the orientational contribution to the Helmholtz energy of a dipolar liquid is always negative and varies with \( {{p^{4} } \mathord{\left/ {\vphantom {{p^{4} } {\left( {V^{{{\text{L}} * }} T} \right)}}} \right. \kern-0pt} {\left( {V^{{{\text{L}} * }} T} \right)}}^{2} \).
Similarly, one may decompose the excess molar Gibbs energy of a binary liquid mixture containing one strongly polar aprotic component, say, component 1, into a central-force contribution and an orientational contribution caused by the permanent electric dipole moment \( \varvec{p}_{1} \):
Again, assuming a face-centered cubic lattice and including interactions beyond the first coordination sphere, to a good approximation
where V L is the molar volume of the mixture. Thus, when mixing a dipolar liquid with a nonpolar liquid, the net destruction of dipolar order results in a positive contribution to \( G^{\text{E}} \) which is proportional to the fourth power of \( \varvec{p}_{1} \), or more precisely, it is proportional to \( {{p_{1}^{4} } \mathord{\left/ {\vphantom {{p_{1}^{4} } {\left( {V^{\text{L}} T} \right)}}} \right. \kern-0pt} {\left( {V^{\text{L}} T} \right)}}^{2} . \)
Alternatively, using a simple Guggenheim model [319] and including also contributions from molecular shape anisotropy, Kalali et al. [320] also showed that the order destruction leads to positive contributions to \( G^{\text{E}} \), \( H^{\text{E}} \) and \( S^{\text{E}} \), and to a negative contribution to \( C_{P}^{\text{E}} \). In this model, the excess molar Gibbs energy is given by
where
is the molar cooperative free energy, and a and b are constants characteristic for a given pair of substances, the excess molar enthalpy is
the excess molar entropy is
and for the excess molar heat capacity at constant pressure one obtains
This latter relation appears to hold well for nonpolar or weakly polar mixtures. However, for mixtures of a strongly polar liquid with an essentially nonpolar liquid, say, an alkane, the experimental \( C_{P}^{\text{E}} \) is usually less negative than demanded by Eq. 113 [6, 7, 17, 320–322]. This indicates that some dipole–dipole orientations have considerably greater stability (one may regard this as weak association) than accounted for by the angle-averaging procedure involved. An intuitively appealing way of treating these non-randomness effects, based on Guggenheim’s quasi-chemical theory, was suggested by Saint-Victor and Patterson [322]. To a reasonable approximation, the excess molar isobaric heat capacity is separated into a random (r) and a non-random (nr) contribution:
where \( \eta = { \exp }\left( {{W \mathord{\left/ {\vphantom {W {zRT}}} \right. \kern-0pt} {zRT}}} \right) \), and z is the coordination number [6, 7, 12, 17]. Note that in their original expression, Eq. 7 of [322], the factor η 2 is missing from the first term inside the wavy brackets. Equation 114 is in agreement with the first-order result of the Taylor expansion of the full quasi-chemical expression as obtained by Cobos [323]. Clearly, the random term is always negative with a parabolic composition dependence, as expected for mixtures where dipole–dipole order is destroyed by the mixing process. In contradistinction, the non-random term is always positive and has zero slope against the mole fraction axis at both ends of the composition range. Thus, the superposition of the two contributions \( C_{P}^{\text{E}} \left( {\text{r}} \right) \) and \( C_{P}^{\text{E}} \left( {\text{nr}} \right) \) accounts qualitatively for the appearance of W-shaped curves \( C_{P}^{\text{E}} \) versus x. The first W-shaped \( C_{P}^{\text{E}} \left( x \right) \) curves ever reported in the literature were for three mixtures of type (1,4-dioxane + an n-alkane) [10, 324], see Fig. 4. Since then, such mixture behavior has been found fairly often [17]. With decreasing temperature, the maximum caused by \( C_{P}^{{\text{E}}} \left( {{\text{nr}}} \right) \) increases, thus making the W-shape more pronounced, which behavior was confirmed by experiment [320, 322, 325–327]. For an analysis of W-shaped excess heat capacities in terms of the non-random two liquid (NRTL) model [328], see Troncoso et al. [329].
However, it is important to note that many of the mixtures showing W-shaped \( C_{P}^{\text{E}} \left( x \right) \) curves are quite close to liquid–liquid phase separation with an upper critical solution temperature (UCST) \( T_{\text{uc}} \). A liquid mixture near its upper critical consolute point has a weak divergence in its heat capacity at constant pressure when determined along a path of constant critical composition \( x = x_{\text{uc}} \) [330–333]. Thus, for the approach through the homogeneous one-phase region (\( T > T_{\text{uc}} \)), the standard power law expression, including the first correction-to-scaling term for extending the theoretical description further away from the critical point [334], is
Here, \( t = {{\left| {\left( {T - T_{\text{uc}} } \right)} \right.} \mathord{\left/ {\vphantom {{\left| {\left( {T - T_{\text{uc}} } \right)} \right.} {\left. {T_{\text{uc}} } \right|}}} \right. \kern-0pt} {\left. {T_{\text{uc}} } \right|}}. \) is the reduced distance, temperature wise, from \( T_{\text{uc}} \), B and E refer to the background heat capacity at constant pressure, A + is the amplitude of the leading divergence (homogeneous region), and D + is the amplitude of the first correction-to-scaling term; α = 0.11 and Δ1 = 0.5 are universal critical exponents [320, 335–338]. Evidently, The quasi-chemical approximation underestimates the non-random contribution to the excess heat capacity and becomes qualitatively incorrect for \( T \to T_{\text{uc}} \).
4 Caloric Properties of Dilute Solutions of Gases in Liquids
Solubility and related phenomena constitute one of the oldest and most important fields of physical chemistry. For more than a century, the study of the solubility of nonelectrolytes in liquids has contributed decisively to the development of the highly formalized general discipline of solution thermodynamics [34], a fact concisely summarized in 1950 by the introductory statement of Hildebrand and Scott to their monograph [141]: “The entire history of chemistry bears witness to the extraordinary importance of the phenomenon of solubility.”
Why, now, my long-term interest in the study of the solubility of gases in liquids? In addition to its profound theoretical interest, practical applications can be found in surprisingly diverse areas of the pure and applied sciences [20, 22, 26–28, 30–34, 339–347]: in other words, it is a fascinating area grounded in both theory and practice. Gas solubility data have led to useful estimates of effective Lennard-Jones parameters [348–350], which in turn allow successful predictions of Henry fugacities and related quantities for many gas–liquid systems over large temperature ranges using scaled particle theory [18, 22, 344, 351–354], ranging from aqueous [22, 23, 29, 355–357] to alcoholic systems [358] to the solubility of gases in perfluoronated hydrocarbons [19]. In particular, experimental solubilities determined in liquid water have been pivotal in developing modern views of hydrophobic effects [311, 312, 359–363], that is hydrophobic solvation and hydrophobic interaction, which field continues to be a highly active research area [313–317, 364–369].
It is far beyond the scope of this review to discuss available experimental methods tailored for determining caloric properties of dilute solutions in general (enthalpies of solution, heat capacity changes on solution), and of solutions of gases in liquids in particular. Those potentially interested in precision apparatus are referred to my review articles covering this topic, say, Refs. [22, 26, 30]. Let it suffice to point out that flow calorimetry involves fairly direct measurement techniques, and despite sophisticated designs they require relatively little additional thermophysical information and data manipulation to obtain the desired quantities from the primary experimental results. In contradistinction to this situation, to obtain thermodynamically well-defined and reliable caloric properties from gas solubility measurements, besides sophisticated instruments, data reduction is more complex and requires more auxiliary thermophysical data. A comprehensive discussion of this so-called van’t Hoff approach and of the relevant thermodynamic fundamentals was recently presented in Refs. [30, 33, 34].
By way of example, I will focus on data reduction associated with the use of our high-precision analytic gas solubility apparatus [23, 24, 29, 356, 357]. By and large, the method adopted for use with our medium-precision synthetic, fully automated Ben-Naim/Baer-type instrument, is similar [370–375]. In this context, high-precision implies an average random error (imprecision) of about ±0.05 % in conjunction with a maximum systematic error (inaccuracy) of about ±0.05 % or less. The imprecision associated with the Ben-Naim/Baer-type apparatus is roughly ±0.5 %, and the corresponding systematic error is estimated to be also about ±0.5 %. Our high-precision analytical method is based on earlier work of Benson and Krause [376, 377]. The technique used to degas the solvent has been described [378]. In order to obtain fully reproducible results, we usually use equilibration times of up to 48 h. The temperature drift of the large water thermostat during equilibration never exceeds ±0.003 K.
After attaining vapor–liquid equilibrium at T and \( P > P_{{\upsigma,1}} \), vapor phase and liquid phase samples of precisely known volumes are isolated, and the quantities of gas contained in each are transferred to the manometric system to determine the amounts of pure gas by classical PVT measurements. From the measured quantities, the Henry fugacity \( h_{2,1} \left( {T,P_{{\upsigma ,1}} \left( T \right)} \right) \), also known as the Henry’s law (HL) constant, of solute 2 (gas) dissolved in liquid solvent 1 at the experimental temperature and at the corresponding vapor pressure of the pure solvent \( P_{{\upsigma,1}} \left( T \right) \) is obtained through straightforward though tedious isothermal extrapolation \( P \to P_{{\upsigma,1}} \left( T \right) \), and concomitantly decreasing liquid phase mole fraction of dissolved gas, x 2 → 0, and decreasing mole fraction of gas in the coexisting vapor phase, y 2 → 0, according to
Here, \( f_{2}^{\text{L}} \left( {T,P,x_{2} } \right) \) is the fugacity of the solute in the liquid phase, and \( \phi_{2}^{\text{V}} \left( {T,P,y_{2} } \right) \) is the vapor phase component fugacity coefficient of the gaseous solute. Equation 116 is directly obtained from the general criterion for phase equilibrium in PVT systems of uniform temperature and pressure, which is formulated advantageously in terms of the equality of the fugacity of each constituent component i in all coexisting phases [42, 43]. For the solute (i = 2) in a binary solution this reads [26, 30, 31, 34]
where the liquid phase fugacity may be expressed by
and the vapor phase fugacity by
Note that the limiting behavior of the unsymmetrically normalized activity coefficient based on Henry’s law is
While the mole fractions are experimentally determined quantities, \( \phi_{2}^{\text{V}} \left( {T,P,y_{2} } \right) \) has to be calculated with a suitable equation of state. For measurements at such low pressures as in our work (P < 120 kPa), the virial equation in pressure at the second-virial-coefficient level,
is entirely adequate and most convenient for the description of real gas behavior: Hence, in a binary vapor mixture
with
B 11 and B 22 are the second virial coefficients of the pure components, B 12 designates the composition-independent interaction virial coefficient (cross-coefficient), and the second virial coefficient of the mixture may be expressed as
The fugacity coefficient of the solute at infinite dilution in the vapor phase is thus given by
and the fugacity coefficient of pure component 2 by
The quite popular rule-of-thumb \( \phi_{2}^{\text{V}} \left( {T,P,y_{2} } \right) = \phi_{2}^{{{\text{V}} * }} \left( {T,P} \right) \) may frequently be rather unsatisfactory. For instance, for the evaluation of \( \phi_{2}^{{{\text{V}}\infty }} \) it only holds if B 12 = (B 11 + B 22)/2.
In brief, the auxiliary quantities needed for a thermodynamically rigorous data reduction of gas solubility measurements in liquids at low pressures with our high-precision apparatus are the vapor pressure of the solvent, the second virial coefficients of the pure components, the second virial cross-coefficient, the molar volume of the pure liquid solvent [23], and the partial molar volume of the gas at infinite dilution in the liquid phase [23] (see also below). Frequently, no experimental data are available for one or more of these properties. Thus for vapor–liquid equilibrium (VLE) data reduction in general, and for gas solubilities in liquids in particular, one depends heavily on semiempirical estimation methods, which are predominantly based on the extended corresponding states theorem. For details I refer to the original articles and to the pertinent reviews [26, 30, 33, 34].
Once experimental Henry fugacities \( h_{2,1} \left( {T,P_{{\upsigma , 1}} \left( T \right)} \right) \) for a given solute/solvent system have been collected over a certain temperature range (but not too close to the critical temperature of the solvent), the question arises as to their most satisfactory mathematical representation as a function of temperature. In the absence of theoretically well-founded models of general validity, one has to rely on essentially empirical correlating equations, subject, however, to some important thermodynamic constraints. Depending on the choice of variables, that is T or 1/T, for expanding the enthalpy of solution (see later), either the Clarke–Glew (CG) equation [379–381]
or the Benson–Krause (BK) equation [376, 377]
are obtained. Both correlating equations are widely used, but on the basis of the ability to fit high-precision Henry fugacities over fairly large temperature ranges, and of simplicity, the BK power series in 1/T appears to be superior. In passing we note that the 3-term version of Eq. 127 is the well-known Valentiner equation [382].
At this juncture I would like to emphasize again that the frequently found sweeping statement “the solubility of a gas in a liquid decreases with increasing temperature” is misleading/incorrect when the entire liquid range between the triple point and the critical point of the solvent is considered. For many systems, the following behavior is well documented: at low temperatures (starting at the solvent triple point), \( h_{2,1} \left( {T,P_{{\upsigma , 1}} } \right) \) increases with increasing temperature, passes through a maximum, and then decreases towards its finite limiting value at the solvent’s critical point:
where use was made of the equilibrium condition prevailing at the critical point, that is
Here, \( \phi_{2}^{{{\text{V}}\infty }} \left( {T_{\text{c,1}} ,P_{\text{c,1}} } \right) \) and \( \phi_{2}^{{{\text{L}}\infty }} \left( {T_{\text{c,1}} ,P_{\text{c,1}} } \right) \) are the fugacity coefficients of component 2 at infinite dilution in the vapor phase and the liquid phase, respectively, at the critical point. Clearly, under these conditions Eq. 125 is no longer adequate and has to be replaced by an expression appropriate for elevated pressures/elevated densities. As I have shown some time ago [12, 25–27, 30, 33–35, 383, 384], this exact limiting value follows directly from the generally valid relation
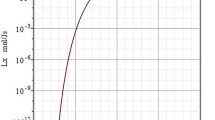
An example of the solubility behavior of gases in liquid water is provided by Fig. 5, where the Henry fugacities, i.e. \( {\text{ln}}\left[ {{{h_{{2,1}} \left( {T,P_{{{{\sigma ,1}}}} } \right)} \mathord{\left/ {\vphantom {{h_{{2,1}} \left( {T,P_{{{{\sigma ,1}}}} } \right)} {{\text{GPa}}}}} \right. \kern-\nulldelimiterspace} {{\text{GPa}}}}} \right] \), of methane dissolved in liquid water, and of krypton dissolved in liquid water, are plotted against temperature [23, 385]. The system {water (1) + methane(2)} plays an important role in discussions of hydrophobic effects [311, 312] as well as in the exploration of offshore oil fields [386].
Plot of \( \ln \left[ {{{h_{2,1} \left( {T,P_{{\upsigma , 1}} } \right)} \mathord{\left/ {\vphantom {{h_{2,1} \left( {T,P_{{\upsigma , 1}} } \right)} {\text{GPa}}}} \right. \kern-0pt} {\text{GPa}}}} \right] \) against temperature T for krypton and methane dissolved in liquid water. \( h_{{2,1}} \left( {T,P_{{{{\sigma ,1}}}} } \right) \) denotes the Henry fugacity (Henry’s law constant) at temperature T and corresponding pressure \( P_{{\upsigma , 1}} \left( T \right) \), the vapor pressure of water. Open circles experimental results of Crovetto et al. [385]: the average percentage deviation of the Henry fugacities from the values calculated via BK-type fitting equations is about ± 2 %. Filled circles experimental results of Rettich et al. [23]: the average percentage deviation of the Henry fugacities from the values calculated via the correlating BK function, Eq. 128, is about ±0.05 %. The temperature where the Henry fugacity exhibits a maximum is about 382 K for H2O + Kr, and about 363 K for H2O + CH4. The limiting values of the respective Henry fugacities \( h_{2,1} \left( {T,P_{{\upsigma,1}} } \right) \) as \( T \to T_{\text{c,1}} \) and \( P_{{\upsigma,1}} \to P_{{{\text{c}},1}} \) are finite and given by Eq. 129, the limiting slope of the curves is −∞, see Eq. 132
While the Henry fugacity remains finite at \( T_{\text{c,1}} \), for volatile solutes the limiting slope diverges to −∞:
when the critical point of the solvent is approached along the coexistence curve [387, 388].
Nonclassically, the temperature derivative diverges as \( \left| {\left. {{{\left( {T - T_{{{\text{c,1}}}} } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{{{\text{c,1}}}} } \right)} {T_{{{\text{c,1}}}} }}} \right. \kern-\nulldelimiterspace} {T_{{{\text{c,1}}}} }}} \right|^{{\beta - 1}} } \right. \), with a critical exponent β = 0.326.
Until the mid 1980s, high-precision measurements of Henry fugacities over temperature ranges large enough to permit van’t Hoff-type data treatment constituted the only reliable source of information on partial molar enthalpy changes on solution,
and a fortiori on partial molar heat capacity changes on solution,
Here, \( H_{2}^{{{\text{L}}\infty }} \) is the partial molar enthalpy of the solute at infinite dilution in the liquid solvent, \( H_{2}^{{{\text{pg}} * }} \) is the molar enthalpy of the pure solute in the perfect gas state, \( C_{P,2}^{{{\text{L}}\infty }} \) is the partial molar heat capacity at constant pressure of the solute at infinite dilution in the liquid solvent, and \( C_{P,2}^{{{\text{pg}} * }} \) is the molar heat capacity at constant pressure of the pure solute in the perfect gas state. Since the temperature dependence of the Henry fugacity is given by
and its pressure dependence by
where \( V_{2}^{{{\text{L}}\infty }} \) is the partial molar volume of the gas at infinite dilution in the liquid solvent, we obtain [23, 26–28, 30–34, 383],
and by analogous arguments
The ordinary differential quotients in Eqs. 137 and 138a, 138b indicate differentiation while maintaining orthobaric conditions: the first term on the right-hand-side of Eq. 137 as well as the first and the second term on the right-hand-side of Eq. 138b may be obtained from any one of the selected fitting equations, say the BK equation Eq. 128. The additional terms on the right-hand-side, containing \( V_{2}^{{{\text{L}}\infty }} \) and its derivatives with respect to T and P together with \( {{{\text{d}}P_{{\upsigma , 1}} } \mathord{\left/ {\vphantom {{{\text{d}}P_{{\upsigma , 1}} } {{\text{d}}T}}} \right. \kern-0pt} {{\text{d}}T}} \) and \( {{{\text{d}}^{2} P_{{\upsigma , 1}} } \mathord{\left/ {\vphantom {{{\text{d}}^{2} P_{{\upsigma , 1}} } {{\text{d}}T^{2} }}} \right. \kern-0pt} {{\text{d}}T^{2} }} \), are referred to in the literature [388, 389] as Wilhelm terms. For aqueous solutions, say, of the rare gases below 100 °C, their contributions are small, usually smaller than the experimental error associated with current precision measurements. However, their contributions increase rapidly with increasing temperature. In fact, the partial molar volume of a volatile solute at infinite dilution in a liquid solvent diverges to +∞ at the critical point of the solvent, see Wood et al. [390, 391], and the partial molar enthalpy at infinite dilution will diverge in exactly the same manner. The partial molar isobaric heat capacity at infinite dilution, \( C_{P,2}^{{{\text{L}}\infty }} \), diverges in a more complex way and much stronger than either \( V_{2}^{{{\text{L}}\infty }} \) or \( H_{2}^{{{\text{L}}\infty }} \) [392–396]. The important experiments of Wood et al. confirm the theoretical expectations. The influences of these divergences are felt relatively far from the critical point.
As pointed out above, direct calorimetric determinations of the high-dilution partial molar enthalpy change when a gas is dissolved in a liquid have been carried out by only a very limited number of research groups, primarily due to the very small heat effects involved. Besides calorimetric sensitivity, achieving the dissolution of an accurately known amount of gas in a time interval compatible with the stability of the calorimeter is another important experimental problem. Battino and Marsh [397] used a modified isothermal displacement calorimeter to measure \( \Updelta H_{2}^{\infty } \left( {T,P_{{\upsigma , 1}} } \right) \) of argon and nitrogen in tetrachloromethane, cyclohexane and benzene at 298.15 K, and of carbon dioxide, methane, ethane, ethene and propane in the same three solvents at 298.15 K and 318.15 K, and derived reasonable \( \Updelta C_{P,2}^{\infty } \left( {T,P_{{\upsigma , 1}} } \right) \) values from
The major step forward for measuring \( \Updelta H_{2}^{\infty } \left( {T,P_{{\upsigma,1}} } \right) \) over extended temperature ranges with a precision high enough to allow the reliable determination of \( \Updelta C_{P,2}^{\infty } \left( {T,P_{{\upsigma,1}} } \right) \) is based on the development of microcalorimeters (batch or flow) by I. Wadsö’s group at the Thermochemistry Laboratory in Lund, Sweden, and by S. J. Gill in the Chemistry Department of the University of Colorado in Boulder, Colorado, USA [398, 399]. There exist only seven sets of directly determined heat capacities of gases dissolved in liquid water, all originating from R. H. Wood’s laboratory at the University of Delaware, Newark, Delaware, USA [394–396]. Regrettably, so far no other research groups have continued work in this field.
Recently, Wilhelm [28, 30] and Wilhelm and Battino [32] presented comprehensive compilations of calorimetrically determined results for \( \Updelta H_{2}^{\infty } \left( {T,P_{{\upsigma,1}} } \right) \) and \( \Updelta C_{P,2}^{\infty } \left( {T,P_{{\upsigma,1}} } \right) \) for many gases dissolved in liquid water at T = 298.15 K and \( P_{{\upsigma,1}} \left( {298.15{\text{ K}}} \right) = 3.1691{\text{ kPa}} \), together with van’t Hoff-derived enthalpy changes on solution and heat capacity changes on solution. As representative examples, Table 1 shows such a comparison for argon [22, 357, 376, 389, 394, 400–403], oxygen [22, 29, 376, 377, 398, 399, 401, 405] and methane [22, 23, 396, 401, 406–408]. Evidently, comparing van’t Hoff derived enthalpy changes (one differentiation step with respect to T) and heat capacity changes (two differentiation steps with respect to T) with high-precision calorimetric results constitutes a severe quality test of solubility data. For nearly all solutions, agreement between these two approaches is entirely satisfactory, that is it is usually within the combined experimental errors. What a credit to the experimental ingenuity, perseverance and skills of solution thermodynamicists!
5 Concluding Remarks and Outlook
By common consent, the liquid state of matter still houses by far the largest group of unsolved/crudely solved problems in modern physical chemistry. Research on pure liquids continues to be an active field, and water is definitely the most enigmatic solvent. When studying liquid mixtures/solutions, the appearance of new phenomena not present in the pure components constitutes a most stimulating theoretical challenge and is of enormous practical importance: these aspects provide the principal reasons for investing so much experimental and theoretical work in the investigation of mixture/solution properties. When combined with advances in the statistical-mechanical treatment and increasingly sophisticated computer simulations, new insights and important connections at the microscopic, mesoscopic and macroscopic level are obtained. Pride of place, of course, is held by aqueous solutions, which are of central importance in biophysics and biophysical chemistry [368, 409–412]. And, of course, studies of aqueous interfaces and of the behavior of solutes therein (in particular ionic solutes) [413–421] have greatly profited from recent advances in surface selective spectroscopic techniques.
Calorimetry, PVT measurements and VLE determinations (and liquid–liquid equilibrium determinations and solid–liquid equilibrium determinations) are the most fundamental and also the oldest experimental disciplines of physical chemistry. Although simple in principle, enormous effort and ingenuity had to be invested into the construction of scientific instruments to provide the vast array of apparatus now at our disposal for the high-precision determination of caloric, PVT and ultrasonic properties of pure and mixed fluids over large ranges of temperature and pressure, and for vapor–liquid, liquid–liquid and solid–liquid equilibrium studies. The major driving forces for progress in instrumentation are the desire to (I) increase the area of applicability (larger temperature and pressure ranges, ever smaller concentrations, etc.), to (II) improve precision and accuracy (in particular for testing and developing theories), to (III) increase the speed of measurements, and to (IV) facilitate application, data management and data transfer. Undoubtedly, automation of instruments will continue, and so will miniaturization. In summary, chemical thermodynamics of liquids and liquid mixtures/solutions in general, and of aqueous systems in particular, will continue to be an exciting, developing field, and cross-fertilization with other disciplines, notably with molecular biology and molecular medicine, will become increasingly important. A rich research area lies ahead with many new and fascinating vistas of importance for mankind, and here the “end of scientific discovery” [422] is nowhere in sight.
The field of chemical thermodynamics has grown too big to be covered in one modest review article, but for the three subsections treated above (to which I have contributed over the years) I hope to have succeeded in providing a feeling for their scope, position in the development of science, and potential. It is a pleasure to acknowledge the many years of fruitful scientific collaboration with my former PhD advisor, Friedrich Kohler (†), with Rubin Battino, now Emeritus Professor at Wright State University (WSU), Dayton, Ohio, USA, with Jean-Pierre E. Grolier, now Emeritus Professor at Université Blaise Pascal, Clermont-Ferrand, France, with Henry V. Kehiaian (†), with Augustinus Asenbaum, now Retired Professor of Experimental Physics at the University of Salzburg, Salzburg, Austria, and about 80 colleagues, post-doctoral fellows and students from 17 countries. Without them, many projects would have been difficult to carry out. My association with chemical thermodynamics led to two extended stays in the United States of America at WSU, Dayton, Ohio, of about 4 years altogether, which I greatly enjoyed, and to more than 5 years, altogether, in France, first at the CRMT/CNRS, Marseille, and then at the Université Blaise Pascal, Clermont-Ferrand, which I also greatly enjoyed. Fortunately, over the years the University of Wien (Vienna), Wien, Austria, was generous enough to grant repeatedly extended Leaves of Absence for scientific research abroad.
6 Glossary of Symbols
In most cases I have adhered to the nomenclature/symbols suggested by IUPAC (see Green Book, Quantities, Units and Symbols in Physical Chemistry [423]). Deviations are due to my desire to present a concise, unequivocal and logically consistent notation in compliance with usage preferred by the scientific community interested in this review’s topics, i.e. by physical chemists, physicists and chemical engineers. Such an approach is in accord with the spirit of the Green Book expressed so admirably by Martin Quack in his Historical Introduction on p. XII of its 3rd edition, 2007: It is not the aim to present a list of recommendations in form of commandments. Rather we have always followed the principle that this manual should help the user in what may be called “good practice of scientific language”. Two quantities in particular I would like to single out to comment on: the Helmholtz energy (Helmholtz function) F and the pressure P. Sometimes the Helmholtz energy is denoted by A, which symbol is, however, almost universally used for the affinity of a chemical reaction as introduced by Th. De Donder in 1922, as quoted by Prigogine and Defay [424]. In addition, when surfaces are involved, A usually denotes the surface area. The symbol P for pressure is now accepted by IUPAC as an alternative to p, as indicated in Tables 2.2 and 2.10 of the Green Book. The reason why I (and many others) prefer P is the following. Temperature and pressure are both intensive quantities, and together with the composition they form a set of basic thermodynamic variables advantageously used for homogeneous fluids in equilibrium states. They are not perceived primarily as properties of the fluids but as conditions imposed on/exhibited by them with the valuable bonus of being (in principle) easily measured and controlled. In other words, temperature and pressure are quantities of “equal rank”, which fact should be reflected in the symbols we use, that is to say capital T and capital P. For heterogeneous PVT systems consisting of several phases in equilibrium with each other, temperature and pressure are identical in the coexisting phases. We note that Griffiths and Wheeler [425] call such variables fields (in contradistinction to variables that are in general not equal in coexisting phases, such as volume, enthalpy and entropy, which they call densities).
Some of the symbols listed below may be modified further, with obvious meaning, by adding appropriate subscripts, such as \( \upsigma \) (saturation or orthobaric condition), and/or superscripts, such as * (pure substance), ∞ (infinite dilution), and L (liquid) or V (vapor). The capital superscript letters are used because (i) they are easy to read, (ii) they are frequently used in the chemical engineering literature, including important monographs (for instance, Prausnitz et al. [43], Poling et al. [55]) and volumes published under the auspices of the International Union of Pure and Applied Chemistry (IUPAC) [69], and (iii) vapor–liquid equilibrium is usually abbreviated by VLE, and not by vle. The values for some fundamental physical constants listed in the glossary below are CODATA recommended values [107, 426].
Variables
- a :
-
Parameter in the expression for the molar cooperative free energy, Eq. 110
- a j :
-
=a j (P, {x i }), j = 1, 2, 3, … dimensionless coefficients used to describe the temperature dependence of \( {{C_{P}^{\text{E}} } \mathord{\left/ {\vphantom {{C_{P}^{\text{E}} } R}} \right. \kern-0pt} R} \), \( {{S^{\text{E}} } \mathord{\left/ {\vphantom {{S^{\text{E}} } R}} \right. \kern-0pt} R} \), \( {{H^{\text{E}} } \mathord{\left/ {\vphantom {{H^{\text{E}} } R}} \right. \kern-0pt} R}T \), and \( {{G^{\text{E}} } \mathord{\left/ {\vphantom {{G^{\text{E}} } R}} \right. \kern-0pt} R}T \), Eqs. 95–98
- a i :
-
i = 0, 1, 2, … dimensionless coefficients used to describe the temperature dependence of the Henry fugacity, i.e. of \( { \ln }\left[ {{{h_{2,1} \left( {T,P_{{\upsigma , 1}} \left( T \right)} \right)} \mathord{\left/ {\vphantom {{h_{2,1} \left( {T,P_{{\upsigma , 1}} \left( T \right)} \right)} {\text{Pa}}}} \right. \kern-0pt} {\text{Pa}}}} \right] \), Eq. 128 (BK)
- A i :
-
i = 0, 1, 2, … dimensionless coefficients used to describe the temperature dependence of the Henry fugacity, i.e. of \( { \ln }\left[ {{{h_{2,1} \left( {T,P_{{\upsigma , 1}} \left( T \right)} \right)} \mathord{\left/ {\vphantom {{h_{2,1} \left( {T,P_{{\upsigma , 1}} \left( T \right)} \right)} {\text{Pa}}}} \right. \kern-0pt} {\text{Pa}}}} \right] \), Eq. 127 (CG)
- A + :
-
Amplitude of the leading critical divergence in the homogeneous one-phase region above the upper critical solution temperature T uc for a path at constant critical composition \( x_{\text{uc}} \): see the power law describing the weak divergence of \( C_{{P,x_{\text{uc}} }} \), Eq. 115
- b :
-
Parameter in the expression for the molar cooperative free energy, Eq. 110
- B :
-
Non-diverging background term in the power law describing the weak divergence of \( C_{{P,x_{\text{uc}} }} \), Eq. 115
- B :
-
Second virial coefficient of a gaseous mixture
- B 11, B 22 :
-
Second virial coefficients of the pure gaseous components 1 and 2 when using the volume-explicit virial equation in pressure Z ≡ PV/RT = 1 + B ii P/RT, i = 1 or 2
- B 12 :
-
Vapor-phase interaction virial coefficient (cross-coefficient)
- c ii :
- \( C_{P}^{\text{L}} ,C_{P}^{\text{V}} \) :
-
Molar heat capacity at constant pressure (molar isobaric heat capacity) of the liquid (L) or of the vapor (V), respectively
- \( C_{P,2}^{{{\text{L}}\infty }} \) :
-
Partial molar heat capacity at constant pressure of solute 2 at infinite dilution in a liquid (L) solvent 1
- ΔC ∞ P.2 :
-
Partial molar heat capacity change on solution of a gas (2) in a liquid (1) at infinite dilution
- \( C_{V}^{\text{L}} ,C_{V}^{\text{V}} \) :
-
Molar heat capacity at constant volume (molar isochoric heat capacity) of the liquid (L) or the vapor (V), respectively
- \( C_{\upsigma}^{\text{L}} \) :
-
Molar heat capacity of a liquid (L) maintained at all temperatures in equilibrium with an infinitesimal amount of vapor (or shorter: molar heat capacity of a liquid at saturation)
- \( C_{\upsigma}^{\text{V}} \) :
-
Molar heat capacity of a saturated vapor (superscript V)
- \( C_{P,2}^{{{\text{pg}} * }} \left( T \right) \) :
-
Molar heat capacity at constant pressure of a pure fluid in the perfect-gas (ideal-gas) state
- \( C_{V}^{\text{pg}} \left( T \right) \) :
-
\(=C_{P}^{\text{pg}} \left( T \right) - R, \) Molar heat capacity at constant volume of a fluid in the perfect-gas (ideal-gas) state
- \( C_{P}^{\text{E}} \) :
-
Excess molar heat capacity at constant pressure
- \( C_{V}^{\text{r}} \) :
-
Residual molar heat capacity at constant volume in (T, V)-space
- \( C_{\text{tr}}^{\text{L}} \) :
-
Translational contribution to \( C_{V}^{\text{L}} \) arising from the motion of the centers of gravity of the molecules under the influence of all the other molecules in the liquid system
- \( C_{\text{rot}}^{\text{L}} \) :
-
Contribution to \( C_{V}^{\text{L}} \) originating from the rotational movement of the molecules as a whole; includes contributions due to hindered rotation (libration)
- \( C_{\text{int}}^{\text{L}} \) :
-
Contribution to \( C_{V}^{\text{L}} \) originating from internal degrees of freedom
- \( C_{\text{or}}^{\text{L}} \) :
-
Contribution to \( C_{V}^{\text{L}} \) originating from the change of the dipole–dipole orientational energy with temperature
- D + :
-
Amplitude of the first correction-to-scaling term (Wegner term), see Eq. 115
- E :
-
Parameter referring to the background heat capacity of a liquid mixture, see Eq. 115
- f :
-
Fugacity
- f i :
-
Fugacity of component i in solution (liquid phase or vapor phase)
- \( f_{i}^{{{\text{V}} * }} \) :
-
\( = \phi_{i}^{{{\text{V}} * }} P, \) fugacity of pure substance i in the vapor phase
- F :
-
Molar Helmholtz energy
- \( g\left( {r,T,\rho_{\text{n}} } \right) \) :
-
Pair distribution function
- G :
-
Molar Gibbs energy
- G E :
-
Excess molar Gibbs energy
- \( G_{\text{or}}^{\text{E}} \) :
-
Orientational contribution to the excess molar Gibbs energy caused by a permanent electric dipole moment of one of the components
- \( G_{i}^{\text{E}} \) :
-
\( = \mu_{i}^{\text{E}} = RT{ \ln }\gamma_{i} \), excess partial molar Gibbs energy of component i of a mixture/solution, also known as excess chemical potential
- h i,j :
-
=h i,j (T, P), Henry fugacity (or Henry’s law constant) of component i dissolved in solvent j. Usually, experimental data are reported at pressures \( P = P_{{\upsigma,j}} \), the vapor pressure of the solvent
- H :
-
Molar enthalpy
- H E :
-
Excess molar enthalpy
- \( \Updelta_{\text{vap}} H \) :
-
Molar enthalpy of vaporization
- ΔH ∞2 :
-
Partial molar enthalpy change on solution of a gas (2) in a liquid (1) at infinite dilution
- k B :
-
=R/N A = 1.380 650 4(24) × 10−23 J·K−1, Boltzmann constant
- k 12 :
-
Scatchard–Hildebrand binary interaction parameter, Eq. 66
- l :
-
=1.2045, lattice-specific constant in the Pople model (face-centered cubic), Eq. 106; for a body-centered cubic lattice l = 1.5317
- m :
-
Mass
- m, n :
-
Mie parameters, Eq. 51; when m = 6 and n = 12 they are called Lennard-Jones parameters, Eq. 53
- \( m_{\text{MTE}} \) :
-
Dimensionless parameter in the modified Tait equation, Eq. 62; for many liquid nonelectrolytes at ordinary temperatures \( m_{\text{MTE}} \) ≈ 10
- \( M_{\text{m}} \) :
-
=m/n, molar mass
- n :
-
\( {=\,\sum_{{i}} {n_{i}}} \), total amount of substance
- n i :
-
Amount of substance of component i of a mixture/solution
- N A :
-
=6.022 141 79(30) × 1023 mol−1, Avogadro constant
- p :
-
Permanent molecular electric dipole moment
- p r :
-
Reduced dipole moment, Eq. 104
- P :
-
Pressure
- \( P_{\text{c}} \) :
-
Critical pressure
- \( P_{\upsigma} \) :
-
Vapor pressure
- P ref :
-
Suitably selected reference pressure, frequently 105 Pa = 0.1 MPa
- r :
-
Distance between molecules
- R :
-
=8.314 472(15) J·K−1·mol−1, (molar) gas constant
- S :
-
Molar entropy
- S E :
-
Excess molar entropy
- t :
-
\( = \left| {{{\left( {T - T_{\text{uc}} } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{\text{uc}} } \right)} {T_{\text{uc}} }}} \right. \kern-0pt} {T_{\text{uc}} }}} \right| \), dimensionless variable measuring the reduced distance, temperature-wise, from the upper critical solution temperature T uc
- T :
-
Thermodynamic temperature
- \( T_{\text{c}} \) :
-
Critical temperature
- \( T_{\text{r}} \) :
-
Reduced temperature
- T ref :
-
Suitably selected reference temperature
- \( T_{\text{mp}} \) :
-
Melting (fusion) temperature
- \( T_{\text{tr}} \) :
-
Triple point temperature
- \( T_{\text{bp}} \) :
-
Normal boiling temperature
- T uc :
-
Upper critical solution temperature
- u(r):
-
Pair-potential-energy function
- U :
-
Molar internal energy
- U r :
-
Molar residual internal energy
- U c :
-
Molar configurational internal energy
- \( U_{\text{coh}}^{\text{L}} \left( {T,P} \right) \) :
-
Molar cohesive energy density of a liquid, Eq. 54
- \( \left( {\frac{\partial U}{\partial V}} \right)_{T} \) :
-
≡Π(T, P), internal pressure
- v 0 :
-
Thermodynamic speed of ultrasound (at low frequencies)
- V :
-
Molar volume
- \( V_{\text{c}} \) :
-
Critical molar volume
- V E :
-
Excess molar volume
- \( \Updelta_{\text{vap}} V \) :
-
Molar volume change on vaporization
- W :
-
Cooperative free energy in the simple Guggenheim model, see Eq. 110
- x i :
-
\( {{ = n_{i}^{\text{L}} } \mathord{\left/ {\vphantom {{ = n_{i}^{\text{L}} } {n^{\text{L}} }}} \right. \kern-0pt} {n^{\text{L}} }} \), liquid-phase mole fraction of component i of a mixture/solution, \( \sum\limits_{i} {n_{i}^{\text{L}} } = n^{\text{L}} \); \( \sum\limits_{i} {x_{i} = 1} \)
- x uc :
-
Critical composition, pertaining to an upper critical solution point (liquid–liquid equilibrium) with an upper critical solution temperature (UCST) T uc
- y i :
-
\( = {{n_{i}^{\text{V}} } \mathord{\left/ {\vphantom {{n_{i}^{\text{V}} } {n^{\text{V}} }}} \right. \kern-0pt} {n^{\text{V}} }} \), vapor-phase mole fraction of component i of a mixture/solution, \( \sum\limits_{i} {n_{i}^{\text{V}} } = n^{\text{V}} \); \( \sum\limits_{i} {y_{i} = 1} \)
- Z :
-
≡PV/RT, compression factor
Greek letters
- α :
-
≈0.11, universal nonclassical critical exponent pertaining to the weak divergence of C V of pure liquids along the critical isochore, or universal nonclassical critical exponent pertaining to the weak divergence of C P of a liquid mixture when determined along a path of constant critical composition x uc as described by the power law, Eq. 115
- α P :
-
≡V −1(∂V/∂T) P , isobaric expansivity
- \( \alpha_{\upsigma}^{\text{L}} \) :
-
\( \equiv \left( {V^{\text{L}} } \right)^{ - 1} \left( {{{\partial V^{\text{L}} } \mathord{\left/ {\vphantom {{\partial V^{\text{L}} } {\partial T}}} \right. \kern-0pt} {\partial T}}} \right)_{\upsigma} \), expansivity of a pure liquid (L) in contact with its vapor (saturation expansivity)
- β S :
-
≡−V −1(∂V/∂P) S , isentropic compressibility
- β T :
-
≡−V −1(∂V/∂P) T , isothermal compressibility
- γ V :
-
≡(∂P/∂T) V = α P /β T , isochoric thermal pressure coefficient
- \( \gamma_{\upsigma} \) :
-
\( \equiv \left( {{{\partial P} \mathord{\left/ {\vphantom {{\partial P} {\partial T}}} \right. \kern-0pt} {\partial T}}} \right)_{\upsigma} \), slope of the vapor pressure curve, \( {{{\text{d}}P_{\upsigma} } \mathord{\left/ {\vphantom {{{\text{d}}P_{\upsigma} } {{\text{d}}T}}} \right. \kern-0pt} {{\text{d}}T}} \)
- γ i :
-
=γ i (T, P, x i ), activity coefficient of component i of a mixture/solution based on the symmetric Lewis–Randall (LR) convention
- \( \gamma_{i}^{\text{HL}} \) :
-
\( = \gamma_{i}^{\text{HL}} \left( {T,P,x_{i} } \right) \), activity coefficient of component i of a mixture/solution based on the unsymmetric Henry’s law (HL) convention
- δ(T, P):
-
Solubility parameter, Eq. 55
- \( \delta \left( {T,P_{\upsigma} } \right) \) :
-
Solubility parameter at saturation condition, Eq. 60
- Δ1 :
-
=0.5, universal critical exponent associated with the first correction-to-scaling term (Wegner term [334]), Eq. 115
- ∆12 :
-
=2B 12 − (B 11 + B 22)
- ɛ :
-
Intermolecular energy parameter characterizing the well-depth of the interaction energy function, say, of the Mie function, Eq. 51
- ε 0 :
-
=8.854187… × 10−12 F·m−1, permittivity of vacuum (electric constant)
- η :
-
=exp(W/zRT), used in Eq. 114 which is based on Guggenheim’s quasi-chemical theory
- Θ :
-
“Reduced” temperature, Eq. 84 (Harrison and Moelwyn-Hughes [116])
- θ :
-
“Reduced” temperature, Eq. 85 (Wilhelm, this work)
- κ :
-
≡C P /C V = β T /β S , ratio of heat capacities or compressibilities, respectively
- μ i :
-
Chemical potential of component i of a mixture/solution
- μ E i :
-
=G E i = RTlnγ i , excess chemical potential of component i of a mixture/solution, LR convention
- Π(T, P):
-
Internal pressure
- ρ :
-
≡M m/V = m/(nV), mass density
- ρ n :
-
≡N A/V, number density
- σ :
-
Intermolecular distance parameter of the Mie intermolecular pair-potential-energy function, see Eq. 51; it is characterized by u(σ) = 0
- τ:
-
≡T ref/T
- ϕ i :
-
Fugacity coefficient of component i in solution (liquid phase or vapor phase)
- ϕ V* i :
-
Fugacity coefficient of pure substance i in the vapor phase
- Φ i :
-
\( \equiv {{x_{i} V_{i}^{{{\text{L}} * }} } \mathord{\left/ {\vphantom {{x_{i} V_{i}^{{{\text{L}} * }} } {\left( {x_{1} V_{1}^{{{\text{L}} * }} + x_{2} V_{2}^{{{\text{L}} * }} } \right)}}} \right. \kern-0pt} {\left( {x_{1} V_{1}^{{{\text{L}} * }} + x_{2} V_{2}^{{{\text{L}} * }} } \right)}}, \, i = 1,2 \), volume fraction of component i in solution
Superscripts
- E:
-
Excess quantity
- HL:
-
Indicates ideal-solution behavior based on Henry’s law
- L:
-
Liquid phase
- LR:
-
Indicates ideal-solution behavior based on the Lewis–Randall rule
- pg:
-
Perfect-gas state (ideal-gas state)
- r:
-
Residual quantity in (T,V)-space
- V:
-
Vapor phase
- *:
-
Indicates a pure-substance property
- ∞:
-
Infinite dilution
Subscripts
- c:
-
Critical property
- cf:
-
Central-force contribution
- i, j, k :
-
General indices; usually i denotes a component of a mixture/solution
- int:
-
Internal
- or:
-
Orientational
- r:
-
Reduced quantity
- rot:
-
Rotational
- tr:
-
Translational
- σ:
-
Saturation (orthobaric) condition
References
Wilhelm, E., Schano, R., Becker, G., Findenegg, G.H., Kohler, F.: Molar heat capacity at constant volume. Binary mixtures of 1,2-dichloroethane and 1,2-dibromoethane with cyclohexane. Trans. Faraday Soc. 65, 1443–1455 (1969)
Wilhelm, E., Rott, E., Kohler, F.: The heat capacities of the mixture trichlorobenzene–hexane. In: Proceedings of 1st International Confference on Calorimetry and Thermodynamics, Warsaw, Poland, pp. 767–771, 31 Aug–4 Sept (1969)
Wilhelm, E., Zettler, M., Sackmann, H.: Molwärmen binärer systeme aus cyclohexan, kohlenstofftetrachlorid, siliziumtetrachlorid und zinntetrachlorid. Ber. Bunsenges. Physik. Chem. 78, 795–804 (1974)
Wilhelm, E., Grolier, J.-P.E., Karbalai Ghassemi, M.H.: Molar heat capacities of binary liquid mixtures: 1,2-dichloroethane + benzene, +toluene, and +p-xylene. Ber. Bunsenges. Physik. Chem. 81, 925–930 (1977)
Grolier, J.-P.E., Wilhelm, E., Hamedi, M.H.: Molar heat capacity and isothermal compressibility of binary liquid mixtures: carbon tetrachloride + benzene, carbon tetrachloride + cyclohexane, and benzene + cyclohexane. Ber. Bunsenges. Physik. Chem. 82, 1282–1290 (1978)
Wilhelm, E.: Thermodynamic properties of nonelectrolyte solutions. High Temp. High Press. 29, 613–630 (1997)
Wilhelm, E.: The fascinating world of pure and mixed nonelectrolytes. Pure Appl. Chem. 77, 1317–1330 (2005)
Chorążewski, M.A., Hrynko, M., Góralski, P., Grolier, J.-P.E., Wilhelm, E.: Thermodynamic and acoustic properties of mixtures of 1,6-dichlorohexane with heptane from 293 K to 313 K. J. Chem. Eng. Data 55, 1700–1710 (2010)
Wilhelm, E.: What you always wanted to know about heat capacities, but were afraid to ask. J. Solution Chem. 39, 1777–1818 (2010)
Grolier, J.-P.E., Inglese, A., Wilhelm, E.: Excess molar heat capacities of (1,4-dioxane + an n-alkane): an unusual composition dependence. J. Chem. Thermodyn. 16, 67–71 (1984)
Inglese, A., Grolier, J.-P.E., Wilhelm, E.: Excess volumes and excess heat capacities of oxane + cyclohexane and 1,4-dioxane + cyclohexane. Fluid Phase Equilib. 15, 287–294 (1984)
Wilhelm, E.: Thermodynamics of solutions: selected aspects. Thermochim. Acta 162, 43–57 (1990)
Grolier, J.-P.E., Wilhelm, E.: Calorimetry, densitometry and ultrasonics: recent contributions to the thermodynamics of fluids. Pure Appl. Chem. 63, 1427–1434 (1991)
Wilhelm, E., Roux-Desgranges, G., Grolier, J.-P.E.: Thermodynamics of liquid mixtures containing alkyl alkanoates: a survey. Calorim. Anal. Therm. 26, 107–112 (1995)
Lainez, A., Lopez, M.R., Caceres, M., Nuñez, J., Rubio, R.G., Grolier, J.-P.E., Wilhelm, E.: Heat capacities and concentration fluctuations in mixtures of 1,2-dibromoethane + alkane. J. Chem. Soc. Faraday Trans. I 91, 1941–1947 (1995)
Wilhelm, E., Egger, W., Vencour, M., Roux, A.H., Polednicek, M., Grolier, J.-P.E.: Thermodynamics of liquid mixtures consisting of a very polar and a nonpolar aromatic: (benzonitrile + benzene or toluene). J. Chem. Thermodyn. 39, 1509–1532 (1998)
Wilhelm, E., Grolier, J.-P.E.: Heat capacities and related properties of liquid mixtures. In: Wilhelm, E., Letcher, T.M. (eds.) Heat Capacities: Liquids, Solutions and Vapours, pp. 54–85. The Royal Society of Chemistry/IACT & IUPAC, Cambridge (2010)
Wilhelm, E., Battino, R.: The solubility of gases in liquids. 1. The solubility of a series of fluorine-containing gases in several non-polar solvents. J. Chem. Thermodyn. 3, 379–392 (1971)
Wilhelm, E., Battino, R.: The solubility of gases in liquids. 4. Calculations on gas solubilities in hexafluorobenzene and benzene. J. Chem. Thermodyn. 3, 761–768 (1971)
Wilhelm, E., Battino, R.: Thermodynamic functions of the solubilities of gases in liquids at 25 °C. Chem. Rev. 73, 1–9 (1973)
Liebermann, E., Wilhelm, E.: On the thermodynamics of binary liquid mixtures of Scatchard–Hildebrand type at infinite dilution. Monatsh. Chem. 107, 367–369 (1976)
Wilhelm, E., Battino, R., Wilcock, R.J.: Low-pressure solubility of gases in liquid water. Chem. Rev. 77, 219–262 (1977)
Rettich, T.R., Handa, Y.P., Battino, R., Wilhelm, E.: Solubility of gases in liquids. 13. High-precision determination of Henry’s constants for methane and ethane in liquid water at 275 to 328 K. J. Phys. Chem. 85, 3230–3237 (1981)
Rettich, T.R., Battino, R., Wilhelm, E.: Solubility of gases in liquids. 16. Henry’s law coefficients for nitrogen in liquid water at 5 to 50 °C. J. Solution Chem. 13, 335–348 (1984)
Wilhelm, E.: The solubility of gases in liquids: a critical review. Pure Appl. Chem. 57, 303–322 (1985)
Wilhelm, E.: Precision methods for the determination of the solubility of gases in liquids. Crit. Rev. Anal. Chem. 16, 129–175 (1985)
Wilhelm, E.: Determination of caloric quantities of dilute liquid solutions. Thermochim. Acta 119, 17–33 (1987)
Wilhelm, E.: Caloric properties of dilute nonelectrolyte solutions: a success story. Thermochim. Acta 300, 159–168 (1997)
Rettich, T.R., Battino, R., Wilhelm, E.: Solubility of gases in liquids. 22. High-precision determination of Henry’s law constants of oxygen in liquid water from T = 274 K to T = 328 K. J. Thermodyn. 32, 1145–1156 (2000)
Wilhelm, E.: Low-pressure solubility of gases in liquids. In: Weir, R.D., de Loos, T.W. (eds.) Experimental Thermodynamics: Measurement of the Thermodynamic Properties of Multiple Phases, vol. VII, pp. 137–176. Elsevier/IUPAC, Amsterdam (2005)
Wilhelm, E.: Thermodynamics of nonelectrolyte solubility. In: Letcher, T.M. (ed.) Developments and Applications in Solubility, pp. 3–18. The Royal Society of Chemistry/IACT, Cambridge (2007)
Wilhelm, E., Battino, R.: Partial molar heat capacity changes of gases dissolved in liquids. In: Wilhelm, E., Letcher, T.M. (eds.) Heat Capacities: Liquids, Solutions and Vapours, pp. 457–471. The Royal Society of Chemistry/IACT & IUPAC, Cambridge (2010)
Wilhelm, E.: Aqueous solutions of nonelectrolytes: a molecular thermodynamics perspective. J. Therm. Anal. Calorim. 108, 547–558 (2012)
Wilhelm, E.: The art and science of solubility measurements: what do we learn? Netsu Sokutei 39, 61–86 (2012)
Wilhelm, E.: Thermodynamics of solutions, especially dilute solutions of nonelectrolytes. In: Teixeira-Dias, J.J.C. (ed.) Molecular Liquids: New Perspectives in Physics and Chemistry. NATO ASI Series C: Mathematical and Physical Sciences, vol. 379, pp. 175–206. Kluwer Academic, Dordrecht (1992)
Popper, K.R.: The Logic of Scientific Discovery. Routledge, London (2002)
Dyson, F.: How we know. The New York Review of Books 58 (4), March 10, 2011
Mach, E.: Die ökonomische Natur der physikalischen Forschung. In: Populärwissenschaftliche Vorlesungen. Leipzig, Germany, 1896. Reprinted by VDM Verlag Dr. Müller, Saarbrücken, Germany (2006). English translation by McCormack, T.J.: Popular Scientific Lectures (1898). Kessinger, Whitefish (2007)
Swinburne, R.: Simplicity as Evidence of Truth (The Aquinas Lecture, 1997). Marquette University Press, Milwaukee (1997)
Katz, J.J.: Realistic Rationalism. MIT Press, Cambridge (1998)
Sober, E.: What is the problem of simplicity? In: Kreuzenkamp, H., McAleer, M., Zellner, A. (eds.) Simplicity, Inference, and Econometric Modelling, pp. 13–32. Cambridge University Press, Cambridge (2002)
Prausnitz, J.M.: Molecular Thermodynamics of Fluid-Phase Equilibria. Prentice-Hall, Englewood Cliffs (1969)
Prausnitz, J.M., Lichtenthaler, R.N., de Azevedo, E.G.: Molecular Thermodynamics of Fluid-Phase Equilibria, 3rd edn. Prentice Hall, Upper Saddle River (1999)
Dymond, J.H., Marsh, K.N., Wilhoit, R.C.: Virial Coefficients of Pure Gases and Mixtures. In: Frenkel, M., Marsh, K.N. (eds.) Landolt-Börnstein, Group IV: Physical Chemistry, Vol. 21A: Virial Coefficients of Pure Gases. Springer–Verlag, Heidelberg, Germany (2002); Vol. 21B: Virial Coefficients of Mixtures. Springer–Verlag, Heidelberg, Germany (2003)
Frenkel, M., Marsh, K.N., Kabo, K.J., Wilhoit, A.C., Roganov, G.N.: Thermodynamics of organic compounds in the gas state, vols. I and II. Thermodynamics Research Center, The Texas A&M System, College Station (1994)
Majer, V., Svoboda, V.: Enthalpies of Vaporization of Organic Compounds. A Critical Review and Data Compilation. Blackwell Scientific/IUPAC, Oxford (1985)
Haar, L., Gallagher, J.S., Kell, G.S.: NBS/NRC Steam Tables (NSRDS). Thermodynamic and Transport Properties and Computer Programs for Vapor and Liquid States of Water in SI Units. Hemisphere, New York (1984)
Hill, P.G., MacMillan, R.D.C.: Virial equation for light and heavy water. Ind. Eng. Chem. Res. 27, 874–882 (1988)
Wagner, W., Pruß, A.: The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. J. Phys. Chem. Ref. Data 31, 387–535 (2002)
Zábranský, M., Růžička Jr., V., Majer, V., Domalski, E.S.: Heat Capacity of Liquids, Volumes I and II: Critical Review and Recommended Values. J. Phys. Chem. Ref. Data, Monograph No. 6, American Chemical Society and American Institute of Physics (1996)
Zábranský, M., Růžička Jr, V., Domalski, E.S.: Heat capacity of liquids: critical review and recommended values. Supplement I. J. Phys. Chem. Ref. Data 30, 1199–1689 (2001)
Chase Jr., M.W.: NIST-JANAF Thermochemical Tables, Parts I and II. J. Phys. Chem. Ref. Data, Monograph No. 9, 4th edn., American Chemical Society and American Institute of Physics (1998)
International DATA Series, SELECTED DATA ON MIXTURES, Series A, published by the Thermodynamics Research Center, Texas A&M University, College Station, TX (1973 through 1994)
Solubility Data Series (IUPAC): Vol. 1. Pergamon Press, Oxford, UK, (1979) and subsequent volumes later; Solubility Data Series (IUPAC-NIST): Vol. 66: J. Phys. Chem. Ref. Data 27, 1289–1470 (1998), and subsequent later volumes
Poling, B.E., Prausnitz, J.M., O’Connell, J.P.: The Properties of Gases and Liquids, 5th edn. McGraw-Hill, New York (2001)
Kazakov, A., Muzny, C.D., Chirico, R.D., Diky, V.V., Frenkel, M.: Web thermo tables—an on-line version of the TRC thermodynamic tables. J. Res. Natl. Inst. Stand. Technol. 113, 209–220 (2008)
NIST SDR 4. NIST Thermophysical Properties of Hydrocarbon Mixtures Database: Version 3.2. NIST, Boulder, Colorado, USA: http://www.nist.gov/srd/nist4.cfm. Accessed 19 Jun 2012
NIST SDR 10. NIST/ASME Steam Properties Database: Version 2.22. NIST, Boulder, Colorado, USA: http://www.nist.gov/srd/nist10.cfm. Accessed 28 Feb 2012
NIST SDR 23: NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP): Version 9.0. NIST, Boulder, Colorado, USA: http://www.nist.gov/srd/nist23.cfm. Accessed 22 Feb 2013
NIST SDR 103b: NIST ThermoData Engine Version 7.0 – Pure Compounds, Binary Mixtures, Ternary Mixtures, and Chemical Reactions. NIST, Boulder, Colorado, USA: http://www.nist.gov/srd/nist103b.cfm Accessed 14 Feb 2013
NIST SDR 203. NIST Web Thermo Tables (WTT) – Professional Edition. NIST, Boulder, Colorado, USA: http://www.nist.gov/srd/nistwebsub3.cfm. Accessed 11 Jan 2013
Dortmund Data Bank Software and Separation Technology: http://www.ddbst.de
McCullough, J.P., Scott, D.W. (eds.): Experimental Thermodynamics: Calorimetry of Non-reacting Systems, Vol. I. Butterworths/IUPAC, London (1968)
Hemminger, W., Höhne, G.: Calorimetry. Fundamentals and Practice. Verlag Chemie, Weinheim (1984)
Trusler, J.P.M.: Physical Acoustics and Metrology of Fluids. Hilger, Bristol (1991)
Marsh, K.N., O’Hare, P.A.G. (eds.): Experimental Thermodynamics, vol. IV: Solution Calorimetry. Blackwell Scientific/IUPAC, Oxford (1994)
Höhne, G., Hemminger, W., Flammersheim, H.-J.: Differential Scanning Calorimetry, an Introduction for Practitioners. Springer, Berlin (1996)
Goodwin, A.R.H., Marsh, K.N., Wakeham, W.A. (eds.): Experimental Thermodynamics: Measurement of the Thermodynamic Properties of Single Phases, vol. VI. Elsevier/IUPAC, Amsterdam (2003)
Weir, R.D., de Loos, ThW (eds.): Experimental Thermodynamics, vol. VII: Measurement of the Thermodynamic Properties of Multiple Phases. Elsevier/IUPAC, Amsterdam (2005)
Letcher, T.M. (ed.): Development and Application in Solubility. The Royal Society of Chemistry/IACT, Cambridge (2007)
Wilhelm, E., Letcher, T.M. (eds.): Heat Capacities: Liquids. Solutions and Vapours. The Royal Society of Chemistry/IUPAC & IACT, Cambridge (2010)
Hildebrand, J.H., Prausnitz, J.M., Scott, R.L.: Regular and Related Solutions. Van Nostrand Reinhold, New York (1970)
Kohler, F.: The Liquid State. Verlag Chemie, Weinheim (1972)
Ben-Naim, A.: Water and Aqueous Solutions. Introduction to a Molecular Theory. Plenum Press, New York (1974)
Marcus, Y.: Introduction to Liquid State Chemistry. Wiley, London (1977)
Rowlinson, J.S., Swinton, F.L.: Liquids and Liquid Mixtures, 3rd edn. Butterworth Scientific, London (1982)
Kreglewski, A.: Equilibrium Properties of Fluids and Fluid Mixtures. Texas A&M University Press, College Station (1984)
Gray, C.G., Gubbins, K.E.: Theory of Molecular Fluids. Vol. 1: Fundamentals. Clarendon Press, Oxford (1984)
Lee, L.L.: Molecular Thermodynamics of Nonideal Fluids. Butterworths, Boston (1988)
Sengers, J.V., Kayser, R.F., Peters, C.J., White, H.J.: Equations of State for Fluids and Fluid Mixtures. Experimental Thermodynamics, vol. V. Elsevier Science/IUPAC, Amsterdam (2000)
Barrat, J.-L., Hansen, J.-P.: Basic Concepts for Simple and Complex Liquids. Cambridge University Press, Cambridge (2003)
Hansen, J.-P., McDonald, I.R.: Theory of Simple Liquids, 3rd edn. Academic Press/Elsevier, London (2006)
Ben-Naim, A.: Molecular Theory of Solutions. Oxford University Press, Oxford (2006)
Lucas, K.: Molecular Models for Fluids. Cambridge University Press, New York (2007)
Wu, J.Z.: Density functional theory for liquid structure and thermodynamics. In: Lu, X., Hu, Y. (eds.) Molecular Thermodynamics of Complex Systems. Structure and Bonding, vol. 131, pp. 1–73. Springer, Berlin (2009)
Goodwin, A.R.H., Sengers, J.V., Peters, C.J. (eds.): Applied Thermodynamics of Fluids. The Royal Society of Chemistry/IUPAC & IACT, Cambridge (2010)
Gray, C.G., Gubbins, K.E., Joslin, C.G.: Theory of Molecular Fluids. Vol. 2: Applications. Oxford University Press, Oxford (2011)
Deiters, U.K., Kraska, T.: High-Pressure Fluid Phase Equilibria: Phenomenology and Computation. Elsevier, Oxford (2012)
Marcus, Y.: Ion Solvation. Wiley, Chichester (1985)
Barthel, J.M.G., Krienke, H., Kunz, W.: Physical Chemistry of Electrolyte Solutions: Modern Aspects. Steinkopff, Darmstadt, Germany, and Springer, New York (1998)
Lee, L.L.: Molecular Thermodynamics of Electrolyte Solutions. World Scientific, Singapore (2008)
Allen, M.P., Tildesley, D.J.: Computer Simulation of Liquids. Oxford University Press, New York (1989)
Haile, J.M.: Molecular Dynamics Simulation: Elementary Methods. Wiley, New York (1997)
Heyes, D.M.: The Liquid State: Applications of Molecular Simulations. Wiley, Chichester (1998)
Sadus, R.J.: Molecular Simulations of Fluids: Theory, Algorithms and Object-Orientation. Elsevier Science, New York (1999)
Leach, A.: Molecular Modelling: Principles and Applications, 2nd edn. Pearson Education, Essex (2001)
Vesely, F.J.: Computational Physics—An Introduction, 2nd edn. Kluwer Academic/Plenum, New York (2001)
Frenkel, D., Smit, B.: Understanding Molecular Simulation, 2nd edn. Academic Press, London (2002)
Cramer, C.J.: Essentials of Computational Chemistry: Theories and Models, 2nd edn. Wiley, Chichester (2004)
Rapaport, D.C.: The Art of Molecular Dynamics Simulation, 2nd edn. Cambridge University Press, Cambridge (2004)
Kaplan, I.G.: Intermolecular Interactions: Physical Picture. Computational Methods and Model Potentials. Wiley, Chichester (2006)
Tuckerman, M.E.: Statistical Mechanics: Theory and Molecular Simulation. Oxford University Press, New York (2010)
Wilhelm, E.: Heat capacities, isothermal compressibilities and related quantities of fluids. In: Tachoire, H. (ed.) Journées d’Étude sur les Capacités Calorifiques des Systems Condensés, pp. 138–163. Société Française de Chimie, Association Française de Calorimétrie et d’Analyse Thermique, Groupement pour l’Avancement des Méthodes Spectroscopiques et Physicochimiques d’Analyse, et Comité des Tables Thermodynamiques de l’IUPAC, Marseille (1987)
Wilhelm, E.: Heat capacities: introduction, concepts and selected applications. In: Wilhelm, E., Letcher, T.M. (eds.) Heat Capacities: Liquids, Solutions and Vapours, pp. 1–27. The Royal Society of Chemistry/IACT & IUPAC, Cambridge (2010)
Hoge, H.J.: Heat capacity of a two-phase system, with applications to vapor corrections in calorimetry. J. Res. Natl. Bur. Stand. 36, 111–118 (1946)
Wieser, M.E., Coplen, T.B.: Atomic weights of the elements 2009 (IUPAC Technical Report). Pure Appl. Chem. 83, 359–396 (2011)
Mohr, P.J., Taylor, B.N., Newell, D.B.: CODATA recommended values of the fundamental physical constants: 2012. Rev. Mod. Phys. 84, 1527–1605 (2012)
Herzfeld, K.F., Litovitz, T.A.: Absorption and Dispersion of Ultrasonic Waves. Academic Press, New York (1959)
Bhatia, A.B.: Ultrasonic Absorption. Oxford University Press, London (1967)
Blandamer, M.J.: Introduction to Chemical Ultrasonics. Academic Press, London (1973)
Kaatze, U., Hushcha, T.O., Eggers, F.: Ultrasonic broadband spectrometry of liquids: a research tool in pure and applied chemistry and chemical physics. J. Solution Chem. 29, 299–368 (2000)
Kaatze, U., Eggers, F., Lautscham, K.: Ultrasonic velocity measurements in liquids with high resolution-techniques, selected applications and perspectives. Meas. Sci. Technol. 19, 06200-1–06200-21 (2008)
Philip, N.M.: Adiabatic and isothermal compressibilities of liquids. Proc. Indian Acad. Sci. A 9, 109–129 (1939)
Staveley, L.A.K., Hart, K.R., Tupman, W.I.: The heat capacities and other thermodynamic properties of some binary liquid mixtures. Disc. Faraday Soc. 15, 130–150 (1953)
Staveley, L.A.K., Tupman, W.I., Hart, K.R.: Some thermodynamic properties of the systems benzene + ethylene dichloride, benzene + carbon tetrachloride, and acetone + carbon disulphide. Trans. Faraday Soc. 51, 323–343 (1955)
Harrison, D., Moelwyn-Hughes, E.A.: The heat capacities of certain liquids. Proc. R. Soc. Lond. A 239, 230–246 (1957)
Nývlt, J., Erdös, E.: P–V–T relations in solutions of liquid non-electrolytes. I. Compressibility. Coll. Czech. Chem. Commun. 26, 485–499 (1961)
Magee, J.W.: Molar heat capacity (C V ) for saturated and compressed liquid and vapor nitrogen from 65 to 300 K at pressures to 35 MPa. J. Res. Natl. Inst. Stand. Technol. 96, 725–740 (1991)
Kuroki, T., Kagawa, N., Endo, H., Tsuruno, S., Magee, J.W.: Specific heat capacity at constant volume for water, methanol, and their mixtures at temperatures from 300 K to 4400 K and pressures to 20 MPa. J. Chem. Eng. Data 46, 1101–1106 (2001)
Kitajima, H., Kagawa, N., Endo, H., Tsuruno, S., Magee, J.W.: Isochoric heat capacities of alkanols and their aqueous mixtures. J. Chem. Eng. Data 48, 1583–1586 (2003)
Aliev, M.M., Magee, J.W., Abdulagatov, I.M.: Volumetric (PVT) and calorimetric (C V VT) measurements for pure methanol in the liquid phase. Int. J. Thermophys. 24, 1527–1549 (2003)
Aliev, M.M., Magee, J.W., Abdulagatov, I.M.: PVTx and isochoric heat capacity measurements for aqueous methanol solutions. Int. J. Thermophys. 24, 1551–1579 (2003)
Perkins, A.R., Magee, J.W.: Molar heat capacity at constant volume for isobutane at temperatures from (114 to 345) K and at pressures to 35 MPa. J. Chem. Eng. Data 54, 2646–2655 (2009)
Asenbaum, A., Wilhelm, E.: Thermodynamics and vibrational dynamics of tetrachloromethane, benzene and cyclohexane. Adv. Mol. Relax. Interact. Process. 22, 187–198 (1982)
Asenbaum, A., Soufi-Siavoch, P., Wilhelm, E.: Brillouinstreung an flüssigem Toluol. Acoustica 67, 284–291 (1989)
Davies, L.A., Gordon, R.B.: Compression of mercury at high pressure. J. Chem. Phys. 46, 2650–2660 (1967)
Vedam, R., Holton, G.: Specific volumes of water at high pressures, obtained from ultrasonic-propagation measurements. J. Acoust. Soc. Am. 43, 108–116 (1968)
Fine, R.A., Millero, F.J.: Compressibility of water as a function of temperature and pressure. J. Chem. Phys. 59, 5529–5536 (1973)
Kell, G.S., Whalley, E.: Reanalysis of the density of liquid water in the range 0–150 °C and 0–1 kbar. J. Chem. Phys. 62, 3496–3503 (1975)
Muringer, M.J.P., Trappeniers, N.J., Biswas, S.N.: The effect of pressure on the sound velocity and density of toluene and n-heptane up to 2600 bar. Phys. Chem. Liq. 14, 273–296 (1985)
Takagi, T., Wilhelm, E.: Speed-of-sound measurements and heat capacities of liquid systems at high pressure. In: Wilhelm, E., Letcher, T.M. (eds.) Heat Capacities: Liquids, Solutions and Vapours, pp. 218–237. The Royal Society of Chemistry/IACT & IUPAC, Cambridge (2010)
Sun, T.F., ten Seldam, C.A., Kortbeek, B.J., Trappeniers, N.J., Biswas, S.N.: Acoustic and thermodynamic properties of ethanol from 273.15 to 333.15 K and up to 280 MPa. Phys. Chem. Liq. 18, 107–116 (1988)
Sun, T.F., Bominaar, S.A.R.C., ten Seldam, C.A., Biswas, S.N.: Evaluation of the thermophysical properties of toluene and n-heptane from 180 to 320 K and up to 260 MPa from speed-of-sound data. Ber. Bunsenges. Physik. Chem. 95, 696–704 (1991)
Daridon, J.L., Lagourette, B., Grolier, J.-P.E.: Experimental measurements of the speed of sound in n-hexane from 293 to 373 K and up to 150 MPa. Int. J. Thermophys. 19, 145–160 (1998)
Dutour, S., Daridon, J.L., Lagourette, B.: Speed of sound, density, and compressibilities of liquid eicosane and docosane at various temperatures and pressures. High Temp. High Press 33, 371–378 (2001)
Gomes de Azevedo, R., Esperança, J.M.S.S., Najdanovic-Visak, V., Visak, Z.P., Guedes, H.J.R., Nunes da Ponte, M., Rebelo, L.P.N.: Thermophysical and thermodynamic properties of 1-butyl-3-methylimidazolium tetrafluoroborate and 1-butyl-3-methylimidazolium hexafluorophosphate over an extended pressure range. J. Chem. Eng. Data 50, 997–1008 (2005)
Zorębski, E., Dzida, M.: Study of the acoustic and thermodynamic properties of 1,2- and 1,3-butanediol by means of high-pressure speed of sound measurements at temperatures from (293 to 318) K and pressures up to 101 MPa. J. Chem. Eng. Data 52, 1010–1017 (2007)
Chorążewski, M., Skrzypek, M.: Thermodynamic and acoustic properties of 1,3-dibromopropane and 1,5-dibromopentane within the temperature range from 293 K to 313 K at pressures up to 100 MPa. Int. J. Thermophys. 31, 26–41 (2010)
Lin, C.-W., Trusler, J.P.M.: The speed of sound and derived thermodynamic properties of pure water at temperatures between (253 and 473) K and at pressures up to 400 MPa. J. Chem. Phys. 136, 094511-1–094511-11 (2012)
Baltasar, E.H., Taravillo, M., Baonza, V.G., Sanz, P.D., Guignon, B.: Speed of sound in liquid water from (253.15 to 348.15) K and pressures from (0.1 to 700) MPa. J. Chem. Eng. Data 56, 4800–4807 (2011)
Hildebrand, J.H., Scott, R.L.: The Solubility of Nonelectrolytes, 3rd edn. Reinhold, New York (1950)
Barton, A.F.M.: Internal pressure: a fundamental liquid property. J. Chem. Educ. 48, 156–162 (1971)
Dack, M.R.J.: The importance of solvent internal pressure and cohesion to solution phenomena. Chem. Soc. Rev. 4, 211–229 (1975)
Marcus, Y.: Internal pressure of liquids and solutions. Chem. Rev. 113, 6536–6551 (2013). doi:10.1021/cr3004423
Goharshadi, E.K., Morsali, A., Mansoori, G.A.: A molecular dynamics study on the role of attractive and repulsive forces in internal energy, internal pressure and structure of dense fluids. Chem. Phys. 331, 332–338 (2007)
Mohazzabi, P., Mansoori, G.A.: Volumetric dependence of interatomic distance in dense nanosystems: a theoretical and molecular dynamics study. J. Comput. Theor. Nanosci. 5, 1–8 (2008)
Mie, G.: Zur kinetischen gastheorie der einatomigen körper. Ann. Phys. 11, 657–697 (1903)
Hergert, W., Wried, T. (eds.): The Mie Theory. Basics and Applications. Springer Series in Optical Sciences, vol. 169. Springer, Berlin (2012)
Jones, J.E.: On the determination of molecular fields. I. From the variation of the viscosity of a gas with temperature. Proc. R. Soc. Lond. A 106, 441–462 (1924)
Jones, J.E.: On the determination of molecular fields. II. From the equation of state of a gas. Proc. R. Soc. Lond. A 106, 463–477 (1924)
Jones, J.E.: On the determination of molecular fields. III. From crystal measurements and kinetic theory data. Proc. R. Soc. Lond. A 106, 709–718 (1924)
Lennard-Jones, J.E.: Cohesion. Proc. Phys. Soc. 43, 46–482 (1931)
Westwater, W., Frantz, H.W., Hildebrand, J.H.: The internal pressure of pure and mixed liquids. Phys. Rev. Ser. II 31, 135–144 (1928)
Hildebrand, J.H.: The compressibilities and thermal pressure coefficients of certain liquids. Phys. Rev. Ser. II 34, 649–651 (1929)
Bianchi, U., Agabio, G., Turturro, A.: Internal pressure of simple liquids. J. Phys. Chem. 69, 4392–4395 (1965)
Orwoll, R.A., Flory, P.J.: Equation-of-state parameters for normal alkanes. Correlation with chain length. J. Am. Chem. Soc. 89, 6814–6822 (1967)
Bagley, E.B., Nelson, T.P., Barlow, J.W., Chen, S.-A.: Internal pressure measurements and liquid-state energies. Ind. Eng. Chem. Fundam. 9, 93–97 (1970)
Bagley, E.B., Nelson, T.P., Chen, S.-A., Barlow, J.W.: Internal pressure measurements and evaluation of external molecular vibrational modes in the liquid state. Ind. Eng. Chem. Fundam. 10, 27–32 (1971)
Few, G.A., Rigby, M.: Thermal pressure coefficient and internal pressure of 2,2-dimethylpropane. J. Phys. Chem. 79, 1543–1546 (1975)
Renuncio, J.A.R., Breedveld, G.J.F., Prausnitz, J.M.: Internal pressures and solubility parameters for carbon disulfide, benzene, and cyclohexane. J. Phys. Chem. 81, 324–327 (1977)
McLure, I.A., Arriaga-Colina, J.L.: Thermal pressure coefficients of ethanenitrile, propanenitrile, and butanenitrile in the region 295–395 K. Int. J. Thermophys. 5, 291–300 (1984)
Compostizo, A., Crespo Colin, A., Vigil, M.R., Rubio, R.G., Diaz Peña, M.: Influence of pressure on the thermodynamic properties of simple molecular fluids: CCl4 + CS2 system. J. Phys. Chem. 92, 3998–4006 (1988)
Polikhronidi, N.G., Batyrova, R.G., Abdulagatov, I.M., Stepanov, G.V., Wu, J.T.: PvT and thermal–pressure coefficient measurements of diethyl ether (DEE) in the critical and supercritical regions. J. Chem. Thermodyn. 53, 67–81 (2012)
Scatchard, G.: Equilibria in non-electrolyte solutions in relation to the vapor pressures and densities of the components. Chem. Rev. 8, 321–333 (1931)
Hansen, C.M.: The universality of the solubility parameter. Ind. Eng. Chem. Prod. Res. Dev. 8, 2–11 (1969)
Barton, A.F.M.: Solubility parameters. Chem. Rev. 75, 731–753 (1975)
Barton, A.F.M.: Handbook of Solubility Parameters and Other Cohesion Parameters, 2nd edn. CRC, Boca Raton (1991)
Hansen, C.M.: Hansen Solubility Parameters: A User’s Handbook, 2nd edn. CRC, Boca Raton (2007)
Panayiotou, C.: Solubility parameter revisited: an equation-of-state approach for its estimation. Fluid Phase Equilib. 131, 21–35 (1997)
Stefanis, E., Tsivintzelis, I., Panayiotou, C.: The partial solubility parameters: an equation-of-state approach. Fluid Phase Equilib. 240, 144–154 (2006)
Gharagheizi, F., Eslamimanesh, A., Mohammadi, A.H., Richon, D.: Group contribution-based method for determination of solubility parameter of nonelectrolyte organic compounds. Ind. Eng. Chem. Res. 50, 10344–10349 (2011)
Gharagheizi, F., Eslamimanesh, A., Farjood, F., Mohammadi, A.H., Richon, D.: Solubility parameters of nonelectrolyte organic compounds: determination using quantitative structure–property relationship strategy. Ind. Eng. Chem. Res. 50, 11382–11395 (2011)
Gharagheizi, F., Eslamimanesh, A., Sattari, M., Mohammadi, A.H., Richon, D.: Corresponding states method for evaluation of the solubility parameters of chemical compounds. Ind. Eng. Chem. Res. 51, 3826–3831 (2012)
Wilhelm, E.: Pressure dependence of the isothermal compressibility and a modified form of the Tait equation. J. Chem. Phys. 63, 3379–3381 (1975)
Wilhelm, E.: Isothermal compressibility of liquids and a modified version of the Tait equation: a van der Waals approach. In: Proceedings of the 14th International Conference on Chemical Thermodynamics, vol. II, pp. 87–94, Montpellier, 26–30 August (1975)
Verdier, S., Andersen, S.I.: Internal pressure and solubility parameter as a function of pressure. Fluid Phase Equilib. 231, 125–137 (2005)
Rai, N., Siepmann, J.I., Schultz, N.E., Ross, R.B.: Pressure dependence of the Hildebrand solubility parameter and the internal pressure: Monte Carlo simulations for external pressures up to 300 MPa. J. Phys. Chem. C 111, 15634–15641 (2007)
van Laar, J.J.: Über dampfspannungen von binären gemischen. Z. Physik. Chem. 72, 723–751 (1910)
van Laar, J.J.: Zur theorie der dampfspannungen von binären gemischen. Erwiderung an Herrn F. Dolezalek. Z. Physik. Chem. 83, 599–608 (1913)
van Laar, J.J., Lorenz, R.: Berechnung von mischungswärmen kondensierter systeme. Z. Anorg. Allg. Chem. 146, 42–44 (1925)
Bridgman, P.W.: Thermodynamic properties of liquid water to 80° and 12000 kg. Proc. Am. Acad. Arts Sci. 48, 307–362 (1912)
Bridgman, P.W.: Thermodynamic properties of twelve liquids between 20° and 80° and up to 12000 kg per cm2. Proc. Am. Acad. Arts Sci. 49, 1–114 (1913)
Gibson, R.E., Kincaid, J.F.: The influence of temperature and pressure on the volume and refractive index of benzene. J. Am. Chem. Soc. 60, 511–518 (1938)
Gibson, R.E., Loeffler, O.H.: Pressure–volume–temperature relations in solutions. I. Observations on the behavior of solutions of benzene and some of its derivatives. J. Phys. Chem. 43, 207–217 (1939)
Gibson, R.E., Loeffler, O.H.: Pressure–volume–temperature relations in solutions. II. The energy–volume coefficients of aniline, nitrobenzene, bromobenzene and chlorobenzene. J. Am. Chem. Soc. 61, 2515–2522 (1939)
Gibson, R.E., Loeffler, O.H.: Pressure–volume–temperature relations in solutions. III. Some thermodynamic properties of mixtures of aniline and nitrobenzene. J. Am. Chem. Soc. 61, 2877–2884 (1939)
Gibson, R.E., Loeffler, O.H.: Pressure–volume–temperature relations in solutions. V. The energy–volume coefficients of carbon tetrachloride, water and ethylene glycol. J. Am. Chem. Soc. 63, 898–906 (1939)
Hayward, A.T.J.: Compressibility equations for liquids: a comparative study. Br. J. Appl. Phys. 18, 977–995 (1967)
Dymond, J.H., Malhotra, R.: The Tait equation: 100 years on. Int. J. Thermophys. 9, 941–951 (1988)
Kratky, O., Leopold, H., Stabinger, H.: Dichtemessungen an Flüssigkeiten und Gasen auf 10−6 g/cm3 bei 0.6 cm3 Präparatvolumen. Z. Angew. Phys. 27, 273–277 (1969)
Picker, P., Tremblay, E., Jolicoeur, C.: A high-precision digital readout flow densimeter for liquids. J. Solution Chem. 3, 377–384 (1974)
Albert, H.J., Wood, R.H.: High-precidion flow densimeter for fluids at temperatures to 700 K and pressures to 40 MPa. Rev. Sci. Instrum. 55, 589–593 (1984)
Simonson, J.M., Oakes, C.S., Bodnar, R.J.: Densities of NaCl(aq) to the temperature 523 K at pressures to 40 MPa measured with a new vibrating-tube densitometer. J. Chem. Thermodyn. 26, 345–360 (1994)
Galicia-Luna, L.A., Richon, D., Renon, H.: New loading technique for a vibrating tube densimeter and measurements of liquid densities up to 39.5 MPa for binary and ternary mixtures of the carbon dioxide–methanol–propane system. J. Chem. Eng. Data 39, 424–431 (1994)
Blencoe, J.G., Drummond, S.E., Seitz, J.C., Nesbitt, B.E.: A vibrating-tube densimeter for fluids at high pressures and temperatures. Int. J. Thermophys. 17, 179–190 (1996)
Ihmels, E.C., Gmehling, J.: Densities of toluene, carbon dioxide, carbonyl sulfide, and hydrogen sulfide over a wide temperature and pressure range in the sub- and supercritical state. Ind. Eng. Chem. Res. 40, 4470–4477 (2001)
Hnedkovský, L., Cibulka, I.: An automated vibrating-tube densimeter for measurements of small density differences in dilute aqueous solutions. Int. J. Thermophys. 25, 1135–1142 (2004)
Aida, T., Yamazaki, A., Akutsu, M., Ono, T., Kanno, A., Hoshina, T.A., Ota, M., Watanabe, M., Sato, Y., Smith, R.L., Inomata, H.: Laser-Doppler vibrating tube densimeter for measurements at high temperatures and pressures. Rev. Sci. Instrum. 78, 11511-11–11511-13 (2007)
Safarov, J., Millero, F., Feistel, R., Heintz, A., Hassel, E.: Thermodynamic properties of standard seawater: extensions to high temperatures and pressures. Ocean Sci. 5, 235–246 (2009)
Randzio, S.L.: Calorimetric determination of pressure effects. In: Marsh, K.N., O’Hare, P.A.G. (eds.) Experimental Thermodynamics, Vol. IV: Solution Calorimetry, pp. 303–324. Blackwell Scientific/IUPAC, Oxford (1994)
Randzio, S.L., Grolier, J.-P.E., Quint, J.R., Eatough, D.J., Lewis, E.A., Hansen, L.D.: n-Hexane as a model for compressed simple liquids. Int. J. Thermophys. 15, 415–441 (1994)
Randzio, S.L., Grolier, J.-P.E., Quint, J.R.: Thermophysical properties of 1-hexanol over the temperature range from 303 K to 503 K and at pressures from the saturation line to 400 MPa. Fluid Phase Equilib. 110, 342–359 (1995)
Randzio, S.L.: Scanning transitiometry and its use to determine heat capacities of liquids at high pressures. In: Wilhelm, E., Letcher, T.M. (eds.) Heat Capacities: Liquids, Solutions and Vapours, pp. 153–184. The Royal Society of Chemistry/IACT & IUPAC, Cambridge (2010)
Navia, P., Troncoso, J., Romani, L.: New calibration methodology for calorimetric determination of isobaric thermal expansivity of liquids as a function of temperature and pressure. J. Chem. Thermodyn. 40, 1607–1611 (2008)
Navia, P., Troncoso, J., Romani, L.: Isobaric thermal expansivity behaviour against temperature and pressure of associating fluids. J. Chem. Thermodyn. 42, 23–27 (2010)
Navia, P., Troncoso, J., Romani, L.: Isobaric thermal expansivity of highly polar nitrogen compounds at temperatures from (278.15 to 348.15) K and at pressures from (5 to 55) MPa. J. Chem. Eng. Data 55, 1537–1541 (2010)
Navia, P., Troncoso, J., Romaní, L.: Isobaric thermal expansivity for nonpolar compounds. J. Chem. Eng. Data 55, 2173–2179 (2010)
Moelwyn-Hughes, E.A.: The determination of intermolecular energy constants from common physicochemical properties of liquids. J. Phys. Chem. 55, 1246–1254 (1951)
Schaafs, W., Hellwege, K.-H., Hellwege, A.M. (eds.): Molecular Acoustics. Landolt–Börnstein, Group II: Atomic and Molecular Physics, vol. 5. Springer, Berlin (1967)
Bartholomé, E., Eucken, A.: The dependence on temperature of the specific heat (C v ) of monoatomic liquids. Trans. Faraday Soc. 33, 45–54 (1937)
Eucken, A.: Assoziation in Flüssigkeiten. Z. Elektrochem. 52, 255–269 (1948)
Bernal, J.D.: An attempt at a molecular theory of liquid structure. Trans. Faraday Soc. 33, 27–40 (1937)
Kincaid, J.F., Eyring, H.: Free volumes and free angle ratios of molecules in liquids. J. Chem. Phys. 6, 620–629 (1938)
Findenegg, G.H., Kohler, F.: Molar heat capacity at constant volume of binary mixtures of 1,2-dibromo- and 1,2-dichloroethane with benzene. Trans. Faraday Soc. 63, 870–878 (1967)
Kohler, F.: Pseudoternäre Mischungen. Monatsh. Chem. 100, 1151–1183 (1969)
Bondi, A.: Estimation of the heat capacity of liquids. Ind. Eng. Chem. Fundam. 5, 442–449 (1966)
Neckel, A., Volk, H.: Über die thermodynamischen Eigenschaften von Mischungen von Aromaten mit halogenierten Kohlenwasserstoffen. Z. Elektrochem. 62, 1104–1115 (1958)
Lielmesz, L., Bondi, A.: Notes on the contribution of hindered internal rotation and rotational isomerism to thermodynamic properties. Chem. Eng. Sci. 20, 706–709 (1965)
Wilhelm, E., Grolier, J.-P.E., Karbalai Ghassemi, M.H.: Molar heat capacity of binary liquid mixtures: 1,2-dichloroethane + cyclohexane and 1,2-dichloroethane + methylcyclohexane. Thermochim. Acta 28, 59–69 (1979)
Shimanouchi, T.: Tables of Molecular Vibrational Frequencies. Consolidated volume I. Nat. Stand. Ref. Data Ser. Nat. Bur. Stand. (U.S.) 39 (1972)
Shimanouchi, T.: Tables of molecular vibrational frequencies. Consolidated volume II. J. Phys. Chem. Ref. Data 6, 993–1102 (1977)
Shimanouchi, T., Matsuura, H., Ogawa, Y., Harada, I.: Tables of molecular vibrational frequencies. Part 10. J. Phys. Chem. Ref. Data 9, 1149–1254 (1980)
Schäfer, K., Lax, E. (eds.): Kalorische Zustandsgrößen. Landolt-Börnstein, 6. Auflage, II. Band, 4. Teil. Springer, Berlin (1961)
Stewart, R.B., Jacobson, R.T.: Thermodynamic properties of argon from the triple point to 1200 K with pressures to 1000 MPa. J. Phys. Chem. Ref. Data 18, 639–798 (1989)
Sackmann, H.: Das Raumproblem bei Tetrahalogeniden der IV. Gruppe. Z. Phys. Chem. Leipzig 208, 235–248 (1958)
Pitzer, K.S., Gwinn, W.D.: Energy levels and thermodynamic functions for molecules with internal rotation. I. Rigid frame with attached tops. J. Chem. Phys. 10, 428–449 (1942)
O’Reilly, D.E., Schacher, G.E.: Rotational correlation times for quadrupolar relaxation in liquids. J. Chem. Phys. 39, 1768–1771 (1963)
Sharp, R.R.: Rotational diffusion and magnetic relaxation of 119Sn in liquid SnCl4 and SnI4. J. Chem. Phys. 57, 5321–5330 (1972)
Narten, A.H., Danford, M.H., Levy, H.A.: Structure and intermolecular potential of liquid carbon tetrachloride derived from X-ray diffraction data. J. Chem. Phys. 46, 4875–4880 (1967)
Egelstaff, P.A., Page, D.I., Powles, J.G.: Orientational correlations in molecular liquids by neutron scattering. Carbon tetrachloride and germanium chloride. Mol. Phys. 20, 881–894 (1971)
van Tricht, J.B.: On the application of the method of interval normalization to neutron diffraction data from molecular liquids. J. Chem. Phys. 66, 85–91 (1978)
Jöllenbeck, K.M., Weidner, J.U.: Röntgenstrukturuntersuchungen des flüssigen Silicium-, Germanium- und Zinntetrachlorids. Ein Beitrag zur Frage einer gemeinsamen Flüssigkeitsstruktur. II. Bestimmung der individuellen partiellen Paarkorrelationsfunktionen. Vorschlag eines einheitlichen Strukturmodells. Ber. Bunsenges. Phys. Chem. 91, 17–24 (1987)
Misawa, M.: Temperature dependence of structure of liquid carbon tetrachloride measured by pulsed neutron total scattering. J. Chem. Phys. 91, 5648–5654 (1989)
Akatsuka, H., Misawa, M., Fukunaga, T., Mizutani, U., Furusaka, M.: Structure of liquid carbon tetrachloride up to the subcritical point measured by wide Q-range neutron diffraction. J. Chem. Phys. 107, 3080–3084 (1997)
Pusztai, L., McGreevy, R.L.: The structure of liquid CCl4. Mol. Phys. 90, 533–539 (1997)
Rey, R., Pardo, L.C., Llanta, E., Ando, K., López, D.O., Tamarit, J.L., Barrio, M.: X-ray and molecular dynamics study of liquid structure in pure methylchloromethane compounds ((CH3)4−n CCl n ). J. Chem. Phys. 112, 7505–7517 (2001)
Jóvári, P., Mészáros, G., Pusztai, L., Sváb, E.: The structure of liquid tetrachlorides CCl4, SiCl4, GeCl4, TiCl4, VCl4, and SnCl4. J. Chem. Phys. 114, 8082–8090 (2001)
Pardo, L.C., Tamarit, J.L., Veglio, N., Bermejo, G.J., Cuello, G.J.: Comparison of short-range-order in liquid- and rotator-phase states of a simple molecular liquid: A reverse Monte Carlo and molecular dynamics analysis of neutron diffraction data. Phys. Rev. B 76, 134203-1–134203-6 (2007)
Pothoczki, S.Z., Temleitner, L., Jóvári, P., Kohara, S., Pusztai, L.: Nanometer range correlations between molecular orientations in liquids of molecules with perfect tetrahedral shape: CCl4, SiCl4, GeCl4, and SnCl4. J. Chem. Phys. 130, 0645031–0645037 (2009)
Pothoczki, S.Z., Ottochian, A., Rovira-Esteva, M., Pardo, L.C., Tamarit, J.L., Cuello, G.J.: Role of steric and electrostatic effects in the short-range order of quasitetrahedral molecular liquids. Phys. Rev. B 85, 0142021–0142029 (2012)
Steinhauser, O., Neumann, M.: Structure and dynamics of liquid carbon tetrachloride. A molecular dynamics study. Mol. Phys. 40, 115–128 (1980)
Steinhauser, O., Bertagnolli, H.: Pair correlation functions of liquid CCl4. A comparison between statistical mechanical theories and computer simulation. Z. Phys. Chem. Neue Folge 124, 33–43 (1981)
Soetens, J.-C., Jansen, G., Millot, C.: Molecular dynamics simulation of liquid CCl4, with a new polarizable potential model. Mol. Phys. 96, 1003–1012 (1999)
Rey, R.: Quantitative characterization of orientational order in liquid carbon tetrachloride. J. Chem. Phys. 126, 164506-1–164506-7 (2007)
Rey, R.: Thermodynamic state dependence of orientational order and rotational relaxation in carbon tetrachloride. J. Chem. Phys. 129, 224509-1–224509-9 (2008)
Rey, R.: Is there a common orientational order for the liquid phase of tetrahedral molecules? J. Chem. Phys. 131, 064502-1–064502-9 (2009)
Lowden, L.J., Chandler, D.: Theory of intermolecular pair correlations for molecular liquids. Applications to the liquids carbon tetrachloride, carbon disulfide, carbon diselenide, and benzene. J. Chem. Phys. 61, 5228–5241 (1974)
Montague, D.G., Chowdhury, M.R., Dore, J.C., Reed, J.: A RISM analysis of structural data for tetrahedral molecular systems. Mol. Phys. 50, 1–23 (1983)
van Tricht, J.B., Sjoerdsma, J.S.: Partial chlorine–chlorine intermolecular scattering functions for XCl4 liquids (X = C, Si, Ge, V, Ti, Sn) from neutron diffraction and the RISM. Mol. Phys. 59, 507–514 (1986)
McGreevy, R.L.: Reverse Monte Carlo modeling. J. Phys. Condens. Matter 13, R877–R913 (2001)
Fredenslund, A., Jones, R.L., Prausnitz, J.M.: Group-contribution estimation of activity coefficients in nonideal liquid mixtures. AIChE J. 21, 1086–1099 (1975)
Kehiaian, H.V.: Thermodynamik flüssiger Mischungen von Kohlenwasserstoffen mit verwandten Substanzen. Ber. Bunsenges. Physik. Chem. 81, 908–921 (1977)
Kehiaian, H.V., Grolier, J.-P.E., Benson, G.C.: Thermodynamics of organic mixtures. A generalized quasichemical theory in terms of group surface interactions. J. Chim. Phys. 75, 1031–1048 (1978)
Kehiaian, H.V.: Thermodynamics of binary liquid organic mixtures. Pure Appl. Chem. 57, 15–30 (1985)
Weidlich, U., Gmehling, J.: A modified UNIFAC model. 1. Prediction of VLE, h E, and γ ∞. Ind. Eng. Chem. Res. 26, 1372–1381 (1987)
Lohmann, J., Joh, R., Gmehling, J.: From UNIFAC to modified UNIFAC (Dortmund). Ind. Eng. Chem. Res. 40, 957–964 (2001)
Gmehling, J.: Present status and potential of group contribution methods for process development. J. Chem. Thermodyn. 41, 731–747 (2009)
Nebig, S., Gmehling, J.: Measurements of different thermodynamic properties of systems containing ionic liquids and correlation of these properties using modified UNIFAC (Dortmund). Fluid Phase Equilib. 294, 206–212 (2010)
Kang, J.W., Diky, V., Chirico, A.D., Magee, J.W., Muzny, C.D., Abdulagatov, I., Kazakov, A.F., Frenkel, M.: A new method for evaluation of UNIFAC interaction parameters. Fluid Phase Equilib. 309, 68–75 (2011)
González, J.A., Alonso, I., Alonso-Tristán, C., de la Fuente, I.G., Cobos, J.C.: Thermodynamics of alkanone + aromatic hydrocarbon mixtures. Fluid Phase Equilib. 337, 125–136 (2013)
Bronneberg, R., Pfennig, A.: MOQUAC, a new expression for the excess Gibbs energy based on molecular orientations. Fluid Phase Equilib. 338, 63–77 (2013)
Bouillot, B., Teychené, S., Biscans, B.: An evaluation of thermodynamic models for the prediction of drug and drug-like molecule solubility in organic solvents. Fluid Phase Equilib. 309, 36–52 (2011)
Klamt, A., Eckert, F.: COSMO-RS: a novel and efficient method for the a priori prediction of thermophysical data of liquids. Fluid Phase Equilib. 172, 43–72 (2000)
Lin, S.-T., Sandler, S.I.: A priori phase equilibrium prediction from a segment contribution solvation model. Ind. Eng. Chem. Res. 41, 899–913 (2002)
Panayiotou, C.: Equation-of-state models and quantum mechanics calculations. Ind. Eng. Chem. Res. 42, 1495–1507 (2003)
Grensemann, H., Gmehling, J.: Performance of a conductor-like screening model for real solvents model in comparison to classical group contribution methods. Ind. Eng. Chem. Res. 44, 1610–1624 (2005)
Wang, S., Sandler, S.I., Chen, C.-C.: Refinement of COSMO-SAC and the applications. Ind. Eng. Chem. Res. 46, 7275–7288 (2007)
Hsieh, C.-M., Lin, S.-T.: First-principle predictions of vapor–liquid equilibria for pure and mixture fluids from the combined use of cubic equations of state and solvation calculations. Ind. Eng. Chem. Res. 48, 3197–3205 (2009)
Diedenhofen, M., Klamt, A.: COSMO-RS as a tool for property prediction of IL mixtures—a review. Fluid Phase Equilib. 294, 31–38 (2010)
Hsieh, C.-M., Sandler, S.I., Lin, S.-T.: Improvements of COSMO-SAC for vapor–liquid and liquid–liquid equilibrium predictions. Fluid Phase Equilib. 297, 90–97 (2010)
Panayiotou, C.: Solvation thermodynamics and non-randomness. Part I: Self-solvation. J. Chem. Eng. Data 55, 5453–5464 (2010)
Panayiotou, C.: Toward a COSMO equation-of-state model of fluids and their mixtures. Pure Appl. Chem. 83, 1221–1242 (2011)
Holderbaum, T., Gmehling, J.: PSRK: a group contribution equation of state based on UNIFAC. Fluid Phase Equilib. 70, 251–265 (1991)
Horstmann, S., Fischer, K., Gmehling, J.: PSRK group contribution equation of state: revision and extension. Fluid Phase Equilib. 167, 173–186 (2000)
Chen, J., Fischer, K., Gmehling, J.: Modification of PSRK mixing rules and results for vapor–liquid equilibria, enthalpy of mixing and activity coefficients at infinite dilution. Fluid Phase Equilib. 200, 411–429 (2002)
Ahlers, J., Gmehling, J.: Development of a universal group contribution equation of state I. Prediction of liquid densities for pure compounds with a volume translated Peng–Robinson equation of state. Fluid Phase Equilib. 191, 177–188 (2001)
Ahlers, J., Gmehling, J.: Development of a universal group contribution equation of state 2. Prediction of vapor–liquid equilibria for asymmetric systems. Ind. Eng. Chem. Res. 41, 3489–3498 (2002)
Ahlers, J., Gmehling, J.: Development of a universal group contribution equation of state III. Prediction of vapor–liquid equilibria, excess enthalpies, and activity coefficients at infinite dilution with the VTPR model. Ind. Eng. Chem. Res. 41, 5890–5899 (2002)
Schmid, B., Gmehling, J.: Revised parameters and typical results of the VTPR group contribution equation of state. Fluid Phase Equilib. 317, 110–126 (2012)
Lei, Z., Chen, B., Li, C., Liu, H.: Predictive molecular thermodynamic models for liquid solvents, solid salts, polymers, and ionic liquids. Chem. Rev. 108, 1419–1455 (2008)
Hwa, S.C.P., Ziegler, W.T.: Temperature dependence of excess thermodynamic properties of ethanol-methylcyclohexane and ethanol-toluene systems. J. Phys. Chem. 70, 2572–2593 (1966)
Holzhauer, J.K., Ziegler, W.T.: Temperature dependence of excess thermodynamic properties of n-heptane-toluene, methylcyclohexane-toluene, and n-heptane-methylcyclohexane systems. J. Phys. Chem. 79, 590–604 (1975)
Maitland, G.C., Rigby, M., Smith, E.B., Wakeham, W.A.: Intermolecular Forces: Their Origin and Determination. Clarendon, Oxford (1981)
Stone, A.J.: The Theory of Intermolecular Forces, 2nd edn. Oxford University Press, Oxford (2013)
Kohler, F.: Zur Berechnung der Wechselwirkungsenergie zwischen ungleichen Molekülen in binären flüssigen Mischungen. Monatsh. Chem. 88, 857–877 (1957)
Kohler, F., Fischer, J., Wilhelm, E.: Intermolecular force parameters for unlike pairs. J. Mol. Struct. 84, 245–250 (1982)
Diaz Peña, M., Pando, C., Renuncio, J.A.R.: Combination rules for intermolecular potential parameters. I. Rules based on approximations for the long-range dispersion energy. J. Chem. Phys. 76, 325–332 (1982)
Diaz Peña, M., Pando, C., Renuncio, J.A.R.: Combination rules for intermolecular potential parameters. II. Rules based on approximations for the long-range dispersion energy and an atomic distortion model for the repulsive interactions. J. Chem. Phys. 76, 333–339 (1982)
Wertheim, M.S.: Theory of polar fluids. V. Thermodynamics and thermodynamic perturbation theory. Mol. Phys. 37, 83–94 (1979)
Wertheim, M.S.: Equilibrium statistical mechanics of polar fluids. Ann. Rev. Phys. Chem. 30, 471–501 (1979)
Haile, J.M., Mansoori, G.A. (eds.): Molecular-Based Study of Fluids. Advances in Chemistry Series, vol. 204. American Chemical Society, Washington, DC (1983)
Boublík, T., Winkelmann, J.: Perturbation theory for fluids of non-spherical polarizable dipolar molecules. Mol. Phys. 96, 435–441 (1999)
Nezbeda, I.: Towards a unified view of fluids. Mol. Phys. 103, 59–76 (2005)
Clark, G.N.I., Haslam, A.J., Galindo, A., Jackson, G.: Developing optimal Wertheim-like models of water for use in statistical associating fluid theory (SAFT) and related approaches. Mol. Phys. 104, 3561–3581 (2006)
Máté, Z., Szalai, I., Boda, D., Henderson, D.: Heat capacities of the dipolar Yukawa model polar fluid. Mol. Phys. 109, 203–208 (2011)
Elrod, M.J., Saykally, R.J.: Many-body effects in intermolecular forces. Chem. Rev. 94, 1975–1997 (1994)
Jakse, N., Bretonnet, J.-L.: Use of state-dependent pair potentials in describing the structural and thermodynamic properties of noble gases. J. Phys. Condens. Matter 15, S3455–S3466 (2003)
Guzmán, O., del Río, F., Eloy Ramos, J.: Effective potential for three-body forces in fluids. Mol. Phys. 109, 955–967 (2011)
Patterson, D.: Effects of molecular size and shape in solution thermodynamics. Pure Appl. Chem. 47, 305–314 (1976)
Grolier, J.-P.E., Inglese, A., Roux, A.H., Wilhelm, E.: Induced conformational changes in mixtures containing n-alkanes. In: Newman, S.A. (ed.) Chemical Engineering Thermodynamics, pp. 483–486. Ann Arbor Science, Ann Arbor (1982)
Patterson, D.: Structure and the thermodynamics of non-electrolyte mixtures. J. Solution Chem. 23, 105–120 (1994)
Jorgensen, W.L.: Theoretical studies of medium effects on conformational equilibria. J. Phys. Chem. 87, 5304–5314 (1983)
Wong, M.W., Frisch, M.J., Wiberg, K.B.: Solvent effects. 1. The mediation of electrostatic effects by solvents. J. Am. Chem. Soc. 113, 4776–4782 (1991)
Meléndez-Pagán, Y., Taylor, B.E., Ben-Amotz, D.: Cavity formation and dipolar contribution to the Gauche-trans isomerization of 1-chloropropane and 1,2-dichloroethane. J. Phys. Chem. B 105, 520–526 (2001)
Thomas, L.L., Christakis, T.J., Jorgensen, W.L.: Conformation of alkanes in the gas phase and pure liquids. J. Phys. Chem. B 110, 21198–21204 (2006)
Marechal, Y.: The Hydrogen Bond and the Water Molecule: The Physics and Chemistry of Water, Aqueous and Bio Media. Elsevier, Amsterdam (2007)
Gilli, G., Gilli, P.: The Nature of the Hydrogen Bond: Outline of a Comprehensive Hydrogen Bond Theory. Oxford University Press, Oxford (2009)
Grabowski, S.J. (ed.): Hydrogen Bonding—New Insights. Springer, Dordrecht (2006)
Kohler, F., Atrops, H., Kalali, H., Liebermann, E., Wilhelm, E., Ratkovics, F., Salamon, T.: Molecular interactions in mixtures of carboxylic acids with amines. 1. Melting curves and viscosities. J. Phys. Chem. 85, 2520–2524 (1981)
Kohler, F., Gopal, R., Götze, G., Atrops, H., Demiriz, M.A., Liebermann, E., Wilhelm, E., Ratkovics, F., Palagyi, B.: Molecular interactions in mixtures of carboxylic acids with amines. 2. Volumetric, conductometric, and NMR properties. J. Phys. Chem. 85, 2524–2529 (1981)
Tanford, C.: The Hydrophobic Effect: Formation of Micelles and Biological Membranes, 2nd edn. Wiley, New York (1980)
Ben-Naim, A.: Hydrophobic Interactions. Plenum, New York (1980)
Pratt, L.R.: Molecular theory of hydrophobic effects: “She is too mean to have her name repeated”. Ann. Rev. Phys. Chem. 53, 409–436 (2002)
Southall, N.T., Dill, K.A., Haymet, A.D.J.: A view of the hydrophobic effect. J. Phys Chem. B 106, 521–533 (2002)
Ben-Amotz, D., Underwood, R.: Unraveling water’s entropic mysteries: a unified view of nonpolar, polar, and ionic hydration. Acc. Chem. Res. 41, 957–967 (2008)
Paschek, D., Ludwig, R., Holzmann, J.: Computer simulation studies of heat capacity effects associated with hydrophobic effects. In: Wilhelm, E., Letcher, T.M. (eds.) Heat Capacities: Liquids, Solutions and Vapours, pp. 436–456. The Royal Society of Chemistry/IACT & IUPAC, Cambridge (2010)
Ben-Naim, A.: The rise and fall of the hydrophobic effect in protein folding and protein–protein association and molecular recognition. Open J. Biophys. 1, 1–7 (2011)
Pople, J.A.: The statistical mechanics of systems with non-central force fields. Disc. Faraday Soc. 15, 35–43 (1953)
Guggenheim, E.A.: Mixtures. Oxford at the Clarendon Press, London (1952)
Kalali, H., Kohler, F., Svejda, P.: Excess properties of the mixture bis(2-dichloroethyl)ether (chlorex) + 2,2,4-trimethylpentane (isooctane). Monatsh. Chem. 118, 1–18 (1987)
Kohler, F., Gaube, J.: Temperature dependence of excess thermodynamic properties of mixtures and intermolecular interactions. Polish J. Chem. 54, 1987–1993 (1980)
Saint-Victor, M.-E., Patterson, D.: The W-shape concentration dependence of C E p and solution non-randomness: ketones + normal and branched alkanes. Fluid Phase Equilib. 35, 237–259 (1987)
Cobos, J.C.: An exact quasi-chemical equation for excess heat capacity with W-shaped concentration dependence. Fluid Phase Equilib. 133, 105–127 (1997)
Inglese, A., Wilhelm, E., Grolier, J.-P.E.: Paper No. 54. In: 37th Annual Calorimetry Conference. Snowbird, Utah, USA, 20–23 July (1982)
Tovar, C.A., Carballo, E., Cerdeiriña, C.A., Paz Andrade, M.I., Romani, L.: Thermodynamic properties of polyoxyethyleneglycol dimethyl ether + n-alkane mixture. Fluid Phase Equilib. 136, 223–234 (1997)
Pardo, J.M., Tovar, C.A., Cerdeiriña, C.A., Carballo, E., Romani, L.: Excess quantities of dialkyl carbonate + cyclohexane mixtures at a variable temperature. Fluid Phase Equilib. 179, 151–163 (2001)
Pardo, J.M., Tovar, C.A., Troncoso, J., Carballo, E., Romani, L.: Thermodynamic behaviour of the binary systems dimethyl carbonate + n-octane or n-nonane. Thermochim. Acta 433, 128–133 (2005)
Renon, H., Prausnitz, J.M.: Local compositions in thermodynamic excess functions for liquid mixture. AIChE J. 14, 135–144 (1968)
Troncoso, J., Cerdeiriña, C.A., Carballo, E., Romani, L.: Quantitative analysis of the W-shaped excess heat capacities of binary liquid mixtures in the light of the local composition concept. Fluid Phase Equilib. 235, 201–210 (2005)
Greer, S.C., Moldover, M.R.: Thermodynamic anomalies at critical points of fluids. Ann. Rev. Phys. Chem. 32, 233–265 (1981)
Levelt Sengers, J.M.H.: The state of the critical state of fluids. Pure Appl. Chem. 55, 437–453 (1983)
Sengers, J.V., Levelt Sengers, J.M.H.: Thermodynamic behavior of fluids near the critical point. Ann. Rev. Phys. Chem. 37, 189–222 (1986)
Anisimov, M.A.: Critical Phenomena in Liquids and Liquid Crystals. Gordon and Breach Science, Philadelphia (1991)
Wegner, F.J.: Corrections to scaling laws. Phys. Rev. B 5, 4529–4536 (1972)
Rebillot, P.F., Jacobs, D.T.: Heat capacity anomaly near the critical point of aniline-cyclohexane. J. Chem. Phys. 109, 4009–4014 (1998)
Heimburg, T., Mirzaev, S.Z., Kaatze, U.: Heat capacity behavior in the critical region of the ionic binary mixture ethylammonium nitrate-n-octanol. Phys. Rev. E 62, 4963–4967 (2000)
Pittois, S., Van Roie, B., Glorieux, C., Thoen, J.: Static and dynamic thermal quantities near the consolute point of the binary liquid mixture aniline-cyclohexane studied with a photopyroelectric technique and adiabatic scanning calorimetry. J. Chem. Phys. 122, 024504-1–024504-8 (2005)
Utt, N.J., Lehman, S.Y., Jacobs, D.T.: Heat capacity of the liquid–liquid mixture nitrobenzene and dodecane near the critical point. J. Chem. Phys. 127, 1045051–1045055 (2007)
Markham, A.E., Kobe, K.A.: The solubility of gases in liquids. Chem. Rev. 28, 519–588 (1941)
Himmelblau, D.M.: Partial molar heats and entropies of solution for gases dissolved in water from the freezing point to near the critical point. J. Phys. Chem. 67, 1803–1808 (1959)
Himmelblau, D.M., Arends, E.: Die Löslichkeit inerter Gase in Wasser bei hohen Temperaturen und Drucken. Chemie Ing. Techn. 31, 791–795 (1959)
Himmelblau, D.M.: Solubilities of inert gases in water. 0 °C to near the critical point of water. J. Chem. Eng. Data 5, 10–15 (1960)
Battino, R., Clever, H.L.: The solubility of gases in liquids. Chem. Rev. 66, 395–463 (1966)
Pierotti, R.A.: A scaled particle theory of aqueous and nonaqueous solutions. Chem. Rev. 76, 717–726 (1976)
Goldman, S.: A modern approach to nonelectrolyte solubility theory. Acc. Chem. Res. 12, 409–415 (1979)
Hepler, L.G.: Thermodynamics of dilute solutions. Pure Appl. Chem. 55, 493–504 (1983)
Hefter, G.T., Tomkins, R.P.T. (eds.): The Experimental Determination of Solubilities. Wiley Series in Solution Chemistry, vol. 6. Wiley, Chichester (2003)
Pierotti, R.A.: Aqueous solutions of nonpolar gases. J. Phys. Chem. 69, 281–288 (1965)
Wilhelm, E., Battino, R.: Estimation of Lennard-Jones (6,12) pair potential parameters from gas solubility data. J. Chem. Phys. 55, 4012–4017 (1971)
Wilhelm, E.: On the temperature dependence of the effective hard sphere diameter. J. Chem. Phys. 58, 3558–3560 (1973)
Pierotti, R.A.: The solubility of gases in liquids. J. Phys. Chem. 67, 1840–1845 (1963)
Pierotti, R.A.: On the scaled-particle theory of dilute aqueous solutions. J. Phys. Chem. 71, 2366–2367 (1967)
Wilhelm, E., Battino, R.: On solvophobic interaction. J. Chem. Phys. 56, 563–566 (1972)
Schaffer, S.K., Prausnitz, J.M.: Correlation of hydrogen solubilities in nonpolar solvents based on scaled-particle theory. AIChE J. 27, 844–848 (1981)
Schulze, G., Prausnitz, J.M.: Solubilities of gases in water at high temperatures. Ind. Eng. Chem. 20, 175–177 (1981)
Rettich, T.R., Battino, R., Wilhelm, E.: Solubility of gases in liquids. 15. High-precision determination of Henry coefficients for carbon monoxide in liquid water at 278 to 323 K. Ber. Bunsenges. Phys. Chem. 86, 1128–1132 (1982)
Rettich, T.R., Battino, R., Wilhelm, E.: Solubility of gases in liquids. 18. High-precision determination of Henry fugacities for argon in liquid water at 2 to 40 °C. J. Solution Chem. 21, 987–1004 (1992)
Battino, R., Evans, F.D., Danforth, W.F., Wilhelm, E.: The solubility of gases in liquids. 2. The solubility of He, Ne, Ar, Kr, N2, O2, CO and CO2 in 2-methyl-1-propanol (1 to 55 °C). J. Chem. Thermodyn. 3, 743–751 (1971)
Frank, H.S., Evans, M.W.: Free volume and entropy in condensed systems. III. Entropy in binary liquid mixtures; partial molal entropy in dilute solutions; structure and thermodynamics in aqueous electrolytes. J. Chem. Phys. 13, 507–532 (1945)
Pratt, L.R., Chandler, D.: Theory of the hydrophobic effect. J. Chem. Phys. 67, 3683–3704 (1977)
Privalov, P.L., Gill, S.J.: The hydrophobic effect: a reappraisal. Pure Appl. Chem. 61, 1097–1104 (1989)
Blokzijl, W., Engberts, J.B.F.N.: Hydrophobic effects. Opinions and facts. Angew. Chem. Int. Ed. Engl. 32, 1545–1579 (1993)
Lum, K., Chandler, D., Weeks, J.D.: Hydrophobicity at small and large length scales. J. Phys. Chem. B 103, 4570–4577 (1999)
Southall, N.T., Dill, K.A.: The mechanism of hydrophobic solvation depends on solute radius. J. Phys. Chem. B 104, 1326–1331 (2000)
Hummer, G., Garde, S., Garcia, A.E., Pratt, L.R.: New perspectives on hydrophobic effects. Chem. Phys. 258, 349–370 (2000)
Chandler, D.: Interfaces and the driving force of hydrophobic assembly. Nature 437, 640–647 (2005)
Levy, Y., Onuchic, J.N.: Water mediation in protein folding and molecular recognition. Annu. Rev. Biophys. Biomol. Struct. 35, 389–415 (2006)
Ball, P.: Water as an active constituent in cell biology. Chem. Rev. 108, 74–108 (2008)
Patel, A.J., Varilly, P., Chandler, D.: Fluctuations of water near extended hydrophobic and hydrophilic surfaces. J. Phys. Chem. B 114, 1632–1637 (2010)
Ben-Naim, A., Baer, S.: Method for measuring solubilities of slightly soluble gases in liquids. Trans. Faraday Soc. 59, 2735–2738 (1963)
Tominaga, T., Battino, R., Gorowara, H.K., Dixon, R.D., Wilhelm, E.: Solubility of gases in liquids. 17. The solubility of He, Ne, Ar, Kr, H2, N2, O2, CO, CH4, CF4, and SF6 in tetrachloromethane at 283–318 K. J. Chem. Eng. Data 31, 175–180 (1986)
Bo, S., Battino, R., Wilhelm, E.: Solubility of gases in liquids. 19. Solubility of He, Ne, Ar, Kr, Xe, N2, O2, CH4, CF4, and SF6 in normal 1-alkanols n-C l H2l+1OH (1 ≤ l ≤ 11) at 298.15 K. J. Chem. Eng. Data 38, 611–616 (1993); Correction. J. Chem. Eng. Data 41, 644 (1996)
Hesse, P.J., Battino, R., Scharlin, P., Wilhelm, E.: Solubility of gases in liquids. 20. Solubility of He, Ne, Ar, Kr, N2, O2, CH4, CF4, and SF6 in n-alkanes n-C l H2l+2 (6 ≤ l ≤ 16) at 298.15 K. J. Chem. Eng. Data 41, 195–201 (1996)
Vosmansky, J., Dohnal, V.: Gas solubility measurements with an apparatus of the Ben-Naim-Baer type. Fluid Phase Equilib. 33, 137–155 (1987)
Fonseca, I.M.A., Almeida, J.P.B., Fachada, H.C.: Automated apparatus for gas solubility measurements. J. Chem. Thermodyn. 39, 1407–1411 (2007)
Benson, B.B., Krause Jr, D.: Empirical laws for dilute aqueous solutions of nonpolar gases. J. Chem. Phys. 64, 689–709 (1976)
Benson, B.B., Krause Jr, D., Peterson, M.A.: The solubility and isotopic fractionation of gases in dilute aqueous solutions. I. Oxygen. J. Solution Chem. 8, 655–690 (1979)
Battino, R., Banzhof, M., Bogan, M., Wilhelm, E.: Apparatus for rapid degassing of liquids. Part III. Analyt. Chem. 43, 806–807 (1971)
Clarke, E.C.W., Glew, D.N.: Evaluation of thermodynamic functions from equilibrium constants. Trans. Faraday Soc. 62, 539–547 (1966)
Bolton, P.D.: Calculation of thermodynamic functions from equilibrium data. J. Chem. Educ. 47, 638–641 (1970)
Wauchope, R.D., Haque, R.: Aqueous solutions of nonpolar compounds. Heat-capacity effects. Can. J. Chem. 50, 133–138 (1972)
Valentiner, S.: Über die Löslichkeit der Edelgase in Wasser. Z. Phys. 42, 253–264 (1927)
Wilhelm, E.: Dilute solutions of gases in liquids. Fluid Phase Equilib. 27, 233–261 (1986)
Wilhelm, E.: The solubility of gases in liquids. Thermodynamic considerations. In: Battino, R. (ed.) Solubility Data Series (IUPAC), vol. 10, pp. XX–XXVIII. Pergamon, Oxford (1982)
Crovetto, R., Fernández-Prini, R., Japas, M.L.: Solubilities of inert gases and methane in H2O and in D2O in the temperature range of 300 to 600 K. J. Chem. Phys. 76, 1077–1086 (1982)
Figura, L.O., Cammenga, H.K.: Die In-line-Strippzelle in der GC-Bestimmung von gelösten Gasen in wäßrigen Matrices. GIT Fachz. Lab., pp. 988–994 (10/1989)
Schotte, W.: Solubilities near the solvent critical point. AIChE J. 31, 154–157 (1985)
Japas, M.L., Levelt Sengers, J.M.H.: Gas solubility and Henry’s law near the solvent’s critical point. AIChE J. 35, 705–713 (1989)
Krause Jr, D., Benson, B.B.: The solubility and isotopic fractionation of gases in dilute aqueous solutions. IIa. Solubilities of the noble gases. J. Solution Chem. 18, 823–873 (1989)
Biggerstaff, D.R., Wood, R.H.: Apparent molar volumes of aqueous argon, ethylene, and xenon from 300 to 716 K. J. Phys. Chem. 92, 1988–1994 (1988)
Hnedkovský, L., Wood, R.H., Majer, V.: Volumes of aqueous solutions of CH4, CO2, H2S, and NH3 at temperatures from 298.15 K to 705 K and pressures to 35 MPa. J. Chem. Thermodyn. 28, 125–142 (1996)
Chang, R.F., Levelt Sengers, J.M.H.: Behavior of dilute mixtures near the solvent’s critical point. J. Phys. Chem. 90, 5921–5927 (1986)
Levelt Sengers, J.M.H.: Thermodynamics of solutions near the solvent’s critical point. In: Bruno, T.J., Ely, J.F. (eds.) Supercritical Fluid Technology: Reviews in Modern Theory and Applications, pp. 1–56. CRC, Boca Raton (1991)
Biggerstaff, D.R., White, D.E., Wood, R.H.: Heat capacities of aqueous argon from 306 to 578 K. J. Phys. Chem. 89, 4378–4381 (1985)
Biggerstaff, D.R., Wood, R.H.: Apparent molar heat capacities of aqueous argon, ethylene, and xenon at temperatures up to 720 K and pressures to 33 MPa. J. Phys. Chem. 92, 1994–2000 (1988)
Hnedkovský, L., Wood, R.H.: Apparent molar heat capacities of aqueous solutions of CH4, CO2, H2S, and NH3 at temperatures from 304 K to 704 K at a pressure of 28 MPa. J. Chem. Thermodyn. 29, 731–747 (1997)
Battino, R., Marsh, K.N.: An isothermal displacement calorimeter for the measurement of the enthalpy of solution of gases. Aust. J. Chem. 33, 1997–2003 (1980)
Gill, S.J., Wadsö, I.: Flow-microcalorimetric techniques for solution of slightly soluble gases. Enthalpy of solution of oxygen in water at 298.15 K. J. Chem. Thermodyn. 14, 905–919 (1982)
Dec, S.F., Gill, S.J.: Steady-state gas dissolution flow microcalorimeter for determination of heats of solution of slightly soluble gases in water. Rev. Sci. Instrum. 55, 765–772 (1984)
Murray, C.N., Riley, J.P.: The solubility of gases in distilled water and sea water—III argon. Deep Sea Res. 17, 203–209 (1970)
Olofsson, G., Oshodj, A.A., Qvarnström, E., Wadsö, I.: Calorimetric measurements on slightly soluble gases in water. Enthalpies of solution of helium, neon, argon, krypton, xenon, methane, ethane, propane, n-butane, and oxygen at 288.15, 298.15, and 308.15 K. J. Chem. Thermodyn. 16, 1041–1052 (1984)
Dec, S.F., Gill, S.J.: Enthalpies of aqueous solutions of noble gases at 25 °C. J. Solution Chem. 14, 417–429 (1985)
Alexander, D.M.: A calorimetric measurement of the heats of solution of the inert gases in water. J. Phys. Chem. 63, 994–996 (1959)
Schäfer, K., Lax, E. (eds.): Landolt-Börnstein, 6. Auflage, II. Band, 4. Teil: Kalorische Zustandsgrößen. Springer, Berlin, (1961)
Klots, C.E., Benson, B.B.: Thermodynamic properties of the atmospheric gases in aqueous solutions. J. Phys. Chem. 67, 933–934 (1963)
Naghibi, H., Dec, S.F., Gill, S.J.: Heat of solution of methane in water from 0 to 50 °C. J. Phys. Chem. 90, 4621–4623 (1986)
Dec, S.F., Gill, S.J.: Heats of solution of gaseous hydrocarbons in water at 25 °C. J. Solution Chem. 13, 27–41 (1984)
Dec, S.F., Gill, S.J.: Heats of solution of gaseous hydrocarbons in water at 15, 25, and 35 °C. J. Solution Chem. 14, 827–836 (1985)
Franks, F. (ed.): Water: A Comprehensive Treatise, vols. I–VII. Plenum, New York (1972–1982)
Cantor, C.R., Schimmel, P.R.: Biophysical Chemistry. Part I: The Conformation of Biological Macromolecules; Part II: Techniques for the Study of Biological Structure and Function; Part III: The Behavior of Biological Macromolecules. W.H. Freeman, San Francisco (1980)
Franks, F.: Water: A Matrix of Life, 2nd edn. The Royal Society of Chemistry, Cambridge (2000)
van Holde, K.E., Johnson, W.C., Shing Ho, P.: Principles of Biophysical Chemistry, 2nd edn. Prentice Hall, Upper Saddle River (2005)
Brovchenko, I.O., Oleinikova, A.: Interfacial and Confined Water. Elsevier, Amsterdam (2008)
Pohorille, A., Wilson, M.A.: Viewpoint 9—molecular structure of aqueous interfaces. J. Mol. Struct. Theochem 284, 271–298 (1993)
Raymond, E.A., Richmond, G.L.: Probing the molecular structure and bonding of the surface of aqueous salt solutions. J. Phys. Chem. B 108, 5051–5059 (2004)
Petersen, P.B., Saykally, R.J.: On the nature of ions at the liquid water surface. Annu. Rev. Phys. Chem. 57, 333–364 (2006)
Wick, C.D., Kuo, I.-F.W., Mundy, J.C., Dang, L.X.: The effect of polarizability for understanding the molecular structure of aqueous interfaces. J. Chem. Theory Comput. 3, 2002–2010 (2007)
Stevens, M.J., Grest, G.S.: Simulations of water at the interface with hydrophilic self-assembled monolayers. Biointerphases 3, FC13–FC22 (2008)
Yancey, J.A., Vellore, N.A., Collier, G., Stuart, S.J., Latour, R.A.: Development of molecular simulation methods to accurately represent protein-surface interactions: The effect of pressure and its determination for a system with constrained atoms. Biointerphases 5, 85–95 (2010)
Zhang, C., Raugei, S., Eisenberg, B., Carloni, P.: Molecular dynamics in physiological solutions: force fields, alkali metal ions, and ionic strength. J. Chem. Theory Comput. 6, 2167–2175 (2010)
Bresme, F., Chacón, E., Tarazona, P., Wynveen, A.: The structure of ionic aqueous solutions at interfaces: an intrinsic structure analysis. J. Chem. Phys. 137, 1147061–11470610 (2012)
Stannard, R.: The End of Discovery: Are We Approaching the Boundaries of the Knowable?. Oxford University Press, Oxford (2010)
International Union of Pure and Applied Chemistry: Quantities Units and Symbols in Physical Chemistry. RSC, Cambridge (2007)
Prigogine, I., Defay, R.: Chemical Thermodynamics. Translated and revised by Everett. D.H. Longmans, Green, London (1954)
Griffiths, R.B., Wheeler, J.C.: Critical points in multicomponent systems. Phys. Rev. A 2, 1047–1064 (1970)
Mohr, P.J., Taylor, B.N., Newell, D.B.: CODATA recommended values of the fundamental physical constants: 2006. Rev. Mod. Phys. 80, 633–730 (2008)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated in part by Emmerich Wilhelm as a Plenary Lecture at the 20. Ulm-Freiberger Kalorimetrietage (20th UFK) in Freiberg, Saxony, Germany, February 27–March 1, 2013.
Rights and permissions
About this article
Cite this article
Wilhelm, E. Chemical Thermodynamics: A Journey of Many Vistas. J Solution Chem 43, 525–576 (2014). https://doi.org/10.1007/s10953-014-0140-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10953-014-0140-0