A hybrid algorithm for the vehicle routing problem with three-dimensional loading constraints and mixed backhauls

Abstract

In this paper, a variant of the vehicle routing problem with mixed backhauls (VRPMB) is presented, i.e. goods have to be delivered from a central depot to linehaul customers, and, at the same time, goods have to be picked up from backhaul customers and brought to the depot. Both types of customers can be visited in mixed sequences. The goods to be delivered or picked up are three-dimensional (cuboid) items. Hence, in addition to a routing plan, a feasible packing plan for each tour has to be provided considering a number of loading constraints. The resulting problem is the vehicle routing problem with three-dimensional loading constraints and mixed backhauls (3L-VRPMB). The simultaneous transport of linehaul and backhaul items presents a particular challenge of the problem. We consider two different loading variants in order to avoid any reloading during the tour: (i) rear loading with separate linehaul and backhaul sections and (ii) loading at a long side. In order to solve the problem, we propose a hybrid metaheuristic consisting of a reactive tabu search for the routing problem and different packing heuristics for the loading problem. Numerical experiments are reported with benchmark instances from the literature for the one-dimensional VRPMB to examine the performance of the routing algorithm and with newly generated instances for the 3L-VRPMB.

1 Introduction

In 2010, the average empty running rate—i.e. the share of trucks driving without transporting any goods—in the European Union amounted to 24% de Angelis (2011). This occurs, for example, if vehicles return empty from their deliveries. By incorporating the pickup of goods (backhauling) during the tours into the logistics system, empty runs can be reduced which subsequently leads to a reduction in travelled distances, fuel consumption and $\hbox {CO}_2$ emission. Therefore, vehicle routing problems (VRPs) with backhauls also gain increasing attention in research.

While backhaul problems can be modelled in different variants (cf e.g. Parragh et al. (2008); Irnich et al. (2014)), this paper will be focused on the (VRPMB). In this problem variant, goods have to be either delivered to customers (linehaul) or picked up from them (backhaul). The sequence of linehaul and backhaul customers within a tour can be chosen arbitrarily.

Moreover, we aim to provide a more realistic modelling of the transportation of (bulky) goods which are of a size that cannot be neglected to ensure feasibility when planning the routes. Therefore, the transported goods are assumed to be three-dimensional (3D) cuboid items. Each solution of the problem must, thus, be equipped with a feasible packing plan per route. A particular challenge of the problem is to transport linehaul and backhaul items simultaneously on the same vehicle. In order to avoid any reloading during a tour, two different loading approaches are considered: (i) loading from the rear side with horizontal separation of the loading space into a delivery section and a pickup section and (ii) loading from one long side. The side from which items are loaded and unloaded is subsequently called loading side. The resulting problem belongs to the group of VRPs with three-dimensional loading constraints (3LVRPs) which was introduced by Gendreau et al. (2006).

We propose a hybrid algorithm for solving the three-dimensional VRPMB. The underlying routing problem is solved with a reactive tabu search (RTS) based on the approach of Nagy et al. (2013). In order to solve the packing subproblem, different packing heuristics have been implemented which can be chosen alternatively. They were tested and compared concerning their performance.

The remainder of this paper is organized as follows: a detailed problem description is presented in Sect. 2. In Sect. 3, an overview of the relevant literature is given. The proposed RTS and the packing heuristics are described in Sect. 4. In Sect. 5, the experiment setup is described, and the results are presented and analysed. Finally, the paper concludes with a summary and an outlook to future research in Sect. 6.

2 Problem description

Let $G=(N,E)$ be a weighted, directed graph with the node set $N=\{0,1,\ldots ,n\}$, where node 0 represents the depot and the nodes $1,\ldots ,n$ represent the n customer locations, and the edge set $E=\{(i, j): i,j \in N, i\ne j\}$. The customers are divided into l linehaul customers and b backhaul customers, i.e. $N=\{0,1,\ldots ,n\} = \{0,1,\ldots ,l,l+1,\ldots ,l+b\}$. Furthermore, let $c_{ij}$ be the cost corresponding to edge $(i,j)\in E$.

A set $I_i=\{1,\ldots ,m_i\}$ of $m_i$ cuboid items (boxes) is assigned to each customer $i\ (i\in N{\setminus }\{0\})$ which must be either delivered to them (linehaul) or picked up from them (backhaul). Each item $I_{ik}\ (i\in N{\setminus }\{0\}, k\in I_i)$ has a known length $l_{ik}$, width $w_{ik}$, height $h_{ik}$ and weight $d_{ik}$ and is assigned with a fragility flag $f_{ik}$ indicating whether it is fragile ($f_{ik}=1$) or not ($f_{ik}=0$). The entire cargo, given by the set of boxes of all n customers, might be strongly heterogeneous (nearly as many box types as boxes), weakly heterogeneous (many boxes, few box types) or even homogeneous. $v_\mathrm{max}$ identical vehicles are available with a given weight capacity D and a three-dimensional cuboid loading space of length L, width W and height H. All vehicles can be loaded and unloaded either from the rear or from one long side (see below).

A solution for the problem must contain information about the allocation of customers to routes, the customer sequences of the routes and the corresponding packing plans.

A packing plan P contains placements for one or more items. It is feasible if it fulfils the following conditions: (P1) all items lie entirely within their loading space, (P2) any two items which are placed simultaneously in one loading space must not overlap, and (P3) all items must be placed orthogonally to the loading space edges. Moreover, the following additional packing constraints must be adhered to [cf. Gendreau et al. (2006)]:

• (PC1) Fixed vertical orientation The items can be rotated by 90$^\circ$ on the horizontal plane, but the height dimensions are fixed.

• (PC2) Vertical stability Each item must be supported by a given percentage $\alpha$ by the top faces of other items or the container floor (see Sect. 5.1).

• (PC3) Fragility A non-fragile item cannot be placed on top of a fragile item, whereas fragile items can be placed on top of any other item.

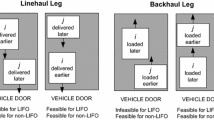
• (PC4) LIFO The last-in, first-out constraint requires that the items are loaded and unloaded solely by straight movements towards the loading side. Therefore, it must be ensured that the (un-)loading is not blocked by items that are delivered later or have already been picked up.

  Let $l_1$ and $l_2$ be two linehaul customers and $b_1$ and $b_2$ two backhaul customers. Assuming $l_1$ precedes $l_2$ in a given route, no item of $l_2$ must be positioned between the loading side and any item of customer $l_1$ or above such item. Analogously, if $b_1$ precedes $b_2$ in a route, no item of $b_1$ can be positioned between the loading side and any item of customer $b_2$ or above such item. Furthermore, if $b_1$ precedes $l_1$ in a route, no item of $b_1$ may be placed between the loading side and any item of $l_1$ or above such item. In addition, no item of $l_1$ can be placed between the loading side and any item of $b_1$ or above such item.

The orientation constraint (PC1) often occurs if technical devices, e.g. household appliances, are to be transported. Constraint (PC2) is also called static stability constraint and prevents boxes from falling down onto the container floor (see Bortfeldt and Wäscher (2013)). By the fragility constraint (PC3), the stacking of boxes is restricted because of their limited load bearing strength. The stability and fragility constraint occur in different variants; see, for example, Paquay et al. (2017, p. 1583).

The LIFO policy (PC4) implies that the reloading of any item during the route is forbidden. Therefore, this constraint is particularly challenging considering that linehaul and backhaul items are transported simultaneously. Two alternative loading approaches are applied here in order to avoid any reloading effort.

In the first variant, double-decker vehicles are used. These vehicles are rear-loaded (the loading side is the rear side), and the loading space is separated horizontally so that two separate compartments are available for each type (linehaul or backhaul). This way, the LIFO constraint must not be considered w.r.t. a mixture of linehaul and backhaul items. It is assumed that both compartments are of the same size. In the following, this variant will be referred to as loading space partition (LSP).

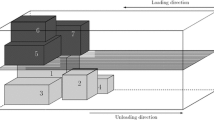
Secondly, side loading (SL) is applied for which so-called tautliners are used. These vehicles can only be loaded and unloaded from the side (the loading side is one long side). An example is illustrated in Fig. 1. By loading linehaul (light grey) and backhaul (dark grey) items from opposing sides (cabin and rear side), space is created for backhaul items when linehaul items are unloaded. $L_\mathrm{LH}$ and $L_\mathrm{BH}$ represent the loading lengths (i.e. maximum front edge) of all linehaul and backhaul items, respectively, which are currently in the loading space. In order to avoid any overlapping, the sum of both lengths must not exceed L. The LIFO constraint must be considered as above ensuring that the (un-)loading is not blocked. In the example in Fig. 1, items 2 and 3 must not be delivered after item 1. Moreover, the constraint must also be considered along the length axis ensuring that the unloading of linehaul items successively creates space for backhaul items. Therefore, item 4 may not be delivered after item 1.

Since we assume uniform vehicles, only one of the loading approaches can be applied for a problem instance, i.e. all vehicles in any generated solution have to be loaded either by the LSP approach or by the SL approach.

Fig. 1

Side loading

A feasible route R is a sequence of locations (0, $i_1$, ..., $i_{n_r}$, 0) which fulfils the following conditions: (R1) it starts and ends at the depot, (R2) it comprises each customer $i\in R{\setminus }\{0\}$ exactly once, (R3) the total weight of all items transported simultaneously does not exceed the vehicle weight capacity D, and (R4) a feasible packing plan $P_L$ exists for all linehaul customers in R at the beginning of the tour and a feasible packing plan $P_B$ exists for all backhaul customers at the end of the tour.

Let v be the number of used vehicles in a solution. Assuming each vehicle travels exactly one tour, a solution consists of a set of v triples $(R_t, P_{t,L}, P_{t,B})$ containing a route $R_t$ for each vehicle $t\ (t=1,\ldots ,v)$ and the corresponding packing plans $P_{t,L}$ and $P_{t,B}$. A solution is feasible if (S1) all routes $R_t$ and packing plans $P_{t,L}, P_{t,B}\ (t=1,\ldots ,v)$ are feasible, (S2) each packing plan $P_{t,L}\ ( P_{t,B})$ contains all of the respective linehaul (backhaul) items (and no others) of all customers visited in $R_t\ (t=1,\ldots ,v)$, (S3) each customer $i\in N{\setminus }\{0\}$ is assigned to exactly one route, and (S4) the number of used vehicles v does not exceed the number of available vehicles $v_\mathrm{max}$. Moreover, a feasible solution for the problem with SL approach must also adhere to the restriction (S5) that the linehaul and backhaul items that are transported simultaneously at any given moment in a route $R_t\ (t=1,\ldots ,v)$ do not overlap, i.e. the sum of the lengths $L_\mathrm{LH}$ and $L_\mathrm{BH}$ must never exceed L (see above).

A feasible solution is to be found that minimizes the total travel distance (TTD). The problem can be classified as a 3L-VRP with mixed backhauls (3L-VRPMB).

3 Literature review

The 3L-VRPMB has so far only been considered once, namely by Reil et al. Reil et al. (2018). The following literature review is focused on the one-dimensional VRPMB and problem variants of the 3L-VRP. In addition, some relevant studies about the VRP with two-dimensional loading constraints are shortly mentioned.

3.1 Vehicle routing problem with mixed backhauls

The (one-dimensional) VRPMB has been studied intensively in the past decades. Straightforward heuristic solution approaches were primarily used in the beginning. They include, for example, Savings and insertions heuristics (Golden et al. 1985; Casco et al. 1988), or cluster-first-route-second heuristics (Halse 1992). In the recent past, the trend shifted towards the use of metaheuristics. One of the first metaheuristics for the VRPMB was presented by Wade and Salhi (2004) who suggested an ant colony optimization (ACO) approach. A hybrid approach presented in Crispim and Brandão (2005) consists of a tabu search (TS) and a variable neighbourhood descent heuristic. An adaptive large neighbourhood search (ALNS) for a great variety of VRPs with backhauls has been described in Ropke and Pisinger (2006). More recently, a reactive tabu search (RTS) to solve the VRPMB was proposed in Nagy et al. (2013) and serves as the base for the solution approach presented in this paper. In addition, a problem variant is also considered in Nagy et al. (2013) where a mixture of linehaul and backhaul customers in a tour is only allowed if a given percentage of the vehicle capacity is available. Hence, if the percentage equals 100%, the VRP with clustered backhauls (VRPCB) is considered, i.e. all linehaul customers have to be visited before the backhaul customers within a tour. Further recent approaches include ACO (Wassan et al. 2013), adaptive local search (Avci and Topaloglu 2015) and evolutionary algorithms (García-Nájera et al. 2015).

3.2 Vehicle routing problems with loading constraints

The capacitated VRP (CVRP) with three-dimensional loading constraints (3L-CVRP) was first presented by Gendreau et al. (2006), who also introduced the above-mentioned constraints regarding the packing subproblem. Subsequently, the problem was studied by various researchers (e.g. Tarantilis et al. (2009); Fuellerer et al. (2010); Bortfeldt (2012)). The 3L-VRP with time windows was first dealt with by Moura (2008) and Moura and Oliveira (2009). They consider two objective criteria. Namely, the TTD and the number of tours as common in research regarding VRPs with time windows (VRPTW). Furthermore, the maximization of the utilized volume as another optimization objective is considered in Moura (2008). The 3L-CVRP with a heterogeneous vehicle fleet is addressed in Wei et al. (2014).

The routing problem is usually tackled with a metaheuristic approach, e.g., genetic algorithm (Moura 2008; Miao et al. 2012), TS (Gendreau et al. 2006; Tarantilis et al. 2009; Wang et al. 2010; Ma et al. 2011; Wisniewski 2011; Zhu et al. 2012; Tao and Wang 2015) or ACO (Fuellerer et al. 2010). Since solving the packing problem requires comparatively much computing time as the packing procedure is called very frequently, the packing problem is often solved by applying simple construction heuristics, e.g. based on bottom-left and touching area heuristics. More complex packing approaches are, for example, applied by Bortfeldt (2012) (tree search) or Zhang et al. (2015) (local-search-based approach). Furthermore, an exact approach for solving the routing subproblem and a GRASP algorithm for solving the packing problem for the obtained routes is used in Escobar-Falcón et al. (2016).

So far, the underlying VRP was mainly assumed to be a CVRP or VRPTW. Variants with pickup and delivery have not been studied intensely yet. The 3L-VRP with clustered backhauls (3L-VRPCB) is approached in Bortfeldt et al. (2015) where ALNS and variable neighbourhood search are used for the routing problem and a tree search procedure is applied to the packing problem. The pickup and delivery problem with three-dimensional loading constraints is studied in Bartók and Imreh (2011) and Männel and Bortfeldt (2016). Here, goods are transported from a loading location to an unloading location (that are not the depot).

Different variants of 3L-VRPs with backhauls and time windows, among them the 3L-VRPMB, are tackled in Reil et al. (2018). The authors propose a two-phase approach following the principle “packing first, routing second”. That is, first for each customer a truck segment is filled by the customer’s boxes by means of a TS packing procedure. In the second phase, the remaining routing task is done with an evolutionary strategy and a TS. The heuristic is able to cope with large instances with up to 1000 customers and 50,000 boxes.

In addition, VRPs with backhauls have been studied considering two-dimensional (2D) loading constraints, e.g. Dominguez et al. (2015) (clustered backhauls), Pinto et al. (2015) (mixed backhauls) or Zachariadis et al. (2016) (simultaneous delivery and pickup). In Pinto et al. (2015) and Zachariadis et al. (2016), variants with simultaneous transportation of linehaul and backhaul items are considered where rearrangements are not allowed.

A detailed overview of the literature on VRP with two- and three-dimensional loading constraints is provided in Pollaris et al. (2015). Packing problems, related constraints and algorithms that are partially of relevance for 3L-VRPs are reviewed in Bortfeldt and Wäscher (2013).

4 Hybrid solution approach

Being a generalization of the CVRP, the 3L-VRPMB is also an NP-hard optimization problem (cf. e.g. Toth and Vigo (2014)). In order to find high-quality solutions within reasonable computing time, a metaheuristic framework is applied to solve the routing problem. As in many previous works, the packing problem is tackled with construction heuristics. In the following subsections, both parts of the solution procedure will be described.

4.1 Reactive tabu search

The routing problem is solved with a reactive tabu search (RTS) based on the work of Nagy et al. (2013). The rough outline of the procedure is depicted in Fig. 2. It starts with the initialization of the search (initial solution, tabu list). In each iteration, a neighbour of the current solution s is generated by applying a selected move $m_s$. Usually, in tabu search algorithms the best non-tabu move is used or a tabu move if it satisfies an aspiration criterion. However, we work with a candidate list CL here, consisting of $n_\mathrm{CL}\ (n_\mathrm{CL}>1)$ moves. In general, the move $m_s$ to be applied to the current solution s is chosen at random from the candidate list. Tabued moves held in the tabu list are expressed in terms of a customer i and a tour t so that i must not be inserted into t for a number of iterations given by the tabu tenure tt.

Reactive elements are included in the tabu list management changing the tabu tenure based on the search progress. In each iteration, a reinitialization of the tabu search can also be triggered. Otherwise, a local optimization procedure is applied to the current solution s after the application of the move $m_s$. The components of the RTS are described in detail in the following subsections.

Fig. 2

Reactive tabu search

4.1.1 Initialization of the search

Two different construction heuristics are applied alternatively to generate the initial solution in order to test their impact on the performance of the RTS.

On the one hand, we use the modified Sweep heuristic as in Nagy et al. (2013). This heuristic extends the classical Sweep heuristic of Gillett and Miller (1974) by leaving the 20% of the customers that are closest to the depot out of the procedure to form single-stop tours. In doing so, poor quality solutions should be avoided and these customers should be left to the RTS algorithm to find the best-fitting routes [see Wassan et al. (2008); Nagy et al. (2013)].

In addition, the Savings heuristic of Clarke and Wright (1964) is also applied in order to construct initial solutions. In this case, all customers are included into the construction process. Initially, they form single-stop tours and are successively merged according to the Savings criterion until no further merging is possible.

At the very beginning of the solution procedure, the tabu search is initialized with an empty tabu list $(\hbox {TL}:=\emptyset$), and a tabu tenure $\hbox {tt}:=\hbox {tt}_\mathrm{init}$, $\hbox {count}_\mathrm{ors}:=0$ and $ma:=0$. The variables $\hbox {count}_\mathrm{ors}$ and ma serve for the reactive operations (see below).

4.1.2 Neighbourhood structures and moves

The two inter-route move types used in Nagy et al. (2013) are applied here. Shift moves remove one customer from one tour and reinsert the customer into another (which can also be an empty tour). Swap moves remove two customers from different tours and reinsert them into the tours of the respective other customer. A move consists of one (Shift) or two (Swap) customer movements. Each customer movement is characterized by a customer to be moved, a source tour, a target tour and a target position. Hence, the swapped customers are not necessarily inserted into the previous (source) position of the respective other customer but can be inserted into any position. Analogously, any position can be considered for the Shift moves. For example, shifting customer i from tour $t_1$ into tour $t_2$ at position $p_1$, and shifting customer i from tour $t_1$ into tour $t_2$ at position $p_2$ are two different moves. This approach is contrary to the original approach of Nagy et al. (2013) who always insert a customer into its best position in the target tour.

Furthermore, in Nagy et al. (2013), the whole neighbourhood is evaluated, i.e. each customer and each target tour are considered for the Shift moves and each pair of customers in different tours for the Swap moves. In contrast, we aim to omit potentially unpromising moves in order to save computing time while maintaining the solution quality. As relevant criterion, we use the distance $\Delta (t_1,t_2)$ between two tours $t_1$ and $t_2$ which is calculated using the minimum and maximum x- and y-values of the coordinates of the customers included in the respective tours:

$$\begin{aligned} \Delta (t_1,t_2)=&\left( \max \left[ \min _{i\in R'_{t_1}}x_i,\min _{i\in R'_{t_2}}x_i\right] -\min \left[ \max _{i\in R'_{t_1}}x_i,\max _{i\in R'_{t_2}}x_i\right] \right) \\&+\left( \max \left[ \min _{i\in R'_{t_1}}y_i,\min _{i\in R'_{t_2}}y_i\right] -\min \left[ \max _{i\in R'_{t_1}}y_i,\max _{i\in R'_{t_2}}y_i\right] \right) . \end{aligned}$$

Here, $R'_{t_i}$ stands for the set of customers served in tour $t_i\ (i=1,2)$ excluding the depot ($R'_{t_i}=R_{t_i}{\setminus }\{0\}$ [see Sect. 2]). Negative distance values indicate two intersecting tours and offer more potential for improvement than pairs of tours that are further away from each other. Only $tp_\mathrm{max}$ of all tour pairs with the smallest distances $\Delta (t_1,t_2)$ are considered. $tp_\mathrm{max}$ is a predefined parameter.

4.1.3 Determining a move for the current solution

In each iteration, a move $m_s$ is determined to construct a new solution from the current one according to $s:=s\oplus m_s$. In order to determine $m_s$, in a first step, a candidate list CL is generated as depicted in Fig. 3 (lines 7 to 22).

In the beginning, the set of all moves M for solution s is generated. All of these moves are then examined. In the end, CL contains up to $n_\mathrm{CL}$ moves m that lead to feasible solutions $s':=s\oplus m$. The feasibility check has the following aspects:

• all tours of a feasible solution $s'$ must not exceed the vehicle weight capacity D and volume capacity $V\ (V=L\cdot W\cdot H)$,

• feasible packing plans $P_{t,L}$ and $P_{t,B}$ must exist for all tours t of $s'$. This includes (S5) in the case of SL.

CL contains the best non-tabu moves leading to feasible solutions. In addition, a tabu move m that yields a new best solution $s':=s\oplus m$ with $f(s')<f(s_\mathrm{best})$ is also accepted for CL, i.e. aspiration by objective is applied.

When the candidate list CL is completely generated, the move $m_s$ is determined as follows:

• (1) If CL is empty (including only dummy moves, see Fig. 3), the tabued move with the shortest remaining tabu tenure is chosen as $m_s$, i.e. aspiration by default is used.

• (2) If CL is not empty and the solution $s':=s\oplus m_\mathrm{best}$ (see Fig. 3, line 26) is a new best solution, $m_s$ is set to $m_\mathrm{best}$; clearly, the best move $m_\mathrm{best}$ is the move for which $f(s\oplus m)$ gets minimal.

• (3) If CL is not empty and there is no new best solution, the move $m_s$ is selected randomly from CL.

Hence, by not necessarily selecting the best neighbour of s, a diversification mechanism is introduced into the search.

Fig. 3

Determination of move $m_s$

4.1.4 Tabu list management

The tabu list contains all customer movements that are currently tabu, i.e. the information which customers must not be inserted into which tours, as well as the iteration number in which the respective moves are allowed again. The tabu tenure tt determines how long a movement is set tabu. If a Shift move removing customer i from tour t was applied in the current iteration, any move that inserts i into t would be tabu for tt iterations. If a Swap move was applied, two movements must be set tabu—one for each customer-tour combination affected: if customer $i_1$ from $t_1$ was swapped with customer $i_2$ from tour $t_2$, then any move inserting $i_1$ into $t_1$or$i_2$ into $t_2$ is not allowed for the next tt iterations.

Three operations to adapt the search can be carried out within the RTS, namely increasing and decreasing of the tabu tenure tt, and reinitialization of the search. These operations are described in detail in Table 1 (see also Nagy et al. (2013)).

Table 1 RTS updating

The parameter GapMax is handled as a constant in Nagy et al. (2013). The results could be improved, though, by taking the size of the instance into account. If an instance contains many customers, there are more possibilities for the algorithm to move around a local optimum and to avoid tabued moves. Therefore, we determine this value as $GapMax =\lambda _{gap}\cdot \sqrt{n}$. In addition, a maximum tabu tenure $\hbox {tt}_\mathrm{max}=\lambda _\mathrm{tt}\cdot n$ is considered. $\lambda _\mathrm{gap}$ and $\lambda _\mathrm{tt}$ are predefined parameters.

4.1.5 Local optimization

At the end of an iteration, two post-optimization procedures are utilized. They are applied only to the tours affected in the current iteration. The first routine is a sequence of intra-route shifts. That is, a customer is moved to another position within the tour if this shift leads to a TTD reduction. This is done iteratively for all customers in the tour until no further improvement is achieved.

In the second routine, the visiting sequence of the customers in a tour is reversed if this reduces the maximum load of a route. In Nagy et al. (2013), the utilization of the capacity is taken into account for this purpose since they consider the one-dimensional case. Here, the maximum loading length needed for linehaul and backhaul items that are simultaneously transported (cf. Fig. 1) is reduced if possible. By this means, an additional customer might be visited in the given route.

4.1.6 Tour number reduction

The heuristics for the construction of the initial solution can lead to solutions with more than $v_\mathrm{max}$ tours. In order to guide the search towards solutions that do not violate the maximum tour number constraint, objective function values of solutions with more than $v_\mathrm{max}$ tours are penalized. A penalty term $(p\cdot c_\mathrm{max}\cdot \max (0, v-v_\mathrm{max}))$ is added to the TTD. p is a fixed parameter, $c_\mathrm{max}$ is the maximum distance between any two customers $(c_\mathrm{max}=\max _{(i,j)\in E} c_{ij})$, and v is the number of vehicles used in the respective solution. The factors $c_\mathrm{max}$ and p serve to ensure a sufficiently large penalty.

Furthermore, in connection with the Shift move, a customer can only be moved into an empty tour if less than $v_\mathrm{max}$ tours are used in the current solution.

4.1.7 Stopping criteria

The algorithm has to run for at least $\hbox {iter}_\mathrm{min}$ iterations. However, the search may continue beyond $iter_\mathrm{min}$ iterations if the last improvement was less than $\hbox {iter}_\mathrm{no\_impr}$ ago. Then, it stops after $\hbox {iter}_\mathrm{no\_impr}$ iterations without improvement.

4.2 Packing heuristics

Three different variants of the deepest-bottom-left-fill (DBLF) heuristic have been integrated into the RTS. It was originally developed for 2D packing (Baker et al. 1980; Hopper 2000) and extended to 3D packing (Karabulut and Inceoglu 2005). The DBLF variants are described here for the 3D container loading problem (3DCLP). In the 3D-CLP, a subset of a set of 3D (cuboid) items has to be packed into one container of fixed dimensions such that the filling rate is maximized. Below, we adapt these heuristics to ensure the feasibility of a route w.r.t. the packing subproblem within the 3L-VRPMB.

4.2.1 DBLF heuristics for the 3D container loading problem

The first variant of the DBLF heuristic that we consider is based on the DBLF implementation presented by Karabulut and Inceoglu (2005) (and by Hopper (2000) for the 2D case). In the approach of Karabulut and Inceoglu (2005), items are packed according to a given sequence. If an item cannot be placed feasibly in a container, it is skipped. Moreover, the spatial orientation is provisionally assumed to be fixed. The priorities for the placement are to position the items as far as possible to the back, (then) to the bottom and (then) to the left of the loading space. In implementations of the DBL heuristic, the final placement is often found using a sliding technique. On the contrary, the Fill method allows to fill gaps by keeping track of all possible placement positions and places each item in the deepest, bottom-most, left-most available position. The different approaches are depicted in Fig. 4. (For the sake of simplicity, the figures in this section show 2D problems). In the case of the Fill approach (Fig. 4a), the potential positions are defined by the top-left-back, bottom-right-back, and bottom-left-front corners of already placed items. The positions are sorted based on the deepest-bottom-left priority which is indicated by the numbers 1-5 in the example figure. It is successively tested whether the placement in the respective positions would be feasible. The tests terminate as soon as a feasible position was identified or all positions have been tested. The position that is nearest to the bottom and (then) nearest to the left and where the placement would be feasible is position 2. Hence, the gap could be filled which is not possible by sliding the item from the top-right corner (Fig. 4b). After a successful placement test for a given position, an item is (if possible) further moved starting from that position as far as possible towards the back, the bottom and the left. In the example in Fig. 4a, the final position of the item would be position $2'$.

Fig. 4

Comparison between BLF and BL approach

The second implementation variant extends the placement test of the heuristic presented above and is subsequently called DBLF⁺. A position where an item cannot be placed feasibly is not considered any further in the DBLF approach. On the contrary, sliding an item into one direction is considered during the placement in the variant DBLF⁺ (regardless of whether a feasible placement is already possible without the sliding). That way, a feasible placement could result from an otherwise infeasible position. The DBLF priority is applied to the sliding, too. That is, first, sliding towards the back, then towards the bottom and then towards the left is tested. If sliding is possible towards one direction, the other ones are not regarded any more. As before, further movements towards the back, bottom and left can be conducted after the placement test was successful.

An example is illustrated in Fig. 5. Testing the placement in position 2 according to the DBLF approach would lead to an infeasible placement (Fig. 5b). The item would overlap with other items. Thus, the next position would be tested now. However, considering sliding for position 2 would lead to a placement further to the bottom which is feasible (Fig. 5c).

Fig. 5

Comparison between BLF and BL approach

The third variant is a combination of the original DBLF implementation and DBLF⁺ in which the sliding of DBLF⁺ is only used once the original DBLF procedure cannot find a feasible placement for an item. The variant is subsequently called DBLF-Comb and is outlined in Fig. 6. The functions placement_DBLF and placement_DBLF$^+$ represent the respective procedure in which the feasibility of a placement is tested.

Furthermore, variants of the TA heuristic [e.g. Lodi et al. (1999)] were also implemented and tested but led to worse results than the DBLF variants. Therefore, they will not be described in further detail here.

Fig. 6

DBLF-Comb

4.2.2 Adaption of the DBLF heuristics to the 3L-VRPMB

In order to apply the three packing heuristics to the packing subproblem described in Sect. 2, the following modifications have been made:

• In the 3L-VRPMB, each item has two possible spatial orientations. Therefore, the following placement rule is applied: if placing an item in a given position with the first orientation fails, the same position is tested again with the second orientation.

• Only those placements are accepted where the geometrical constraints [(P1)–(P3)] as well as the packing constraints vertical stability, fragility and LIFO are satisfied.

• In order to facilitate finding a feasible packing plan for a given route, the following sequence of items is chosen: the first items to be placed are the ones of the last (first) customers to be visited in the case of linehaul (backhaul) customers. The items of one customer are sorted by the item fragility (non-fragile items first), breaking ties by non-increasing volume, breaking ties by non-increasing length and breaking ties by non-increasing width.

• The packing problem to be solved is the orthogonal packing problem (OPP), i.e. the objective is not to maximize the filling rate but to load all items belonging to a route feasibly into the loading space. Thus, the procedure is aborted as soon as one item cannot be placed feasibly in any available position.

• For the SL approach, the heuristics were modified. The LIFO restriction as described above must be considered along the width axis of the loading space in order to avoid rearrangements when (un-)loading items. Moreover, it should also be considered along the length axis in order to guarantee that the unloading of linehaul items gradually decreases $L_\mathrm{LH}$ and, thus, creates space for the backhaul items (see Fig. 1). However, simply extending the restriction in this manner resulted in packing patterns as in Fig. 7a. Let the visiting sequence here be $\{4,3,2,1\}$. Items of neither customer 3 nor 4 can be placed behind item $I_{22}$ (from the view of the unloading side). In order to avoid such gaps, the placement priorities have been adjusted for the SL: with first priority, an item is to be placed as close as possible towards the origin of the loading space, where the distance is defined as the sum of length and width coordinate of a given placement position. Subsequently, the DBLF rule is applied again, i.e. ties are broken by non-increasing length coordinate, then by height coordinate and then by width coordinate. This rule results in patterns like in Fig. 7b where items tend to be stacked first and then to be arranged towards the side from which they are loaded (cabin or rear side).

Fig. 7

Example packing patterns for side loading

4.3 Integration of routing and packing

The packing procedure is executed in order to check whether the items transported on a tour can be packed feasibly according to the above-formulated packing constraints. In the course of a packing check, (generally) two packing plans—one for the linehaul items and one for the backhaul items of a tour—are determined. Moreover, in the case of the SL approach, the procedure tests whether linehaul and backhaul items would overlap at any stop of the route according to the generated packing plans (see restriction (S5), Sect. 2).

A packing check is made when a route is tested for feasibility (see Fig. 3). Feasibility tests are conducted whenever a new solution is generated, i.e. during the generation of the initial solution, during the generation of neighbour solutions and in connection with the local optimization. Firstly, it is checked whether the items transported simultaneously exceed the weight and volume capacity of the vehicle at any stop of the tour. If this is not the case, the packing procedure is called. Note that not every neighbour of the current solutions is tested for feasibility during the TS. Only if the corresponding move can potentially be added to the candidate list, the routes affected by the move are tested. That way, the efficiency is increased significantly (cf. Fig. 3, lines 11,18).

In the course of the packing procedure, the maximum loading length of a packing plan is determined. This is needed (i) for the tests regarding the SL approach, and (ii) for the second routine of the local optimization (reverse operator).

The application of the packing procedure is usually computationally very expensive. Therefore, a cache is used which stores routes that have already been tested for packing feasibility. The cache is organized as a map with a maximum size of 1,000,000 elements. The oldest route in the map is removed if the size is exhausted.

5 Computational experiments

5.1 Benchmark instances

5.1.1 One-dimensional instances

In order to make sure the implemented routing approach is working properly, it was applied to one-dimensional (1D) benchmark instances and the results were compared to the ones obtained by recently published methods for the VRPMB. Three instance sets were used. Two of them, namely GJB89 and TV97, were originally proposed for the VRPCB by Goetschalckx and Jacobs-Blecha (1989) and Toth and Vigo (1997), respectively. Later these sets were used as VRPMB instances in Halse (1992) and Wade (2002) by relaxing the delivery-before-pickups assumption. At the same time, the “fixed fleet” restriction of the original instances, i.e. constraint (S4) in our problem formulation, was dropped. This specification of the VRPMB instance sets GJB89 and TV97 has been maintained in all further VRPMB papers (see Wassan et al. (2008), p. 154 and Wassan et al. (2013)), and we will also observe it. As a consequence, the GJB89 set for the VRPMB includes only 46 instances (not 62 as for the VRPCB) while the TV97 set has 33 instances as in the original version. In the set GJB89, the number of customers varies between 25 and 150 customer locations and there are 50%, 66% or 80% linehaul customers. The instances of the set TV97 have 21 to 100 customer locations and the shares of linehaul customers are the same as in set GJB89. Finally, the third set (SN99) was generated by Salhi and Nagy (1999) for the VRPMB. This set consists of 42 instances with 50–199 customer locations with 10%, 25% and 50% backhaul customers. Again, there is no constraint in the set SN99 with regard to the number of vehicles (routes). Note that we consider only those 21 instances that do not include tour length limits and drop times.

5.1.2 Three-dimensional instances

New 3L-VRPMB instances were generated which cover different features of the problem. The number of customers is set to 20, 60 and 100, and the share of linehaul customers to 50% and 80%. The locations of the customers were determined randomly. Moreover, we keep the total number fixed to 200 items so that the number of items per customer depends on the number of customers in an instance (5–15 for $n=20$, 2–5 for $n=60$, 1–3 for $n=100$).

We consider different levels of heterogeneity with respect to the items, that is, instances were generated with 3, 10 or 100 different item types. The edge dimensions and weights of each item type were generated randomly. There are instances with large items and instances with small items. The length and width of large items were uniformly randomly generated in the intervals [0.2L, 0.6L] and [0.2W, 0.6W], respectively (cf. Gendreau et al. (2006)). The height of an item was determined in the interval [0.2H, 0.5H]. The factor 0.5 was chosen for the upper limit of the interval to ensure that the items can be placed inside the partitioned loading space (cf. Sect. 2). For instances with 20 customers, only small items are considered, since all large items of one customer would nearly completely fill the loading space due to the comparatively large number of items per customer. The length (respectively, width and height) of small items is generated in the interval [0.1L, 0.3L] (respectively, [0.1W, 0.3W] and [0.1H, 0.3H]). In addition, instances with mixed item size were also generated which have ca. 50% small items and 50% large items. Any instance with mixed items results by merging an instance with small items and an instance with large items where both instances share the same characteristics (except item size).

The weight (in weight units (WU)) of an item type was randomly generated between $0.001[\frac{WU}{VU}] \cdot \ hbox{vol} [VU]$ and $0.01\ [\frac{WU}{VU}] \cdot \hbox {vol} [VU]$, where vol is the item’s volume (in volume units (VU)). 20%, but at least one, of the item types is fragile. The loading space dimensions are $L=60$, $W=25$, $H=30$ and the weight capacity $D = 200$. The percentage $\alpha$ in the stability constraint (PC2) is set to 75%.

For the 3D instances, constraint (S4) on the available number of vehicles $v_\mathrm{max}$ is in force. $v_\mathrm{max}$ is determined by applying the Savings heuristic to the instances. The resulting number of routes is used as $v_\mathrm{max}$. This way, feasible solutions regarding the vehicle constraint (S4) are ensured.

Taking into account the variation of the customer number, percentage of linehaul customers, item size and heterogeneity of items, there are 42 feature combinations. For each combination, 10 instances were generated randomly resulting in 420 3L-VRPMB instances, among them 120 instances contain a mix of small and large items.

The 3L-VRPMB instances as well as our best solutions can be found online at http://www.mansci.ovgu.de/Forschung/Materialien.html. In addition, the well-known 27 3L-CVRP instances introduced in Gendreau et al. (2006) were used for a numerical comparison.

5.2 Parameter setting

The parameter settings were mostly adapted from Nagy et al. (2013). The values for the newly introduced parameters were determined in pretests with a set of test instances taken from the three sets for the VRPMB. Their settings are given in Table 2.

Table 2 Parameter settings

5.3 Computational results

The hybrid algorithm was implemented in C++, and the experiments were conducted on a Haswell system with up to 3.2 GHz and 16 GB RAM per core.

5.3.1 One-dimensional instances

The RTS in combination with the Savings procedure for the construction of the initial solutions will be referred to as RTS_Sav in the following. The combination with the Sweep heuristic shall be called RTS_Sweep. Moreover, we consider the combination of RTS_Sav and RTS_Sweep, denoted as RTS_Comb, where first RTS_Sav and then RTS_Sweep are applied each with the same parameter setting. Due to some random components in the algorithm, five runs for each variant of the RTS were conducted for each instance. The results for the 1D instances are summarized in Tables 3 and 4. Note that only 45 GJB89 instances are considered here as one of the compared methods (Wassan et al. (2008)) does not provide results for one instance.

For each instance set, the obtained solutions are compared to the best solutions of Nagy et al. (2013) (NWS13) and the best known solutions from the literature (BKS). Furthermore, an analogue comparison is done with a second well performing VRPMB method; in the case of the instance sets GJB89 and TV97, the RTS by Wassan et al. (2008) (WNA08) is taken while the ALNS by Ropke and Pisinger (2006) is used for the (reduced) set SN99.

In the first column of Table 3, the instance set and the RTS variant are indicated. The columns Dev-best (2–4) contain for each compared method and BKS the average percentage deviation of the best found TTD per instance from the best TTD of the compared method and the BKS, respectively. The columns Dev-avg (5–7) contain for each compared method and BKS the average percentage deviation of the average obtained TTDs over five runs per instance from the best TTD of the compared method and the BKS, respectively. For each instance set and each compared method (including our RTS), the number of used vehicles over all instances per set is calculated. Note that in the BKS case the number of used vehicles is calculated using the solutions with best TTD values. The columns Dec-veh (8–10) contain for each compared method and BKS the difference of the sums of used vehicles over all instances of a set between our RTS and the compared method and the BKS, respectively. Negative values indicate lower numbers of used vehicle in the solutions provided by the RTS.

Table 3 RTS results for 1D instances (A)

In the first two columns of Table 4, the instance sets and related numbers of instances are given. In the third column, the numbers of new best solutions provided by the proposed RTS are indicated while the last three columns show the average run times per instance (in seconds).

Table 4 RTS results for 1D instances (B)

The comparison of best solutions in terms of total travel distance can be summed up as follows where only our combined RTS is considered. Compared to the method provided in Nagy et al. (2013) (NWS13), an improvement of $-1.21$% could be reached by our RTS over all 99 instances (note that negative values indicate that our results are better than results of a compared method). Taking the sets GJB89 and TV97, our RTS is slightly better than the method proposed in Wassan et al. (2008) (WNA08) with a mean improvement of $-0.5$%. Among the compared methods, only the ALNS presented in Ropke and Pisinger (2006) (RP06) is clearly dominating our method, for instance set SN99 with an improvement of 1.59 %.

The number of used vehicles (or routes) represents a second optimization criterion that is often taken into account in vehicle routing problems. Our combined RTS achieves mostly the same numbers of vehicles as the compared methods. Significant differences only occur compared to the ALNS proposed in Ropke and Pisinger (2006) (the numbers of vehicles used by the ALNS of Ropke and Pisinger (2006) were picked up from Nagy et al. (2013), p. 212). In total, 80 vehicles less are used in the solutions of RTS_Comb.

The deviations of our best solutions from the BKS (see Table 3, column 4) indicate RTS_Sav produces better results than RTS_Sweep. The difference amounts to $0.66\%$-points over all 99 instances. Applying the Savings heuristic instead of or combined with the Sweep heuristic did enable us to improve the results obtained by Nagy et al. (2013).

However, Table 4 makes clear that this improvement was only possible on the cost of higher run times. Note that Nagy et al. (2013) state that less than a minute was needed for the majority of the instances. Nevertheless, the run times for all variants of our RTS seem to be acceptable. Finally, the numbers of new best solutions in Table 4 prove that the RTS performs relatively well for the well-known VRPMB instance sets.

5.3.2 Three-dimensional instances

The test of the hybrid algorithm deals with three different aspects. First, as the final hybrid algorithm must be equipped with a packing heuristic, the available packing heuristics were initially tested and compared. Second, the impact of the initial solution construction heuristic as well as of the loading approach is studied. Third, a numerical comparison with the 3L-VRPMB heuristic by Reil et al. (2018) is conducted. The parameter settings determined with the one-dimensional instances were also applied to the 3D case. Third, a numerical comparison with the 3L-VRPMB heuristic by Reil et al. (2018) as well as the 3L-CVRP heuristics by Gendreau et al. (2006) and Zhang et al. (2015) is conducted.

Determination of the best packing heuristic

For this purpose, a test set of 30 out of 420 instances was formed. The instances were chosen at random from the instances with small and large items so that all remaining feature attributes (number of customers, number of item types, etc.) are combined.

To determine the best packing heuristic, we compare six variants of the hybrid algorithm with the Savings heuristic which differ regarding the used packing heuristic and the loading approach. Each of the available packing heuristics (DBLF, DBLF+ and DBLF-Comb) is combined with each loading approach (loading space partition (LSP) and side loading (SL)). Each of the selected instances was run five times with each of the six variants. In Table 5, the obtained TTD results for each of the variants are compared to the best found solutions over all six hybrid algorithm variants. Per variant, the table contains the average (Dev-avg) and maximum (Dev-max) percentage deviations of the obtained TTDs from the best found ones.

The best results were obtained with the SL approach and the DBLF heuristic. However, in combination with LSP, DBLF-Comb produced better results than the plain DBLF heuristic. Hence, the respective results were examined in more detail with the conclusion that DBLF seems to work better for instances with small items whereas the combination dominates in the case of large items. Therefore, in the final tests, the packing heuristic is chosen depending on the item sizes: DBLF for small items and DBLF-Comb for large items. DBLF is also used in later experiments for instances with mixed items.

Table 5 Comparison of packing heuristics (TTD)

Impact of initial solution heuristic and loading approach

To study these issues, experiments were conducted with all 420 instances each of which was solved five times by four variants of the hybrid algorithm. These variants result by using both loading approaches combined with both initial solution heuristics. The combined variant of the hybrid algorithm is not applied here (as in the 1D case) since the run time effort would be presumably too high.

The results are presented first in Tables 6 and 7. They contain in the first three columns a description of the different instance groups. Then, for each of the four variants of the hybrid algorithm mean values of average and best obtained TTDs over five runs and of related numbers of used vehicles are indicated.

Table 6 Results for the hybrid algorithm with the Savings heuristic and both loading approaches

Table 7 Results for the hybrid algorithm with the Sweep heuristic and both loading approaches

Reading the last lines of the tables, one can realize that the Savings heuristic performs better than the Sweep heuristic and the SL approach dominates the LSP approach. Nevertheless, a more detailed presentation regarding the impact of the initial solution heuristic and loading approach should be given in the next two tables.

The results regarding the initial solution construction heuristics are summarized in Table 8. The results obtained with RTS_Sav and the respective loading approaches serve as a benchmark here. The column Dev-avg contains the average percentage deviations of the TTDs obtained with RTS_Sweep from the average benchmark TTDs aggregated over both loading approaches.

The results support the findings from the 1D tests (Table 3) indicating that RTS_Sav slightly outperforms RTS_Sweep. The TTDs obtained with RTS_Sweep deviate on average 0.77% from the TTDs obtained with RTS_Sav.

Table 8 Results for 3D instances: Initial solution construction heuristics

Table 9 provides a comparison of the two different loading approaches. Here, the results obtained with LSP were used as benchmark for each initial solution heuristic. In the table, the average deviations (Dev-avg) of the SL solutions (w.r.t. the TTDs) from the LSP solutions (aggregated over both initial solution heuristics) and the average numbers of used vehicles of the best solutions (v-best) are reported. Furthermore, the average computing times (in seconds) are listed in the columns “Run times (s)”.

Not surprisingly, much better results can be obtained with the SL approach. The respective TTDs are on average about 16% lower than the TTDs obtained with the LSP and less vehicles are needed. These results could be expected as the SL approach allows making use of the whole loading space, whereas half of it is left empty at least at the very beginning and the very end of a tour if the loading space is separated. However, differences can be observed among the different instance classes. The SL approach seems to be particularly beneficial if the items are large (as smaller items can be placed more easily also within a smaller loading space), and if the share of linehaul and backhaul items is unequal. Moreover, the differences decrease with an increasing number of customers, i.e. with a decreasing number of items per customer.

Table 9 Results for 3D instances: Loading approaches

Moreover, the hybrid algorithm with the LSP requires less computing time than the variant with the SL approach. Two reasons can be identified. Firstly, checking feasibility for the SL approach takes longer because the two generated packing plans need to be compared for each backhaul stop of a tour to avoid any overlapping of linehaul and backhaul items. Secondly, the SL approach allows to form longer tours which also require a higher packing effort. Independently of the loading approach, it can be observed that the computing times increase with the size of the underlying VRP, i.e. with the number of customers, and that the computing times depend on the item sizes. Instances with large items can be solved much faster than instances with small items. In the case of small items, much more customers can be merged into one tour (resulting in more items per tour) which requires higher efforts for the packing checks.

Numerical comparison with the 3L-VRPMB heuristic by Reil et al. Reil et al. (2018)

For the numerical comparison, 128 of the 3L-VRPMB instances introduced above were selected among the 420 instances. Thirty-two instances were chosen at random from the instances with 20 customers. As mentioned above, those contain only instances with small items. Forty-eight instances were chosen at random for instances with 60 and with 100 customers. More instances were selected for those instance groups as they contain instances with small, mixed and large items.

The heuristic by Reil et al. (2018) (RBM18) is able to work with different loading approaches and strategies. In this comparison, the side loading approach is taken which turned out to be the strongest available loading approach for the 3L-VRPMB(TW) (see Reil et al. (2018), p. 14). The observed constraints for packing and routing are similar to the RTS heuristic; in particular, a supporting rate of 75% in constraint (PC2) is required for the heuristic by Reil et al. (2018), too. The RTS heuristic is applied with the Savings heuristic and with both loading approaches. Since only one run of the procedure of Reil et al. (2018) was performed on each selected instance, we randomly chose the result of one run (out of five) of the RTS on each one of those instances for comparison purposes.

Tables 10 and 11 contain the results of the comparison which are again organized by instance groups. In the first two columns of Table 10 and 11, the instance groups are characterized. In the following nine columns of Table 10, for each of the compared methods, average values per instance group are given for the total travel distance, the number of used vehicles and the run time (in seconds). In the last four columns of Table 11, the minimum and average deviations per instance group of the total travel distances gained by the heuristic of Reil et al. (2018) to the ones yielded by RTS(LSP) and RTS(SL) are listed. Negative values indicate better solutions obtained by Reil et al. (2018).

Table 10 Results for 3D instances: Comparison with Reil et al. (2018) (A)

Both hybrid RTS variants (LSP and SL) perform considerably better than the heuristic by Reil et al. (2018) for the given set of instances in terms of total travel distance as well as number of used vehicles while the running times are comparable. In the heuristic of Reil et al. (2018), each customer of a route has a special compartment, i.e. segment of the loading space, that is filled exclusively by the boxes of this customer. In the instances used here, very often a customer has only few and/or small boxes. In this case, the volume of a customer compartment cannot be utilized very well. Hence, more vehicles (or routes) and also longer travel distances are needed for transporting all the goods. It is our belief that for differently constructed instances the compared heuristic could perform better. This is proven by those instances in which the heuristic by Reil et al. (2018) achieved better results than the RTS (see Table 11, column 3). On the other hand, our instances do reflect situations where individuals make purchases in department stores consisting of few or small things and therefore make sense. We can conclude that—as in other vehicle routing areas—several heuristics with different abilities are necessary to cover the full range of requirements.

Table 11 Results for 3D instances: Comparison with Reil et al. (2018) (B)

Table 12 Results for instances of Gendreau et al. (2006) and comparison with Gendreau et al. (2006) and Zhang et al. (2015)

Numerical experiments on the instances of Gendreau et al.Gendreau et al. (2006)

Finally, the RTS was applied to the well-known 3L-CVRP instances of Gendreau et al. (2006). In this regard, its results are compared to those of Gendreau et al. (2006) and Zhang et al. (2015). The latter have developed an evolutionary local search which proved to be one of the best approaches for the 3L-CVRP to date.

Table 12 presents the results of these experiments. Instance information is provided in the first columns [name, number of customers (n), total number of items (m), maximum number of vehicles ($v_\mathrm{max}$)]. The RTS heuristic was applied with both the Savings and Sweep heuristic and with both loading approaches. For the rear loading approach, the loading space separation was omitted as a 3L-CVRP instance does not contain any backhaul customers.

In Table 12, the TTD and number of routes (v) of the best solutions among all runs are listed. In addition, the average run times are given in seconds (t (s)). For the comparison with the approaches from the literature, the best TTDs and average run times of Gendreau et al. (2006) and Zhang et al. (2015) are presented as well as the deviations of the TTDs provided by the RTS from the TTDs of the comparison procedures.

As can be seen, our approach achieves slightly better solutions than the ones of Gendreau et al. (2006). The local search of Zhang et al. (2015) provides considerably better results. The RTS does outperform the approach of Zhang et al. (2015) in one case (E016-05m). However, it must be noted that the RTS did not achieve to find a solution where the vehicle number restriction is satisfied. The found solution requires one vehicle more than allowed. As mentioned above, the only mechanism to handle this restriction is the penalization of additional tours. For the presented instances, this approach seems to be insufficient as the maximum number of vehicles is often violated by the best found solutions.

An advantage of our approach is, though, that moderate solutions are provided rather fast requiring on average only about 9 seconds of run time.

6 Conclusions

Transporting linehaul and backhaul goods in the same tours can be a useful mean to reduce empty running trucks, travelled distances, fuel consumption and, in consequence, to reduce costs. Although the integration of backhauls into the VRP was studied frequently in the research, the transported goods and available capacities were mostly considered to be one-dimensional. Applying solutions obtained by solving such problems could turn out to be infeasible when the transported goods are bulky. Therefore, we present a 3L-VRPMB which includes not only the backhauls into the VRP but also three-dimensional loading constraints so that, for example, load stability or loading sequences can be considered. In order to solve it, a hybrid algorithm consisting of a reactive tabu search (which was originally developed for the one-dimensional VRPMB) combined with a packing construction heuristic was implemented.

The procedure was tested for both one-dimensional and three-dimensional test instances. The one-dimensional tests indicate that the implemented RTS is comparable to the original approach. Moreover, a second heuristic for constructing initial solutions was applied which led to further improvements of the results.

New instances were generated for the 3L-VRPMB and different packing construction heuristics were implemented and compared. The final hybrid algorithm combined the RTS with variants of the deepest-bottom-left-fill approach. Since linehaul and backhaul customers can be visited in any sequence in the VRPMB, linehaul and backhaul items are (partly) transported simultaneously. In the hybrid approach, this is realized by two different loading approaches which ensure that any reloading during a tour is avoided. They include rear-loaded vehicles with horizontally separated loading spaces into linehaul and backhaul sections, and side-loaded vehicles. The best results—in terms of both total travel distance and number of tours—were obtained with the side loading approach.

A comparison has been conducted with the 3L-VRPMB heuristic by Reil et al. (2018). In this comparison, our hybrid algorithm performed considerably better than the method of Reil et al. (2018) in terms of total travel distance and number of routes. This may have been caused partially by the use of benchmark instances for which the method of Reil et al. (2018) is less suitable. In addition, the hybrid RTS heuristic was compared to further heuristics presented in the literature using the 3L-CVRP instances of Gendreau et al. (2006). In terms of solution quality, the RTS is comparable to the approach of Gendreau et al. (2006). The local search of Zhang et al. (2015) performs significantly better. Yet, our approach is able to provide moderate solutions in rather small run times.

The mixture of linehaul and backhaul items within a route leads to the application of the presented loading approaches. Both face limitations which could be tackled further in future research regarding the 3L-VRPMB. For example, the side loading approach could provide more flexibility if a mixture of linehaul and backhaul items along the length axis of the loading space was allowed. This would make packing more complicated but might lead to better utilization of the loading space and, thus, better solutions. Future studies on the 3L-VRPMB and other VRPs with backhauls should also integrate further and more complicated packing constraints, e.g. axle weight constraints, to cope with even more difficult real-world situations.

Appendix

Table 13 Results RTS for GJB89 instance set

Followingly, the detailed results of the one-dimensional tests are presented. Tables 13, 14 and 15 state the instance characteristics in the first columns. The columns “BKS” contains the TTD and the number of vehicles (v) of the best known solution from the literature. The next columns contain the best found solutions (TTD-best) of our RTS and the number of vehicles corresponding to the best solution (v-best). The last column states whether the best solution was obtained in connection with the Sweep (Sw) heuristic, the Saving (Sav) heuristic, or both.

Table 14 Results RTS for TV97 instance set

Table 15 Results RTS for SN99 instance set