1 Introduction

Job scheduling is an optimization problem mainly studied in operations research and computer science in which the jobs are assigned to resources at particular times Pinedo (2012). The objective of the job scheduling problem may take different forms, such as minimizing the makespan, minimizing the total completion time, and minimizing the total waiting time. If we want to use minimum cost to get the jobs done, then the job length is one of the important factors to be considered. Besides the length of the processing time, the cost may also be related to the time period during which the job is processed. For example, the electricity price is varying for different time slots because the electricity company needs to give extra effort to satisfy the requirements from the public in rush hours. If we insist on finishing the job earlier in those rush hours, then the electricity price may be higher than postponing the jobs to non-rush hours. Another example comes from the delivering company where the delivery costs are higher during the Thanksgiving day or Christmas because there are too many orders. If we want the package delivered earlier during those holidays, then we probably have to pay extra money so that the package could have a higher priority to be delivered. Notice that if the time slot costs are increasing, then the earlier the jobs are done, the less cost we need to pay. Hence we do not need to care about the time slot costs if they are increasing. Therefore, in this paper, we consider the case when the time slot costs are non-increasing.

Recently Wan and Qi (2010) proposed a new scheduling model with variable time slot costs. In such problems, a schedule is measured not only by the standard scheduling objective but also the incurred machine costs. The standard scheduling objectives that are considered in Wan and Qi (2010) include minimizing the total completion time, minimizing the maximum lateness/tardiness, minimizing the total weighted number of tardy jobs, and minimizing the total tardiness. Specifically, the planning horizon is partitioned into multiple time slots with a unit length, where each time slot may have a different cost to use. The machine cost of a schedule depends on which time slots of the machine are occupied by the jobs. Such problems have applications when the revenue of a schedule needs to be considered Aydinliyim and Vairaktarakis (2010).

One common way to simultaneously consider both the time slot cost and the traditional scheduling criteria is to minimize the weighted summation of the total time slot cost and one traditional scheduling criterion. In Zhong and Liu (2012), Zhong and Liu consider to minimize the makespan plus the total time slot costs. They prove that the general problem is strongly NP-hard and analyze a special case with non-increasing time slot costs. In Wan and Qi (2010), they discussed the case that the time slot costs were non-decreasing with respect to time. In such a case, no one would like to postpone the jobs, hence their models could be reduced to the corresponding classical scheduling models. For the case that the time slot costs varied arbitrarily with respect to time, all their models became NP-hard in the strong sense. When the time slot costs were non-increasing with respect to time, they showed that the optimal schedules were different from the optimal schedules for the counterparts without the time slot costs. They found that some structured properties of classical scheduling models, like shortest processing time first and earliest due data first, still held in the modified forms. While most such basic problems have been shown to be either NP-hard or polynomially solvable, there is one important open case: the problem with non-increasing time slot costs and the traditional scheduling criterion being the total weighted completion time.

The same model was rediscovered in 2012 by Kulkarni and Munagala (2012) in the computer science setting with the data centers as the motivation. They study online algorithms to minimize the total weighted completion time plus time slot costs by providing a \((1+\epsilon )\)-speed \(O(poly(\frac{1}{\epsilon }))\)-competitive algorithm. Most recently Chen et al. (2015) investigated the preemptive scheduling of jobs to minimize certain scheduling objective plus the time slot costs. When the scheduling objective is makespan, for unrelated machines, they designed a polynomial-time algorithm. When the scheduling objective is total weighted completion time, they can calculate the optimal schedule in polynomial time if the job execution sequence is given. They also gave a PTAS for the general weighted jobs.

Before presenting our results, we formally define the problem as follows.

Suppose that there are n non-preemptive jobs to be processed on a single machine where each job j has an integer processing time \(p_j\) and a weight \(w_j\). Denote \(\bar{p}_j=p_1+\cdots +p_j\) for \(j=1,\ldots ,n\), and \(P=\bar{p}_n\). Assume that the planning horizon is divided into K time slots with unit length, where all the jobs have to be completed by time K. Note that, under the definition of the time slot, the kth time slot starts at time \(k-1\) and ends at time k. To ensure feasibility, we assume that \(P\le K\).

Each time slot k has a cost \(\pi _k\). We further define \(\bar{\pi }_{a,b}=\pi _{a+1}+\cdots +\pi _{b}\) for \(0\le a < b \le K\). In this paper, we concentrate on the case of non-increasing cost, i.e., \(\pi _1 \ge \pi _2 \ge \cdots \ge \pi _K\). Under this case, there is an incentive to delay processing the jobs in order to reduce the time slot cost.

In a feasible schedule without preemption, if a job is started at time \(S_j\), then it is completed at time \(C_j=S_j+p_j\), and incurs total time slot cost \(\bar{\pi }_{S_j,C_j}=\pi _{S_j+1}+\cdots +\pi _{C_j}\). The objective of the scheduling problem is to minimize the total time slot cost plus the total weighted completion time, i.e.,

$$\begin{aligned} \min \sum _{j=1}^n\big (\bar{\pi }_{S_j,C_j}+w_jC_j\big ). \end{aligned}$$

From a practitioner’s point of view, it is more reasonable to define the objective function as a weighted sum of the two terms, i.e., \(\min \sum _{j=1}^n\big (\bar{\pi }_{S_j,C_j}+\alpha w_jC_j\big )\) with \(\alpha \ge 0\) being a controllable coefficient. The methods we used in this paper can also be extended and applied to this general case by changing all \(w_j\) to \(\alpha w_j\).

We address the open problem by the following results.

  • First, we consider the case of time slot costs decreasing linearly at a constant rate, where we show the optimality of weighted shortest processing time first (WSPT) order (possibly with idle times in the actual schedule) and find that there is an optimal schedule having only one possible interval of idle time. As a result, the problem can be solved by sorting jobs according to their weighted processing times, and then identifying the optimal position of the single idle time period.

  • Second, we consider the case with decreasing concave time slot costs, where we find again that there is only one possible interval of idle time in an optimal schedule. The situation is a bit complicated because of the lack of the global WSPT property. A dynamic programming algorithm is developed to cope with this case.

  • Third, we consider the case with decreasing convex time slot costs, where there are possibly many idle time intervals in an optimal schedule. We propose a polynomial-time repetitive merge algorithm to solve the problem.

  • Finally, we prove that the problem is NP-hard in the strong sense when the time slot costs follow an arbitrary non-increasing function.

The remainder of the paper is organized as follows. We discuss the case of linearly decreasing time slot cost in Sect. 2. In Sects. 3 and 4, decreasing concave and decreasing convex time slot costs are considered. In Sect. 5, we prove the complexity of the general decreasing case. Finally we conclude the paper in Sect. 6.

2 Linearly decreasing time slot cost

We start with the case where the time slot cost decreases as a linear function of the time index k. Specifically, we assume \(\pi _k - \pi _{k+1} = \varepsilon \), \(\varepsilon >0\), for \(k=1,\ldots ,K-1\). Clearly, we have \(\pi _i-\pi _k=(k-i)\varepsilon \) for any two time slots i and k.

We first show the optimality of WSPT order and then give the algorithm on how to schedule all the jobs in the linearly decreasing time slot cost case.

Lemma 1

For a job j, if \(\frac{w_j}{p_j}> \varepsilon \), then it is optimal to process this job as early as possible.

Proof

Suppose that the job starts at time k, where the total cost c incurred by this job is

$$\begin{aligned} c=w_j(k+p_j)+ \bar{\pi }_{k,k+p_j}. \end{aligned}$$

If the job starts x time slots earlier, then the new cost \(c{^\prime }\) is

$$\begin{aligned} c{^\prime }=w_j(k+p_j-x)+\bar{\pi }_{k-x,k-x+p_j}. \end{aligned}$$

Comparing c and \(c{^\prime }\), we can see that

$$\begin{aligned} c-c{^\prime }=w_j\cdot x-\varepsilon \cdot p_j\cdot x=\left( \frac{w_j}{p_j}-\varepsilon \right) p_j\cdot x>0. \end{aligned}$$

Hence the earlier the job is processed, the less cost it will have. \(\square \)

Similarly, we have the following lemmas, where the proofs are omitted.

Lemma 2

For a job j, if \(\frac{w_j}{p_j}<\varepsilon \), then it is optimal to process the job as late as possible.

Lemma 3

For a job j, if \(\frac{w_j}{p_j}=\varepsilon \), then the job has the same cost no matter when it is processed.

Based on the above three lemmas, we can prove the following theorem which describes the order of jobs in an optimal schedule.

Theorem 1

If the time slot cost decreases linearly with respect to time k, then for each optimal schedule to the problem, the jobs are scheduled in WSPT order.

Proof

Suppose that in an optimal schedule there exist two successive jobs where job i precedes job j with \(\frac{w_i}{p_i}<\frac{w_j}{p_j}\). Comparing \(\frac{w_i}{p_i}\), \(\frac{w_j}{p_j}\) with \(\varepsilon \), there are five cases to be discussed.

Case 1 \(\frac{w_i}{p_i}<\frac{w_j}{p_j}=\varepsilon \) By Lemmas 2 and  3, we can switch job i and job j to reduce the total cost.

Case 2 \(\frac{w_i}{p_i}<\varepsilon <\frac{w_j}{p_j}\) By Lemmas 2 and  1, switching job i and job j can reduce the total cost.

Case 3 \(\frac{w_i}{p_i}=\varepsilon <\frac{w_j}{p_j}\) By Lemmas 3 and  1, switching job i and job j can reduce the total cost.

Case 4 \(\frac{w_i}{p_i}<\frac{w_j}{p_j}<\varepsilon \) In this case, job i and job j both prefer being processed as late as possible by Lemma 2. Therefore, there will be no idle time slots between these two jobs. Suppose that job i starts at x, then the cost for processing i and j is

$$\begin{aligned} c=w_i(x+p_i)+w_j(x+p_i+p_j)+\bar{\pi }_{x, x+p_i+p_j} \end{aligned}$$

If we switch job i and job j and let job j start at x, then the new cost

$$\begin{aligned} c{^\prime }=w_j(x+p_j)+w_i(x+p_i+p_j)+\bar{\pi }_{x, x+p_i+p_j} \end{aligned}$$

Comparing c with \(c{^\prime }\), we can see that

$$\begin{aligned} c-c{^\prime }=w_jp_i-w_ip_j=p_ip_j\left( \frac{w_j}{p_j}-\frac{w_i}{p_i}\right) >0 \end{aligned}$$

which means that switching job i and job j could further decrease the total cost.

Case 5 \(\varepsilon <\frac{w_i}{p_i}<\frac{w_j}{p_j}\) This case is very similar to Case 4 where there is no idle time between these two jobs. The cost calculation is the same of Case 4. Hence we can get the same conclusion that switching job i and job j is better.

All the five cases show that switching job i and job j can decrease the total cost and do not affect other jobs, which contradicts our assumption of optimality. Hence for every optimal solution, the jobs are processed in WSPT order. \(\square \)

Based on the above lemmas and Theorem 1, we see that in an optimal schedule jobs can be partitioned into three subsets \(J_1\), \(J_2\), and \(J_3\), where \(J_1\) consists of jobs with \(w_j/p_j > \varepsilon \) that are sequenced in WSPT order without any idle time and started at time zero, \(J_3\) consists of jobs with \(w_j/p_j < \varepsilon \) that are sequenced in WSPT order without any idle time and completed at time K, and \(J_2\) consists of jobs with \(w_j/p_j = \varepsilon \) that are scheduled anywhere between \(J_1\) and \(J_3\). The algorithm can be summarized as in Algorithm 1.

figure a

3 Decreasing concave time slot cost

In this case, the cost differences between successive time slots become larger with respect to the time index k, i.e., \(\pi _{k}-\pi _{k+1}>\pi _{k-1}-\pi _{k}\) for \(1<k<K\). This also implies \(\pi _{k}-\pi _{k+p_j}>\pi _{k-1}-\pi _{k+p_j-1}\) for any j. An interesting property for this case is that there is only one possible interval of idle times in an optimal schedule, similar to the case of linearly decreasing cost.

Lemma 4

When \(\pi _{k}-\pi _{k+1}>\pi _{k-1}-\pi _{k}\) holds for \(1<k<K\), there is no job processed between two idle time intervals in an optimal schedule.

Proof

We prove it by contradiction. Assume that there is a set of t jobs \(J_{a1}, J_{a2},\ldots , J_{at}\) processed between two idle time slots in the optimal schedule. If the first job \(J_{a1}\) starts at time k and the last job \(J_{at}\) ends at time \(k+p_{a}\), then the cost for this set of t jobs is

$$\begin{aligned} c_a^0=\sum _{i=1}^{t}{w_{ai}C_{ai}}+\bar{\pi }_{k, k+p_a} \end{aligned}$$

where \(w_{ai}\) is the weight for job \(J_{ai}\) and \(C_{ai}\) is the completion time of job \(J_{ai}\).

Since these t jobs are between two idle time slots, we can process them one time slot earlier or later with cost \(c_a^L\) and \(c_a^R\), respectively.

$$\begin{aligned} c_a^L= & {} \sum _{i=1}^{t}{w_{ai}(C_{ai}-1)}+\bar{\pi }_{k-1,k-1+p_a}\\ c_a^R= & {} \sum _{i=1}^{t}{w_{ai}(C_{ai}+1)}+\bar{\pi }_{k+1,k+1+p_a}. \end{aligned}$$

Because of the optimality assumption, we have \( c_a^0\le c_a^L\) and \(c_a^0\le c_a^R \), which implies that

$$\begin{aligned} \sum _{i=1}^{t}{w_{ai}}\le & {} \bar{\pi }_{k-1, k-1+p_a}-\bar{\pi }_{k, k+p_a} , \end{aligned}$$
(1)
$$\begin{aligned} \sum _{i=1}^{t}{w_{ai}}\ge & {} \bar{\pi }_{k, k+p_a}-\bar{\pi }_{k+1, k+1+p_a}. \end{aligned}$$
(2)

However, it violates the property of decreasing concave time slot cost. Therefore, inequalities (1) and (2) cannot hold at the same time, which contradicts our assumption. \(\square \)

Since for each job j and each k holds that \(\pi _{k}-\pi _{k+p_j}<\pi _{k+1}-\pi _{k+p_j+1}\), we can find a proper \(k{^\prime }_j\) such that \(\pi _{k{^\prime }_j+1}-\pi _{k{^\prime }_j+p_j+1}\ge w_j\ge \pi _{k{^\prime }_j}-\pi _{k{^\prime }_j+p_j}\). Let \(c_j^0\) denote the cost when job j starts at time \(k{^\prime }_j\). Let \(c_j^L\) and \(c_j^R\) denote the cost when job j starts at time \(k{^\prime }_j-1\) and \(k{^\prime }_j+1\), respectively. We have \(c_j^0-c_j^L\ge 0\) and \(c_j^0-c_j^R\ge 0\) (the details are shown in the proof of Lemma 5), which means that the cost will be reduced if we can change the schedule of this job, no matter earlier or later. We call such \(k{^\prime }_j\) as job j’s worst starting time.

Lemma 5

In the optimal schedule, if job j starts before its worst starting time \(k_j{^\prime }\), then there is no idle time before it; if job j starts after its worst starting time \(k_j{^\prime }\), then there is no idle time after it; if job j starts at its worst starting time \(k{^\prime }_j\), then there is no idle time before and after it.

Proof

By Lemma 4, we can see that no job can be adjacent to two idle time slots at both ends. As shown in the proof of Lemma 4 we have \(c_j^0-c_j^L=w_j-(\pi _{k}-\pi _{k+p_j})\) and \(c_j^0-c_j^R=(\pi _{k+1}-\pi _{k+p_j+1})-w_j\) for a job j starting at time k.

We now focus on the cost caused by each job when this job’s starting time is before or after its worst starting time. There are three cases where we redefine our notation as follows.

  • If job j starts at \(k{^\prime }_j\), then we denote the cost of job j as \(c_j^0\).

  • If job j starts x time slots earlier than \(k{^\prime }_j\), then we denote this cost as \(c_j^L(x)\).

  • If job j starts y time slots later than \(k{^\prime }_j\), then we denote this cost as \(c_j^R(y)\).

Comparing \(c_j^0\) with \(c_j^L(x)\), we can find that

$$\begin{aligned}&c_j^0-c_j^L(x)\\&\quad =w_j\cdot x-\sum _{i=1}^x \pi _{k{^\prime }_j-x+i}+\sum _{i=1}^x \pi _{k{^\prime }_j+p_j-x+i}\\&\quad =w_j\cdot x-\sum _{i=1}^x \left( \pi _{k{^\prime }_j-x+i}-\pi _{k{^\prime }_j+p_j-x+i}\right) . \end{aligned}$$

Because \(w_j\ge \pi _{k{^\prime }_j}- \pi _{k{^\prime }_j+p_j}>\pi _{k{^\prime }_j-1}-\pi _{k{^\prime }_j+p_j-1}>\cdots >\pi _{k{^\prime }_j-x+1}-\pi _{k{^\prime }_j+p_j-x+1}\), we can see that \(c_j^0-c_j^L(x)\) is always nonnegative and the value of \(c_j^0-c_j^L(x)\) is increasing with respect to the index x, which means that, if job j is started before its worst starting time, then it is optimal to start it as early as possible.

Similarly, comparing \(c_j^0\) and \(c_j^R(y)\), we can see that

$$\begin{aligned}&c_j^0-c_j^R(y)\\&\quad =-w_j\cdot y+\sum _{i=1}^y \pi _{k{^\prime }_j+i}-\sum _{i=1}^y \pi _{k{^\prime }_j+p_j+i}\\&\quad =-w_j\cdot y+\sum _{i=1}^y \left( \pi _{k{^\prime }_j+i}-\pi _{k{^\prime }_j+p_j+i}\right) . \end{aligned}$$

Because \(w_j\le \pi _{k{^\prime }_j+1}-\pi _{k{^\prime }_j+p_j+1}<\pi _{k{^\prime }_j+2}-\pi _{k{^\prime }_j+p_j+2}<\cdots <\pi _{k{^\prime }_j+y}-\pi _{k{^\prime }_j+p_j+y}\), we can see that \(c_j^0-c_j^R(y)\) is also nonnegative and increases with respect to the index y, which means that, if job j is started after its worst starting time, then it is optimal to start it as late as possible. Hence if a job j starts after its worst starting time in an optimal schedule, then it is impossible to have idle time directly after job j.

If job j is started at its worst starting time in the optimal schedule, then we can see that there should be no idle time slots before and after it. Otherwise, we can start job j either earlier or later to decrease the total cost. \(\square \)

According to the above properties, we can see that, in an optimal schedule, the jobs are partitioned into two groups. The first group starts from time zero, the second group ends at time K, and idle time only exists between these two groups. In addition, the jobs belonging to the same group must be processed in WSPT order. Such an observation leads to the following dynamic programming algorithm, where the jobs are sorted in nonincreasing order of w / p, i.e., \(\frac{w_1}{p_1}\ge \frac{w_2}{p_2}\ge \cdots \ge \frac{w_n}{p_n}\).

Consider a subproblem with jobs 1 to m under the condition that the first group ends at time x and the second group ends at time \(K_0\). Let \(f(x,m,K_0)\) be the minimum total cost corresponding to the above subproblem. Then the second group should start at time \(K_0-(\bar{p}_{m} - x)\). Due to the WSPT property, job m is the last job of either the first or second group. Hence, we have the following recursion, \(f(x,m,K_0)\)

$$\begin{aligned} =\min \left\{ \begin{array}{l} f(x-p_m,m-1,K_0) + w_m \cdot x + \bar{\pi }_{x-p_m, x}, \\ f(x,m-1,K_0-p_m) + w_m \cdot K_0 + \bar{\pi }_{K_0-p_m, K_0} \end{array}\right. \end{aligned}$$

with boundary conditions

$$\begin{aligned} f(x,m,K_0)=+\infty , if \left\{ \begin{array}{l}x<0 \\ x> \min \{K_0, \bar{p}_m\}\\ K_0>K \\ \bar{p}_m >K_0 \end{array}\right. \end{aligned}$$

The initial conditions are

$$\begin{aligned} f(x,1,K_0)\!=\!{\left\{ \begin{array}{ll} w_1\cdot K_0+ \bar{\pi }_{K_0-p_1,K_0}&{} \text {if } x=0 \text{ and } K_0 \le K\\ w_1\cdot p_1+ \bar{\pi }_{0,p_1}&{} \text {if } x=p_1 \le K_0\\ \infty &{} \text {otherwise }\\ \end{array}\right. } \end{aligned}$$

The total cost of the optimal schedule corresponds to the minimum value of f(x, n, K), i.e., \(\min _{x}\{ f(x,n,K ) |\) \(x=0,1,\ldots ,P \}.\) In the dynamic programming, the range of m is in O(n) and the ranges of x and \(K_0\) are in O(P) and O(K), respectively. Each \(f(x,m,K_0)\) is evaluated in constant time. Therefore, the time complexity is O(nPK).

We summarize the result in this case as the following theorem.

Theorem 2

If the time slot cost function is decreasing concave with respect to time k, then in an optimal schedule the jobs are partitioned into two groups. The first part starts from time zero, the second part ends at time K, and idle time only exists between these two groups. In addition, the jobs belonging to the same part must be processed in WSPT order. The optimal schedule can be computed by dynamic programming in O(nPK) time.

If the time slot costs are represented as a series of K discrete values, then the input size of the time slot cost is in O(K), which means that the algorithm with O(nPK) running time is a polynomial-time algorithm because the total processing time P is no larger than K. If the time slot costs are represented as a function of time t, then the above algorithm is pseudo-polynomial. It is not known whether there is an algorithm that can find the optimal schedule in polynomial time if the input does not specify the time slot cost for each time slot individually. We leave it as an open question.

4 Decreasing convex time slot cost

In this case, the cost differences between successive time slots become smaller with respect to the time index k, i.e., \(\pi _{k}-\pi _{k+1}<\pi _{k-1}-\pi _{k}\) for \(1<k<K\), which implies that \(\pi _{k}-\pi _{k+p_j}<\pi _{k-1}-\pi _{k+p_j-1}\) for any j. This case is different from the previous cases in that an optimal solution may have multiple intervals of idle times.

Suppose that a job j starts at time k. Then its cost is

$$\begin{aligned} c_j^0=w_j(k+p_j)+(\pi _{k+1}+\cdots +\pi _{k+p_j}). \end{aligned}$$

If we process this job one time slot earlier or later, the new costs are \(c_j^L\) and \(c_j^R\), respectively, where

$$\begin{aligned} c_j^L= & {} w_j(k+p_j-1)+(\pi _{k}+\cdots +\pi _{k+p_j-1}),\\ c_j^R= & {} w_j(k+p_j+1)+(\pi _{k+2}+\cdots +\pi _{k+p_j+1}). \end{aligned}$$

Notice that \(c_j^0-c_j^L=w_j-(\pi _{k}-\pi _{k+p_j})\) and \(c_j^0-c_j^R=(\pi _{k+1}-\pi _{k+p_j+1})-w_j\). Because \(\pi _{k}-\pi _{k+p_j}>\pi _{k+1}-\pi _{k+p_j+1}\), we can find a proper \(k^*_j\) such that \(\pi _{k^*_j}-\pi _{k^*_j+p_j}\ge w_j > \pi _{k^*_j+1}-\pi _{k^*_j+p_j+1}\). If job j starts at time \(k^*_j\), then we have \(c_j^0-c_j^L\le 0\) and \(c_j^0-c_j^R<0\). Hence, we call such \(k^*_j\) as job j’s preferred starting time and the time interval \([k^*_j, k^*_j+p_j]\) as job j’s preferred processing interval.

Finding out all jobs’ preferred starting times and preferred processing intervals could help us get properties of the optimal schedule. Similarly, we explore a job’s cost when its starting time is before or after its corresponding preferred starting time. For job j with preferred starting time \(k^*_j\), we consider the following three costs.

  • If job j starts at \(k^*_j\), then we denote the cost of job j as \(c_j^0\).

  • If job j starts x time slots earlier than \(k^*_j\), then we denote this cost as \(c_j^L(x)\).

  • If job j starts y time slots later than \(k^*_j\), then we denote this cost as \(c_j^R(y)\).

Comparing \(c_j^0\) with \(c_j^L(x)\), we can find that

$$\begin{aligned}&c_j^0-c_j^L(x)\\&\quad =w_j\cdot x-\sum _{i=1}^x \pi _{k^*_j-x+i}+\sum _{i=1}^x \pi _{k^*_j+p_j-x+i}\\&\quad =w_j\cdot x-\sum _{i=1}^x \left( \pi _{k^*_j-x+i}-\pi _{k^*_j+p_j-x+i}\right) . \end{aligned}$$

Because \(w_j\le \pi _{k^*_j}- \pi _{k^*_j+p_j}<\pi _{k^*_j-1}-\pi _{k^*_j+p_j-1}<\cdots <\pi _{k^*_j-x+1}-\pi _{k^*_j+p_j-x+1}\), we can see that \(c_j^0-c_j^L(x)\) is always non-positive and the value of \(c_0-c_L(x)\) is decreasing with respect to the index x, which means that the earlier job j is processed, the more cost this job will have, as long as its starting time is before its preferred starting time.

Similarly, we can compare \(c_j^0\) and \(c_j^R(y)\) and get

$$\begin{aligned}&c_j^0-c_j^R(y)\\&\quad =-w_j\cdot y+\sum _{i=1}^y \pi _{k^*_j+i}-\sum _{i=1}^y \pi _{k^*_j+p_j+i}\\&\quad =-w_j\cdot y+\sum _{i=1}^y \left( \pi _{k^*_j+i}-\pi _{k^*_j+p_j+i}\right) . \end{aligned}$$

Because \(w_j> \pi _{k^*_j+1}-\pi _{k^*_j+p_j+1}>\pi _{k^*_j+2}-\pi _{k^*_j+p_j+2}>\cdots >\pi _{k^*_j+y}-\pi _{k^*_j+p_j+y}\), we can see that \(c_j^0-c_j^R(y)\) is always non-positive and the value of \(c_j^0-c_j^R(y)\) is decreasing with respect to the index y, which means that the later job j is processed, the more cost this job will have as long as its starting time is after its preferred starting time. Hence we have the following lemma.

Lemma 6

If job j starts before its preferred starting time \(k^*_j\), then the earlier it is processed, the more cost it will have; if job j starts after its preferred starting time \(k_j^*\), then the later it is processed, the more cost it will have; if job j starts at its preferred starting time \(k^*_j\), then it will have the least possible cost.

If every job can feasibly start at its preferred time without any overlap, then such a schedule will be optimal. In most problems, this is not the case. Hence an algorithm is needed to resolve the overlaps.

Lemma 7

If two jobs’ preferred processing intervals do not completely contain each other, then the job with earlier preferred starting time has a greater ratio of \(\frac{w}{p}\) than the other job.

Proof

Without loss of generality, assume that two jobs, \(J_1\) and \(J_2\), have preferred starting times \(k^*_1<k^*_2\), and their preferred processing intervals do not completely contain each other, i.e., \(k^*_1+p_1< k^*_2+p_2\). We want to prove that \(\frac{w_1}{p_1}>\frac{w_2}{p_2}\).

By the definition of preferred starting time, we have the following two inequalities.

$$\begin{aligned} \pi _{k^*_1+1}-\pi _{k^*_1+p_1+1}< w_1\le & {} \pi _{k^*_1}-\pi _{k^*_1+p_1} \end{aligned}$$
(3)
$$\begin{aligned} \pi _{k^*_2+1}-\pi _{k^*_2+p_2+1}< w_2\le & {} \pi _{k^*_2}-\pi _{k^*_2+p_2} \end{aligned}$$
(4)

There are two cases to be considered. The first case is \(p_1\le p_2\). The second case is \( p_1 >p_2\).

Case 1 \(p_1 \le p_2\). We get the following deductions.

$$\begin{aligned} \frac{w_1}{p_1}> & {} \frac{\pi _{k^*_1+1}-\pi _{k^*_1+p_1+1}}{p_1} \end{aligned}$$
(5)
$$\begin{aligned}\ge & {} \frac{\pi _{k^*_2}-\pi _{k^*_2+p_1}}{p_1}\end{aligned}$$
(6)
$$\begin{aligned}> & {} \frac{\pi _{k^*_2}-\pi _{k^*_2+p_2}}{p_2} \end{aligned}$$
(7)
$$\begin{aligned}\ge & {} \frac{w_2}{p_2} \end{aligned}$$
(8)

which implies that \(\frac{w_1}{p_1}>\frac{w_2}{p_2}\).

Inequality (5) comes from Inequality (3). Inequality (6) holds because \(k^*_1<k^*_2\) and the decreasing convex time slot cost. Inequality  (7) holds because \(p_1 \le p_2\) and the decreasing convexity time slot cost. Inequality (8) is derived from Inequality (4) directly.

Case 2 \(p_1 > p_2\). we get the following inequalities.

$$\begin{aligned} \frac{w_1}{p_1}> & {} \frac{\pi _{k^*_1+1}-\pi _{k^*_1+p_1+1}}{p_1} \end{aligned}$$
(9)
$$\begin{aligned}> & {} \frac{\pi _{k^*_1+p_1+1-p_2}-\pi _{k^*_1+p_1+1}}{p_2} \end{aligned}$$
(10)
$$\begin{aligned}\ge & {} \frac{\pi _{k^*_2}-\pi _{k^*_2+p_2}}{p_2} \end{aligned}$$
(11)
$$\begin{aligned}\ge & {} \frac{w_2}{p_2} \end{aligned}$$
(12)

which also implies that \(\frac{w_1}{p_1}>\frac{w_2}{p_2}\).

Inequality (9) comes from Inequality (3), and Inequality (12) is derived from Inequality (4) directly. Now we discuss how the other inequalities can be derived.

Notice that the interval \([k^*_1+1,k^*_1+p_1+1]\) completely contains the interval \([k^*_1+p_1+1-p_2, k^*_1+p_1+1]\) since they have the same end point and \(p_1 > p_2\). Combining with decreasing convex time slot cost, we can get Inequality (10). Because the two jobs’ preferred processing intervals do not completely contain each other, i.e., \(k^*_1+p_1< k^*_2+p_2\), we have \(k^*_1+p_1+1-p_2< k^*_2+p_2+1-p_2=k^*_2+1\), which implies \(k^*_1+p_1+1-p_2 \le k^*_2\). With decreasing convex time slot cost, we can see that Inequality (11) holds. \(\square \)

The above lemma gives the relationship between the ratio \(\frac{w}{p}\) and the preferred starting time. Although in general decreasing convex cases, not all the jobs can start at their preferred starting times, this relationship can still help us get some useful properties as shown in the following lemma.

Lemma 8

The jobs are scheduled in WSPT order in the optimal solution.

Proof

In the optimal solution, the jobs must be processed in several intervals.

First, we consider the jobs processed in the same interval. Because of the optimality, these jobs must be processed by WSPT order in each interval.

Next, we consider jobs in different intervals. Choose any two successive intervals A and B such that A is before B and there are only some idle time slots between A and B. Suppose that job i is processed at the end of interval A and job j is processed at the beginning of interval B. Because of the optimality, job i will not gain benefit if it is processed later, and job j will not gain benefit if it is processed earlier. Hence we can see that job i starts no earlier than its preferred starting time and job j starts no later than its preferred starting time. Since there are time slots between job i and job j, they must have no overlap even if they both start at their preferred starting times. Applying Lemma 7, we can see that job i has larger value of \(\frac{w}{p}\), which means that \(\frac{w_i}{p_i}>\frac{w_j}{p_j}\).

From the above analysis, we can see that job i has the smallest value of \(\frac{w}{p}\) among all the jobs in interval A and job j has the largest value of \(\frac{w}{p}\) among the jobs in interval B. Hence jobs in different intervals are also processed in WSPT order. \(\square \)

Lemma 8 shows the processing order of jobs in the optimal solution. The only remaining task is to decide where idle time slots are. The following lemma will give some properties about the positions of idle time slots.

Lemma 9

If two jobs are successive in WSPT order and their preferred processing intervals have overlap, then there exist no idle time slots between these two job in the optimal solution.

Proof

Consider job i and job j which are successive in WSPT order and whose preferred processing intervals have overlap. Without loss of generality, we assume that \(\frac{w_i}{p_i}\ge \frac{w_j}{p_j}\). Because their preferred processing intervals have overlap, the width between their preferred starting times is shorter than the processing time of job i. From Lemma 8, we can see that these two jobs must be successive in the optimal solution.

Then we prove this lemma by contradiction. Suppose that there are idle time slots between job i and job j in the optimal solution. Because of the optimality, the preferred starting time of job i is no later than the current starting time of job i, otherwise job i could gain benefit by moving several time slots later. By the same reason, the preferred starting time of job j is no earlier than the current starting time of job j. Hence the width between these two preferred starting times is longer than the processing time of job i, which contradicts our assumption that these two jobs’ preferred processing intervals have overlap.

Therefore, once two successive jobs’ preferred processing intervals have overlap, there exist no idle time slots between these two jobs in the optimal solution. \(\square \)

By Lemmas 8 and 9, we can use Algorithm 2 to find the optimal schedule for the case with the decreasing convex cost.

figure b

Because of Lemma 9, we can see that once two successive jobs in WSPT order have overlap on their preferred processing intervals, they will be processed one after another without idle time slots between them. Hence we can consider such two jobs as a new composite job whose weight is the sum of the two jobs’ weights, and the processing time is the sum of the two jobs’ processing times. Such composite job also has a preferred starting time and a preferred processing interval. Notice that the new composite job’s ratio \(\frac{w}{p}\) is just between the two ratios of the original two jobs. Hence replacing such two jobs with the new composite job will not change the ratio order in stack S. Since step c in each while loop will decrease the number of jobs, there will be at most n jobs in stack S. Hence step b and step c will be run for at most O(n) times, and the running time for step a and step d are also O(n).

If the cost for each time slot is given as a function of time, then we can compute the preferred processing interval for each job in constant time. The first step needs \(O(n\log n)\) time to sort these n jobs, and the remaining steps take up to O(n) time to deal with the stack. Hence the overall time complexity is \(O(n\log n)\), which is polynomial in the input size.

If the cost for each time slot is given as a discrete number, then computing preferred processing interval for each job requires \(O(\log n)\) time by binary search. Step 2 takes \(O(n\log K)\) time to find all the preferred processing intervals, while remaining steps takes up to \(O(n\log n)\) time. Hence the overall time complexity is \(O(n\log K)\), which is also polynomial in the input size because we have at least K costs in the input.

Hence we have the following theorem.

Theorem 3

If the time slot cost function is decreasing convex with respect to time k, then Algorithm 4 can compute the optimal schedule in \(O(n\log n)\) if the cost for each time slot is given as a function of time and in \(O(n\log K)\) if the cost is given individually for each time slot.

5 The general case

When the time slot cost is arbitrarily non-increasing with respect to the time index k, it is strongly NP-hard to find an optimal schedule. The strong NP-hardness can be proved by a reduction from 3-PARTITION, a well known NP-complete problem in the strong sense.

3-PARTITION problem: Given positive integers \(a_1,\ldots , a_{3q}\) and b with \(\frac{b}{4} < a_j < \frac{b}{2}\), \(j = 1,\ldots , 3q\) and \(\sum _{j=1}^{3q}{a_j}=q\cdot b\), do there exist q pairwise disjoint three element subsets \(S_i\subset \{1,\ldots ,3q\}\) such that \(\sum _{j\in S_i}{a_j}=b\) for \(i=1,\ldots ,q\)?

Theorem 4

The problem with arbitrary non-increasing time slot cost is NP-hard in the strong sense.

Proof

Given an instance of 3-PARTITION, we construct a corresponding instance of the decision version of our scheduling problem.

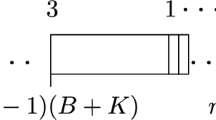
Let there be \(n=3q\) jobs. The j-th job has processing time \(a_j\) and weight \(w_j=\varepsilon \cdot a_j\) for \(j=1,\ldots ,n\). Here \(\varepsilon \) is a positive number. Let the planning horizon be \(K=q\cdot (b+1)\). The cost of the k-th time slot is defined as follows, as shown in Fig. 1,

$$\begin{aligned} \pi _k = \left\{ \begin{array}{ll} (q\cdot (b+1)+2-k)\epsilon , &{} k\!=\! t\cdot (b+1), t=1,\ldots ,q\\ (q\cdot (b+1)+1-k)\epsilon , &{} \mathrm{otherwise}\\ \end{array} \right. \end{aligned}$$

where we refer to slots \(b+1, 2(b+1),\ldots ,q\cdot (b+1)\) as “special” time slots. Note that the above construction can be done in O(nb) time. Since 3-Partition is strongly NP-hard, even all of its numerical parameters are bounded by a polynomial in the length of the input (Garey and Johnson 1978). We can assume that b is bounded by a polynomial in the length of the input, hence our instance construction can be done in polynomial-time.

Fig. 1
figure 1

Demonstration for the proof of Theorem 4

Full size image

Let \(z=\sum _{j=1}^n(\sum _{i=1}^{a_j}{\pi _i}+w_j\cdot a_j)\). Because \(w_j=\epsilon p_j\), we have \(\frac{w_j}{p_j}=\epsilon \) which is just the cost difference between any two adjacent time slots in the intervals that exclude the “special” time slots. By Lemma 2, we can see that each job j will have the same cost as long as its processing interval excludes those “special” time slots. Therefore we can calculate the cost for job j as \(\sum _{i=1}^{a_j}{\pi _i}+w_j\cdot a_j\), which is the cost when job j is processed from the first time slot. The value of z corresponds to the total cost when all the jobs’ processing intervals exclude those “special” time slots. The question asks whether there exists a schedule such that the total cost is no more than the threshold value z.

We have the following important observation. The time slot cost is almost linearly decreasing with time, except for those special time slots. Because \(w_j/p_j = \varepsilon \) for any job j, by Lemma 2, we know that a job will have the same cost as long as its processing interval does not include any special time slot. Since each job has processing time no more than \(\frac{b}{2}\) and the interval between two successive special time slots is b, the processing interval of each job could include at most one special time slot. If some job is processed during some special time slot, then its cost will be \(\varepsilon \) more than the case that the job’s processing interval excludes the special time slot.

We claim that the 3-PARTITION instance has a YES solution if and only if the scheduling instance has a solution with total cost no more than \(\sum _{j=1}^n\Big (\sum _{i=1}^{p_j}{\pi _i}+w_j\cdot p_j\Big )\).

First, assume that the 3-PARTITION instance has a YES solution. Then we can schedule each group of three jobs in one of the q intervals \([(t-1)(b+1),t\cdot (b+1)-1]\), \(t=1,\ldots ,q\), leaving all the q special time slots idle. Since no job is processed during the special time slot, their costs can be expressed as \(\sum _{i=1}^{p_j}{\pi _i}+w_j\cdot p_j\) for \(j=1,\ldots , n\), which is just the cost when the job starts at the first time slot. Calculating the total cost of this schedule, we can see that it is just \(\sum _{j=1}^n\Big (\sum _{i=1}^{p_j}{\pi _i}+w_j\cdot p_j\Big )=z\).

Then assume that the scheduling instance has a solution such that the total cost is no more than z. According to the analysis above, we can see that all the idle time slots must be the q special time slots. Since \(K=q\cdot (b+1)\) and the total processing time is qb, all the jobs are processed in the q intervals \([(t-1)(b+1),t\cdot (b+1)-1]\), \(t=1,\ldots ,q\). Note that all the intervals \([(t-1)(b+1),t\cdot (b+1)-1]\) have length b. Because each job has its processing time between \(\frac{b}{4}\) and \(\frac{b}{2}\), and no preemption is allowed, there must exist three jobs in each interval. This means that 3-PARTITION problem has a YES solution.

When all the parameters of our scheduling instance are bounded by a polynomial in the length of the input, the reduction still holds, which proves the NP-hardness in the strong sense. \(\square \)

6 Conclusion

This paper focuses on the problem of minimizing the total weighted completion time on a single machine with variable time slot costs. The results answer an open question in the literature. Scheduling with variable time slot costs is a new and practically relevant scheduling model that deserves more in-depth study. So far only the very basic problems have been addressed. More research on extended models, such as with release times, is worth investigating in the future.