1 Introduction

For pure scientific purposes, it is usually considered best and sufficient to classify earthquake size solely according to the physically defined seismic moment M 0, or to the product between rupture area and average slip, termed seismic potency P. However, both M 0 and P are pure static measures of earthquake size, i.e. of the earthquake’s cumulative tectonic effect. For seismic hazard and risk assessment, more relevant would be the knowledge of the amount of radiated seismic wave energy E S, of its high-frequency content in particular. E S is closely related to stress drop and rupture velocity, i.e. to the rupture dynamics and kinematics and the related earthquake strength in terms of its potential of cause shaking damage. Therefore, the complementary determination and joint assessment of both M 0 and E S is particularly useful for a more realistic quantification and assessment of the actual type of seismic or tsunami hazard (e.g., Newman and Okal 1998; Choy and Kirby 2004; Bormann and Di Giacomo 2011). Yet, there is a great disadvantage for practical application, early warning of people at risk included, of these linear earthquake size and strength classifiers. For relevant damaging earthquakes, when expressed in common physical international standard (SI) units for energy (Joule) and moment (Newton-metre), the latter reach numbers in the range from terra (1012) to yotta (1024) and even 107 times more in centimetre-gram-second (cgs) units, till now still widely used in the USA. Such astronomical numbers are hardly comprehensibly and tractable for both ordinary people and decision-makers. This makes them not suitable for public information, guiding rapid and widely accepted disaster assessment and response actions or for calculating and communicating generally understandable seismic activity and probability of reoccurrence rates.

Therefore, the physical measures M 0 and E S have been scaled to empirically derived logarithmic magnitude classifiers. Values of the latter vary in about the same range as the realistically discernible and thus relevant degrees of macroseismic intensities and related perceptibility and damage patterns or as the fractions of strong-motion ground accelerations in terms of earth gravity g. No wonder that the Global Earthquake Model (GEM) initiative insisted to get from the International Seismological Center (ISC) as a deliverable of particular importance for their efforts to improve probabilistic seismic hazard assessment on a global scale a homogenized Global Instrumental Earthquake Catalogue (1900–2009). It classifies earthquake size magnitude-wise solely according to moment magnitude M w, also for events for which no direct M 0 measurements were available (Storchak et al. 2015). Then proxy estimates of M w via classical magnitudes had to be made (Di Giacomo et al. 2015). But the problem is that there exist several empirical magnitude scales. They are based on different types of seismic waves and ranges of periods measured. Therefore, it is not a trivial question to decide to which type of magnitude M 0 and E S should be scaled best in order to derive meaningful and reasonably reliable conversion relationships and with which purpose in view. This will be illustrated in this paper by way of scaling logE S data and thus M e either to teleseismic surface or body-wave magnitudes.

First, the paper looks critically into the history of tackling these problems. It also investigates whether the currently common formulas to scale M 0 and E S to magnitude are still appropriate and backed by standardized modern data. In fact, the original intermagnitude and magnitude-energy relationships used as well as some of the parameter assumptions made when deriving the formulas for calculating M w and M e are based on not well-constrained data sets, or questionable for some other reasons. The new data presented here have been measured according to recently adopted and in future to be applied International Association of Seismology and Physics of the Earth’s Interior (IASPEI) magnitude measurement standards. Moreover, these data have been regressed with more appropriate statistical procedures than most of the classical relationships. The agreement between the magnitude relationships derived on the basis of old and new data is of different quality. It is better for M w than for M e. By far the best correlation exists, however, as reasoned already by Gutenberg (1956), when scaling logE S to the new IASPEI (2005, 2013) broadband body-wave magnitude m B(BB). The latter is based, with slight modifications, on Gutenberg (1945a, b) original medium- to long-period body-wave magnitude concept and thus an important complement to the dominating narrow-band short-period m b since the mid 1970s. Reasons for discrepancies between old and new relationships for scaling M 0 and E S to magnitude and recommendable actions will finally be discussed.

2 History

In the 1970s, Kanamori was interested in estimating the seismic energy E S released in great earthquakes with rupture lengths of 100 km or more. At that time, neither E S nor seismic moment data M 0 based on direct high-quality instrumental recordings were available en masse. The M 0 values available to Kanamori had mostly been estimated using long-period body waves, surface waves, very long-period free oscillations and geodetic data. In the absence of such data, M 0 of great earthquakes was derived via estimates of the area and slip of surface rupturing events and/or inferred from the 100-s magnitudes determined by Brune and Engen (1969).

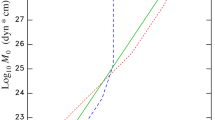
Kanamori and Anderson (1975) had shown via dimension analysis that 20-s surface wave magnitudes M S scaled for values between about 6.5 and 8 rather well with M 0 but that M S tends to saturate for much larger M 0 values. Therefore, Kanamori (1977) proposed a “work magnitude” M w scaled to and conceived as a linear extension of the not yet saturated M S. Pursuing this, he assumed an average shear modulus μ in the crust and upper mantle of about 3–6 × 104 MPa and, according to Kanamori and Anderson (1975) and Abe (1975), a more or less constant stress drop Δσ of large earthquakes ranging between about 2 and 6 MPa. With such values, Kanamori (1977) and Hanks and Kanamori (1979) arrived—via the Wyss and Brune (1968) relationship E S/M 0 = Δσ/2μ = apparent stress τ a/μ—at E S ≈ M 0/(2 × 104). This agreed on average reasonably well with the few scattering E S-M 0 data available at that time (Fig. 1).

Fig. 1
figure 1

Relations between seismic moment M 0 and energy E S for shallow and deep earthquakes (according to Vassiliou and Kanamori 1982). The solid line indicates the relation E S = M0/(2 × 104), suggested by Kanamori (1977) on the basis of elastostatic considerations. Note that the real data may deviate from it by ±1 order or even more. Copy from Kanamori 1983, Tectonophysics, Vol. 93, p. 191, with permission from Elsevier Science

Full size image

Inserting this E S-M 0 relation into the relationship proposed by Richter (1958) between E S and surface-wave magnitude Ms measured at periods around 20 s, which reads, when corrected for a typo,

$$ \log {E}_{\mathrm{S}}=1.5{M}_{\mathrm{S}}+4.8, $$
(1)

it follows

$$ \log {M}_0=1.5{M}_{\mathrm{S}}+9.1, $$
(2)

when E S and M 0 are given here and in the following in SI units Joule J and Newton-metre Nm, respectively.

When substituting in (2) M S by M w and resolving it for M w yields, then the definition formula for M w calculations is

$$ {M}_{\mathrm{w}}=\left( \log {M}_0\hbox{--}\ 9.1\right)/1.5=\left(2/3\right)\left( \log {M}_0\hbox{--} 9.1\right) $$
(3)

This way of writing has been accepted by IASPEI (2005, 2013) as the standard form. I has been derived by strictly following Kanamori’s way of reasoning but without prior resolving (3) and then rounding the constant with a different degree of precision. In contrast to various slightly different published M w formulas, e.g. formulas (4) to (6) in Hanks and Kanamori (1979), there all given in units of dyne centimetre, (3) yields unambiguous results. Reasons of the IASPEI Working Group on magnitude measurements in favour of (3) have been outlined by Bormann and Dewey (2014):

The order of operations in the right-hand sides of equations for Mw, subtraction prior to division by 1.5, respectively multiplication by 2/3, avoids an ambiguity that arises if this operation is performed prior to subtraction, which in a certain percentage of cases leads to Mw being different according to whether the moment is expressed in CGS or SI units (Utsu 2002).

The effect of rounding the constant in the resolved formula (3) to one or two decimal places may lead in some cases to a difference of 0.1 magnitude units (m.u.) in the derived magnitude values. Therefore, Bormann and Choy (personal correspondence 2007) also agreed on the same way of standardized writing of the energy magnitude relationship [see formula (8)] instead of the earlier used expanded version with the constant rounded-off to one decimal place, i.e. M e = (2/3) logE S-2.9.

Both the US National Earthquake Information Center (NEIC) and the Global Centroid Moment Tensor (GCMT) Project (http://www.globalcmt.org) adopted (3) but with units in dyn cm. On the GCMT search front page, this change is commented as follows:

The moment magnitude is calculated by this software using the formula of Kanamori (1977), MW = (2/3) · (log M0 - 16.1), where M0 is given in units of dyne-cm. Prior to February 1, 2006, the quantity (2/3)*16.1 was rounded to the value 10.73. For a small number of earthquakes, searches conducted after 2006/02/01 will give values for MW that differ by 0.1 magnitude unit from values given by searches prior to 2006/02/01.

In the following, we will relate only to the standard M w relationship (3) and the respective M e relationship (8) in SI units. M w, although developed as a very adequate non-saturating magnitude scale for great earthquakes, is—because of its linear relationship with logM 0—also suitable for M w determinations down to very small earthquakes, consistent and compatible M 0 determination provided. The same holds for the M e formula (8). Regrettably, however, so far neither the procedures for M 0 nor those for E S determination are standardized. They may differ significantly depending on observations made in the teleseismic, regional or local range (Lolli et al. 2014) and on earthquake size, duration and complexity (e.g. Tsai et al. 2005), whether the records are analysed in the frequency or time domain (Edwards and Fäh 2013) and in which magnitude-dependent period range (Stein and Okal 2005), and corrected, or not, for empirically confirmed or theoretically expected biases (Boatwright and Choy 1986 and discussion below). This may lead to incompatible results for equal events, with differences up to several tenths of magnitude units but all being labelled as “M w”. To avoid confusion and misinterpretation of such data, a unique specification of magnitude nomenclature is urgently required. Therefore, we flag in the following magnitude values of equal type differently when they have been produced by different institutions with different procedures. But with respect to M w, only GCMT data are considered. They are based on a consistent centroid moment tensor inversion procedure according to Dziewonski et al. (1981) with some recent modifications (Ekström et al. 2012).

Because of

$$ {M}_0=\mu \kern0.5em \overline{D}\kern0.5em S $$
(4)

(with μ—rigidity or shear modulus of the source medium, \( \overline{D} \)—average final displacement after the rupture, S—the surface area of the rupture), M w is principally a pure static measure of earthquake size in terms of the irreversible inelastic deformation in the rupture area. With (1) and (2), the M w formula (3) can be decomposed according to Bormann and Di Giacomo (2011) into the following general formula:

$$ {M}_{\mathrm{w}}=\left( \log {M}_0\hbox{--} \mathbf{a}+\mathbf{b}\right)/\mathbf{c}, $$
(5)

where a is the constant and c the slope in the logE S-M S relation (1) and b the average ratio Θ = log(E S/M 0). According to Kanamori’s (1977) condition E S ≈ M 0/(2 × 104), one gets Θ = −4.3.

In contrast to (1), the only E S-M relationship proposed and authorized by Gutenberg (1956) (see Fig. 2) and jointly also by Gutenberg and Richter (1956) had been

Fig. 2
figure 2

Primary relation between seismic energy E S and the “unified” magnitude m = m B, with E S in units of dyne centimetre, as published first by Gutenberg (1956). Note that this fundamental relationship is just an eye fit through only 21 data points. Copy of Fig. 1 in Gutenberg (1956)

Full size image
$$ \log {E}_{\mathrm{S}}=2.4{m}_{\mathrm{B}}-1.2. $$
(6)

Gutenberg (1945a, b) m B is a medium- to long-period body-wave magnitude, measuring the largest ratio (A/T)max between the displacement amplitude A and period T in the range T = 2 to 20 s (see Abe 1981, 1984). Thus, m B is more closely related to seismic energy release, also of smaller earthquakes, than 20-s M S.

However, with the deployment in the 1960s and 1970s of the World-Wide Seismic Standard Network (WWSSN), which lacked medium-period broadband instrumentation, m B determination was disbanded in western seismological practice. But the obvious benefits of m B, being an important complement to the much earlier saturating short-period m b, let the IASPEI (2005, 2013) Working Group on Magnitude Measurement recommend the reintroduction into global seismological practice of m B as a broadband P wave body-wave magnitude complement, termed m B(BB) (Bormann and Saul 2008; Bormann and Dewey 2014). It is based on direct measurement of the largest velocity amplitude V max = 2π(A/T)max in the period range 0.2 s < T < 30 s and correlates excellent with logE S (Fig. 4).

Note that Eq. (1) has been derived by inserting into (6) the Gutenberg and Richter (1956) relationship between body- and surface-wave magnitudes

$$ {m}_{\mathrm{B}}=0.63{M}_{\mathrm{S}}+2.5. $$
(7a)

Thus, (7a), although not yet well constrained by data, has become the fundamental classical intermagnitude relationships that provided the very basis for the derivation of (3). Therefore, it is important to know that (7a) could be reproduced rather well by orthogonal regression of hundreds of IASPEI standard magnitudes m B(BB) over M S(20) (Bormann et al. 2009):

$$ {m}_{\mathrm{B}}\left(\mathrm{B}\mathrm{B}\right)=0.61{M}_{\mathrm{S}}(20)+2.63\pm 0.24. $$
(7b)

According to (7a) and (7b), m B = M S for 6¾, m B > M S for smaller and m B < M S for larger values.

Two decades later, Choy and Boatwright (1995) were in a better position when proposing the energy magnitude scale M e. They regressed hundreds of E S values, calculated via the integration of squared P wave velocity amplitudes over the whole P wave train in the wide period range between about 1 and 100 s (Boatwright and Choy 1986), over 20-s M S values of the US National Earthquake Information Center (NEIC). M S(20) has been confirmed by IASPEI (2005, 2013) as one of the two standard surface-wave magnitudes, besides the newly proposed velocity broadband version M S(BB). The latter, however, is better tuned than M S(20) to the log(A/T)-based M S calibration function according to Vanĕk et al. (1962), IASPEI standard since 1967, applicable in a much wider range of periods and epicentral distance down to 2°, and differs less than M S(20) from M w for values <6.5 (Bormann et al. 2013; Bormann and Dewey 2014).

Choy and Boatwright (1995) least square fitted the logE S-M S(20) data available to them with a prescribed slope of 1.5, as in (1). Their intention was to assure as far as possible continuity with this widely accepted and applied Richter formula. But for the constant, they then got 4.4, instead of 4.8, as in (1). Substituting in the so revised formula M S by M e and resolving it for M e, they arrived at (when written in the now recommended standard form for better recognition of its origin)

$$ {M}_{\mathrm{e}}=\left( \log {E}_S\hbox{--} a\right)/c=\left( \log {E}_{\mathrm{S}}\hbox{--} 4.4\right)/1.5. $$
(8)

Because of the similar approaches of deriving and scaling M w and M e via M S(20) and due to the ratio Θ = log(E S/M 0) with E S/M 0 = Δσ/2μ, Bormann and Di Giacomo (2011) derived the following general relationship between M e and M w:

$$ {M}_{\mathrm{e}}={M}_{\mathrm{w}}+\left[ \log \left(\varDelta \sigma /2\mu \right)+4.7\right]/1.5={M}_{\mathrm{w}}+\left[ \log \left({E}_{\mathrm{S}}/{M}_0\right)+4.7\right]/1.5. $$
(9)

According to (9), the Choy and Boatwright M e and the Hanks and Kanamori (1979) M w are equal only for log(E S/M 0) = −4.7, i.e. for a lower global average stress drop than the one assumed by Kanamori (1977) and later by Hanks and Kanamori when deriving (3). However, for earthquakes with significantly different stress drop, and thus related kinematic-dynamic source parameters such as rupture velocity and radiation efficiency, M e and M w may differ by about one magnitude unit (m.u.) or even more (Choy and Kirby 2004; Kanamori and Brodsky 2004; Bormann and Di Giacomo 2011; Choy 2011). This illustrates the importance of measuring, as fast as possible, both M w and M e. While the former is just a measure of the cumulative average static tectonic effect of an earthquake, M e is largely controlled by the variable dynamics and kinematics of individual earthquake ruptures. Accordingly, earthquakes of equal M w may have a very different potential for causing either shaking damage or generating a tsunami (e.g., Choy and Kirby 2004; Di Giacomo et al. 2008).

3 Modern data

The above basic relationships, on which the current M w and M e formulas are based, could not or only marginally be reproduced by orthogonally regressing nowadays available directly measured logE S data over standard m B(BB) and M S(20) (see Fig. 3 and for regression procedure Castellaro et al. 2006 and Castellaro and Bormann 2007). logE S(GFZ) has been calculated with an automatic procedure developed at the GFZ German Research Centre for Geosciences, described by Di Giacomo et al. (2008, 2010a, b). It can run in real time and thus be of great benefit in conjunction with near real-time M w data or good proxy estimates of M w in tsunami early warning and related emergency response activities. No corrections for different source radiation patterns are applied to logE S(GFZ). The same applies to m B(GFZ) = m B(BB) according to Bormann and Saul (2008), M S(USGS) = M S(20) or other types of classical catalogued magnitudes such as the Gutenberg m B and M S and the Richter M L or to m b. The plot shows that logE S(GFZ)-m B(BB) data fit rather well whereas the scatter of logE S(GFZ)-M S(USGS) is about twice as large. Also the slopes of the two regressions differ strongly.

None of the GFZ logE S-m B(BB) regression relationships agrees with the respective Gutenberg-Richter formula (6), but the orthogonal logE S(GFZ)-M S(NEIC) relationship agrees almost perfectly with the semi-heuristic Choy and Boatwright (1995) formula. This is not the case, however, for the regression relationships between m B(BB) and M S(20) when compared with the Gutenberg-Richter m B-M S relationship (7) (Bormann et al. 2013).

The methods for M 0 and E S determination are not yet standardized. There exist procedural differences that may lead to different results. LogE S and M e data published by the NEIC are the result of interactive off-line data analysis. They aim at best precision and the use of these data also for geo-diagnostic research problems (e.g. Choy 2011). This goes well beyond the common operational use of magnitude data. Since theory predicts a dependence of energy radiation on the source mechanism (Boatwright and Choy 1986), corrections, for strike-slip earthquakes in particular, are applied to USGS logE S and thus M e values, as soon as final CMT fault plane values are available. But E S data corrected for idealized fault radiation pattern may differ significantly from respective uncorrected GFZ data (Fig. 3), also when calculating Θ = log(E S/M 0) (Fig. 5). Reasons are given below.

Fig. 3
figure 3

Orthogonal standard (OR—solid line), standard (SR—broken line) and inverse standard regression (ISR—dot-hatched line) relationships between logE S(GFZ) over m B(GFZ) (left-hand panel) and 20-s M S(USGS) (right-hand panel); rms root-mean-square data scatter. The E S values are based on broadband records of earthquakes with different source mechanism. The new logE S-magnitude relationships are compared with the original Gutenberg and Richter (1956) logE S-m B relationship (GR, multi-dot hatched line) and the Choy and Boatwright (1995) logE S-M S relationships (C&B, multi-dot hatched line). Compiled from Figs. 3.85 and 3.86 in Bormann et al. (2013), © IASPEI

Full size image

Striking are the systematically larger logE S values for strike-slip events and the generally larger (approximately doubled) data scatter of the USGS relations. The reason may be just the source mechanism corrections which are supposed to improve the accuracy of the data. They are, however, based on idealized theoretical calculations of source radiation and wave propagation. Generally, plane earthquake rupture surfaces and a homogeneous 1-D Earth velocity model with minimum path P wave propagation are assumed. But CMT fault plane solutions are smoothed average representations of the real rupture surface in space. They are derived from wavelengths larger than the rupture itself, thus considering the source as a point and not as a complex finite rupture. Accordingly, they cannot account for fault bending, branching and/or step overs. The orientation and radiation pattern of such non-planar fault segments and other rough rupture irregularities may significantly differ (up to more than 10°) from the calculated average planar fault plane. This may have a significant influence on the actual angular radiation pattern, especially of high-frequency energy s, which is not accounted for by simplified rupture and wave propagation models. Also the Earth medium along the propagation paths is more or less heterogeneous, resulting in scattering and multi-pathing, especially of short-period waves which contribute much to the E S estimates (see the pronounced signal codas in SP records). Therefore, Newman and Okal (1998), Pérez-Campos and Beroza (2001) and Bormann and Di Giacomo (2011) pointed out that the short-period energy will find its way to the stations irrespective of idealized theoretical assumptions. Okal and Talandier (1989) expressed that a “..magnitude concept, which ignores the exact focal geometry, could be a more robust measure of the true size of the event than one correcting for an expected small source excitation, but failing to account for non-geometrical effects”. The rather stable estimation of wave attenuation via coda-Q measurements, independent of the unknown actual source mechanism, is explained by multi-path wave scattering as well. Also Schweitzer and Kværna (1999) could not confirm a significant source mechanism effect for short-period m b.

4 Consequences for the M w and M e formulas

The new data raise the question whether there is a need to revise the current commonly used formulas (3) and (8) for M w and M e estimation. According to Figs. 3 and 4, the following orthogonal regression relationships hold, with RMSO being the rout-mean-square data scatter orthogonal to the linear regression lines:

$$ \log {E}_{\mathrm{S}}\left(\mathrm{G}\mathrm{F}\mathrm{Z}\right) = 1.51{M}_{\mathrm{S}}\left(\mathrm{USGS}\right)+4.51\kern0.37em \mathrm{with}\ \mathrm{RMSO}=0.24 $$
(10)
$$ \log {E}_{\mathrm{S}}\left(\mathrm{USGS}\right)=1.79{M}_{\mathrm{S}}\left(\mathrm{USGS}\right)+2.41\kern0.75em \mathrm{with}\ \mathrm{RMSO}=0.30 $$
(11)
$$ \log {E}_{\mathrm{S}}\left(\mathrm{G}\mathrm{F}\mathrm{Z}\right) = 1.92{m}_{\mathrm{B}}\left(\mathrm{G}\mathrm{F}\mathrm{Z}\right)+1.39\kern0.5em \mathrm{with}\ \mathrm{RMSO}=0.13. $$
(12)

According to Fig. 5, the global average values for Θ are

$$ \varTheta \left(\mathrm{G}\mathrm{F}\mathrm{Z}\right)=-4.6 $$
(13)

and

$$ \varTheta \left(\mathrm{USGS}\right)=-4.8, $$
(14)

respectively. The answer should be based on quantifying the difference between the values derived by the currently used and possible alternative new formulas. Moreover, new formulas should pay credit to the basic intention, methodology and arguments of Kanamori and Choy and recognize, with respect to the derivation of M w, also the quantitatively and qualitatively inferior data available at that time. With this in view, we have first to acknowledge what remains valid and what has changed since the 1970s.According to the ISC-GEM Global Instrumental Earthquake Catalogue (1900–2009), the M S(20) type of magnitude is the longest available and most complete long-period magnitude (Di Giacomo et al. 2015). Therefore, transforming non-saturating M 0 data of great earthquakes into an equivalent magnitude scale by relating M w to M S remains the correct choice. Whether at a later time a scaling to M S(BB) that is measured in the much wider range of periods between 3 s < T < 60 s will be more appropriate may be looked at when masses of standard M S(BB) values are available. But different to Gutenberg’s and early Kanamori’s time, now hosts of both instrumentally measured M 0, E S and thus Θ = log(E S/M 0) values as well as a much better constrained and directly measured logE S-M S relationship are available. When inserting into the general M w formula (5), which reflects best the essence of Kanamori’s approach, the slope and constant of (10) would yield, together with the Θ of (13), as an alternative M w formula

$$ {M}_{\mathrm{w}}=\left( \log {M}_0\hbox{--} 9.11\right)/1.51. $$
(15)

(15) is practically identical with the current standard formula (3) although the constant in (10) and Θ = −4.6 differ more strongly from the respective values assumed by Kanamori. But since the constant in (1), being b in (5), depends on the average value for Θ, being c in (5), their interrelationship balances off this difference. M w values calculated via (15) for logM 0 between about 17 and 23 (i.e. M w ≈ 5.3 to 9.3) differ only within −0.04 and −0.07 m.u. from those calculated via (3). Thus, formula (15) confirms the correctness of the current M w formula within the IASPEI aimed tolerance limits of <0.1 m.u. for different procedures of magnitude estimation. Yet, this also hints to the general correctness of regressing logE S(GFZ) data—which have not been corrected for source mechanism-dependent radiation coefficients—orthogonally over M S(USGS) = M S(20). In contrast, the constants based on orthogonally regressed logE S(USGS) data over M S(USGS) according to Fig. 4 (right) and formula (11) are, together with Θ(USGS) = −4.8, a = 2.41, b = −4.8 and c = 1.79 These values would yield as a new M w formula

$$ {M}_{\mathrm{w}}=\left( \log {M}_0\hbox{--} 7.21\right)/1.79. $$
(16)

M w values calculated via (16) with logM 0 (respectively M w) values in the same range as above would differ from those derived with the current M w standard formula (3) between +0.20 und −0.45 m.u. Such large differences, if accepted as correct, might suggest the need to replace formula (3) by (16). Interestingly, however, the more heuristically derived relationship by Choy and Boatwright (1995)

$$ \log {E}_{\mathrm{S}}=1.5{M}_{\boldsymbol{S}}+4.4, $$
(17)

aimed at preserving the Richter slope of 1.5 for the sake of data continuity, would yield together with the new average Θ(USGS) = −4.8 according to Fig. 5, instead of Kanamori’s (1977) value of Θ = −4.3,

$$ {M}_{\mathrm{w}}=\left( \log {M}_0\hbox{--} 9.2\right)/1.5. $$
(18)
Fig. 4
figure 4

Linear regression relationships between logE S(USGS) over m B(GFZ) (left-hand panel) and logE S(USGS) over 20-s M S(USGS) (right-hand panel), based on broadband records of earthquakes with different source mechanism, and their comparison with the original Gutenberg and Richter (1956) logE S-m B and Choy and Boatwright (1995) logE S-M S relationships (multi-dot hatched lines). For legend of earthquake mechanism symbols, see Fig. 3. Compiled from Figs. 3.85 and 3.86 in Bormann et al. (2013), © IASPEI

Full size image
Fig. 5
figure 5

Comparison between Θ = log(E S/M 0) calculated as the difference between logE S of the US Geological Service (USGS), respectively, logE S(GFZ) and logM 0 according to the Global Centroid Moment Tensor Catalog (GCMT; http://www.globalcmt.org/CMTsearch.html) for earthquakes in the magnitude range 5.5 < M w ≤ 9.0. The different symbols relate to different types of source mechanism, e.g. upright triangles to strike-slip (SS) earthquakes (for detailed legend, see Fig. 3). Note the much larger data scatter of the USGS data set with its distinct separation of SS earthquakes which have been corrected for theoretically expected reduced radiation coefficients according to Boatwright and Choy (1986). Copy of Fig. 3.89 in Bormann et al. (2013), © IASPEI

Full size image

Again, this is very close to (3). (18) yields, on average, M w values that are constantly only 0.07 m.u. smaller than those derived with the current standard formula. Thus, the current M w standard formula is well supported within these error limits by modern instrumentally measured logE S data, better than the currently used M e formula.

With respect to logE S and M e, the following conclusions can be drawn from Figs. 4 and 5:

  • Relationship (10), i.e. when scaling logE S(GFZ) to M S(USGS), yields in the whole considered magnitude range between M S 5.2 and 8.8 values of logE S that are only between +0.16 and +0.20 log units larger than those calculated via (17). This is less than the general uncertainty of energy calculations. According to McGarr and Fletcher (2002), E S released by earthquakes can probably be estimated only within a factor of 2–3 (i.e. within 0.30 to 0.47 log units), if multi-station high-quality seismic broadband data are available. This corresponds to an uncertainty of about 0.2 to 0.3 m.u. in M e.

  • In contrast, when converting M S into logE S via (11), the differences reach for M S = 5.2 and 8.8 already values of −0.42 and +0.56 logE S units, respectively. This is unacceptably large.

  • Thus, the orthogonal regression between logE S(GFZ) and M S(USGS) constrains the Choy and Boatwright (1995) formula (8) much better than the orthogonal regression between logE S(USGS) and M S(USGS) data.

Substituting in the relationships (10) and (11) M S by M e, and resolving them for M e, yields

$$ {M}_{\mathrm{e}}=\left[ \log {E}_{\mathrm{S}}(GFZ)\hbox{--} 4.51\right]/1.51 $$
(19)

and

$$ {M}_{\mathrm{e}}=\left[ \log {E}_{\mathrm{S}}(USGS)\hbox{--} 2.41\right]/1.79 $$
(20)

respectively.

Calculating M e via relationship (19) for logE S values of 12 and 18, i.e. M e between about 5 and 9, yields values that are in this range only between 0.11 and 0.14 m.u. smaller than those calculated with the current M e formula (8). This is acceptable within the uncertainty range of M e determinations, not, however, when calculating M e with (20). Values will then in the considered magnitude range differ from those calculated with (8) between +0.40 and −0.36 m.u. Again it holds that logE S(GFZ) data better justify the current semi-heuristic USGS M e formula than a more correct orthogonal regression of logE S(USGS) data over M S(USGS).

Generally, it holds, however, that E S and M e values are more “noisy” than asymptotic long-period M 0 and thus M w estimates. Reliable energy calculations require inclusion of about one decade of frequencies higher than the corner frequency of the source spectrum (Bormann and Di Giacomo 2011). However, high-frequency waves are more difficult to treat theoretically and much more affected than low-frequency waves by unknown attenuation and velocity heterogeneities along the propagation paths, local site effects in particular.

In conclusion, the current IASPEI standard M w formula according to Kanamori (1977) and the currently common teleseismic M e formula according to Choy and Boatwright (1995), both being scaled to M S(20), yield magnitude values that agree within acceptable limits with alternative orthogonal regression relationships based on almost thousand logE S(GFZ) and USGS M S(20) data as well as on the average of many hundreds of related Θ = log(E SGFZ/logM 0GCMT) values. This, however, is achieved only by not applying source mechanism corrections to logE S(GFZ).

5 Should M e better be scaled to m B(BB)?

The above notwithstanding, it remains the principal question whether it is reasonable at all to scale E S, estimated via the analysis of broadband P wave records, to narrowband long-period 20-s surface wave M S. Would it not be more appropriate and data compatible to compare such E S estimates with m B that is measured too on broadband velocity P wave records in a wide range of periods? The advantage is obvious from Fig. 4. Gutenberg’s (1956) energy-magnitude relationship (Fig. 2) had already been of this type. But such an approach could not be considered at the USGS in the 1980s, because m B determinations had been disbanded at the NEIC in the 1970s. Yet m B(BB) is now being accepted and recommended by IASPEI as one of the important complementary broadband standard magnitudes to be determined in future day-to-day practice at regional and global seismological data centres (see Resolution 1 of the 2013 IASPEI Assembly; http://www.iaspei.org/resolutions/resolutions_2013_gothenburg.pdf). This makes an alternative—or at least complementary—scaling of M e a realistic option again. What are the likely consequences?

Taking the orthogonal logE S(GFZ)-m B(BB) relationship in Fig. 3 (left) as a good starting data set for deriving such a new M e formula, one would get, by replacing in (12) m B by M emB and resolving it for the latter,

$$ {M}_{\mathrm{emB}}=\left[ \log {E}_S(GFZ)\hbox{--} 1.39\right]/1.92. $$
(21)

The factor 1.92 is close to 2 which one would expect if logE S is proportional to squared ground velocity amplitudes. It is also very close to the factor of 1.96 in the logE S-M L relationship for California derived by Kanamori et al. (1993). Energy-wise any factor near 2 makes much more sense than the factor 1.5 in the Richter relationship (1). However, such a new type of M e, tentatively termed M emB in contrast to M eMs scaled M S, would yield rather different values for the same logE S values of 12 and 18 as assumed above:

$$ \begin{array}{cc}\hfill \log {E}_{\mathrm{S}}=12\hfill & \hfill \to {M}_{\mathrm{e}\mathrm{mB}}=5.53; {M}_{\mathrm{e}\mathrm{Ms}}=5.06;\kern0.5em \varDelta {M}_{\mathrm{e}}=+0.47\hfill \end{array} $$
$$ \begin{array}{cc}\hfill \log {E}_{\mathrm{S}}=18\hfill & \hfill \to {M}_{\mathrm{e}\mathrm{mB}}=8.65; {M}_{\mathrm{e}\mathrm{Ms}}=9.07;\kern0.5em \varDelta {M}_{\mathrm{e}}=-0.42\hfill \end{array} $$

Because of (7a) and (7b), formula (21) will on average yield larger logE S values for high stress-drop earthquakes and those with magnitudes <≈ 6¾. The corner period of the source spectrum and thus the maximum of energy radiation occurs then at periods <<20 s. In contrast, for stronger, low stress-drop and low rupture earthquakes, M eMs, scaled to 20-s surface waves, tends to yield larger logE S values. This property would make M emB particularly suitable for applications in earthquake engineering, engineering seismology and shaking hazard assessment. Moreover, for slow and very slow tsunamigenic and tsunami earthquakes, the difference between M w and M emB would become even larger than for M eMs and thus even more indicative and alarming. This would make the joint assessment of M w and M emB even more useful in actual event-related risk assessment, disaster response and management. Ideally, in the years to come, regional and global data centres should aim at testing these conclusions by calculating for several thousands of earthquakes M e according to these two different but complementary approaches of M e determination.

6 Summary discussion and conclusions

Classical magnitude and energy relationships, on which currently accepted formulas for calculating M w and M e are based, have been derived from either rather insufficient and inhomogeneous data and/or by applying not optimal statistical and correction procedures. Rich homogeneous modern data, amongst them magnitudes measured according to recently accepted and IASPEI (2005, 2013) recommended standards, yield after homogeneous orthogonal regression new relationships. These sometimes differ significantly from the classical M w- and M e-defining relationships and related parameter assumptions. However, the mutual relationship of these differences sometimes balances off. Thus, the correctness of Richter’s (1958) logE S-M S relationship, originally derived via Gutenberg’s logE S-m B and m B-M S relationships, could now for the first time be confirmed with well-constrained and orthogonal-regressed, direct instrumentally measured logE S(GFZ) over M S(USGS) = M S(20) data, not, however, by orthogonally regressing source mechanism-corrected logE S (USGS) over M S(USGS) data.

On the other hand, also the combination of the semi-heuristic Choy and Boatwright logE S-M S relationship (17) with Θ(USGS) = −4.8 instead of Kanamori’s (1977) Θ = −4.3 yields an M w formula that yields values which agree on average within <0.1 m.u. with those derived via the alternative new relationships based on rich modern data. This small average deviation is less than the IASPEI acceptable tolerance for magnitudes of the same type that have been estimated via different procedures.

Also the M e formula (8) could be well reproduced with formula (19) via formula (10). In the considered M S and logE S range, the values calculated with both formulas differ less than 0.15 m.u. This is negligible when compared with the uncertainty of about 0.2–0.3 m.u. even of very good M e determinations. Thus, there is no need for revising the current M w and M e formulas. However, the suitability of source mechanism corrections applied to logE S data prior to M e calculation, practice at the NEIC, is questioned.

The best correlation between E S and magnitudes exists with the newly proposed IASPEI (2005, 2013) broadband body-wave magnitude m B(BB). It is the modern version of the original medium-period body-wave magnitude proposed by Gutenberg (1945a, b) and Gutenberg and Richter (1956). The easy to measure m B(BB) allows to estimate M e with a standard deviation SD = ±0.19 m.u. only. This is within the inherent error range of direct M e determinations. When estimating M e via M S(20) instead, SD is twice as large. Therefore, scaling body-wave logE S estimates derived from velocity broadband P wave records to velocity broadband m B(BB) body-wave magnitude would be more appropriate and physically more correct than scaling them to long-period and nearly monochromatic 20-s surface-wave M S. m B(BB) is measured in a wide range of periods, thus covering a wide range of the magnitude-dependent corner frequencies of seismic source spectra, at which the maximum of seismic energy is radiated (Bormann and Di Giacomo 2011). Using currently available m B(BB) and logE S data, a new M emB formula has been derived. Values calculated with it may differ up to almost 0.5 m.u. from those calculated with the current formula scaled to M S(20). The new formula more correctly represents, as does mB(BB), the energy release of medium to smaller size as well as of faster rupturing and high stress-drop earthquakes but underestimates the dominatingly long-period energy release of great, slow and low-stress-drop earthquakes (e.g. Fig. 3 of Bormann and Saul 2008) which is better represented by the current M e formula scaled to M S(20). This would make M emB very attractive for engineering seismological and hazard assessment applications and a useful complement to the currently common M eMs.

But generally, one has to accept that both M w(GCMT) and M e(USGS), consistently determined and published for 30 to 40 years already in authoritative catalogues, constitute valuable data bases in their own right. Already for this reason alone, their calculation should be continued with the current formulas (3) and (8). Most important in seismic hazard assessment is not how these M w or M e scales were initially calibrated but how we can infer from the available M w and M e values’ hazard relevant ground motion and source parameters. Numerous subsequent equations are based on the existing formulae, so far mainly for M w, e.g., estimating model-dependent ground motion parameters such as peak ground acceleration and response spectral accelerations and prediction of next-generation attenuation models (Douglas et al. 2014), determining source parameters from catalogued M w (Edwards and Fäh 2013), historical earthquake M w calibration based on M w-intensity relationships (Stucchi et al. 2013), determining magnitude-frequency relations from catalogued M w (Wiemer et al. 2009). Changing these formulas now, even if the original calibration data and parameter assumptions were not optimal, would therefore not be beneficial. But important is the understanding of the physical reasons for systematic differences between the various scales. Formula (9) illustrates this for the difference between M w and M e. With such an understanding, one may derive from classical empirical magnitudes still reasonably good proxy estimates for the more physically defined modern magnitudes M w and M e. Up to now, M w proxies are still favoured for unifying magnitude data in long-term instrumental earthquake catalogues needed for probabilistic seismic hazard assessment (e.g. Grünthal et al. 2009, Wiemer et al. 2009; Stucchi et al. 2013; Di Giacomo et al. 2015). Hosts of mutual relationships between M w and other magnitude scales have been published. Summaries with helpful discussions can be found, e.g. in Kanamori (1983), Bormann et al. (2009; 2013), Edwards et al. (2010), Di Giacomo et al. (2015) and Lolli et al. (2014). In future, however, the joint consideration of M w and M e is needed for a better understanding of the differences in earthquake rupture kinematics and dynamics and thus for a more realistic fast assessment of the specific nature and related hazard potential of individual earthquakes (e.g. Newman and Okal 1998; Choy and Kirby 2004; Di Giacomo et al. 2010a, b). Good correlation relationships between M e and classical magnitudes such as m B, m b and M S are still rare although for many significant pre-1990 earthquakes, a comparison between M w and M e proxy estimates would be highly desirable too, e.g. via the m B and M S values in the Abe (1981, 1984) catalogues. First regression relationships between M e and the four IASPEI teleseismic standard magnitudes have been published by Bormann et al. (2009).