1 Introduction

Great attention towards perovskites, especially oxide based, has been paid in the recent past because of their countless different applications and device fabrication [1,2,3,4]. Perovskite oxides particularly with ABO3 composition containing f-electrons are very important, because of the properties that result from their highly correlated electron systems. These perovskite oxides are extensively investigated in several technological domains, and these are considered as the best candidate for multiferroic materials, spintronic devices and solid oxide fuel cells [5, 6]. BaAmO3 is one of the ABO3-type perovskite oxides, crystallizes in cubic form with the space group pm-3m (221). The divalent cation (Ba) is located at the (0, 0, 0) position; (O) at the (0.5, 0.5, 0), (0.5, 0, 0.5) and (0, 0.5, 0.5) positions; and (Am) at the body-centred position (0.5, 0.5, 0.5) of the cubic unit cell. The molar enthalpy of formation was found to be −15,446.6 kJ mol −1 [7]. Extensive theoretical studies have been made using first-principles calculations for closely related compounds like BaMO3 (M = Pr, Th, U) and SrUO3 perovskites [8,9,10]. As far as the previous literature study is concerned, not much attention has so far been paid to understand the physical behaviour of such a highly correlated f electron system, BaAmO3. This glaring lack of information on the physical behaviour of BaAmO3 and the absence of many experimental and theoretical studies especially elastic, magnetic, thermodynamic and mechanical properties have motivated us to accomplish this study. In the present work, we have employed density functional theory (DFT) as implemented in Wien2k with different exchange correlations to investigate structural properties, band profile, density of states, bulk modulus, elastic constants, magnetic moments and thermodynamic properties using the quasi-harmonic Debye model. Therefore, the present work will overcome the lack of available data for this compound and will endow as reference data which can serve as a tool for further advance in experimental as well as theoretical studies.

2 Computational Details

The structural, electronic, elastic and magnetic properties were calculated using the full-potential linearized augmented plane wave (FP-LAPW) method as implemented in the Wien2k code, which is based on density functional theory (DFT) [11, 12]. Structural optimization was performed within the generalized gradient approximation (GGA) scheme of Perdew, Burke and Ernzerhof (PBE) [13], LSDA [14], WC-GGA [15], PBEsol-GGA [16] and Hubbard approximation (GGA + U) [17]. The energy convergence function used R MT K max = 7, where R MT is the small atomic radius in the unit cell and K max refers to the size of the largest k vector in the plane wave expansion. In the fullpotential scheme the unit cell of the crystal is partitioned into two different regions: (1) atomic spheres and (2) interstitial region (a region which belongs outside the atomic spheres). The wave function is expanded into two different basis sets. Within the atomic sphere the wave function is extended in atomic-like functions (radial part times spherical harmonics) while in the interstitial region it is extended in a plane wave basis. Inside the sphere L max = 10, while the charge density is Fourier expanded up to G max = 12 a.u. −1. The self-consistent calculations are converged when the total energy of the system is stable within 10 −4 Ry. A dense mesh of 1000 K points is used, and the tetrahedral method [18] has been used for Brillouin zone integration. The calculations have been performed on cubic BaAmO3 with the space group number (221) considering the experimental lattice constant value of 4.357 Å [7, 19].

Elastic constant calculations require knowledge of the derivative of the energy as a function of the lattice strain. The symmetry of the cubic lattice is such that it reduces the 21 elastic constants to three independent elastic constants, namely C 11, C 12 and C 44. The elastic stability criteria for a cubic crystal at ambient conditions are C 11 + 2 C 12 >0, C 44 >0, C 11 − C 12 >0 and C 12 <B < C 11. In the present work, the elastic constants are calculated by the method developed by Charpin as integrated in the Wien2k package [20]. For thermodynamic calculations, the quasi-harmonic Debye model has been implemented [21].

3 Results and Discussion

3.1 Structural Properties

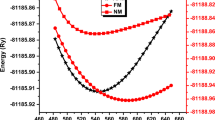
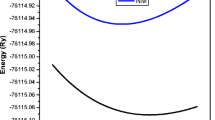
The optimum volume of BaAmO3 is obtained by fitting the total energy as a function of its unit cell volume using Birch–Murnaghan’s equation of state [22]. We have computed the total energy of the BaAmO3 perovskite in ferromagnetic (FM), anti-ferromagnetic (AFM) and non-magnetic (NM) states as depicted in Fig. 1. One can notice from the figure that BaAmO3 is found to be stable in the FM state as it is having minimum energy in this state. The relaxed lattice constants, bulk moduli and groundstate energy are evaluated at the optimum volume. These calculated groundstate results using different approaches are compared with the available results as shown in Table 1. The calculated value of the lattice constant is found to be 4.4169 Å in GGA-PBE which is overestimated from the experimental value and in the case of LSDA it is underestimated to be 4.3172 Å.

Fig. 1
figure 1

Energy as a function of volume for ferromagnetic (FM), non-magnetic (NM) and anti-ferromagnetic (AFM) phases of BaAmO3

Full size image
Table 1 Calculated value of lattice constant a 0, bulk modulus B 0 and pressure derivative \(B\prime \) under various schemes
Full size table

3.2 Electronic Properties

The electronic band structure along the principal symmetry directions in the Brillouin zone for FM BaAmO3 using GGA, GGA + U (where the Hubbard (U) term was taken as 5 eV) and modified Becke–Johnson exchange potential (mBJ) are shown in Fig. 2a–c, respectively The Fermi level E f is set to 0 eV. Inspection of Fig. 2a–c reveals the half-metallic nature of BaAmO3. Using all the three approximations: GGA, GGA + U and mBJ, the compound shows a conducting nature for spinup (majority spin states) and for spindown (minority spin states); the compound behaves as a semiconductor. The band gap value increases as we approach from GGA to GGA + U from 3.64 to 4.16 eV and in the case of mBJ there is a further increase in the band gap value to 4.47 eV.

Fig. 2
figure 2

a Band structure of BaAmO3 for spinup and spindown states with GGA. b Band structure of BaAmO3 for spinup and spindown states with GGA + U. c Band structure of BaAmO3 for spinup and spindown states with mBJ

Full size image

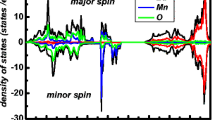
In order to visualize the electronic origin of the band structure, the total density of states (DOS) has been calculated for both the spins using GGA, GGA + U and mBJ and is plotted in Fig. 3. In the majority spin case using GGA, GGA + U and mBJ, the Fermi level falls on Am-f states; nevertheless, in the case of the minority spin case, the Fermi level falls in a gap. Overall, the total DOS diagram shows the half-metallic nature of BaAmO3.

Fig. 3
figure 3

Total density of states for spin-up and spin-down states for BaAmO3 with GGA, GGA + U and mBJ

Full size image

In order to understand the elemental contribution to BaAmO3, the partial density of states has been calculated and is depicted in Fig. 4. One can easily understand the elemental contribution to BaAmO3 for majority and minority spin states. The most contributing orbitals towards DOS which surround the Fermi level are the Ba-d, Am-d, Am-f and O-p states. At the Fermi level, the localized f states of Am are present in the spin-up states in all three cases: GGA, GGA + U and mBJ, while for the spin-down states, the f states of Am are pulled deep inside the conduction band (shown for GGA only). The Am-d and Ba-d states are found in the valence band crossing one another, and the p states of O are present in the valance band for both the spins. Thus, from the overall electronic study, we conclude that BaAmO3 is a spin-dependent half-metallic compound.

Fig. 4
figure 4

DOS contribution of Ba-d, Am-d, Am-f and O-p states in BaAmO3 for spin-up and spin-down states in GGA

Full size image

3.3 Magnetic Properties and Phase Stability

As discussed in Section 3.1 that the total energy of BaAmO3 is found to be minimum in the ferromagnetic state, also as far as the evidence are concerned, the ferromagnetic character is most common for ABO3 perovskite oxides [10]. This ferromagnetic character is based on two types of indirect exchange interactions between Am-Am via oxygen, one is the double-exchange mechanism, which favours ferromagnetism, and the other is the superexchange mechanism [10], which favours anti-ferromagnetism. In this compound, double-exchange interaction between americium atoms via a non-magnetic oxygen anion takes place. As far as the magnetism in BaAmO3 is concerned, it is discussed with a special reference to the associated magnetic moments of the material. These magnetic moments in a material come from the atoms constituting the material and the interstitial sites. The interstitial individual and total magnetic moments using different exchange potential approaches for BaAmO3 are presented in Table 2. The main contribution to the total magnetic moment of BaAmO3 is due to americium. It is clear that the effective magnetic moment of Am is large in all the approximations used while the remaining part is due to Ba and O and from the interstitial sites giving us the total magnetic moment of the material. The total magnetic moment of the material in every approximation is found to be the integer value 5 µB, which is one of the consequences of the halfmetallic nature of the material. With the insertion of the U term (where U = 5 eV) an increase in the magnetic moment of americium is calculated but the overall magnetic moment remains the same.

Table 2 Total magnetic moment of ferromagnetic BaAmO3 under ambient conditions in B2 phase (in Bohr magneton (μ B))
Full size table

3.4 Elastic Properties

The elastic properties of solids are important as they are related to various essential solid-state phenomena, such as inter-atomic potential, equation of state and phonon spectra. The elastic properties are also linked thermodynamically with specific heat, thermal expansion, Debye temperature, melting point and the Grüneisen parameter [25]. The knowledge of elastic constants is vital for many practical applications related to the mechanical properties of a solid. The elasticity of a solid material is its ability to recover its original profile after being slightly altered by some external agency. This property is very significant to study mechanical properties like ductility and stiffness, which result in the determination of elastic constants of the studied material. Several theoretical models have been developed for the determination of elastic constants. They are based on the study of reaction in terms of energy of a material under the effect of an external force. In the present study, we have used the theoretical model of Charpin [26] to determine the elastic constants of the BaAmO3 perovskite. BaAmO3 has a cubic symmetry, hence three elastic constants, C 11, C 12 and C 44, to be calculated. The value of these elastic constants was obtained by calculating the total energy as a function of volume-conserving strains and is presented in Table 3. To the best of our knowledge there is no experimental or theoretical data available on elastic moduli for BaAmO3; therefore we could not compare our results with the others’ work; nevertheless the elastic constants of some of the similar perovskites were found to be in the same range [27,28,29]. As far as the criteria [30, 31] for cubic elastic constants are concerned our predicted values (Table 3) well satisfy the following criteria:

  • (C 11 − C 12) > 0

  • C 11 > 0, C 44 > 0

  • (C 11 + 2C 12) > 0

  • C 12 <B <C 11

Table 3 Calculated elastic constants C 11, C 12 and C 44 (in GPa) of BaAmO3
Full size table

Poisson’s ratio (ν), Young’s modulus (E), and shear modulus (G) are often measured for materials when their hardness is to be investigated. These quantities are calculated from the computed data of the elastic constants by using the following expressions [32,33,34] and presented in Table 4

$$ \nu =\frac{3B-2G}{2(3B+G)} $$
(1)
$$ E=\frac{9BG}{3B+G} $$
(2)

where B is the bulk modulus and G is the average shear modulus. As per Hill [35], the average shear modulus, G, is defined as the arithmetic mean of Voigt, G V, and Reuss, G R, values, which can be calculated as:

$$ G_{\mathrm{V}}=\frac{1}{5}\left( C_{11}-C_{12}+3C_{44} \right) $$
(3)
$$ G_{\mathrm{R}}=\frac{5(C_{11}-C_{12})C_{44}}{3(C_{11}-C_{12})+4C_{44}} $$
(4)

The ductility and brittleness of the BaAmO3 perovskite can be defined by the B/G ratio. According to Pugh [36], a material is brittle if the B/G ratio is less than a limit value of 1.75 and is ductile if it is higher than this limit value. The B/G ratio for BaAmO3 is calculated to be 2.02, which is higher than the limit value; thus BaAmO3 shows a ductile nature

Table 4 The calculated values of shear modulus G (GPa), Young’s modulus E (GPa), Poisson’s ratio ν, Zener anisotropy factor A, B/G ratio, Cauchy’s pressure (C 12– C 44) and B/ C 44
Full size table

In solid state physics, anisotropy (opposite of isotropy) is a property in which an anisotropic material can present different characteristics (such as mechanical, electronic and optical properties) in the different directions of its structure. The degree of anisotropy in solids can be defined by the Zener anisotropy factor, ‘A’ For a material which is completely isotropic, the A factor takes the value 1; when the value of A is smaller or greater than unity then the material behaves as an anisotropic material. The value of anisotropy is determined by:

$$ A=\frac{2C_{44}}{C_{11}-C_{12}} $$
(5)

The calculated value of the Zener anisotropy for BaAmO3 is less than 1; consequently, the material is anisotropic in nature and will have different characteristic properties like optical and mechanical in different directions of its structure.

The behaviour of the heat capacity of solids can be understood by calculating the Debye temperature, 𝜃 D. The Debye temperature further provides us a lot of information about the characteristics of a solid material under the effect of temperature. One of the standard methods to calculate the Debye temperature 𝜃 D is from elastic constant data, since 𝜃 D may be estimated from the average sound velocity, ν m, by the following equation [34]

$$ \theta_{\mathrm{D}}=\frac{h}{k_{\mathrm{B}}}\left[ \frac{3}{4\pi V_{\mathrm{a}}} \right]^{1/3}v_{\mathit{m}} $$
(6)

where h is Planck’s constant k B is Boltzmann’s constant and V a is the average atomic volume. The average wave velocity is given by v m and is determined by the following relation:

$$ v_{m}=\left[ \frac{1}{3}\left( \frac{2}{v_{\mathrm{t}}^{3}}+\frac{1}{v_{\mathrm{l}}^{3}} \right) \right]^{-\frac{1}{3}} $$
(7)

where v l is the longitudinal elastic wave velocity and v t is the transverse elastic wave velocity and these are determined by the following relations [34]:

$$ v_{\mathrm{t}}=\left( \frac{G}{\rho} \right)^{\frac{1}{2}} $$
(8)
$$ v_{\mathrm{l}}=\left( \frac{3B+4G}{3\rho} \right)^{\frac{1}{2}} $$
(9)

The above calculated values are grouped in Table 5.

Table 5 Calculated density ρ (g/cm 3); longitudinal, transverse and average sound velocity (v l,v tandv m respectively in m/s) calculated from elastic moduli; and Debye temperature (𝜃 D in K) calculated from average sound velocity for BaAmO3 compound
Full size table

3.5 Thermodynamic Properties

Thermal properties provide us valuable information on the specific performance of solids under the application of temperature and pressure. In this paper, we have calculated the thermal properties of BaAmO3 by applying the quasi-harmonic Debye model [21] in the temperature range of 0 to 600 K, while the pressure variation is done in the range of 0 to 40 GPa.

The quasi-harmonic Debye model has been applied to investigate the thermodynamic properties of the perovskite oxide BaAmO3. In this model, the Gibbs function takes the form;

$$ G\ast \left( V,P,T \right)=E\left( V \right)+ P\left( V \right)+ F_{\text{vib}}\left( \theta \left( V \right); T \right) $$
(10)

where E(V ) is the total energy per unit cell, P(V ) corresponds to the constant hydrostatic pressure, 𝜃(V) is the Debye temperature and F vib is the vibration term written as;

$$ F_{\text{vib}}\left[ \theta \left( V \right);T \right]=NK_{\mathrm{B}}T\left[ \frac{9\theta} {8T} +3\ln \left( 1-e^{\frac{-\theta} {T}} \right)-D\left( \frac{\theta} {T} \right) \right] $$
(11)

where \(D\left (\frac {\theta } {T} \right )\) represents the Debye integral, N is the number of atoms per formula unit and K B is Boltzmann’s constant. For an isotropic solid, the Debye temperature 𝜃 D is expressed as [37, 38]

$$ \theta_{\mathrm{D}}= \frac{h}{K_{\mathrm{B}}}(6\pi^{2}V^{1/2}N)^{1/3}f(v)\sqrt{\frac{B_{\mathrm{s}}}{M}} $$
(12)

In the above equation B s is the adiabatic bulk modulus and M is the molecular mass per unit cell; the bulk modulus is expressed by

$$ B_{\mathrm{s}}=V\left( \frac{d^{2}E(V)}{dV^{2}} \right) $$
(13)

The non-equilibrium Gibbs function G*(V;PT) can be minimized with respect to volume V;

$$ \left[ \frac{dG\ast (V;P,T)}{dV} \right]_{P,T} $$
(14)

The solution to (14) helps one to get thermodynamic quantities like thermal expansion α heat capacity at constant volume C V and heat capacity at constant pressure C P, given respectively by [37];

$$ \alpha =\frac{\gamma C_{\mathrm{V}}}{B_{\mathrm{T}}V} $$
(15)
$$ C_{\mathrm{V}}=3nk\left[ 4D\left( \frac{\theta_{D}}{T} \right)-\frac{3\theta_{D/T}}{e^{\frac{\theta_{\mathrm{D}}}{T}}-1} \right] $$
(16)
$$ C_{\mathrm{P}}=C_{\mathrm{V}}(1+\gamma \alpha T) $$
(17)

In (17) γ represents the Grüneisen parameter, which is approximated as

$$ \gamma = -\frac{dln\theta_{\mathrm{D}}(V)}{dlnV} $$
(18)

In this section, we discuss the temperature and pressure dependence of volume, bulk modulus and various thermodynamic quantities like specific heat, entropy, Grüneisen parameter and thermal expansion coefficient.

Figure 5 shows the variation of unit cell volume with temperature (range 0 to 600 K) at various pressure points. Since the reality is concerned, temperature tends to increase the unit cell volume, while pressure decreases the cell volume. For the present case in BaAmO3, temperature increases the unit cell volume with a moderate pace, and this increase is found in a linear fashion. In Fig. 6, we have plotted the variation of bulk modulus with temperature at different pressure values of 0, 10, 20, 30 and 40 GPa. One can notice the linear decrease in bulk modulus with temperature. This is because the increase in temperature results in the reduction in material hardness. We have also calculated heat capacity at constant volume, C v, for BaAmO3. In Fig. 7, we have plotted the variation of C v with temperature. One understands from this figure that the specific heat varies rapidly up to a temperature of 200 K and beyond that, it approaches a constant value; the reason behind this is that at high temperature, the Debye model reaches a limit known as the Dulong–Petit limit [39]. The value of C v is calculated to be 67.35 at 300 K. Figure 8 shows the variation of thermal expansion coefficient, ‘ α’, with temperature. It is clear from the figure that the value of ‘ α’ increases with increasing temperature; this increase in thermal expansion coefficient is very fast at low temperatures, and at high temperatures, it gradually increases. Pressure has a very small effect on the thermal expansion coefficient at low temperatures, but at higher temperature values, the effect of pressure gets dominant and the thermal expansion coefficient decreases rapidly; this is because of the shortfall of quasi-harmonic approximation at high temperature and low pressure.

Fig. 5
figure 5

Variation of unit cell volume as a function of temperature at various pressures

Full size image
Fig. 6
figure 6

Bulk modulus variation with temperature at different pressure points

Full size image
Fig. 7
figure 7

Temperature-dependent heat capacity C v at constant volume

Full size image
Fig. 8
figure 8

Variation of thermal expansion (α) as a function of temperature at different pressure values

Full size image

Further, the effect of temperature and pressure on the entropy ‘S’ of the system is calculated. In Fig. 9, we have presented the variation of entropy ‘S’ with temperature at various pressure values. The figure provides us a clear understanding that the entropy increases with increase in temperature; one can also understand that it decreases as pressure increases. We have calculated the entropy value 74.93 J mol −1 K under ambient conditions. From (18), we have calculated the Grüneisen parameter and depicted its variation with temperature and pressure in Fig. 10. The variation is in such a way that at low temperature, the value of γ is almost constant; nevertheless, a small increase is noticed as temperature increases. On the other hand, one can see a decrease in the γ value as pressure increases.

Fig. 9
figure 9

Variation of entropy S as a function of temperature at different pressure points

Full size image
Fig. 10
figure 10

Variation of Grüneisen parameter γ as a function of temperature at various pressures

Full size image

4 Conclusion

In summary, the structural, electronic and mechanical properties of BaAmO3 were calculated at T = 0 K by DFT calculations. The exchange-correlation potentials (GGA, GGA + U, mBJ) were used to check ground-state properties such as lattice constant, bulk modulus and its pressure derivative, and the obtained values were found to be in good agreement with available results. According to our calculations, BaAmO3 was found to have a stable ferromagnetic state, with a magnetic moment of 5 µB. The spin-polarized band and DOS diagrams show its half-metallic nature. The elastic constants were predicted; from the knowledge of elastic constants, elastic moduli were calculated. The elastic anisotropy and Debye temperature have also been evaluated. In addition to this, the thermodynamic properties were calculated in the temperature range of 0 to 600 K and the pressure variation from 0 to 40 GPa. The specific heat at constant volume was found to follow the well-known Dulong–Petit law. The variations of thermal expansion coefficient, entropy, bulk modulus, Grüneisen parameter and volume with temperature and pressure were presented and open a scope for experimental observations.