1 Introduction

Owing to their potential for computing complex structural and electronic properties of solids with great accuracy has made first-principle calculations an important tool of materials research [1–4]. This advancement in simulation techniques has brought many breakthroughs in condensed matter physics. For instance, we can analyze those (non-magnetic and magnetic) properties of materials [5–8] which were very hard to be studied through experiments. Also, such properties which needed very intense imaginative insight are now possible to be explained through virtual reality with the help of computational methods.

Dilute magnetic semiconductors (DMS) [9] are renowned magnetic materials which can be made by doping traditional semiconductors with transition metal impurities. In order to use DMS based on II–VI and III–V semiconductor compounds practically, it is necessary that these compounds possess a unique combination of structural, electronic, and magnetic properties. In DMS solid solution, the cations are usually replaced by magnetic transition metal and/or rare-earth anions. Hence, the nature and concentration of the dopant firmly decides the structural, electronic, and magnetic properties of DMS. It is worth pointing out here that doping does not enforce the host to drop off its semiconducting properties rather than it furnishes magnetic effects in the host [10].

Another important feature of doped semiconductors is that the dopant composition can control energy band gaps and other important physical properties [11]. Also, doped semiconductors have the ability to regulate charge as well as electronic spin current which makes them among the promising candidates for spintronic devices [12]. The prime purpose behind the wide spread research on magnetic materials is to manufacture the feasible devices like ultra-fast optical switches, spin LEDs, spin valves, and magnetic sensor in spintronic industry [13]. Many researchers [14–17] have analyzed (theoretically and experimentally) the response of adding the magnetic transition elements (Ti, Mn, Fe, Co, Ni, and Cr) and rare-earth elements (like Sm, Er, Dy, Gd) into the conventional semiconductors (either II–VI or III–V) compounds.

The II–VI systems, magnesium chalcogenides, MgX (X = S, Se, Te), in fourfold coordinate ZB structure that can be crystallized at low pressure. Their small ionic radii and strong covalent binding nature are the prime features which make them distinct from all other alkaline-earth metal chalcogenides. For these compounds, the Philips ionicity, band gap, and bulk modulus values increases while going from MgTe to MgS [18, 19]. Larger values of bulk modulus make them more stable materials. Furthermore, MgS and MgTe have lattice constants closer to those of gallium arsenide and zinc selenide. Keeping in view all these appealing characteristics, magnesium chalcogenides are promising materials for optoelectronic devices [20, 21]. In the present study, we have investigated structural, electronic, and magnetic properties of Ti doped on zinc blende MgY (Y = S, Se, and Te) semiconductor. The 3d transition element Ti is adopted with the purpose to introduce magnetism in the paramagnetic MrY compounds for which no theoretical work has been carried out yet, to the best of our knowledge.

2 Method of Calculations

To evaluate the ground state properties of Ti-doped Mg-chalcogenides, full-potential linearized augmented plane (FP-LAPW + lo) method is used which has its basis on density functional theory (DFT) and incorporated into wien2k code to solve the many electron system [22]. From this method, eigenvalue and eigenfunction of Kohn-Sham equations are calculated systematically [23]. In order to solve the electron core interaction problem (exchange co-relation potential), generalized gradient approximation (GGA) is used to evaluate the ground state parameters of material and its mechanical response [24]. The electronic and magnetic properties are computed by the implementation both modified Becke-Johnson exchange potential [25] and local density approximation combinedly called as mBJLDA. The joint effect of semi-local exchange potential and local spin density gives the improved energy band gap of spin polarized semiconductors and transition metal (TM)-doped materials [26–29].

In this work, the core and valence states of the Mg, Ti, and Y = S, Se, Te are behaved as self-consistently in relativistically relaxed, spherical approximation and semi-relativistic approximation (without spin-orbit coupling), respectively. The charge density, wave function, and potential expanded within the non-overlapping spheres surrounded by the atomic sties and the residual (interstitial) space of the unit cell by the plane-wave basis set. For the wave expansion in the atomic sphere, maximum quantum number l max is chosen as 10 and the Fourier-expanded charge density G max up to 20 (Ry)1/2. R MT×k max known as convergence parameter, that controls the dimension of the basis set, is fixed to 8. The average radius of the muffin tin spheres is represented by R MT, and for reciprocal lattice, the maximum modulus is represented by k max. We have used the muffin tin radius values for the Ti, Mg, S, Se, and Te as 1.96, 1.68, 2, and 1.73 atomic units (a.u.), respectively. The 10 × 10 × 10 Monkhorst–Pack mesh along with sufficient k-vectors in the irreducible Brillion zone is used to model the reciprocal space. In each evaluation, we have converged the total energy of crystal up to 10−5 Ry by recurrence process.

3 Result and Discussion

3.1 Structural Properties

On computational grounds, structural optimization is of enormous concern to obtain the ground state properties of a material. In this process, we have performed the structural optimization for ZB Mg0.75Ti0.25Y (Y = S, Se, Te) compounds with WC-GGA through total energy minimization as a function of unit cell volume in order to obtain optimized lattice parameters (a 0) and bulk moduli (B 0). The total energy versus volume curves at x = 0.25 are displayed in Fig. 1; however, the optimized structural parameters are enumerated in Table 1. For the ZB Mg0.75 Ti0.25Y (Y = S, Se, Te) crystal structures, we have premeditated the difference in energy (ΔE = E NM − E FM) between FM and NM states by optimization of the crystal structure. The plots of optimization are displayed in Fig. 1, and energy difference values are given in Table 1 which implies that FM states of Mg0.75Ti0.25S, Mg0.75Ti0.25Se, and Mg0.75Ti0.25Te are of lower energies than that of their NM states. Consequently, the compounds being studied are stable in FM state. To confirm the thermodynamic permanence in FM state, with ZB crystal structures, we also premeditated the enthalpy of formation (ΔH) from the following relation:

$$\begin{array}{@{}rcl@{}} {\Delta} H\,=\,E_{\text{Total}} \left( {\text{Ti}_{\mathrm{l}} \text{Mg}_{\mathrm{m}} \mathrm{S}_{\mathrm{n}} /\text{Sen}/\text{Te}_{\mathrm{n}} } \right)\\ -lE_{\text{Ti}} -mE_{\text{Mg}} -nE_{\mathrm{S}/\text{Se}/\text{Te}} \end{array} $$
(1)

where the energies E Total(TilMgmSn/Sen/Ten), E Ti, E Mg, and E S/Se/Te are related to the lowest total ground state energy of MgmTil Y n (Yn = S n, Sen, and Ten) alloys and the individual ground state energies per atom of Ti, Mg, S, Se, and Te correspondingly, where l, m, n show contribution from Ti, Be, and S/Se/Te atoms for the unit cell formation. The enthalpy of formation gives the negative values as given in Table 1, which makes sure that ZB Mg0.75Ti0.25Y (Y = S, Se, Te) have high stability and their evolution in FM phase are moderately conceivable.

Fig. 1
figure 1

Total energy verses unit cell volume for Mg0.75Ti0.25Y (Y = S, Se, Te) alloys in non-magnetic (NM) and ferromagnetic (FM) phase

Full size image
Table 1 Equilibrium lattice constant a (Å), bulk modulus B (GPa), total energy difference ΔE (eV), crystal field energy (ΔE crystal), band gap values E g (eV) and enthalpies of formation ΔH f (eV) calculated for MgTiY (Y = S, Se, Te)
Full size table

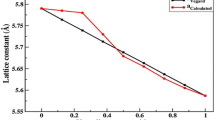
From the structural optimization (Fig. 1), the equilibrium lattice constant (a 0) and bulk modulus (B 0) were derived for binary semiconductors and their ternary Mg0.75Ti0.25S, Mg0.75Ti0.25Se, and Mg0.75Ti0.25Te alloys (see data in Table 1). The analysis of data shows that the lattice constant of ternary Mg0.75Ti0.25S, Mg0.75Ti0.25Se, and Mg0.75Ti0.25Te alloys increases and bulk modulus decreases as compared to binary alloys MgS, MgSe, and MgTe. However, the lattice constant (a 0) increases from Mg0.75Ti0.25S, Mg0.75Ti0.25Se, to Mg0.75Ti0.25Te because ionic radius down the group (S to Te) increases due to addition of shells. The value of ΔE also increases from S to Te that shows that the ternary alloys Mg0.75Ti0.25S, Mg0.75Ti0.25Se, and Mg0.75Ti0.25Te have different values of ferromagnetism with different Curie temperatures [30–33].

3.2 Mechanical Properties

To elaborate the mechanical and dynamical behavior of crystals, the knowledge of elastic constants is highly meaningful. Moreover, elastic constants describe materials behavior before and after applied stress [34]. We have performed ab initio calculations to compute elastic moduli Cij by calculating stress tensor components for small strain. These constants perform a magnificent part in revealing substantial information regarding the steadiness and stiffness of materials. The method used to evaluate these constants was developed by Chapin and implemented in Wien2k code [35] which already has been applied in some prior studies [36–38] with successful results. Since the investigated materials have cubic symmetry, it is necessary to calculate merely three independent elastic parameters C11, C12, and C44 for complete description of their mechanical properties. Hence, three equations are needed to perceive these constants [39]. The generalized Hooke’s law provide a connection between stresses (s) and strains (ε) to obtain elastic moduli as follows: The Born stability criteria was used to [40] defines mechanical stability of a cubic crystal. The bulk modulus estimated by using the relation B = (1/3) (C 11 + 2C 12), as well as by energy minimization, has nearly the equal values (see Table 2). This is the reliability of the determined results for the studied compounds. Kleinman parameter (ζ) speaks about dominate character of either bond bending or bond stretching in cubic materials. Its value drops to 0 and 1 for minimizing bond bending and stretching, respectively. In the present study, bond stretching is dominating over bond bending [41].

Table 2 Calculated elastic constants C ij (GPa), Kleinman parameters (ζ), shear modulus G (GPa), Young’s modulus E (GPa), Poisson’s ratio, anisotropy factor (A) and B/G ratio at equilibrium for binary compounds and their alloys Mg1−x Ti x Y (Y = S, Se and Te) at x = 0, 0.25
Full size table

In engineering sciences, the knowledge of elastic anisotropy is of great importance as it states that how micro-cracks are possible to be infiltrated in materials [42]. In this context, we have evaluated the anisotropy factor A using obtained elastic constants and it stands 1 for an isotropic material while any deviation (lower or higher) from 1 indicates anisotropy [43]. The degree of anisotropy is measured as magnitude of the deviation from 1. Referring to Table 2, the studied compounds are anisotropic materials as A undergoes deviation from unity. For the sake of evaluation of moduli for the proposed materials, the Voigt-Reuss-Hill [44] approximation has been employed because our materials are generally polycrystalline. According to this approximation, the approximated modulus can be driven from the average of the two recognized bounds for mono-crystals as suggested by Voigt [45] and Reuss [46]. In this regard, the abovementioned moduli for cubic structures are worked out from the relations given in Ref. [47]. Moreover, Young’s modulus (E) and the Poisson’s ratio (ν) have also been premeditated. Both of these factors are linked with bulk modulus (B), and Shear modulus (G) by the equations given in Ref. [48, 49]. The estimated elastic moduli for the binary MgY and its alloys Mg0.75Ti0.25S, Mg0.75Ti0.25Se, and Mg0.75Ti0.25Te are listed in Table 2. Higher value of E places a material in the category of stiffer materials. Since the value of E decreases while going from S to Te, the alloy Mg0.75Ti0.25S is stiffer than that of Mg0.75Ti0.25Se and Mg0.75Ti0.25Te. Among the determined elastic parameters, Poisson’s ratio is more capable of explaining bonding forces operational in a material. The upper and lower limits defined for ν are 0.5 and 0.25, respectively [50]. Since the value of ν is laying within 0.25–0.5 for all under observation alloys, so the central inter-atom forces are set in these alloys. The covalent and ionic materials can also be distinguished with Poisson’s ratio value which is typically 0.1 and 0.25 for covalent and ionic materials, respectively. On the basis of estimated values of ν, all alloys are ionic. Furthermore, the critical value 0.26 of Poisson’s ratio separates a brittle material from a ductile one [51]. It is obvious from our ν values that all the proposed materials are ductile. The brittle and ductile nature of a compound can also be characterized by Pugh’s ratio (B/G) whose critical value is 1.75. Referring to Table 2, B/G value is 2.47 for Mg0.75Ti0.25S, 2.29 for Mg0.75Ti0.25Se, and 1.79 for Mg0.75Ti0.25Te classifying these compounds as ductile. So, ductile nature makes them suitable candidate for device fabrication.

3.3 Electronic Properties

The electronic band structures and density of states (DOS) are embraced in the electronic properties of Ti0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te compounds for spin-up and spin-down arrangements along the high symmetry directions in the first Brillouin zone have been calculated by using mBJLDA functional. In this study, the calculated equilibrium lattice constants were used to run the self-consistent calculations. It is clear from Fig. 2 that the band gap is symmetric in spin-down channel across the E F because of splitting of Ti atom 3d degenerate states without losing the semiconducting character of MgS, MgSe, and MgTe, while the spin-up channel shows the metallic character. Therefore, the overall contributions of both spin-up and spin-down channel show the half-metallic character in these compounds. Furthermore, it is clear that in the spin-down channel, less number of electrons exist as likened to that in spin-up channel. A valuable explanation about total (TDOS) and partial density of states (PDOS) delivers profound apprehend of band structures of Ti0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te, as depicted in Fig. 3a–c. The density of states (DOS) plot clearly shows that 3d-state of Ti splits across the E F within E g of host semiconductors and retains a band gap in down spin channel. Therefore, the doping of Ti impurity does not disturb the semiconducting property of MgS, MgSe, and MgTe in the spin-down channel. This behavior of Ti0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te compounds depicts the half-metallic character. Moreover, the low energy region from −5 to −3 eV for Ti0.25Mg0.75S, −5 to −2.5 eV for Ti0.25Mg0.75Se, and −5 to −2 eV for Ti0.25Mg0.75Te compounds shows the weak interaction of p-state and s-state of S/Se/Te with 3d-state of Ti, while across the Fermi level (from energy region −1 to 6 eV), the interaction of p-state of anion with 3d-state of Ti impurity exhibit strong p−d hybridization. The cause of this hybridization being week in the low energy region is due to the tendency of Ti d-states of being localized. There is a creation of extensive energy band gap in spin-down channel across the Fermi level.

Fig. 2
figure 2

Spin polarized band structures of Mg0.75Ti0.25Y (Y = S, Se, Te) alloys in majority spin-up (upwards arrow) and minority spin-down (downwards arrow) states using mBJGGA functional

Full size image
Fig. 3
figure 3figure 3figure 3

a The calculated total density of states (TDOS) along DOS with partial Ti, Mg, and S sites for Mg0.75Ti0.25S alloy for majority spin-up (upwards arrow) and minority spin-down (downwards arrow) configuration using mBJGGA functional. b The calculated total density of states (TDOS) along DOS with partial Ti, Mg, and Se sites for Mg0.75Ti0.25Se alloy for majority spin-up (upwards arrow) and minority spin-down (downwards arrow) configuration using mBJGGA functional. c The calculated total density of states (TDOS) along DOS with partial Ti, Mg and Te sites for Mg0.75Ti0.25Te alloy for majority spin-up (upwards arrow) and minority spin-down (downwards arrow) configuration using mBJGGA functional

Full size image

From Fig. 3a, b and c the p states of S, Se and Te respectively, and the d states of Ti show hybridization, which leads to the bandgap in the spin down channel. As well as unraveling the symmetry of two- and threefold perverted states (e g and t 2g), the p−d hybridization performs a significant part in the creation of FM in the studied materials by producing the dual exchange interaction. The states e g and t 2g appear owing to drive of fivefold perverted 3d-states of Ti, and the central cause of state splitting is the tetrahedral atmosphere created by S/Se/Te atoms. Furthermore, in the spin-up case, the e g states exist in the energy zone E F<0, whereas the t 2g states are enclosed in the situated of E F in VB and CB as shown in Fig. 3a–c. Conversely in spin-down, both of the symmetry states are completely situated in CB (E F>0). Moreover, the difference of spin-up and spin-down peaks of Ti-3 dcorresponds to the spin exchange splitting energy (Δ x (d)). The values of spin interchange splitting energies between the spin-up and spin-down Ti 3d-states and crystal field energies for Ti0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te alloys are presented in Table 3. The greater values of exchange splitting energies than crystal field energies lower the energy of the system because strong p−d hybridization favors the ferromagnetism in Ti0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te alloys [18].

Table 3 Energy splitting Δx(d), conduction band edge splitting (ΔE C) and valance band edge splitting (ΔE V) and exchange constants (N α and N β) calculated for all three Mg0.75Ti0.25S, Mg0.75Ti0.25Se and Mg0.75Ti0.25Te DMS alloys
Full size table

3.4 Electron Charge Density

The charge density for Ti0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te alloys was also examined (by implementing mBJLDA approximation) by taking into account the spin-up and spin-down configuration in (110) crystallographic plane. Figure 4 shows the spin-polarized contour plots of Ti0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te alloys for spin-up (↑) and spin-down (↓) configuration. The contour plot (Fig. 4) shows the partially ionic and partially covalent nature of bonds between Ti-S, Ti-Se, and Ti-Te atoms. The charge transfer was observed between cations and anions which reflected the electronegativity difference among Mg, Te, and Ti. Thus, stronger ionic bond was found in Ti-S/Ti-Se/Ti-Te than Mg-S/Mg-Se/Mg-Te due to greater electronegativity difference in Mg-S/Se/Te as compared to Ti-S/ Ti-Se/ Ti-Te atoms. Comparing the contour plots of all three DMS, more charge transfer was observed in Ti0.25Mg0.75S and Ti0.25Mg0.75Se than Ti0.25Mg0.75Te alloys. Further, it can also be seen that the d-states of magnetic ion has strong contribution in bonding for spin-up (↑) state, thus leading to major part of spin charge density. While d-states of magnetic ion has less contribution in bonding for spin-down (↓) state, thus disturbing the spherically symmetric charge distribution. On the other hand, Ti-S, Ti-Se, and Ti-Te bonds have a higher ionic character due to the higher electronegativity difference. The charge residing around Mg atom is contributed from s states; however, both s and p states are responsible gather charge around anions.

Fig. 4
figure 4

Electron density plots of Mg0.75Ti0.25Y (Y = S, Se, Te) alloys for both spin-up (upwards arrow) and spin-down (downwards arrow) configurations using mBJGGA functional

Full size image

3.5 Magnetic Behavior

To evaluate the magnetic properties of Ti0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te alloys, the total and local magnetic moments are calculated with mBJLDA and are listed in Table 4. Although, the calculated values of magnetic moment vary by employing different exchange correlation functional, it is noticeable that total magnetic moment values are identical for all the investigated compounds and main contribution comes from local magnetic moment of Ti ion. The electrons spin density (shown in Fig. 5) explains the overall atomic contribution to magnetic moment (taking the net contribution of electrons spin-up and spin-down state magnetic moments). The yellow flowers around the Ti atoms show its major contribution to magnetic moment as illustrated earlier in Table 3.

Table 4 Calculated magnetic moment at Mg, Ti and Y (Y = S, Se, Te) sites in Mg0.75Ti0.25Y alloys
Full size table
Fig. 5
figure 5

Plots of spin density for (a) Mg0.75Ti0.25S, (b) Mg0.75Ti0.25Se, and (c) Mg0.75Ti0.25Te alloys, where yellow flowers represent magnetic moment contribution of each atom

Full size image

For the sake of studying the role of conduction and valence bands in exchange splitting process, the knowledge of exchange constants (N 0 α and N 0 β) is necessary. The realization of these bands’ role is appropriate to parameterize conduction and valence bands spin splitting. This explanation is consistent with Hamiltonian-based mean field theory by the following equation [52, 53]:

$$ H~=~-N_{\mathrm{0}} \beta s.S $$
(2)

where N 0 is cation concentration, β denotes the pd exchange integral, s and S represent hole spin and Ti spin, respectively. Similarly, the conduction band spin-splitting can be calculated on the basis of same Hamiltonian with exchange constant N 0 α. So, the edge splitting of conduction band \(({\Delta E}_{\mathrm {C}}=E_{\mathrm {C}}^{\downarrow }-E_{\mathrm {C}}^{\uparrow })\) and valence band \(({\Delta E}_{\mathrm {V}}=E_{\mathrm {V}}^{\downarrow }-E_{\mathrm {V}}^{\uparrow })\) are serving to estimate both of the exchange constants using the following equations:

$$ N_{\mathrm{O}}\alpha =\frac{{\Delta E}_{\mathrm{C}}}{x\langle S\rangle }\; \text{and}\; N_{\mathrm{O}}\beta =\frac{{\Delta E}_{\mathrm{V}}}{x\langle S\rangle } $$
(3)

Table 3 shows the obtained values of ΔE c, ΔE v, N 0 α, and N 0 β. The exchange splitting energy Δ x (p d) which is the difference between maxima’s of valence bands for spin-down and spin-up (i.e., \({\Delta }_{x}(pd)~=~E_{\mathrm {V}}^{\downarrow }-E_{\mathrm {V}}^{\uparrow }\)), respectively. This energy is commonly used to compute magnetic properties of magnetic semiconductors [9, 29]. From Table 3, it is evident that the exchange splitting energy Δ x (pd) decreases while going from S to Te which is explained by the increasing differences in the electronegativity values and the increasing covalent bonding nature discussed earlier. The effective potential is more attractive for spin-down than that of spin-up as evident from the negative values of Δ x (pd), and it is in accordance with previous studies of the Ti-doped systems [54]. These findings confirm that pd coupling in the conduction band of Ti0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te alloys, due to Ti impurity, is ferromagnetic in nature.

4 Conclusion

In conclusion, the structural, mechanical, electronic, and magnetic behavior of Ti0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te DMS system have been investigated by means of first-principles DFT calculations based on the FP-LAPW + lo method. On the basis of our results, following main conclusions are drawn:

  1. (i)

    The equilibrium lattice constant of MgY compounds increase with the addition of Ti-dopant.

  2. (ii)

    T he Ti0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te alloys are found to be in ferromagnetic (FM) phase. The negative enthalpies of formation for all three alloys confirm the stability of FM phase.

  3. (iii)

    TheTi0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te alloys exhibit strong ductile behavior.

  4. (iv)

    The density of states and band structures Ti0.25Mg0.75S, Ti0.25Mg0.75Se, and Ti0.25Mg0.75Te alloys exhibit half-metallic ferromagnetic behavior.

  5. (v)

    For all three alloys, large magnetic moment is observed at the magnetic atomic sites, while small magnetic moments also appear at the non-magnetic sites (Mg and S/Se/Te) caused by the hybridization of p- and d-states.