1 Introduction

Since the pioneering work of Yablonovitch [1] and John [2], the photonic crystals (PCs) have attracted a lot of researchers’ interests in theory and experiment. The PCs are the artificial medium, which are composed of different materials, and are repeated periodically along one, two, or three directions of space, respectively. Similar to the electronic band gaps in a semiconductor, the PCs can exhibit magic frequency regions called photonic band gaps (PBGs) where the propagation of electromagnetic wave (EM wave) is forbidden. The main mechanisms responsible for the PBGs formation are based on Bragg scattering and the localized resonances [3]. Thus, the PCs have opened up a method for controlling the EM wave, and lead to proposals for many novel applications [4–6], and some of them have been confirmed in practical devices. If the EM wave incident at any angle with any polarization is forbidden in PCs, the omnidirectional photonic band gaps (OBGs) or high-reflectance ranges (reflectance greater than 0.99) can be obtained. The larger OBGs have potential application in the omnidirectional high reflector [7], all-dielectric coaxial waveguide [8], omnidirectional mirror fiber [9], etc. In the past two decades, the researchers just focused on the PBGs and OBGs of conventional PCs composed of conventional dielectrics [10–12], which are the multilayer periodic structures. However, quasiperiodic or aperiodic dielectric structures arranged according to a recursion rule have attracted the attention of researchers because they show many interesting properties. The most classic of those sequences are Fibonacci [13], Cantor [14], and the Thue–Mores sequence [15], respectively. The Thue–Mores sequence also has been extended to investigate the PBGs and OBGs of 1D PCs [16–19]. As time passed, the metamaterial also is introduced in PCs [20] to obtain a new kind of OBG named the zero-\(\bar{n}\) gap. Such gap originates from the EM wave tunneling of evanescent modes, and is insensitive to the lattice parameter changed in contrast with OBG originating from the Bragg gap. Recently, the researchers use the dispersive or dissipative materials to realize a new kind of PCs to obtain the tunable PBGs, such as semiconductor [21], metal [22], plasma [23–25], superconductor [26], and liquid crystals [27]. Thus, the SDPCs have received great attention of many researchers. If the superconductor is introduced in the conventional PCs, the frequency ranges of PBGs can be in the terahertz frequencies region [28–30]. Lyubchanskii et al. [31, 32] focused on the properties of 1D SDPCs with a complex defect layer. They found the position and transmittance of the defect mode can be tuned by the superconductor sublayer as well as the temperature. Li et al. [33] have systematically investigated the properties of PBGs for 1D SDPCs based on the TMM. They found that the bandwidth of PBG is more sensitive to the thicknesses of superconductor layers, and the damp coefficient does not affect the PBG under low-temperature conditions. Cheng et al. [34] studied the complex PBGs in two-dimensional (2D) PCs composed of a high-temperature for the case of TM polarization. They found that the contribution of a normal conducting electron is nonnegligible with increasing the temperature. Chen et al. [35] also investigate the properties of PBGs for 2D SDPCs by the plane wave expansion method. They found that the PBG is strongly dependent on the temperature, which makes it possible for 2D SDPCs to be used as a temperature-controlled optical shutter. Dai et al. [36] used the superconductor to design the omnidirectional reflector by a ternary periodical structure. Simulation results showed that the OBG can be extended markedly in the 1D ternary PCs and the bandwidth of OBG can also be tuned by varying the external temperature. Zhang et al. [37, 38] enlarged the OBGs of 1D SDPCs with the binary Fibonacci sequence and binary graded structure.

All the works mentioned above focused on the OBGs or PBGs of 1D and 2D SDPCs and only consisted of a single binary, ternary periodic structure, or Fibonacci quasiperiodic structure, respectively. To the best of our knowledge, the OBGs in ternary PCs with the Thue–Mores sequence containing superconductor have been rarely reported. In this paper, the OBG of 1D ternary PCs based on a new Thue–Mores sequence aperiodic structure containing superconductor is investigated by the TMM in detail, and simulation results show that such OBG is insensitive to the incident angle and the polarization of the EM wave. The reflectance is used to analyze the effects of the thickness of superconductor layer, the thickness of dielectric layer, the ambient temperature of the system, and the damping coefficient of superconductor layer on the properties of OBG, respectively. The results show that the bandwidth and central frequency of OBG can be notably enlarged by changing the thicknesses of superconductor and dielectric layers but cease to change with increasing the Thue–Mores order. The OBG also can be tuned by the ambient temperature of the system especially close to the critical temperature. However, the damping coefficient of superconductor layer has no effects on the OBG. The relative bandwidth of OBG also is investigated by the parameters as mentioned above. It is shown that such new 1D ternary SDPCs have a superior feature in the enhancement of bandwidth of OBG compared with the conventional ternary SDPCs and conventional ternary SDPCs with the Thue–Mores aperiodic structure (as depicted in Fig. 1(c)).

Fig. 1
figure 1

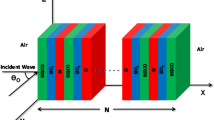
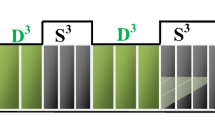
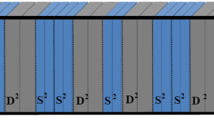
Schematic diagram of three kinds of 1D ternary SDPCs consisting of quartz glass (A), air (B) and superconductor (S) under any incidence angle (θ) for TE and TM waves, (a) conventional 1D ternary SDPCs, (b) conventional 1D Thue–Mores aperiodic ternary SDPCs, and (c) 3th Thue–Mores aperiodic 1D ternary SDPCs with a new structure, respectively

Full size image

2 Theoretical Model and Method

Schematic view of oblique indent EM wave in three kinds of 1D SDPCs composed of two kinds of dielectric layers and superconductor layers are described in Fig. 1. The conventional 1D ternary SDPCs is plotted in Fig. 1(a). As shown in Figs. 1(b)–(c), we consider a 1D periodic layered structure in each cell following the Thue–Mores sequence. The Thue–Mores sequence can be generated by the rule \(S_{n} = S_{n-1}\widetilde{S_{n-1}}\) for level n≥1; here, n represents the Thue–Mores order and \(\widetilde{S_{n-1}}\) is the complement of S n−1, where all letters are interchanged to their opposite. In the case of Fig. 1(b), starting from a double layers S 0={AB}, one obtains S 1={ABS}, S 2={ABSSAB}, S 3={ABSSABSABABS}, and so forth, with each step giving a sequence of generation number increased by one. However, the new 1D ternary Thue–Mores aperiodic SDPCs start from four layers S 0={SABS}; one obtains S 1={SABSS}, S 2={SABSSSSABS}, S 3={SABSSSSABSSSABSSABSS}, and so forth. Layers A, B, and S represent quartz glass with a thickness of d A , air with thickness of d B , and superconductor with thickness of d P , respectively. As an example, the third sequence of S 3 is S 3={SABSSSSABSSSABSSABSS} as depicted in Fig. 1(c). Here, we use ε a , ε b , and ε s to describe the relative permittivity for dielectric A, B, and superconductor, respectively, as we know the superconductor is a kind of frequency dependence dielectric. In order to define the properties of superconductor, the Gorter–Casimir two-fluid model [33] is adopted to describe the electromagnetic response of the superconductor layer with the absence of an external magnetic field. The effective relative dielectric function of the superconductor is represented as follows [33]:

$$ \varepsilon_{\mathrm{s}}(\omega ) = \varepsilon_\mathrm{c} \biggl[ 1 - \frac{\omega_\mathrm{sp}^{2}}{\omega ^{2}} - \frac{\omega_\mathrm{np}^{2}}{\omega (\omega + j\gamma )} \biggr] $$
(1)

with

$$ \omega_\mathrm{sp} = \sqrt{\frac{n_\mathrm{s}e^{2}}{m\varepsilon_{0} \varepsilon_\mathrm{c}}}, \quad \omega_\mathrm{np} = \sqrt{\frac{n_{n}e^{2}}{m\varepsilon_{0}\varepsilon_\mathrm{c}}}, $$
(2)

where ε c is the dielectric constant of the crystal, ω np and ω sp are the plasma frequencies of the normal conducting electrons and the superconducting electrons, respectively. γ is the damping term of normal conducting electrons. n s and n n are densities of superconducting electrons and normal conducting electrons, respectively. e and m are the charge and mass of the electron. We can rewrite Eq. (2) in the form by using the Gorter–Casimir result [31]:

$$ \everymath{\displaystyle }\begin{array}[b]{@{}l} \omega_\mathrm{sp} = \frac{c}{\lambda_{0}\sqrt{\varepsilon_\mathrm{c}}} \sqrt{ \biggl( 1 - \biggl( \frac{T}{T_\mathrm{c}} \biggr)^{4} \biggr)}, \qquad \omega_\mathrm{np} = \frac{c}{\lambda_{0}\sqrt{\varepsilon_\mathrm{c}}} \biggl(\frac{T}{T_\mathrm{c}} \biggr)^{2} \\ \noalign {\vspace {12pt}} \end{array} $$
(3)

where λ 0 is the London penetration length at temperature T=0, and T c is the critical temperature of a superconductor. ω is electromagnetic wave frequency, and c is the light speed in vacuum. Substituting Eq. (3) into Eq. (1), the temperature dependent dielectric function of the superconductor can be expressed as

$$ \everymath{\displaystyle }\begin{array}[b]{@{}l} \varepsilon_{\mathrm{s}}(\omega ) = \varepsilon_\mathrm{c} - \frac{c^{2}}{\omega ^{2}\lambda_{0}^{2}} \biggl[ 1 - \biggl( \frac{T}{T_{\mathrm{c}}} \biggr)^{4} \biggr] - \frac{c^{2}}{\omega (\omega + j\gamma )\lambda_{0}^{2}} \biggl( \frac{T}{T_{\mathrm{c}}} \biggr)^{4} \\ \noalign {\vspace {11pt}} \end{array} $$
(4)

The EM wave is incident from the vacuum to the nth order Thue–Mores multilayer with incident angle θ. For the transverse electric (TE) wave, the electric field E is polarized along the y direction. Suppose wave vectors K(ω) lie in xz plane. In order to calculate the reflectance for a Thue–Mores multilayered structure, the TMM is used [35–37]. According to this method, we can set up the characteristic corresponding to the electric and magnetic fields at any two positions in the adjacent layer, which is given as

$$ \mathrm{M}_{l} = \left ( \begin{array}{c@{\quad }c} \cos \beta_{l} & \frac{j}{p_{l}}\sin \beta_{l} \\ jp_{l}\sin \beta_{l} & \cos \beta_{l} \end{array} \right ) $$
(5)

where β l =k 0 n l d l cosθ l and \(p_{l} = \frac{n_{l}}{Z_{0}} \cos \theta_{l}\) (TE wave), \(p_{l} = \frac{1}{Z_{0}n_{l}}\cos \theta_{l}\) (TM wave) with l=A, B, S, and impedance of vacuum \(Z_{0} =\sqrt{\mu_{0}} /\sqrt{\varepsilon_{0}}\). Here, d l is the thickness of periodic length of the d A , d B , and d P with refractive indices n A , n B , and n S , respectively. Thus, the transfer matrices M j are M 1(=M S M A M B M S M S ), M 2(=M S M A M B M S M S M S M S M A M B M S ), and M 3(=M S M A M B M S M S M S M S M A M B M S M S M S M A M B M S M S M A M B M S M S ) for S 1, S 2, and S 3, respectively. If the order of the Thue–Mores sequence is N, the total transfer matrix of the Nth order Thue–Mores sequence M N can be deduced from the following recursion relations:

$$ \mathbf{M}_{N} = \mathbf{M}_{N - 1}\widetilde{\mathbf{M}_{N - 1}} \quad (N \ge 2) $$
(6)

So, the total translation matrix M is obtained to be

$$ \mathbf{M} = \prod_{k = 1}^{N_{1}} \mathbf{M}_{k} = \left ( \begin{array}{c@{\quad }c} M_{11} & M_{12} \\ M_{21} & M_{22} \end{array} \right ) $$
(7)

N 1 refers to the number of layers in the SDPCs. The reflection coefficient of the considered structure is given by

$$ r = \frac{(M_{11} + M_{12}p_\mathrm{s})p_{0} - (M_{21} + M_{22}p_\mathrm{s})}{ (M_{11} + M_{12}p_\mathrm{s})p_{0} + (M_{21} + M_{22}p_\mathrm{s})} $$
(8)

Here, p 0 and p s are the first and last mediums of the structure, which given as p 0=n 0cosθ 0/Z0, p s=n scosθ s/Z0 (TE wave) and p 0=cosθ 0/(n 0Z0), p s=cosθ s/n 10Z0 (TM wave). In our case, we have taken n 0=n 10=1 for the vacuum. The reflectance is related by

$$ R = | r |^{2} $$
(9)

In order to study the properties of OBG for such 1D ternary SDPCs, the relative bandwidth is defined

$$ \Delta \omega /\omega_{i} = 2(\omega_\mathrm{up} - \omega_\mathrm{low})/(\omega_\mathrm{up}\ + \omega_\mathrm{low}) $$
(10)

where ω up and ω low are the upper and lower limits of a OBG, respectively.

3 Results and Discussion

In order to investigate the OBG in the terahertz frequency region, we choose the structure parameters as follows: ε A =4, μ A =1, d A =400 nm, ε B =1, μ B =1, and d B =200 nm, respectively. The superconductor layer is taken to be T c=9.2 K, λ 0=83.4 nm, and γ=1×105 Hz, respectively. Assumed the thickness of superconductor layer d P =30 nm, the ambient temperature of system T=4.2 K, and ε c=1, respectively. The Thue–Mores order is 5. Here, we only focus on the Bragg gap in the frequency domain 100–300 THz.

3.1 Superior Feature in the Enhancement of the Frequency Range of OBG

Firstly, we investigate the OBG of 1D conventional binary dielectric PCs consisting of alternate dielectric A and B. The dependence of the PBG on the frequency and incident angle for TM polarizations is plotted in Fig. 2(a). In Fig. 2(a), the red areas indicate the Bragg gaps or high-reflectance ranges. As shown in Fig. 2(a), there do not exist OBGs obviously for such binary dielectric PCs, and the PBGs of TM polarization are closed at an incident angle of 66∘ due to Brewster’s angle [37]. The criterion for the existence of OBG is that there are no propagating modes which can couple with incident wave. Thus, we can combine the superconductor, dielectric A and dielectric B with a new Thue–Mores aperiodic structure to form a ternary SDPC as depicted in Fig. 1(c) to open the Brewster’s window. For comparison, we plot the dependence of the PBGs on the frequency and incident angle for both polarizations of such new 1D ternary SDPCs in Fig. 2(b). The gray areas indicate the OBGs. As shown in Fig. 2(b), there exists an OBG obviously, and the PBGs are opened at an incident angle of 66∘. The both edges of OBG are upward to higher frequencies with increasing the incident angle for both polarizations. The OBG frequency region runs from 168.74 to 215.38 THz, and the frequency range is 46.64 THz. From Fig. 2(b), it is clearly seen that the OBG is sensitive to the incident angle for TM polarization but is insensitive for TE polarization. For TM polarization, the OBG frequency region spans from 168.74 to 215.38 THz. The OBG for TE polarization in the frequency range runs from 125.15 to 215.38 THz. Therefore, we can draw a conclusion that OBG for TM polarization determine the bandwidth of OBG. Such property is different obviously from that of the OBG in a conventional 1D dielectric PCs since the OBG for TM polarization is narrower than that for TE polarization, except for normal incidence. Consequently, we can obtain the OBG by introducing the superconductor in 1D dielectric PCs with the new Thue–Mores aperiodic structure as we proposed, and the frequency range of OBG can be enlarged.

Fig. 2
figure 2

(a) Photonic band structure of 1D binary dielectric-air PCs in terms of angular frequency and incidence angle. The red areas (background) correspond to Bragg gaps or high-reflectance ranges, and (b) reflectance spectra of 1D ternary SDPCs with a new Thue–Mores aperiodic structure at various incident angles. The black solid (read dash dot) curves are for TM (TE) polarization, and the gray areas correspond to the OBG

Full size image

In order to illustrate such new 1D SDPCs have a superior feature in the enhancement of the frequency range of OBG, we plot the dependence of the PBGs of different PCs structures on the normal incident with analogous structure parameters chosen as mentioned above in Fig. 3. As shown in Figs. 3(a)–(d), the 1D ternary SDPCs based on the new Thue–Mores aperiodic structure have a superior feature in enlarging the PBGs. The frequency range and relative bandwidth of PBG are larger than those for other three structures obviously. Figure 3(d) shows that the PBG displays from 119.43 to 215.38 THz, and the bandwidth is 95.95 THz. As compared to Figs. 3(a)–(c), the PBG is obviously enlarged, and the bandwidth of PBG is increased by 58.16, 37.58, and 31.34 THz, respectively. Thus, the 1D ternary SDPCs as we proposed have a superior feature in increasing the frequency range of PBG. For comparison, we also plot the dependence of the PBG for 1D ternary SDPCs based on the new Thue–Mores aperiodic structure on the incident angle and angular frequency for both polarizations with analogous structure parameters chosen as above in Fig. 4, where the area between two white lines is the OBG. As shown in Fig. 4(a), the OBG region runs 168.74 to 215.38 THz and the frequency range is 46.64 THz. However, there is not the OBG as shown in Figs. 4(c) and (b) (PCs structure as depicted in Figs. 1(a) and (b)). The bandwidth of OBG is increased by 46.64 THz as compared to Figs. 4(b)–(c), respectively. Thus, the 1D ternary SDPCs based on the new Thue–Mores aperiodic structure have a superior feature in increasing the bandwidth of OBG compared with the conventional ternary SDPCs and conventional ternary Thue–Mores aperiodic SDPCs.

Fig. 3
figure 3

Reflectance of 1D PCs versus frequency at normal incidence with different structure, (a) binary PCs without superconductor, (b) 1D conventional ternary Thue–Mores aperiodic SDPCs, (c) 1D conventional ternary SDPCs, and (d) the SDPCs with the new Thue–Mores aperiodic structure, respectively

Full size image
Fig. 4
figure 4

Photonic band structure of (a) 1D ternary SDPCs with the new Thue–Mores aperiodic structure, (b) conventional 1D ternary Thue–Mores aperiodic SDPCs, and (c) conventional 1D ternary SDPCs in terms of angular frequency and incidence angle, respectively. The area between two white lines is the OBG, and the red areas (background) indicate Bragg gaps or high-reflectance ranges

Full size image

3.2 Effects of Thue–Mores Order on OBG

Secondly, we study the dependence of the OBG on the Thue–Mores order (N≥1) for normal incidence. We plot the normal incidence reflection spectra for the different order Thue–Mores structures as a function of the frequency with S 1 (Fig. 5(a)), S 2 (Fig. 5(b)), S 3 (Fig. 5(c)), and S 4 (Fig. 5(d)) in Fig. 5. It can see from Fig. 5 that, only one unit cell of such SDPCs cannot form the PBG as shown in Fig. 5(a). With increasing order of the Thue–Mores sequence, the central frequency of the PBG (167.41 THz), which we focus on remains invariant and the edges of the PBG become much shaper. However, the narrow transmission peeks appear between the reflectance bands. It also can be seen from Fig. 5 that, as increasing the Thue–Mores order N from 1 to 4, the upper edge of the PBG shifts up to higher frequencies, but the lower edge of the PBG shifts down to lower frequencies, and the frequency region of PBG becomes larger. If we continue to increase the Thue–Mores order as shown in Fig. 6. As shown in Fig. 6, the reflection spectra for normal incidence are shown in the cases of such new ternary Thue–Mores structures where S 5 (Fig. 6(a)), S 6 (Fig. 6(b)), S 7 (Fig. 6(c)), and S 9 (Fig. 6(d)). It is shown that, if increasing the Thue–Mores order N from 5 to 9, the both edges of the PBG remain unchanged but the some transmission peeks decrease or disappear. The frequency range of the PBG runs from 119.43 to 215.38 THz and the bandwidth is 95.95 THz. Consequently, the bandwidth and central frequency of OBG cease to change with increasing the Thue–Mores order.

Fig. 5
figure 5

Normal incident reflection spectra for the different order Thue–Mores structures as a function of the frequency with (a) S 1, (b) S 2, (c) S 3, and (d) S 4, respectively

Full size image
Fig. 6
figure 6

Normal incident reflection spectra for the different order Thue–Mores structures as a function of the frequency with (a) S 5, (b) S 6, (c) S 7, and (d) S 9, respectively

Full size image

3.3 Effects of the Thickness of Superconductor Layer on OBG

Thirdly, we analyze the effect of thickness of the superconductor layer on the OBG in theory. We plot the reflectance of 1D ternary SDPCs based on the new Thue–Mores aperiodic structure as a function of the thickness of superconductor layer at normal incidence in Fig. 7. The red regions denote Bragg gaps or the high-reflectance ranges. As shown in Fig. 7, the edges of the PBG which we focus on are sensitive to increasing the thickness of superconductor layer, and the frequency shifts of the edges are obvious. With increasing the thickness of superconductor layer, the upper edge of PBG shifts upward to higher frequencies but the lower edge is downward to lower frequencies. Thus, the frequency range of PBG can be broadened by increasing the thickness of superconductor layer. To take a close look at the dependence of the OBG on the thickness of superconductor layer, the frequency range of OBG as a function of the superconductor layer thickness also is plotted in Fig. 8. From Fig. 8, one can see, the lower edge of OBG is downward to lower frequencies but the upper edge of OBG is upward to higher frequencies as the thickness of superconductor layer increased. The bandwidth of OBG is notably enlarged with increasing the superconductor thickness. As shown in Fig. 8, the frequency rang of OBG runs from 145.21 to 243.76 THz, and the frequency width is 98.55 THz as the thickness of superconductor layer is creased from d P =20 nm to d P =80 nm. The bandwidth of OBG is increased by 80.13 THz as compared to the case of d P =20 nm. We also plot the relative bandwidth as a function of the superconductor thickness for the OBG in Fig. 9. As shown in Fig. 9, the relative bandwidth of OBG increases with increasing the thickness of superconductor layer. The maximum relative bandwidth is 50.74 %, which can be found at the case of d P =80 nm. The relative bandwidth of OBG is increased by 40.78 % in as compared to the case of d P =20 nm. From the aforementioned discussions, the frequency ranges and relative bandwidth of OBG are obviously enlarged with increasing the thickness of superconductor layer. Consequently, the bandwidth of OBG is enlarged.

Fig. 7
figure 7

Reflection coefficients of 1D ternary SDPCs with the new Thue–Mores aperiodic structure as a function of the superconductor thickness at normal incidence. The red areas (background) indicate Bragg gaps or high-reflectance ranges

Full size image
Fig. 8
figure 8

The frequency range of OBG for 1D ternary SDPCs with the new Thue–Mores aperiodic structure as a function of the superconductor thickness

Full size image
Fig. 9
figure 9

The relative bandwidth of OBG as a function of the superconductor thickness

Full size image

3.4 Effects of the Thickness of Dielectric Layer on OBG

In order to analyze the influence of the thickness of dielectric layer on the OBG, we just need study the effects of the thickness of dielectric layer A on the OBG since the similar conclusion also can be obtained by investigating the effects of the thickness of dielectric layer B. We plot the reflection coefficients of 1D ternary SDPCs based on the new Thue–Mores aperiodic structure as a function of the thickness of dielectric layer A at normal incidence in Fig. 10. The red areas denote Bragg gaps or the high-reflectance ranges. It can be seen from Fig. 10 that the edges of PBGs are sensitive to increasing the thickness of dielectric layer A, and the frequency shifts of the edges are obvious. The bandwidths of PBGs are notably narrowed, and the edges and central frequencies of PBGs are downward to lower frequencies with increasing the thickness of dielectric layer A. The number of PBGs is also sensitive to increasing the thickness of dielectric layer A, and the more PBGs appear. Thus, the bandwidths of PBGs are narrowed, and the central frequencies shift downward to lower frequencies with increasing the thickness of dielectric layer A. The number of PBGs also can be increased. To take a close look at the dependence of OBG on the thickness of dielectric layer A, the frequency range of OBG for such new 1D ternary SDPCs as a function of the thickness of dielectric layer A is plotted in Fig. 11. As shown in Fig. 11, the edges and central frequency of OBG shift downward to lower frequencies, and the frequency range of OBG is narrowed obviously with increasing the thickness of dielectric layer A. The OBG spans from 100.50 to 121.84 THz, and the bandwidth is 21.34 THz, as the thickness of dielectric layer A is creased from d A =300 nm to d A =800 nm. The bandwidth of OBG is decreased by 8.89 THz as compared to the case of d A =300 nm. In Fig. 12, the relative bandwidth of OBG as a function of the thickness of dielectric layer A is plotted. As shown in Fig. 12, the relative bandwidth of the OBG has an increasing trend with increasing the thickness of dielectric layer A. The maximum and minimum relative bandwidths of OBG are 19.86 % and 12.84 %, which can be found at the cases of d A =800 nm and d A =300 nm, respectively. As mentioned above, the frequency range of OBG is narrowed, and the number of PBGs is increased with increasing the thickness of dielectric layer A. The relative bandwidth of OBG also can be tuned by the thickness of dielectric layer A. Consequently, the bandwidth and the number of PBGs can be modulated by the thickness of the dielectric layer.

Fig. 10
figure 10

Reflection coefficients of 1D ternary SDPCs with the new Thue–Mores aperiodic structure as a function of the thickness of dielectric layer A at normal incidence. The red areas (background) indicate Bragg gaps or high-reflectance ranges

Full size image
Fig. 11
figure 11

The frequency range of OBG for 1D ternary SDPCs with the new Thue–Mores aperiodic structure as a function of the thickness of dielectric layer A

Full size image
Fig. 12
figure 12

The relative bandwidth of OBG as a function of the thickness of dielectric layer A

Full size image

3.5 Effects of the Damp Coefficient of Superconductor Layer on OBG

Next, we investigate the influence of the damp coefficient of superconductor layer on the OBG. If temperature of superconductor is larger then 4.55 K, the damp coefficient of superconductor layer should be considered [33]. Based on T=6 K for different damp coefficient of superconductor layer, the reflectance of 1D ternary SDPCs based on the new Thue–Mores aperiodic structure versus frequency at normal incident is plotted in Fig. 13. As shown in Figs. 13(a)–(d), the frequency ranges of PBG as we focus on at normal incident are obviously unchanged with increasing the damp coefficient of superconductor layer. It can be seen from Fig. 13(d) that the bandwidth of PBG is 119.43 to 215.38 THz and the bandwidth is 95.95 THz, as the damp coefficient of superconductor layer is γ=1×1011 Hz. When the damp coefficient of superconductor layers is decreased to null, the PBG is till unchanged as shown in Fig. 13(a) compared to Fig. 13(d). To study the dependence of OBG on the damp coefficient of the superconductor layer, the reflectance of 1D ternary SDPCs based on the new Thue–Mores aperiodic structure as a function of \(\log _{10} ^{\gamma}\) at T=6 K is plotted in Fig. 14. From Fig. 14, we can clearly see that the edges of OBG are almost unchanged with increasing the value of \(\log _{10} ^{\gamma}\). The frequency range of OBG runs from 168.74 to 215.38 THz and the frequency range is 46.64 THz, as the \(\log _{10} ^{\gamma}\) is creased from \(\log _{10}^{\gamma} =0\) to \(\log _{10} ^{\gamma} =11\) at T=6 K. To take a close look at the dependence of the relative bandwidth for OBG on the damp coefficient of superconductor layer, we present the relative bandwidth as a function of \(\log _{10} ^{\gamma}\) is plotted in Fig. 15. As shown in Fig. 15, the relative bandwidth of OBG is 24.33 %, which is never changed with increasing the value of \(\log _{10} ^{\gamma}\). As mentioned above, the frequency range and relative bandwidth of OBG can not be changed by increasing the damp coefficient of superconductor layer. Consequently, whether or not the contribution of the normal conducting electrons is considered, the damping coefficient of superconductor layer has no effect on the frequency range and relative bandwidth of OBG under low-temperature conditions.

Fig. 13
figure 13

Reflectance of 1D ternary SDPCs with the new Thue–Mores aperiodic structure versus frequency at normal incidence with different damp coefficient of superconductor layers at T=6 K

Full size image
Fig. 14
figure 14

The frequency range of OBG for 1D ternary SDPCs with the new Thue–Mores aperiodic structure as a function of \(\log_{10} ^{\gamma}\) at T=6 K

Full size image
Fig. 15
figure 15

The relative bandwidth of OBG as a function of \(\log _{10} ^{\gamma}\) for the OBG at T=6 K

Full size image

3.6 Effects of the Ambient Temperature on OBG

Finally, we investigate the influence of the ambient temperature on the OBG. The reflectance of 1D ternary SDPCs based on the new Thue–Mores aperiodic structure as a function of the ambient temperature at normal incidence is plotted in Fig. 16. As shown in Fig. 16, the PBG which we focus on is hardly changed, as the ambient temperature is less than 6 K. If the ambient temperature is larger than 6 K, the edges and central frequency of PBG shift downward to lower frequencies, and the bandwidth of PBG significantly reduced especially close to the critical temperature. Therefore, we can draw a conclusion that the PBG is not changed obviously at the low ambient temperature (T<6 K). If the ambient temperature is larger than 6 K, the PBG can be broadened by decreasing the ambient temperature. To investigate the dependence of OBG on the ambient temperature, we plot the bandwidth of OBG as a function of the ambient temperature in Fig. 17. As shown in Fig. 17, the both edges of OBG are unchanged first then shift to the lower frequencies. The frequency range of OBG spans from 295.22 to 347.01 THz, and the bandwidth is 51.79 THz, as the ambient temperature is creased from T=1 K to T=9 K. The bandwidth of the OBG is decreased by 44.79 THz as compared to the case of T=1 K. To take a close look at the dependence of the relative bandwidth for OBG on the ambient temperature, the relative bandwidth as a function of the ambient temperature for the OBG is plotted in Fig. 18. From Fig. 18, it is clearly seen that the relative bandwidth of OBG is unchanged first then shift to the smaller value regions. If the ambient temperature is less than 6 K, the maximum the relative bandwidth of OBG is 25.40 %, which can be found at the case of T=4 K. The minimum relative bandwidth of OBG is 16.23 %, which can be found at the case of T=9 K. As mentioned above, the OBG can be tuned by changing the ambient temperature as the temperature is very close to the critical temperature. The larger frequency range and relative bandwidth of OBG can be obtained at lower ambient temperature. Consequently, we can obtain the wider OBG by controlling the ambient temperature.

Fig. 16
figure 16

Reflection coefficients of 1D ternary SDPCs with the new Thue–Mores aperiodic structure as a function of the ambient temperature. The red areas (background) correspond to Bragg gaps or high-reflectance ranges

Full size image
Fig. 17
figure 17

The frequency range of OBG for 1D ternary SDPCs with the new Thue–Mores aperiodic structure as a function of the ambient temperature system

Full size image
Fig. 18
figure 18

The relative bandwidth of OBG as a function of the ambient temperature

Full size image

4 Conclusion

In summary, the PBG and OBG of 1D ternary SDPCs composed of homogeneous, isotropic dielectric quartz glass (dielectric A), air (dielectric B), and superconductor, arranged according to a recursion rule of the new Thue–Mores sequence have been investigated by the TMM in detail. In contrast to the OBG originating from a zero-\(\bar{n}\) gap or single negative gap, an OBG originating from the Bragg gap can be found in such 1D SDPCs, which originates from EM wave scattering of propagating modes. The numerical results show that the bandwidth and central frequency of OBG can be notably enlarged by changing the thicknesses of superconductor and dielectric layers but cease to change with increasing the Thue–Mores order. The OBG also can be manipulated by the ambient temperature of system especially close to the critical temperature. The relative bandwidth of OBG also can be tuned obviously by above parameters except for the damping coefficient of superconductor. However, the damping coefficient of superconductor has no effect on the bandwidth and central frequency of OBG. It is shown that such 1D ternary SDPCs based on the new Thue–Mores aperiodic structure as we proposed have a superior feature in the enhancement of bandwidth of OBG compared with the conventional ternary SDPCs and conventional ternary Thue–Mores aperiodic SDPCs. These results may provide theoretical instructions to design the future SDPCs devices.