1 Introduction

One dimensional Superconducting Photonic quasicrystals (SPQCs) are composed of alternating Dielectric and superconductor layers. They intervene in many experimental and theoretical investigations due to their interesting physical properties (Rahimi 2016; Wu and Gao 2015; Segovia-Chaves and Vinck-Posadaa 2018; Trabelsi et al. 2019a; Lee and Wu 2010).The concept of photonic quasicrystal was first introduced by Shechtman (Shechtman et al. 1984), as an artificial superlattice which is built according to quasiperiodic sequences. We note that the quasiperiodic arrangement is more different than conventional photonic crystals (PCs) since it can be considered as an intermediate class between the random and the periodic media with perfect long-range order and lack translational symmetry. We mention that these multilayer’s stacks contain pile of two different layers H and L arranged according to specific inflation rule obeying to a mathematical sequence called photonic quasicrystals (PQCs).

A great deal of attention had been paid to improve optical devices (Trabelsi et al. 2019b, c; Ji and Jin-xia 2012) via deterministic aperiodic Fibonacci sequence. In particular, Photonic crystal containing superconductor has attracted researcher’s interest due to their important properties such as lower losses, lower dispersion and wider bandwidths compared to metals (Aly et al.2012). Hence, the superconductor into photonic crystal lies on many potential applications like reflectors (Zang et al. 2014) and filters (Upadhyay et al. 2015; Lin et al. 2010; Barvestani 2015; Zhang et al. 2013; Talebzadeha and Bavagha 2018) thanks to their ability to improve the characteristics of main Photonic Band Gaps (PBGs).

Moreover, the well-studied PBG may change with quasiperiodic order, operating temperature of system, and constituent materials lead to the design of large OBG (Wu et al. 2009; Hu et al. 2019). Also, the autosimilarity of distributed (L/H) in photonic quasicrystals can be reappear in the spectrum. It is well-known that the combination of the reflected waves in phase and incident waves at each interface produces a standing wave that does not allow to propagate through the multilayers stack (Aly et al. 2020) and allows the existence of forbidden zones of signal propagation at OBG frequency range. The OBG is made generally from periodic or quasiperiodic structure which is built according certain quasiperiodic matching rules. These PBGs prohibit the propagation of wave in a given frequency range for both transverse electric/magnetic modes.

The destructive interference at all interfaces of the multilayered stacks causes high reflectivity band gaps. These forbidden bands without propagative modes are very sensitive to refractive index materials, thickness of the constituent dielectric, the kind of arrangement of layers within the multilayered stacks and external parameters, such as temperature, pressure (Segovia-Chaves et al. 2020).Therefore, the insert defects into graded photonic quasicrystals provides an interesting properties like localized states, band edge resonance, ability to manipulate and confine the propagating light. This allows to develop efficient optical devices (Trabelsi et al. 2020).

Recently, the authors in Herrera et al. (2018) and Ramanujam et al. (2019) treated superconductor instead of dielectric into heterostructure, this improves the characteristics of PBG and enhances the OBG behavior by tuning the temperature of superconductor and thicknesses of the non-dispersive materials. Indeed, inserting defect within the new type of superconducting photonic devices offers a broad OBG with structural resonance that allows the propagation of photon at selective frequency. These effects divided the PBG in sub band gaps. It may be useful in several areas as the Dense Wavelength Division Multiplexing (DWDM) (Trabelsi 2019).

In this work, we develop an extending omnidirectional high reflector with tenability around visible wavelengths, based on hybrid superconducting photonic quasicrystals (SPQC). In order to obtain a structural Bragg gap along the visible light spectrum, we organize the main multilayered stacks following Generalized Fibonacci (GF) sequence. For estimated GF (m, n) sequences, the main limited band gaps are enhanced by tuning the operating superconductor’s temperature. The strategy for improving the characteristics of OBG, is applying a simple deformation on layers thicknesses. The reorganization of heterolayers by juxtaposition of regular GF sequence as (GF)p with \(p \ge 2\), estimated deformation h permits to enhance the proper PBG. To open structural peaks within the OBG spectrum, we apply specific defect along the main SPQC structure. In which, the insert defect within the GF stacks opens sharply microcavities with high localization modes that dependent significantly to optical parameters of system and on superconductor temperature.

2 Problem formulation

In the present work, we use the Transfer Matrix Method (TMM) to determine the photometric responses through the 1D SPQCs for TE/TM incident wave. We report also the theoretical Gorter–Casimir two-fluid model (GCTFM) (Trabelsi 2019; Baraket et al. 2017) to depict the response of the superconducting materials.

We start by noting that according to the GCTFM (Trabelsi 2019; Baraket et al. 2017), the complex conductivity of a superconductor obeys to the following expression:

$$\sigma (\omega ){ = }\frac{{ - {\text{ie}}^{2} n_{s} }}{{{\text{m}}\omega }}$$
(1)

With, ns is the electron density and \({\upomega }\) represents the frequency of incident electromagnetic wave. e and m define electron charge and mass, respectively.

Based on the approximation condition indicated in (Trabelsi 2019; Baraket et al. 2017), the conductivity can be expressed in terms of the complex conductivity as:

$$\sigma (\omega ) \approx \frac{ - {\text{i}}}{{\omega \mu_{{0}} \lambda_{L}^{2} {\text{(T)}}_{{_{{}} }} }}$$
(2)

where, \({\uplambda }_{{\text{L}}}\) is the London temperature penetration depth (Trabelsi 2019; Baraket et al. 2017) given by

$$\lambda_{{\text{L}}} {\text{(T) = }}\frac{{\lambda {(0)}}}{{\sqrt {{1} - {\text{G(T)}}} }}$$
(3)

where, \({\text{G(T) = (}}{{\text{T}} \mathord{\left/ {\vphantom {{\text{T}} {{\text{T}}_{{\text{c}}} {)}^{{4}} }}} \right. \kern-\nulldelimiterspace} {{\text{T}}_{{\text{c}}} {)}^{{4}} }}\) denotes the Gorter–Casimir function (Trabelsi 2019) with \({\text{T}}_{{\text{c}}}\) and \({\text{T}}\) are the critical and the operating temperatures of the considered superconductor, respectively. The refractive index of the superconductor.

(ns) can be derived from the above equation (Trabelsi 2019; Baraket et al. 2017):

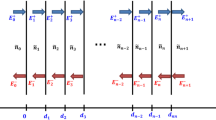
$${\text{n}}_{{\text{s}}} { = }\sqrt {{1 - }\frac{{1}}{{{\upomega }^{{2}} {\upmu }_{{0}} {\upvarepsilon }_{{0}} {\uplambda }_{{\text{L}}}^{{2}} }}}$$
(4)

Before stating our results, we note that the transmittance spectrum of our structure can be well calculated by a TMM method. We assume that the refractive index of limit media of quasiperiodic structure is equal to 1.

For both modes TE and TM waves, the entrance amplitude fields \({\text{E}}_{{0}}^{ + }\), \({\text{E}}_{{0}}^{ - }\) and the output field of stratified medium \({\text{E}}_{{\text{m + 1}}}^{ + }\) are related by the \({\text{2x2}}\) transfer matrix coefficients (Trabelsi et al. 2013; BenAli et al. 2020):

$$\left[ {\begin{array}{*{20}c} {{\text{E}}_{{0}}^{ + } } \\ {{\text{E}}_{{0}}^{ - } } \\ \end{array} } \right]{ = }\prod\limits_{{\text{i = 1}}}^{{\text{m}}} {\frac{{{\text{C}}_{{\text{j}}} }}{{{\text{t}}_{{\text{j}}} }}} \left[ {\begin{array}{*{20}c} {{\text{E}}_{{\text{m + 1}}}^{ + } } \\ {{\text{E}}_{{\text{m + 1}}}^{ - } } \\ \end{array} } \right]$$
(5)

where, \({\text{C}}_{{\text{j}}}\) denotes the transfer matrix and it can be written for both propagation modes TE and TM as in Trabelsi et al. (2013):

$${\text{C}}_{{\text{j}}} { = }\left( {\begin{array}{*{20}c} {{\text{e}}^{{{\text{i}}\varphi _{{\text{j}} - 1} }} } & {{\text{r}}_{{\text{j}}} {\text{e}}^{{-{\text{i}}\varphi _{{\text{j}} - 1} }} } \\ {{\text{r}}_{{\text{j}}} {\text{e}}^{{{\text{i}}\varphi_{{\text{j}} - 1}}} } & {{\text{e}}^{{- {\text{ i}}\varphi _{{\text{j}} - 1} }} } \\ \end{array} } \right)$$
(6)

where, \({\text{t}}_{{\text{j}}}\) and \({\text{r}}_{{\text{j}}}\) are the Fresnel coefficients that take the following form (see Trabelsi et al. 2013; BenAli et al. 2020):

For TE mode, \({\text{t}}_{{\text{j}}}\) and \({\text{r}}_{{\text{j}}}\) can be defined as follows:

$${{\text{r}}_{\text{j}}} = \frac{{{{\hat n}_{{\text{j}} - 1}}\cos {\theta _{\text{j}}} - {{\hat n}_{\text{j}}}\cos {\theta _{{\text{j}} - 1}}}}{{{{\hat n}_{{\text{j}} - 1}}\cos {\theta _{\text{j}}} + {{\hat n}_{\text{j}}}\cos {\theta _{{\text{j}} - 1}}}};\;{{\text{t}}_{\text{j}}} = \frac{{{\text{2}}{{\hat n}_{{\text{j}} - 1}}\cos {\theta _{{\text{j}} - 1}}}}{{{{\hat n}_{{\text{j}} - 1}}\cos {\theta _{\text{j}}} + {{\hat n}_{\text{j}}}\cos {\theta _{{\text{j}} - 1}}}}$$
(7)

As well as, for TM mode, the two Fresnel coefficients can be defined as:

$${{\text{t}}_{\text{j}}}{\text{ = }}\frac{{{\text{2}}{{\hat n}_{{\text{j}} - 1}}{\text{cos}}{\theta _{{\text{j}} - 1}}}}{{{{\hat n}_{{\text{j}} - 1}}{\text{cos}}{\theta _{{\text{j}} - 1}}{\text{ + }}{{\hat n}_{\text{j}}}{\text{cos}}{\theta _{\text{j}}}}};\;\;{{\text{r}}_{\text{j}}}{\text{ = }}\frac{{{{\hat n}_{{\text{j}} - {\text{1}}}}{\text{cos}}{\theta _{{\text{j}} - 1}} - {{\hat n}_{\text{j}}}{\text{cos}}{\theta _{\text{j}}}}}{{{{\hat n}_{{\text{j}} - {\text{1}}}}{\text{cos}}{\theta _{{\text{j}} - 1}}{\text{ + }}{{\hat n}_{\text{j}}}{\text{cos}}{\theta _{\text{j}}}}}$$
(8)

Here \({\uptheta }\) and \({\hat{\text{n}}}\) represent the incident angle and the complex refractive index that follow the Snell’s low. With \(\varphi\) is the phase between two alternating layers along the structure that can be written as (Trabelsi et al. 2013; BenAli et al. 2020):

$$\varphi _{{{\text{j}} - 1}} {\text{ = }}\frac{{2\pi }}{\lambda }{\text{x}}_{0} {\text{cos}}\theta _{{{\text{j}} - 1}}$$
(9)

Here, the optical thickness \({\text{x}}_{{0}} { = }\frac{{{\uplambda }_{{0}} }}{{4}}\left( {{\text{j}}^{{\text{h + 1}}} - ({\text{ j}} - 1)^{{\text{h + 1}}} } \right)\) and h denotes the value of deformation and j defines the number of jth layer. For both propagating modes s and p, the transmittances are related according to the following equations (Trabelsi et al. 2013; BenAli et al. 2020):

$${{\text{T}}_s}{\text{ = Re}}\left( {\frac{{{{\hat n}_{{\text{m + 1}}}}{\text{cos}}{\theta _{{\text{m + 1}}}}}}{{{{\hat n}_{\text{0}}}{\text{cos}}{\theta _{\text{0}}}}}} \right){\left| {{{\text{t}}_{\text{s}}}} \right|^{\text{2}}};\;{{\text{T}}_{\text{p}}}{\text{ = Re}}\left( {\frac{{{\text{cos}}{\theta _{{\text{m + 1}}}}/{{\hat n}_{{\text{m + 1}}}}}}{{{\text{cos}}{\theta _{\text{0}}}/{{\hat n}_{\text{0}}}}}} \right){\left| {\frac{{{{\hat n}_{{\text{m + 1}}}}}}{{{{\hat n}_{\text{0}}}}}{{\text{t}}_{\text{s}}}} \right|^{\text{2}}}$$
(10)

3 Theoretical model and numerical results

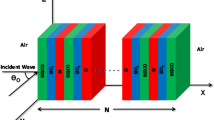
We present a one-dimensional quasiperiodic multilayered structure built according the GF(m, n) sequence. The two constituent materials S (superconductor) and D (Dielectric) of considered multilayered stacks follow the GF substitution rule: \({\text{S}}_{k - 1} {\text{ = S}}_{k}^{m} {\text{ S}}_{k - 1}^{n}\) for \({\text{k}} \ge 0\) \(\mathrm{H}\to {\mathrm{H}}^{\mathrm{m}}{\mathrm{L}}^{\mathrm{n}}\)(Trabelsi et al. 2013). In our structure, the two building blocks S, and D denote YBCO with a thickness dS, and SiO2 with a thickness dD.

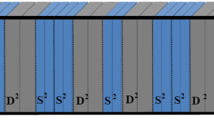
The Fibonacci sequence GFk can be generated by a substitution rule: \(\sigma_{GF} (S,D):S \to S^{m} D^{n} ,D \to S\) with k is the GF order. We begin by Fig. 1 which shows the distributed layers S and D along z axis organized following the third generation of GF3(m, n) with m = n = 3.

Fig. 1
figure 1

Representation of 1D SPQCs, with S and D as the two constituent materials ordered according to the third generation of GF(3, 3)

Full size image

In this subsection, we evaluate the transmission spectrum for different incident angles in order to obtain a complete band gap for both modes. We assume that all constituent materials are isotropic and homogeneous. The medium of input and output ports are considered as free space with a refractive index n0 = 1. We recall that our heterostructure is composed of alternating superconductors (YBCO) and Dielectrics (SiO2). In particular, the superconductors are assumed to be YBa2Cu3O7 with a critical high-Tc temperature (Tc = 93 K) and a London penetration depth at zero temperature \(\lambda_{{\text{L}}} {(0) = }\lambda_{{0}} {\text{ = 145nm}}\). The dielectric and superconductor thicknesses were supposed to be dD = 80 nm and ds = 30 nm, respectively.

First, we examined the transmission spectra of a 1D GF(m, n) SPQCs without deformation (h = 0). Figure 2 reveals that under our assumptions, opened gaps are found for both polarizations within the spectrum of GF3. So, both edges of PBG are \(\Delta {\uplambda } = \left[ {0.43 - 0.49} \right]\;\mu {\text{m}}\) and \(\Delta {\uplambda } = \left[ {0.43 - 0.52} \right]\;\mu {\text{m}}\) for TE and TM modes, respectively. The 3D GF spectrum exhibits the largest stop band gaps for TE mode and ensures a commune prohibited region of transmissions with half bandwidth \(\Delta {\uplambda } = 0.06\;\mu {\text{m}}\). So, the transmission and the band gap appeared in both spectrum are related to the strong Bragg reflection derived from periodic modulation of two refractive indices along the quasiperiodic multilayered stacks. So, it is relevant for the multiple scattering processes that lead to the formation of the significant band gaps.

Fig. 2
figure 2

The 3D transmittance spectrum through hybrid GF3(3, 3) multilayer stacks as function of wavelength and wave incidence angle for both polarization modes

Full size image

We are now in position to apply a deformation h satisfying the low \(y = x^{h + 1}\), where, \(x\) and \(y\) represent the coordinates of the main and deformed GF-SPQC thicknesses, respectively. This improves the characteristics of reflector. Figure 3 shows the transmittance spectrum through the deformed GF-SPQC. For the optimum value h, the system exhibits an omnidirectional band gap. Besides, the spectrum exhibits an oscillation beam transmission around the two PBGs. As claimed, the typical broadening of all heterolayers thicknesses enhances the main PBG. Similarly, the intensity of transmission in all structures is reduced. So, the increasing of all thicknesses causes a decrease of crystallite size that leads to a large decrease of the localized states and defects modes. This increment improves the optical band gap. For both mode, the commune size of the two output gaps can covers the maximum of visible light range for h = 0.01. Thus, we note that the reflector characteristics are sensitive to optimized deformation h applied along the crystals.

Fig. 3
figure 3

A schematic view of 1D deformed SPQC and its corresponding PBG at given deformation stack h = 0.01

Full size image

We examine the influence of superconductor temperature on propagation wave of 1D hybrid SPQC structure. Thus, we evaluate the characteristics of distributed electric field through the considered heterostructure at given deformation h = 0.01. Figure 4 shows a forbidden zone with zero transmission (the blue area) for different incident angles. The yellow and graded blue areas in figure indicate the propagating states of TE and TM polarized wave, respectively. The dark blue areas represent regions of the omnidirectional band gap. The forbidden band is sensitive to the temperature T of YBCO. Thus, the bandwidth of PBG increases with T. So, an enhanced reflected band is also obtained for T = 80 K. It covers a considerable portion of visible light range and exhibits perfect omnidirectional reflectors. Therefore, the surface reflected band of the SPQC changes under different temperature values. When T increases, the edge of band shifts to higher wavelength. The wave properties of SPQC can be tunable by the temperature of system. This is so because the response to an electromagnetic wave is mainly dependent on the London penetration depth, which is a function of the temperature and the external magnetic field as well.

Fig. 4
figure 4

Distributed electric fields of deformed SPQC versus wavelength and incident angle at T = 20 k, and 80 K, respectively

Full size image

In this subsection, we reorganized the distribution of layers within the SPQC in order to achieve a complete forbidden band that covering all visible rays. We apply the repetition of Fibonacci stacks as (GF)p with p is a positive integer. The new configuration multiplies the constructive reflected waves at interfaces by increasing the alternating (L/H) layers. As a result, the bandwidth of prohibited zone can be strongly enhanced due to the repetition of the gradient of translational symmetry along all structure that increases the constructive reflectance at each interface.

Consequently, an OBG is obtained (Fig. 5) covering an extremely broad range of visible light spectrum for specific arrangement of layers within the SPQC.

Fig. 5
figure 5

Distributed electric field through (GF)p stacks under TM / TE polarizations with p is set to be p = 3

Full size image

In order to achieve relative peaks within the main OBG, we insert a typical quasiperiodic Generalized Thue Morse (GTM) defect between two GF3 distributed Bragg reflectors. The present hybrid heterostructure becomes GF3/GTM3(2, 2)/GF3. Here, the present defect blocks A and B are built according to the third generation of Thue Morse sequence.

Figure 6 shows the transmittance spectrum of the cascading GF/GTM/GF model as a function of wavelength and incident angle (\(\theta {\text{ (rad)}}\)). We claim that sharp transmission peaks are appreciated into wavelength range whose positions are sensitive to superconductor temperature. The localized resonant modes can be shifted by tuning the operating temperature of the superconductor layers. Moreover, the peak center wavelength (\({\uplambda }_{c} { (}\mu {\text{m)}}\)) shifted toward the higher wavelength for an increase of T. Then, the additional micro defect into the considered structure affects the Q value of resonant mode. Since the distributed layers show broken translational symmetries within the whole structure, the present system opens an efficient gradient of transmission gaps without significant off band oscillations. Consequently, the system with inserted defect modes behaves like a cascading high reflector ordered by the temperature.

Fig. 6
figure 6

Evaluation of inserted propagating mode through hybrid GF/GTM/GF heterostructure versus wavelength at given temperature with T(K) set at 20, 40,60 and 80

Full size image

4 Conclusion

We studied the properties of the 1D hybrid SPQCs hetrostructure built according to the GF, (GF)p and defective GF/GTM/GF arrangements. We found that the simple GF(m, n) distribution exhibits an OBG for m = n, in which the bandwidth of obtained OBG are notably improved by applying a structural deformation along the whole thickness of constituent layers. We showed that the tunable PBGs of considered heterostructure can be adjusted by the temperature of YBCO and juxtposition (GF)p of main GF form. By introducing a repetitive and structural defect inside the main structure, resonant peaks appear from the proper transmittance that is very sensitive to temperature and juxtaposition insert defect. Such supposed heterolayers can be used as high reflector that dependent to temperature.