1 Introduction

Superconducting vortex lattice pinning and vortex lattice dynamics are strongly modified by arrays of nanodefects embedded in superconducting films [1]. This effect can be studied using arrays of holes (antidotes) [2] which thread the films or dots [3] embedded in the sample. In the latter many effects have been reported on these hybrid samples, as for instance (i) reconfiguration of the vortex lattice [4], effects induced by (ii) arrays made with different materials [5], (iii) different diameters of the pinning centers [6], channeling effects [7], and so on.

Magnetoresistance measurements are a perfect tool to study these effects, since resistance vs. applied magnetic fields shows deep minima when the vortex lattice matches the unit cell of the array [1] due to geometric matching occurs when the vortex density is an integer multiple of the pinning center density. These phenomena are ruled by the balance among different interactions, (i) vortex–vortex, (ii) vortex–artificially induced pinning center (array of nanodefects), (iii) vortex–intrinsic and random pinning centers. The magnetoresistance minima show up only when the temperature is close to T c , since, at these temperatures, the effect of the vortex–array interaction is enhanced [8].

The large roughness of the sample surface precludes the use of standard local probe methods to detect experimentally the vortex position and symmetry of the vortex lattice, which could be only inferred from the experimental matching conditions.

Therefore, theoretical approaches have been undertaken by computer simulation methods. In a pioneering work, in the framework of molecular dynamics, Reichhardt et al. [9], integrating numerically the Langevin equation of motion, were able to predict some of the matching fields at which commensurate vortex arrangements happen. According to this approach the superconducting penetration depth is the crucial parameter. These authors use cut-off conditions, pinning strengths and other relevant parameters governed by the penetration superconducting depth. In a similar scenario, Langevin equation of motion of the vortices, Dinis et al. [10] have been able to simulate the rectifier behavior of the vortex lattice [11] in the transverse ratchet effect [12]. In this case the parameters are taken from the experiment and the random intrinsic pinning of the superconductor plays a crucial role.

Recently, Rodríguez-Pascual et al. [13] have explored the possibility to simulate the commensurability experiments in the frame work of the Langevin equation of motion, but without any initial conditions neither constraints and using only as input the vortex–vortex interaction and the periodic pinning sites (array unit cell). These preliminary results [13] show that this simulation could be performed in a reasonable amount of time. In this work, we will show that the experimental magnetoresistance minima permit obtaining the number of vortices in the array unit cell and improving this computer simulation allows figuring out not only the vortices position for different arrays and matching fields, besides evaluating the vortex lattice interaction.

2 Experiment and Implemented Simulation

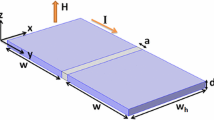
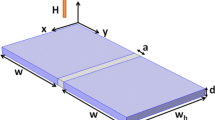
Superconducting/magnetic hybrids have been grown by magnetron sputtering, electron beam lithography and etching techniques, for more details see for example [11]. In brief, the samples are Nb film on top of array of submicrometric Ni dots which have been fabricated by electron beam lithography on Si (100) substrates. Thus, 400×500 nm2 and 400×600 nm2 rectangular arrays of Ni dots have been selected as the artificially fabricated pinning arrays for the present work. In both hybrids, the thickness of the Ni dots is 40 nm, while the thickness of the Nb film is 100 nm. The diameter of the Ni dots is 200 nm. The maximum number of vortices that could accommodate one of these pinning sites, i.e. the so-called filling factor could be estimated [14] as one vortex per dot.

A cross-shaped bridge of 40 μm is patterned in the hybrids for magnetotransport measurements by means of standard photolithography and etching techniques. The magnetic fields are applied perpendicular to the sample and magnetoresistance measurements have been done in a commercial cryostat with superconducting solenoid.

Figures 1 and 2 show the experimental magnetoresistance data for both hybrids at temperature close to T c , i.e. the periodic pinning potential overcomes the effects of the intrinsic random pinning potentials, and therefore, the effect related to the periodic pinning is enhanced [8]. Minima appear at applied magnetic fields H n =n⋅ϕ 0/(a⋅b), where a and b are the lattice parameters of the rectangular array and ϕ 0=2.07⋅10−15 Wb is the fluxoid. The number of vortices n per array unit cell can be known by simple inspection of the magnetoresistance curves, in which the first minimum corresponds to one vortex per unit cell, the second minimum to two vortices per unit cell, and so on.

Fig. 1
figure 1

Resistance vs. applied magnetic field for a 100 nm Nb film on top of a rectangular (400×500 nm2) array of Ni circular dots (40 nm thickness, 200 nm in diameter) at 0.96T c (T c =8.5 K)

Full size image
Fig. 2
figure 2

Resistance vs. applied magnetic field for a 100 nm Nb film on top of a rectangular (400×600 nm2) array of Ni circular dots (40 nm thickness, 200 nm in diameter) at 0.99T c (T c =8.5 K)

Full size image

The next step is to model these behaviors by computer simulation. Computer simulation reproduces the aforementioned experimental effects, but different geometries of lattices have been also evaluated by calculating the interaction of each possible vortices configuration and choosing the most convenient, i.e. the one with the lowest energy according to the desired specifications (physical parameters) used as input data. This code has been implemented from scratch; it does not take advantages neither of matching conditions with respect to the vortices lattices nor computational cut-off approximations to place the vortices.

Several interactions are present and the code obtains the configuration with the lowest energy, so the interactions in the overdamped equation of vortex motion can be described as follows [9]:

(1)

where f i is the total force per unit length acting on vortex \(i, f_{i}^{vv}\) is caused by the vortex–vortex interaction and \(f_{i}^{vp}\) is the pinning force.

The first sum runs up to the total number of vortices N v and K 0 is the zero order modified Bessel function, which depends on the distance r ij and the penetration depth λ, being λ (at 0.99T c )=2.6 μm in the experiment. Specifically, f 0 is

$$ f_{0} = \frac{\phi_{0}^{2}}{8\pi^{2}\lambda^{3}} $$
(2)

the value of which is 3.08⋅10−6 T2nm in our experiment.

In addition, the second sum related to pinning force has k as the index referring to the different pinning sites in the system, Θ as the Heaviside step function, f p as the maximum pinning force (it has been considered as 0.5 times the constant f 0) and r p as the pinning radius (100 nm in our experiment).

The possible vortices’ positions are evaluated by also using some heuristics in order to represent the symmetry of the system and reduce the complexity of the problem. Since the vortices are not randomly distributed [1], but follow certain patterns that can be implemented reducing the problem size in several orders of magnitude, the used heuristics have been: (i) the candidates in which two or more vortices are placed closely can be discarded (a minimum distance of a/N v was imposed, being a the smallest side of the lattice); (ii) the sum of the distances from each vortex to the rest should be constant for any of them. The different periodic solutions (vortices and pinning positions) obtained with the code for different values of the matching field and single lattices, either square, rectangular or triangular, were computed on the EGI Grid infrastructure and lately stored (see [13] for details about this computational pool of resources). Last, a Java program was implemented where as many lattices as requested by the user are configured with the aforementioned values. Gradient-driven simulations are then performed so the final position with minimum energy is finally settled in accordance with Eq. (1); later on, the final result can be retrieved. By doing so, neither cutting off of the potential beyond a distance of several times the penetration depth λ, or matching conditions for vortices lattices are needed.

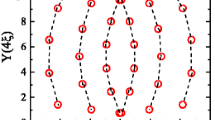
The obtained positions of the vortices are in agreement with those results provided by the experimental data and as an example some of them (the ones related to the minima in Fig. 1) can be found in Fig. 3. No other geometrical rules that those aforementioned in the heuristics have been employed. For a matching field of two, the overall vortices lattice is square but rotated 45° with respect to the pinning array since the interstitial vortices occupy the regions in between the pinning sites and the rest of them are settled upon this array. When matching field is three, there is an alternating position (90° rotation) of the pair of interstitial vortices.

Fig. 3
figure 3

Position obtained by the simulation performed for a matching field values which correspond to two vortices per array unit cell (upper panel) and three vortices per array unit cell (lower panel) corresponding to the sample depicted in Fig. 1. Only 20 (5×4) lattices are shown out of the whole 8000. The circular dots represent the pinning centers, the points represent the vortices

Full size image

Table 1 shows the interaction obtained by the simulation for different matching fields and lattice geometries with the experimental conditions and parameters previously mentioned (λ,r p ). They also correspond to a sample of 40 μm2 where 400×500 nm2 (Fig. 1) and 400×600 nm2 (Fig. 2) rectangular Ni nanodots lattices have been grown. The code can simulate these geometries with other sizes and matching field values and also different ones such as square or triangular lattices. Thus, results related to a square 400×400 nm2 lattice and 400 nm equilateral triangular lattices are also shown just as the two more relevant situations connected to the rectangular array.

Table 1 Interaction values calculated in this work for a 40 μm2 sample
Full size table

3 Conclusions

In summary, hybrid superconducting/magnetic samples are fabricated with superconducting films on top of array of pinning centers. The magnetoresistance of these hybrids, close to critical temperature, shows deep and equal spaced minima which are due to commensurability effects between the vortex lattice and the unit cell of the array. The first minimum appears when the density of the pinning centers equals the density of the vortex lattice, upper order minima take place at H n =n(Φ 0/S), where n>1 is an integer number and Φ 0 is the quantum fluxoid. Taking into account the vortex–vortex and the vortex–pinning center interactions, a grid computing simulation code has been implemented. This code can calculate different values and positions for different lattices in size, matching field values and geometry of the pinning sites, which allows having a picture of the different vortex lattices which develop for the main and upper order matching conditions as well as an estimated magnitude of their interactions.