Introduction

The first software tool to facilitate nonlinear mixed effects analysis in the context of pharmacokinetic (PK) and pharmacodynamic (PD) modeling was the NONlinear Mixed Effect Modeling package NONMEM (Nonmem) developed by Stuart Beal, Lewis Sheiner, and Alison Boeckmann [1]. The Nonmem methodology was based on maximum likelihood methods that use various approximations to compute and minimize the objective function (−2 log likelihood of the model parameters given the data) in order to estimate population PK and PK-PD model parameters. While several other software packages [2–6] for nonlinear mixed effect modeling were later developed, Nonmem remains the standard in the pharmaceutical industry. In the last 10–15 years, a number of new methods for population analysis were proposed, investigated, and implemented in the publicly available software [7–12]. The review of the population analysis methods and further references can be found in [13]. These new methods were introduced in Nonmem 7.1 and were further improved in the current Nonmem 7.2 release [14].

This work compares the performance (closeness of parameter estimates to simulation values, standard errors of estimates, and the run time) of all estimation methods implemented in Nonmem 7.2.0 (first order conditional (FOCEI), iterative two-stage (ITS), Monte-Carlo importance sampling (IMP), IMP assisted by mode a posteriori estimation (IMPMAP), stochastic approximation expectation maximization (SAEM), and full Markov chain Monte-Carlo (MCMC) Bayesian analysis (BAYES)) on the datasets simulated from two complex models with continuous dependent variables described by the system of nonlinear differential equations. To aid the readers, a very brief description of the nonlinear mixed-effect problem and the Nonmem estimation methods is provided below.

A nonlinear mixed-effect model aims to describe the data observed in a population of subjects. The observed data and the individual subject model parameters are assumed to include random components. The model consists of the population or fixed-effect parameters, a variance–covariance matrix that best describes the distribution of individual model parameters among the subjects, and the residual variance parameters that describe the within-subject data variability. To fit the model, a joint probability density of the data, called the posterior density, is evaluated. The posterior density depends on the fixed-effect parameters, on the distribution of individual model parameters, and the distribution of the observed data. To obtain the set of the population parameters that best fit the entire set of the data while taking into account all possible individual subject parameter values, the integral of the posterior density over all possible individual parameters is evaluated for each subject, and multiplied over all subjects. The result is a marginal density that depends only on the fixed-effect parameters. The set of the fixed-effect parameters that yields the maximal marginal density (maximum likelihood) is obtained, and is considered to be the final estimate. Even the simplest mixed-effect problems are analytically intractable. Various methods were proposed to solve this general problem numerically.

FOCEI evaluates the integration step by assuming that the posterior density can be approximated by a multivariate normal density with respect to the individual parameters. Such an assumption is suitable when the observed data are normally distributed, the model is not highly nonlinear with respect to the model parameters, and/or there is a reasonable number of data samples obtained for each individual. FOCEI has the advantage of providing highly reproducible values, and is rapid for simple PK models. Monte Carlo expectation–maximization (EM) methods (IMP, IMPMAP, and SAEM) integrate the posterior density by performing a Monte Carlo sampling over all possible individual parameters during the expectation step, and then use a single iteration maximization step that is easy to compute in order to advance the fixed-effect parameters towards the maximum likelihood. The Monte Carlo methods have the advantage of not using a linearized approximation to the integral, providing less bias. The efficient maximization step of the EM algorithms allow them to be faster than FOCEI for complex PK/PD problems, but the Monte Carlo expectation step causes the EM algorithms to be slower than FOCE for simple PK models. The stochastic nature of the methods provides less precise and not exactly reproducible results, but it is less likely than deterministic methods to be locked into a local minimum. Iterative two-stage (ITS) is a hybrid method that uses the deterministic, linearized approximation to the posterior density during the expectation step, similar to FOCEI, but utilizes the fast maximization step of EM methods to advance fixed-effect parameters towards the maximum likelihood. The advantage of the ITS method is very rapid advancement of the fixed-effect parameters, but it can occasionally have more bias than the FOCEI method. The Markov chain Monte Carlo Bayesian analysis method does not seek the parameter estimates that most likely fit the data, but uses a Monte Carlo search of the individual parameters as well as the fixed-effect parameters, to provide a series of fixed-effect parameter values that are distributed according to their ability to fit the data. The advantage is therefore in obtaining a set of descriptive statistics, such as mean estimates, empirical standard errors of the estimates, and confidence ranges for the estimates, that cannot be easily obtained, or are impossible to be obtained, by maximization methods. The disadvantage to MCMC Bayesian is that it can sometimes take considerably longer for this analysis than to obtain a maximum.

Two simulated data sets were created. The first dataset was simulated using the quasi-steady-state (QSS) approximation [15] of the target-mediated drug disposition (TMDD) model [16]. With the rich data for the free drug and total target concentrations from 224 subjects, the model is well-posed, with easily identifiable model parameters. The second data set was simulated from the QSS approximation of the two-target TMDD model [17] that describes the pharmacokinetics of the drug that can bind to soluble (S) and membrane-expressed (M) targets. The parameters of the membrane-expressed target were selected to create a poorly identifiable problem, with the membrane-target contribution to elimination that is difficult to distinguish from the non-specific linear elimination [17].

The TMDD equations were selected for two reasons. First, they provide an example of the model described by the nonlinear system of differential equations, with multiple fixed and random effect parameters. Some of those parameters could be poorly identifiable. Thus, long run time and computational complexities of the problem present a rigorous test of the estimation methods performance. Second, the TMDD equations are important by themselves because they describe the pharmacokinetic and pharmacodynamic properties of many new biologic drugs. Modeling of these drugs is a challenging and important problem. This work is intended to investigate and report how to apply the Nonmem estimation methods to the TMDD equations.

The full TMDD system [16] is rarely identifiable given the available data because it describes the processes with very different time scales, resulting in stiff differential equations with insufficient sampling to describe the drug–target binding processes. Therefore, the quasi-steady state approximation [15, 17] of the TMDD model was used. This approximation simplifies the TMDD equations by assuming that the binding process is nearly instantaneous and the drug, target and the drug–target complex are in quasi-steady state. This approximation was shown to preserve all characteristic features of the full TMDD model, and provide a robust platform to describe the observed data for drugs with target-mediated disposition. Further details and references can be found in the recent review [18].

All estimation methods were applied in two versions. The first set of control streams (also called ‘naive’) employed the default estimation options (where available), no formal convergence criteria (except for the FOCEI method), and very large number of iterations to guarantee convergence or stationarity of the estimates. The control streams of the second set employed ‘expert’ options and convergence criteria designed to attain the best possible results and the shortest run time. The parameter estimates (PEs) and relative standard errors of the parameter estimates (RSEs) were compared between the methods, and also for PEs with the known true values and for RSEs with predictions of the optimal design software PFIM 3.2 [19]. The motivation behind the “expert choice” of the estimation method options and interpretation of the results are discussed.

PFIM is a collection of R functions for population designs evaluation and optimization. It is based on the expression of the Fisher information matrix in nonlinear mixed-effect models. The version 3.2 includes evaluation of the multiple response models that allows application of the software to the TMDD models with two dependent variables. In this work, only design evaluation feature was used since the goal was to compute the expected standard errors of the parameter estimates for comparison with those obtained by various Nonmem estimation methods. No optimization of the study designs was attempted.

Many complex PK/PD models (such as the TMDD model used in this paper) are expressed with differential equations that must be numerically integrated, and may require many hours of computation. The most recent Nonmem version introduced the parallel computing option that can reduce the actual time of analysis by many folds. Parallel computing is the process of splitting the computational load of a particular problem across two or more CPU’s. The parallel processing feature of Nonmem allows use of several CPU’s attached to the same computer, such as with the multi-core workstations, or several computers connected via the network. One of the goals of this work was to test the efficiency of Nonmem 7.2.0 parallel computing for all tested estimation methods.

Run time of the models that require solution of differential equations greatly depends on the performance of the integration methods. Nonmem includes several subroutines (ADVAN6, ADVAN8, ADVAN9, and ADVAN13) for solving the system of differential equations. These subroutines differ by the implemented integration methods. Selecting the appropriate numerical integrator algorithm may reduce the time of the analysis. Also, some differential equation solvers are more efficient than others for certain kinds of problems. Performance of various ADVAN integrators for the TMDD model was tested for all estimation methods.

Thus, this work has two goals: to compare speed and accuracy of different estimation methods for the chosen problems, and to illustrate how to best use the estimation methods and parallel computing available in the latest release of the Nonmem software.

Methods

Models

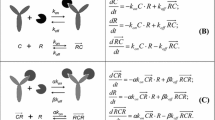
The following system of equations describes the QSS approximation of the two-target TMDD system [17]:

$$ \frac{{{\text{d}}A_{\text{d}} }}{\text{dt}} = - k_{\text{a}} A_{\text{d}} ;\quad A_{\text{d}} (0) = D_{1} $$
(1)
$$ \frac{{{\text{d}}A_{\text{tot}} }}{\text{dt}} = F_{\text{SC}} k_{\text{a}} A_{\text{d}} + \frac{Q}{{V_{2} }}A_{\text{p}} - \left( {\frac{CL}{{V_{1} }}\, + \,\frac{Q}{{V_{1} }}} \right)C \cdot V_{1} - \frac{{R_{\text{tot}} k_{\text{int}} C \cdot V_{c} }}{{K_{\text{SS}}^{\text{S}} + C}} - \frac{{V_{\max } C \cdot V_{1} }}{{K_{\text{SS}}^{\text{M}} + C}}; $$
(2)
$$ \frac{{{\text{d}}A_{\text{p}} }}{{{\text{d}}t}} = \frac{Q}{{V_{1} }}C \cdot V_{1} - \frac{Q}{{V_{2} }}A_{p} ; $$
(3)
$$ \frac{{{\text{d}}R_{\text{tot}} }}{\text{dt}} = k_{\text{syn}} - k_{{\text{deg }}} R_{\text{tot}} - \left( {k_{\text{int}} - k_{{\text{deg }}} } \right)\frac{{R_{\text{tot}} C}}{{K_{\text{SS}}^{\text{S}} + C}}; $$
(4)
$$ A_{\text{tot}} (0) = D_{2} ;\quad R_{\text{tot}} (0) = R_{0} = k_{\text{syn}} /k_{{\text{deg }}} ;\quad C_{\text{tot}} = A_{\text{tot}} /V_{1} ; $$
(5)
$$ C = \frac{1}{2}\left[ {\left( {C_{\text{tot}} - R_{\text{tot}} - K_{\text{SS}}^{\text{S}} } \right) + \sqrt {\left( {C_{\text{tot}} - R_{\text{tot}} - K^{\text{S}}_{\text{SS}} } \right)^{2} + 4K_{\text{SS}}^{\text{S}} C_{\text{tot}} } } \right], $$
(6)

Here A d and A p are the free drug amounts in the depot and peripheral compartments, respectively; A tot is the total (free and bound to the S-target) drug amount in the central compartment; C and C tot are the free and total concentrations of the drug in the central compartment; R, R tot, and RC are the concentrations of the free (unbound) S-target, total (unbound and bound to the drug) S-target, and the drug-S-target complex in the central compartment; all other parameters are described in Table 1. The initial conditions correspond to the case where the free drug that is not present endogenously is administered as a subcutaneous dose D 1 and bolus dose D 2. Further details and discussion of the model can be found in [17].

Table 1 True model parameters and relative standard errors predicted by PFIM 3.2
Full size table

In the case when the membrane target influence is negligible (V max = 0), the model degenerates to the QSS approximation of the TMDD model proposed in [15]. The resulting system is well-posed with easily identifiable parameters. Further in the paper this model is referred to as Model 1. When the membrane target influence is not zero (V max ≠ 0) but is relatively small, the model is poorly identifiable (Model 2) since it cannot distinguish between linear elimination and M-target-mediated elimination. For the selected set of the parameters, this was confirmed by performing a sensitivity analysis in which, when V max was set to 0 and CL was adjusted to take up the difference, the shape of the predicted curve changed little. This was also confirmed by the convergence rate of the estimation methods that easily found the true solution for Model 1 while spent much more time iterating toward the solution of Model 2.

Datasets

The data from two studies were simulated as described in Table 2. The free drug and total S-target concentration–time data from these trials (“true data”) were simulated using the QSS model (Eq. 1–6) for both, one-target (Model 1) and two-target (Model 2) settings. The drug and target parameters (Table 1) were chosen to reflect the values typical for fully human therapeutic monoclonal antibodies. The targets were selected to correspond to the typical parameters of the soluble and membrane-bound targets. Details and references can be found in [17] where this model was used for different simulations. The rich sampling scheme typical for phase 1–2 trials of monoclonal antibodies was selected. Moderate log-normal inter-individual variability with diagonal OMEGA-matrix and moderate log-normal residual variability (as specified in Table 1) were assumed. A total of 3312 pairs of unbound drug and total S-target observations from 224 subjects were simulated for each of the two models. The simulated data below the hypothetical assay quantification limit of 0.1 nM were removed from the datasets. The exponential error model was used for the simulations. To avoid linearization of the error model at the estimation step, the error model was implemented as an additive error for the log-transformed dependent variables. Example of the Nonmem simulation model and the subset of the simulated data set are available in the Supplemental Material.

Table 2 Dosing and sampling scheme in the simulated studies
Full size table

Hardware and software

The computer simulations and the analysis were conducted using Nonmem® 7.2.0 [1] under Windows 7 Professional 64 bit operating system and Intel Fortran Professional 11.0 compiler. Nonmem runs were performed on Dell Precision T5500 workstation with two Intel Xeon X5690 (3.47 MHz) six-core processors.

Defining random effects for the estimation methods

BAYES, IMP, IMPMAP, ITS, and SAEM estimation methods benefit from the so-called MU-referencing where each model parameter is presented (whenever possible) as a function of the sum of the MU-parameter and the random effect. In this work, MU-referencing with the random effects on all model parameters was used for all estimation runs as illustrated below for the clearance parameter CL

$$ {\text{MU}}\_ 1= {\text{THETA}}\left( 1\right) $$
(7)
$$ {\text{CL}} = {\text{EXP}}\left( {{\text{MU}}\_ 1+ {\text{ETA}}\left( 1\right)} \right) $$
(8)

In addition, the NONMEM 7.2.0 manual [14] recommends employing linear MU referencing, where MU parameters are linear combinations of THETA parameters as it greatly increases speed and incidence of successful convergence of the EM methods. The EM algorithms advance the population parameters very efficiently and more reliably towards the maximum likelihood. For BAYES analysis, linear MU referencing allows the more efficient Gibbs sampling process to be used, rather than the less efficient but more general Metropolis–Hastings process. When MU referencing is not performed, the EM algorithms are forced to create computationally expensive gradient equations in order to advance the fixed effects towards the maximum likelihood position. The EM analysis will take many more times longer, especially with the complex PK/PD problem used here. The price for the speed up is that with linear MU referencing THETA parameters are in log domain (e.g. THETA(1) in (7) represents log of population value of CL), and final results need to be exponentiated to represent mechanistically understandable values.

Although FOCEI does not utilize the MU equations and therefore its speed of analysis is not improved, parameterization of the THETAs into their log-transformed versions may stabilize FOCE analyses as well, and result in fewer function calls or increase probability of successful completion. Therefore, estimation using FOCEI method was performed both ways, with and without MU-referencing.

In the examples of this paper, covariate effects were not explored. If there were covariates (e.g. continuous and categorical covariates for body weight (WT) and gender (SEX = 0 for males and = 1 for females), respectively), linear MU-referencing would be preserved by expressing THETAs associated with the covariates linearly in MU, e.g.

$$ {\text{MU}}\_ 1= {\text{THETA}}\left( 1\right) + {\text{THETA}}\left( 2\right)*{\text{LOG}}\left( {{\text{WT}}/{\text{WT}}_{\text{REF}} } \right) + {\text{THETA}}\left( 3\right)*{\text{SEX}} $$
$$ {\text{CL}} = {\text{EXP}}\left( {{\text{MU}}\_ 1+ {\text{ETA}}\left( 1\right)} \right) $$

With this representation, MU linearly depends on THETAs while the covariate data, in this case WT, may enter the expression non-linearly, in any appropriate functional form. Examples of the Nonmem estimation models with and without MU-referencing are provided in the Supplemental Material.

Estimation methods options

Two runs, with ‘naive’ and ‘expert’ estimation options for each method were performed for each of the two problems. The summaries of the options for all model runs are presented in Tables 3 and 4. Options that were not mentioned explicitly were assigned the default values. Generally, ‘expert’ options turned on testing of the convergence criteria (CTYPE = 2), allowed larger number of iterations (to greatly exceed the likely number of iterations needed for conversion), decreased (where appropriate) the number of significant digits considered at different stages of estimation process (SIGL, NSIG, TOL), and added (where appropriate) additional steps to improve accuracy of the final estimates. Glossary of Nonmem estimation options can be found in Table 5.

Table 3 Estimation options for Model 1
Full size table
Table 4 Estimation options for Model 2
Full size table
Table 5 Nonmem glossary of terms
Full size table

For estimation, all parameters were assumed to have associated random effects, even for Model 2 where the simulation (true) model had zero inter-subject variability for F SC , \( K_{\text{SS}}^{\text{M}} \), and \( K_{\text{SS}}^{\text{S}} \) parameters. In addition, for the FOCEI method Model 2 was fitted with the inter-subject variability for F SC, \( K_{\text{SS}}^{\text{M}} \), and \( K_{\text{SS}}^{\text{S}} \) fixed to the true value of zero.

Typical Nonmem control steams of the simulation and estimation models are reproduced in the Supplemental Material. The control streams also indicate initial conditions that were kept identical for all methods, unless noted otherwise. The code for Model 1 can be obtained from the corresponding code for Model 2 by removing the terms related to the membrane target (V M and K M parameters in the control stream).

Expert choice of the estimation options for Model 1

As all estimation methods for the data and the model with well identifiable parameters (Model 1) were expected to produce similar results, the main purpose of the ‘expert’ options was to reduce the duration of the analysis.

By default, the convergence tester for Monte Carlo and EM methods is off (CTYPE = 0), and very large number of iterations were requested in ‘naive’ options to guarantee convergence or stationarity of the estimates. ‘Expert’ options turned on the convergence tester (CTYPE = 2, which tests the objective function, THETAs, SIGMAs, and OMEGA diagonals), allowing the software to decide when the objective function and the parameters are no longer changing, and thus reducing the analysis time. For the classical NONMEM methods (FO, FOCE, Laplace) and ITS, where the convergence is tested by default, the criterion of convergence, NSIG, that specifies the number of significant digits used for evaluation of whether parameters have not changed from the previous iteration was reduced from the default value of 3.

Further reduction of the analysis time was sought by decreasing SIGL that specifies the number of significant digits that NONMEM uses during evaluation of the mode of the posterior density (of the ETA parameters) for each subject. It also specifies the accuracy of the total objective function. Reducing SIGL decreases the duration of this step. The TOL setting (TOL specifies the accuracy of evaluation of the numerical integral of the predictive function) could have also been reduced for all methods to further reduce the run time, but was only reduced for FOCEI.

Finally, the parameter MAPITER was set to 0 in the refining step of the IMP and IMPMAP methods (and in the IMP objective function evaluation that follows SAEM). By default (MAPITER = 1), on the first iteration of the IMP method mode a posteriori (MAP) estimation [14] is performed to assist in obtaining the conditional means and variances. In the refining step, setting MAPITER = 0 tells Nonmem to use conditional means and variances from the last iteration of the previous estimation to assist in obtaining new conditional means and variances, thus maintaining continuity of the estimation from the previous IMP (or SAEM) step.

An additional refining step (10 iterations of 3,000 Monte Carlo samples per subject) was also performed following IMP, IMPMAP and SAEM convergence to obtain more precise final estimates.

Expert choice of the estimation options for Model 2

Compared to Model 1, Model 2 had an additional saturable clearance mechanism through a membrane-bound target described by two additional parameters (Vmax and K MSS ). Contribution of this extra clearance was difficult to distinguish from linear clearance CL. As a consequence, all of the methods had difficulty efficiently moving these three parameters, thus requiring many more iterations than in Model 1. Therefore, in addition to turning on the convergence tester and decreasing SIGL, the number of burn-in (NBURN) and accumulation (NITER) iterations in SAEM and BAYES methods were set higher than in runs of Model 1 to ensure convergence to the true values. The SAEM method also required to increase ISAMPLE, the number of Monte Carlo samples used to evaluate the expectation step of a Monte Carlo EM algorithm. This was necessary because the change of poorly identifiable parameters from iteration to iteration was very slow, and the iteration pattern tended to be highly correlated. Thus, the convergence tester was often fooled into thinking the analysis was complete, resulting in estimates for these parameters that were far from the true values. Increase of ISAMPLE was to make the change of parameter values quicker per iteration, and more monotonic.

For the IMP and IMPMAP methods, the SIGL parameter was not reduced, but it could have been reduced as in Model 1. As in Model 1, an additional refining step (10 iterations of 3,000 Monte Carlo samples per subject) was performed following IMP, IMPMAP and SAEM convergence to obtain more precise final estimates.

Parallel computing

Parallel computation was tested for all methods using Model 1 with the ‘naive’ options and using PARSE_TYPE = 4 option that distributes computations to the specified number of CPUs aiming to minimize the overall run time. The same model was tested on 1, 4, 8, and 12 processors. The computational efficiency was characterized by the ratio

$$ {\text{Efficiency}} = 100\% \, \left( {\text{time of single CPU run}} \right)/\left( {\text{time of multi{-}CPU run}} \right)/\left( {\text{number of CPUs}} \right) $$

Choice of ADVAN subroutines

Nonmem 7.2.0 has four PREDPP subroutines (ADVAN6, ADVAN8, ADVAN9, and ADVAN13) that solve differential equations. ADVAN6 is a Runge–Kutta-Verner fifth and sixth order method of numerical integration, for non-stiff problems. ADVAN8 is the Gear method of numerical integration, for stiff problems. ADVAN9 is the Livermore solver for ordinary differential equations, implicit form (LSODI), using the backward differentiation formulas (BDF) for stiff problems. ADVAN13 is the Livermore solver for ordinary differential equations (LSODA), with automatic method switching for stiff (BDF) and non-stiff (Adams method) problems [1, 20, 21]. The performance of these routines (number of iterations required for convergence and the run time) was compared for all methods using Model 1 with the ‘naive’ options.

Expected standard errors of parameter estimates

PFIM [19] is the optimal design software that can be used to evaluate a study design (that is, it provides the expected standard errors of the parameter estimates given the true model and sampling schedule) and to optimize various features of the study design. In this work, only design evaluation option was used while the study design and sampling schedule were not optimized. The expected standard errors of the parameter estimates (Table 1) were obtained using PFIM version 3.2 applied to the system with two response variables with the block-diagonal information matrix (PFIM 3.2 option 1) that was shown to provide more reliable estimates of the expected standard errors [22, 23]. The models without MU-referencing (with the fixed-effect model parameters expressed in the original rather than log-transformed parameter space) and with zero inter-subject variability for F SC, \( K_{\text{SS}}^{\text{M}} \), and \( K_{\text{SS}}^{\text{S}} \) parameters (for Model 2) were used to compute the expected standard errors. The models with MU-referencing, and the models with a very small variance (ω2 = 0.0001) of F SC, \( K_{\text{SS}}^{\text{M}} \), and \( K_{\text{SS}}^{\text{S}} \) parameters were also tested. They provided nearly identical results (not shown). Models with the residual errors expressed in the original and log-transformed dependent variables were also tested and compared.

Results

One-target QSS model (Model 1)

The results are presented in Figs. 1 and 2 that illustrate the parameter estimates and 95% confidence intervals of the parameter estimates for all estimated parameters and all estimation methods. The 95% confidence intervals were computed using the estimated standard errors of the parameter estimates. In these figures, values of the parameters are normalized by their known true values. The solid horizontal lines correspond to the true values. The dashed lines show the 95% confidence intervals computed using standard errors predicted by the PFIM. The circles correspond to the obtained parameter estimates while the stars indicate the Nonmem-computed 95% confidence intervals of the normalized parameter estimates. The estimation methods are indicated at the horizontal axes x. For each method, the points to the left and to the right of the method number correspond to the ‘naive’ and ‘expert’ options (Table 3), respectively. The FOCEI run in the center (x = 1) corresponds to the MU-referenced run (Table 3). For the models with MU-referencing, the confidence intervals were computed by exponentiation of the confidence intervals obtained for MU-parameters. Variances (rather than standard deviations) of the random effects and the residual errors are presented. The run times are illustrated in the last plot of Fig. 2. Number of iterations to convergence and estimation time for each run is shown in Table 6.

Fig. 1
figure 1

Parameter estimates and confidence intervals: One-Target QSS Model. For each parameter, the estimated value (PE) and the 95% confidence interval (CI), both normalized by the true value are presented. The solid lines show the true normalized values (equal to 1). The dashed lines illustrate the expected CI predicted by PFIM software. The circles and the stars illustrate PE and CI for each of the estimation methods. CIs were computed using Nonmem or PFIM standard errors. For models with MU-modeling, CIs were computed by exponentiation of CIs obtained for MU-parameters. The method is indicated by the number on the x-axis. The details of the runs for each method are described in the text

Full size image
Fig. 2
figure 2

Parameter estimates and confidence intervals: One-target QSS model (Continuation). See legend of Fig. 1. The last plot illustrates the run time of each model

Full size image
Table 6 Convergence and estimation time for Model 1
Full size table

As can be seen, for this well-identifiable rich sampling problem all methods obtained very similar results. The unexpected result was an excellent performance of the FOCEI method with the reduced requirement for numerical precision (NSIG, SIGL and TOL values) implemented in the ‘expert’ run. The estimation time was about 3 times shorter than with ‘naive’ options without any adverse effects on the obtained estimates. Also unexpected was a good performance of the Bayesian method used without specifying OMEGA-priors. Estimates of the ‘naive’ run that started far from the true values (as for all other methods) and without OMEGA-priors were as good as for the ‘expert’ run that had the initial values of the parameters and OMEGA priors taken from the solution of IMP method. The IMP step that followed SAEM method provided RSEs similar to SAEM RSEs. Thus, the only additional result of this step was evaluation of the objective function value. ITS, IMP and IMPMAP methods had the shortest run times, while FOCEI with ‘naive’ precision had the longest run time. Application of the convergence criteria for all methods provided the objective criteria for stopping the iterations and reduced the run time without compromising quality of the fit.

All fixed-effect parameter estimates were close to their true values (well within 15% of the true values) while variance parameter estimates were less precise. In particular, variances of R 0 and k deg were, respectively, under- and over-estimated. Note that the variance of the target production rate (k syn = R 0 k deg; ω 2Ksyn  = ω 2R0  + ω 2Kdeg ) was estimated close to the true value. Confidence intervals on the parameter estimates were similar or slightly wider than predicted by PFIM.

Two-target QSS model (Model 2)

The results are presented in Figs. 3 and 4 and follow the same notations as in Fig. 1. The left and center points for the Bayesian method correspond to the ‘naive’ options of Table 4 with 10,000 and 20,000 burn-in iterations, respectively. The last plot in Fig. 4 shows the run time for each run. Number of iterations to convergence and estimation time for each run is also shown in Table 7.

Fig. 3
figure 3

Parameter estimates and confidence intervals: Two-target QSS model, Fixed-Effect Parameters. See legend of Fig. 1

Full size image
Fig. 4
figure 4

Parameter estimates and confidence intervals: Two-target QSS model, Variance Parameters. See legend of Fig. 1

Full size image
Table 7 Convergence and Estimation Time for Model 2
Full size table

For this poorly-identifiable rich sampling problem differences between the estimation methods were larger. Similar to Model 1, the reduced numerical precision requirements for the FOCEI method (‘expert’ options) resulted in significantly shorter run time (about seven times shorter) without affecting the estimates of the parameters. The IMPMAP and SAEM(Only) methods with the default settings provided wider confidence intervals for many parameters. The ITS method had visibly larger deviation from the true parameter values for V 2 and \( K_{\text{SS}}^{\text{M}} \). The BAYES method with the ‘naive’ options (i.e. with the initial values not at the solution and without OMEGA priors) had large deviation for CL, Q, V 2, V max, \( \omega_{\text{Q}}^{ 2} \), and \( \omega_{{{\text{V}}_{ \max } }}^{ 2} \) parameters. The ‘expert’ options (i.e. where the initial values and OMEGA priors were taken from the final values of the IMPMAP run) improved the estimates of these parameters, but the estimates had still more deviation from the true values than in the other methods. Figure 5 illustrates the ability of the methods to estimate variances of F 1, \( K_{\text{SS}}^{\text{M}} \), and K SS that were set to zero at the simulation stage. Values in this figure are not normalized, and the plot of \( \omega_{{{\text{V}}_{ \max } }}^{ 2} \) is added (same as in Fig. 4 but non-normalized). All methods were able to correctly estimate variances of F 1 and K SS (except for the BAYES method that was a little worse than the other methods). However, the variability of the M-target parameters was attributed to \( K_{\text{SS}}^{\text{M}} \) rather than V max by all methods except one IMP and one SAEM run (for two FOCEI runs, variances ω 2F1 , ω 2KSSS , and ω 2KMSS were fixed to zero). And the BAYES method with the ‘naive’ options again had a larger deviation from true values. The low-precision FOCEI method and the ITS, IMP and IMPMAP methods with the convergence criteria had the shortest run times while FOCEI with high precision had the longest run time. Application of the convergence criteria for all methods provided the objective criteria for stopping the iterations and reduced the run time without compromising the quality of the fit. Confidence intervals on the parameter estimates were very similar to those predicted by PFIM.

Fig. 5
figure 5

Parameter estimates and confidence intervals: Two-target QSS model, Absolute values of Variance Parameters, For each parameter, the estimated value (PE) and the 95% confidence interval (CI) are presented. The solid and dashed lines show the true values and expected CI. The circles and the stars illustrate PE and CI for each of the estimation methods. CIs were computed using Nonmem or PFIM standard errors. For models with MU-modeling, CIs were computed by exponentiation of CIs obtained for MU-parameters. The method is indicated by the number on the x-axis. The details of the runs for each method are described in the text

Full size image

Parallel computing

The results are presented in Fig. 6 where the fold-decrease of the run time and computational efficiency are presented. Efficiency was very high and it slowly declined with the number of processors. At 12 processors, it varied between 85 and 95% for all methods except BAYES that had the lowest (about 70% at 12 processors) efficiency of parallel processing.

Fig. 6
figure 6

Run time speed-up and efficiency of nonmem parallel computing. Top: Fold difference between the multi-processor and single-processor run time versus number of processors. Bottom: Computation efficiency of the multi-processor run versus number of processors. Efficiency is defined as the fold difference (illustrated in the top plot) divided by the number of processors, and multiplied by 100%. The estimation method is specified in the legend

Full size image

For the FOCEI and ITS methods, the results were exactly reproducible and independent of the number of processors. However, for the stochastic methods (IMP, IMPMAP, SAEM and BAYES), distribution of subjects to different nodes for computations is dependent on number of processors. This leads to differences in sequences of random numbers generated during computations that made the results dependent on the number of processors. Moreover, with the parallel processing option PARSE_TYPE = 4, the results of the stochastic methods may not be exactly reproducible even when repeated on the same number of processors, because the distribution of the subjects to each processor may depend on the computer load. The option PARSE_TYPE = 1 (equal number of subjects at each node) guarantees the results to be independent of the computer load. Still, the results will depend on the number of used processors.

Choice of ADVAN subroutines

All runs provided similar if not identical parameter estimates. For all problems except FOCEI, ADVAN13 provided the fastest solution (Table 8), ADVAN6 required the same or slightly longer run time, while ADVAN8 and ADVAN9 were significantly less efficient. For the FOCEI method, comparison is not as straightforward since use of different ADVAN routines resulted in different number of iterations and function calls required for convergence. ADVAN6 was less efficient at each function evaluation but required fewer function calls and iterations for convergence, thus providing overall a shorter run time than ADVAN13. Note that the performance of these subroutines may depend on the stiffness of the underlying differential equations. The results obtained in this work may not be generalizable to problems with stiffer differential equations.

Table 8 Relative run times for various ADVAN subroutines
Full size table

Expected standard errors of parameter estimates

The expected standard errors for models without MU-referencing, zero inter-subject variability for F SC, \( K_{\text{SS}}^{\text{M}} \), and K SSS parameters (for Model 2), and exponential error model were used for comparison with the Nonmem results. The results for the models with the residual error expressed in the original and log-transformed dependent variables were identical. The models with the MU-referencing provided nearly identical results (not shown). The Model 2 with 1% variance (ω2 = 0.0001) for the F SC, \( K_{\text{SS}}^{\text{M}} \), and \( K_{\text{SS}}^{\text{S}} \) parameters was also tested. It provided nearly identical results for all the parameters (not shown) except for variances of F SC, \( K_{\text{SS}}^{\text{S}} \) (with small standard errors of about 0.003), \( K_{\text{SS}}^{\text{M}} \) (with large standard error of 0.04), and V max that was estimated to have a slightly higher relative standard error (41 vs. 30%) compared to the model where variances of F SC, \( K_{\text{SS}}^{\text{M}} \), and \( K_{\text{SS}}^{\text{S}} \) were fixed to zero.

Discussion

Model 1

For the data and the model with well identifiable parameters (Model 1), all of the methods gave similar results. Therefore, the main purpose of the ‘expert’ options was to reduce the duration of the analysis.

The ‘naive’ options did not take advantage of the convergence test for the Monte Carlo and EM methods, and due to the large numbers of the requested iterations these methods took a long time to complete. For almost all methods, turning on the convergence tester considerably reduced the analysis time. Further reduction came from decreasing the precision requirements of intermediate evaluations.

For the ITS method, the run with the ‘expert’ options converged after 67 iterations reducing total run time 3.7-fold while reducing duration of each iteration from 45 to 37 s. Thus, the main reduction in time was due to running no more iterations than necessary, and there was a small additional reduction in time per iteration due to decreasing the SIGL parameter.

The importance sampling methods, IMP and IMPMAP with the ‘expert’ options converged in 70 and 48 iterations respectively, shortening the estimation time 2.8- and 5.4-fold, compared with the runs with the ‘naive’ options. In addition to the main estimation, the refining step with 10 iterations of 3,000 Monte Carlo samples per subject was performed following convergence to obtain more precise final estimates. This step took longer (43 and 50 min for IMP and IMPMAP, respectively) than the main estimation (31 and 25 min), and the parameter estimates with and without this step were nearly identical for both methods. Therefore, for the well-behaved Model 1 addition of this step was unnecessary.

The SAEM method with the ‘expert’ options completed the burn-in phase in 850 iterations reducing the estimation time 2.2-fold.

The ‘naive’ options for the BAYES method specified 4,000 burn-in iterations and 10,000 stationary distribution iterations, which took 593 min. With the ‘expert’ options including convergence testing, burn-in completed in 500 iterations, and the total analysis time was reduced to 400 min. The comparison of convergence and time is not meaningful in this example as beside turning on the convergence tester and reducing precision of intermediate evaluations, the ‘expert’ run also used the final results from IMPMAP as the initial values and OMEGA-priors. Motivation for this was a notion that for more accurate assessments of the OMEGAS the BAYES method generally requires that the uninformative priors should be provided for OMEGAs, with the number of degrees of freedom equivalent to the dimension size of the OMEGA block. Thus, this method was thought to be used as an add-on following use of other methods rather than as a stand-alone analysis. However, in the Model 1 example, accurate OMEGA values were obtained with no prior settings, and all the other results were accurate for both the ‘naive’ and ‘expert’ options.

The FOCEI method with the default options terminated with rounding error message (of less than 3 significant digits precision) at 129 iterations. Re-parameterization of the fixed-effect parameters into the log-domain form (consistent with linear MU referencing) lead to successful completion at 140 iterations (but slightly longer run time). Lowering, instead, the convergence criteria (NSIG = 2) and reducing SIGL and TOL to save time resulted in termination of the run with the rounding error message (of less than 2 significant digits) at 97 iterations. However, the estimation time was reduced 2.6-fold, and the terminated analyses had the same final objective function value as the successfully completed one.

Model 2

Similar to Model 1, implementation of the convergence tester and decrease of precision requirement of intermediate evaluations significantly reduced the run time of the ITS (2.5-fold), IMP (3.4-fold), and IMPMAP (5.7-fold) methods.

The additional refining step performed following IMP and IMPMAP convergence to obtain more precise final estimates added 0.9 and 1.4 h to the total run time. Unlike Model 1 where these steps took longer than the main estimation, they only increased the total run time by 10 and 15%, respectively. As in Model 1, this additional step did not change anything for the IMP method. For IMPMAP, it did not change the parameter estimates, but reduced the standard errors for several parameters.

For the SAEM method, ‘expert’ options besides turning on the convergence tester also increased ISAMPLE from 3 to 10. With these settings, convergence was achieved in 49 h at 4,650 iterations which was longer than 43 h that the ‘naive’ run took. It shows that occasionally, when the parameter versus iteration pattern is highly irregular, it may be better not to have convergence testing on, and, instead, analyze the progress in the raw output file (root.ext) to decide when the burn-in is completed. Then, the burn-in process can be terminated by entering ctrl-K, or, if keyboard interruption is suspended (which happens, for example, during parallelization with MPI) by entering the command “sig next” from another command window that is pointing to the run directory.

Two BAYES runs with the ‘naive’ options were performed first, with 10,000 and 20,000 burn-in iterations respectively, and 5,000 stationary distribution iterations in both runs. The runs took 13 and 22 h. Surprisingly, the omega values in the longer burn-in analysis had more deviation from true values than in the shorter analysis. This suggested that this problem needed OMEGA-priors for stabilization that were added in the ‘expert’ run. As in the Model 1, these priors as well as initial values of parameters were taken from the final estimates of the IMPMAP run. For the ‘expert’ run, the convergence tester was turned on. In addition, 30,000 statistical samples after burn-in were requested, because of the high MCMC correlation observed in the parameter iteration history plot. This may typically be caused by poor identifiability of some parameters. When this occurs, the number of statistical samples needs to be increased, to obtain a more accurate mean and standard error of the parameters. As a result of the ‘expert’ measures stationarity was reached after 500 burn-in iterations, and the analysis completed in 27 h. Thus, the ‘expert’ options for this method did not decrease the run time, but decreased deviation from the true parameter estimates.

All three FOCEI runs converged successfully for Model 2 and provided similar objective functions and the parameter estimates. As with Model 1, the run with re-parameterized parameters took longer (99 vs. 71 h) despite fewer iterations that were needed for convergence (474 vs. 575). And as in Model 1, the run with decreased NSIG, SIGL and TOL drastically decreased the run time, more than 5-fold, to 14 h.

Summarizing the above examples of a complex PK/PD problem requiring numerical integration of ordinary differential equations, we can see that in rich sampling setting the EM methods facilitated by linear MU referencing can be much more efficient than FOCEI, especially IMP and IMPMAP. It should be noted though that the EM algorithms are much less efficient in the problems where there are many fixed-effect THETA parameters that are not associated with any etas, the situation that has not been explored in the considered examples.

The Monte Carlo EM methods use exact likelihood algorithms, and therefore, may produce more accurate results in the problems with sparse data and/or considerable non-normality of the posterior density. Also, the Monte Carlo variability of these methods (especially the SAEM algorithm) allows a stochastic method of search, and therefore allows these methods to be less susceptible to locking into a local minimum. According to the above examples, where the quality of the results was similar between FOCEI and the Monte Carlo EM methods, these theoretical advantages did not extend to the rich data situations.

There are a number of options to improve accuracy of the EM algorithms for complex problems, very sparse or non-normally distributed data. In our example of the ill-posed problem, ISAMPLE was increased for the SAEM method, and OMEGA-priors were used to stabilize the BAYES method. If it were needed, in addition to increasing ISAMPLE, the IMP and IMPMAP methods could have reduced IACCEPT to improve accuracy.

As we saw in the examples, the FOCE algorithm may spend considerable time trying to pin-point a parameter value to 3 significant digits for a parameter that has little impact on the final objective function. This is why FOCE can spend many more iterations moving the objective function by only 0.01 unit, when the convergence tester is set to NSIG = 3, requiring parameters to not change by 0.001 unit before it completes. One way to keep FOCE from doing this is to set NSIG to 2, and also set SIGL lower, so the analysis is quicker, and NONMEM reduces its convergence requirement without compromising the accuracy of the gradient calculations. Doing so greatly reduced the run time in our examples. Still, even with these lower requirements, the ITS, IMP, and IMPMAP algorithms were more efficient.

On the other hand, the drawback of the Monte Carlo methods is that there is no perfect convergence algorithm, and the one in NONMEM is prone to either being fooled into ending the analysis too early, because a particular parameter moved very slowly relative to its Monte Carlo noise, or be never satisfied because the convergence algorithm is too sensitive to some parameters, with the analysis going to the limit of the maximum iteration number. Also, there is still some aesthetic discomfort in obtaining variable Monte Carlo results instead of deterministic results that are reproducible to 2 or 3 significant digits. However, Monte Carlo variations in the values of the parameters are typically only 10–20% of the size of the standard errors associated with those parameters, so that Monte Carlo derived results are sufficiently reproducible from a statistical perspective, although not necessarily from a strict numerical standpoint.

The MCMC Bayesian method was the slowest of all the methods. For the ill-posed problem, it also required at least uninformative priors on OMEGA parameters, the values that needed to be obtained from a previous maximum likelihood analysis. It also required the increased number of stationary samples (NITER = 30,000) compared with the usual 1,000–10,000 samples for well-behaved problems, to offset high iteration-to-iteration correlation that poorly identifiable parameters are particularly prone to. But the BAYES method can serve as a replacement for the much more time-consuming bootstrap process, as during stationary iterations after burn-in iterations are completed it obtains a large set of likely population parameters that fit the data, so that one can obtain empirical confidence ranges and variances of all parameters. Therefore, even though the BAYES method as a stand-alone tool takes longer than the other methods, used in conjunction with another method, it may save a lot of time by providing empirical confidence intervals for the parameters at the same time as the parameters themselves.

Conclusions

In the examples of the one-target and two-target QSS TMDD models with rich sampling, the new Nonmem 7.2.0 ITS, IMP, IMPMAP, SAEM and BAYES estimation methods generally provided parameters estimates and standard errors similar to the FOCEI method, although a larger deviation from the true parameter values was observed using the BAYES method for poorly identifiable parameters. Standard errors of the parameter estimates were in general agreement with the PFIM 3.2 predictions. The ITS, IMP, and IMPMAP methods with the convergence tester were the fastest methods, reducing the computation time by about ten times relative to the FOCEI method. Use of lesser precision for the FOCEI method reduced the estimation time by 3–5 times without compromising the quality of the parameter estimates, and equaling or exceeding the speed of the SAEM and BAYES methods. Use of parallel computations with 4–12 processors running on the same computer, improved the speed proportionally to the number of processors with the efficiency (for 12 processor run) in the range of 85–95% for all methods except BAYES that had parallelization efficiency of about 70%.