Introduction

Model evaluation is a crucial part of model building. The modeler requires appropriate numerical and graphical tools to decide whether a proposed model adequately describes the underlying process. Due to the complexity of pharmacometric models, which can involve mixed effects, non-linearities, categorical and/or continuous covariates, residual errors, below the limit of quantification (BLQ) data, etc., diagnostics must be performed extremely carefully to avoid misinterpretation.

A Visual Predictive Check (VPC) is a tool used to compare the distribution of real observations with that of simulated data [1–4]. Summary statistics of the observed and simulated data are compared visually. The simulated data itself is generated from the mathematical model expected to characterize the underlying biological process. Inter-individual variability (IIV), residual variability and possibly inter-occasion variability (IOV) are also accounted for in the simulation. Typically, the summary statistics are related to the median and two extreme percentiles, for example the 10 and 90th. The choice of percentiles depends on how much data is available; less data leads to poorer estimation of extreme percentiles.

For time-course data one can thus plot the relevant median and percentiles of both the real and simulated data with respect to time, and visually compare them. If the model is good, we would expect the simulated median and percentiles to be systematically “close” to the real data ones.

Further developments to VPCs have been suggested to improve model diagnosis. One strategy is to create a confidence interval (CI) for the percentiles based on the simulated data, and then visually check how well the percentiles calculated on the real data “fit inside” the interval [5]. Another, “reverse” strategy, is to create a CI on the percentiles of the real data by bootstrapping, then see how well the simulated percentiles “fit inside” this interval [6]. However, the bootstrap has limitations when the data is sparse; this may be the case in the tails of the distributions, leading for example to uninformative CIs for the 10 and 90th percentiles. Other interesting developments have been proposed more recently [7–9].

When trying to visually compare real and simulated data, the real data are usually first binned into specific time intervals. Otherwise, the predicted CIs may exhibit overly “bumpy” patterns, making visual interpretation difficult. However, binning leads to two fundamental questions: How should we bin? and, What is the effect of our choice of binning on the conclusions we draw from a VPC?

A partial reply is that there are two “simple” binning strategies for pharmacometric time-course data. Either make the bins equal-width, or make them equal-size, i.e., each containing the same number of (real) data points. Unfortunately, as we will show further on, the design of typical experiments makes both these options inherently poor “representations” of the real data. This may end up hiding the evidence of a poor model choice, or incorrectly rejecting the correct model when doing a VPC.

In this contribution, we present a binning strategy for pharmacometric time-course data that automatically determines a “good” binning, i.e., a well-chosen number of bins and their edges. A modified least-squares criteria and dynamic programming determine the edges, and a model-selection approach selects the number of bins. In practice, this leads to irregularly sized bins that better correspond to the clusters we see in the data. Consequently, we improve the match between the real data and the VPC “summary”, leading to better model diagnosis in practice. In particular, we show how this automatic binning leads to better VPC diagnosis of correct and incorrect models compared to the other “simple” binning strategies. The new algorithm is implemented in version 4.0 of Monolix.

Methods for VPC construction

What are VPCs?

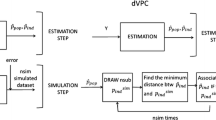
Visual Predictive Checks are commonly-used model evaluation methods for evaluating stochastic models. They provide a fundamental way to evaluate whether a model correctly describes given data and decide if the model is likely to accurately predict responses in future subjects. For CI VPCs, several sets of data are simulated with the proposed model. Then, the distribution of the simulated data is compared with the empirical distribution of the true data. What follows is a detailed description of how basic CI VPCs are constructed in Monolix, also illustrated in Fig. 1.

  1. (a)

    Observations (y i ; 1 ≤ i ≤ n) are measured at times (t i ; 1 ≤ i ≤ n). Here, n is the total number of observations across the whole set of individuals, i.e., in a population context, data is pooled. Figure 1a displays an example of pharmacokinetic (PK) data (t i , y i ).

  2. (b)

    Data is grouped into adjacent time intervals (bins).

  3. (c)

    To summarize the distribution, empirical percentiles are computed for the data in each bin. Here, the 10, 50 and 90th percentiles are calculated.

  4. (d)

    A large number of datasets are simulated under the model being evaluated, using the design of the original dataset.

  5. (e)

    The data from each simulated dataset is grouped into the same original bins.

  6. (f)

    The same percentiles are computed in each bin for each of the simulated datasets.

  7. (g)

    CIs for each percentile are calculated using these simulated percentiles. Here, 90% CIs are computed.

  8. (h)

    Observed percentiles are compared with these CI.

  9. (i)

    Regions where the observed percentiles are not found within the CIs are filled in with red, in order to help detect misspecified models. A small number of regions filled in with red does not necessarily mean a misspecified model; indeed, it is expected, and the modeler must make a decision as to whether there are too many such regions.

Fig. 1
figure 1

Visual Predictive Check construction: a the data, b data grouped into bins, c empirical 10, 50 and 90th percentiles computed for each bin, d several simulated data sets, e these simulated data sets grouped into the same bins, f the 10, 50 and 90th percentiles of each simulated data set computed for each bin, g 90% CI computed from the percentiles of the simulated data, h observed percentiles and 90% CI, i zones outside of the CI are filled in with red (Color figure online)

Full size image

Remark

Ideally, we would like to associate VPCs with a decision rule based on a statistical test, to accept or reject a proposed model. However, the data is not independent in successive bins, so multiple testing strategies such as [10] are not directly applicable to quantifying the regions filled in with red. It was also shown by [11] that there was no clear decision rule for CI VPCs. Creating a statistical test that leads to a decision rule is an interesting line of research, but out of the scope of the paper.

Binning

In general, the distribution of the observations (here, measures of concentration) changes with time. Binning the data, i.e., grouping observations into time intervals, leads to an approximation of this distribution by a piecewise-constant distribution (constant in each time interval).

The choice of the set of bins is crucial, as binning will always lead to a certain distortion between the true and estimated distributions. A binning strategy should aim to be “good”, in the following senses:

  • for a given number of bins, the locations of the bin edges must be chosen so as to minimize heterogeneity of the data in each bin.

  • the number of bins must be carefully chosen, i.e., we require a good tradeoff between a large number of bins and a large number of observations in each bin; the true distribution can be accurately approximated by a piecewise-constant distribution with a large number of bins, while a large number of observations in each bin is required to accurately estimate this true distribution.

Remark

We only consider “basic” CI VPCs as described above. Several authors have proposed different corrections in order to take into account a large variability in doses or covariates [6, 8, 9]. As suggested in [7] and implemented in Monolix 4, the same methodology can also be used for a graphical representation of the (weighted) residuals and the normalized prediction distribution error (npde). The proposed binning strategies described below also applied to these extensions.

Standard binning strategies

There are various ways to implement binning. The two simplest are:

  • equal-width binning: K bins of length (t max  − t min )/K.

  • equal-size binning: K bins, each with n/K data points. If n is not a multiple of K, we can correct so that each bin has either [n/K] or [n/K] + 1 data points.

Figure 2 shows these two strategies applied to theophylline PK data. Equal-width binning (Fig. 2b) is clearly not appropriate when time-points are inhomogenously distributed; some bins contain many data points whereas others are completely empty. Due to this inherent poor adaptability, we do not consider this method in the following.

Fig. 2
figure 2

a Theophylline PK data, b equal-width binning, c equal-size binning

Full size image

In other situations, several observations are obtained from different patients at the same time points. This is the case for example in the warfarin PK data shown in Fig. 3a. This poses obvious problems for equal-size binning. We may wonder if the equal-size binning procedure can be modified to deal with this case of identical time points, but different number of measurements at each time point? In Fig. 3b, we see that it is possible to obtain bins with “similar” amounts of data in each. Such a construction is of course possible “by hand”. Our first objective is to propose a procedure which automatically gives bins with sizes as similar as possible. Let \(t_1 < t_2 < \ldots < t_M\) be the M different time points and \(m_1, m_2, \ldots, m_M\) the number of measurements taken at each of these time points. As before, n = ∑ m j is the total number of data. For a given number K of bins, we look for the bins \(I=(I_1, I_2,\ldots,I_K)\) that minimize the following criteria:

$$ J_{\rm size} = \sum_{k=1}^K \left|\sum_{j \in I_k}m_j - \frac{n}{K} \right|. $$
(1)

This minimization can be performed using dynamic programming [12]. The segmentation displayed in Fig. 3b was obtained by minimizing the criteria J size with K = 8 bins.

Fig. 3
figure 3

a The warfarin PK data, b “approximately” equal-size binning

Full size image

A new binning procedure

Selection of bin boundaries

So far, we have shown that as soon as time points are inhomogeneously distributed, equal-width binning breaks down, and that the equal-size method can be relaxed to perform relatively well using similar-sized bins. Often however, we have data where all time points are different and the data is “clustered” around various time points (Fig. 4a, simulated data). In this case, the similar-size solution obtained by minimizing J size no longer provides a plausible binning (Fig. 4b) as it does not take into account knowledge of the clusters.

Fig. 4
figure 4

a Simulated data, b equal-size binning, c optimal binning obtained by minimizing J opt

Full size image

One way to resolve this more general problem is to interpret binning as clustering or 1D-segmentation, i.e., grouping the n time points \(t_1 \leq t_2 \leq \ldots \leq t_n\) into K clusters or segments along the time axis. One possible way to do this is by 1D K-means clustering [13]. Let us define

$$ J_{\rm opt}(I) = \sum_{k=1}^K \sum_{j \in I_k} \left(t_j - \overline{t}_{k} \right)^2 , $$
(2)

where \(\overline{t}_{k}\) is the empirical mean of the t j ’s in bin I k :

$$ \overline{t}_{k} = \frac{1}{n_k}\sum_{j \in I_k} t_j, $$

with n k the number of points in bin k. Then, the K-means solution is found by minimizing J opt over all possible segmentations \(I=(I_1, I_2,\ldots,I_K)\) of the data into K bins. In practice, we do this using dynamic programming [12]. Figure 4c shows the optimal binning obtained by minimizing J opt.

J opt is a least-squares criteria that supposes that we are dealing with a homoscedastic model, i.e., the data spread (with respect to time) inside each cluster is similar. This is not always the case, as for example in Fig. 5a. Here the combined variability of the first two clusters is similar to that of each of the third, fourth and fifth, whereas the variability of the sixth cluster is significantly greater than all the others. In this case, the J opt criteria may not be optimal; Fig. 5b shows that it groups the first two clusters together, and splits the sixth cluster in two. In order to avoid this, we can generalize J opt to better take into account heteroscedacity:

$$ J_{{\rm opt},\beta}(I) = \sum_{k=1}^K n_k (\sigma^{2}_k)^{\beta}, $$
(3)

where \(\beta \in (0,1]\) and σ 2 k is the empirical variance of the t j ’s in bin I k :

$$ \sigma^{2}_k = \frac{1}{n_k}\sum_{j \in I_k} \left(t_j - \overline{t}_{k} \right)^2. $$
Fig. 5
figure 5

a Simulated data, b binning minimizing J opt,β with β = 1, c binning minimizing J opt,β with β = 0.2

Full size image

We see that J opt = J opt,β when β = 1. Fig. 5b shows the binning obtained when β = 1. Then, as β is set closer and closer to 0, more emphasis is made on selecting bins with differing variability. We refer the reader to [14] for more details that motivate this approach. Figure 5c shows an intuitively optimal binning, obtained by minimizing J opt,β when β = 0.2, which is the default value proposed by Monolix 4. Exactly the same binning is obtained with any value of β in [0.05 , 0.35].

Remark 1

Binning consists in summarizing the probability distribution of the observations (y i ) into K probability distributions, one for each of the K bins. In other words, if t i belongs to the k-th bin B k , we approximate the marginal distribution \({P_{t_i}}\) of the observation y i measured at time t i with the marginal distribution \({P_{B_k}}\) estimated using the set of observations found in the k-th bin. After pooling the data, let us suppose that each measurement y i can be written: \(y_i = f(t_i,\psi_i) + \epsilon_i, \) where we suppose a continuous data model with f the regression function, ψ i a vector of (random) parameters and \(\epsilon_i\) some residual error. Then, we can approximately rewrite this as \(y_i \simeq f(\overline{t}_{k},\psi_i) + \epsilon_i + (t_i - \overline{t}_{k}) f^\prime(\overline{t}_{k},\psi_i)\) when t i is in bin k, and \(\overline{t}_{k}\) is defined as before. In order to minimize the distance between the true distribution \({P_{t_i}}\) and the approximation \({P_{B_k}}\), the correction term \((t_i - \overline{t}_{k}) f^\prime(\overline{t}_{k},\psi_i)\) can then either be dealt with by taking more into account the form of f (and thus \(f^\prime\)), or by trying to make \((t_i - \overline{t}_{k})\) small on average. The latter option is the one invoked in our method, whereas supposing prior knowledge of f (the first option) may in the future lead to alternative approaches.

Remark 2

Percentiles of \({P_{B_k}}\) are estimated empirically. The variance of these empirical percentiles decreases as the number of observations in bin B k increases. Minimizing simultaneously the bias and the variance of the estimated percentiles requires bins with small width and large size: this is exactly what our clustering approach does.

Selection of the number of bins

For any given number of bins K, the binning that minimizes the criteria can be calculated. The question then arises as to which K to choose. We have seen in the previous section that a small number of bins leads to a poor approximation (large bias) but a good estimation (small variance) of the estimated percentiles. On the other hand, a large number of bins will lead to a good approximation (small bias) but a poor estimation (large variance). In order to obtain a good compromise between these two criteria, we propose here to automatically select the number of bins using a model selection approach with the following penalized criteria:

$$ U(I,\lambda) = \log\left(J_{{\rm opt},\beta}(I))\right) + \lambda \beta K(I) , $$
(4)

where K(I) is the number of bins in binning I. We choose the I (and thus the K) that minimizes U(I, λ) for λ fixed. The larger λ is, fewer bins are selected. Extensive numerical trials suggest the use of λ = 0.3. Modelers can see for themselves whether this value of λ gives plausible binnings for their own data, and if necessary, modify the value of λ to penalize to a higher or lesser degree. The β term is included in the penalty as it can be shown that when the t j ’s are uniformly distributed, \(\log\left(J_{{\rm opt},\beta}(I))\right)\) decreases as a linear function of β.

Results

Data was simulated under a PK model, then two VPCs were constructed, one using the correct model that had generated the simulated data, the other using an incorrect model. The true model is a 1-compartment oral model with first-order absorption and a proportional residual error model. The incorrect model assumes a zero-order absorption and a constant residual error model. The data is presented in Fig. 6a, along with the binning produced using the similar-size binning algorithm with 10 bins. We see that the visually-obvious clusters are split unnaturally; parts of several clusters end up in a bin to the left, shared with the previous cluster, and a bin to the right, shared with the next cluster. Critically, this has an effect on the VPCs, as shown in Fig. 6b–c. In b, the simulated CIs are generated from the true model for the simulated data, yet several “red” areas exist where the data quantiles slip outside the 90% CIs from data simulated from the true model. In particular, the artificial splitting of the data cluster just after t = 10 h helps provide the largest area of red. Similarly, c shows simulated CIs from the wrong model. Again, several red areas exist, but not significantly more than in b. This shows that poorly binned data does not lead to easily differentiating the right model from the wrong one.

Fig. 6
figure 6

a Simulated PK data with equal-size binning, b VPC obtained from the correct model, c VPC obtained from the wrong model (Color figure online)

Full size image

In Fig. 7a, the same simulated data is binned using the proposed binning strategy with the default β = 0.2 setting in Monolix 4.0, and model-selection for K with λ = 0.3.

Fig. 7
figure 7

a Simulated PK data and optimal binning with β = 0.2, b VPC obtained from the correct model, c VPC obtained from the wrong model

Full size image

Each visually-obvious cluster is now contained within its own bin. In b, the simulated CIs were again generated from the true model. However, unlike before, the VPC indicates, correctly, that we should not reject the suggested model. In c, it is now clearer that we should reject the proposed, incorrect, model, due to how often the data quantiles slip outside the simulated 90% CIs.

It should be pointed out that in this example, the result is relatively insensitive to the choice of the parameters β and λ: the same binning with 10 bins is obtained with any β in [0.01 , 1] and any λ in [0.26 0.53]. The two first bins are grouped with λ in [0.53 , 0.77] while a value of λ in [0.17 , 0.26] leads to split the sixth bin into two bins.

Discussion

Visual diagnostic methods are increasingly used in pharmacometric modeling to help determine the quality of a model thought to represent a given biological process and its relationship to various covariates. Typically, we have measured time-course data from a cohort of patients undergoing a treatment, and we want to see if a given model could have plausibly generated the real data we obtain from these patients. One way to do this is to calculate pertinent statistics of the real data and of data simulated from the suggested model, and compare them visually in some way.

Visual Predictive Checks, or VPCs, are a class of methods that do just that, and various implementations and extensions are possible. In each of these methods, the real data are typically binned into specific time intervals, because otherwise, predicted CIs may exhibit overly “bumpy” patterns, making visual interpretation difficult. Simple, automatic binning strategies such as putting the same number of data points in each bin, or having bins of equal length, are not adaptive enough to cleanly summarize typical pharmacometric time-course data. This is a fundamental problem, and can lead to poor model diagnosis when performing VPCs. We have shown that when using such binning strategies, it is easy to incorrectly discard the true model, or accept the wrong model.

We have introduced a binning algorithm that improves the “binned” representation of data before performing VPC diagnoses of a suggested pharmacometric model. It selects variable-width bins that better capture the cluster of data around each time point; clusters visible to the naked eye intuitively end up in their own bins. The algorithm, implemented in Monolix 4.0, automatically proposes a solution – no user input is initially required, greatly simplifying the modeler’s task. We have shown with a typical PK example how this better “binned” summary of the data improves model diagnosis, whether it be improved likelihood of discarding an incorrect model, or correctly accepting the true model.