Introduction

Mechanistic pharmacokinetic models are typically expressed as systems of ordinary differential equations (ODE) with several parameters that are determined either in vitro or estimated by in vivo experiments. Especially in Whole Body Physiologically Based Pharmacokinetic models (WBPBPK), fairly large systems are considered for the distribution of drug in the body [1]. Furthermore with the expansion of Systems Biology models to describe the drug action on a detailed mechanistic basis, even larger systems may need to be studied [2]. On the other hand clinical pharmacology utilises mainly empirical mathematical modelling to describe the typically sparse and noisy data obtained from clinical trials. The need to bridge the gap between these two opposite directions can be assisted by mathematical techniques including model order reduction.

Model order reduction methods are formal methods of reducing the dimensionality (i.e. number of states or dependent variables) and number of parameters of dynamical systems, which are typically defined by ordinary differential equations. With these methods, the reduced systems are supposed to be able to describe the basic features of the original models leaving out some less important details. Various methods have appeared in the literature for model order reduction including lumping and elimination of states [3].

In elimination, states which are not important for the overall behaviour of the system, mainly because their time scale is different from the time scale of interest, are replaced by steady state values or expressions derived from a quasi-steady state approximation.

On the other hand, in lumping methods, the states described by the model are transformed to a set of states, fewer in number, typically a linear combination of the original states, thus reducing the number of equations and parameters accordingly. More interesting is the special case of proper lumping, where each one of the original states, contributes to only one of the states of the reduced system. This constraint means that the original states form groups which retain a clear physical interpretation and so do the corresponding parameters.

Most of the work carried out on lumping of chemical networks has been based on the early work of Wei and Kuo in the late ‘60s [4]. Building on that work, several papers have appeared presenting different lumping strategies [5–8], but mostly not on proper lumping. Formal methods for lumping of mathematical models have also been applied in pharmacokinetics. Examples include the work of Nestorov et al. [9] which derives lumping rules and Brochot et al. [10] which applies the method presented in [7] to a PK model. Recently, Dokoumetzidis and Aarons [11] proposed an intuitive algorithm for proper lumping, which is completely automatic and can be applied on nonlinear systems.

Model order reduction in general, is valid only locally, for the specified set of parameter values. For a different set of parameter values, the kinetics of the system change and the lumping scheme chosen may not be appropriate. In compartmental pharmacokinetics a 3-compartment model may collapse to a 2-compartment, when the corresponding parameters of the two peripheral compartments are the same. This reduction may even be approximately valid if these values are not identical but are still close. However this lumping scheme is completely wrong if the condition of equal or similar parameter values for the peripheral compartments does not hold. This simple example demonstrates the local nature of model reduction. For a mathematical analysis of this example please refer to the appendix of [11].

There is therefore a necessity for robust model reduction methodology. Recent work in this field includes Refs. [12] and [13] in systems biology and chemical kinetics, considering specific types of reactions. Earlier, Gueorguieva et al. [14], applied global sensitivity analysis for the selection between lumped model candidates of a PBPK model, including parameter variability. In this report we present our contribution in this area, a method inspired from robust or Bayesian decision theory, which utilises the efficient optimisation algorithm developed in [11]. The methodology was applied to a linear PBPK model developed for barbiturates [1] however it is directly applicable to nonlinear models also. Further, we include a discussion on the generality of lumping as a model reduction strategy as opposed to the elimination of states.

Methods

The lumping methodology this work is based on has been described in detail in [11]. Briefly we go through the basics of this approach in the following section.

A system of ordinary differential equations with a vector state y of length n

$$ {\frac{dy}{dt}}\, = \,f(y) $$
(1)

where f(y) is a nonlinear function, can be transformed to a new vector of states, , of length \( \hat{n} < n \) such that \( \hat{y} = My \), where M is a lumping matrix of dimension \( \hat{n} \times n \) which determines the transformation from y to \( \hat{y} \). When all columns of M are unit vectors then the lumping scheme is referred to as proper [11]. The inverse transformation involves \( \bar{M} \), the generalised inverse of M, such that \( M\bar{M} = I_{{\hat{n}}} . \) Although there are infinite generalised inverse matrices for a matrix M, it has been shown that the Moore–Penrose inverse, denoted as M +, which is a unique matrix, is a good choice for the purpose used here [7].

A new set of differential equations is then defined which describes the reduced model

$$ {\frac{{d\hat{y}}}{dt}}\, = \,\hat{f}(\hat{y}) $$
(2)

Given the original system f(y) and the lumping matrix M, a reduced system may be obtained by the following expression which in the general case is an approximation [7].

$$ \hat{f}(\hat{y})\, = \,Mf(\bar{M}\hat{y}) $$
(3)

The lumping matrix M is of size \( \hat{n} \times n \) and contains 1s and 0s which describe the lumping scheme. A list of pairs of lumps can be converted to an appropriate lumping matrix. Only pairs of lumps have to be considered in the list because from these, larger sizes of lumps can be included in the matrix, M, by appropriate combinations of pairs with common elements [11]. This list of lumps may include either all combinations of states or a subset of these if one wants to include constraints in the model reduction.

In model order reduction the objective is to find an appropriate matrix M, such that a property or a criterion is satisfied. Typically the criterion is the difference of the original model from the reduced model. The problem then becomes an optimisation problem where one searches for the optimal matrix M, such that an objective function is minimised.

This optimisation problem can be a challenging one since the obvious choice of trying out every single one of the possible lumping matrices fails because of combinatorial explosion, where the number of combinations grows fast with the size and the degree of reduction. For example, for a model of size n = 30 reduced to 10, the number of combinations is in the order of 1034. So exhaustive search is not a realistic option.

In order to combat combinatorial explosion, in [11], a greedy algorithm was developed which works in steps and locates one pair of states to be lumped at each step. Then each successive step is conditional on the result of the previous step. The search within each step is an exhaustive one throughout all possible combinations of pairs of lumps, but these are normally not many. This approach is much faster than the exhaustive search and the number of objective function calls grows linearly with the degree of reduction. For the previous example of a model of size 30 reduced to size 10 the number of objective function calls is only about 8500 instead of 1034. The reason why this greedy algorithm works is not intuitive and is justified by an apparent property of this kind of systems, where lumps remain consistent over different levels of order reduction when the reduced and the original systems are close enough. Further, numerical examples comparing this algorithm with the exhaustive search, have given the same results [11]. It is also implied that when the reduced and the original systems are not close enough the algorithm may fail to produce the same result as the exhaustive search. However the purpose of this effort is that the two systems are kept as close as possible, therefore this assumption holds. Note that in terms of implementation, the search within each step can be parallelised to run over several processors if available. The details of this algorithm can be found in [11].

Initially a list of allowed pair of lumps is considered. This may include all the possible combinations or may include a subset of them, putting in this way constraints that may have some physiological meaning or forcing certain states of special interest to remain unlumped. Although only pairs of lumps are considered in this initial list, in fact all the combinations of all possible sizes of lumps are considered since when a new pair is considered, for which one of the states contributes to a previously established lump, a larger lump is formed.

A reasonable objective function to consider is one that takes the sum of squares of the differences of the responses of the reduced and original models for all the different states.

$$ d\, = \,\sum\limits_{i = 1}^{{\hat{n}}} {\left[ {w_{i} \int\limits_{0}^{T} {\left( {{\frac{{y_{i} (t) - \hat{y}_{i} (t)}}{{Y_{i} (t)}}}} \right)^{2} dt} } \right]} $$
(4)

where Y i is a normalisation factor, used to scale all states such that these are comparable and it may be the maximum of y i (t). T is the time span of the profile and should be that which produces a representative trajectory of the system. w i are weights which can make some states to have a higher contribution to the value of the objective function when the interest is not same for all the states.

A known problem of model reduction is that the whole analysis is valid only locally, for a specific set of model parameters. For a different set of model parameters the lumping scheme may be different. However model parameters always carry uncertainty or variability and are not single values, but instead are random variables following statistical distributions. A way of implementing a more robust lumping scheme that explicitly incorporates parameter variability is to use Bayesian decision theory. So given a prior distribution of the parameter values, one can take the average over that prior distribution of the local objective function, Eq. 4:

$$ d_{B} \, = \,\int\limits_{S} {(P(\theta )d)d\theta } $$
(5)

where P(θ) is the probability density function of the prior distribution of parameters θ, S is the parameter space and d is the local objective function of Eq. 4. This objective function, Eq. 5, may not produce the optimal lumping scheme for the nominal parameter values, and in fact the lumping scheme may not be optimal for any set of parameter values but it will be optimal in the average sense. In other words it will be a compromise over all possible parameter values.

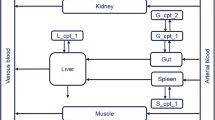
In this report we applied the methodology described above to a PBPK model developed for barbiturates in the rat [1]. It has 19 states, which are listed together with the corresponding parameter values of partition coefficients Kpu, flows, Q, and volumes, V, in Table 1. These parameter values correspond to the first compound in the homologue series, 5-methyl barbituric acid. Clearance values are 0.011 and 0.52 ml/min for hepatic and renal, respectively. All other parameters can be found in [1]. The dose was considered to be 7500 nanomoles injected over 5 s. We introduced variability of 20% CV to the 52 reported parameter values: a lognormal distribution with variance 0.04 and geometric mean equal to the nominal parameter values was used. Since the integration over the multi-dimensional parameter space may be very computationally intensive, an efficient sampling strategy is necessary. In this report we used hyper-cube sampling [15] in order to carry out this integration. All the calculations were performed in MATLAB version 7.8 (Mathworks, Natick, MA). Function “ode15s” was used for solving the ODEs, function “lshnorm” was used to generate the Latin hypercube samples and also the Parallel Toolbox was used to speed up the calculations since the algorithm is parallel. The MATLAB code is provided as online supplementary material. Simulations where run on an 8 core, 2.66 MHz Xeon computer.

Table 1 The 18 states of the PBPK model for barbiturates [1] together with parameters values
Full size table

Results and discussion

The local nature with respect to parameter values, of the validity of a reduced model is a serious problem in model reduction. Especially in PBPK modelling it is a known issue with important implications. A lumping scheme of certain tissues in a PBPK model may not be optimal across different animal species, as some of the parameter values, namely flows and volumes are different between species. This compromises the applicability of model reduction in PBPK.

The methodology proposed here is a Bayesian version of a methodology presented previously in [11]. It has all the advantages of the original algorithm, including that it handles nonlinear models and constraints, it is completely automatic and can be used very easily as a black box. Using an appropriate filter that converts a Systems Biology Mark-up Language (SBML) file to a MATLAB subroutine, any model described in SBML can be easily plugged into this algorithm. Although the PBPK model used as example in this paper is a linear model, this fact makes no difference and a nonlinear model can be used instead in exactly the same way without any additional considerations or modifications to the MATLAB code. Furthermore, the code can be easily expanded to handle other types of models such as partial differential equations and even adapted to do more than lumping such as elimination as we will see further down in the discussion. However, the feature we are focussing our attention in this report is robust model reduction.

In the results produced here we simulated profiles from all the states of the PBPK model adding also variability to the nominal reported parameter values. We compared the agreement of the lumped model to the original model. Comparison was performed in terms of the lumped states. In order for the original states to be comparable to the lumped states, the original states were also grouped in the same way as the lumped states but after the simulation. So effectively, in order to have comparable states, what we compared was the lumped system, where the reduction was performed using Eq. 3 before simulation and the original system, where the same states were grouped after the simulation. Agreement between the two, means that a good lumping scheme is being considered.

A first task was to run the lumping algorithm using the nominal parameter values without variability. The number of initial states of the system is 19, and therefore the list of pairs of lumps for the first step of the algorithm is n(n − 1)/2, i.e. 171 and the run takes only a few seconds to complete since the steps are as many as the degree of reduction and at each step no more than 171 calls of the objective function are made. The lumping schemes determined for reduction of the 19 original states to 10 and 7 states, respectively, are shown in Table 2, columns 2 and 3, respectively. In Figs. 1 and 2, the profiles of amount of drug in the different tissues simulated by the reduced and the original models are co-plotted for different levels of reduction. Figure 1a shows the simulations of a reduction from 19 original states to 10 final states and on Fig. 1b, plots of the reduced versus the original model together with the identity line appear. Figure 2 corresponds to a reduction down to 7 final states. We can observe that generally there is agreement between the original and reduced models and predictably the agreement is closer for larger reduced models, i.e. smaller degree of reduction. The lumping schemes from this method group states based on kinetics. Having applied no constraints, any state can be grouped with any other and not just neighbouring ones. It has also been demonstrated formally in PBPK that two parallel compartments may be grouped if they exhibit similar kinetics while two compartments in series may be grouped if their time scales are very different, and therefore one is the limiting step [9]. However with the presented algorithm more complex patterns are also possible but mostly in large systems. Looking at Table 2 we can observe the choices made by the more aggressive lumping scheme of size 7, which do not necessarily have a clear anatomical interpretation. For example, an obvious non-anatomical lump is the combination of compartments 16 and 18 which correspond to the extravascular portions of the brain and the testes, respectively. The lumping scheme of Table 2 is different to the one produced by the lumping rules and anatomical arguments in [9] for the same model of barbiturates. This may partly be due to the fact that our methodology is automatic, as opposed to the guided, manual methodology. The automatic method could also be guided towards a specific direction by introducing constraints or weights in the objective function to give emphasis to specific tissues of interest, something we have not tried here. By including constraints, which is a readily available feature of the algorithm, we could have forced the algorithm to avoid choices that have no anatomical meaning. However we have to stress here that this type of lumping is based on the kinetics and not the anatomy or the physiology. Of course one hopes that the kinetic information corresponds to the physiological properties of the tissues and the physicochemical properties of the drug, but this is an ideal scenario. So, biological relevance of the lumped model is conditional to the original model being perfectly correct. Further, the study of barbiturates is not the scope of our work and this PBPK model is used only as an example to test our methodology. Note that all simulations performed with the model and the calculations of the various lumping schemes are based on amounts since these are the states of the system, rather than concentrations, which are the observable quantities. It is straightforward to convert the lumped amounts to concentrations and one would only have to add up the corresponding volumes in order to determine the volume of each lump. However one has to be careful, because two compartments of completely different concentration scales, may lump well based on their kinetics, but the average concentration of the lump may not be representative of any of the concentrations of individual compartments.

Table 2 Local lumping schemes of size 10 and 7 final states. The first column refers to the state number in the reduced system while the number in the other columns refer to the original state numbers
Full size table
Fig. 1
figure 1

a The dashed lines correspond to simulation of the original model at the nominal parameter values and the solid lines to simulation using the reduced model of 10 final states. The y-axis is on a log scale. The curves are basically indistinguishable. b The trajectory of the reduced system of 10 final states is plotted against the original, for the nominal parameter values. We visually verify that there is agreement between the reduced and the original systems, since the points lie close to the identity line

Full size image
Fig. 2
figure 2

a The dashed lines correspond to simulation of the original model at the nominal parameter values and the solid lines to simulation using the reduced model of 7 final states. The y-axis is on a log scale. Reasonable agreement is observed. b The trajectory of the reduced system of 7 final states is plotted against the original, for the nominal parameter values. We visually verify that there is agreement between the reduced and the original systems, since the points lie close to the identity line. Generally good agreement is observed

Full size image
Fig. 3
figure 3

a The trajectories of a reduced system of size 10, produced by the local scheme of Table 2 (column 2), are plotted against the original, for parameter values sampled from the prior distribution (20% variability, 1000 Latin hypercube samples). One can observe significant dispersion, indicating that although this lumping scheme was optimal for the nominal parameter values (Fig. 1), for most of other parameter values it is not adequate, as a result of its local character. b The same as in a, but now the lumping scheme used is the Bayesian one shown in Table 3. We can see that the dispersion of a has reduced significantly, indicating that although this lumping scheme may not be optimal for the nominal parameter values, or in fact for any other individual set of parameter values, it is optimal on average for the given prior distribution

Full size image

The next step is to assess the robustness of the produced lumping scheme with respect to parameter variability. Profiles were simulated including a modest, arbitrary variability of 20% CV for all parameters. For each parameter set, the same lumping scheme was used, the optimal one for the nominal parameter set shown in Table 2. Five-hundred parameter sets were drawn using Latin hypercube sampling. Plots of the simulated profiles of the reduced model versus the original model, are shown in Figs. 3a and 4a, for the final reduced models of order 10 and 7, respectively, exhibiting considerable spread around the identity line, indicating that although the lumping schemes of Table 2 were optimal for the nominal parameter values they are not appropriate for most parameter sets within the variability range around these nominal values. This failure demonstrates the lack of robustness of model reduction which is not a weakness of the way the algorithm determines the reduction scheme. It is simply due to the fact that the reduction scheme is based on kinetics and when the parameters controlling the kinetics change the reduction scheme may not be valid.

Fig. 4
figure 4

a The trajectories of a reduced system of size 7, produced by the local scheme of Table 2 (column 3), are plotted against the original, for parameter values sampled from the prior distribution (20% variability, 1000 Latin hypercube samples). b The same as in a, but now the lumping scheme used is the Bayesian one shown in Table 3

Full size image

One way to determine a lumping scheme which is more robust to changes in parameter values is to take into account their variability during the optimisation as expressed by the Bayesian objective function of Eq. 5. One thousand samples were drawn by Latin hypercube sampling from a lognormal distribution with geometric mean equal to the nominal parameter values and standard deviation of 0.2. These samples are stored and used for the original model and all the subsequent objective function calls involving the reduced model candidates. The calculation of each value for this Bayesian objective function is computationally intensive as it solves the ODE system 1000 times, which slows considerably the process, i.e. by a factor of a thousand. The ability to parallelise the optimisation on 8 processors helps to reduce the run time, which totalled a few hours. The lumping scheme determined by the Bayesian method is shown in Table 3, and one can observe that it is different from the one produced by the local method shown in Table 2. In Figs. 3b and 4b, plots of the reduced versus the original model are shown, for the final reduced models of order 10 and 7, respectively, exhibiting some spread around the identity line but significantly reduced compared to the local lumping scheme plotted in Figs. 3a and 4a. We can therefore conclude that this lumping scheme determined by the Bayesian method is more robust. It may not be optimal for any specific parameter set, but it is optimal on average, as opposed to the local scheme which is optimal for the nominal parameter set but poor for most other parameter sets and on average.

Table 3 Bayesian lumping schemes of size 10 and 7 final states
Full size table

As already mentioned lumping of states is only one of the ways of reducing a model. Alternative methods include elimination of states. Elimination of states is also based on the kinetics, basically the time scale of each state. The principle is that if a state is much faster (or even much slower) than the states of interest in the time span of interest, this state can be replaced by a steady state value and is therefore eliminated. The optimisation algorithm that we have described here, with some modifications, can be applied to solve this problem also, and in fact we have tested this in systems biology models. The algorithm works stepwise, on the same optimisation principle eliminating one state at each step while every next step is conditional to the previous ones. For each step each one of the states is replaced by its steady state value and the resulting model is compared to the original with an objective function. In this way the state needed less is eliminated and the algorithm moves to the next step. According to our experience, the algorithm performs as expected producing smaller models with similar kinetics, but elimination of states is not as flexible as lumping and so a poorer quality system compared to lumping, for the same size, is expected.

Also, we have gone one step further, developing an automated algorithm based on the same optimisation principle, that combines the two methods of lumping and elimination of states into one. The basic motivation behind this, is that it implements automatically what a modeller would do empirically when trying to reduce a model. One would either group a state with another one, or would delete it. The algorithm, as before, works on the same optimisation principle of reducing by one state at a time, while every next step is conditional to the previous scheme, but at each step it performs a dual search where either a state is lumped with another one, or a state is eliminated, which ever produces a system closer to the original. In our experience, this algorithm outperforms the reduction based on elimination alone, as expected, due to the additional flexibility, but does not perform better compared to lumping on its own. The conclusion is that lumping on its own is a very efficient and general way or reducing a system because all the slow states which are candidates for elimination can also be lumped into one single state. Therefore the only additional task the combined algorithm does, is to delete that lumped steady state. Figure 5 pictures schematically the different scenarios of elimination and lumping. In elimination, all states that can be replaced by steady state are eliminated from the system, while the rest remain intact. In lumping the states with similar kinetics are lumped, including all states which are good candidates for elimination, which are all lumped into a single state with nearly steady state kinetics. The only additional thing the combined algorithm accomplishes is to eliminate this single lumped steady state, and therefore lumping is the most important task which in a way renders elimination obsolete.

Fig. 5
figure 5

Schematic representation of elimination versus lumping, model order reduction approaches. Elimination replaces near steady states with fixed values thus reducing the system, but has no effect on non-steady state species. Lumping groups kinetically similar species, and hence combines all near steady states in one single near steady state, as well as grouping other kinetically similar states. Therefore, lumping almost includes the action of elimination. A combined method which performs both lumping and elimination, basically ends up performing lumping and only eliminates the final single steady state group

Full size image

Conclusions

We demonstrated that a Bayesian optimality criterion can offer a robust lumping scheme that addresses to some extent the inherent local character of model reduction, for large systems expressed by differential equations. In pharmacokinetics this approach may be applied in other scenarios also, such as model reduction which is robust over different animal species. In this case the differences in model parameter values over the different animal species do not follow lognormal distributions as in the example presented here, but instead they follow multimodal distributions or even discrete parameter sets corresponding to the different animal species with appropriate weights. In any case a Bayesian model reduction scheme does not overcome completely the inherent local nature of model reduction, but instead it determines a compromise reduction scheme, which may not be optimal for any specific parameter set, but it is optimal in the average sense. Our proposed methodology is based on our previous work of an efficient optimisation algorithm, which works stepwise and is very fast. Without such a fast search strategy the use of a computationally expensive Bayesian objective function would be prohibitive. This algorithm is very easy to use, it can be used on nonlinear systems, supports constraints and can be expanded to be used with other types of models such as PDEs. Further, motivated by the results of a combined algorithm of elimination and lumping, which we developed, we discussed the generality of a lumping strategy to reduce a model. We argued that this is much more powerful than elimination of states and in fact elimination is almost a special case of lumping since all the states to be eliminated can be grouped into a single lump.